Заключается в том, что эти массы и моменты инерции заменяются одним эквивалентным моментом инерции на валу двигателя. При этом необходимым условием приведения является равенство кинетической энергии, в определенном эквивалентном моменте энергии на валу двигателя, сумме кинетической энергии двигателя всех движущих масс в механической части привода т.е.
w-скорость вращения вала двигателя
J– приведенный момент инерции к валу двигателя;
Jдв – момент инерции ротора двигателя (кгм2)
Если в каталоге указана величина махового момента, то в системе СИ момент инерции будет: 
Ji– момент инерцииi-ого вращающего механизма,
mj– массаjпоступательно-движущегося элемента (кг),
- передаточное отношение редукторов от вала двигателя доiвращательного элемента,
- радиус приведения поступательно-движущегося элемента.
При приведении вращающего движения к поступательному, на рабочем органе величина приведенного усилия будет зависеть от направления передачи энергии.
1 случай: передача энергии от двигателя к поступательно движущимся элементам привода
2 случай: направление передачи механической энергии от механизма к валу двигателя.
;
Fp– приведенное усилие,
М– момент, создаваемый на валу двигателя,
ро– радиус приведенного поступательно-движущегося элемента к валу.
В случае приведения маховых масс к рабочему органу, максимальные массы заменяются одной результирующей массой на рабочем органе, которая определяется из условия сохранения полного запаса кинетической энергии.
Из приведенного выше соотношения следует, что при приведении инерционных масс и моментов сопротивления к вращающему движению, сложная в кинематическом отношении механическая часть электропривода, заменяется эквивалентным или приведенным механическим звеном. Это звено представляет собой твердое тело, вращающееся вокруг осевой линии со скоростью двигателя, которая обладает моментом инерции равной Jпри находится под воздействием момента двигателя и приведенного момента сопротивления.
В случае приведения инерционных масс и момента сопротивления к поступательному движению приведенное механическое звено представляет собой поступательно-движущуюся массу, к которой приложены две силы - приведенная и сила рабочего органа.
Таким образом полученная простая модель механической части электропривода в виде одномассовой системы, справедлива для механических звеньев без упругости и зазоров. Такое представление о кинетической системе электропривода (в виде одномассовой системы) может быть сохранено в большинстве случаев для механических звеньев, обладающих небольшими зазорами и незначительной механической упругостью.
Пример: привести статический момент и момент инерции к валу кинематической схемы грузоподъемной лебедки.
G=mгрg; Mcбар=mгрgRбар; 
.
Активный статический момент на валу барабана создается силой тяжести груза на крюке лебедки.
Момент, прикладываемый к валу лебедки. Для случая подъема груза, приведенный статический момент на барабане к валу двигателя будет равен
Приведенный момент инерции поступательного движения к вращающему движению барабана определяется:
;
Тогда суммарный приведенный момент энергии к валу двигателя равен:
studfiles.net
Изобретение относится к способам бестормозных испытаний двигателей внутреннего сгорания. Технический результат достигается тем, что способ позволяет определить момент инерции двигателя внутреннего сгорания без проведения тормозных испытаний. Способ определения момента инерции двигателя внутреннего сгорания заключается в том, что на фланец коленчатого вала устанавливается диск с эталонным моментом инерции. Измеряется угловое ускорение системы вращающихся масс «диск с эталонным моментом инерции, двигатель внутреннего сгорания». Далее диск с эталонным моментом инерции демонтируется и определяется угловое ускорение системы вращающихся масс «двигатель внутреннего сгорания». А момент инерции двигателя внутреннего сгорания определяется как отношение произведения углового ускорения системы вращающихся масс системы «диск с эталонным моментом инерции, двигатель внутреннего сгорания» на момент инерции диска с эталонным моментом инерции к разности углового ускорения системы вращающихся масс «двигатель внутреннего сгорания» и углового ускорения системы вращающихся масс «диск с эталонным моментом инерции, двигатель внутреннего сгорания». 1 ил.
Изобретение относится к способам определения момента инерции двигателя внутреннего сгорания (ДВС).
Известен способ измерения момента инерции двигателя внутреннего сгорания, основанный на предварительном измерении мощности ДВС на тормозном стенде и последующем определении угловых ускорений во всем диапазоне скоростных режимов работы коленчатого вала (Лоскутов А.С. Испытание двигателей внутреннего сгорания: учебное пособие. - Йошкар-Ола: МарГТУ, 2007).
Недостаток известного способа заключается в необходимости проведения тормозных испытаний.
Изобретение направлено на обеспечение возможности определения момента инерции ДВС без проведения стендовых испытаний.
Сущность изобретения заключается в том, что на фланец коленчатого вала устанавливается диск с эталонным моментом инерции, измеряется угловое ускорение системы вращающихся масс «диск с эталонным моментом инерции, двигатель внутреннего сгорания», далее диск с эталонным моментом инерции демонтируется и определяется угловое ускорение системы вращающихся масс «двигатель внутреннего сгорания», а момент инерции двигателя внутреннего сгорания определяется как отношение произведения углового ускорения системы вращающихся масс системы «диск с эталонным моментом инерции, двигатель внутреннего сгорания» на момент инерции диска с эталонным моментом инерции к разности углового ускорения системы вращающихся масс «двигатель внутреннего сгорания» и углового ускорения системы вращающихся масс «диск с эталонным моментом инерции, двигатель внутреннего сгорания».
Новизна заключается в том, что момент инерции ДВС определяется с помощью диска с эталонным моментом инерции, то есть с помощью диска, момент инерции которого однозначно определяется из его геометрических размеров в соответствии с зависимостью: 
, где m - масса диска, R - наружный радиус диска, r - радиус посадочного отверстия диска на вал (Яблонский А.А. Курс теоретической механики. Ч.II. Динамика. Учебник для ВТУЗов. Изд. 5-е, испр. - М.: Высш. школа, 1977).
На чертеже изображена схема реализации предлагаемого способа определения момента инерции ДВС без проведения тормозных испытаний.
Двигатель внутреннего сгорания 1 через фланец коленчатого вала 2, угловое ускорение которого определяется посредством датчика положения коленчатого вала 3, соединен с диском с эталонным моментом инерции 4.
Реализуется предлагаемый способ определения момента инерции двигателя внутреннего сгорания следующим образом.
На фланец коленчатого вала 2 устанавливается диск 4 с эталонным моментом инерции J∂. С помощью органов регулирования устанавливается определенная угловая скорость ω коленчатого вала ДВС 1, при которой развивается определенный крутящий момент М. Затем измеряется угловое ускорение ε1 системы вращающихся масс «диск с эталонным моментом инерции, двигатель внутреннего сгорания», имеющей момент инерции J1+J∂ при изменении угловой скорости вращения коленчатого вала ДВС в диапазоне от ω до ω+1. Крутящий момент М для диапазона угловых скоростей от ω до ω+1 равен:
Из выражений (1) и (2) определяется момент инерции системы вращающихся масс «двигатель внутреннего сгорания»:
Таким образом, используя один диск с эталонным моментом инерции, можно определить момент инерции двигателя, а после этого и параметры внешней скоростной характеристики двигателя внутреннего сгорания, что позволит значительно повысить экономическую эффективность испытаний ДВС.
Способ определения момента инерции двигателя внутреннего сгорания, отличающийся тем, что на фланец коленчатого вала устанавливается диск с эталонным моментом инерции, измеряется угловое ускорение системы вращающихся масс «диск с эталонным моментом инерции, двигатель внутреннего сгорания», далее диск с эталонным моментом инерции демонтируется и определяется угловое ускорение системы вращающихся масс «двигатель внутреннего сгорания», а момент инерции двигателя внутреннего сгорания определяется как отношение произведения углового ускорения системы вращающихся масс системы «диск с эталонным моментом инерции, двигатель внутреннего сгорания» на момент инерции диска с эталонным моментом инерции к разности углового ускорения системы вращающихся масс «двигатель внутреннего сгорания» и углового ускорения системы вращающихся масс «диск с эталонным моментом инерции, двигатель внутреннего сгорания».
www.findpatent.ru
Cтраница 2
Кратность момента инерции механизма главного привода к моменту инерции двигателя составляет от Мжш % для токаР - ных станков до J / J 3 - 5 - 5 для сверлильных. Поэтому время переходных процессов относительно велико. Однако его можно значительно снизить при пуске с повышенным напряжением на якоре и обеспечении прямоугольной диаграммы тока во всем диапазоне изменения частоты вращения. Поэтому преобразователи в якорном канале для приводов главного движения должны иметь большой запас по напряжению, для них больше всего подходят двигатели с низким номинальным напряжением якоря - 110, 220, 340 В. [16]
Момент инерции насосного агрегата пожарного автомобиля складывается из момента инерции двигателя, рабочего колеса насоса, вала и трансмиссии. [17]
Параметрами такой системы являются следующие величины: J - момент инерции двигателя и нагрузки, приведенный к выходному валу; Mv - коэффициент вязкого трения, приведенный к выходному валу; Мн - момент внешней нагрузки; Мдр - вращающий момент на валу двигателя; i - передаточное число редуктора; Qex-Qeblx - угол рассогласования; Мтр - момент сухого трения, приведенный к выходному валу. [18]
Так как в расчет введены приведенные значения демпфирования и момента инерции двигателя, то общая требуемая мощность является функцией передаточного числа. Описанные ниже приемы позволяют проверить, может ли двигатель развить указанную выше мощность PL и одновременно определить оптимальное передаточное число. Момент двигателя Т, соответствующий скорости v, может быть определен из кривой характеристики скорость - момент. [20]
Рабочие характеристики снимают при различных сочетаниях включаемых обмоток, моментах инерции двигателя и нагрузки и пр. [21]
Если зазоры относительно невелики и приведенный момент инерции не превышает момента инерции двигателя ( - у е 2), специального формирования плавного выбора зазоров обычно не требуется. При этом удовлетворительная плавность выбора зазоров обеспечивается формированием оптимальной зависимости М f ( t) с ограниченной производной и максимальным значением. [22]
При вычислении суммарного приведенного момента инерции привода следует учесть, что моменты инерции двигателя и шкива трения суммируются непосредственно, поскольку они находятся на одном валу. Моменты инерции направляющих шкивов необходимо привести к валу двигателя, так как скорости их различны. Кроме того, должен быть прибавлен приведенный момент инерции масс, движущихся поступательно. [23]
Нм; / - момент инерции привода, включающий в себя момент инерции двигателя JaB и приведенный к валу двигателя момент инерции механизма / пр ( см. разд. [25]
Следует отметить, что конвейеры принадлежат к инерционным механизмам, в которых момент инерции двигателя составляет лишь ( 0 03 - 0 1) JK, где JK - суммарный момент инерции конвейера. [27]
При определении момента инерции, приведенного к скорости вала двигателя, следует учитывать моменты инерции двигателя, всех звеньев передачи, а также момент инерции исполнительного механизма. Для приведения моментов инерции звеньев привода к скорости вала двигателя заменяют действительную систему, содержащую все перечисленные звенья, условной эквивалентной системой, состоящей из одного звена. Такая замена правомерна лишь в том случае, если запасы кинетической энергии действительной и эквивалентной систем равны. [28]
Время пуска и торможения такого привода с приведенным моментом инерции механизма, равным моменту инерции двигателя, не должно превышать 0 1 с. Привод должен обеспечивать позиционирование с точностью до 1 мкм за секунду. Жесткие требования выдвигаются также к равномерности перемещений на пониженных скоростях. [29]
В работе [107] рассматривается частный случай оптимальной следящей системы, в которой можно пренебречь моментом инерции двигателя и моментом нагрузки на выходном валу. Для вывода расчетных формул и иллюстрации движения системы используется энергетическая плоскость. [30]
Страницы: 1 2 3 4 5
www.ngpedia.ru
Санкт-Петербургский Государственный Политехнический Университет
Факультет Технической Кибернетики
Кафедра «Систем автоматического управления»
Пояснительная записка ПЗ08.24.04.1986
к курсовому проекту по механике
Выполнил:
группа: 3083/2
Преподаватель:
2009 г.
1. Выбор двигателя:
Используя формулу 
,высчитаем величину потребляемой мощности двигателя: Wпот=10
996Вт,
где 
С помощью каталога выберем двигатель:
|
Типоразмер двигателя |
Мощность |
Скорость |
Номинальный ток , Iн |
Номинальное напряжение, u н |
Сопротив- |
Индуктивность |
Момент инерции ротора, Jр |
|
Nдн |
nдн |
ление, R |
L |
||||
|
Вт |
об/мин |
А |
В |
Ом |
Гн |
кгм2 |
|
|
2ПН112L |
2 200 |
1 500 |
11 |
220 |
0,968 |
0,014 |
0,018 |
Двигатель 2ПН112L удовлетворяет всем условиям:
1) Wдн=2200Вт≥ Wпот=996Вт
2) неравенство:
. Верно (440 кгм
>183,3кгм)
Использовались
формулы 
и 
,
где g - коэффициент перегрузки задан равным
2.
Параметры этого двигателя:
а)
число оборотов в минуту на холостом ходу 
б)
электромагнитную постоянную времени 
в)
крутизну статической характеристики двигателя 
.
Передаточное число редуктора: 
2. Динамическое исследование машинного агрегата:
«Задачей
динамического исследования машины является определение закона движения входного
звена исполнительного механизма 
с учетом
динамических свойств приводного двигателя, движущего момента 
и динамической нагрузки в приводе 
, а также оценка неравномерности
вращения входного звена и проверка перекладки зазоров в приводе, улучшение
динамических показателей качества машины»
Машинный агрегат состоит из двигателя, передаточного и исполнительного механизмов. Динамический расчет машинного агрегата связано с определением и исследованием стационарного решения системы дифференциальных уравнений
Первое
уравнение системы представляет собой уравнение механической системы агрегата,
рассматриваемой как механизм с жесткими звеньями, обладающими одной степенью
свободы (подвижности). В этом уравнении 
-
обобщенная координата; 
- приведенный момент
инерции механической системы; 
- приведенный
момент сил сопротивления.
Второе
уравнение системы является приведенной динамической характеристикой двигателя.
Здесь 
- постоянная времени двигателя; 
- приведенная статическая
характеристика двигателя, разрешенная относительно момента.
Первым этапом динамического исследования машинного агрегата является определение коэффициентов, входящих в систему дифференциальных уравнений:
а) Приведённый момент инерции определяется по формуле
, где 
- переменная часть приведённого момента инерции, 
-момент инерции двигателя, которые вычисляется по формулам:
Полученную функцию 
с целью
упрощения динамических расчетов разложить в ряд Фурье с точностью до пяти
гармоник:
, где 
без маховика
Коэффициенты ряда Фурье для приведённого момента инерции:
|
J1c= |
-0,001 |
J1s= |
-0,0339 |
|
J2c= |
-0,0727 |
J2s= |
0,0003 |
|
J3c= |
0,001 |
J3s= |
0,0341 |
|
J4c= |
0,0132 |
J4s= |
-0,0006 |
|
J5c= |
-0,0002 |
J5s= |
-0,005 |
Построим графики функции переменной части приведённого момента инерции(Ĵпр) и её разложения в ряд Фурье(Ĵпр*) для 12и точек:
|
q |
Ĵпр |
Ĵпр* |
|
0 |
-0,0612 |
-0,0599 |
|
30 |
-0,0278 |
-0,029 |
|
60 |
0,0024 |
0,0035 |
|
90 |
0,0143 |
0,0132 |
|
120 |
0,004 |
0,0052 |
|
150 |
-0,0258 |
-0,027 |
|
180 |
-0,0607 |
-0,0594 |
|
210 |
-0,0557 |
-0,0573 |
|
240 |
0,0557 |
0,0576 |
|
270 |
0,1604 |
0,1582 |
|
300 |
0,0509 |
0,0529 |
|
330 |
-0,0565 |
-0,0581 |
|
360 |
-0,0612 |
-0,0599 |
Производная
от приведенного момента инерции по обобщенной координате вычисляется по
формуле: 
.
Её график для 12и точек:
б) Приведенный момент сил сопротивления определяется по формуле:
, где 
Функция 
раскладывается
в ряд Фурье с точностью до пяти гармоник:
Коэффициенты ряда Фурье для приведённого момента сил сопротивления:
|
Q1c= |
-1,7745 |
Q1s= |
-136,4172 |
|
Q2c= |
-33,8325 |
Q2s= |
1,4001 |
|
Q3c= |
0,6003 |
Q3s= |
9,477 |
|
Q4c= |
2,6261 |
Q4s= |
-0,0184 |
|
Q5c= |
0,0527 |
Q5s= |
-0,7169 |
Построим графики функции переменной части приведённого момента сил сопротивления(Õс) и её разложения в ряд Фурье(Õс*) для 12и точек:
|
q |
Õc |
Õc* |
|
0 |
-32,5198 |
-32,3279 |
|
30 |
-77,534 |
-77,7051 |
|
60 |
-102,308 |
-102,1493 |
|
90 |
-110 |
-110,1525 |
|
120 |
-101,836 |
-101,6841 |
|
150 |
-76,7772 |
-76,9336 |
|
180 |
-30,2541 |
-30,0849 |
|
210 |
43,8337 |
43,6397 |
|
240 |
135,5808 |
135,8128 |
|
270 |
183,3333 |
183,0698 |
|
300 |
130,1772 |
130,4335 |
|
330 |
38,3046 |
38,0818 |
|
360 |
-32,5198 |
-32,3279 |
в) Определим
приведенную статическую характеристику двигателя: 
где
- угловая скорость холостого хода
ротора двигателя.
3. Решение уравнений движения машины:
Система
дифференциальных уравнений движения (см.п.2) содержит две неизвестные функции
времени и .
Для отыскания стационарного решения этих уравнений воспользуемся методом
последовательных приближений. Для этого уравнения запишем в такой форме,
чтобы в правых частях стояли только те слагаемые, которые явно содержат , поскольку они вызывают отклонения
закона движения от программного (равномерного) вращения:
где волнистой линией обозначены переменные части соответствующих функций.
В нулевом
приближении, т.е. при 
получаем систему
уравнений
Пусть 
Известно, что 
, а 
Тогда решение этой системы:
При установленном тормозе, с моментом Qt=180Нм:
При 
получим систему уравнений
Выражение, стоящее в правой части
первого уравнения – возмущающий момент:
характеризует
внутреннюю виброактивность исполнительного механизма.
Решение системы
уравнений в первом приближении (
разыскиваем в
виде 
Здесь 
- отклонение закона движения
входного звена от программного (равномерного) движения, называемое динамической
ошибкой по углу; 
- отклонение движущего
момента от среднего значения. Подставив эти решения в систему уравнений,
получим
Разложим возмущающий момент на программном движении 
в ряд Фурье с точностью до пяти
гармоник: 
где 
;
L1=136,46;L2=34,3;L3=10,51;L4=3,6;L5=1,36;
Построим график возмущающего момента для 12 точек:
|
w0t |
L* без тормоза |
L* с тормозом |
|
0 |
-34,7422 |
-34,5548 |
|
30 |
-81,5967 |
-81,2946 |
|
60 |
-104,4439 |
-104,2658 |
|
90 |
-110,2599 |
-110,2516 |
|
120 |
-99,5017 |
-99,6711 |
|
150 |
-72,9946 |
-73,3004 |
|
180 |
-27,4575 |
-27,6615 |
|
210 |
38,4535 |
38,8561 |
|
240 |
119,1166 |
120,4127 |
|
270 |
183,5101 |
183,4759 |
|
300 |
147,0289 |
145,7405 |
|
330 |
42,8877 |
42,5146 |
|
360 |
-34,7422 |
-34,5548 |
Заметим, что наличие тормоза на форму графика почти не повлияло.
Видим, что графики возмущающего момента и приведённого момента
vunivere.ru
Изобретение относится к способам бестормозных испытаний электрических двигателей. Способ заключается в том, что на фланец выходного вала устанавливается диск с эталонным моментом инерции, а момент инерции электрического двигателя определяется как отношение произведения углового ускорения системы вращающихся масс системы «диск с эталонным моментом инерции, электрический двигатель» на момент инерции диска с эталонным моментом инерции к разности углового ускорения системы вращающихся масс «электрический двигатель» и углового ускорения системы вращающихся масс «диск с эталонным моментом инерции, электрический двигатель». Технический результат заключается в возможности определения момента инерции электрического двигателя без проведения тормозных испытаний. 1 ил.
Изобретение относится к способам определения момента инерции электрических двигателей (ЭД) и может быть использовано для проведения их испытаний
Известен способ измерения момента инерции электрического двигателя, основанный на предварительном измерении мощности электрического двигателя на тормозном стенде и последующем определении угловых ускорений во всем диапазоне частот вращения вала ротора (Справочник по электрическим машинам. Том.1 / Под редакцией И.П.Копылова. - М.: Энергоатомиздат, 1988, 679 с).
Недостаток известного способа заключается в необходимости проведения тормозных испытаний.
Изобретение направлено на обеспечение возможности определения момента инерции электрического двигателя без проведения тормозных испытаний.
Сущность изобретения заключается в том, что на конец выходного вала ЭД устанавливается диск с эталонным моментом инерции, а момент инерции ЭД определяется как отношение произведения углового ускорения системы вращающихся масс системы «диск с эталонным моментом инерции, ЭД» на момент инерции диска с эталонным моментом инерции к разности углового ускорения системы вращающихся масс «ЭД» и углового ускорения системы вращающихся масс «диск с эталонным моментом инерции, ЭД».
Новизна заключается в том, что момент инерции ЭД определяется с помощью диска с эталонным моментом инерции.
На чертеже изображена схема реализации предлагаемого способа определения момента инерции ЭД без проведения тормозных испытаний.
ЭД 1 через фланец выходного вала 2, угловое ускорение которого определяется посредством датчика 3, соединен с диском с эталонным моментом инерции 4.
Реализуется предлагаемый способ определения момента инерции ЭД следующим образом.
На фланец выходного вала 2 устанавливается диск 4 с эталонным моментом инерции Jд. С помощью органов регулирования устанавливается определенная угловая скорость ω выходного вала 1, при которой развивается определенный крутящий момент М. Затем измеряется угловое ускорение ε1 системы вращающихся масс «диск с эталонным моментом инерции, электрический двигатель», имеющей момент инерции J1+Jд при изменении угловой скорости вращения выходного вала в диапазоне от ω до ω+1. Крутящий момент М для диапазона угловых скоростей от ω до ω+1 равен:
Далее диск с эталонным моментом инерции 4 демонтируется, и определяется угловое ускорение ε2 системы вращающихся масс «электрический двигатель» с моментом инерции J1 при изменении угловой скорости вращения выходного вала в диапазоне от ω до ω+1, то есть при том же начальном значении крутящего момента М. Крутящий момент М для диапазона угловых скоростей от ω до ω+1 равен:
Из выражений (1) и (2) определяется момент инерции системы вращающихся масс «ЭД»:
Таким образом, используя один диск с эталонным моментом инерции, можно определить момент инерции ЭД, а после этого и параметры скоростной характеристики электрического двигателя, что позволит значительно повысить экономическую эффективность испытаний ЭД.
Способ определения момента инерции электрического двигателя, отличающийся тем, что на фланец выходного вала устанавливается диск с эталонным моментом инерции, а момент инерции электрического двигателя определяется как отношение произведения углового ускорения системы вращающихся масс системы «диск с эталонным моментом инерции, электрический двигатель» на момент инерции диска с эталонным моментом инерции к разности углового ускорения системы вращающихся масс «электрический двигатель» и углового ускорения системы вращающихся масс «диск с эталонным моментом инерции, электрический двигатель».
www.findpatent.ru
Теория электропривода
Обычно значительная часть производственных механизмов работает при небольшой скорости рабочих органов (100-300 об/мин.), в то время как двигатели исходя из экономических соображений конструируются на скорости 750-3000 об/мин. Поэтому между двигателем и механизмом размещается передаточное устройство (редуктор), отдельные элементы которого движутся с различными скоростями.
Кинематическая схема эл. привода дает представление о кинематических связях между движущимися массами конкретной установки, однако она не отражает того, что инерционные массы движутся с разными скоростями, поэтому момент инерции J отдельных вращающихся элементов или поступательно движущиеся массы ”m” непосредственно сравнивать невозможно, так же как сложно определять (сравнивать) силы и моменты, действующие в движущихся с разными скоростями элементах. Кроме того, кинематическая схема не отражает того обстоятельства, что все элементы системы при нагружении испытывают деформации, т. к. обладают жесткостью. Поэтому при практических расчетах с помощью кинематической схемы составляется расчетная схема механической части эл. привода, в которой Мс, Fc, J, m, а также реальные жесткости “С” механических связей заменяются эквивалентными величинами, приведенными к одной расчетной скорости. Обычно за нее принимается скорость вала двигателя. При замене реальной системы эквивалентной, приведенной системой все J, Mc, Fc, j, m и С должны быть пересчитаны таким образом, чтобы сохранились кинетические и динамические свойства исходной системы, т. е. необходимо обеспечить сохранение запаса кинетической и потенциальной энергии системы, а также элементарной работы всех действующих в системе сил и моментов на возможных перемещениях.
Если система эл. привода состоит из нескольких инерционных элементов (см. рис.), имеющих моменты инерции J1,J2,…Jn, вращающихся с угловыми скоростями w1,w2,...wn, и параметры системы таковы, что влиянием упругих связей можно пренебречь, их динамическое действие можно заменить действием одного момента инерции Jпр, приведенного к расчетной скорости (валу двигателя). Под ним понимают момент инерции простейшей системы, состоящей только из элементов, вращающихся со скоростью оси, к которой производится приведение, и которая обладает
 |  |
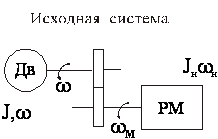при этом запасом кинетической энергии, равной запасу энергии в исходной системе.
В этом случае
Отсюда
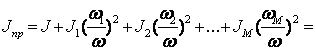
, где
J1,j2,…,jn – передаточные отношения между осью (валом) двигателя и осями отдельных вращающихся элементов (звеньев).
Часто приведенный момент инерции системы считают равным сумме моментов инерции двигателя и приведенного момента инерции рабочей машины, а моменты инерции звеньев передаточного механизма (редуктора) учитывают увеличением момента инерции двигателя в “d” раз, т. е.
, где d=1,1¸1,3
При привидении момента любого i-го элемента к расчетной скорости должно выполняться условие:
, откуда 
.
Аналогично выполняется приведение масс, движущихся поступательно со скоростью V, к расчетной скорости w.
Заменим, например, систему подъемника, изображенную на рис., эквивалентной системой, содержащей только вращающиеся элементы.
 |  |
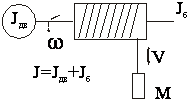Исходная система Приведенная система
Баланс кинетической энергии 
Отсюда 
В этом случае приведенная к вращательному движению масса эквивалентна моменту инерции J`
В общем случае приведение поступательно движущейся со скоростью Vj массы mj к расчетной скорости w производится из условий равенства запасов энергии: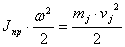 
;
Отсюда 
, где
Rj – радиус приведения к расчетной скорости (валу двигателя) j-го поступательно движущегося элемента.
Приведение углов поворота jj и поступательных перемещений Sj к расчетной угловой скорости w осуществляется с учетом того, что передаточное число и радиус приведения определяются соотношением скоростей. Исходя из этого в общем случае перемещения в системе связан так:
; 
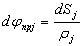; а при ji =const и rj=const формулы приведения имеют следующий вид: 
; 
.
Привидение статических моментов сопротивления и статических усилий элементов кинематической цепи должно осуществляться на основе равенства элементарной работы на возможных перемещениях.
и 
; отсюда
; 
;
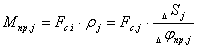Приведение жесткостей упругих элементов осуществляется при условии сохранения неизменной величины потенциальной энергии деформации реальной и эквивалентной систем.
Отметим, что приведенной жесткостью элемента называется крутящий момент (усилие), необходимый для получения крутильной деформации упругого элемента 1 радиан (или линейной деформации 1 м).
Приведенная жесткость может быть определена, если известен фактический коэффициент жесткости упругого элемента и кинематические параметры системы. Пусть, например, участок кинематической цепи с жесткостью Сi (см. рис.) при закручивании получает деформацию ji радиан.
Потенциальная энергия деформации при этом 
Эквивалентный упругий элемент должен иметь такую же потенциальную энергию.
msd.com.ua
Министерство образования и науки Российской Федерации
НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
ФАКУЛЬТЕТ МЕХАТРОНИКИ И АВТОМАТИЗАЦИИ
Кафедра электропривода и автоматизации промышленных установок
Расчётно-графическое задание
Задача 1, 2, 3
Вариант 51
Выполнил:
Студент гр. ЭМ – 51 « » 2008 г. Солнцев А.С.
Проверил:
К.т.н., доцент « » 2008 г. Абакумов И.Д.
Новосибирск 2008
Технические данные электродвигателя 4MTF(H) 112LB6:
− номинальная мощность;
– номинальное напряжение;
− частота питающей сети;
− номинальная частота вращения;
− максимальная частота вращения;
– максимальный момент;
– момент инерции электродвигателя;
− продолжительность включения;
– число ступеней пуска.
Статор:
− номинальный ток статора;
− коэффициент мощности в номинальном режиме;
− ток холостого хода;
− коэффициент мощности при холостом ходе;
;
− активное сопротивление обмотки;
− индуктивное сопротивление обмотки;
Ротор:
− номинальная эдс ротора;
− номинальный ток ротора;
− активное сопротивление обмотки;
− индуктивное сопротивление обмотки;
− коэффициент приведения обмоток.
− сопротивление обмоток при 
.
Технические данные механизма подъёма:
− диаметр барабана;
− масса поднимаемого груза;
− передаточное число редуктора;
− высота подъёма груза;
.
Кинематическая схема механизма подъёмника представлена на рисунке 1.
Рисунок 1 Кинематическая схема механизма подъёмника
Принимаем механическую схему электродвигателя жёсткой одномассовой, т.е. не учитываем упругие деформации в кинематических звеньях привода.
Задача №1
Пункт 1
Привести моменты инерции движущихся инерционных масс привода к скорости вращения электродвигателя. Определить суммарный момент инерции расчётной эквивалентной механической системы привода. При этом принять суммарный момент инерции соединительных муфт и шестерни редуктора, вращающихся со скоростью двигателя 
, равным 
, а суммарный момент инерции соединительных муфт и шестерни редуктора, вращающихся со скорость механизма 
, равным 
.
На рисунке 2 представлена расчётная схема механизма.
Рисунок 2. Расчётная схема механизма
Общее управление движения электропривода:
,
где 
− момент электродвигателя;
− статический момент сил сопротивления;
− момент инерции приведённой системы.
Расчёт выполним из условия равенства кинетической энергии реальной схемы и кинетической энергии приведенной массы 
.
Приведём моменты инерции движущихся инерционных масс привода к скорости вращения электродвигателя. Кинематическая схема электропривода показана на рисунке 1.
Принимаем:
и
.
Тогда с учётом этого запишем уравнение:
где 
− энергия электродвигателя;
− энергия барабана;
− энергия груза;
− суммарная энергия соединительных муфт СМ1 и шестерни редуктора, вращающихся со скоростью двигателя 
;
− суммарная энергия соединительных муфт СМ2 и колеса редуктора, вращающихся со скоростью барабана 
.
Т.к. и 
, то можно записать:
Помножим это уравнение на 
, тогда получим:
Введём обозначения:
.
Запишем:
Подставив численные значения, получим:
.
Пункт 2
Определить приведенные к скорости вращения электродвигателя моменты статического сопротивления для двух режимов работы электродвигателя:
1. Двигательный режим при подъёме груза.
2. Генераторный режим (торможения) при спуске груза.
При этом КПД механизма принять равным 
, а КПД редуктора 
.
1. Для двигательного режима работы:
Приведение моментов статического сопротивления осуществляется на основе равенства элементарных работ, выполняемых в реальной и эквивалентной расчётных схемах.
Работа, совершаемая электродвигателем:
.
Работа, затрачиваемая на вращение механизма:
,
где 
− время работы электродвигателя.
Часть работы двигателя затрачивается на потери в редукторе и в рабочем органе, эти потери учитывают КПД механизма и редуктора.
и
Работа, затрачиваемая на подъём груза:
.
Учёт потерь в механизме:
.
После учёта потерь в механизме получим:
.
Учитывая, что 
и 
, получим:
.
Приведём механический момент к скорости вращения электродвигателя с учётом потерь в редукторе:
, тогда
,
,
подставим численные значения:
.
2. Генераторный (тормозной) режим работы электродвигателя:
vunivere.ru
