ДВС

РОТОРНЫЙ

EMDRIVE

РАСКОКСОВКА

HONDA

ВИДЫ

Глава 6. Выбор двигателя и тепловые процессы в приводе. Теплоотдача двигателя

Процессы нагрева и охлаждения электродвигателей

Для обеспечения нормального режима эксплуатации электрических машин необходимы знания теплового режима работы изоляции электродвигателя.

Учет всех тепловых процессов, происходящих в электрической машине, задача далеко не из легких, так как существует различие материалов, использованных при изготовлении электродвигателя (медь, изоляция, электротехническая сталь), условия работы элементов (вращающиеся и неподвижные), а также довольно сложные процессы обмена тепла между отдельными частями электродвигателя.

В процессе работы электродвигателя избежать потерь в нем невозможно. Эти потери будут вызывать нагрев отдельных компонентов и создавать процессы теплообмена. Поэтому при изучении процессов нагрева и охлаждения электрическую машину рассматривают как систему нескольких однородных тел, которые связаны взаимными тепловыми потоками.

Например, асинхронный электродвигатель следовало бы рассматривать как систему четырех тел, а именно: сталь и медь статора, которые разделены изоляцией, медь и сталь ротора, а также охлаждающая среда. При подобных допущениях тепловые процессы внутри асинхронного электродвигателя будут описываться довольно сложной системой дифференциальных уравнений. В случае же переменной нагрузки система уравнений значительно усложняется, что делает расчет практически невозможным.

Более простым случаем является нагрев двух тел. В таком случае нагревание статора и ротора рассматривается отдельно друг от друга. Нагрев каждого из этих элементов рассматривают как процессы теплообмена между медью и сталью под действием соответствующих потерь. Однако даже такое весьма упрощенное и приближенное рассмотрение процессов теплообмена электрических двигателей требует значительного количества конструктивных и расчетных параметров, таких как теплоотдача лобовых частей обмотки статора, теплоотдача между медью и сталью ротора через пазовую изоляцию и другие параметры. Эти данные в каталогах производители не приводят, что делает подобные методы расчета практически недоступными для проектировщиков систем электроприводов, не говоря уже об эксплуатирующем персонале. В случаях необходимости установления нагрева электродвигателя при определенной нагрузке используют более грубые и простые методы.

Упрощение достигается тем, что процесс нагревания электрической машины заменяют процессом нагревания однородного твердого тела, обладающего бесконечно большой теплопроводимостью. Этому телу на единицу времени по всему объему будет передано определенное количество тепла, которое определяется потерями:

Где Р – мощность полезная на валу машины; η – КПД соответствующий данной нагрузке.

При нагревании электромашины ее температура повышается. Как только она превысит температуру окружающей среды — электродвигатель станет излучать тепло и, соответственно, процесс нагрева замедлится. С увеличением температуры электродвигателя будет увеличиваться и количество теплоты, отдаваемое им в окружающую среду. При определенной температура наступает тепловое равновесия – это когда количество теплоты, получаемое объектом, равно количеству теплоты отдаваемой им. При достижении равновесия температура установится на определенном уровне и не будет изменятся.

Отдача тепла телом может происходить тремя способами – конвекцией, лучеиспусканием, теплопроводностью.

Тепло, отдаваемое лучеиспусканием, будет пропорционально разности четвертых степеней абсолютных температур тела и среды.

Тепло, отдаваемое при конвекции, пропорционально разности температур в степени 1,25; а в случае с теплопроводностью – пропорционально данной разности.

Ввиду того, что температуры нагрева в электромашиностроении не велики, количество тепла, отдаваемое путем лучеиспускания, будет весьма невелико и им, как правило, пренебрегают. Наиболее существенное влияние оказывают процессы конвекции и теплопроводимости, поэтому для упрощения расчетов в дальнейшем принимается, что отдаваемое тепло пропорционально разности температур.

В соответствии с принятыми ранее допущениями можно записать условия теплового равновесия:

Где: Q – количество теплоты, которое сообщается телу за единицу времени, размерность        кал/сек или дж/сек;

С – теплоемкость тела (количества тепло необходимого для повышения температуры на 10 ), размерность кал/град или дж/град;

А – теплоотдача (количество тепла, рассеиваемое поверхностью в секунду при разности температур тела и среды в 10 ), размерность кал/сек∙град или дж/сек∙град;

τ – превышение температуры тела над температурой окружающей среды;

Проинтегрировав выражение (2) получим:

Постоянную интегрирования можно найти из начальных условий: при t = 0 и τ = τнач, подставив которые получим:

или:

Использовав значение постоянной интегрирования:

Отношение теплоемкости электродвигателя к его теплоотдаче назовем постоянной времени нагрева и обозначим:

В соответствии с размерностью входящих в формулу (5) величин размерность постоянной времени будет равна:

Подставив Θ в выражение (4) получим:

Полученная в результате вычислений кривая нагрева будет иметь следующий вид:

Кривая показывает, что в начальном этапе (при t = 0) начальное превышение температуры было равно τ = τнач. По истечению бесконечно большого времени (t = ∞) превышение температуры достигнет какого-то установившегося значения:

Используя понятия об установившейся температуре выражению можно придать вид:

Если в начальный момент времени превышение температуры тела над окружающей средой τнач = 0 уравнение процесса нагрева примет более простой вид:

Выражение (7) показывает, что установившаяся температура перегрева тела определяется только количеством выделяемого в теле тепла и его теплоотдачей и совершенно не зависит от теплоемкости тела. Отсюда следует, что при сохранении постоянства теплоотдачи установившаяся температура перегрева будет пропорциональна количеству тепла, сообщаемого телу.

Но с другой стороны, улучшив отвод тепла от тела (принудительное охлаждение) мы пропорционально снижаем его перегрев.

Соотношение (7) позволяет наметить основные пути, направленные к более рациональному использованию материалов при конструировании электрических машин. Правильно рассчитанный  электродвигатель должен иметь при номинальной нагрузке максимально допустимую температуру перегрева изоляции:

Подставив значение потерь при номинальном режиме, выраженное через КПД и номинальную мощность, а также значение теплоотдачи и решив все относительно Рном получим:

Выражение (12) показывает, что для получения максимальной мощности электродвигателя необходимо иметь максимальный КПД. В этом случае потери будут сведены к минимуму. Мощность электрической машины будет больше в случае более интенсивного охлаждения  и большей охлаждаемой площади. С этой целью в электрических машинах широкое распространение получили вентиляторы, которые улучшают охлаждение. Для увеличения площади охлаждающей поверхности корпус электрических машин очень часто выполняют ребристым (особенно наглядно видно на примере асинхронных электродвигателей). Также существует еще один способ повышения мощности – это повышение теплостойкости изоляции.

Формула (12) позволяет сделать вывод, что открытая машина при одинаковых габаритах будет иметь мощность больше, чем закрытая. Это связано с тем, что воздух, проходящий через внутренние части открытой машины, лучше охлаждает ее компоненты чем в закрытой, так как площадь охлаждения внешней поверхности в закрытой машине будет значительно ниже.

Для различного рода приближенных расчетов по формуле (10) удобно использовать номограмму:

Задавшись значениями Θ и t и проведя через эти точки прямую до третьей вертикали получают повышение температуры в долях установившегося перегрева тела.

Продолжим анализ выражения (10). Температура перегрева тела представляет собой сумму трех слагаемых. Соотношение этих слагаемых будут определять характер процесса. При сообщении телу какого-то количества теплоты Q, которому соответствует установившаяся температура перегрева τу, при τу> τнач будет иметь место нагрев тела до температуры τу.

В случае подведения меньшего количества теплоты Q, а именно при τнач> τу>0, произойдет понижение температуры от τнач до τу.

При отсутствии подвода тепла Q = 0 и τу = 0 превышение температуры будет равно:

Вследствие наличия разности температур в сторону превышения τнач>0  и Q = 0, тело начнет охлаждаться, то есть отдавать тепло.

Очевидно, что процесс теплообмена будет продолжатся до тех пор, пока температуры окружающей среды и тела не сравняются.

На рисунке ниже показана кривая нагрева электрической машины и ее составляющие:

Кривая τ1 соответствует нагреву, τ2 охлаждению при сообщении тепла, а τ3 – охлаждение до температуры окружающей среды. Таким образом, в зависимости от значений τнач и τу можно иметь любой характер теплового процесса.

При охлаждении электродвигателя с самовентиляцией в отключенном состоянии с неподвижным якорем или ротором условия отдачи тепла будут хуже и отдача А меньше, чем в процессе работы машины. Поэтому постоянная Θ0 = С/А будет при охлаждении больше, чем при нагреве, то есть Θ0>Θ.

Кривая охлаждения неподвижной электрической машины приведена ниже, для сравнения там приведена и кривая нагрева:

elenergi.ru

Тепловыделения от электродвигателей

Тепловыделения от электродвигателей насосов и вентиляторов, не имеющих принудительного охлаждения с отводом тепла за пределы помещения, ккал/ч:

, (4)

где: Ny- установочная или номинальная мощность электродвигателя, кВт;

η1 = Кп η - КПД электродвигателя при данной загрузке; здесь Кп - поправочный коэффициент, учитывающий загрузку двигателя: при Кзагр ≥ 0,8 значение Кп = 1, при Кзагр < 0,8 значение Кп принимается в следующих пределах:

Кзагр 0,7 0,6 0,5 0,4 0,3

Кп 0,99 0,98 0,97 0,95 0,91

η - КПД электродвигателя при полной загрузке, определяемый по каталогу;

η = 0,8 - 0,95

Ксп – коэффициент спроса на электроэнергию, принимаемый по электротехнической части проекта, Ксп = 0,9;

 

Тепловыделения от нагретых поверхностей

При составлении баланса тепла для помещения должно учитываться поступление (удаление) тепла от нагретых (охлажденных) поверхностей воздуховодов вентиляции, местных отсосов, зонтов и укрытий оборудования. Теплоотдача от нагретых поверхностей, если известна их температура, ккал/ч:

, (5)

где : F - площадь нагретой поверхности, м2;

tпов и tв - температура соответственно нагретой поверхности и воздуха в помещении, °С;

a - коэффициент теплоотдачи от поверхности к воздуху помещения, ккал/(чм2 оС). Значения a определяют по формуле:

, (6)

где: v - скорость движения воздуха у наружной поверхности, м/с.

в зоне комфорта v = 0,5 м/с.

 

 

2.4. Тепловыделения от искусственного освещения

Принято считать, что вся энергия, затрачиваемая на освещение, переходит в тепло, нагревающее воздух помещения. Тепловыделения от освещения, ккал/ч:

(7)

где: N осв - суммарная мощность источников освещения, кВт.

 

Выделение тепла людьми

Выделение тепла и влаги людьми зависит от затрачиваемой ими энергии и температуры воздуха в помещении (табл.5). В табл. 5 приведены средние данные для мужчин. Принято считать, что женщины выделяют 85%, а дети, в среднем - 75% тепла, выделяемого мужчинами.

 

Таблица 5

Количество тепла, выделяемого взрослыми людьми (мужчинами)

Показатели	Количество тепла, ккал/ч., выделяемого людьми при температуре воздуха в помещении, °С
	При легкой работе
Тепло:
явное
скрытое
полное
	При работе средней тяжести
Тепло:
явное
скрытое
полное
	При тяжелой работе
Тепло:
явное
скрытое
полное

 

Выбор кондиционера

Необходимый воздухообмен для всего помещения в целом:

, (8)

 

где: n – число работающих в данном помещении;

L1 – расход воздуха на одного работающего, м3/ч.

Когда неизвестно количество выделяющихся вредных веществ количество воздуха определяется по кратности вентиляционного воздухообмена. Кратность воздухообмена k (час-1) показывает, сколько раз в час меняется воздух в помещении (принимается по СНиП 2.04.05-91):

, (9)

где: L – объем воздуха, подаваемого или удаляемого из помещения, м3/ч;

V – объем вентилируемого помещения, м3.

Величина k обычно составляет значения от 1до10.

 

Таблица 6

studopedya.ru

Основы расчета жидкостной системы охлаждения

Для расчета системы охлаждения автомобильного или тракторного двигателя исходной величиной является количество отводимого от него в единицу времени тепла Qохл. Это количество может быть определено из уравнения теплового баланса:

,

где qохл – доля количества тепла, отводимого от двигателя. Для бензиновых ДВС qохл = 800–1300 КДж/КВт  с, для дизельных ДВС qохл = 1100–1150 КДж/КВт  с.

Определив величину Qохл, находят затем количество жидкости, циркулирующей в системе охлаждения в единицу времени,

,

где Сж – теплоемкость циркулирующей жидкости.

Для воды Сж = 4.22 КДж/кг К, для этиленгликолевых смесей Сж = 2–3.8 КДж/кг К;

tвыхж, tвхж – температуры выходящей из радиатора жидкости и входящей в него, °С.

Для радиаторов автомобильных и тракторных двигателей значение tвыхж – tвхж = 5–10  С.

Систему охлаждения двигателя обычно рассчитывают для двух режимов работы двигателя: при номинальной мощности и максимальном крутящем моменте.

Величина поверхности охлаждения радиатора (м2) определяется по формуле:

,

где k – полный коэффициент теплопередачи через стенки радиатора,

tохлж – средняя температура охлаждающей жидкости в радиаторе, °С;

,

где tвхохлж = 90°  С – температура охлаждающей жидкости на входе в радиатор;

tвыхохлж = 80–85°  С – температура охлаждающей жидкости на выходе из радиатора;

tохлв – средняя температура проходящего через радиатор воздуха, °С,

,

где tвхохлв = 40° С – температура воздуха на входе в радиатор;

tвыхохлв= 60–70°С – температура воздуха на выходе из радиатора.

Коэффициент k зависит от многих факторов: материала охлаждающей решетки, формы и состояния ее внутренней и наружной поверхностей, характера движения воздушного потока и т. д. Теплопередача радиатора значительно ухудшается при образовании в нем накипи, ржавчины или при покрытии грязью.

Величина k может быть определена по формуле:

,

где a 1 = 8500–14500 КДж/м2 ч К – коэффициент теплоотдачи от жидкости к стенкам радиатора;

l – коэффициент теплопроводности металла стенок (трубок) ра-диатора. Для латуни значение  = 300–450 КДж/м ч К, для алюминия = 300–350 КДж/м ч К, для нержавеющей стали = 35–70 КДж/м ч К;

b– толщина стенки трубки, м;

a 2 – коэффициент теплоотдачи от стенок радиатора (трубок) к воздуху,  = 150–1100 КДж/м2чК.

Коэффициент  2 в основном зависит от скорости воздуха ?воз , проходящего через радиатор, и выражается зависимостью:

.

Для предварительных расчетов площади радиатора системы охлаждения можно использовать формулу:

,

где f – удельная площадь охлаждения, м2/КВт.

Для легковых автомобилей f = 0.14–0.3, для грузовых автомобилей f = 0.2–0.4, для тракторов f = 0.4–0.55.

Емкость системы жидкостного охлаждения л. (Ne в КВт) изменяется в следующих пределах: для легковых автомобилей – (0.13–0.35) Ne, для грузовых автомобилей – (0.27–0.8) Ne, для тракторов – (0.5–1.7) Ne.

Размеры вентилятора автомобильного или тракторного двигателя должны быть таковы, чтобы обеспечить подачу воздуха в количестве, необходимом для охлаждения жидкости в радиаторе.

Тип вентилятора определяют по условному коэффициенту быстроходности:

,

где Vвоз – производительность вентилятора, м3/с.

,

где  Vвоз = 1.07 кг/м3 – плотность воздуха;

Своз = 1 КДж/кг К – теплоемкость воздуха;

Н – напор вентилятора. Н = 600–1000 Па.

При nусл = 15–100 используют центробежные вентиляторы, при nусл = 80–300 – осевые одноступенчатые вентиляторы.

Воздушная система охлаждения

В двигателях с воздушным охлаждением для обеспечения нормального теплового состояния двигателя площади наружных поверхностей головок и цилиндров увеличивают путем их оребрения. От поверхности оребрения тепло, поступающее к ней от стенок камеры сгорания и стенок цилиндра, отводится охлаждающим потоком воздуха.

Положительными особенностями системы воздушного охлаждения являются несложное обслуживание, надежность в эксплуатации, меньший по сравнению с системой жидкостного охлаждения вес и простота конструкции, упрощение эксплуатации двигателя в безводных районах, а также устранение опасности замерзания воды в радиаторе и рубашке двигателя (в случае заполнения их водой) при низких температурах.

Схема движения воздуха, охлаждающего однорядный четырехцилиндровый двигатель, представлена на рис. 3.8. Каналы, по которым движется воздух, разделены на участки: входа воздуха, прохождения воздуха через вентилятор 1, распределения воздуха по цилиндрам,прохождения воздуха по межреберным каналам и отводного трубопровода. В рассматриваемой схеме охлаждаемые поверхности находятся на линии нагнетаемого воздуха. В некоторых случаях воздух через межреберные каналы не нагнетается, а просасывается.

Для получения эффективного и равномерного охлаждения при минимальной затрате мощности в двигателях с воздушным охлаждением применяют дефлекторы. Дефлекторы представляют собой направляющие устройства для подачи охлаждающего потока воздуха к оребренным поверхностям с определенными скоростью и направлением.

Рис. 3.8. Схема системы воздушного охлаждения двигателя

При проектировании системы воздушного охлаждения стремятся обеспечить подачу охлаждающего воздуха в первую очередь к наиболее горячим местам головки цилиндров (перемычки между гнездами клапанов и др.), а также к свечам зажигания (в бензиновых двигателях) и форсункам (в дизелях). Для улучшения теплопередачи поток охлаждающего воздуха должен омывать поверхности охлаждения равномерно и с достаточно высокой скоростью.

Расчет системы воздушного охлаждения автомобильных и тракторных двигателей сводится к определению параметров оребрения двигателя, производительности и размеров вентилятора, а также затрачиваемой на привод вентилятора мощности.

Проведение этого расчета вследствие влияния ряда трудно учитываемых факторов, а также из-за отсутствия данных о взаимозависимости расчетных параметров системы охлаждения весьма сложно и связано с большими трудностями. В особенности сложен теоретический расчет теплопередачи и аэродинамического сопротивления оребрения двигателя. Поэтому на практике при проектировании системы воздушного охлаждения обычно задаются удельной поверхностью оребрения и широко пользуются экспериментальными данными прототипов двигателей.

В начале расчета задаются его исходными параметрами, к которым относятся: а) температура, давление и влажность окружающего двигатель воздуха, б) рабочие температуры деталей двигателя и в) расчетный режим работы двигателя.

В качестве расчетной температуры окружающего воздуха принимают температуру, равную 40 °С.

Превышение рабочих допустимых температур может вызвать нарушение работы (увеличение нагарообразования, коробление головки цилиндра, закоксовывание и зависание иглы форсунки в дизелях, детонацию и калильное зажигание в бензиновых двигателях, повышенный износ цилиндра, поршня и поршневых колец).

Средняя температура у оснований чугунных ребер цилиндров 130–170 °С; у оснований чугунных ребер головки цилиндров 170–220 °С. При алюминиевых сплавах средние температуры соответственно 130–150 и 160–200 °С.

Минимальные температуры внутренних поверхностей цилиндра и его головки стремятся обеспечить не ниже 130–140 °С, т. е. значительно выше точки росы выпускных газов.

studfiles.net

Выбор ЭП. Тепловые процессы.

Воронин Сергей Григорьевич

Выбор двигателя является одним из важнейших этапов проектирования привода, так как именно двигатель в значительной степени определяет эксплуатационные свойства, динамические характеристики, энергетические и габаритно-массовые показатели привода. Исходя из особенностей системы или объекта, в котором используется привод, двигатель выбирают по таким параметрам и показателям: роду тока и номинальному напряжению; виду естественной механической характеристики; пусковым и тормозным свойствам; особенностям регулирования скорости; конструктивному исполнению и т.д. При этом общие критерии выбора достаточно очевидны. Следует выбирать наиболее простой двигатель по устройству и управлению, надежный в эксплуатации, имеющий минимальную массу, габариты и стоимость, работоспособный в условиях окружающей среды и т.д.

Если с учетом перечисленных требований тип выбран, необходимо выбрать конкретный типоразмер двигателя. В гл. 1 мы рассматривали вопросы выбора типоразмера по добротности, мощности и скорости из условия обеспечения сформулированных тем или иным образом динамических свойств привода. Однако при этом не учитывались условия эксплуатации и тепловые режимы. Между тем в процессе работы за счет потерь энергии происходит нагрев двигателя, поэтому при форсировании его, например, для обеспечения заданной добротности его обмотка может перегреться, что приведет к выходу двигателя из строя. С другой стороны, завышение установленной мощности двигателя не только удорожает привод, повышает его габариты и массу, но и ведет к увеличению потерь, т.е. к ухудшению энергетических показателей.

Таким образом, для правильного выбора типа двигателя и его мощности необходимо учитывать тепловые процессы и выбирать двигатель так, чтобы он, с одной стороны, не был недогружен по теплу, а с другой не перегревался. Так как нагрев осуществляется за счет потерь в двигателе, рассмотрим их.

6.1. Потери энергии в электроприводах

6.1.1. Потери энергии в неуправляемых электроприводах

Потери в двигателе складываются из переменных, зависящих от нагрузки, и постоянных, не зависящих от нагрузки. Для электроприводов постоянного тока суммарные потери

(6.1)

$ΔP_с = K + V$,

где $K,~V$ – соответственно постоянные и переменные потери; $K=ΔP_в+ΔP_{ст}+ΔP_{мех}$, где $ΔP_в$, $ΔP_{ст}$, $ΔP_{мех}$ – соответственно потери на возбуждение, потери в стали и механические; $V=I^2 R$ – переменные потери в якорной цепи двигателя.

Аналогично для асинхронного двигателя

$ΔP_с = ΔP_{ст} + ΔP_{мех} + 3 (I_1^2 R + I'_2^2 R'_2)$.

Переменные потери можно выразить через момент и скорость

(6.2)

$V = M (ω_0 - ω)$,

а также через номинальные значения тока и момента

(6.3)

$V = V_н (I / I_н)^2 = V_н (M / M_н)^2$.

Выражение (6.3) позволяет рассчитать потери в двигателе в статических режимах. Рассмотрим, как определить потери в переходных режимах. Здесь целесообразно искать расход и потери мощности за время всего переходного процесса. Потери энергии за время переходного процесса равны

В переходных процессах постоянные потери чаще всего много меньше переменных, поэтому в дальнейшем мы их учитывать не будем. Для двигателя постоянного тока независимого возбуждения потери при пуске с учетом (6.2)

.

Раскрывая $M$ в соответствии с уравнением движения привода (1.14) в виде

$M = J dω/dt + M_с$,

после преобразований получим:

или

(6.4)

,

где $ω_с$ – установившееся значение скорости.

Первый член выражения (6.4) представляет собой потери энергии в якорной цепи, обусловленные разгоном инерционных масс привода ($ΔA_д$), а второй – потери, вызванные наличием момента нагрузки ($ΔA_с$).

Если принять $M_с=0$, то потери энергии определятся выражением

(6.5)

$ΔA_п = J ω_0^2 / 2$.

Следовательно, потери энергии при пуске двигателя вхолостую равны запасу кинетической энергии, накопленной движущимися массами привода к концу пуска. И суммарная энергия, затраченная на пуск и потребленная из сети

$A_{эл} = J ω_0^2$.

При $M_с≠0$ и известной зависимости $ω(t)$ для расчета потерь необходимо использовать выражение (6.4). Если указанная зависимость аналитически не выражена, то необходимо использовать приближенные методы.

При торможении противовключением под нагрузкой $M_с=\const$ потери энергии можно определить по формуле

(6.6)

Из выражения (6.6) следует, что потери энергии при торможении под нагрузкой меньше, чем вхолостую. Это объясняется тем, что нагрузка сама по себе является тормозящим фактором. При $M_с=0$ потери при торможении противовключением равны

$ΔA_{тп} = 3 J ω_0^2 / 2$.

При динамическом торможении вхолостую якорь двигателя отключается от сети и замыкается на резистор, поэтому кинетическая энергия, запасенная в движущихся частях привода, определяемая согласно (6.5), выделяется в якорной цепи, распределяясь пропорционально величине сопротивлений. Если динамическое торможение производится под нагрузкой ($M_с = \const$), то потери энергии в якорной цепи

(6.7)

Потери энергии в якорной цепи двигателя при реверсировании без нагрузки

(6.8)

Выражение (6.8) показывает, что потери энергии при реверсе равны сумме потерь при торможении противовключением и пуске.

Потери при реверсировании под нагрузкой определяются по формуле

(6.9)

$ΔA_р = ΔA_п + ΔA_{тп}$.

На основе полученных нами соотношений можно заключить, что при управлении двигателем постоянного тока от источника постоянного напряжения и $M_с=0$ потери при пуске определяются только кинетической энергией движущихся частей привода, имеющейся после пуска, и не зависят от способа пуска и времени переходного процесса.

Пусковые потери в асинхронном двигателе, если пренебречь постоянной составляющей потерь и влиянием тока холостого хода, можно определить по формуле

(6.10)

При $M_с = 0$

$dt = -(J ω / M) ds$.

Выражая потери мощности в роторной цепи через мощность скольжения, т.е.

$3 I'_2 (R'_2 + R'_{2доб}) = M ω_0 s$,

в результате несложных преобразований получаем:

(6.11)

или, учитывая, что $s_{нач} = 1$ и $s_{кон} = 0$,

(6.12)

$Δ A_{п0} = J ω _0^2 / 2 × (1 + R_1 / (R'_2 + R'_{2доб}))$.

Из полученного уравнения следует, что потери при пуске состоят:

1) из потерь в роторной цепи

$ΔA_{п02} = J ω_0^2 / 2$,

определяемых запасом кинетической энергии, которую приобретает привод к концу пуска;

2) из потерь в статорной цепи

$ΔA_{п01} = J ω_0^2 / 2 × R_1 / (R'_2 + R'_{2доб})$,

зависящих от активных сопротивлений статора и роторной цепи.

Для двигателей с короткозамкнутым ротором можно принять $R'_2_{доб}≈0$. Для уменьшения потерь при пуске в этом случае делают, например, двигатели с двойной беличьей клеткой, обеспечивающие повышенное сопротивление ротора, изменяющееся в функции от скольжения.

Потери энергии при пуске асинхронного двигателя под нагрузкой могут быть определены по формуле

(6.13)

$ΔA_п ≈ A_{п0} × M_{пср} / (M_{пср} - M_с)$,

где $M_{пср}=(λ+k_п)M_{ном}/2$ – средний пусковой момент; $λ=M_к/M_{ном}$; $k_п=M_п/M_{ном}$.

Потери энергии в асинхронном двигателе при торможении противовключением могут быть найдены по (6.11) при подстановке пределов $s_{нач}=2$ и $s_{кон}=1$, тогда

(6.14)

$ΔA_{тп} = 3 J ω_0^2 / 2 × (1 + R_1 / (R'_2 + R'_{2доб}))$.

Если торможение происходит под нагрузкой, то потери равны

(6.15)

$ΔA_{тп~н} ≈ A_{тп} × M_{тср} / (M_{тср} + M_с)$,

где $M_{тср}$ – средний момент, развиваемый двигателем при торможении противовключением.

Потери энергии в роторной цепи двигателя при торможении вхолостую определяются запасом кинетической энергии, который имеет привод к началу торможения, т.е.

$ΔA_{т~дин02} = J ω_0^2 / 2$.

Потери в статоре в этом случае

(6.16)

$ΔA_{т~дин1} = 3 I_{экв}^2 R_1 t_т$.

Здесь $I_{экв}$ – эквивалентный ток статора, $t_т$ – время динамического торможения.

Если динамическое торможение происходит под нагрузкой, то потери в роторной цепи

(6.17)

$ΔA_{т~дин2} = ΔA_{т~дин02} × M_{т~дин1} / (M_{т~дин1} + M_с)$.

Потери в статоре в этом случае определяются по (6.17) с учетом того, что время торможения будет меньше при том же значении $I_{экв}$.

6.1.2. Потери энергии в управляемом электроприводе

Для уменьшения потерь при пуске необходим управляемый источник напряжения. Например, в случае линейного изменения напряжения на обмотке якоря линейно изменяется и скорость холостого хода двигателя, как это показано на рис. 6.1. Здесь, если пренебречь электромагнитной постоянной двигателя, при $t≤t_п$ скорость изменяется в соответствии с выражением:

$ω(t) = ε_п t - T_м ε_п (1 - e ^{-t / T_м})$,

$M = J ε_п (1 - e ^{-t / T_м})$,

при $t ≥ t_п$

$ω(t) = ω_{0н} - (ω_{0н} - ω_п) e ^{-t / T_м}$,   $M = M_п e ^{-t / T_м}$,

где $ε_п$ – ускорение, с которым меняется напряжение; $ω_п$, $M_п$ – скорость и момент при $t = t_п$, т.е. в конце первого этапа. Отсчет времени на втором этапе пуска необходимо вести от $t_п$, тогда потери энергии

Рис. 6.1. Изменение скорости холостого хода и истинной скорости двигателя при спуске

Полагая $t_п \gt\gt T_м$ и допуская для упрощения линейную зависимость $ω(t)$, получаем

$ω(t) ≈ ε_п t - T_м ε_п$.

Кроме того,

$ω_0 - ω = T_м ε_п$;   $M = J dω/dt = J ε_п$;   $ε_п t_п ≈ ω_{0ном}$.

Тогда:

(6.18)

$ΔA_п = J ω_{0ном}^2 / 2 × 2 T_м / t_п$.

Сравнивая (6.5) и (6.10) можно отметить, что за счет медленного наращивания напряжения на двигателе можно существенно сократить потери на пуске.

В частотно-управляемом приводе с асинхронным двигателем потери определим ориентировочно аналитически, пренебрегая электромагнитными процессами. Примем, что процессы в приводе протекают с абсолютным скольжением меньше критического, т.е. $β \lt β_к$. При указанном ограничении потери можно найти из следующей системы уравнений:

(6.19)

$M = φ (β, α)$,   $M = M_с + J dω/dt$, $ω = ω_{1ном} (α - β)$,   $α = Ψ(t)$,

где $α = f_1 / f_{1ном}$ – относительная частота напряжения статора, $β = Δω/Δω_{1ном} = f_2 / f_{1ном}$ – абсолютное скольжение или относительная частота ротора. Уравнение движения, в свою очередь, можно выразить так:

(6.20)

$M = M_с + J ω_{1ном} dα/dt - J ω_{1ном} dβ/dt$.

Из (6.20) видно, что динамический момент представляется двумя составляющими:

(6.21)

$M_{дин~α} = J ω_{1ном} dα/dt = J ε$, $M_{дин~β} = J ω_{1ном} dβ/dt$,

где $ε = dω_1/dt$.

Момент двигателя при управлении с $β \lt β_к$ можно представить линейным уравнением

(6.22)

$M = k_β β$,

где $k_β = M_{ном} / s_{ном}$.

Учитывая из (6.19) третье уравнение и (6.22), получим выражение механической характеристики двигателя при частотном управлении

$M = k_β α - k_β ω / ω_{1ном}$

и уравнение движения

(6.23)

$k_β + J ω _{1ном} × dβ/dt = M_с + J × dω_1/dt$;

или

(6.24)

$k_β α (t) = M_с + k_β × ω / ω_{1ном} + J × dω/dt$.

Для линейного изменения частоты во времени, $ε = \const$, параметр абсолютного скольжения можно определить по формуле

(6.25)

$β = (M_с + J ε) / k_β × (1 - e ^{-t / T_м}) + β_с e ^{-t / T_м}$,

где $T_м = J ω_{1ном} s_{ном} / M_{ном}$; $β_с = M_с / k_β$.

Потери энергии при пуске

(6.26)

Зная зависимость $β=f(t)$, можно определить потери. Принимая для упрощения при пуске без нагрузки $t_п \gt\gt T_м$, получим $β=Jε/k_β$. Отсюда найдем

(6.27)

$Δ A_{п0} = J ω_{1ном}^2 / 2 × (1 + R_1 / R'_2) × 2 T_м / t_{п0}$.

Таким образом, формула (6.27) аналогична (6.18), что и следовало ожидать, и пуск двигателя при плавном наращивании частоты существенно уменьшает потери при пуске. Аналогично могут быть найдены потери при торможении.

6.2. Нагрев и охлаждение двигателей

6.2.1. Закон изменения температуры двигателей

Потери энергии вызывают нагрев двигателей. Допустимый нагрев определяется нагревостойкостью применяемых изоляционных материалов. Чем больше нагревостойкость, тем при той же мощности меньше размеры двигателя. Лучшему использованию двигателя способствует также более совершенная система его охлаждения.

Изоляционные материалы, применяемые в электрических машинах, делятся на ряд основных классов, обозначаемых A, E, B, F, H и C, с допустимой температурой от 105 до 180 °C.

Соблюдение допустимых ограничений по температуре обеспечивает заданный срок службы электродвигателей 15…20 лет. Превышение допустимых температур ведет к сокрушению срока эксплуатации. Так, для изоляции класса A превышение допустимой температуры нагрева на 8÷10 °C. сокращает срок службы изоляции вдвое.

Предельные температуры достигаются двигателем при номинальной нагрузке, температуре окружающей среды 40 °C и при высоте над уровнем моря до 1000 м. При более высокой температуре окружающей среды или при увеличении высоты нагрузка двигателя должна быть снижена относительно номинального значения. При выполнении оговоренных условий для двигателя нормируется не допустимая температура, а превышение температуры обмотки и других частей машины над температурой окружающей среды.

Условия нагрева различных частей машины различны. Большему нагреву подвергаются части обмоток, расположенных во внутренних частях машины. Так же не одинаково выделение теплоты в различных режимах работы. Эти обстоятельства весьма усложняют тепловые расчеты, и поэтому без соответствующих упрощений описать процессы нагрева и охлаждения двигателя сложно.

В последующем мы примем следующие допущения:

• двигатель рассматривается как однородное тело, обладающее бесконечно большой теплопроводностью, с одинаковой температурой во всех точках выделения тепла и точках, соприкасающихся с охлаждающей средой;
• передача тепла в окружающую среду пропорциональна разности температур двигателя и окружающей среды;
• температура окружающей среды постоянна;
• теплоемкость двигателя, потери и теплоотдача двигателя не зависят от температуры.

Уравнение теплового баланса двигателя при неизменных потерях имеет вид

(6.28)

$Q dt = A τ dt + C dτ$,

где $Q$ – количество теплоты, выделяемое двигателем в единицу времени, Дж/с; $A$ – теплоотдача двигателя – количество теплоты, отдаваемой двигателем в окружающую среду в единицу времени при разности температур в 1 °C, Дж/с°C; $τ$ – превышение температуры двигателя над температурой окружающей среды, °C:

$τ = Θ_д – Θ_{ос}$,

где $Θ_д,~Θ_{ос}$ – соответственно температуры двигателя и окружающей среды, °C; $C$ – теплоемкость двигателя – количество теплоты, необходимое для повышения температуры двигателя на 1 °C.

Уравнение (6.28) преобразуем к виду

$τ + T_н dτ/dt = τ_у$,

где $T_н$ – постоянная времени нагрева двигателя, $τ_у$ – установившееся значение превышения температуры двигателя над температурой окружающей среды:

$T_н = C / A$;   $τ_у = Q / A$.

Решение последнего уравнения имеет вид

(6.29)

$τ = τ_у (1 - e^{-t / T_н}) + τ_0 e^{-t / T_н}$,

где $τ_0$ – начальное значение превышения температуры двигателя над температурой окружающей среды.

Таким образом, кривая переходного процесса нагрева двигателя приближенно имеет вид экспоненты, как кривая изменения скорости двигателя постоянного тока при пуске без учета электромагнитной постоянной.

Действительная кривая нагрева несколько отличается от экспоненты. В начале процесса нагрева повышение температуры идет быстрее, чем по теоретической кривой, и лишь начиная с $τ=(0,5÷0,6)τ_у$ действительная кривая приближается к экспоненциальной. Поэтому определение постоянной времени нагрева на начальном участке по методу касательной может привести к ошибке.

Количественное значение тепловой постоянной определяется габаритами двигателя и его конструктивным исполнением. У исполнительных двигателей систем автоматики мощностью в несколько десятков или сотен ватт она может составлять десятки минут, у двигателей средней мощности открытого исполнения около 1 ч, у двигателей большой мощности открытого исполнения несколько часов. При отключении самовентилируемых двигателей постоянная времени охлаждения оказывается больше постоянной нагрева. Это объясняется ухудшением теплоотдачи, которое характеризуется коэффициентом ухудшения

$β = A_0 / A$,

где $A_0,~A$ – теплоотдача соответственно при неподвижном двигателе и при номинальной скорости.

Так как для принятого закона изменения температура двигателя теоретически достигнет установившегося значения при $t=∞$, практически нагрев считают законченным при $t=(3÷4)T_н$.

6.2.2. Нагрузочные диаграммы и режимы работы электроприводов

Для расчета тепловых режимов необходимо знать, как меняется во времени их нагрузка. Для этого используются нагрузочные диаграммы, характеризующие зависимость тока, момента или мощности, развиваемой двигателем от времени. Нагрузочная диаграмма электропривода учитывает статические и динамические нагрузки, преодолеваемые электроприводом в течение цикла работы механизма.

Статические нагрузки определяются на основании технологических данных, характеризующих работу того или иного класса механизмов, а динамические нагрузки оцениваются инерционными моментами, которые развиваются электроприводом для создания соответствующих угловых ускорений, обеспечивающих заданную производительность механизмов.

С точки зрения тепловых процессов различают восемь режимов работы электропривода с условными обозначениями от S1 до S8.

1. Продолжительным номинальным режимом работы (S1) называют режим работы двигателя при неизменной нагрузке, продолжающийся столько времени, что температура его перегрева достигнет установившегося значения (рис. 6.2, где $P,~ΔP$ – соответственно мощность на валу двигателя и мощность потерь).

Рис. 6.2. Зависимость мощностей и температуры перегрева двигателя в продолжительном режиме

2. Кратковременным номинальным режимом работы (S2) называют режим, при котором периоды неизменной номинальной нагрузки чередуются с периодами отключения; при этом в период нагрузки температура перегрева двигателя не достигает установившегося значения, а в период отключения его температура достигает температуры окружающей среды (рис. 6.3). В этом режиме принимаются стандартные продолжительности включения: $t_р=10,~30,~60$ и 90 мин.

Рис. 6.3. Зависимость мощностей и температуры от времени при кратковременном режиме работы

3. Повторно-кратковременным режимом работы называют режим, при котором кратковременные рабочие периоды неизменной номинальной нагрузки чередуются с периодами отключения (паузами), причем как рабочие периоды, так и паузы не настолько длительны, чтобы превышения температуры могли достигнуть установившихся значений (рис. 6.4).

Рис. 6.4. Зависимость мощностей и температуры при повторно-кратковременном режиме

В этом режиме продолжительность цикла не превышает 10 мин и режим характеризуется относительной продолжительностью включения ($ПВ$) в процентах, которая определяется по выражению

$ПВ = (t_р / t_ц) 100 %$.

Стандартные значения $ПВ = 15,~25,~40~и~60%$.

Рис. 6.4. Зависимость мощностей и температуры при повторно-кратковременном режиме

Остальные режимы в той или иной степени являются разновидностями перечисленных трех режимов: S4 – повторно-кратковременный режим с частыми пусками; S5 – повторно-кратковременный режим с частыми пусками и электрическим торможением; S6 – перемежающийся режим работы; S7 – перемежающийся режим с частыми реверсами; S8 – перемежающийся режим с двумя или более скоростями.

6.3. Расчет мощности двигателей по тепловым перегрузкам

В зависимости от режима работы привода осуществляется выбор двигателей по мощности и их расчет по тепловым нагрузкам. Рассмотрим наиболее характерные случаи.

6.3.1. Расчет мощности двигателя в продолжительном режиме работы. Метод эквивалентного тока, момента и мощности

Существует большое число приводов механизмов, работающих продолжительно с неизменной или мало меняющейся нагрузкой, т.е. в режиме S1. Это приводы ротора гироскопа, лентопротяжных механизмов, насосов, вентиляторов и др. Расчет мощности двигателя в таких приводах весьма прост, если известна требуемая мощность. Выбрав двигатель на указанную мощность можно быть уверенным, что он окажется полностью использованным по допустимому превышению температуры. Так как в продолжительном режиме двигатель пускается редко, то пусковые потери не могут сказаться на нагреве двигателя. Иногда, возможно, потребуется проверка двигателя на достаточность пускового момента, так как у некоторых механизмов он бывает повышен по отношению к номинальному.

При продолжительной переменной нагрузке, пример графика которой показан на рис. 6.5, предварительно выбранный для продолжительного режима работы двигатель необходимо проверить по нагреву путем определения наибольшего превышения температуры за цикл $τ_{max}$ и сравнить его с допустимым $τ_{доп}$. При этом должно выполняться условие $τ_{max} ≤ τ_{доп}$.

Рис. 6.5. Диаграмма изменения мощности и потерь двигателя при переменной нагрузке

Таким образом, для проверки двигателя по нагреву придется построить диаграмму нагрузки, определить потери на каждом интервале $t_i$ и по ним рассчитать с помощью уравнения (6.29) температуру перегрева в конце этого интервала. Учитывая, что многие из необходимых для этого параметров двигателя в каталогах не указываются, такой путь является довольно сложным и трудоемким.

На практике пользуются хотя и менее точными, но более простыми методами проверки. Наиболее часто она производится по методу средних или эквивалентных потерь. Сущность метода заключается в том, что превышение температуры двигателя при неизменной теплоотдаче определяется средними потерями за цикл:

(6.30)

,

где $ΔP_{i}$ – мощность потерь на $i$-м интервале; $t_i$ – продолжительность $i$-го интервала; $m$ – число интервалов в цикле; $t_ц$ – время цикла, по формуле

(6.31)

$τ_{кц} = ΔP_{ср} / A$.

Действительное максимальное превышение температуры отличается от вычисленного по выражению (6.31), но при $t_ц \lt\lt T_н$ и $q t_ц \gt 4T_н$, где $q$ – число циклов, это расхождение незначительно и только при соблюдении этих условий можно пользоваться методом средних потерь. При правильном выборе двигателя должно выполняться условие

(6.32)

$τ_{кц} ≤ τ_{доп} = τ_{ном}$.

В том случае, когда на протяжении цикла теплоотдача двигателя на отдельных интервалах различная, например, в случае изменения угловой скорости самовентилируемого двигателя, это необходимо учитывать коэффициентом ухудшения теплоотдачи.

Использование метода эквивалентных потерь неудобно тем, что не всегда удается их вычислить достаточно точно, поэтому вводятся понятия других эквивалентных величин – тока, момента и мощности. Переход к ним осуществляется следующим образом.

Подставим потери мощности в электродвигателе на каждом $i$-м интервале, выраженные согласно (6.1) и (6.2), в уравнение (6.30) и получим:

Подставим в (6.32) $τ_{кц}$ из (6.31), где $ΔP_{ср}$ определим согласно последнему уравнению, а $τ_{ном}$ представим в виде

$τ_{доп} = ΔP_н / A = (K + V_н) / A$.

Тогда условие проверки двигателя по нагреву получит вид:

(6.32.а)

.

Ток в левой части выражения (6.32) является эквивалентным действительному, изменяющемуся во времени току по условиям нагрева.

Часто для проверки двигателя по нагреву и, особенно, при предварительном его выборе приходится пользоваться графиками момента или мощности механизма. Принимая момент пропорциональным току, перейдем от эквивалентного тока к эквивалентному моменту:

(6.33)

.

Умножим обе части уравнения (6.33) на скорость и получим уравнение для эквивалентной мощности

(6.34)

.

Проверку или выбор двигателя по эквивалентному моменту или мощности осуществляем так же, как и по эквивалентному току – путем сравнения их с номинальным значением указанных величин.

6.3.2. Расчет мощности при кратковременном режиме работы (S2)

График работы двигателя в кратковременном режиме приведен на рис. 6.6. Исходя из определения этого режима, можно ограничиться рассмотрением одного периода работы двигателя. Превышение температуры определяется уравнением

$τ = τ_у (1 - e^{-t / T_н})$.

Рис. 6.6. График работы двигателя в кратковременном режиме

Если выбрать двигатель, предназначенный для продолжительного режима работы мощностью $P_{ср}$, то при кратковременном режиме работы превышение температуры не достигнет допустимого значения ($τ_{доп}$) (рис. 6.6, кривая 1). Поэтому в этом режиме двигатель оказывается недоиспользован по нагреву.

При заданной нагрузке и времени рабочего периода $t_р$ в тепловом отношении будет полностью использован двигатель меньшей мощности, превышение температуры которого ко времени $t_р$ будет равно $τ_{доп}$ (рис. 6.6, кривая 2). При этом двигатель будет кратковременно перегружаться, а установившаяся температура для него окажется равной $τ_у^1 \gt τ_у=τ_{доп}$. Перегрузка может быть значительной при малых $t_р$.

Соотношение между $τ_у^1$ и $τ_у$ может быть найдено из выражения

(6.35)

$τ_у = τ_у^1(1 - e ^{-t / T_{н~ср}})$,

где $T_{н~ср}$ – среднее значение постоянной времени нагрева в начале и в конце процесса нагрева, $τ_у=ΔP_{ном}/A$ и $τ_у^1=ΔP_{кр}/A$; $ΔP_{кр}$ – потери мощности в двигателе при нагрузке $P_{кр}$. Отношение потерь при кратковременной нагрузке к потерям при номинальной нагрузке при условии одинакового перегрева двигателя называется коэффициентом термической перегрузки. Значение этого коэффициента может быть получено из (6.35):

(6.36)

$p_т = ΔP_{кр} / ΔP_{ном} = 1 / (1 - e^{-t_р / T_{н~ср}})$.

По коэффициенту термической перегрузки можно найти коэффициент механической перегрузки, который представляет собой отношение момента при кратковременном режиме работы к моменту при продолжительном режиме работы при условии одинаковой температуры перегрева обмотки, т.е. $p_м=M_{кр}/M_{ном}$.

Раскроем в выражении (6.36) потери мощности через момент

(6.37)

$p_т = (K + V_н × (M_{кр} / M_н)^2) / (K + V_н) = (a + (p_м)^2) / (a + 1)$.

Отсюда, раскрывая $p_т$ по (6.36),

(6.38)

.

Пренебрегая постоянными потерями ($a = 0$), выражение (6.38) представим в виде

(6.39)

Если нагрузка на валу двигателя в процессе кратковременной работы меняется, то необходимо найти эквивалентные значения тока, момента или мощности. Отметим, что уже при отношении $t/T_{н~ср}≤0,35$ и допустимой перегрузке по нагреву коэффициент механической перегрузки становится равным 2,5, что для асинхронных двигателей уже недопустимо. Поэтому для кратковременного режима используют специальные двигатели с нормированной длительностью работы в 10, 30, 60 и 90 мин. Следовательно, выбранный по каталогу двигатель может быть загружен номинальной мощностью в течение указанного времени и будет полностью использоваться по нагреву.

Если же время работы двигателя отличается от каталожного, то можно найти нагрузку, при которой двигатель будет полностью использован по нагреву из следующих соображений.

Превышение температуры двигателя с номинальной нагрузкой и нормированным временем $t_{р~кат}$ равно

(6.40)

$τ_{доп} = ΔP_{ном} / A × (1 - e^{-t_{р~кат} / T_н})$.

В течение фактического времени $t_р$ с нагрузкой, отличной от номинальной, превышение температуры будет

(6.41)

$τ_{доп} = ΔP_{кр} / A × (1 - e^{-t_р / T_н})$,

где $ΔP_{кр}$ – потери при кратковременной нагрузке, отличной от номинальной.

Приравнивая правые части уравнений (6.40) и (6.41) и принимая во внимание выражение для коэффициента термической перегрузки (6.37), найдем

(6.42)

.

Если $t_р \lt t_{р~кат}$ – двигатель должен быть проверен по допустимой перегрузке.

Отметим, что двигатели, предназначенные для кратковременного режима, не могут быть использованы в длительном режиме, так как они имеют значительные постоянные потери.

6.3.3. Расчет мощности при повторно-кратковременном режиме работы (S3)

К такому виду могут быть сведены графики, имеющие чередование рабочего режима и режима паузы. Когда в рабочем режиме нагрузка меняется (для режимов S4, S5), необходимо воспользоваться формулами для эквивалентной нагрузки и привести график к простому виду (рис. 6.7).

Рис. 6.7. График работы двигателя в повторно-кратковременном режиме

В повторно-кратковременном режиме работы после окончания теплового переходного процесса колебания температуры осуществляются в пределах от $τ_0$ до $τ_у=τ_{доп}$.

Выбор мощности двигателя, если мы имеем стандартную продолжительность включения, не вызывает затруднения. Просто необходимо выбрать двигатель на заданный ток, момент или мощность, при имеющейся $ПВ$. Но, если фактическая продолжительность включения отличается от стандартной, требуется расчет. Здесь на основании метода эквивалентных потерь можно утверждать, что средняя температура перегрева двигателя при его работе с мощностью $P_1≠P_н$ при $ПВ_1≠ПВ_{ст}$ не будет превышать допустимую в том случае, если средние потери за цикл при $P_1$ и $ПВ_1$ не будут превышать средние потери за тот же цикл при $P_н$ и $ПВ_{ст}$, т.е. если

$(ΔP_1 t_{р1}) / (t_{р1} + t_{01}) ≤ (ΔP_н t_р) / (t_р + t_0)$,

или

$ΔP_1 ПВ_1 ≤ ΔP_н ПВ_{ст}$.

Отсюда условие выбора двигателя

(6.43)

$ΔP_н ≥ ΔP_1 × ПВ_1 / ПВ_{ст}$.

Если в выражении (6.43) выразить потери через постоянную и переменную составляющие, после преобразований получим уравнение для выбора двигателя по току

(6.44)

.

Для двигателей постоянного тока независимого возбуждения и асинхронных двигателей, работающих на линейном участке, аналогично могут быть представлены уравнения для выбора двигателей по моменту и мощности. Там вместо токов записываются соответствующие значения моментов и мощностей.

Уравнение (6.44) может быть использовано не только для пересчета двигателя при $ПВ$, отличающейся от стандартной, но и в случае использования в повторно-кратковременном режиме двигателя, предназначенного для длительного режима работы. Для этого достаточно принять в (6.44) $ПВ_{ст}=1$.

model.exponenta.ru

Нагревание и охлаждение электродвигателей

При работе любого электродвигателя часть поступающей к тему энергии затрачивается на потери, связанные с нагревом обмоток и магнитопроводов, трением в подшипниках и враща­ющихся частей о воздух. Хотя потери энергии в современных электродвигателях невелики, при их работе все же выделяется значительное количество тепла, что приводит к нагреву элек­тродвигателей. Различают постоянные и переменные потери в электрических машинах. Величина первых не зависит или мало зависит от нагрузки машины. К ним относятся потери на перемагничивание, на вихревые токи, на нагрев параллельных об­моток возбуждения и на трение (о воздух, в подшипниках, на щетках и т. п.). К переменным относят потери, пропорциональ­ные квадрату тока нагрузки. Это потери на нагрев обмотки якоря или статора), последовательных обмоток возбуждения, коллектора и т. п. На холостом ходу нагрев машин определяется постоянными потерями. По мере загрузки машины увеличиваются переменные потери и нагрев ее повышается.

Таким образом, вопросы нагрева электродвигателей имеют большое практическое значение, так как нагревом должна оп­ределяться допустимая нагрузка электродвигателя. Темпера­тура неработающей машины равна температуре окружающего воздуха. Если машина приведена в рабочее состояние и нагруз­ка на ,нее постоянна, то в каждую единицу времени в ней на­чинают выделяться определенные порции тепла. В начальный момент работы все выделенное в машине тепло почти полно­стью идет на ее нагрев, при этом повышается температура ма­шины, т. е. появляется температурный перепад ? между темпе­ратурой машины и температурой окружающей среды. При по­явлении температурного перепада машина начинает часть вы­деляющегося в ней тепла отдавать окружающей среде путем конвекции, лучеиспускания и теплопроводности.

Чем выше перепад ?, тем больше тепла машина будет отда­вать окружающей среде. Наконец, перепад достигает такого предельного значения ?пр, когда все выделяемое в машине тепло станет отводиться в окружающую среду и нагрев машины прекратится, т. е. ее температура достигнет значения, предель­ного для данной нагрузки.

В случае, когда нагрузка на машину превышает допусти­мую, установившаяся температура может оказаться слишком высокой и превысит допустимую. Установившаяся температу­ра работающей машины не должна превосходить величины, оп­ределяемой теплоемкостью ее изоляции.

Современные электроизоляционные материалы, используе­мые в электрических машинах, делятся на классы: А, В и др. К материалам класса А относятся хлопок, шелк и другие подоб­ные органические материалы, пропитанные специальными лака­ми или маслами, различные эмали. К материалам класса В отно­сятся материалы из слюды или асбеста, пропитанные органиче­скими связующими составами.

Для всех изоляционных материалов классов А и В ГОСТом установлены допускаемые превышения температуры при температуре охлаждающего воздуха +35°С. Номинальная мощность электродвигателей нормируется для температуры охлаждающего воздуха до 40°С. Если кран или другой механизм предназначается для работы при температуре окружающей среды более 40°С, при выборе электродвигателей нужно учи­тывать это обстоятельство и вводить соответствующую (поправку, повышающую мощность электродвигателей. В качестве первого приближения можно рекомендовать следующее эмпирическое правило: учитывать повышенную температуру воздуха, увели­чивая мощность выбираемого двигателя на 1% при повышении температуры воздуха на 1 ?С.

Для максимального использования (по тепловым возмож­ностям) всех применяемых в электродвигателе материалов не­обходимо, чтобы при полной нагрузке его отдельные части на­гревались до температур, близких к предельно допустимым. С этой же целью используется искусственное охлаждение элек­тродвигателей, позволяющее большую часть выделяющегося при работе машины тепла отдавать окружающей среде и тем самым повышать нагрузку без опасности разрушения изоляции машины. Большинство электродвигателей, используемых для привода подъемно-транспортных машин, оборудуется самовентиляцией. Лишь электродвигатели, работающие в особо тя­желых условиях, могут иметь независимую вентиляцию. В этом случае воздух через внутренние полости машины продувается независимым вентилятором.

Напрев электрической машины характеризует зависимость вида ? = f(t). Аналитическое определение этой зависимости за­труднено тем, что электрическая машина не является однород­ным телом. Отдельные ее части имеют различные теплоемкости, теплопроводности и теплоотдачу. Они по-разному нагреваются и по-разному отдают тепло окружающей среде. Если для упро­щения принять, что электрическая машина является однород­ным телом, то задача определения зависимости вида ? = f(t) может быть решена следующим образом.

Предварительно примем следующие обозначения:

? — температурный перепад, град;

q — количество тепла, выделяемого в машине, кал/сек;

с — теплоемкость машины, кал/град;

А — теплоотдача машины, кал/град • сек.

За время dt в машине выделится Q=qdt калорий тепла.

где Q1 — тепло, затрачиваемое за время dt на нагрев машины;

Q2 — тепло, отданное окружающей среде за это же время. За время dt температурный перепад машины возрастет на вели­чину d?. Следовательно,

Подставив эти выражения в уравнение (8), получим диф­ференциальное уравнение теплового баланса машины

Интеграл этого уравнения, решаемого относительно t,

Примем за начальные условия t = 0 и ? = ?0 (?0 — темпера­турный перепад машины). Тогда

Теперь выражение (12) примет вид

Подставив это выражение в уравнение (11) и произведя пре­образования, получим

Полученное уравнение и является аналитически выраженной зависимостью температурного перепада ? от времени t. Поло­жив в этом уравнении t = ? , получим значение ?пр:

Следовательно, величина предельного или установившегося пе­репада ?пр, а значит, и установившаяся температура машины зависят лишь от количества тепла, выделяемого в машине за единицу времени, и от ее теплоотдачи.

Величина входящая в показатель степени в уравнении (15), имеет размеренность времени и называется по­стоянной времени нагревания. Эта величина от нагрузки ма­шины не зависит и физически является тем временем, в течение которого машина достигла бы перегрева, равного предель­ному, при отсутствии теплоотдачи в окружающую среду. Зна­чение постоянной времени нагревания зависит от мощности и конструктивных особенностей машины и колеблется в пределах от 1 до 4 ч. Приближенно величину постоянной времени нагревания можно определить по эмпирической формуле:

где ?1, ?2 и ?3 — значения температуры машины, измеренные че­рез равные промежутки времени ?t.

Таким образом, уравнение (15) примет вид:

Из этого уравнения вытекает, что теоретически предельный перегрев достигается машиной по истечении бесконечно боль­шого периода времени.

Однако практически можно считать, что машина достигает предельного (установившегося) перегрева по истечении времени, равного (3?4)Т. Действительно, подставив в уравнение (18) значение t = 3Т, получим, что ? = 0,95?пр, а при t = 4Т ? = 0,98 ?пр

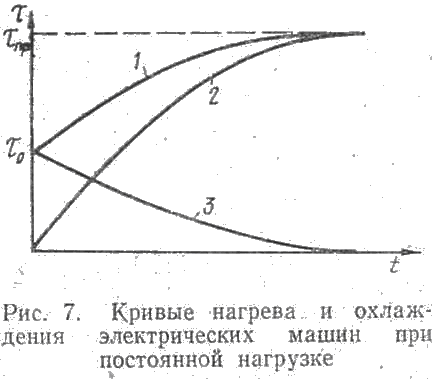
Кривая, соответствующая уравнению (18), называется экспонентой (рис. 7). Уравне­нию (18) соответствует кри­вая 1. Кривой 2 соответствует уравнение

которое можно получить, при­няв ?0=0. Кривые охлаждения электрических машин подобны кривым нагрева. Действитель­но, если выделение тепла в ма­шине прекратится (q = 0), то уравнения (15) и (18) примут вид:

которому соответствует кривая 3, представляющая собой кривую охлаждения машины от начального перегрева до нуля.

Следует иметь в виду, что значения Т в уравнениях (19) и (20) должны быть одинаковыми, если принять электрическую машину за однородное тело. В действительности же постоян­ная времени нагревания вращающейся машины меньше посто­янной времени охлаждения этой же машины и составляет в среднем 0,25?0,7 Тохл.

vdvizhke.ru

Тепло ДВС и ГТУ. Потери теплоты, отводимой системой охлаждения и уносимой с газами. Часть №2.

Содержание:

   2. ПОТЕРИ ТЕПЛОТЫ, ОТВОДИМОЙ СИСТЕМОЙ ОХЛАЖДЕНИЯ И УНОСИМОЙ С ГАЗАМИ

   Большее количество тепловой энергии отводится от двигателя в систему охлаждения и уносится с отработавшими газами. Отвод теплоты в систему охлаждения необходим для того, чтобы воспрепятствовать пригоранию поршневых колец, обгоранию седел клапанов, задиру и заклиниванию поршня, растрескиванию головок цилиндров, возникновению детонации и т. п.

   Время сгорания очень мало, но за этот период давление газов значительно возрастает, а температура достигает 2 300 – 2 500 °С. При сгорании в цилиндре интенсивно протекают процессы перемещения газов, способствующие теплоотдаче в стенки цилиндра. Теплоту, сэкономленную в этой фазе рабочего цикла, можно преобразовать в полезную работу в течение последующего хода расширения. При сгорании около 6 % тепловой энергии, содержащейся в топливе, теряется из-за теплопередачи стенкам камеры сгорания и цилиндра.

   В течение хода расширения стенкам цилиндра передается около 7 % тепловой энергии топлива. При расширении поршень перемещается из ВМТ в НМТ и постепенно освобождает все большую поверхность стенок цилиндра. Однако лишь около 20 % теплоты, сэкономленной даже при продолжительном по времени ходе расширения, можно преобразовать в полезную работу.

   Около половины теплоты, отводимой в систему охлаждения, приходится на такт выпуска. Отработавшие газы выходят из цилиндра с большой скоростью и имеют высокую температуру. Часть их теплоты отводится в систему охлаждения через выпускной клапан и выпускной канал головки цилиндра. Непосредственно за клапаном поток газов изменяет направление почти на 90°, при этом возникают вихри, что интенсифицирует теплоотдачу в стенки выпускного канала.

   Отработавшие газы необходимо отводить из головки цилиндра кратчайшим путем, так как переданная ей их теплота заметно нагружает систему охлаждения и для ее отвода в окружающий воздух требуется использование части эффективной мощности двигателя. В период выпуска газов в систему охлаждения отводится около 15 % теплоты, содержащейся в топливе. Тепловой баланс бензинового двигателя приведен на рисунке №1.

Рисунок №1. Тепловой баланс бензинового двигателя, 

где 32% - теплота, преобразованная в полезную работу; 

28% - теплота, отведённая в систему охлаждения; 

2% - теплота, возникшая при трении поршня; 

38% - теплота, отведённая с отработавшими газами.

   У дизельного двигателя условия отвода теплоты другие. Вследствие более высокой степени сжатия температура газов на выходе из цилиндра гораздо ниже. По этой причине количество теплоты, отведенное во время хода выпуска, меньше и составляет в ряде случаев около 25 % всей теплоты, отданной в систему охлаждения. 

   Давление и температура газов при сгорании в дизеле выше, чем у бензинового двигателя. Совместно с большими скоростями вращения газов в цилиндре эти факторы способствуют увеличению количества теплоты, передаваемой стенкам камеры сгорания. В процессе сгорания эта величина составляет около 9 %, а при ходе расширения - 6 %. За время хода выпуска в систему охлаждения отводится 9 % энергии, содержащейся в топливе. Тепловой баланс дизельного двигателя приведён на рисунке №2. 

Рисунок №2. Тепловой баланс дизельного двигателя,

где 45% - теплота, преобразованная в полезную работу; 

23% - теплота, отведённая в систему охлаждения; 

2% - теплота, возникшая при трении поршня; 

30% - теплота, отведённая с отработавшими газами.

   Теплота, возникающая при трении поршня о стенки цилиндра у бензинового двигателя, составляет около 1,5 %, а у дизеля - около 2 % от ее общего количества. Эта теплота также отводится в систему охлаждения. Следует учесть, что приведенные примеры представляют результаты измерений, выполненных на исследовательских одноцилиндровых двигателях, и могут характеризовать двигатели, работающие в автомобильной технике, для привода различных агрегатов, в том числе и для привода электрогенераторов в мини-ТЭЦ, лишь приблизительно. Однако эти данные могут быть вполне использованы для оценочного расчета тепловых потерь. 

   Системой охлаждения отводится от 23 до 32% теплоты, которая подводится с топливом в двигатель. Сюда входит как непосредственно теплота, возникшая при горении топлива, так и теплота, возникшая при трении поршня о цилиндр двигателя, что требует обеспечения хорошего смазывания этой трущейся пары. Температура масла при этом не должна превышать допустимых границ, что ограничивает в свою очередь температуру стенки цилиндра. Для современных моторных масел температура стенки цилиндра не должна быть выше 220 °С, в то время как температура газов в цилиндре при сгорании и ходе расширения на порядок выше, и цилиндр по этой причине необходимо охлаждать. 

     Другая проблема связана с поддержанием нормальной температуры выпускного клапана. Прочность стали при высокой температуре падает. При использовании специальных сталей в качестве материала выпускного клапана его максимально допустимая температура может быть доведена до 900 °С.

   Для того, чтобы охлаждающая жидкость смогла отвести все необходимое тепло от двигателя, её температура, как на входе, так и на выходе должна находится в строго определённых температурных границах. По различным сведениям на сегодняшний момент температура охлаждающей жидкости на выходе из двигателя должна быть не выше 90 … 110 °С для различных моделей. Превышение этой температуры может привести к аварийному останову двигателя. В свою очередь температура охлаждающей жидкости на выходе зависит от её температуре на входе, что характеризует работу системы охлаждения охлаждающей жидкости. 

     Наравне с системой охлаждения большое количество теплоты, подведённой с топливом в двигатель, уносится выхлопными газами. На сегодняшний день большей части эту теплоту используют для отопления, а также для работы турбонаддува. 

     Подогрев воздуха отработавшими газами в газовоздушном теплообменнике системы отопления опасен из-за возможности прогорания или негерметичности его трубок. Поэтому для переноса теплоты используют масло или другую незамерзающую жидкость, нагреваемую отработавшими газами.

   Еще целесообразнее использовать отработавшие газы для привода вентилятора системы охлаждения. При больших нагрузках двигателя отработавшие газы имеют наиболее высокую температуру, а двигатель нуждается в интенсивном охлаждении. Поэтому использование турбины, работающей на отработавших газах для привода вентилятора системы охлаждения, весьма целесообразно и в настоящее время начинает находить применение. Такой привод может автоматически регулировать охлаждение, хотя это достаточно дорого.

   Основным способом использования энергии отработавших газов служит их расширение в турбине, которая, как говорилось выше, наиболее часто используется для привода центробежного компрессора наддува двигателя Ее можно использовать также и для других целей, например, для упомянутого привода вентилятора. Однако использование энергии выхлопных газов для срабатывании их в турбине ведёт к тому, что их температура уменьшается. 

   Степень наддува зависит от назначения двигателя. При более высоких давлениях наддува воздух в компрессоре сильно нагревается и на входе в двигатель и его необходимо охлаждать, что также требует теплообменного оборудования. В настоящее время турбонаддув применяют в основном в дизелях, повышение мощности которых на 25 – 30 % не требует большого форсирования по давлению наддува, и охлаждение двигателя при этом не вызывает трудностей. Такой способ повышения мощности дизеля применяют чаще всего.

© Н.Д. Денисов-Винский

www.denisov-vinskiy.ru

Потери теплоты, отводимой в систему охлаждения и уносимой с отработавшими газами

Автор: Юлиюс Мацкерле (Julius Mackerle)Источник: «Современный экономичный автомобиль» [1] 12482 0 Большая часть тепловой энергии отводится от двигателя в систему охлаждения и уносится с отработавшими газами. Отвод теплоты в систему охлаждения необходим для того, чтобы воспрепятствовать пригоранию поршневых колец, обгоранию сёдел клапанов, задиру и заклиниванию поршня, растрескиванию головок цилиндров, возникновению детонации и т. п. Для отвода теплоты в атмосферу часть эффективной мощности двигателя расходуется на привод вентилятора и водяного насоса. При воздушном охлаждении мощность, расходуемая на привод вентилятора, выше из-за необходимости преодоления большого аэродинамического сопротивления, создаваемого оребрением головок и цилиндров. Для снижения потерь важно выяснить, сколько теплоты необходимо отводить в систему охлаждения двигателя и каким способом можно уменьшить это количество. Г. Рикардо уделял этому вопросу большое внимание уже на начальном этапе развития двигателестроения. На экспериментальном одноцилиндровом двигателе с раздельными системами охлаждения для головки блока цилиндра и для цилиндра проводились опыты по измерению количества теплоты, отводимой в эти системы. Измерялось также количество теплоты, отводимой охлаждением в течение отдельных фаз рабочего цикла. Время сгорания очень мало, но за этот период давление газов значительно возрастает, а температура достигает 2300—2500 °C. При сгорании в цилиндре интенсивно протекают процессы перемещения газов, способствующие теплоотдаче в стенки цилиндра. Теплоту, сэкономленную в этой фазе рабочего цикла, можно преобразовать в полезную работу в течение последующего хода расширения. При сгорании около 6 % тепловой энергии, содержащейся в топливе, теряется из-за теплопередачи стенкам камеры сгорания и цилиндра. В течение хода расширения стенкам цилиндра передается около 7 % тепловой энергии топлива. При расширении поршень перемещается из ВМТ в НМТ и постепенно освобождает все большую поверхность стенок цилиндра. Однако лишь около 20 % теплоты, сэкономленной даже при продолжительном по времени ходе расширения, можно преобразовать в полезную работу. Около половины теплоты, отводимой в систему охлаждения, приходится на такт выпуска. Отработавшие газы выходят из цилиндра с большой скоростью и имеют высокую температуру; часть их теплоты отводится в систему охлаждения через выпускной клапан и выпускной канал головки цилиндра. Непосредственно за клапаном поток газов изменяет направление почти на 90°, при этом возникают вихри, что интенсифицирует теплоотдачу в стенки выпускного канала. Отработавшие газы необходимо отводить из головки цилиндра кратчайшим путем, так как переданная ей их теплота заметно нагружает систему охлаждения и для ее отвода в окружающий воздух требуется использование части эффективной мощности двигателя. В период выпуска газов в систему, охлаждения отводится около 15 % теплоты, содержащейся в топливе. Тепловой баланс бензинового двигателя приведен в табл. 1. Табл. 1 Тепловой баланс бензинового двигателя Составляющие теплового баланса Доля в балансе, % Теплота, преобразованная в полезную работу 32 Теплота, отведённая в систему охлаждения в фазе сгорания 6 28 при ходе расширения 7 при ходе выпуска 15 Теплота, отведённая с отработавшими газами и излучением 40 Итого 100 У дизельного двигателя условия отвода теплоты другие. Вследствие более высокой степени сжатия температура газов на выходе из цилиндра гораздо ниже. По этой причине количество теплоты, отведенное во время хода выпуска, меньше и составляет в ряде случаев около 25 % всей теплоты, отданной в систему охлаждения. Давление и температура газов при сгорании в дизеле выше, чем у бензинового двигателя. Совместно с большими скоростями вращения газов в цилиндре эти факторы способствуют увеличению количества теплоты, передаваемой стенкам камеры сгорания. В процессе сгорания эта величина составляет около 9 %, а при ходе расширения — 6 %. За время хода выпуска в систему охлаждения отводится 9 % энергии, содержащейся в топливе. Тепловой баланс дизеля приведен в табл. 2. Табл. 2 Тепловой баланс дизеля Составляющие теплового баланса Доля в балансе, % Теплота, преобразованная в полезную работу 45 Теплота, отведённая в систему охлаждения в фазе сгорания 8 23 при ходе расширения 6 при ходе выпуска 9 Теплота, возникающая при трении поршня 2 Теплота, отведённая с отработавшими газами и излучением 30 Итого 100 Теплота, возникающая при трении поршня о стенки цилиндра у бензинового двигателя, составляет около 1,5 %, а у дизеля — около 2 % от её общего количества. Эта теплота также отводится в систему охлаждения. Следует учесть, что приведённые примеры представляют результаты измерений, выполненных на исследовательских одноцилиндровых двигателях, и не характеризуют автомобильные двигатели, а служат лишь для демонстрации различий в тепловых балансах бензинового двигателя и дизеля. Теплота, отводимая в систему охлаждения Системой охлаждения отводится около 33 % тепловой энергии, содержащейся в используемом топливе. Уже на заре развития двигателей внутреннего сгорания начались поиски путей преобразования хотя бы части теплоты, отводимой в систему охлаждения, в эффективную мощность двигателя. В то время широко и достаточно эффективно применялся паровой двигатель с теплоизолированным цилиндром и поэтому, естественно, стремились применить этот метод теплоизоляции и для двигателя внутреннего сгорания. Опыты в этом направлении проводили крупные специалисты, такие, например, как Р. Дизель. Однако в ходе опытов выявились значительные проблемы. В применяемом в двигателях внутреннего сгорания кривошипном механизме давление газов на поршень и сила инерции поступательно-движущихся масс прижимают поршень к стенке цилиндра, что при высокой скорости поршня требует обеспечения хорошего смазывания этой трущейся пары. Температура масла при этом не должна превышать допустимых границ, что ограничивает в свою очередь температуру стенки цилиндра. Для современных моторных масел температура стенки цилиндра не должна быть выше 220 °C, в то время как температура газов в цилиндре при сгорании и ходе расширения на порядок выше, и цилиндр по этой причине необходимо охлаждать. Другая проблема связана с поддержанием нормальной температуры выпускного клапана. Прочность стали при высокой температуре падает. При использовании специальных сталей в качестве материала выпускного клапана его максимально допустимая температура может быть доведена до 900 °C. Температура газов в цилиндре при сгорании достигает 2500—2800 °C. Если бы теплота, передаваемая стенкам камеры сгорания и цилиндра, не отводилась, то их температура превысила бы допустимые значения для материалов, из которых изготовлены эти детали. Теплота, отводимая охлаждением через стенки камеры сгорания, рассчитывается по формуле Q = S∙Δt∙α∙τ, где S — площадь охлаждаемой поверхности, м2; Δt — перепад температур между стенкой камеры сгорания и газом, °C; α — коэффициент теплоотдачи, Дж/м2∙с∙град.; τ — время, с. Установить значение α — коэффициента теплоотдачи от газов к стенкам достаточно сложно, поскольку он в значительной мере зависит от скорости газа около стенки. В камере сгорания определить эту скорость практически невозможно, так как она меняется в течение всего рабочего цикла. Точно так же сложно определить перепад температур между стенкой цилиндра и воздухом. При впуске и в начале сжатия воздух холоднее, чем стенки цилиндра и камеры сгорания, и поэтому теплота передается от стенки воздуху. Начиная с некоторого положения поршня при такте сжатия, температура воздуха становится выше температур стенок, и тепловой поток изменяет направление, т. е. теплота передается от воздуха стенкам цилиндра. Расчет теплопередачи при таких условиях представляет собой задачу большой сложности. Резкие изменения температуры газов в камере сгорания оказывают влияние и на температуру стенок, которая на поверхности стенок и глубине менее 1,5—2 мм колеблется в течение одного цикла, а глубже — устанавливается на некотором среднем значении. При расчетах теплопередачи именно это среднее значение температуры нужно принимать для наружной поверхности стенки цилиндра, с которой теплота передается охлаждающей жидкости. Поверхность камеры сгорания включает в себя не только принудительно охлаждаемые детали, но и днище поршня, тарелки клапанов. Теплоотдача в стенки камеры сгорания тормозится слоем нагара, а в стенки цилиндра — масляной пленкой. Головки клапанов должны быть плоскими, чтобы под воздействием горячих газов находилась минимальная площадь. При открывании впускной клапан охлаждается потоком входящего заряда, тогда как выпускной клапан в процессе работы сильно нагревается отработавшими газами. Стержень этого клапана защищен от воздействия горячих газов длинной направляющей, доходящей почти до его тарелки. Как уже отмечалось, максимальная температура выпускного клапана ограничена температурной прочностью материала, из которого он изготовлен. Теплота от клапана отводится главным образом через его седло к охлаждаемой головке цилиндра и отчасти через направляющую, которую также необходимо охлаждать. У выпускных клапанов, работающих в тяжелых температурных условиях; стержень делается полым и частично заполняется натрием. Когда клапан нагрет, натрий находится в жидком состоянии, и поскольку он не заполняет всю полость стержня; то при движении клапана интенсивно перемещается в ней, отводя тем самым теплоту от тарелки клапана к его направляющей и далее — в охлаждающую среду. Тарелка выпускного клапана имеет наименьший перепад температур с газами в камере сгорания и поэтому при сгорании ему передается относительно небольшое количество теплоты. Однако при открывании выпускного клапана теплопередача от потока отработавших газов к тарелке клапана весьма велика, что и определяет его температуру. Отвод теплоты в воздух и его регулирование Отвод теплоты системой охлаждения вызывает не только потери тепловой энергии, которая могла бы быть реализована в работу, но также и прямые потери части эффективной мощности двигателя, вследствие привода вентилятора и водяного насоса. Отвод теплоты с охлаждаемой поверхности S в воздушную среду зависит от перепада температур между этой поверхностью и воздухом Δt, а также от коэффициента теплоотдачи охлаждающей поверхности в воздух α. Этот коэффициент не меняется сколько-нибудь значительно независимо от того, образована ли охлаждающая поверхность пластинами радиатора системы жидкостного охлаждения или ребрами деталей двигателя воздушного охлаждения. Прежде всего, рассмотрим двигатели с системами жидкостного охлаждения. Количество охлаждающего воздуха тем меньше, чем больше теплоты отводится в единицу его объема, т. е. чем больше будет нагреваться охлаждающий воздух. Это требует равномерного распределения воздуха по всей охлаждающей поверхности и максимального перепада температур между, ней и воздухом. В радиаторе системы жидкостного охлаждения создаются условия, при которых охлаждаемая поверхность имеет почти равномерное поле температур, а температура охлаждающего воздуха по мере движения его через радиатор постепенно, повышается, достигая максимального значения на выходе из него. Перепад температур между воздухом и охлаждаемой поверхностью постепенно, уменьшается. На первый взгляд кажется, что предпочтителен глубокий радиатор, поскольку в нем воздух нагревается больше, однако следует рассмотреть этот вопрос с энергетической позиции. Коэффициент теплоотдачи поверхности α представляет собой сложную зависимость от ряда факторов, однако наибольшее влияние на его величину оказывает скорость потока воздуха около охлаждающей поверхности. Связь между ними можно представить, соотношением α ~ v0,6–0,7. При увеличении скорости воздуха на 10 %, отвод теплоты увеличивается лишь на 7 %. Скорость потока воздуха пропорциональна его расходу через радиатор. Если конструкция радиатора не меняется, то для увеличения количества отводимого тепла на 7 % следует увеличить частоту вращения вентилятора на 10 %, поскольку подаваемое вентилятором количество воздуха прямо зависит от нее. Давление воздуха при постоянной площади сечения вентилятора зависит от второй степени его частоты вращения, а мощность привода вентилятора пропорциональна ее третьей степени. Таким образом, при увеличении частоты вращения вентилятора на 10 % мощность привода увеличивается на 33 %, что имеет отрицательные последствия, проявляющиеся в ухудшении механического КПД двигателя. Зависимость количества охлаждающего воздуха от количества отводимой теплоты, а также от увеличения давления воздуха и мощности привода вентилятора показана на рис. 1. С позиции уменьшения затрат энергии эта номограмма очень полезна. Если лобовую поверхность радиатора увеличить на 7 %, то пропорционально увеличиваются площади проходного сечения и охлаждающей поверхности радиатора, и, следовательно, количество охлаждающего воздуха достаточно увеличить на те же 7 %, чтобы отвести на 7 % больше теплоты, т. е. как и в описанном выше примере. При этом мощность вентилятора повышается лишь на 22,5 % вместо 33 %. Если расход воздуха через вентилятор Vz0,5 увеличить на 20 % (точка и стрелки 1 на рис. 1), то количество отведенной теплоты Q, пропорциональное Vz0,5 возрастет на 11,5 %. Изменение расхода воздуха увеличением частоты вращения вентилятора на те же 20 % приводит к увеличению давления воздушного потока на 44 %, а мощность привода вентилятора — на 72,8 %. Для увеличения теплоотвода на 20 % тем же путем следует увеличить расход воздуха на 35,5 % (точка и пунктирные стрелки 2 на рис. 1), что влечет за собой рост давления воздуха на 84 %, а мощность привода вентилятора — почти в 2,5 раза (на 149 %). Поэтому выгоднее увеличить лобовую поверхность радиатора, чем при тех же радиаторе и вентиляторе увеличивать частоту вращения последнего. Рис. 1 Зависимость относительных величин отводимой теплоты Q, напора h и мощности привода Nv вентилятора от относительного расхода воздуха Vz. Если радиатор разделить по его глубине на две равные части, то в передней перепад температур Δt1 будет больше, чем в задней Δt2, и, следовательно, передняя часть радиатора будет охлаждаться воздухом сильнее. Два радиатора, получаемые при разделении одного на две части, по глубине будут иметь меньшие сопротивления потоку охлаждающего воздуха. Поэтому слишком глубокий радиатор невыгоден для применения. Радиатор должен быть изготовлен из материала с хорошей теплопроводностью и его сопротивления потокам воздуха и жидкости должны быть небольшими. Масса радиатора и объем находящейся в нем жидкости должны быть также невелики, так как это важно для быстрого прогрева двигателя и включения системы отопления в автомобиле. Для современных легковых автомобилей с низкой передней частью кузова требуются радиаторы небольшой высоты. Для минимизации энергетических затрат важно достичь высокого КПД вентилятора, для чего используется направляющий воздуховод, имеющий небольшой зазор по наружному диаметру крыльчатки вентилятора. Крыльчатка вентилятора часто делается из пластмассы, что гарантирует точную форму профиля лопаток, их гладкую поверхность и малую шумность. При высоких частотах вращения такие лопатки деформируются, снижая тем самым расход воздуха, что весьма целесообразно. Высокая температура радиатора повышает его КПД. Поэтому в настоящее время применяют герметизированные радиаторы, избыточное давление в которых повышает температуру кипения охлаждающей жидкости и, следовательно, температуру всей матрицы радиатора, который может быть меньших размеров и более легким. Для двигателя воздушного охлаждения действуют те же закономерности, что и для двигателя жидкостного охлаждения. Разница состоит в том, что ребра деталей двигателя воздушного охлаждения имеют более высокую температуру, чем матрица радиатора, поэтому на отвод такого же количества теплоты при воздушном охлаждении требуется меньшее количество охлаждающего воздуха. Это преимущество имеет большое значение при эксплуатации автомобилей в условиях жаркого климата. В табл. 3 приведены режимы работы двигателей жидкостного и воздушного охлаждения при изменении температуры окружающего воздуха от 0 до 50 °C. Для двигателя жидкостного охлаждения степень охлаждения уменьшается на 45,5 %, тогда как у двигателя воздушного охлаждения в тех же условиях — только на 27,8 %. Для двигателя жидкостного охлаждения это означает более громоздкую и более энергоемкую систему охлаждения. Для двигателя воздушного охлаждения достаточна небольшая переделка вентилятора. Табл. 3 Эффективность охлаждения двигателя системами жидкостного и воздушного охлаждения в зависимости от внешней температуры Вид охлаждения Жидкостная Воздушная Температура охлаждающей поверхности, °C 110 180 Температура охлаждающего воздуха, °C 0 0 Разница температур, °C 110 180 Температура охлаждающего воздуха, °C 50 50 Разница температур, °C 60 130 Ухудшение режима при температуре 50 °C по сравнению с 0 °C, % 45,5 27,5 Регулирование охлаждения дает большую экономию энергии. Охлаждение можно отрегулировать так, чтобы оно было удовлетворительным при максимальной нагрузке двигателя и при максимальной температуре воздуха. Но при более низкой температуре окружающей среды и частичной нагрузке двигателя такое охлаждение, естественно, является избыточным и для снижения износа и механического КПД двигателя необходимо вновь отрегулировать охлаждение. У двигателей жидкостного охлаждения это обычно делают дросселированием потока жидкости через радиатор. В этом случае потребляемая мощность вентилятора не изменяется, и с энергетической точки зрения такое регулирование не приносит никакой выгоды. Например, для охлаждения двигателя мощностью 50 кВт при температуре 30 °C расходуется 2,5 кВт, а при температуре 0 °C и нагрузке двигателя 50 % от полной потребовалось бы лишь 0,23 кВт. При условии, что требуемое количество охлаждающего воздуха пропорционально перепаду температур между поверхностью радиатора и воздухом, при 50 %-ной нагрузке двигателя для его охлаждения достаточно также половины расхода воздуха, регулируемого частотой вращения вентилятора. Экономия энергии и, следовательно, расхода топлива при таком регулировании может быть достаточно значительной. Поэтому регулированию охлаждения в настоящее время уделяется особое внимание. Наиболее удобное регулирование — изменение частоты вращения вентилятора, но для его осуществления необходимо иметь регулируемый привод. Отключение привода вентилятора преследует ту же цель, что и изменение его частоты вращения. Для этого удобно применять электромагнитную муфту, включаемую термостатом в зависимости от температуры жидкости (или головки цилиндра). Если муфта включается термостатом, то регулирование осуществляется не только в зависимости от температуры окружающей среды, но и от нагрузки двигателя, что весьма эффективно. Выключение вентилятора при помощи вязкостной муфты производится несколькими способами. В качестве, примера рассмотрим вязкостную муфту фирмы «Холсет» (США). При наиболее простом способе используется ограничение передаваемого момента. Поскольку с ростом частоты вращения момент, необходимый для вращения, вентилятора, увеличивается, то увеличивается также и пробуксовка вязкостной муфты, и при некотором значении потребляемой мощности вентилятора его частота вращения уже более не повышается (рис. 2). Частота вращения вентилятора с нерегулируемым клиноременным приводом от коленчатого вала двигателя увеличивается пропорционально частоте вращения двигателя (кривая Б), тогда как в случае привода вентилятора через вязкостную муфту его частота вращения растет лишь до величины nv = 2500 мин-1 (кривая А). Мощность, потребляемая вентилятором с нерегулируемым приводом, растет пропорционально третьей степени частоты вращения и на режиме максимальной мощности составляет 8,8 кВт. У вентилятора, приводимого через вязкостную муфту, частота вращения увеличивается, как отмечено, до 2500 мин-1, и требуемая на режиме мощность вентилятора составляет 2 кВт. Поскольку в вязкостной муфте при 50 %-ной пробуксовке в теплоту дополнительно рассеивается еще 1 кВт, то общая экономия энергии на приводе вентилятора составляет 5,8 кВт, однако и это снижает расход топлива. Такое регулирование охлаждения можно считать удовлетворительным, так как расход воздуха не растет прямо пропорционально частоте вращения двигателя и, кроме того, с повышением скорости движения сохраняется рост скоростного напора воздуха, содействующего охлаждению двигателя. Рис. 2 Изменение частоты вращения и мощности, потребляемой вентилятором при использовании вязкостной муфты:nh — частота вращения двигателя; nv — частота вращения вентилятора; Nv — мощность, потребляемая вентилятором; А — привод вентилятора через вязкостную муфту; Б — нерегулируемый клиноременный привод вентилятора. Другой тип вязкостной муфты фирмы «Холсет» обеспечивает регулирование теплового режима двигателя дополнительно и от температуры окружающего воздуха (рис. 3). От ранее рассмотренной эта муфта отличается тем, что объем жидкости в ней, передающий крутящий момент, зависит от внешней температуры. Картер муфты разделен перегородкой 5 (см. рис. 4) на камеру ведущего диска 1 и камеру резервного объема 2, соединенные между собой клапаном 3. Клапан управляется биметаллическим термостатом 4 в зависимости от температуры воздуха. Черпачок 6, прижатый к диску пружиной, служит для сброса жидкости с диска и ускорения перетекания ее из камеры диска в объем 2. Часть жидкости постоянно находится в камере ведущего диска и способна передавать вентилятору небольшой крутящий момент. При температуре воздуха 40 °C, например, максимальная частота вращения вентилятора составляет 1300 мин-1, а потребляемая мощность — не более 0,7 кВт. При нагревании двигателя биметаллический термостат открывает клапан, и часть жидкости поступает в камеру ведущего диска. По мере роста проходного сечения клапана поступающее в камеру диска количество жидкости увеличивается и при полном открытии клапана уровень её в обеих половинах одинаков. Изменение передаваемого при этом крутящего момента и частоты вращения вентилятора показано кривыми А2 (см. рис. 3). Рис. 3 Изменение частоты вращения и мощности, потребляемой вентилятором, в зависимости от внешней температуры воздуха при использовании вязкостной муфты «Холсет Т 60» с биметаллическим термостатом:nh — частота вращения двигателя; nv — частота вращения вентилятора; Nv — мощность, потребляемая вентилятором; А1 — привод вентилятора через вязкостную муфту при холодном двигателе; А2 — привод вентилятора через вязкостную муфту при прогретом двигателе; Б — нерегулируемый клиноременный привод вентилятора. В этом случае максимальная частота вращения вентилятора составляет 3200 мин-1, а потребляемая мощность увеличивается до 3,8 кВт. Максимальное открытие клапана соответствует температуре окружающего воздуха, равной 65 °C. Описанным регулированием охлаждения двигателя можно снизить расход топлива в легковых автомобилях на 1 л/100 км. Рис. 4 Схема работы вязкостной муфты «Холсет Т 60» с биметаллическим термостатом:1 — ведущий диск; 2 — камера резервного объема; 3 — клапан; 4 — термостат; 5 — перегородка; 6 — черпачок. Мощные двигатели имеют еще более совершенные системы регулирования охлаждения. У дизелей «Татра» привод вентилятора осуществляется через гидромуфту, объем масла, в которой регулируется термостатом в зависимости от температур отработавших газов и окружающего воздуха. Показания датчика температуры в выпускном трубопроводе зависят в основном от нагрузки двигателя и, в меньшей степени, от его частоты вращения. Запаздывание этого датчика очень невелико, поэтому регулирование охлаждения с его помощью более совершенно. Регулирование охлаждения частотой вращения вентилятора относительно легко осуществляется в двигателе внутреннего сгорания любого типа; при этом уменьшается общий шум, издаваемый автомобилем. При переднем расположении двигателя поперек автомобиля механический привод вентилятора вызывает некоторые трудности и поэтому чаще применяют электропривод вентилятора. В этом случае регулирование охлаждения весьма упрощается. Вентилятор с электроприводом не должен иметь большой потребляемой мощности, поэтому стремятся использовать эффект охлаждения скоростным напором воздуха при движении автомобиля, поскольку с увеличением нагрузки двигателя скорость легкового автомобиля и, следовательно, скоростной напор обтекающего его воздуха растут. Электропривод вентилятора работает только в течение короткого времени при преодолении затяжных подъемов или же при высокой температуре окружающего воздуха. Расход охлаждающего воздуха через вентилятор регулируется включением электродвигателя с помощью термостата. Если радиатор расположен далеко от двигателя, например в автобусе с задним расположением двигателя, то вентилятор обычно имеет гидрообъемный привод. Приводимый двигателем автобуса гидронасос подает масло под давлением в поршневой гидродвигатель с качающейся шайбой. Такой привод более сложен и его применение целесообразно в двигателях большой мощности. Использование теплоты, уносимой с отработавшими газами Отработавшие газы двигателя содержат значительное количество тепловой энергии. Ее можно использовать, например, для отопления автомобиля. Подогрев воздуха отработавшими газами в газовоздушном теплообменнике системы отопления опасен из-за возможности прогорания или негерметичности его трубок. Поэтому для переноса теплоты используют масло или другую незамерзающую жидкость, нагреваемую отработавшими газами. Еще целесообразнее использовать отработавшие газы для привода вентилятора системы охлаждения. При больших нагрузках двигателя отработавшие газы имеют наиболее высокую температуру, а двигатель нуждается в интенсивном охлаждении. Поэтому использование турбины, работающей на отработавших газах для привода вентилятора системы охлаждения, весьма целесообразно и в настоящее время начинает находить применение. Такой привод может автоматически регулировать охлаждение, хотя это достаточно дорого. Более приемлемым с точки зрения стоимости можно считать эжекционное охлаждение. Отработавшие газы отсасывают из эжектора охлаждающий воздух, который смешивается с ними и отводится в атмосферу. Такое устройство дешево и надежно, так как не имеет никаких движущихся деталей. Пример эжекционной системы охлаждения показан на рис. 5. Рис. 5 Схема эжекторного охлаждения Эжекционное охлаждение было с успехом применено в гоночных автомобилях «Татра» и в некоторых специализированных автомобилях. Недостатком системы является высокий уровень шума, так как отработавшие газы необходимо непосредственно подводить в эжектор, а расположение глушителя шума за ним вызывает трудности. Но основным способом использования энергии отработавших газов является наддув двигателя (см. по ссылке турбонаддув и динамический наддув). Отработавшие газы расширяются в турбине, которая наиболее часто используется для привода центробежного компрессора, также её можно применить и для других целей, например, для упомянутого привода вентилятора; в турбокомпаундных двигателях она непосредственно соединяется с коленчатым валом двигателя. В двигателях, использующих в качестве топлива водород, теплоту отработавших газов, а также отведенную в систему охлаждения можно использовать для нагревания гидридов, извлекая тем самым содержащийся в них водород. При таком способе эта теплота аккумулируется в гидридах, и при новой заправке гидридных баков водородом она может быть использована в различных целях для нагревания воды, отопления зданий и т. д. Последнее обновление 02.03.2012Опубликовано 29.09.2011 Читайте также Свойства водорода Плотность энергии в единице массы у водорода уникальна, поэтому он может быть отличным аккумулятором и с успехом применяться в двигателях внутреннего сгорания, газовых турбинах, двигателях Стирлинга и других источниках механической энергии. Паровой двигатель За время своего развития паровые машины значительно усовершенствовались, поэтому на них было обращено внимание при поиске замены двигателя внутреннего сгорания. Сноски ↺ Мацкерле Ю. Современный экономичный автомобиль/Пер. с чешск. В. Б. Иванова; Под ред. А. Р. Бенедиктова. - М.: Машиностроение, 1987. - 320 с.: ил.//Стр. 154 - 164 (книга есть в библиотеке сайта). – Прим. icarbio.ru Комментарии

icarbio.ru

---

Смотрите также

• 
  G4Ea двигатель
• 
  G4Cs двигатель
• 
  Многофазный двигатель
• Двигатель многофазный
• 
  Двигатель 306dt
• 
  F14D двигатель
• 
  490Bpg двигатель
• 
  Двигатель 490bpg
• 
  Радиоактивный двигатель
• 
  Двигатель х5м
• K10A двигатель