Коэффициент полезного действия определяется как отношение полезной, или отдаваемой, мощности P2 к потребляемой мощности P1:
 | (1) |
или в процентах
 | (2) |
Современные электрические машины имеют высокий коэффициент полезного действия (к. п. д.). Так, у машин постоянного тока мощностью 10 кВт к. п. д. составляет 83 – 87%, мощностью 100 кВт – 88 – 93% и мощностью 1000 кВт – 92 – 96%. Лишь малые машины имеют относительно низкие к. п. д.; например, у двигателя постоянного тока мощностью 10 Вт к. п. д. 30 – 40%.
 |
| Рисунок 1. Зависимость коэффициента полезного действия электрической машины от нагрузки |
Кривая к. п. д. электрической машины η = f(P2) сначала быстро растет с увеличением нагрузки, затем к. п. д. достигает максимального значения (обычно при нагрузке, близкой к номинальной) и при больших нагрузках уменьшается (рисунок 1). Последнее объясняется тем, что отдельные виды потерь (электрические Iа2rа и добавочные) растут быстрее, чем полезная мощность.
Прямой метод определения к. п. д. по экспериментальным значениям P1 и P2 согласно формуле (1) может дать существенную неточность, поскольку, во-первых, P1 и P2 являются близкими по значению и, во-вторых, их экспериментальное определение связано с погрешностями. Наибольшие трудности и погрешности вызывает измерение механической мощности.
Если, например, истинные значения мощности P1 = 1000 кВт и P2 = 950 кВт могут быть определены с точностью 2%, то вместо истинного значения к. п. д.
η = 950/1000 = 0,95
можно получить
или
Поэтому ГОСТ 25941-83, "Машины электрические вращающиеся. Методы определения потерь и коэффициента полезного действия", предписывает для машин с η% ≥ 85% косвенный метод определения к. п. д., при котором по экспериментальным данным определяется сумма потерь pΣ.
Подставив в формулу (1) P2 = P1 - pΣ, получим
 | (3) |
Применив здесь подстановку P1 = P2 + pΣ, получим другой вид формулы:
 | (4) |
Так как более удобно и точно можно измерять электрические мощности (для двигателей P1 и для генераторов P2), то для двигателей более подходящей является формула (3) и для генераторов формула (4). Методы экспериментального определения отдельных потерь и суммы потерь pΣ описываются в стандартах на электрические машины и в руководствах по испытанию и исследованию электрических машин. Если даже pΣ определяется со значительно меньшей точностью, чем P1 или P2, при использовании вместо выражения (1) формул (3) и (4) получаются все же значительно более точные результаты.
Различные виды потерь различным образом зависят от нагрузки. Обычно можно считать, что одни виды потерь остаются постоянными при изменении нагрузки, а другие являются переменными. Например, если генератор постоянного тока работает с постоянной скоростью вращения и постоянным потоком возбуждения, то механические и магнитные потери являются также постоянными. Наоборот, электрические потери в обмотках якоря, добавочных полюсов и компенсационной изменяются пропорционально Iа², а в щеточных контактах – пропорционально Iа. Напряжение генератора при этом также приблизительно постоянно, и поэтому с определенной степенью точности P2 ∼ Iа.
Таким образом, в общем, несколько идеализированном случае можно положить, что
или
где коэффициент нагрузки
Kнг = I / Iн = P2 / P2н | (6) |
Определяет относительную величину нагрузки машины.
Суммарные потери также можно выразить через kнг:
pΣ = p0 + kнг × p1 + kнг² × p2, | (7) |
где p0 – постоянные потери, не зависящие от нагрузки; p1 – значение потерь, зависящих от первой степени kнг при номинальной нагрузке; p2 – значение потерь, зависящих от квадрата kнг, при номинальной нагрузке.
Подставим P2 из (5) и pΣ из (7) в формулу к. п. д.
Тогда
 | (8) |
Установим, при каком значении kнг к. п. д. достигает максимального значения, для чего определим производную dη/dkнг по формуле (8) и приравняем ее к нулю:
Это уравнение удовлетворяется, когда его знаменатель равен бесконечности, т. е. при kнг = ∞. Этот случай не представляет интереса. Поэтому необходимо положить равным нулю числитель. При этом получим
Таким образом, к. п. д. будет максимальным при такой нагрузке, при которой переменные потери kнг² × p2, зависящие от квадрата нагрузки, становятся равными постоянным потерям p0.
Значение коэффициента нагрузки при максимуме к. п. д., согласно формуле (9),
 | (10) |
Если машина проектируется для заданного значения ηмакс, то, поскольку потери kнг × p1 обычно относительно малы, можно считать, что
p0 + p2 ≈ pΣ = const.
Изменяя при этом соотношение потерь p0 и p2, можно достичь максимального значения к. п. д. при различных нагрузках. Если машина работает большей частью при нагрузках, близких к номинальной, то выгодно, чтобы значение kнг [смотрите формулу (10)] было близко к единице. Если машина работает в основном при малых нагрузках, то выгодно, чтобы значение kнг [смотрите формулу (10)] было соответственно меньше.
Источник: Вольдек А. И., "Электрические машины. Учебник для технических учебных заведений" – 3-е издание, переработанное – Ленинград: Энергия, 1978 – 832с.
Видео 1. Общее определение коэффициента полезного действия
www.electromechanics.ru
Физика — это наука, которая изучает процессы, происходящие в природе. Наука эта очень интересная и любопытная, ведь каждому из нас хочется удовлетворить себя ментально, получив знания и понимание того, как и что в нашем мире устроено. Физика, законы которой выводились не одно столетие и не одним десятком ученных, помогает нам с этой задачей, и мы должны только радоваться и поглощать предоставленные знания.
Но в то же время физика — наука далеко непростая, как, собственно, и сама природа, но разобраться в ней было бы очень интересно. Сегодня мы будем говорить о коэффициенте полезного действия. Мы узнаем, что такое КПД и зачем он нужен. Рассмотрим все наглядно и интересно.
Расшифровка аббревиатуры — коэффициент полезного действия. Однако и такое толкование с первого раза может оказаться не особо понятным. Этим коэффициентом характеризуется эффективность системы или какого-либо отдельного тела, а чаще — механизма. Эффективность характеризуется отдачей или преобразованием энергии.
Этот коэффициент применим практически ко всему, что нас окружает, и даже к нам самим, причём в большей степени. Ведь совершаем мы полезную работу все время, только вот как часто и насколько это важно, уже другой вопрос, с ним и используется термин «КПД».
Важно учесть, что этот коэффициент — величина неограниченная, она, как правило, представляет собой либо математические значения, к примеру, 0 и 1, либо же, как это чаще бывает — в процентах.
В физике этот коэффициент обозначается буквой Ƞ, или, как её привыкли называть, Эта.
При использовании каких-либо механизмов или устройств мы обязательно совершаем работу. Она, как правило, всегда больше той, что необходима нам для выполнения поставленной задачи. Исходя из этих фактов различается два типа работы: это затраченная, которая обозначается большой буквой, А с маленькой з (Аз), и полезная — А с буквой п (Ап). Для примера, возьмем такой случай: у нас есть задача поднять булыжник определенной массой на определенную высоту. В этом случае работа характеризует только преодоление силы тяжести, которая, в свою очередь, действует на груз.
В случае когда для подъема применяется какое-либо устройство, кроме силы тяжести булыжника, важно учесть еще и силу тяжести частей этого устройства. И кроме всего этого, важно помнить, что, выигрывая в силе, мы всегда будем проигрывать в пути. Все эти факты приводят к одному выводу, что затрачиваемая работа в любом варианте окажется больше полезной, Аз > Ап, вопрос как раз заключается в том, насколько её больше, ведь можно максимально сократить эту разницу и тем самым увеличить КПД, наш или нашего устройства.
Полезная работа — это часть затрачиваемой, которую мы совершаем, используя механизм. А КПД — это как раз та физическая величина, которая показывает, какую часть составляет полезная работа от всей затраченной.
Итог:
Существует определенная формула для нахождения КПД. Она звучит следующим образом: чтобы найти КПД в физике, нужно количество энергии разделить на проделанную системой работу. То есть КПД — это отношение затраченной энергии к выполненной работе. Отсюда можно сделать простой вывод, что тем лучше и эффективнее система или тело, чем меньше энергии затрачивается на выполнение работы.
Сама формула выглядит кратко и очень просто Ƞ будет равняться A/Q. То есть Ƞ = A/Q. В этой краткой формулы и фиксируют нужные нам элементы для вычисления. То есть A в этом случае является использованной энергией, которая потребляется системой во время работы, а большая буква Q, в свою очередь, будет являться затраченной A, или опять же затраченной энергией.
В идеале КПД равен единице. Но, как это обычно бывает, он её меньше. Так происходит по причине физики и по причине, конечно же, закона о сохранении энергии.
Все дело в том, что закон сохранения энергии предполагает, что не может быть получено больше А, чем получено энергии. И даже единице этот коэффициент будет равняться крайне редко, поскольку энергия тратится всегда. И работа сопровождается потерями: к примеру, у двигателя потеря заключается в его обильном нагреве.
Итак, формула КПД:
Ƞ=А/Q, где
Примечательно, что КПД не существует как понятие нейтральное, для каждого процесса есть свой КПД, это не сила трения, он не может существовать сам по себе.
Рассмотрим несколько из примеров процессов с наличием КПД.
К примеру, возьмем электрический двигатель. Задача электрического двигателя — преобразовывать электрическую энергию в механическую. В этом случае коэффициентом будет являться эффективность двигателя в отношении преобразования электроэнергии в энергию механическую. Для этого случая также существует формула, и выглядит она следующим образом: Ƞ=P2/P1. Здесь P1 — это мощность в общем варианте, а P2 — полезная мощность, которую вырабатывает сам двигатель.
Нетрудно догадаться что структура формулы коэффициента всегда сохраняется, меняются в ней лишь данные, которые нужно подставить. Они зависят от конкретного случая, если это двигатель, как в случае выше, то необходимо оперировать затрачиваемой мощностью, если работа, то исходная формула будет другая.
Теперь мы знаем определение КПД и имеем представление об этом физическом понятии, а также об отдельных его элементах и нюансах. Физика — это одна из самых масштабных наук, но её можно разобрать на маленькие кусочки, чтобы понять. Сегодня мы исследовали один из этих кусочков.
Это видео поможет вам понять, что такое КПД.
liveposts.ru
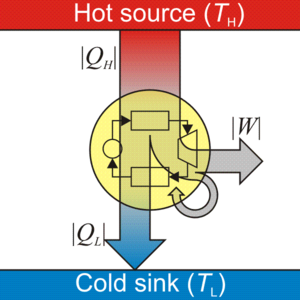
Баланс энергии за цикл можно получить на основе первого закона термодинамики. Рабочему телу передано путем теплообмена количество теплоты Q1, и над ним совершена работа A2. Рабочее тело совершило работу при расширении A1 и передало количество теплоты Q2 холодильнику. Для идеального теплового двигателя изменение внутренней энергии ΔU = 0, ибо рабочее тело вернулось в исходное состояние.
\(~Q_1 + A_2 = Q_2 + A_1 .\)Отсюда
\(~A = A_1 - A_2 = Q_1 - Q_2 .\)Отношение полезной работы к количеству теплоты, которое рабочее тело получило от нагревателя, называется коэффициентом полезного действия теплового двигателя (КПД):
\(~\eta = \frac{A}{Q_1} = \frac{Q_1 - Q_2}{Q_1} = 1 -\frac{Q_2}{Q_1} . \qquad (1)\)Из формулы (1) видно, что даже у идеального теплового двигателя η < 1. Наибольший КПД, как показал впервые С. Карно, можно получить для идеального двигателя в случае, если рабочее тело совершает цикл Карно с тем же нагревателем и холодильником. Цикл Карно состоит из двух изотермических (рис. 3 — кривые 1-2 и 3-4) и двух адиабатных (кривые 2-3 и 4-1) процессов:
\(~\eta_{max} = \frac{T_1 - T_2}{T_1} . \qquad (2)\)
Рис. 3
Из формулы (2) видно, что для повышения КПД необходимо увеличивать T1 и уменьшать T2. Так как холодильником в большинстве случаев служит окружающая среда, то основной способ повышения КПД состоит в повышении температуры нагревателя.
Цикл Карно — идеальный цикл. В реальных циклах нельзя осуществить идеальную адиабатность и изотермичность. Кроме того, не устранимы потери на трение. Поэтому КПД в реальных тепловых двигателях всегда меньше, чем рассчитанный по формуле (2).
Из формул (1) и (2) имеем
\(~1 - \frac{Q_2}{Q_1} = 1 - \frac{T_2}{T_1} \Rightarrow \frac{Q_2}{Q_1} = \frac{T_2}{T_1} \Rightarrow \frac{Q_1}{T_1} = \frac{Q_2}{T_2} .\)где Q2 — количество теплоты, отданной рабочим телом холодильнику, поэтому оно отрицательно.
Следовательно, можно записать алгебраическую сумму:
\(~\frac{Q_1}{T_1} + \frac{Q_2}{T_2} = 0 .\)Величина \(~\frac QT\) называется приведенным количеством теплоты.
Следовательно, в цикле Карно сумма приведенных количеств теплоты равна нулю.
Строгий теоретический анализ показывает, что не только для цикла Карно, а для любого обратимого кругового процесса сумма приведенных количеств теплоты равна нулю. Это значит, что в обратимом процессе сохраняется некоторая величина, изменение которой равно приведенному количеству теплоты:
\(~\Delta S = \frac QT .\)Как показал Р. Клаузиус, S — это энтропия.
Следовательно, в обратимых процессах энтропия не изменяется. При необратимых процессах энтропия замкнутой и адиабатически изолированной системы возрастает: ΔSнеобр > 0.
В общем случае: при любых процессах, протекающих в замкнутой или адиабатически изолированной макроскопической системе, ее энтропия не убывает, т.е. ΔS ≥ 0.
Это заключение можно рассматривать как наиболее общую формулировку второго начала термодинамики.
Из формулы (2) имеем \(~\eta = 1 - \frac{T_2}{T_1}\). Следовательно, видим, что η < 1. КПД был бы η = 1, если бы температура холодильника была равна абсолютному нулю: T2 = 0 К. Но еще в 1912 г. немецкий физик В. Нернст теоретически доказал невозможность достижения такой температуры. Это утверждение называют третьим началом термодинамики; абсолютный нуль темпера туры недостижим; к нему можно лишь асимптотически приближаться.
Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — C. 163-165.
www.physbook.ru
Работу многих видов машин охарактеризовывает таковой принципиальный показатель, как КПД термического мотора. Инженеры с каждым годом стремятся создавать более совершенную технику, которая при наименьших издержек горючего давала бы наибольший итог от его использования.
До того как разбираться в том, что такое КПД (коэффициент полезного деяния), нужно осознать, как работает этот механизм. Без познания принципов его деяния нельзя узнать суть этого показателя. Термическим движком именуют устройство, которое совершает работу благодаря использованию внутренней энергии. Неважно какая термическая машина, превращающая термическую энергию в механическую, употребляет термическое расширение веществ при повышении температуры. В твердотельных движках может быть не только лишь изменение объема вещества, да и формы тела. Действие такового мотора подчинено законам термодинамики.
Для того чтоб осознать, как работает термический движок, нужно разглядеть базы его конструкции. Для функционирования прибора нужны два тела: горячее (нагреватель) и прохладное (холодильник, охладитель). Принцип деяния термических движков (КПД термических движков) находится в зависимости от их вида. Часто холодильником выступает конденсатор пара, а нагревателем — хоть какой вид горючего, сгорающий в топке. КПД безупречного термического мотора находится по таковой формуле:
КПД = (Тнагрев. — Тхолод.)/ Тнагрев. х 100%.
При всем этом КПД реального мотора никогда не сумеет превысить значения, приобретенного согласно этой формуле. Также этот показатель никогда не превзойдет вышеупомянутого значения. Чтоб повысить КПД, в большинстве случаев наращивают температуру нагревателя и уменьшают температуру холодильника. Оба эти процесса будут ограничены реальными критериями работы оборудования.
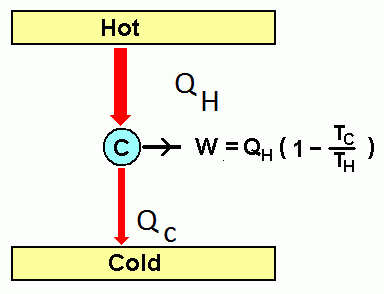
При функционировании термического мотора совершается работа, по мере которой газ начинает терять энергию и охлаждается до некоторой температуры. Последняя, обычно, на несколько градусов выше окружающей атмосферы. Это температура холодильника. Такое особое устройство создано для остывания с следующей конденсацией отработанного пара. Там, где имеются конденсаторы, температура холодильника время от времени ниже температуры среды.
В термическом движке тело при нагревании и расширении не способно дать всю свою внутреннюю энергию для совершения работы. Какая-то часть теплоты будет передана холодильнику вкупе с выхлопными газами либо паром. Эта часть термический внутренней энергии безизбежно пропадает. Рабочее тело при сгорании горючего получает от нагревателя определенное количество теплоты Q1. При всем этом оно еще совершает работу A, в процессе которой передает холодильнику часть термический энергии: Q2<Q1.
КПД охарактеризовывает эффективность мотора в сфере преобразования и передачи энергии. Этот показатель нередко измеряется в процентах. Формула КПД:
η*A/Qx100 %, где Q — затраченная энергия, А — нужная работа.
Исходя из закона сохранения энергии, можно прийти к выводу, что КПД будет всегда меньше единицы. Другими словами, полезной работы никогда не будет больше, чем на нее затрачено энергии.
КПД мотора — это отношение полезной работы к энергии, сообщенной нагревателем. Его можно представить в виде таковой формулы:
η = (Q1-Q2)/ Q1, где Q1 — теплота, приобретенная от нагревателя, а Q2 — отданная холодильнику.
Работа, совершаемая термическим движком, рассчитывается по таковой формуле:
A = |QH| — |QX|, где А — работа, QH — количество теплоты, получаемое от нагревателя, QX — количество теплоты, отдаваемое охладителю.
КПД термического мотора (формула):
|QH| — |QX|)/|QH| = 1 — |QX|/|QH|
Он приравнивается отношению работы, которую совершает движок, к количеству приобретенной теплоты. Часть термический энергии при этой передаче пропадает.
Наибольшее КПД термического мотора отмечается у прибора Карно. Это обосновано тем, что в обозначенной системе он зависит только только от абсолютной температуры нагревателя (Тн) и охладителя (Тх). КПД термического мотора, работающего по циклу Карно, определяется по последующей формуле:
(Тн — Тх)/ Тн = — Тх — Тн.
Законы термодинамики позволили рассчитать наибольший КПД, который вероятен. В первый раз этот показатель вычислил французский ученый и инженер Сади Карно. Он вымыслил термическую машину, которая работала на безупречном газу. Она работает по циклу из 2 изотерм и 2 адиабат. Принцип ее работы достаточно прост: к сосуду с газом подводят контакт нагревателя, вследствие чего рабочее тело расширяется изотермически. При всем этом оно работает и получает определенное количество теплоты. После сосуд теплоизолируют. Невзирая на это, газ продолжает расширяться, но уже адиабатно (без термообмена с окружающей средой). В это время его температура понижается до характеристик холодильника. В этот момент газ контактирует с холодильником, вследствие чего дает ему определенное количество теплоты при изометрическом сжатии. Позже сосуд опять теплоизолируют. При всем этом газ адиабатно сжимается до начального объема и состояния.
В наше время существует много типов термических движков, которые работают по различным принципам и на различном горючем. У всех у их собственный КПД. К ним относятся последующие:
• Бензиновый двигатель (поршневой), представляющий из себя механизм, где часть хим энергии сгорающего горючего перебегает в механическую энергию. Такие приборы могут быть газовыми и жидкостными. Различают 2- и 4-тактные движки. У их может быть рабочий цикл непрерывного деяния. По способу изготовления консистенции горючего такие движки бывают карбюраторными (с наружным смесеобразованием) и дизельными (с внутренним). По видам преобразователя энергии их делят на поршневые, реактивные, турбинные, комбинированные. КПД таких машин не превосходит показателя в 0,5.
• Движок Стирлинга — прибор, в каком рабочее тело находится в замкнутом пространстве. Он является разновидностью мотора наружного сгорания. Принцип его деяния основан на повторяющемся охлаждении/нагреве тела с получением энергии вследствие конфигурации его объема. Это один из самых действенных движков.
• Турбинный (роторный) движок с наружным сгоранием горючего. Такие установки в большинстве случаев встречаются на термических электростанциях.
• Турбинный (роторный) ДВС употребляется на термических электростанциях в пиковом режиме. Не так очень всераспространен, как другие.
• Турбиновинтовой движок за счет винта делает некую часть тяги. Остальное он получает за счет выхлопных газов. Его конструкция представляет собой роторный движок (газовая турбина), на вал которого насаживают воздушный винт.
• Ракетные, турбореактивные и реактивные движки, которые получают тягу за счет отдачи выхлопных газов.
• Твердотельные движки употребляют в качестве горючего жесткое тело. При работе меняется не его объем, а форма. При эксплуатации оборудования употребляется максимально малый перепад температуры.
Может быть ли увеличение КПД термического мотора? Ответ необходимо находить в термодинамике. Она изучает обоюдные перевоплощения различных видов энергии. Установлено, что нельзя всю имеющуюся термическую энергию конвертировать в электронную, механическую и т. п. При всем этом преобразование их в термическую происходит без каких-то ограничений. Это может быть из-за того, что природа термический энергии базирована на неупорядоченном (беспорядочном) движении частиц.
Чем посильнее разогревается тело, тем резвее будут двигаться составляющие его молекулы. Движение частиц станет еще больше хаотичным. Вместе с этим все знают, что порядок можно просто перевоплотить в хаос, который очень тяжело упорядочить.
www.tipsboard.ru
