







В термодинамических циклах поршневых ДВС процессы сжатия и расширения рабочего тела принимаются адиабатными, а рабочим телом является идеальный газ. Различают термодинамические циклы поршневых ДВС с изохорным подводом теплоты – цикл Отто (рис. 3а), изобарным подводом теплоты – цикл Дизеля (рис. 3б) и со смешанным подводом теплоты – цикл Сабатэ–Тринклера (рис. 3в).
Основными характеристиками термодинамических циклов поршневых ДВС являются:

Рис. 3. Термодинамические циклы поршневых ДВС:
а) Отто, б) Дизеля, в) Сабатэ–Тринклера
Термический КПД цикла ДВС со смешанным подводом теплоты определяется по соотношению
 . (36)
. (36)
Анализ соотношения (36) свидетельствует, что термический КПД цикла возрастает с повышением степени сжатия  , показателя адиабаты
, показателя адиабаты , степени повышения давления
, степени повышения давления и с уменьшением степени предварительного расширения
и с уменьшением степени предварительного расширения .
.
При одинаковых исходных значениях параметров рабочего тела и степени сжатия справедливо следующее неравенство:
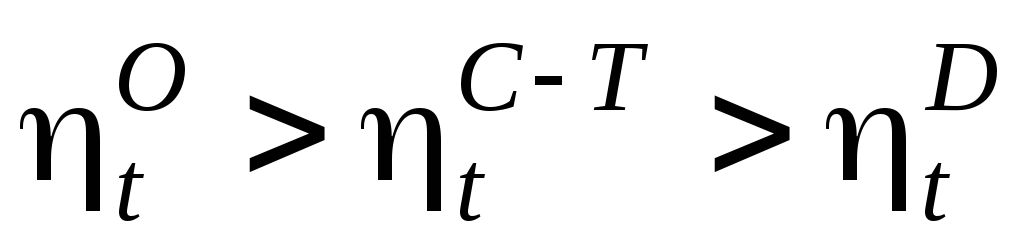 . (37)
. (37)
В то же время следует отметить, что более корректно проводить сравнение значений термического коэффициента полезного действия циклов в условиях одинаковых максимальных параметров рабочего тела ( ,
,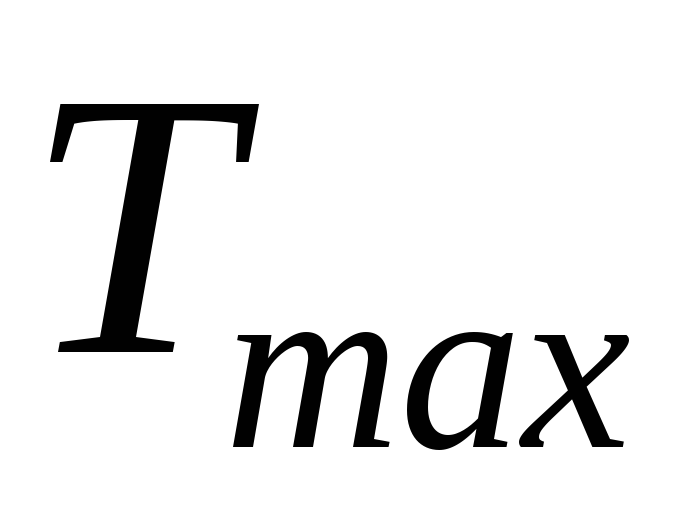 ).
).
В этом случае справедливо неравенство
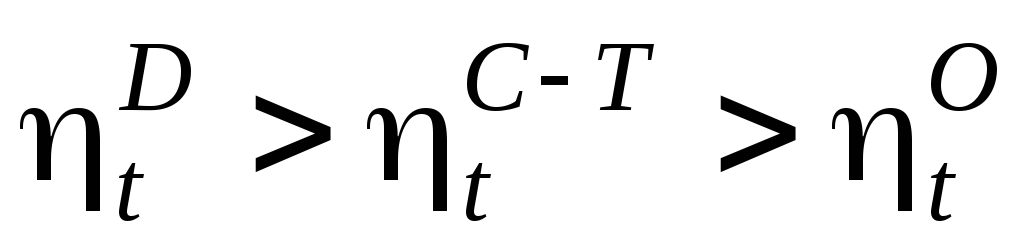 . (37а)
. (37а)
Термический КПД циклов ДВС может достигать 60–65%.
В реальных двигателях внутреннего сгорания, вследствие необратимых потерь работы, действительный КПД меньше термического и в среднем составляет 30-40% для дизелей и 20-30% для карбюраторных двигателей.
Различают два термодинамических цикла ГТУ: циклы с изобарным подводом теплоты – цикл Брайтона (рис. 4а) и с изохорным подводом теплоты – цикл Гемфри (рис. 4б).

Рис. 4. Термодинамические циклы ГТУ:
а) Брайтона, б) Гемфри
Основными характеристиками термодинамических циклов ГТУ являются:
Термический коэффициент полезного действия цикла Гемфри может быть определен из соотношения
 , (38)
, (38)
а термический КПД цикла Брайтона по формуле
 . (39)
. (39)
Сопоставление значений термических КПД циклов газотурбинных установок при одинаковых исходных параметрах и степени повышения давления рабочего тела в процессе сжатия показывает, что
 . (40)
. (40)
Следует отметить, что циклы поршневых ДВС характеризуются изохорным отводом, а циклы ГТУ – изобарным отводом теплоты.
В реальных ГТУ и ДВС процессы сжатия и расширения не являются адиабатными. С достаточной для технических расчетов точностью их можно считать политропными с постоянными показателями политропы.
studfiles.net
Двигатели внутреннего сгорания (ДВС) со смешанным подводом теплоты являются главными двигателями подавляющего большинства (95%) морских судов. Для исследования цикла такого ДВС решим ряд задач.
Задача 1. Для цикла ДВС со смешанным подводом теплоты заданы начальные параметры рабочего тела: р1 = 0,095 МПа, t1 = 40°С и характеристики цикла: ε = 14, λ = 1,35, ρ = 1,6.
Изобразить цикл на рабочей и тепловой диаграммах. Определить параметры в характерных точках цикла, работы расширения, сжатия и полезную, количества подводимой, отводимой и превращаемой в работу теплоты, а также термический КПД цикла.
Решение.

Рис. 2.1. Термодинамический цикл ДВС со смешанным подводом теплоты на рабочей и тепловой диаграммах: 1-2 – адиабатное сжатие, 2-3 – изохорный подвод теплоты, 3-4 – изобарный подвод теплоты, 4-5 – адиабатное расширение, 5-1 – изохорный отвод теплоты.
В курсе термодинамики полагают, что рабочим телом ДВС является идеальный газ со свойствами воздуха. Поскольку воздух является смесью двухатомных газов, его теплоёмкости cv и cp и показатель адиабаты k равны
 ;
;
 ;
;
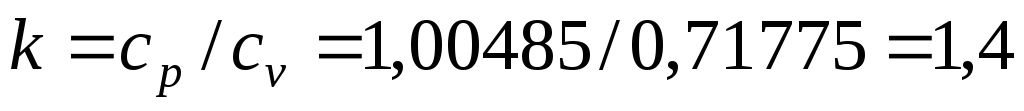 .
.
Значение удельного объема в точке 1 определяем по уравнению состояния идеального газа
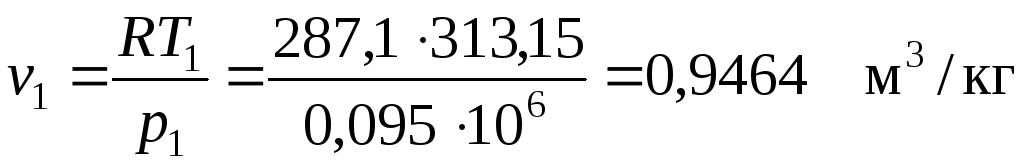 .
.
Точка 2. Рассчитываем значение v2 из определения степени сжатия
 .
.
Температуру рассчитываем по уравнению изоэнтропы
 .
.
Давление определяем из уравнения состояния идеального газа
 .
.
Точка 3. При изохорном подводе теплоты значение удельного объема v3= =v2 = 0,0676 м3/кг. Давление и температуру определяем, зная степень повышения давления λ
р3 = р2·λ = 3,822·1,45 = 5,160 МПа,
Т3 = Т2λ = 899,92·1,35 = 1214,89 К.
Точка 4. При изобарном подводе теплоты значение давления р4 = р3 = =5,160 МПа. Удельный объем и температуру рассчитываем, используя значение степени предварительного расширения ρ
v4 = v3ρ = 0,0676·1,6 = 0,1082 м3/кг
Т4 = Т3ρ = 1214,89·1,6 = 1943,82 К
Точка 5. Значение удельного объема в конце адиабатного расширения принимаем из принципа построения термодинамического цикла ДВС v5 = v1= =0,9464 м3/кг. Температуру рассчитываем по уравнению изоэнтропы
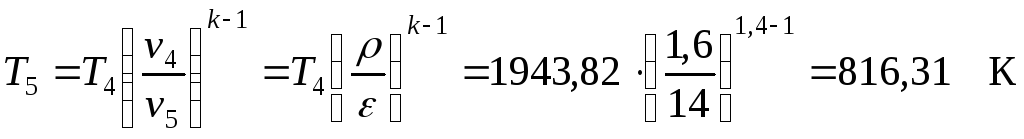
Давление находим из уравнения состояния

Результаты расчетов записываем в таблицу:
| Точки | р, МПа | v, м3/кг | Т, К |
| 1 | 0,095 | 0,9464 | 313,15 |
| 2 | 3,822 | 0,0676 | 899,92 |
| 3 | 5,160 | 0,0676 | 1214,89 |
| 4 | 5,160 | 0,1082 | 1943,83 |
| 5 | 0,248 | 0,9464 | 816,31 |
На основании найденных значений параметров рабочего тела ДВС (идеального газа со свойствами воздуха) рассчитываем энергетические эффекты во всех процессах, образующих термодинамический цикл.
Работа в изоэнтропном процессе сжатия 1-2

Работа в изобарном процессе расширения 3-4

Работа в изоэнтропном процессе расширения 4-5

Полезная работа в цикле

Количества теплоты, подводимые в изохорном процессе 2-3 и в изобарном 3-4, равны

 Количество теплоты, отводимой в процессе 5-1
Количество теплоты, отводимой в процессе 5-1
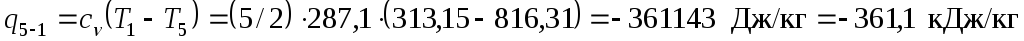
Полезно использованная теплота (превращенная в работу)

Результаты расчетов записываем в таблицу
| Процесс | l, кДж/кг | q, кДж/кг |
| 1-2 адиабатное сжатие | -421,1 | 0 |
| 2-3 изохорный подвод теплоты | 0 | 226,1 |
| 3-4 изобарный подвод теплоты | 209,5 | 732,5 |
| 4-5 адиабатное расширение | 809,0 | 0 |
| 5-1 изохорный отвод теплоты | 0 | -361,1 |
| Сумма | 597,4 | 597,5 |
Рассчитанные суммарные значения q и l согласуются в пределах 0,02%. Это свидетельствует о высокой точности выполненных расчетов.
Термический КПД цикла
 .
.
Для проверки рассчитываем значение термического КПД по заданным характеристикам цикла
 Полученные значения ηt совпали, что также подтверждает высокую точность всех рассчитанных величин.
Полученные значения ηt совпали, что также подтверждает высокую точность всех рассчитанных величин.
Задача 2. В цикле поршневого двигателя со смешанным подводом теплоты начальное давление р1 = 0,09 МПа, начальная температура t1 = 50°С, степень сжатия ε = 15, максимальное давление — 5,4 МПа, количество подводимой теплоты q1 = 900 кДж/кг, рабочее тело — воздух.
Какая часть теплоты подводится в изохорном процессе и каково значение термического КПД цикла.
Решение.
Для ответа на первый вопрос необходимо определить значения температуры в начале и в конце изохорного процесса 2-3 (Т2 и Т3). Значение Т2 рассчитываем из уравнения изоэнтропы

Для расчета значения Т3 необходимо знать степень повышения давления λ = =р3/р2.Поэтому определяем р2 по уравнению изоэнтропы
 .
.
Поскольку в рассматриваемом цикле р3 = рмакс = 5,4 МПа, значение λ равно
λ = р3/р2 = 5,4/3,988 = 1,354.
Температура в конце изохорного подвода теплоты
Т3 = Т2λ = 954,65·1,354 = 1292,60 К.
Количество теплоты, подводимой в изохорном процессе
 , что составляет 27,0% от всей подведенной теплоты.
, что составляет 27,0% от всей подведенной теплоты.
Для расчета значения термического КПД цикла необходимо определить количество отведенной теплоты, то есть температуру в точке 5, либо определить третью характеристику цикла — степень предварительного расширения ρ. Значение ρ можно найти, рассчитав предварительно температуру Т4 из уравнения для количества теплоты, подводимой в изобарном процессе

Отсюда
 .
.
Степень предварительного расширения равна
ρ = Т4/Т3 = 1946,83/1292,60 = 1,506
Зная характеристики цикла, определяем значение термического КПД

Для проверки определяем температуру Т5 и количество отводимой теплоты


На основании величин q1 и q2 можно также рассчитать значение термического КПД

Значения ηt, рассчитанные двумя способами, согласуются в пределах 0,02%, что свидетельствует о высокой точности проведенных расчетов.
Задача 3. Рассчитать параметры рабочего тела во всех характерных точках идеализированного обратимого термодинамического цикла ДВС со смешанным процессом подвода теплоты. Сделать заключение об его эффективности, если известны следующие данные: температура воздуха в начале процесса сжатия t1 = 24°С; удельный объем газов в точке 5 v5 = 0,47071 м3/кг; теплота, подводимая в цикле q1 = 722,64 кДж/кг; работа адиабатного сжатия воздуха l1-2 = – 501,85 кДж/кг; изменение энтропии в изохорном процессе подвода теплоты  = 0,35943кДж/(кг·К).
= 0,35943кДж/(кг·К).
Решение
Параметры рабочего тела в точке 1:
удельный объем
 ,
,
исходя из принципа построения теоретического цикла ДВС.
давление

Параметры рабочего тела в точке 2:
температура определяется на основании заданного значения работы адиабатного процесса сжатия
 ; тогда
; тогда 
удельный объем и давление определяются из уравнения адиабаты
 , откуда
, откуда 
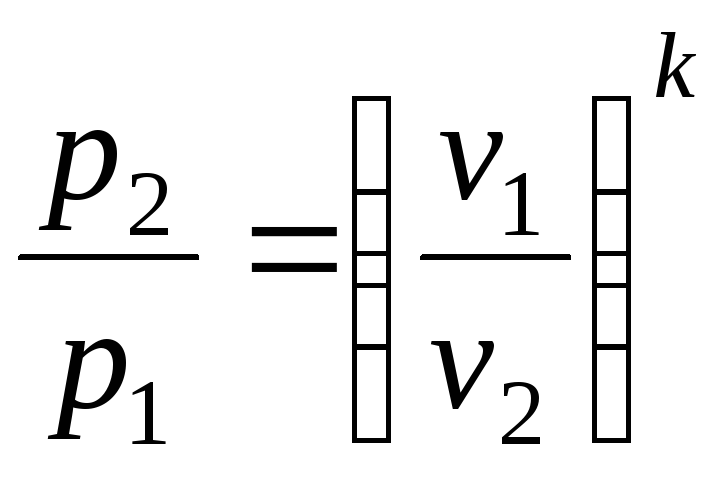 ,откуда
,откуда
Параметры рабочего тела в точке 3:
Процесс 2-3 – изохорный, поэтому 
В условии задачи задано изменение энтропии в процессе 2-3
 , тогда
, тогда 
Как известно, в изохорном процессе температура и давление изменяются прямопропорционально
 , отсюда
, отсюда 
Проверка: из уравнения состояния идеального газа

Значения р3 рассчитанные по двум независимым соотношениям согласуются вполне удовлетворительно (с погрешностью 0,12%)
Параметры рабочего тела в точке 4:
Процесс 3-4 – изобарный, поэтому 
В условии задачи задано общее количество теплоты q1, подводимой в цикле
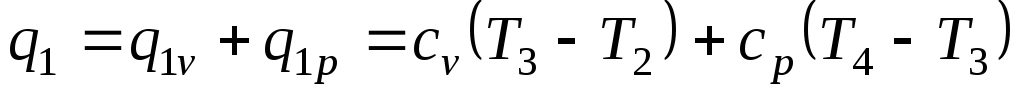 .
.
Следовательно, количество теплоты, подводимое в процессе 3-4, равно
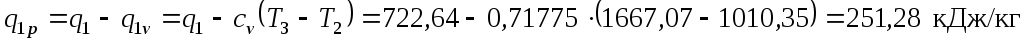 С другой стороны
С другой стороны
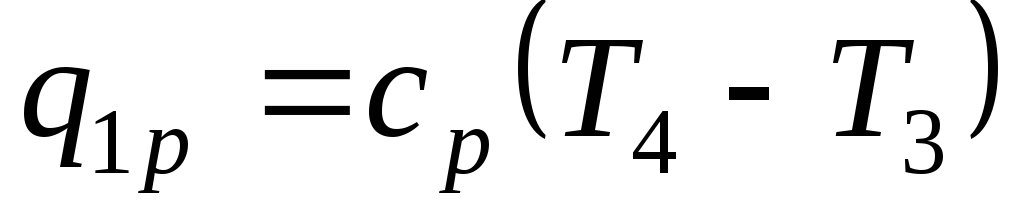 , отсюда
, отсюда 
В изобарном процессе температура и удельный объем изменяются прямо пропорционально:
 , тогда
, тогда 
Проверка: 
Значение v4, рассчитанные по двум независимым соотношениям, совпали.
Параметры рабочего тела в точке 5:
Процесс 4-5 – адиабатный, тогда:
температура
 , отсюда
, отсюда 
давление
 , отсюда
, отсюда 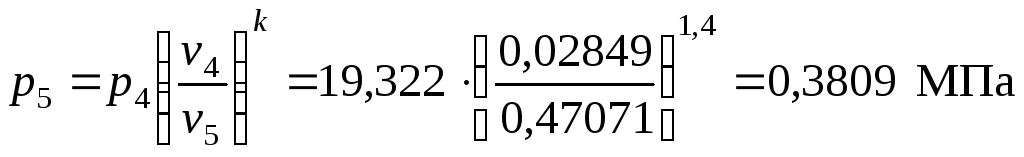
Результаты расчетов записываем в таблицу:
| Точки | р, МПа | v, м3/кг | Т, К |
| 1 | 0,1900 | 0,47071 | 311,15 |
| 2 | 11,725 | 0,02477 | 1010,35 |
| 3 | 19,322 | 0,02477 | 1667,07 |
| 4 | 19,322 | 0,02849 | 1917,14 |
| 5 | 0,3809 | 0,47071 | 624,35 |
Первая комплексная проверка точности выполненных расчетов термических параметров состояния рабочего тела ДВС в характерных точках цикла состоит в сопоставлении суммарной работы цикла, рассчитанной через p и v, c суммарной теплотой, рассчитанной через T, сp и сv. Вторая проверка точности расчетов состоит в сопоставлении значений термического КПД, рассчитанных из различных соотношений, включающих как термические, так и калорические параметры состояния.
Первоначально рассчитываем значения деформационной работы:
в адиабатном процессе сжатия 1-2:
 в изохорном процессе 2-3 :
в изохорном процессе 2-3 :  ;
;
в изобарном процессе расширения 3-4:
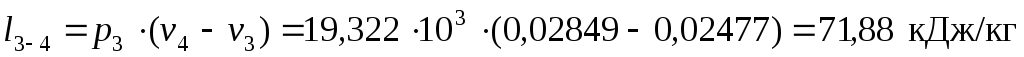 ,
,
в адиабатном процессе расширения 4-5:

в изохорном процессе 5-1: 
После расчёта значений работы рассчитываем значение теплоты:
в адиабатном процессе сжатия 1-2: 
в изохорном процессе 2-3:

в изобарном процессе 3-4:
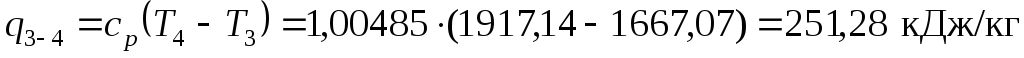
в адиабатном процессе расширения 4-5: 
в изохорного процесса 5-1:

Результаты проверки записываем в таблицу
| Процесс | l, кДж/кг | q, кДж/кг |
| 1-2 адиабатное сжатие | -502,4 | 0 |
| 2-3 изохорный подвод теплоты | 0 | 471,36 |
| 3-4 изобарный подвод теплоты | 71,88 | 251,28 |
| 4-5 адиабатное расширение | 928,02 | 0 |
| 5-1 изохорный отвод теплоты | 0 | -224,80 |
| Сумма | 497,50 | 497,84 |
Из таблицы видна хорошая точность расчётов, так как сумма теплот мало отличается от суммы работ (на 0,34 кДж/кг, то есть на 0,07%).
Теперь проверяем точность выполненных расчетов, сопоставляя значения термического КПД, рассчитанные из следующих соотношений:
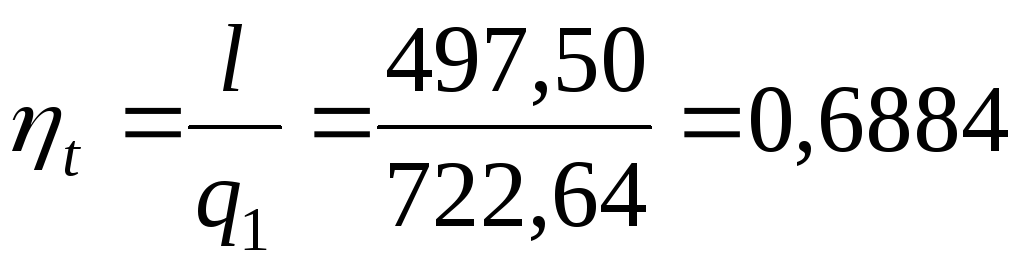 ,
,
где l – суммарная работа цикла (см. предыдущую таблицу).


где q1 и q2 – значения подводимой и отводимой теплоты
 ,
,
где 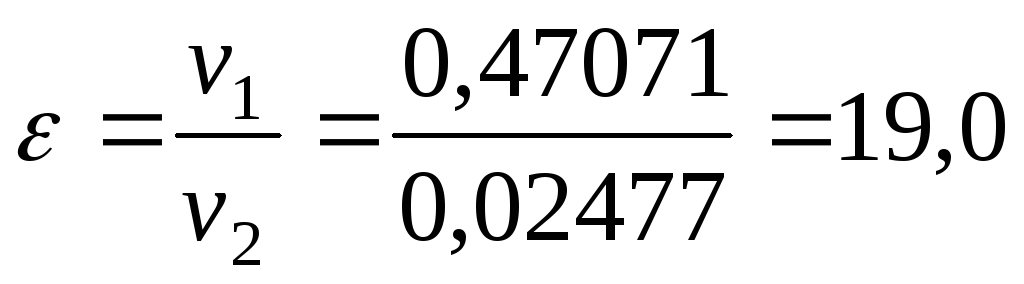 — степень сжатия;
— степень сжатия;
 —степень повышения давления;
—степень повышения давления;
 —степень предварительного расширения.
—степень предварительного расширения.
Термический КПД эквивалентного цикла Карно:
 ,
,
где  — средняя температура отвода теплоты
— средняя температура отвода теплоты
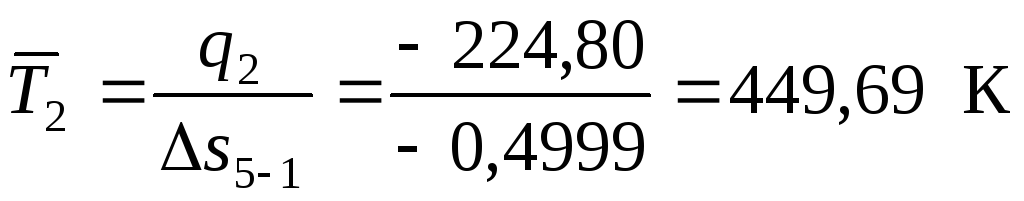 ,
,
Δs5-1 — изменение энтропии в изохорном процессе отвода теплоты 5-1
 ,
,
 —средняя температура подвода теплоты
—средняя температура подвода теплоты

Δs2-3-4 — изменение энтропии в процессе 2-3-4:

Таким образом, значения КПД, рассчитанные из 4-х независимых соотношений, хорошо согласуются. Небольшое расхождение (0,07%) между значениями КПД, рассчитанными через работу цикла l и через значения теплот q1 и q2, объясняется отмеченным выше расхождением между суммами работ и теплот.
Термический КПД предельного цикла Карно:
 ,
,
где Тmin, и Tmax– минимальное и максимальное значения температуры в рассматриваемом цикле.
Степень совершенства исследуемого цикла ДВС:

Следовательно, эффективность данного цикла ДВС ниже, чем предельного цикла Карно почти на 18%.
Задача 4. Какую дополнительную работу можно получить, расширив отработавшие газы ДВС, рассмотренного в предыдущей задаче, до атмосферного давления в газовой турбине комбинированного двигателя?
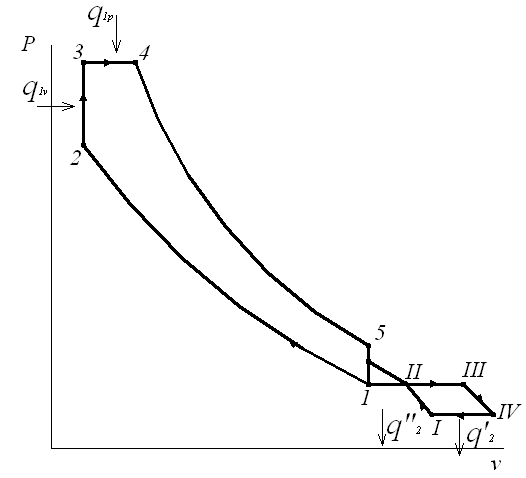

Рис. 2.2. Термодинамический цикл комбинированного двигателя на рабочей и тепловой диаграммах:
I-II – изоэнтропное сжатие в компрессоре, II-I – изобарный отвод теплоты от наддувочного воздуха, II-III – подвод теплоты к газу перед турбиной, III-IV – изоэнтропное расширение в турбине, IV-I – изобарный отвод теплоты в окружающую среду,
1-2 – изоэнтропное сжатие в цилиндре дизеля, 2-3 и 3-4 – изохорный и изобарный подвод теплоты к газу в цилиндре, 4-5 – изоэнтропное расширение в цилиндре, 5-1 – изохорный отвод теплоты от газа после расширения.
Решение
Комбинированный двигатель состоит из поршневого ДВС и открытой газотурбинной установки (ГТУ), которая используется как для наддува ДВС, так и для производства полезной работы. Термодинамический цикл комбинированного двигателя приведен на рис. 2.2.
В предыдущей задаче 3 начальное давление воздуха равно 0,19 МПа и обеспечивается благодаря предварительному сжатию окружающего воздуха в компрессоре ГТУ, работающей на выхлопных газах ДВС.
Как известно, в открытой ГТУ теплота к рабочему телу подводится по изобаре (см. рис. 2.2). Тогда

где TII — температура воздуха после компрессора, которая определяется из уравнения адиабатного процесса I-II
 , тогда
, тогда  .
.
При расчете ТII приняты значения атмосферного давления 0,1 МПа и температуры воздуха 20°С.
Из выражения для подведенной теплоты определяем температуру рабочего тела перед турбиной
 .
.
Определяем удельный объем в точках I, II и III
точка I 
точка II 
точка III 
Температура в конце адиабатного расширения газов в турбине (точка IV)
 , тогда
, тогда 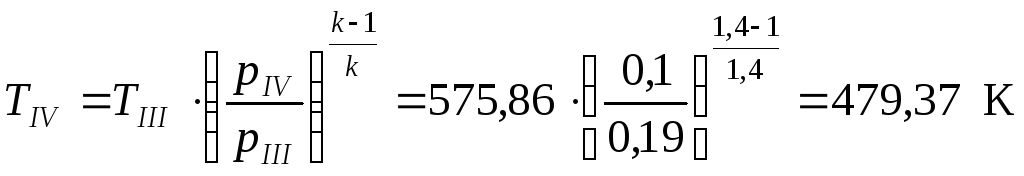
Удельный объем газов в конце расширения

Теплота, отводимая в цикле ГТУ I-II-III-IV

Количество теплоты превращаемой в работу в цикле ГТУ
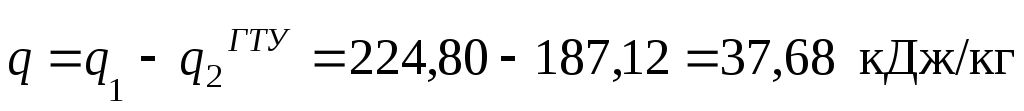
Определим также работу цикла путем непосредственного расчета значений работы отдельных процессов.
Техническая работа, получаемая при адиабатном расширении газов в ГТУ (процесс III-IV)

Техническая работа, затрачиваемая на адиабатное сжатие воздуха в компрессоре (процесс I-II)

Техническая работа изобарных процессов II-III и IV-I равна нулю
Работа в цикле ГТУ равна

Значения работы, рассчитанные двумя способами, практически совпали.
Итак, используя энергию отработавших газов ДВС в комбинированном двигателе, можно дополнительно получить полезную работу помимо работы, используемой для сжатия наддувочного воздуха. В данной задаче такая работа равна 37,67 кДж/кг. Дополнительную работу можно использовать, например, для привода насосов охлаждающей воды. В любом случае это повысит эффективность судовой энергетической установки (но несколько усложнит её).
studfiles.net
Рассчитать термодинамический цикл поршневого ДВС (рис. 5), если рабочим телом является 1 кг смеси идеальных газов следующего состава:
Процессы сжатия и расширения в цикле политропные. Показатель политропы в процессе сжатия (1-2) равен  , а в процессе расширения (4-5) –
, а в процессе расширения (4-5) – . Температура и давление рабочего тела в начале процесса сжатия равны соответственно
. Температура и давление рабочего тела в начале процесса сжатия равны соответственно и
и .
.
Кроме того, заданы степень сжатия  , степень повышения давления
, степень повышения давления и степень предварительного расширения
и степень предварительного расширения в процессе подвода теплоты.
в процессе подвода теплоты.
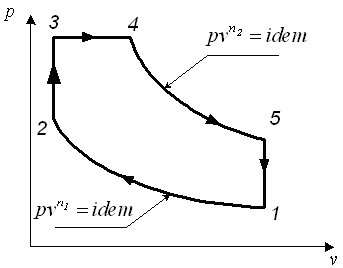
Рис. 5. Термодинамический цикл ДВС
со смешанным подводом теплоты
Определить:
Значения параметров и функций состояния в характерных точках цикла 
Изменения функций состояния  термодинамическую
термодинамическую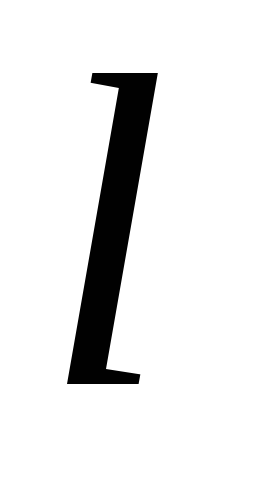 и потенциальную
и потенциальную работы и теплообмен
работы и теплообмен во всех процессах цикла.
во всех процессах цикла.
Работу цикла  , его термический КПД
, его термический КПД и КПД цикла Карно
и КПД цикла Карно , осуществляемого в том же интервале температур.
, осуществляемого в том же интервале температур.
Как измениться термический КПД цикла и его термодинамическое совершенство, если политропный процесс расширения (4-5) заменить на изотермический?
Изобразить цикл в координатах  и
и .
.
1. Определение характеристик рабочего тела.
Из справочной литературы определяются молярные массы компонентов газовой смеси  (
( ) (Приложение. Табл. 1) [3]
) (Приложение. Табл. 1) [3]
 .
.
Средняя молярная масса смеси
 .
.
Газовая постоянная смеси
 .
.
Интерполируя справочные данные (Приложение. Табл. 1) [3], находятся значения изобарной теплоемкости идеальных газов – компонентов смеси 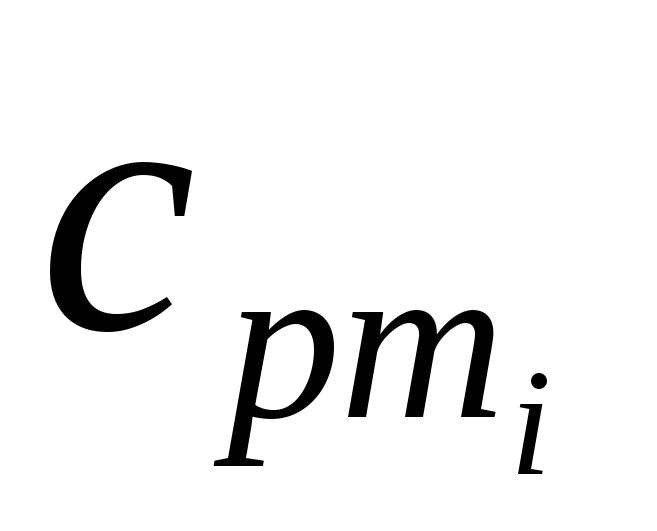
 при температуре рабочего тела в начале процесса сжатия
при температуре рабочего тела в начале процесса сжатия

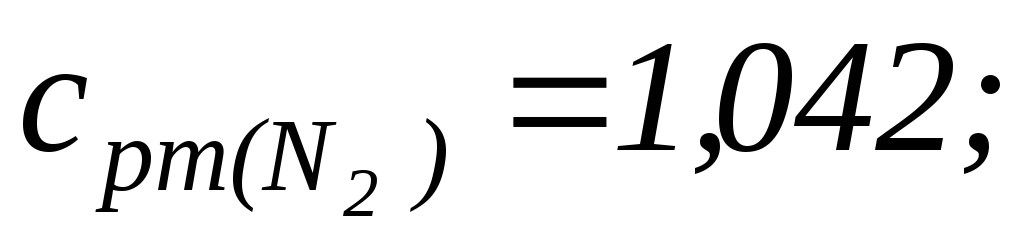
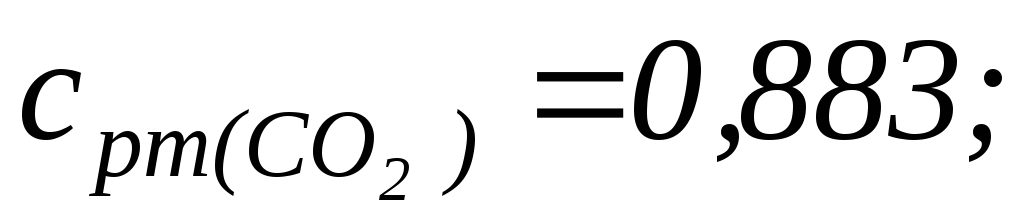

а затем определяются средняя удельная изобарную теплоемкость

средняя удельная изохорная теплоемкость

и показатель адиабаты смеси идеальных газов
 .
.
2. Расчет термодинамических параметров состояния рабочего тела в характерных точках цикла (рис. 5).
Точка 1
 ;
;
 .
.
Точка 2
 ;
;
 ;
;
 ;
;
 .
.
Точка 3
 ;
;
 ;
;
 ;
;
 .
.
Точка 4
 ;
;
 ;
;
 ;
;
 .
.
Точка 5
 ;
;
 ;
;
 ;
;
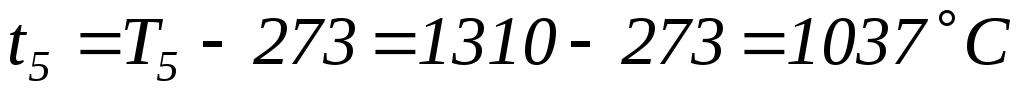 .
.
Результаты расчета заносятся в таблицу 1.
Таблица 1
Значения параметров и функций состояния в характерных точках цикла
| Номер точки |
|
|
|
|
|
|
|
| 1 2 3 4 5 | 0,105 4,53 6,34 6,34 0,413 | 0,924 0,062 0,062 0,124 0,924 | 60 691,2 1076,4 2425,8 1037,0 | 333,0 964,2 1349,4 2698,8 1310,0 | 256,1 741,5 1037,7 2075,4 1007,4 | 353,0 1022,1 1430,4 2860,7 1388,6 | 0,199 0,230 0,489 1,223 1,252 |
3. Определение функции состояния рабочего тела в характерных точках цикла ( ).
).
а) Внутренняя энергия ( ):
):

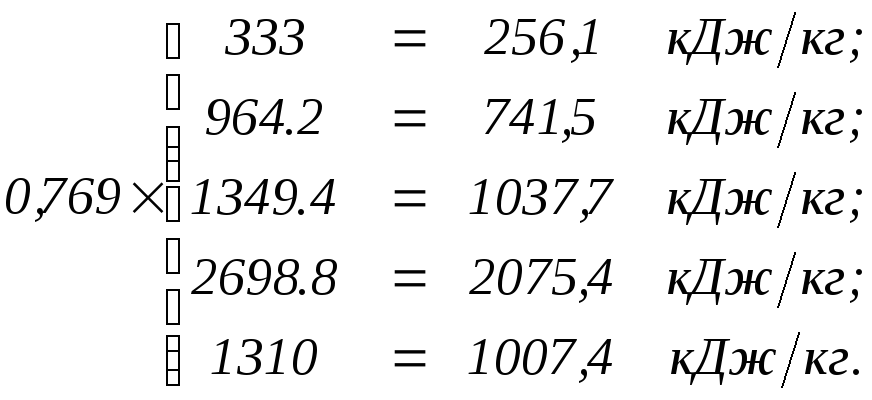
б) Энтальпия (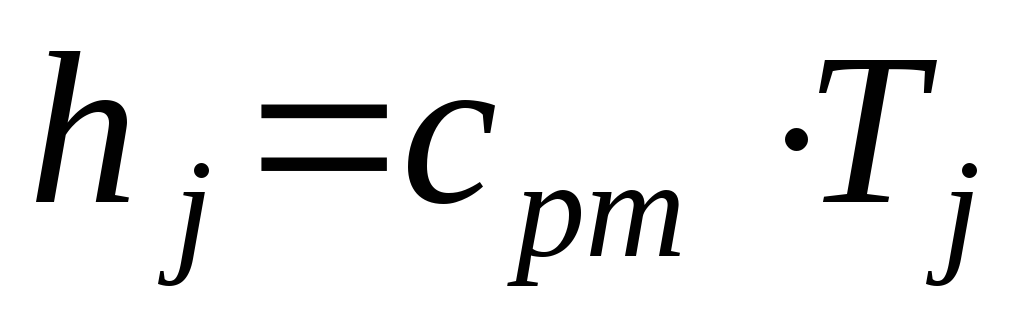 ):
):
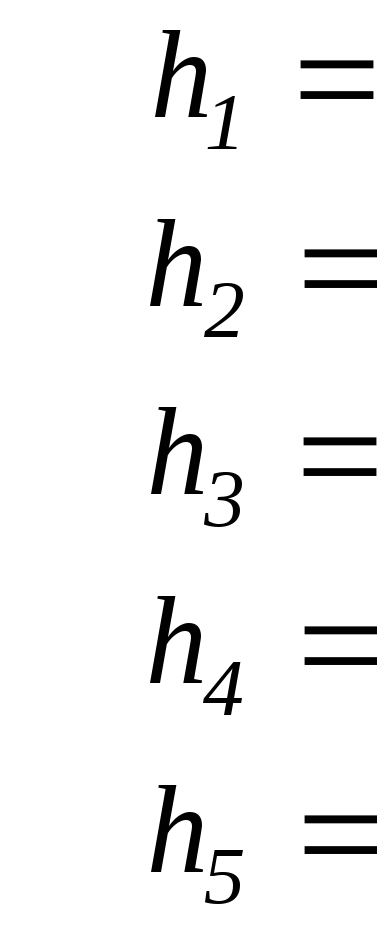

в) Энтропия (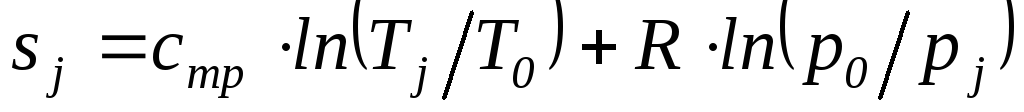 ).
).
Принимаем, что теплоемкость рабочего тела не зависит от температуры, тогда  ,
, , и:
, и:
 ;
;
 ;
;
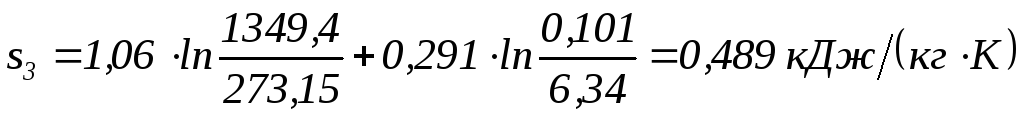 ;
;
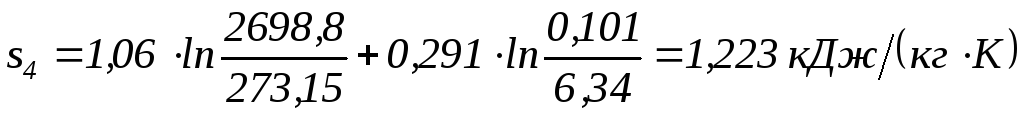 ;
;
 .
.
Найденные значения функций состояния рабочего тела заносятся в таблицу 1.
4. Изменение функций состояния в каждом процессе цикла  определяются как разность значений этих функций в конечной
определяются как разность значений этих функций в конечной и начальной
и начальной точках процесса
точках процесса .
.
Результаты этих вычислений заносятся в таблицу 2.
Таблица 2
Изменение функций процесса и состояния в процессах цикла
| Процесс |
|
|
|
|
|
|
| 1-2 2-3 3-4 4-5 5-1 | 485,4 296,2 1037,7 - 1068,0 - 751,3 | 669,1 408,3 1430,3 - 1472,1 - 1035,6 | - 471,7 0 393,1 1124,7 0 | - 655,7 - 112,2 0 1529,6 284,6 | 15,0 296,2 1430,3 53,6 - 751,3 | 0,031 0,259 0,734 0,029 - 1,053 |
|
| 0 | 0 | 1046,1 | 1046,3 | 1043,8 | 0 |
5. Находим термодинамическую  ,потенциальную
,потенциальную  работы и теплообмен
работы и теплообмен  во всех процессах цикла.
во всех процессах цикла.
Процесс 1-2 – политропное сжатие.
Характеристика сжатия
 ;
;
 ;
;
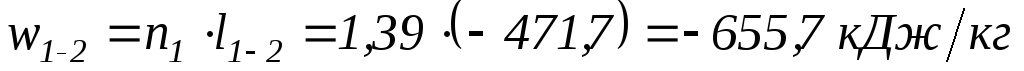 ;
;
 .
.
Процесс 2-3 – изохорный подвод теплоты.
 ;
;
 ;
;
 .
.
Процесс 3-4 – изобарный подвод теплоты.
 ;
;
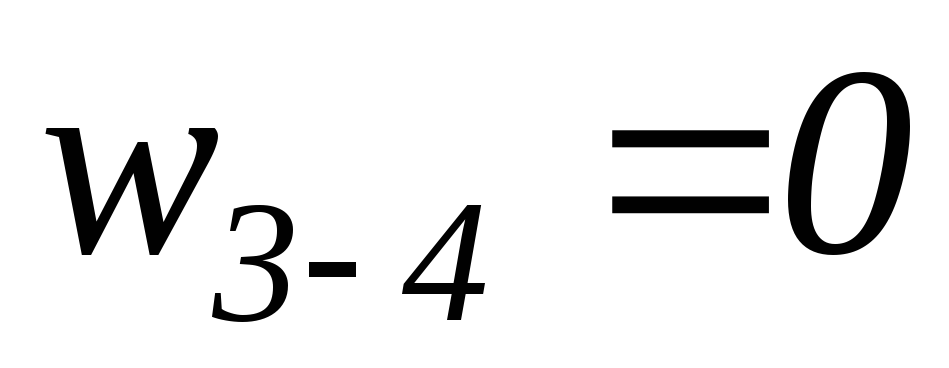 ;
;
 .
.
Процесс 4-5 – политропное расширение.
Характеристика расширения
 ;
;
 .
.
 ;
;
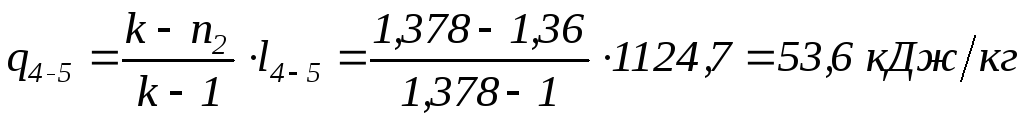 .
.
Процесс 5-1 – изохорный отвод теплоты.
 ;
;
 ;
;
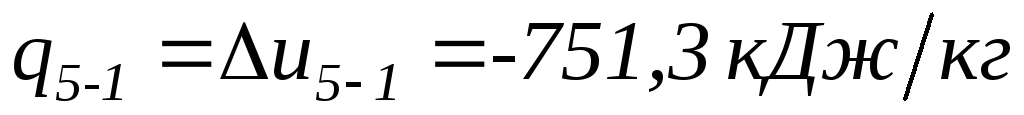 .
.
Результаты вычислений заносятся в таблицу 2.
Проверка полученных результатов проводится по первому началу термодинамики для каждого процесса и цикла в целом
 ,
,
 .
.
Проверка полученных результатов показывает, что относительная погрешность расчетов, наличие которой связано с проводимыми округлениями, составляет  , что допустимо для приближенных термодинамических расчетов.
, что допустимо для приближенных термодинамических расчетов.
6. Определяем работу цикла 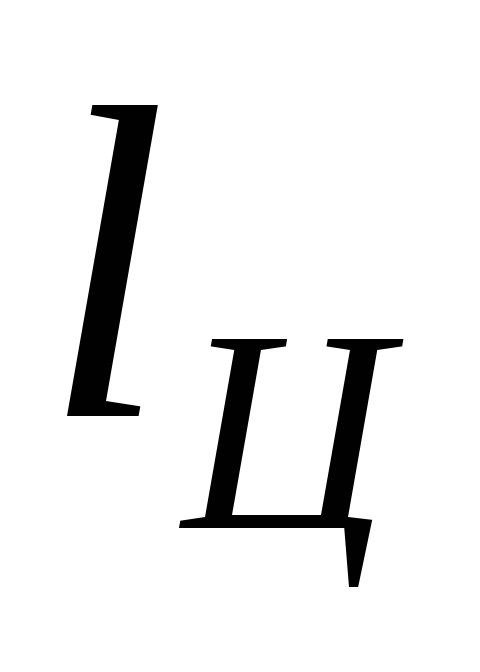 ,термический КПД цикла
,термический КПД цикла  иКПД цикла Карно
иКПД цикла Карно 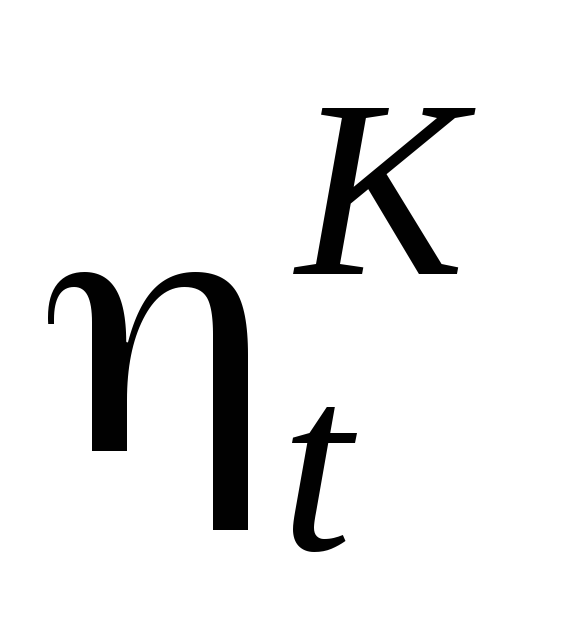 :
:

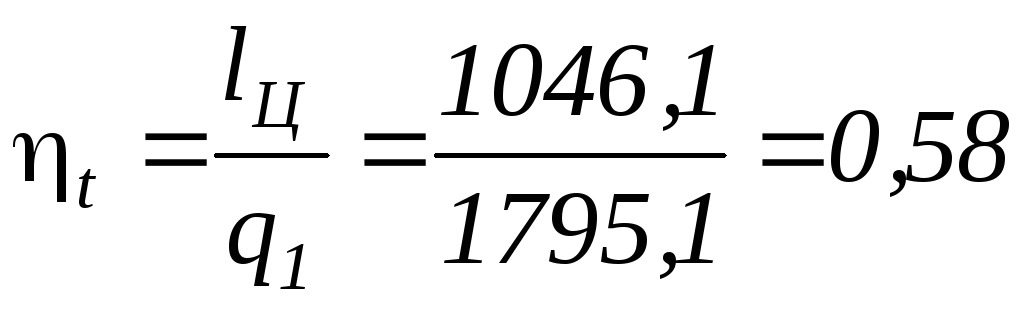 или
или  ,
,
где  – удельное количество подведенной теплоты,
– удельное количество подведенной теплоты,
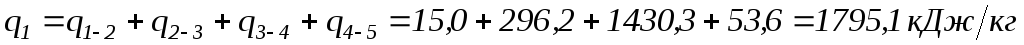 ;
;
 или
или  .
.
7. Изобразим цикл поршневого ДВС в координатах  и
и (рис. 6). Для этого определим координаты промежуточных точек в процессах цикла.
(рис. 6). Для этого определим координаты промежуточных точек в процессах цикла.

Рис. 6. Термодинамический цикл поршневого ДВС
со смешанным подводом теплоты
а) Расчет промежуточных точек для построения цикла в координатах  .
.
Промежуточная точка  в процессе политропического сжатия 1-2
в процессе политропического сжатия 1-2
Выбираем 
 , тогда из уравнения политропы
, тогда из уравнения политропы
 .
.
Промежуточная точка  в процессе политропического расширения 4-5
в процессе политропического расширения 4-5
Принимаем 
 , тогда из уравнения политропы
, тогда из уравнения политропы
 .
.
б) Расчет промежуточных точек для построения цикла в координатах  .
.
Промежуточная точка  в процессе 1-2
в процессе 1-2
Принимаем 
 , тогда:
, тогда:
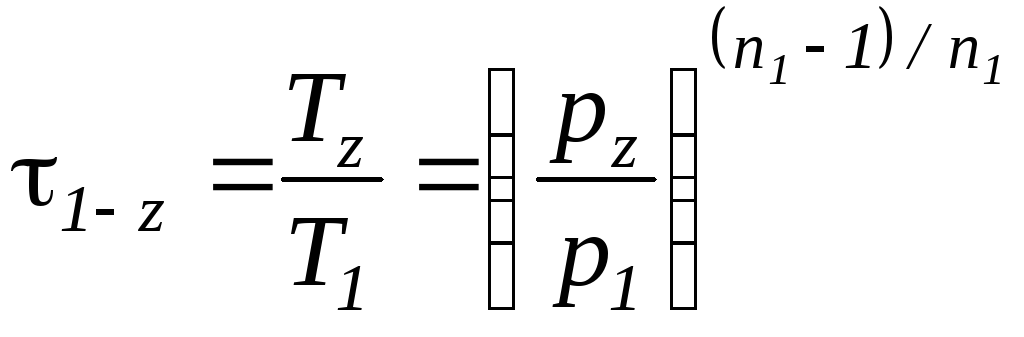 ,
,
 ,
,

Промежуточная точка  в процессе изохорного подвода теплоты 2-3
в процессе изохорного подвода теплоты 2-3
Принимаем 
 . Так как
. Так как ,
,
 ,
,
 .
.
Промежуточная точка  в процессе изобарного подвода теплоты 3-4
в процессе изобарного подвода теплоты 3-4
Принимаем 
 , при этом:
, при этом:
 ,
,
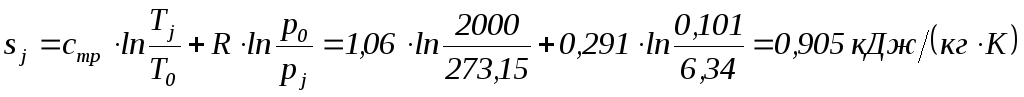 .
.
Промежуточная точка  в процессе 4-5
в процессе 4-5
Принимаем 
 . При этом:
. При этом:
 ,
,

Промежуточная точка  в процессе изохорного отвода теплоты 5-1
в процессе изохорного отвода теплоты 5-1
Принимая 
 , и учитывая, что
, и учитывая, что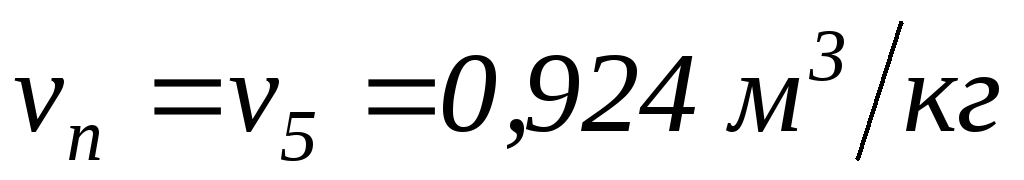 , получим:
, получим:
 ,
,
 .
.
8. Проведем расчет термодинамического цикла поршневого ДВС с изотермическим расширением рабочего тела в процессе 4-5.
При данном изменении в цикле определяем термодинамические параметры состояния в точке 5′:
 ;
;
 ;
;
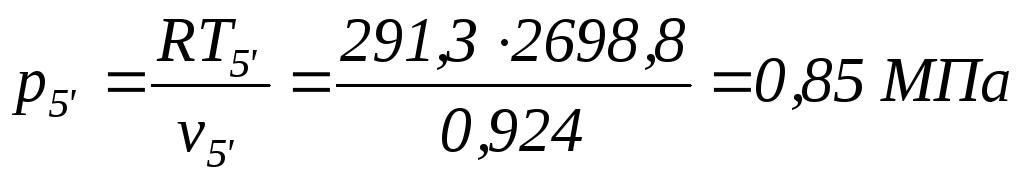 .
.
Рассчитываем термодинамическую работу  и теплообмен
и теплообмен .
.
Процесс 4-5′
 .
.
Процесс 5′-1
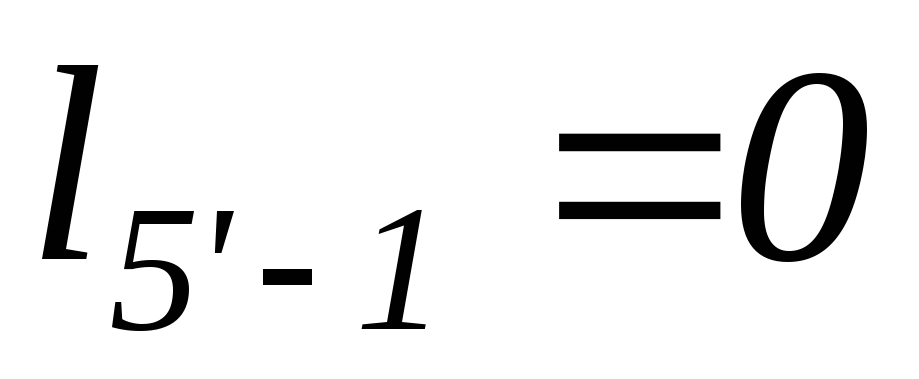 ;
;
 .
.
Находим работу цикла
 ,
,
где  – число процессов в цикле,
– число процессов в цикле,
удельное количество теплоты, подведенной к рабочему телу
 ,
,
термический КПД цикла
 или
или  .
.
КПД цикла Карно остался неизменным, так как не изменились минимальная 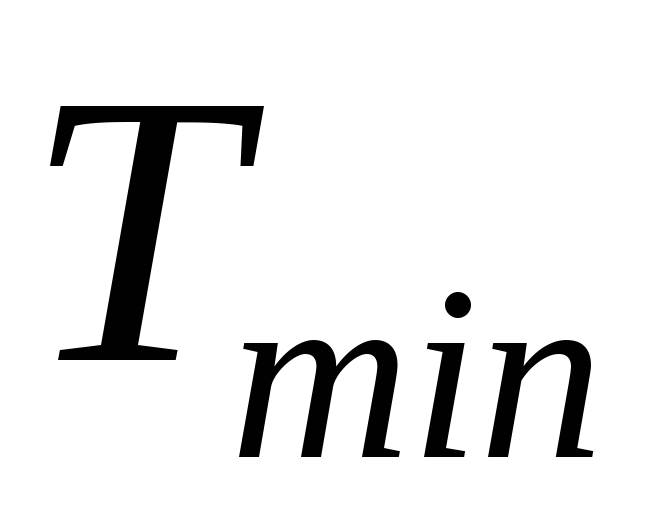 и максимальная
и максимальная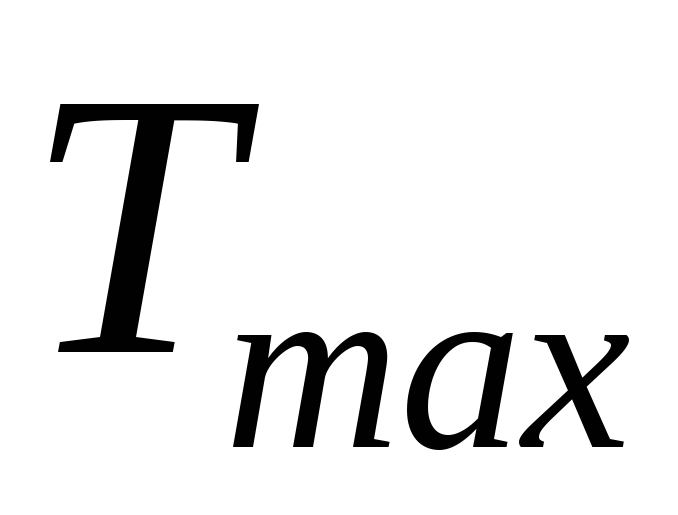 температуры рабочего тела в цикле.
температуры рабочего тела в цикле.
9. Замена политропического процесса расширения с показателем политропы  на изотермический, приводит к снижения термического коэффициента полезного действия. Кроме того, снижается и термодинамическое совершенство цикла, так как в первом случае работа цикла
на изотермический, приводит к снижения термического коэффициента полезного действия. Кроме того, снижается и термодинамическое совершенство цикла, так как в первом случае работа цикла составляет 66% от теоретически возможной работы цикла
составляет 66% от теоретически возможной работы цикла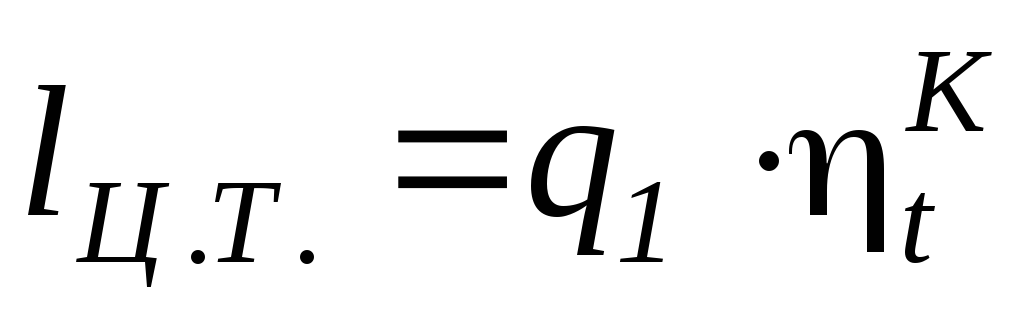 , а во втором случае этот показатель, называемый коэффициентом заполнения, снижается до 51%.
, а во втором случае этот показатель, называемый коэффициентом заполнения, снижается до 51%.
studfiles.net
Энергетические установки тепловых и атомных электростанций представляют собой тепловые двигатели (паросиловые установки), способные превращать полученное при теплообмене рабочим телом количество теплоты в механическую энергию. Механическая работа в тепловых двигателях производится в процессе расширения некоторого вещества, называемого рабочим телом. В качестве рабочего тела используется питательная вода и водяной пар. Механическая энергия вращения паровой турбины с помощью электрогенератора преобразуется в электрическую энергию.
К тепловым двигателям относят не только паровые машины, но и двигатели внутреннего сгорания, дизельные двигатели и т.д. Характерной особенностью работы таких машин является циклический процесс теплопередачи и преобразования полученного количества теплоты в работу. Для этого рабочее тело должно совершать круговой процесс или термодинамический цикл, при котором периодически восстанавливается исходное состояние рабочего тела. Наибольшее распространение в производстве механической энергии получили тепловые двигатели, работающие по термодинамическим циклам Ранкина и Карно. Именно они определяют теоретические и реальные показатели эффективности, экономичности работы того или иного теплового двигателя и энергетической установки в целом. Различным типам тепловых двигателей присущи различные круговые термодинамические циклы рабочего тела.
В 1824 году французский инженер С. Карно рассмотрел круговой процесс, состоящий из двух изотерм и двух адиабат (рис. 2.2.).

Рис. 2.2. Термодинамический цикл Карно
Ц
(2.3)
икл Карно совершает газ, находящийся в цилиндре под поршнем. На изотермическом участке (1–2) газ нагревают тепловым резервуаром с температурой T1, подводя к газу некоторое количество теплоты Q1. Газ изотермически расширяется, совершая работу A12. На адиабатическом участке (2–3) газ помещают в адиабатическую оболочку, и он продолжает расширяться без теплообмена, совершая работу A23 . При этом температура газа падает до значения T2. На изотермическом участке (3–4) газ приводят в тепловой контакт с холодным резервуаром, и происходит его сжатие. При этом газ отдает тепло Q2 , совершая отрицательную работу A34 . На последнем участке адиабатического сжатия (4–1) газ вновь помещают в адиабатическую оболочку. При сжатии газа его температура повышается до значения T1 и совершается отрицательная работа A41. Полная работа газа за цикл равна сумме работ на отдельных участках:A = A12 + A23 + A34 + A41 .
На диаграмме (P,V) эта работа равна площади цикла. Заметим, что в замкнутом цикле A23 = – A41. Тогда
A
(2.4)
= A12 + A34 .КПД цикла Карно представляет собой отношение теплоты, израсходованной на совершение работы, к подведенной теплоте:

(2.5)
.Карно предложил выражать КПД цикла через температуры нагревателя и холодильника:
(2.6)
 .
. Цикл Карно – наиболее эффективный круговой процесс из всех возможных при неизменных температурах нагревателя и холодильника, поскольку отсутствует теплообмен рабочего тела и окружающей среды при конечной разности их температур, когда тепло может передаваться без совершения работы. Заметим, что идеальное устройство, работающее по циклу Карно, является обратимой тепловой машиной, т.к. обход цикла против часовой стрелки будет соответствовать холодильной машине.
Один из самых распространенных тепловых двигателей – двигатель внутреннего сгорания (ДВС) – работает по тому или иному термодинамическому циклу, соответствующему реальному циклу Карно. Существуют два типа ДВС – бензиновый и дизельный. Круговые термодинамические процессы изображаются на диаграмме (P,V) газообразного рабочего тела (смеси паров бензина или дизельного топлива с воздухом) с помощью замкнутых кривых (рис. 2.3).
Цикл карбюраторного бензинового двигателя состоит из двух изохор (1–2, 3–4) и двух адиабат (2–3, 4–1). При расширении газ совершает положительную работу, равную площади под кривой 2–3, при сжатии – отрицательную работу, равную площади под кривой 4–1. Полная работа за цикл определяется разницей этих площадей.

Рис. 2.3. Термодинамические циклы карбюраторного
бензинового ДВС (1) и дизельного двигателя (2)
Дизельный двигатель работает по циклу, состоящему из двух адиабат (1–2, 3–4), одной изобары (2–3) и одной изохоры (4–1). Площадь внутри цикла отражает полную работу газа за цикл.
Реальный КПД карбюраторного двигателя порядка 30 %, дизельного – порядка 40 %.
studfiles.net
Идеальные термодинамические циклы поршневых двигателей (циклы Карно, Отто, Дизеля и Сабатэ-Тринклера) описывают процессы, происходящие в цилиндрах двигателя из условий максимального использования тепловой энергии. Эти циклы различаются, в основном, способом подвода тепла – при постоянной температуре рабочего тела, при постоянном объеме, при постоянном давлении и смешанным образом.

Чтобы нагляднее понять суть процессов, составляющих эти циклы, попробуем отбросить стереотипы, зачастую мешающие реально осмыслить причины, приводящие в движение поршень теплового двигателя и, в конечном итоге, заставляющие двигатель выполнять определенную работу. Для этих целей откажемся от подачи топливо-воздушной смеси в цилиндры, уберем клапана, систему зажигания, и представим себе простейшую систему (поршневой двигатель), состоящую из цилиндра, поршня и заключенного между ними любого газа, например, обычного воздуха. Верхнее донышко цилиндра «сделаем» из тонкого (но прочного) и прозрачного материала, способного пропускать тепловые лучи.
А теперь представим, как протекают процессы подвода теплоты в разных термодинамических циклах, рассматривая описанную выше простейшую модель поршневого двигателя. Итак, никакого топлива у нас нет – только цилиндр, поршень, и воздух между ними.
Разместим над прозрачным донышком цилиндра маломощную лампу накаливания, которая способна медленно передавать тепло воздуху, размещенному между цилиндром и поршнем (см. рис. 2). Поскольку подогрев осуществляется медленно, повышение давления воздуха сопровождается одновременным увеличением его объема (поршень перемещается вниз), при этом температура воздуха в цилиндре остается практически постоянной. Процесс подвода теплоты осуществляется по изотерме, как в цикле, описанном С. Карно.  Примерно в средней части хода поршня лампу выключаем, и наш поршень продолжает перемещаться вниз уже за счет внутренней энергии молекул воздуха, накопленной во время подвода теплоты.
Примерно в средней части хода поршня лампу выключаем, и наш поршень продолжает перемещаться вниз уже за счет внутренней энергии молекул воздуха, накопленной во время подвода теплоты.
Достигнув нижней мертвой точки, наш поршень должен остановиться - ведь для того, чтобы он начал двигаться в обратном направлении, воздух в цилиндре необходимо охлаждать. Именно в этом месте цикла Сади Карно ввел свой знаменитый холодильник – устройство, способное отнимать тепло у системы, т. е. у нашего воздуха в цилиндре. Итак, вместо лампы подогрева мы должны обложить цилиндр со всех сторон льдом или снегом – только в этом случае охлаждаемый воздух начнет уменьшаться в объеме, и поршень поползет вверх. В цикле Карно этот процесс называется изотермическим отводом теплоты – т. е. температура воздуха остается неизменной, а отвод теплоты сопровождается уменьшением объема воздуха (отрицательная работа цикла). Примерно в средней части хода поршня удаляем лед, и далее поршень перемещается к верхней точке за счет внутренней энергии, совершая все также отрицательную работу. Цикл замкнулся (см. графическое отображение цикла карно на рис. 1).
***
А теперь давайте эту модель применим для цикла Отто (или, как его еще называют – цикла Бо де Роша). Как и в предыдущем случае, поршень вверху, между поршнем и цилиндром воздух. Вместо лампочки накаливания на короткое время включаем мощный лазер, способный достаточно быстро разогреть воздух в цилиндре. Моментально возрастает давление в цилиндре, при этом поршень (в силу своей инертности и расположения кривошипно-шатунного звена) не успевает уйти из мертвой точки, т. е. процесс подвода теплоты протекает при постоянном объеме (изохорно).
Далее – рабочий ход (выполнение поршнем полезной работы), который сопровождается увеличением объема и постепенным уменьшением давления. Температура воздуха тоже несколько снижается. В идеальной системе для продолжения цикла необходимо отвести тепло с помощью холодильника (обложить цилиндр льдом), тогда диаграмма цикла на этом участке будет мало отличаться от диаграммы цикла Карно. В реальном двигателе отвод теплоты осуществляется выпуском горячего рабочего тела и замена его холодным рабочим телом (выпуск газов и впуск свежего заряда), по этой причине цикл не является замкнутым и разрывается в зоне отвода тепла (см. рис. 1). Итак, для реализации цикла Отто мы использовали очень быстрый подвод теплоты с помощью лазерного луча.
Для моделирования цикла Дизеля вместо лазера разместим над стеклянным донышком цилиндра опять же лампу накаливания, только значительно мощнее, чем в первом случае.
Тогда воздух в цилиндре будет интенсивно разогреваться (но значительно медленнее, чем от разогрева лазером), при этом поршень будет успевать уйти от верхней точки таким образом, что увеличение объема воздуха не сопровождается изменением давления.  В результате мы получим процесс подвода теплоты с помощью мощной лампы, протекающий при изобарном процессе (при постоянном давлении и переменных объеме и температуре), т. е. аналогичный процессу подвода теплоты в цикле Дизеля.
Рабочий ход, отвод тепла и сжатие воздуха в цикле Дизеля протекают по таким же процессам, как и в цикле Отто (см. график на рис. 1).
В результате мы получим процесс подвода теплоты с помощью мощной лампы, протекающий при изобарном процессе (при постоянном давлении и переменных объеме и температуре), т. е. аналогичный процессу подвода теплоты в цикле Дизеля.
Рабочий ход, отвод тепла и сжатие воздуха в цикле Дизеля протекают по таким же процессам, как и в цикле Отто (см. график на рис. 1).
Ну а цикл Сабатэ-Тринклера, как вы уже догадались, будет заключаться для нашего «двигателя» кратковременным подводом тепла с помощью лазера, а затем подменой лазера на мощную лампочку накаливания. Тогда воздух получит мощную порцию тепла от лазера, в цилиндре резко увеличится давление при постоянном объеме, после чего поршень относительно медленно переместится вниз, получая тепло от лампы при неизменном давлении в цилиндре (см. рис. 1).
На основании анализа приведенных выше виртуальных моделей термодинамических циклов становится очевидным, что суть процессов, происходящих в двигателе, в общем случае, не зависит от того, какое топливо сжигается в цилиндре (можно обойтись вообще без топлива), а лишь от способа подвода теплоты к рабочему телу. В реальности все выглядит несколько иначе и, конечно же, сложнее.
***
Реальные циклы двигателей внутреннего сгорания
Скачать теоретические вопросы к экзаменационным билетам по учебной дисциплине "Основы гидравлики и теплотехники" (в формате Word, размер файла 68 кБ)
Скачать рабочую программу по учебной дисциплине "Основы гидравлики и теплотехники" (в формате Word):
Скачать календарно-тематический план по учебной дисциплине "Основы гидравлики и теплотехники" (в формате Word):
k-a-t.ru
В термодинамических циклах поршневых ДВС процессы сжатия и расширения рабочего тела принимаются адиабатными, а рабочим телом является идеальный газ. Различают термодинамические циклы поршневых ДВС с изохорным подводом теплоты – цикл Отто (рис. 3а), изобарным подводом теплоты – цикл Дизеля (рис. 3б) и со смешанным подводом теплоты – цикл Сабатэ–Тринклера (рис. 3в).
Основными характеристиками термодинамических циклов поршневых ДВС являются:
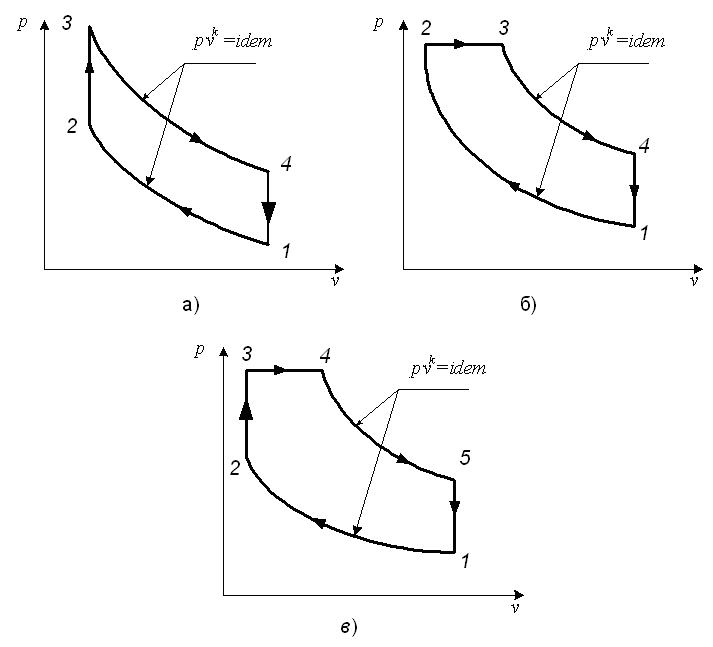
Рис. 3. Термодинамические циклы поршневых ДВС:
а) Отто, б) Дизеля, в) Сабатэ–Тринклера
Термический КПД цикла ДВС со смешанным подводом теплоты определяется по соотношению
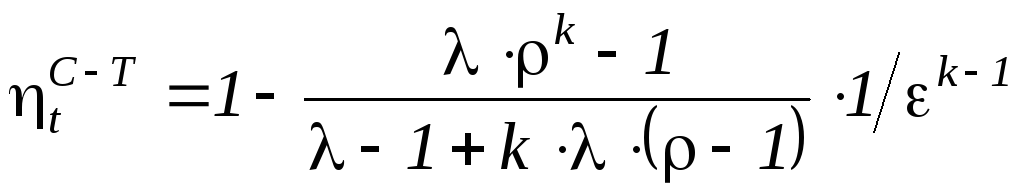 . (36)
. (36)
Анализ соотношения (36) свидетельствует, что термический КПД цикла возрастает с повышением степени сжатия  , показателя адиабаты
, показателя адиабаты , степени повышения давления
, степени повышения давления и с уменьшением степени предварительного расширения
и с уменьшением степени предварительного расширения .
.
При одинаковых исходных значениях параметров рабочего тела и степени сжатия справедливо следующее неравенство:
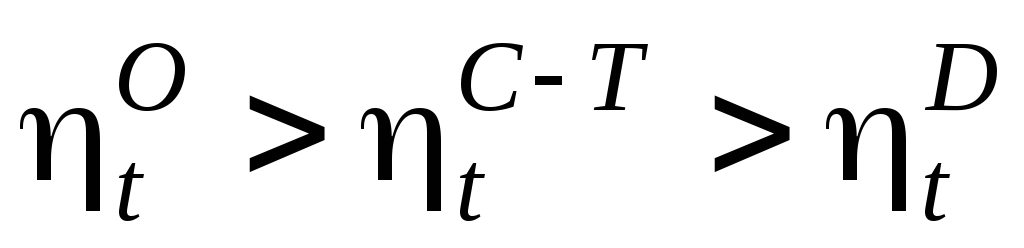 . (37)
. (37)
В то же время следует отметить, что более корректно проводить сравнение значений термического коэффициента полезного действия циклов в условиях одинаковых максимальных параметров рабочего тела ( ,
,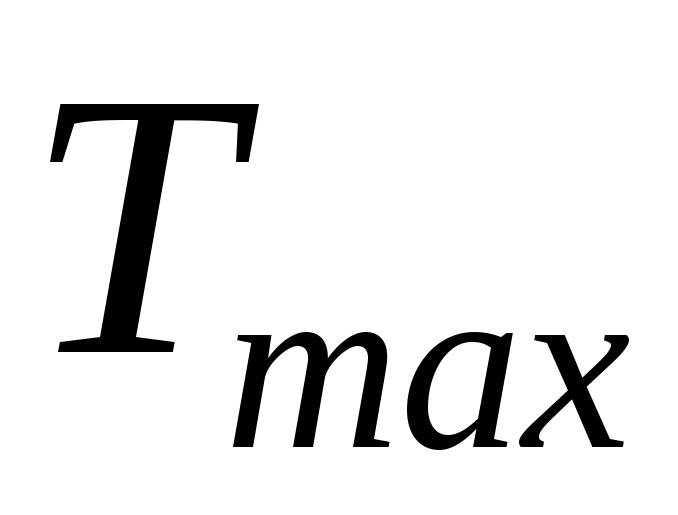 ).
).
В этом случае справедливо неравенство
 . (37а)
. (37а)
Термический КПД циклов ДВС может достигать 60–65%.
В реальных двигателях внутреннего сгорания, вследствие необратимых потерь работы, действительный КПД меньше термического и в среднем составляет 30-40% для дизелей и 20-30% для карбюраторных двигателей.
Различают два термодинамических цикла ГТУ: циклы с изобарным подводом теплоты – цикл Брайтона (рис. 4а) и с изохорным подводом теплоты – цикл Гемфри (рис. 4б).

Рис. 4. Термодинамические циклы ГТУ:
а) Брайтона, б) Гемфри
Основными характеристиками термодинамических циклов ГТУ являются:
Термический коэффициент полезного действия цикла Гемфри может быть определен из соотношения
 , (38)
, (38)
а термический КПД цикла Брайтона по формуле
 . (39)
. (39)
Сопоставление значений термических КПД циклов газотурбинных установок при одинаковых исходных параметрах и степени повышения давления рабочего тела в процессе сжатия показывает, что
 . (40)
. (40)
Следует отметить, что циклы поршневых ДВС характеризуются изохорным отводом, а циклы ГТУ – изобарным отводом теплоты.
В реальных ГТУ и ДВС процессы сжатия и расширения не являются адиабатными. С достаточной для технических расчетов точностью их можно считать политропными с постоянными показателями политропы.
studfiles.net
ГЛАВА 7. КОГЕНЕРАЦИОННЫЕ УСТАНОВКИ НА БАЗЕ ГАЗОПОРШНЕВЫХ ДВИГАТЕЛЕЙ
Термодинамические циклы двигателей внутреннего сгорания (ДВС)
Первые поршневые двигатели внутреннего сгорания (ДВС) работали на газообразном топливе, используя светильный газ. Значительный вклад в развитие таких двигателей внес немецкий изобретатель Н.Отто, разработавший двигатель с предварительным сжатием и искровым зажиганием.
Несколько позднее Рудольф Дизель разработал двигатель, до сих пор носящий его имя, в котором используется специальное дизельное топливо. Благодаря высокой концентрации энергии в единице объема, оно практически вытеснило газообразное топливо в двигателях внутреннего сгорания.
Рассмотрим следующие основные циклы ДВС, работающие на жидком топливе при различных способах воспламенения топлива или при различных способах подвода теплоты.
Различают следующие циклы ДВС. Двигатели с подводом теплоты при постоянном объеме (V = const), двигатели с подводом теплоты при постоянном давлении (Р = const) и двигатели, работаю-
щие по смешанному циклу.
Идеальный цикл ДВС при подводе теплоты V = const (цикл Отто) в P-V и T-S диаграммах представлен на рис.7.1.
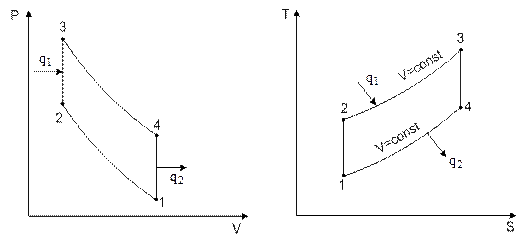
Рис.7.1. Идеальный цикл двигателя внутреннего сгорания с подводом теплоты при V = const в P-V и T-S диаграммах
В этом цикле процесс сжатия рабочей смеси происходит по адиабате 1-2. Изохора 2-3 соответствует горению топлива, воспламеняемого от электрической искры и подводу теплоты q1. Рабочий ход поршня осуществляется при адиабатическом расширении продуктов сгорания, изображен линией 3-4. Отвод теплоты q2 осуществляется по изохоре 4-1, соответствующей выхлопу отработанных газов в атмосферу.
Термический КПД рассматриваемого цикла, характеризующий эффективность использования теплоты сжигаемого топлива, вычисляется следующим образом:
 . (7.1)
. (7.1)
Сравнение адиабат 1-2 и 3-4 позволяет сделать вывод, что
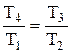 (7.2)
(7.2)
и, следовательно, получить
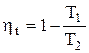 . (7.3)
. (7.3)
Отношение всего объема рабочего цилиндра V1 к объему камеры сжатия V2 называется степенью сжатия и является основной характеристикой цикла Отто
 . (7.4)
. (7.4)
Для адиабатического процесса справедливо следующее соотношение, устанавливающее связь между V и Т:
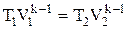 , (7.5)
, (7.5)
которое позволяет записать уравнение для термического КПД в следующем виде:
 . (7.6)
. (7.6)
Из последнего соотношения видно, что термический КПД двигателей, работающих по циклу Отто, зависит только от степени сжатия  и с ее увеличением возрастает. При этом температура в конце сжатия Т2 не должна достигать температуры самовоспламенения горючей смеси. Поэтому степень сжатия в реальных двигателях такого типа не превышает 10 и зависит от характеристик применяемого топлива.
и с ее увеличением возрастает. При этом температура в конце сжатия Т2 не должна достигать температуры самовоспламенения горючей смеси. Поэтому степень сжатия в реальных двигателях такого типа не превышает 10 и зависит от характеристик применяемого топлива.
Степень сжатия в цикле может быть повышена, если сжимать не горючую смесь, а воздух, и затем, получив высокие давление и температуру, обеспечить самовоспламенение распыленного в цилиндре топлива. В этом случае процесс горения затягивается и двигатели такого типа характеризуются постепенным (или медленным) сгоранием топлива при постоянном давлении. Идеальный цикл такого двигателя внутреннего сгорания называется циклом Дизеляи осуществляется следующим образом (рис. 7.2). Рабочее тело (воздух) сжимается по адиабате 1-2, изобарный процесс 2-3 соответствует процессу горения топлива, т.е. подводу теплоты q1 а рабочий ход выражен адиабатным расширением продуктов сгорания 3-4. Наконец, изохора 4-1характеризует отвод теплоты q2, заменяя для четырехтактных двигателей выхлоп продуктов сгорания и всасывание новой порции воздуха.
Формула для расчета термического КПД в этом случае принимает вид
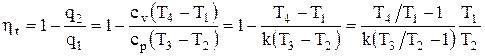 . (7.7)
. (7.7)
Кроме степени сжатия  , у цикла Дизеля имеется еще одна характеристика - степень предварительного расширения
, у цикла Дизеля имеется еще одна характеристика - степень предварительного расширения 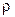 :
:
 . (7.8)
. (7.8)
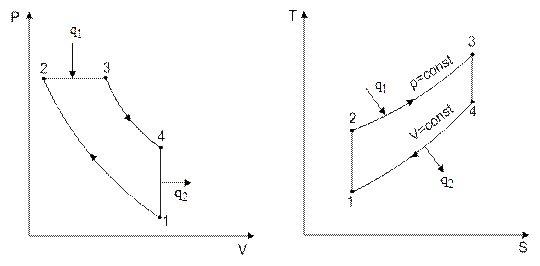
Рис.7.2. Идеальный цикл двигателя внутреннего сгорания с подводом теплоты при Р = const (цикл Дизеля) в P-V и T-S диаграммах
Для изобары 2-3 можно записать V3/V2=Т3/Т2. Рассматривая изохору 4-1 и учитывая, что P4Vk4=P3Vk3,  P1Vk1=P2Vk2 и V4=V1 , получаем
P1Vk1=P2Vk2 и V4=V1 , получаем
 . (7.9)
. (7.9)
Окончательно с учетом соотношения (7.9) формула для расчета термического КПД цикла Дизеля имеет вид:
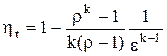 . (7.10)
. (7.10)
Выражение (7.10) показывает, что основным фактором, определяющим экономичность двигателей, работающих по циклу Дизеля, также является величина степени сжатия  , с увеличением которой термический КПД цикла возрастает. Как указывалось, нижний предел
, с увеличением которой термический КПД цикла возрастает. Как указывалось, нижний предел  определен необходимостью получения в конце сжатия температуры, значительно превышающей температуру самовоспламенения топлива. Верхний предел
определен необходимостью получения в конце сжатия температуры, значительно превышающей температуру самовоспламенения топлива. Верхний предел  (до 20) ограничен допустимым давлением в цилиндре, превышение которого приводит к утяжелению конструкции и увеличению потерь на трение. Повышение степени предварительного расширения
(до 20) ограничен допустимым давлением в цилиндре, превышение которого приводит к утяжелению конструкции и увеличению потерь на трение. Повышение степени предварительного расширения 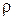 вызывает снижение термического КПД цикла с подводом теплоты при постоянном давлении. Отсюда следует, что с увеличением нагрузки и удлинением процесса горения топлива экономичность двигателя уменьшается. Это следует учитывать наряду с другими обстоятельствами при определении оптимального режима работы двигателя.
вызывает снижение термического КПД цикла с подводом теплоты при постоянном давлении. Отсюда следует, что с увеличением нагрузки и удлинением процесса горения топлива экономичность двигателя уменьшается. Это следует учитывать наряду с другими обстоятельствами при определении оптимального режима работы двигателя.
Цикл Тринклера или цикл со смешанным подводом теплоты, по которому работают современные бескомпрессорные дизели (рис.7.3), осуществляется по следующей схеме. Адиабата 1-2соответствует сжатию в цилиндре воздуха до температуры, превышающей температуру самовоспламенения топлива. Изохора 2-3 соответствует процессу горения топлива, впрыскиваемого в цилиндр, а изобара 3-4 изображает процесс горения остальной части топлива по мере поступления его из форсунки. Расширение продуктов сгорания идет по адиабате 4-5, а изохора 5-1соответствует выхлопу отработавших газов в атмосферу. Таким образом, теплота q1подводится в двух процессах 2-3 и 3-4.
q1= q11 + q12 . (7.11)
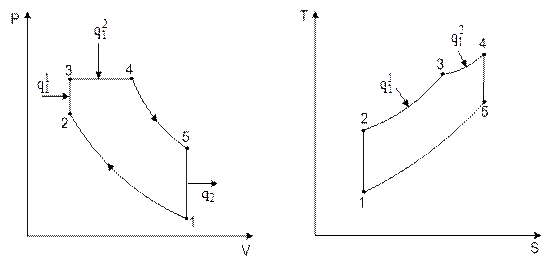
Рис.7.3. Идеальный цикл Тринклера со смешанным подводом теплоты в P-V и T-S диаграммах
Выражение для термического КПД цикла со смешанным подводом теплоты записывается в следующем виде:
 . (7.12)
. (7.12)
Параметр 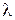 называется степенью повышения давления в изохорном процессеи рассчитывается по формуле
называется степенью повышения давления в изохорном процессеи рассчитывается по формуле
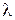 = Рз/Р2 . (7.13)
= Рз/Р2 . (7.13)
В двигателях, работающих по циклу Тринклера, распыление топлива производится топливным насосом высокого давления, а компрессор, применяемый при пневматическом распылении топлива, отсутствует. Степень сжатия в рассматриваемом цикле может достигать 18.
Выражение (7.12) является общим для циклов поршневых ДВС и при 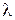 =1 и
=1 и 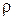 =1 переходит в соответствующие формулы для термического КПД циклов с подводом теплоты при постоянном давлении или постоянном объеме. Сравнение эффективности рассмотренных циклов проведем с помощью T-S диаграммы (рис. 7.4), предположив, что в каждом из них достигается одинаковая максимальная температура Т3. Одинаковы и количества отведенной теплоты q2в каждом цикле (площадь 14ав). При таких условиях полезно используемая теплота цикла, равная полезной работе цикла, будет наибольшей для цикла Дизеля 12'34 и наименьшей для цикла Отто 1234. Цикл Тринклера 1dс34занимает промежуточное положение.
=1 переходит в соответствующие формулы для термического КПД циклов с подводом теплоты при постоянном давлении или постоянном объеме. Сравнение эффективности рассмотренных циклов проведем с помощью T-S диаграммы (рис. 7.4), предположив, что в каждом из них достигается одинаковая максимальная температура Т3. Одинаковы и количества отведенной теплоты q2в каждом цикле (площадь 14ав). При таких условиях полезно используемая теплота цикла, равная полезной работе цикла, будет наибольшей для цикла Дизеля 12'34 и наименьшей для цикла Отто 1234. Цикл Тринклера 1dс34занимает промежуточное положение.

Рис.7.4. Идеальные циклы ДВС при V=const, P=const и цикл Тринклера с одинаковой температурой Т3
Таким образом, термический КПД, характеризующий степень термодинамического совершенства цикла, будет наибольшим для цикла с подводом теплоты при постоянном давлении и наименьшим для цикла с подводом теплоты при постоянном объеме.
megalektsii.ru