







Рассуждая аналогично пункту 4.3 составим основные уравнения асинхронного двигателя.
Напряжение U1, приложенное к фазе обмотки статора, уравновешивается основной ЭДС E1, ЭДС рассеяния и падением напряжения на активном сопротивлении обмотки статора.
В роторной обмотке аналогичное уравнение будет иметь вид:
Но т.к. роторная обмотка замкнута, то напряжение U2=0, и если учесть еще, что E2s=SE2и x2s=Sx2 , то уравнение можно переписать в виде:
Уравнение токов асинхронного двигателя повторяет аналогичное уравнение трансформатора:
,
где
.
Для того чтобы параметры ротора и статора изобразить на одной векторной диаграмме, произведем приведение параметров обмотки ротора к параметрам обмотки статора. При этом обмотку ротора с числом фаз m2, обмоточным коэффициентом k2и числом витков W2заменяют обмоткой с m1×k1×W1, соблюдая при этом энергетический баланс в роторе.
Не останавливаясь на методике приведения параметров, которая повторяется из раздела "трансформаторы", перепишем основные уравнения приведенного асинхронного двигателя:
1. 2.3.
Используя принципы построения векторной диаграммы для трансформатора, построим ее для асинхронного двигателя.
Вначале во втором основном уравнении величину r2' представим в виде:
,
что математически не противоречит друг другу.
Тогда само уравнение можно переписать:
Используя три основных уравнения двигателя, построим векторную диаграмму, которая, будет несколько напоминать диаграмму трансформатора (рис. 5.7.1).
Вторичное напряжение определяется вектором:
,
иначе говоря, асинхронный двигатель в электрическом отношении работает как трансформатор при активной нагрузке.
Мощность, отдаваемая вторичной обмоткой данного трансформатора
,
представляет собой полную механическую мощность, развиваемую двигателем.
Уравнениям ЭДС и токов соответствует эквивалентная схема замещения (рис. 5.8.1.). Таким образом, сложную магнитную цепь электрической машины можно заменить электрической схемой. Сопротивление r2'(1 - S)/S можно рассматривать как внешнее сопротивление, включенное в обмотку ротора. Оно является единственным переменным параметром схемы. Изменение этого сопротивления эквивалентно изменению нагрузки на валу двигателя, а следовательно, изменению скольжения S.
В обмотку статора из сети поступает мощность P1. Часть этой мощности идет на потери в стали Pсl, а также потери в обмотке статора Рэ1:
Оставшаяся мощность посредством магнитного потока передается на ротор и называется электромагнитной мощностью:
Часть электромагнитной мощности затрачивается на покрытие электрических потерь в обмотке ротора:
Оставшаяся мощность преобразуется в механическую, получившую название полной механической мощности:
Р2'=Рэм-Рэ2
Воспользовавшись ранее полученной формулой
запишем выражение полной механической мощности:
тогда
или
Рэ2=SРэм,
т.е. мощность электрических потерь пропорциональна скольжению.
Мощность на валу двигателя P2меньше полной механической мощности Р2’ на величину механических Рмехи добавочных Рдобпотерь:
Р2=Р2’-(Рмех.+Рдоб.).
Таким образом:
Р2=Р1-SP,
где
SP=Pсl+Рэ1+Рэ2+Рмех.+Рдоб.
Коэффициент полезного действия есть отношение мощности на валу P2к потребляемой мощности P1:
studfiles.net
Основной магнитный поток Ф в асинхронном двигателе создается совместным действием МДС обмоток статора F1 и ротора F2:
= (1 + 2) / Rм = 0 / Rм (12.10)
где Rм — магнитное сопротивление магнитной цепи двигателя потоку Ф; F0 — результирующая МДС двигателя, численно равная МДС обмотки статора в режиме х.х. [см. (9.16)]:
F0 = 0,45m1 I1 ω1 kоб1/ P (12.11)
I0 — ток х.х. в обмотке статора, А.
МДС обмоток статора и ротора на один полюс в режиме нагруженного двигателя
F1 = 0,45 m1 I1 ω1 kоб1/ P
F2 = 0,45 m2 I2 ω2 kоб2/ P (12.2)
где m2 — число фаз в обмотке ротора; ko62 — обмоточный коэффициент обмотки ротора.
При изменениях нагрузки на валу двигателя меняются токи в статоре I1, и роторе I2. Но основной магнитный поток Ф при этом сохраняется неизменным, так как напряжение, подведенное к обмотке статора, неизменно (U1 = const) и почти полностью уравновешивается ЭДС Е1 обмотки статора [см. (12.3)]:
1 ≈ (-1) (12.13)
Так как ЭДС Е1 пропорциональна основному магнитному потоку Ф [см. (7.20)], то последний при изменениях нагрузки остается неизменным. Этим и объясняется то, что, несмотря на изменения МДС F1 и F2, результирующая МДС остается неизменной, т. е. 0 = 1 +2 = const.
Подставив вместо F0, F1 и F2 их значения по (12.11) и (12.12), получим
0,45 m1 0 ω1 kоб1/ p = 0,45m1 1 ω1 kоб1/ p + 0,45 m2 2 ω2 ko62/ р.
Разделив это равенство на m1 ω1 kоб1/ p, определим уравнение токов асинхронного двигателя:
0 = 1 + 2 =1 + ′2 (12.14)
где
′2=2(12.15)
- ток ротора, приведенный к обмотке статора.
Преобразовав уравнение (12.14), получим уравнение токов статора асинхронного двигателя
1 =0 + (-′2) (12.16)
из которого следует, что ток статора в асинхронном двигателе 1 имеет две составляющие: 0 - намагничивающую (почти постоянную) составляющую ( I0 ≈ I1μ ) и -′2 —переменную составляющую, компенсирующую МДС ротора.
Следовательно, ток ротора I2 оказывает на магнитную систему двигателя такое же размагничивающее влияние, как и ток вторичной обмотки трансформатора (см. § 1.5). Таким образом, любое изменение механической нагрузки на валу двигателя сопровождается соответствующим изменением тока в обмотке статора I1 так изменение этой нагрузки двигателя вызывает изменение скольжения s. Это, в свою очередь, влияет на ЭДС обмотки ротора [см.(12.6)], а следовательно, и на ток ротора I2. Но так как этот ток развивает размагничивающее действие на магнитную систему двигателя, то его изменения вызывают соответствующие изменение тока в обмотке статора I1 за счет составляющей – I′2 . Так, в режиме холостого хода, когда нагрузка на валу двигателя отсутствует и s ≈ 0, ток I2≈ 0. В этом случае ток в обмотке статора 1 ≈0. Если же ротор двигателя затормозить, не отключая обмотку статopa от сети (режим короткого замыкания), то скольжение s = 1 и ЭДС обмотки ротора Е2s достигает своего наибольшего значения Е2. Также наибольшего значения достигнет ток I2, а следовательно, и ток в обмотке статора I1.
studfiles.net
Рассуждая аналогично пункту 4.3 составим основные уравнения асинхронного двигателя.
Напряжение U1, приложенное к фазе обмотки статора, уравновешивается основной ЭДС E1, ЭДС рассеяния и падением напряжения на активном сопротивлении обмотки статора.
В роторной обмотке аналогичное уравнение будет иметь вид:
Но т.к. роторная обмотка замкнута, то напряжение U2=0, и если учесть еще, что E2s=SE2 и x2s=Sx2 , то уравнение можно переписать в виде:
Уравнение токов асинхронного двигателя повторяет аналогичное уравнение трансформатора:
,
где
.
Для того чтобы параметры ротора и статора изобразить на одной векторной диаграмме, произведем приведение параметров обмотки ротора к параметрам обмотки статора. При этом обмотку ротора с числом фаз m2, обмоточным коэффициентом k2 и числом витков W2 заменяют обмоткой с m1×k1×W1, соблюдая при этом энергетический баланс в роторе.
Не останавливаясь на методике приведения параметров, которая повторяется из раздела "трансформаторы", перепишем основные уравнения приведенного асинхронного двигателя:
1. 2.3.
Используя принципы построения векторной диаграммы для трансформатора, построим ее для асинхронного двигателя.
Вначале во втором основном уравнении величину r2' представим в виде:
,
что математически не противоречит друг другу.
Тогда само уравнение можно переписать:
Используя три основных уравнения двигателя, построим векторную диаграмму, которая, будет несколько напоминать диаграмму трансформатора (рис. 5.7.1).
Вторичное напряжение определяется вектором:
,
иначе говоря, асинхронный двигатель в электрическом отношении работает как трансформатор при активной нагрузке.
Мощность, отдаваемая вторичной обмоткой данного трансформатора
,
представляет собой полную механическую мощность, развиваемую двигателем.
Уравнениям ЭДС и токов соответствует эквивалентная схема замещения (рис. 5.8.1.). Таким образом, сложную магнитную цепь электрической машины можно заменить электрической схемой. Сопротивление r2'(1 - S)/S можно рассматривать как внешнее сопротивление, включенное в обмотку ротора. Оно является единственным переменным параметром схемы. Изменение этого сопротивления эквивалентно изменению нагрузки на валу двигателя, а следовательно, изменению скольжения S.
В обмотку статора из сети поступает мощность P1. Часть этой мощности идет на потери в стали Pсl, а также потери в обмотке статора Рэ1:
Оставшаяся мощность посредством магнитного потока передается на ротор и называется электромагнитной мощностью:
Часть электромагнитной мощности затрачивается на покрытие электрических потерь в обмотке ротора:
Оставшаяся мощность преобразуется в механическую, получившую название полной механической мощности:
Р2'=Рэм-Рэ2
Воспользовавшись ранее полученной формулой
запишем выражение полной механической мощности:
тогда
или
Рэ2=SРэм,
т.е. мощность электрических потерь пропорциональна скольжению.
Мощность на валу двигателя P2 меньше полной механической мощности Р2’ на величину механических Рмех и добавочных Рдоб потерь:
Р2=Р2’-(Рмех.+Рдоб.).
Таким образом:
Р2=Р1-SP,
где
SP=Pсl+Рэ1+Рэ2+Рмех.+Рдоб.
Коэффициент полезного действия есть отношение мощности на валу P2 к потребляемой мощности P1:
studfiles.net
Аналогично трансформатору можно представить эквивалентные схемы ротора и статора (Рис.3.12 и 3.13):
Рис.3.12 Рис.3.13
Согласно II закону Кирхгофа запишем уравнения соответствующие данным схемам:
где: U1 - напряжение сети;
X1, R1 - реактивное и активное сопротивления статора;
X2s, R2 - реактивное и активное сопротивления ротора;
E1 ,E2s - э.д.с. статора и ротора.
Для пуска двигателя (s = 1) имеем:
Когда ротор вращается (0 < s < 1), первое уравнение остается неизменным, а второе трансформируется в:
откуда .
Подставляя в уравнение следующее выражение
,
получим ,
где: - эквивалентная нагрузка двигателя.
Активная электрическая мощность трехфазного асинхронного двигателя известна
,.
где два первых члена уравнения соответствуют электрическим потерям в статоре и роторе, а третий определяет электрическую мощность, которая преобразуется в механическую.
Согласно классической формуле механики имеем
Pмех = M = Ms (1 - s),
где: M - механический момент [Н м];
- угловая скорость [рад/сек].
Приравнивая электрическую и механическую мощности, получим
= M s (1 - s),
откуда формула момента будет
.
Считая, что аналогично трансформатору, выделим из основных уравнений асинхронного двигателя ток ротора I2, исключая при этом э.д.с. E2 :
Пренебрегая падениями напряжения I1R1 и I1X1 по сравнению с U1, получим:
.
И тогда окончательно в действующих значениях будем иметь:
В результате выражение для вращающего момента будет иметь вид:
Зависимость М = f(s) имеет кубический характер (Рис.3.14).
Рис.3.14
Эта кривая имеет четыре характерных точки:
1)s = 0, M = 0 холостой ход;
2) s = sкр, M = Mмакс;
3) s = sкр, M = Mн;
4) s = 1, M = Mп.
В интервале 0 < s < 1 электрическая машина работает в режиме двигателя и вращающий момент достигает максимума при s = sкр = R2 /X2.
Для скольжения больше чем критическое sкр работа двигателя носит неустойчивый характер, поэтому на участке sкр s 1 происходит пуск двигателя.
Зная sкр и Ммаксможно записать эмпирическую формулу Клосса для вращающего момента:
.
На практике номинальный момент двигателя достигает половины максимального момента, при этом скольжение составляет около 5%.
Характеристика момент-частота вращения М = f(n) называется двигателя. Зная, что n = ns ( 1 - s ), представим эту кривую на рисунке 3.15.
Рис.3.15
Уравнение баланса мощностей для АД представлено следующим выражением:
P1 = P2 + Pмг + Pэл + Pмех,
где: P1 - потребляемая, электрическая мощность;
P2 - полезная, механическая мощность;
Pмех - механические потери на трение в подшипниках, независящие от нагрузки;
Pмг = Pмгс + P мгр- магнитные потери в статоре и роторе, независящие от нагрузки;
Pэл = Pэлс + Pэлр - электрические потери в статоре и роторе.
Преобразование электрической энергии в механическую осуществляется с помощью энергии электромагнитного поля (мощность электромагнитного поля Рэлм). Можно представить баланс мощностей в виде диаграммы (Рис.3.16) и тогда КПД двигателя будет
.
Электрические потери зависят от нагрузки, а значит и КПД тоже является функцией нагрузки. Для большинства асинхронных двигателей КПД достаточно высок и находится в интервале от 80% до 90%.
Рис.3.16
studfiles.net
Рабочими характеристиками называют графические зависимости частоты вращения п2 (или скольжения s),момента на валу М2 , тока статора I1 , коэффициента полезного действия η и cos φ1от полезной мощности Р2 при U1 = const и f1 = const. Их определяют экспериментально или путем расчета по схеме замещения или круговой диаграмме.
Примерный вид рабочих характеристик асинхронного двигателя показан на рис. 4.25. Частота вращения, ток статора, момент на валу, потребляемая и полезная мощности приведены на графике в относительных единицах. Рабочие характеристики строят только для зоны практически устойчивой работы двигателя, т. е. до скольжения (1,1 ÷ l,2)sном .
Из последнего выражения видно, что вращающий момент асинхронного двигателя зависит от скольжения. На фиг. 224 изображена кривая А зависимости вращающего момента двигателя от скольжения. Из кривой видно, что в момент пуска, когда s=l и n = 0, вращающий момент двигателя невелик. Это объясняется тем, что в момент пуска частота тока в обмотке ротора наибольшая и индуктивное сопротивление обмотки велико. Вследствие этого cos имеет малое значение (по-
При некотором скольжении S1 вращающий момент двигателя будет иметь максимальное значение. При дальнейшем уменьшении скольжения или, иначе говоря, при даль, нейшем увеличении скорости вращения двигателя его момент будет быстро умень-
шаться и при скольжении s = 0 момент вращения двигателя бу- • дет также равен нулю.
Следует оговориться, что у асинхронного двигателя скольжение, равное нулю, практически быть не может. Это возможно лишь в том случае, если ротору сообщить извне вращающий момент в сторону вращения поля статора.
Пусковой момент можно увеличить, если в момент пуска уменьшить сдвиг фаз между током и э. д. с. ротора. Из формулы
видно, что если при постоянном индуктивном сопротивлении обмотки ротора увеличить активное сопротивление, то и сам угол будут уменьшаться, что приведет к тому, что и вращающий момент двигателя станут больше. Этим пользуются на практике для увеличения пускового вращающего момента двигателя. В момент пуска в цепь ротора вводят активное сопротивление (пусковой реостат), которое затем выводят, как только двигатель увеличит скорость. Увеличение пускового момента приводит к тому, что максимальный вращающий момент двигателя получается при большем скольжении (точка S2 кривой B на фиг. 224). Путем увеличения активного сопротивления цепи ротора при пуске можно добиться того, что максимальный вращающий момент будет в момент пуска (s = 1 кривой С). Вращающий момент асинхронного двигателя пропорционален квадрату напряжения, поэтому даже небольшое уменьшение напряжения сопровождается резким уменьшением вращающего момента.
studfiles.net
Как следует из принципа действия асинхронного двигателя (см. § 6.2), обмотка ротора не имеет электрической связи с обмоткой статора. Между этими обмотками существует только магнитная связь, и энергия из обмотки статора передается в обмотку ротора магнитным полем. В этом отношении асинхронная машина аналогичнатрансформатору: обмотка статора является первичной, а обмотка ротора - вторичной.
В процессе работы асинхронного двигателя токи в обмотках статора и ротора создают две магнитодвижущие силы; МДС статора и МДС ротора. Совместным действием эти МДС наводят в магнитной системе двигателя результирующий магнитный поток, вращающийся относительно статора с синхронной частотой вращения n1. Так же как и в трансформаторе, этот магнитный поток можно рассматривать состоящим из основного потока Ф, сцепленного как с обмоткой статора, так и с обмоткой ротора (магнитный поток взаимоиндукции), и двух потоков рассеяния: Фσ1 — потока рассеяния обмотки статора и Ф σ2 — потока рассеяния обмотки ротора (см. § 11.3). Рассмотрим, какие ЭДС наводят указанные потоки в обмотках двигателя.
Электродвижущие силы, наводимые в обмотке статора. Основной магнитный поток Ф, вращающийся с частотой n1 наводит в неподвижной обмотке статора ЭДС Е1, значение которой определяется выражением [см. (7.20)] E1 = 4,44 f1 Ф ω1 kоб1.
Магнитный поток рассеяния Фσ1 наводит в обмотке статора ЭДС рассеяния, значение которой определяется индуктивным падением напряжения в обмотке статора:
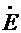 σ1 = - j
σ1 = - j  1x1
1x1 (12.1)
(12.1)
где х1 — индуктивное сопротивление рассеяния фазной обмотки статора [см. (11.6)],Ом.
Для цепи обмотки статора асинхронного двигателя, включенной в сеть с напряжением U1, запишем уравнение напряжений по второму закону Кирхгофа:
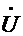 1 +
1 + 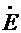 1 +
1 + 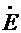 σ1 =
σ1 =  1 r1, (12.2)
1 r1, (12.2)
где I1 r1 - падение напряжения в активном сопротивлении обмотки статора r1.
После переноса ЭДС E1, и Eσ1 , в правую часть уравнения (12.2) с учетом (12.1) получим уравнение напряжений обмотки статора асинхронного двигателя:
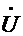 1 = (-
1 = (- 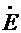 1) + j
1) + j  1 x1 +
1 x1 +  1r1 (12.3)
1r1 (12.3)
Сравнив полученное уравнение с уравнением (1.13), видим, что оно не отличается от уравнения напряжений для первичной цепи трансформатора.
Электродвижущие силы, наводимые в обмотке ротора.В процессе работы асинхронного двигателя ротор вращается в сторону вращения поля статора с частотой n2. Поэтому частота вращения поля статора относительно ротора равна разности частот вращения (n1 – n2). Основной магнитный поток Ф, обгоняя ротор с частотой вращения ns = (n1 - n2), индуцирует в обмотке ротора ЭДС
Е2 = 4,44 f2 Ф ω2 коб2 (12.4)
где f2— частота ЭДС Е2s в роторе, Гц; ω2 — число последовательно соединенных витков одной фазы обмотки ротора; ko62 — обмоточный коэффициент обмотки ротора.
Частота ЭДС (тока) в обмотке вращающегося ротора пропорциональна частоте вращения магнитного поля относительно ротора ns = n1 - n2, называемой частотой скольжения:
f2 = pns / 60 = p(n1 – n2) / 60,
или
f2 = 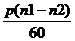
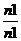 =
= 
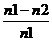 = f1s (12.5)
= f1s (12.5)
т. е. частота ЭДС (тока) ротора пропорциональна скольжению. Для асинхронных двигателей общепромышленного назначения эта частота обычно невелика и при f1 = 50 Гц не превышает нескольких герц, так при s = 5% частота f2 = 50 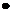 0,05 = 2,5 Гц. Подставив (12.5) в (12.4), получим
0,05 = 2,5 Гц. Подставив (12.5) в (12.4), получим
E2s = 4,44 f1 s Ф ω2 kоб2 = E2 s. (12.6)
Здесь Е2 - ЭДС, наведенная в обмотке ротора при скольжении s = 1, т. е. при неподвижном роторе, В.
Поток рассеяния ротора Фσ2 индуцирует в обмотке ротора рассеяния, значение которой определяется индуктивным падением напряжения в этой обмотке:
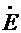 σ2 = - j
σ2 = - j  2 x2 s (12.7)
2 x2 s (12.7)
где х2 - индуктивное сопротивление рассеяния обмотки ротора при неподвижном роторе [см. (11.8)], Ом.
Обмотка ротора асинхронного двигателя электрически не связана с внешней сетью и к ней не подводится напряжение. Ток в этой обмотке появляется исключительно за счет ЭДС, наведенной основным магнитным потоком Ф. Поэтому уравнение напряжений для цепи ротора асинхронного двигателя по второму закону Кирхгофа имеет вид
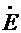 2s +
2s + 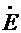 σ2 =
σ2 =  2 r2
2 r2
где r2 — активное сопротивление обмотки ротора. С учетом (12.6) и (12.7) получим
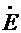 2s - j
2s - j  2 x2 s -
2 x2 s -  2 r2 (12.8)
2 r2 (12.8)
Разделив все слагаемые равенства (12.8) на s, получим
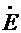 2 - j
2 - j  2 x2 -
2 x2 -  2 r2 / s = 0 (12.9)
2 r2 / s = 0 (12.9)
-уравнение напряжений для обмотки ротора.
§ 12.2. Уравнения МДС и токов асинхронного двигателя
Основной магнитный поток Ф в асинхронном двигателе создается совместным действием МДС обмоток статора F1 и ротора F2:
 = (
= ( 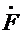 1 +
1 + 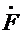 2) / Rм =
2) / Rм = 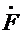 0 / Rм (12.10)
0 / Rм (12.10)
где Rм — магнитное сопротивление магнитной цепи двигателя потоку Ф; F0 — результирующая МДС двигателя, численно равная МДС обмотки статора в режиме х.х. [см. (9.16)]:
F0 = 0,45m1 I1 ω1 kоб1/ P (12.11)
I0 — ток х.х. в обмотке статора, А.
МДС обмоток статора и ротора на один полюс в режиме нагруженного двигателя
F1 = 0,45 m1 I1 ω1 kоб1/ P
F2 = 0,45 m2 I2 ω2 kоб2/ P (12.2)
где m2 — число фаз в обмотке ротора; ko62 — обмоточный коэффициент обмотки ротора.
При изменениях нагрузки на валу двигателя меняются токи в статоре I1, и роторе I2. Но основной магнитный поток Ф при этом сохраняется неизменным, так как напряжение, подведенное к обмотке статора, неизменно (U1 = const) и почти полностью уравновешивается ЭДС Е1 обмотки статора [см. (12.3)]:
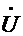 1 ≈ (-
1 ≈ (- 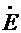 1) (12.13)
1) (12.13)
Так как ЭДС Е1 пропорциональна основному магнитному потоку Ф [см. (7.20)], то последний при изменениях нагрузки остается неизменным. Этим и объясняется то, что, несмотря на изменения МДС F1 и F2, результирующая МДС остается неизменной, т. е. 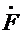 0 =
0 = 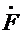 1 +
1 + 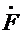 2 = const.
2 = const.
Подставив вместо F0, F1 и F2 их значения по (12.11) и (12.12), получим
0,45 m1 0 ω1 kоб1/ p = 0,45m1
0 ω1 kоб1/ p = 0,45m1 1 ω1 kоб1/ p + 0,45 m2
1 ω1 kоб1/ p + 0,45 m2  2 ω2 ko62/ р.
2 ω2 ko62/ р.
Разделив это равенство наm1 ω1 kоб1/ p, определим уравнение токов асинхронного двигателя:
 0 =
0 =  1 +
1 +  2
2 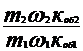 =
=  1 +
1 +  ′2
′2  (12.14)
(12.14)
где
 ′2
′2  =
=  2
2 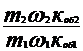 (12.15)
(12.15)
- ток ротора, приведенный к обмотке статора.
Преобразовав уравнение (12.14), получим уравнение токов статора асинхронного двигателя
 1 =
1 =  0 + (-
0 + (-  ′2
′2  ) (12.16)
) (12.16)
из которого следует, что ток статора в асинхронном двигателе  1 имеет две составляющие:
1 имеет две составляющие:  0 - намагничивающую (почти постоянную) составляющую ( I0 ≈ I1μ ) и -
0 - намагничивающую (почти постоянную) составляющую ( I0 ≈ I1μ ) и -  ′2 —переменную составляющую, компенсирующую МДС ротора.
′2 —переменную составляющую, компенсирующую МДС ротора.
Следовательно, ток ротора I2 оказывает на магнитную систему двигателя такое же размагничивающее влияние, как и ток вторичной обмотки трансформатора (см. § 1.5). Таким образом, любое изменение механической нагрузки на валу двигателя сопровождается соответствующим изменением тока в обмотке статора I1 так изменение этой нагрузки двигателя вызывает изменение скольжения s. Это, в свою очередь, влияет на ЭДС обмотки ротора [см.(12.6)], а следовательно, и на ток ротора I2. Но так как этот ток развивает размагничивающее действие на магнитную систему двигателя, то его изменения вызывают соответствующие изменение тока в обмотке статора I1 за счет составляющей – I′2 . Так, в режиме холостого хода, когда нагрузка на валу двигателя отсутствует и s ≈ 0, ток I2≈ 0. В этом случае ток в обмотке статора  1 ≈
1 ≈  0. Если же ротор двигателя затормозить, не отключая обмотку статopa от сети (режим короткого замыкания), то скольжение s = 1 и ЭДС обмотки ротора Е2s достигает своего наибольшего значения Е2. Также наибольшего значения достигнет ток I2, а следовательно, и ток в обмотке статора I1.
0. Если же ротор двигателя затормозить, не отключая обмотку статopa от сети (режим короткого замыкания), то скольжение s = 1 и ЭДС обмотки ротора Е2s достигает своего наибольшего значения Е2. Также наибольшего значения достигнет ток I2, а следовательно, и ток в обмотке статора I1.
stydopedya.ru
Блок реализует математическую модель асинхронного двигателя (ДА).
В системах автоматического регулирования применяют как трехфазные, так и двухфазные асинхронные электродвигатели. Трехфазные ДА являются двигателями общепромышленного применения, двухфазные ДА – это специальные двигатели, получившие название исполнительных асинхронных двигателей (ИДА).
Расчетная схема и дифференциальные уравнения
Как двухфазные, так и трехфазные ДА принято описывать системой дифференциальных уравнений в неподвижной системе координат. При этом трехфазные машины приводят к двухфазным. Расчетная схема ДА представлена на рисунках 1 и 2:
Рисунок 1
Рисунок 2
Система дифференциальных уравнении ДА для неподвижной системы координат, связанной со статором, и вращающейся системы координат, связанной с ротором, имеет вид:
(1)
где– активные сопротивления обмоток статора и ротора;
– потокосцепления статора и ротора по осямисоответственно.
ЭДС вращения, вводимые в уравнения обмоток ротора, определяются как
(2)
где– частота вращения ротора,– число пар полюсов,– частота вращения электромагнитного поля (частота питающего напряжения),.
Потокосцепления обмоток машины равны:
(3)
где– коэффициенты самоиндукции обмоток статора и ротора, – коэффициент взаимоиндукции между контурами статора и ротора при совпадении их осей.
Решая систему линейных уравнений (3), получаем:
(4)
Уравнение равновесия моментов:
(5)
(6)
s — коэффициент скольжения вектора скорости вращения ротора относительно вектора вращающегося магнитного поля.
При записи через потокосцепления и токи, электромагнитный момент для двухфазного ДА равен:
(7)
Электромагнитный момент для трехфазного ДА равен
(8)
Уравнения состояния асинхронного электродвигателя
Результирующий магнитный поток, созданный какой-либо обмоткой обобщенной машины принято подразделять на основной магнитный поток и поток рассеяния, например, поток, созданный обмоткой статора, равен, где– основной магнитный поток, – поток рассеяния. Соответственно индуктивности обмоток можно разделить на основные и индуктивности рассеяния:
(9)
и индуктивные сопротивления:
Введем равенство:
или
где– индуктивность цепи намагничивания;
– индуктивное сопротивление цепи намагничивания;
– индуктивность рассеяния обмотки статора;
– приведенная индуктивность рассеяния обмотки ротора;
– индуктивность основного потока обмотки статора;
– приведенная индуктивность основного потока обмотки ротора;
– приведенные взаимоиндуктивности обмоток.
Систему уравнений ДА (1) – (7) запишем в форме Коши, одновременно заменяя токи обмоток через функции потокосцеплений, а индуктивности обмоток через основные и индуктивности рассеяния. Из системы уравнений (3) находим:
(10)
Заменяя токи в выражении (7) получаем
(11)
где– число фаз питающего напряжения.
Подставляем полученные значения токов и момента в уравнения (1) и (4), обозначая, имеем
(12)
Уравнения (12) можно рассматривать как уравнения состояния ДА. В качестве переменных состояния здесь выступают проекции потокосцеплений на ортогональные оси, угловая скорость вращения ротора и угол поворота ротора. Внешними воздействиями на двигатель являются напряжения статора (образующие вектор управления) и момент сил сопротивления.
Блок имеет 3 входных и 3 выходных сигнала.
Входные сигналы:
Напряжение на обмотке статорав неподвижной системе координат, В.
Напряжение на обмотке статорав неподвижной системе координат, В.
Возмущающий момент , Н·м.
Выходные сигналы:
Угол поворота вала, рад.
Угловая скорость (частота) вращения , рад/с.
Электромеханический момент на валу ротора двигателя, Н·м;
Дополнительно на третий выход можно выводить:
Ток в обмотке статора, А.
Ток в обмотке статора, А.
Свойства:
Сопротивление цепи статора, Ом;
Сопротивление цепи ротора, Ом;
Индуктивность цепи статора, Гн;
Индуктивность цепи ротора, Гн;
Взаимная индуктивность, Гн;
Момент инерции, приведённый к валу ротора, кг·м2.
Число полюсов, шт.
Число фаз питающего напряжения, шт.
Начальный угол поворота ротора, рад.
Начальная частота вращения ротора, рад/c.
Начальное потокосцепление в обмотке q статора, В·с.
Начальное потокосцепление в обмотке q ротора, В·с.
Начальное потокосцепление в обмотке d статора, В·с.
Начальное потокосцепление в обмотке d ротора, В·с.
Дополнительный вывод.
simintech.ru