





При частотном регулировании
При частотном регулировании частоту переменных статора и синхронную скорость поля обычно представляют в относительных единицах
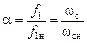 , (2.31)
, (2.31)
где 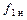 - номинальная частота,
- номинальная частота, 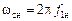 - синхронная скорость поля при номинальной частоте.
- синхронная скорость поля при номинальной частоте.
От скольжения s переходят к абсолютному скольжению
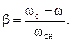 (2.32)
(2.32)
Здесь за базовую величину принята синхронная скорость поля при номинальной частоте.
Связь между 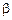 и s описывается равенством
и s описывается равенством
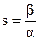 (2.33)
(2.33)
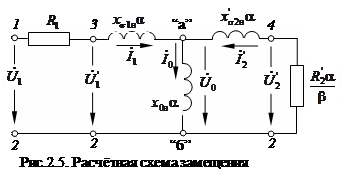 В схеме замещения (рис.2.5) в качестве переменных характеризующих нагрузку и частоту выступают: абсолютное скольжение
В схеме замещения (рис.2.5) в качестве переменных характеризующих нагрузку и частоту выступают: абсолютное скольжение 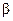 и относительная частота
и относительная частота 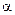 .
.
Ротор, как и ранее, представляется заторможенным, а его параметры приведены к числу витков статора. Все индуктивные сопротивления и напряжения на отдельных участках схемы замещения зависят от частоты:
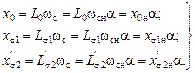 (2.34)
(2.34)
Уравнения для напряжений (2.13) принимают вид:
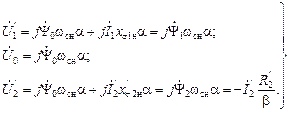 (2.35)
(2.35)
В этих уравнениях индуктивные сопротивления 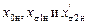 соответствуют номинальной частоте. Разделив обе части уравнений (2.35) на
соответствуют номинальной частоте. Разделив обе части уравнений (2.35) на 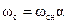 , и перейдя к действующим значениям, получим:
, и перейдя к действующим значениям, получим:
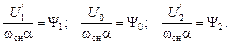 (2.36)
(2.36)
Эти равенства очень важные, так как характеризуют основные законы частотного регулирования:
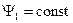 ,
, 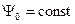 ,
, 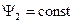 .
.
При частотном регулировании скорости вниз от номинальной скорости ( 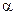 < 1) одновременно регулируют и модуль напряжения на определённом участке схемы замещения. В этом случае стабилизируется соответствующее потокосцепление.
< 1) одновременно регулируют и модуль напряжения на определённом участке схемы замещения. В этом случае стабилизируется соответствующее потокосцепление.
Регулирование скорости вверх от номинальной скорости выполняют при ослабленном поле. В этом случае напряжение поддерживают на постоянном уровне.
Выражения для ЭДС статора и ротора можно представлять в разных формах записи:
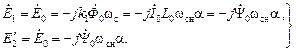 (2.37)
(2.37)
Связь между токами устанавливается по ранее рассмотренной методике.
Из схемы замещения видно, что при 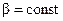 с уменьшением частоты, то есть
с уменьшением частоты, то есть 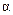 , уменьшаются все индуктивные сопротивления, что приводит к возрастанию тока статора и тока намагничивания. Это, в свою очередь, приводит к повышению степени насыщения магнитной системы. Так, если при идеальном холостом ходе уменьшить частоту в два раза, то магнитный поток
, уменьшаются все индуктивные сопротивления, что приводит к возрастанию тока статора и тока намагничивания. Это, в свою очередь, приводит к повышению степени насыщения магнитной системы. Так, если при идеальном холостом ходе уменьшить частоту в два раза, то магнитный поток 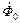 должен увеличиться в два раза, а ток намагничивания с учётом насыщении магнитопровода может увеличиться во много раз и стать больше номинального тока статора.
должен увеличиться в два раза, а ток намагничивания с учётом насыщении магнитопровода может увеличиться во много раз и стать больше номинального тока статора.
Выводы:
1. Магнитный поток 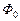 зависит не только от напряжения, но и от частоты.
зависит не только от напряжения, но и от частоты.
2. При частотном регулировании приходится регулировать не только частоту, но и модуль напряжения.
Схемы замещения асинхронного двигателя
С добавочными ЭДС
В электроприводах переменного тока вопросы динамики обычно решаются с помощью теории обобщённой электрической машины. В работах [9,10] отмечается, что с помощью схем замещения можно решать не только задачи статики, но и динамики.
Покажем, что между схемой замещения АД и теорией обобщённой электрической машины имеется тесная связь.
На рис.2.6 изображены две схемы замещения АД. Первая схема (а) относится к процессам в неподвижных системах координат: 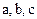 и
и  . Вторая схема относится к процессам во вращающихся системах координат:
. Вторая схема относится к процессам во вращающихся системах координат:  .
.
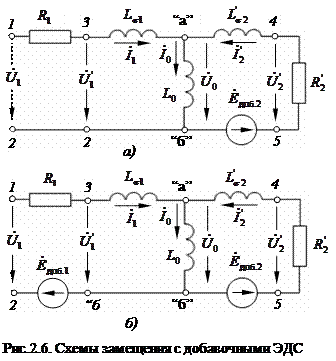
В приведенных схемах предполагается, что переменные и параметры ротора приведены к числу витков статора. Обмотки статора и ротора находятся в магнитном поле, вращающемся со скоростью 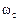 . Вращение машины и системы координат учитывается с помощью добавочных ЭДС вращения, которые должны удовлетворять условиям:
. Вращение машины и системы координат учитывается с помощью добавочных ЭДС вращения, которые должны удовлетворять условиям:
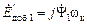 ,
, 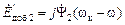 . (2.38)
. (2.38)
Положительные направления для этих ЭДС приняты совпадающими с направлением токов. В частном случае, когда система координат неподвижна, дополнительная ЭДС вводится только в ротор
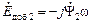 . (2.39)
. (2.39)
Вначале рассмотрим математическое описание процессов при неподвижной системе координат (рис.2.6а).
В контуре тока статора последовательно соединены две индуктивности 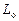 и
и 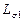 . В сумме они представляют полную индуктивность фазы статора
. В сумме они представляют полную индуктивность фазы статора 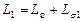 . В контуре тока ротора тоже имеется полная индуктивность
. В контуре тока ротора тоже имеется полная индуктивность 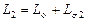 .
.
Проходя последовательно вдоль контуров, получаем уравнения для напряжений в контурах статора и ротора:
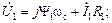
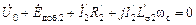
Если для контура ротора напряжение 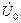 выразить через главное потокосцепление
выразить через главное потокосцепление 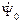 , то оно принимает вид:
, то оно принимает вид:
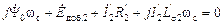 .
.
Первый и последний члены этого уравнения в сумме характеризуют ЭДС самоиндукции, наводимую в роторе потокосцеплением 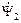
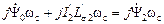 .
.
С учётом (2. 38) уравнение для контура ротора может быть записано в одной из следующих форм записи:
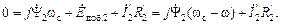
Таким образом, электромагнитные процессы в одной фазе описываются системой уравнений:
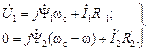 (2.40)
(2.40)
В этой системе уравнений скорость 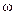 учитывается угловой частотой скольжения
учитывается угловой частотой скольжения 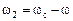 . Если в качестве переменной принимать эту частоту, то расчёт электромагнитных процессов можно выполнять без учёта механического процесса. Его можно проводить для одной фазы, не переходя к теории обобщённой электрической машины. Расчёт можно выполнять в аналитическом виде по методике предложенной в [4] или путём моделирования с помощью компьютера.
. Если в качестве переменной принимать эту частоту, то расчёт электромагнитных процессов можно выполнять без учёта механического процесса. Его можно проводить для одной фазы, не переходя к теории обобщённой электрической машины. Расчёт можно выполнять в аналитическом виде по методике предложенной в [4] или путём моделирования с помощью компьютера.
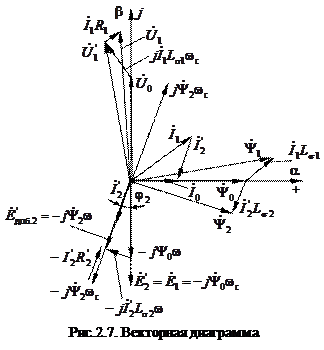 |
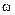 <
< 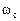 .
.
Раскроем физическую сущность отдельных составляющих в системе уравнений (2.40).
Выражение 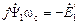 представляет собой ЭДС самоиндукции, наведённую в статоре потокосцеплением
представляет собой ЭДС самоиндукции, наведённую в статоре потокосцеплением 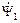 , в комплексной форме записи. Во временной форме записи эта ЭДС записывается так:
, в комплексной форме записи. Во временной форме записи эта ЭДС записывается так: 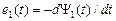 . На векторной диаграмме она действует встречно напряжению
. На векторной диаграмме она действует встречно напряжению 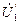 .
.
Выражение 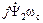 представляет собой ЭДС самоиндукции, наведённую в роторе потокосцеплением
представляет собой ЭДС самоиндукции, наведённую в роторе потокосцеплением 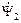 . Во временной форме записи это выражение принимает вид
. Во временной форме записи это выражение принимает вид 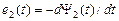 .
.
Выражение 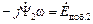 представляет собой ЭДС вращения наводимую в роторе потокосцеплением
представляет собой ЭДС вращения наводимую в роторе потокосцеплением 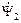 .
.
Из рис.2.6 и уравнения (2.40) следует, что при неподвижном роторе 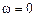 ток в роторе
ток в роторе 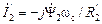 потребляется от источника питания. Знак минус характеризует фактическое направление тока
потребляется от источника питания. Знак минус характеризует фактическое направление тока 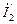 . Часть тока
. Часть тока 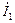 идёт на создание тока возбуждения
идёт на создание тока возбуждения 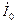 , а другая его часть, того же направления, передаётся в ротор для создания полезной мощности. При вращающемся роторе появляется добавочная ЭДС (2.39), ток в роторе пропорционален частоте скольжения
, а другая его часть, того же направления, передаётся в ротор для создания полезной мощности. При вращающемся роторе появляется добавочная ЭДС (2.39), ток в роторе пропорционален частоте скольжения 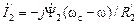 . В режиме идеального холостого хода
. В режиме идеального холостого хода 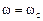 он становится равным нулю.
он становится равным нулю.
Перейдём к схеме замещения на рис.2.6б. Проходя, как и раньше, последовательно по контурам, получим:
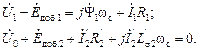
Выражая 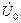 через потокосцепление
через потокосцепление 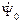 , и выполнив простые преобразования с учётом (2.38), получим:
, и выполнив простые преобразования с учётом (2.38), получим:
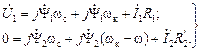 (2.41)
(2.41)
В правой части этих уравнений присутствуют ЭДС двух видов с разной физической сущностью:
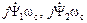 - ЭДС самоиндукции, наводимые периодически изменяющимися токами статора и ротора;
- ЭДС самоиндукции, наводимые периодически изменяющимися токами статора и ротора;
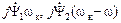 - ЭДС вращения или ЭДС взаимоиндукции с учётом взаимодействия с другими фазами. Эти ЭДС как раз и являются добавочными ЭДС (2.38).
- ЭДС вращения или ЭДС взаимоиндукции с учётом взаимодействия с другими фазами. Эти ЭДС как раз и являются добавочными ЭДС (2.38).
Векторная диаграмма на рис.2.7 отражает процессы в одной фазе. Для создания электромагнитного момента обязательно нужна ещё одна или две фазы. В этом случае состояния переменных рассматривают с помощью пространственных векторных диаграмм. Направим вдоль действительной оси + геометрическую ось фазы “а”, а вдоль мнимой оси расположим геометрическую ось фазы “b”. Получили пространственную плоскость поперечного сечения машины. На этой плоскости уже изображены в виде векторов все переменные.
Известно, что в ортогональных системах координат модули временных и пространственных векторов одинаковы. В этом случае временные и пространственные векторные диаграммы принимают одинаковый вид, изменяется лишь символика для переменных. Изменив символику, то есть, заменив точку над переменной чертой над переменной, получим пространственную векторную диаграмму.
Если теперь сравнивать процессы во временной и пространственной областях, то они совершенно разные.
В пространственной области изображающие вектора вращаются относительно геометрических осей отдельных фаз и отражают процессы во всех фазах.
Во временной области вектора вращаются относительно комплексной плоскости и отражают процессы только в одной фазе. Если их поведение рассматривать относительно геометрической оси рассматриваемой фазы, то они пульсируют во времени.
Вернёмся к уравнениям (2.41), которые описывают процессы во временной области, Если в этих уравнениях изменить всего лишь символику для переменных, то получим математическое описание процессов в пространственной области:
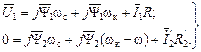 (2.42)
(2.42)
Эти уравнения являются основополагающими в теории обобщённой электрической машины, так как описывают электромагнитные процессы в статике и динамике.
Таким образом, путём простых преобразований, установлена связь между схемой замещения и теорией обобщённой электрической машины. Эта связь стала возможной благодаря введению в схему замещения добавочных ЭДС, которые описываются уравнениями (2.38) и (2.39).
2.5. Процесс преобразования энергии и
Электромагнитный момент
Асинхронный двигатель потребляет от источника питания активную и реактивную мощность.
Активную мощность можно записать в виде скалярного произведения вектора напряжения на вектор тока
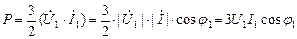 . (2.43)
. (2.43)
Напомним, что здесь 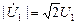 и
и 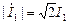 .
.
Реактивная мощность идёт на создание главного поля и полей рассеяния
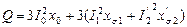 .
.
Важным энергетическим показателем является коэффициент мощности
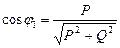 .
.
Активная мощность состоит из двух составляющих
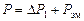 .
.
Первая составляющая представляет собой мощность потерь в активных сопротивлениях статора
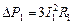 .
.
Разность между мощностью 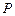 и потерями мощности в активных сопротивлениях статора
и потерями мощности в активных сопротивлениях статора 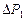 принято называть электромагнитной мощностью
принято называть электромагнитной мощностью 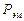 . Эта мощность через воздушный зазор передаётся в ротор.
. Эта мощность через воздушный зазор передаётся в ротор.
Если в (2-43) напряжение 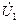 заменить вектором напряжения за активным сопротивлением статора
заменить вектором напряжения за активным сопротивлением статора 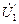 (рис.2.2) , то получим уравнение для электромагнитной мощности
(рис.2.2) , то получим уравнение для электромагнитной мощности
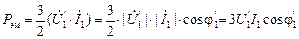 . (2.44)
. (2.44)
 Здесь
Здесь 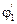 представляет собой угол между векторами
представляет собой угол между векторами 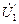
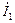 (рис.2.8).
(рис.2.8).
В (2.44) перейдём от 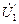 к
к 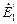 , а затем к
, а затем к 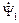
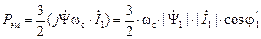
При выполнении операций с векторами целесообразно пользоваться одной методикой. Дополнив угол 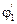 до
до 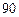 градусов, выполним формальный переход от скалярного произведения к векторному произведению
градусов, выполним формальный переход от скалярного произведения к векторному произведению
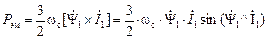 (2.45)
(2.45)
Напомним, что при вычислении векторного произведения отсчёт углов производится против часовой стрелки от первого вектора 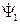 ко второму вектору
ко второму вектору 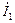 [11].
[11].
Электромагнитная мощность, проходя через воздушный зазор, преобразуется в механическую мощность, и её можно выразить через электромагнитный момент. Так как поле вращается со скоростью 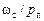 , то можно записать
, то можно записать
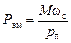 . (2.46)
. (2.46)
При совместном решении (2.45) и (2.46) находим
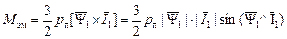 (2.47)
(2.47)
Ранее было показано, что процесс преобразования электрической энергии в механическую энергию происходит в пространственной области. В ортогональных системах координат можно выполнять формальный переход от временных векторов к пространственным векторам. Такой переход выполнен в (2.47).
Если от электромагнитной мощности отнять мощность электрических потерь в сопротивлениях ротора, то оставшаяся часть преобразуется в механическую мощность на валу двигателя
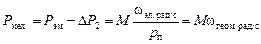 ;
;
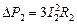 .
.
В ряде случаев удобно представлять электромагнитный момент в виде векторного произведения двух других векторов. В этом случае следует записать уравнение связи между этими векторами и перейти от одного вектора к другому.
Потокосцепления связаны уравнениями
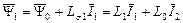 ,
,
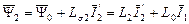 .
.
Здесь 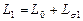 ,
, 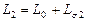 - полные индуктивности фазы статора и ротора.
- полные индуктивности фазы статора и ротора.
Токи связаны равенством 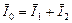 .
.
Допустим, что хотим выразить электромагнитный момент через потокосцепление 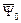 и ток статора
и ток статора 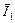 . Процесс преобразований описывается равенствами
. Процесс преобразований описывается равенствами
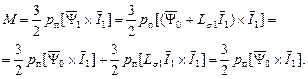
Если эту методику повторить для других векторов, то число уравнений для электромагнитного момента возрастёт. Его можно вычислять с помощью одного из следующих уравнений:
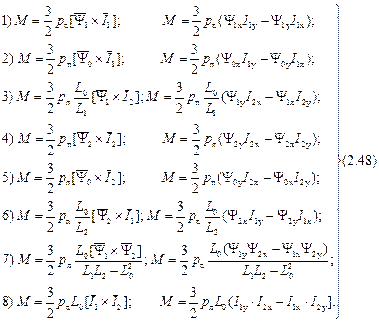
Здесь, в левой части момент представлен в виде векторного произведения двух результирующих векторов. Этими уравнениями можно пользоваться в любой из известных систем координат. В правой части записаны уравнения во вращающейся системе координат “xy”.
Если нужно перейти к неподвижной системе координат a, b, то достаточно изменить лишь символику для переменных. Символ x следует заменить символом 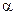 , а символ y заменить на
, а символ y заменить на 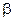 .
.
Так, например уравнение с номером 2 в системах координат x, y и a, b принимает вид
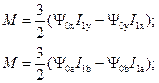
В первом уравнении вектора 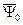 и
и 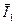 не совершают вращательного движения, они лишь поворачиваются на определённые углы и меняются по модулю. В вычислениях электромагнитного момента нет синусоидальных функций.
не совершают вращательного движения, они лишь поворачиваются на определённые углы и меняются по модулю. В вычислениях электромагнитного момента нет синусоидальных функций.
Во втором уравнении эти же вектора совершают вращательное движение со скоростью 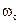 . Проекции этих векторов меняются по законам синуса и косинуса и участвуют в процессе вычисления электромагнитного момента.
. Проекции этих векторов меняются по законам синуса и косинуса и участвуют в процессе вычисления электромагнитного момента.
Сам процесс вычислений в разных системах координат имеет принципиальные отличия, а результат вычислений получается одинаковым.
Система координат 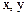 удобна для организации процесса управления объектом и хорошо воспринимается в процессе анализа отдельных явлений.
удобна для организации процесса управления объектом и хорошо воспринимается в процессе анализа отдельных явлений.
Процессы в неподвижных системах координат 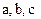 и
и 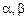 максимально приближены к реальным процессам в электрических цепях переменного тока.
максимально приближены к реальным процессам в электрических цепях переменного тока.
Выводы:
1. Полезная работа совершается за счёт преобразования активной мощности, потребляемой из сети, в механическую мощность.
2. Реактивная мощность идёт на создание магнитного поля, с помощью которого возникает электромагнитный момент.
infopedia.su
При частотном регулировании частоту переменных статора и синхронную скорость поля обычно представляют в относительных единицах
, (2.31)
где - номинальная частота, -синхронная скорость поля при номинальной частоте.
От скольженияs переходят к абсолютному скольжению
(2.32)
Здесь за базовую величину принята синхронная скорость поля при номинальной частоте.
Связь между иsописывается равенством
(2.33)
В схеме замещения (рис.2.5) в качестве переменных характеризующих нагрузку и частоту выступают: абсолютное скольжение и относительная частота.
Ротор, как и ранее, представляется заторможенным, а его параметрыприведены к числу витков статора. Все индуктивные сопротивленияи напряжения на отдельных участках схемы замещения зависят от частоты:
(2.34)
Уравнения для напряжений (2.13) принимают вид:
(2.35)
В этих уравнениях индуктивные сопротивления соответствуют номинальной частоте. Разделив обе части уравнений (2.35) на, и перейдя к действующим значениям, получим:
(2.36)
Эти равенства очень важные, так как характеризуют основные законы частотного регулирования:
,,.
При регулировании скорости вниз от номинальной скорости (< 1) для стабилизации одного из потокосцеплений следует регулировать не только частоту, но и модуль напряжения на соответствующем участке схемы замещения. Регулирование скорости вверх от номинальной скорости выполняют при ослабленном поле. В этом случае напряжение поддерживают на постоянном уровне.
Выражения для ЭДС статора и ротора можно представлятьв разных формах записи:
(2.37)
Связь между токами устанавливается по ранее рассмотренной методике.
Из схемы замещения видно, что при с уменьшением частоты, то есть, уменьшаются все индуктивные сопротивления, что приводит к возрастанию тока статора и тока намагничивания. Это, в свою очередь, приводит к повышению степени насыщения магнитной системы. Так, если при идеальном холостом ходе уменьшить частоту в два раза, то магнитный потокдолжен увеличиться в два раза, а ток намагничивания с учётом насыщении магнитопровода может увеличиться во много раз и стать больше номинального тока статора.
Выводы:
1. Магнитный поток зависит не только от напряжения, но и от частоты.
2. При частотном регулировании приходится регулировать не только частоту, но и модуль напряжения.
В электроприводах переменного тока вопросы динамики обычно решаются с помощью теории обобщённой электрической машины. В работах [9,10] отмечается, что с помощью схем замещения можно решать не только задачи статики, но и динамики.
Покажем, что между схемой замещения АД и теорией обобщённой электрической машины имеется тесная связь.
На рис.2.6 изображены две схемы замещения АД. Первая схема (а) относится к процессам в неподвижных системах координат: и. Вторая схема относится к процессам во вращающихся системах координат: . Будем рассматривать общий случай, когда система координат вращается с произвольной скоростью.
В приведенных схемах предполагается, что переменные и параметры ротора приведены к числу витков статора. Обмотки статора и ротора находятся в магнитном поле, вращающемся со скоростью . Вращение машины и системы координат учитывается с помощью добавочных ЭДС вращения, которые должны удовлетворять условиям:
,. (2.38)
Положительные направления для этих ЭДС приняты совпадающими с направлением токов. В частном случае, когда система координат неподвижна, дополнительная ЭДС вводится только в ротор
. (2.39)
Вначале рассмотрим математическое описание процессов при неподвижной системе координат (рис.2.6а).
В контуре тока статора последовательно соединены две индуктивности и. В сумме они представляют полную индуктивность фазы статора. В контуре тока ротора тоже имеется полная индуктивность.
Проходя последовательно вдоль контуров, получаем уравнения для напряжений в контурах статора и ротора:
Если для контура ротора напряжение выразить через главное потокосцепление, то оно принимает вид:
.
Первый и последний члены этого уравнения в сумме характеризуют ЭДС самоиндукции, наводимую в роторе потокосцеплением
.
С учётом (2. 38) уравнение для контура ротора может быть записано в одной из следующих форм записи:
Таким образом, электромагнитные процессы в одной фазе описываются системой уравнений:
(2.40)
В этой системе уравнений скорость учитывается угловой частотой скольжения. Если в качестве переменной принимать эту частоту, то расчёт электромагнитных процессов можно выполнять без учёта механического процесса. Его можно проводить для одной фазы, не переходя к теории обобщённой электрической машины. Расчёт можно выполнять в аналитическом виде по методике предложенной в [4] или путём моделирования с помощью компьютера.
Взаимную ориентацию переменных во временной области удобно рассматривать с помощью векторной диаграммы на рис.2.7. В этой диаграмме учитывается добавочная ЭДС в роторе и выполнены дополнительные построения в предположении, что<.
Процессы будут более понятными, если укажем физическую сущность отдельных составляющих в системе уравнений (2.40).
Выражение представляет собой ЭДС самоиндукции, наведённую в статоре потокосцеплением, в комплексной форме записи. Во временной форме записи эта ЭДС записывается так:. На векторной диаграмме она действует встречно напряжению.
Выражение представляет собой ЭДС самоиндукции, наведённую в роторе потокосцеплением. Во временной форме записи это выражение принимает вид.
Выражение представляет собой ЭДС вращения наводимую в роторе потокосцеплением.
Из рис.2.6 и уравнения (2.40) следует, что при неподвижном роторе ток в роторепотребляется от источника питания. Знак минус характеризует фактическое направление тока. Часть токаидёт на создание тока возбуждения, а другая его часть, того же направления, передаётся в ротор для создания полезной мощности. При вращающемся роторе появляется добавочная ЭДС (2.39), ток в роторе пропорционален частоте скольжения. В режиме идеального холостого ходаон становится равным нулю.
Перейдём к схеме замещения на рис.2.6б. Проходя, как и раньше, последовательно по контурам, получим:
Выражая через потокосцепление, и выполнив простые преобразования с учётом (2.38), получим:
(2.41)
В правой части этих уравнений присутствуют ЭДС двух видов с разной физической сущностью:
- ЭДС самоиндукции, наводимые периодически изменяющимися токами статора и ротора;
- ЭДС вращения или ЭДС взаимоиндукции с учётом взаимодействия с другими фазами. Эти ЭДС как раз и являются добавочными ЭДС (2.38).
Векторная диаграмма на рис.2.7 отражает процессы в одной фазе. Для создания электромагнитного момента обязательно нужна ещё одна или две фазы. В этом случае состояния переменных рассматривают с помощью пространственных векторных диаграмм. Направим вдоль действительной оси + геометрическую ось фазы “а”, а вдоль мнимой оси расположим геометрическую ось фазы “b”. Получили пространственную плоскость поперечного сечения машины. На этой плоскости уже изображены в виде векторов все переменные.
Известно, что в ортогональных системах координат модули временных и пространственных векторов одинаковы. В этом случае временные и пространственные векторные диаграммы принимают одинаковый вид, изменяется лишь символика для переменных. Изменив символику, то есть, заменив точку над переменной чертой над переменной, получим пространственную векторную диаграмму.
Если теперь сравнивать процессы во временной и пространственной областях, то они совершенно разные.
В пространственной области изображающие вектора вращаются относительно геометрических осей отдельных фаз и отражают процессы во всех фазах.
Во временной области вектора вращаются относительно комплексной плоскости и отражают процессы только в одной фазе. Если их поведение рассматривать относительно геометрической оси рассматриваемой фазы, то они пульсируют во времени.
Вернёмся к уравнениям (2.41), которые описывают процессы во временной области, Если в этих уравнениях изменить всего лишь символику для переменных, то получим математическое описание процессов в пространственной области:
(2.42)
Эти уравнения являются основополагающими в теории обобщённой электрической машины, так как описывают электромагнитные процессы в статике и динамике.
Таким образом, путём простых преобразований, установлена связь между схемой замещения и теорией обобщённой электрической машины. Эта связь стала возможной благодаря введению в схему замещения добавочных ЭДС, которые описываются уравнениями (2.38) и (2.39).
studfiles.net
Трехфазный асинхронный двигатель состоит из двух основных частей: неподвижного статора и вращающегося ротора.
Статор (рис. 1) представляет собой полый цилиндр 2, помещенный внутри стального или алюминиевого корпуса3. Цилиндр собран из кольцеобразных изолированных пластин электротехнической стали. На его внутренней стороне имеются пазы, в которых размещаются симметрично три фазные обмотки1, состоящие из одной или нескольких катушек медного изолированного провода. Фазные обмотки соединяются звездой или треугольником и подключаются к трехфазной сети. Схема соединения фазных обмоток зависит от линейных напряжений трехфазной сети, указанных на клеммной коробке электродвигателя, например, 220/380 В. При напряжении меньше 220 В фазные обмотки соединяются треугольником, а при напряжении больше 380 В —
| звездой, | что | обеспечивает | |
| при каждом способе соедине- | |||
| ния фазное напряжение об- | |||
| моток 220 В. |
|
| |
| Ротор | асинхронного | дви- | |
| гателя представляет собой за- | |||
| крепленный на валу цилиндр, | |||
| собранный из изолированных | |||
| пластин, | выполненных | из | |
| электротехнической стали. На | |||
| внешней | стороне цилиндра | ||
| имеются пазы. В пазах распо- | |||
| ложена его обмотка, которая | |||
| может быть короткозамкну- | |||
Рис. 1 | той и фазной. | Соответствен- | ||
но различают асинхронный двигатель с короткозамкнутым и фазным ротором.
Обмотка короткозамкнутого ротора (рис. 2) выполняется в виде круглой («беличьей») клетки, образованной расположенными в пазах ротора медными или алюминиевыми стержнями 1, замкнутыми накоротко с двух сторон кольцами2 из того же материала.
Фазная обмотка ротора (рис. 3) изготавливается так же, как и обмотка статора, изолированным медным проводом. Ее катушки соединяются звездой, а их свободные концы присоединяются
Рис. 2
Рис. 3
к трем контактным кольцам 1, находящимся на валу ротора. Кольца изолированы друг от друга и от вала. К контактным кольцам прижаты графитовые щетки2, с помощью которых к обмотке ротора подключается трехфазный реостат3. Его включение в цепь обмотки ротора позволяет регулировать частоту вращения асинхронного двигателя, а также существенно улучшить его пусковые свойства, т. е. уменьшить пусковой ток и одновременно увеличить пусковой момент.
Ротор асинхронного двигателя помещается внутри статора и фиксируется в этом положении с помощью боковых подшипниковых щитов.
Для анализа характеристик асинхронного двигателя в установившихся режимах используют его электрическую схему замещения. На рис. 4 изображена Г-образнаясхема замещения асинхронного двигателя. Она представляет собой составленную из идеализированных элементов электрическую схему замещения одной фазы электродвигателя, в которой магнитная связь между статором и ротором заменена электрической.
Рис. 4
По аналогии со схемой замещения трансформатора в ней переменный резистор R2 (1s)/s представляет эквивалент полезной
нагрузки. Поэтому мощность, выделяемая в нем, будет равна одной трети механической мощности Рмех, развиваемой асинхронным двигателем. По схеме замещения можно определить мощность потерь в сталиРст, мощности потерь в обмотках статораРэ1 и ро-
тора Рэ2, а также потребляемую асинхронным двигателем мощностьР1.
Естественные механические характеристики асинхронного двигателя
Механической характеристикой асинхронного двигателя называют зависимость развиваемого им момента от скольжения M =f (s) и зависимость частоты вращения ротора от развиваемого моментаn2 =f (M). Механическая характеристика двигателя, полученная при номинальных (паспортных) напряжении и частоте сети по основной схеме включения обмоток двигателя без включенных в их цепи дополнительных электротехнических элементов, являетсяестественной. Если указанные условия не соблюдаются, то механическая характеристика будетискусственной.
Расчет естественной механической характеристики асинхронного двигателя выполняют по формуле, представляющей собой аналитическую зависимость его электромагнитного момента от скольжения:
M |
| 3U12н pR2 |
| , | (1) |
2 f1нs R1 | R2 s2 X1 | X22 | |||
|
|
|
|
| |
где p — число пар полюсов обмотки статора.
Механическая характеристика асинхронного двигателя — нелинейная, поэтому при расчете рекомендуется задаться значения-
ми скольжения s = 0; 0,5sн;sн; 1,5sн;sк; 0,6; 0,8; 1,0 и определить соответствующий им электромагнитный момент.
Скольжению s = 0 соответствует режим идеального холостого хода электродвигателя, при работе в котором его частота вращения равна частоте вращения магнитного поля, т. е. синхронной частоте вращения
n1 60 f1н , p
а электромагнитный момент М = 0.
Скольжение асинхронного двигателя вычисляют по формуле
s n1 n2 . n1
При расчете номинального скольжения электродвигателя в этой формуле принимают n2 =n2н. Критическое скольжение, при кото-
ром асинхронный двигатель развивает максимальный (критический) момент Мк, зависит от параметров его обмоток:
Значению s = 1 соответствует пусковой режим электродвигателя, при котором его частота вращения равнаn2 = 0, а развиваемый электромагнитный момент называется пусковым моментомМп. Построение механической характеристикиn2 =f(M) осуществляют по данным, полученным при расчете зависимостиM =f(s) с помощью следующего соотношения:
n2 n1(1s).
Примерный вид естественных механических характеристик асинхронного двигателя с указанием характерных точек показан на рис. 5, 6. При выполнении домашнего задания естественные механические характеристики строят совместно с искусственными механическими характеристиками.
Рис. 5
Рис. 6
studfiles.net