







Для получения высокого качества управления ЭП в статических и динамических (переходных) режимах необходимо иметь возможность быстрого непосредственного управления моментом двигателя.
Момент любого двигателя в каждый отрезок времени определяется величиной (амплитудой) и фазой двух моментообразующих составляющих: тока и магнитного потока. В АД токи и потокосцепления статора и ротора вращаются с одинаковыми скоростями, имеют разные, изменяющиеся во времени фазовые параметры и не подлежат непосредственному измерению и управлению. Доступной управляемой переменной в АД является ток статора, имеющий составляющие, образующие магнитный поток и момент. Фазовая ориентация этих двух составляющих может быть осуществлена только внешним управляющим устройством, чем и обусловлен термин “векторное управление”.
В структуре электропривода двигатель рассматривается как электромеханический преобразователь ЭМП в виде идеализированного двигателя. Его ротор не обладает массой и механической энергией, не имеет механических потерь энергии и жестко связан с реальным физическим ротором, относящимся к механической части ЭП. Такой двигатель может быть представлен электромеханическим многополюсником, содержащим n пар электрических выводов по числу n обмоток, и одну пару механических выводов (смотри рисунок 2). На механических выводах в результате электромеханического преобразования (ЭМТ) энергии при скорости w развивается электромагнитный момент M. Момент M является выходной величиной ЭМП и входной для механической части электропривода. Скорость w определяется условиями движения механической части, но для ЭМП может рассматриваться как независимая переменная. Механические переменные M и w связывают ЭМП с механической частью в единую взаимосвязанную систему. Все процессы в двигателе описываются системой уравнений электрического равновесия (число уравнений равно числу обмоток) и уравнением электромеханического преобразования энергии. Для этого в теории ЭП используют двухфазную модель обобщенного ЭП (смотри рисунок 1), к которой приводятся абсолютно все виды и типы электрических машин:

Рисунок 1 – Модель обобщенного ЭМП.
α, β – неподвижные оси статора; d, q – вращающиеся оси ротора; φ – угол поворота ротора;  — угловая скорость ротора;
— угловая скорость ротора;
Уравнение электрического равновесия i— обмотки:

где  — потокосцепление i—ой обмотки;
— потокосцепление i—ой обмотки;
i=1a,…2q; j=1a,…2q, Ri – активное сопротивление обмотки, Li,j – собственные и взаимные индуктивности обмоток. Величина взаимных индуктивностей зависит от угла j поворота ротора и от пространственного сдвига обмоток, т.е. является функцией скорости (и времени). Именно поэтому невозможно получить cos φ = 1.
Синтез алгоритмов и систем векторного управления АД базируется на анализе двухфазной d – q модели АД (d и q – ортогональная система координат ротора).

Рисунок 2 – Схема векторного управления
Схема векторного управления состоит из трех основных функциональных частей:
БРП – блок регуляторов переменных;
БВП – блок вычисления переменных;
БЗП – блок задания переменных;
На вход БРП поступают задающие сигналы скорости и потока, и сигналы обратной связи (с выхода БВП) – ориентированные по полю значения составляющих тока статора, потокосцепления ротора, и скорости. БРП содержит набор регуляторов потока, момента, тока, на выходе которых формируются также ориентированные по полю сигналы задания составляющих тока статора.
БЗП осуществляет фазовые и координатные преобразования задающих d – q переменных в систему трехфазных сигналов управления ШИМ АИН. Блок БВП вычисляет текущие значения амплитудных и фазовых параметров d – q переменных АД, осуществляя фазовые и координатные преобразования реальных трёхфазных сигналов токов и напряжений АД, поступающих с выходов соответствующих датчиков.
Координатные преобразования, осуществляемые блоком БВП, заключаются в переходе от реальных координат трёхфазной системы статора АД с осями d,q (преобразование 3 → 2). Блок БЗП осуществляет обратные координатные преобразования (2 → 3), от d—q к a,b,c.
Фазовые преобразования в этих блоках обеспечивают привязку фазовых параметров переменных в двух системах координат.
На надежность, стоимость и качество характеристик ЭП влияют число измеряемых параметров и точность измерений. Для векторного управления АД надо измерять хотя бы две из четырех, доступных к измерению переменных:
Векторное управление позволяет практически в любой момент времени, при любом положении ротора относительно статора, при любой угловой скорости и нагрузке на машину, получить максимальный cos φ АД. Это, в свою очередь, ощутимо повышает К.П.Д и момент эл. машины, который, в данном случае, практически не зависит от угловой скорости двигателя.
plc24.ru
 В предыдущей статье «Векторное управление электродвигателем «на пальцах» рассматривалась векторная система управления для синхронных электродвигателей. Статья получилась большой, поэтому вопрос про асинхронные электродвигатели (induction motors) был вынесен в отдельную публикацию. Данная статья является продолжением предыдущей и опирается на приведенные там объяснения принципов работы электродвигателей. Она расскажет об особенностях работы асинхронного двигателя применительно к векторному управлению, а также покажет отличия в структуре векторной системы управления между синхронной и асинхронной машиной. Как работает асинхронный электродвигатель? Наиболее популярное объяснение говорит что-то типа «статор создает вращающееся магнитное поле, которое наводит ЭДС в роторе, из-за чего там начинают течь токи, в результате ротор увлекается полем статора и начинает вращаться». Лично я от такого объяснения всю физику процесса понимать не начинаю, поэтому давайте объясню по-другому, «на пальцах». Все же видели видео, как магнит взаимодействует с медным цилиндром? Особенно обратите внимание на диапазон времени с 0:49 до 1:03 – это уже самый настоящий асинхронный двигатель:
В предыдущей статье «Векторное управление электродвигателем «на пальцах» рассматривалась векторная система управления для синхронных электродвигателей. Статья получилась большой, поэтому вопрос про асинхронные электродвигатели (induction motors) был вынесен в отдельную публикацию. Данная статья является продолжением предыдущей и опирается на приведенные там объяснения принципов работы электродвигателей. Она расскажет об особенностях работы асинхронного двигателя применительно к векторному управлению, а также покажет отличия в структуре векторной системы управления между синхронной и асинхронной машиной. Как работает асинхронный электродвигатель? Наиболее популярное объяснение говорит что-то типа «статор создает вращающееся магнитное поле, которое наводит ЭДС в роторе, из-за чего там начинают течь токи, в результате ротор увлекается полем статора и начинает вращаться». Лично я от такого объяснения всю физику процесса понимать не начинаю, поэтому давайте объясню по-другому, «на пальцах». Все же видели видео, как магнит взаимодействует с медным цилиндром? Особенно обратите внимание на диапазон времени с 0:49 до 1:03 – это уже самый настоящий асинхронный двигатель:Эффект происходит из-за появления в цилиндре вихревых токов. Согласно закону электромагнитной индукции, открытого Майклом Фарадеем, при изменении магнитного потока замкнутого контура в нем возникает ЭДС (по-простому считайте, что напряжение). Эта ЭДС, применительно к медному цилиндру, тут же вызывает появление в цилиндре тока. При этом этот ток тоже создает свой, ответный магнитный поток, направленный ровно в противоположную сторону от изменения потока магнита, который мы подносим:
Индукционный ток, возникающий в замкнутом проводящем контуре, имеет такое направление, что создаваемое им магнитное поле противодействует тому изменению магнитного потока, которым был вызван данный ток.
Это можно понимать так, что замкнутый контур сопротивляется изменению магнитного потока внутри себя. Если вы резко поднесёте магнит к медному цилиндру, т.е. сделаете резкое изменение магнитного потока, то в цилиндре потекут такие ответные токи, что магнитное поле внутри цилиндра в первый момент времени будет равно нулю: магнитное поле поднесенного магнита будет полностью скомпенсировано магнитным полем токов цилиндра (с допущениями, конечно). Если магнит поднести и держать, то токи в цилиндре из-за наличия активного сопротивления меди постепенно спадут, а поле цилиндра, создаваемое его токами, пропадет: магнитный поток постоянного магнита «прорвется» внутрь цилиндра, как будто никакого цилиндра и нет. Но стоит попытаться убрать магнит, как цилиндр отреагирует снова – теперь он будет пытаться сам «воссоздать» внутри себя пропадающий магнитный поток, т.е. будет опять сопротивляться изменению магнитного потока, в данном случае его исчезновению. Но что значит «воссоздать магнитный поток»? Это значит, что на какое-то время медный цилиндр можно считать условно «постоянным магнитом» – в нем циркулирует вихревой ток, создающий магнитное поле (на этом же принципе «висят» сверхпроводники в магнитном поле, но это совсем другая история).
Давайте теперь обратимся к конструкции асинхронного двигателя. Ротор асинхронного двигателя условно можно представлять себе также в виде медного цилиндра. Но в реальных конструкциях это некая решётка в виде «беличьей клетки» (рисунок 1) из меди или алюминия, совмещенная с магнитопроводом (шихтованное железо).
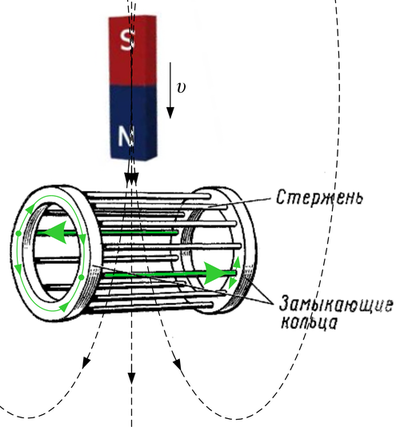 Рисунок 1. Ротор асинхронного двигателя типа «беличья клетка» с током в одной из «рамок» беличьей клетки, реагирующей на нарастание внешнего магнитного поля.
Рисунок 1. Ротор асинхронного двигателя типа «беличья клетка» с током в одной из «рамок» беличьей клетки, реагирующей на нарастание внешнего магнитного поля.На рисунке схематично показано протекание тока в одной из «рамок», т.е. в некоторых прутьях беличьей клетки, если сверху поднести магнит (создать ток в статоре). На самом деле ток в этом случае протекает во всех прутьях, кроме, условно, верхнего и нижнего, для которых изменения потока нет (но они бы среагировали на горизонтально поднесенный магнит).
Помните ещё из начала прошлой статьи картинку со схематическим изображением двухфазной синхронной машины, где ротором был магнит? Давайте теперь сделаем из неё асинхронный двигатель: вместо магнита поставим две перпендикулярные короткозамкнутые катушки, символизирующие медный цилиндр ротора (рисунок 2).
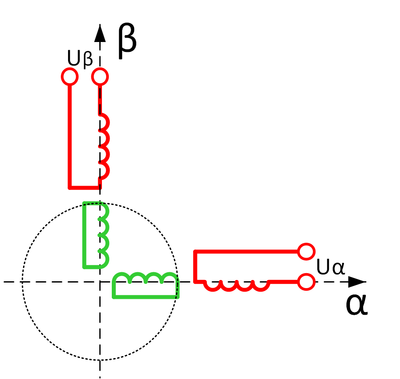 Рисунок 2. Схематическое изображение двухфазного асинхронного двигателя с короткозамкнутым ротором.
Рисунок 2. Схематическое изображение двухфазного асинхронного двигателя с короткозамкнутым ротором.Замена цилиндра на две катушки для пояснения принципа работы (или моделирования) корректна, точно также как корректна замена трехфазной обмотки на двухфазную. Только в этом случае мы заменяем… «бесконечнофазную обмотку» цилиндра (бесконечное число рамок) на две катушки с эквивалентной индуктивностью и сопротивлением. Ведь двумя катушками можно создать точно такой же вектор тока и магнитного потока, как и цилиндром.
А теперь давайте сделаем на короткое время из асинхронной машины синхронную. Подадим в катушку оси β постоянный ток и подождем секунды две-три, пока в роторе перестанут течь ответные токи: «поднесем внешний магнит». То есть дождемся спадания токов в роторе, чтобы магнитное поле статора «пронзило ротор» и никто ему не мешал. Что теперь будет, если выключить ток в статоре? Правильно, на те же две-три секунды, пока ток ротора этому противится, мы из ротора получим «обычный магнит» (рисунок 3).
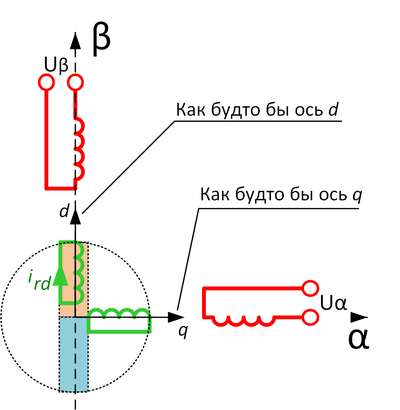 Рисунок 3. Асинхронный двигатель, когда только что выключили постоянный ток по фазе β – течет ток в роторе ird.
Рисунок 3. Асинхронный двигатель, когда только что выключили постоянный ток по фазе β – течет ток в роторе ird.Что же мы ждем? Быстрее, пока магнит не пропал, рисуем вдоль него привычную ось d (как в синхронной машине) и перпендикулярную ей ось q, привязанные к ротору. Включаем структуру векторного управления синхронной машиной, подаем ток по оси q, создавая момент, поехали!
Так можно даже действительно сделать несколько оборотов, пока наш сахарный магнит не растаял, а ось d не ушла в небытие. Что же делать? Давайте не будем выключать ток по оси d, подпитывая наш магнит! И опять же сохраним структуру векторного управления синхронной машиной, просто подав задание по оси d (раньше там был ноль). Итак, смотрим на рисунок 4: оси d, q по датчику положения «приделаны» к ротору, двигатель стоит, подан ток по оси d в статоре, что в данном случае для стоячей машины совпадает с осью β. Тока по оси q пока нет: ждем, пока ротор «намагнитится». И вот подаем ток isq (s – статор)! Поехали!
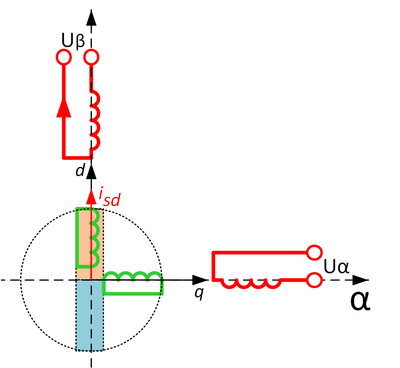 Рисунок 4. Подадим ток в ось d, намагнитив машину, подготовив всё для подачи тока в ось q статора.
Рисунок 4. Подадим ток в ось d, намагнитив машину, подготовив всё для подачи тока в ось q статора.Далеко ли мы уедем таким методом барона Мюнхгаузена? К сожалению, нет. Смотрите, что произошло (рисунок 5):
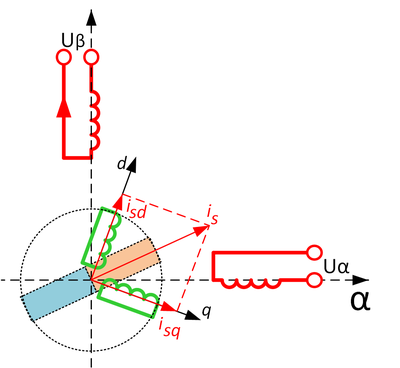 Рисунок 5. А магнит-то сполз!
Рисунок 5. А магнит-то сполз!Двигатель начал крутиться, но через некоторое время после того, как мы подали ток в ось q, образовав суммарный ток is и «прибив» этот вектор к положению ротора, магнит в роторе «съехал»! И встал ровно вдоль вектора is. Ротор же не понимает, где мы нарисовали ему оси d, q… Ему все равно, крутился он или нет. Важно, что его внутренний «наведенный магнит» в конечном счете хочет стать сонаправленным с магнитным потоком статора, «подчиниться» внешнему потоку. Из-за съехавшего магнита двигатель перестанет крутиться: мало того, что между магнитом ротора и током iq нет желаемых 90 градусов, так еще и ток оси d теперь его тянет в противоположную сторону, компенсируя момент, создаваемый током iq. Метод барона Мюнхгаузена не удался.
Что же делать с ускользающим магнитом ротора? А давайте сделаем структуру векторного управления асинхронного двигателя не в осях d,q, приделанных к ротору, а в других осях, приделанных именно к текущему положению «магнита ротора» – назовем их оси x,y, чтобы отличать от d,q. По «научному» – это оси, ориентированные по потокосцеплению ротора. Но как же узнать, где конкретно сейчас это потокосцепление ротора, т.е. куда повернут магнит в роторе? Его положение зависит… во-первых, от положения самого ротора (датчик положения у нас есть, хорошо), во-вторых, от токов статора (создающих поток статора, по которому и собирается в конечном счете повернуться магнит ротора), а в-третьих от параметров роторной цепи – индуктивности и сопротивления «медного цилиндра» (он же беличья клетка, он же роторная обмотка, он же цепь ротора). Поэтому… зная всё это, положение «магнита» ротора можно просто вычислять по нескольким дифференциальным уравнениям. Делает это так называемый наблюдатель потокосцепления ротора, выделенный цветом на итоговой структурной схеме векторного управления асинхронным двигателем (рисунок 6).
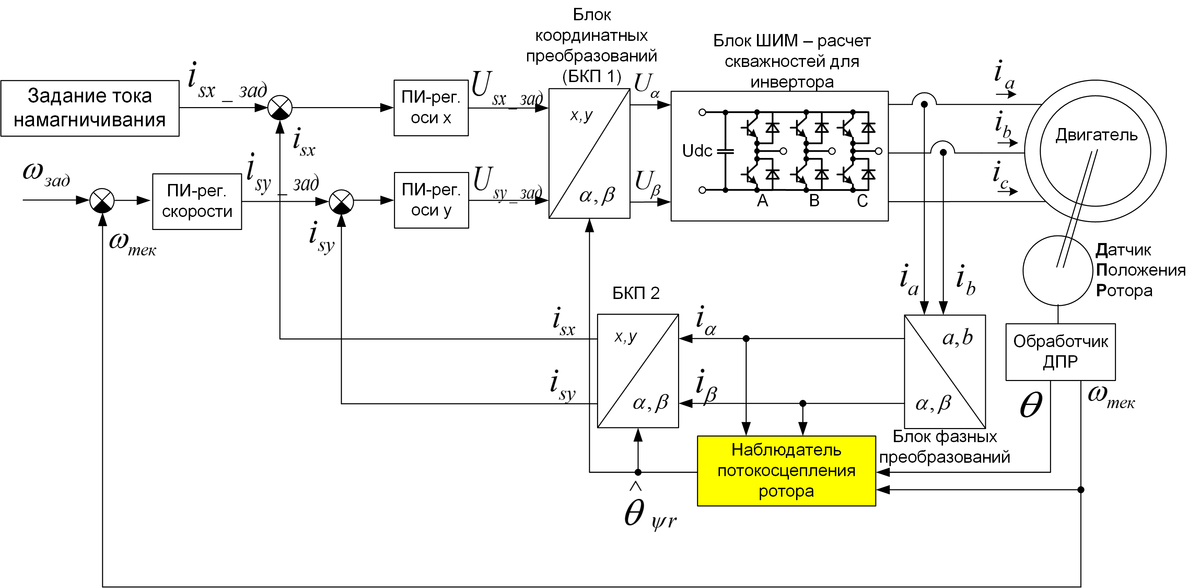 Рисунок 6. Векторная датчиковая структура управления асинхронным двигателем
Рисунок 6. Векторная датчиковая структура управления асинхронным двигателемВ наблюдатель заводятся показания с датчика положения ротора, а также текущие токи статора в осях α, β. На выходе наблюдателя – положение «магнита» ротора, а именно угол наблюдаемого потокосцепления ротора 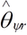 . В остальном структура полностью аналогична таковой для синхронной машины, только оси d,q переименованы в x,y, а на ось x подано задание тока, который будет поддерживать наш «магнит» в роторе. Также на многих обозначениях добавлен индекс “s”, чтобы показать, что данная величина имеет отношение к статору, а не к ротору. Также надо отметить, что в западной литературе не используют оси x,y: у них ось d всегда направлена по полю ротора, что для асинхронного двигателя, что для синхронного. Наши ученые еще в советское время разделили оси d,q и x,y, чтобы исключить путаницу: d,q прикреплены к ротору, а x,y к полю ротора.
. В остальном структура полностью аналогична таковой для синхронной машины, только оси d,q переименованы в x,y, а на ось x подано задание тока, который будет поддерживать наш «магнит» в роторе. Также на многих обозначениях добавлен индекс “s”, чтобы показать, что данная величина имеет отношение к статору, а не к ротору. Также надо отметить, что в западной литературе не используют оси x,y: у них ось d всегда направлена по полю ротора, что для асинхронного двигателя, что для синхронного. Наши ученые еще в советское время разделили оси d,q и x,y, чтобы исключить путаницу: d,q прикреплены к ротору, а x,y к полю ротора.
Что же получается? Магнит ротора всё время скользит, сползает от текущего положения на роторе в сторону тока оси y. Чем больше этот ток, тем сильнее скольжение. Наблюдатель в реальном времени вычисляет положение этого магнита и «подкручивает» оси x,y всё время вперед по отношению к осям d,q (положению ротора). Ось x всегда соответствует текущему положению потокосцепления в роторе – положению «магнита». Т.е. оси x,y бегут всегда (в двигательном режиме) немного быстрее вращения ротора, компенсируя скольжение в нем. Токи в роторе, если их измерить или промоделировать, получаются синусоидальными. Только изменяются они не с частотой статорных токов, а с частотой этого скольжения, т.е. очень медленно. Если в статоре промышленного асинхронника 50Гц, то при работе под нагрузкой частота тока в роторе – единицы герц. Вот, собственно, и весь секрет векторного управления для асинхронного двигателя.
Чем векторное управление асинхронным двигателем лучше, чем скалярное? Скалярное управление это такое, когда к двигателю прикладывается напряжение заданной частоты и амплитуды – например, 380В 50Гц. И от нагрузки на роторе оно не зависит – никаких регуляторов токов, векторов… Просто задается частота напряжения и его амплитуда – скалярные величины, а токи и потоки в двигателе пусть сами себе удобное место находят, как хотят. В установившемся режиме работы двигателя векторное управление неотличимо от скалярного – векторное точно также будет прикладывать при номинальной нагрузке те же, скажем, 380В, 50Гц. Но в переходных режимах… если нужно быстро запустить двигатель с заданным моментом, если нужно отрабатывать диаграмму движения, если есть импульсная нагрузка, если нужно сделать генераторный режим с определенным уровнем мощности – всё это скалярное управление или не может сделать, или делает это с отвратительными, медленными переходными процессами, которые могут к тому же «выбить защиту» преобразователя частоты по превышению тока или напряжения звена постоянного тока (двигатель колеблется и может запрыгивать в генераторный режим, к которому преобразователь частоты не всегда приспособлен).
В векторной же структуре «всё под контролем». Момент вы задаете сами, поток тоже. Можно ограничить их на нужном уровне, чтобы не превысить уставок защиты. Можно контролируемо форсировать токи, если кратковременно нужно сделать в несколько раз больший момент. Можно регулировать не только момент двигателя, но и поток (ток оси x): если нагрузка на двигателе мала, то нет никакого смысла держать полный поток в роторе (делать магнит «номинального режима») – можно ослабить его, уменьшив потери. Можно стабилизировать скорость регулятором скорости с высокой точностью и быстродействием. Можно использовать асинхронный привод в качестве тягового (в транспорте), задавая требуемый момент тяги. В общем, для сложных применений с динамичной работой двигателя векторное управление асинхронным двигателем незаменимо.
Также есть отличительные особенности векторного управления асинхронного двигателя от синхронного. Первая – это датчик положения. Если для синхронного привода нам нужно знать абсолютное положение ротора, чтобы понять, где магнит, то в асинхронном приводе этого не требуется. Ротор не имеет какой-то выраженной полюсной структуры, «магнит» в нем постоянно скользит, а если посмотреть в формулы наблюдателя потокосцепления ротора, то там не требуется знания положения: в формулы входит только частота вращения ротора (на самом деле есть разные формулы, но в общем случае так). Поэтому на датчике можно сэкономить: достаточно обычного инкрементального энкодера для отслеживания частоты вращения (или даже тахогенератора), абсолютные датчики положения не требуются. Вторая особенность – управление потоком в асинхронном электродвигателе. В синхронной машине с постоянными магнитами поток не регулируется, что ограничивает максимальную частоту вращения двигателя: перестает хватать напряжения на инверторе. В асинхронном двигателе, когда это случается… просто уменьшаете задание по оси x и едете дальше! Максимальная частота не ограничена! Да, от этого будет снижаться момент двигателя, но, главное, ехать «вверх» можно, в отличие от синхронной машины (по-правде там тоже можно, но недалеко, не для всех двигателей и с кучей проблем).
Точно также существуют бездатчиковые алгоритмы векторного управления асинхронным двигателем, которые оценивают угол потокосцепления ротора не используя сигнал датчика положения (или скорости) вала ротора. Точно также, как и для синхронных машин, в работе таких систем есть проблемы на низкой частоте вращения ротора, где ЭДС двигателя мала.
Также следует сказать пару слов о роторе. Если для промышленных асинхронных двигателей его удешевляют, используя алюминиевую беличью клетку, то в тяге, где массогабаритные показатели важнее, наоборот, могут использовать медный цилиндр. Так, во всеми любимом электромобиле Tesla стоит именно асинхронный электродвигатель с медным ротором (рисунок 7)
 Рисунок 7. Ротор асинхронного электродвигателя Tesla Model S в стальной обшивке (фото из разных источников за разные годы)
Рисунок 7. Ротор асинхронного электродвигателя Tesla Model S в стальной обшивке (фото из разных источников за разные годы)Вот, собственно, и всё, что я хотел сказать про асинхронный двигатель. В данной обзорной статье не рассмотрены многие тонкости, такие как регулятор потока ротора, возможное построение векторной структуры в других осях координат, математика наблюдателя потокосцепления ротора и многое другое. Как и в конце прошлой статьи, за дальнейшими подробностями отсылаю читателя к современным книгам по приводу, например к «Анучин А. С. Системы управления электроприводов. МЭИ, 2015».
На каком микроконтроллере можно сделать полноценное векторное управление, читайте, например, в статье «Новый отечественный motor-control микроконтроллер К1921ВК01Т ОАО «НИИЭТ», а как это отлаживать в статье «Способы отладки ПО микроконтроллеров в электроприводе». Также наша фирма ООО «НПФ Вектор» предлагает разработку на заказ систем управления электродвигателями и другим электрооборудованием, примеры выполненных проектов можно посмотреть на нашем сайте.
P.S. У специалистов прошу прощения за не совсем корректное обращение с некоторыми терминами, в частности с терминами «поток», «потокосцепление», «магнитное поле» и другими – простота требует жертв…
habr.com
Современный асинхронный электропривод реализуется на базе силовой полупроводниковой техники с применением микропроцессорного управления. Его возможности позволяют организовать регулирование выходных координат электропривода в широком диапазоне, с высокой точностью и быстродействием.
Современные преобразователи частоты с микропроцессорным управлением позволяют реализовывать традиционные или создавать новые программные алгоритмы и синтезировать асинхронные электроприводы с широким набором эксплуатационных характеристик.
Цель: Обзор алгоритмов управления асинхронными электроприводами и выбор более подходящего алгоритма для тягового электропривода троллейбусов.
Основным условием для выбора алгоритма управления тяговым электроприводом троллейбуса это поддержание момента на валу двигателя, как при разгоне, так и при торможении. Так как мощность тягового электропривода большая необходимо учитывать тепловые потери. Исходя из этого, рассмотрим и сделаем анализ существующих алгоритмов управления
Векторное управление, ориентированное по роторному потоку, для асинхронного двигателя, питающегося от источника тока
Для создания источника тока, управление элементами инвертора определяются быстрыми местными петлями тока, контролируемыми заранее описанными мгновенными значениями фазовых токов
Двухфазные компоненты статорного тока в установленной системе координат (id*, iq*) полученных из петли управления скоростью (позицией). Они определяют мгновенные заранее описанные значения статорного тока (ia*, ib*, ic*), сравниваемые с реальными, измеренными, значениями статорных токов ia, ib, ic. Управление элементами инвертора (всегда для каждой фазы противоположные состояния) определяются таким образом, чтобы, независимо от каждой фазы, лимитировать частоту переключений, предусматривая гистерезис в процентах от максимального значения заранее описанного тока.

Рис. 1. Принцип широтной модуляции с реакцией по току
Главными преимуществами этой стратегии модуляции являются:
1. Простота реализации;
2. Возможность реализации на аналоговых компараторах;
3. Хорошие динамические характеристики;
4. Нечувствительность системы векторного управления скоростью к изменениям параметров асинхронного двигателя.
Описанная стратегия имеет ряд недостатков:
1. Поскольку компараторы каждой фазы независимы, не существует способа генерации нулевого вектора напряжения;
2. На маленьких частотах существует тенденция появления переключений на высокой частоте в результате неправильной работы компаратора.
Система управления скоростью (позицией) вращения асинхронного двигателя в косвенной форме.
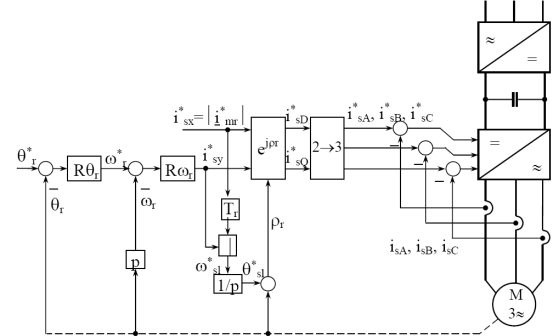
Рис. 2. Система управления позицией ротора косвенным методом
Регулятор позиции Rθr (пропорционального типа) перемещает заданное значение скорости ротора  , которое сравнивается с реальным значением скорости ротора ωr, а у регулятора скорости Rωr в качестве выходного параметра выступает активное значение тока статора i*sy.
, которое сравнивается с реальным значением скорости ротора ωr, а у регулятора скорости Rωr в качестве выходного параметра выступает активное значение тока статора i*sy.
На этой основе вместе с реактивной составляющей тока статора i*sx, рассчитывается частота скольжения. Полученная величина суммируется с позицией ротора и таким образом определяется позиция ρr вектора потока ротора.
Блоки (ejρr) и (2→3) осуществляют трансформацию координат из вращающейся системы в фиксированную, из двухфазных ортогональных значений в трехфазные:
Система управления скоростью (позицией) вращения асинхронного двигателя в непосредственной форме
В случае этого метода управления позиция ротора ρr, необходимая для трансформации координат, получается на основании измеренных значений токов статора, используя модель потока.
В результате получаются два пути управления: моментом (активный ток) и потоком (реактивный ток).

Рис. 3. Система управления позицией асинхронного двигателя прямым методом
В случае управления моментом заданной величиной может быть позиция или скорость ротора. В случае управления позицией её заданная величина θ*r сравнивается с измеренной, полученной в результате интегрирования скорости ротора. Разница между этими двумя параметрами передается регулятору позиции (пропорционального типа). Его выходное значение определяет заданное значение скорости вращения, которое сравнивается с реальной скоростью. Разница между этими двумя параметрами передается регулятору скорости (пропорционально интегрального типа), на выходе которого получается заданное значение электромагнитного момента. Значение момента сравнивается с измеренным параметром (рассчитанным на основании компонентов статорных токов в результате использования модели потока). Регулятор момента передает заданное значение активной составляющей статорного тока в систему потока ротора i*sy.
В случае управления потоком заданное значение тока намагничивания ротора, полученное на выходе трансформатора, сравнивается с измеренным значением, являющимся результатом работы модели потока. Результат сравнения используется регулятором реактивного тока, который в свою очередь передает заданное значение реактивной составляющей статорного тока в систему потока ротора i*sх.
Угол позиции вектора потока ротора, необходимого для трансформации координат (ejρr), получается из модели потока на базе измеренных значений статорных токов и скоростей ротора.
Представленные варианты схем управления применяются как для маленьких, так и для средних мощностей, где могут быть использованы инверторы напряжения с заданными токами. Соответственно, модуляция каждой фазы является результатом сравнения заданных фазных токов, полученных в схеме векторного управления, с измеренными значениями статорных токов. Поэтому, не во всех тяговых электроприводах троллейбусов возможно это использовать, поскольку троллейбусы выпускаются с разными мощностями электродвигателей.
Векторное управление с ориентацией по потоку ротора для асинхронного двигателя, питающегося от инвертора напряжения
В системах с большими и очень большими мощностями, из-за потерь при переключениях, невозможно использовать инверторы напряжения как источник тока, поэтому здесь используются инверторы напряжения как источник напряжения. Эти инверторы являются обобщенным случаем автоматических систем векторного управления с широтной модуляцией. Системы управления передают мгновенные заранее заданные значения фазных напряжений независимо от стратегии модуляции. Управление полупроводниковыми элементами осуществляется в зависимости от типа модуляции.
Считая машину ненасыщенной (постоянные индуктивности), электромагнитный момент асинхронного двигателя определяется компонентами статорных токов в различных системах координат. Так как инверторы напряжения являются источниками напряжения, а контроль моментом осуществляется статорными токами, необходимо осуществлять этот контроль посредством питающих напряжений. Таким образом, для управления моментом необходимо осуществить следующие преобразования: напряжение → ток → момент.
Система управления скоростью (позицией) асинхронного двигателя с заданием токов i*sx, i*sy

Рис. 4. Система управления позицией асинхронного двигателя с заданием токов i*sx, i*sy
Важен тот факт, что статорное сопротивление Rs, которое участвует в расчете компонентов ûsx, ûsy, не является лишь собственным сопротивлением двигателя, определяемое адекватными измерительными приборами, а эквивалентное сопротивление (большее) статора, включающее также сопротивления полупроводниковых элементов, находящихся в управлении, эквивалентное сопротивление промежуточной цепи, сопротивления проводников и др.
Блоки (ejρr) и (2→3) осуществляют трансформации координат из вращающейся системы координат в фиксированную, соответственно, из двухфазных ортогональных величин в трехфазные, используя в качестве переменных составляющие напряжения.
ЗАКЛЮЧЕНИЕ
В результате проведенного анализа схем видно, что метод, где инвертор выступает в качестве источника тока, позволяет «мягко» управлять как моментом, так и скоростью вращения, что позволяет добиться хороших динамических характеристик.
Другими преимуществами этой стратегии модуляции являются:
- простота реализации системы;
- возможность реализации на аналоговых компараторах;
- нечувствительность системы векторного управления скоростью к изменениям параметров асинхронного двигателя.
Однако реализация привода мощностью выше 10 кВт таким методом не является эффективной. Это связанно с тем, что частота переключений силовых элементов составляет порядка 10–20кГц, вследствие чего выделяется большое количество тепла на коллекторе IGBT транзистора. Следовательно он не может использоваться в тяговом электроприводе троллейбусов.
В схемах, где инвертор выступает в качестве источника напряжения, частота переключений может быть ниже 10кГц, в следствии количество тепла, выделяемое на инверторе, в 2 и более раза меньше, чем в предыдущем методе. Также преобразования проще, поскольку мы управляем только частотой и амплитудой напряжения.
Но при данном способе управления изменения параметров двигателя в процессе работы (изменение сопротивления и индуктивности обмоток) не позволяют добиться таких же динамических характеристик, как при управлении инвертором, выступающем в качестве источника тока.
Точность в электроприводе транспортных средств не самое важное: даже если скорость троллейбуса будет изменяться в пределах нескольких километров в час — это не существенно.
Исходя из этого, можно сделать вывод, что данный алгоритм управления походит для тягового электропривода троллейбусов.
Литература:
1. Шрейнер Р. Т. «Математическое моделирование электроприводов переменного тока с полупроводниковыми преобразователями частоты» Екатеринбург: УРО РАН, 2000
2. Соколовский Г. Г. «Электроприводы переменного тока С частотным регулированием» Москва: ACADEMA, 2006
Основные термины (генерируются автоматически): асинхронный двигатель, система управления, векторное управление, трансформация координат, инвертор напряжения, тяговый электропривод троллейбусов, статорный ток, позиция ротора, случай управления, стратегия модуляции.
moluch.ru
Санкт-Петербургский государственный институт точной механики и оптики
(технический университет)
Кафедра электротехники и прецизионных электромеханических систем
Усольцев А.А.
ВЕКТОРНОЕ УПРАВЛЕНИЕ АСИНХРОННЫМИ ДВИГАТЕЛЯМИ
Учебное пособие по дисциплинам электромеханического цикла
Санкт-Петербург 2002
Содержание
Развитие асинхронного электропривода с векторным управлением
1. ВЕКТОРНАЯ МОДЕЛЬ АСИНХРОННОГО ДВИГАТЕЛЯ
1.1. Понятие обобщенного вектора
1.2. Основные соотношения между токами и потокосцеплениями АД
1.3. Индуктивность составляющей нулевой последовательности
1.4. Уравнения статора и ротора в векторной форме
1.5. Обобщённая электрическая машина
1.5.1. Электромагнитный момент АД
1.6. Модель короткозамкнутого АД при частотном управлении
2. ВЕКТОРНОЕ УПРАВЛЕНИЕ АСИНХРОННЫМИ ДВИГАТЕЛЯМИ
2.1. Общий принцип векторного управления АД
2.2. Модель АД, управляемого током статора, в системе координат, ориентированной по потокосцеплению ротора
2.3. Модель АД, управляемого напряжением статора, в системе координат, ориентированной по потокосцеплению ротора
2.4. Основные элементы систем векторного управления АД
2.4.1. Усилитель мощности релейного типа
2.4.2. Преобразователи числа фаз
2.4.3. Вектор-анализаторы и ротатор
2.5. Замкнутые системы векторного управления АД
2.5.1. Характеристики системы с П-регулятором скорости
2.5.2. Характеристики системы с ПИ-регулятором скорости
Список литературы
Современные системы векторного управления прошли долгий путь развития и в настоящее время являются наиболее распространенными среди систем электропривода переменного тока. Они позволяют просто и эффективно управлять такими сложными объектами как асинхронный двигатель с короткозамкнутым ротором (АД), что в свою очередь, позволяет существенно расширить область его применения, почти полностью вытесняя из автоматизированных управляемых приводов двигатели постоянного тока. Это связано в первую очередь с развитием силовой электроники, позволяющей создавать надежные и относительно дешевые преобразователи, а также с развитием быстродействующей микроэлектроники, способной реализовать алгоритмы управления практически любой сложности. Поэтому высококачественный асинхронный векторный электропривод (АВП) в настоящее время является по существу техническим стандартом.
Первым этапом процесса развития АВП была разработка универсальной векторно-матричной математической модели, получившей название обобщенной электрической машины, которая началась в конце 20-х годов и завершилась в конце 40-х годов ХХ века. Эта модель позволяет описывать электромагнитные процессы в идеализированной электрической машине с помощью аппарата линейной алгебры. Практическое использование модели было отложено на несколько десятилетий, т.к. при ручных расчетах она не давала каких-либо преимуществ, но требовала существенных вычислительных затрат, теоретически же ее успешно использовали для анализа переходных процессов в электрических машинах.
В 1971 году F. Blaschke предложил принцип построения системы управления асинхронным двигателем, в котором использовалась векторная модель АД с ориентацией системы координат по потокосцеплению ротора. Сущность предложенного метода, получившего впоследствии название векторного, заключалась в использовании в системе управления передаточных функций обратных по отношению к передаточным функциям векторной модели АД, что позволяло получить в качестве независимых входных переменных системы величины, входящие в уравнение электромагнитного момента. Поэтому этот принцип называется также прямым управлением моментом. Кроме того, для упрощения задачи в векторной модели АД использовалась система координат, ориентированная по одному из векторов, входящих в уравнение электромагнитного момента, что существенно упрощало передаточные функции системы и позволяло определить момент двумя независимыми переменными аналогично тому, как это делается в двигателях постоянного тока.
За три прошедшие десятилетия были разработаны десятки вариантов исходных моделей АВП, реализованы сотни устройств на разной элементной базе, опубликованы тысячи статей и монографий, но принцип и первая модель, предложенная F. Blaschke, по-прежнему доминируют в технических реализациях.
Большинство электрических машин переменного тока предназначено для работы в трехфазных сетях, поэтому они строятся с симметричными трехфазными обмотками на статоре, причем МДС этих обмоток распределены в пространстве по закону близкому к синусоидальному, т.е. МДС, создаваемая k-й обмоткой в точке, отстоящей от оси этой обмотке на угол k равна –F k=Fk0cos k, где Fk0 – МДС, соответствующая оси k-й обмотки. Синусоидальность распределения позволяет представить МДС или пропорциональные им токи обобщенным пространственным вектором на комплексной плоскости, т.е. вектором, представляющим собой геометрическую сумму отрезков, построенных на пространственных осях фазных обмоток и соответствующих мгновенным значениям фазных МДС или токов. При этом проекции обобщенного вектора на оси фазных обмоток в любой момент времени будут соответствовать мгновенным значениям соответствующих величин.
При симметричной трехфазной системе обмоток обобщенный вектор тока можно представить в виде
|
| (1.1.1) |
где  – операторы поворота, аia, ib и ic – мгновенные значения токов соответствующих обмоток. Обозначение вектора строчным символом принято для указания на то, что его координаты являются функциями времени аналогично тому, как строчные символы при обозначении скалярных величин указывают на мгновенное значение.
– операторы поворота, аia, ib и ic – мгновенные значения токов соответствующих обмоток. Обозначение вектора строчным символом принято для указания на то, что его координаты являются функциями времени аналогично тому, как строчные символы при обозначении скалярных величин указывают на мгновенное значение.

При таком представлении фазные токи ia, ib и ic можно рассматривать как проекции вектора i на соответствующие оси фазных обмоток (рис. 1.1 а)). Если произвести построение вектора i , откладывая значения фазных токов ia, ib и ic на осях обмоток (рис. 1.1 б)), то суммарный вектор окажется в полтора раза больше того вектора, проекции которого соответствуют фазным токам. Поэтому в выражении (1.1.1) присутствует коэффициент 2/3, приводящий модуль суммарного вектора к такому значению, которое при проецировании на оси фазных обмоток даст истинные значения фазных токов.
Если статор машины имеет нулевой провод, то фазные токи могут содержать нулевую составляющую и их значения можно представить в виде ia+io, ib+io и ic+io. Тогда вектор тока будет равен

Таким образом, обобщенный вектор тока статора не содержит нулевой составляющей и ее при анализе следует учитывать особо.
Обобщенный вектор, как и любой вектор на комплексной плоскости, можно представить алгебраической формой записи комплексного числа. Обычно это делают, совмещая вещественную ось с осью обмотки a (рис. 1.1), тогда
 .
.
Подставляя в выражение (1.1.1) значения операторов поворота, записанные в алгебраической форме, и разделяя вещественную и мнимую части получим

Если фазные токи содержат нулевую составляющую, то ее значение будет равно 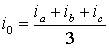 .
.
Переход от представления обобщенного вектора через проекции на оси трехфазных обмоток к представлению через проекции на оси комплексной плоскости эквивалентно преобразованию трехфазной системы обмоток в эквивалентную двухфазную. В матричной форме это преобразование можно записать в виде
|
|
(1.1.2) |
Отсюда обратное преобразование координат обобщенного вектора –
|
|
(1.1.3) |
Обобщенный вектор можно представить также во вращающейся системе координат. Если вектор тока представлен в неподвижной системе координат - , то переход к новой системе координат x-y, развернутой относительно исходной на некоторый угол (xy) (рис. 1.2 а)), осуществляется из очевидного соотношения аргументов комплексных чисел в виде
|
| (1.1.4) |
При этом следует заметить, что на угол (xy) не накладывается никаких ограничений, т.е. он может иметь постоянное значение, но может также изменяться произвольным образом. Для системы координат вращающейся с постоянной угловой частотой (xy) он равен – (xy) = (xy)t.
Преобразование координат можно записать в развернутом виде следующим образом

 .
.
Отсюда можно найти составляющие вектора ix и iy.или в матричной форме
|
| (1.1.5) |
а также обратное преобразование
|
| (1.1.6) |
Преобразование координат можно осуществить не только от неподвижной системы к вращающейся, но и для двух систем координат, вращающихся с различными угловыми частотами. Пусть вектор i представлен в системе координат d-q, текущий угол которой относительно неподвижных координат составляет (dq) (рис. 1.2 б). Тогда из очевидных соотношений углов преобразование координат можно записать в виде
|
| (1.1.7) |
Обобщенными векторами можно представить также напряжения u и потокосцепления , при этом все свойства рассмотренного выше обобщенного вектора тока будут присущи и этим векторам.
studfiles.net
Векторное управление является методом управления синхронными и асинхронными двигателями, не только формирующим гармонические токи (напряжения) фаз (скалярное управление), но и обеспечивающим управление магнитным потоком ротора. Первые реализации принципа векторного управления и алгоритмы повышенной точности нуждаются в применении датчиков положения (скорости) ротора.
В общем случае под "векторным управлением" понимается взаимодействие управляющего устройства с так называемым "пространственным вектором", который вращается с частотой поля двигателя.

Для СД и АД принцип векторного управления можно сформулировать следующим образом:
Необходимо определить направление и угловое положение вектора потокосцепления ротора двигателя. Ортогональные оси d,q (в отечественной литературе для асинхронных машин применяют оси x,y) направляют так, что ось d совпадает с направлением вектора потокосцепления ротора. Вектор напряжения статора двигателя регулируют в осях d,q. Составляющая напряжения по оси d регулирует величину тока статора по оси d.
Изменяя ток статора по оси d следует добиваться требуемого значения амплитуды вектора потокосцепления ротора. Ток статора по оси q, контролируемый напряжением по этой оси, определит момент развиваемый двигателем. В таком режиме работы СД и АД подобны двигателю постоянного тока, так по оси d формируется поле машины (обмотка возбуждения для двигателя постоянного тока, т.е. индуктор), а ток по оси q задаёт момент (якорная обмотка двигателя постоянного тока).
Векторное управление может быть реализовано не только при определении направления и углового положения вектора потокосцепления ротора (система «Transvektor»). Практический интерес представляют аналогичные устройства с управлением по вектору главного потокосцепления двигателя, которые в нашей стране стали именоваться векторными системами. Указанные устройства управления имеют свои особенности. Применение вектора потокосцепления ротора теоретически обеспечивает большую перегрузочную способность АД. При использовании устройства управления по вектору главного потокосцепления и стабилизации модуля главного потокосцепления двигателя во всех режимах работы исключается чрезмерное насыщение магнитной системы, упрощается структура управления АД. Для составляющих вектора главного потокосцепления (по осям α, β статора) возможно прямое измерение, например, с помощью датчиков Холла, устанавливаемых в воздушном зазоре двигателя.
Питание АД и СД в режиме векторного управления осуществляется от инвертора, который может обеспечить в любой момент времени требуемые амплитуду и угловое положение вектора напряжения (или тока) статора. Измерение амплитуды и положение вектора потокосцепления ротора производится с помощью наблюдателя (математический аппарат позволяющий восстанавливать неизмеряемые параметры системы).
Для векторного управления асинхронным двигателем следует сначала привести его к упрощенной двухполюсной машине, которая имеет две обмотки на статоре и роторе, в соответствии с этим имеется системы координат связанные со статором, ротором и полем.
Векторное управление подразумевает наличие в звене управления математической модели (далее - ММ) регулируемого электродвигателя. В зависимости от условий эксплуатации электропривода возможно управление электродвигателем как в режимах с обычной точностью, так и в режимах с повышенной точностью отработки задания на скорость или момент.
В связи с вышесказанным представляется возможным произвести классификационное разделение режимов управления по точности ММ электродвигателя, используемой в звене управления:
В зависимости от наличия или отсутствия датчика обратной связи по скорости (датчика скорости) векторное управление можно разделить на:
Поскольку принцип векторного управления был изобретен в ФРГ, то в русскоязычной литературе нередко встречается термин "векторное регулирование", являющийся калькой с немецкого "Vektorregelung". Такое определение нельзя считать ошибочным, однако по установившемся нормам русского технического языка более правильным будет использование именно термина "векторное управление".
dic.academic.ru
Чтобы понять что означает термин ВЕКТОРНОЕ УПРАВЛЕНИЕ давайте сначала разберемся что такое электродвигатель
Электродвигатель — это электромеханическое устройство, предназначенное для преобразования электрической энергии в механическую и наоборот — механическую в электрическую.
Электродвигатели нас окружают повсюду — это трамваи, троллейбусы, электрички, холодильники, кофемолки, кофеварки. Все они имеют по одному двигателю, а иногда и не по одному.
Электродвигатели потребляют около 60 % всей энергии вырабатываемой электростанциями по всему миру.
Условно все двигатели можно разделить на двигатели постоянного и переменного тока.
Двигатели переменного тока намного надежнее и проще по своей конструкции, поэтому они дешевле.
Однако управлять двигателем постоянного тока намного проще.Он содержит две обмотки. Первая — это обмотка возбуждения двигателя, вторая — это якорная обмотка. Благодаря тому что обмотка возбуждения никак не зависит от якорной обмотки, управление возбуждением является очень простым. Конечно все просто — подал напряжение на обмотку — появилось возбуждение, снял напряжение — возбуждение исчезло.
Основной недостаток двигателей постоянного тока — это коллектор. Он быстро выходит из строя, потому что вешь достаточно ненадежная.
Двигатель переменного тока не содержит обмотки возбуждения, потому что и возбуждение и вращающий момент создается статорной обмоткой. Уже становится невозможным так легко и просто создать в двигателе возбуждение. При подаче напряжения сначала появляется возбуждение, только после этого двигатель начинает вращатся.
Обычное (скалярное) управление двигателем переменного тока не позволяет регулировать возбуждение. Тут на помощь и приходит векторное управление. Хочется сразу заметить что векторное управление применимо только для двигателей переменного тока (асинхронных и синхронных машин).
Суть векторного управления заключается в псевдоуправлении возбуждением (потоком) двигателя.
Асинхронная машина представляется как двигатель постоянного тока (ДПТ) с независимым возбуждением (раздельными обмотками). Благодаря этому управление асинхронником становится таким же простым как ДПТ.
Однако даже векторное управление асинхронным двигателем не позволяет получить такой точности управления по сравнению с системами управления двигателя постояного тока. Плюс появляется необходимость использования дорогостоящего оборудования — силовых IGBT транзисторов. Поэтому векторное управление нашло себе применение в основном в приводах мощьностью до 100 кВт.
xn----8sbecmada0aoptggbsmf4a0a.xn--p1ai