Как было выяснено в разделе 4.3.1, потери в роторной цепи асинхронного двигателя пропорциональны его скольжению, поэтому стремятся, чтобы в рабочем режиме двигатель работал с минимальным скольжением. Однако в процессе пуска двигатель разгоняясь проходит скольжение от 1 до sн. В этот период в роторе двигателя могут выделиться значительные по величине потери энергии, что особенно неблагоприятно для асинхронных короткозамкнутых двигателей, где эти потери не могут быть вынесены из машины в пусковые сопротивления.
Определим потери в цепи ротора 
за один пуск асинхронного двигателя без нагрузки (без статического момента на валу двигателя).
Потери энергии за один пуск будут
. (4.38)
При отсутствии статического момента уравнение движения будет 
, подставляя которое в (4.38) и соответственно заменяя пределы интегрирования, получим:
,
откуда
. (4.39)
Отсюда вытекает правило, что при пуске асинхронного двигателя вхолостую потери в цепи его ротора равны тому запасу кинетической энергии, который получают приходящие в движение маховые массы (ротора и рабочего механизма) при их разгоне до установившейся скорости.
Заметим, что потери в роторе не зависят от времени пуска, пусковых токов и других параметров. Потери в статоре, напротив, зависят от параметров пуска.
Во избежание перегрева для каждого короткозамкнутого двигателя существует предельное значение суммарного момента инерции, который может преодолеть данный двигатель. При пуске значение 
указывается в каталогах. При отсутствии этих данных величина
может быть определена из следующих соображений.
Допустимая величина энергии, выделяющейся в клетке ротора и массой mкл, не должна приводить к ее перегреву более чем на 
. Отсюда
,
где Скл – Дж/кг.гр – теплоемкость материала клетки ротора.
Расчет проводится исходя из необходимости обеспечения двух пусков подряд. Поэтому 
.
Потери энергии в роторной цепи двигателя при динамическом торможении от скорости 
до минимальной скорости (затормозить двигатель до нулевой скорости при динамическом торможении нельзя) также равны запасу кинетической энергии, которой обладали движущиеся массы ротора и рабочей машины.
При торможении противовключением двигатель работает при еще больших скольжениях – от sнач=2 до s=1. Подставляя эти значения в (4.38), получим, что
.
Для асинхронного двигателя важно определить потери при пуске и торможении не только в роторной, но и в статорной цепи. Ориентировочно эти потери можно найти, зная потери в роторе и пользуясь соотношением
.
Потери в статоре могут быть сокращены, используя, например, снижение напряжения на статоре при пуске (если это возможно).
Для нерегулируемых электроприводов большой мощности (свыше 250кВт) широко применяются синхронные электродвигатели с электромагнитным возбуждением. Схема включения такого двигателя показана на рис.4.22.
Конструкция статора синхронного двигателя аналогична конструкции статора асинхронного двигателя. Токи, протекающие по трехфазной обмотке статора, создают намагничивающие силы, результирующий вектор которых образует вращающееся в пространстве электромагнитное поле статора Ф1. Скорость вращения поля статора равна
(4.40)
и является рабочей скоростью синхронного двигателя.
Рис.4.22. Схема включения Рис.4.23. Пространственные векторы
синхронного двигателя электромагнитных полей синхронного
двигателя а) идеальный холостой ход;
б) при нагрузке на валу
На роторе синхронного двигателя расположена обмотка возбуждения, которая питается постоянным током от независимого регулируемого источника напряжения – возбудителя. Ток возбуждения создает электромагнитное поле Ф0, неподвижное относительно ротора и вращающееся в установившемся режиме вместе с ротором со скоростью
. Магнитные силовые линии поля ротора сцепляются с вращающимся синхронно с ним электромагнитным полем статора. Взаимодействие полей статора и ротора создает электромагнитный момент на валу синхронной машины.
.
П
ри отсутствии нагрузки векторы поля статора
и поля ротора
совпадают в пространстве (см.рис.4.23) и совместно вращаются со скоростью
. При появлении на валу двигателя момента сопротивления векторы
и
, называемый углом нагрузки, причем, если вектор
отстает от вектора
(см.рис. 4.23б), то синхронная машина работает в двигательном режиме и электромагнитный момент на ее валу положителен. Если синхронная машина работает генератором, приводимым во вращение первичным двигатель, то вектор поля ротора опережает вектор поля статора на угол (-
) и электромагнитный момент на валу машины отрицателен. Изменению нагрузки на валу машины соответствует изменение угла
. Образно это соответствует растяжению-сжатию пружины. Максимальный момент будет иметь место при
Рис.4.24. Механические характеристики синхронного двигателя
1 – характеристика синхронного режима
2 – пусковая характеристика (асинхронный режим)
Механическая харак-теристика синхронной машины представляют собой прямую, парал-лельную оси абсцисс и ограниченную значени-ями момента
(рис. 4.24). Жесткость механической характе-ристики равна бесконечности. Поскольку ротор двигателя вращается с синхронной скоростью и скольжение отсутствует, то вся мощность электромагнитного поля статора Рэм преобразуется в механическую мощность на валу синхронного двигателя. Если пренебречь потерями в статоре, то 
. (4.41)
Рассмотрим векторную диаграмму неявнополюсной синхронной машины (рис.4.25). Двигатель с неявнополюсным ротором имеет симметричную в магнитном отношении конструкцию. Пренебрегая активным сопротивлением статора получим 
.
З
десьЕ1 – э.д.с., наводимая в обмотках статора вращающим-ся вместе с ротором полем Ф0.
Из векторной диаграммы следует:
или 
П
Рис.4.25. Векторная диаграмма синхронного двигателя
одставляя эти значения в (4.41), получим выражение для угловой характеристики неявнополюсной синхронной машины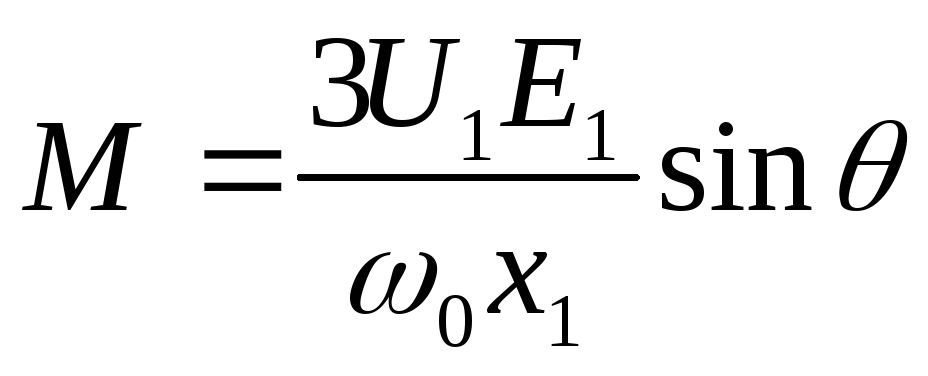 
. (4.42)
Из этого выражения и соответствующей ему угловой характеристики (рис.4.26) следует, что по мере нагружения синхронной машины угол нагрузки увеличивается и момент достигает максимума при 
. Учитывая пропорциональность между э.д.с.Е1 и магнитным потоком Ф0 (т.е. током возбуждения IВ), получим, что максимальный момент синхронной машины будет равен
, (4.43)
т.е. максимальный момент синхронного двигателя (в отличие от асинхронного) зависит от величины питающего напряжения в первой степени и в определенных пределах (когда не сказывается насыщение магнитной цепи) пропорционален величине тока возбуждения. Исходя из соотношения (4.43) в большинстве схем автоматического регулирования возбуждения синхронных двигателей для сохранения постоянной перегрузочной способности двигателя предусматривается автоматическое увеличение тока возбуждения при приложении ударной нагрузки или снижении величины питающего напряжения.
Рис.4.26. Угловая характеристика синхронного двигателя: а) неявнополюсной машины; б) – явнополюсной машины
1 – при номинальном потоке возбуждения;
2 – при форcировке возбуждения
Для синхронной машины с несимметричной магнитной цепью, когда ротор имеет явнополюсную конструкцию, кроме момента, вызванного полем ротора, возникает реактивный момент, определяемый стремлением ротора занять такое положение в пространстве, при котором магнитная проницаемость пути, по которому замыкается магнитное поле статора, была бы максимальной. Возникновение реактивного момента соответствует закону Ленца, который определяет: «При всяком изменении магнитного потока возникают силы электрического и механического характера, стремящиеся сохранить этот поток».
Для анализа угловой характеристики явнополюсного синхронного двигателя разложим векторы токов и падений напряжения по продольной d (согласно вектору э.д.с. Е1) и поперечной q осям ротора. Очевидно, что индуктивные сопротивления двигателя по этим осям будут разными, причем xd>xq. Преобразуем выражения (4.41) в соответствии с векторной диаграммой 4.25, где 
.
.
Обозначив 
, получим
. (4.44)
Из векторной диаграммы следует:
(4.45)
Подставляя I1d и I1q из (4.45) в (4.44), после преобразований получим:
. (4.46)
Первый член выражения представляет электромагнитный момент M’, возникающий в результате взаимодействия полей статора и ротора, второй член – реактивный момент M”, возникающий из-за несимметрии магнитной цепи двигателя и связанного с ней стремления ротора ориентироваться по оси поля статора. Угловая характеристика синхронной машины с явнополюсным ротором показана на рис.4.26б. Максимальная величина реактивного момента составляет обычно 15-20% от момента, определяемого взаимодействием полей.
Заметим, что явнополюсная синхронная машина развивает момент даже при отсутствии тока возбуждения – за счет реактивного момента. Это свойство синхронной машины легло в основу создания синхронных электроприводов без возбуждения на базе синхронных реактивных двигателей. У этих машин индуктивность по продольной и поперечной осям различается значительно, что обуславливает создание достаточного по величине реактивного момента на валу двигателя. Синхронные реактивные двигатели используются, как правило, для приводов небольшой мощности (менее 1кВт).
studfiles.net
В асинхронном двигателе, являющемся трёхфазным, возникает два типа потерь. Вот эти потери:
1. Постоянные или фиксированные потери.
2. Переменные потери.
Постоянными потерями называют такие потери, которые остаются постоянными в нормальном режиме работы асинхронного двигателя. Такие потери могут быть легко получены путём проведения теста без нагрузки трёхфазного двигателя. Эти потери подразделяются на следующие виды:
1. Потери железа или потери сердечника.
2. Механические потери.
3. Потери трения щёток.
Данные потери также можно подразделить на гистерезисные потери и потери вихревого тока. Потери вихревого электрического тока минимизируются за счёт использования наслоения на сердечнике. Раз применяется наслоение на сердечнике, область уменьшается, и поэтому увеличивается сопротивление, вследствие чего уменьшаются вихревые токи.
Гистерезисные потери минимизируются при помощи кремнистой стали высокого качества. Потери сердечника зависят от частоты поступаемого напряжения. Частота статора всегда является подающейся частотой, f, а частота ротора является проскальзыванием, умноженным на подающуюся частоту, (sf), которая всегда меньше частоты статора.
Частота статора составляет 50 герц. Частота ротора составляет около 1,5 герц. Так происходит потому, что в нормальном рабочем состоянии проскальзывание составляет 3%. Отсюда потери сердечника ротора очень малы по сравнению с потерями сердечника статора, и ими обычно пренебрегают при рабочих состояниях.
Механические потери имеют место быть в подшипнике, потери трения щёток возникают в асинхронном двигателе с обмотанным ротором. Эти потери составляют ноль на старте. По мере того, как возрастает скорость, данные потери увеличиваются. В трёхфазных двигателях скорость обычно остаётся постоянной. Отсюда следует, что и данные потери почти остаются постоянными.
Эти потери также называются потерями меди. Данные потери происходят из-за электрического тока, идущего по обмоткам статора и ротора. Когда нагрузка меняется, данный электрический ток также изменяется, а потому и потери эти тоже претерпевают изменения. Поэтому их и назвали переменными потерями. Их можно получить при помощи проведения теста с заблокированным ротором трёхфазного двигателя.
Основная функция асинхронного двигателя состоит в том, чтобы преобразовывать электрическую энергию в механическую энергию. В течение данного преобразования одной энергии в другую, энергия проходит через различные этапы. Данная энергия, проходящая через разные ступени, отображается на диаграмме течения энергии.
Как известно, на входе трёхфазного асинхронного двигателя трёхфазная подача. Так что эта трёхфазная подача идёт на статор трёхфазного электродвигателя.Допустим, Pin = электрическая энергия, которая идёт на статор трёхфазного двигателя,VL = линейное напряжение, поступающее статору трёхфазного двигателя,IL = линейный ток,Cos = коэффициент мощности трёхфазного двигателя.Вход электрической энергии на статор, Pin = 3VLILcos.
Часть этой энергии на входе используется для поддержки потери статора, которыми являются потери железа статора и потери меди статора. Сохраняющаяся энергия (электроэнергия на входе – потери статора) идёт на ротор как вход на ротор.Так что вход на ротор, P2 = Pin – потери статора (потери меди статора и потери железа статора). Теперь ротор должен преобразовать этот вход на ротор в механическую энергию, но этот завершённый вход не может быть преобразован в механический выход, поскольку он должен поддерживать потери ротора.
Бывает два типа потерь ротора, а именно потери меди и потери железа. Потери железа зависят от частоты ротора, которая очень мала, когда ротор вращается. Поэтому этим обычно пренебрегают. Так что можно сказать, что ротор имеет лишь потери меди. По этой причине вход на ротор должен поддерживать эти потери меди. После этой поддержки, оставшаяся часть входа ротора, P2 преобразовывается в механическую энергию, Pm.
Допустим, Pc будет потерями меди ротора,I2 будет током ротора в рабочем состоянии,R2 – сопротивлением ротора,Pm – общая производимая механическая энергия.Pc = 3I22R2Pm = P2 – Pc
Теперь эта создаваемая механическая энергия идёт на нагрузку за счёт вала, но появляются некоторые механические потери, такие как потери трения и потери сопротивления воздуха. Так что общая воспроизводимая механическая энергия должна быть подана на поддержание этих потерь.
Поэтому выход образуемой энергии идёт на вал, который в конечном итоге подаёт её нагрузке, Pout.Pout = Pm – механические потери (потери трения, а также потери, связанные с сопротивлением воздуха).Pout зовется энергией вала. Также его называют полезной энергией.
Пишите комментарии, дополнения к статье, может я что-то пропустил. Загляните на карту сайта, буду рад если вы найдете на моем сайте еще что-нибудь полезное.
elektronchic.ru
Потери энергии в переходных режимах, как правило, возрастают, поскольку эти процессы сопровождаются большими бросками тока.Так, при пуске асинхронного короткозамкнутого двигателя пусковые токи составляют 5-6 номинального. В процессе разгона двигатель должен не только преодолевать момент сопротивления, но и создавать динамический момент, идущий на увеличение кинетической энергии движущихся масс.
Рассмотрим потери энергии в короткозамкнутом асинхронном двигателе за время пуска вхолостую (М^О). В процессе пуска двигатель, разгоняясь, проходит скольжения от 1 до 0. В этот период в роторе выделяются значительные потери энергии, что особенно неблагоприятно для короткозамкнутых двигателей, где эти потери не могут быть вынесены из машины в пусковые сопротивления.
Так как потери в роторе пропорциональны моменту и скольжению
ΔP = M · ω0s
то потери энергии за один пуск будут:
(11.7)
При пуске вхолостую М = J∑(dω/dt) подставляя это значение момента в (11.7) и соответственно заменяя пределы интегрирования, получим:
(11.8)
Отсюда вытекает правило, что при пуске асинхронного двигателя вхолостую потери в цепи его ротора равны запасу кинетической энергии, который получают приходящие в движение маховые массы ротора двигателя и рабочего механизма при их разгоне до установившейся скорости.
Заметим, что потери в роторе не зависят от времени пуска, пусковых токов и других параметров. Потери в статоре, напротив, зависят от параметров пуска.
Во избежание перегрева для каждого короткозамкнутого двигателя существует предельное значение суммарного момента инерции, который может преодолеть данный двигатель. При пуске значение J∑пред указывается в каталогах. При отсутствии этих данных величина J∑пред может быть определена из следующих соображений.
Допустимая величина энергии, выделяющейся в клетке ротора массой ткл„ не должна приводить к перегреву более чем на Тпер = 3000С. Отсюда
ΔАдоп = тклСклТпер
где Скл – Дж/кг.гр – теплоемкость материала клетки ротора.
Расчет проводится исходя из необходимости обеспечения двух пусков подряд. Поэтому 2ΔА < тклСклТпер300. Из этих условий получим:
Потери энергии в роторной цепи двигателя при динамическом торможении от скорости ω до минимальной скорости (затормозить двигатель до нулевой скорости при динамическом торможении нельзя) также равны запасу кинетической энергии, которой обладали движущиеся массы ротора и рабочей машины.
При торможении противовключением двигатель работает при еще больших скольжениях - от sнач=2 до s=1. Подставляя эти значения в (11.7), получим, что
Для асинхронного двигателя важно определить потери при пуске и торможении не только в роторной, но и в статорной цепи. Ориентировочно эти потери можно найти, зная потери в роторе и пользуясь соотношением
Потери в статоре могут быть сокращены, используя, например, снижение напряжения на статоре при пуске (если это возможно).
При плавном изменении ω0 в соответствии с заданным темпом разгона (при частотном управлении асинхронным двигателем или плавном повышением напряжения в приводах постоянного тока) двигатель работает с малыми скольжениями и потери в двигателе, как и в установившемся режиме, определяются величиной развиваемого момента.
studfiles.net
П
усть в начале ротор не вращается. Магнитное поле, пересекая проводники ротора индуктируют в них ЭДС. При замкнутой цепи ротора по обмотке его потечет ток.
Взаимодействие потока статора и тока ротора вызовет усилие, действующее на проводник, под действием которого ротор начнет вращаться. Вращение будет в ту же сторону, что магнитный поток. Скорость ротора будет меньше скорости вращения магнитного поля статора. Скольжение
.
Разберемся, в каких пределах будет изменяться скольжение.
Момент зависит от потока Ф и тока I2 при U = const, поток также постоянен. Если увеличивается момент на валу, то увеличивается и момент двигателя за счет увеличения тока I2, а I2 Е2 S, S за счет увеличения интенсивного пересечения проводников ротора.
При неподвижном роторе n = 0, S = 1
Если ротор будет вращаться с n = n1, S = 0
Это диапазон скольжений соответствует двигательному режиму. Мощность потребляемая из сети будет преобразована в механическую на валу.
Но если под действием спускаемого груза раскрутить ротор до скорости больше синхронной, то машина перейдет в генераторный режим
n > n1, S < 0 - скольжение отрицательное
При этом режиме механическая мощность будет преобразована в электрическую, которая будет отдаваться в сеть Р1, а реактивная будет потребляться для создания магнитного потока - Q.
Режим противовключения.
Если например в приводе имеется большой маховик, то если отключить двигатель, то маховик будет вращаться длительное время до остановки, но если же мы переключим две фазы асинхронного двигателя, то его момент будет направлен против вращения маховика и время останова его резко сократиться. При этом режиме мощность будет потребляться из сети и механическая мощность будет теряться в роторе. Это тяжелый режим для асинхронной машины. Поэтому, если используется двигатель с фазным ротором, то на период работы в цепь ротора включают значительное сопротивление для ограничения тока. Если же используется короткозамкнутый двигатель, то пускают его при пониженном напряжении. Ниже на рисунке представлены все три режима работы асинхронной машины.
Рассмотрим два крайних режима двигателя:
а) холостой ход двигателя
При холостом ходе нет нагрузки на валу, ротор под действием вращающего магнитного поля статора разгонится до скорости близкой к синхронной, а ток статора равен току холостого хода. Мощность, потребляемая из сети пойдет на покрытие потерь, т.е.
Ро = Рэл1 + Рмг + Рмех + Рдоб
Разница между тр-м и двигателем будет только конструктивная. В двигателе имеется воздушный зазор. Поэтому ток холостого хода двигателя равен 20 - 30 от номинального.
б) режим короткого замыкания
При этом режиме ротор механически заторможен, а обмотка ротора закорочена. К статору подводится пониженное напряжение, при котором ток имеет значение близкое к номинальному. Мощность короткого замыкания пойдет на покрытие потерь в стали и обмотках. При номинальном напряжении пусковой ток
Iп = (5 7)Iн.
Используя данные режима холостого хода и короткого замыкания можно построить круговую диаграмму, а по ней определить рабочие характеристики работы двигателя при нагрузке.
studfiles.net
Последнее время активно внедряются асинхронные электроприводы, и наиболее распространенными из них являются с короткозамкнутым ротором, которые довольно часто работают в повторно-кратковременном режиме. Асинхронные электрические машины нашли широкое применение в механизмах кузнечно-прессовых, металлорежущих станках, а также в подъемно-транспортных механизмах и многих других. Большинство из этих механизмов имеют довольно напряженный режим работы – по 1000-1500 и иногда и по 2000 включений в час.
Условия работы АД с КЗ ротором более тяжелые, чем тех же электродвигателей постоянного тока или асинхронных с фазным ротором. В двигателях с КЗ ротором тепло, которое выделится на обмотке ротора при пуске или торможении должно рассеиваться самой обмоткой ротора. Чтоб уменьшить нагрев при повторно-кратковременном режиме работы нужно, чтобы двигатель имел минимальный маховый момент на роторе, а также ток пусковой как можно меньше и обладать повышенным скольжением.
При расчете количества пусков в час не рекомендуют использовать методы эквивалентного момента, тока и мощности. Это связано с тем, что при пуско-тормозных режимах происходит изменение потерь в стали, из-за значительного нагрева обмоток ротора растет и сопротивление в них, следствием чего становится не возможность связать потери в статоре и роторе каким-то коэффициентом.
Более менее точные расчеты получают методом средних потерь. В этом случае составляют баланс тепла, которое выделяется в двигателе в виде потерь и тепла, которое отдается охлаждающей среде.
Допустимое число циклов работы в час можно определить отношением количества тепла, которое отдаст двигатель за час окружающей среде при τ=τдоп к количеству тепла, которое выделится в нем за один цикл работы. Пусть рабочий цикл асинхронной машины будет состоять из разгона, некоторого времени работы с установившейся скоростью, ну и, естественно, торможения и паузы. Отдача тепла при состоянии покоя будет равно 
, а в динамических режимах (пуск и торможение) 
. А потери за цикл составят:
Где: ∆Апуск и ∆Ат – потери, которые возникает в электродвигателе при торможении и пуске; qc – потери, возникающие в двигателе в установившемся режиме; ty – длительность работы в продолжении одного цикла;
Также должно существовать равенство между теплом, которое выделится в двигателе, и теплом, которое отведется окружающей средой:
Если предположить что электродвигатель работает с Z циклами в час, то можно определить длительность цикла:
Продолжительность рабочего участка в каждом цикле составит
, где ԑ — относительная заданная продолжительность работы.
А длительность работы двигателя с установившейся скорость составит:
И получаем продолжительность паузы:
Подставив значения tу и t0 в уравнение теплового баланса получим:
Решив уравнения относительно Z:
Полагая что β=0,25 и приравняв qс= qном, получим:
При токе 3-4 Iном в режимах торможения и пуска потери превысят номинальные в 10-15 раз:
Исходя из этого третий член знаменателя оценивается примерно в 3% от суммы потерь ∆Апуск+ ∆Ат. Тогда выражение решенное относительно Z примет вид:
Анализ выше показанного выражения показывает, что для того, чтоб повысить допустимое количество включений в час необходимо стремится к снижению потерь в переходных режимах и увеличивать теплоотдачу в период пауз.
Снижение потерь в переходных режимах можно достигнуть за счет снижения запаса кинетической энергии системы рабочая машина – электродвигатель, а также подбора рационального метода торможения. Как правило, большая часть кинетической энергии системы будет приходится на долю ротора или якоря электродвигателя. Поэтому для подобных приводов должны применять специальные двигатели, обладающие особо малыми маховыми массами ротора. Не последнюю роль играет и тип торможения. При торможении противовключением потери будут равны утроенному запасу кинетической энергии системы. Как следствие отказ от торможения противовключением и замена его на динамическое торможение позволяет уменьшить потери примерно в 2 раза.
Для увеличения теплоотдачи иногда применяется принудительная вентиляция электродвигателя, при которой β стремится к единице. Также иногда при конструировании электрических машин могут закладываться обмотки с повышенной теплостойкостью изоляции. Использование таких не хитрых приемов позволяет увеличить количество включений в час до 2000 и более.
elenergi.ru
Потери в двигателе складываются из переменных, зависящих от нагрузки, и постоянных потерь, не зависящих от нагрузки.
Для электропривода постоянного тока суммарные потери мощности равны:
ΔРΣ=ΔРк+ ΔРυ = ΔРв+ ΔРст+ ΔРмех+I2R , (9.5)
где ΔРк — постоянные потери, ΔРк = ΔРв+ ΔРст+ +ΔРмех ; ΔРв , ΔРст , ΔРмех — соответственно потери на возбуждение, потери в стали и механические; I2R = ΔРυ — потери в силовой (якорной) цепи двигателя.
Аналогично для асинхронного двигателя
ΔРΣ= ΔРст+ ΔРмех+3(I12R1+ I2’2R2). (9.6)
Переменные потери ΔРυ могут быть выражены также через электромагнитный момент и относительную скорость (или скольжение), а именно:
1
) для двигателя постоянного тока независимого воз- буждения
(9.7)
где Р12 — электромагнитная мощность; Δω, ω0 — соответственно перепад угловой скорости, обусловленный моментом М, и угловая скорость идеального холостого хода;
2) для асинхронного двигателя
(9.8)
Выше при рассмотрении различных способов регулирования угловой скорости электроприводов постоянного и переменного тока приводились необходимые соотношения для определения потерь в двигателях при установившемся режиме.
Более подробно остановимся на определении потерь и расходе энергии в переходных процессах. Здесь целесообразно находить не среднее значение потерь мощности, а расход и потери энергии за время переходного процесса.
Потери энергии в двигателе за время переходного процесса tп.п в общем случае равны:
(9.9)
Так как по сравнению с переменными постоянные потери в переходном процессе малы, то в дальнейшем они учитываться не будут.
Д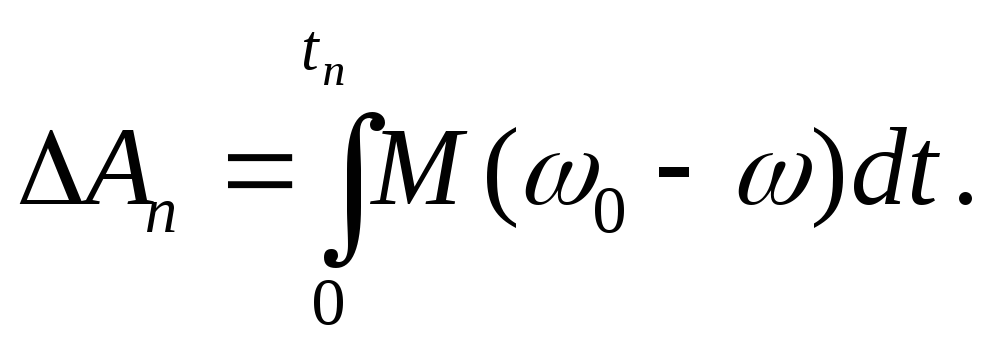
ля двигателя постоянного тока независимого возбуждения потери при пуске равны:
(9.10)
Если пуск совершается вхолостую (при Мс = 0), то из
уравнения движения следует: 
тогда
или (9.11)
Следовательно, потери энергии при пуске двигателя вхолостую определяются запасом кинетической энергии, накопленной массами привода к концу пуска.
П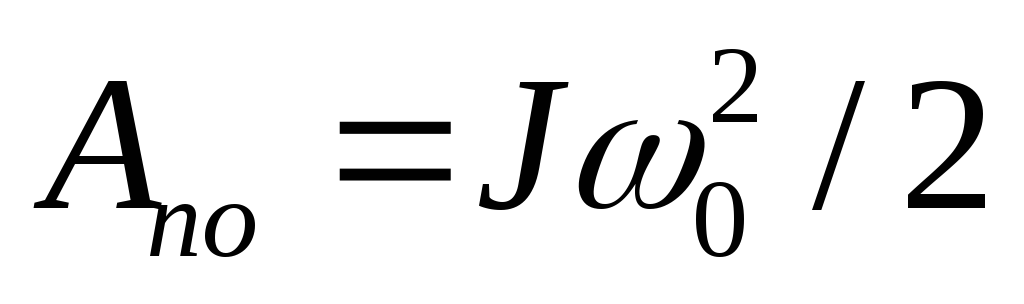
олезная работа (затраченная на пуск привода), произведенная двигателем за время пуска вхолостую, также равна запасу кинетической энергии, накопленной массами за этот период:
(9.12)
Расход электрической энергии из сети равен:
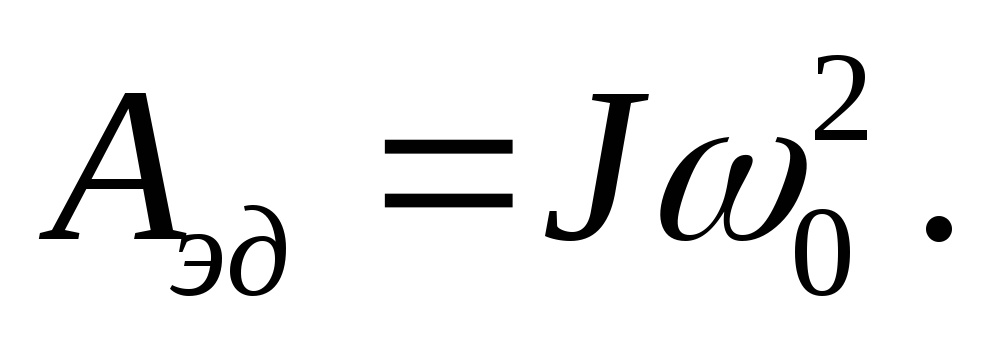(9.13)
На рис. 9.6 приведены идеализированные графики угловой скорости и развиваемой (полезной) и потребляемой из сети мощности двигателя постоянного тока независимого возбуждения. Суммарная потребляемая за время пуска из сети энергия отображается прямоугольником Обве; постоянные потери соответствуют площади абвг. Полезная мощность двигателя растет по прямой Ог, принимая максимальное значение к концу пуска, затем падает до 0, так как Мс = 0; при этом не учитываются постоянные потери,
о
тмеченные отрезкомде-вг. Энергия, потребляемая якорной цепью двигателя, пропорциональна площади Оаге, площадь треугольника Оаг — потерям в якорной цепи двигателя, а Оге — полезной работе. График изменения угловой скорости ω (t) при постоянном моменте показан отрезком Ож. При пуске двигателя под нагрузкой в предположении, что Мc = const, потери энергии
Т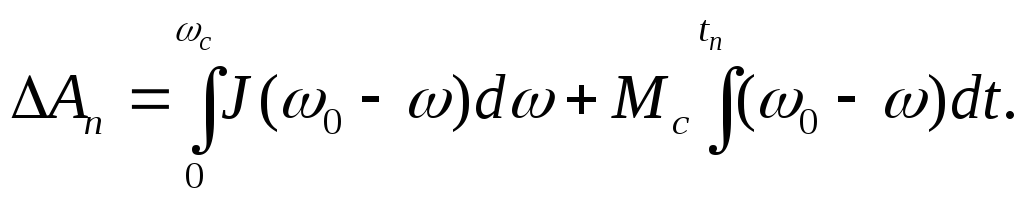
ак какdt=J dω/Мдин , то после преобразований
И
ли
(9.14)
Первый член выражения (9.14) представляет собой потери энергии в якорной цепи, обусловленные разгоном инер-
Рис. 9.6. Идеализированные Рис. 9.7. К графическому оп-
графики угловой скорости и раз- ределению потерь при пуске
виваемой и потребляемой из се- двигателя постоянного тока не-
ти мощностей двигателя постоян- зависимого возбуждения под
ного тока независимого возбуж- нагрузкой. дения при пуске вхолостую.
ционных масс привода (ΔАп.дин), а второй — потери, вызванные наличием момента нагрузки (ΔАп.с).
Формулу (9.14) можно записать так:
(9.15)
ΔАп = ΔАп.дин+ ΔАп.с
Если ωс мало отличается от ω0, то
Подсчет ΔАпс можно произвести, воспользовавшись следующим графиком (рис. 9.7), на котором дается зависимость ω = f (t).
Н
а рис. 9.7 заштрихованная площадь равна:
Следовательно,
ΔAп.c=McFп (9.16)
Тогда потери в якорной цепи двигателя
(9.17)
П
отери энергии при торможении противовключениемвхолостую определяются по формуле
Или
ΔАт.п0 = 3Jω02/2 (9.18)
энергии, т. е. в 3 раза превышают потери энергии при пуске вхолостую. Графическая интерпретация изменения механической и электрической мощности при торможении противовключением с МС = 0 показана на рис. 9.8. Механическая мощность, поступающая с вала, преобразуется в элект-
Рис. 9.8. Графическая интерпретация изменения механической и электрической мощностей при торможении противовключением вхолостую двигателя постоянного тока независимого возбуждения.
рическую и выделяется в якорной цепи двигателя, что определяет одну составляющую потерь, прямо пропорциональ-
ную площади треугольника Оаб. Так как напряжение сети постоянно во время торможения, то вторая составляющая потерь обусловлена потреблением электрической энергии из сети и пропорциональна площади, ограниченной прямоугольником Обвг. Как видно, сумма этих составляющих и определяет тройной запас кинетической энергии.
П
ри торможении противовключением под нагрузкойМс = const) потери энергии можно определить по формуле
(9.19)
или
(9.20)
Аналогично предыдущему можно обозначить:
Окончательно
(9.21)
Из (9.21) следует, что потери энергии при торможении двигателя под нагрузкой меньше, чем вхолостую.
При динамическом торможении якорь двигателя отклю чен от сети и замкнут на резистор, поэтому кинетическая энергия, запасенная в массах электропривода, в процессе торможения превращается в электрическую и выделяется в виде теплоты в якорной цепи.
Потери энергии в якорной цепи двигателя при динамическом торможении вхолостую
Или
(9.22)
Если динамическое торможение производится под нагрузкой (Мс = const), то потери энергии в якорной цепи
(9.23)
Второй член (9.23) легко подсчитать, как и ранее, если известна зависимость ω = f(t).
П
отери энергии в якорной цепи двигателя при реверсировании без нагрузки
(9.24)
Формула (9.24) подтверждает, что потери энергии при реверсировании складываются из суммы потерь энергии при торможении противовключением и пуске.
Для определения потерь энергии при реверсировании под нагрузкой можно воспользоваться формулой
ΔАр= ΔАп + ΔАт.п (9.25)
Следует подчеркнуть, что при управлении двигателем независимого возбуждения от источника с постоянным напряжением и Мс = 0 на потери в переходном режиме не влияет значение тока в якорной цепи, с которым пускается или тормозится двигатель, а следовательно, и электромагнитный момент. Эти потери остаются неизменными при любом числе ступеней пускового или тормозного резистора, так же как и при безрезисторном управлении. Отсюда следует, что и длительность переходного процесса не оказывает влияния на потери энергии в переходных режимах, если Мс = 0, а постоянные потери не учитываются.
Иначе, чем в случае двигателя постоянного тока независимого возбуждения, определяются потери при переходных процессах в двигателе постоянного тока последовательного возбуждения, у которого магнитный поток зависит от тока якоря, т. е. имеет место нелинейная зависимость между током якоря и моментом. Здесь для определения потерь необходимо построить график зависимости квадрата тока якоря в переходном процессе от времени и, проводя численное интегрирование этой кривой, вычислить потери энергии. Так же определяются при переходных режимах потери энергии в двигателе постоянного тока сме-шйнного возбуждения и для других типов двигателей в случае существенного изменения магнитного потока или статического момента в течение переходного процесса. Следует отметить, что при пуске и торможении противовключе-
нием двигателя постоянного тока последовательного возбуждения при неизменном напряжении потери энергии в нем могут быть меньше, больше или равны соответствующим потерям в двигателе постоянного тока независимого возбуждения. Если среднее значение тока в переходном режиме у двигателя последовательного возбуждения больше номинального, то вследствие увеличенного магнитного потока момент, развиваемый двигателем, окажется больше, а время переходного процесса и потери энергии меньше, чем у двигателя независимого возбуждения, при прочих равных условиях (в частности, при одинаковых токах).
Рис. 9.9. Схема пуска двухдвигателыюго привода постоянного тока с двигателем независимого возбуждения изменением напряжения в две ступени,
а — схема для первой ступени; б — для второй ступени.
Если же ток в среднем меньше номинального, то момент двигателя последовательного возбуждения меньше, чем у двигателя независимого возбуждения, а время и потери энергии будут больше. Только при номинальном токе для обоих типов двигателей время и потери энергии будут одинаковыми в переходных режимах.
Если при управлении переходными процессами напряжение, подводимое к двигателю, изменяется от меньшего значения в начале процесса до большего в конце его, то потери в якорной цепи становятся меньшими, чем при неизменном напряжении.
Рассмотрим простейший случай пуска изменением напряжения в две ступени двухдвигательного привода постоянного тока с двигателями независимого возбуждения, каждый из которых рассчитан на номинальное напряжение. Вначале (рис. 9.9, а) якорные цепи обоих двигателей вклю-
чены последовательно, и напряжение, приходящееся на выводы якоря каждого из двигателей, равно половине не-минального — оба двигателя разгоняются до половинной
Рис. 9.10. Графики процесса разгона двухдвигательного привода постоянного тока с двигателями независимого возбуждения в две ступени.
а — графики напряжения и угловой скорости; б — графики электрической и механической мощностей.
у
гловой скорости. Очевидно (если считать для упрощенияМс = 0) потери энергии при пуске до угловой скорости, равной ω0/2, составят:
а при последующем разгоне от угловой скорости ω0/2 до ω0,
о
существляемом переключением с последовательного соединения двух двигателей на параллельное (рис. 9.9, б), потери энергии равны:
Таким образом, суммар-
н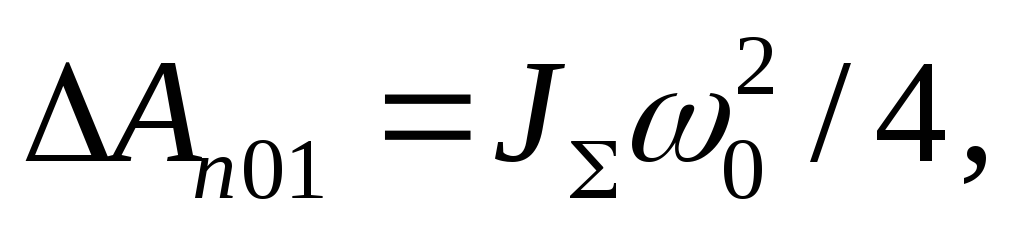
ые потери (пуск в две сту- Рис. 9.11. Зависимости ш„.(0 и пени т. е. со (t) при пуске вхолостую двига-
в 2 раза меньше, чем при теля постоянного тока независимо- пуске в одну ступень (сра- го возбуждения путем линейного
зу ω0). Графики, приве- го изменения во времени.
денные на рис. 9.10, а и б,
иллюстрируют в упрощенном виде процесс пуска двух-двигательного привода в две ступени; площади заштри-
кованных треугольников пропорциональны потерям энергии.
В случае линейного во времени изменения напряжения, подводимого к якорю двигателя постоянного тока независимого возбуждения (линейно изменяется и задаваемая угловая скорость идеального холостого хода), зависимости ω0(t) и ω (t) при пуске вхолостую можно представить, как это показано на рис. 9.11. Здесь на первом этапе пуска
п
риt > tп0
н
а втором этапе приt > tп0
(9.26)
г
деεп — угловое ускорение ; Tм — электромеханическая постоянная времени привода ; ωп и Мп — соответственно угловая скорость и момент при t = tп0; t' = t — tп0.
Потери энергии
Полагая tп0 > Тм и допуская для упрощения линейную зависимость для ω (t), получаем:
Кроме того,
Тогда
И
ли окончательно
(9.27)
Из (9.27) следует, что когда Тм < tп0, потери энергии при пуске с линейным изменением напряжения значительно меньше (в 5—6 раз), чем в случае пуска с постоянным напряжением.
Если пуск двигателя постоянного тока независимого возбуждения производится в системе Г — Д путем включе-
н
ия обмоток возбуждения генератора на полное напряжение и ЭДС генератора изменяется по экспоненциальному закону, то потери в якорной цепи
(9.28)
Для пуска вхолостую с учетом, что
(9.29)
п
осле преобразования получим:
(9.30)
где ΔAп0 = Jω02/2; т = Тв / Тм — отношение постоянной времени обмотки возбуждения к электромеханической постоянной времени привода.
Из (9.29) и (9.30) следует, что чем больше Тв по сравнению с Тм, тем медленнее нарастает ЭДС генератора, замедляется пуск двигателя и уменьшаются потери энергии. Форсирование процесса возбуждения приводит к возрастанию потерь энергии.
Можно показать, что при пуске под нагрузкой потери в якорной цепи системы Г — Д равны:
(9.31)
г
де Рс, Асос — соответственно мощность, потребляемая двигателем, и перепад угловой скорости, обусловленный моментом нагрузки УИС при установившейся ЭДС генератора. В процессе рекуперативного торможения вхолостую путем снятия напряжения с обмотки возбуждения генератора потери в якорной цепи составят:
(9.32)
То же при Мс = const :
(9.33)
Потери при торможении под нагрузкой при том же времени оказываются меньшими, чем вхолостую, из-за меньшего тока в якоре.
Пусковые потери в асинхронном двигателе, если пренебречь постоянной составляющей потерь ΔРк и влиянием
т
ока холостого хода (т. е. считатьI1 ≈ I2’), можно определить по формуле
(9.34)
При Мс = 0
dt = - ( Jω / M ) ds.
Выражая потери мощности в роторной цепи через мощность скольжения, т. е. 3I2’(R'2 + R’2доб) = Мω0s, в результате несложных преобразований получаем:
(9.35)
или, учитывая, что sнач = 1 и sкон = 0,
(9.36)
где ω0 —синхронная угловая скорость двигателя; R1, R2, R’2доб — соответственно сопротивление фазы статора, приведенные к цепи статора сопротивление фазы ротора и сопротивление добавочного резистора в цепи ротора; для двигателя с короткозамкнутым ротором R’2доб = 0.
Из (9.36) следует, что потери при пуске состоят:
и
з потерь в роторной цепи: ΔАп02 = Jω02/2, опре - деляемых запасом кинетической энергии, которую приобре тает привод к концу пуска;
из потерь в статорной цепи:
зависящих от активных сопротивлений статора и роторной цепи; чем больше сопротивление роторной цепи, тем меньше потери в статоре асинхронного двигателя. Уменьшение потерь в статоре с ростом вторичного сопротивления объясняется уменьшением пускового тока.
Для двигателя с короткозамкнутым ротором R’2доб = 0, и составляющая потерь в статоре равна:
В двигателях общего назначения (единой серии) с короткозамкнутым ротором R1 ≈ R'2, т. е. в этом случае составляющая потерь энергии в статоре численно равна запасу кинетической энергии, т. е. потерям в роторе.
За счет применения двигателей со специальной конструкцией короткозамкнутого ротора, имеющего повышенное сопротивление, может быть достигнуто уменьшение потерь в статоре. Это двигатели со сплошным стальным ротором и двигатели с повышенным номинальным скольжением. Двигатели, имеющие ротор с глубокими пазами или ротор с двойной беличьей клеткой (двигатели типа Бушеро), также обладают повышенным сопротивлением ротора, изменяющимся в функции скольжения, что приводит к уменьшению переменных потерь в статоре. Потери в роторной цепи при пуске вхолостую для всех типов двигателей определяются запасом кинетической энергии.
П
отери энергии при пуске асинхронного двигателя поднагрузкой (Мс = const) могут быть определены по формуле
(9.37)
где Мп.ср = (λ + kn) Mном / 2 — средний пусковой момент асинхронного двигателя; λ = Мк / Мном; kп = Мк / Мном; Мп — пусковой момент (момент короткого замыкания двигателя).
Потери энергии в асинхронном двигателе при торможении противовключением могут быть найдены по (9.35) при подстановке в нее пределов интегрирования sнач = 2 и
s
кон = 1, тогда
(9.38)
Е
сли торможение противовключением производится под нагрузкой (Мс — const), то потери равны:
(9.39)
где Мт,ср — средний момент, развиваемый асинхронным двигателем при торможении противовключением.
Потери энергии в роторной цепи двигателя в период динамического торможения вхолостую определяются запасом кинетической энергии, который приобретет привод к началу торможения, т. е.
Потери в статоре в этом случае
(9.40)
здесь Iэкв — эквивалентный ток статора; tт — время динамического торможения.
Н
аконец, если динамическое торможение происходитпод нагрузкой (Мс = const), то потери в роторной цепи
(9.41)
Потери в статоре для этого случая определяются по (9.40) с учетом того, что время торможения будет меньше при том же значении Iэкв.
У
двух- или многоскоростных двигателей потери энергии значительно выше, чем у односкоростного двигателя такой же мощности, имеющего номинальную угловую скорость, равную максимальной угловой скорости многоскоростного двигателя, обладающего значительно большими габаритами и моментом инерции. Поэтому прямой пуск многоскоростного двигателя на максимальную угловую скорость нежелателен. Целесообразно для уменьшения пусковых потерь энергии использовать ступенчатый пуск. В случае двухскоростного двигателя пуск осуществляется . в две ступени. При включении обмотки статора при пуске на первую ступень таким образом, что синхронная угловая скорость будет равна половине верхней (ω0/2), потери энергии составят (Mc= 0):
(9.42)
П
уск на вторую ступень от угловой скоростиω0/2 до ω0вызовет потери
(9.43)
Суммарные пусковые потери составят:
(9.44)
Следовательно, при двухступенчатом пуске потери энергии окажутся вдвое меньше, чем при пуске в одну ступень, если отношение R1/R'2 сохранится неизменным с переключением числа полюсов. Ступенчатый пуск двухскоростного двигателя аналогичен пуску двигателя постоянного тока независимого возбуждения изменением подводимого к якорю напряжения в две ступени.
При многоступенчатом пуске трех- или четырехскорост-ного двигателя потери энергии еще в большей мере сни-
жаются. Например, если осуществить ступенчатый пуск четырехскоростного двигателя, имеющего синхронные частоты вращения 500/1000/1500/3000 об/мин, то потери энергии на первой, второй, третьей ступенях пуска составят по 1/36 и на четвертой 1/4, а общие пусковые потери энергии V3 потерь при прямом пуске в одну ступень до 3000 об/мин.
Для двигателя с частотами вращения 500/750/1000/ 1500 об/мин при четырехступенчатом пуске общие потери энергии составят 5/18 пусковых потерь в одну ступень до 1500 об/мин.
Торможение двух- или многоскоростных асинхронных двигателей с целью снижения потерь также может быть ступенчатым.
Е
сли двухскоростной двигатель имеет две синхронныеугловые скорости ω02 и ω01, то торможение от ω02 до ω01можно осуществить с рекуперацией энергии в сеть, а с ω1до 0 — противовключением или динамическим торможением. На первой ступени потери энергии при рекуперативном торможении вхолостую можно определить по формуле
(9.45)
где т = ω02/ω01; k' = (R2’ + R1)/R2’
Потери энергии на второй ступени (торможение противо-включением)
(9.46)
С
уммарные потери при ступенчатом торможении (в предположении, что k' = k" = k)
(9.47)
здесь С0 = 
Если осуществить торможение противовключением с максимальной угловой скорости до остановки, то
(9.48)
Отношение потерь по (9.47) к потерям по (9.48)
(9.49)
Например, если осуществляется ступенчатое торможение двухскоростного двигателя с m = 2, то потери энергии составят f 2/3 потерь при торможении противовключением в одну ступень. С увеличением т уменьшаются потери энергии в полюсопереключаемом двигателе при ступенчатом торможении по сравнению с потерями при торможении противовключением в одну ступень. Еще меньшими оказываются потери энергии в частотно-управляемом асинхронном электроприводе, которые могут быть ориентировочно определены аналитически, если пренебречь электромагнитными процессами. Примем, что электромеханический процесс протекает с абсолютным скольжением, меньшим критического, т. е. β < βК.
При указанном ограничении потери можно найти из следующей системы уравнений:
(9.50)
У
равнение движения в свою очередь можно выразитьтак:
(9.51)
И
з (9.51) видно, что динамический момент представляетсядвумя составляющими:
(9.52)
(9.53)
где ε = dω1/ dt.
Момент двигателя при управлении с β < βк можно представить линейным уравнением
M = kβ β, (9.54)
где kβ = Mном / sном .
Учитывая из (9.50) третье уравнение и (9.54), получаем выражение механической характеристики двигателя при частотном управлении
М = kβ а - kβ ω / ω1ном(9.55)
и
уравнение движения
(9.56)
или
(9.57)
Для линейного изменения частоты во времени, ε = =const, параметр абсолютного скольжения можно определить по формуле
(9.58)
г
деТм = Jω1номsном / Мном ; βc =M c / kβ. Потери энергии при пуске
Зная зависимость β = f (t), можно определить ΔAп ; при Мс = 0, принимая для упрощения, что tп > Тм, получаем: β = Jε/kβ;
(9.60)
Таким образом, (9.60) совершенно аналогично (9.27), что и следовало ожидать. Из (9.60) следует, что для Тм < < tп0 потери при частотном пуске с β < βк значительно меньше, чем в случае прямого включения-асинхронного двигателя с а = 1.
Так же могут быть найдены потери при частотном торможении .
Необходимо отметить, что минимальные потери при частотном управлении могут быть достигнуты в результате установления оптимального значения абсолютного скольжения βопт. Его можно выбирать, исходя из режима минимума потерь или режима минимума тока.
Значение βопт в режиме минимума тока выбирается так, чтобы заданному току статора соответствовал максимум электромагнитного момента, что обеспечивает необходимое быстродействие, а следовательно, при выбранном токе и минимум электрических потерь. Пользуясь механическими характеристиками М = f(β) построенными для фиксированных значений токов статора, можно установить общую закономерность независимо от типа и параметров асинх-
ронного двигателя, заключающуюся в том, что с ростом тока статора увеличивается критическое скольжение βк. Линия оптимального скольжения проходит через точки максимума моментов, каждый из которых отвечает своему постоянному значению тока статора. Таким образом, сравнительно просто находится βопт.
Определение βопт в режиме минимума потерь связано со значительно более сложными расчетами и практически не всегда оправдано, так как потери энергии при частотном пуске и торможении, полученные в режиме минимума потерь, всего на несколько процентов отличаются от рассчитанных из условия минимума тока.
Приведенные выше соотношения для определения потерь энергии в переходных режимах при различных способах управления асинхронными двигателями не учитывают влияния электромагнитных процессов и насыщения магнитной цепи. Их влияние можно оценить в результате решения дифференциальных уравнений асинхронного двигателя при питании его как непосредственно от сети, так и от соответствующего преобразователя частоты. Эти уравнения, дополненные уравнениями для мощности потерь и потерь энергии, сложные и нелинейные и аналитически не решаются. Их решение возможно с использованием средств вычислительной техники.
studfiles.net
В энергетике электропривода важное место занимают вопросы потребления, расхода и потерь электроэнергии при ее преобразовании в механическую энергию.
Если пренебречь потерями в стали и механическими потерями из-за их относительной малости, а также пренебречь влиянием тока холостого хода (при этом I1= I’2), то потери энергии при пуске асинхронного двигателя в цепях статора и ротора можно определить следующим образом:
(7.1)
При пуске двигателя без нагрузки Мс=0 и
(7.2)
потери мощности в цепи ротора:
(7.3)
Поэтому при пуске двигателя из неподвижного состояния до синхронной скорости потери энергии будут равны:
… (7.4)
где J -приведенный момент инерции системы, кг*м2;
R1 — сопротивление статорной цепи, Ом;
R’2 — приведенное к статору сопротивление роторной цепи.
Потери энергии в двигателе при пуске с нагрузкой
(7.5)
где Мс — момент сопротивления рабочей машины, Н*м;
Мпуск.ср.— среднее значение момента двигателя за период пуска, Н*м.
Потери электроэнергии при переходных режимах увеличивают нагревэлектродвигателя и общее потребление электроэнергии. При частых пусках,реверсе, торможении потери энергии достигают значительных величин. Потери при пуске и торможении нагревают электродвигатель и ограничиваютчастоту пусков.
Допустимое число включений в час определяется по соотношению
(7.6)
где e — относительная продолжительность включения;
DРн — номинальные потери мощности.
(7.7)
где tри t0 — соответственно продолжительность периода работы и паузы.
(7.8)
где Рн,hн— значение номинальной мощности и КПД электродвигателя.
Пример 7
Периодически действующий конвейер приводится в движение электродвигателем с короткозамкнутым ротором типа 4А80А2УЗ: Рн= 1,5 кВт; nн= 2850 об/мин; hн= 0,81; mп= 2,1; mк =2,6; GD2= 0,0073 кг*м2. Приведенный к валу двигателя момент сопротивления Мс = 4,9 Н*м; GD2рм = 0,26 кг*м2; t0= 24 с; tp= 6 с; R1/R2= 1,25. Определить значение пусковых потерь, действительное и допустимое число включений электродвигателя в час.
Решение
1. Определим номинальный момент:
2. Максимальный, пусковой, а также средний моменты за период пуска
3.Скорость идеального холостого хода
4.Приведенный момент инерции системы
5.Потери энергии
6.Относительная продолжительность включения
7.Допустимое число включений в час
8.Действительное число включений
Из материала, изложенного выше, видно, что потери энергии в переходных режимах могут быть снижены за счет уменьшения момента инерции электропривода или при ступенчатом пуске многоскоростных двигателей.
refac.ru
