





Единицы силы. Вес. Перегрузка
Сила, приложенная к телу, в системе единиц СИ измеряется в ньютонах (1 Н = 1 кг·м/с2). В технических дисциплинах в нередко качестве единицы измерения силы традиционно используют килограмм-силу (1 кгс, 1 кГ) и аналогичные единицы: грамм-силу (1 гс, 1 Г), тонна-силу (1 тс, 1 Т). 1 килограмм-сила определена как сила, сообщающая телу массой 1 кг нормальное ускорение, равное по определению 9,80665 м/с2 (это ускорение приблизительно равно ускорению свободного падения). Таким образом, по второму закону Ньютона, 1 кгс = 1 кг · 9,80665 м/с2 = 9,80665 Н. Можно сказать также, что тело массой 1 кг, покоящееся на опоре, имеет вес 1 кгс Часто ради краткости килограмм-силу называют просто «килограммом» (а тонна-силу, соответственно, «тонной»), что порождает порой путаницу у людей, не привыкших к использованию разных единиц.
Русская терминология, сложившаяся в ракетостроении, традиционно использует «килограммы» и «тонны» (точнее, килограмм-силы и тонна-силы) в качестве единиц тяги ракетных двигателей. Таким образом, когда говорят о ракетном двигателе с тягой 100 тонн, имеют в виду, что данный двигатель развивает тягу 105кг · 9,80665 м/с2 $\approx$ 106Н.
Путая ньютоны и килограмм-силы, некоторые считают, что сила в 1 килограмм-силу сообщает телу массой 1 килограмм ускорение 1 м/с2, т. е. пишут ошибочное «равенство» 1 кгс / 1 кг = 1 м/с2. В то же время очевидно, что на самом деле 1 кгс / 1 кг = 9,80665 Н / 1 кг = 9,80665 м/с2 — таким образом, допускается ошибка почти в 10 раз.
Ю. И. Мухин в книге «Антиаполлон. Лунная афера США» (2006) ведет расчет ускорения частиц песка под воздействием газов из двигателя лунного модуля:
<…> Соответственно, сила которая давит на частицы в пределах средневзвешенного радиуса будет равна: 0,74 Гс/мм2 · 0,00024 = 0,00018 Гс/мм2 или 0,18 мГс/мм2. Соответственно, на среднюю частицу с поперечным сечением в 0,01 мм2 будет давить сила в 0,0018 мГс.Эта сила придаст частице ускорение, равное ее отношению к массе средней частицы: 0,0018 мГс / 0,0014 мГ = 1,3 м/сек2. <…>
(Выделение apollofacts.) Разумеется, сила величиной 0,0018 миллиграмм-сил сообщила бы частице массой 0,0014 миллиграмм ускорение почти в 10 раз больше того, что насчитал Мухин: 0,0018 миллиграмм-сил / 0,0014 миллиграмм = 0,0018 мг · 9,81 м/с2 / 0,0014 мг $\approx$ 13 м/сек2. (Можно заметить, что с исправлением одной только этой ошибки насчитанная Мухиным глубина кратера, который якобы должен был бы образоваться под лунным модулем при посадке, сразу упадет с 1,9 м, которые требует Мухин, до 20 см; однако весь остальной расчет настолько нелеп, что эта поправка не способна его исправить).
По определению, вес тела есть сила, с которой тело давит на опору или подвес. Вес тела, покоящегося на опоре или подвесе (т. е. неподижного относительно Земли или иного небесного тела) равен
(1)\begin{align} \mathbf{W} = m \cdot \mathbf{g}, \end{align}
где $\mathbf{W}$ — вес тела, $m$ — масса тела, $\mathbf{g}$ — ускорение свободного падения в данной точке. На поверхности Земли ускорение свободного падения близко к нормальному ускорению (часто округляемому до 9,81 м/с2). Тело массой 1 кг имеет вес $\approx$ 1 кг · 9,81 м/с2 $\approx$ 1 кгс. На поверхности Луны ускорение свободного падения примерно в 6 раз меньше, чем у поверхности Земли (точнее, близко к 1,62 м/с2). Таким образом, на Луне тела примерно в 6 раз легче, чем на Земле.
Путают вес тела и его массу. Масса тела не зависит от небесного тела, она постоянна (если пренебречь релятивистскими эффектами) и всегда равна одной и той же величине — и на Земле, и на Луне, и в невесомости
В газете «Дуэль», № 47, 2005 г. «объясняется», почему лунный модуль якобы не мог взлететь с Луны [2]:
<…> на такую фразу хиви (добровольного помощника) NASA: «Достаточно комфортные условия были и при взлёте с Луны. Сухая (т.е. без топлива) масса взлётной ступени — 2,2 тонны, а сила тяги ее двигателя — 1,6 тонны (1590 кг). Поэтому взлетная ступень не может развить ускорение свыше 7,3 м/с2, а это значит, что вес находящихся в ней астронавтов опять-таки менее их земного веса».Эту фразу я бы назвал шедевром тупости хиви, не требующим других доказательств лунной аферы NASA. Какое ускорение может развить взлётная ступень, если ее тяговооруженность (отношение тяги двигателя к ее весу) меньше единицы и равна 1590 кг/ 2200 кг = 0,72. При взлете с Земли тяговооруженность ракеты (имеется в виду «Сатурн-5» — apollofacts) составляла 3 470 000 кг/ 2 913 000 кг = 1,19. Да она бы просто не сумела оторваться от поверхности Луны, это же школьная физика, закон Ньютона. Любой желающий может это проверить дома.
Разумеется, в своем разоблачительском порыве автор этого «опровержения» позабыл, что масса и вес — это разные вещи. Вес сухой взлетной ступени составляет $\approx$ 2200 кг · 1,62 м/с2$\approx$ 3560 Н $\approx$ 360 кгс. Топливо и астронавты увеличивали эту цифру примерно до 800 кгс, поэтому стартовая тяговооруженность составляла около $\approx$ 1590 кгс/800 кгс $\approx$ 2 — эта величина больше, чем у большинства ракет-носителей на земле.
Перегрузкой называется вес тела, выраженный в единицах его нормального веса, т. е. веса этого тела, покоящегося при нормальном ускорении свободного падения $\approx$ 9,81 м/с2. Единицей измерения перегрузки традиционно является 1 g (1 «же»). Фактически, g есть безразмерная величина. Если вес тела меньше его нормального веса, то величина перегрузки меньше единицы, и можно условно говорить о «недогрузке» (термин не употребляется). Например, двигатель лунного модуля тягой $\approx$ 10 тс сообщает модулю массой $\approx$ 15 т [1] ускорение $\approx$ 9,81·104Н / 15·103кг $\approx$ 6,5 м/с2 (это верно как в совершенно пустом пространстве, так и вблизи Луны: гравитация не оказывает прямого влияния на вес тел). Таким образом лунный модуль и находящиеся в нем астронавты под воздействием этого двигателя испытывают перегрузку $\approx$ 6,5 / 9,81 $\approx$ 0,66 g — то есть их вес при этом меньше, чем их вес на земле.
Иногда путают вес тела и его силу тяжести (силу, действующую на тело со стороны планеты). При этом приходят к абсурдному выводу о том, что корабль, движущийся в поле тяжести планеты с выключенным двигателем, все-таки испытывает перегрузку из-за действия на корабль гравитационной силы. Гравитационная сила сама по себе не может вызывать перегрузки. Ее вызывает лишь действие на тело опоры (подвеса). Для ракеты и космического корабля перегрузка обычно связана либо с действием тяги его двигателя, либо с тормозящим действием атмосферы (или суммой этих действий).
Другая распространенная ошибка — путают ускорение тела и перегрузку. Однако даже когда речь идет об ускорениях, связанных с работой двигателя (или торможением атмосферой), перегрузка должна рассчитываться в единицах нормального ускорения; таким образом, перегрузка в $\approx$ 9,81 раза меньше ускорения.
В газете «Дуэль», № 20, 2002 г. автор живописует страдания, которые должны испытывать астронавты лунного модуля при посадке на Луну, и настаивает на невозможности такой посадки [3]:
Космонавты <…> испытывают длительную перегрузку, максимальное значение которой — 5. Перегрузка направлена вдоль позвоночника (самая опасная перегрузка). Спросите у военных летчиков, можно ли устоять в самолете в течение 8 мин. при пятикратной перегрузке да еще и управлять им. Представьте себе, что после трех дней пребывания в воде (три дня полета к Луне в невесомости) вы выбрались на сушу, вас поместили в Лунную кабину, а ваш вес стал 400 кг (перегрузка 5), комбинезон на вас — 140 кг, а рюкзак за спиной — 250 кг. Чтобы вы не упали, вас держат тросом, прикрепленным к поясу, 8 минут, а затем еще 1,5 мин. (никаких кресел, ложементов нет). Не подгибайте ноги, опирайтесь на подлокотники (руки должны быть на органах управления). Кровь отлила от головы? Глаза почти не видят? Не умирайте и не падайте в обморок <…>уж совсем плохо заставлять космонавтов управлять посадкой в положении «стоя» при длительной 5-кратной перегрузке — это просто НЕВОЗМОЖНО.
Однако, как уже было показано, в начале спуска астронавты испытывали перегрузку $\approx$ 0,66 g — то есть заметно меньше их нормального земного веса (и никакого рюкзака за спиной у них не было — они были непосредственно подключены к системе жизнеобеспечения корабля). Перед посадкой тяга двигателя почти уравновешивала вес корабля на Луне, поэтому связанное с ней ускорение составляет $\approx$ 1/6 g — таким образом, в течение всей посадки они испытывали меньшую нагрузку, чем при простом стоянии на земле. По сути, одна из задач описыванной тросовая системы как раз и была в том, чтобы помочь астронавтам удержаться на ногах в условиях пониженного веса.
Ссылки
2. «Тяга», В. Б. Селиванчик, «Дуэль», 47, 2005apollofacts.wikidot.com
Следует различать понятия двигатель и силовая установка.
Двигателем принято называть устройство, участвующее в создании тяги (или мощности), необходимой для движения летательного аппарата. Двигатель является составной частью силовой установки, той ее частью, которая изготавливается и поставляется двигательным заводом.
Авиационной силовой установкой называют конструктивно объединенную совокупность двигателя с входным и выходным устройствами (с теми их элементами, которые изготавливаются на самолетостроительном заводе), встроенную в конструкцию планера (фюзеляжа или крыла) или скомпонованную в отдельных двигательных гондолах.
Силовая установка, помимо двигателя, входного и выходного устройств, включает в себя еще системы топливопитания, автоматического управления, обеспечивающие ее надежное функционирование, а также узлы крепления, необходимые для передачи усилий от двигателя к планеру. В теории авиационных двигателей эти системы и узлы не рассматриваются.
Под тягой двигателя Р понимают тягу, которую развивала бы силовая установка, если бы её внешнее обтекание было идеальным (т.е. без трения, отрывов потока и скачков уплотнения). Б.С. Стечкин еще в 1929 г. показал, что в этом случае тяга реактивного двигателя равна
, (2.1)
где Gв и Gг расходы воздуха на входе в двигатель и газа на выходе из сопла, V и сс – скорость полёта и скорость истечения газа в выходном сечении сопла (направленная параллельно вектору скорости V), а Fс и рс – площадь выходного сечения сопла и давление газа в этом сечении.
Эта формула получила наименование формулы Стечкина.
В формуле Стечкина в ряде случаев могут быть сделаны упрощения. Так, если пренебречь тем, что расходы воздуха на входе в двигатель и газа на выходе из негонесколько различны, получим.
. (2.2)
отличается от из-за подвода топлива и отборов воздуха на нужды летательного аппарата.
При полном расширении газа в сопле до атмосферного давления
(рс=рН) эта формула тяги приобретает еще более простой вид
. (2.3)
Под эффективной тягой силовой установки Рэф понимают тягу двигателя Р за вычетом всех внешних сопротивлений, создаваемых самой силовой установкой.
По физическому смыслу Рэф является равнодействующей всех сил давления и трения, действующих на элементы проточной части со стороны газового потока, протекающего через силовую установку изнутри, и внешнего потока воздуха, обтекающего силовую установку снаружи. Задача определения эффективной тяги сводится к нахождению векторной суммы всех указанных сил. Эти силы принято разделять на внутренние (Rвн) и наружные (Rнар).
Внутренние силы представляют собой сумму сил давления и трения, действующих на рабочие поверхности силовой установки, со стороны воздуха и газа, протекающих через силовую установку. Величина равнодействующей внутренних сил практически не зависит от способа установки двигателя на летательном аппарате.
Наружные силы представляют собой совокупность сил давления и трения, действующих на силовую установку со стороны обтекающего ее внешнего потока. Эти силы существенно зависят от способа размещения силовой установки на летательном аппарате.
Рассмотрим наиболее простой с точки зрения учета условий внешнего обтекания случай, когда силовая установка расположена в отдельной мотогондоле. Рассмотрим ее обтекание в полёте (рис. 2.1). При этом предположим, что векторы скорости полёта и скорости истечения газа из соплапараллельны оси двигателя.
Рис. 2.1. Схема обтекания двигательной гондолы
Сечения в невозмущенном потоке перед силовой установкой, на входе в воздухозаборник и на выходе из сопла двигателя обозначим Н-Н, вх-вх и с-с. Соответственно, площади этих нормальных сечений будут FН, Fвх и Fс. Наружную поверхность силовой установки здесь условно разделим на три части: лобовую часть вх-М, центральную часть М-и кормовую часть-c.
Набегающий поток воздуха разделяется поверхностью тока Н-вх на внутренний, проходящий через двигатель, и внешний, обтекающий силовую установку снаружи.
Главной причиной возникновения внешнего сопротивления силовой установки является повышение давления на головном участке гондолы вх-М (р>pH) и наличие разрежения на ее кормовом участке -c (p<pH). К этому прибавляется сопротивление от сил трения по всей поверхности гондолы от сечения вх-вх до сечения с-с.
Эффективная тяга силовой установки представляет собой следующую векторную сумму
, (2.4)
где – равнодействующая сил давления и трения газа, действующих на внутренние поверхности силовой установки, а– равнодействующая сил давления и трения, действующих на наружную поверхность гондолы.
Силу можно определить непосредственным интегрированием сил давления и трения по внешней поверхности гондолы. Тогда
, (2.5)
где и– равнодействующие сил давления и трения, приложенные к наружной поверхности гондолы.
Величину определим, используя теорему Эйлера. Для этого выделим объем струи газа, ограниченный следующей контрольной поверхностью (рис. 2.1): слева – сечениемН-Н; между сечениями Н - Н и вх - вх – боковой поверхностью струи; между сечениями вх - вх и с - с – внутренней поверхностью силовой установки, а справа, на выходе из силовой установки, – сечением с-с. На рис. 2.1 границы этой контрольной поверхности обозначены пунктиром. Отбросим газ вне контрольной поверхности от сечения Н-Н до сечения вх-вх и в сечении с-с и заменим его воздействие на газ внутри этой поверхности силами давления.
Силовая установка воздействует на газ, протекающий через неё, с силой , равной по модулю силе, но противоположно ей направленной.
Тогда в соответствии с теоремой Эйлера
, (2.6)
где FН и Fс – силы давления, приложенные к торцевым поверхностям вы
деленного участка струи; – равнодействующая сил давления, приложенных к боковой поверхности струи на участкеН - вх, – количество движения на выходе из контрольной поверхности, а – количество движения на входе в неё. Причем в уравнениях (2.5) и (2.6) dF– это площадь проекции элемента контрольной поверхности или поверхности гондолы на плоскость, перпендикулярную направлению полета.
Так как =, то из формулы (2.6) получим
. (2.7)
Подставив (2.5) и (2.7) в (2.4), определим эффективную тягу силовой установки
. (2.8)
Для перехода от абсолютных давлений к избыточным давлениям воспользуемся следующим очевидным тождеством:
+. (2.9)
Вычтем из (2.8) выражение (2.9), тогда
Спроектировав полученное выражение на направление полета, получим
. (2.10)
Эта формула является общим выражением эффективной тяги для силовой установки рассмотренной схемы. Первые три члена её правой части соответствуют формуле Стечкина (2.1) для тяги двигателя. Поэтому можно сказать, что эффективная тяга силовой установки
равна тяге двигателя за вычетом внешнего сопротивления силовой установки, равного .
Необходимо отметить, что тяга реактивного двигателя, вообще говоря, является векторной величиной, так как векторы инеобязательно могут быть направлены вдоль оси двигателя, как это было принято выше, а могут отклоняться от нее, например, при полетах со значительными углами атаки или при повороте сопла. Поэтому, например, для определения тяги двигателя при полном расшире
нии газа в сопле в общем случае формула (2.1) примет вид: .
studfiles.net
Реактивная тяга — сила, возникающая в результате взаимодействия реактивной двигательной установки с истекающей из сопла струёй расширяющейся жидкости или газа, обладающих кинетической энергией[1].
В основу возникновения реактивной тяги положен закон сохранения импульса. Реактивная тяга обычно рассматривается как сила реакции отделяющихся частиц. Точкой приложения её считают центр истечения — центр среза сопла двигателя, а направление — противоположное вектору скорости истечения продуктов сгорания (или рабочего тела, в случае не химического двигателя). То есть, реактивная тяга:
Среди растений реактивное движение встречается у созревших плодов бешеного огурца. При созревании растения его плод отцепляется от плодоножки. Под большим давлением из плода выбрасывается жидкость с семенами, которая направлена в противоположное направление движению плода[3].
Среди животного мира реактивное движение встречается у кальмаров, осьминогов, медуз, каракатиц, морских гребешков и других. Перечисленные животные передвигаются, выбрасывая вбираемую ими воду.
Если нет внешних сил, то ракета вместе с выброшенным веществом является замкнутой системой. Импульс такой системы не может меняться во времени.
F→p=mp⋅a→=−u→⋅ΔmtΔt{\displaystyle {\vec {F}}_{p}=m_{p}\cdot {\vec {a}}=-{\vec {u}}\cdot {\frac {\Delta m_{t}}{\Delta t}}}, где
mp{\displaystyle m_{p}} — масса ракеты a→{\displaystyle {\vec {a}}} — её ускорение u→{\displaystyle {\vec {u}}} — скорость истечения газов ΔmtΔt{\displaystyle {\frac {\Delta m_{t}}{\Delta t}}} — расход массы топлива в единицу времениПоскольку скорость истечения продуктов сгорания (рабочего тела) определяется физико-химическими свойствами компонентов топлива и конструктивными особенностями двигателя, являясь постоянной величиной при не очень больших изменениях режима работы реактивного двигателя, то величина реактивной силы определяется в основном массовым секундным расходом топлива[1].
До начала работы двигателей импульс ракеты и горючего был равен нулю, следовательно, и после включения сумма изменений векторов импульса ракеты и импульса истекающих газов равна нулю: mp⋅Δv→+Δmt⋅u→=0{\displaystyle m_{p}\cdot \Delta {\vec {v}}+\Delta m_{t}\cdot {\vec {u}}=0}, где
Δv→{\displaystyle \Delta {\vec {v}}} — изменение скорости ракетыmp⋅Δv→=−Δmt⋅u→{\displaystyle m_{p}\cdot \Delta {\vec {v}}=-\Delta m_{t}\cdot {\vec {u}}}
Разделим обе части равенства на интервал времени t, в течение которого работали двигатели ракеты:
mp⋅Δv→Δt=−ΔmtΔt⋅u→{\displaystyle m_{p}\cdot {\frac {\Delta {\vec {v}}}{\Delta t}}=-{\frac {\Delta m_{t}}{\Delta t}}\cdot {\vec {u}}}
Произведение массы ракеты m на ускорение её движения a по определению равно силе, вызывающей это ускорение:
F→p=mp⋅a→=−u→⋅ΔmtΔt{\displaystyle {\vec {F}}_{p}=m_{p}\cdot {\vec {a}}=-{\vec {u}}\cdot {\frac {\Delta m_{t}}{\Delta t}}}
Если же на ракету, кроме реактивной силы F→p{\displaystyle {\vec {F}}_{p}}, действует внешняя сила F→{\displaystyle {\vec {F}}}, то уравнение динамики движения примет вид:
mp⋅Δv→Δt=F→+F→p⇔{\displaystyle m_{p}\cdot {\frac {\Delta {\vec {v}}}{\Delta t}}={\vec {F}}+{\vec {F}}_{p}\Leftrightarrow } mp⋅Δv→Δt=F→+(−u→⋅ΔmtΔt){\displaystyle m_{p}\cdot {\frac {\Delta {\vec {v}}}{\Delta t}}={\vec {F}}+(-{\vec {u}}\cdot {\frac {\Delta m_{t}}{\Delta t}})}
Формула Мещерского представляет собой обобщение второго закона Ньютона для движения тел переменной массы. Ускорение тела переменной массы определяется не только внешними силами F→{\displaystyle {\vec {F}}}, действующими на тело, но и реактивной силой F→p{\displaystyle {\vec {F}}_{p}}, обусловленной изменением массы движущегося тела:
a→=F→p+F→mp{\displaystyle {\vec {a}}={\frac {{\vec {F}}_{p}+{\vec {F}}}{m_{p}}}}
Применив уравнение Мещерского к движению ракеты, на которую не действуют внешние силы, и проинтегрировав уравнение, получим формулу Циолковского[4]:
mtm=ev→u→{\displaystyle {\frac {m_{t}}{m}}=e^{\frac {\vec {v}}{\vec {u}}}}
Релятивистское обобщение этой формулы имеет вид:
mtm=(c→+v→c→−v→)c→2u→{\displaystyle {\frac {m_{t}}{m}}=\left({\frac {{\vec {c}}+{\vec {v}}}{{\vec {c}}-{\vec {v}}}}\right)^{\frac {\vec {c}}{2{\vec {u}}}}} , где c→{\displaystyle {\vec {c}}} — скорость света.
wikiredia.ru
Реактивная тяга — сила, возникающая в результате взаимодействия реактивной двигательной установки с истекающей из сопла струёй расширяющейся жидкости или газа, обладающих кинетической энергией[1].
В основу возникновения реактивной тяги положен закон сохранения импульса. Реактивная тяга обычно рассматривается как сила реакции отделяющихся частиц. Точкой приложения её считают центр истечения — центр среза сопла двигателя, а направление — противоположное вектору скорости истечения продуктов сгорания (или рабочего тела, в случае не химического двигателя). То есть, реактивная тяга:
Среди растений реактивное движение встречается у созревших плодов бешеного огурца. При созревании растения его плод отцепляется от плодоножки. Под большим давлением из плода выбрасывается жидкость с семенами, которая направлена в противоположное направление движению плода[3].
Среди животного мира реактивное движение встречается у кальмаров, осьминогов, медуз, каракатиц, морских гребешков и других. Перечисленные животные передвигаются, выбрасывая вбираемую ими воду.
Если нет внешних сил, то ракета вместе с выброшенным веществом является замкнутой системой. Импульс такой системы не может меняться во времени.
F→p=mp⋅a→=−u→⋅ΔmtΔt{\displaystyle {\vec {F}}_{p}=m_{p}\cdot {\vec {a}}=-{\vec {u}}\cdot {\frac {\Delta m_{t}}{\Delta t}}}, где
mp{\displaystyle m_{p}} — масса ракеты a→{\displaystyle {\vec {a}}} — её ускорение u→{\displaystyle {\vec {u}}} — скорость истечения газов ΔmtΔt{\displaystyle {\frac {\Delta m_{t}}{\Delta t}}} — расход массы топлива в единицу времениПоскольку скорость истечения продуктов сгорания (рабочего тела) определяется физико-химическими свойствами компонентов топлива и конструктивными особенностями двигателя, являясь постоянной величиной при не очень больших изменениях режима работы реактивного двигателя, то величина реактивной силы определяется в основном массовым секундным расходом топлива[1].
До начала работы двигателей импульс ракеты и горючего был равен нулю, следовательно, и после включения сумма изменений векторов импульса ракеты и импульса истекающих газов равна нулю: mp⋅Δv→+Δmt⋅u→=0{\displaystyle m_{p}\cdot \Delta {\vec {v}}+\Delta m_{t}\cdot {\vec {u}}=0}, где
Δv→{\displaystyle \Delta {\vec {v}}} — изменение скорости ракетыmp⋅Δv→=−Δmt⋅u→{\displaystyle m_{p}\cdot \Delta {\vec {v}}=-\Delta m_{t}\cdot {\vec {u}}}
Разделим обе части равенства на интервал времени t, в течение которого работали двигатели ракеты:
mp⋅Δv→Δt=−ΔmtΔt⋅u→{\displaystyle m_{p}\cdot {\frac {\Delta {\vec {v}}}{\Delta t}}=-{\frac {\Delta m_{t}}{\Delta t}}\cdot {\vec {u}}}
Произведение массы ракеты m на ускорение её движения a по определению равно силе, вызывающей это ускорение:
F→p=mp⋅a→=−u→⋅ΔmtΔt{\displaystyle {\vec {F}}_{p}=m_{p}\cdot {\vec {a}}=-{\vec {u}}\cdot {\frac {\Delta m_{t}}{\Delta t}}}
Если же на ракету, кроме реактивной силы F→p{\displaystyle {\vec {F}}_{p}}, действует внешняя сила F→{\displaystyle {\vec {F}}}, то уравнение динамики движения примет вид:
mp⋅Δv→Δt=F→+F→p⇔{\displaystyle m_{p}\cdot {\frac {\Delta {\vec {v}}}{\Delta t}}={\vec {F}}+{\vec {F}}_{p}\Leftrightarrow } mp⋅Δv→Δt=F→+(−u→⋅ΔmtΔt){\displaystyle m_{p}\cdot {\frac {\Delta {\vec {v}}}{\Delta t}}={\vec {F}}+(-{\vec {u}}\cdot {\frac {\Delta m_{t}}{\Delta t}})}
Формула Мещерского представляет собой обобщение второго закона Ньютона для движения тел переменной массы. Ускорение тела переменной массы определяется не только внешними силами F→{\displaystyle {\vec {F}}}, действующими на тело, но и реактивной силой F→p{\displaystyle {\vec {F}}_{p}}, обусловленной изменением массы движущегося тела:
a→=F→p+F→mp{\displaystyle {\vec {a}}={\frac {{\vec {F}}_{p}+{\vec {F}}}{m_{p}}}}
Применив уравнение Мещерского к движению ракеты, на которую не действуют внешние силы, и проинтегрировав уравнение, получим формулу Циолковского[4]:
mtm=ev→u→{\displaystyle {\frac {m_{t}}{m}}=e^{\frac {\vec {v}}{\vec {u}}}}
Релятивистское обобщение этой формулы имеет вид:
mtm=(c→+v→c→−v→)c→2u→{\displaystyle {\frac {m_{t}}{m}}=\left({\frac {{\vec {c}}+{\vec {v}}}{{\vec {c}}-{\vec {v}}}}\right)^{\frac {\vec {c}}{2{\vec {u}}}}} , где c→{\displaystyle {\vec {c}}} — скорость света.
ru.wikibedia.ru
Изобретение относится к авиадвигателестроению, а именно к способам измерения тяги турбореактивных двухконтурных двигателей (ТРДЦ) для летательных аппаратов по термогазодинамическим параметрам, измеряемым в условиях эксплуатации. Техническим результатом изобретения является определение тяги ТРДД в полете с использованием только тех параметров, которые измеряются и используются в электронных САУ двигателя и летательного аппарата, без установки на двигателе дополнительных приемников и датчиков. При формировании тарированной функциональной зависимости в качестве функции используют отношение тяги двигателя к полному давлению воздуха за компрессором высокого давления, измерения которого используют из электронной САУ двигателя, а в качестве аргумента используют критерий подобия режимов работы двигателя. В процессе эксплуатации двигателя на земле измеряют полное давление воздуха за компрессором высокого давления, вычисляют критерий подобия режимов двигателя Ппр i и тягу двигателя определяют по формуле
, где Р*кизм - измеренное значение полного давления воздуха за компрессором высокого давления; - вычисленное значение
. 2 з.п. ф-лы, 3 табл.
Изобретение относится к авиадвигателестроению, а именно к способам измерения тяги турбореактивных двухконтурных двигателей (ТРДД) для летательных аппаратов по термогазодинамическим параметрам, измеряемым в условиях эксплуатации.
Известен способ определения тяги турбореактивного двухконтурного двигателя («Теория воздушно-реактивных двигателей». / Под редакцией С.М.Шляхтенко. М.: «Машиностроение», 1975, стр.46), при котором в процессе летной эксплуатации измеряют расход газа через двигатель Gг; скорость истечения газа Vистечения газа из реактивного сопла; расход воздуха Gв через двигатель и определяют тягу R по разности между выходным и входным импульсом по формуле
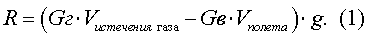
Такой способ определения тяги используют при летных испытаниях ТРДД на летающих лабораториях. Для его осуществления требуется:
- установка от 46 до 85 приемников и датчиков давления и температур на срезах реактивных сопел;
- установка от 24 до 36 приемников и датчиков во входном воздухозаборнике ТРДД;
- установка на летающей лаборатории систем измерения и регистрации со всех установленных на двигателе датчиков;
- разработка алгоритмов и обработка данных для определения тяги двигателя в соответствии с формулой (1).
Известен способ определения тяги ТРДД (Патенты НМЦ «Норма» №223-03-02 от 10.06.2004 г.; №169-92-43 от 29.03.1993 г.; №210-07-088 от 27.12.1997 г. «Способы определения тяги ТРДД на земле и тяги реактивного сопла в полете (выходного импульса)»).
Этот способ обеспечивает измерение тяги двигателя только на земле, а в полете обеспечивает определение только тяги реактивного сопла.
Данный способ не требует установки системы измерения расхода воздуха и поля скоростей на срезе сопла, так как вместо нее используют установку системы измерения выходного импульса на срезе реактивного сопла, основанную на измерении нагружения струны или специального аэродинамического профиля, которые помещают диаметрально на срезе сопла, и установке специальных датчиков статического давления газа на срезе реактивного сопла для учета недорасширения истекающего из сопла газового потока.
Для определения тяги двигателя в полете этим способом, также как и в ранее рассмотренном способе определения тяги, требуется измерение расхода воздуха через двигатель и скорости полета самолета, что также требует установки от 4 до 36 приемников и датчиков во входном воздухозаборнике ТРДД.
Известен способ определения и контроля тяги ТРДД при наземном опробовании двигателя или при взлете летательного аппарата (Методические указания МУ 1.1.227-90 «Контроль тяги авиационных ГТД в эксплуатации», 1990 г.).
Этот способ определения тяги двигателя основан на использовании общей теории подобия характеристик и режимов работы ГТД, при использовании которой экспериментальные или расчетные характеристики двигателя, в том числе и тяговые, могут представляться в виде функциональных обобщенных зависимостей. В данном способе обобщенная или приведенная к одинаковым полным давлениям воздуха на входе в двигатель тяговая характеристика двигателя формируется после проведения приемосдаточных испытаний (ПСИ) в виде функциональной зависимости 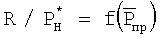 , в которой приведенная тяга
, в которой приведенная тяга 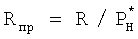 является функцией для любого типа двигателей, аргумент которой по физическому смыслу является критерием подобия режимов работы двигателя и для различных типов ГТД определяется по формулам:
является функцией для любого типа двигателей, аргумент которой по физическому смыслу является критерием подобия режимов работы двигателя и для различных типов ГТД определяется по формулам:
- для ТРД 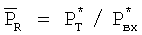 ,
,
где Р* T - полное давление газа за турбиной;
Р* вх - полное давление воздуха на входе в двигатель;
- для ТРДД с нерегулируемыми соплами без смешения потоков
 ,
,
где 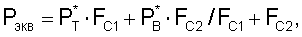
где Р* В - полное давление воздуха за вентилятором в наружном контуре;
FC1 - площадь сопла на срезе внутреннего контура;
FC2 - площадь сопла наружного контура;
- для ТРДД с нерегулируемым реактивным соплом и смешением потоков
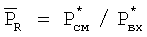 ,
,
где 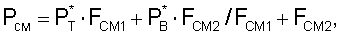
где FCM1 - площадь сечения на выходе из внутреннего контура в камеру смешения,
FCM2 - площадь сечения на выходе из наружного контура в камеру смешения.
При таком способе тяга двигателя на земле определяется:
- путем установки на двигателе приемников и датчиков для измерений полных давлений в различных сечениях двигателя;
- осуществления измерений и обработки в процессе ПСИ двигателя с целью вычисления критериев подобия режимов работы двигателя  ;
;
- измерения в процессе ПСИ тяги двигателя и полных давлений воздуха на входе в двигатель и вычисления приведенной тяги Rпр;
- формирования на основе полученных при ПСИ данных по Rпр и  тарировочной зависимости
тарировочной зависимости 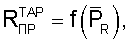 которая аппроксимируется уравнением;
которая аппроксимируется уравнением;
- измерением в процессе наземной эксплуатации двигателя Р* вх, полных давлений воздушных и газовых потоков в различных сечениях двигателя и за турбиной и вычислением тяги двигателя по формуле:
 ,
,
где  - значение приведенной тяги двигателя, вычисленное по уравнению тарировочной функциональной зависимости в соответствии с вычисленным значением
- значение приведенной тяги двигателя, вычисленное по уравнению тарировочной функциональной зависимости в соответствии с вычисленным значением  .
.
Недостатком этого способа определения тяги ТРДД является необходимость установки на двигателе специальных датчиков и приемников полного давления в различных сечениях двигателя и за турбиной и на входе в двигатель, которые в электронных САУ ТРДД летательных аппаратов не используются. При этом для приемников полного давления на входе в двигатель необходимо создание специального обогрева для предотвращения его обледенения в эксплуатации, что неприемлемо для малоразмерных ТРДД.
Кроме этого, в процессе эксплуатации ТРДД на самолетах единичные измерения полных давлений воздуха на входе в двигатель не в полной мере отражают интегральное значение полного давления из-за неравномерностей воздушного потока, который вызывается воздухозаборниками самолета.
Этот способ обеспечивает достоверное определение тяги только в условиях наземного опробования двигателя при Vп=0 с целью диагностирования технического состояния двигателя или достаточности тяги двигателя перед взлетом самолета и не обеспечивает определение тяги в летных условиях, так как по полученной при ПСИ тарировочной зависимости 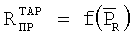 и измеренному в процессе эксплуатации значению
и измеренному в процессе эксплуатации значению  достоверно определяется только скорость истечения газа из сопла при условии Рн=Рн*, что соответствует Vп=0 (Мп=0).
достоверно определяется только скорость истечения газа из сопла при условии Рн=Рн*, что соответствует Vп=0 (Мп=0).
Для обеспечения достоверного определения тяги ТРДД в полете помимо использования тарированной контрольной зависимости 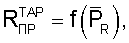 которая характеризует выходной импульс при Мп=0, необходимо:
которая характеризует выходной импульс при Мп=0, необходимо:
- измерение числа М полета, которое характеризует изменение выходного импульса при изменениях числа Мп;
- измерение расхода воздуха и скорости полета летательного аппарата для учета изменений входного импульса воздушного потока GВ·VП.
Все вышеуказанные способы определения тяги ТРДД используют приемники и датчики измеряемых параметров газовоздушного тракта двигателя, которые не используются в электронных системах автоматического управления ТРДД.
Наиболее близким прототипом к предлагаемому способу определения тяги ТРДД является способ определения тяги по термогазодинамическим параметрам в соответствии с МУ 1.1.227-90.
В предлагаемом способе определения тяги во всех ожидаемых условиях эксплуатации ТРДД технический результат достигается путем осуществления следующей последовательности действий.
1. Используют измеряемые в современных электронных САУ двигателя частоты вращения роторов двигателя, мгновенный расход топлива, полную температуру воздуха на входе в двигатель, или за вентилятором, или за компрессором низкого давления, полную осредненную температуру газа за турбиной и полное или статическое давление воздуха за компрессором высокого давления.
2. Измеряют в специальной системе число М полета летательного аппарата, на котором устанавливается данный тип ТРДД, или используют число М полета из системы управления летательным аппаратом, или используют вычисленное число М полета летательного аппарата по данным внешнетраекторных измерений высоты и скорости полета.
3. Проводят приемосдаточные испытания (ПСИ) двигателя с одновременным измерением:
- тяги двигателя;
- параметров двигателя в электронной САУ, указанных в п.1;
- параллельно этих же параметров в стендовой метрологически аттестованной системе измерений;
- имитированного числа М полета в стендовой системе наддува и подогрева в случае, если ПСИ двигателя осуществляются с этой системой.
4. На основе полученной по п.3 после проведения ПСИ базы измеренных данных производят тарировку всех измерительных каналов электронной САУ двигателя, используя в качестве эталонных значений измерения в метрологически аттестованной стендовой системе измерений по п.3, и формируют новую базу измеренных параметров двигателя с учетом выполненных тарировок измерительных каналов электронной САУ двигателя.
5. На основе полученной базы данных по п.4 вычисляются:
5.1. Отношение тяги двигателя к полному или статическому давлению воздуха за компрессором высокого давления, которое также является параметром подобия тяговых характеристик двигателя, и при числе Мп=0 однозначно определяет приведенную тягу двигателя.
5.2. Критерии подобия режимов работы двигателя следующего вида:

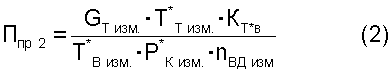
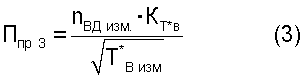
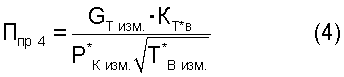
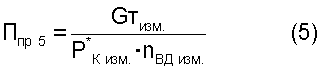
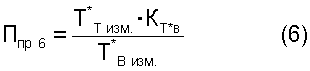
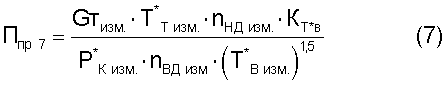
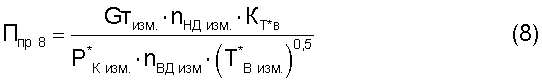
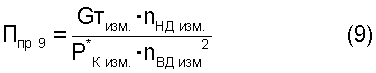
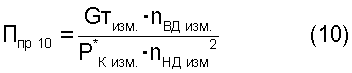
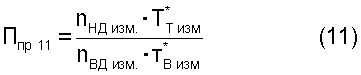
где Gтизм. - весовой расход топлива в ТРДД;
Р*кизм. - полное давление воздуха за компрессором высокого давления;
nвд изм. - частота вращения ротора высокого давления;
nнд изм. - частота вращения ротора низкого давления;
Т*в изм. - полная температура воздуха в любом сечении двигателя;
Т*т изм. - полная средняя температура газа за турбиной;
Кт*в - безразмерный коэффициент, функционально зависимый от измеренной температуры воздуха Т*в изм.
6. На основе полученной в процессе ПСИ при числе Мп=0 базы вычисленных значений 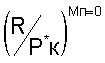 и Ппр i от Ппр 1 до Ппр 11 формируют индивидуально для каждого двигателя экспериментальные обобщенные обобщенные тарировочные функциональные зависимости, в которых в качестве функции используют
и Ппр i от Ппр 1 до Ппр 11 формируют индивидуально для каждого двигателя экспериментальные обобщенные обобщенные тарировочные функциональные зависимости, в которых в качестве функции используют 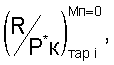 а в качестве аргумента - любой из критериев подобия режимов работы двигателя Ппр i от Ппр 1 до Ппр 11. Полученные функциональные зависимости
а в качестве аргумента - любой из критериев подобия режимов работы двигателя Ппр i от Ппр 1 до Ппр 11. Полученные функциональные зависимости
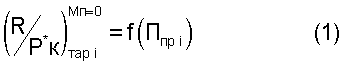
аппроксимируют уравнениями.
После выполнения аппроксимации тягу двигателя в эксплуатации при Мп=0 определяют по формуле

где Р*кизм. - измеренное в процессе эксплуатации значение давления воздуха за компрессором высокого давления с учетом тарировочных поправок, полученных по п.4;
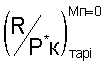 - численные значения по аппроксимированным тарировочным зависимостям при определенных значениях Ппр i от Ппр 1 до Ппр 11 по измеренным параметрам в САУ двигателя с учетом тарировочных поправок, полученных по п.4.
- численные значения по аппроксимированным тарировочным зависимостям при определенных значениях Ппр i от Ппр 1 до Ппр 11 по измеренным параметрам в САУ двигателя с учетом тарировочных поправок, полученных по п.4.
7. На основе математической модели типа ТРДД и предварительно рассчитанных с использованием этой модели высотно-скоростных характеристик (ВСХ) двигателя во всех ожидаемых условиям эксплуатации формируют вторую обобщенную функциональную зависимость
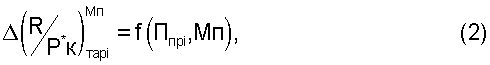
где функцией являются расчетные отклонения
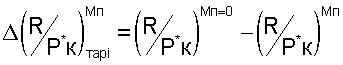
при одинаковых значениях любого из Ппр i от Ппр 1 до Ппр 11 и различных значений чисел М полета, а аргумент формируется от двух переменных, в которых Ппр i являются любым из критериев подобия режимов работы двигателя от Ппр 1 до Ппр 11, а число Мп является критерием подобия режимов полета самолета.
Полученные функциональные зависимости аппроксимируют уравнением в зависимости от двух переменных.
8. После выполнения аппроксимации этих функциональных зависимостей тягу двигателя в любых условиях эксплуатации, включая летную, определяют по формуле
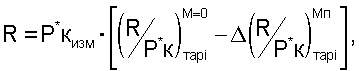
где Р*кизм - измеренное значение давлений воздуха за компрессором высокого давления;
 - вычисленные по уравнениям (1) п.6 тарировочные значения в зависимости от любого из определенных Ппр i от Ппр 1 до Ппр 11;
- вычисленные по уравнениям (1) п.6 тарировочные значения в зависимости от любого из определенных Ппр i от Ппр 1 до Ппр 11;
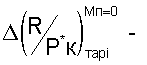 вычисленные по уравнению (2) п.7 тарировочные значения в зависимости от любого из определенных Ппр i от Ппр 1 до Ппр 11 и определенных чисел М полета летательного аппарата.
вычисленные по уравнению (2) п.7 тарировочные значения в зависимости от любого из определенных Ппр i от Ппр 1 до Ппр 11 и определенных чисел М полета летательного аппарата.
9. В тех случаях, когда ПСИ двигателя осуществляются с имитацией числа М полета летательного аппарата, первую функциональную зависимость формируют при любом выбранном из имитированных значений числа М полета в процессе ПСИ двигателя в виде

где 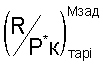 - экспериментальные значения функции при выбранном имитированном числе М полета;
- экспериментальные значения функции при выбранном имитированном числе М полета;
- Ппр i - значения аргументов, которыми являются критерии подобия режимов работы двигателя, вычисленные по п.5.2. от Ппр 1 до Ппр11, при выбранном имитированном числе М полета.
Вторую функциональную зависимость формируют в виде
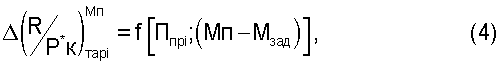
где 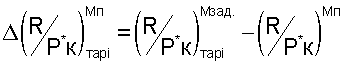 - экспериментально определенные отклонения от функциональной зависимости, определенной при выбранном числе М полета и одинаковых значениях Ппрi при отклонениях имитированных чисел М полета от выбранного числа М полета при формировании первой функциональной зависимости;
- экспериментально определенные отклонения от функциональной зависимости, определенной при выбранном числе М полета и одинаковых значениях Ппрi при отклонениях имитированных чисел М полета от выбранного числа М полета при формировании первой функциональной зависимости;
(Мп-Мзад.) - отклонения имитированных при ПСИ двигателя чисел М полета от выбранного числа М полета при формировании первой функциональной зависимости.
Аппроксимируют полученные зависимости уравнениями и определяют тягу двигателя, включая летную, по формуле
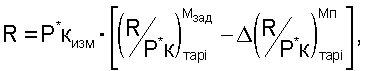
где Р*к изм. - измеренное в полете полное давление воздуха за компрессором высокого давления с учетом тарировочных поправок по п.4;
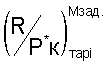 - численные значения, полученные по тарировочному уравнению (3) в зависимости от любого из вычисленных значений Ппр i от Ппр1 до Ппр11, при выбранном имитированном числе М полета;
- численные значения, полученные по тарировочному уравнению (3) в зависимости от любого из вычисленных значений Ппр i от Ппр1 до Ппр11, при выбранном имитированном числе М полета;
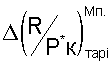 - численные значения, полученные по тарировочному уравнению (4) в зависимости от любого из вычисленных значений Ппр i от Ппр1 до Ппр11 и от вычисленных отклонений, измеренных и определенных в других системах чисел М полета от заданного числа М полета, при котором были сформированы первые зависимости.
- численные значения, полученные по тарировочному уравнению (4) в зависимости от любого из вычисленных значений Ппр i от Ппр1 до Ппр11 и от вычисленных отклонений, измеренных и определенных в других системах чисел М полета от заданного числа М полета, при котором были сформированы первые зависимости.
Таким образом, по приведенной последовательности действий обеспечивается поставленная цель - определение тяги ТРДД в полете с использованием только тех параметров, которые измеряются и используются в электронных САУ двигателя и летательного аппарата, без установки на двигателе дополнительных приемников и датчиков.
Новым в предлагаемом способе определения тяги ТРДД в эксплуатации является:
- использование после проведения приемосдаточных испытаний двигателя с измерением тяги двигателя при формировании тарировочной обобщенной (приведенной) функциональной зависимости
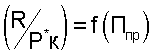
в которой в качестве приведенной тяги используются не отношение тяги двигателя к полному давлению воздуха на его входе, а отношение тяги двигателя к полному давлению воздуха за компрессором, то есть тяга двигателя, приводится не к входу в компрессор, а к его выходу, что не противоречит теории ВРД и не требует установки приемников полного давления воздуха на входе в двигатель;
- использование при формировании тарировочной обобщенной функциональной зависимости
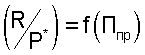
с последующим определением тяги ТРДД в качестве аргумента обобщенного критерия подобия режимов работы ТРДД не по отношениям 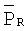 , а любого из одиннадцати ранее представленных критериев подобия режимов работы ТРДД, определение которых не требует установки дополнительных приемников и датчиков и обеспечиваются при любом сочетании используемых измеряемых параметров ТРДД в электронных САУ;
, а любого из одиннадцати ранее представленных критериев подобия режимов работы ТРДД, определение которых не требует установки дополнительных приемников и датчиков и обеспечиваются при любом сочетании используемых измеряемых параметров ТРДД в электронных САУ;
- использование после проведения ПСИ двигателя с измерением тяги двигателя не одной, а двух функциональных тарировочных обобщенных зависимостей с целью обеспечения определения тяги не только на земле, но и в полете, из которых
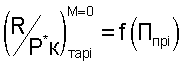 определяется экспериментально по данным ПСИ индивидуально для каждого двигателя,
определяется экспериментально по данным ПСИ индивидуально для каждого двигателя,
а  определяется расчетным путем по данным математической модели типа ТРДД.
определяется расчетным путем по данным математической модели типа ТРДД.
При этом 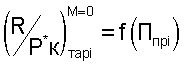 обеспечивает определение выходного импульса газового потока, который однозначно определяет тягу ТРДД при Мп=0, а вторая зависимость
обеспечивает определение выходного импульса газового потока, который однозначно определяет тягу ТРДД при Мп=0, а вторая зависимость 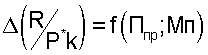 обеспечивает одновременный учет изменения входного импульса воздушного потока и изменение выходного импульса газового потока при изменениях числа М полета, при этом тяга двигателя определяется по формуле
обеспечивает одновременный учет изменения входного импульса воздушного потока и изменение выходного импульса газового потока при изменениях числа М полета, при этом тяга двигателя определяется по формуле

- в случае проведения ПСИ с имитацией чисел М полета летательного аппарата используются индивидуально для каждого двигателя две тарировочные обобщенные зависимости с целью обеспечения определения тяги не только на земле, но и в полете из которых и первая и вторая определяются экспериментально в виде
 а
а
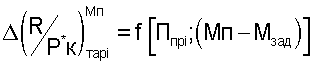
При этом 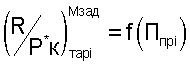 обеспечивает определение выходного импульса газового потока, который однозначно определяет тягу ТРДД при заданном числе М полета, а вторая зависимость обеспечивает одновременный учет изменения входного импульса воздушного потока и изменение выходного импульса газового потока при отклонениях числа М полета от выбранного числа Мзад, при этом тяга двигателя определяется по формуле
обеспечивает определение выходного импульса газового потока, который однозначно определяет тягу ТРДД при заданном числе М полета, а вторая зависимость обеспечивает одновременный учет изменения входного импульса воздушного потока и изменение выходного импульса газового потока при отклонениях числа М полета от выбранного числа Мзад, при этом тяга двигателя определяется по формуле
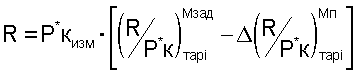
Примеры реализации предлагаемого способа определения тяги ТРДД в эксплуатации
После проведения стендовых испытаний с имитацией различных чисел М полета при заданном числе Мзад. полета формируют две дроссельные тарированные характеристики двигателя:
- отношение 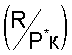 тяги к давлению воздуха за компрессором высокого давления при выбранном числе полета Мзад. в зависимости от приведенного комплекса Ппр
тяги к давлению воздуха за компрессором высокого давления при выбранном числе полета Мзад. в зависимости от приведенного комплекса Ппр
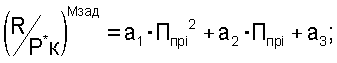
- отклонение 
b1·(Мзад.-Мизм.)+b2·(М2зад.-M2изм.)+b3·Ппр i(Мзад.-Мизм.)
в зависимости от приведенного комплекса Ппр и отклонения имитированных чисел М полета ΔМп=Мзад.-Мизм. от выбранного Мзад., при котором определена первая функциональная зависимость.
В полете в электронной системе автоматизированного управления двигателя измеряют следующие параметры двигателя:
- Gтизм. - весовой расход топлива;
- nвд изм. - частота вращения ротора высокого давления;
- Т*в изм. - полная температура воздуха за вентилятором;
- Р*кизм. - полное давление воздуха за компрессором высокого давления.
Эти данные корректируют с учетом поправок, полученных путем тарировки системы автоматизированного управления в процессе стендовых испытаний двигателя, по формулам
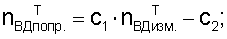
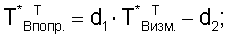
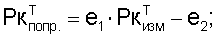

С учетом выполненных измерений частоты вращения ротора nВД изм высокого давления и полной температуры воздуха Т*в изм. за вентилятором получают безразмерный коэффициент Кт* в, учитывающий влияние свойств воздуха на приведенный комплекс Ппр при изменении полной температуры воздуха на входе в двигатель. Затем определяют приведенный комплекс Ппр
по формуле 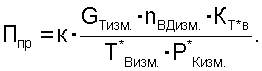
Из уравнения обобщенной характеристики 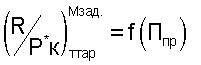 определяют соотношение
определяют соотношение 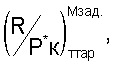 затем определяют величину поправки
затем определяют величину поправки 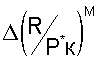 к величине
к величине 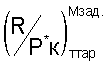 для измеренного числа М полета, и с учетом этой поправки определяют тягу двигателя как произведение отношения
для измеренного числа М полета, и с учетом этой поправки определяют тягу двигателя как произведение отношения 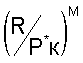 и давления воздуха за компрессором высокого давления Р*к при измеренном числе М полета.
и давления воздуха за компрессором высокого давления Р*к при измеренном числе М полета.
Пример конкретного выполнения способа с использованием приведенного комплекса Ппр1 по формуле (1)
В таблице 1 приведены уточненные по тарировочным зависимостям параметры, взятые из электронного регулятора системы автоматического управления двигателя в процессе летной эксплуатации.
| Таблица 1 | |||
| nвд, % | Gт, % | Т* в, К | Рк, кгс/см2 |
| 91,58 | 67,89 | 365,52 | 13,315 |
В таблице 2 приведены значения коэффициентов поправочных уравнений, которые были использованы для получения данных таблицы 1.
| Таблица 2 | ||||||||
| с1 | с2 | d1 | d2 | e1 | е2 | f1 | f2 | |
| nвд | 1,005106 | -50,97180 | ||||||
| Т* B | 1,001905 | -3,505247 | ||||||
| Рк | 1,060384 | -0,255828 | ||||||
| Gт | 1,025536 | -3,775783 |
По данным измерений числа М полета ЛА отклонение Мзад.-Мполета=0,0261.
Приведенный комплекс Ппр 1 определяли по формуле
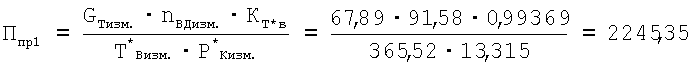
где к=1689,6 - коэффициент согласования размерности измерений;
КТ*в - поправочный коэффициент, учитывающий изменения СP и СV при изменении полной температуры воздуха, и определен в зависимости от измеренных nвд и Т*в
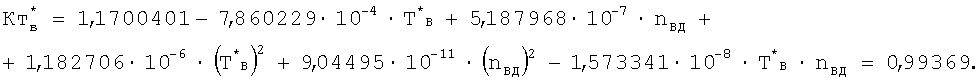
В соответствии с измеренным числом М полета и определенным приведенным комплексом Ппр 1 из уравнения дроссельной характеристики 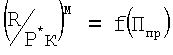 определяли соотношение
определяли соотношение 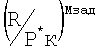 при числе полета Mзад.
при числе полета Mзад.

где к=0,39 - коэффициент согласования размерности измерений.
Так как измеренное число М полета отличается от величины Мзад., то определяли величину соответствующей поправки Δ к величине
к величине 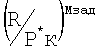 при Мизм.-Мзад.=-0,0261;
при Мизм.-Мзад.=-0,0261;
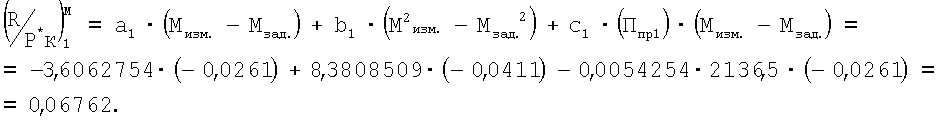
Выполнено приведение к условию М=Мизм. величины 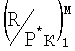 по формуле
по формуле
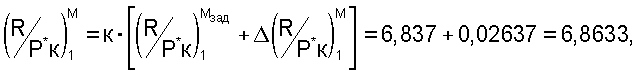
где к=0,39 - коэффициент согласования размерности измерений и представления тяги в эксплуатации.
С учетом этой поправки определяли тягу двигателя как произведение отношения 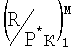 и давления воздуха за компрессором высокого давления Р*к при измеренном числе М полета:
и давления воздуха за компрессором высокого давления Р*к при измеренном числе М полета:
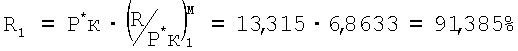
Пример конкретного выполнения способа с использованием приведенного комплекса Ппр3 по формуле (3)
В таблице 3 приведены уточненные по тарировочным зависимостям измеренные в электронном регуляторе системы автоматического управления двигателя в процессе летной эксплуатации параметры.
| Таблица 3 | ||
| nвд, % | Т*в, К | Рк, кгс/см2 |
| 91,58 | 365,52 | 13,315 |
По данным измерений числа М полета ЛА отклонение Мзад.-Мполета=0,0261.
Приведенный комплекс Ппр 3 определяли по формуле
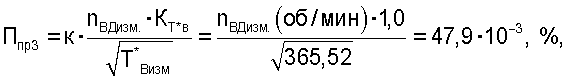
где К=0,000018656 - коэффициент согласования размерности измерений;
КT*в - поправочный коэффициент, учитывающий влияние свойств воздуха (СP и СV) при изменении его полной температуры на входе в двигатель, на данный комплекс, принятый равным 1.
В соответствии с измеренным числом М полета и определенным приведенным комплексом Ппр 3 из уравнения дроссельной характеристики 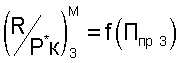 определяли отношение
определяли отношение 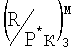 при заданном числе М полета, равном Мзад..
при заданном числе М полета, равном Мзад..
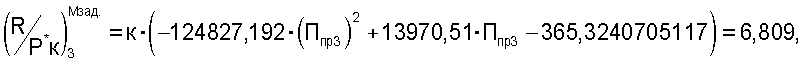
где к=0,39 - коэффициент согласования размерности измерений.
Так как текущее число М полета отличается от величины Мзад., то определяли величину соответствующей поправки  к величине
к величине 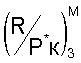 для соответствующего отклонения Мизм.-Мзад=-0,0261
для соответствующего отклонения Мизм.-Мзад=-0,0261
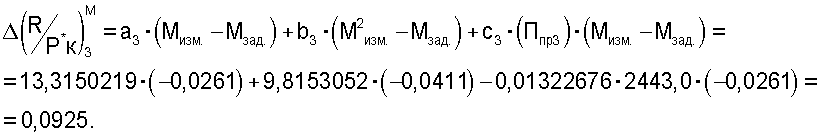
Далее производят вычисление приведенной к условию М=Мизм. величины 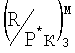 по формуле
по формуле

С учетом этой поправки определяли тягу двигателя как произведение отношения 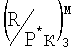 и давления воздуха за компрессором высокого давления Р*к при измеренном числе М полета:
и давления воздуха за компрессором высокого давления Р*к при измеренном числе М полета:
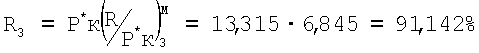
Вывод: Результаты расчетов тяги двигателя по приведенным комплексам Ппр 1 и Ппр 3 практически совпали. Отличие составило 0,3%.
Аналогичным образом производится определение тяги ТРДД и по другим вышеуказанным формулам.
Таким образом, предлагаемый способ позволяет определить тягу ТРДД только по тем параметрам, которые измеряются в электронных системах автоматического управления (САУ) ТРДД и летательного аппарата, без установки дополнительных приемников и датчиков.
1. Способ определения тяги турбореактивного двухконтурного двигателя в эксплуатации, при котором на двигателе устанавливают приемники и датчики для измерения полных давлений воздуха, осуществляют измерение с этих датчиков в системах измерения и обработки и в процессе приемосдаточных испытаний (ПСИ) двигателя измеряют тягу двигателя, по результатам проведенных ПСИ формируют тарировочную функциональную зависимость, в которой функцию задают в виде отношения тяги двигателя к полному давлению воздуха, а в качестве аргумента используют критерий подобия режимов работы двигателя, аппроксимируют полученную функциональную зависимость уравнением и определяют тягу двигателя, отличающийся тем, что при формировании тарировочной функциональной зависимости в качестве функции используют отношение тяги двигателя к полному давлению воздуха за компрессором высокого давления, измерения которого используют из электронной САУ двигателя, а при определении аргумента используют любой из критериев подобия режимов работы двигателя Ппрi; от Ппр1 до Ппр10, которые определяют по формулам
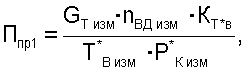 или
или
 или
или
 или
или
 или
или
 или
или
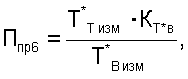 или
или
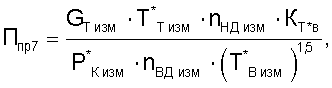 или
или
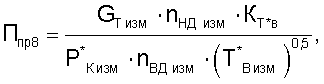 или
или
 или
или
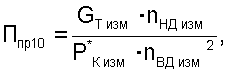 или
или
измеренные в электронных САУ
GТ изм - весовой расход топлива в ТРДД;
Р*К изм - полное давление воздуха за компрессором высокого давления;
nвд изм - частота вращения ротора высокого давления;
nнд изм - частота вращения ротора низкого давления;
Т*В изм - полная температура воздуха в любом сечении двигателя;
Т*т изм - полная средняя температура газа за турбиной;
Кт*в - безразмерный коэффициент, функционально зависимый от измеренной температуры воздуха Т*визм и режима работы двигателя, предварительно определяемый для данного типа ТРДД по математической модели двигателя, аппроксимируют полученные экспериментально функциональные зависимости уравнениями
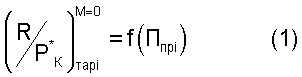
и в процессе эксплуатации двигателя на земле измеряют полное давление воздуха за компрессором высокого давления, вычисляют любой выбранный критерий подобия режимов работы двигателя Ппрi от Ппр1 до Ппр10 и тягу двигателя определяют по формуле
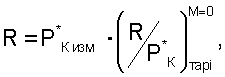
где Р*К изм - измеренное значение полного давления воздуха за компрессором высокого давления;
 - вычисленные значения по уравнениям (1) в зависимости от любого выбранного и определенного Ппрi.
- вычисленные значения по уравнениям (1) в зависимости от любого выбранного и определенного Ппрi.
2. Способ определения тяги турбореактивного двухконтурного двигателя по п.1, отличающийся тем, что, с целью определения тяги во всех ожидаемых условиях эксплуатации, включая летную, измеряют число М полета на летательном аппарате или используют число М полета из систем управления летательного аппарата, или определяют число М полета по данным внешнетраекторных измерений высоты и скорости полета летательного аппарата, по результатам ПСИ двигателя формируют и аппроксимируют уравнениями две тарировочные функциональные зависимости, из которых первая формируется и аппроксимируется при числе Мп=0 в процессе ПСИ двигателя по экспериментальным данным, а вторую формируют с использованием расчетных высотно-скоростных характеристик (ВСХ) двигателя по математической модели типа ТРДД в виде 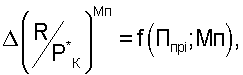 где в качестве функции используют отклонения отношений тяги к полному давлению воздуха за компрессором при числе Мп=0 от этого же отношения, при значениях чисел М полета летательного аппарата в ожидаемых скоростных условиях эксплуатации двигателя
где в качестве функции используют отклонения отношений тяги к полному давлению воздуха за компрессором при числе Мп=0 от этого же отношения, при значениях чисел М полета летательного аппарата в ожидаемых скоростных условиях эксплуатации двигателя 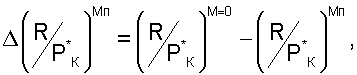 а в качестве аргументов используют два критерия подобия, из которых одним является любой из критериев подобия режимов работы двигателя Ппрi от Ппр1 до Ппр10, а вторым является число М полета, аппроксимируют эти зависимости уравнениями от двух переменных
а в качестве аргументов используют два критерия подобия, из которых одним является любой из критериев подобия режимов работы двигателя Ппрi от Ппр1 до Ппр10, а вторым является число М полета, аппроксимируют эти зависимости уравнениями от двух переменных
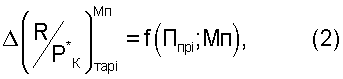
и в процессе эксплуатации двигателя, включая летную, тягу двигателя определяют по формуле
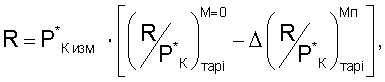
где Р*К изм - измеренное значение полного давления воздуха за компрессором высокого давления;
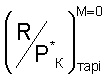 - любые вычисленные значения по уравнениям (1) п.1 первых тарировочных функциональных зависимостей в зависимости от любого выбранного и определенного Ппрi;
- любые вычисленные значения по уравнениям (1) п.1 первых тарировочных функциональных зависимостей в зависимости от любого выбранного и определенного Ппрi;
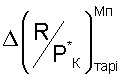 - любые вычисленные тарировочные значения по уравнениям (2) вторых функциональных зависимостей, с использованием полученных чисел М полета и любого выбранного и определенного критерия подобия режимов работы двигателя Ппрi.
- любые вычисленные тарировочные значения по уравнениям (2) вторых функциональных зависимостей, с использованием полученных чисел М полета и любого выбранного и определенного критерия подобия режимов работы двигателя Ппрi.
3. Способ определения тяги турбореактивного двухконтурного двигателя по п.1, отличающийся тем, что, если ПСИ двигателя проводятся с использованием имитации чисел М полета ЛА, первую функциональную зависимость формируют и аппроксимируют уравнениями по экспериментальным данным при любом выбранном из имитируемых значений числа М полета в процессе ПСИ двигателя в виде

где 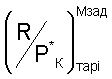 - экспериментальные значения тарировочных функций при выбранном числе Мп из диапазона имитированных чисел Мп в процессе ПСИ двигателя в зависимости от любого из определенных критериев подобия режимов работы двигателя Ппрi от Ппр1 до Ппр10;
- экспериментальные значения тарировочных функций при выбранном числе Мп из диапазона имитированных чисел Мп в процессе ПСИ двигателя в зависимости от любого из определенных критериев подобия режимов работы двигателя Ппрi от Ппр1 до Ппр10;
Ппрi - значения аргументов, которыми являются любые из выбранных критериев подобия режимов работы двигателя от Ппр1 до Ппр10,
вторую функциональную тарировочную зависимость формируют и аппроксимируют уравнениями от двух переменных также по экспериментальным данным

где 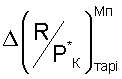 - экспериментальные значения тарировочной функции, определяемые отклонениями имитированного числа Мп от выбранного Мпзад в процессе ПСИ двигателя;
- экспериментальные значения тарировочной функции, определяемые отклонениями имитированного числа Мп от выбранного Мпзад в процессе ПСИ двигателя;
Ппрi - значения критериев подобия режимов работы двигателя, определенные по п.1 от Ппр1 до Ппр10;
(Мп-Мпзад) - отклонения имитируемого числа Мп в процессе ПСИ двигателя от выбранного числа Мпзад при формировании первой функциональной тарировочной зависимости и в процессе эксплуатации двигателя, включая летную, тягу двигателя определяют по формуле
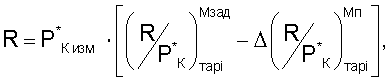
где P*К изм - измеренное значение полного давления воздуха за компрессором высокого давления;
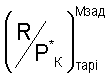 - любые вычисленные значения по уравнениям (3) первой тарировочной функциональной зависимости в зависимости от любого выбранного и определенного критерия подобия режимов работы двигателя Ппрi от Ппр1 до Ппр10;
- любые вычисленные значения по уравнениям (3) первой тарировочной функциональной зависимости в зависимости от любого выбранного и определенного критерия подобия режимов работы двигателя Ппрi от Ппр1 до Ппр10;
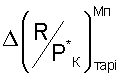 - любые вычисленные тарировочные значения по уравнениям (4) второй функциональной зависимости, полученной экспериментально в процессе ПСИ, с использованием отклонений измеренного числа М полета от выбранного имитированного числа М полета в процессе ПСИ и любых выбранных и определенных критериев подобия режимов работы двигателя Ппрi от Ппр1 до Ппр10.
- любые вычисленные тарировочные значения по уравнениям (4) второй функциональной зависимости, полученной экспериментально в процессе ПСИ, с использованием отклонений измеренного числа М полета от выбранного имитированного числа М полета в процессе ПСИ и любых выбранных и определенных критериев подобия режимов работы двигателя Ппрi от Ппр1 до Ппр10.
www.findpatent.ru
Количество просмотров публикации Тяга двигателя - 386
В ракетном двигателе струя истекающих газов формируется в сопловой, сначала сужающейся, а затем расширяющейся части камеры. Скорость текущих вдоль сопла газов постепенно нарастает, а давление соответственно падает. Возникает вопрос, где следует провести границу между отбрасываемыми газами и тем предметом, который мы будем называть ракетой.
Такое разделение можно произвести различными способами, но предпочтительным будет тот, который даст наибольшие удобства для определения действующих сил.
Самое простое и очевидное — это отделить струю истекающих газов по крайнему срезу сопла, а все то, что находится в пределах внешней поверхности корпуса и плоскости среза, и считать ракетой (рис. 1.3).
Отделяя мысленно, часть механической системы, мы, в соответствии с правилами механики, обязаны заменить действие отброшенной части на оставшуюся силами взаимодействия. Поскольку окружающая среда нами пока не рассматривается, мы заменяем ее действие на ракету невозмущенным атмосферным давлением рh, распределенным по внешней поверхности. Отбрасывая струю газов, мы также должны заменить ее действие на оставшуюся по другую сторону сечения массу давлением, ĸᴏᴛᴏᴩᴏᴇ возникает в струе на срезе сопла. Это давление принято обозначать через ра(рис. 1.3). Оно не обязательно равно атмосферному и должна быть как больше, так и меньше его.
Теперьостается условиться о том, что же следует понимать под тягой двигателя. Для ракеты это та движущая сила, первопричину возникновения которой мы усматриваем в работе двигателя. Она обладает тем удобным свойством, что должна быть непосредственно замерена на стенде (рис. 1.4).
Рис. 1.3. К выводу формулы тяги.
Для закрепленной ракеты сила тяги уравновешивается реакцией связи R, равной тяге Р . По этой причине ускорение равно нулю, и уравнение движения для точки переменной массы (1.4) примет вид
где Sa — площадь выходного сечения сопла, а Wа— скорость истечения потока в данном сечении.
Рис. 1.4. Силы, действующие на закрепленную ракету.
Так как R = P, то тяга
Следует особо подчеркнуть, что под давлением р принято понимать исключительно барометрическое давление окружающей среды, но не истинное давление на поверхности ракеты, значение и закон распределения которого зависят от условий обтекания. Все добавочные силы, связанные со скоростью полета в атмосфере, относятся к категории аэродинамических и в выражение тяги не включаются.
Выражение для тяги на высоте h получим в окончательном виде:
(1.5)
или
Важно заметить, что для стартующей с поверхности Земли ракеты тяга непрерывно возрастает от своего начального значения
(где ро— давление у поверхности Земли) до наибольшего значения, называемого пустотной тягой —
(1.6)
Отличие стартовой тяги от пустотной определяется площадью выходного сечения сопла и для реальных двигателей лежит в пределах 10 — 15%.
После того как введено понятие тяги, мы получаем возможность написать уравнение для поступательного движения ракеты в обычной форме закона Ньютона (1.1):
Здесь М — текущее значение массы ракеты, а под знак суммы вынесены составляющие не рассмотренных нами пока сил, таких как аэродинамическое сопротивление и вес ракеты.
Итак, истекающую струю газов мы отделили от ракеты плоскостью, проходящей через выходное сечение сопла. Но как было сказано ранее, это не единственное решение. В частности, разделение можно произвести по внутренней поверхности камеры, заменив действие отброшенных газов на стенки камеры некоторым изменяющимся вдоль оси давлением рг, приводящим к возникновению результирующей силы Рг (рис. 1.5). Нетрудно догадаться, что результирующая Рг как раз и представляет собой пустотную тягу Рп, из которой для определения тяги на высоте h следует вычесть произведение Saph,т. е.
(1.7)
Τᴀᴋᴎᴍ ᴏϬᴩᴀᴈᴏᴍ, пустотная тяга представляет собой результирующую сил давления, распределенных по внутренней поверхности камеры. В дальнейшем мы увидим, что это давление не зависит ниот скорости полета͵ ни от условий окружающей среды, и в связи с этим пустотная тяга представляет собой одну из базовых характеристик собственно самого двигателя, а не условий полета.
Часто выражение тяги в пустоте записывают в форме реактивной силы
(1.8)
где Wе - так называемая эффективная скорость истечения.
Рис.1.5. Распределение сил давления по поверхности ракеты и по внутренней поверхности камеры.
Из сопоставления выражений (1.6) и (1.8) следует, что эффективная скорость истечения
(1.9)
Основной особенностью эффективной скорости истечения является то, что она не зависит от секундного расхода , поскольку, как это будет показано позже, давление рана выходе из сопла пропорционально , а сама скорость истечения Waтакже отрасхода не зависит (правда, в некоторых определенных пределах). В реально существующих двигателях эффективная скорость истечения превышает действительную примерно на 10—15%.
В заключение можно отметить, что при выводе выражения тяги нами были сделаны некоторые замаскированные упрощения. Ускорение закрепленной на стенде ракеты мы приняли равным нулю. Между тем центр масс ракеты вследствие сгорания топлива смещается. По этой причине уравнение равновесия следовало бы, строго говоря, заменить уравнением движения, введя производные от координаты центра масс по времени. Рассматривая пустотную тягу как равнодействующую сил внутрикамерного давления рг, мы пренебрегли тягой, создаваемой жидким топливом при впрыске в камеру. Наконец, масса находящихся в камере газов должна либо включаться, либо не включаться в общую массу ракеты М, смотря по тому, где проводится поверхность, отделяющая ракету от отбрасываемого рабочего тела. Учёт перечисленных особенностей, однако, приводит к совершенно ничтожным числовым поправкам, и ими с полным основанием пренебрегают.
referatwork.ru