







Уравнения электрического состояния. По аналогии с трансформатором можно написать уравнения второго закона Кирхгофа обмоток статора и ротора. Для статора
(3.15) и для вращающего ротора
и для вращающего ротора
(3.16) 
где  - параметры ротора, приведенные к числу витков статора; – соответственно ЭДС ротора и напряжение рассеяния у вращающегося ротора (см. (3.9) и (3.10)). Уравнения (3.15) и (3.16) являются основой для описания электромагнитных процессов в асинхронном двигателе и его математического моделирования.
- параметры ротора, приведенные к числу витков статора; – соответственно ЭДС ротора и напряжение рассеяния у вращающегося ротора (см. (3.9) и (3.10)). Уравнения (3.15) и (3.16) являются основой для описания электромагнитных процессов в асинхронном двигателе и его математического моделирования.


 с уравнением для вращающейся обмотки ротора (3.16), можно видеть несоответствие между ними. В уравнении для трансформатора правая часть имеет три слагаемых, а уравнение (3.16) – два слагаемых.
с уравнением для вращающейся обмотки ротора (3.16), можно видеть несоответствие между ними. В уравнении для трансформатора правая часть имеет три слагаемых, а уравнение (3.16) – два слагаемых.
С учетом (3.17) уравнение (3.16) примет вид 
(3.18)
 Если теперь сравнить уравнение для вторичной обмотки трансформатора с (3.18), то из закона сохранения энергии следует, что механическая мощность на валу двигателя соответствует величине .
Если теперь сравнить уравнение для вторичной обмотки трансформатора с (3.18), то из закона сохранения энергии следует, что механическая мощность на валу двигателя соответствует величине .

 Схема замещения. Если построить схему замещения двигателя, то она будет иметь вид, аналогичный схеме замещения трансформатора, в которой вместо сопротивления нагрузки Z′н будет сопротивление (рис. 3.15).
Схема замещения. Если построить схему замещения двигателя, то она будет иметь вид, аналогичный схеме замещения трансформатора, в которой вместо сопротивления нагрузки Z′н будет сопротивление (рис. 3.15).
 В этой схеме величина равна сопротивлению, на котором при токе I′2 рассеивается электрическая мощность , равная мощности на валу двигателя, т.е.
В этой схеме величина равна сопротивлению, на котором при токе I′2 рассеивается электрическая мощность , равная мощности на валу двигателя, т.е.
где  - угловая скорость ротора.
- угловая скорость ротора.
Векторная диаграмма фазы двигателя при этом оказывается аналогичной векторной диаграмме фазы трансформатора.
Формула тока. По схеме замещения (рис. 3.15), если пренебречь током холостого хода Ix, можно определить ток Ix, потребляемый двигателем из сети:
electrono.ru
В фазной обмотке статора ЭДС индуктируются не только потоком вращающегося магнитного поля, магнитные линии которого сцепляются одновременно с проводниками статора и ротора. Каждая фазная обмотка статора имеет также потокосцепление рассеяния  рас1. Это та часть линий магнитной индукции, которые замыкаются помимо ротора. Потокосцепление рассеяния статора
рас1. Это та часть линий магнитной индукции, которые замыкаются помимо ротора. Потокосцепление рассеяния статора  рас1 складывается (рис. 14.13) из потокосцеплений магнитных линий поля, замыкающихся поперек пазов сердечника
рас1 складывается (рис. 14.13) из потокосцеплений магнитных линий поля, замыкающихся поперек пазов сердечника  n, вокруг лобовых соединений
n, вокруг лобовых соединений  л, между зубцами статора и ротора, т. е. в воздушном зазоре машины
л, между зубцами статора и ротора, т. е. в воздушном зазоре машины  3. Чем больше воздушный зазор, чем длиннее лобовые соединения и чем глубже заложены проводники обмотки в пазы, тем больше потокосцепление рассеяния
3. Чем больше воздушный зазор, чем длиннее лобовые соединения и чем глубже заложены проводники обмотки в пазы, тем больше потокосцепление рассеяния  рас1. Так как большая часть пути магнитных линий проходит в воздухе, то на тех же основаниях, что и для трансформатора, можно считать потокосцепление рассеяния прямо пропорциональным току статора и совпадающим по фазе с этим током. Потокосцепление рассеяния индуктирует в каждой из фаз обмотки статора ЭДС рассеяния Ерас1, которая отстает по фазе от этого потокосцепления,
рас1. Так как большая часть пути магнитных линий проходит в воздухе, то на тех же основаниях, что и для трансформатора, можно считать потокосцепление рассеяния прямо пропорциональным току статора и совпадающим по фазе с этим током. Потокосцепление рассеяния индуктирует в каждой из фаз обмотки статора ЭДС рассеяния Ерас1, которая отстает по фазе от этого потокосцепления,

а следовательно, и от тока на четверть периода. Как и для трансформатора, напряжение — рас1, уравновешивающее ЭДС рассеяния, можно выразить через произведение тока статора
рас1, уравновешивающее ЭДС рассеяния, можно выразить через произведение тока статора  1 на индуктивное сопротивление xpacl =
1 на индуктивное сопротивление xpacl =  Lpacl, т. е.
Lpacl, т. е.
—  рас1 =j xpacl
рас1 =j xpacl 1 =j
1 =j  Lpacl
Lpacl 1 ,
1 ,
где Lpacl — индуктивность рассеяния фазной обмотки статора. Таким образом, ток в каждой из фазных обмоток можно рассматривать как создаваемый совместным действием фазного напряжения сети U1 и двух ЭДС — одной, индуктируемой вращающимся магнитным полем, и второй, индуктируемой потокосцеплением рассеяния.
Следовательно,
I1=( 1+
1+ 1+
1+ рас1)/rB1,
рас1)/rB1,
где rB1 — активное сопротивление витков фазной обмотки статора, на основании чего напряжение
 1 = (-
1 = (- 1) + (rB1 + jxрас1)
1) + (rB1 + jxрас1)  1 = (-
1 = (- 1) + Zo61
1) + Zo61 1. (14.11а)
1. (14.11а)
Здесь величина
Zo61=rB1+jxрас1
— комплексное сопротивление фазной обмотки статора.
Это уравнение ничем не отличается от уравнения электрического состояния первичной обмотки трансформатора (8.11а), что естественно, так как в асинхронной машине, а также и в трансформаторе передача энергии во вторичную цепь (передача энергии ротору) осуществляется при посредстве магнитного поля.
В уравнении электрического состояния фазы статора асинхронного двигателя Zo61  1 существенно больше, чем в уравнении первичной обмотки трансформатора. Это — результат наличия воздушного зазора в магнитной цепи машины.
1 существенно больше, чем в уравнении первичной обмотки трансформатора. Это — результат наличия воздушного зазора в магнитной цепи машины.
Все же падение напряжения Zo61  1 в машинах средней и большой мощности в рабочем режиме при I1 == I1ном относительно мало и приближенно определяется согласно (7.2в):
1 в машинах средней и большой мощности в рабочем режиме при I1 == I1ном относительно мало и приближенно определяется согласно (7.2в):
U1 E1 = 4,44f
E1 = 4,44f kоб1Фв. (I4.116)
kоб1Фв. (I4.116)
Так как напряжение между выводами фазной обмотки U1 неизменно, то приближенно можно считать магнитный поток вращающегося поля машины Фв также неизменным, не зависящим от ее нагрузки.
studfiles.net
В отличие от синхронного генератора в синхронном двигателе ось полюсов ротора отстает от оси полюсов вращающегося магнитного поля статора (см. рис. 15.3, б). Возникающий при этом электромагнитный момент равен противодействующему тормозному моменту на валу двигателя Мэм = Mтop. В синхронном двигателе осуществляется преобразование электрической энергии в механическую. На рис. 15.15 приведена схема замещения фазы синхронного двигателя, подключенного к электрической системе большой мощности (U = const). Эта схема замещения совпадает со схемой замещения фазы синхронного генератора, подключенного к системе большой мощности (см. рис. 15.7), с той разницей, что в первом случае электрическая энергия поступает из системы в двигатель, а во втором случае электрическая энергия поступает из генератора в систему.
Из схемы замещения фазы синхронного двигателя следует уравнение электрического состояния фазы синхронного двигателя

где Ėо = jωψo, х = xрас + xя совпадают по своему физическому смыслу с аналогичными понятиями, обсуждавшимися при анализе синхронного генератора (см. § 15.5).
У равнению электрического состояния (15.16) соответствует векторная диаграмма фазы синхронного двигателя на рис. 15.16. На векторной диаграмме сдвиг фаз θ соответствует геометрическому углу между осью полюсов ротора и осью результирующего магнитного поля синхронного двигателя, деленному на число пар полюсов. Для синхронной машины, работающей в режиме двигателя, значение угла 6 всегда больше нуля (θ > 0).
равнению электрического состояния (15.16) соответствует векторная диаграмма фазы синхронного двигателя на рис. 15.16. На векторной диаграмме сдвиг фаз θ соответствует геометрическому углу между осью полюсов ротора и осью результирующего магнитного поля синхронного двигателя, деленному на число пар полюсов. Для синхронной машины, работающей в режиме двигателя, значение угла 6 всегда больше нуля (θ > 0).
Электрическая мощность трехфазного синхронного двигателя определяется подобно мощности трехфазного синхронного генератора (15.9) и равна:
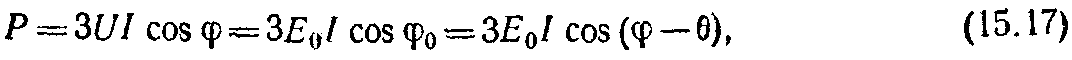
где для синхронного двигателя θ > 0.
Преобразуя (15.17) аналогично (15.9) и учитывая, что θ > 0, получим выражение для электромагнитного момента синхронного двигателя, совпадающее с выражением электромагнитного момента синхронного генератора (15.11):

Так как механическая мощность синхронного двигателя равна Рмех = Р = Мэмωр, то, учитывая (15.18), получим:

Напряжение U и частота f в электрической системе большой мощности являются постоянными величинами.
Учитывая это обстоятельство, можно сделать вывод, что значения электромагнитного момента Мэя и мощности Р синхронного двигателя, подключенного к такой системе, при постоянном токе возбуждения Iв = const зависят только от угла 6. Такие зависимости Мьа (б) и Р (0) называются угловыми характеристиками синхронного двигателя и имеют вид, аналогичный угловым характеристикам синхронного генератора (см. рис. 15.10).
Угловые характеристики позволяют анализировать процессы, происходящие в синхронном двигателе при изменении нагрузки.
При увеличении тормозного момента на валу синхронного двигателя

ротор машины замедляет частоту своего вращения и значения угла θ и электромагнитного момента Мэм начинают возрастать. Равновесие тормозного и электромагнитного моментов восстановится (Mтор2 = Мзм2) через некоторый промежуток времени при новом значении угла θ2 > θ1.
Для того, чтобы сохранить запас устойчивости π/2 — θ при возросшем тормозном моменте, необходимо увеличить ток возбуждения.
studfiles.net
Вращающееся магнитное поле индуктирует в фазной обмотке ротора ЭДС е2 с частотой /2 = p(nx—ri)/60 (см. 14.5). Чтобы выразить эту частоту через частоту питающей сети /, разделим и умножим правую часть этой формулы на щ и, учитывая (14.1) и (14.8), получим частоту
к = /я. (14.12)
называемую частотой скольжения, равной частоте сети, умноженной на скольжение.
Электродвижущая сила егв фазной обмотке статора и ЭДС е2 в фазной обмотке ротора индуктируются общим для этих обмоток вращающимся магнитным полем двигателя, создаваемым совместным действием МДС токов статора и ротора. Однако ЭДС ехпрепятствует изменению тока ixв фазной обмотке статора, а ЭДС е2 возбуждает ток г2 в фазной обмотке ротора. Поэтому если положительные направления ЭДС еги тока цв фазной обмотке статора выбирают совпадающими (см. рис. 14.13), то в фазной обмотке ротора положительное направление тока г2 обычно выбирают противоположным направлению ЭДС е2. Это соответствует встречному включению фазных обмоток статора и ротора, при котором результирующая МДС двигателя равна разности МДС токов статора и ротора. Аналогичные соотношения между ЭДС, токами и МДС были ранее по-jsajLpac2
Рис. 14.15
Лучеиы для первичной и вторичной обмоток трансформатора (см. рис. 9.4, б).
Токi2фазной обмотки ротора создает магнитное поле, часть магнитных линий которого замыкается помимо обмотки статора. Совокупность этих магнитных линий определяет потокосцепление рассеяния Фрас2 фазной обмотки ротора.
Запишем в комплексной форме уравнение электрического состояния фазы ротора с учетом противоположных положительных направлений ЭДС и тока:
—Е2 =RB2h+jsuLp.dc2I2,
где = 2-7г/2 = w2; Rb2—активное сопротивление витков; Lpac2= = ФраС2/г2— индуктивность рассеяния; su)Z/pac2— индуктивное сопротивление фазной обмотки ротора.
Действующее значение ЭДС фазы ротора определим по аналогии с (14.116):
Е2 =4,44/^2^2$,
где для короткозамкнутого ротораw2= 1/2 и коС)2 = 1.
Уравнению (14.13) соответствуют схема замещения фазной обмотки ротора на рис. 14.15 и векторная диаграмма на рис. 14.16.
Заметим, что уравнение электрического состояния фазы ротора (14.13) аналогично уравнению электрического состояния вторичной цепи трансформатора (9.116) в режиме короткого замыкания, т.е. приU2= 0.
Баланс магнитодвижущих сил в асинхронном двигателе
Вращающиеся магнитные поля токов статора и ротора, как было показано, неподвижны относительно друг друга. На этом основании при вращении ротора МДС токов статора и ротора можно рассматривать как векторы, геометрическая сумма которых определяет
МДС, возбуждающую вращающееся магнитное поле двигателя. При расчете этих МДС необходимо учитывать то обстоятельство, что они создаются токами в обмотках, секции которых распределены по нескольким пазам, вследствие чего магнитные поля токов отдельных секций обмоток не совпадают в пространстве. Чтобы учесть это, можно ввести в выражения МДС коэффициент, меньший единицы и приближенно равный обмоточному коэффициенту.
Следовательно, по аналогии с балансом МДС в трансформаторе [см. (9.4)] в асинхронном двигателе как при неподвижном, так и при вращающемся роторе справедливо условие
lWlkoeJl ~ = lWlkoeJlx- (14Л5>
Здесь учтено, что результирующие МДС трехфазной и га2-фазной обмоток статора и ротора соответственно в 3/2 раза [по (14.5)] и т2/2 раз больше МДС одной фазы.
Из последнего уравнения можно выразить ток статора следующим образом:
А =+ Л* = 4 +'u- (1416>
1 об1
Величина
j! =™2™2к<*2 / 2 Ъп к 2
Называется приведенным током ротора; это та часть тока статора, которая уравновешивает размагничивающее действие тока ротора.
Ток намагничивания /1х в рабочем режиме двигателя(s ^sHOM) практически равен току статора при идеальном холостом ходе двигателя. Чтобы определить последний из опыта, необходимо сообщить ротору с помощью вспомогательного двигателя синхронную частоту вращения, т. е. равную частоте вращения магнитного поля(s = 0), при которой ток в роторе станет равным нулю. Таким образом, ток холостого хода двигателя при отсутствии нагрузки на валу больше тока идеального холостого хода вследствие потерь энергии на преодоление трения в подвижных частях, на нагревание обмоток ротора и т. п.
Дата добавления: 2018-02-28; просмотров: 7; ЗАКАЗАТЬ РАБОТУ
studopedia.net
Cтраница 1
Уравнение электрического состояния для контура является следствием закона сохранения энергии. [1]
Уравнение электрического состояния фазы статора асинхронного двигателя иллюстрирует векторная диаграмма на рис. 14.14, гдеZ Д существенно больше, чем в уравнении первичной обмотки трансформатора. [2]
Уравнение электрического состояния фазы статора асинхронного двигателя иллюстрирует векторная диаграмма на рис. 14.14, где Z & Ji существенно больше, чем в уравнении первичной обмотки трансформатора. [3]
Анализ уравнения электрического состояния фазы статора (14.116) показывает, что при постоянном значении напряжения U между выводами фазной обмотки статора и тока 1 1ном магнитный поток вращающегося поля двигателя 4в также постоянен и не зависит от ее нагрузки. Это означает, что энергия, запасаемая в магнитном поле асинхронного двигателя, и реактивная мощность двигателя также постоянны и не зависят от его нагрузки. Но так как с ростом нагрузки активная мощность двигателя увеличивается, то из (14.21) следует, что с ростом нагрузки и коэффициент мощности двигателя увеличивается. [4]
Анализ уравнения электрического состояния фазы статора (14.116) показывает, что при постоянном напряжении t / x между выводами фазной обмотки статора и / х g / 1ном магнитный поток вращающегося поля машины Фв также постоянен и не. Это означает, что энергия, запасаемая в магнитном поле асинхронного двигателя, и реактивная мощность двигателя также постоянны и не зависят от ее нагрузки. Но так как с увеличением нагрузки активная мощность двигателя увеличивается, то из (14.21) следует, что с увеличением нагрузки коэффициент мощности двигателя увеличивается. [5]
Анализ уравнения электрического состояния фазы статора (14.116) показывает, что при постоянном значении напряжения Ut между выводами фазной обмотки статора и тока / 2 1ном магнитный поток вращающегося поля двигателя Ф также постоянен и не зависит от ее нагрузки. Это означает, что энергия, запасаемая в магнитном поле асинхронного двигателя, и реактивная мощность двигателя также постоянны и не зависят от его нагрузки. Но так как с ростом нагрузки активная мощность двигателя увеличивается, то из (14.21) следует, что с ростом нагрузки и коэффициент мощности двигателя увеличивается. [6]
С помощью уравнения электрического состояния рассчитывают и анализируют режимы цепи. [7]
Решение системы уравнений электрического состояния узлов и контуров, если количество ветвей в электрической цепи более трех, создает известные трудности. [8]
При составлении уравнения электрического состояния ветви слагаемые берут со знаком минус, если на заданном участке происходит падение потенциала, и со знаком плюс, если потенциал возрастает. [9]
Докажите, что уравнение электрического состояния для любого контура схемы рис. 8 является следствием закона сохранения энергии. [10]
Вышеприведенное уравнение называют иногда уравнением электрического состояния цепи или уравнением баланса напряжения замкнутой цепи. [12]
Аналитически эти характеристики описываются уравнением электрического состояния цепи якоря. Характер этих зависимостей определяется способом возбуждения основного поля. [13]
Это уравнение ничем не отличается от уравнения электрического состояния первичной обмотки трансформатора ( 9.11 а), что естественно, так как и в асинхронном двигателе, и в трансформаторе передача энергии во вторичную цепь ( передача энергии ротору) осуществляется посредством магнитного поля. [14]
При анализе таких цепей для составления уравнений электрического состояния схем замещения необходимо знать, как направлены по отношению друг к другу магнитные потоки самоиндукции и взаимной индукции. Для этого прибегают к разметке зажимов элементов цепи с магнитной связью. [15]
Страницы: 1 2 3
www.ngpedia.ru
Как следует из принципа действия асинхронного двигателя (см. § 6.2), обмотка ротора не имеет электрической связи с обмоткой статора. Между этими обмотками существует только магнитная связь, и энергия из обмотки статора передается в обмотку ротора магнитным полем. В этом отношении асинхронная машина аналогична трансформатору: обмотка статора является первичной, а обмотка ротора - вторичной.
В процессе работы асинхронного двигателя токи в обмотках статора и ротора создают две магнитодвижущие силы; МДС статора и МДС ротора. Совместным действием эти МДС наводят в магнитной системе двигателя результирующий магнитный поток, вращающийся относительно статора с синхронной частотой вращения n1. Так же как и в трансформаторе, этот магнитный поток можно рассматривать состоящим из основного потока Ф, сцепленного как с обмоткой статора, так и с обмоткой ротора (магнитный поток взаимоиндукции), и двух потоков рассеяния: Фσ1 — потока рассеяния обмотки статора и Ф σ2 — потока рассеяния обмотки ротора (см. § 11.3). Рассмотрим, какие ЭДС наводят указанные потоки в обмотках двигателя.
Электродвижущие силы, наводимые в обмотке статора. Основной магнитный поток Ф, вращающийся с частотой n1 наводит в неподвижной обмотке статора ЭДС Е1, значение которой определяется выражением [см. (7.20)] E1 = 4,44 f1 Ф ω1 kоб1.
Магнитный поток рассеяния Фσ1 наводит в обмотке статора ЭДС рассеяния, значение которой определяется индуктивным падением напряжения в обмотке статора:
 σ1 = - j
σ1 = - j 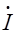 1x1
1x1 (12.1)
(12.1)
где х1 — индуктивное сопротивление рассеяния фазной обмотки статора [см. (11.6)],Ом.
Для цепи обмотки статора асинхронного двигателя, включенной в сеть с напряжением U1, запишем уравнение напряжений по второму закону Кирхгофа:
 1 +
1 +  1 +
1 +  σ1 =
σ1 = 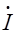 1 r1, (12.2)
1 r1, (12.2)
где I1 r1 - падение напряжения в активном сопротивлении обмотки статора r1.
После переноса ЭДС E1, и Eσ1 , в правую часть уравнения (12.2) с учетом (12.1) получим уравнение напряжений обмотки статора асинхронного двигателя:
 1 = (-
1 = (-  1) + j
1) + j 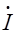 1 x1 +
1 x1 + 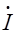 1r1(12.3)
1r1(12.3)
Сравнив полученное уравнение с уравнением (1.13), видим, что оно не отличается от уравнения напряжений для первичной цепи трансформатора.
Электродвижущие силы, наводимые в обмотке ротора.В процессе работы асинхронного двигателя ротор вращается в сторону вращения поля статора с частотой n2. Поэтому частота вращения поля статора относительно ротора равна разности частот вращения (n1 – n2). Основной магнитный поток Ф, обгоняя ротор с частотой вращения ns = (n1 - n2), индуцирует в обмотке ротора ЭДС
Е2 = 4,44 f2 Ф ω2 коб2(12.4)
где f2— частота ЭДС Е2s в роторе, Гц; ω2 — число последовательно соединенных витков одной фазы обмотки ротора; ko62 — обмоточный коэффициент обмотки ротора.
Частота ЭДС (тока) в обмотке вращающегося ротора пропорциональна частоте вращения магнитного поля относительно ротора ns = n1 - n2, называемой частотой скольжения:
f2 = pns / 60 = p(n1 – n2) / 60,
или
f2 = 
 =
= 
 = f1s (12.5)
= f1s (12.5)
т. е. частота ЭДС (тока) ротора пропорциональна скольжению. Для асинхронных двигателей общепромышленного назначения эта частота обычно невелика и при f1 = 50 Гц не превышает нескольких герц, так при s = 5% частота f2 = 50  0,05 = 2,5 Гц. Подставив (12.5) в (12.4), получим
0,05 = 2,5 Гц. Подставив (12.5) в (12.4), получим
E2s = 4,44 f1 s Ф ω2 kоб2 = E2 s. (12.6)
Здесь Е2 - ЭДС, наведенная в обмотке ротора при скольжении s = 1, т. е. при неподвижном роторе, В.
Поток рассеяния ротора Фσ2 индуцирует в обмотке ротора рассеяния, значение которой определяется индуктивным падением напряжения в этой обмотке:
 σ2 = - j
σ2 = - j 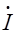 2 x2 s (12.7)
2 x2 s (12.7)
где х2 - индуктивное сопротивление рассеяния обмотки ротора при неподвижном роторе [см. (11.8)], Ом.
Обмотка ротора асинхронного двигателя электрически не связана с внешней сетью и к ней не подводится напряжение. Ток в этой обмотке появляется исключительно за счет ЭДС, наведенной основным магнитным потоком Ф. Поэтому уравнение напряжений для цепи ротора асинхронного двигателя по второму закону Кирхгофа имеет вид
 2s +
2s +  σ2 =
σ2 = 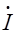 2 r2
2 r2
где r2 — активное сопротивление обмотки ротора. С учетом (12.6) и (12.7) получим
 2s - j
2s - j 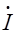 2 x2 s -
2 x2 s - 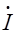 2 r2 (12.8)
2 r2 (12.8)
Разделив все слагаемые равенства (12.8) на s, получим
 2 - j
2 - j 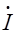 2 x2 -
2 x2 - 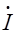 2 r2 / s = 0 (12.9)
2 r2 / s = 0 (12.9)
-уравнение напряжений для обмотки ротора.
Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
zdamsam.ru