6.3 Работа асинхронной машины при вращающемся роторе. Уравнение движения ротора асинхронного двигателя

3.2. Уравнение движения ротора синхронной машины

В наиболее общем виде уравнение движения ротора синхронной машины будет представляться в соответствии со вторым законом Ньютона в следующем виде

, (3.1)

где J– момент инерции ротора агрегата: турбины и генератора; ω – угловая скорость вращения ротора генератора, которая может рассматриваться как сумма синхронной угловой скорости вращения ротора ω0 и скорости перемещения ротора относительно синхронно вращающейся оси Δω, т. е. ω = ωо + Δω; Mт – момент, создаваемый турбиной, который имеет вращательный характер; М– электромагнитный момент на валу ротора генератора, несущий тормозящий характер.

Переходный процесс в соответствии с данным выражением можно характеризовать отклонениями координат Δω, ΔMт, ΔM от их нормальных установившихся значений: ω0, Mто, Mо. Для системы, содержащей n число синхронных машин, таких уравнений (3.1) также будет n.

В нормальном установившемся режиме угловая скорость ω = ωо = const, а также Mт = Mо . Для отклонений координат Δω , ΔMт , ΔM, т. е. для анализа переходного процесса, уравнение движения ротора (3.1) сохраняет свою структуру и принимает следующий вид

(3.2)

или сокращенно:

. (3.3)

В неподвижной системе координат положение ротора синхронной машины в каждый момент времени можно характеризовать некоторым положением угла γ, который отсчитывается между поперечной осью синхронной машины q и магнитной осью статорной обмотки фазы А: γ = (q^А). И

(3.4)

Здесь угол δ отсчитывается от оси, которая вращается с постоянной угловой скоростью исходного установившегося режима ωо и называется синхронно вращающейся осью. Обычно также угол δ называют еще абсолютным углом. Разность этих абсолютных углов для любой пары синхронных машин образует относительные или взаимные углы: . Поскольку

(3.5)

или

, (3.6)

то вторая производная

. (3.7)

Тогда с учетом соотношений (3.6) и (3.7) уравнение (3.3) может быть переписано:

. (3.8)

Преобразуем (3.8), для чего разделим левую и правую части на отношение , тогда

. (3.9)

Левую часть (3.9) умножим на и разделим на:

. (3.10)

Здесь , где подTJпонимается постоянная инерции ротора генератора, которая имеет размерность времени в секундах. И тогда с учетом этого обозначения (3.10) перепишем:

. (3.11)

Далее перейдем от моментов к мощностям:

. (3.12)

Тогда с учетом (3.12) уравнение (3.11) перепишем следующим образом

. (3.13)

Это есть не что иное, как полное уравнение движения ротора. Как видно из данного выражения, правая часть уравнения представляет собой безразмерную величину, и поэтому, чтобы получить такую же безразмерную величину в левой части, необходимо подставить в левую часть (3.13): синхронную угловую скорость ωо ,; Δδ,;t,;ТЈ ,. Тогда в левой части также будет получаться безразмерная величина. Можно переписать уравнение (3.13) при применении системы относительных единиц для всех величин, входящих в это уравнение. В такой системе базисными величинами дополнительно принимают угол в один радиан и синхронную угловую скорость ωо. В этом случае единица времени, принимаемая за базисное время (tбаз), будет определяться как промежуток времени в секундах, в течение которого при синхронной угловой скорости вращения ротора ωо будет достигаться изменение угла, равное одному радиану. Тогда

где синхронная скорость вращениярад/с.

И тогда время, выраженное в относительных единицах или, как иногда говорят, в радианах, будет определяться как

. (3.14)

Если применить (3.14) ко времени t и постоянной инерции ТЈ в выражении (3.13), тогда последнее перепишется следующим образом

. (3.15)

Если допустить Δω* = 0, то получим приближенное уравнение движения ротора синхронной машины:

. (3.16)

Следует отметить, что применение этого приближенного уравнения движения ротора не вносит неприемлемых погрешностей в результат расчета синхронной динамической устойчивости. Это объясняется тем, что в действительности размах синхронных динамических качаний Δδ = (100–120)° при длительности качаний T = (0,5–0,8) с (рис. 3.4).

В этих условиях Δω = 200 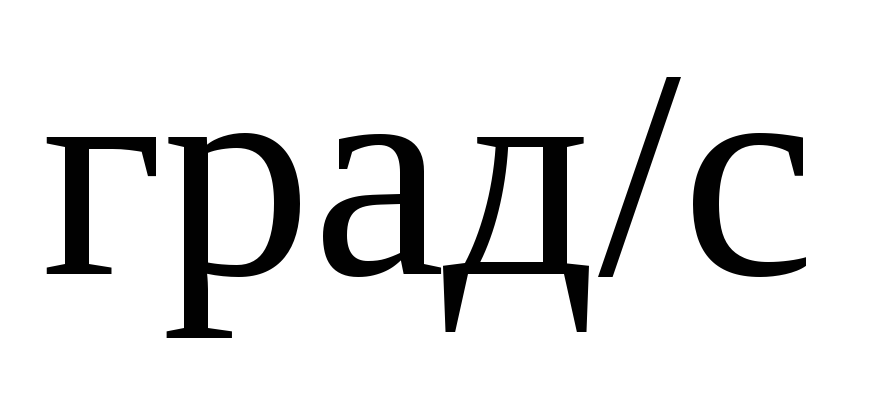что, отнесенное к ωном, составит

Рис. 3.4. Изменение угла во времени и определение

размаха колебаний и периода качаний

Таким образом, отсюда видно, что скорость перемещения ротора Δω относительно синхронно вращающейся оси, выраженная в относительных единицах, будет немного превышать один процент, что с полным основани-

ем доказывает, что этим можно пренебречь при выполнении приближенных упрощенных расчетов динамической устойчивости. При выполнении же расчетов длительных переходных процессов, таких как синхронизация генераторов, этим допущением Δω = 0 пользоваться не следует, и тогда анализ процесса синхронизации следует проводить по полному уравнению движения ротора синхронной машины, т. е. уравнению (3.13).

Постоянная ТЈ, входящая в уравнение движения ротора, представляет собой физически промежуток времени, в течение которого ротор генератора изменит свою скорость вращения от состояния покоя до синхронной угловой скорости вращения ωо при постоянном вращающем моменте, подведенном к валу ротора генератора, равном номинальному. И наоборот, постоянная инерции ТЈ равна промежутку времени, необходимому для полного останова ротора от синхронной угловой скорости ωо при постоянном тормозящем моменте, подведенном к валу ротора генератора, равном номинальному. Эта постоянная инерции ТЈ в секундах обычно задается в паспортных (каталожных) данных генератора или ее можно определить по эмпирическим формулам следующего вида:

– в паспортных данных задан маховый момент, т. е. GD2:

где GD2 − произведение веса на диаметр ротора, тм2; n – частота вращения ротора, об/мин; Sном − номинальная мощность генератора, МВ·А;

– указан момент инерции J, тм2:

Для большинства серийно выпускаемых генераторов ТЈ = 5−10 с.

studfiles.net

6.3 Работа асинхронной машины при вращающемся роторе

В статорной обмотке при переходе от неподвижного ротора к подвижному практически ничего не меняется, если U1 = const и f1 = const. В роторной же обмотке изменяется частота ЭДС из-за возникновения скольжения,

f2S=f1s. (6.8)

Таким образом, частота ЭДС (тока), наводимая вращающимся полем в роторе, равна частоте сети, умноженной на скольжение.

При работе асинхронной машины двигателем частота f2Sобычно весьма невелика; если, например,f1= 50 Гц, а скольжениеsHпри номинальной нагрузке составляет 1–4 %, то

f2S= 50∙(0,01 – 0,04) = 0,5 – 2 Гц.

ЭДС и индуктивное сопротивление обмотки вращающегося ротора:

; (6.9)

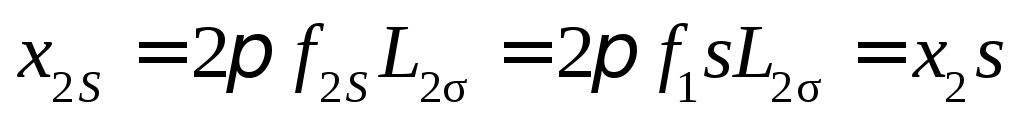, (6.10)

где L2σ– индуктивность рассеяния фазной обмотки ротора;

E2иx2– ЭДС и индуктивное сопротивление фазной обмотки неподвижного ротора.

Активное сопротивление обмотки ротора при малой частоте тока в ней можно считать неизменным, т. е. r2=const, тогда по закону Ома ток в роторной обмотке

. (6.11)

Уравнение (6.11) позволяет режим двигателя с вращающимся ротором привести к эквивалентному режиму при неподвижном роторе. В этом режиме во вторичной цепи при вращении ротора вместо ЭДС E2Sс частотойf2Sбудет существовать ЭДС при неподвижном ротореE2с частотойf1, а вместо индуктивного сопротивления при вращении ротораx2Sво вторичной цепи действует индуктивное сопротивление при неподвижном ротореx2. Для сохранения величины и фазы токаI2необходимо вместоr2ввести новое со

противление r2/s. Представимr2/sкак

. (6.12)

Тогда эквивалентная схема роторной цепи имеет вид рисунка 6.1, а Т–образная схема замещения для приведенной машины – вид рисунка 6.2. Последняя получена на основании основных уравнений асинхронной машины:

;

; (6.13)

Рисунок 6.1 – Эквивалентная схема роторной цепи

Рисунок 6.2 – Т-образная схема замещения асинхронного двигателя

На схеме замещения r1и x1 – фазное активное и индуктивное сопротивления статорной обмотки; r2 и x2 – аналогичные приведенные сопротивления роторной обмотки; rm и xm – параметры намагничивающей ветви; – элемент, на котором выделяется электрическая мощность, равнаямеханической мощности на валу двигателя.

6.4 Вращающий момент асинхронного двигателя

Если считать, что двигатель работает в установившемся режиме, т. е. при n=const, то в этом случае, по условию равновесия моментов,

M=M0+M2,

где M – вращающий момент, развиваемый двигателем;

M0иM2– моменты сопротивления при холостом ходе двигателя и его нагрузки.

Момент M2задаётся рабочим механизмом, на который работает двигатель. Соответствующая ему полезно развиваемая двигателем мощностьР2определяется в виде

где ω – угловая частота вращения ротора.

Моменту холостого хода М 0соответствует мощность

Вращающий момент двигателя Мобразуется в результате взаимодействия вращающегося магнитного потока Ф и тока в ротореI2. Но поле Ф вращается с угловой частотойω1, следовательно, развиваемая им электромагнитная мощность

Рэм=Мω1 .

Из энергетической диаграммы также следует, что

Рэм=Рмех+ ∆РМ2=Мω+ ∆РМ2,

где ∆РМ2– потери в обмотке ротора,.

Следовательно, Рэм – Рмех = М (ω1 – ω) = ∆PM2или, откуда

. (6.14)

Если в Т-образной схеме замещения асинхронного двигателя намагничивающую ветвь (xm,rm) вынести на входные зажимы так, чтобы токI0не изменился, то получим Г-образную схему замещения двигателя. Последняя имеет вид рисунка 6.3.

Из Г-образной схемы замещения двигателя имеем

. (6.15)

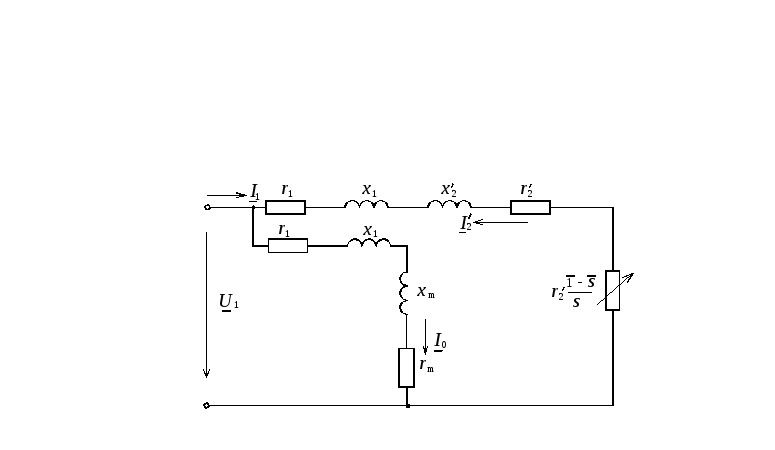
Рисунок 6.3 – Г-образная схема замещения асинхронного двигателя

Подставляя значение тока в (6.14), получим

,(6.16)

где .

Из выражения (6.16) следует, что вращающий момент асинхронного двигателя пропорционален квадрату приложенного напряжения питания. Отмеченное является недостатком асинхронного двигателя. Так, если напряжение сети уменьшится на 20 %, то развиваемый двигателем момент снизится на 36 %.

Вращающий момент двигателя также зависит от соотношения параметров его рабочей цепи и.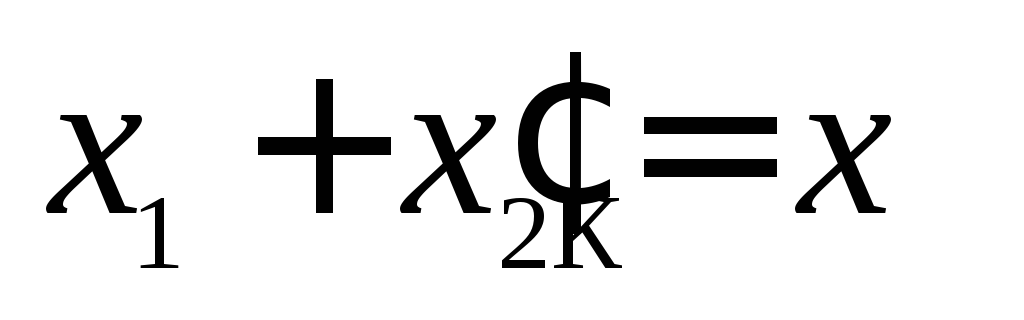

При пуске двигателя n= 0,s= +1, имеем пусковой моментМП. Если моментМПдостаточен для преодоления статического моментаМ0+М2, то

начнется разгон двигателя, т. е. двигатель будет увеличивать частоту вращения до тех пор, пока его момент Мне станет равным моментуМ0+М2. В соответствии с этим скольжение будет уменьшаться от значенияs= +1 до определенной величины.

Так как обычно xК > rК, то при уменьшении s (см. формулу (6.16)) будут одновременно увеличиваться и числитель, и знаменатель; сначала, при больших s, преобладающее значение имеет числитель, вследствие чего момент М возрастает, а затем, при скольжениях s = 0,12 … 0,2, преобладающее значение получает знаменатель, куда отношение входит в квадрате. Этоприводит к тому, что момент М, достигнув наибольшего значения МКР = Мmax, начинает уменьшаться и при s = 0 становится равным нулю.

Зависимость М = f(s) при постоянстве U1 и f1 называется механической характеристикой асинхронного двигателя. Последняя имеет вид рисунка 6.4.

Рисунок 6.4 – Механическая характеристика асинхронного двигателя

Чтобы определитьМКР, сначала находят то скольжение sКР, при котором двигатель развивает этот момент. Для того, по общему правилу, берут производную и приравнивают ее к нулю, т. е. решают уравнение.

Так как эта операция носит обычный математический характер, то дос

таточно привести её конечный результат. При некоторых допущениях имеем

,(6.17)

тогда максимальный момент (критический момент) будет

.(6.18)

При номинальном режиме работы двигатель имеет sН и МН. Отношение максимального момента к номинальному характеризует перегрузочную способность двигателя

λ.(6.19)

Для короткозамкнутых асинхронных двигателей λ = 1,8 … 2,5. Более высокие значения λ соответствуют двигателям с меньшим числом полюсов.

Критическое скольжение двигателя

. (6.20)

Для расчета механической характеристики можно использовать упрощенную формулу Клосса,

,(6.21)

где s– скольжение, при котором определяется моментМ.

Имея каталожные данные о МН,sНи, из формулы (6.21) определяемsКРи, задаваясь скольжениемs, находим моментМдля данногоs.

Формула Клосса вместе с выражением для определения частоты вращения ротора n=n1(1 –s) позволяет получить механическую характеристику в виде зависимостиn=f(M), которая представлена на рисунке 6.5. Анализ данного рисунка показывает, что асинхронные двигатели на рабочем участке имеют жесткую механическую характеристику, т. е. такую, при которой частота вращения мало изменяется при увеличении нагрузки.

Рисунок 6.5 –Механическая характеристика асинхронного двигателя

Анализ зависимости M= f(s), (см. уравнение (6.16)) показывает, что максимальный моментМКРне зависит от активного сопротивления обмотки ротора(см. формулу (6.18)), однако согласно выражению (6.17) это сопротивление оказывает влияние на скольжениеsКР, при котором асинхронный двигатель развивает максимальный момент. Отмеченное используют в двигателях с фазным ротором. При пуске таких двигателей в цепь ротора включают пусковой реостатr2 пуск, при этом возрастаетsКР, максимальный моментМКР, не изменяясь по величине, смещается в сторону больших скольжений, отчего возрастает пусковой моментМП, что облегчает пуск двигателя (кривая 2 на рисунке 6.4). Одновременно включениеr2пускуменьшает пусковой токI2пуск, а следовательно, иI1пуск.

Полезная мощность, отдаваемая двигателем рабочему механизму, Вт,

, (6.22)

где M– момент на валу двигателя, Н·м;

n – частота вращения ротора, об/мин.

Активная мощность, потребляемая двигателем из сети,

, (6.23)

где U1Л– линейное напряжение сети;

I1Л– линейный ток, потребляемый из сети;

φ1– угол сдвига фаз между током и напряжением.

Коэффициент полезного действия двигателя

. (6.24)

studfiles.net

Уравнение движения электропривода

Уравнение движения электропривода учитывает все силы и моменты, действующие в переходных режимах и имеет следующий вид:

. (3-3)

Уравнение движения (3-3) показывает, что электромагнитный момент двигателя уравновешивается: статическим моментом на его валуи

инерционным динамическим моментом .

В расчётах принимается, что при работе электропривода массы тел и их моменты инерции не изменяются.

Из анализа уравнения движения (3-3) следует, что:

1) при , происходит ускорение электропривода;

при 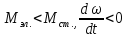,происходит замедление электропривода;
при , ускорение равно нулю, привод работает в установившемся режиме (то есть с постоянной скоростью

Момент, двигателя, положительный, если он направлен в сторону движения привода. Если момент двигателя направлен в противоположную сторону, то он отрицательный.

Знак минус перед статическим моментом указывает на тормозящее действие механизма.

При спуске груза, раскручивании сжатой пружины, движении электротранспорта под уклон и т.п. перед статическим моментом ставитсязнак плюс, так как статический момент направлен в сторону движения привода и способствует движению исполнительного механизма.

Правая часть уравнения (3-3) динамический (или инерционный) момент – проявляется только при переходных режимах, то есть когда изменяется скорость привода.

При ускорении привода динамический момент направлен против движения, а при торможении в сторону движения, так как он поддерживает движение за счёт инерции.

Из уравнения движения электропривода (3-3) рассчитываются времена: пуска, разгона и торможения электропривода.

Время пуска двигателя в холостом режиме и под нагрузкой

Цикл пуска электропривода включает пуск и торможение ЭД. Для некоторых судовых механизмов пуски и торможения повторяются очень часто и оказывают существенное влияние на их работу. При расчете электроприводов механизмов необходимо знать длительность переходных процессов.

Время переходных процессов определим из уравнения движения.

t = (3-4)

Если динамический момент 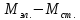=const решение значительно упрощается. Найдем частное решение для наиболее типичных режимов работы электропривода.

Пуск двигателя в холостом режиме

Многие асинхронные двигатели с короткозамкнутым ротором при разгоне до рабочих скоростей развивают электромагнитный момент, который незначительно изменяется за время разгона. Поэтому этот разгонный момент можно принять равным среднему значению.

где;= 1.22.

Для рассматриваемого режима (пуск в холостую)

момент инерции, равен только моменту инерции двигателя, так как двигатель не нагружен механизмом. Из уравнения (3-4) получим tххвремя разгона двигателя без нагрузки до скоростипри холостом ходе

tхх = , (3-5)

где: 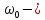скорость в режиме холостого хода;331 130313

= 2.

studfiles.net

3. Решение дифференциальных уравнений относительного движения ротора генератора

(ПРИ Eq = const ИЛИ Е = const)

Дифференциальное уравнение и его особенности. При принятых выше допущениях переходные процессы могут быть описаны дифференциальным уравнением второго порядка:

, (1)

где Tj - постоянная инерции; Ро - вращающий момент, в соответствии со сделанными ранее допущениями замененный мощностью турбины; Рт-амплитуда той характеристики, мощность которой соответствует изучаемому режиму.

Преобразуем (1), введя новые параметры: τ =и Р* = P0/Pm.

Назовем последнюю величину приведенной мощностью первичного двигателя. Тогда (1) примет вид

∂2δ/∂τ2 = Р*—sinδ, (2)

где Р* = const.

Любые начальные изменения режима получат свое отражение в изменении угла б0, значениях мощности Ро, амплитуды характеристики Рт и, следовательно, в величине Р* = Р0/Рm.

В таком простейшем виде интеграл уравнения (2), т. е. зависимость δ = (τ), не выражается через конечную комбинацию известных трансцендентных величин. Здесь не удается воспользоваться и известными (заранее вычисленными и сведенными в таблицы) функциями. Приближенное решение такого рода довольно громоздко, а случай, когда Р* = 0, соответствующий отсутствию вращающего момента у первичного двигателя (Р* = 0), не представляет практического интереса, поэтому эти случаи здесь не будут рассматриваться.

4. Численное интегрирование уравнения движения.

При приближенном представлении процесса (E’ = const) на основе уравнения (2) легко найти изображение на фазовой плоскости Δω= ψ(δ)

или

С помощью графического интегрирования функции Δω = ψ(δ) можно приближенно получить зависимость τ = f(δ). Для этого соответствующая кривая Δω = ψ(δ) разбивается по оси б на интервалы и на каждом из интервалов участок кривой заменяется горизонтальным отрезком с ординатой, равной среднему значению Δω на этом интервале — Δω ср. Для i-го интервала

Δω ср = (Δωi+ Δωi+1)/2 = Δ δ1/Δ τi

Откуда, Δ τi = Δ δi / Δω срi

Проводя такие вычисления по всем интервалам, получим искомую зависимость τ =f(δ), представленную на рис. 8.2 б, от которой легко перейти к зависимости

t =

Построение ее будет тем точнее, чем меньше будет взята величина интервала Δ δ.

Численные методы решения дифференциальных нелинейных уравне-

ний. Метод последовательных интервалов.

Качественную оценку переходного процесса смены режимов при больших возмущениях (к каковым относится и КЗ) можно выполнить по зависимости Δ=f(t), которую можно получить численным решением системы нелинейных дифференциальных уравнений. Существует немало методов решений таких уравнений (методы решения с помощью рядов Тейлора, метод Эйлера, метод Рунге-Кутта и др.) Эти методы находят широкое применение при анализе переходных процессов в электрических системах. Мы рассмотрим здесь более простой, но в то же время дающий достаточно точные результаты при исследовании переходных процессов СЭС, который носит название метода последовательных интервалов. Этот метод позволяет учесть влияние управляющих

воздействий на характер переходного процесса от регулирования элемента,

АПВ и др.

Переходный процесс описывается уравнением

где . δ – рад

где . δ – град

Обосновывая метод последовательных интервалов, что поставленная задача уже решена и подлежащие определению зависимости построены, разобьём весь процесс на малые интервалы времени Δt и будем рассматривать его последовательно от интервала к интервалу. Выбирая одинаковые интервалы по времени, очевидно, будем иметь неодинаковые интервалы по углу. Каждый интервал может характеризоваться некоторыми начальными и конечными значениями угла, скорости, ускорения, действующими в данном интервале. Начальные значения этих величин в последующих интервалах будут равны конечным в предыдущих. Выберем интервал настолько малым, чтобы на протяжении его ускорение можно было считать неизменным. Практически при расчётах современных мощных систем выбирается интервал Δt=0,02 – 0,05 с. Наиболее точные результаты получаются, разумеется, при меньшем интервале, который должен выбираться тем меньше, чем меньше постоянная времени. При меньшем интервале погрешность расчёта на каждом интервале будет меньше, но при этом увеличится длительность расчёта.

В первом интервале начальная скорость равна нулю и при постоянном ускорении α0 (см. рис.5.2).

Изменение угла будет происходить по закону равномерно ускоренного движения.

Решение

граничные условия для определения С1

а) при t = 0 ∆ω = 0 С1 = 0

т.о.

граничные условия для определения С1

б) при t = 0 ∆δ = 0 С2 = 0

I интервал

Во втором интервале времени ротор генератора движется под действием избытка мощности ΔР1=Р0 – Pmax авsinδ1 и некоторой начальной скорости, приобретённой в первом интервале:

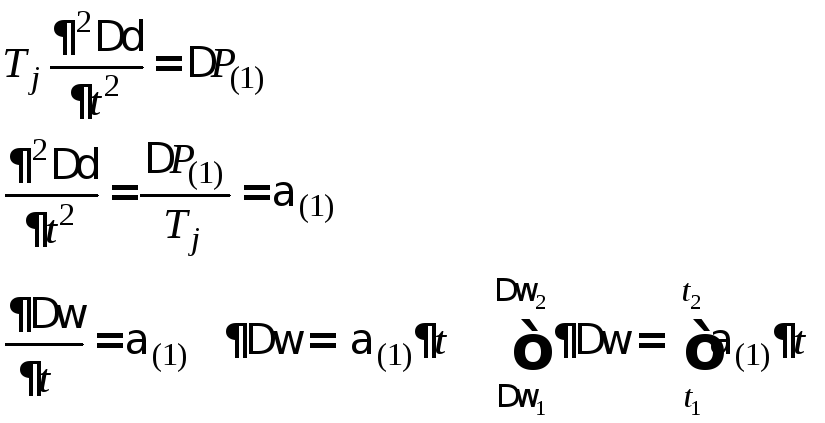
Решив уравнение (5.5) относительно приращения во втором интервале

времени, получим

После преобразования этого уравнения найдём

Для n-го интервала времени

Δδn=Δδ1+ kΔРn -1.

Если в i-м интервале времени происходит изменение режима с пере-

ходом из одной угловой характеристики мощности на другую, то прира-

щение угла определяется приращением

Δδ1=Δδi-1+0,5k(ΔР'i-1+ΔР''i-1).__

Упрощенные (приближенные) решения. Современные вычислительные средства (АВМ, ЦВМ) дают возможность численного интегрирования уравнений вида (2), однако для общего анализа процессов и многих практических инженерных решений важно уметь находить приближенное решение таких уравнений.

Трудность решения уравнения (2) обусловлена наличием синусоидальной функции угла δ. Поэтому простейшая возможность обеспечить интегрирование уравнения (2) — это заменить синусоиду отрезком прямой (рис. 8.3,а). Можно провести линию АВ через точку, соответствующую установившемуся (точка а) и начальному (точка А) режимам. Разность между приведенной мощностью первичного двигателя Р*’’ и электрической мощностью, равной sin δ, т. е. относительное ускорение ΔP* = P*’’—sin δ, представлена на рис. 8.3,а отрезком 1 2.

Заменяя участок синусоиды А2а соответствующим отрезком прямой ΔP* = (δ011— δ01)tgε и обозначая тангенс наклона аппроксимирующей прямой через

C = (P*II - P*I)/ (δ011— δ01)

вместо (2) будем иметь

∂2δ/∂τ2 = Cδ011—Cδ. (3)

Уравнение (3) легко интегрируется:

δ = δ011 - (δ011— δ01) cos Cτ, (4)

где τ =

Напомним, как интегрируется (3).

Его характеристическое уравнение p2δ—Cδ = 0 имеет корни

р1,2 = ±jC = ±jγ.

Решение полного уравнения имеет вид

Постоянные интегрирования A1 и A2находятся из начальных условий. При t = 0 начение δ = δ0 и, следовательно, δ'0 == δ"0 + А1 + А2; при t = 0 значение ∂δ/∂τ= 0, откуда

A1 = A2 = A = (δ01— δ011)/2;

δ = δ011 + (δ01— δ011)(ejγτ + e-jγτ)/2 = δ011 - Δδcos√CΔτ

Выражение (4) будет справедливо и при изменении наклона аппроксимирующей прямой, проходящей через точку а (например, кривая А' В' на рис. 8.3, а). Разумеется, результат приближенного расчета будет справедлив только в том интервале, где аппроксимирующая прямая достаточно близка к соответствующему отрезку синусоиды, а площадки ускорения и торможения не слишком отличаются от действительных (определенных при синусоидальной зависимости). Сопоставление характера точного решения и решения при замене синусоиды прямой дано на рис. 8.3,б. Для повышения точности расчетов применяются различные корректирующие приемы, вводятся поправочные коэффициенты и т. д. Здесь на этом останавливаться не будем.

Рассмотренный подход к приближенному интегрированию справедлив и в случае, когда характеристика аварийного режима РIIm < Ро или P*III > 1. Проводя при этом линеаризацию так, как это показано на рис. 8.4 будем иметь

δ = δ0III - (δ0III— δ0I)cos√Cτ (5)

Согласно (5) и соответственно рис. 8.4, можно определить предельное время отключения короткого замыкания. Полагая δ = δ ОТКЛ, находим

cos√Cτ = (δоткл— δ0III)/ (δ0I— δ0III)

или

Если принять

С = (sinδ0ТКЛ - sinδ0I)/(8откл- δ0I),

то время отключения

(6)

Уточненная аппроксимация синусоиды. Замена синусоиды прямой линией может привести к погрешностям в определении δ = f(t) и соответственно в определении времени отключения аварии. Можно повысить точность решения, заменяя синусоидальную характеристику зависимостью

Р = sinδ ≈ C0δ – bδ3 (7)

Варьируя коэффициенты Со и b, можно получить наилучшее совпадение кривой C0δ – bδ3 с тем или иным участком синусоиды. Минимальная квадратичная ошибка, обусловленная аппроксимацией при изменении δ от 0 до π, будет, если принять Со = 0,855, b = 0,094.

После подстановки (7) в (2) уравнение движения приобретает вид

где Р* = P0/Pm.

Такое уравнение может быть проинтегрировано.

Случай полного сброса мощности. рассматривалось. Случай движения ротора генератора под действием только механического момента турбины при Рт = 0, т. е. без отдачи генератором мощности в сеть имеет большое практическое значение, отвечая трехфазному короткому замыканию у шин генератора или отключению генератора от линии (х12 =оо). При этом прекращается связь генератора с нагрузкой и вся мощность турбины (Рмех = Ро) идет на ускорение ротора генератора. Это, следовательно, наиболее опасный случай в смысле разгона генератора и нарушения устойчивости.

Дифференциальное уравнение (1) при этом принимает вид

Tj∂2δ/∂t2 = Ро, (9)

Уравнение (9) интегрируется весьма просто. В самом деле, движение происходит при постоянном ускорении α, причем α = ∂ω/∂t = P0/Tj. Интеграл этого уравнения хорошо известен.

Рост скорости происходит линейно, а угла - по квадратичной параболе; время t, отвечающее какому-либо значению угла δ.

Если бы в начальный момент (t = 0) ротор имел некоторую скорость ∆ω = 0, то решение имело бы другой вид.

Влияние демпфирования и уменьшения момента турбины при полном сбросе мощности. Демпферные моменты, препятствующие движению, и уменьшение вращающего момента турбины с ростом скорости (уменьшение «естественное», вызванное трением, потерями на гистерезис, действием регуляторов скорости) изменяют характер движения.

Основное уравнение (1) при учете демпфирования имеет вид

Tj∂2δ/∂t2 + Рd∂δ/∂t = Ро, (10)

Решение (10) получаем в виде

(11)

Следовательно, скорость не возрастает непрерывно, а экспонен-циально стремится к некоторому установившемуся значению Р0/Кd = ωуст.

Литература: : [1], §10.6–10.11.

[7], § 8.3 – 8.8.

studfiles.net

Уравнение - движение - ротор

Cтраница 1

Уравнение движения ротора нелинейно и не может быть решено в общем виде. Исключением является полный сброс мощности в аварийном режиме, т.е. Рш пах 0, рассмотренный выше. Одним из них является метод последовательных интервалов, иллюстрирующий физическую картину протекания процесса. Для малого интервала At можно допустить, что избыток мощности в течение этого интервала остается неизменным. [2]

Уравнение движения ротора (1.49) остается при этом без изменения. [3]

Уравнение движения ротора составим так, чтобы использовать его в исследованиях устойчивости регулирования при изучении малых колебаний. [4]

Уравнение движения ротора может быть использовано при анализе вынужденных и свободных колебаний синхронных машин. [5]

Уравнение движения ротора для любой формы записи дифференциальных уравнений асинхронной машины остается без изменения. [6]

Уравнение движения ротора, совершающего колебания с большой амплитудой, не может быть линеаризировано и сведено к уравяению гармонического осциллятора, как это обычно делается при изучении качаний синхронных машин. [7]

Уравнение движения ротора двигателя в переходном режиме может быть получено следующим образом. [9]

Уравнение движения ротора асинхронного двигателя при этом всегда является дифференциальным уравнением первого порядка, ибо в силу полной ( электрической и магнитной) симметрии асинхронного двигателя угол 6 между магнитными осями фаз а статора и ротора в уравнения цепей его статора и ротора не входит. [10]

Исследование уравнения движения ротора приводит к весьма существенным для проектирования выводам. [11]

Решение уравнения движения ротора (2.26) при неизменном во времени расходе потока носит название статической характеристики расходомера. Участок статической характеристики, ограниченный диапазоном измерения расходомера, представляет собой градуировочную зависимость расходомера. Выражение для статической характеристики осевого турбинного преобразователя (2.42) получено ранее. Выясним теперь, каково влияние на статическую характеристику различных конструктивных параметров преобразователей с тем, чтобы найти оптимальные соотношения между размерами ротора. [12]

Решение уравнения движения ротора двигателя (10.16) позволяет судить об устойчивости двигателя. Если эта зависимость отражает затухающие колебания, то двигатель устойчив. [13]

При этом уравнение движения ротора в подлежащую решению систему уравнений машины не входит и служит лишь для проверки того, насколько постоянной остается угловая скорость ротора со на протяжении исследуемого промежутка времени. [14]

Чем отличаются уравнения движения ротора синхронной и асинхронной машины. [15]

Страницы: 1 2 3 4

www.ngpedia.ru

Основные уравнения асинхронного двигателя

⇐ ПредыдущаяСтр 11 из 17Следующая ⇒

Рассуждая аналогично пункту 4 составим основные уравнения асинхронного двигателя.

Напряжение U1, приложенное к фазе обмотки статора, уравновешивается основной ЭДС E1, ЭДС рассеяния и падением напряжения на активном сопротивлении обмотки статора.

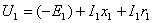
В роторной обмотке аналогичное уравнение будет иметь вид:

Но т.к. роторная обмотка замкнута, то напряжение U2=0, и если учесть еще, что E2s=SE2 и x2s=Sx2 , то уравнение можно переписать в виде:

Уравнение токов асинхронного двигателя повторяет аналогичное уравнение трансформатора:

где

Приведение параметров обмотки ротора к обмотке статора

Для того чтобы параметры ротора и статора изобразить на одной векторной диаграмме, произведем приведение параметров обмотки ротора к параметрам обмотки статора. При этом обмотку ротора с числом фаз m2, обмоточным коэффициентом k2 и числом витков W2 заменяют обмоткой с m1×k1×W1, соблюдая при этом энергетический баланс в роторе.

Не останавливаясь на методике приведения параметров, которая повторяется из раздела "трансформаторы", перепишем основные уравнения приведенного асинхронного двигателя:

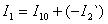
Векторная диаграмма асинхронного двигателя

Используя принципы построения векторной диаграммы для трансформатора, построим ее для асинхронного двигателя.

Вначале во втором основном уравнении величину r2' представим в виде:

что математически не противоречит друг другу.

Тогда само уравнение можно переписать:

Используя три основных уравнения двигателя, построим векторную диаграмму, которая, будет несколько напоминать диаграмму трансформатора (рис. 5.7.1).

Вторичное напряжение определяется вектором:

иначе говоря, асинхронный двигатель в электрическом отношении работает как трансформатор при активной нагрузке.

Мощность, отдаваемая вторичной обмоткой данного трансформатора

представляет собой полную механическую мощность, развиваемую двигателем.

Схема замещения асинхронного двигателя

Уравнениям ЭДС и токов соответствует эквивалентная схема замещения (рис. 5.8.1.). Таким образом, сложную магнитную цепь электрической машины можно заменить электрической схемой. Сопротивление r2'(1 - S)/S можно рассматривать как внешнее сопротивление, включенное в обмотку ротора. Оно является единственным переменным параметром схемы. Изменение этого сопротивления эквивалентно изменению нагрузки на валу двигателя, а следовательно, изменению скольжения S.

Потери и КПД асинхронного двигателя

В обмотку статора из сети поступает мощность P1. Часть этой мощности идет на потери в стали Pсl, а также потери в обмотке статора Рэ1:

Оставшаяся мощность посредством магнитного потока передается на ротор и называется электромагнитной мощностью:

Часть электромагнитной мощности затрачивается на покрытие электрических потерь в обмотке ротора:

Оставшаяся мощность преобразуется в механическую, получившую название полной механической мощности:

Р2'=Рэм-Рэ2

Воспользовавшись ранее полученной формулой

запишем выражение полной механической мощности:

тогда

или

Рэ2=SРэм,

т.е. мощность электрических потерь пропорциональна скольжению.

Мощность на валу двигателя P2 меньше полной механической мощности Р2’ на величину механических Рмех и добавочных Рдоб потерь:

Р2=Р2’-(Рмех.+Рдоб.).

Таким образом:

Р2=Р1-SP,

где

SP=Pсl+Рэ1+Рэ2+Рмех.+Рдоб.

Коэффициент полезного действия есть отношение мощности на валу P2 к потребляемой мощности P1:

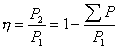
Уравнение вращающего момента

Вращающий момент в асинхронном двигателе создается взаимодействием тока ротора с магнитным полем машины. Вращающий момент математически можно выразить через электромагнитную мощность машины:

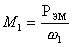где w1=2pn1/60 - угловая частота вращения поля.

В свою очередь, n1=f160/Р, тогда

Подставим в формулу M1 выражение Рэм=Рэ2/S и, разделив на 9,81, получим:

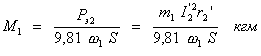Отсюда следует, что момент двигателя пропорционален электрическим потерям в роторе. Подставим в последнюю формулу значение тока I2’:

получим

где U1 - фазное напряжение обмотки статора.

Основные уравнения асинхронного двигателя

Поиск Лекций

Напряжение U1, приложенное к фазе обмотки статора, уравновешивается основной ЭДС E1, ЭДС рассеяния и падением напряжения на активном сопротивлении обмотки статора:

В роторной обмотке аналогичное уравнение будет иметь вид:

Но так как роторная обмотка замкнута, то напряжение U2=0, и если учесть еще, что E2s=SE2 и x2s=Sx2 , то уравнение можно переписать в виде:

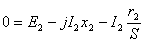Уравнение токов асинхронного двигателя повторяет аналогичное уравнение трансформатора:

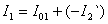где

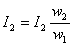
40. Чтобы векторы ЭДС, напряжений и токов обмоток статора и ротора можно было изобразить на одной векторной диаграмме, следует параметры обмотки ротора привести к обмотке статора, т. е. обмотку ротора с числом фаз m2, обмоточным коэффициентом ko62 и числом витков одной фазной обмоткиω2 заменить обмоткой с m1, ω1 и kоб1. При этом мощности и фазовые сдвиги векторов ЭДС и токов ротора после приведения должны остаться такими же, что и до приведения. Пересчет реальных параметров обмотки ротора на приведенные выполняется по формулам, аналогичным формулам приведения параметров вторичной обмотки трансформатора (см. § 1.6).

При s = 1 приведенная ЭДС ротора

E'2 = E2 ke, (12.17)

где ke = E1/ E2 =ko61 ω1 /(ko62/ ω2) - коэффициент трансформации напряжения в асинхронной машине при неподвижном роторе. Приведенный ток ротора

I′2 = I2/ ki, (12.18)

где ki = m1 ω1 koб1/ (m2 ω2 ko62) = m1 ke/ m2 - коэффициент трансформации тока асинхронной машины.

В отличие от трансформаторов в асинхронных двигателях коэффициенты трансформации напряжения и тока не равны ( kе ≠ ki ). Объясняется это тем, что число фаз в обмотках статора и ротора в общем случае не одинаково ( m1 ≠ m2 ). Лишь в двигателях с фазным ротором, у которых m1 = m2, эти коэффициенты равны.

Активное и индуктивное приведенные сопротивления обмотки ротора:

r′2 = r2 ke ki ;

x′2 = x2 ke ki. (12.19)

Следует обратить внимание на некоторую специфику определения числа фаз m2 и числа витков ω2 для короткозамкнутой обмотки ротора (см. рис. 10.3). Каждый стержень этой обмотки рассматривают как одну фазу, а поэтому число витков одной фазы короткозамкнутой обмотки ротора ω2 = ,0,5; обмоточный коэффициент такой обмотки kоб2 = 1, а число фаз m2 = Z2, т. е. равно числу стержней в короткозамкнутой обмотке ротора.

41. В обмотку статора из сети поступает мощность P1. Часть этой мощности идет на потери в стали Pсl, а также потери в обмотке статора Рэ1:

Часть электромагнитной мощности затрачивается на покрытие электрических потерь в обмотке ротора:

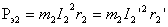
Оставшаяся мощность преобразуется в механическую, получившую название полной механической мощности:

Р2'=Рэм-Рэ2

Воспользовавшись ранее полученной формулой

запишем выражение полной механической мощности:

тогда

или

Рэ2=SРэм,

т.е. мощность электрических потерь пропорциональна скольжению.

Р2=Р2’-(Рмех.+Рдоб.).

Таким образом:

Р2=Р1-SP,

где

SP=Pсl+Рэ1+Рэ2+Рмех.+Рдоб.

Коэффициент полезного действия есть отношение мощности на валу P2 к потребляемой мощности P1:

42. Электромагнитный момент асинхронной машины создается в результате взаимодействия тока в обмотке ротора с вращающимся магнитным полем. Связь между моментом и скоростью вращения ротора можно получить из уравнения механической мощности. Если в него подставить выражение для тока ротора, то с учетом того, что угловая частота вращения равна ,получим

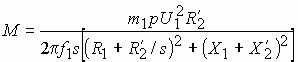
Все величины, входящие в это выражение константы, кроме скольжения s. Взяв производную и приравнивая ее нулю, найдем экстремумы функции . Они наступают при критическом скольжении . К приближенному равенству для критического скольжения можно перейти с учетом того, что . Подставляя критическое скольжение в выражение , получим значение максимального момента

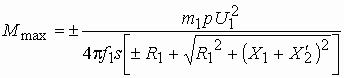. Знак плюс в этих выражениях соответствует двигательному режиму, а минус – генераторному.

Из выражения для 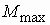следует, что максимальный момент в генераторном режиме больше, чем в двигательном. Однако, пренебрегая также, как это было сделано для 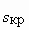, мы получим упрощенное выражение для максимального момента более удобное для качественного анализа –

Полагая в выражении , получим выражение для пускового момента асинхронного двигателя

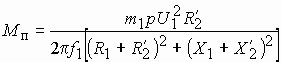
Полученная зависимость представлена на рисунке. Точка 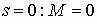соответствует идеальному холостому ходу машины. Этот режим может быть получен только за счет внешнего вращающего момента.Точка 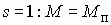соответствует пусковому режиму или режиму короткого замыкания. Устойчивая работа машины возможна только в пределах скольжений от до 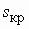, т.к. вне этого участка при увеличении скольжения момент двигателя уменьшается, что приводит к дальнейшему увеличению скольжения (снижению скорости) и этот процесс будет развиваться до полной остановки двигателя. Переход на участок неустойчивой работы называется "опрокидыванием" двигателя. Это происходит, если момент нагрузки больше или равен максимальному, поэтому максимальный момент называют также опрокидывающим.

Номинальный режим работы двигателя соответствует скольжению . Отношение называется перегрузочной способностью. Превышение максимального момента над номинальным является необходимым условием надежной работы двигателя.

Если за счет внешнего вращающего момента вал двигателя раскручивается до скорости выше синхронной , то скольжение становится отрицательным и машина переходит в генераторный режим.

При скольжениях скорость вращения будет отрицательной, т.е. ротор двигателя будет вращаться в направлении противоположном направлению вращения магнитного поля и машина перейдет в тормозной режим или режим противовключения.

На рисунке для наглядности критическое скольжение составляет около 0,5. Такие значения в реальных машинах нормального исполнения не бывают. Они находятся в пределах от 0,1 до 0,02, причем меньшие значения соответствуют машинам большей мощности. Поэтому рабочий участок характеристики практически линейный и может быть заменен прямой .

Выражение не позволяет анализировать свойства характеристики в общем виде. Однако, если его разделить на 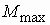, то получится удобное выражение в относительных единицах, называемое по имени автора формулой Клосса

В теории электрических машин и электропривода вместо характеристики принято пользоваться механической характеристикой. Механическая характеристика двигателя это зависимость скорости вращения от момента нагрузки на валу, т.е. . Эту характеристику легко можно получить из характеристики , если учесть, что , т.е. она получается смещением оси момента в точку и изменением масштаба оси скольжений. При этом в новой системе координат режимы работы машины (генераторный, двигательный и тормозной) оказываются в различных квадрантах плоскости 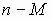, а режимы холостого хода и короткого замыкания – в точках пересечения механической характеристики с осями координат.

Линеаризованная механическая характеристика рабочего участка примет вид

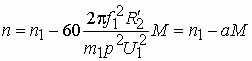
43. Рабочие характеристики асинхронного двигателя представляют собой графически выраженные зависимости частоты вращения n2, КПД η, полезного момента (момента на валу) М2, коэффициента мощности cos φ, и тока статора I1 от полезной мощности Р2 при U1 = const f1 = const.

Скоростная характеристика n2 = f(P2). Частота вращения ротора асинхронного двигателя n2 = n1(1 - s).

Скольжение s = Pэ2/Pэм, т. е. скольжение асинхронного двигателя, а следовательно, и его частота вращения определяются отношением электрических потерь в роторе к электромагнитной мощности. Пренебрегая электрическими потерями в роторе в режиме холостого хода, можно принять Рэ2 = 0, а поэтому s ≈ 0 и n20 ≈ n1.

По мере увеличения нагрузки на валу асинхронного двигателя отношение s = Pэ2/Pэм растет, достигая значений 0,01 - 0,08 при номинальной нагрузке. В соответствии с этим зависимость n2 = f(P2) представляет собой кривую, слабо наклоненную к оси абсцисс. Однако при увеличении активного сопротивления ротора двигателя r2' угол наклона этой кривой увеличивается. В этом случае изменения частоты асинхронного двигателя n2 при колебаниях нагрузки Р2 возрастают. Объясняется это тем, что с увеличением r2' возрастают электрические потери в роторе.

Рис. 1. Рабочие характеристики асинхронного двигателя двигателя

Зависимость М2 =f(P2). Зависимость полезного момента на валу асинхронного двигателя М2 от полезной мощности Р2 определяется выражением M2 = Р2/ ω2 = 60 P2/ (2πn2) = 9,55Р2/ n2,

где Р2 — полезная мощность, Вт; ω2 = 2πf 2/ 60 — угловая частота вращения ротора.

Из этого выражения следует, что если n2 = const, то график М2 =f2(Р2) представляет собой прямую линию. Но в асинхронном двигателе с увеличением нагрузки Р2 частота вращения ротора уменьшается, а поэтому полезный момент на валу М2 с увеличением нагрузки возрастает не сколько быстрее нагрузки, а следовательно, график М2 =f (P2) имеет криволинейный вид.

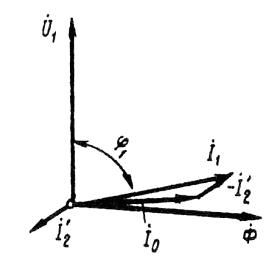
Рис. 2. Векторная диаграмма асинхронного двигателя при небольшой нагрузке

Зависимость cos φ1 = f (P2). В связи с тем что ток статора асинхронного двигателя I1 имеет реактивную (индуктивную) составляющую, необходимую для создания магнитного поля в статоре, коэффициент мощности асинхронных двигателей меньше единицы. Наименьшее значение коэффициента мощности соответствует режиму холостого хода.Объясняется это тем, что ток холостого хода электродвигателя I0 при любой нагрузке остается практически неизменным. Поэтому при малых нагрузках двигателя ток статора невелик и в значительной части является реактивным (I1 ≈ I0). В результате сдвиг по фазе тока статора относительно напряжения получается значительным (φ1 ≈ φ0), лишь немногим меньше 90° (рис. 2).

44. Пусковые свойства асинхронного двигателя зависят от особенностей его конструкции, в частности от устройства ротора.

Пуск асинхронного двигателя сопровождается переходным процессом машины, связанным с переходом ротора из состояния покоя в состояние равномерного вращения, при котором момент двигателя уравновешивает момент сил сопротивления на валу машины.

При пуске асинхронного двигателя имеет место повышенное потребление электрической энергии из питающей сети, затрачиваемое не только на преодоление приложенного к валу тормозного момента и покрытие потерь в самой асинхронном двигателе, но и на сообщение движущимся звеньям производственного агрегата определенной кинетической энергии. Поэтому при пуске асинхронный двигатель должен развить повышенный вращающий момент.

Для асинхронного двигателя с фазным ротором начальный пусковой момент, соответствующий скольжению sп= 1, зависит от активных сопротивлений регулируемых резисторов, введенных в цепь ротора.

Рис. 1. Пуск трехфазного асинхронного двигателя с фазным ротором: а — графики зависимости вращающего момента двигателя с фазным ротором от скольжения при различных активных сопротивлениях резисторов в цепи ротора, б — схема включения резисторов и замыкающих контактов ускорения в цепь ротора.

Так, при замкнутых контактах ускорения У1, У2, т. е. при пуске асинхронного двигателя с замкнутыми накоротко контактными кольцами, начальный пусковой момент Мп1 = (0,5 -1,0) Мном, а начальный пусковой ток Iп = (4,5 - 7) Iном и более.

Малый начальный пусковой момент асинхронного электродвигателя с фазным ротором может оказаться недостаточным для приведения в действие производственного агрегата и последующего его ускорения, а значительный пусковой ток вызовет повышенный нагрев обмоток двигателя, что ограничивает частоту его включений, а в маломощных сетях приводит к нежелательному для работы других приемников временному понижению напряжения. Эти обстоятельства могут явиться причиной, исключающей использование асинхронных двигателей с фазным ротором с большим пусковым током для привода рабочих механизмов.

45. Для пуска асинхронного двигателя с короткозамкнутым ротором применяются следующие способы:

· прямой включение,

· пуск при пониженном напряжении питания.

40.2.1. Прямое включение

Прямое включениеасинхронного двигателя в сеть является наиболее простым способом пуска двигателя. В то же время в этом случае обмотки статора и ротора двигателя обтекаются большим пусковым током (током КЗ), равным 4—7-кратному значению номинального. Поэтому очень важно, чтобы время пуска двигателя было при этом как можно меньшим. Такой метод пуска применяется для небольших двигателей, или для двигателей, приводящих во вращение небольшие механические нагрузки.

40.2.2. Пуск при пониженном, напряжении

Пуск при пониженном напряжении питания осуществляется обычно в тех случаях, когда прямой пуск не допускается по условиям работы сети.

Обычно применяют один из четырех способов пуска при пониженном напряжении:

двигателя через понижающий автотрансформатор;
переключение обмотки статора со звезды на треугольник;
включение двигателя через полупроводниковый регулятор напряжения.

Во всех этих случаях снижение напряжения ведет не только к пропорциональному уменьшению пускового тока (положительный эффект), но и к резкому (квадратичному) уменьшению пускового момента (отрицательный эффект).

а) Пуск асинхронного двигателя через автотрасформатор

На рис.40.1. показана схема пуска асинхронного двигателя через автотрансформатор.

Рис.40.1. Пуск асинхронного двигателя с помощью автотрансформатора

Уменьшения напряжения при пуске можно достигать включением между сетью и двигателем понижающего автотрансформатора Т(рис. 40.1). При пуске сначала замыкают рубильник QS1,и пониженное напряжение попадает на обмотки двигателя. По достижении ротором достаточной частоты вращения замыкают рубильник OS2,шунтируя автотрансформатор так, что полное напряжение сети попадает на обмотки двигателя.

б) Пуск с переключением обмоток статора со звезды на треугольник

К способам пуска с понижением напряжения можно отнести также пуск с переключением обмоток статора со звезды на треугольник (рис. 40.2).

Рис.40.2. Схема пуска двигателя с переключением обмоток со звезды на треугольник

В режиме пуска переключатель QSнаходится в положении , причем обмотка статора включена по схеме звезды. После того как ротор достигнет установившейся частоты вращения, переключатель необходимо перевести в положение и обмотки статора будут включены по схеме треугольника.

При данном способе пуска фактически снижается напряжение, подводимое к каждой фазе двигателя, поскольку при одинаковом напряжении сети фазное напряжение в схеме звезды в 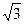раз меньше, чем в схеме треугольника. Пусковой ток в сети при соединении обмотки статора и звезду снижается в 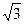раза по сравнению с пусковым током при соединении в треугольник. Однако пусковой момент, пропорциональный квадрату напряжения, снижается в 3 раза.

46. Частота вращения асинхронного двигателя

n = n1 (1 – s) = (60f1/p) (1-s) (85)

Из этого выражения видно, что ее можно регулировать, изменяя частоту f1 питающего напряжения, число пар полюсов р и

Рис. 266. Схема переключения катушек обмотки статора (одной фазы) для изменения числа полюсов: а — при четырех полюсах; б — при двух полюсах

скольжение s. Последнее при заданных значениях момента на валу Мвн и частоты f1 можно изменять путем включения в цепь обмотки ротора реостата.

Регулирование путем изменения частоты питающего напряжения.Этот способ требует наличия преобразователя частоты, к которому должен быть подключен асинхронный двигатель. На основе управляемых полупроводниковых вентилей (тиристоров) созданы статические преобразователи частоты и построен ряд опытных электровозов и тепловозов с асинхронными двигателями, частота вращения которых регулируется путем изменения частоты питающего напряжения. Такой способ регулирования частоты вращения ротора асинхронного двигателя является весьма перспективным.

Регулирование путем изменения числа пар полюсов. Этот способ позволяет получить ступенчатое изменение частоты вращения. Для этой цели отдельные катушки 1, 2 и 3, 4, составляющие одну фазу (рис. 266), переключаются так, чтобы изменялось соответствующим образом направление тока в них (например, с последовательного согласного соединения на встречное). При согласном включении катушек (рис. 266, а) число полюсов равно четырем, при встречном включении (рис. 266, б) — двум. Катушки двух других фаз, сдвинутые в пространстве на 120°, соединяются таким же образом. Такое же уменьшение числа полюсов можно осуществить при переключении катушек с последовательного на параллельное соединение. При изменении числа полюсов изменяется частота вращения n1магнитного поля двигателя, а следовательно, и частота вращения n его ротора. Если нужно иметь три или четыре частоты вращения n1, то на статоре располагают еще одну обмотку, при переключении которой можно получить еще две частоты. Существуют двигатели, которые обеспечивают изменение частоты вращения n1 при постоянном наибольшем моменте или при приблизительно постоянной мощности (рис. 267).

В асинхронном двигателе число полюсов ротора должно быть равно числу полюсов статора. В короткозамкнутом роторе это условие выполняется автоматически и при переключении обмотки статора никаких изменений в обмотке ротора выполнять не требуется.

Рис. 267. Механические характеристики двухскоростных асинхронных двигателей с постоянным наибольшим моментом (а) и постоянной мощностью (б)

Рис. 268. Механические характеристики асинхронного двигателя при регулировании частоты вращения путем включения реостата в цепь обмотки ротора

Рис. 269. Схемы подключения асинхронного двигателя к сети при изменении направления его вращения

В двигателе же с фазным ротором в этом случае надо было бы изменять число полюсов обмотки ротора, что сильно усложнило бы его конструкцию, поэтому такой способ регулирования частоты вращения используется только в двигателях с коротко-замкнутым ротором. Такие двигатели имеют большие габаритные размеры и массу по сравнению с двигателями общего применения, а следовательно, и большую стоимость. Кроме того, регулирование осуществляется большими ступенями; при частоте f1 = 50 Гц частота вращения поля n1 при переключениях изменяется в отношении 3000:1500:1000:750.

Регулирование путем включения в цепь ротора реостата. При включении в цепь обмотки ротора реостата с различным сопротивлением (Rп4, RпЗ, Rп2 и т. д.) получаем ряд реостатных механических характеристик 4, 3 и 2 двигателя. При этом некоторому нагрузочному моменту Мном (рис. 268) будут соответствовать меньшие частоты вращения n4, n3, n2 и т. д., чем частота nе при работе двигателя на естественной характеристике 1 (при Rп = 0). Это способ регулирования может быть использован только для двигателей с фазным ротором. Он позволяет плавно изменять частоту вращения в широких пределах. Недостатками его являются большие потери энергии в регулировочном реостате, поэтому его используют только при кратковременных режимах работы двигателя (при пуске и пр.).

47. Конденсаторные двигатели — разновидность асинхронных двигателей, в обмотки которого включены конденсаторы для создания сдвига фазы тока.[1] Подключаются в однофазную сеть посредством специальных схем. По количеству фаз статора делятся на двухфазные и трехфазные.

Существует разные схемы подключения, больше вариантов для трёхфазных двигателей, различающиеся способом соединения обмоток двигателя и составом дополнительных элементов, но минимальная работоспособная схема содержит один конденсатор, от чего и происходит название.

Как правило, одна из обмоток («фаза двигателя») запитывается напрямую от однофазной сети, а другие обмотки запитывается через электрический конденсатор, который сдвигает фазу подводимого тока почти на +90°, или через катушку индуктивности, которая сдвигает фазу почти на −90°. Чтобы результирующее вращающееся магнитное поле не было эллиптическим, последовательно с конденсатором включается переменный проволочный резистор, с помощью которого добиваются кругового вращающегося магнитного поля.

Однофа́зный дви́гатель — электродвигатель, конструктивно предназначенный для подключения к однофазной сети переменного тока. Фактически является двухфазным, но вследствие того, что рабочей является только одна обмотка, двигатель называют однофазным.

48. Большинство синхронных машин имеет электромагнитное возбуждение. Источниками постоянного тока для обмоток возбуждения являются специальные системы возбуждения, к которым предъявляется ряд важных требований:

1) надежное и устойчивое регулирование тока возбуждения в любых режимах работы машины;

2) достаточное быстродействие, для чего применяется форсировка возбуждения, т. е. быстрое увеличение напряжения возбуждения до предельного значения, называемого потолочным. Форсировка возбуждения применяется для поддержания устойчивой работы машины во время аварий и в процессе ликвидации их последствий. Потолочное напряжение возбуждения выбирают не менее 1,8-2 номинального напряжения возбуждения. Скорость нарастания напряжения при форсировке возбуждения должна быть не менее 1,5-2 номинальных напряжений на контактных кольцах ротора в секунду;

3) быстрое гашение магнитного поля, т. е. уменьшение тока возбуждения машины до нуля без значительного повышения напряжения на ее обхмотках. Необходимость в гашении поля возникает при отключении генератора или повреждении в нем.

Для возбуждения синхронных машин применяется несколько систем. Простейшей из них является электромашинная система возбуждения с возбудителем постоянного тока (рис. 15). В этой системе в качестве источника используют специальный генератор постоянного тока GE, называемый возбудителем; он приводится во вращение от вала синхронного генератора, а его мощность составляет 1- 3 % мощности синхронного генератора. Ток возбуждения синхронной машины Iв относительно велик и составляет несколько сотен и даже тысяч ампер. Поэтому его регулируют с помощью реостатов, установленных в цепи возбуждения возбудителя. Возбуждение возбудителя осуществляют по схеме самовозбуждения (рис. 15) или независимого возбуждения от специального генератора постоянного тока GEA, называемого подвозбудителем (рис. 16). Подвозбудитель работает с самовозбуждением, и сопротивление резистора Rш2при работе генератора не изменяется.

49. Метод асинхронного пуска. Синхронный двигатель не имеет начального пускового момента. Если его подключить к сети переменного тока, когда ротор неподвижен, а по обмотке возбуждения проходит постоянный ток, то за один период изменения тока, электромагнитный момент будет дважды изменять свое направление, т. е. средний момент за период равняется нулю. При этих условиях двигатель не сможет прийти во вращение, так как его ротор, обладающий определенной инерцией, не может быть в течение одного полупериода разогнан до синхронной частоты вращения. Следовательно, для пуска синхронного двигателя необходимо разогнать его ротор с помощью внешнего момента до частоты вращения, близкой к синхронной.

В настоящее время для этой цели применяют метод асинхронного пуска. При этом методе синхронный двигатель пускают как асинхронный, для чего его снабжают специальной коротко-замкнутой пусковой обмоткой, выполненной по типу «беличья клетка». Чтобы увеличить сопротивление стержней, клетку изготовляют из латуни. При включении трехфазной обмотки статора в сеть образуется вращающееся магнитное поле, которое, взаимодействуя с током Iпв пусковой обмотке (рис. 6.48, а), создает электромагнитные силы F и увлекает за собой ротор. После разгона ротора до частоты вращения, близкой к синхронной, постоянный ток, проходящий по обмотке возбуждения, создает синхронизирующий момент, который втягивает ротор в синхронизм.

Применяют две основные схемы пуска синхронного двигателя. При схеме, изображенной на рис. 6.48, б,обмотку возбуждения сначала замыкают на гасящий резистор, сопротивление которого Rдоб превышает в 8 — 12 раз активное сопротивление Rв обмотки возбуждения. После разгона ротора до частоты вращения, близкой к синхронной (при s ≈ 0,05), обмотку возбуждения отключают от гасящего резистора и подключают к источнику постоянного тока (возбудителю), вследствие чего ротор втягивается в синхронизм. Осуществить пуск двигателя с разомкнутой обмоткой возбуждения нельзя, так как во время разгона ротора при s > 0 в ней вращающимся магнитным полем индуцируется ЭДС Ев = 4,44f2wвФm = 4,4f1swвФm , где f2 = f1s — частота изменения тока в обмотке возбуждения; wв — число витков обмотки возбуждения; Фm — амплитуда магнитного потока вращающегося поля.

В начальный момент пуска при s = 1 из-за большого числа витков обмотки возбуждения ЭДС Ев может достигать весьма большого значения и вызвать пробой изоляции. При схеме, изображенной на рис. 6.48, в, обмотка возбуждения постоянно подключена к возбудителю, сопротивление которого по сравнению с сопротивлением Rв весьма мало, поэтому эту обмотку в режиме асинхронного пуска можно считать замкнутой накоротко. С уменьшением скольжения до

s = 0,3 ÷ 0,4 возбудитель возбуждается и в обмотку возбуждения подается постоянный ток, обеспечивающий при s ≈ 0,05 втягивание ротора в синхронизм. Различие пусковых схем обусловлено тем, что не во всех случаях может быть применена более простая схема с постоянно подключенной к возбудителю обмоткой возбуждения (рис. 6.48, в), так как она имеет худшие пусковые характеристики, чем более сложная схема, приведенная на рис. 6.48,б. Главной причиной ухудшения пусковых характеристик является возникновение одноосного эффекта — влияние тока, индуцируемого в обмотке возбуждения при пуске, на характеристику пускового момента.

50. Под реакцией якоря в синхронных машинах понимают воздействие магнитного поля статора (якоря) на магнитное поле ротора. Реакция якоря оказывает сильное влияние на все электромагнитные процессы в машине. Явление реакции по определению связано с магнитным полем статора, поэтому характер и степень влияния реакции определяется током статора, т.е. нагрузкой машины.

Рассмотрим этот процесс на примере синхронного генератора. Изобразим вращающееся магнитное поле ротора вектором . При вращении оно пересекает неподвижные проводники обмоток статора и наводит в них ЭДС , отстающую от потока на 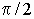. Ток статора 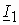создает магнитный поток статора , совпадающий с ним по направлению. В зависимости от характера нагрузки ток статора может иметь фазовый сдвиг по отношению к ЭДС в пределах .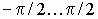

При чисто активной нагрузке (R) ток 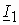и магнитный поток статора совпадают по фазе с и результирующий магнитный поток машины оказывается смещенным относительно потока ротора на некоторый угол в сторону запаздывания. В результате смещения потока магнитное поле ослабляется под набегающими краями полюсов ротора и усиливается под сбегающими. Несмотря на то, что в результате смещения сбегающие края полюсов подмагничиваются, результирующее поле машины ослабляется, т.к. из-за насыщения полюсов в зоне подмагничивания оно проявляется слабее, чем размагничивание на набегающих краях. В целом при активной нагрузке магнитное поле ослабляется и деформируется.

При чисто индуктивной нагрузке (L) ток статора и магнитный поток отстают от ЭДС на 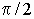. Поток статора оказывается направленным встречно по отношению к потоку ротора и сильно размагничивает машину. Однако, в отличие от активной нагрузки, искажения поля за счет смещения потока не происходит.

При чисто емкостной нагрузке (C) ток статора и магнитный поток опережают ЭДС на 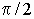и поле в машине усиливается потоком реакции, направленным согласно с потоком ротора. Искажения поля в этом случае также не происходит, а усиление поля вследствие насыщения оказывается выраженным слабо.

В случае активно-реактивной нагрузки (RL и RC) поток статора оказывается смещенным на угол меньший, чем 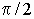, в сторону запаздывания или опережения. В этом случае магнитный поток статора , можно разложить на продольную 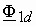и поперечную 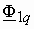составляющие. Продольная составляющая будет оказывать при RL нагрузке размагничивающее действие, а при RC нагрузке – подмагничивающее. Поперечная составляющая будет вызывать деформацию поля, аналогичную деформации при активной нагрузке.

Таким образом реакция якоря в синхронной машине изменяет величину и направление магнитного потока, в отличие от асинхронной машины, у которой . Негативное влияние реакции якоря в синхронных машинах снижают увеличением рабочего зазора.

Магнитный поток вызывает искажение магнитного поля ротора, которое проявляется в статоре в виде ЭДС . Так как поток линейно связан с током статора 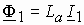, то эту ЭДС можно представить в комплексной форме через некое индуктивное сопротивление в виде .