





Рассмотрим асинхронный двигатель, подключенный к узловой точке системы.
Характеристика мощности для таких асинхронных двигателей представлена на рис. 2.30.
Рис. 2.30. Характеристика мощности асинхронного двигателя
В этом случае для асинхронных двигателей статическая устойчивость проверяется по скольжению и из соотношения механической мощности, которая присоединена к валу ротора двигателя и имеет тормозящий характер, и электрической мощности – той, которая подводится к двигателю. Исходя из этого, практический критерий статической устойчивости асинхронных двигателей имеет вид (на возрастающей части характеристики). В отличие от генератора расчетным возмущением для асинхронных двигателей будет являться изменение скольжения на величинуs. При этом электрическая мощность, подводимая к асинхронному двигателю, будет ускорять вращение ротора двигателя и тем самым уменьшать скольжение. Механическая мощность рабочих агрегатов, приводимых во вращение асинхронным двигателем, носит тормозящий характер. При преобладании этой мощности будет происходить увеличение скольжения асинхронного двигателя.
Под действием случайных факторов баланс мощности может нарушаться. Кроме отклонения нагрузки, которая вызывает изменение баланса мощности, могут быть и другие причины его нарушения:
1. Отключения генераторов, трансформаторов или ЛЭП, которые приводят к малым возмущениям режима в электроэнергетической системе. Такие изменения при нахождении режима вблизи границы области статической устойчивости могут вызвать нарушение режима. Это является первой причиной обеспечения необходимого запаса статической устойчивости.
2. Некоторая неопределенность самой границы области статической устойчивости, которая объясняется тем, что нет возможности учесть влияние на эту границу устойчивости всех параметров ЭЭС.
3. Неизбежны погрешности самих расчетов, которые обусловлены упрощением схемы, применением упрощенных математических моделей элементов ЭЭС, приближенного задания параметров элементов ЭЭС и т. д.
По указанным причинам допустимые режимы работы ЭЭС должны задаваться с некоторым запасом по отношению к рассчитываемому режиму. И геометрически запас статической устойчивости для ЭЭС будет характеризоваться удаленностью отображающей точки от границы устойчивости.
При этом возникает вопрос определения количественных показателей запаса статической устойчивости. Такими общепринятыми показателями в настоящее время являются:
а) для ЭЭС – коэффициент запаса статической устойчивости по активной мощности – КР;
б) для оценки запаса статической устойчивости узла нагрузки используется коэффициент запаса по напряжению KU.
Для определения коэффициента запаса по активной мощности рассчитываемый переток мощности исходного режима Р0 сравнивается с рассчитываемым перетоком в предельном по статической устойчивости режиме Рпр (рис. 2.31)
%.
Причины, требующие введения запаса по напряжению, те же самые, что и при введении запаса статической устойчивости по активной мощности:
– возможность самопроизвольного утяжеления режима;
– наличие множества трудно учитываемых в расчетах факторов, влияющих на границу устойчивости;
– неизбежность погрешности самих расчетов.
Рис. 2.31. Графическая иллюстрация определения коэффициента
запаса статической устойчивости
Для определения запаса статической устойчивости по напряжению для узла нагрузки напряжение U0 в исходном режиме заданного узла сравнивается с критическим напряжением Uкр в этом же узле нагрузки. Тогда
% ,
.
Значение Uкр определяется свойствами нагрузки, главным образом двигательной нагрузки, а также протяженностью ЛЭП, входящей в узел нагрузки.
Выбор обеспечения запасов статической устойчивости представляет собой сложную технико-экономическую задачу. Увеличение запаса статической устойчивости позволяет снизить количество нарушений устойчивости и связанных с ними аварий в энергосистеме. В то же время увеличение запаса статической устойчивости ведет к недоиспользованию пропускной способности ЛЭП, эксплуатируемых в ЭЭС, и как следствие, увеличению затрат на строительство новых ЛЭП.
В соответствии с ПУЭ и ПТЭ в нормальном установившемся режиме работы коэффициент запаса должен быть KP ≥ 20 %, коэффициент по напряжению KU ≥ 15 %.
В кратковременных послеаварийных установившихся режимах коэффициент запаса может быть снижен, но при этом должен быть не меньше дляKP≥ 8 % и KU≥ 10 %.
Под кратковременным послеаварийным установившимся режимом понимается режим, который устанавливается в энергосистеме после возмущения и переходного процесса и существует в течение времени, необходимого диспетчеру для восстановления нормальной схемы ЭЭС; обычно время существования послеаварийного установившегося режима составляет не более 40 мин.
studfiles.net
Под устойчивостью работы электродвигателя понимают способность двигателя восстанавливать установившуюся частоту вращения при кратковременных возмущениях (изменениях нагрузки, напряжения питающей сети и т. д.).
Электромагнитный момент двигателя М, который является вращающим, уравновешивает тормозящие моменты: момент 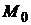 , соответствующий потерям холостого хода (
, соответствующий потерям холостого хода ( 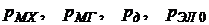 ), покрываемым за счет механической мощности;
), покрываемым за счет механической мощности; 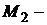 момент нагрузки на валу, создаваемый рабочей машиной или механизмом;
момент нагрузки на валу, создаваемый рабочей машиной или механизмом; 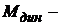 динамический момент, зависящий от момента инерции вращающихся масс
динамический момент, зависящий от момента инерции вращающихся масс 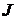 и ускорения ротора
и ускорения ротора 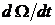 ;
;
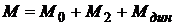 .
.
Обозначив статический момент сопротивления 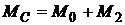 , получим
, получим
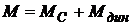 .
.
При 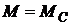 ускорение ротора
ускорение ротора
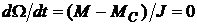 ,
,
т. е. ротор вращается с установившейся частотой. Если 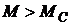 , ротор ускоряется, а при
, ротор ускоряется, а при 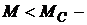 замедляется.
замедляется.
Устойчивость зависит от конкретных условий, при которых работает электродвигатель, в частности от формы механических характеристик двигателя и приводимого им во вращение производственного механизма.
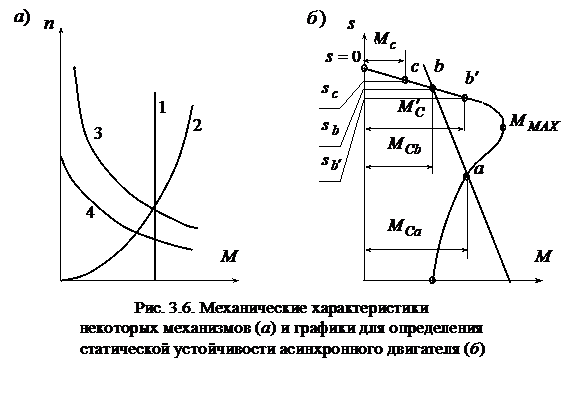 Типичные механические характеристики производственных механизмов приведены на рис. 3.6, а. Независимость статического момента от частоты вращения (
Типичные механические характеристики производственных механизмов приведены на рис. 3.6, а. Независимость статического момента от частоты вращения ( 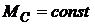 , кривая 1) характеризует грузоподъемные механизмы (лифты, краны, лебедки и т. д.). У вентиляторов, центробежных насосов, гребных винтов нагрузочный момент пропорционален (кривая 2) второй степени частоты вращения (
, кривая 1) характеризует грузоподъемные механизмы (лифты, краны, лебедки и т. д.). У вентиляторов, центробежных насосов, гребных винтов нагрузочный момент пропорционален (кривая 2) второй степени частоты вращения ( 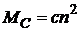 ). Эту характеристику называют вентиляторной. Тяговый электропривод, как правило, имеет характеристику, соответствующую уравнению
). Эту характеристику называют вентиляторной. Тяговый электропривод, как правило, имеет характеристику, соответствующую уравнению 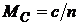 (кривая 3). Большое трение в состоянии покоя и при малых частотах вращения характерно для бетономешалок и шаровых мельниц. В таких механизмах при увеличении частоты вращения нагрузочный момент падает (кривая 4).
(кривая 3). Большое трение в состоянии покоя и при малых частотах вращения характерно для бетономешалок и шаровых мельниц. В таких механизмах при увеличении частоты вращения нагрузочный момент падает (кривая 4).
Условия устойчивой работы рассмотрим на примере работы двигателя совместно с механизмом, у которого нагрузочный момент 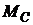 падает при увеличении частоты вращения (рис. 3.6, б). Пусть двигатель работает в точке
падает при увеличении частоты вращения (рис. 3.6, б). Пусть двигатель работает в точке 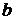 и развивает момент
и развивает момент 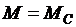 при
при 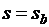 . Если со стороны механизма момент увеличится до
. Если со стороны механизма момент увеличится до 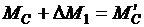 , то частота вращения двигателя несколько замедлится, а скольжение увеличится до
, то частота вращения двигателя несколько замедлится, а скольжение увеличится до 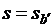 . При этом возрастут ЭДС
. При этом возрастут ЭДС 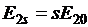 , ток в роторе
, ток в роторе 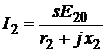 и электромагнитный момент до значения
и электромагнитный момент до значения 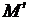 . Двигатель войдет в новое равновесное состояние, работая с повышенным моментом и скольжением (точка
. Двигатель войдет в новое равновесное состояние, работая с повышенным моментом и скольжением (точка 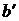 ).
).
При уменьшении статического момента до значения, соответствующего точке с, под действием положительного динамического момента 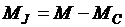 , частота вращения увеличится, уменьшится скольжение и ЭДС, а следовательно, ток ротора и электромагнитный момент до значения
, частота вращения увеличится, уменьшится скольжение и ЭДС, а следовательно, ток ротора и электромагнитный момент до значения 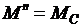 .
.
Изменение момента на валу двигателя, работающего в режиме, соответствующему точке а (рис. 3.6, б) неизбежно приведет к остановке двигателя (если момент 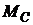 увеличить) или значительному увеличению частоты вращения и уменьшению скольжения до
увеличить) или значительному увеличению частоты вращения и уменьшению скольжения до 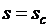 (если момент нагрузки уменьшить).
(если момент нагрузки уменьшить).
Таким образом, асинхронный двигатель при работе на части 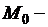
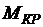 механической характеристики обладает свойством внутреннего саморегулирования, благодаря которому его вращающий момент автоматически регулируется по закону
механической характеристики обладает свойством внутреннего саморегулирования, благодаря которому его вращающий момент автоматически регулируется по закону 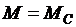 . Это регулирование осуществляется за счет увеличения или уменьшения частоты вращения ротора
. Это регулирование осуществляется за счет увеличения или уменьшения частоты вращения ротора 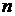 , т. е. система регулирования является статической.
, т. е. система регулирования является статической.
Сравнивая условия работы двигателя в точках а и 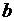 , делаем вывод, что работа двигателя устойчивая, если при увеличении частоты вращения
, делаем вывод, что работа двигателя устойчивая, если при увеличении частоты вращения 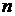 статический момент
статический момент 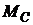 уменьшается медленнее, чем электромагнитный момент двигателя
уменьшается медленнее, чем электромагнитный момент двигателя 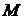 :
:
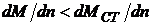 .
.
Данное условие является необходимым, но недостаточным. При резком изменении режима работы двигателя, работающего при скольжениях, близких к 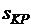 , перегрузка двигателя может привести к его останову при
, перегрузка двигателя может привести к его останову при 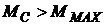 , поэтому максимальный момент называют иногда опрокидывающим моментом.
, поэтому максимальный момент называют иногда опрокидывающим моментом.
Повышению устойчивости асинхронного двигателя способствует увеличение его максимального момента (кратности максимального момента или его перегрузочной способности).
Увеличение перегрузочной способности асинхронного двигателя ведет к возрастанию его габаритов и массы или к снижению энергетических показателей.
Вращающий момент асинхронного двигателя зависит от квадрата питающего напряжения, поэтому качество электроснабжения имеет большое значение для обеспечения устойчивой работы двигателей, поскольку даже незначительное уменьшение напряжения сказывается на величине максимального момента, а значительное уменьшение может привести к останову двигателя.
Дата добавления: 2018-04-15; просмотров: 11; ЗАКАЗАТЬ РАБОТУ
studopedia.net
Для анализа статической устойчивости асинхронного двигателя вновь построим зависимости электрической и механической мощностей от скольжения (рис.4.8).Из графиков видно, что установившийся режим работы двигателя возможен в двух точках пересечения характеристик : в точках a и b.
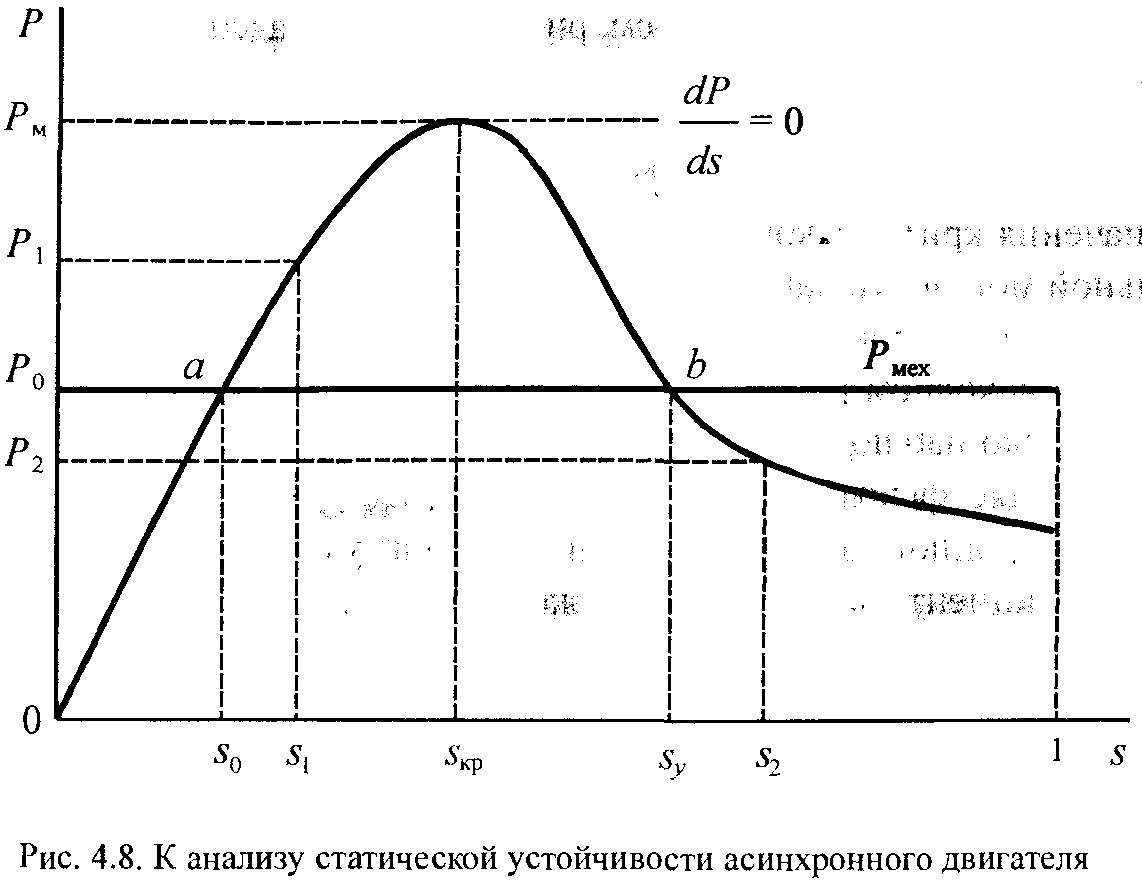
Предположим, что исходный режим характеризуется мощностью P0 и скольжением s0. Далее допустим, что скольжение увеличилось до значения s1 в результате какого-либо малого возмущения.Это вызовет увеличение активной мощности двигателя с P0 до значения P1 . При этом механическая мощность останется постоянной и равной P0 .в этом случае, согласно (1.49) и принимая в относительных единицах P=M, скольжение ротора будет определяться уравнением
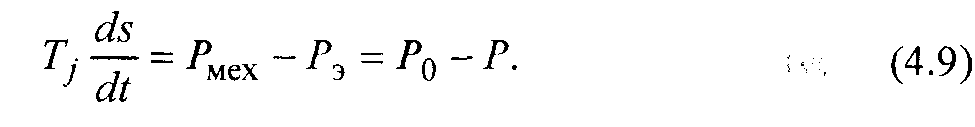
Поскольку в рассматриваемом случае P=P1>P0, то на валу машины возникает ускоряющий электромагнитный момент, под влиянием которого скольжение начнет уменьшаться, а скорость увеличиваться. В результате этого устанавливается исходный режим работы двигателя в точке а. Иной исход процесса имеет место при работе двигателя в точке b со скольжением sy В этом случае при увеличении скольжения до значения s2 электрическая мощность Р2 становится меньше механической Р0, что, согласно (4.9), обусловливает дальнейший рост скольжения вплоть до остановки двигателя.
Сохранение статической устойчивости асинхронного двигателя будет осуществлено не только в точке а, но и на всей восходящей части характеристики активной мощности двигателя, для которой справедливо соотношение dP/ds>0.Следовательно, критерием статической устойчивости асинхронного двигателя является положительный знак производной

У асинхронного двигателя имеется только одна область устойчивой работы - область, лежащая между синхронной скоростью и критическим скольжением. Область между критическим скольжением и скольжением, равным единице, оказывается неустойчивой. В нормальных условиях двигатель работает на устойчивой части своей характеристики при скольжении меньше критического и потребляемой мощности меньше Pм. Нарушение устойчивой работы может быть вызвано увеличением механической мощности или снижением напряжения. Напряжение, при котором электромагнитная мощность, развиваемая двигателем, становится равной механической мощности (Pм=P0) называют критическим.
Значения критического напряжения, критического скольжения и мак-симальной мощности характеризуют предельное состояние режима по ус-тойчивости асинхронной нагрузки. Зная эти предельные параметры и па-раметры в исходном режиме, можно оценить запас статической устойчи-вости. Однако наблюдение за текущей величиной, например, скольженияне представляется возможным. Поэтому уровень статической устойчивос-ти как асинхронного двигателя, так и узлов нагрузки оценивают путем рас-чета коэффициента запаса по напряжению:

Для обеспечения устойчивости нагрузки коэффициент запаса по напряжению должен быть не менее 0,15 в нормальных и 0,1 в аварийных режимах электроэнергетических систем.
Изменение частоты в системе оказывает влияние на условия устойчивой работы асинхронных двигателей. Для качественной её оценки запишем реактивное сопротивление рассеяния двигателя
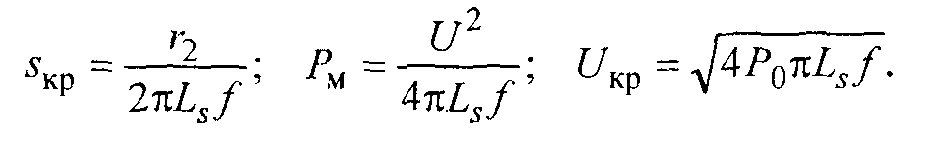
Таким образом, из полученных формул видно, что критическое сколь-жение, максимальная мощность у двигателя, работающего при понижен-ной частоте, увеличиваются, а критическое напряжение уменьшается.Снижение частоты, таким образом, положительно влияет на условия рабо-ты двигателя. Поэтому в режимах со снижением частоты можно, не опаса-ясь нарушения устойчивости, допускать более глубокие снижения напря-жения, чем при нормальной частоте, так как критическое напряжение припонижении частоты становится меньше. Однако полученные выводы спра-ведливы для режимов, имеющих запасы по реактивной мощности. В усло-виях дефицита реактивной мощности рост потребления реактивной мощ-ности асинхронных двигателей при снижении частоты может вызвать на-столько глубокое снижение напряжения, что приведет к нарушению ус-тойчивости значительной части потребителей. Поэтому положительноевлияние снижения частоты на устойчивость двигательной нагрузки можетсмениться весьма отрицательным из-за роста потребления реактивноймощности двигателями. В каждом конкретном случае необходима провер-ка и оценка режимов при снижениях как частоты, так и напряжения.
Статическая устойчивость синхронного двигателя оценивается так же, как и синхронного генератора, критерием dP/dδ>0.при отсутствии АРВ максимальная мощность и критическое напряжение определяются выражениями
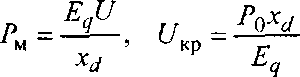
cyberpedia.su
Cтраница 1
Устойчивая работа асинхронного двигателя возможна лишь на участке характеристики, заключенном в пределах s 0; s SK. [1]
Определим область устойчивой работы асинхронного двигателя. Пусть двигатель работает в точке / механической характеристики ( рис. 12 - 18), развивая скорость пг и вращающий момент Mt. [3]
Определим область устойчивой работы асинхронного двигателя. Пусть двигатель работает в точке 1 механической характеристики фис. [5]
Определим область устойчивой работы асинхронного двигателя. Пусть двигатель работает в точке / механической характеристики ( рис. 12 - 19), развивая скорость i и вращающий момент Mt. [6]
Большое значение для обеспечения устойчивой работы асинхронных двигателей имеет качество электроснабжения. Поэтому даже незначительное уменьшение напряжения сказывается на величине максимального момента, а значительное уменьшение может вызвать остановку двигателя. [8]
Большое значение для обеспечения устойчивой работы асинхронных двигателей имеет качество электроснабжения. [9]
Большое значение для обеспечения устойчивой работы асинхронных двигателей имеет качество электроснабжения. Поэтому даже незначительное уменьшение напряжения влияет на максимальный момент, а значительное уменьшение может вызвать остановку двигателя. [11]
Весьма большое значение для обеспечения устойчивой работы асинхронных двигателей имеет качество электроснабжения. [13]
Вывод этот очевиден и указывает на то, что при Мет const нельзя обеспечить устойчивой работы асинхронного двигателя в разомкнутых системах при скольжениях, больших SK. Если ппк, &0 в этом случае двигатель является устойчивым апериодическим звеном. [14]
Таким образом, при достижении электромагнитного момента максимального значения наступает предел устойчивой работы двигателя. Следовательно, для устойчивой работы асинхронного двигателя необходимо, чтобы номинальный момент был меньше максимального. В этом случае двигатель будет работать устойчиво не только при номинальной нагрузке, но будет способен выдерживать некоторые перегрузки, что необходимо для надежной работы двигателя в электроприводе. [15]
Страницы: 1 2
www.ngpedia.ru
Количество просмотров публикации Динамическая устойчивость асинхронного двигателя - 120
Снижение напряжения на зажимах двигателя или механического момента на его валу вызывает появление избыточного тормозящего момента ΔМ (см. рисунок 15.1). Как при снижении напряжения, так и при увеличении механического момента скольжение двигателя будет увеличиваться и он опрокинется. Чтобы этого не произошло, нужно своевременно восстановить напряжение или уменьшить механический момент. В случае если прежнее значение напряжения или момента будет восстановлено при скольжении S1 (см. рисунок 15.2), то на вал двигателя будет действовать ускоряющий избыточный момент ΔМ1, который вернет двигатель в устойчивый режим со скольжением S0.
Рисунок 15.2
В случае если восстановление напряжения или момента произойдет при скольжении S3, то избыточный момент ΔМ2 будет иметь тормозной характер и двигатель опрокинется. Необходимо знать время, в течение которого будет достигнуто то или иное значение скольжения. Для этого крайне важно решить уравнение движения ротора двигателя.
При возникновении избыточного момента на валу двигателя ускорение ротора прямо пропорционально избыточному моменту и обратно пропорционально моменту инерции и должна быть записано в виде
(15.1)
где ΔМ = Мдв – Мс – разность электромагнитного момента двигателя и момента сопротивления приводимого механизма;
J – момент инерции, причем J = Jдв + Jмех. пр, Jдв – момент инерции двигателя, Jмех. пр. = Jмех. (ωном. мех /ωном.дв) – приведенный момент механизма с учетом разных номинальных скоростей вращений;
ω – угловая скорость вращения двигателя, которая должна быть выражена через скольжение следующим образом:
ω = (1 – S) ω1 ном . (15.2)
Подставляя уравнение (15.2) в (15.1) и выражая ΔМ в относительных номинальных единицах двигателя, получим
(15.3)
где , а - номинальная мощность двигателя.
Уравнение (15.3) описывает движение ротора двигателя при больших возмущениях и принято называть уравнением движения ротора двигателя. Это уравнение нелинейно, его решение должна быть получено с помощью любого из методов численного интегрирования. Наиболее просто это решение получается, в случае если разбить ось абсцисс функции ΔМ(S) на ряд равных интервалов Δ S (см. рисунок 15.3).
Рисунок 15.3
Тогда уравнение движения на всем интервале будет иметь вид
,
и время от момента нарушения режима до конца любого n-го интервала определится как
.
Точность решения зависит от величины ΔS и возрастает с ее уменьшением.
Получив таким образом зависимость S(t), можно определить скольжение, соответствующее времени t1 на рисунке 15.1. Зная это значение, можно судить о динамической устойчивости двигателя.
referatwork.ru
Снижение напряжения на зажимах двигателя или механического момента на его валу вызывает появление избыточного тормозящего момента ΔМ (см. рисунок 15.1). Как при снижении напряжения, так и при увеличении механического момента скольжение двигателя будет увеличиваться и он опрокинется. Чтобы этого не произошло, надо своевременно восстановить напряжение или уменьшить механический момент. Если прежнее значение напряжения или момента будет восстановлено при скольжении S1 (см. рисунок 15.2), то на вал двигателя будет действовать ускоряющий избыточный момент ΔМ1, который вернет двигатель в устойчивый режим со скольжением S0.
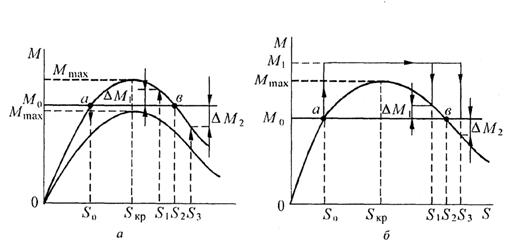
Рисунок 15.2
Если восстановление напряжения или момента произойдет при скольжении S3, то избыточный момент ΔМ2 будет иметь тормозной характер и двигатель … опрокинется. Необходимо знать время, в течение которого будет достигнуто то или иное значение скольжения. Для этого необходимо решить уравнение движения ротора двигателя.
При возникновении избыточного момента на валу двигателя ускорение ротора прямо пропорционально избыточному моменту и обратно пропорционально моменту инерции и может быть записано в виде

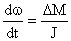 (15.1)
(15.1)
где ΔМ = Мдв – Мс – разность электромагнитного момента двигателя и момента сопротивления приводимого механизма;
J – момент инерции, причем J = Jдв + Jмех. пр, Jдв – момент инерции двигателя, Jмех. пр. = Jмех. (ωном. мех /ωном.дв) – приведенный момент механизма с учетом разных номинальных скоростей вращений;
ω – угловая скорость вращения двигателя, которая может быть выражена через скольжение следующим образом:
ω = (1 – S) ω1 ном . (15.2)
Подставляя уравнение (15.2) в (15.1) и выражая ΔМ в относительных номинальных единицах двигателя, получим
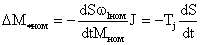 (15.3)
(15.3)
где 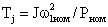 , а
, а 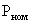 — номинальная мощность двигателя.
— номинальная мощность двигателя.
Уравнение (15.3) описывает движение ротора двигателя при больших возмущениях и называется уравнением движения ротора двигателя. Это уравнение нелинейно, его решение может быть получено с помощью любого из методов численного интегрирования. Наиболее просто это решение получается, если разбить ось абсцисс функции ΔМ(S) на ряд равных интервалов Δ S (см. рисунок 15.3).
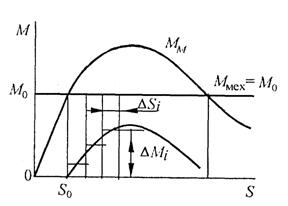
Рисунок 15.3
Тогда уравнение движения на всем интервале будет иметь вид
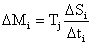 ,
,
и время от момента нарушения режима до конца любого n-го интервала определится как
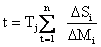 .
.
Точность решения зависит от величины ΔS и возрастает с ее уменьшением.
Получив таким образом зависимость S(t), можно определить скольжение, соответствующее времени t1 на рисунке 15.1. Зная это значение, можно судить о динамической устойчивости двигателя.
refac.ru
Под статической устойчивостью понимается способность асинхронной машины возвращаться в исходный режим после малого возмущения со стороны сети или вала.
Рис.4.13
Рассмотрим в качестве примера двигательный режим (4.13). Пусть на ротор действует электромагнитный момент М и момент сопротивлений Мвн1, обусловленный рабочим
механизмом. Разность этих моментов определяет динамический момент:
Принимая во внимание, что n = (1 - s)n1, получим
(4.17)
Задача заключается в том, чтобы при pflfyys[ зависимостях M(s) и Mвн1(s) определить устойчивость режима в точке 1.
Для решения этой задачи выполним линеаризацию нелинейных функций M[s) и Мщ (s) в малой окрестности точки 1:
Данные соотношения позволяют записать дифференциальное уравнение (4.17) в малых приращениях:
Это уравнение является линейным, его решение хорошо известно:
(4.18)
С - постоянная, определяемая начальными условиями.
Согласно (4.18) асинхронная машина вернется в исходный режим (Δs→ 0 при t →∞) после снятия малого возмущения, если
(4.19)
Частные производные определяет угол наклона касательных к кривым М(s) и Mвн1(s) в точке 1. Как следует из рис. 4.13, поэтому А > 0. Следовательно, режим в точке 1 статически устойчив.
Если момент сопротивления рабочего механизма определяется кривой Мвн2, то согласно критерию статической устойчивости (4.19) в точках 2 и 4 режим работы асинхронного двигателя будет устойчивым, а в точке 3 - неустойчивым. При постоянном моменте сопротивления на валу предельным по устойчивости будет режим в точке 5, соответствующий максимуму электромагнитного момента. Поэтому устойчивой зоной работы двигателя является диапазон скольжений от 0 до sk. Кратность максимального момента Кm =Mmax /Mном характеризует перегрузочную способность двигателя. Для того, чтобы обеспечить устойчивую работу асинхронного двигателя при возможных колебаниях напряжения сети и момента нагрузки, кратность Кm должна быть не ниже 1,7 ±1,9.
Экспериментальное исследование асинхронных двигателей
Экспериментальное исследование асинхронных двигателей проводится с целью определения параметров схемы замещения (рис. 4.8). Программа исследований включает два опыта: опыт холостого хода и опыт короткого замыкания. Эти опыты легко реализуются, для их проведения требуется минимальная мощность установленного оборудования. Экспериментальные исследования асинхронных двигателей в рабочих режимах, как правило, не проводятся в виду их большой трудоемкости и стоимости. Характеристики асинхронных двигателей в рабочих режимах получают расчетным путем по схеме замещения.
Опыт холостого хода
Схема экспериментальной установки представлена на рис. 4.14. Схема включает кроме испытуемого двигателя (АД) индукционный регулятор (ИР) для регулирования напряжения статора АД, измерительный комплект (ИК) для регистрации тока, активной мощности и напряжения статора, тахогенератор (ТГ) для измерения частоты вращения n и машину постоянного тока (МПТ) для затормаживания ротора.
Рис.4.15
Опыт холостого хода проводится без нагрузки на валу (ключ К разомкнут) для нескольких значений напряжения U1 в диапазоне (1,2 - 0,4)Uн. Измеряются фазные токи I10 и активная мощность Pо подводимая к обмотке статора. По данным опыта строят зависимости I10, P0, cosφo = f(U1). Вид этих зависимостей представлен на рис. 4.15. Согласно энергетической диаграмме (рис. 4.10) потребляемая на холостом ходу мощность расходуется на покрытие потерь в обмотке статора рэл1 , потерь в стали рмг и механических потерь рмех. Потерями в роторной обмотке рэл2 = sPэм, можно пренебречь, так как в опыте холостого хода скольжение весьма мало (s < 0,001). Вычитая из потерь холостого хода P0 электрические потери рэл1=m1r1I210, получим сумму потерь в стали и механических потерь:
Рис.4.16
Разделение этих потерь производится путем экстраполяции зависимости рмг +рмех =f(U21) до пересечения с осью ординат (рис, 4.16). Данный способ разделения потерь основан на том, что потери в стали пропорциональны рмг ~ В2δ ~ Ф2 ~ U2, а потери механические рмех не зависят от напряжения U1, так как частота вращения ротора во время опыта холостого хода остается практически постоянной. Однако при очень малых значения напряжения U1 частота вращения ротора снижается, растут скольжение и потери в обмотке ротора, не учитываемые при разделения потерь. Этим объясняется отклонение зависимости рмг +рмех =f(U21) от прямой в зоне малых напряжений. Его не следует учитывать при экстраполяции.
Полученные данные позволяют рассчитать следующие параметры схемы замещения асинхронного двигателя:
Расчет проводится по данным опыта холостого хода при номинальном напряжении (U1 = 1,0о.е.). Сопротивление обмотки статора r1 определяется постоянным током перед опытом холостого хода.
poisk-ru.ru