







Трехфазные асинхронные электродвигатели, или как их еще называют индукционные электродвигатели, являются наиболее распространенными в промышленности. Данный тип электродвигателя, аналогично машинам постоянного тока тоже обладают свойствами обратимости, и может работать как в двигательном, генераторном, так и в тормозных режимах – противовключение, динамическое торможение. Режим работы асинхронного электродвигателя характеризуют знаком и величиной скольжения.
Пожалуй, основным методом анализа установившихся режимов индукционного электродвигателя является использование эквивалентных схем замещения. В таком случае обычно рассматривают явление, которое относится к одной фазе многофазного двигателя при соединении его обмоток звездой.
Упрощенная картина магнитных потоков работающего асинхронного электродвигателя позволяет представить его в виде эквивалентной схемы:

Электромагнитная связь первичной и вторичной цепи осуществляется потоком взаимоиндукции Ф, индуктирующим в роторной обмотке ЭДС Е2S. Сопротивление индуктивное первичной цепи Х1 обусловлено наличием потока рассеивания, связанного только с этой цепью. Аналогично сопротивления Х2 обусловлено потоком рассеивания Ф25.
Частота тока ротора будет определяться скоростью его вращения относительно скорости вращения магнитного поля статора, то есть зависеть от скольжения и будет равна f2 = f1S.
Ток вторичной цепи при вращающемся роторе:

Также выражения для I2 может иметь:

Выше показанные выражения имеют не только различную форму записи, но и имеют совершенно разный физический смысл. А смысл его в том, что вместо вращающегося ротора можно рассматривать неподвижный, в котором будет индуцироваться ЭДС Е2. При этом индуктивное сопротивление будет равно Х2, а активное возрастет на величину  так как
так как  . При этом I1 останется прежним по фазе и величине, что не повлияет на потребляемую из сети мощность. Поскольку I1 и I2 не изменятся, то естественно и потери в первичных и вторичных цепях также не изменятся, соответственно мощность тоже не будет изменяться, а мощность развиваемая двигателем при вращении, будет равна мощности, потребляемой в добавочном сопротивлении
. При этом I1 останется прежним по фазе и величине, что не повлияет на потребляемую из сети мощность. Поскольку I1 и I2 не изменятся, то естественно и потери в первичных и вторичных цепях также не изменятся, соответственно мощность тоже не будет изменяться, а мощность развиваемая двигателем при вращении, будет равна мощности, потребляемой в добавочном сопротивлении  . Таким образом, эквивалентная схема замещения асинхронной машины может быть заменена схемой замещения с добавочным сопротивлением rд во вторичной цепи:
. Таким образом, эквивалентная схема замещения асинхронной машины может быть заменена схемой замещения с добавочным сопротивлением rд во вторичной цепи:

После приведения первичной и вторичной ЭДС они будут равны Е1 = Е2/ и это дает возможность соединить эквивалентные точки и получить такую схему:

Недостатком Т – образной схемы замещения помимо сложностей расчета, является зависимость всех токов I1, I2/, Iμ от скольжения s.
Из Т – образной схемы замещения видно, что в режиме холостого хода, при I2/ = 0 и s = 0, ток в контуре будет обуславливаться сопротивлениями намагничивающего контура и первичной цепи и совсем не будет зависеть от скольжения. Данное обстоятельство позволит вынести на зажимы электродвигателя намагничивающий контур и перейти к Г – образной схеме замещения.
Данная схема замещения позволяет изучать процессы в асинхронном электродвигателе, которые имеют место при изменении скольжения электрической машины.

Учет контура намагничивания необходим при определении I1, который потребляется из сети. Но Г — образная схема замещения будет справедлива лишь при наличии определенных допущений:
Следует также помнить и то, что в Г – образной схеме замещения в величины сопротивлений необходимо внести соответствующие поправки:

Где:

В выше перечисленных уравнениях величины имеющие индекс «дейст» соответствуют реальным значениям параметров асинхронной машины, а без индексов – те, которые используют в эквивалентной схеме.
Поскольку отношение r1/xμ довольно таки мало, то практически довольно часто принимают:

Обычно δ лежит в пределах 1,05 – 1,1.
Первичный ток I1 будет равен при любом скольжении:

Приведенный роторный ток:

Показанное выше выражение показывает, что ток ротора является функцией скольжения. При s = 0 I2/ = 0. При увеличении скольжения I2/ также будет расти, а при s = 1 достигнет своего максимума, или тока короткого замыкания, или пускового:

Если в роторной цепи отсутствует добавочное сопротивление (АД с КЗ ротором), пусковой ток может достигнуть довольно приличных значений, а именно 5 – 8 раз больше чем его номинальное значение.
Данная зависимость показана ниже:

Отношения пускового значения к номинальному является очень важным параметром для асинхронных машин с короткозамкнутым ротором, так как наличие пусковых токов приводит к просадкам напряжения, что особо ощутимо при использовании электродвигателей средней и большой мощности. Поэтому данная характеристика приводится в каталогах по выбору электрических машин.
elenergi.ru
При практических расчетах вместо реального асинхронного двигателя, на схеме его заменяют эквивалентной схемой замещения, в которой электромагнитная связь заменена на электрическую. При этом параметры цепи ротора приводятся к параметрам цепи статора.
По сути, схема замещения асинхронного двигателя аналогична схеме замещения трансформатора. Различие в том, что у асинхронного двигателя электрическая энергия преобразуется в механическую энергию (а не в электрическую, как это происходит в трансформаторе), поэтому на схеме замещения добавляют переменное активное сопротивление r2'(1-s)/s, которое зависит от скольжения. В трансформаторе, аналогом этого сопротивления является сопротивление нагрузки Zн.
Величина скольжения определяет переменное сопротивление, например, при отсутствии нагрузки на валу, скольжение практически равно нулю s≈0, а значит переменное сопротивление равно бесконечности, что соответствует режиму холостого хода. И наоборот, при перегрузке двигателя, s=1, а значит сопротивление равно нулю, что соответствует режиму короткого замыкания.


В Г-образной схеме, намагничивающая ветвь вынесена к входным зажимам. Таким образом, вместо трех ветвей получают две ветви, первая – намагничивающая, а вторая – рабочая. Но данное действие требует внесение дополнительного коэффициента c1, который представляет собой отношение напряжения подводимого к двигателю, к ЭДС статора.

Величина c1 приблизительно равна 1, поэтому для максимального упрощения, на практике принимают значение c1≈1. При этом следует учитывать, что значение коэффициента c1 уменьшается с увеличением мощности двигателя, поэтому более точное приближение будет соответствовать более мощному двигателю.
Другой источник
Для расчета характеристик асинхронного двигателя и исследования различных режимов его работы удобно использовать схемы замещения.
При этом реальная асинхронная машина с электромагнитными связями между обмотками заменяется относительно простой электрической цепью, что позволяет существенно упростить расчет характеристик.
С учетом того, что основные уравнения асинхронного двигателя (2.25) аналогичны таким же уравнениям трансформатора (1.23), схема замещения двигателя такая же, как и у трансформатора, представлена она на рисунке 2.6.


Рисунок 2.6 – T-образная схема замещения асинхронного двигателя
Изображенная на рисунке 2.6 схема называется T-образной схемой замещения (сопротивления  ,
, и
и образуют буквуТ), в ней: r1 и x1– активное и индуктивное сопротивления фазной обмотки статора;
образуют буквуТ), в ней: r1 и x1– активное и индуктивное сопротивления фазной обмотки статора;  и
и – при-веденные активное и индуктивное сопротивления фазной обмотки ротора.
– при-веденные активное и индуктивное сопротивления фазной обмотки ротора.
Сопротивление  определяет параметры намагничивающей ветви схемы. Индуктивная составляющая
определяет параметры намагничивающей ветви схемы. Индуктивная составляющая является индуктивным сопротивлением взаимной индукции. Посредством сопротивления
является индуктивным сопротивлением взаимной индукции. Посредством сопротивления учитываются магнитные потери в стали статора
учитываются магнитные потери в стали статора . Как и в трансформаторе, сопротивление
. Как и в трансформаторе, сопротивление зависит от подведенного напряженияU1. С повышением U1 сопротивление
зависит от подведенного напряженияU1. С повышением U1 сопротивление 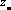 уменьшается.
уменьшается.
При расчете характеристик асинхронного двигателя с использованием схемы замещения ее параметры должны быть известны. Схема рисунка 2.6 полностью отражает физические процессы, происходящие в двигателе, но имеет узловую точку между сопротивлениями  и
и , что усложняет расчет токов при различных значениях скольжения. Поэтому большое практическое применение для анализа режимов работы асинхронных машин находит другаясхема замещения, в которой намагничивающая ветвь подключена непосредственно на входе схемы, куда подводится напряжение U1 (рисунок 2.7). Данная схема называется Г-образной схемой замещения.
, что усложняет расчет токов при различных значениях скольжения. Поэтому большое практическое применение для анализа режимов работы асинхронных машин находит другаясхема замещения, в которой намагничивающая ветвь подключена непосредственно на входе схемы, куда подводится напряжение U1 (рисунок 2.7). Данная схема называется Г-образной схемой замещения.


Рисунок 2.7 – Г-образная схема замещения асинхронного
двигателя (а) и ее упрощенный вариант (б)
На рисунке 2.7, а комплексный коэффициент
 или
или  .
.
Так как x1 >> xm, то  незначительно больше единицы (
незначительно больше единицы ( ).
).
Если пренебречь коэффициентом  , то получим упрощеннуюГ-образную схему замещения (рисунок 2.7, б), которую используют при практических расчетах асинхронных двигателей средних и больших мощностей. При этом погрешность в расчете не превышает 1–5%.
, то получим упрощеннуюГ-образную схему замещения (рисунок 2.7, б), которую используют при практических расчетах асинхронных двигателей средних и больших мощностей. При этом погрешность в расчете не превышает 1–5%.
Необходимость учета коэффициента  возникает главным образом при анализе асинхронных двигателей небольшой мощности.
возникает главным образом при анализе асинхронных двигателей небольшой мощности.
Согласно (2.22) активное сопротивление обмотки ротора двигателя разбито на две части: 
 . Первое сопротивление не зависит от режима работы, и потери в нем равны электрическим потерям реального ротора. Второе сопротивление зависит от скольжения, и мощность, выделяемая в нем, численно равна механической мощности двигателя Рмех. Следовательно сопротивление
. Первое сопротивление не зависит от режима работы, и потери в нем равны электрическим потерям реального ротора. Второе сопротивление зависит от скольжения, и мощность, выделяемая в нем, численно равна механической мощности двигателя Рмех. Следовательно сопротивление в схеме замещения выполняет роль нагрузки двигателя.
в схеме замещения выполняет роль нагрузки двигателя.
Из упрощенной Г-образной схемы замещения можно определить приведенный ток роторной обмотки
 . (2.26)
. (2.26)
В дальнейшем (2.26) используется при выводе уравнения электромагнитного момента асинхронного двигателя.
25. энергетическая диаграмма асинхронного двигателя Все преобразования энергии и потери, которые происходят в асинхронном двигателе, можно иллюстрировать при посредстве так называемой "энергетической" диаграммы.
На фиг. 88 показана такая диаграмма в форме "потока энергии", который течет слева направо. Как видно из фиг. 88, этот "поток" состоит из ряда "рукавов". Притекающая к статору асинхронного двигателя из сети электрическая энергия Р1 изображена на фиг. 88 в виде потока наибольшей ширины. По мере течения направо главное "русло" этого потока делается все уже и уже.
"Рукав" потокаVFe изображает потери железа в двигателе (токи Фуко и гистерезис).
Рукав потока V1 =m1I12•r1 изображает потери меди в статоре.
Потери меди в роторе m2 •I22 •r2 изображены рукавом потокаV2 и, наконец, рукав потокаVρ изображает механические потери.
Таким образом притекающая к статору мощность Р1 оказывается больше тормозной мощности двигателяР2 на величину суммарных потерь фиг. 88.
На диаграмме фиг. 88, кроме того, очень наглядно представлены весьма характерные в теории асинхронных двигателей величины мощности Р'2 иPs.
|
|
| Фиг. 88. Энергетическая диаграмма асинхронного двигателя |
а) Мощность Р'2 есть мощность ротора; эта мощность меньше мощности, подведенной к статору, на величину суммы потерьVFe+ V1 +V2; если из мощности ротораР2 вычесть мощность, соответствующую механическим потерямVρ, то получится мощность на валу двигателяW2.
b) Мощность Ps носит обычно название мощности вращающегося потока;Ps равно сетевой мощностиР1 за вычетом суммарных потерь в статоре
VFe + V1.
Мощность Ps является, как будет видно ниже, весьма характерной величиной в теории асинхронных двигателей.
25.вопрос Энергетическая диаграмма асинхронного двигателя
Энергетическая диаграмма позволяет судить о характере распределения мощности, потребляемой двигателем из сети. Ее можно получить с помощью векторной диаграммы (рис.4.9). При работе асинхронный двигатель потребляет из сети активную мощность  . Из векторной диаграммы можно получить следующие соотношения:
. Из векторной диаграммы можно получить следующие соотношения: С учетом этих соотношений выражение для мощности
С учетом этих соотношений выражение для мощности  преобразуется к виду
преобразуется к виду  . Отсюда следует, что мощность
. Отсюда следует, что мощность  расходуется в статоре на покрытие электрических потерь в обмотке статора,
расходуется в статоре на покрытие электрических потерь в обмотке статора,  и на покрытие потерь в стали,
и на покрытие потерь в стали,  . Остальная мощность поступает через воздушный зазор в ротор. Эта мощность определяет электромагнитный момент двигателя, поэтому ее называют электромагнитной мощностью
. Остальная мощность поступает через воздушный зазор в ротор. Эта мощность определяет электромагнитный момент двигателя, поэтому ее называют электромагнитной мощностью  . Из векторной диаграммы можно получить следующее соотношение:
. Из векторной диаграммы можно получить следующее соотношение: , поэтому для электромагнитной мощности справедливо второе выражение:
, поэтому для электромагнитной мощности справедливо второе выражение: . Часть электромагнитной мощности, как мы выяснили выше, теряется в виде электрических потерь в обмотке ротора,
. Часть электромагнитной мощности, как мы выяснили выше, теряется в виде электрических потерь в обмотке ротора,  , а остальная часть мощности
, а остальная часть мощности  преобразуется в механическую мощность
преобразуется в механическую мощность  . Часть механической мощности
. Часть механической мощности  теряется внутри самой машины в виде механических потерь
теряется внутри самой машины в виде механических потерь  , магнитных потерь
, магнитных потерь  и добавочных потерь
и добавочных потерь  . Механические потери включают потери на трение и на вентиляцию. Их расчет выполняется по эмпирическим формулам. Магнитные потери
. Механические потери включают потери на трение и на вентиляцию. Их расчет выполняется по эмпирическим формулам. Магнитные потери  обычно малы и отдельно не определяются , а учитываются в
обычно малы и отдельно не определяются , а учитываются в  вместе с потерями в стали статора. Добавочные потери вызваны в основном высшими гармониками магнитных полей. Они трудно поддаются расчету. Поэтому добавочные потери оценивают приближенно величиной 0,5% от номинальной мощности двигателя. Полезная мощность на валу двигателя
вместе с потерями в стали статора. Добавочные потери вызваны в основном высшими гармониками магнитных полей. Они трудно поддаются расчету. Поэтому добавочные потери оценивают приближенно величиной 0,5% от номинальной мощности двигателя. Полезная мощность на валу двигателя
 .
.
|
|
В соответствии с изложенным энергетическую диаграмму двигателя можно представить в виде, показанном на рис. 4.10. Сумма потерь  определяет КПД двигателя
определяет КПД двигателя  . КПД двигателей мощностью от 1 кВт до 1000 кВт лежит в пределах
. КПД двигателей мощностью от 1 кВт до 1000 кВт лежит в пределах 
26. вопрос Векторная диаграмма асинхронного двигателя
Для построения векторной диаграммы асинхронного двигателя необходимо чтобы параметры цепи ротора были приведены к цепи статора. Это достигается заменой числа витков одной фазной обмотки w2, с числом фаз m2 и обмоточным коэффициентом kоб2 на w1, m1, kоб1.
Энергетические параметры должны быть пересчитаны правильно, для того чтобы сохранить энергетические соотношения в двигателе.
ЭДС приведенной вторичной обмотки
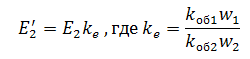
Коэффициент трансформации токов

Отсюда приведенный ток вторичной обмотки

В асинхронном двигателе с короткозамкнутым ротором числа фаз m1 и m2 не равны, потому что каждый стержень короткозамкнутой обмотки рассматривается как отдельная фаза, число витков такой обмотки w2=0.5, а число фаз равно числу стержней m2=Z2. Обмоточный коэффициент для такой обмотки kоб2=1. Исходя из этого ke≠ki, в отличие от трансформатора.
Активное и индуктивное сопротивления вторичной обмотки

Угол сдвига фаз между E2’ и I2’

Уравнения токов, напряжений статора и ротора

На основании этих уравнений выполняется построение векторной диаграммы асинхронного двигателя

Построение векторной диаграммы начинается с вектора основного магнитного потока Ф. Затем откладываются вектора E2’ и E1, которые отстают от вектора Ф на 90⁰. Затем зная угол сдвига фаз ψ2 между I2’ и E2’, строят вектор I2’. Вектор I0 опережает Ф на угол δ, а вектор I1 находят как векторную сумму I0 и -I2’. Вектор U1 строим, добавляя к вектору –E1 падение напряжения I1r1 параллельно вектору I1, затем откладываем jI1x1 и получаем вектор I1Z1, который складываем с –E1 и в итоге получаем U1.
Так как асинхронный двигатель в данном случае можно рассматривать как трансформатор, работающий на активную нагрузку, то вектор –I2’r2’(1-s)/s откладываем под тем же углом, что и I2', затем прибавляем к нему –I2’r2’ и –jI2’x2, получаем вектор –I2’Z2.
27.вопрос Электромеханическая (скоростная) и механическая характеристики асинхроннй машины
Механическая характеристика. Зависимость частоты вращения ротора от нагрузки (вращающегося момента на валу) называется механической характеристикой асинхронного двигателя (рис. 262, а). При номинальной нагрузке частота вращения для различных двигателей обычно составляет 98—92,5 % частоты вращения n1 (скольжение sном = 2 – 7,5 %). Чем больше нагрузка, т. е. вращающий момент, который должен развивать двигатель, тем меньше частота вращения ротора. Как показывает кривая
 Рис. 262. Механические характеристики асинхронного двигателя: а — естественная; б — при включении пускового реостата
Рис. 262. Механические характеристики асинхронного двигателя: а — естественная; б — при включении пускового реостата
на рис. 262, а, частота вращения асинхронного двигателя лишь незначительно снижается при увеличении нагрузки в диапазоне от нуля до наибольшего ее значения. Поэтому говорят, что такой двигатель обладает жесткой механической характеристикой.
Наибольший вращающий момент Mmax двигатель развивает при некоторое скольжении skp, составляющем 10—20%. Отношение Mmax/Mном определяет перегрузочную способность двигателя, а отношение Мп/Мном — его пусковые свойства.
Двигатель может устойчиво работать только при обеспечении саморегулирования, т. е. автоматическом установлении равновесия между приложенным к валу моментом нагрузки Мвн и моментом М, развиваемым двигателем. Этому условию соответствует верхняя часть характеристики до достижения Mmax (до точки В). Если нагрузочный момент Мвн превысит момент Mmax, то двигатель теряет устойчивость и останавливается, при этом по обмоткам машины будет длительно проходить ток в 5—7 раз больше номинального, и они могут сгореть.
При включении в цепь обмоток ротора пускового реостата получаем семейство механических характеристик (рис. 262,б). Характеристика 1 при работе двигателя без пускового реостата называется естественной. Характеристики 2, 3 и 4, получаемые при подключении к обмотке ротора двигателя реостата с сопротивлениями R1п (кривая 2), R2п (кривая 3) и R3п (кривая 4), называют реостатными механическими характеристиками. При включении пускового реостата механическая характеристика становится более мягкой (более крутопадающей), так как увеличивается активное сопротивление цепи ротора R2 и возрастает sкp. При этом уменьшается пусковой ток. Пусковой момент Мп также зависит от R2. Можно так подобрать сопротивление реостата, чтобы пусковой момент Мп был равен наибольшему Мmax.
В двигателе с повышенным пусковым моментом естественная механическая характеристика приближается по своей форме к характеристике двигателя с включенным пусковым реостатом. Вращающий момент двигателя с двойной беличьей клеткой равен сумме двух моментов, создаваемых рабочей и пусковой клетками. Поэтому характеристику 1 (рис. 263) можно получить путем суммирования характеристик 2 и 3, создаваемых этими клетками. Пусковой момент Мп такого двигателя значительно больше, чем момент М’п обычного короткозамкнутого двигателя. Механическая характеристика двигателя с глубокими пазами такая же, как и у двигателя с двойной беличьей клеткой.
Рабочие характеристики. Рабочими характеристиками асинхронного двигателя называются зависимости частоты вращения n (или скольжения s), момента на валу М2, тока статора I1коэффициента полезного действия ? и cos?1, от полезной мощности Р2 = Рmx при номинальных значениях напряжения U1 и частоты f1 (рис. 264). Они строятся только для зоны практической устойчивой работы двигателя, т. е. от скольжения, равного нулю, до скольжения, превышающего номинальное на 10—20%. Частота вращения n с ростом отдаваемой мощности Р2 изменяется мало, так же как и в механической характеристике; вращающий момент на валу М2 пропорционален мощности Р2, он меньше электромагнитного момента М на значение тормозящего момента Мтр, создаваемого силами трения.
Ток статора I1, возрастает с увеличением отдаваемой мощности, но при Р2 = 0 имеется некоторый ток холостого хода I0. К. п. д. изменяется примерно так же, как и в трансформаторе, сохраняя достаточно большое значение в сравнительно широком диапазоне нагрузки.
Наибольшее значение к. п. д. для асинхронных двигателей средней и большой мощности составляет 0,75—0,95 (машины большой мощности имеют соответственно больший к. п. д.). Коэффициент мощности cos?1 асинхронных двигателей средней и большой мощности при полной нагрузке равен 0,7—0,9. Следовательно, они загружают электрические станции и сети значительными реактивными токами (от 70 до 40% номинального тока), что является существенным недостатком этих двигателей.
 Рис. 263. Механическая характеристика асинхронного двигателя с повышенным пусковым моментом (с двойной беличьей клеткой)
Рис. 263. Механическая характеристика асинхронного двигателя с повышенным пусковым моментом (с двойной беличьей клеткой)
 Рис. 264. Рабочие характеристики асинхронного двигателя
Рис. 264. Рабочие характеристики асинхронного двигателя
При нагрузках 25—50 % номинальной, которые часто встречаются при эксплуатации различных механизмов, коэффициент мощности уменьшается до неудовлетворительных с энергетической точки зрения значений (0,5—0,75).
При снятии нагрузки с двигателя коэффициент мощности уменьшается до значений 0,25—0,3, поэтому нельзя допускать работу асинхронных двигателей при холостом ходе и значительных недогрузках.
Электромеханическая
Для АД существуют два типа характеристик:  (S) и
(S) и  (S).
(S).
Уравнение для второй электромеханической характеристики уже получено ранее в виде (8.13).
Ток ротора  является основной величиной для оценки работы двигателя.
является основной величиной для оценки работы двигателя.
Ввиду отсутствия подробных данных о сопротивлениях двигателя, для построения электромеханической характеристики удобно воспользоваться параметрами, используемыми для построения механических характеристик двигателя поформуле Клосса (8.18).
Для анализа формы электромеханической характеристики ее уравнение (без вывода) можно представить в виде [1,2]
 . (8.20)
. (8.20)
Из формулы (8.20) видим, что ток ротора интенсивно растет при увеличении скольжения от нуля до Sк. При S=Sк  . При дальнейшем росте скольжения S > Sк ток
. При дальнейшем росте скольжения S > Sк ток  увеличивается медленно (рис. 8.4).
увеличивается медленно (рис. 8.4).

Рис. 8.4. Электромеханические характеристики АД
Для схемы замещения с вынесенным на зажимы сети контуром намагничивания ток намагничивания Iμ сохраняется неизменным во всех режимах. С достаточной степенью точности его можно считать чисто реактивным, пренебрегая потерями мощности на перемагничивание стали статора.
Ток  определяется как [1,2,4]
определяется как [1,2,4]
 , (8.21)
, (8.21)
где  – коэффициент.
– коэффициент.
Для выпускающих промышленностью машин значение  лежит в пределах 0,4–0,8 и соответствующие им токи
лежит в пределах 0,4–0,8 и соответствующие им токи  = 3–8. Поэтому в среднем
= 3–8. Поэтому в среднем  0,13–0,115. Зависимости
0,13–0,115. Зависимости и
и  показаны на рис. 8.4.
показаны на рис. 8.4.
Необходимо обратить внимание, что при одинаковых значениях скольжения ток ротора в двигательном режиме меньше тока в генераторном режиме.
28.вопрос Пуск асинхронных двигателей
studfiles.net
Т-образная схема замещения. Полная схема замещения асинхронной машины при вращающемся роторе отличается от схемы замещения асинхронной машины с заторможенным ротором только наличием в цепи ротора активного сопротивления, зависящего от нагрузки (рис.9-7). Эту схему замещения называют Т-образной. Следовательно, и в этом случае удается свести теорию асинхронной машины к теории трансформатора.

Рис. 9-7. Т-образная схема замещения асинхронной машины
Сопротивления Rm и Хт намагничивающего контура значительно меньше соответствующих значений для схемы замещения трансформатора, так как ток холостого хода асинхронного двигателя гораздо больше, чем у трансформатора. Если при рассмотрении работы трансформатора часто можно пренебречь намагничивающим контуром, то при рассмотрении работы асинхронного двигателя этого сделать нельзя, так как ошибка может получиться значительной.
Г-образная схема замещения. Можно упростить вычисления, преобразовав Т-образную схему замещения в Г-образную, как это показано на рис.9-8,а.
Для Г-образной схемы замещения (рис.9-8,а) имеем  где
где 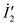 и
и  — токи рабочих контуров для Т- и Г-образной схем замещения.
— токи рабочих контуров для Т- и Г-образной схем замещения.

Рис. 9-8. Г-образные схемы замещения асинхронной машины (а, б)
Появившийся в этой схеме замещения комплекс  практически всегда можно заменить модулем С1 который для асинхронных двигателей мощностью 10 кВт и выше равен 1,02...1,05. При анализе электромагнитных процессов в машинах общего применения часто полагают С1≈1, что существенно облегчает расчеты и мало влияет на точность полученных результатов. Г-образную схему замещения при С1 = 1называют упрощенной схемой замещения с вынесенным намагничивающим контуром (рис.9-8,б). В этой схеме ток
практически всегда можно заменить модулем С1 который для асинхронных двигателей мощностью 10 кВт и выше равен 1,02...1,05. При анализе электромагнитных процессов в машинах общего применения часто полагают С1≈1, что существенно облегчает расчеты и мало влияет на точность полученных результатов. Г-образную схему замещения при С1 = 1называют упрощенной схемой замещения с вынесенным намагничивающим контуром (рис.9-8,б). В этой схеме ток  без большой погрешности можно приравнять току I0.
без большой погрешности можно приравнять току I0.
При подключении нагрузки к вторичной обмотке во вторичной цепи возникает ток нагрузки, создающий магнитный поток в магнитопроводе, направленный противоположно магнитному потоку, создаваемому первичной обмоткой. В результате в первичной цепи нарушается равенство ЭДС индукции и ЭДС источника питания, что приводит к увеличению тока в первичной обмотке до тех пор, пока магнитный поток не достигнет практически прежнего значения.
Схематично, процесс преобразования можно изобразить следующим образом:

Мгновенный магнитный потокв магнитопроводе трансформатора определяется интегралом по времени от мгновенного значения ЭДС в первичной обмотке и в случае синусоидального напряжения сдвинут по фазе на 90° по отношению к ЭДС. Наведённая во вторичных обмотках ЭДС пропорциональна первой производной от магнитного потока и для любой формы тока совпадает по фазе и форме с ЭДС в первичной обмотке. Векторная диаграмма напряжений и токов в трансформаторе с нагрузкой при согласном включении обмоток приведена на рис В

Электродвигатели выпускаются сериями, а для массового применения – едиными сериями. Для единых серий характерен высокий уровень унификации деталей и узлов, максимальная взаимозаменяемость. Для этого используют одни и те же штампы. Например, для того, чтобы пластины роторов и статоров использовались в машинах разной мощности, наращивание мощности достигается изменением длины пакетов пластин. Выпускаются специальные серии – крановые, металлургические, судовые, тяговые и т.д.
studfiles.net
При практических расчетах вместо реального асинхронного двигателя, на схеме его заменяют эквивалентнойсхемой замещения, в которой электромагнитная связь заменена на электрическую. При этом параметры цепи ротора приводятся к параметрам цепи статора.
По сути, схема замещения асинхронного двигателя аналогична схеме замещения трансформатора. Различие в том, что у асинхронного двигателя электрическая энергия преобразуется в механическую энергию (а не в электрическую, как это происходит в трансформаторе), поэтому на схеме замещения добавляют переменное активное сопротивление r2'(1-s)/s, которое зависит от скольжения. В трансформаторе, аналогом этого сопротивления является сопротивление нагрузки Zн.
Величина скольжения определяет переменное сопротивление, например, при отсутствии нагрузки на валу, скольжение практически равно нулю s≈0, а значит переменное сопротивление равно бесконечности, что соответствует режиму холостого хода. И наоборот, при перегрузке двигателя, s=1, а значит сопротивление равно нулю, что соответствует режиму короткого замыкания.
Как и у трансформатора, у асинхронного двигателя есть Т-образная схема замещения.

Более удобной при практических расчетах является Г-образная схемазамещения.

В Г-образной схеме, намагничивающая ветвь вынесена к входным зажимам. Таким образом, вместо трех ветвей получают две ветви, первая – намагничивающая, а вторая – рабочая. Но данное действие требует внесение дополнительного коэффициента c1, который представляет собой отношение напряжения подводимого к двигателю, к ЭДС статора.

Величина c1приблизительно равна 1, поэтому для максимального упрощения, на практике принимают значение c1≈1. При этом следует учитывать, что значение коэффициента c1уменьшается с увеличением мощности двигателя, поэтому более точное приближение будет соответствовать более мощному двигателю.
Параметры схемы замещения рассматриваются подробнее в статье векторная диаграмма асинхронного двигателя
Для построения векторной диаграммы осуществим приведение параметров обмотки ротора к параметрам обмотки статора. При этом обмотку ротора с числом фаз m2, обмоточным коэффициентом k2 и числом витков W2заменяют обмоткой с соответствующими параметрами статора m1, k1, W1, соблюдая при этом энергетический баланс в роторе.
Методика приведения параметров асинхронного двигателя аналогична методике приведения вторичной обмотки трансформатора. При этом уравнение обмотки ротора (5.4) примет вид

где 


 ;
;

Как уже говорилось, взаимодействие тока I2 в обмотке ротора с потоком асинхронной машины Ф создает механическую силу, приводящую ротор во вращение. При определении вращающего момента, создаваемого этой силой, необходимо исходить из известного физического соотношения, согласно которому мощность, затрачиваемая на приведение тела во вращение, определяется произведением приложенного к нему момента на скорость вращения данного тела.
Как было указано в § 3, на ротор двигателя через вращающийся магнитный поток Ф передается некоторая электромагнитная мощность, рассчитываемая по формуле (33). Однако не вся мощность, переносимая на ротор магнитным потоком, расходуется на приведение его во вращение, поскольку часть ее тратится на нагревание проводников обмотки ротора.
Механическая мощность двигателя, равная разности электромагнитной мощности и мощности потерь [см. формулу (34)], будет равна произведению вращающего момента на частоту вращения ротора:
Рмех = Мп/9,55, (39)
где М — момент, Н∙м; n — частота вращения, об/мин.
Частота вращения ротора может быть связана с частотой вращения магнитного поля машины, если вспомнить формулу (9), из которой следует:
n = n1(1— s). (40)
Во многих случаях для понимания сущности явлений, происходящих в асинхронной машине, полезно иметь в виду еще одно выражение для вращающего момента. Выше мы уже упоминали, что механическая сила, действующая на проводники ротора, создается в результате взаимодействия тока в проводниках обмотки ротора с магнитным полем. Момент асинхронного двигателя можно рассчитать, зная значение приведенного тока в роторе и потока машины
М = cмI2Фмакс cos ψ2 , (43)
где ψ2 — угол сдвига между э. д. с. Е'2, наводимой в роторе и током ротора I'2; cм — постоянный коэффициент; Фмакс — магнитный поток, Вб; I'2 — ток ротора, А.
В области малых скольжений асинхронной машины справедливой является приближенная формула
М = cмI'2Фмакс , (44)
поскольку cos ψ2 при малых скольжениях близок к единице
studfiles.net
На основании исходных данных необходимо определить скольжение в номинальном режиме, номинальный момент на валу двигателя, пусковой и критический моменты на валу, мощность, потребляемую двигателем из сети в номинальном режиме, линейный ток АД в номинальном режиме при соединении обмоток статора по схеме звезда и треугольник.
1.1.1 Скольжение в номинальном режиме

где n1 – частота вращения поля статора, об/мин.
Частота вращения поля статора равна

где f1 – циклическая частота питающей сети, Гц;
р – число пар полюсов двигателя.
1.1.2 Номинальный момент на валу двигателя
 ,
,
где ωн – номинальная угловая скорость на валу двигателя, рад/с.
Номинальная угловая скорость на валу двигателя

1.1.3 Пусковой и критический моменты на валу двигателя
Пусковой момент определяем из уравнения кратности пускового момента

Критический или максимальный момент определяем из уравнения кратности максимального момента

1.1.4 Мощность, потребляемую двигателем из сети в номинальном режиме
Мощность, потребляемая из сети, зависит от номинальной мощности на валу двигателя и от коэффициента полезного действия

тога  .
.
1.1.5 Линейный ток АД в номинальном режиме при соединении обмоток статора по схеме звезда и треугольник
При соединении фаз звездой линейные токи равны фазным токам

При соединении фаз треугольником линейные токи больше фазных токов в  раз
раз

Определение параметров асинхронной машины является весьма важным
этапом при анализе АД, так как от них зависит степень точности расчета характеристик. Параметрами АД являются активные и индуктивные сопротивления обмоток статора r1, х1, ротора r2, х, сопротивление взаимной индуктивности xм и расчетное сопротивление rм, учитывающее потери в стали.
 Физические процессы в АД наглядно отражает схема замещения (рис.1.1)
Физические процессы в АД наглядно отражает схема замещения (рис.1.1)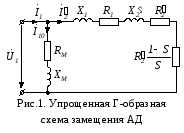
Полное сопротивление короткого замыкания


Активное и индуктивное сопротивления короткого замыкания


Активное сопротивление обмотки статора при расчетной температуре, которая зависит от высоты оси вращения
 ,
,
где tр – расчетная температура, 0С.
Расчетная температура для двигателей с высотой оси вращения
Н ≤ 132 мм, tр = 75 0С и Н ≥ 160 мм, tр = 115 0С .
Приведенное значение активного сопротивления ротора

где С1 – комплексный коэффициент Г-образной схемы замещения.
С1 = 1,04 …1,06.
Реактивное сопротивление обмотки статора
 .
.
Приведенное значение реактивного сопротивления ротора
 .
.
Активное сопротивление холостого хода

Полное сопротивление холостого хода

Активное сопротивление намагничивающего контура
 .
.
Реактивное сопротивление холостого хода

Реактивное сопротивление намагничивающего контура
 .
.
studfiles.net
37) Схемы замещения асинхронной машины.
Схема замещения позволяет определить токи, потери мощности и падения напряжения в асинхронной машине. При этом нужно учитывать, что в обмотке вращающегося ротора проходит ток, действующее значение и частота которого зависят от частоты вращения.
Схема замещения обмотки ротора. Из электрической схемы замещения ротора при его вращении (рис. 5.14, а) следует, что ток ротора

При вращении ротора [см. (5.13а) и (5.12а)] ЭДС E2s в обмотке ротора и ее частота пропорциональны скольжению s. Следовательно, и индуктивное сопротивление обмотки ротора зависит от скольжения:

где Х2—индуктивное сопротивление обмотки заторможенного ротора.
Подставляя значения E2s и X2s в (5.30), получаем

В числителе и знаменателе (5.32) есть переменная величина s, поэтому преобразуем его к виду

Уравнению (5.32а) соответствует электрическая схема замещения, показанная на рис. 5.14, б. Здесь ЭДС Е2 и индуктивное сопротивление Х2 неизменны, а активное сопротивление R2/s изменяется в зависимости от скольжения.
Схемы, представленные на рис. 5.14, а, б, с энергетической точки зрения не эквивалентны. Так, в схеме, приведенной на рис. 5.14, а, электрическая мощность ротора Рр равна электрическим потерям
|
|
| Рис. 5.14. Схемы замещения ротора асинхронной машины (а —в) |

а мощность, потребляемая в схеме, приведённой на рис. 5.14, б,

Отношение этих мощностей

Однако поскольку s = ΔPэл2/Pэм, получим, что Р'р = Рэм. Следовательно, электрическая мощность Р'р в схеме, представленной на рис. 5.14, б, равна всей электромагнитной мощности, подводимой от статора к ротору.
По известным значениям ΔРэл2 и Рэм можно определить и механическую мощность ротора:

Полученный результат наглядно представлен электрической схемой (рис. 5.14, в), в которой активное сопротивление обмотки ротора состоит из двух частей: R2 и R2(1—s)/s. Первое сопротивление не зависит от режима работы, и потери в нем равны электрическим потерям реального ротора. Второе сопротивление зависит от скольжения, и мощность, выделяющаяся в нем, численно равна механической мощности двигателя. Таким образом, рассматриваемая схема замещения позволяет заменить реальный вращающийся ротор неподвижным, в цепь обмотки которого включено активное сопротивление, зависящее от частоты вращения ротора.
Т-образная схема замещения. Полная схема замещения асинхронной машины при вращающемся роторе отличается от схемы замещения асинхронной машины с заторможенным ротором только наличием в цепи ротора активного сопротивления, зависящего от нагрузки (рис. 5.15, а). Эту схему замещения называют Т-образной. Следовательно, и в этом случае удается свести теорию асинхронной машины к теории трансформатора. Векторная диаграмма для Т-образной схемы замещения приведена на рис. 5.15, б.
Сопротивления Rm и Хт намагничивающего контура значительно меньше соответствующих значений для схемы замещения трансформатора, так как ток холостого хода асинхронного двигателя гораздо больше, чем у трансформатора. Если при рассмотрении работы трансформатора часто можно пренебречь намагничивающим контуром, то при рассмотрении работы асинхронного двигателя этого сделать нельзя, так как ошибка может получиться значительной.
Г-образная схема замещения. Можно упростить вычисления, преобразовав Т-образную схему замещения в Г-образную, как это показано на рис. 5.16, а. Подобные преобразования изучаются в курсе ТОЭ, поэтому математические выкладки здесь не приводятся.

Рис. 5.15. Т-образная схема замещения (а) асинхронной машины
и ее векторная диаграмма (б)
Для Г-образной схемы замещения (рис. 5.16, а) имеем  где
где  и
и  — токи рабочих контуров для Т- и Г-образной схем замещения.
— токи рабочих контуров для Т- и Г-образной схем замещения.
Появившийся в этой схеме замещения комплекс  практически всегда можно заменить модулем С1 который для асинхронных двигателей мощностью 10 кВт и выше равен 1,02...1,05. При анализе электромагнитных процессов в машинах общего применения часто полагают С1≈1, что существенно облегчает расчеты и мало влияет на точность полученных результатов. Г-образную схему замещения при С1 = 1 называют упрощенной схемой замещения с вынесенным намагничивающим контуром (рис. 5.16, б). В этой схеме ток
практически всегда можно заменить модулем С1 который для асинхронных двигателей мощностью 10 кВт и выше равен 1,02...1,05. При анализе электромагнитных процессов в машинах общего применения часто полагают С1≈1, что существенно облегчает расчеты и мало влияет на точность полученных результатов. Г-образную схему замещения при С1 = 1 называют упрощенной схемой замещения с вынесенным намагничивающим контуром (рис. 5.16, б). В этой схеме ток  без большой погрешности можно приравнять току I0.
без большой погрешности можно приравнять току I0.
|
|
Рис. 5.16. Г-образные схемы замещения асинхронной машины (а, б)
3
studfiles.net
Для расчетов рабочих процессов асинхронного двигателя часто используется схема замещения фазы двигателя, состоящая из резистивных и индуктивных элементов с постоянными параметрами, а также резистивного элемента с переменным сопротивлением, замещающим механическую нагрузку на валу двигателя.
Для обоснования такой схемы замещения преобразуем соответствующим образом основные уравнения состояния двигателя. Для этого все роторные величины приведем к числу витков, обмоточному коэффициенту и числу фаз статора подобно тому, как мы приводили к числу витков первичной обмотки трансформатора величины, относящиеся ко вторичной обмотке (см. § 8.5). Асинхронный двигатель является трехфазным устройством, но его фазы симметричны, поэтому достаточно составить схему замещения для одной фазы.
Электродвижущая сила фазы статора Е1 связана с ЭДС фазы неподвижного эквивалентного ротора Е2н соотношением
Е1 = (w1ko61/w2ko62) Ег н = keE2 H,
где ke — коэффициент трансформации напряжений асинхронной машины.
Согласно векторной диаграмме фазы двигателя (рис. 14.18)
— 2н =(
2н =( +j
+j Lрас2)
Lрас2)  2 = (rВ2 + r2 +j
2 = (rВ2 + r2 +j Lpac2)
Lpac2)  2 = Zo62
2 = Zo62 2 + г2
2 + г2 2.
2.
Следовательно,
— 1 = (Zo62 + r2)ke
1 = (Zo62 + r2)ke 2.
2.
Ток фазы ротора  2 можно заменить приведенным током:
2 можно заменить приведенным током:
 2= (Зw1kоб1/m2w2kоб2)
2= (Зw1kоб1/m2w2kоб2)  ’2 = ki
’2 = ki ’2
’2
где ki — коэффициент трансформации токов асинхронной машины. Сделав подстановку, получим:
 1 = — (Zo62 + r2) keki
1 = — (Zo62 + r2) keki ’2.
’2.
Произведение keki = k есть коэффициент трансформации асинхронной машины.
Введем теперь в уравнения электрического состояния фазы статора асинхронного двигателя приведенные сопротивления цепи ротора:
keki Zоб2 = Z’0б2 И keki r2 = r’2.
Элементы с такими сопротивлениями в цепи фазы статора будут потреблять такую же энергию и при том же сдвиге фаз между током и напряжением, как это имеет место в соответствующих сопротивлениях элементов цепи фазы ротора по схеме на рис. 14.17.
Таким образом, ЭДС фазы статора равна:
 1 = - (Z’об2 + r’2)
1 = - (Z’об2 + r’2)  ’2
’2
а напряжение статора (фазное)
 1 = (-
1 = (- 1 ) + Zo61
1 ) + Zo61 1 = Zo61
1 = Zo61 1 + (Zo62 + r’2)
1 + (Zo62 + r’2)  ’2. (14.18)
’2. (14.18)
С другой стороны, ЭДС 1 пропорциональна намагничивающему току
1 пропорциональна намагничивающему току  1x и по тем же соображениям, как и для трансформатора, напряжение
1x и по тем же соображениям, как и для трансформатора, напряжение
(— 1) = Z12
1) = Z12 1x,
1x,
где условная величина Z12, модуль которой имеет размерность сопротивления, в эквивалентной схеме замещения соответствует магнитной цепи двигателя. Следовательно, для напряжения фазы статора справедливо также второе уравнение
 1 = Z0б1
1 = Z0б1 1 + Z12
1 + Z12 1х. (14.19)
1х. (14.19)
Вместе с уравнением тока статора
 1 =
1 =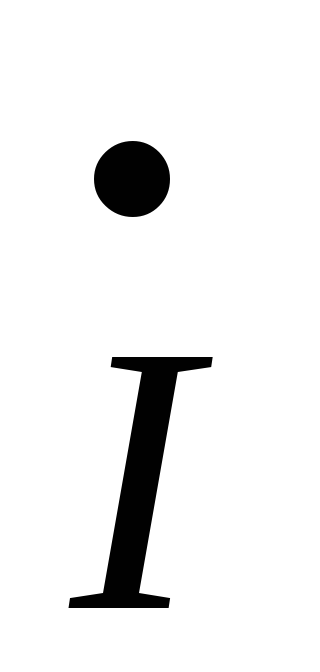 1х +
1х + ’2 (14.20)
’2 (14.20)
два уравнения напряжения фазы статора (14.18) и (14.19) можно рассматривать как уравнения, соответствующие законам Кирхгофа для цепи на рис. 14.19. В ней элементы Zo61 изображают схему замещения обмотки фазы статора, Z’qб2 — обмотки фазы ротора, Z12 — магнитную цепь машины, a r'2 — механическую нагрузку.

Уточним, что ток  1х является током фазы статора идеального холостого хода двигателя, т. е. это ток двигателя в условиях, когда ток в роторе отсутствует (I2 = 0). Ток 11x можно измерить, если посредством внешнего двигателя довести ротор до синхронной частоты вращения (s = 0).
1х является током фазы статора идеального холостого хода двигателя, т. е. это ток двигателя в условиях, когда ток в роторе отсутствует (I2 = 0). Ток 11x можно измерить, если посредством внешнего двигателя довести ротор до синхронной частоты вращения (s = 0).
При такой синхронной частоте вращения сопротивление резистивного элемента, соответствующего механической нагрузке в эквивалентной схеме замещения, равно (14.16):
r'2 = r'B2/s — r'B2 = r'B2 (1 — s)/s = .
.
Если затормозить двигатель до полной остановки, то s = 1 и, следовательно,
r'2= 0.
По этой причине опыт полной остановки двигателя именуется опытом короткого замыкания — обычно он осуществляется при сильно пониженном напряжении на статоре.
studfiles.net