







Федосов Борис Трофимович Рудненский индустриальный институт, Рудный, КазахстанОб авторе
УДК 681.51.01 Ф338
В настоящее время разработаны и применяются весьма подробные математические модели асинхронных двигателей, учитывающие как механическую, так и электромагнитную природу физических явлений, происходящих в них [3, 4]. Недостаток таких моделей в методическом отношении состоит в их сложности, трудности восприятия смысла модели, содержащей довольно большое число электрических элементов и трудности получения параметров электрических элементов конкретного двигателя, которые требуется задать.
Ниже приводятся довольно простые в понимании и, особенно, в применении в системах управления, механодинамические модели асинхронных двигателей, основанные на формуле Клосса и ее модификации, позволяющие применять их как в системах дискретного управления (включить - выключить), так и скалярного регулирования частоты вращения вала в довольно широких пределах.
Использование современных программ объектно-ориентированного виртуального моделирования систем управления требует от разработчика системы автоматического регулирования вынести готовую модель объекта, в качестве которого в данной статье будем подразумевать асинхронный двигатель, на рабочее поле программы и задать параметры этого двигателя. К настоящему времени разработаны весьма подробные, электромагнитно - механические динамические модели асинхронных двигателей классического исполнения. Однако, эти модели содержат в себе множество параметров, которые рядовой разработчик САР получить, найти, вычислить для конкретного двигателя оказывается в затруднении, поскольку в технических характеристиках, приводимых в справочниках, даются только основные эксплуатационные параметры АД. Кроме того, для асинхронных двигателей с повышенным пусковым моментом эти модели должны быть доработаны.
Нормированные естественные механические характеристики реальных АД приведены на рис. 1.1 [1]. Здесь же приведены такие же характеристики простой механодинамической модели, естественная механическая характеристика которой определена по формуле Клосса [2].

Рис. 1.1. Разновидности ЕМХ (естественных механических характеристик) реальных асинхронных двигателей и ЕМХ, построенные по формуле Клосса
Как видно, классическая модель, основанная на формуле Клосса для ЕМХ, состоятельна для двигателей базового ряда, а также для двигателей с повышенным скольжением, но существенно занижает пусковой момент для двигателей с повышенным пусковым моментом.
Для целей дискретного и даже скалярного (но не векторного) регулирования частоты вращения асинхронного двигателя могут быть применены простые в настройке и восприятии принципа работы механодинамические модели, предлагаемые ниже. Эти модели учитывают главную, механическую инерционность асинхронных двигателей, пренебрегая их сравнительно малой электромагнитной инерционностью. И для задания параметров такой модели вполне достаточно тех параметров, которые как правило приводятся в технических характеристиках двигателей.
Аналитическое описание механодинамической модели очень простое и основывается на следующих уравнениях [2].
Уравнение углового ускорения ротора (рад/сек2):
(1.1)

где: М - электромагнитный вращающий момент двигателя; Мс - момент сопротивления (тороможения) нагрузки, приведенный к валу АД.
Уравнение угловой скорости ротора (рад/сек):
(1.2)

Модифицированное выражение формулы Клосса, учитывающее влияние напряжения U и частоты f сети, а также частоты вращения n ротора и критической частоты nкр на электромагнитный момент (Н м) вращения двигателя:
(1.3)

Отметим, что на угловое ускорение ротора влияет и производная по времени момента инерции J, однако во многих технических задачах этот момент постоянен, что позволяет использовать формулу (1.1) в вышеприведенном воде. Учет влияния производной по времени момента инерции, приведенного к валу в механизмах непрерывного транспорта приведен ниже, в параграфе 6.
Виртуальная объектная модель, основанная на вышеприведенных формулах и построенная в VisSim'е:

Рис.1.2. Механодинамическая модель асинхронного двигателя представляет собой контур с одним интегратором, охваченным обратной связью, которая замыкается через блок, осуществляющий вычисление вращающего момента по модифицированной формуле Клосса. На блок "Механическая характеристика" подаются значения параметров конкретного асинхронного двигателя и значения частоты и напряжения сети. Вспомогательные нелинейные блоки обеспечивают отсутствие электромагнитного вращающего момента в выключенном состоянии
Суммарное действие вращающего момента АД и момента сопротивления механической нагрузки, приведенной к валу двигателя, с учетом момента инерции определяет угловое ускорение ротора. Интеграл от этого ускорения дает угловую скорость вращения вала. Текущая угловая скорость вращения вала в совокупности с естественной механической характеристикой АД определяет вращающий момент - контур модели замкнулся.
Дискретной управляющей величиной является команда на включение двигателя. Его начальное состояние (исходная частота вращения вала) определяется постоянной интегрирования. Возмущениями являются момент сопротивления (торможения или ускорения от механической нагрузки), а также совокупный, приведенный к валу двигателя момент инерции, учитывающий как момент инерции ротора, так и нагрузки.
На основании формул (1.1) - (1.3) построена простая модель асинхронного двигателя, способная воспроизводить разгон и остановку двигателя и учитывающая основные возмущения: момент торможения на валу АД и момент инерции нагрузки, приведенный к его валу:

Рис.2.1. Экспериментальная естественная механическая характеристика виртуального трехфазного асинхронного двигателя базового ряда
Динамические свойства модели характеризует диаграмма:

Рис.2.2. Динамика АД. Осциллограмма иллюстрирует влияние изменения возмущений (момента торможения и момента инерции, приведенного к валу АД) на пуск, работу и остановку АД. Несмотря на простоту и прозрачность физического смысла, модель хорошо отображает динамику реального АД во всех основных режимах его работы, что позволяет использовать ее при моделировании и оптимизации систем автоматического регулирования, имеющих асинхронные двигатели, управляемые дискретно
Особенность модели: изменение момента инерции на участках разгона и торможения ротора влияет на вращающий момент и его поведение во времени, но изменение момента инерции в случае, когда АД находится в режиме динамического равновесия момента сопротивления и вращающего момента, не сказывается на вращающем моменте (см. уравнение (1.1) и раздел 6).

Рис.2.3. Панель задания параметров конкретного асинхронного двигателя
Структуру субмоделей можно непосредственно увидеть, запустив модели из первой папки архива из Приложения, также, см. [2].
Там же, в Приложении имеются файлы Маткада, версий 10 и 14 с вычислением и построением ЕМХ.
Т.о. простая модель АД не имеет управляемых непрерывно величин, имеет одну дискретную бинарную управляющую величину (Пуск - Стоп), две потенциально контролируемые величины (частоту вращения вала и электромагнитный вращающий момент), которые могут в принципе измеряться в процессе работы АД, а также два непрерывных возмущения (момент торможения и момент инерции, приведенные к валу АД).
Для обеспечения вращения вала АД в противоположную сторону изменяют на 1800 начальную фазу одного из напряжений, подаваемых на АД, например при механическом переключении меняют местами два провода, подводящих к АД трехфазное напряжение. Если напряжение сети вырабатывает тиристорный преобразователь, изменение фазы на противоположную осуществляется электронной схемой.
В модели команда реверса условно задается значением -1, подаваемым на управляющий вход, в отличие от команды Пуск, имеющей значение 1. Статические характеристики (естественные механические) приведены на рис. 3.1:

Рис.3.1. ЕМХ АД, включаемого в прямом и обратном направлениях
Принцип экспериментального построения ЕМХ состоит в предварительном разгоне ротора в реверсном направлении с последующим включением двигателя в прямом направлении, что поясняется рисунком:

Рис.3.2. Принцип экспериментального определения ЕМХ виртуального АД
Динамика АД с реверсированием иллюстрируется рисунком:

Рис.3.3. Динамика реверсивного АД. Изменение момента инерции сказывается на динамике АД, в частности на частоте вращения вала и вращающем моменте в моменты времени, когда вращающий момент не равен тормозящему
Модель может быть применена при моделировании и оптимизации систем автоматического регулирования, когда требуется осуществлять реверс двигателя.
Модели АД, основанные на классической формуле Клосса, хорошо соответствуют двигателям обычного исполнения и двигателям с повышенным скольжением, но недостаточно точны в области пусковых значений для двигателей с повышенным пусковым моментом, см. рис.1.1.
Формулу Клосса можно модифицировать, чтобы она была состоятельной и для двигателей с повышенным пусковым моментом:

Рис. 4.1. Фрагмент рабочего поля Маткада. Модификация формулы Клосса путем повышения значения критического скольжения в области малых частот вращения ротора АД
Модификация формулы Клосса позволяет исправить поведение ЕМХ в области пусковых значений для АД с повышенным пусковым моментом:

Рис.4.2. Естественные механические характеристики моделей АД, построенные по классической и модифицированной формулам Клосса, а также значения ЕМХ реального двигателя с повышенным пусковым моментом
В соответствии с предложенной модификацией формулы Клосса построена и виртуальная объектная модель в VisSim'е. Статические характеристики ее имеют вид:

Рис. 4.3. ЕМХ модели совпадает со значениями ЕМХ реального двигателя с повышенным пусковым моментом
Сравнение динамики двигателя базового ряда и двигателя с повышенным пусковым моментом:

Рис.4.4. Двигатель с повышенным пусковым моментом разгоняется и осуществляет реверс несколько быстрее двигателя нормального ряда
Непрерывное частотное регулирование скорости вращения ротора асинхронного двигателя весьма важная и актуальная задача. Частотное регулирование осуществляется с применением электронных преобразователей напряжения и частоты сети в двух основных видах.
Исторически первым видом было т.н. скалярное регулирование, когда частота вращения вала задавалась плавным изменением частоты трехфазного напряжения (частоты сети), подаваемого на двигатель. В номинальном режиме работы асинхронного двигателя частота вращения его ротора близка, с точностью 5 - 10 %, к частоте сети, деленной на число пар полюсов, которое в разных двигателях может быть от 1 до 4 и более. Поскольку при изменении частоты сети изменяется и критический вращающий момент, то для того, чтобы не выводить двигатель из строя одновременно с изменением частоты вниз от номинальной требуется пропорционально уменьшать и величину напряжения. При увеличении частоты выше номинальной, по той же причине не следует увеличивать величину напряжения сети, что уменьшает номинальный и критический моменты вращения.
Достоинство скалярного регулирования состоит в простоте организации регулирования в довольно широком диапазоне: в два - три раза ниже номинальной частоты и в полтора - два раза выше номинальной. Недостаток - сравнительно невысокая точность поддержания требуемого значения частоты, определяемая крутизной, жесткостью рабочего участка естественной механической характеристики. Отметим, что применение сравнительно простых САР с управлением по отклонению позволяет существенно, на один - два порядка повысить точность регулирования частоты вращения АД. Векторное управление позволяет регулировать частоту вращения ротора в очень широких пределах, практически от нуля до величин, вдвое превышающих номинальную. При этом вращающий момент практически равен номинальному критическому, что весьма немаловажно.
Такое достоинство требует весьма сложной системы управления, которая должна анализировать состояние двигателя, возмущения, поступающие на него, моделировать в режиме реального времени двигатель и вырабатывать такое трехфазное напряжение, величина напряжения фаз которого, частота и начальные фазы линейных напряжений сети должны строго соответствовать текущему и требуемому поведению двигателя. Система управления поддерживает момент вращения двигателя на критическом уровне, т.е. двигатель, как объект управления, находится в неустойчивом состоянии, и система управления им должна успевать сохранять это неустойчивое состояние.
Существенным недостатком векторного управления является то, что система управления может "потерять" двигатель, выйти из режима регулирования, что может повлечь за собой экономические потери. Однако, ввиду высокой точности регулирования и широты диапазона регулирования, а также надежности управляющих систем, векторное управление находит достаточно широкое применение. Модели АД, способные работать в системах векторного регулирования см. [2, 3].
Тем не менее, при решении достаточно простых производственно-технических задач, где требуется частотное управление асинхронным двигателем, целесообразно использовать скалярное управление частотой. Модель двигателя, в котором возможно скалярное управление частотой вращения ротора приведена ниже:

Рис.5.1. Естественные механические характеристики (ЕМХ) асинхронного двигателя при разных значениях напряжения и частоты сети

Рис.5.2. Экспериментальное определение ЕМХ виртуальной модели АД с повышенным пусковым моментом в прямом включении при изменении частоты вращения ротора в широких пределах

Рис. 5.3. Динамика АД с повышенным пусковым моментом
Выше, в первом параграфе, из методических соображений, чтобы не перегружать изложение деталями, в уравнении (1.1) положено, что момент инерции на валу влияет на угловое ускорение только во время, когда сумма вращающего и тормозящего моментов не равна нулю. Такая модель учитывает изменения момента вращения в динамике, во время разгона и торможения двигателя.
Но, на частоту вращения вала может сказываться и изменение момента инерции в процессе динамического равновесия ускоряющего электромагнитного момента АД и тормозящего момента на его валу. Действительно, пусть АД приводит в движение ленту транспортера или мельницу. При этом, на ленту или в барабан подается материал, и если подача осуществляется неравномерно, то момент инерции, приведенный к валу АД будет меняться.
При добавлении материала, в силу закона сохранения импульса (или момента импульса) скорость ленты или частоты вращения барабана будет в первый момент уменьшаться, а затем двигатель в меру возможностей (жесткости рабочего участка ЕМХ) будет восстанавливать рабочую частоту.
Если же момент вращения, приведенный к валу уменьшится, то двигатель этого не заметит, поскольку, например, если с ленты упадет большой камень, это не повлияет на скорость ленты. Камень унесет с собой импульс, не тормозя и не ускоряя ленту.
Итак, при добавлении инерционности, следует учитывать закон сохранения момента импульса
(6.1)

Отсюда
(6.2)

Поскольку, как было показано, в вышеназванных транспортных задачах только увеличение момента инерции приводит в уменьшению частоты вращения вала, а уменьшение момента инерции не сказывается на частоте вращения, то для ускорения вала получим выражение:
(6.3)

частота вращения вала:
(6.4)

и вращающий момент
(6.5)

Отметим, что изменение момента инерции, приведенного к валу на практике сопровождается и изменением момента сопротивления (торможения) на валу, которое двигатель компенсирует, изменяя вращающий момент. При моделировании это изменение момента сопротивления следует учитывать.
В итоге, схема модели принимает вид:

Рис.6.1. Механодинамическая модель асинхронного двигателя с регулированием пускового момента, с дискретным (Вкл - Выкл - Реверс) и с непрерывным (частота и напряжение сети) управлением и учетом влияния скорости изменения момента инерции на частоту вращения вала и вращающий момент в транспортных задачах (увеличение момента инерции уменьшает скорость двигателя, а уменьшение момента инерции не влияет на нее)
Отметим, что приведенная модель справедлива для двигателей, работающих в качестве привода транспортных устройств (конвейер, барабан мельницы и т.п.). Если же момент инерции меняется без потери вращающейся (движущейся) массы, то изменение момента вращения как в сторону увеличения, так и в сторону уменьшения будет сопровождаться соответствующим обратным изменением скорости вращения, и в уравнении (6.3) ускорение будет определяться верхним равенством как при положительных, так и при отрицательных скоростях изменения момента вращения. Поэтому в модели рис. 6.1 нужно будет убрать ограничитель снизу производной совокупного момента вращения.

Рис. 6.2. Динамика АД при изменении управляющих воздействий и возмущений при учете влияния скорости увеличения момента инерции на частоту вращения вала и вращающий момент в приводах транспортных машин
Модель см. в Приложении
Механодинамические модели асинхронных двигателей содержат их основную инерционность, наглядны и могут быть использованы для моделирования управляемых приводов в системах управления. Управление моделями может быть как дискретным, так и непрерывным по частоте (скалярное управление), с учетом главных возмущений - момента сопротивления на валу и момента инерции, приведенного к валу АД.
Архив файлов моделей bt_354_AD_MechDin_Mdl_Appl.zip (953 КБ), выполненных в программе Vissim (версия 6) и Маткад (версии 10 и 14) и снимки экрана в составе:
18.03.2011
* * *
<< К началу статьи
model.exponenta.ru
Данная работа является продолжением опубликованной статьи [1], в которой были подробно показаны без сокращений способы и технологии получения пространственных векторов  ,
,  ,
, 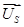 ,
,  ,
, 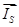 ,
, 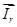 , в системе абсолютных едениц. Для неподвижной системы координат, основное уравнение в векторной форме переведены в систему относительных едениц.
, в системе абсолютных едениц. Для неподвижной системы координат, основное уравнение в векторной форме переведены в систему относительных едениц.
В работах [2; 3] приведено множество вариантов конечных результатов электромагнитного момента в зависимости от произведения проекций двух векторов 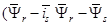 и т.д.). В этой статье сделан вывод одного из множества математических моделей асинхронного двигателя и сравнение полученных уравнений и структурной схемы с фундаментальной работой [3].
и т.д.). В этой статье сделан вывод одного из множества математических моделей асинхронного двигателя и сравнение полученных уравнений и структурной схемы с фундаментальной работой [3].
Система уравнений описывающих АД с короткозамкнутым ротором в неподвижной системе:
|
|
(1) |
|
(2) |
|
|
(3) |
|
|
(4) |
|
|
(5) |
|
|
(6) |
Так как электромагнитный момент определяется переменными  , то из системы уравнений (1) … (4) исключаем переменные
, то из системы уравнений (1) … (4) исключаем переменные 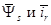 .
.
Из уравнения (4) выразим ток 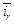 :
:

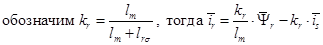 (7)
(7)
Далее, из уравнения (3) исключаем 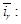
 ,
,
где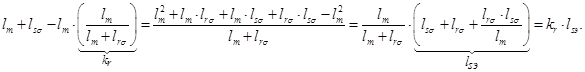
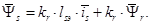 (8)
(8)
Из уравнения (2) исключаем переменную 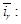
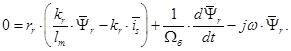 (9)
(9)
Выразим 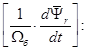
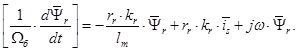 (10)
(10)
Из уравнения (9):
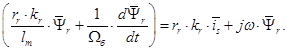
Переведем полученное уравнение из оригинала в изображение 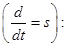
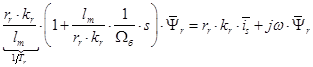 (11)
(11)
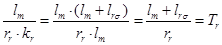
Умножим обе части уравнения (11) на 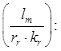
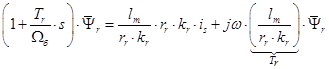
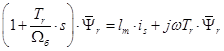 (12)
(12)
Разложим векторы по проекциям: 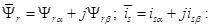
Подставим их в уравнение (12):
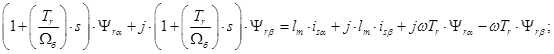 (13)
(13)
Проекция уравнения (13) на ось +1:
 (14)
(14)
Проекция уравнения (14) на ось +j:
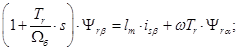 (15)
(15)
Из уравнения (14) определим 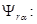
 (16)
(16)
Уравнению (16) соответствует следующая структурная схема (рис. 1):
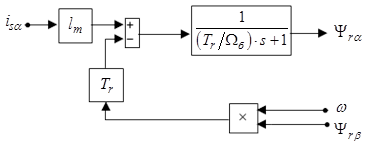
Рис. 1. Структурная схема для определения  .
.
Из уравнения (15) определим 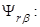
 (17)
(17)
Уравнению (17) соответствует следующая структурная схема (рис. 2):

Рис. 2. Структурная схема для определения  .
.
В уравнении (1) подставим 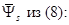
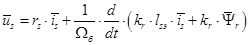
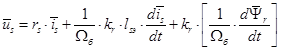
Подставим значение  из уравнения (10):
из уравнения (10):
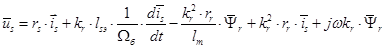

Переведем полученное уравнение из оригинала в изображение 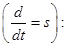
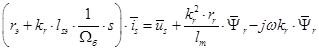


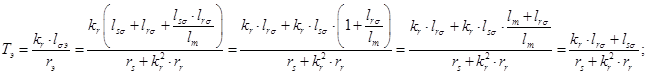
 (18)
(18)
Разложим векторы по проекциям:
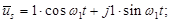


Подставим их в уравнение (18):
 (*)
(*)
Проекция уравнения (*) на ось +1:
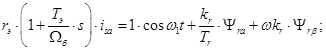 (19)
(19)
Проекция уравнения (*) на ось +j:
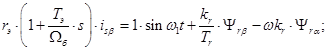 (20)
(20)
Из уравнения (19) выразим статорный ток 
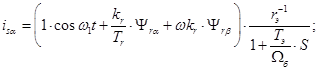 (21)
(21)
Уравнению (21) соответствует следующая структурная схема (рис. 3):

Рис. 3. Структурная схема для определения 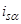 .
.
Из уравнения (20) выразим статорный ток 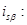
 (22)
(22)
Уравнению (22) соответствует следующая структурная схема (рис. 4):
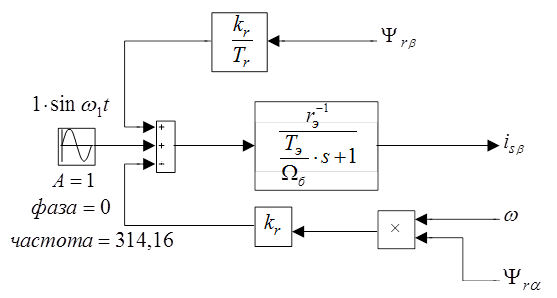
Рис. 4. Структурная схема для определения  .
.
Электромагнитный момент определяется по формуле (5)
 (**)
(**)
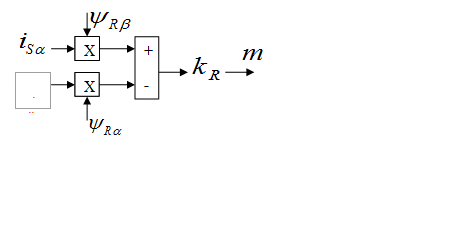
Структурная схема для реализации уравнения (5) дана на (рис. 5):
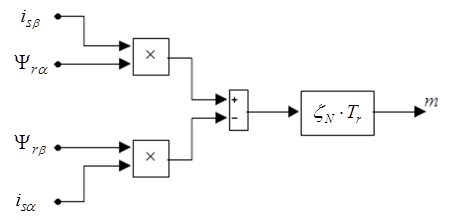
Рис. 5. Структурная схема для определения электромагнитного момента.
Наконец, для уравнения (6) структурная схема (рис. 6):
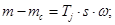

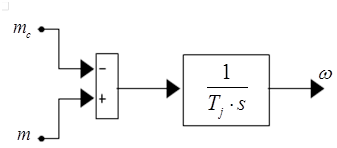
Рис. 6. Структурная схема для определения скорости.
В работе Шрейнера в главе 6 «Примеры» дан образец расчета параметров асинхронного двигателя. В наших дальнейших работах направленных на подготовку студентов к исследовательской работе, глава 6 окажет неоценимую помощь. Можно было бы по аналогии рассмотреть паспортные данные любого другого двигателя, но для проверки правильности выводов уравнений сделанных исследовательской группой самостоятельно, необходимо постоянно выходить на многие полученные результаты в работе [3]. Поэтому, этот пример рассчета окажется очень полезным.
Номинальные данные:
Номинальный режим работы S1;
Номинальная мощность 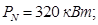
Номинальное фазное напряжение 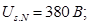
Номинальный фазный ток 
Номинальная частота 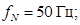
Номинальная синхронная скорость 
Номинальная скорость ротора 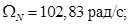
Номинальный КПД 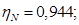
Номинальный коэффициент мощности 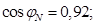
Число пар полюсов 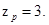
Параметры Т-образной схемы замещения при номинальной частоте:
Активное сопротивление обмотки статора 
Инуктивное сопротивления рассеяния обмотки статора 
Активное сопротивление обмотки ротора, приведенное к статору 
Индуктивное сопротивление рассеяния обмотки ротора, приведенное статору 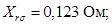
Главное индуктивное сопротивление 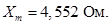
Базисные величины системы относительных единиц:
Напряжение 
Ток 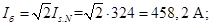
Частота 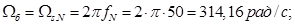
Скорость ротора 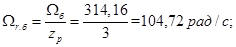
Сопротивление 
Потокосцепление 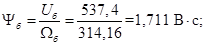
Индуктивность 
Используя номинальные данные двигателя, определяем:

где 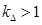 – коэффициент, учитывающий различие значений электромагнитного момента и момента на валу двигателя в номинальном режиме (
– коэффициент, учитывающий различие значений электромагнитного момента и момента на валу двигателя в номинальном режиме (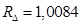 ).
).
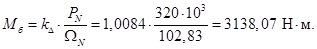
В качестве базисной мощности выбираем значение электромагнитной мощности двигателя в номинальном режиме, определяемое по следующей формуле:
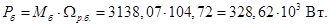
Относительные значения параметров схемы замещения двигателя:
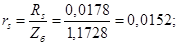
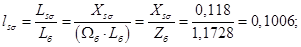
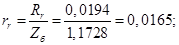

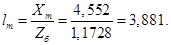
Механическая постоянная времени:
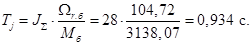
Номинальное значение скольжения:
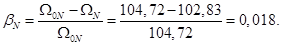
Относительное значение номинальной скорости ротора:
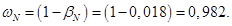
Нормирующий энергетический коэффициент:
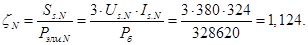

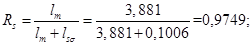
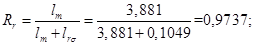
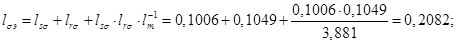
При расчете режимов работы, для того чтобы 

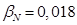 необходимо откорректировать
необходимо откорректировать 
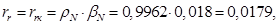
где 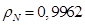 – корректирующий коэффициент [5, с. 296].
– корректирующий коэффициент [5, с. 296].
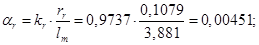
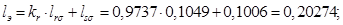

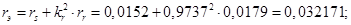
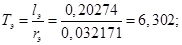

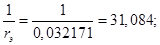
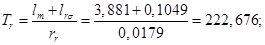
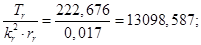

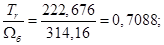
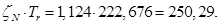
Математическая модель асинхронного двигателя в неподвижной системе координат представлена на рисунке 7. Результаты математического моделирования приведены на рисунках 8…10.
moluch.ru
Емельянов А. А., Медведев А. В., Медведев А. В., Кобзев А. В., Шепельков А. В., Зарубин Е. А., Воробьев А. Н. Математическая модель асинхронного двигателя во вращающейся системе координат c переменными // Молодой ученый. 2011. №5. Т.1. С. 7-15. URL https://moluch.ru/archive/28/3216/ (дата обращения: 26.06.2018).
При выполнении студентами дипломных и курсовых работ, связанных с моделированием асинхронного двигателя, возникает необходимость увеличения вариантов их модификаций. Одним из способов решения этой задачи является возможность выразить электромагнитный момент через различную комбинацию переменных токов и потокосцеплений двигателя [1, c.238] и [2]. Данная статья позволяет сформировать у студентов представление об одном из множества вариантов моделирования АД в «Matlab-Simulink». Вывод уравнений даем без сокращений, т. к. важен не только конечный результат, но и путь, ведущий к цели.
Основные уравнения математической модели АД, записаны в векторной форме в относительных единицах, имеют следующий вид [3]:
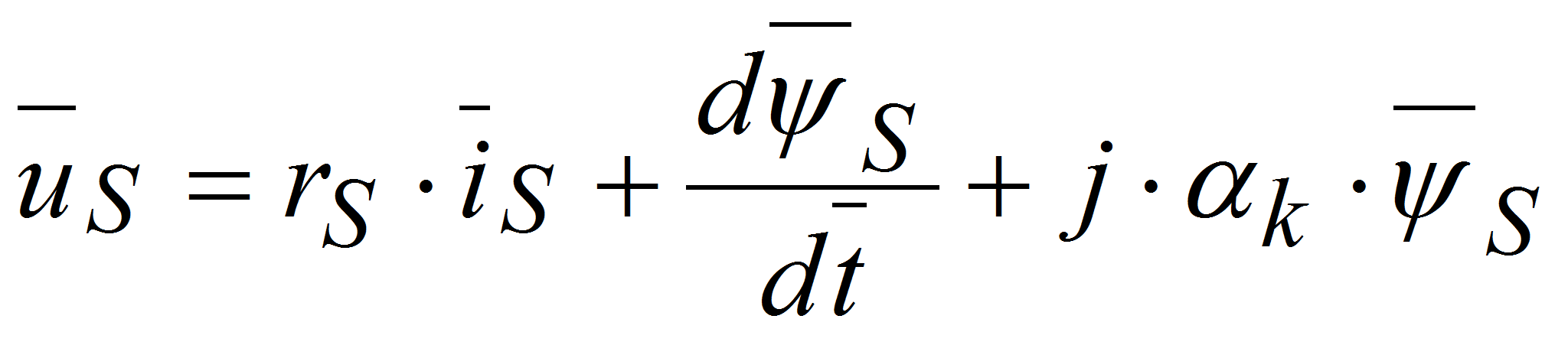
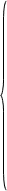 (1)
(1)
 (2)
(2)
 (3)
(3)
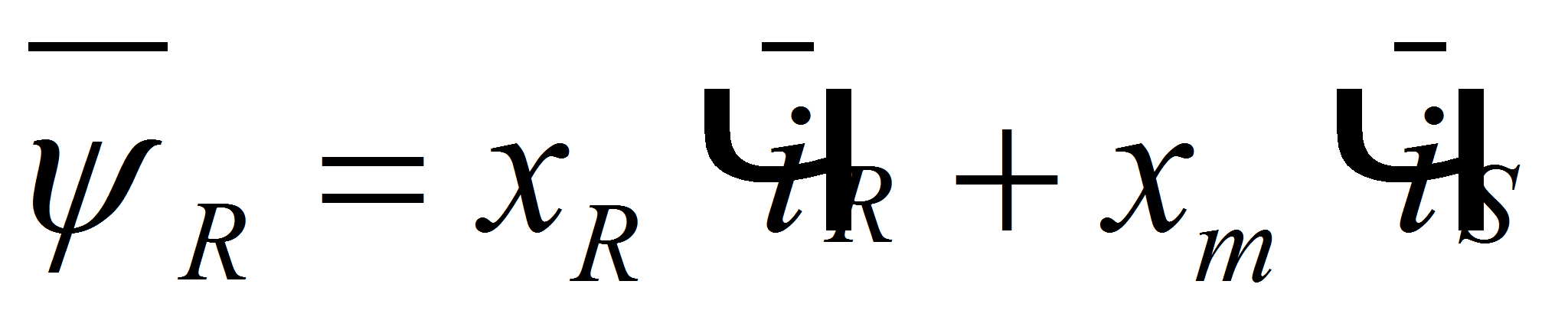 (4)
(4)
Рассмотрим асинхронный двигатель с К.З. ротором (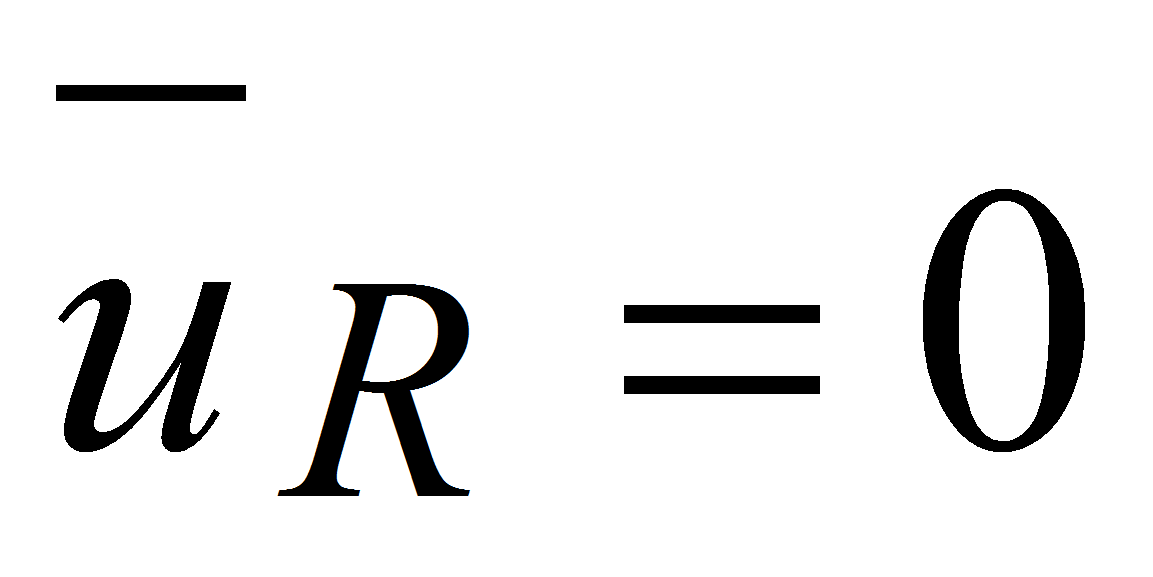 ),
кроме того, определим электромагнитный момент по следующей формуле
[1, с.238]
),
кроме того, определим электромагнитный момент по следующей формуле
[1, с.238]
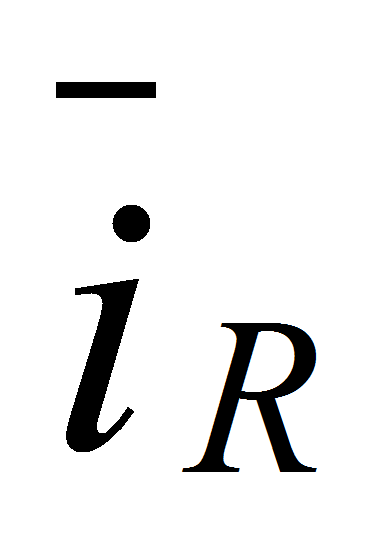 тогда,
тогда,
 .
.
Подставим
 в (3) уравнение:
в (3) уравнение:
 .
.
Обозначим
 и
и
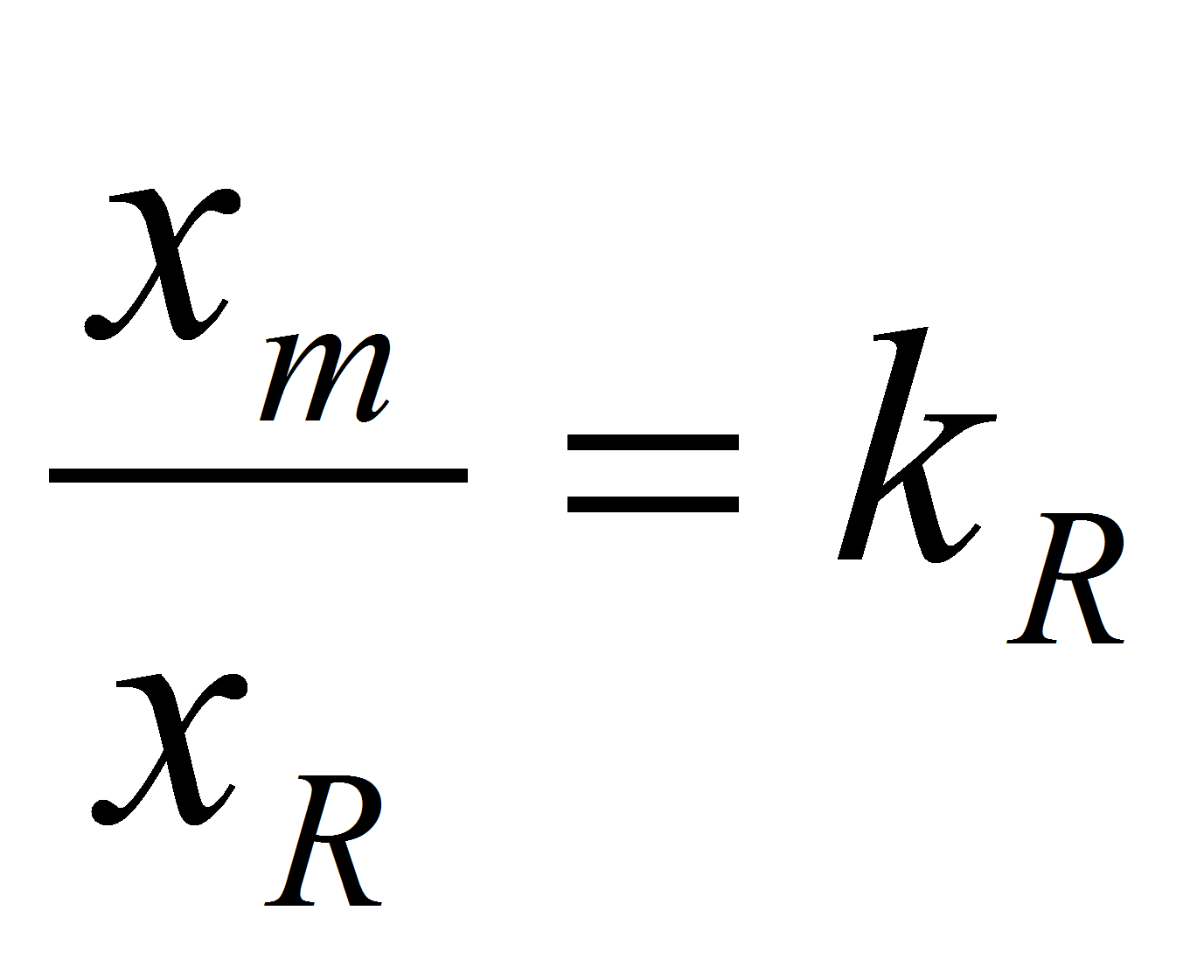 ,
тогда
,
тогда
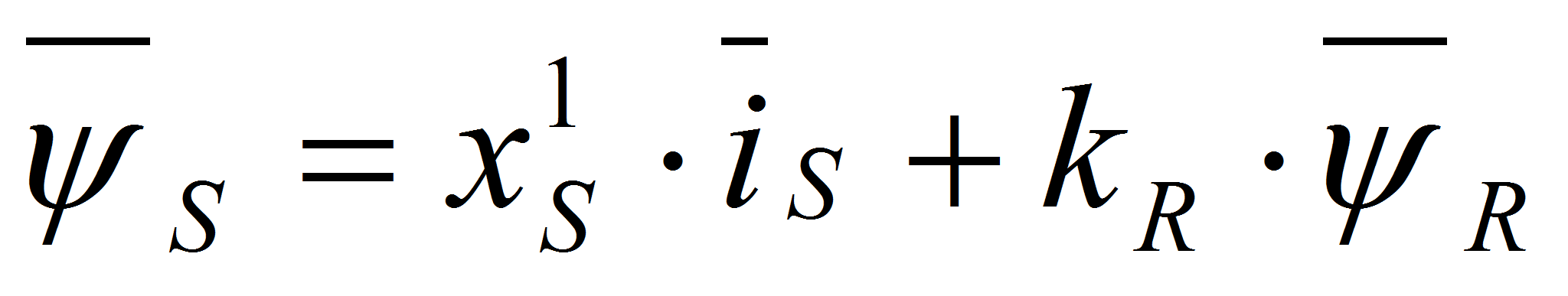
В уравнении (2) исключим
 :
:
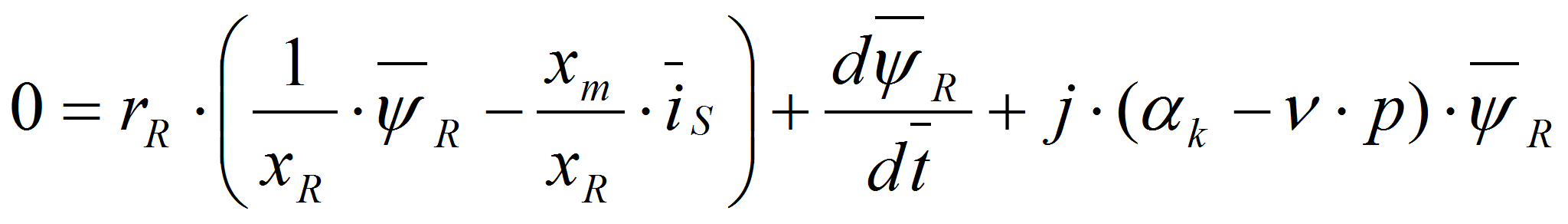 ,
,
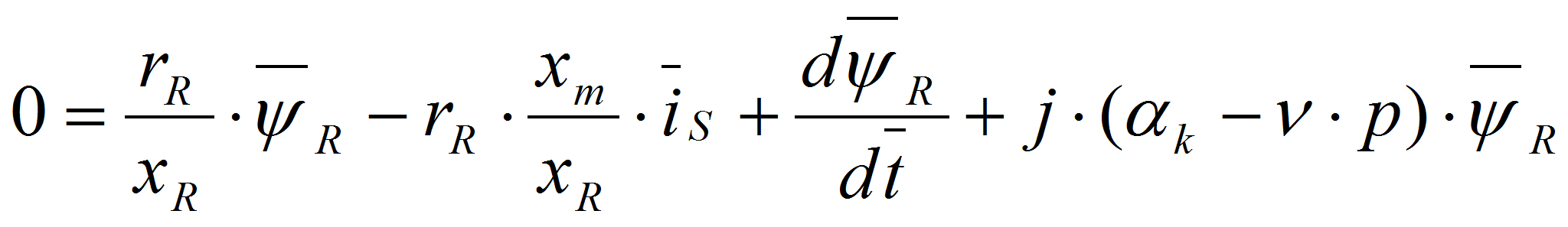 .
.
Обозначим
 ,
тогда:
,
тогда:
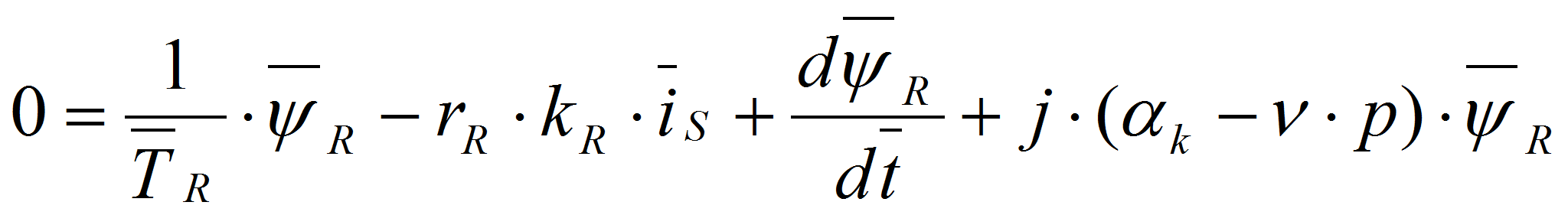 .
.
Из последнего уравнения выделим
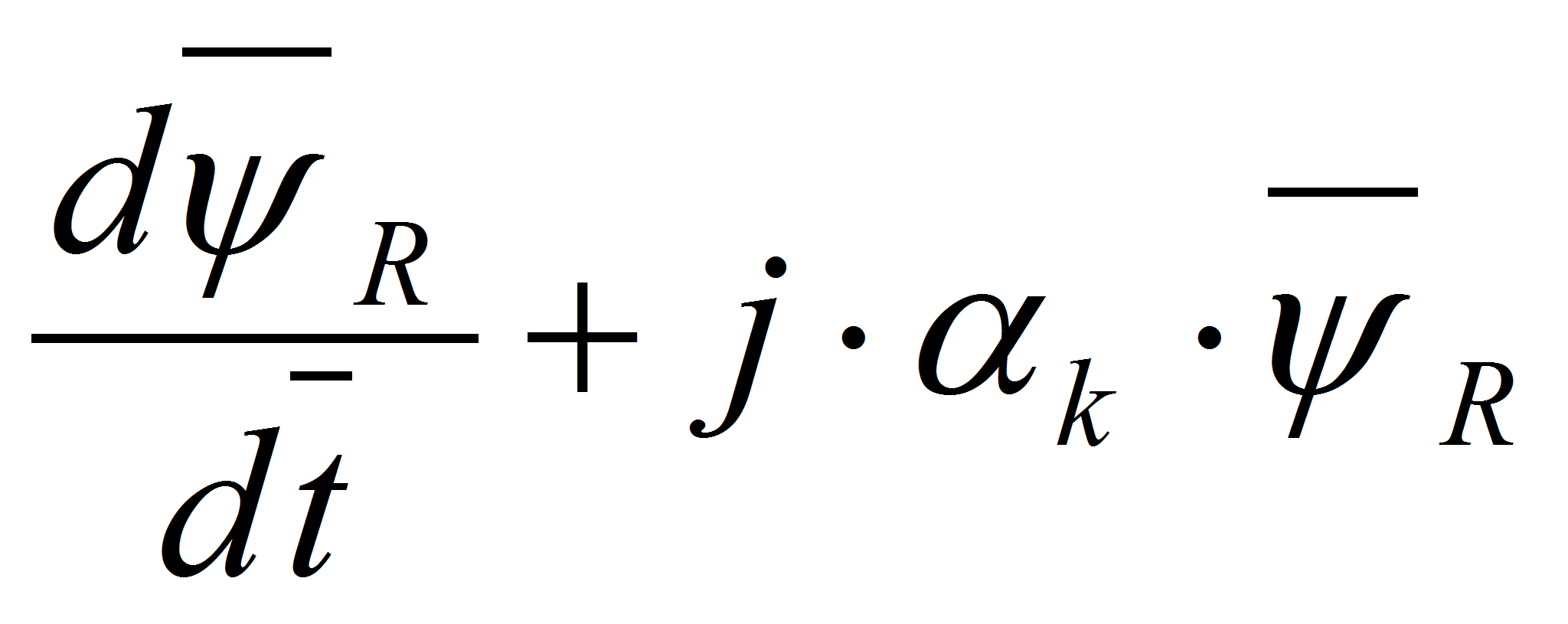 ,
которые в дальнейшем подставим в уравнение (1):
,
которые в дальнейшем подставим в уравнение (1):
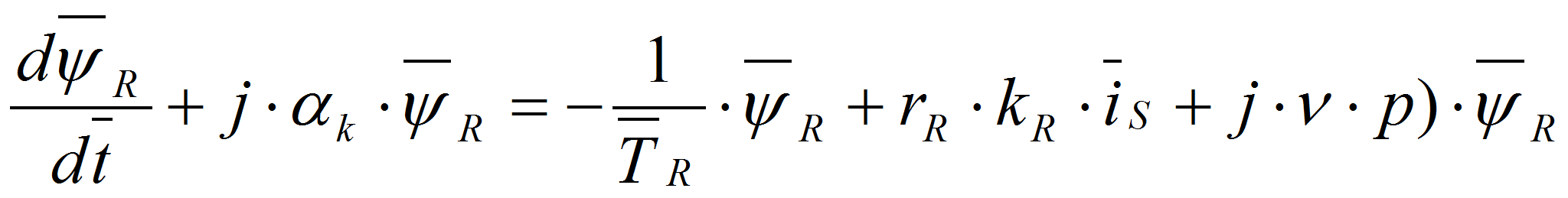
В уравнение (1) сделаем следующие преобразования:
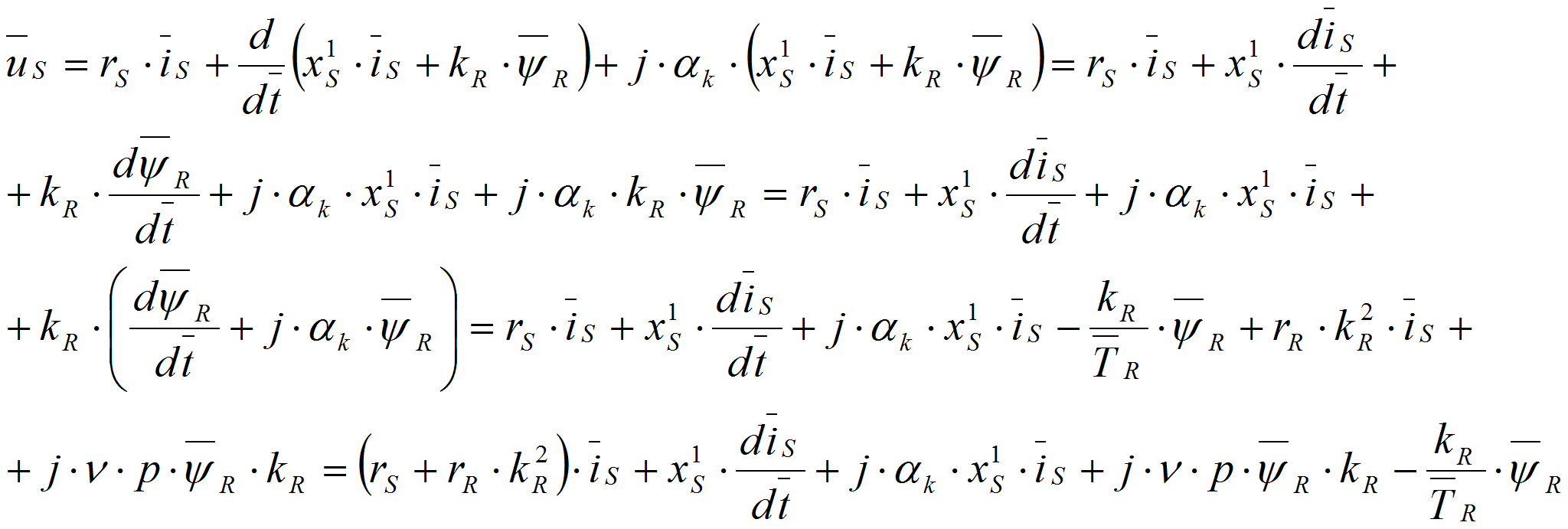
Обозначим
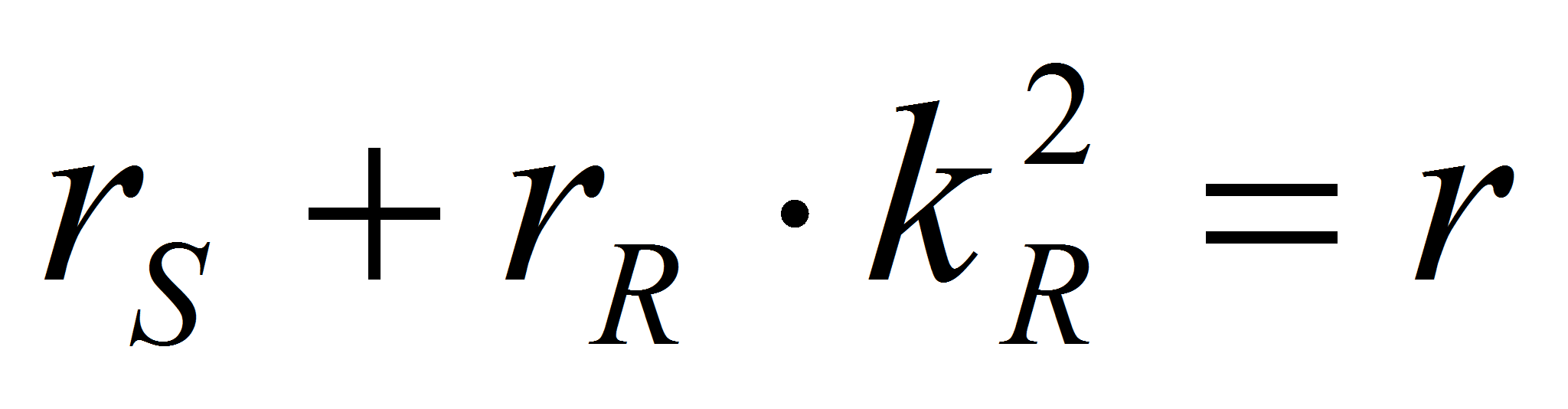 ,
тогда:
,
тогда:
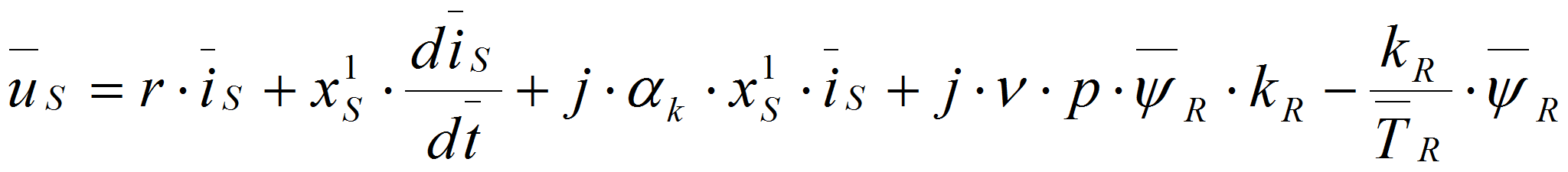 .
.

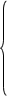
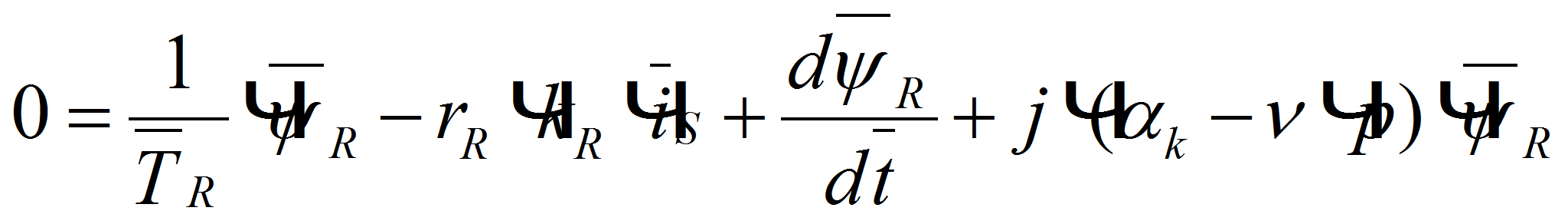
Вещественную ось обозначим , а мнимую через . Пространственные векторы в этом случае раскладываются по осям:
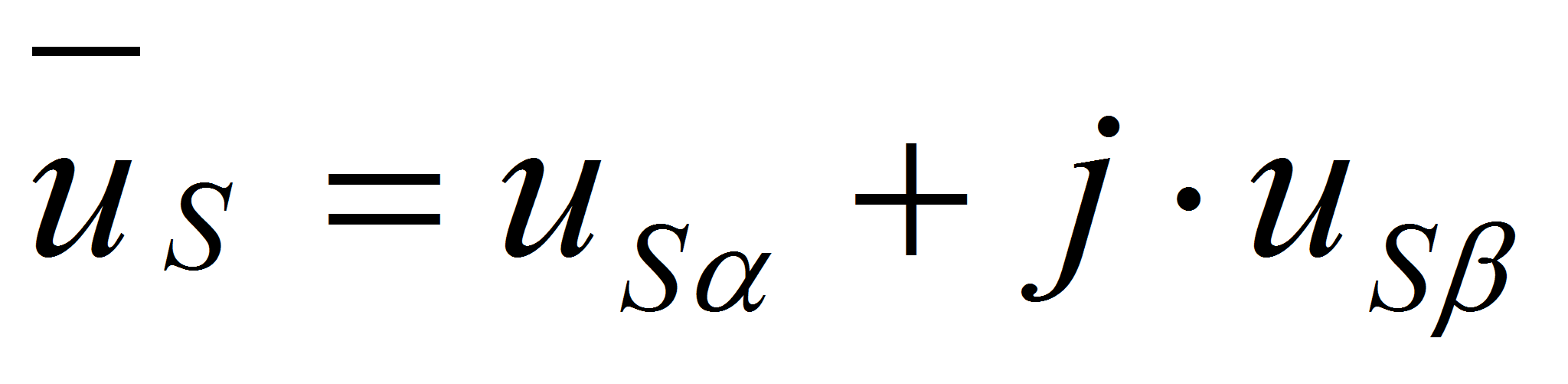 ;
;
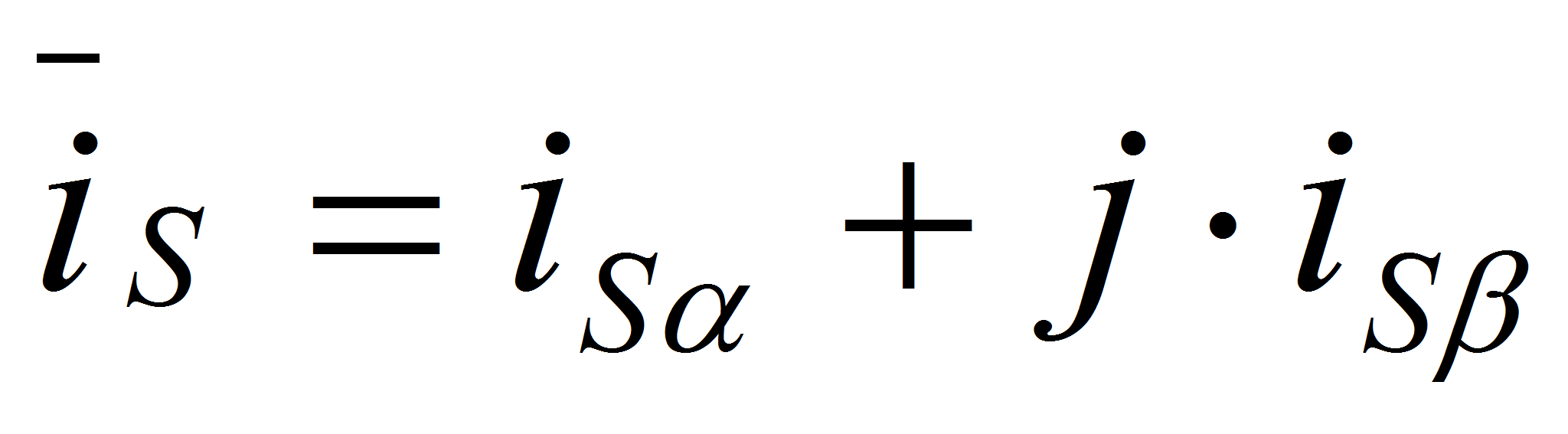 ;
;
 .
.
Подставим эти значения в уравнения и, приравняв отдельно вещественные и мнимые части, получим:


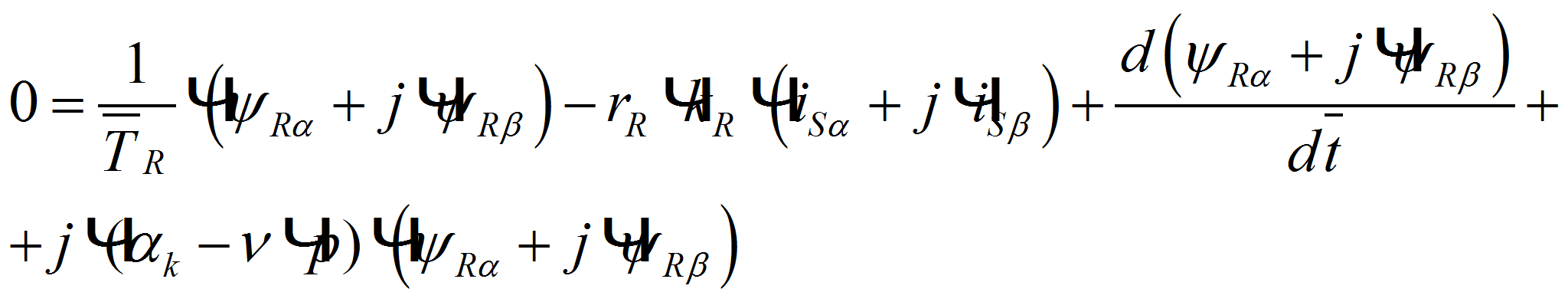
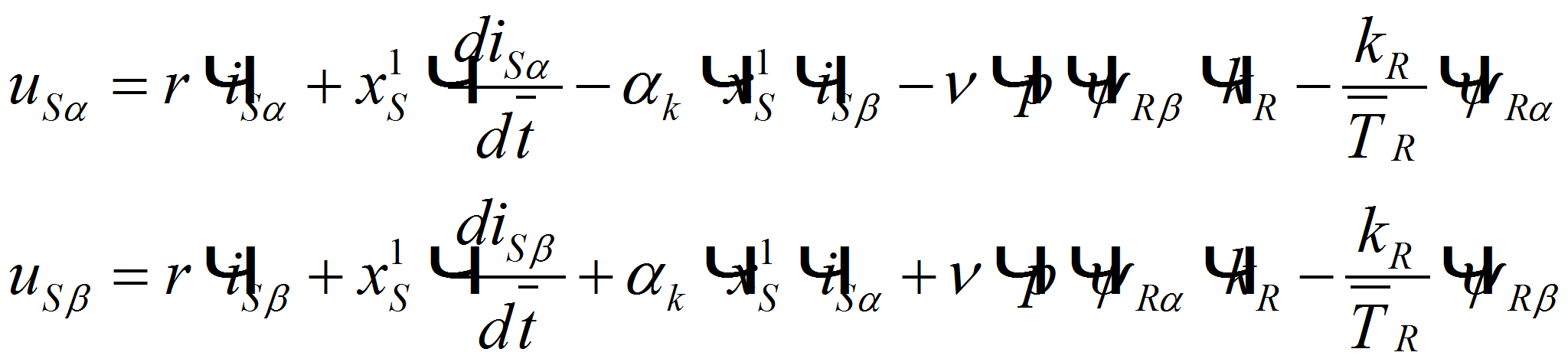

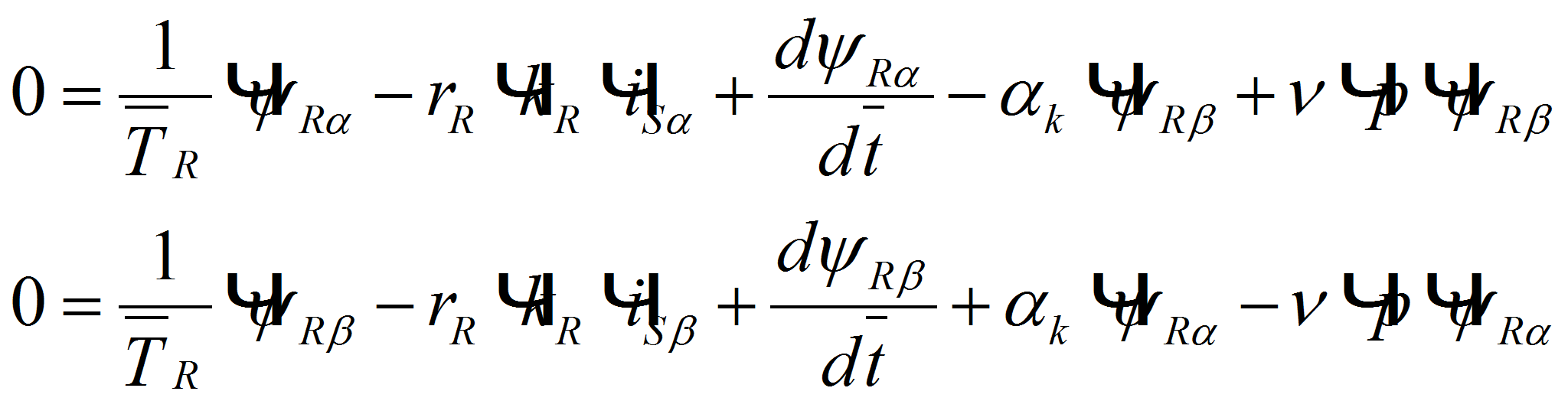
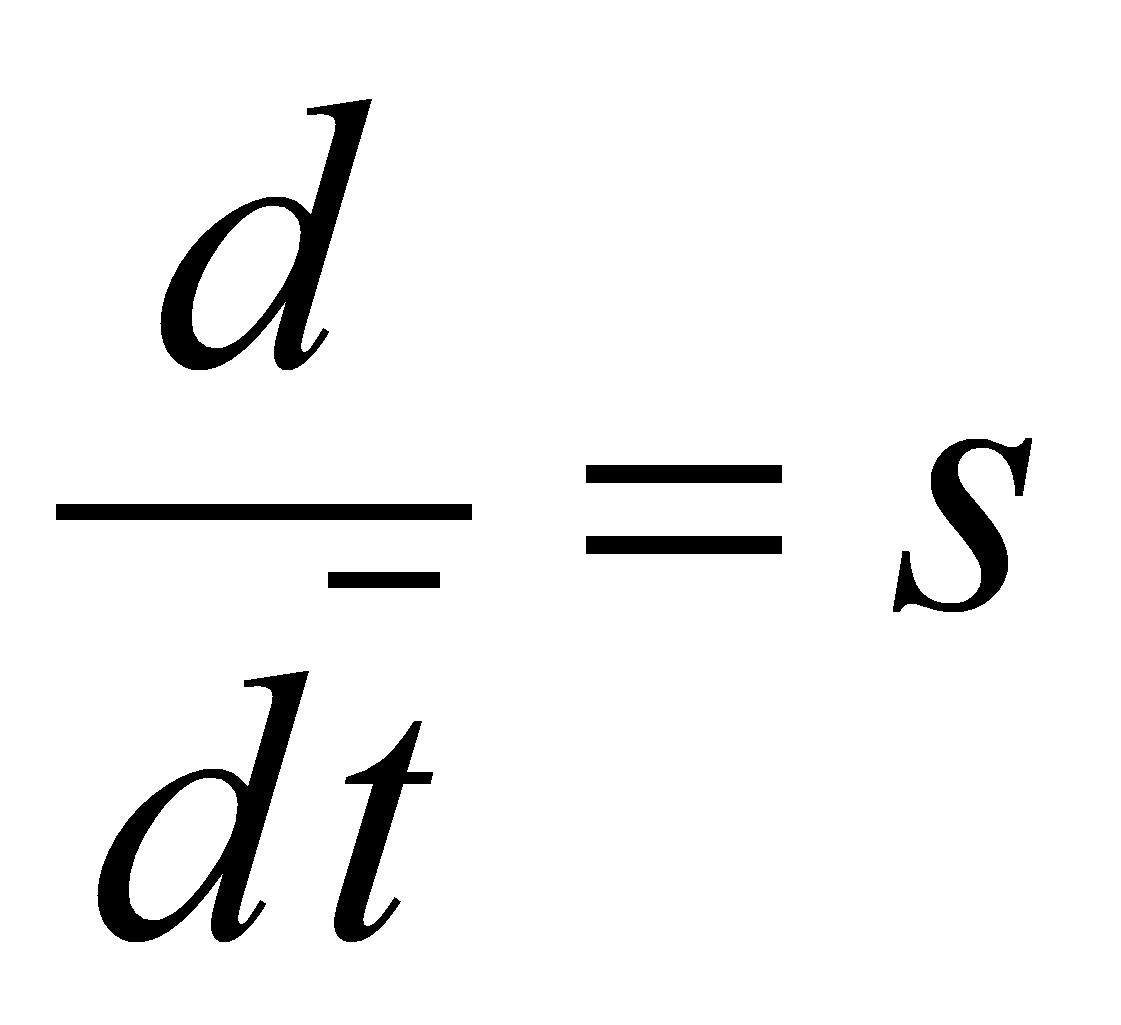 примет вид:
примет вид:

 (1)
(1)
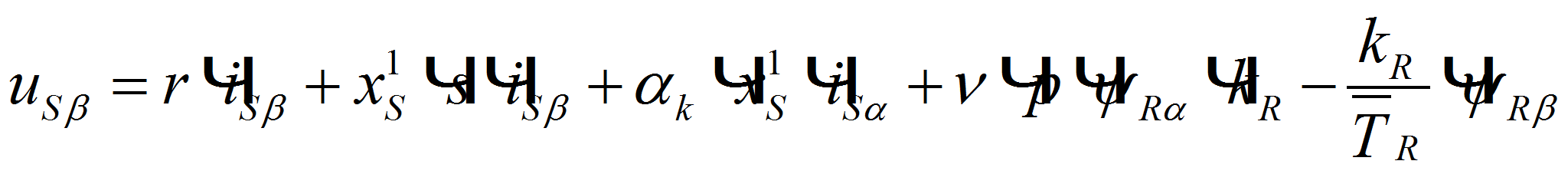 (2)
(2)
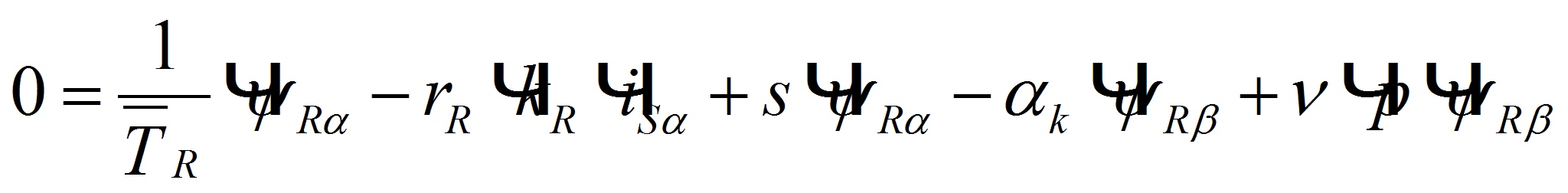 (3)
(3)
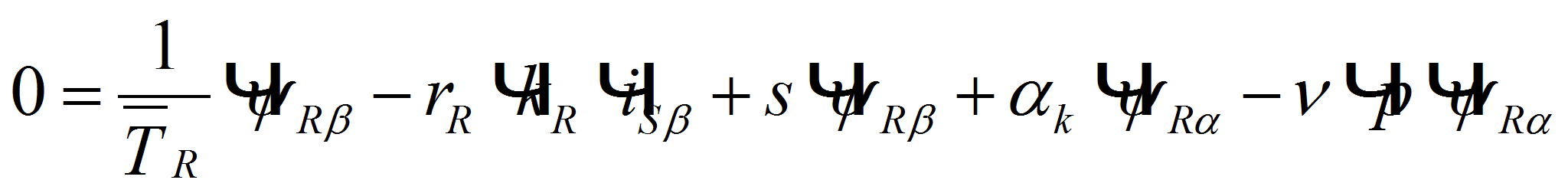 (4)
(4)
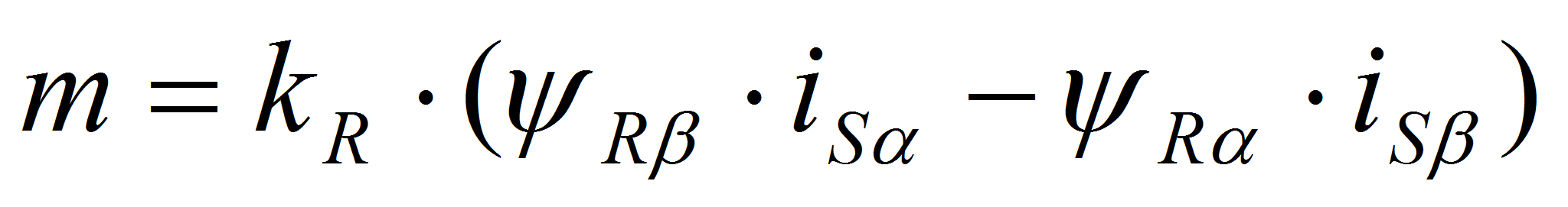 (5)
(5)
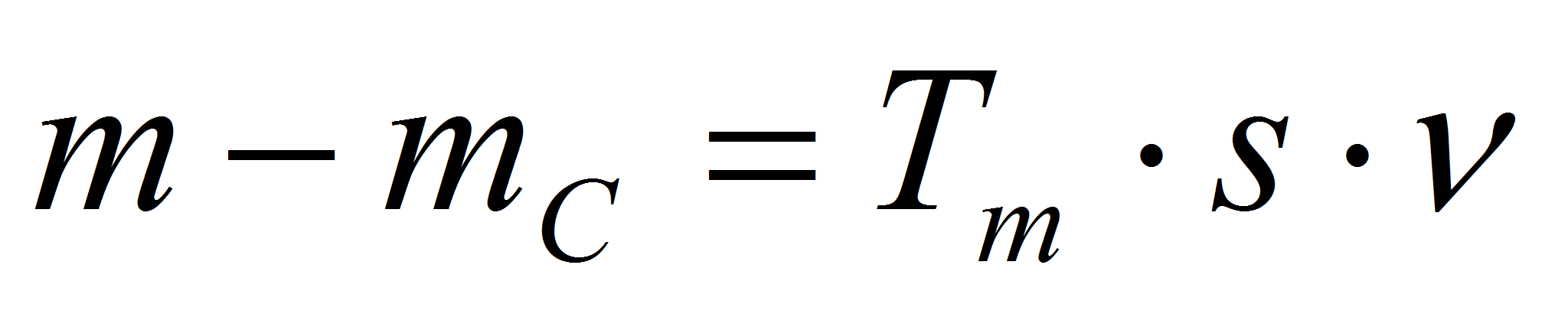 (6)
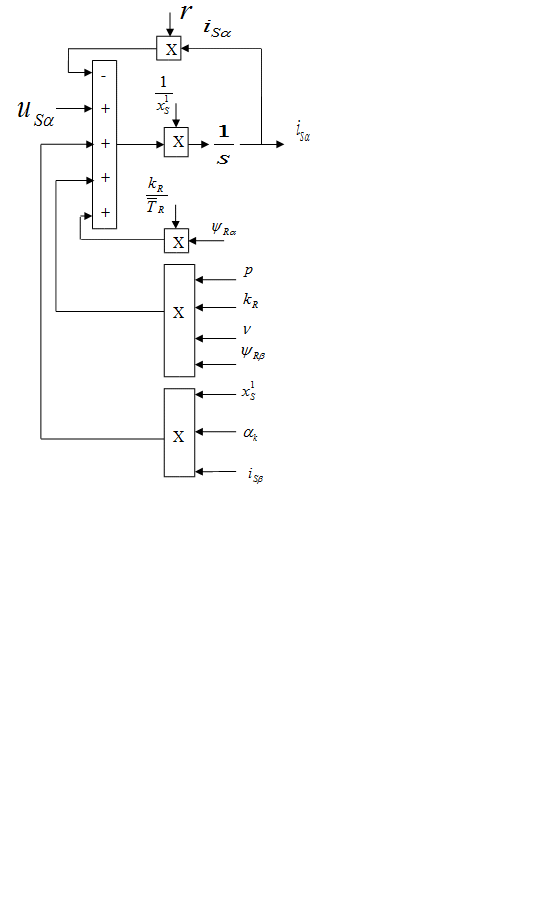
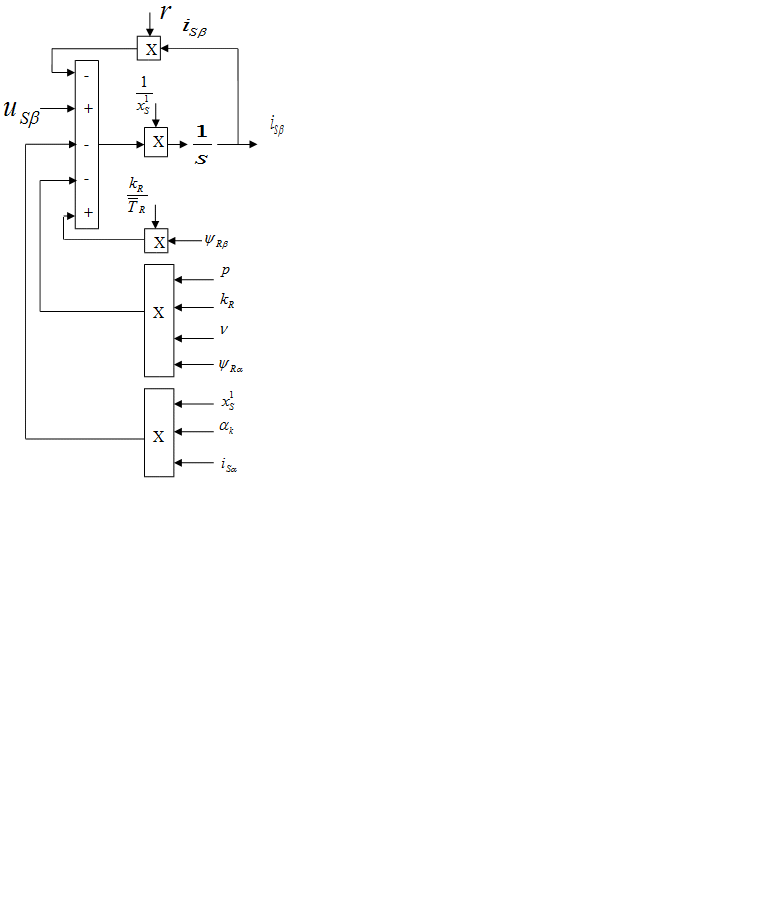
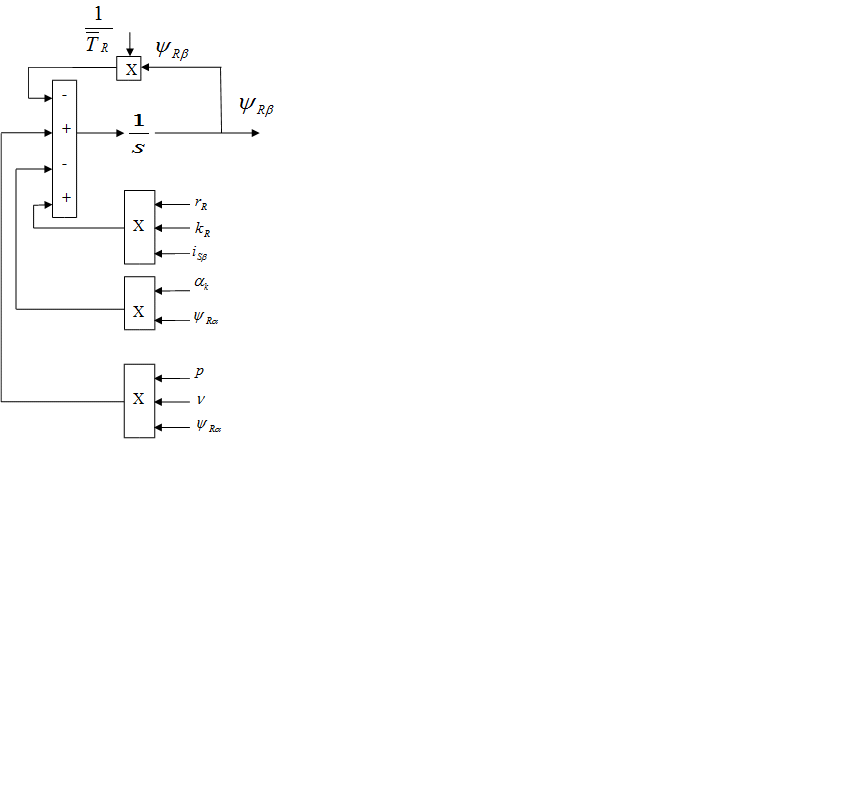
Структурная схема для уравнений (1) и (2):
(6)
Структурная схема для уравнений (1) и (2):
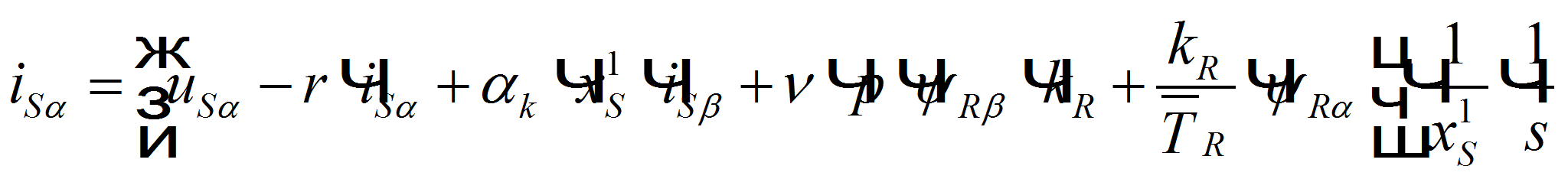




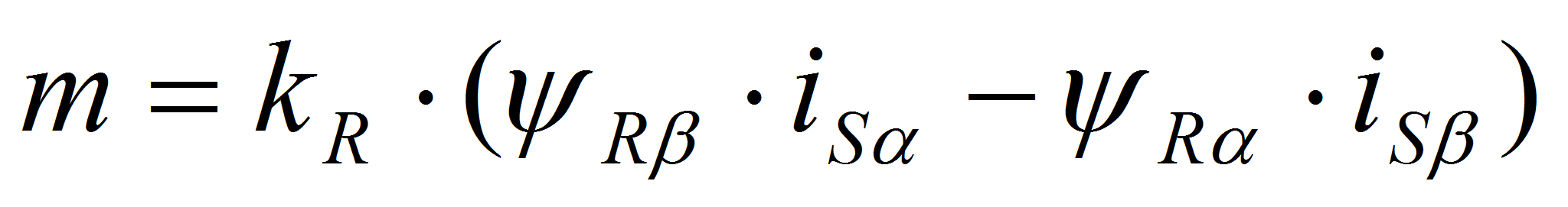
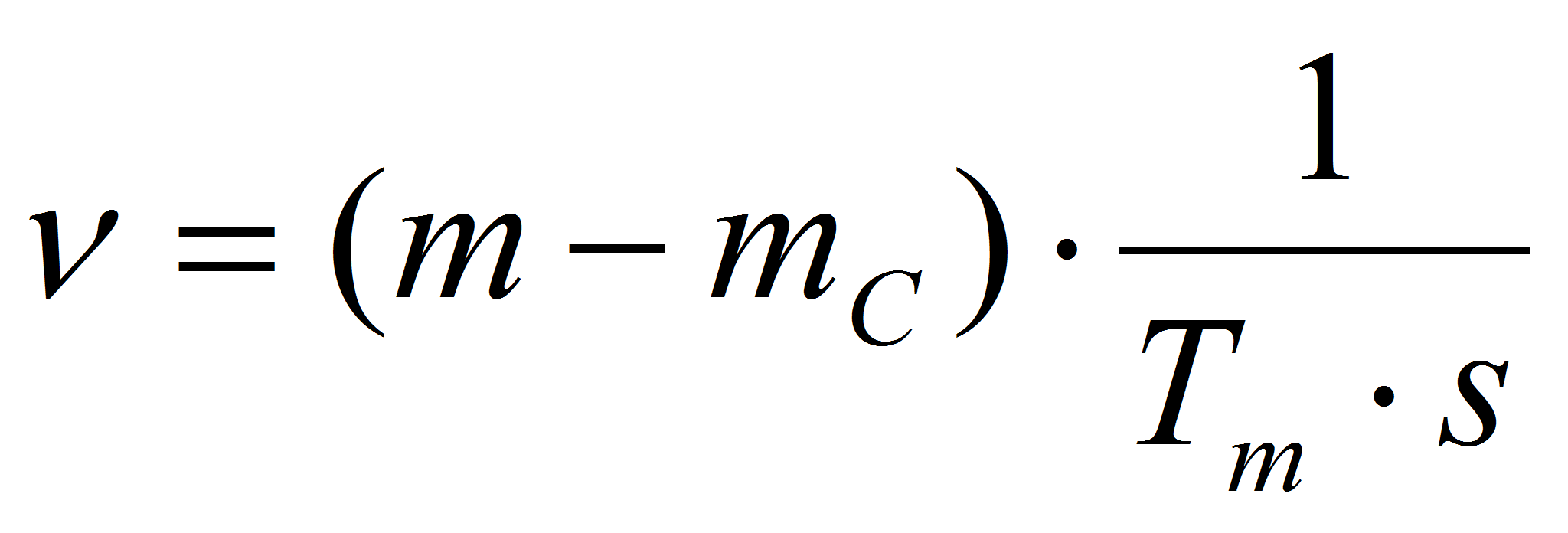

Рассмотрим трехфазный асинхронный короткозамкнутый двигатель со следующими номинальными данными и параметрами схемы замещения [4].
Номинальные данные:
номинальная мощность…………………………………………………
номинальное фазное напряжение……………………………………..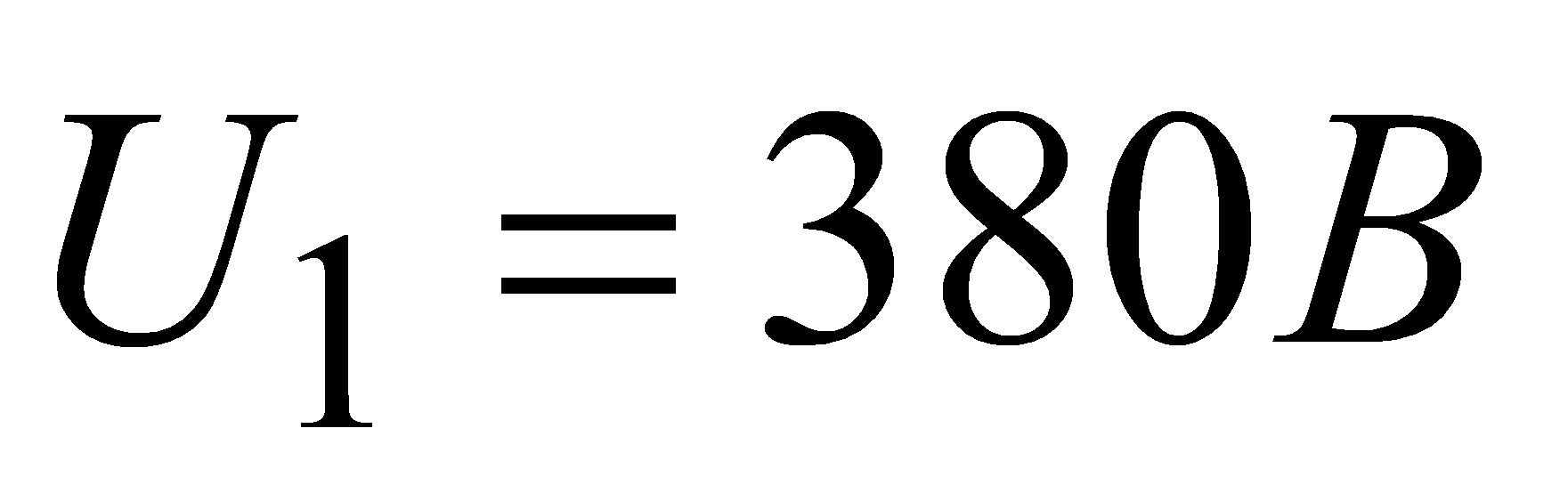
номинальный фазный ток……………………………………………...
номинальная частота……………………………………………………
номинальная синхронная скорость……………………………………
номинальная скорость ротора………………………………………….
номинальный КПД……………………………………………………...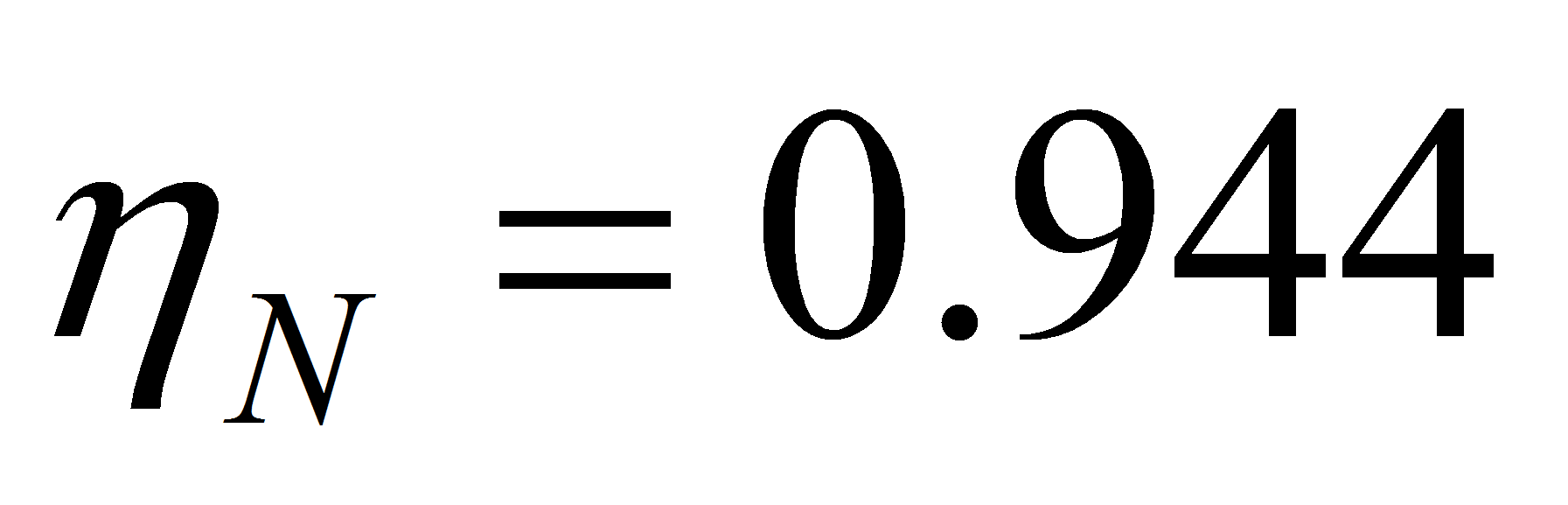
номинальный коэффициент мощности……………………………….
число пар полюсов………………………………………………………
Параметры Т-образной схемы замещения при номинальной частоте:
активное сопротивление обмотки статора…………………………….
индуктивное сопротивление рассеянья обмотки статора……………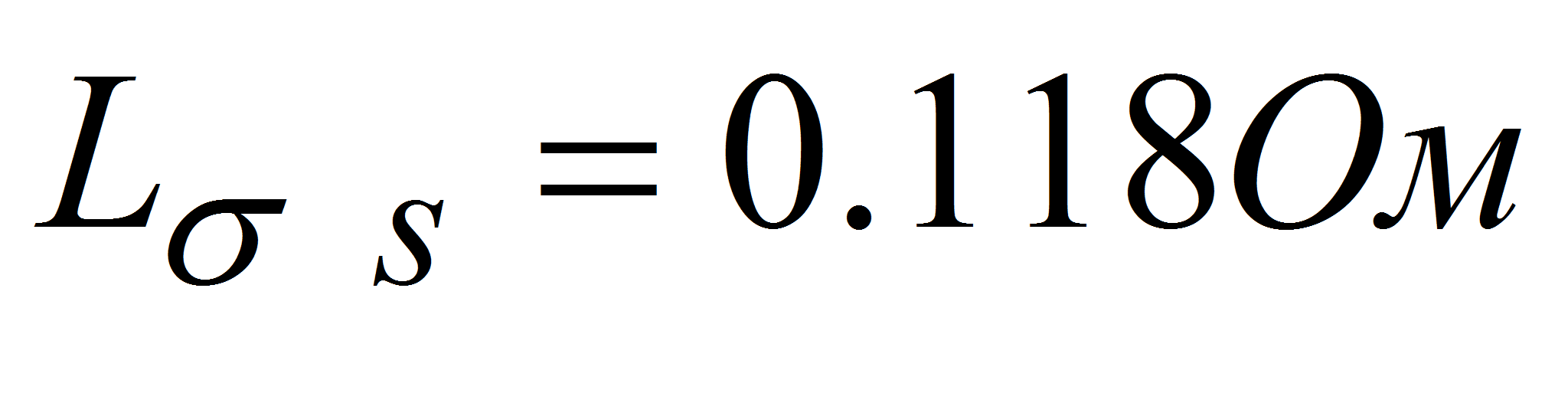
активное сопротивление обмотки ротора, приведенное к статору….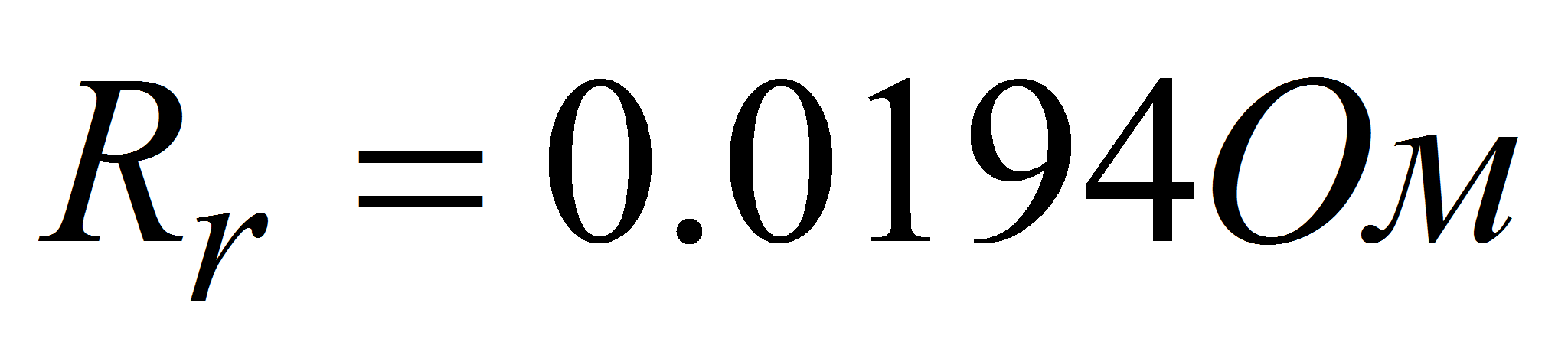
индуктивное сопротивление рассеянья обмотки ротора, приведенного к
статору…………………………………………………………………………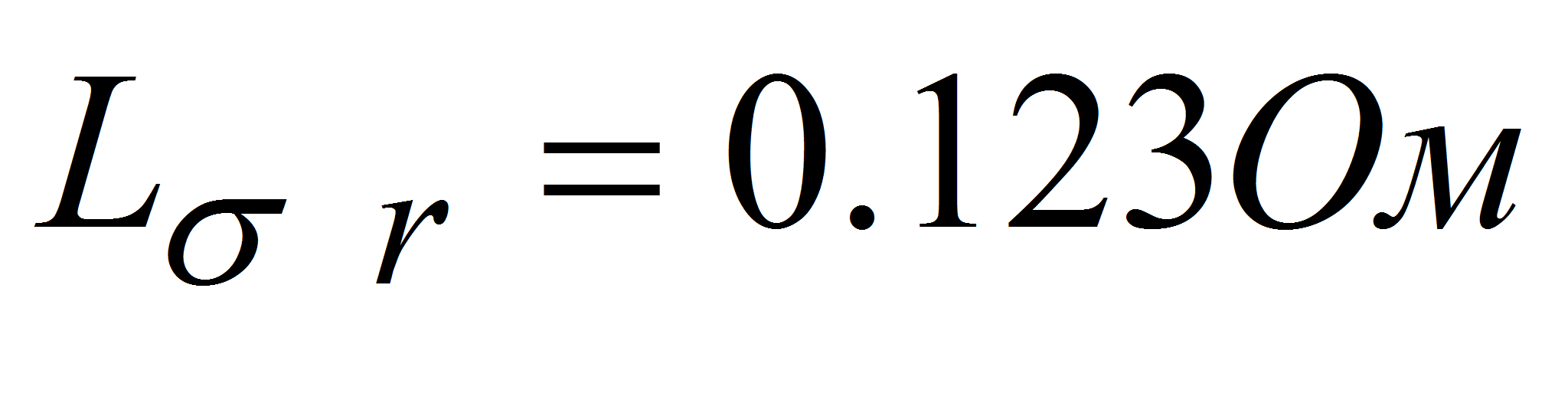
главное индуктивное сопротивление…………………………………..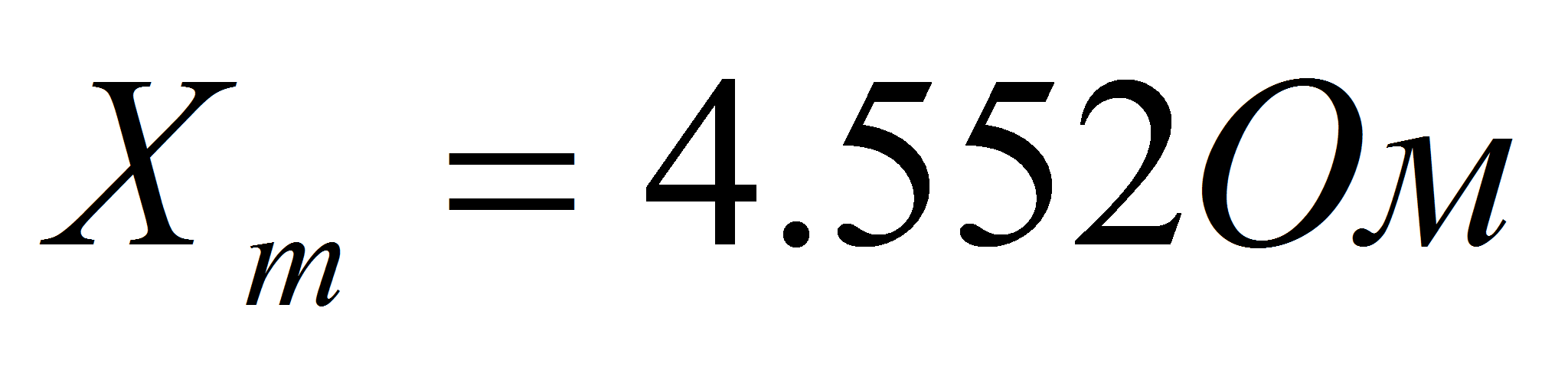
Суммарный момент инерции двигателя и механизма, приведенный к валу
двигателя:
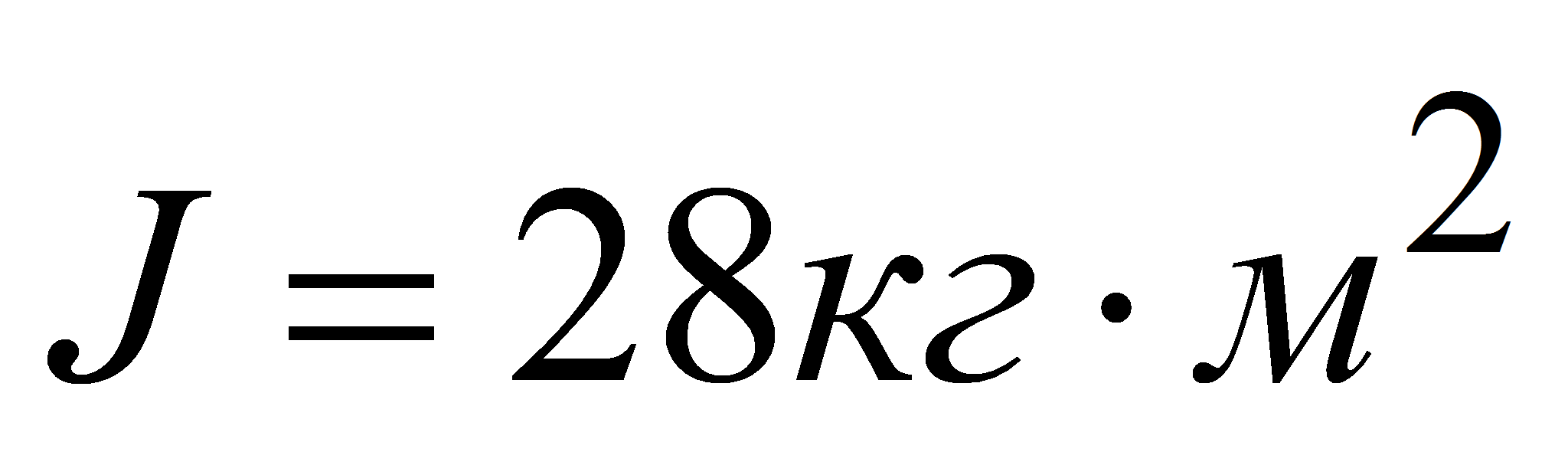
Базисные величины системы относительных единиц.
напряжение……….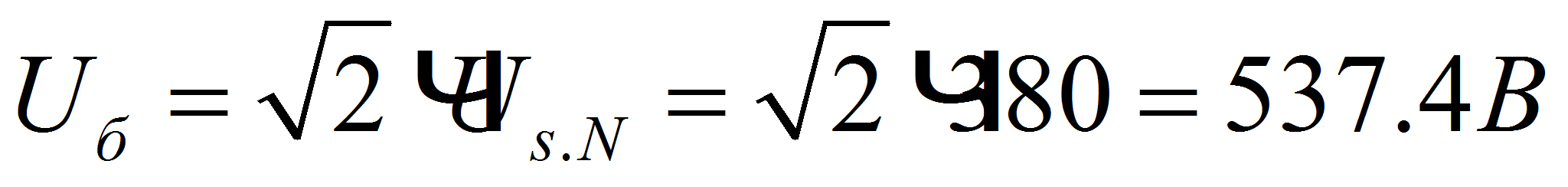
ток………………....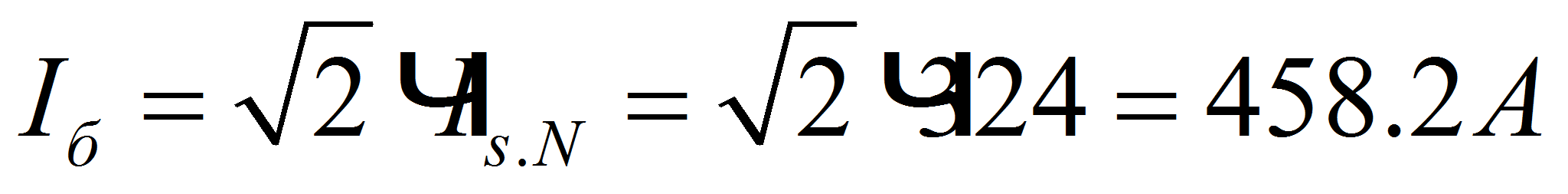
частота…………….
скорость ротора…..
сопротивление……..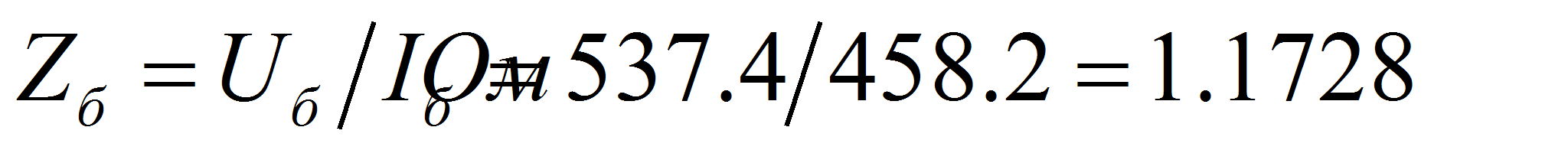
потокосцепление…..
индуктивность……...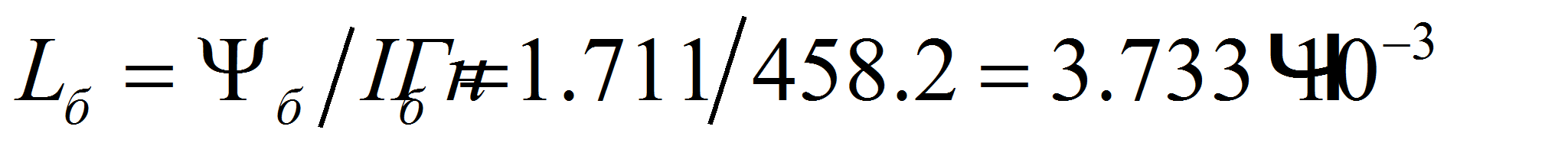
В качестве базисного значения моментов двигателя и статического механизма выбираем значение электромагнитного момента двигателя в номинальном режиме:
 ,
,
где
 – коэффициент, учитывающий различие значений электромагнитного
момента и момента на валу двигателя в номинальном режиме.
– коэффициент, учитывающий различие значений электромагнитного
момента и момента на валу двигателя в номинальном режиме.
В качестве базисной мощности выбираем значение электромагнитной мощности двигателя в номинальном режиме, определяемое по следующей формуле:
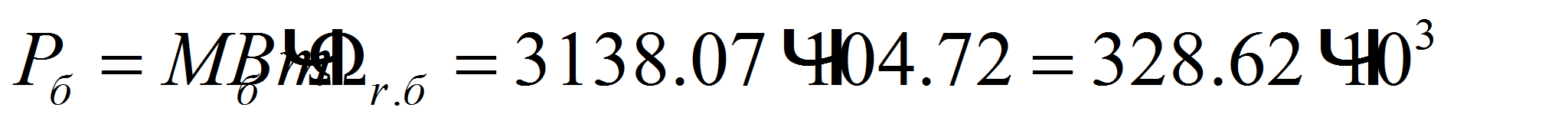 .
.
Относительные значения параметров схемы замещения двигателя.

Механическая постоянная времени системы «двигатель-механизм» составляет:
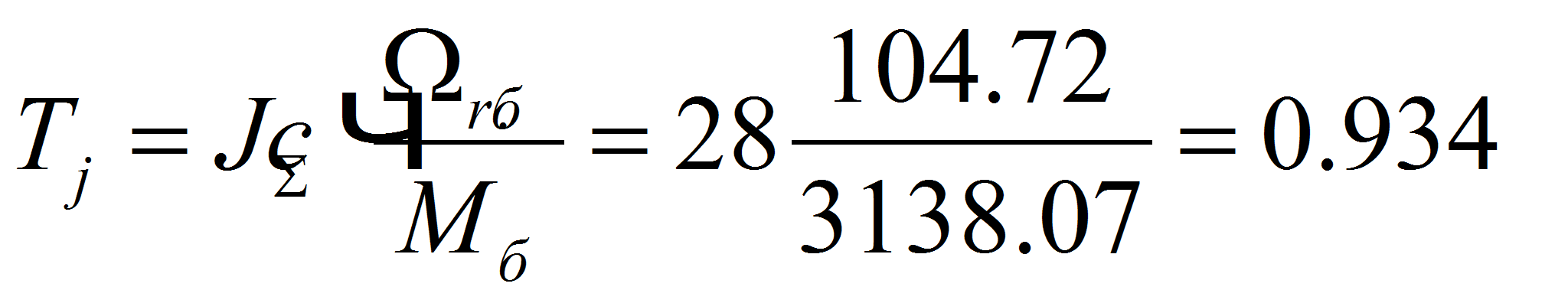 .
.
Значения безразмерных коэффициентов в уравнениях, рассчитанные по выражениям, приведенным выше:
|
Коэффициент |
|
|
|
|
|
|
Значение |
234.639 |
0.974 |
0.031 |
0.203 |
783.496 |
Модель АКЗ, построенная по уравнениям (1) – (6), представленная на рис. 1.
На вход модели в момент времени
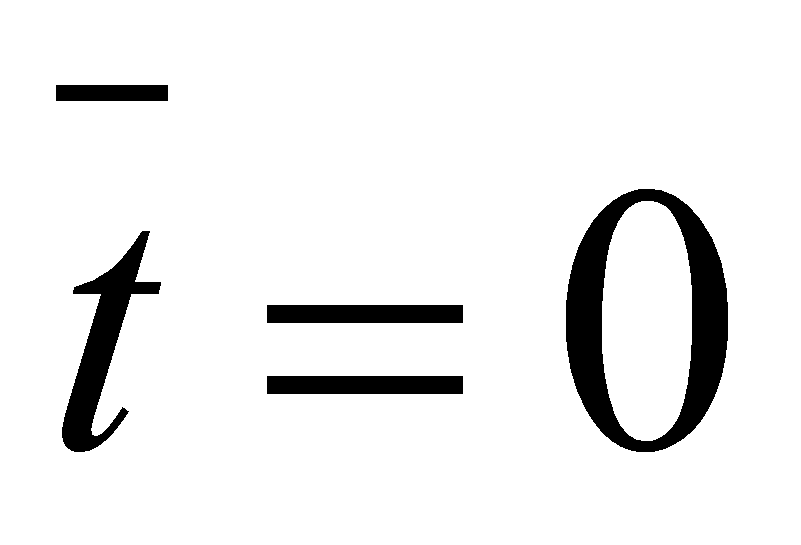 подаются
напряжения
подаются
напряжения
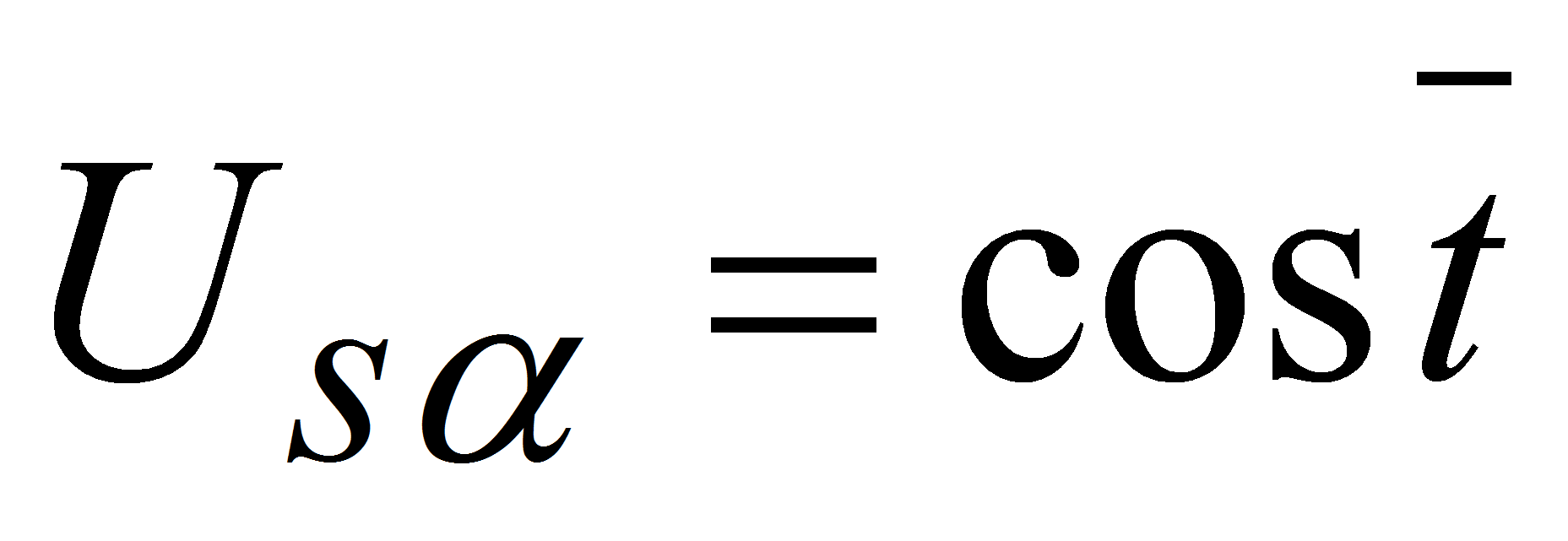 ,
,
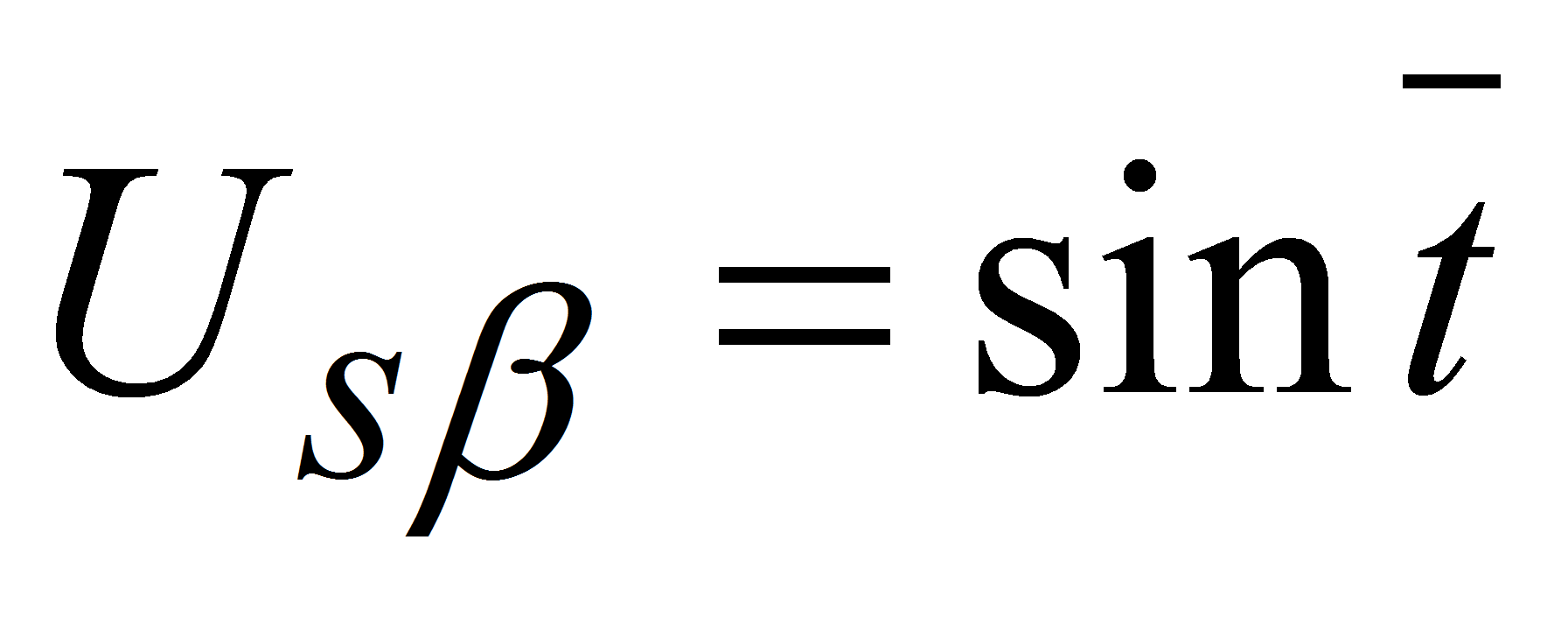 ,
(
,
( ),
тем самым реализуя прямой пуск.
),
тем самым реализуя прямой пуск.
Осциллоскопы измеряют относительные значения электромагнитного момента и скорости. Результаты моделирования представлены на рис. 2. Они показывают, что при прямом пуске вначале наблюдается значительные колебания момента. Такие же колебания наблюдаются в токе и скорости.
Р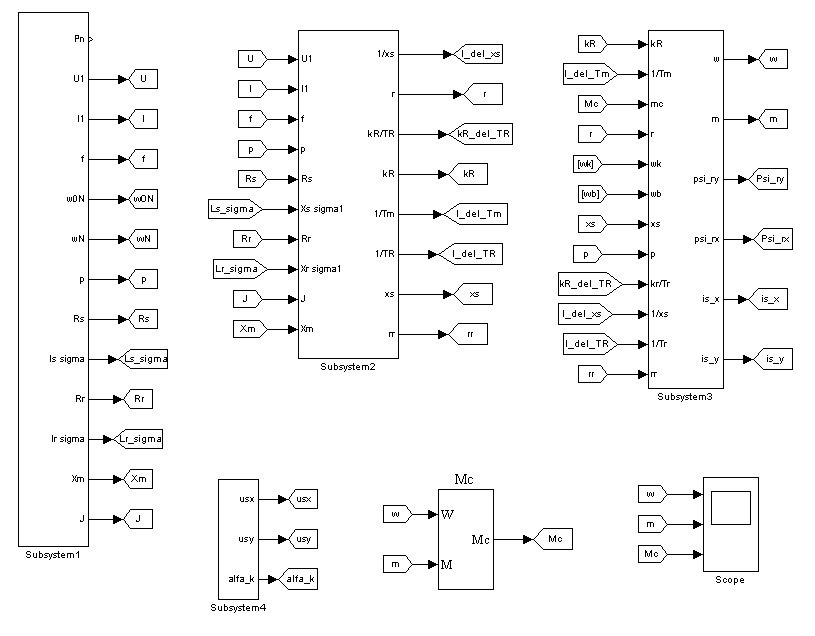 ис.
1.Полная модель АКЗ во вращающейся системе координат с
переменными
ис.
1.Полная модель АКЗ во вращающейся системе координат с
переменными
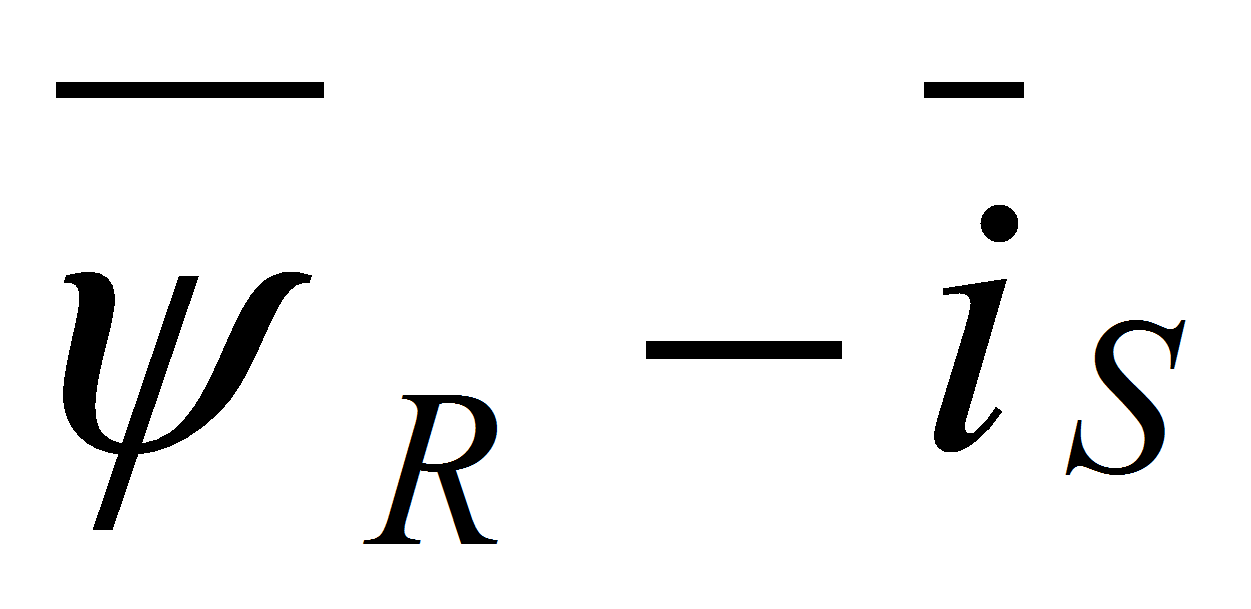

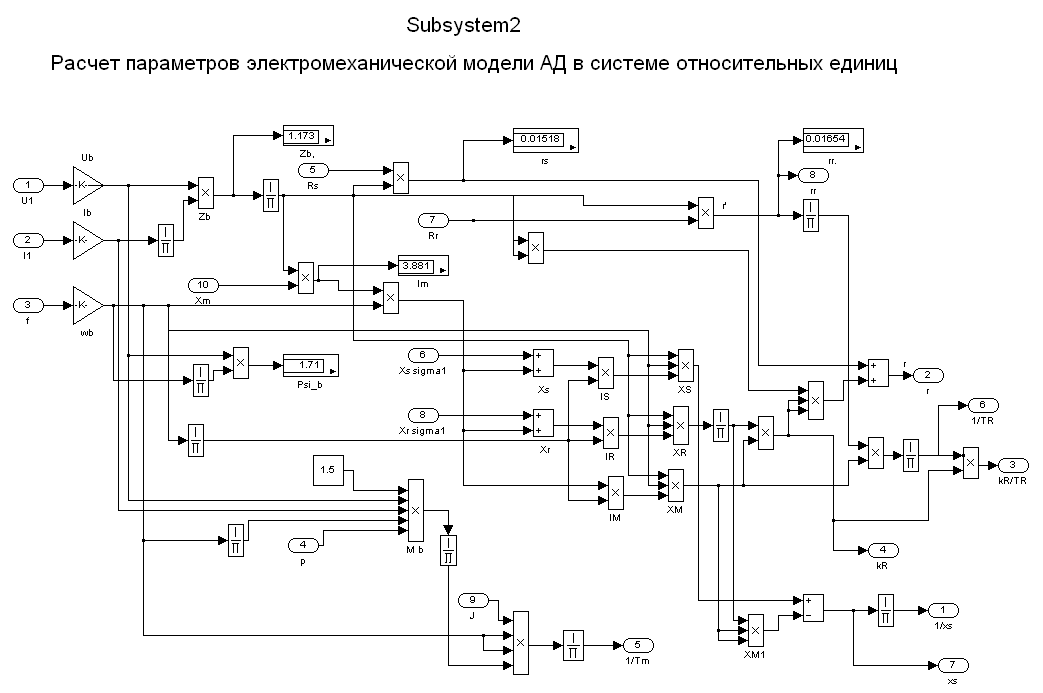
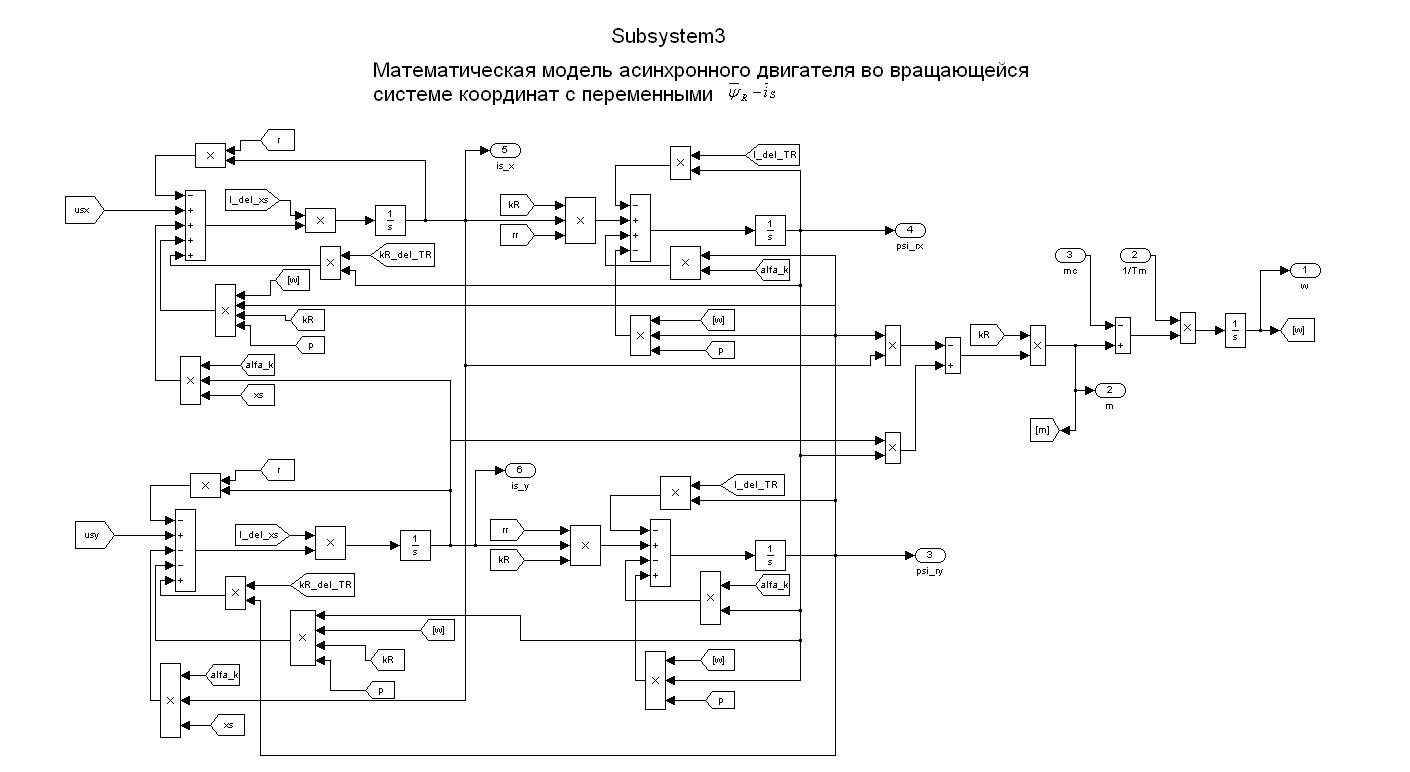
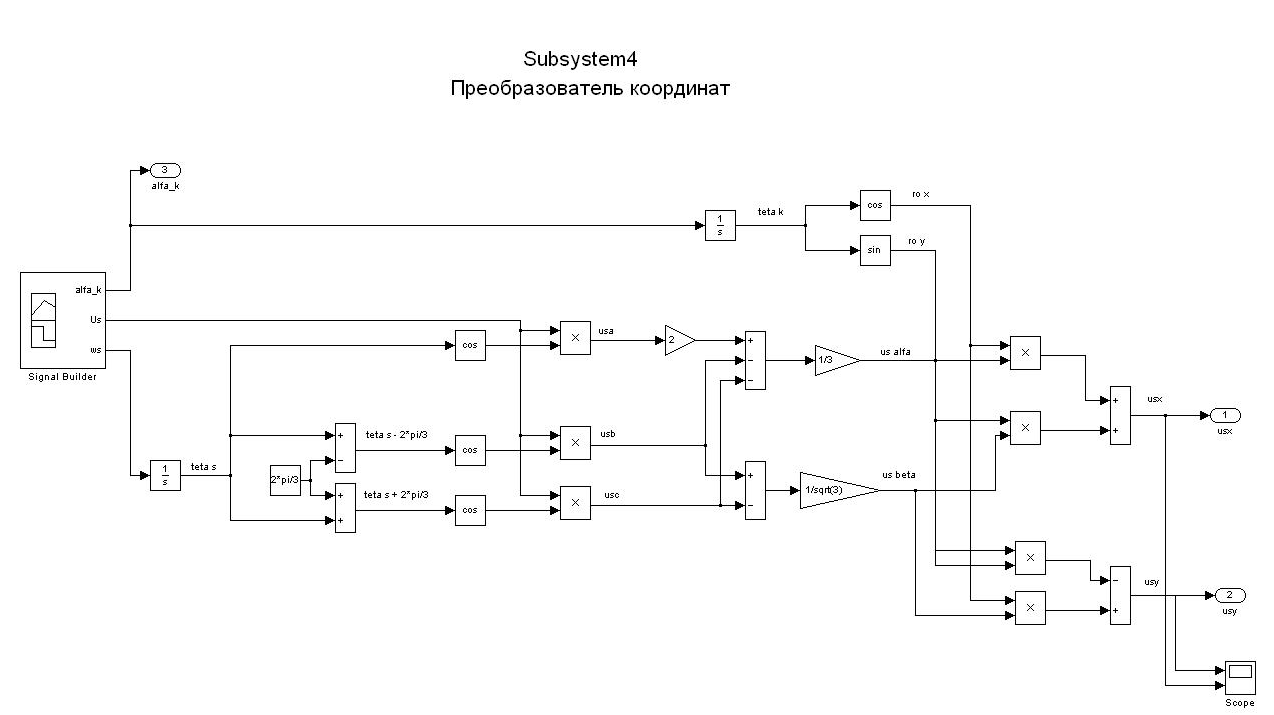
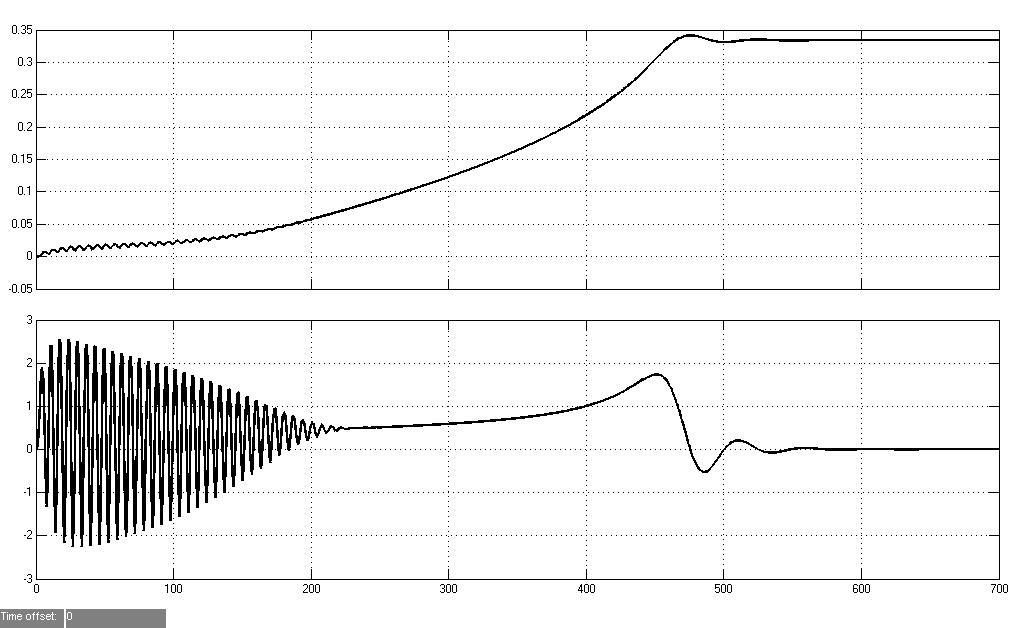
Рис. 2. Результаты моделирования, относительные
значения электромагнитного момента и скорости (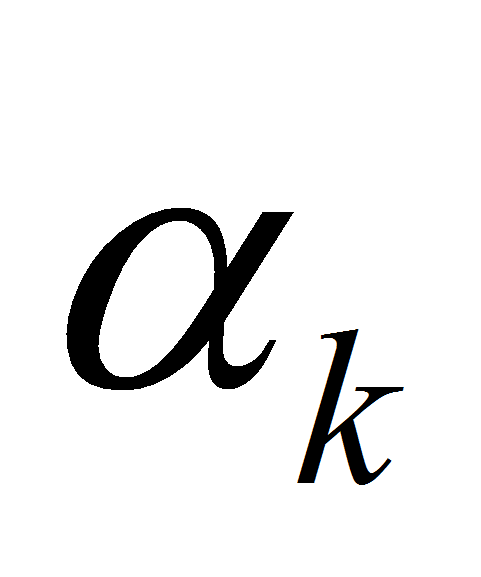 =1).
=1).
Литература:
Шрейнер Р.Т. Математическое моделирование электроприводов
переменного тока с полупроводниковыми преобразователями частоты. Екатеринбург: УРО РАН, 2000. 654 с.
Герман-Галкин С.Г. Компьютерное моделирование полупроводниковых систем Matlab 6.0: Учебное пособие. – Спб.: Корона принт. 2001. – 320с., ил.
Емельянов А.А., Клишин А.В., Медведев А.В. Математическая модель АД
в неподвижной системе координат с переменными
 [Текст] / Молодой ученый. – 2010. -№4. – С.
8-24.
[Текст] / Молодой ученый. – 2010. -№4. – С.
8-24.
Шрейнер Р.Т. Электромеханические и тепловые режимы асинхронных двигателей в системах частотного управления. Екатеринбург: ГОУ ВПО «Рос. гос. проф.-пед. ун-т», 2008. 361 с.
Основные термины (генерируются автоматически): электромагнитный момент, уравнение, структурная схема, номинальный режим, результат моделирования, вал двигателя, прямой пуск, номинальная частота, асинхронный двигатель.
moluch.ru
В наших статьях, рассматривающих электромеханические переходные процессы в линейных асинхронных двигателях, математическое моделирование дано в системе абсолютных единиц. При рассмотрении системы автоматического регулирования скорости в асинхронных двигателях регуляторы тока и скорости определяются из параметров математической модели асинхронного двигателя. В зависимости от принятой системы единиц (абсолютных или относительных) параметры регуляторов будут различны.
Данная работа является развитием статьи [1], в которой переменные  и
и 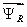 определялись на выходе апериодических звеньев. В этой статье эти переменные получены с интегрирующих звеньев, что существенно изменяет возможности математической модели асинхронного двигателя.
определялись на выходе апериодических звеньев. В этой статье эти переменные получены с интегрирующих звеньев, что существенно изменяет возможности математической модели асинхронного двигателя.
| | (1) |
| (2) | |
| (3) | |
| (4) | |
| (5) | |
| (6) |
Так как электромагнитный момент определяется через переменные 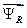 и
и  , то из этих уравнений исключим переменные
, то из этих уравнений исключим переменные  и
и 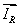 .
.
Из уравнения (4) выразим 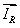 :
:

Обозначим  , где о. е.
, где о. е. 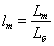 и
и 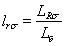 , тогда
, тогда
| | (7) |
Из уравнения (3) исключим 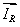 :
:

Обозначим  , тогда
, тогда
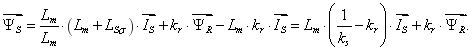
Преобразуем выражение в скобке:
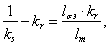 где
где

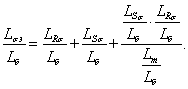
Тогда

| | (8) |
В уравнение (2) подставим  :
:
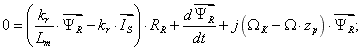
| | (9) |
где 

Отсюда выразим:
| | (10) |
В уравнении (9) перейдем к оператору 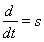 и разложим векторы
и разложим векторы  и
и 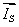 на проекции:
на проекции:
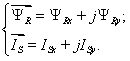
| | (11) |
Проекция уравнения (11) на ось +1:
| | (12) |

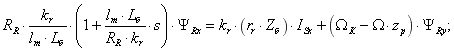
Обозначим 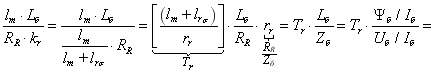
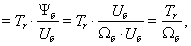
где 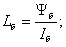
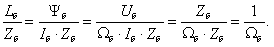
В результате получим уравнение, которое было рассмотрено нами в работе [1] при получении переменной 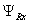 на выходе апериодического звена:
на выходе апериодического звена:



Для получения переменной 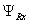 на выходе интегрирующего звена раскроем скобки в левой части:
на выходе интегрирующего звена раскроем скобки в левой части:
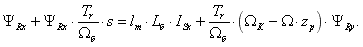
Перенесем первое слагаемое в правую часть:
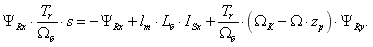
Наконец, переменная 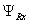 выразится через интегрирующее звено:
выразится через интегрирующее звено:
| | (13) |
Этому уравнению (13) соответствуют структурная схема и оболочка, представленные на рис. 1 и 2.

Рис. 1. Структурная схема для определения 
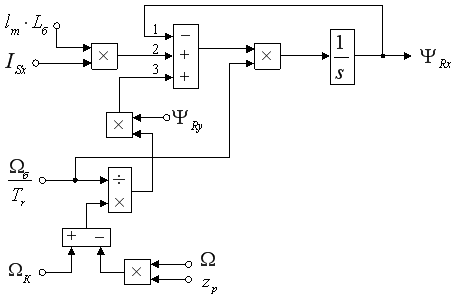
Рис. 2. Оболочка для определения 
Проекция уравнения (11) на ось+j:
| | (14) |
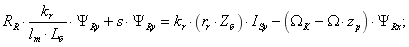



Для получения переменной  на выходе интегрирующего звена раскроем скобки в левой части перенесем первое слагаемое в правую часть:
на выходе интегрирующего звена раскроем скобки в левой части перенесем первое слагаемое в правую часть:

| | (15) |
Полученному уравнению (15) соответствуют структурная схема и оболочка, показанные на рис. 3 и 4.
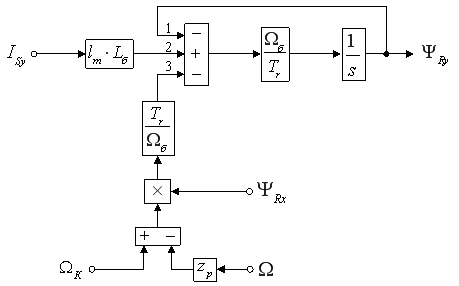
Рис. 3. Структурная схема для определения 
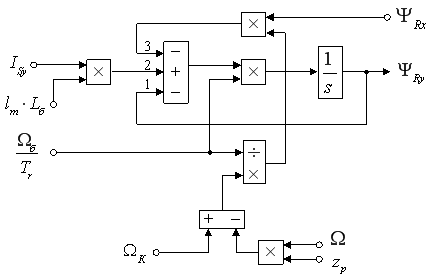
Рис. 4. Оболочка для определения 
Из уравнения (1) исключим 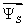 :
:
| | (*) |
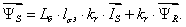
Подставим 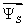 в (*):
в (*):
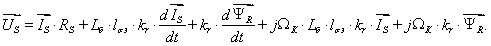
Подставим в это уравнение  из уравнения (10):
из уравнения (10):
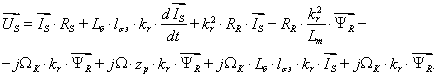
Переведем уравнение 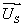 в изображения, для этого выразим
в изображения, для этого выразим  :
:
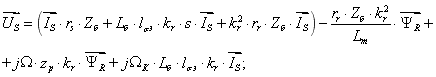

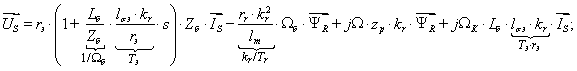
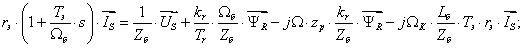
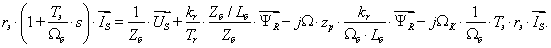
Выразим векторы 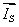 ,
,  и
и 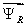 через проекции:
через проекции:
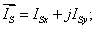
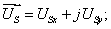
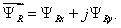
| | (16) |
Проекция уравнения (16) на действительную ось +1:
| | (17) |
Проекция уравнения (16) на мнимую ось +j:
| | (18) |
Из уравнения (17) выразим 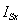 :
:
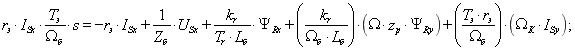
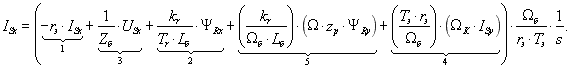
Структурная схема и оболочка для реализации тока 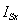 в Matlab-Simulink даны на рис. 5 и 6.
в Matlab-Simulink даны на рис. 5 и 6.

Рис. 5. Структурная схема проекции статорного тока 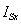 на ось+1
на ось+1

Рис. 6. Оболочка проекции статорного тока 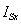 на ось+1
на ось+1
Аналогично из уравнения (18) выразим  :
:

Структурная схема и оболочка, соответствующие этому уравнению, представлены на рис. 7 и 8.

Рис. 7. Структурная схема проекции статорного тока 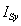 на ось+j
на ось+j

Рис. 8. Оболочка проекции статорного тока 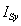 на ось+j
на ось+j
Структурная схема для реализации уравнения электромагнитного момента дана на рис. 9:
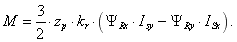

Рис. 9. Математическая модель электромагнитного момента M
Наконец для уравнения (6):


Структурная схема дана на рис. 10.
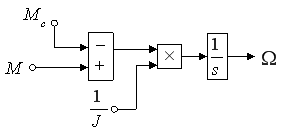
Рис. 10. Математическая модель уравнения движения
В работе [2] в главе 6 «Примеры» дан образец расчета параметров асинхронного двигателя. В наших дальнейших работах направленных на подготовку студентов к исследовательской работе, глава 6 окажет неоценимую помощь. Можно было бы по аналогии рассмотреть паспортные данные любого другого двигателя, но для проверки правильности выводов уравнений сделанных исследовательской группой самостоятельно, необходимо постоянно выходить на многие полученные результаты в работе [3]. Поэтому, этот пример расчета окажется очень полезным.
Номинальные данные:
Номинальный режим работыS1;
Номинальная мощность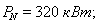
Номинальное фазное напряжение
Номинальный фазный ток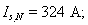
Номинальная частота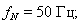
Номинальная синхронная скорость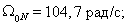
Номинальная скорость ротора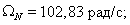
Номинальный КПД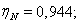
Номинальный коэффициент мощности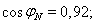
Число пар полюсов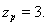
Параметры Т-образной схемы замещения при номинальной частоте:
Активное сопротивление обмотки статора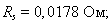
Индуктивное сопротивление рассеяния обмотки статора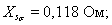
Активное сопротивление обмотки ротора, приведенное к статору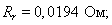
Индуктивное сопротивление рассеяния обмотки ротора, приведенное статору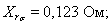
Главное индуктивное сопротивление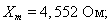
Суммарный момент инерции двигателя и механизма
Базисные величины системы относительных единиц:
Напряжение
Ток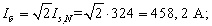
Частота
Скорость ротора
Сопротивление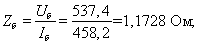
Потокосцепление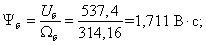
Индуктивность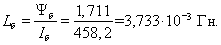
Используя номинальные данные двигателя, определяем:

где  – коэффициент, учитывающий различие значений электромагнитного момента и момента на валу двигателя в номинальном режиме (
– коэффициент, учитывающий различие значений электромагнитного момента и момента на валу двигателя в номинальном режиме ( ).
).
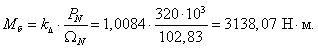
В качестве базисной мощности выбираем значение электромагнитной мощности двигателя в номинальном режиме, определяемое по следующей формуле:
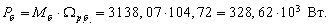
Относительные значения параметров схемы замещения двигателя:
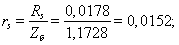
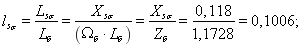



Механическая постоянная времени:

Номинальное значение скольжения:
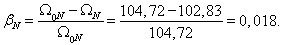
Относительное значение номинальной скорости ротора:
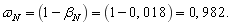
Нормирующий энергетический коэффициент:

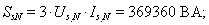


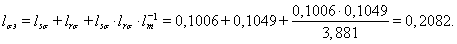
При расчете режимов работы, для того чтобы 
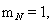
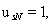
 и
и 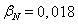 необходимо откорректировать
необходимо откорректировать 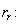
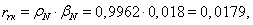
где – корректирующий коэффициент [2, с. 296].
– корректирующий коэффициент [2, с. 296].
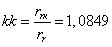 - коэффициент, показывающий отношение
- коэффициент, показывающий отношение 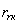 к
к 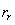 .
.
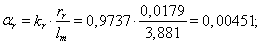

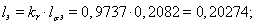
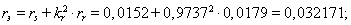
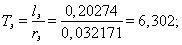
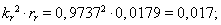
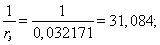

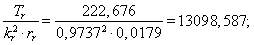
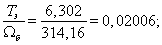
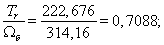
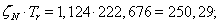
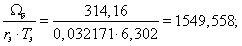
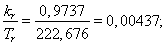

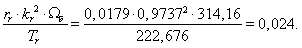
Основным отличием данной модели от модели двигателя, приведенного в работе [1], является то, что переменные  и
и 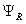 формируются на выходе интегрирующих звеньев. Это позволяет вынести расчет коэффициентов модели в отдельную подсистему (Raschetkoefficientov). В результате этого выноса остается оболочка из сумматоров, блоков перемножения и интеграторов (Obolochkadvigatela). Общая структура двигателя дана на рис. 11.
формируются на выходе интегрирующих звеньев. Это позволяет вынести расчет коэффициентов модели в отдельную подсистему (Raschetkoefficientov). В результате этого выноса остается оболочка из сумматоров, блоков перемножения и интеграторов (Obolochkadvigatela). Общая структура двигателя дана на рис. 11.

Рис. 11. Модель асинхронного двигателя
Оболочка двигателя дана на рис. 12.
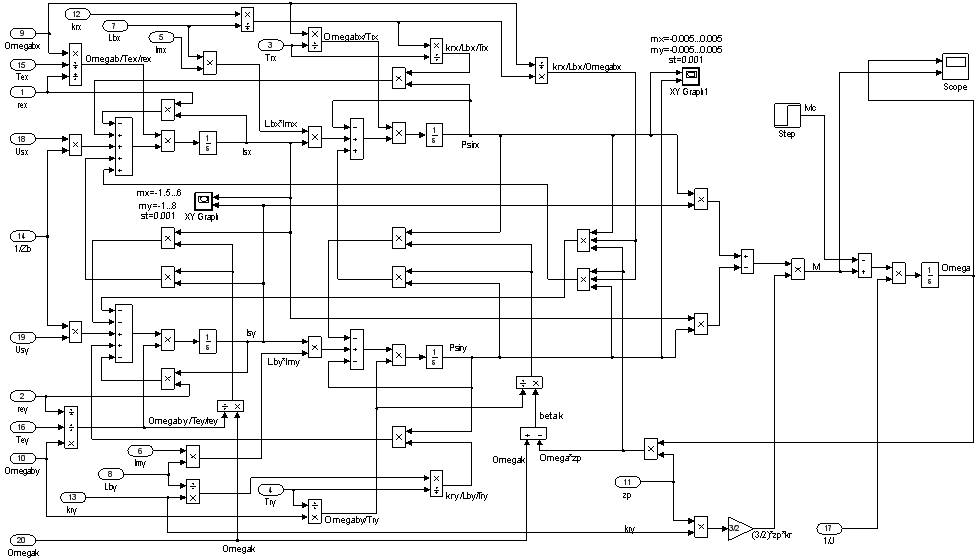
Рис. 12. Оболочка математической модели асинхронного двигателя с переменными 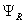 —
—  в системе абсолютных единиц
в системе абсолютных единиц
Ввод паспортных данных двигателя показан на рис. 13.

Рис. 13. Паспортные данные
Расчет коэффициентов осуществляется в подсистеме Raschetkoefficientov, приведенной на рис. 14.

Рис. 14. Расчет коэффициентов
Результаты моделирования представлены на рис. 15.
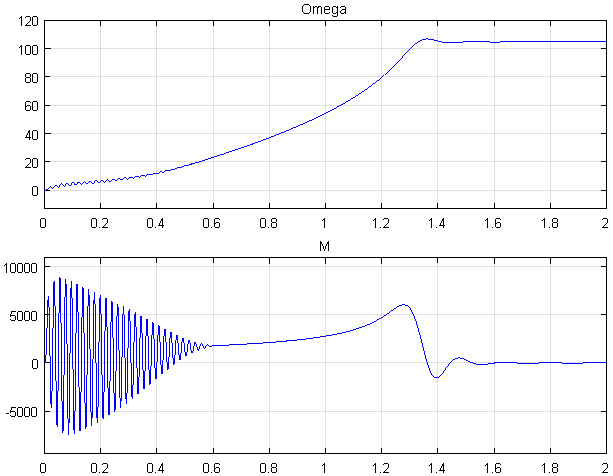
Рис. 15. Графики скорости и момента
Литература:Основные термины (генерируются автоматически): структурная схема, асинхронный двигатель, уравнение, статорный ток, проекция уравнения, математическая модель, получение переменной, номинальный режим, интегрирующее звено, электромагнитный момент.
moluch.ru
координат при ориентации оси  по вектору потокосцепления ротора(Лекция 5)
по вектору потокосцепления ротора(Лекция 5)
. Рассмотрение структурной схемы асинхронного двигателя во вращающейся системе координат, в которой ось направлена по вектору потокосцепления ротора, представляет особый интерес, так как на ее базе строится система векторного управления асинхронным двигателем, имеющая широкое применение в практике электропривода. В основу построения структурной схемы положена система уравнений [Л.1. подраздел 2.4]:




 ,
,
а также основное уравнение механики и равенство 0эл=pп+р. Построенная на основании этих уравнений структурная схема приведена на рис. 19, см. также [Л.1, рис. 2.5].
Стру
 Рис.19. Структурная схема асинхронного двигателя при направлении оси вещественных по вектору потокосцепления ротора
Рис.19. Структурная схема асинхронного двигателя при направлении оси вещественных по вектору потокосцепления ротора
Из структурной схемы видно, что на входы блоков (1/R1)/(T1p) воздействуют сигналы перекрестных связей по проекциям вектора тока статораi1иi1. Если влияние этих перекрестных связей свести к минимуму, что достигается применением быстродействующих контуров проекций тока статора, то, задавая значениеu1, можно независимо устанавливать потокосцепление ротора2. При данном значении2сигнал задания составляющей напряженияu1будет задавать значение электромагнитного момента и скорости двигателя. Таким образом, задачи управления потокосцеплением ротора и электромагнитным моментом двигателя будут разделены подобно тому, как это имеет место в двигателе постоянного тока независимого возбуждения.
В этой модели используется математическое описание асинхронного двигателя в виде структурной схемы рис. 19. Используя его сходство электроприводом .постоянного тока, система строится по принципам подчиненного регулирования и включает в себя две подсистемы: регулирования скорости и регулирования потокосцепления ротора. При рассмотрении настроек контуров можно воспользоваться материалом подраздела 8.8 в учебнике [Л.1]. При этом следует иметь в виду, что в нем рассматривается система, содержащая в канале регулирования скорости внутренний контур регулирования электромагнитного момента, применение которого целесообразно, если в каких-то режимах используется регулирование скорости путем воздействия на потокосцепление ротора. Если регулирование скорости потоком не применяется, то контур регулирования момента не предусматривается, как это сделано в структуре привода, приведенной на рис.20.
Одна из сложностей, возникающих при расчетах электропривода с векторным управлением, состоит в недостаточности параметров токового контура, которыми располагает исследователь, выполняющий расчеты параметров модели. Эти параметры приходится определять косвенными методами, используя элементы подбора данных и анализируя их путем проб и ошибок.
1.4.4. Функциональная схема системы векторного регулирования скорости электропривода с асинхронным двигателем
Функциональная схема электропривода Компании SEWEurodriveпокзана на рис.21.
СИЛОВАЯ ЧАСТЬ ПРИВОДА И РЕЖИМ УПРАВЛЕНИЯ. Силовая часть схемы электропривода представляет собой преобразователь частоты со звеном постоянного тока, от которого получает питание асинхронный двигатель М. При тормозном режиме двигателя в звено постоянного тока cпомощью транзисторного ключаBRCвключается тормозной резисторBW, на который сбрасывается тормозная мощность.
ДАТЧИК СКОРОСТИ. Режим управления при питании от преобразователя, управляемого током, требует для управления двигателем и регулирования скорости контроля истинного значения скорости с использованием датчика скорости, который встраивается в корпус двигателя. Это может быть либо инкрементный датчик (прямоугольные сигналы) либо синусно-косинусный датчик (синусоидальные сигналы). Инкрементный датчик имеет максимальное позиционное разрешение в 8192 инкрементов на один оборот вала двигателя (при 2048 имп./об). Сигналы синусно-косинусного датчика можно использовать таким


Рис. 20,а. Структура векторной системы регулирования скорости

Рис. 20,б. Структура векторной системы регулирования скорости (субсистема к рис..20,а)

что позиционное разрешение составит 262144 инкрементов на оборот. Благодаря этому можно получить более жесткую характеристику привода.

Рис.21. Функциональная схема векторной системы регулирования электропривода с асинхронным двигателем. (SEWEurodrive. Справочное пособие. Приводные преобразователиMOVIDRIVE. Основы приводной техники
РЕГУЛЯТОР СКОРОСТИ. Входными величинами регулятора скорости являются сигнал задания скорости и её истинное значение, определяемое датчиком. Разность этих величин создает на выходе регулятора сигнал рассогласования, который является сигналом задания момента. . Решению задачи повышения быстродействия способствует упреждение по ускорению.
БЛОК УПРАВЛЕНИЯ ДВИГАТЕЛЕМ. Задача блока управления двигателем состоит в обеспечении, максимально быстрого формирования на валу двигателя момента, значение которого задается регулятором скорости. Этот блок состоит из двух частей: блока расчета уставки тока и регулятора тока. По значениям заданного момента Msetp, истинного значения частоты вращенияnactи углового положения ротора блок расчета уставки тока определяет необходимые фазные токи. Регулятор тока оптимально корректирует действительные токи двигателя до необходимых заданных значений. В этом случае при использовании асинхронного двигателя получение фазного тока и, вместе с тем, создание вращающего момента обеспечивает быстродействующий цифровой регулятор тока. При этом возможен контроль даже самых малых значений тока.
БЛОК РАСЧЕТА УСТАВКИ ТОКА
По уставке вращающего момента от регулятора частоты вращения блок управления двигателем рассчитывает составляющую тока iqдля создания момента. Кроме того, рассчитывается составляющая токаidдля создания магнитного поля. Основой такого расчета в модели магнитных потоков является действительная частота вращения двигателя. При частоте вращения ниже базовой магнитное поле стабилизируется, а из-за ограниченности выходного напряжения преобразователя оно еще может ослабевать для увеличения скорости (эффект ослабления поля). В модели двигателя по составляющим токаiq, idи данным двигателя рассчитывается соответствующая частота скольжения. Из этой частоты и углового положения ротора выводится угловое положение вектора магнитного поля ротора. Наконец, это положение определяет частоту системы трехфазного напряжения. Исходя из параметров моделиiq, idи углового положения поля, блок расчета фазных токов формирует уставки трех фазных токов.
РЕГУЛЯТОР ТОКА
Входными величинами регулятора тока являются заданные и истинные значения тока в фазах двигателя. Через вычитание действительных значений тока из соответствующих заданных определяется их рассогласование. Исходя из этого рассогласования ПИ-регулятор генерирует фазные напряжения таким образом, что разность токов стремится к нулю. Сочетание этих трех фазных напряжений называют также „вектором фазных напряжений".
СИСТЕМА ТРЕХФАЗНОГО НАПРЯЖЕНИЯ
Величина и направление вектора напряжения на статоре соответствуют сумме трех составляющих для трех фазных напряжений. Этот вектор напряжения обрабатывается в широтно-импульсном модуляторе. По трем составляющим вектора напряжения этот модулятор формирует коммутационные сигналы для силовых транзисторов.
studfiles.net
Обобщенная асинхронная машина показана на рис. 1 [1] ÷ [3]:


rs, ls, lms – параметры статорной обмотки,
rr, lr, lmr – параметры роторной обмотки,
|lmsr|=|lmrs|=|lm| – коэффициенты взаимоиндуктивности.
Рис.1. Обобщённая асинхронная машина
Основные уравнения математической модели АД в мгновенных значениях переменных:
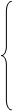
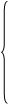
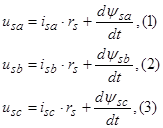

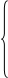
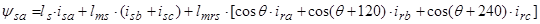
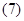
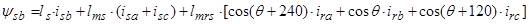
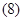
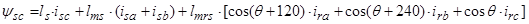


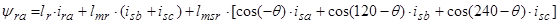
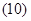
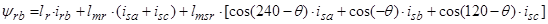
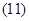

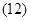
1. Вектор потокосцепления статора АД
Вектор потокосцепления статора является центральным понятием при математическом моделировании асинхронного двигателя, который в дальнейшем будут использован в замкнутых системах векторного управления.
Пространственный вектор потокосцепления статора:
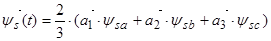 , (13)
, (13)
где 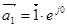 ,
, 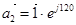 ,
, 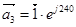 - единичные пространственные векторы.
- единичные пространственные векторы.
Уравнения (7) ÷ (9) представим по трем столбцам соответствующих индуктивностей:

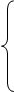
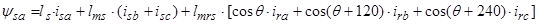
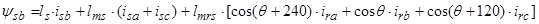
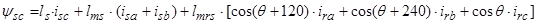
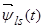
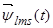
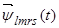
Первое уравнение умножим на единичный пространственный вектор 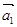 , второе – на
, второе – на  , и последнее уравнение - на
, и последнее уравнение - на 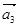 . С целью уменьшения громоздкости получаемых выражений вначале произведем суммирование отдельно по вертикальным столбцам, а затем приведем сумму в соответствии с формулой (13).
. С целью уменьшения громоздкости получаемых выражений вначале произведем суммирование отдельно по вертикальным столбцам, а затем приведем сумму в соответствии с формулой (13).
Мгновенные значения токов в АД:

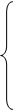
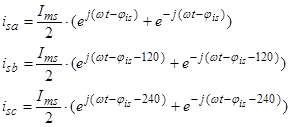

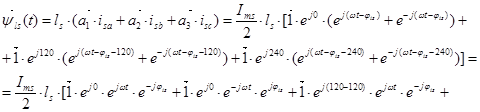
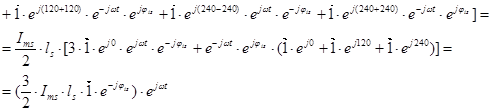

 ,
,
где 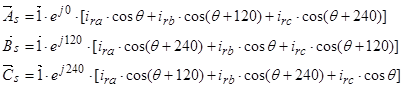 .
.
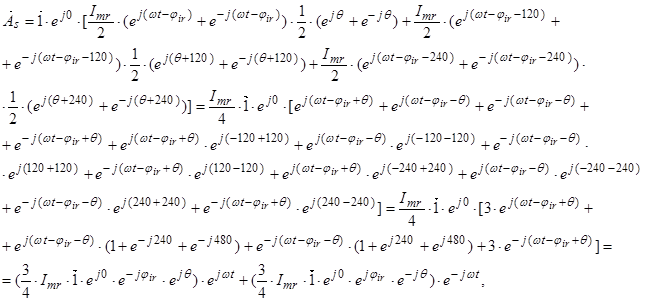 где
где 
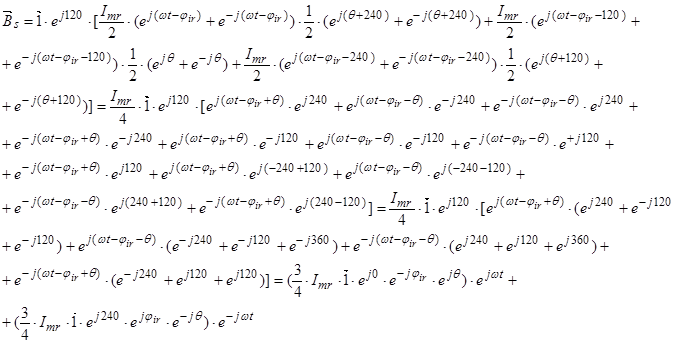
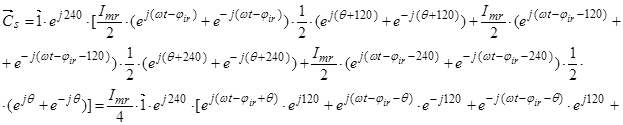


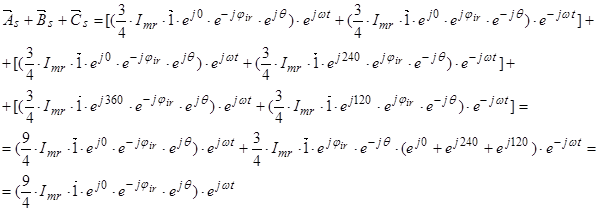

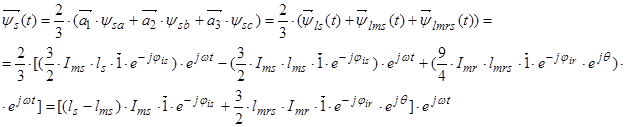 Обозначим
Обозначим  ;
; 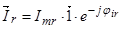 ;
;  ;
;  .
.
Окончательно, вектор потокосцепления статора[1] ÷ [3]:
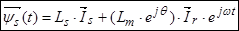 (14)
(14)
2. Вектор потокосцепления ротора АД
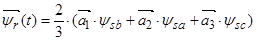 , (15)
, (15)
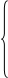
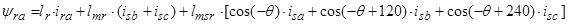


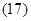
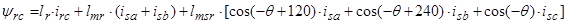
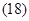

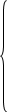
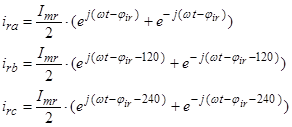
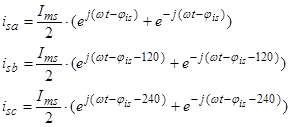
 Уравнения (16) ÷ (18) представим по трём столбцам соответствующих индуктивностей:
Уравнения (16) ÷ (18) представим по трём столбцам соответствующих индуктивностей:

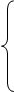
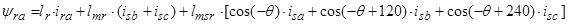

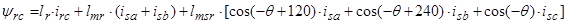
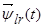

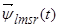
Первое уравнение умножим на 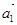 , второе – на
, второе – на  , третье – на
, третье – на 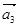 . Вначале произведем суммирование отдельно по вертикальным столбцам, а затем приведем полную сумму в соответствии с формулой (15).
. Вначале произведем суммирование отдельно по вертикальным столбцам, а затем приведем полную сумму в соответствии с формулой (15).
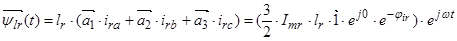
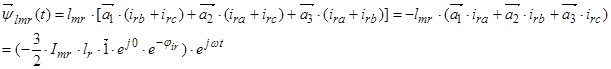
 ,
,
где 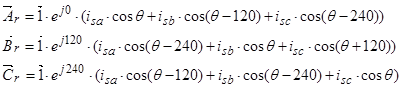
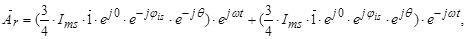


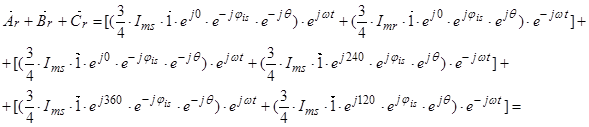
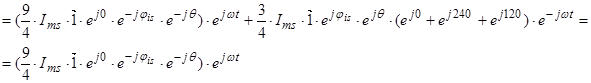


Обозначим  ;
;  ;
; 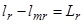 ;
; 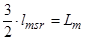 .
.
Окончательно, вектор потокосцепления ротора:
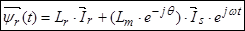 (19)
(19)
3. Векторные уравнения АД в различных системах координат
Основные уравнения асинхронного двигателя в векторной форме имеют вид:
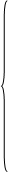
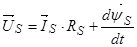
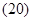
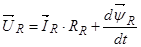
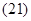

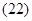
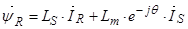
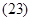
Сделаем существенное замечание по полученным обобщенным векторам. В уравнении (20) векторы  ,
, 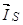 ,
, 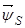 записаны в неподвижной системе координат статора, но в некоторых задачах их необходимо привести к системе координат связанных с ротором. Рассмотрим схему преобразования одного из векторов, например,
записаны в неподвижной системе координат статора, но в некоторых задачах их необходимо привести к системе координат связанных с ротором. Рассмотрим схему преобразования одного из векторов, например,  из одной системы координат в другую. Поясним это преобразование на следующем рис.2.
из одной системы координат в другую. Поясним это преобразование на следующем рис.2.
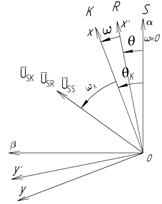
Рис.2. Система координат S, R, K.
 – неподвижная система координат статора
– неподвижная система координат статора  ;
; 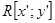 – система координат, связанная с ротором,
– система координат, связанная с ротором,  – произвольная система координат,
– произвольная система координат,  - угол сдвига к
- угол сдвига к 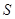 и
и  .
.
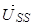 – обобщенный вращающийся вектор напряжения статора.
– обобщенный вращающийся вектор напряжения статора.
 и
и  – этот же вращающийся вектор напряжения статора в системах координат ротора
– этот же вращающийся вектор напряжения статора в системах координат ротора 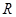 и
и 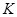 соответственно.
соответственно.
Связь между векторами в разных системах координат:
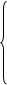
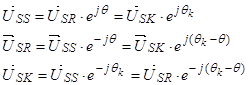
Система уравнений (20) – (23) примет следующий вид:
 , (24)
, (24)
где 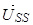 ,
, 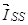 ,
,  – записаны в не подвижной системе координат статора
– записаны в не подвижной системе координат статора 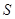 .
.
 (25)
(25)
где  ,
,  ,
,  – обобщённые вектора роторных величин в роторной системе координат R.
– обобщённые вектора роторных величин в роторной системе координат R.
 , (26)
, (26)
где 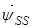 ,
,  , – векторы потокосцепления и ток статора в неподвижной системе координат S, а
, – векторы потокосцепления и ток статора в неподвижной системе координат S, а 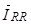 – в роторной системе координат сдвинутой в неподвижной системе на угол
– в роторной системе координат сдвинутой в неподвижной системе на угол  .
.
 (27)
(27)
где  ,
,  , – векторы потокосцепления и ток ротора в роторной системе координат R, а
, – векторы потокосцепления и ток ротора в роторной системе координат R, а  – в неподвижной системе координат
– в неподвижной системе координат 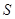 .
.
3.1 Рассмотрим приведение вышеприведённых уравнений к неподвижной системе координат статора
Уравнение (20) уже записано в статорной системе координат, поэтому показываем процесс приведения следующего уравнения. Для этого умножим обе части уравнение (21) на 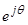 :
:
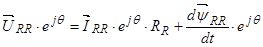 .
.
В соответствии с вышерассмотренной схемой приведения векторов из одной системы координат в другую, получим:
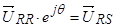 и
и 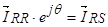 .
.
Выражение 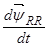 преобразуем к следующему виду:
преобразуем к следующему виду:
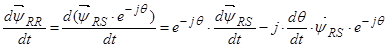
Окончательно 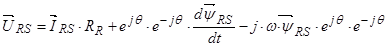 .
.
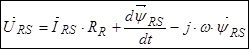 (28)
(28)
В выражении  представим:
представим: 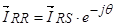 тогда
тогда

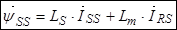 . (29)
. (29)
В уравнении (27) умножим обе части на 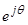 :
:
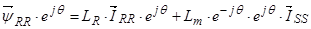 ,
,
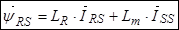 . (30)
. (30)
Окончательно уравнения (24) ÷ (27) в статорной системе координат примет следующий вид:


3.2 Выполним приведение уравнений (24) ÷ (27) к роторной системе координат
Умножим обе части уравнение (24) на  :
:
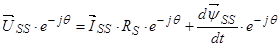
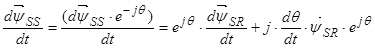
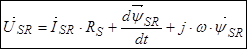
Уравнение (25) перепишем без изменений, т.к. оно уже записано в роторной системе координат:
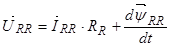
Уравнение (26) умножим обе части на  :
:
 ,
,

В уравнении (27) выразим  , тогда
, тогда
 ,
,
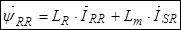
Окончательно в роторной системе координат уравнения (24) ÷ (27) имеют следующий вид:

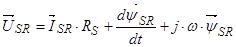
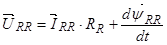
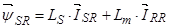
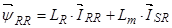
3.3 Приведение уравнений (24) ÷ (27) к системе координат вращающейся с произвольной скоростью 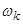
Уравнение (24) умножим на  и сразу выразим
и сразу выразим 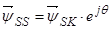 :
:
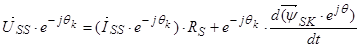 ,
,
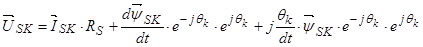 ,
,
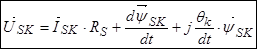 .
.
Уравнение (25) умножим на  :
:
 ,
,
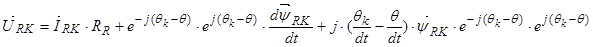
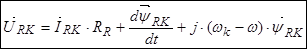 .
.
Уравнение (26) умножим на  , тогда
, тогда
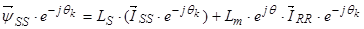 , т.к.
, т.к.  , то
, то
 .
.
Уравнение (27) умножим на  , тогда
, тогда
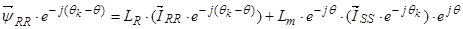
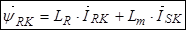 .
.
Для системы координат вращающейся с произвольной скоростью 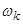 система уравнений:
система уравнений:
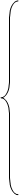
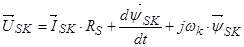 (31)
(31)
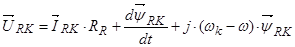 (32)
(32)
 (33)
(33)
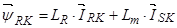 (34)
(34)
 (35)
(35)
Зададим базовые величины (параметры):
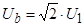 ;
; 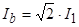 ;
;  ,
,
где 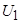 - номинальные действующее фазное напряжение двигателя;
- номинальные действующее фазное напряжение двигателя; 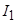 - номинальный фазный ток двигателя.
- номинальный фазный ток двигателя.
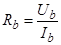 ;
;  ;
; 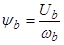 ;
; 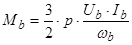 ;
; .
.
Обозначим относительные величины (параметры):
 ;
; ;
;  ;
; 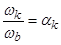 ;
; 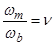 ;
; 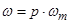 ,
,
где 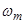 – механическая скорость вращения вала;
– механическая скорость вращения вала;  - число пар полюсов.
- число пар полюсов.
 ;
; 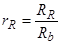 ;
; 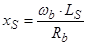 ;
; ;
; 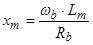 ;
; 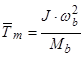 ;
; 
В уравнении (31) сделаем следующие преобразования, обе части разделим на  :
:
 .
.
В квадратных скобках выделены соответствующие относительные величины.
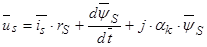
Аналогичные преобразования произведем в (32) уравнении:
 ,
,
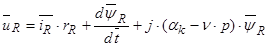
Для уравнения (33), умножим обе части уравнения на 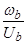 :
:
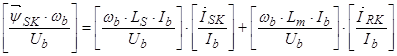 ,
,
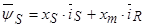
Аналогично в уравнении (34), умножим обе части на 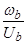 :
:
 ,
,
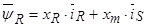
В уравнении (35) обе части разделим на  :
:
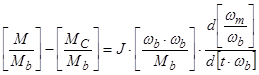 ,
,
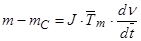
Система уравнения асинхронного двигателя с коротко замкнутым. ротором:
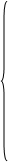
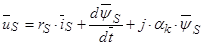 (36)
(36)
 (37)
(37)
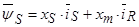 (38)
(38)
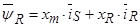 (39)
(39)
Определим электромагнитный момент через векторное произведение [1, c. 238]:
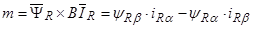
Выразим из уравнения (39)  :
:

В уравнение (38) подставим  :
:

Обозначим  ,
, 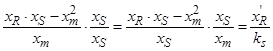 ,
,  , тогда
, тогда
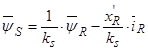 .
.
В уравнение (36) исключим 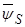 и
и  :
:
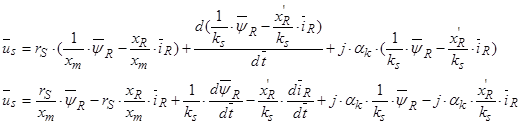
Из уравнения (37) выразим  :
:
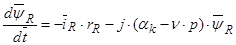 .
.
Подставим в предыдущее уравнение:
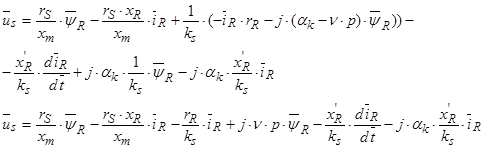

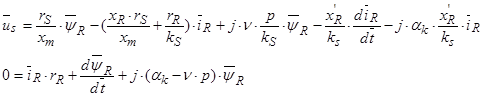
Обозначим 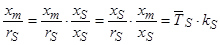 ,
,  , где
, где 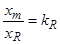 ,
, 
В итоге получилось два уравнения:
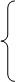
 (40)
(40)
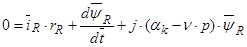 (41)
(41)
В уравнении (40) разделим обе части на 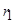 и обозначим
и обозначим 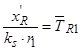 :
:

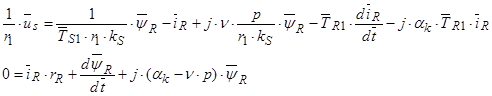
Рассмотрим процессы в неподвижной системе координат, 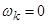 ,
, 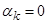 :
:

 (42)
(42)
 (43)
(43)
Вещественную ось обозначим  , мнимую через -
, мнимую через - 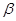 . Пространственные вектора в этом случае разложим по осям:
. Пространственные вектора в этом случае разложим по осям:
 ;
;  ;
; 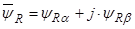 .
.
Подставим эти значения в уравнения (42) ÷ (43) и, приравняв отдельно вещественные и мнимые части, получим:
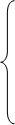
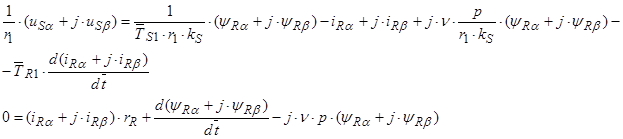


С учетом электромагнитных моментов [1, c. 238] система уравнений в операторной форме 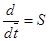 примет вид:
примет вид:
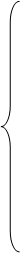
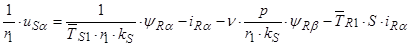 (44)
(44)
 (45)
(45)
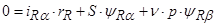 (46)
(46)
 (47)
(47)
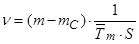 (48)
(48)
 (49)
(49)
Структурная схема для уравнения(44):
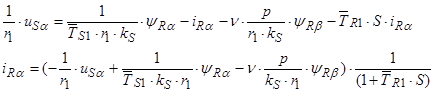


Структурная схема для уравнения(45):
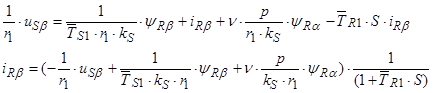
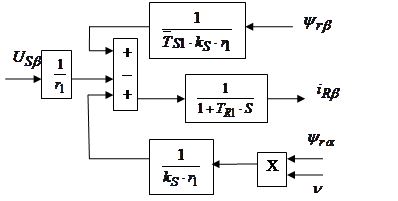

Структурная схема для уравнения(46):
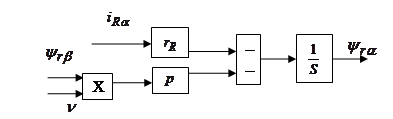


Структурная схема для уравнения(47):
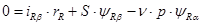
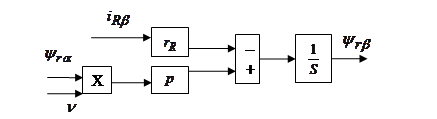
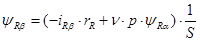

Структурная схема для уравнения (48):
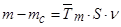
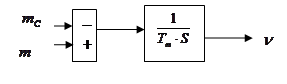

Структурная схема для уравнения (49):
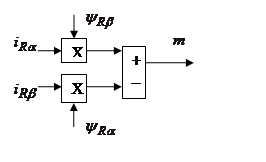


Для моделирования выберем АКЗ со следующими паспортными данными и параметрами:  ,
,  ,
,  ,
, 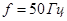 ,
, 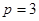 ,
, 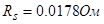 ,
, 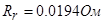 ,
, 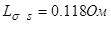 ,
,  ,
, 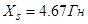 ,
,  ,
,  ,
, 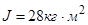 .
.
Значения безразмерных коэффициентов в уравнениях, рассчитанные по выражениям, приведенным выше:
|
Коэффициент |
|
|
|
|
|
|
|
|
|
Значение |
262.36 |
6.4 |
0.97 |
0.97 |
0.0152 |
0.0165 |
0.203 |
200 |
Модель АКЗ, построенная по уравнениям (44) ÷ (49), представленная на рис. 3.
На вход модели в момент времени 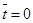 подаются напряжения
подаются напряжения  ,
, 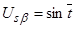 , (
, (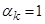 ), тем самым реализуя прямой пуск.
), тем самым реализуя прямой пуск.
Осциллоскопы измеряют относительные значения электромагнитного момента и скорости. Результаты моделирования представлены на рис. 4. Они показывают, что при прямом пуске вначале наблюдается значительные колебания момента. Такие же колебания наблюдаются в токе и скорости. Кроме того они показывают, что при приложении момента нагрузки наблюдается уменьшение скорости.
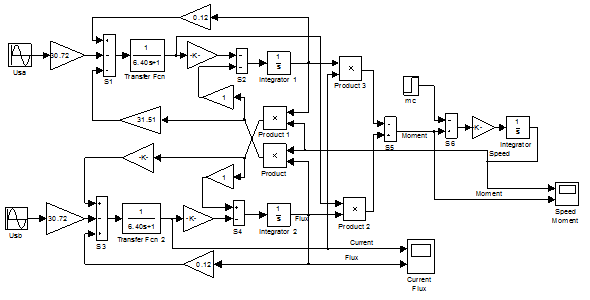
Рисунок 3. Модель АКЗ в неподвижной системе координат с переменными 

Рисунок 4. Результаты моделирования, относительные значения электромагнитного момента и скорости
1. Шрейнер Р.Т. Математическое моделирование электроприводов
переменного тока с полупроводниковыми преобразователями частоты. Екатеринбург: УРО РАН, 2000. 654 с.
2. Герман-Галкин С.Г. Компьютерное моделирование полупроводниковых систем Matlab 6.0: Учебное пособие. – Спб.: Корона принт. 2001. – 320с., ил.
3. Ковач К.П., Рац И. Переходные процессы в машинах переменного тока/Пер. с нем. М.Л.: Госэнергоиздат, 1963. 735 с.: ил.
moluch.ru
1. Введение
Из числа различных видов современных электрических машин самой распространённой в наши дни является асинхронная бесколлекторная машина, применяемая обычно в качестве двигателя.
Асинхронная машина – это машина, в которой при работе возбуждается вращающееся магнитное поле, но ротор вращается асинхронно, т.е. с угловой скоростью, отличной от угловой скорости поля. Она была изобретена М. О. Доливо – Добровольским в 1888 г., но до настоящего времени сохранила ту простую форму, которую ей придал русский изобретатель.
Причины исключительно широкого распространения асинхронного двигателя – его простота и дешевизна. Можно сказать, что в основном асинхронная машина состоит из трёх неподвижных катушек (точнее, обмоток), размещённых на общем сердечнике, и помещенной между ними четвёртой, вращающейся катушки. В машине отсутствуют какие-либо легко повреждающиеся или быстро изнашивающиеся части (например, коллектор).
Асинхронные машины малой мощности часто выполняются однофазными для устройств, питающихся от двухпроводной сети. Такие машины находят широкое применение в бытовой технике.
Общий недостаток асинхронных машин – это относительная сложность и неэкономичность регулирования их режимов работы.
Представление механической части электропривода 2-массовой системой даёт наиболее полное представление о динамических процессах, происходящих в реальном приводе, т. к. даже сложные механические системы, связанные с приводом, сводятся к 2-массовой или 3-массовой системам.
2. Исходные данные
Моделируемая машина – асинхронный электродвигатель с короткозамкнутым ротором типа 4А160S4У3
Справочные данные:
Мощность АД, Pn (кВт)18.5
Число пар полюсов 2
К.П.Д. η (%)89.5
сosφ0.88
Номинальное скольжение Sn (%)2.2
Номинальная частота f1(Гц) 50, Unф (В)220
Момент инерции ротора Jд.р. .0,13
Параметры Т-образной схемы замещения двигателя (в относительных единицах):
Активное сопротивление обмотки статора Rs = 0.042
Индуктивное сопротивление рассеяния обмотки статора Xs = 0.085
Приведённое активное сопротивление обмотки ротора Rr ' = 0.024
Приведённое индуктивное сопротивление рассеяния обмотки ротора Xr’ = 0.13
Индуктивное сопротивление магнитной цепи Xµ = 4.3
3. Обработка исходных данных для моделирования
Угловая скорость вращения магнитного поля:
ω0 = 2×π×f1 /p = 2×π×50/2 = 157 рад/с
Номинальная угловая скорость ротора определяется на основе выражения скольжения:
Sн = ( ω0 - ωн )/ ω0 , откуда
ωн = ω0 × (1- Sн ) = 157× (1-0.022) =153.546 рад/с
Номинальный момент двигателя:
Мн = Рн / ωн = 18500/153.546 = 120,485 Н×м
Номинальный ток двигателя определяется из выражения потребляемой мощности:
Р1 =3×Uнф ×Iнф ×cosj.
Потребляемая мощность, в свою очередь равна:
Р1=Рн/h = 3000/0.895 = 20670,39 Вт , тогда
Iнф = Р1 /(3×Uнф ×cosj.) = 20670,39 /(3×220×0.88) = 35,589 A
Номинальное сопротивление двигателя, на которое необходимо умножить активные и индуктивные сопротивления в относительных единицах, чтобы получить параметры двигателя в абсолютных единицах (Ом):
Zн = Uнф / Iнф = 220/35,589 = 6,18 Ом
Пересчитаем параметры Т – образной схемы замещения двигателя из относительных единиц в абсолютные.
Активное сопротивление обмотки статора:
Rs = 0.042×6,18 = 0,2596 Ом
Приведённое активное сопротивление обмотки ротора:
Rr ' = 0.024×6,18 = 0,148358 Ом
Собственная индуктивность статора:
Lσs = Xs /2×π×f1 = 0.085×6,18 /2×π×50 = 0.00167 Гн
Собственная индуктивность ротора:
Lσr = Xr’ /2×π×f1 = 0.13×6,18/2×π×50 = 0.0025573 Гн
Взаимная индуктивность:
Lm = Xµ /2×π×f1 = 4.3×6,18/2×π×50 = 0.084587 Гн
Индуктивность обмотки статора:
L1 = Lm + Lσs = 0.084587 + 0.00167 = 0.086257 Гн
Индуктивность обмотки ротора:
L2 = Lm + Lσr = 0.084587 + 0.0025573 = 0.0871443 Гн
3. Разработка модели

Пуск двигателя будем выполнять на холостом ходу, и после выхода АД на синхронную скорость нагрузим номинальным моментом.
Момент инерции привода подобран таким образом, чтобы в динамической кривой скорости вращения двигателя ω (t) не было колебаний при выходе на установившийся режим.

Схема прямого пуска асинхронного двигателя в осях XY .

Схема прямого пуска асинхронного двигателя в осях  .
.

4. Результаты моделирования
В результате моделирования нами получены следующие зависимости угловой скорости вращения якоря и момента:

Зависимость тока статора от времени в неподвижной (связанной со статором) системе координат имеет следующий вид (для фазы А):

Зависимость тока статора от времени в неподвижной (связанной со статором) системе координат под номинальной нагрузкой.

Зависимость тока статора от времени в неподвижной (связанной со статором) системе координат на холостом ходу.

График зависимости w=f(M) имеет следующий вид:

Зависимость тока ротора от времени в вращающейся со скоростью ротора (связанной с ротором) системе координат имеет следующий вид (d q):

5. Адекватность модели прямого пуска асинхронного двигателя
Проведём анализ адекватности разработанной нами модели прямого пуска асинхронного двигателя на основе расчета процентного совпадения параметров номинального режима, полученных при моделировании и рассчитанных по справочным данным.
В установившемся режиме при нагрузке на валу двигателя, соответствующей номинальной, значение угловой скорости будет равно:

В результате моделирования получено значение:

Определим расхождение сравниваемых параметров в процентах:

Такое расхождение результатов моделирования и номинальных данных двигателя даёт основание полагать, что разработанная нами модель адекватно отражает прямой пуск реального асинхронного двигателя.
По результатам моделирования определить номинальный ток, номинальную скорость, ток холостого хода, пусковой ток, кратность пускового тока, кратность пускового момента.
Номинальный ток равен Iном=32,6 А
Ток холостого хода Iх.х.=8,13 А
Пусковой ток Iп=166 А
Кратность пускового тока

Кратность пускового момента

Я ознакомился с методом моделирования прямого пуска АД с короткозамкнутым ротором на основе обобщённой машины.
mirznanii.com