Емельянов А. А., Бесклеткин В. В., Устинов А. П., Патерило А. С., Авдеев А. С., Габзалилов Э. Ф. Моделирование прямого пуска асинхронного двигателя с ШИМ в пакете SimPowerSystems // Молодой ученый. 2016. №17. С. 4-11. URL https://moluch.ru/archive/121/33531/ (дата обращения: 26.06.2018).
Целью данной работы является овладение технологией сборки модели прямого пуска асинхронного двигателя с ШИМ в пакете SimPowerSystems для использования в лабораторных работах по дисциплинам «Математическое моделирование электромеханических систем» и «Электрический привод». За основу принята математическая модель из электронного ресурса [1]. Показаны пути поиска разделов необходимых элементов схемы электропривода, позволяющих студентам без больших потерь времени получить необходимые характеристики. Полезные рекомендации по работе в SimPowerSystems даны в работах [2], [3], [4], [5].
Общая схема модели электропривода приведена на рис. 1.
Рис. 1. Электропривод на базе трехфазного асинхронного двигателя с ШИМ
Блок асинхронного двигателя (Asynchronous Machine SI Units) находится в разделе Machines библиотеки SimPowerSystems (рис. 2). Напряжения с ШИМ поступают на асинхронный двигатель через блоки согласования Simulink и SimPowerSystems Vab и Vbc (Controlled Voltage Source) из раздела Electrical Sources (рис. 2).
Параметры асинхронного двигателя представлены на рис. 3. Параметры блоков Vab и Vbc задаются нулевыми.
Рис. 2. Расположение блоков асинхронного двигателя (Asynchronous Machine SI Units) и согласования Simulink и SimPowerSystems (Controlled Voltage Source)
Рис. 3. Параметры асинхронного двигателя
Задание скорости ωm* производится блоком Step1, наброс нагрузки Tm – блоком Step2 (библиотека Simulink, раздел Sources). Параметры этих блоков даны на рис. 4.
Рис. 4. Параметры блоков задания скорости (Step 1) и наброса нагрузки (Step 2)
Блок Gain, а также блоки Math Function и Trigonometric Function находятся в разделе Math Operations библиотеки Simulink (рис. 5). Блок одномерной матрицы 1-D Lookup Table – в разделе Lookup Tables (рис. 5). Параметры этих блоков даны на рис. 6.
Рис. 5. Расположение блоков Gain, Math Function, Trigonometric Function и 1-D Lookup Table
Рис. 6. Параметры блоков Math Function, Trigonometric Function и 1-D Lookup Table
В источнике временного сигнала Clock (раздел Simulink/Sources) следует установить параметр Decimation равным 10. С помощью блока Constant с выражением 2*pi/3*[0,-1,1] обеспечивается сдвиг трехфазных синусоидальных напряжений на 120°.
В блоках Relay (раздел Simulink/Discontinuities) по фазам A, B и C задаются одинаковые параметры, приведенные на рис. 7.
Рис. 7. Параметры блоков Relay A, B и C
Блок шинного селектора (Bus Selector) предназначен для измерения характеристик машины. В библиотеке Simulink раскрываем следующий путь до группы блоков «Разводка сигнала» (Signal Routing) (рис. 8). Переносим блок Bus Selector на рабочее поле.
Рис. 8. Расположение блока Bus Selector в окне библиотеки Simulink
Открываем блок шинного селектора. Из списка механических характеристик (Mechanical) выбираем электромагнитный момент (Electromagnetic torque Te (N*m)) и скорость вращения ротора (Rotor speed (wm)) и добавляем их в список выбранного (Selected signals) кнопкой Select (рис. 9).
Рис. 9. Выбор характеристик в блоке Bus Selector
Для перевода скорости из рад/с в об/мин необходимо добавить блок Gain и установить в нём значение 30/pi.
Для работы модели необходим блок Powergui (раздел Fundamental Blocks библиотеки SimPowerSystems), параметры которого приведены на рис. 10.
Рис. 10. Параметры блока Powergui
Результаты моделирования электропривода на базе трехфазного асинхронного двигателя с ШИМ даны на рис. 11.
Рис. 11. Графики скорости (w) и электромагнитного момента (Te) с набросом нагрузки на двигатель при t = 1,8 с
Примечания:
Рис. 12. Окно параметров модели
Номинальные данные:
Номинальный режим работыS1;
Номинальная мощность
Номинальное фазное напряжение
Номинальный фазный ток
Номинальная частота
Номинальная синхронная скорость
Номинальная скорость ротора
Номинальный КПД
Номинальный коэффициент мощности
Число пар полюсов
Параметры Т-образной схемы замещения при номинальной частоте:
Активное сопротивление обмотки статора
Индуктивное сопротивление рассеяния обмотки статора
Активное сопротивление обмотки ротора, приведенное к статору
Индуктивное сопротивление рассеяния обмотки ротора, приведенное статору
Главное индуктивное сопротивление
Индуктивность рассеяния обмотки статора
Индуктивность рассеяния обмотки ротора
Суммарный момент инерции двигателя и механизма
Основные термины (генерируются автоматически): асинхронный двигатель, блок, параметр блоков, параметр, раздел, электромагнитный момент, шинный селектор, трехфазный асинхронный двигатель, номинальная частота, расположение блоков.
moluch.ru
Данная работа является продолжением статьи [1]. Проекции векторов 
и 
выведены на основе интегрирующих звеньев с моделированием в Simulink.
В работе [1] было получено уравнение (13) для расчета ψsx в Script-Simulink:
Выразим потокосцепление ψsx по оси (+1):
Структурная схема для определения ψsx представлена на рис. 1.
Рис. 1. Структурная схема для определения потокосцепления ψsx в Script-Simulink
Преобразуем структурную схему на рис. 1 в оболочку, позволяющую производить расчет коэффициентов в отдельном блоке Subsystem. Для этого вместо операторов с коэффициентами, рассчитываемыми в Script, установим блоки перемножения, к которым подведены сигналы с результатами расчетов в Simulink, как показано на рис. 2.
Рис. 2. Структурная схема для определения потокосцепления ψsx в Simulink
Для определения ψmx приведем уравнение (14) из работы [1]:
Перенесем слагаемое 
в левую часть:
Умножим обе части уравнения на 
:
Обозначим 
и 
.
Выразим ψmx по оси (+1):
Структурная схема для определения ψmx приведена на рис. 3.
Рис. 3. Структурная схема для определения ψmx в Script-Simulink
Расчет коэффициентов будем производить в отдельном блоке Subsystem, поэтому вносим в структурную схему на рис. 3 блоки перемножения (рис. 4).
Рис. 4. Структурная схема для определения ψmx в Simulink
Аналогично, определим ψsy и ψmy по оси (+j).
Из уравнения (15), полученного в работе [1], выразим ψsy:
Структурная схема для определения ψsy представлена на рис. 5.
Рис. 5. Структурная схема для определения ψsy в Script-Simulink
Схема для расчета ψsy в Simulink приведена на рис. 6.
Рис. 6. Структурная схема для определения ψsy в Simulink
Для определения ψmy приведем уравнение (16) из работы [1]:
Перенесем слагаемое 
в левую часть и умножим обе части уравнения на :
Отсюда ψmy определится в следующей форме:
Структурная схема для определения ψmy приведена на рис. 7.
Рис. 7. Структурная схема для определения ψmy в Script-Simulink
Схема для расчета ψmy в Simulink дана на рис. 8.
Рис. 8. Структурная схема для определения ψmy в Simulink
На рис. 9 приведена структурная схема для реализации уравнения электромагнитного момента:
Рис. 9. Математическая модель определения электромагнитного момента m в Simulink
Из уравнения движения выразим механическую угловую скорость вращения вала двигателя (рис. 10):
Рис. 10. Математическая модель уравнения движения в Simulink
Математическая модель асинхронного двигателя с короткозамкнутым ротором с переменными ψs – ψm на выходе интегрирующих звеньев в Simulink дана на рис. 11, …, 15.
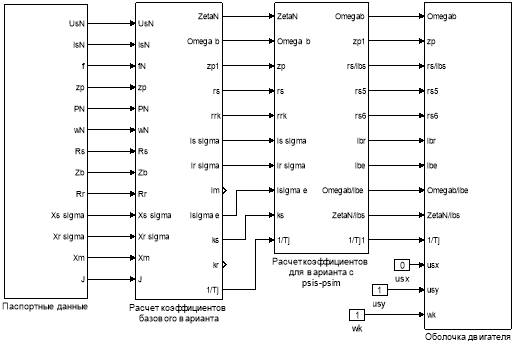
Рис. 11. Общая схема математической модели асинхронного двигателя с переменными ψs – ψmна выходе интегрирующих звеньев в Simulink
Рис. 12. Паспортные данные
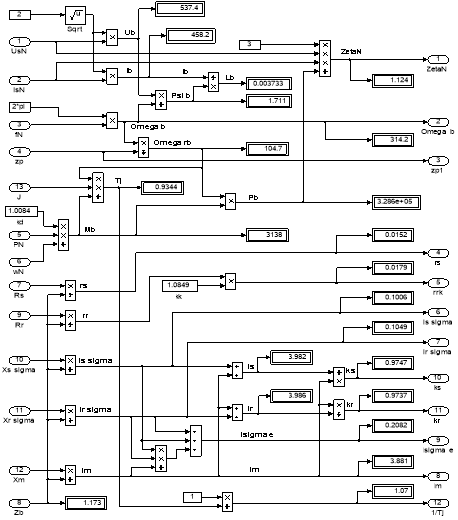
Рис. 13. Расчет коэффициентов базового варианта
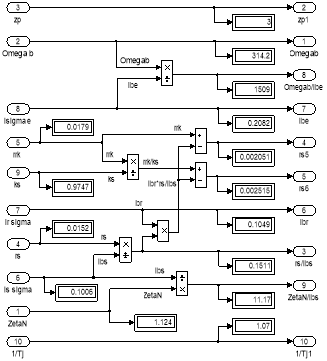
Рис. 14. Расчет коэффициентов для варианта с переменными ψs – ψm
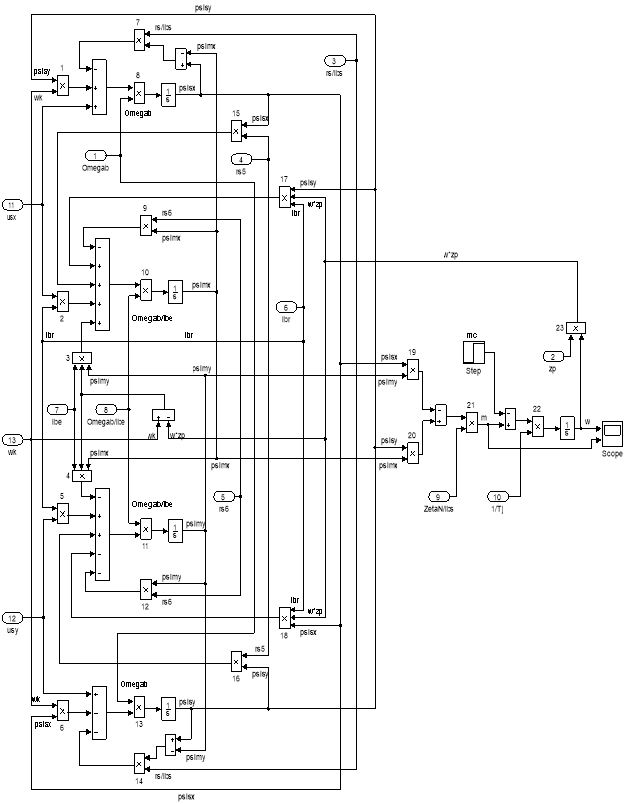
Рис. 15. Оболочка модели асинхронного двигателя с переменными ψs – ψm на выходе интегрирующих звеньев в Simulink
Эту же схему можно представить в более компактной форме с использованием блоков Goto и From (рис. 16) и отдельных субблоков с расчетами потокосцеплений, приведенных на рис. 17 и 18.
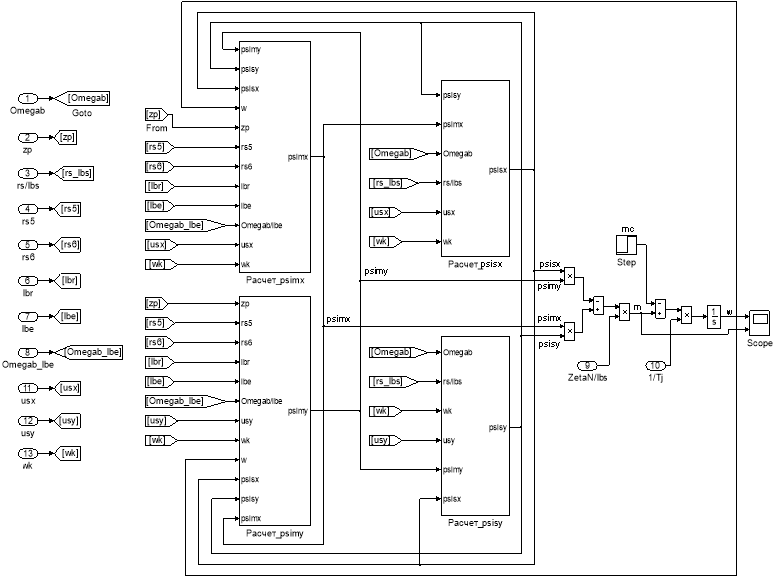
Рис. 16. Оболочка модели асинхронного двигателя с применением блоков Goto и From
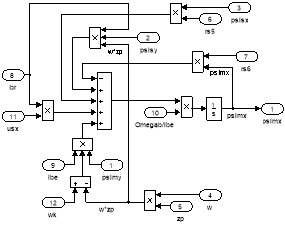
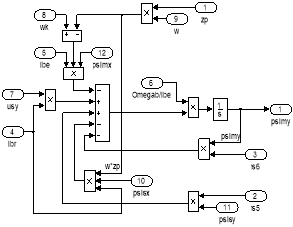
Рис. 17. Схемы для расчета ψmx и ψmy
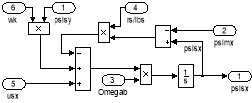
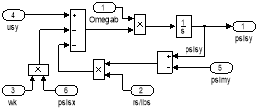
Рис. 18. Схемы для расчета ψsx и ψsy
В работах [2] и [3] дан образец расчета параметров асинхронного двигателя.
Номинальные данные:
Номинальный режим работыS1;
Номинальная мощность
Номинальное фазное напряжение
Номинальный фазный ток
Номинальная частота
Номинальная синхронная скорость
Номинальная скорость ротора
Номинальный КПД
Номинальный коэффициент мощности
Число пар полюсов
Параметры Т-образной схемы замещения при номинальной частоте:
Активное сопротивление обмотки статора
Индуктивное сопротивление рассеяния обмотки статора
Активное сопротивление обмотки ротора, приведенное к статору
Индуктивное сопротивление рассеяния обмотки ротора, приведенное статору
Главное индуктивное сопротивление
Суммарный момент инерции двигателя и механизма
Базисные величины системы относительных единиц:
Напряжение
Ток
Частота
Скорость ротора
Сопротивление
Потокосцепление
Индуктивность
Используя номинальные данные двигателя, определяем:
где 
– коэффициент, учитывающий различие значений электромагнитного момента и момента на валу двигателя в номинальном режиме (k∆ = 1,0084).
В качестве базисной мощности выбираем значение электромагнитной мощности двигателя в номинальном режиме, определяемое по следующей формуле:
Относительные значения параметров схемы замещения двигателя:
Механическая постоянная времени:
Номинальное значение скольжения:
Относительное значение номинальной скорости ротора:
Нормирующий энергетический коэффициент:
При расчете режимов работы, для того чтобы isн = 1, mN = 1, usN = 1, ωsN = 1 и βN = 0,018, необходимо откорректировать rr:
где
– корректирующий коэффициент [3, с. 296].
- коэффициент, показывающий отношение 
к 
.
Расчет коэффициентов для математической модели с переменными ψs – ψm:
Результаты моделирования асинхронного двигателя представлены на рис. 19.
Рис. 19. Графики скорости и момента
Литература:Основные термины (генерируются автоматически): структурная схема, асинхронный двигатель, расчет коэффициентов, математическая модель, электромагнитный момент, номинальный режим, левая часть, номинальная частота, отдельный блок, номинальная скорость ротора.
moluch.ru
По умолчанию модель асинхронного двигателя из раздела библиотеки SimPowerSystems даётся для фазного ротора (рисунок 3.13,а).
Рисунок 3.13 – Виртуальная модель асинхронной машины: а) модель в абсолютных единицах двигателя с фазным ротором; б) модель короткозамкнутого двигателя; в) измерительный инструмент
Клеммы A, B, C служат для подключения к трёхфазному напряжению, клеммы a, b, c – выходы обмотки ротора. Параметры двигателя для модификации SI Units вводятся через диалоговое окно в абсолютных единицах, которое вызывается двойным щелчком по изображению двигателя (рисунок 3.14).
Рисунок 3.14 – Окно ввода параметров двигателя в абсолютных единицах
В строке Rotor type предлагается два варианта: Wound – двигатель с фазным ротором и Squirrel – cage – короткозамкнутый двигатель (с беличьей клеткой). В строке Reference frame предлагается три варианта выбора системы координат:Rotor – вращающаяся с ротором с одинаковой частотой; Stationary – неподвижная, наиболее естественная для нас; Synchronous – система координат, синхронно вращающаяся с частотой сетевого напряжения. Параметры асинхронного двигателя вводятся в следующие строки в абсолютных единицах.
Чаще всего применяется короткозамкнутый двигатель (рисунок 3.13,б). К выходу m подключается специальный демультиплексор Machines Measurement Demux, находящийся в разделе SimPowerSystems в подразделе Machine.
Тип машины переменного тока отражается в строке Machine type, открываемого двойным щелчком левой кнопки мыши (рисунок 3.15).
Рисунок 3.15 – Окно выбора типа машины и перечня выходных переменных
Следует иметь в виду, что эти параметры в справочниках и каталогах не приводятся, а рассчитываются с помощью различных методик, например, так, как это рассмотрено в предыдущем пункте.
По входу Tm задаётся активный момент нагрузки в Нм. По требованию программы Simulink на рабочем поле модели должен быть размещён блок Multimeter (рисунок 3.13, в), иначе процесс моделирования блокируется.
асинхронный электропривод – центробежный насос
Одним из наиболее эффективных путей развития энергосберегающих технологических режимов при управлении центробежными насосами является регулируемый электропривод. В настоящее время, доминирующее положение занимают частотно – регулируемые асинхронные электроприводы с системами автоматического управления, что позволяет решить не только технологические задачи насосных агрегатов, но и проблему энергосбережения [1].
Формирование требуемых статических и динамических свойств асинхронного частотно-регулируемого электропривода возможно лишь в замкнутой системе регулирования его координат, функциональная схема которого представлена на рисунке 3.16 [2].
Р – регулятор; Д – датчик переменных электропривода; ПЧ – преобразователь частоты.
Рисунок 3.16 – Функциональная схема замкнутой системы ПЧ-АД.
Для увеличения диапазона регулирования по скорости в данную систему регулирования необходимо введение отрицательной обратной связи по скорости. Поэтому в математическом описании переходных процессов электропривода учитывается обратная связь по скорости. Структурная схема системы ПЧ-АД с отрицательной обратной связью по скорости будет иметь вид [2]:
Отметим, что структурная схема, в соответствии с рисунком 3.17,
является линеаризованной системой электропривода.
Рисунок 3.17 – Структурная схема системы ПЧ-АД с обратной связью по скорости.
На схеме приняты следующие обозначения:
β – модуль жесткости механической характеристики ;
Тэ – эквивалентная электромагнитная постоянная времени цепей статора и ротора АД;
kПЧ – передаточный коэффициент функции ПЧ;
ТПЧ – постоянная времени цепи управления ПЧ;
Тм – электромеханическая постоянная времени.
Уравнение движения, согласно передаточной функции W1 структурной
схемы, можно записать в следующем виде:
, (3.15)
или
, (3.16)
где 
приращение скорости;
приращение момента;
приращение статического момента нагрузки.
Согласно передаточной функции W2 будем иметь следующее
соотношение:
, (3.17)
которое можно написать в виде дифференциального уравнения:
, (3.18)
где 
приращение угловой скорости электромагнитного поля АД.
Уравнение ПЧ, исходя из передаточной функции W3, запишем:
, (3.19)
а РС ( передаточная функция W4) представим уравнением:
, (3.20)
или
, (3.21)
Приращение 
запишем в следующем виде:
, (3.22)
где 
- приращение задающего сигнала;
- коэффициент обратной связи по скорости.
Таким образом, математическое описание частотно – регулируемого
электропривода центробежного насоса можно представить следующей
системой уравнений:
,
,(3.23)
,
,
.
studfiles.net
Габзалилов Эльвир Фиргатович, студент.
Уральский государственный горный университет (г. Екатеринбург)
Данная работа является продолжением статьи [1]. Проекции векторов 
и 
выведены на основе интегрирующих звеньев с моделированием в Simulink.
В работе [1] было получено уравнение (12) для расчета потокосцепления ψrx в Script-Simulink:
Выразим ψrx по оси (+1):
Структурная схема для определения ψrx представлена на рис. 1.
Рис. 1. Структурная схема для определения потокосцепления ψrx в Script-Simulink
Преобразуем структурную схему на рис. 1 в оболочку, позволяющую производить расчет коэффициентов в отдельном блоке Subsystem. Для этого вместо операторов с коэффициентами, рассчитываемыми в Script, установим блоки перемножения, к которым подведены сигналы с результатами расчетов в Simulink, как показано на рис. 2.
Рис. 2. Структурная схема для определения потокосцепления ψrx в Simulink
Для определения тока isx приведем уравнение (13) из работы [1]:
Перенесем 
в левую часть:
Обозначим 
и разделим обе части уравнения на kr:
Определим ток isx по оси (+1):
Структурная схема для определения тока isx приведена на рис. 3.
Рис. 3. Структурная схема для определения тока isx в Script-Simulink
Расчет коэффициентов будем производить в отдельном блоке Subsystem, поэтому вносим в структурную схему на рис. 3 блоки перемножения (рис. 4).
Рис. 4. Структурная схема для определения тока isx в Simulink
Аналогично, определим ψry и isy по оси (+j).
Из уравнения (15), полученного в работе [1], выразим ψry:
Структурная схема для определения ψry приведена на рис. 5.
Рис. 5. Структурная схема для определения ψry в Script-Simulink
Схема для расчета ψry в Simulink приведена на рис. 6.
Рис. 6. Структурная схема для определения ψry в Simulink
Для определения isy приведем уравнение (16) из работы [1]:
Перенесем 
в левую часть:
Разделим обе части уравнения на kr:
Отсюда isy определится в следующей форме:
Структурная схема для определения isy представлена на рис. 7.
Рис. 7. Структурная схема для определения isy в Script-Simulink
Схема для расчета isy в Simulink дана на рис. 8.
Рис. 8. Структурная схема для определения isy в Simulink
На рис. 9 представлена структурная схема для реализации уравнения электромагнитного момента:
Рис. 9. Математическая модель определения электромагнитного момента m в Simulink
Из уравнения движения выразим механическую угловую скорость вращения вала двигателя (рис. 10):
Рис. 10. Математическая модель уравнения движения в Simulink
Математическая модель асинхронного двигателя с короткозамкнутым ротором с переменными is– ψr на выходе интегрирующих звеньев в Simulink дана на рис. 11, …, 15.
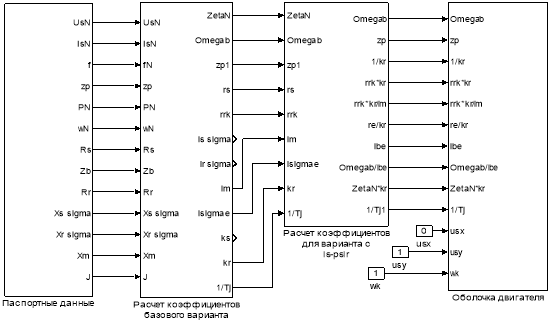
Рис. 11. Общая схема математической модели асинхронного двигателя с переменными is– ψr на выходе интегрирующих звеньев в Simulink
Рис. 12. Паспортные данные
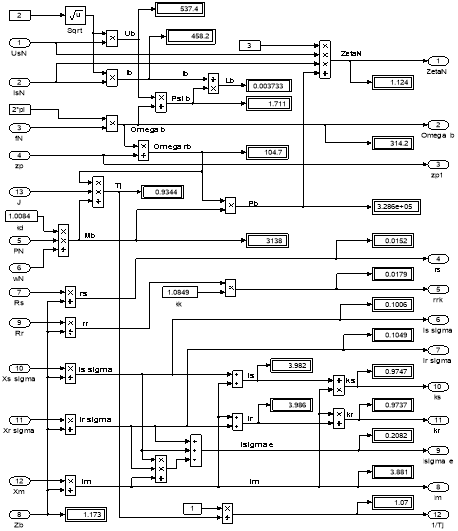
Рис. 13. Расчет коэффициентов базового варианта
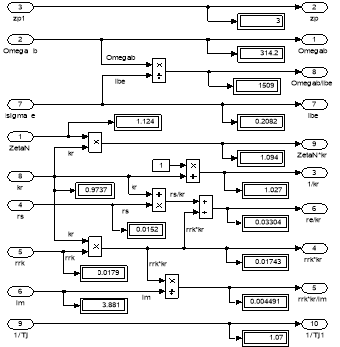
Рис. 14. Расчет коэффициентов для варианта с переменными is – ψr
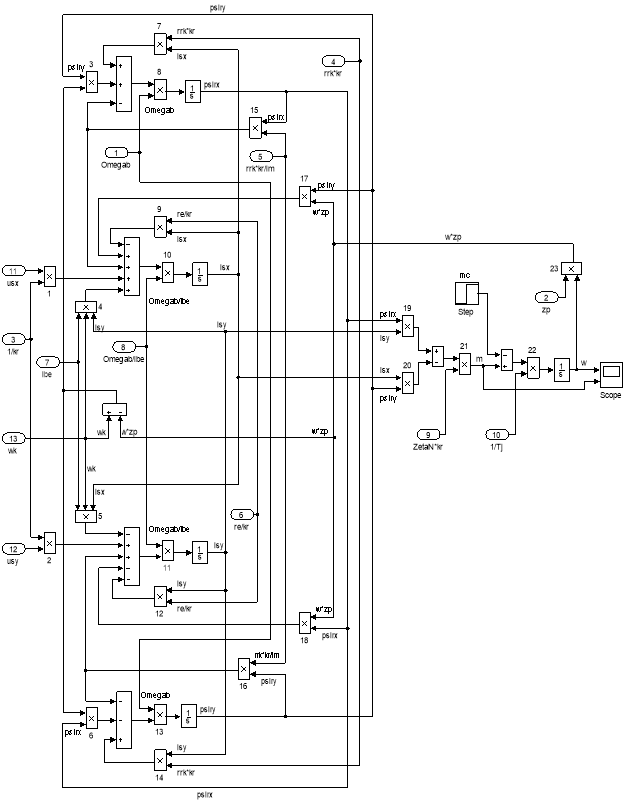
Рис. 15. Оболочка модели асинхронного двигателя с переменными is – ψr на выходе интегрирующих звеньев в Simulink
Эту же схему можно представить в более компактной форме с использованием блоков Goto и From (рис. 16) и отдельных субблоков с расчетами потокосцеплений, приведенных на рис. 17 и 18.
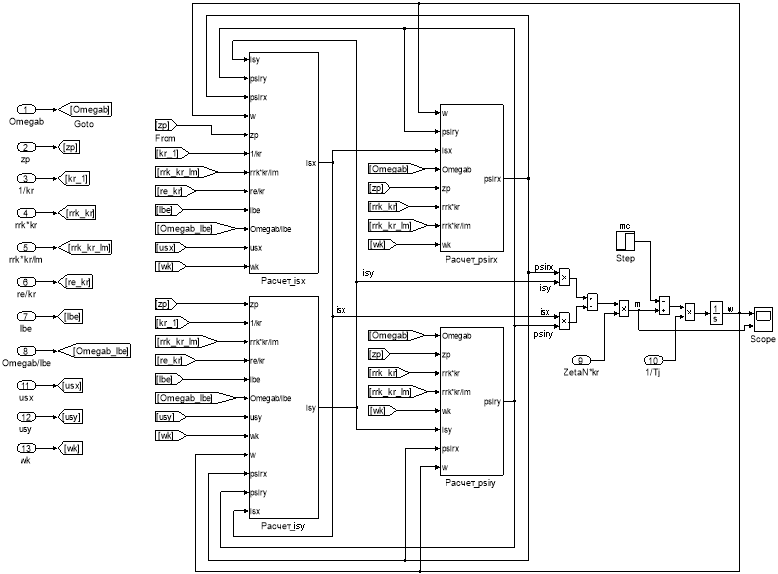
Рис. 16. Оболочка модели асинхронного двигателя с применением блоков Goto и From
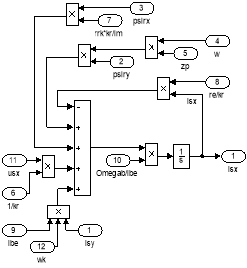
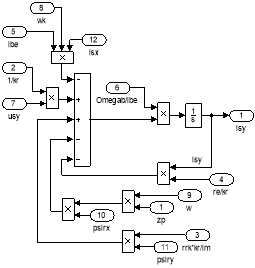
Рис. 17. Схемы для расчета isx и isy
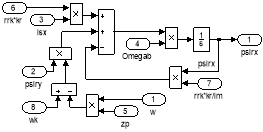
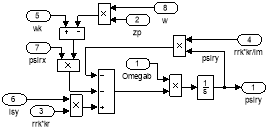
Рис. 18. Схемы для расчета ψrx и ψry
В работах [2] и [3] дан образец расчета параметров асинхронного двигателя.
Номинальные данные:
Номинальный режим работыS1;
Номинальная мощность
Номинальное фазное напряжение
Номинальный фазный ток
Номинальная частота
Номинальная синхронная скорость
Номинальная скорость ротора
Номинальный КПД
Номинальный коэффициент мощности
Число пар полюсов
Параметры Т-образной схемы замещения при номинальной частоте:
Активное сопротивление обмотки статора
Индуктивное сопротивление рассеяния обмотки статора
Активное сопротивление обмотки ротора, приведенное к статору
Индуктивное сопротивление рассеяния обмотки ротора, приведенное к статору
Главное индуктивное сопротивление
Суммарный момент инерции двигателя и механизма.
Базисные величины системы относительных единиц:
Напряжение
Ток
Частота
Скорость ротора
Сопротивление
Потокосцепление
Индуктивность
Используя номинальные данные двигателя, определяем:
где 
– коэффициент, учитывающий различие значений электромагнитного момента и момента на валу двигателя в номинальном режиме (k∆ = 1,0084).
В качестве базисной мощности выбираем значение электромагнитной мощности двигателя в номинальном режиме, определяемое по следующей формуле:
Относительные значения параметров схемы замещения двигателя:
Механическая постоянная времени:
Номинальное значение скольжения:
Относительное значение номинальной скорости ротора:
Нормирующий энергетический коэффициент:
При расчете режимов работы, для того чтобы 
и 
, необходимо откорректировать 
где
– корректирующий коэффициент [3, с. 296].
- коэффициент, показывающий отношение 
к 
.
Расчет коэффициентов для математической модели с переменными is–ψr:
Результаты моделирования асинхронного двигателя представлены на рис. 19.
Рис. 19. Графики скорости и момента
Литература:Основные термины (генерируются автоматически): структурная схема, асинхронный двигатель, расчет коэффициентов, математическая модель, электромагнитный момент, номинальный режим, левая часть, номинальная частота, отдельный блок, номинальная скорость ротора.
moluch.ru
Корректный учет нагрузки на валу электрических двигателей является важным условием получения достоверных результатов математического моделирования электрифицированных механизмов. В теории электропривода моменты статического сопротивления механизмов подразделяются на две характерные группы: активные и реактивные. Активные моменты порождаются силами гравитации и упругой деформации и отличаются способностью вызвать движение механизма даже при отключенном двигателе. Реактивные моменты порождаются силами трения и неупругой деформации и всегда проявляют себя как силы, противодействующие движению. Они возникают и в состоянии покоя, как равное противодействие активному усилию двигателя и активной составляющей момента статического сопротивления механизма.
Широко распространенным инструментом решения задач электромеханики является пакет «Matlab – Simulink», где содержится обширная библиотека моделей электрических машин постоянного и переменного тока. Обобщенная структура таких моделей показана на рис. 1.
Рис. 1 Обобщенная структура моделей электрических машин
Здесь выделены два основных блока, моделирующих процессы в электромагнитных контурах машины и ее механической части. Момент нагрузки вводится в качестве независимой переменной 
. Такое внешнее воздействие интерпретируется моделью как активный момент статического сопротивления механизма. Отсутствие блока формирования реактивной составляющей момента сопротивления ограничивает область использования подобных моделей в задачах электромеханики. Известны усовершенствованные модели, где порождаемые силами сухого и вязкого трения реактивные моменты статического сопротивления формируются как нелинейные функции скорости [1]. Однако такие модели не учитывают особенностей возникновения и действия сил статического сопротивления механизмов в состоянии покоя.
Целью данной работы является создание функционального блока, позволяющего моделировать режимы работы электрифицированных механизмов с активными и реактивными моментами статического сопротивления, как при движении, так и при покое.
Теоретическая основа построения такого блока дана в работе [2], где приводится следующая математическая модель вычисления нагрузки на валу двигателя:
(1)
где 
– активный момент статического сопротивления механизма;
– модуль реактивного момента статического сопротивления, возникающего при движении механизма;
– модуль реактивного момента статического сопротивления при трогании механизма;
– скорость вращения вала двигателя;
– электромагнитный момент двигателя;
– результирующий момент статического сопротивления механизма, приведенный к валу двигателя.
Алгоритм функционирования этого блока показан на рис. 2. Правая ветвь алгоритма определяет величину и направление действия реактивной составляющей момента статического сопротивления при движении механизма, как фактора, противодействующего движению. Левая ветвь определяет величину и направление реактивной составляющей момента статического сопротивления в состоянии покоя, как равного противодействия активным усилиям со стороны двигателя и механизма. Средняя ветвь описывает ситуацию, возникающую при трогании механизма, и позволяет учесть различие сил трения в состоянии покоя и движения. Для обеспечения устойчивости численного решения уравнений модели «двигатель-нагрузка» строгие условия идентификации движения (
) и покоя (
) из выражений (1) заменены на менее жесткое условие 
, где 
– малая положительная величина.
Использование данного алгоритма позволяет корректно учесть нелинейные свойства сил трения и неупругой деформации, как при движении, так и при покое, включая условия трогания и остановки механизмов.
Рис.2 Алгоритм вычисления момента статического сопротивления механизма
Как следует из описанной выше математической модели, момент статического сопротивления механизма представляет собой нелинейную функцию четырех переменных 
. Для учета сухого и вязкого трения, а также особенностей полезной нагрузки различных механизмов, целесообразно представление модуля реактивной составляющей момента их статического сопротивления, как комбинации постоянной составляющей, линейной, квадратичной и кубической функций скорости:
, (2)
где 
– постоянная составляющая модуля реактивного момента;
, 
, 
– весовые коэффициенты переменных составляющих модуля реактивного момента сопротивления механизма.
Обобщенная структура модели электрического двигателя с блоком моделирования нагрузки приобретает вид, показанный на рис. 3. В отличие от структуры рис.1 здесь присутствуют связи по электромагнитному моменту и скорости двигателя, необходимые для корректного вычисления реактивной составляющей момента статического сопротивления на валу двигателя в блоке модели нагрузки. Модуль реактивной составляющей формируется нелинейным блоком в соответствии с формулой (2).
Рис. 3 Обобщенная структура модели электрического двигателя с блоком моделирования нагрузки
В приложение к библиотеке моделей электрических машин пакета «Matlab – Simulink» разработан блок моделирования нагрузки двигателя, структура которого показана на рис. 4. Здесь скорость обозначена как W.
Рис.4 Блок моделирования нагрузки на валу двигателя
В соответствии с алгоритмом вычисления (рис. 2), в модели нагрузки сформированы три субсистемы (Subsystem1, 2, 3), моделирующие три ветви исходного алгоритма. Модели этих субсистем показаны на рис. 5, 6 и 7. Блоки Relay в структурах Subsystem1 и 3 реализуют релейную функцию 
, принимающую значение 1 при 
и 0 при 
.
Рис.5 Функциональная модель Subsystem1
Рис.6 Функциональная модель Subsystem2
Рис.7 Функциональная модель Subsystem3
Нелинейный блок Subsystem4 позволяет реализовать различные функциональные зависимости модуля реактивного момента от скорости. Соответствующая выражению (2) функциональная модель изображена на рис. 8.
Рис.8 Функциональная модель нелинейного блока
Разработанный блок моделирования нагрузки апробирован в сочетании с моделями различных двигателей постоянного и переменного тока из приложения SimPowerSystems/Machines. В качестве примера использования данного блока на рис. 9 изображена модель электрифицированного механизма с асинхронным короткозамкнутым двигателем, питаемым от управляемого по частоте и амплитуде источника синусоидального напряжения.
Рис. 9 Модель частотно-регулируемого асинхронного
короткозамкнутого двигателя с блоком моделирования нагрузки
Источник питания двигателя Subsystem1 (структура его модели приведена на рис. 10) обеспечивает пропорциональный закон частотного управления (
) и линейное изменение частоты и амплитуды напряжения на зажимах двигателя в режимах пуска, торможения и реверса.
Рис.10 Функциональная модель источника питания двигателя
Асинхронный короткозамкнутый двигатель (Asynchronous Mashine) имеет следующие паспортные данные и параметры схемы замещения: 
, 
, 
, 
, 
, 
, 
, 
, 
. Приведенный к валу электродвигателя суммарный момент инерции механической системы 
. Механизм характеризуется переменным реактивным моментом, включающим постоянную и квадратичную составляющие зависимости момента сопротивления от скорости. Момент трогания превышает постоянную составляющую на 30%. Принятые при моделировании численные значения параметров нагрузки , , , и величины ε в блоке моделирования нагрузки Subsystem (Рис. 9) показаны на рис. 4 и 5.
На рис. 10 приведены результаты моделирования процессов частотного пуска, установившегося движения и реверса механизма. Графики изменения во времени величин скорости 
, электромагнитного момента 
и момента статического сопротивления на валу двигателя 
представлены в физических единицах. Как видно, модель адекватно воспроизводит соответствующие реалиям люфты в графиках скорости на начальной стадии пуска и при реверсе, пики момента статического сопротивления при троганиях механизма, а также изменения момента нагрузки 
при изменении скорости. Колебания момента обусловлены электромагнитными переходными процессами в двигателе.
Рис.10 Временная диаграмма пуска, установившегося движения
и реверса электрифицированного механизма с асинхронным короткозамкнутым двигателем
Результаты апробации подтвердили возможность моделирования режимов работы электрифицированных механизмов с различными двигателями и механизмами с активными и реактивными моментами статического сопротивления.
Литература
1. Герман-Галкин С.Г. Matlab & Simulink. Проектирование мехатронных систем на ПК. [Текст] / Спб.: КОРОНА-Век, 2008. – 368 с., ил.
2. Шрейнер Р. Т. Системы подчиненного регулирования электроприводов. [Текст] / Р. Т. Шрейнер. Екатеринбург: Изд-во ГОУ ВПО «Рос. гос. проф.-пед. ун-т», 2008. 279 с.
moluch.ru
1 ВЕСТНИК ПНИПУ 204 Электротехника, информационные технологии, системы управления УДК ДА Даденков, ЕМ Солодкий, АМ Шачков Пермский национальный исследовательский политехнический университет, Пермь, Россия МОДЕЛИРОВАНИЕ СИСТЕМЫ ВЕКТОРНОГО УПРАВЛЕНИЯ АСИНХРОННЫМ ДВИГАТЕЛЕМ В ПАКЕТЕ MATLAB/IMULINK Рассмотрены вопросы синтеза и моделирования системы векторного управления асинхронным двигателем Приведены структура векторного управления и этапы настройки контуров регулирования скорости и тока Особое внимание уделено проработке отдельных узлов системы управления, связанных с компенсацией перекрестных связей и ограничением момента Выполнена реализация комплексной модели системы управления в среде имитационного моделирования MatLab/imulink Приведены и проанализированы результаты моделирования, которые подтверждают правильность настройки контуров регулирования Предложенные в статье подходы и разработанные модели позволят выполнять отладку проектируемых систем частотного управления перед непосредственной реализацией на микроконтроллере Полученные в работе результаты планируется дополнить использованием алгоритмов автоматической идентификации параметров модели двигателя и задействовать при разработке и исследовании бездатчиковых систем управления электроприводом переменного тока Ключевые слова: асинхронный двигатель, частотное векторное управление, регулятор, имитационное моделирование, синтез контура регулирования DA Dadenkov, EM olodky, AM hachkov Perm National Research Polytechnic University, Perm, Russian Federation IMULATION OF VECTOR CONTROL YTEM OF AYNCHRONOU MOTOR THROUGH THE MATLAB/IMULINK ENVIRONMENT The synthesis and simulation of systems of vector control of an induction motor are discussed The structure of the vector control and configuration steps of speed and current regulators are shown pecial attention is paid to the study of the individual components of the control system related to compensation of cross-connections and torque limit Еhe implementation of a comprehensive model of the control system in the Matlab/imulink simulation environment is done The simulation results Presented and analyzed that confirm the correct configuration of the control system The proposed approaches and the models allow to debug the design frequency control systems before carrying on the microcontroller The results are planned to complement with usage of algorithms for automatic identification of model parameters of the motor and to engage in the development and study of sensorless control systems of AC drives Keywords: induction motor, frequency vector control, regulator, simulation, control loop synthesis 7
2 ДА Даденков, ЕМ Солодкий, АМ Шачков Качество векторного управления асинхронным двигателем (АД) зависит во многом от настройки регуляторов скорости и тока, дискретности аналого-цифрового преобразователя (АЦП) и алгоритмов векторной широтно-импульсной модуляции (ВШИМ) Для качественной настройки систем векторного управления необходимо разработать и реализовать алгоритмы настройки контуров регулирования по параметрам схемы замещения АД, а также алгоритмы ВШИМ, стремясь их максимально адаптировать для системы управления двигателем на базе микроконтроллера С этой целью для моделирования и отладки алгоритмов векторного управления АД могут быть использованы программно-аппаратные симуляторы электропривода [, 2], средства имитационного моделирования В данной работе предлагается использовать среду имитационного моделирования MatLab/imulink Структурная схема системы векторного управления, выбранная для исследования и моделирования [3], представлена на рис Рис Упрощенная структура системы векторного управления АД Для построения модели системы векторного управления необходимо выполнить синтез контуров регулирования скорости и тока Синтез и настройку регуляторов тока по осям d и q производим по известной методике [4, 5] На рис 2 изображен контур регулирования составляющей тока I Для силового преобразователя принимаем пропорциональный 2 коэффициент kп = U нф и постоянную времени Tп = 2Tшим = f шим 8
3 Моделирование системы векторного управления асинхронным двигателем * I W ( р) рт kп T p + п k0 T p + э I k от Рис 2 Контур регулирования тока I С учетом компенсации перекрестных обратных связей [3] получаем коэффициенты для составляющей цепи статора по оси q: где R сопротивление статора; k0 =, () R L σr Lm Tэ = Lσ + / R, (2) LσR + Lm L σ индуктивность рассеяния статора; L σ R индуктивность рассеяния ротора; L m главная индуктивность Коэффициент обратной связи датчика тока k от = Настройку контура тока производим на технический оптимум [4, 5], компенсируя большую постоянную времени T, поэтому T T В результате процедуры синтеза получена передаточная функция ПИ-регулятора тока: W = 2T p T p k k T p + T p + п 0 ( + ) µ µ Передаточная функция замкнутого контура тока статора по оси q п W ЗКТ = = q 2 2T p( T p + ) + 2T p + 2T p + 2T + (4) µ µ µ µ µ p Аналогично выполняются синтез и настройка контура регулирования составляющей тока I Далее рассмотрим настройку контура регулирования скорости В результате процедуры синтеза [4, 5] получена схема контура регулирования скорости (рис 3), который включает в себя непосредственно э э µ = п (3) 9
4 ДА Даденков, ЕМ Солодкий, АМ Шачков сам регулятор скорости W рс (p), вычислитель тока I, замкнутый контур регулирования тока (ЗКРТ q ), механическую часть АД и обратную связь в виде датчика скорости (K с ) * ω W рс (р) * М 2 3Z Р ψ R ЗКРТ q * I 2Tµ p + М М с Мех часть АД ω 2Hp + F тр ω ос K c Рис 3 Контур регулирования скорости Передаточная функция механической части АД определяется из математического описания АД в среде имитационного моделирования MatLab/imulink [6]: dω = ω dt 2H ( M Fтр Mс ) где M электромагнитный момент, F тр коэффициент трения, Н суммарная инерционная постоянная машины, M с статический момент нагрузки Принимая M с = 0, получаем передаточную функцию механической части АД: W МЕХ / Fтр = = 2Hp + Fтр 2H p + F тр Коэффициент обратной связи датчика скорости принимаем k от = Настройку контура скорости выполняем на технический оптимум [4, 5], меньшую постоянную времени принимаем Tµ C = 2 Tµ В результате процедуры синтеза [4, 5] получена передаточная функция ПИ-регулятора скорости: Wрс = (7) 2 2Tµ C ( Tµ C p + ) 3 Z ψ 2 T p + 2 Hp + F P R µ, тр (5) (6) 20
5 Моделирование системы векторного управления асинхронным двигателем При построении системы модели векторного управления необходимо также учесть компенсацию нелинейных обратных связей [3, 7] Для этого воспользуемся векторной диаграммой двигателя (рис 4) при ψ R = const и выразим потокосцепление в уравнениях равновесия статора через токи статора: ( ), ψ = L I + ψ = L + L I (8) σ md σ m ψ = L I + ψ = L I + L I = L + L L I σr m σ mq σ m mq σ Lσ R + Lm (9) Рис 4 Векторная диаграмма АД при ψ R = const Подставляя найденные выражения (8) и (9) для ψ, ψ в уравнения равновесия ЭДС статора [3], получим систему уравнений: di LσR Lm U = ( Lσ + Lm ) + R I Lσ + I, dt LσR + Lm (0) L σrl di m U = Lσ + + R I + ω ( Lσ + Lm ) I LσR + Lm dt Анализируя полученную систему уравнений (0), видим, что в напряжении U присутствует составляющая, зависящая от I, а в напряжении U составляющая, зависящая от I Следовательно, при синтезе системы управления между каналами регулирования составляющих I и I будет существовать взаимовлияние Каналы будут оказывать друг на друга возмущающее воздействие, особенно сильно проявляющееся в переходных режимах Чтобы этого избежать, 2
6 ДА Даденков, ЕМ Солодкий, АМ Шачков выполним компенсацию перекрестных связей и получим компенсирующие составляющие Компенсационная составляющая канала управления по току I U kd = ω L L L σr m σ + I () Lσ + Lm Компенсационная составляющая канала управления по току I kq ( L L ) I U = ω σ + (2) При реализации модели в MatLab/imulink для компенсации перекрестных связей суммируем компенсационные составляющие с получаемыми на выходе регуляторов тока составляющими векторов статорного напряжения При реализации векторного управления необходимо учесть, что при работе на номинальном напряжении с повышением частоты ограничивается предельно достижимый двигателем момент [3, 8] Рассмотрим закон сохранения механической мощности при работе АД на различных скоростях: m P = Mω = const (3) Согласно выражению (3) максимальный момент, который двигатель способен обеспечить, зависит от частоты и определяется следующим соотношением [3]: M M ω н max = н, (4) ω где М н номинальный момент двигателя; ω н номинальная скорость двигателя Следовательно, в первом приближении можно считать, что зависимость момента от скорости вращения гиперболическая [3] Таким образом, ток реального силового преобразователя всегда ограничен предельным значением, связанным с его физической реализацией, поэтому необходимо ограничивать момент на уровне некоторого перегрузочного момента M Зная предельно допустимый ток силового преобразователя ( I max max ), определим допустимый момент перегрузки: M max 3Z ψ I L = ψ p R max m R 2( Lσ R + Lm ) 22
7 Моделирование системы векторного управления асинхронным двигателем На рис 5 представлена схем реализации расчета перегрузочного момента и ограничения момента в среде Matlab/imulink Рис 5 Реализация ограничения момента На рис 6 представлена комплексная модель векторного управления асинхронным двигателем в пакете Matlab/imulink Рис 6 Модель системы векторного управления АДв Matlab/imulink Паспортные данные двигателя, используемого при моделировании, представлены в таблице Параметры двигателя, используемые при моделировании, BA L σ, Гн 4 0, U НЛ, B L σr, Гн 8 0, f Н, Гц 0 50 J,кг*м 2 2 0,03 3 R, Ом 4,405 5 Z P R R, Ом 8,395 9 F TP, Н*м*с 20 0, L m, Гн 22 0, n 2, об/мин
8 ДА Даденков, ЕМ Солодкий, АМ Шачков Графики переходных процессов по результатам имитационного моделирования представлены на рис 7 Рис 7 Результаты имитационного моделирования в Matlab/imulink На рис 7 при рассмотрении сверху вниз первый график отражает изменение скорости, второй электромагнитного момента, третий статорных токов в трехфазной неподвижной системе координат При моделировании в начальный момент времени задание скорости составляет 0 рад/с Двигатель запускается вхолостую и выходит на эту скорость без нагрузки После выхода на заданную скорость происходит наброс нагрузки в момент времени t = с Далее в момент времени t =,5 с происходит снижение задания скорости до 70 рад/с И наконец, в момент времени 2,5 с происходит увеличение задания скорости до 80 рад/с По графикам переходных процессов скорости, момента и токов (рис 7) видно, как регуляторы качественно отрабатывают задающие и возмущающие воздействия При этом, анализируя картину статорных токов в трехфазной неподвижной системе координат, видно, что токи имеют меньшую ам- 24
9 Моделирование системы векторного управления асинхронным двигателем плитуду при моменте двигателя, близком к моменту M зад (заданному при расчете оптимального потокосцепления ротора), и большую амплитуду при увеличении разницы между моментом двигателя и M зад Таким образом, сначала при задании скорости ω = 0 рад/с и набросе нагрузке амплитуда статорных токов минимальна, а затем при снижении скорости ω = 70 рад/с разность между моментом двигателя и M зад изменяется, что приводит к увеличению амплитуды статорных токов Далее при увеличение скорости до ω = 80 рад/с сокращается разница между моментом двигателя и M зад, что приводит к уменьшению амплитуды статорных токов Из полученных результатов анализа графиков переходных процессов следует, что все расчеты были произведены правильно и векторная система управления (ВСУ) работает согласно настроенному критерию оптимизации Данная ВСУ с косвенной ориентацией по потокосцеплению ротора может быть реализована на микроконтроллере [9] для последующей оценки работоспособности системы на реальном АД Заметим, что при получении результатов моделирования, отвечающих определенным требованиям, следует всегда помнить об адекватности модели и принятых допущениях В ходе исследования в среде имитационного моделирования Matlab/imulink реализована структура векторного управления асинхронным двигателем Моделирование системы управления позволило сделать вывод об адекватности настройки регуляторов по параметрам схемы замещения двигателя, а также о правильной работе алгоритмов в блоках оценки потокосцепления ротора и ограничения момента Моделирование векторной системы управления АД позволяет исключить ошибки и неточности при проектировании системы управления двигателем, а также произвести отладку алгоритмов управления во многих режимах работы системы управления Рассмотренная в работе система векторного управления АД может быть использована для создания программной части системы управления частотно-регулируемым электроприводом в датчиковом режиме (с использованием энкодера или датчика Холла) Дальнейшее развитие данная система управления может получить добавлением алгоритмов идентификации параметров АД и реализацией бездатчикового управления [0] 25
10 ДА Даденков, ЕМ Солодкий, АМ Шачков 26 Библиографический список Зюзев АМ, Нестеров КЕ, Мудров МВ Программноаппаратный симулятор электропривода // Энергетика Инновационные направления в энергетике CAL-технологии в энергетике Пермь: Изд-во Перм нац исслед политехн ун-та, 203 С Кычкин АВ, Даденков ДА, Билалов АБ Автоматизированная информационная система полунатурного моделирования статической нагрузки электроприводов // Вестник Пермского национального исследовательского политехнического университета Электротехника, информационные технологии, системы управления С Качачев ЮН Векторное регулирование (заметки практика) [Электронный ресурс] URL: (дата обращения: ) 4 Казанцев ВП Теория автоматического управления Линейные системы управления: учеб пособие Пермь: Изд-во Перм гос техн ун-та, Даденков ДА, Шиляев ДВ Сравнительный анализ методов синтеза систем регулирования скорости микроприводов постоянного тока // Вестник Пермского национального исследовательского политехнического университета Электротехника, информационные технологии, системы управления 203 Т 7 С Герман-Галкин СГ Компьютерное моделирование полупроводниковых систем в МatLab 60: учеб пособие СПб: КОРОНА принт, с 7 Башарин АВ, Новиков ВА, Соколовский ГГ Управление электроприводами Л: Энергоиздат, Осипов ПА, Карякин АЛ Метод измерения координат асинхронного электродвигателя в частотно регулируемом электроприводе механизмов карьерного экскаватора // Электротехника С Проекты на микроконтроллерах AVR [Электронный ресурс] (дата обращения: ) 0 Браславский ИЯ, Зюзев АМ, Нестеров КЕ Асинхронный тиристорный электропривод с бездатчиковым измерителем скорости // Электромашиностроение и электрооборудование С 35 36
11 Моделирование системы векторного управления асинхронным двигателем References Ziuzev AM, Nesterov KE, Mudrov MV Programmnoapparatnyi simuliator elektroprivoda [Hardware-software simulator of the electric drive] Energetika Innovatsionnye napravleniia v energetike CALtekhnologii v energetike Permskii natsional'nyi issledovatel'skii politekhnicheskii universitet, 203, no, pp Kychkin AV, Dadenkov DA, Bilalov AB Avtomatizirovannaia informatsionnaia sistema polunaturnogo modelirovaniia staticheskoi nagruzki elektroprivodov [The automated information system of seminatural modeling of static loading of electric drives] Vestnik Permskogo natsional'nogo issledovatel'skogo politekhnicheskogo universiteta Elektrotekhnika, informatsionnye tekhnologii, sistemy upravleniia, 203, no 8, pp Kachachev IuN Vektornoe regulirovanie (zametki praktika) [Vector regulation (practician's note)] Available at: (accessed 2 eptember 204) 4 Kazantsev VP Teoriia avtomaticheskogo upravleniia Lineinye sistemy upravleniia [Theory of automatic control Linear control systems] Izdatel'stvo Permskogo gosudarstvennogo tekhnicheskogo universiteta, Dadenkov DA, hiliaev DV ravnitel'nyi analiz metodov sinteza sistem regulirovaniia skorosti mikroprivodov postoiannogo toka [Comparative analysis of synthesis methods of speed control systems for direct current micro drives] Vestnik Permskogo natsional'nogo issledovatel'skogo politekhnicheskogo universiteta Elektrotekhnika, informatsionnye tekhnologii, sistemy upravleniia, 203, vol, no 7, pp German-Galkin G Komp'iuternoe modelirovanie poluprovodnikovykh sistem v MatLab 60 [Computer modeling of semiconductor systems in MATLAB 60] aint Petersburg: Korona print, 200, 320 P 7 Basharin AV, Novikov VA, okolovskii GG Upravlenie elektroprivodami [Control of electric drives] Leningrad: Energoizdat, Osipov PA, Kariakin AL Metod izmereniia koordinat asinkhronnogo elektrodvigatelia v chastotno reguliruemom elektroprivode mekhanizmov kar'ernogo ekskavatora [The method of measuring the coordinates of the asynchronous motor in frequency controlled electric drive mechanisms career excavator] Elektrotekhnika, 202, no 9, pp
12 ДА Даденков, ЕМ Солодкий, АМ Шачков 9 Proekty na mikrokontrollerakh AVR [Projects on microcontrollers] Available at: (accessed 27 October 204) 0 Braslavskii IIa, Ziuzev AM, Nesterov KE Asinkhronnyi tiristornyi elektroprivod s bezdatchikovym izmeritelem skorosti [Asynchronous thyristor electric drive with sensorless speed meter] Elektromashinostroenie i elektrooborudovanie, 2006, no 66, pp Сведения об авторах Даденков Дмитрий Александрович (Пермь, Россия) старший преподаватель кафедры микропроцессорных средств автоматизации Пермского национального исследовательского политехнического университета (64990, Пермь, Комсомольский пр, 29, Солодкий Евгений Михайлович (Пермь, Россия) старший преподаватель кафедры микропроцессорных средств автоматизации Пермского национального исследовательского политехнического университета (64990, Пермь, Комсомольский пр, 29, Шачков Алексей Михайлович (Пермь, Россия) магистрант -го курса кафедры микропроцессорных средств автоматизации Пермского национального исследовательского политехнического университета (64990, Пермь, Комсомольский пр, 29, About the authors Dadenkov Dmitry Alexandrovich (Perm, Russian Federation) is a enior Lecturer at the Department of Automation Microprocessors, Perm National Research Polytechnic University (64990, Perm, 29, Komsomolsky pr, olodkiy Eugene Mikhailovich (Perm, Russian Federation) is a enior Lecturer at the Department of Automation Microprocessors, Perm National Research Polytechnic University (64990, Perm, 29, Komsomolsky pr, hachkov Alexey Mikhailovich (Perm, Russian Federation) undergraduate student at Department of Automation Microprocessors, Perm National Research Polytechnic University (64990, Perm, 29, Komsomolsky pr, Получено
docplayer.ru
По умолчанию модель асинхронного двигателя из раздела библио_ теки SimPowerSystems даётся для фазного ротора (рис. 1.53, а).
| Tm | ir_abc | |||
| Tm | m | |||
| is_abc | ||||
| A | a | A | ||
| m | m | |||
| B | b | B | wm | |
| C | ||||
| C | c | Te | ||
| Asynchronous Machine | Multimeter | |||
| Asynchronous Machine | Machines | |||
| SI Units1 | ||||
| SI Units | Measurement | |||
Demux
Рис. 1.53. Виртуальная модель асинхронной машины (Fig 1_53):
а) модель в абсолютных единицах двигателя с фазным ротором; б) модель короткозамкнутого двигателя; в) измерительный инструмент
Рис. 1.54. Окно ввода параметров двигателя в абсолютных единицах
Клеммы A, B, C служат для подключения к трёхфазному напряже_ нию, клеммы a, b, c – выходы обмотки ротора. Параметры двигателя для модификации SI Units в абсолютных единицах вводятся через диа_ логовое окно, которое вызывается двойным щелчком по изображению двигателя (рис. 1.54). В строке Rotor type предлагается два варианта: Wound – двигатель с фазным ротором и Squirrel*cage – короткозамкну_тый двигатель (с беличьей клеткой). В строке Reference frame предлага_
ется три варианта выбора системы координат: Rotor – вращающаяся с ротором с одинаковой частотой; Stationary – неподвижная, наиболее естественная для нас; Synchronous – система координат, синхронно вра_ щающаяся с частотой сетевого напряжения. Параметры асинхронного двигателя вводятся в следующие строки в абсолютных единицах. Сле_ дует иметь в виду, что эти параметры в справочниках и каталогах не приводятся, а рассчитываются с помощью различных методик, напри_ мер так, как это рассмотрено в предыдущем пункте.
Чаще всего применяется короткозамкнутый двигатель (рис. 1.53, б). К выходу m подключается специальный демультиплексор Machines Measure* ment Demux, находящийся в разделе SimPowerSystems в подразделе Machine.
Тип машины переменного тока отражается в строке Machine type, открываемой двойным щелчком левой кнопки мыши (рис. 1.55).
Рис. 1.55. Окно выбора типа машины и перечня выходных переменных
По входу Tm задаётся активный момент нагрузки в Н.м. По требова_ нию программы Simulink на рабочем поле модели должен быть размещён блок Multimeter (рис. 1.53, в), иначе процесс моделирования блокируется.
На рис. 1.56 представлена схема моделирования процессов пуска и реверса асинхронного короткозамкнутого двигателя при включении на фазное напряжение 220 В, 50 Гц (380 В линейное) с реверсом путём из_ менения порядка чередования фаз с помощью переключателей Switch и Switch2. Время моделирования принято 0,6 с и реверса – через 0,3 с. Ак_тивный момент нагрузки задан 30 Н.м. Для построения динамической механической характеристики использован графопостроитель XY Graph.
Step
Sine Wave
+ ++
s -s-s-
Sine Wave1
Clock
Switch Switch2
Sine Wave2
| Tm | ir_abc | |||
| A | ||||
| m | is_abc | |||
| B | m | |||
| C | w m | |||
| Asynchronous Machine | Te | |||
| SI Units | ||||
| Machines | Scope | |||
| Measurement | ||||
| Demux | ||||
| Multimeter |
XY Graph
Рис. 1.56. Модель реверсивного электропривода переменного тока с прямым включением двигателя в сеть (Fig 1_56)
Настройка задающих генераторов синусоидального сигнала, упра_ вляемых источников напряжения и переключателей показана на рис. 1.57.
Рис. 1.57. Настройка блоков управления модели привода переменного тока
Результаты моделирования процессов пуска и реверса представле_ ны на рис. 1.58. Текущее значение токов представлено в каждой фазе.
Рис. 1.58. Переходные процессы пуска и реверса асинхронного двигателя
На первом временном отрезке от 0 до 3 с на двигатель подаётся на_ пряжение с прямым чередованием фаз. Двигатель разгоняется под на_ грузкой 30 Н.м «вперёд» (положительный знак частоты вращения). Пу_ сковой ток в обмотке статора достигает амплитудного значения 86,93 А. Примерно такое же значение достигает ток в обмотке ротора 77,6 А, так как выводится значение тока ротора в обмотке ротора, приведённое к об_ мотке статора. Электромагнитный момент двигателя носит колебатель_ ный характер, что приводит к ухудшению пусковых свойств двигателя и является недостатком асинхронного двигателя. Максимальное значение текущего значения момента составило при пуске «вперёд» 147 Н.м. При увеличении частоты вращения, колебания момента двигателя затухают, интенсивность роста частоты вращения возрастает. При этом ток стато_ ра уменьшается при неизменной частоте 50 Гц, в то же время ток в обмот_ ке ротора тоже уменьшается, но с уменьшением частоты тока ротора. Это объясняется выбором неподвижной системы координат. В установив_ шемся режиме (текущее время чуть менее 3 с) частота вращения достига_ ет значения 150,4 1/с (при ω0 = (1500.2π)/60 = 157 1/c), момент двигате_ ля – 29,94 Н.м (при нагрузке 30 Н.м), амплитудное значение тока ста_ тора – 11,6 А, амплитудное значение тока ротора – 11,02 А.
В момент времени 3 с производится реверс двигателя путём измене_ ния порядка чередования фаз. Эту задачу выполняют переключатели Switch. Идет переходный процесс реверса: ток в обмотке ротора достига_ет 106,9 А амплитудного значения (рис. 1.58), частота тока в обмотке ро_ тора чуть менее 100 Гц. Происходит противоточное торможение (двига_ тель включен «назад», а ещё вращается «вперёд»). Момент двигателя по_ прежнему имеет колебательный характер, максимальное значение соста_ вляет –170,1 Н.м. По мере уменьшения частоты вращения колебатель_ ность момента затухает, частота вращения достигает нулевого значения и начинает расти в отрицательной области, которую мы уже назвали «на_ зад». Частота вращения достигает значения –162,3 1/с (рис. 1.58), превы_ шающего частоту идеального холостого хода 157 1/с, это свидетельствует о том, что двигатель работает в режиме генераторного торможения и раз_ вивает положительный момент +30,52 Н.м, равный заданному моменту нагрузки 30 Н.м. Ток ротора и статора уменьшился до установившегося значения, соответствующего нагрузке 30 Н.м.
Рис. 1.59. Динамическая механическая характеристика асинхронного
двигателя при пуске и реверсе с активным моментом нагрузки 30 Н.м
На рис. 1.59 приведена снятая при пуске и реверсе механическая характеристика двигателя. Колебательный характер момента при пуске и реверсе весьма существенно изменяет вид механической характери_ стики. При пуске максимальное значение момента достигает значения около 150 Н.м, однако среднее значение, определяющее интенсивность пуска, невелико. Наиболее близка к статической механическая харак_ теристика, рассчитанная при пуске двигателя «назад». Двигатель разви_ вает пусковой момент –51,77 Н.м (рис. 1.59), максимальный момент –76,6 Н.м при частоте вращения –111,2 1/с и разгоняется до частоты вращения, большей, чем частота идеального холостого хода.
Основной вывод состоит в том, что в модель двигателя можно вве_ сти только активный момент. Виртуальный двигатель из библиотеки SimPowerSystems не способен работать с реактивной нагрузкой, тем бо_лее со смешанной.
Дата добавления: 2015-12-07; просмотров: 197 | Нарушение авторских прав
mybiblioteka.su - 2015-2018 год. (0.059 сек.)mybiblioteka.su
