







Для нерегулируемых электроприводов большой мощности (свыше 160кВт) широко применяются синхронные электродвигатели с электромагнитным возбуждением. Схема включения такого двигателя показана на рис.3.23.
Конструкция статора синхронного двигателя аналогична конструкции статора асинхронного двигателя. Токи, протекающие по трехфазной обмотке статора, создают намагничивающие силы, результирующий вектор которых образует вращающееся в пространстве электромагнитное поле статора Ф,. Скорость вращения поля статора равна согласно (3.3)

и является рабочей скоростью синхронного двигателя.
На роторе синхронного двигателя расположена обмотка возбуждения, которая питается постоянным током от независимого регулируемого источника напряжения - возбудителя. Ток возбуждения создает электромагнитное поле Ф0, неподвижное относительно ротора и вращающееся в установившемся режиме вместе с ротором со скоростью а>0. Магнитные силовые линии поля ротора сцепляются с вращающимся синхронно с ним электромагнитным полем статора. Взаимодействие полей статора и ротора создает электромагнитный момент на валу синхронной машины.


Рис.3.23. Схе- Рис.3.24. Пространственные векторы электро-
ма включения магнитных полей синхронного двигателя
синхронного а) идеальный холостой ход;
двигателя б) при нагрузке на валу
При отсутствии нагрузки векторы поля статора Ф1 и поля ротора Ф0 совпадают в пространстве (см. рис.3.24,а) и совместно вращаются со скоростью ω0. При появлении на валу двигателя момента сопротивления векторы Ф1, и Ф0 расходятся (как бы растягиваются подобно пружине) на угол θ, называемый углом нагрузки, причем, если вектор Ф0 отстает от вектора Ф1 (см. рис. 3.24,6), то синхронная машина работает в двигательном режиме и электромагнитный момент на ее валу положителен. Если синхронная машина работает генератором, приводимым во вращение первичным двигателем, то вектор поля ротора опережает вектор поля статора на угол (–θ ) и электромагнитный момент на валу машины отрицателен. Изменению нагрузки на валу машины соответствует изменение угла θ. Образно это соответствует растяжению-сжатию пружины. Максимальный момент Ммакс будет иметь место при θ – π/2 . Если нагрузка на валу машины будет больше Ммахс, то синхронный режим нарушается и машина выпадает из синхронизма.
Механическая характеристика синхронной машины представляют собой прямую, параллельную оси абсцисс и ограниченную значениями момента ± Ммакс (рис.3.25). Жесткость механической характеристики равна бесконечности.

Рис.3.25. Механические характеристики синхронного двигателя
1 - характеристика синхронного режима
2 - пусковая характеристика (асинхронный режим)
Поскольку ротор двигателя вращается с синхронной скоростью и скольжение отсутствует, то вся мощность электромагнитного поля статора Рэм преобразуется в механическую мощность на валу синхронного двигателя. Если пренебречь потерями в статоре, то Рэм = 3U1I1 соsφ = Мω0, откуда
 (3.39)
(3.39)
Рассмотрим векторную диаграмму неявнополюсной синхронной машины (рис. 3.26). Двигатель с неявнополюсным ротором имеет симметричную в магнитном отношении конструкцию. Пренебрегая активным сопротивлением статора, получим Ů1 – Ė1 = jI1x1.
Здесь Е, – э.д.с., наводимая в обмотках статора вращающимся вместе с ротором полем Ф0.

Рис.3.26. Векторная диаграмма синхронного двигателя
Из векторной диаграммы следует:
U1 sin θ = I1x1 cos (φ – θ)

U1cos φ = E1 cos(φ – θ)
Подставляя эти значения в (3.39), получим выражение для угловой характеристики неявнополюсной синхронной машины
 (3.40)
(3.40)
Из этого выражения и соответствующей ему угловой характеристики (рис.3.27) следует, что по мере нагружения синхронной машины угол нагрузки увеличивается и момент достигает максимума при θ = π/2. Для сохранения постоянной перегрузочной способности двигателя предусматривается автоматическое увеличение тока возбуждения при приложении ударной нагрузки или снижении величины питающего напряжения.

Рис.3.27. Угловая характеристика синхронного двигателя:
а) неявнополюсной машины; б) явнополюсной машины
1 - при номинальном потоке возбуждения;
2 - при форсировке возбуждения
Для синхронного двигателя явнополюсной конструкции, который имеет несимметричную магнитную цепь, кроме момента, вызванного полем ротора, возникает реактивный момент, определяемый стремлением ротора занять такое положение, при котором магнитная проницаемость для пути потока статора была бы максимальной. Угловая характеристика (см. рис.3.27,б) для такого двигателя описывается уравнением:
 +
+ 
где хd и хq– индуктивное сопротивление по продольной и поперечной осям.
studfiles.net
П ринципиальная схема двигателя независимого возбуждения (ДНВ) изображается так, как показано на рис. 3.1.
ринципиальная схема двигателя независимого возбуждения (ДНВ) изображается так, как показано на рис. 3.1.
Обмотка возбуждения (ОВ) питается от независимого источника постоянного тока. При подключении ОВ к обмотке якоря машина превращается в двигатель параллельного возбуждения. Для регулируемых электроприводов обычно используется ДНВ.
Процессы электромеханического преобразования энергии ДНВ описываются следующими уравнениями.



Здесь 

 –электромагнитная постоянная обмотка возбуждения
–электромагнитная постоянная обмотка возбуждения  .
.
 –электромагнитная постоянная обмотка якоря
–электромагнитная постоянная обмотка якоря  .
.
К – конструктивный коэффициент, равный  , где
, где
N – число активных проводников обмотки якоря;
 –число пар полюсов машины;
–число пар полюсов машины;
a – число пар параллельных ветвей обмотки якоря;
 –ЭДС вращения якоря;
–ЭДС вращения якоря;
 –коэффициент ЭДС машины;
–коэффициент ЭДС машины;
 –сопротивление обмотки якоря;
–сопротивление обмотки якоря;
 –сопротивление обмотки добавочных полюсов;
–сопротивление обмотки добавочных полюсов;
 –сопротивление компенсационной обмотки (для машины мощностью 100 и выше кВт).
–сопротивление компенсационной обмотки (для машины мощностью 100 и выше кВт).
Обычно ДНВ работает при Ф=Фн=const. При этом выше написанные уравнения линеаризуются и после преобразований (решение относительно скорости ω) получим уравнение электромеханической характеристики.

Выразив ток якоря через момент  , получим уравнение механической характеристики
, получим уравнение механической характеристики

В установившимся режиме 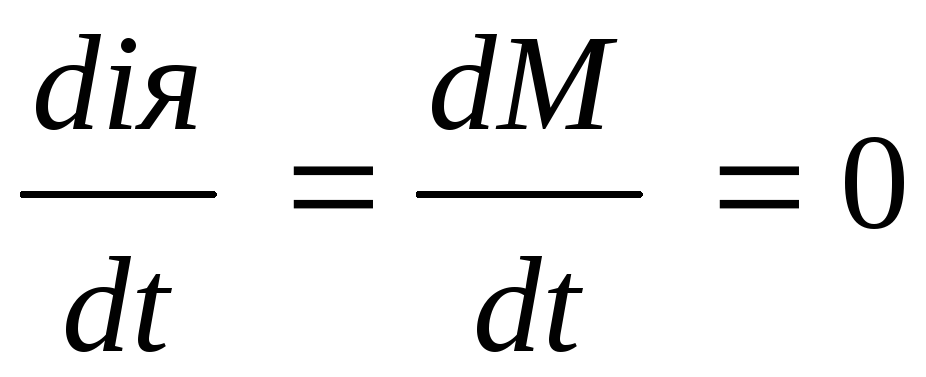 . Поэтому уравнения запишутся в следующем виде:
. Поэтому уравнения запишутся в следующем виде:


Эти уравнения показывают, что при U=Uя=const и ф=const характеристики являются прямыми с начальной ординатой  , соответствующей скорости идеального холостого хода двигателя (рис. 3.2).
, соответствующей скорости идеального холостого хода двигателя (рис. 3.2).

Характеристики, соответствующие отсутствию в цепи якоря добавочного сопротивления, являются естественными. Статическую жесткость характеристики, определяющую ее наклон, можно найти, продифференцировав выражение момента М по скорости ω, найдя предварительно М из уравнения механической характеристики.
 ;
; 
Модуль статической жесткости

Используя понятие жесткости, уравнение статической механической характеристики ДНВ можно представить в виде:

Чем больше модуль жесткости естественной механической характеристики, тем стабильнее является скорость ω электропривода при широких пределах изменения его нагрузки.
Другой оценкой стабильности рабочей скорости ω является статизм механической характеристики, количественной оценкой которого служит номинальный перепад скорости.
 , где
, где
 –скорость идеального холостого хода на естественной характеристике.
–скорость идеального холостого хода на естественной характеристике.
Относительный перепад скорости для двигателей

большой мощности составляет (1,53)%.
На вид естественных механической и электромеханический характеристик значительное влияние оказывает реакция якоря, ослабляющая магнитный поток машины. Из-за ее размагничивающего действия в механической характеристике двигателя могут появиться участки с положительной жесткостью (рис. 3.3, участок а-б), что приводит к неустойчивости электропривода.

Реакция якоря, может снизить магнитный поток двигателя на 10-20%, вследствие чего уменьшится его перегрузочная способность. Она неблагоприятно сказывается и на динамических свойствах электропривода. Поэтому в двигателях без компенсационной обмотки мощностью до 100 кВт применяют так называемую стабилизирующую обмотку, размещаемую на сердечниках главных полюсов. Она включается цепь якоря последовательно и создает небольшую МДС, компенсирующую действие реакции якоря. Но двигатели с такой обмоткой нельзя применять для реверсивных электроприводов, т.к. при изменении направления вращения ток якоря имеет противоположное направление, и стабилизирующая обмотка будет усугублять действие реакции якоря.
Отметим, что механическая характеристика ДНВ представляет собой зависимость от электромагнитного момента М двигателя. Если же изобразить зависимость от момента на валу, то это будет не прямая, а ломанная (рис. 3.4). В двигательном режиме  , а в тормозном (генераторном)
, а в тормозном (генераторном)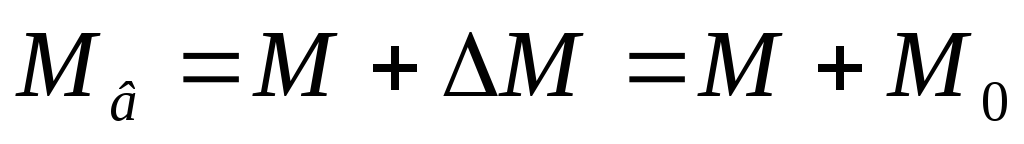 (пунктирная линия). При=0 возникает разрыв непрерывности. Это создает неудобства при расчетах. Поэтому момент
(пунктирная линия). При=0 возникает разрыв непрерывности. Это создает неудобства при расчетах. Поэтому момент  прибавляют к нагрузке (кМс) и характеристику двигателя считают линейной.
прибавляют к нагрузке (кМс) и характеристику двигателя считают линейной.


Часто для удобства расчетов уравнение механической характеристики представляют в относительных единицах. Характеристики двигателей, различных по своим номинальным данным, становятся универсальными. В относительных единицах напряжение, ЭДС, ток, момент, магнитный поток, скорость можно представить в следующем виде:

(для двигателей последовательного и смешанного возбуждения  ),
), , где
, где – номинальное сопротивление, т.е. сопротивление якорной цепи, которое при приложении к якорю номинального напряжения и ω=0 ограничивает ток в якоре до
– номинальное сопротивление, т.е. сопротивление якорной цепи, которое при приложении к якорю номинального напряжения и ω=0 ограничивает ток в якоре до  (см. рис. 3.5).
(см. рис. 3.5).
Для написания уравнения механической характеристики относительных единицах разделим обе части уравнения механической характеристики на ω0.
 , отсюда
, отсюда
 .
.
т.е. 
Т.к. у ДНВ при Ф=const МIя, то  и
и .
.
Это уравнение электромеханической характеристики в относительных единицах.
Характеристики двигателя, соответствующие изменениям параметров двигателя или специальным схемам его включения, являются искусственными. Так, при введении в цепь якоря добавочного сопротивления наклон характеристик увеличивается, их жесткость уменьшается. Семейство механических характеристик, соответствующих различным значениям Rдоб, изображено на следующем рис. 3.6. Скорость якоря двигателя при этом уменьшается, ибо увеличивается падение напряжения на якоре, уменьшается ток, а следовательно и вращающий момент. Отсюда видна возможность регулирования скорости двигателя изменением сопротивления в якорной цепи.

При изменении напряжения, подводимого двигателю, изменяется скорость идеального холостого хода  , а жесткость характеристик остается неизменной. Семейство механических характеристик, соответствующих различным напряжениям на якоре, изображено на рис. 3.7. Для получения таких характеристик двигатель нужно питать от источника, напряжение которого можно регулировать. Это позволяет регулировать скорость двигателя.
, а жесткость характеристик остается неизменной. Семейство механических характеристик, соответствующих различным напряжениям на якоре, изображено на рис. 3.7. Для получения таких характеристик двигатель нужно питать от источника, напряжение которого можно регулировать. Это позволяет регулировать скорость двигателя.

Для ряда производственных механизмов в соответствие с требованиями технологического процесса иногда возникает необходимость увеличения рабочей скорости, превышающей скорость при U= UН и φ=φН. Этого достигается ослаблением магнитного потока двигателя (уменьшением тока возбуждения).
Если уменьшенное значение магнитного потока, равно  , где<1, то новое, увеличенное значение скорости идеального холостого хода будет
, где<1, то новое, увеличенное значение скорости идеального холостого хода будет
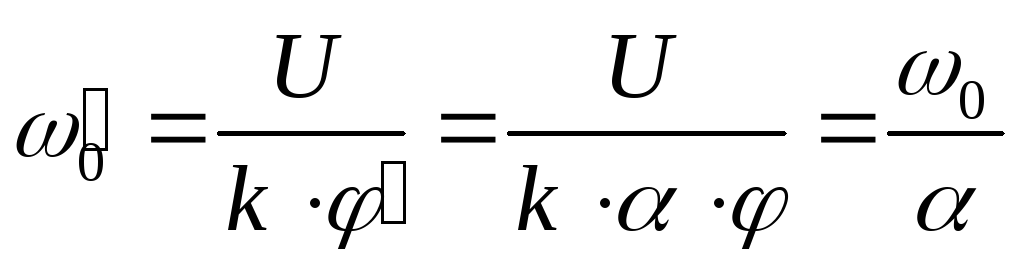 .
.
При ослабленном потоке и прежнем значении момента ток якоря увеличивается. Его можно найти из уравнения момента
 , откуда
, откуда

Уравнение механической характеристики при ослабленном потоке будет
 , где
, где
 –перепад скорости при номинальном потоке.
–перепад скорости при номинальном потоке.

Ослабление потока вызывает увеличение не только 0, но и скорости якоря двигателя (при нагрузках, допустимых по условиям коммутации), что, собственно, и требуется. Но при нагрузках, не допустимых по условиям коммутации, скорость будет уменьшаться, и двигатель может перейти в тормозной режим, что отраженно на рис. 3.8, где изображено семейство механических характеристик двигателя, соответствующих различным значениям магнитного потока.
studfiles.net
ЭП с трехфазным асинхронным двигателем (АД) является самым массовым видом привода в промышленности, в коммунальном и сельском хозяйстве. Такое положение определяется простотой изготовления и эксплуатации АД, меньшими по сравнению с ДПТ массой, габаритными размерами и стоимостью, а также высокой надежностью в работе. В народном хозяйстве наибольшее распространение получили АД с короткозамкнутым ротором.
Основной областью применения АД вплоть до недавнего времени являлся нерегулируемый электропривод. В последние годы в связи с разработкой и выпуском электротехнической промышленностью тиристорных преобразователей частоты и напряжения стали создаваться регулируемые асинхронные ЭП с характеристиками, не уступающими по своим показателям ЭП постоянного тока.
Основная схема включения трехфазного АД в сеть и соответствующая ей однофазная схема замещения с вынесенным контуром намагниченности показаны на рисунке 8.1 [1,2].
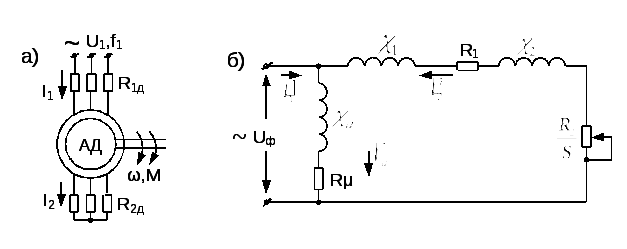
Рис.8.1. Схема включения (а) и однофазная схема замещения (б) АД
На схеме приняты следующие обозначения:
Uф – действующее значение фазного напряжения сети, В;
 –фазные токи соответственного намагничивания, обмотки статора и приведенный ток ротора, А;
–фазные токи соответственного намагничивания, обмотки статора и приведенный ток ротора, А;
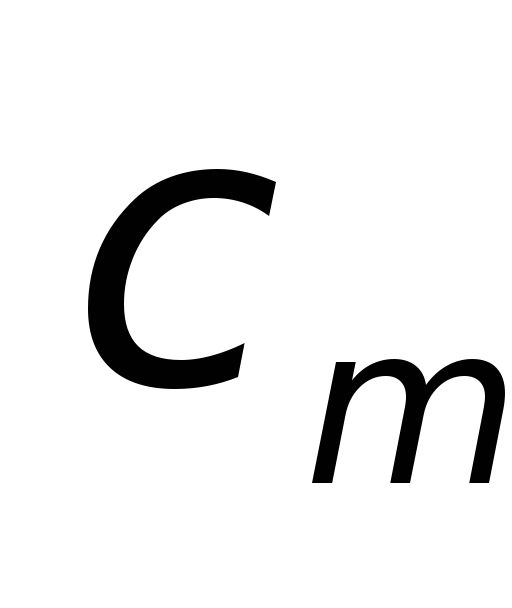 –индуктивное сопротивление контура намагничивания, Ом;
–индуктивное сопротивление контура намагничивания, Ом;
 –активные фазные сопротивления обмоток, соответственно статора и ротора; последнее приведено к обмотке статора, Ом;
–активные фазные сопротивления обмоток, соответственно статора и ротора; последнее приведено к обмотке статора, Ом;
R1д и R2д – добавочные сопротивления в фазах статора и ротора;
 –индуктивные фазные сопротивления, обусловленные полями рассеяния обмоток статора и ротора; последнее приведено к обмотке статора, Ом.
–индуктивные фазные сопротивления, обусловленные полями рассеяния обмоток статора и ротора; последнее приведено к обмотке статора, Ом.
S – скольжение двигателя, определяется по выражению [1,4]:
 , (8.1)
, (8.1)
где  – угловая скорость ротора, рад/с;
– угловая скорость ротора, рад/с;  – угловая скорость магнитного поля статора, называемая синхронной, рад/с.
– угловая скорость магнитного поля статора, называемая синхронной, рад/с.
 (8.2)
(8.2)
В выражении (8.2):
 –частота напряжения питающей сети, Гц; р – число пар полюсов двигателя.
–частота напряжения питающей сети, Гц; р – число пар полюсов двигателя.
Рассматриваемая схема замещения АД получена при определенных допущениях. В частности, ее параметры считаются не зависящими от режима работы, не учитываются насыщение магнитопровода, добавочные потери, а также влияние пространственных и временных высших гармонических составляющих (н.с.) обмоток статора и ротора.
При подведении к обмотке статора переменного трехфазного напряжения в статоре образуется вращающееся магнитное поле со скоростью  . Это поле пересекает обмотку ротора и наводит в ней ЭДС [1]:
. Это поле пересекает обмотку ротора и наводит в ней ЭДС [1]:
 , (8.3)
, (8.3)
где  < 1 – обмоточный коэффициент, учитывающий уменьшение ЭДС ротора вследствие геометрического сложения ЭДС, и укорочение шага обмотки ротора;
< 1 – обмоточный коэффициент, учитывающий уменьшение ЭДС ротора вследствие геометрического сложения ЭДС, и укорочение шага обмотки ротора;
 –частота тока в обмотке ротора, Гц;
–частота тока в обмотке ротора, Гц;
 –число витков обмотки фазы ротора;
–число витков обмотки фазы ротора;
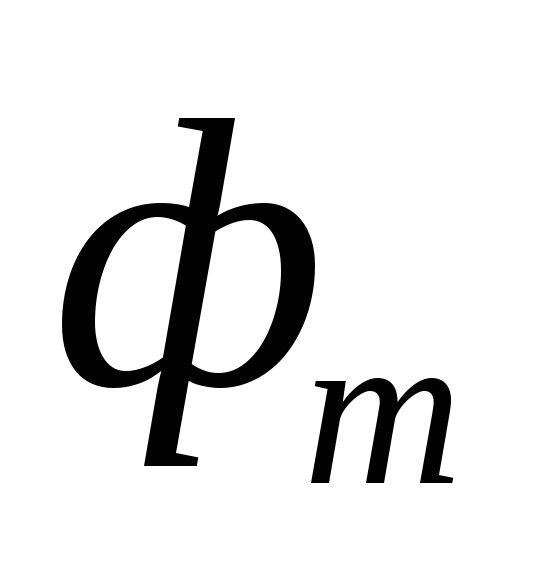 –максимальное значение магнитного потока статора, Вб.
–максимальное значение магнитного потока статора, Вб.
Эта ЭДС создает ток в обмотке ротора
 (8.4)
(8.4)
где  – активное сопротивление фазной обмотки ротора;
– активное сопротивление фазной обмотки ротора;
 –индуктивное сопротивление рассечения фазы роторной обмотки.
–индуктивное сопротивление рассечения фазы роторной обмотки.
Взаимодействуя с полем статора, активный ток создает пусковой вращающий момент, и двигатель запускается, вращаясь в дальнейшем со скоростью
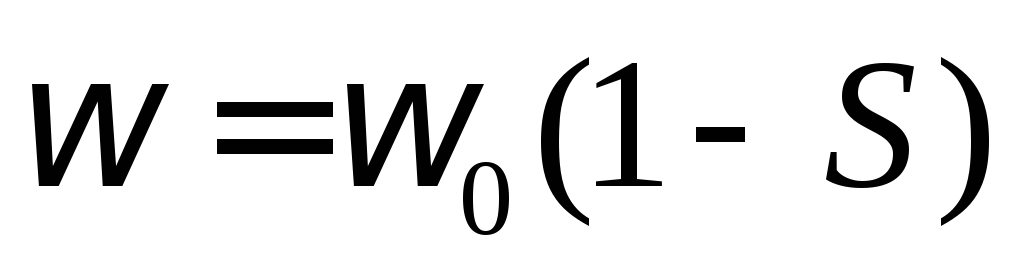 . (8.5)
. (8.5)
При номинальном скольжении  номинальная скорость
номинальная скорость  .
.
Для обычных двигателей  = 0,02÷0,06, для двигателей с повышенным скольжением
= 0,02÷0,06, для двигателей с повышенным скольжением  = 0,08÷0,18.
= 0,08÷0,18.
Запуск электродвигателя происходит по следующей механической характеристике (рис. 8.2).

Рис. 8.2. Механическая характеристика АД
На рисунке 8.2 обозначено: Мп – пусковой момент; Мк – критический момент; Мн – номинальный момент; Sк – критическое скольжение.
Так как ЭДС, индуктированная в обмотке ротора в момент пуска имеет максимальное значение (при S=1, f2=50 Гц), то ток в обмотке ротора I2 = (4–8)Iн.д. (Iн.д – номинальный ток двигателя).
Однако на пусковой момент влияет не эта величина пускового тока (I2 = Iп), а сдвиг фаз между током I2 и ЭДС Е2s ротора.
Если индуктивность обмотки ротора велика, то будет большим и сдвиг фаз между током ротора I2 и ЭДС ротора Е2s.
В момент пуска, когда ротор еще неподвижен, частота тока в обмотке ротора наибольшая ( =
= =50 Гц), и поэтому индуктивное сопротивление
=50 Гц), и поэтому индуктивное сопротивление имеет наибольшее максимальное значение
имеет наибольшее максимальное значение  :
:
 , (8.6)
, (8.6)
где  – индуктивность рассеяния фазы обмотки ротора.
– индуктивность рассеяния фазы обмотки ротора.
Вращающий момент АД определяется по формуле [1]
 , (8.7)
, (8.7)
а коэффициент мощности  - по выражению [1]
- по выражению [1]
 . (8.8)
. (8.8)
В формуле (8.7): 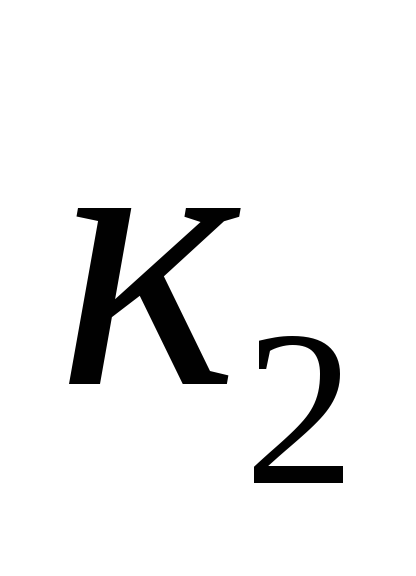 – обмоточный коэффициент;
– обмоточный коэффициент;  – угол сдвига фаз между ЭДС и током фазы обмотки ротора.
– угол сдвига фаз между ЭДС и током фазы обмотки ротора.
Таким образом, момент двигателя определяется активной слагающей пускового полного тока ротора  .
.
Пусковой момент двигателя можно увеличить, если в момент пуска уменьшить сдвиг фаз меду током I2 и ЭДС E2S ротора. Это приведет к тому, что увеличится  . ПриR2доб = 0 и ω = 0
. ПриR2доб = 0 и ω = 0  = 0,1÷0,2. ПриR2доб ≠ 0
= 0,1÷0,2. ПриR2доб ≠ 0  = 0,3–0,6. При ω = ωн
= 0,3–0,6. При ω = ωн  = 0,8÷0,9. На практике этим способом часто пользуются. Для этого в цепь ротора вводят активное сопротивление, которое затем выводят как только двигатель увеличит скорость, либо применяют двигатель, у которого на роторе глубокие пазы для стержней, либо две клетки (две короткозамкнутые обмотки).
= 0,8÷0,9. На практике этим способом часто пользуются. Для этого в цепь ротора вводят активное сопротивление, которое затем выводят как только двигатель увеличит скорость, либо применяют двигатель, у которого на роторе глубокие пазы для стержней, либо две клетки (две короткозамкнутые обмотки).
Таким образом, пусковой момент двигателя зависит от конструкции ротора.
При пуске АД с уменьшением скольжения от S = 1 до S = Sк уменьшаются частота  и ЭДС Е2, полный ток I2 уменьшается очень медленно (всего на 29 % от I2п), а
и ЭДС Е2, полный ток I2 уменьшается очень медленно (всего на 29 % от I2п), а  и активный токI2а значительно увеличиваются. При дальнейшем пуске АД от S = Sк до S = 0 токи I2 и I2а резко уменьшаются при незначительном росте
и активный токI2а значительно увеличиваются. При дальнейшем пуске АД от S = Sк до S = 0 токи I2 и I2а резко уменьшаются при незначительном росте 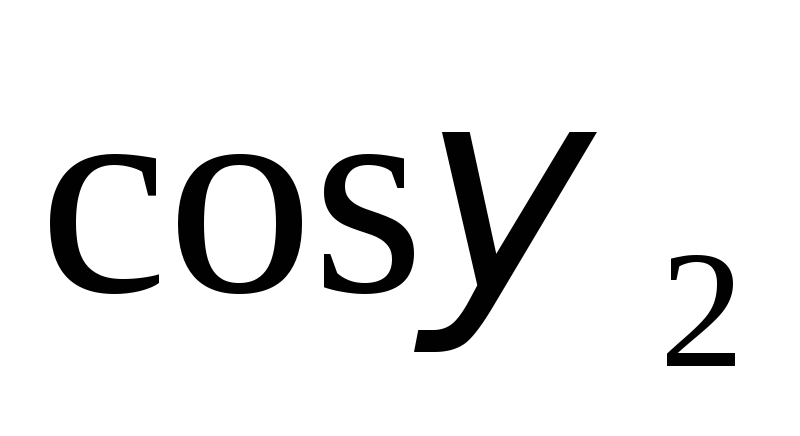 . Такие изменения параметров в цепи ротора и определяют вид характеристики (рис. 8.2).
. Такие изменения параметров в цепи ротора и определяют вид характеристики (рис. 8.2).
Для вывода уравнения механической характеристики и ее построения обычно пользуются схемой замещения двигателя (рис. 8.1б), рассматривая баланс мощности в двигателе.
Электромагнитная мощность Р12, передаваемая ротору от статора, определяется электромагнитным моментом М, развиваемым двигателем: Р12 = М ω0. Здесь, как и ранее, считается, что электромагнитный момент двигателя приблизительно равен моменту на его валу, т.е. не учитываются механические потери.
ω0. Здесь, как и ранее, считается, что электромагнитный момент двигателя приблизительно равен моменту на его валу, т.е. не учитываются механические потери.
Мощность, передаваемую ротору, можно разделить на две составляющие: мощность, преобразуемую в механическую Рм, и мощность потерь ∆Рэл.2 в роторе. Первая составляющая может быть определена следующим образом: Рм = М ω. Вторая составляющая представляет собой электрические потери в обмотках ротора и потери на перемагничивание.
ω. Вторая составляющая представляет собой электрические потери в обмотках ротора и потери на перемагничивание.
Как правило, потери в стали ротора существенно меньше электрических потерь, в связи с чем последними можно пренебречь. Тогда
Р12 =Рм + ∆Рэл.2, (8.9)
или М ω0 = М
ω0 = М ω +∆Рэл.2.
ω +∆Рэл.2.
Отсюда
∆Рэл.2 = М(ω0 – ω) = М ω0
ω0 S. (8.10)
S. (8.10)
Учитывая, что
∆Рэл.2 =  , (8.11)
, (8.11)
где 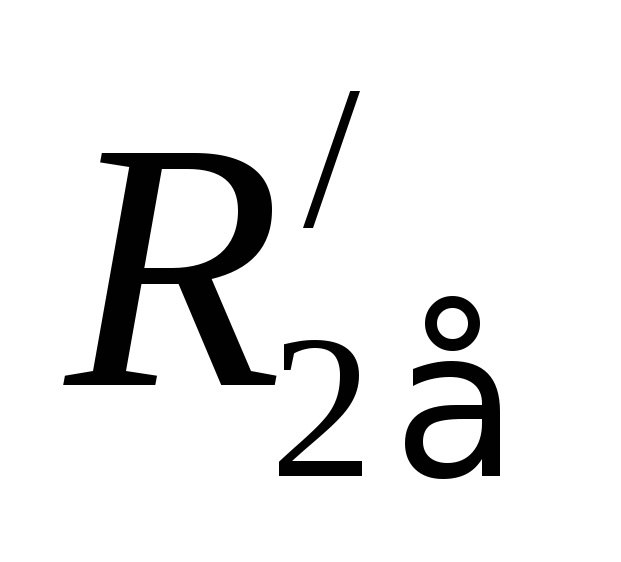 =
= , можно записать выражение для момента в виде
, можно записать выражение для момента в виде
 . (8.12)
. (8.12)
Из схемы замещения [1,2]
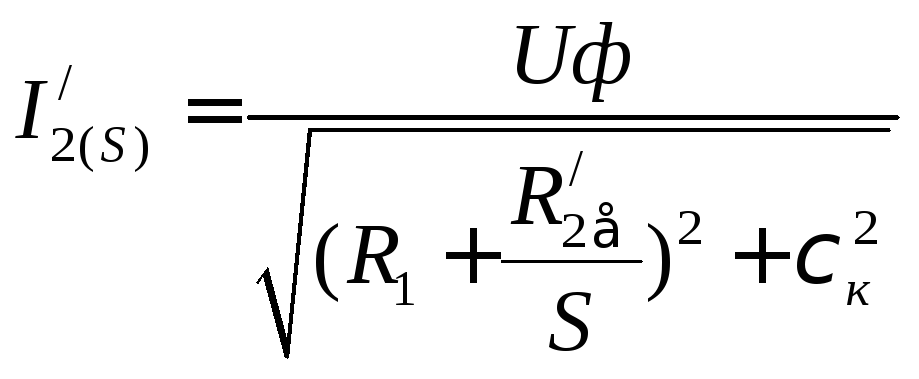 , (8.13)
, (8.13)
где  – индуктивное фазное сопротивление короткого замыкания.
– индуктивное фазное сопротивление короткого замыкания.
Выражение (8.13) представляет собой уравнение электромеханической характеристики двигателя  , так как скольжение
, так как скольжение  однозначно определяет величину скорости двигателя
однозначно определяет величину скорости двигателя  .
.
Отметим, что для АД обычно под электромеханическими и механическими характеристиками понимаются зависимости момента и тока от скольжения. В этом случае соответствующие уравнения получают более компактную форму записи и оказываются удобными для вычисления.
Подстановка (8.13) в (8.12) дает уравнение механической характеристики [1,2,3,4]:
 . (8.14)
. (8.14)
Максимальное значение момента Мк принято называть критическим (допустимым перегрузочным моментом). Соответствующее ему скольжение Sк также называется критическим. Для определения Sк необходимо решить уравнение вида  , подставив в него М(S).
, подставив в него М(S).
Решение этого уравнения дает:
 . (8.15)
. (8.15)
Подставляя значение  в уравнение (8.14), находим:
в уравнение (8.14), находим:
 . (8.16)
. (8.16)
Знак (+) соответствует S > 0, а (–) – S < 0. Знаки « » в уравнении (8.16) означают, что максимум момента может иметь место при S > 0 в двигательном режиме или в режиме противовключения, а при S < 0 – в генераторном режиме.
» в уравнении (8.16) означают, что максимум момента может иметь место при S > 0 в двигательном режиме или в режиме противовключения, а при S < 0 – в генераторном режиме.
Из уравнения (8.16) видно, что при работе в генераторном режиме с рекуперацией энергии критический момент больше, чем при работе в двигательном режиме или режиме противовключения.
Из уравнений (8.14) и (8.16) с учетом (8.15) может быть получена другая формула для механической характеристики:
 , (8.17)
, (8.17)
где  .
.
Для крупных машин сопротивление  невелико, поэтому практически
невелико, поэтому практически 
 . В этом случае получится формула, более удобная для расчетов [1,2]:
. В этом случае получится формула, более удобная для расчетов [1,2]:
 , (8.18)
, (8.18)
Критическое скольжение можно определять по следующему выражению:
 , (8.19)
, (8.19)
где  – коэффициент перегрузочной способности.
– коэффициент перегрузочной способности.
Для уравнения (8.18) достаточно знать лишь параметры, которые обычно указываются в каталогах, или могут быть найдены по данным каталогов, тогда как такие параметры, как  и
и  обычно неизвестны.
обычно неизвестны.
Анализ формулы (8.18) показывает, что при S > Sк (нерабочая часть характеристики) получается гипербола. Эта часть характеристики соответствует лишь пусковым и тормозным режимам.
При малых значениях скольжения (S < Sк) для М = f(S) получится уравнение прямой линии. Эта линейная часть характеристики является ее рабочей частью, на которой двигатель обычно работает в установившемся режиме. На этой же части характеристики находятся точки, соответствующие номинальным данным Мн, Iн, ωн, Sн … .
Величина номинального скольжения зависит от сопротивления ротора и мощности двигателя. Двигатель с малым сопротивлением (большой мощности) ротора имеет малые Sк и Sн и более жесткую механическую характеристику.
Анализ уравнений (8.15) и (8.16) показывает, что Мк и Sк уменьшаются с увеличением индуктивных сопротивлений обмоток  и активного сопротивления
и активного сопротивления  обмотки статора.
обмотки статора.
Критическое скольжение не зависит от питающего напряжения и прямо пропорционально  . Это свойство используется для увеличения пускового момента АД с фазным ротором при включении в цепь ротора добавочного сопротивления R2д (рис. 8.1а).
. Это свойство используется для увеличения пускового момента АД с фазным ротором при включении в цепь ротора добавочного сопротивления R2д (рис. 8.1а).
Механические характеристики АД с фазным ротором приведены на рисунке 8.3.

Рис. 8.3. Механические характеристики АД с фазным ротором
С увеличением сопротивления R2д снижается жесткость механических характеристик аналогично как и для ДПТ независимого возбуждения.
Момент Мк не зависит от активного сопротивления цепи ротора и пропорционален квадрату напряжения питающей сети. Снижение напряжения питающей сети на ~15 % приводит к уменьшению Мк и соответственно λ на 28 %.
studfiles.net
ЭЛЕКТРИЧЕСКИЙ ПРИВОД
Наиболее распространенными типами нерегулируемых электроприводов являются электроприводы с короткозамкнутыми асинхронными двигателями. Для нерегулируемых электроприводов характерен пуск электродвигателя прямым включением в сеть с помощью контактной аппаратуры без промежуточных преобразователей электрической энергии.
Стандартная схема силовых цепей включения короткозамкнутого асинхронного двигателя с помощью контактов пускателя приведена на рис. 5.1.
|
|
Рис. 5.1. Схема включения короткозамкнутого асинхронного двигателя с использованием контактного пускателя
Для расчета характеристик асинхронного двигателя, как правило, пользуются его математической моделью, которая в общем случае представляется различными схемами замещения. Наиболее простой и удобной для инженерных расчетов асинхронного двигателя является Т-образная схема замещения (см. рис. 5.2).
Нарис. 5.2 приняты следующие обозначения:
Uij - фазное напряжение обмотки статора;
Щ - активное сопротивление обмотки статора;
Х1о - индуктивное сопротивление рассеяния обмотки статора;
11 - ток обмотки статора;
Ei - ЭДС обмотки статора;
і
- активное сопротивление обмотки ротора, приведенное к обмотке статора;
і
Х2а - индуктивное сопротивление рассеяния обмотки ротора, приведенное к обмотке статора;
і
12 - ток обмотки ротора, приведенный к обмотке статора; s = (со0 - со)/со0 - скольжение;
оо0 = 2 ■ л ■ fi/zp - синхронная угловая скорость; со - угловая скорость асинхронного двигателя; zp - число пар полюсов;
fx - значение частоты напряжения переменного тока, подводимого к обмотке статора;
Ет - ЭДС от главного магнитного потока машины;
і
Е 2 ЭДС обмотки ротора, приведенная к обмотке статора.
|
Рис. 5.2. Схема замещения асинхронного двигателя |
Векторная диаграмма токов, ЭДС и напряжений, удовлетворяющая системе уравнений (5.1), изображена на рис. 5.3.
|
|
| 7о Рис. 5.3. Векторная диаграмма асинхронного двигателя |
Ток ротора /2, приведенный к обмотке статора асинхронного дви
|
|
| гателя, определяется зависимостью, получаемой непосредственно из схемы замещения асинхронного двигателя: |
где XKYl = XiQ + Xiv - индуктивное сопротивление короткого замыкания.
і
Уравнение /2 = /( v) называется электромеханической характери-
стикой асинхронного двигателя.
Для короткозамкнутого асинхронного двигателя представляет интерес другая электромеханическая характеристика I= f ( v), отражающая зависимость тока статора! от скольжения s.
Задаваясь скольжением s можно по (5.10) и (5.2) построить, соответственно, механические и электромеханические характеристики асинхронного двигателя, которые представлены на рис. 5.4.
|
Рис. 5.4. Статические характеристики асинхронного двигателя: а - механическая; б - электромеханическая |
При скольжениях 0 < s < 1 асинхронная машина работает в двигательном режиме, при s < 0 - в генераторном режиме параллельно с сетью (рекуперативное торможение), при s > 1 - в генераторном режиме последовательно с сетью или в режиме торможения противовключени-
Механические характеристики, приведенные на рис 5.4, а имеют в двигательном режиме три характерные точки:
1) ,v = 0; М= 0, при этом скорость двигателя равна синхронной ®о = 2-л-/і/-р;
2) s = sK; М = Мвд, что соответствует точке с критическим скольжением и критическим моментом двигательного режима;
3) s = 1, при этом скорость двигателя будет равна нулю, а момент равен пусковому М = Ми.
Электромеханические характеристики, приведенные на рис 5.4, б, имеют две характерные точки в двигательном режиме:
і
1) ^ = 0; /2 = 0, при этом скорость двигателя равна синхронной ®о = 2-^-/1/zP ;
2) s = 1, при этом скорость двигателя будет равна нулю, а ток рото-
t (
ра - току короткого замыкания (/2 = /2кз )•
Механические и электромеханические характеристики асинхронного двигателя не совпадают даже построенные в безразмерных единицах.
Различают естественную и искусственные механические характеристики асинхронного двигателя.
Под естественной механической характеристикой асинхронного двигателя будем понимать зависимость момента двигателя М от его скольжения s при номинальной схеме включения двигателя, номинальных параметрах питающей сети (£/1н, /ін) и отсутствии добавочных сопротивлений в цепях двигателя. Все остальные характеристики называются искусственными. С помощью искусственных характеристик асинхронного двигателя регулируют его скорость в соответствие с требованиями технологического процесса.
Как следует из уравнения механической характеристики асинхронного двигателя (5.7), регулировать его скорость можно, изменяя один или несколько параметров:
U j - фазное напряжение обмоток статора двигателя;
Л’їдоб - добавочное активное сопротивление статора;
А"| Доб - добавочное индуктивное сопротивление статора;
і
і?2доб - добавочное активное сопротивление ротора, приведенное к обмотке статора;
і
Х2доб - добавочное индуктивное сопротивление ротора, приведенное к обмотке статора;
©о = 2 • л • flZp - синхронную угловую скорость изменением числа пар полюсов Zp или частоты fx напряжения переменного тока, подводимого к обмотке статора.
Из всего многообразия искусственных механических характеристик асинхронного двигателя практический интерес в настоящее время могут представлять только следующие способы регулирования:
• регулирование скорости изменением добавочного активного сопротивления в цепи обмотки ротора асинхронного двигателя с фазным ротором;
• регулирование скорости изменением фазного напряжения короткозамкнутого асинхронного двигателя;
• частотное регулирование скорости короткозамкнутого асинхронного двигателя.
Статические механические и электромеханические характеристики асинхронных двигателей благоприятны для пусков двигателей прямым включением в сеть. Поскольку пуск двигателя происходит достаточно быстро, то кратковременная перегрузка по току даже в 6 - 8 раз не опасна для него ни с точки зрения больших ударных динамических моментов, ни с точки зрения больших пусковых токов, которые много меньше пусковых токов естественной характеристики двигателей постоянного тока независимого возбуждения той же мощности. Ограничения на прямой пуск асинхронных двигателей накладываются не самим двигателем, а питающей сетью.
Если сеть имеет ограниченную мощность или большое внутреннее сопротивление, то пусковые токи двигателя будут вызывать в этой сети большие падения напряжения. Естественно, что это скажется на режимах работы других потребителей энергии. По правилам Ростехнадзора напрямую можно запускать асинхронные двигатели, если их мощность
Рдв<0,25-аеТи, (5.12)
где (2сети - мощность питающего трансформатора подстанции в том случае, если от сети не питается осветительная аппаратура.
При питании осветительной аппаратуры от общей сети асинхронный двигатель можно пускать прямым включением в сеть, когда
Рдв<0,05-бсети - (5.13)
Если условия (5.12) и (5.13) не выполняются, то способы токоогра-
ничения вытекают из уравнения тока короткого замыкания асинхронно
го двигателя.
В частотно-регулируемых асинхронных электроприводах векторное управление связано как с изменением частоты и текущих значений переменных (напряжения, тока статора, потокосцепления), так и со взаимной ориентацией их векторов в декартовой системе координат. …
Сигналом тока можно воздействовать как на канал напряжения, так и на канал частоты. Функциональная схема электропривода с положительными обратными связями по току в канале регулирования напряжения и частоты приведена на …
Если вектор напряжения Uj формируется векторным сложением напряжения задания U з, и сигнала / • /^ • ккм, вводимого с целью компенсации падения напряжения в фазах А, В и С …
msd.com.ua
Механическая и электромеханическая характеристики.
Если рассматривать статику когда d/dt=0, тогда
 (2,5) – уравнение электромеханической характеристики.
(2,5) – уравнение электромеханической характеристики.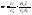 (2,6) – уравнение механической характеристики.
(2,6) – уравнение механической характеристики.
Т.к первый член U/Ce=ω0 (скорость идеального хх) постоянная величина, то обе характеристики механическая и электромеханическая будут представлять прямые линии и характеристики будут совпадать только по оси абсцисс будут разные масштабы.
 Мдоп=(2-3)Мн
Мдоп=(2-3)Мн
Iдоп=(2-3)Iн
Мкз=(15-20)Мн
Iкз=(15-20)Iн
Двигатель постоянного тока не в кое случае нельзя включать на номинальное напряжение без добавочного сопротивления.
Двигатели постоянного тока имеют допустимые значения которые нельзя превышать и указываются в паспортных данных.
Если характеристика получена при номинальном напряжении, номинальном потоке и отсутствии добавочного сопротивления то она называется естественной.
Если имеется добавочное сопротивление либо не номинальное напряжение, либо не номинальный поток, то характеристика называется искусственной.
Построение механической и электромеханической характеристик производится по 2 точкам.


1т. В паспортных данных даются следующие значения: Рн, Uн, Iн, nн → ωн=πnн/30 (c-1)

Внутреннее сопротивление якорной цепи можно определить следующими 3 способами.
1. По каталогу. Raд=(Rа+Rко+Rдп)кт+Rщ
2. Определяют по номограмме.
ρ=f(Рн)
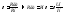 ,
, 
3. Если нет каталога, нет справочных данных, то пользуются эмпирической формулой.

2т. Мн=СмIн=Мэм
1 - соединим 1 и 2 точки получим характеристику ω=f(Мэ)
3т. 
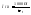
Однако 2 характеристика также не является механической характеристикой. Чтобы получить механическую характеристику откладываем от начала координат Мхх=Мн-Мнв. С Мхх поднимаем перпендикуляр до пересечения с 2. Эта точка определяет скорость идеального хх.
3 это и будет искомая механическая характеристика ω=f(Мнв).
Механические и токовые характеристики.
Для вывода механических и токовых характеристик рассмотрим схему замещения одной фазы.

Вынесем намагничивающий контур на зажимы.

Как следует из схемы замещения ток в роторной цепи равен:
 (3,1) Хк=Х1+Х’2
(3,1) Хк=Х1+Х’2 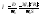
 (3,2)
(3,2)
Взяв производную момента по S и приравняв к 0 получим:
 (3,3)
(3,3)
Подставим 3,3 в 3,2 получим.
 (3,4)
(3,4)
Разделив 3,2 на 3,4 получим при некоторых допущениях упрощенную формулу Клосса.

По формуле Клосса рассматривать влияние параметров неудобно поэтому рассматриваются формулы (3,2), (3,3), (3,4).
Рассмотрим вид механической характеристики или зависимости момента от скольжения используя формулу 3,2.


В формуле 3,4 «+» в двигательном режиме, «-» в генераторном режиме. Поэтому момент в генераторном режиме больше чем в двигательном в 2 и более раз.
Рассмотрим вид токовой характеристики в соответствии с выражением 3,1 при:
1. S=0, I’2=0
2. При скольжении S=±∞, ток 
3. При S=1, 
4. R1=R’2/2, S=- R’2/R1, I’2=Uф/Хк.

В электроприводе как правило механическую и токовую (эл мех) характеристики не в зависимости от скольжения, а в зависимости от скорости.

 1. ω=ω0 S=0 2. ω=0 S=1 3. ω=-ω0 S=2 4. ω=2ω0 S=-1
1. ω=ω0 S=0 2. ω=0 S=1 3. ω=-ω0 S=2 4. ω=2ω0 S=-1
Намагничивающий ток составляет 20-30% от номинального,
I’2n=(4-7)Iн, 4 - для маломощных, 7 – для двигателей большой мощности.
studfiles.net
Правильный выбор электродвигателя для производственного механизма – залог его нормальной и экономичной работы. Если электродвигатель подобран правильно, это упростит систему управления электроприводом и возможно удешевит стоимость электропривода. Как известно электропривод должен обеспечивать не только постоянство установившихся значений (скорость, момент), но и динамических (переходных процессов, таких как ускорение, тормозной момент, пусковой момент и т.д.).
Основным критерием для подбора электродвигателей используют зависимость, на которой отображают значение момента М электродвигателя и скорости вращения вала n при действии этого момента. Такая зависимость имеет название механическая характеристика n=f(M). По механическим характеристикам производят анализ электромеханических свойств двигателя, а также оценивают целесообразность применения его для различного рода механизмов и устройств. Они могут быть двух видов: естественные и искусственные.
Естественные механические характеристики: они снимаются при влиянии на двигатель номинальных параметров (номинальный ток, сопротивление обмоток, напряжение, момент сопротивления и т.д.). То есть двигатель подключается к источнику питания без каких-либо преобразовательных устройств – прямым включением.

Искусственные механические характеристики: их снимают при введении в цепь двигателя дополнительных элементов (резистор добавочный) или при пониженном напряжении питания, частоте (если двигатель переменного напряжения) и т.д. То есть на механическую характеристику двигателя производят искусственное влияние.

Также различают механические характеристики по изменению скорости вращения вала в зависимости от увеличения момента. Они оцениваются по жесткости:

и крутизне наклона:

Чтоб определить жесткость механической характеристики необходимо знать изменение скорости и момента на заданном участке зависимости n=f(M). Соответственно все расчеты жесткости ведутся либо в процентах, либо в относительных единицах.
Также механические характеристики можно отсортировать по группам:

Ниже приведен график различных механических характеристик электродвигателей:

Подбор электродвигателя определяется требованиями производственных механизмов. В таком производстве как прокатка металла, изготовление бумаги или картона, требуется четкое поддержание постоянства скорости, а такие механизмы, как подъемные и транспортные, не требуют жестких характеристик (в тяговых электроприводах используется ДПТ ПВ, также он применяется в некоторых крановых механизмах).
elenergi.ru
Электромеханическая характеристика асинхронного двигателя определяется как зависимость  .
.
Из схемы замещения видно:
 , (5.6)
, (5.6)
где 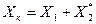 - индуктивное фазное сопротивление короткого замыкания [13; 14].
- индуктивное фазное сопротивление короткого замыкания [13; 14].
В этом случае рассматривают зависимость тока ротора не от скорости, как у ДПТ, а от скольжения S; уравнения получаются более компактные и удобные.
Если возникает необходимость перейти к традиционной электромеханической характеристике как  , то можно воспользоваться выражением
, то можно воспользоваться выражением 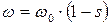 . Отметим основные точки электромеханической характеристики, изменяя
. Отметим основные точки электромеханической характеристики, изменяя  от
от  до
до  (рис. 5.3).
(рис. 5.3).
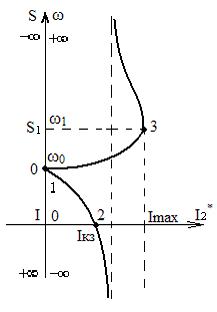
Рис. 5.3. Электромеханическая характеристика АД
1)  ;
; 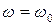 ;
;  - точка идеального холостого хода;
- точка идеального холостого хода;
2)  ;
; 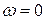 ;
;  - точка короткого замыкания;
- точка короткого замыкания;
3) 
 ;
;  =
=  ;
;  - точка максимального значения тока ротора. Она располагается в области отрицательных скольжений.
- точка максимального значения тока ротора. Она располагается в области отрицательных скольжений.
4)  ;
; 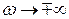 ;
;  - асимптотическое значение тока ротора.
- асимптотическое значение тока ротора.
Механическую характеристику асинхронного двигателя можно определить из уравнения потерь в цепи ротора [13; 14]:
 .
.
Потери в роторе часто называют потерями скольжения.
С другой стороны, пренебрегая магнитными потерями в роторе, получаем:
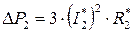 .
.
Приравнивая  , получаем:
, получаем:
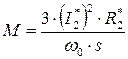 .
.
Подставив в это выражение 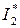 (5.6), получим уравнение механической характеристики (рис. 5.4):
(5.6), получим уравнение механической характеристики (рис. 5.4):

 . (5.7)
. (5.7)
Если исследовать уравнение момента на экстремум 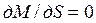 , то обнаружим наличие двух экстремальных точек. Обозначив экстремальное значение момента через
, то обнаружим наличие двух экстремальных точек. Обозначив экстремальное значение момента через 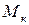 , получим:
, получим: 
 (5.8)
(5.8)
при этом соответствующее значение критического скольжения определяется как:
 . (5.9)
. (5.9)
Знак “+” в обоих уравнениях относится к области положительных скольжений, а знак “-” к области отрицательных скольжений. Экстремальное значение момента и соответствующее ему скольжение получили название критических.

Рис. 5.4. Механическая характеристика АД
Часто уравнение момента записывают в иной форме, которая может быть получена, если разделить уравнение момента на 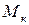 :
:
 ,
,где  .
.
Характерные точки механической характеристики (рис. 5.4):
1)  ,
, 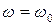 ,
,  - точка идеального холостого хода;
- точка идеального холостого хода;
2)  ,
, 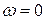 ,
,  - точка короткого замыкания;
- точка короткого замыкания;
3)  ,
, 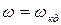 ,
,  ,
,  ,
,  ,
, 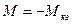 - точки максимума момента в двигательном и генераторном режимах соответственно;
- точки максимума момента в двигательном и генераторном режимах соответственно;
4)  ;
; 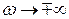 ;
;  - асимптотическое значение (асимптотой является ось скорости).
- асимптотическое значение (асимптотой является ось скорости).
Приведенная механическая характеристика соответствует прямому порядку чередования фаз питающего напряжения. Если изменить порядок чередования фаз на обратный, то получим симметричную относительно начала координат характеристику. При этом двигательному режиму будет соответствовать третий квадрант.
Учитывая незначительную величину активного сопротивления статора R1, им часто пренебрегают. В этом случае а=0, а уравнение (5.10) механической характеристики выглядит так:
 ,
,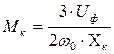 ,
, 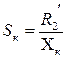 . (5.12)
. (5.12)
Если в уравнения моментов вместо текущих значений подставить номинальные, то есть  и
и 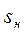 , а отношение
, а отношение  выразить через
выразить через  , то:
, то:
 . (5.13)
. (5.13)
Используя это выражение, по каталожным данным АД можно найти  . Для АД серий 4А и АИ кратность максимального момента
. Для АД серий 4А и АИ кратность максимального момента  составляет примерно
составляет примерно  и, следовательно, критическое скольжение примерно в
и, следовательно, критическое скольжение примерно в 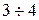 раза превышает номинальное (при знаке + в формуле (5.13)).
раза превышает номинальное (при знаке + в формуле (5.13)).
В некоторых случаях рабочий участок характеристики можно описать еще более простым выражением. Учитывая, что  , можно записать:
, можно записать:
 .
.
Это выражение может использоваться только на рабочем участке характеристики.
poznayka.org