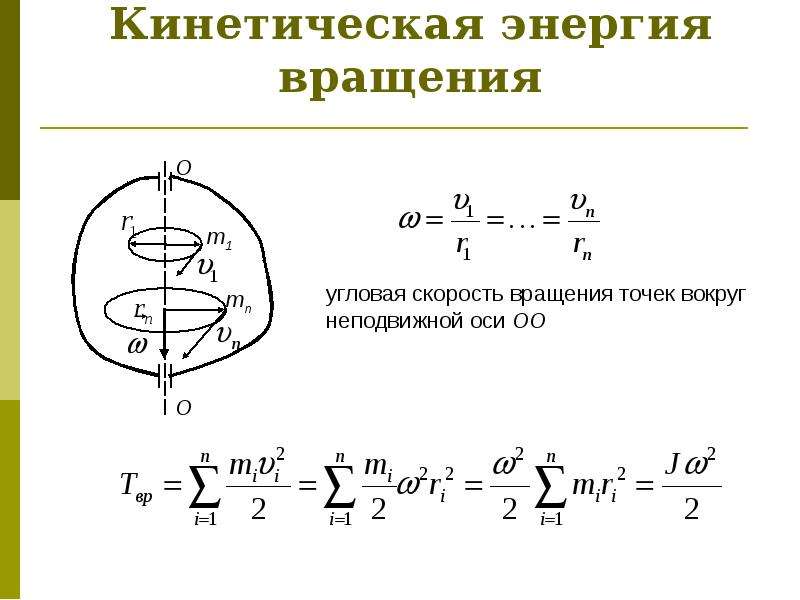
Содержание
4 способа расчета угловой скорости колеса барабана
Пример решения задачи по определению угловой скорости колеса заданного радиуса и приводимого в движение приложенным моментом из состояния покоя, которое посредством невесомой нити двигает груз по шероховатой поверхности.
Задача
Однородное колесо 1 массой M и радиусом r1 приводится в движении из состояния покоя приложенным моментом mвр. Груз 2 массой m посредством невесомой нити, намотанной на колесо барабана, движется по шероховатой поверхности, коэффициент трения скольжения которой равен f (рисунок 3.6).
Рисунок 3.6
Определить угловую скорость колеса в 4 случаях:
- а) mвр=A;
- б) mвр=a∙t, где a – постоянная, t – время;
- в) mвр=b∙φ, где b – постоянная, φ – угол поворота барабана;
- г)
где c – постоянная,
– угловая скорость колеса.
Другие примеры решений >
Помощь с решением задач >
Пример решения
Механическая система состоит из двух тел: барабана 1, вращающегося вокруг оси x, и груза 2, движущегося поступательно.
Выделим все силы, действующие на систему:
P1 = M∙g – сила тяжести барабана;
R1 и R2 – составляющие реакции колеса по осям Oz и Oy;
mвр – вращающий момент;
P2 = M∙g – сила тяжести груза;
N – нормальная реакция плоскости;
Fтр = f∙N = f∙m∙g – сила трения при скольжении груза о плоскость.
Согласно теореме об изменении момента количества движения механической системы относительно оси
где
Kx – кинетический момент системы.
Кинетический момент системы определяется по формуле
где kб – кинетический момент барабана;
kгр – кинетический момент груза;
Тогда
Итак,
Окончательно получим
Решим последнее соотношение относительно угловой скорости колеса в четырех случаях, указанных в условии задачи.
Случай (а) mвр=A (A = const).
Для удобства в выражении (3. 15) введем для момента инерции системы обозначение
15) введем для момента инерции системы обозначение
Тогда
Разделив переменные и проинтегрировав обе части уравнения, получим
Окончательно будем иметь
Случай (б) mвр = a∙t.
Разделив переменные и проинтегрировав обе части этого уравнения
получим
Случай (в) mвр = b∙φ.
Так как правая часть зависит от угла поворота φ и прямого разделения переменных совершить невозможно, произведем замену переменной t:
тогда
Разделим переменные и проинтегрируем полученное уравнение
откуда
Случай (г)
Разделив переменные, проинтегрируем и определим угловую скорость
Другие примеры решения задач >
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
Стоимость мы сообщим в течение 5 минут
на указанный вами адрес электронной почты.
Если стоимость устроит вы сможете оформить заказ.
НАБОР СТУДЕНТА ДЛЯ УЧЁБЫ
На нашем сайте можно бесплатно скачать:
— Рамки A4 для учебных работ
— Миллиметровки разного цвета
— Шрифты чертежные ГОСТ
— Листы в клетку и в линейку
Сохранить или поделиться с друзьями
Заказать решение
Поиск формул и решений задач
Формула угловой скорости в физике
Содержание:
- Определение и формула угловой скорости
- Равномерное вращение
- Формула, связывающая линейную и угловую скорости
- Единицы измерения угловой скорости
- Примеры решения задач
Определение и формула угловой скорости
Определение
Круговым движением точки вокруг некоторой оси называют движение, при котором траекторией точки является окружность
с центром, который лежит на оси вращения, при этом плоскость окружности перпендикулярна этой оси.
Вращением тела вокруг оси называют движение, при котором все точки тела совершают круговые движения около этой оси.
Перемещение при вращении характеризуют при помощи угла поворота
$(\varphi)$ . Часто используют вектор элементарного поворота
$\bar{d\varphi}$ , который равен по величине элементарному углу поворота тела
$(d \varphi)$ за маленький отрезок времени dt и направлен по мгновенной оси вращения в сторону,
откуда этот поворот виден реализующимся против часовой стрелки. Надо отметить, что только элементарные угловые перемещения являются векторами.
Углы вращения на конечные величины векторами не являются.
Определение
Угловой скоростью называют скорость изменения угла поворота и обозначают ее обычно буквой
$\omega$ . Математически определение угловой скорости записывают так:
$$\bar{\omega}=\frac{d \bar{\varphi}}{d t}=\dot{\bar{\varphi}}(1)$$
Угловая скорость — векторная величина (это аксиальный вектор). Она имеет направление вдоль мгновенной оси вращения совпадающее
с направлением поступательного правого винта, если его вращать в сторону вращения тела (рис. 1).
1).
Вектор угловой скорости может претерпевать изменения как за счет изменения скорости вращения тела вокруг оси (изменение модуля угловой скорости),
так и за счет поворота оси вращения в пространстве ($\bar{\omega}$ при этом изменяет направление).
Равномерное вращение
Если тело за равные промежутки времени поворачивается на один и тот же угол,
то такое вращение называют равномерным. При этом модуль угловой скорости находят как:
$$\omega=\frac{\varphi}{t}(2)$$
где $(\varphi)$ – угол поворота, t – время, за которое этот поворот совершён.
Равномерное вращение часто характеризуют при помощи периода обращения (T), который является временем, за которое тело производит один оборот
($\Delta \varphi=2 \pi$). Угловая скорость связана с периодом обращения как:
$$\omega=\frac{2 \pi}{T}(3)$$
С числом оборотов в единицу времени ($\nu) угловая скорость связана формулой:
$$\omega=2 \pi \nu(4)$$
Понятия периода обращения и числа оборотов в единицу времени иногда используют и для описания неравномерного вращения,
но понимают при этом под мгновенным значением T, время за которое тело делало бы один оборот, если бы оно вращалось равномерно
с данной мгновенной величиной скорости. {3} \approx 20(\mathrm{rad})$$
{3} \approx 20(\mathrm{rad})$$
Ответ. $\varphi = 20$ рад.
Читать дальше: Формула удельного веса.
6.1 Угол поворота и угловая скорость – College Physics 2e
Цели обучения
К концу этого раздела вы сможете:
- Задайте длину дуги, угол поворота, радиус кривизны и угловую скорость.
- Рассчитайте угловую скорость вращения колеса автомобиля.
В кинематике мы изучали движение по прямой и ввели такие понятия, как перемещение, скорость и ускорение. Двумерная кинематика имеет дело с движением в двух измерениях. Движение снаряда — это частный случай двумерной кинематики, в котором объект проецируется в воздух, подвергаясь действию силы гравитации, и приземляется на расстоянии. В этой главе мы рассмотрим ситуации, когда объект не приземляется, а движется по кривой. Начнем изучение равномерного кругового движения с определения двух угловых величин, необходимых для описания вращательного движения.
Угол поворота
Когда объекты вращаются вокруг некоторой оси — например, когда CD (компакт-диск) на рис. 6.2 вращается вокруг своего центра — каждая точка объекта движется по дуге окружности. Рассмотрим линию от центра компакт-диска к его краю. Каждая яма, используемая для записи звука вдоль этой линии, проходит под одним и тем же углом за одно и то же время. Угол поворота представляет собой величину поворота и аналогичен линейному расстоянию. Определим угол поворота ΔθΔθ как отношение длины дуги к радиусу кривизны:
Δθ=Δср.Δθ=Δср.
6.1
Рисунок
6.2
Все точки на компакт-диске движутся по дугам окружности. Ямки вдоль линии от центра к краю все перемещаются на один и тот же угол ΔθΔθ за время ΔtΔt.
Рисунок
6.3
Радиус окружности повернут на угол ΔθΔθ. Длина дуги ΔsΔs описана на окружности.
Длина дуги ΔsΔs — это расстояние, пройденное по круговому пути, как показано на рис.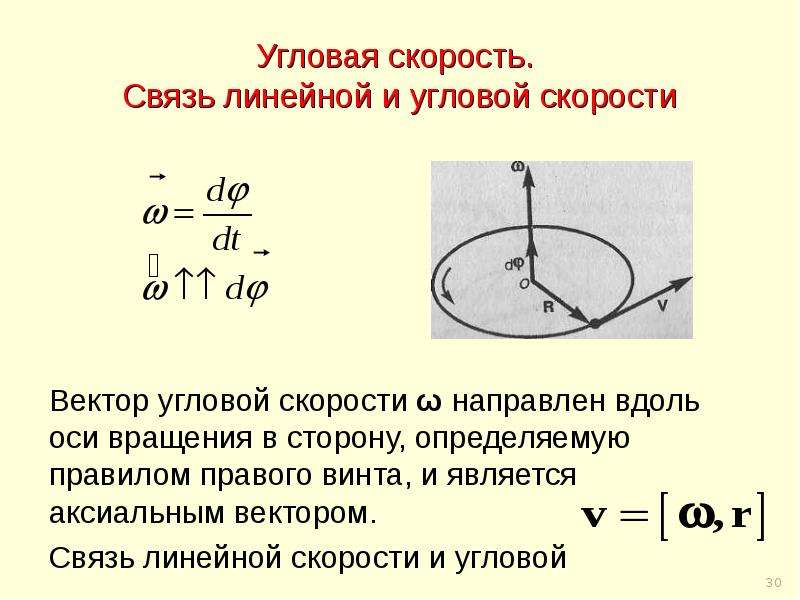 6.3. Обратите внимание, что rr — это радиус кривизны кругового пути.
6.3. Обратите внимание, что rr — это радиус кривизны кругового пути.
Мы знаем, что для одного полного оборота длина дуги равна длине окружности радиуса rr. Длина окружности равна 2πr2πr. Таким образом, за один полный оборот угол поворота равен
Δθ=2πrr=2π.Δθ=2πrr=2π.
6.2
Этот результат является основой для определения единиц, используемых для измерения углов поворота, ΔθΔθ – радианы (рад), определенные таким образом, что
2πрад = 1 оборот. 2πрад = 1 оборот.
6.3
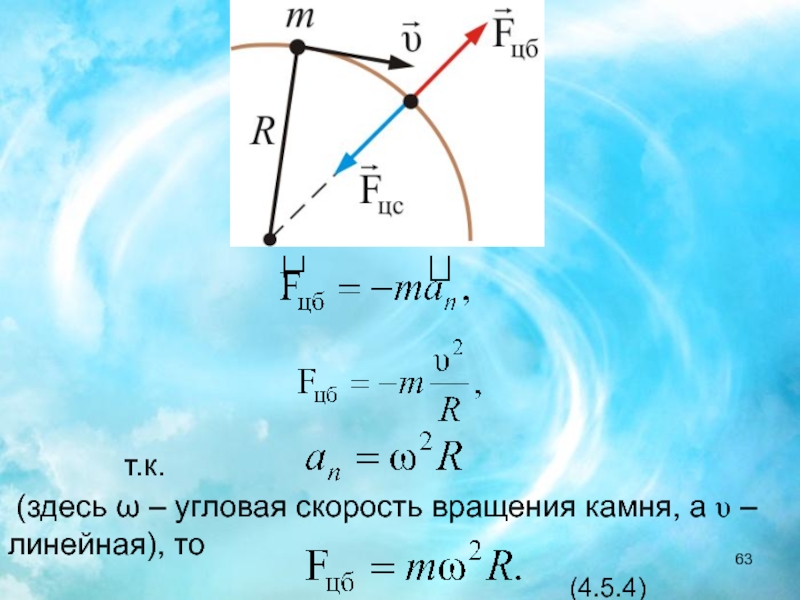
Сравнение некоторых полезных углов, выраженных как в градусах, так и в радианах, показано в таблице 6.1.
| Градусы | Измерение в радианах |
|---|---|
| 30º30º | π6π6 |
| 60º60º | π3π3 |
| 90º90º | π2π2 |
| 120º120º | 2π32π3 |
| 135º135º | 3π43π4 |
| 180º180º | номер |
Стол
6. 1
1
Сравнение угловых единиц
Рисунок
6.4
Точки 1 и 2 поворачиваются на один и тот же угол (ΔθΔθ), но точка 2 перемещается на большую длину дуги ΔsΔs, поскольку она находится на большем расстоянии от центра вращения (r)(r).
Если Δθ=2πΔθ=2π рад, то компакт-диск совершил один полный оборот, и каждая точка на компакт-диске вернулась в исходное положение. Поскольку в окружности или одном обороте 360º360º, соотношение между радианами и градусами будет таким образом 7,3º.1рад=360º2π≈57,3º.
6,5
Угловая скорость
Как быстро вращается объект? Мы определяем угловую скорость ωω как скорость изменения угла. В символах это
ω=ΔθΔt,ω=ΔθΔt,
6.6
где угловой поворот ΔθΔθ происходит за время ΔtΔt. Чем больше угол поворота за данный промежуток времени, тем больше угловая скорость. Единицами угловой скорости являются радианы в секунду (рад/с).
Угловая скорость ωω аналогична линейной скорости vv. Чтобы получить точное соотношение между угловой и линейной скоростью, мы снова рассмотрим ямку на вращающемся компакт-диске. Эта яма перемещается на длину дуги ΔsΔs за время ΔtΔt, поэтому она имеет линейную скорость
Чтобы получить точное соотношение между угловой и линейной скоростью, мы снова рассмотрим ямку на вращающемся компакт-диске. Эта яма перемещается на длину дуги ΔsΔs за время ΔtΔt, поэтому она имеет линейную скорость
v=ΔsΔt.v=ΔsΔt.
6,7
Из Δθ=ΔsrΔθ=Δsr мы видим, что Δs=rΔθΔs=rΔθ. Подстановка этого в выражение для vv дает
v=rΔθΔt=rω.v=rΔθΔt=rω.
6,8
Мы запишем это отношение двумя разными способами и получим два разных понимания:
v=rω или ω=vr.v=rω или ω=vr.
6,9
Первое соотношение в v=rω или ω=vrv=rω или ω=vr утверждает, что линейная скорость vv пропорциональна расстоянию от центра вращения, поэтому она наибольшая для точки на ободе (самый большой rr), как и следовало ожидать. Мы также можем назвать эту линейную скорость vv точки на ободе тангенциальная скорость . Второе соотношение в v=rω или ω=vrv=rω или ω=vr можно проиллюстрировать на примере шины движущегося автомобиля. Обратите внимание, что скорость точки на ободе шины равна скорости vv автомобиля. См. рисунок 6.5. Таким образом, чем быстрее движется автомобиль, тем быстрее вращается шина — большое vv означает большое ωω, потому что v=rωv=rω. Точно так же шина большего радиуса, вращающаяся с той же угловой скоростью (ωω), будет производить большую линейную скорость (vv) автомобиля.
Обратите внимание, что скорость точки на ободе шины равна скорости vv автомобиля. См. рисунок 6.5. Таким образом, чем быстрее движется автомобиль, тем быстрее вращается шина — большое vv означает большое ωω, потому что v=rωv=rω. Точно так же шина большего радиуса, вращающаяся с той же угловой скоростью (ωω), будет производить большую линейную скорость (vv) автомобиля.
Рисунок
6,5
Автомобиль, движущийся со скоростью vv вправо, имеет шину, вращающуюся с угловой скоростью ωω. Скорость протектора шины относительно оси равна vv, как если бы автомобиль был поднят домкратом. Таким образом, автомобиль движется вперед с линейной скоростью v=rωv=rω, где rr — радиус шины. Большая угловая скорость шины означает большую скорость автомобиля.
Пример
6.1
Как быстро вращается автомобильная шина?
Рассчитайте угловую скорость автомобильной шины радиусом 0,300 м, когда автомобиль движется со скоростью 15,0 м/с15,0 м/с (около 54 км/ч54 км/ч). См. рисунок 6.5.
См. рисунок 6.5.
Стратегия
Поскольку линейная скорость обода шины равна скорости автомобиля, мы имеем
v=15,0 м/с. v=15,0 м/с.
Радиус шины принимается равным
r=0,300 м. r=0,300 м. Зная
vv и rr, мы можем использовать второе соотношение в v=rω, ω=vrv=rω, ω=vr для вычисления угловой скорости.
Решение
Для расчета угловой скорости воспользуемся следующим соотношением:
ω=vr.ω=vr.
6.10
Подставляя известные,
ω=15,0м/с0,300м=50,0рад/с.ω=15,0м/с0,300м=50,0рад/с.
6.11
Обсуждение
Когда мы исключаем единицы в приведенном выше расчете, мы получаем 50,0/с. Но угловая скорость должна иметь единицы рад/с. Поскольку радианы на самом деле безразмерны (радианы определяются как отношение расстояния), мы можем просто вставить их в ответ для угловой скорости. Также обратите внимание, что если бы землеройная машина с гораздо большими шинами, скажем, радиусом 1,20 м, двигалась с той же скоростью 15,0 м/с, ее шины вращались бы медленнее. Они будут иметь угловую скорость
Они будут иметь угловую скорость
ω=(15,0 м/с)/(1,20 м)=12,5 рад/с. ω=(15,0 м/с)/(1,20 м)=12,5 рад/с.
6.12
И ωω, и vv имеют направления (следовательно, они являются угловой и линейной скоростями соответственно). Угловая скорость имеет только два направления относительно оси вращения — либо по часовой стрелке, либо против часовой стрелки. Линейная скорость касается траектории, как показано на рис. 6.6.
Домашний эксперимент
Привяжите предмет к концу веревки и раскачивайте его по горизонтальному кругу над головой (раскачивая на запястье). Поддерживайте постоянную скорость при раскачивании объекта и измеряйте угловую скорость движения. Какова примерная скорость объекта? Определите точку рядом с вашей рукой и выполните соответствующие измерения, чтобы рассчитать линейную скорость в этой точке. Определите другие круговые движения и измерьте их угловые скорости.
Рисунок
6,6
Поскольку объект движется по кругу, в данном случае муха на краю старомодной виниловой пластинки, ее мгновенная скорость всегда касается окружности. Направление угловой скорости в этом случае – по часовой стрелке.
божья коровка революция
Вместе с божьей коровкой исследуйте вращательное движение. Вращайте карусель, чтобы изменить ее угол, или выберите постоянную угловую скорость или угловое ускорение. Узнайте, как круговое движение связано с положением жука по осям x, y, скоростью и ускорением, используя векторы или графики.
Нажмите, чтобы просмотреть содержимое.
Угол поворота и угловая скорость
Цели обучения
К концу этого раздела вы сможете:
- Определять длину дуги, угол поворота, радиус кривизны и угловую скорость.
- Рассчитайте угловую скорость вращения колеса автомобиля.
В кинематике мы изучали движение по прямой и ввели такие понятия, как перемещение, скорость и ускорение. Двумерная кинематика имеет дело с движением в двух измерениях. Движение снаряда — это частный случай двумерной кинематики, в котором объект проецируется в воздух, подвергаясь действию силы гравитации, и приземляется на расстоянии. В этой главе мы рассмотрим ситуации, когда объект не приземляется, а движется по кривой. Начнем изучение равномерного кругового движения с определения двух угловых величин, необходимых для описания вращательного движения.
Двумерная кинематика имеет дело с движением в двух измерениях. Движение снаряда — это частный случай двумерной кинематики, в котором объект проецируется в воздух, подвергаясь действию силы гравитации, и приземляется на расстоянии. В этой главе мы рассмотрим ситуации, когда объект не приземляется, а движется по кривой. Начнем изучение равномерного кругового движения с определения двух угловых величин, необходимых для описания вращательного движения.
Угол поворота
Когда объекты вращаются вокруг некоторой оси — например, когда CD (компакт-диск) на рис. 1 вращается вокруг своего центра, — каждая точка объекта движется по дуге окружности. Рассмотрим линию от центра компакт-диска к его краю. Каждая яма , используемая для записи звука вдоль этой линии, перемещается под одним и тем же углом за одно и то же время. Угол поворота представляет собой величину поворота и аналогичен линейному расстоянию. Определим угол поворота Δ θ как отношение длины дуги к радиусу кривизны: [латекс]\displaystyle\Delta\theta=\frac{\Delta{s}}{r}\\[/latex]
Рисунок 1. Все точки на компакт-диске движутся по дугам окружности. Ямы вдоль линии от центра к краю все перемещаются на один и тот же угол Δθ за время Δt .
Все точки на компакт-диске движутся по дугам окружности. Ямы вдоль линии от центра к краю все перемещаются на один и тот же угол Δθ за время Δt .
Рис. 2. Радиус окружности повернут на угол Δθ . Длина дуги Δs описана на окружности.
длина дуги Δs это расстояние, пройденное по круговому пути, как показано на рисунке 2. Обратите внимание, что r – это радиус кривизны кругового пути.
Мы знаем, что для одного полного оборота длина дуги равна длине окружности радиусом r . Длина окружности равна 2π r . Таким образом, для одного полного оборота угол поворота равен
[латекс]\displaystyle\Delta\theta=\frac{2\pi{r}}{r}=2\pi\\[/latex].
Этот результат является основой для определения единиц, используемых для измерения углов поворота, Δ θ до радиан (рад), определенных таким образом, что 2π рад = 1 оборот.
Сравнение некоторых полезных углов, выраженных как в градусах, так и в радианах, показано в таблице 1.
| Таблица 1. Сравнение угловых единиц | |
|---|---|
| Градусы | Измерение в радианах |
| 30° | [латекс]\displaystyle\frac{\pi}{6}\\[/латекс] |
| 60º | [латекс]\displaystyle\frac{\pi}{3}\\[/латекс] |
| 90º | [латекс]\displaystyle\frac{\pi}{2}\\[/латекс] |
| 120º | [латекс]\displaystyle\frac{2\pi}{3}\\[/латекс] |
| 135º | [латекс]\displaystyle\frac{3\pi}{4}\\[/латекс] |
| 180º | № |
Рис. 3. Точки 1 и 2 поворачиваются на один и тот же угол (Δθ), но точка 2 перемещается по большей дуге (Δs), поскольку находится на большем расстоянии от центра вращения (r). 9{\circ}\\[/латекс].
Угловая скорость
Как быстро вращается объект? Мы определяем угловую скорость ω как скорость изменения угла. В символах это [латекс]\omega=\frac{\Delta\theta}{\Delta{t}}\\[/latex], где угловой поворот Δ θ происходит за время Δ t . Чем больше угол поворота за данный промежуток времени, тем больше угловая скорость. Единицами угловой скорости являются радианы в секунду (рад/с).
В символах это [латекс]\omega=\frac{\Delta\theta}{\Delta{t}}\\[/latex], где угловой поворот Δ θ происходит за время Δ t . Чем больше угол поворота за данный промежуток времени, тем больше угловая скорость. Единицами угловой скорости являются радианы в секунду (рад/с).
Угловая скорость ω аналогична линейной скорости v . Чтобы получить точное соотношение между угловой и линейной скоростью, мы снова рассмотрим ямку на вращающемся компакт-диске. Эта яма движется по дуге длиной Δ с за время Δ t , поэтому она имеет линейную скорость [латекс]v=\frac{\Delta{s}}{\Delta{t}}\\[/ латекс].
Из [латекс]\Delta\theta=\frac{\Delta{s}}{r}\\[/latex] мы видим, что Δ s = r Δ θ . Подставляя это в выражение для v дает [латекс]v=\frac{r\Delta\theta}{\Delta{t}}=r\omega\\[/latex].
Мы запишем это отношение двумя разными способами и получим два разных понимания:
[latex]v=r\omega\text{ или }\omega\frac{v}{r}\\[/latex].
Первое соотношение в [latex]v=r\omega\text{ или }\omega\frac{v}{r}\\[/latex] утверждает, что линейная скорость v пропорциональна расстоянию от центр вращения, таким образом, он является наибольшим для точки на ободе (наибольшая р ), как и следовало ожидать. Мы также можем назвать эту линейную скорость v точки на ободе тангенциальной скоростью . Второе соотношение в [latex]v=r\omega\text{ или }\omega\frac{v}{r}\\[/latex] можно проиллюстрировать, рассмотрев шину движущегося автомобиля. Обратите внимание, что скорость точки на ободе шины равна скорости автомобиля v . См. рис. 4. Таким образом, чем быстрее движется автомобиль, тем быстрее вращается шина — большие против означают большие ω , потому что v = rω . Точно так же шина большего радиуса, вращающаяся с той же угловой скоростью (90 205 ω 90 136), будет производить большую линейную скорость (90 205 v 90 136) для автомобиля.
Рис. 4. Автомобиль, движущийся со скоростью v вправо, имеет шину, вращающуюся с угловой скоростью ω. Скорость протектора шины относительно оси равна v , такая же, как если бы автомобиль были подняты. Таким образом, автомобиль движется вперед с линейной скоростью v = r ω, где r — радиус шины. Большая угловая скорость шины означает большую скорость автомобиля.
4. Автомобиль, движущийся со скоростью v вправо, имеет шину, вращающуюся с угловой скоростью ω. Скорость протектора шины относительно оси равна v , такая же, как если бы автомобиль были подняты. Таким образом, автомобиль движется вперед с линейной скоростью v = r ω, где r — радиус шины. Большая угловая скорость шины означает большую скорость автомобиля.
Пример 1. Как быстро вращается автомобильная шина?
Рассчитайте угловую скорость автомобильной шины радиусом 0,300 м, когда автомобиль движется со скоростью 15,0 м/с (около 54 км/ч). См. рис. 4.
Стратегия
Поскольку линейная скорость обода шины равна скорости автомобиля, мы имеем v = 15,0 м/с. Радиус шины равен 9.0205 r = 0,300 м. Зная v и r , мы можем использовать второе соотношение в [latex]v=r\omega\text{ или }\omega\frac{v}{r}\\[/latex] для вычисления угловой скорости .
Решение
Для расчета угловой скорости мы будем использовать следующую зависимость: [латекс]\омега\фрак{в}{г}\\[/латекс].
Подстановка известных,
[латекс]\omega=\frac{15,0 \text{ м/с}}{0,300\text{ м}}=50,0\text{ рад/с}\\[/latex].
Обсуждение
Если мы отменим единицы измерения в приведенном выше расчете, мы получим 50,0/с. Но угловая скорость должна иметь единицы рад/с. Поскольку радианы на самом деле безразмерны (радианы определяются как отношение расстояния), мы можем просто вставить их в ответ для угловой скорости. Также обратите внимание, что если бы землеройная машина с гораздо большими шинами, скажем, радиусом 1,20 м, двигалась с той же скоростью 15,0 м/с, ее шины вращались бы медленнее. У них будет угловая скорость [латекс]\omega=\frac{15,0\text{ м/с}}{1,20\text{ м}}=12,5\text{ рад/с}\\[/latex].
Оба ω и v имеют направления (следовательно, они являются угловой и линейной скоростями соответственно). Угловая скорость имеет только два направления относительно оси вращения — либо по часовой стрелке, либо против часовой стрелки. Линейная скорость касается траектории, как показано на рис. 5.
5.
Самостоятельный эксперимент
Привяжите предмет к концу веревки и раскачивайте его по горизонтальному кругу над головой (раскачивая на запястье). Поддерживайте постоянную скорость при раскачивании объекта и измеряйте угловую скорость движения. Какова примерная скорость объекта? Определите точку рядом с вашей рукой и выполните соответствующие измерения, чтобы рассчитать линейную скорость в этой точке. Определите другие круговые движения и измерьте их угловые скорости.
Рис. 5. Поскольку объект движется по кругу, здесь муха на краю старой виниловой пластинки, ее мгновенная скорость всегда касается окружности. Направление угловой скорости в этом случае – по часовой стрелке.
Исследования PhET: Революция божьей коровки
Присоединяйтесь к божьей коровке в исследовании вращательного движения. Вращайте карусель, чтобы изменить ее угол, или выберите постоянную угловую скорость или угловое ускорение. Узнайте, как круговое движение связано с ошибкой x , y положение, скорость и ускорение с использованием векторов или графиков.
Нажмите, чтобы загрузить. Запуск с использованием Java.
Резюме раздела
- Равномерное круговое движение — это движение по окружности с постоянной скоростью. Угол поворота [латекс]\Delta\theta\\[/latex] определяется как отношение длины дуги к радиусу кривизны: [latex]\Delta\theta=\frac{\Delta{s}}{r }\\[/latex], где длина дуги Δ с — это расстояние, пройденное по круговой траектории, а 9{\circ}\\[/латекс].
- Угловая скорость ω — скорость изменения угла, [латекс]\omega=\frac{\Delta\theta}{\Delta{t}}\\[/latex], где вращение [латекс]\Delta\ theta\\[/latex] происходит во времени [latex]\Delta{t}\\[/latex]. Единицами угловой скорости являются радианы в секунду (рад/с). Линейная скорость v и угловая скорость ω связаны соотношениями [latex]v=\mathrm{r\omega}\text{ или }\omega =\frac{v}{r}\text{.}[/latex]
Концептуальные вопросы
- Существует аналогия между вращательными и линейными физическими величинами.
 6\text{ м}\\[/латекс] на экваторе, какова линейная скорость на поверхности Земли?
6\text{ м}\\[/латекс] на экваторе, какова линейная скорость на поверхности Земли? - Бейсбольный питчер вытягивает руку вперед во время подачи, вращая предплечье вокруг локтя. Если скорость мяча в руке питчера 35,0 м/с, а мяч находится на расстоянии 0,300 м от локтевого сустава, какова угловая скорость предплечья?
- В лакроссе мяч выбрасывается из сетки на конце клюшки путем вращения клюшки и предплечья вокруг локтя. Если угловая скорость мяча относительно локтевого сустава равна 30,0 рад/с, а мяч находится на расстоянии 1,30 м от локтевого сустава, какова скорость мяча?
- Грузовик с шинами радиусом 0,420 м движется со скоростью 32,0 м/с. Какова угловая скорость вращающихся шин в радианах в секунду? Что это в об/мин?
- Интегрированные концепции. При ударе по футбольному мячу бьющий игрок вращает ногой вокруг тазобедренного сустава. (a) Если скорость носка ботинка игрока составляет 35,0 м/с, а тазобедренный сустав находится на расстоянии 1,05 м от носка ботинка, какова угловая скорость носка ботинка? (b) Башмак находится в контакте с изначально неподвижным футбольным мячом массой 0,500 кг в течение 20,0 мс.

 6\text{ м}\\[/латекс] на экваторе, какова линейная скорость на поверхности Земли?
6\text{ м}\\[/латекс] на экваторе, какова линейная скорость на поверхности Земли?