|
Пожалуйста активируйте JavaScript в настройках браузера.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
определение, физический смысл, расчеты, причины понижения
При оценке эффективности энергопотребления принимаются во внимание значения потребляемой электроэнергии и полной мощности, поставляемой электросетями. Потребляемая энергия определяется как активная мощность, которая идет на выполнение полезной механической работы, нагрева или освещения. При этом часть энергии затрачивается на трансформацию электрического тока отдельными элементами цепи (конденсаторами, катушками индуктивности, обмотками электродвигателей и т. д.) – так называемая реактивная составляющая. Для описания соотношения этих видов энергии вводят такое понятие, как коэффициент мощности.
Потребляемая энергия определяется как активная мощность, которая идет на выполнение полезной механической работы, нагрева или освещения. При этом часть энергии затрачивается на трансформацию электрического тока отдельными элементами цепи (конденсаторами, катушками индуктивности, обмотками электродвигателей и т. д.) – так называемая реактивная составляющая. Для описания соотношения этих видов энергии вводят такое понятие, как коэффициент мощности.
- Определение и физический смысл
- Математические расчеты
- Причины низкого коэффициента мощности
- Коррекция коэффициента мощности
Определение и физический смысл
Коэффициент мощности (PF) определяется как отношение активной мощности (P) к полной (S). В проводниках переменного тока с постоянно меняющимися показателями последняя складывается из активной и реактивной (Q) мощностей, равняясь при этом произведению среднеквадратичных значений напряжения и силы тока. Для ее измерения используют внесистемную единицу вольт-ампер. Для простого выражения мощностного коэффициента используется процентное соотношение.
Для простого выражения мощностного коэффициента используется процентное соотношение.
В физических расчетах для обозначения коэффициента мощности также используют «cos φ», имея в виду косинус сторон P/S в так называемом треугольнике мощностей, а также угол сдвига фаз напряжения и тока. Фазовый угол при этом может принимать значения от -1 до 1. Положительными величинами характеризуется рабочая мощность, отрицательными — энергия, вырабатываемая реактивными элементами.
Наличие в цепи реактивной составляющей при имеющемся расхождении тока и напряжения, а значит, и определенной величине коэффициента мощности, как правило, увеличивает нагрузку на источник энергии, что повышает теплоотдачу в проводниках и влечет за собой энергопотери. Значительное количество электроэнергии может теряться на подстанциях или в трансформаторных будках. Вместе с тем, при учете энергии, передаваемой конечному потребителю, в расчет принимается только активная мощность, потребляемая электрическими устройствами.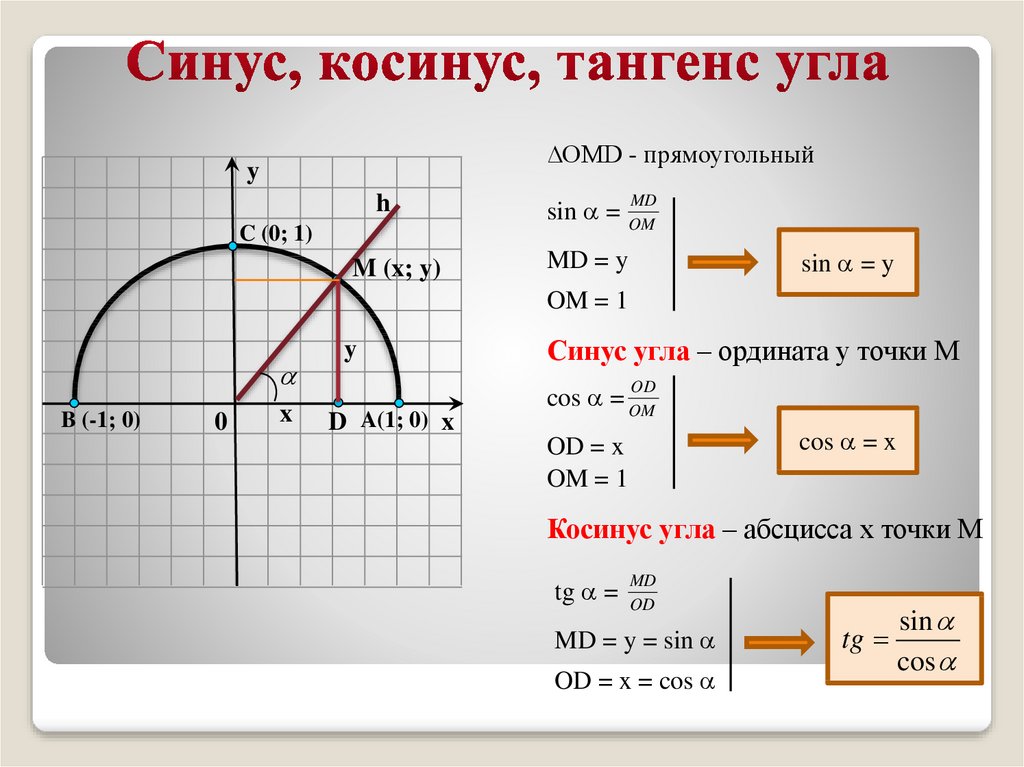
Математические расчеты
Являясь существенным параметром для цепей синусоидального тока, коэффициент мощности подлежит обязательному учету при разработке энергосистем. Для их корректного функционирования необходимо правильное определение этого параметра электроцепи. В противном случае велик риск избыточного энергопотребления, а также уменьшения коэффициента полезного действия электроприборов, включенных в неотрегулированную цепь.
Причиной же потерь электроэнергии могут служить низкие значения «косинуса фи». Будучи вызванным импульсной нагрузкой, недостаточный коэффициент мощности может стать причиной неправильного напряжения. Для цепей с непостоянными значениями силы тока (I) и напряжения (U) для вычисления ключевых параметров применяются следующие формулы:
Простейший расчет мощностного коэффициента можно показать на следующем примере. В цепь на 120 В включен электроприемник мощностью 1 кВт при силе тока в 1 А.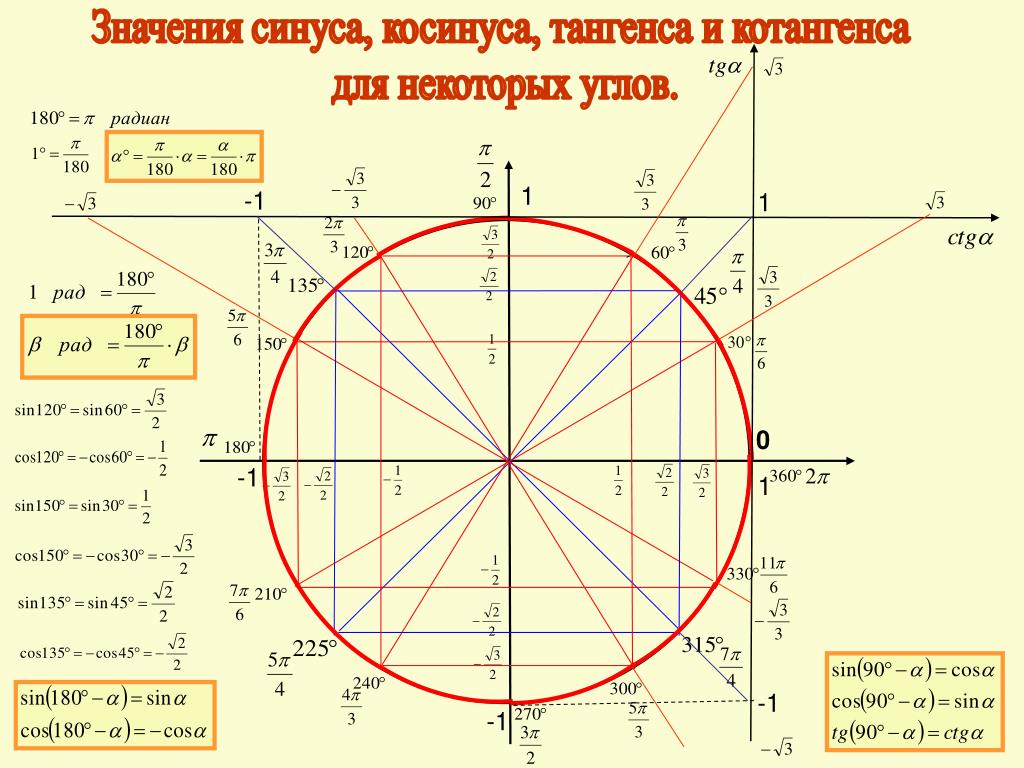 В соответствии с вышеприведенными формулами, cos φ равняется: 1000 / 120 × 10 = 0,83, или же 83%.
В соответствии с вышеприведенными формулами, cos φ равняется: 1000 / 120 × 10 = 0,83, или же 83%.
Причины низкого коэффициента мощности
Учитывая все вышесказанное, можно сказать, что чем выше показатель PF, тем более эффективно используются базовые элементы сети, включая генераторы на электростанции, трансформаторы и линии электропередач. Если же мощностной коэффициент снижается, то на энерговырабатывающих станциях возрастают эксплуатационные затраты с необходимостью привлечения дополнительных источников электроэнергии.
Снижению же коэффициента мощности очень часто способствуют особенности эксплуатации оборудования на некоторых предприятиях. Так как активная работа тех или иных аппаратов в разных цехах то прекращается, то начинается снова, уровень рабочей мощности может непрерывно изменяться, следовательно, изменяются соотношение мощностей и «косинус фи».
Понижение PF непосредственно возникает из-за прерывистой работы электротехнического оборудования, включающего в себя реактивные детали. В их число входят:
В их число входят:
- асинхронные двигатели;
- трансформаторы;
- выпрямители переменного тока;
- люминесцентные лампы с электромагнитными балластами и электронными пускорегуляторами;
- электросварочные аппараты;
- дуговые печи.
В активном режиме с почти полной нагрузкой электродвигатель, например, выдает достаточно большой cos φ. Однако этот показатель уменьшается по мере снижения мощности агрегата, притом что загруженность его реактивной части при неизменности электромагнитного тока практически остается на одном и том же уровне. Минимальных значений коэффициент мощности достигает при холостом режиме, находясь в диапазоне 0,1-0,3, в зависимости от основных характеристик электроприбора.
Ощутимое снижение PF наблюдается и в трансформаторных установках при активной загруженности менее чем на три четверти. При этом сохранение индуктивной составляющей ведет к увеличению полномощностной нагрузки.
Коррекция коэффициента мощности
Ввиду повышенной энергозатратности работы реактивных систем с нерезистивными нагрузками и в целях оптимизации энергопотребления проводят мероприятия по увеличению мощностного коэффициента. Коррекция «косинуса фи» в нужную сторону повышает пропускную способность электросистемы, оптимизируя энергопотери. Стабилизация энергопотребления предотвращает нежелательные падения напряжения в электросети, а значит, и критические сбои в работе оборудования. Кроме того, улучшение отношений мощностей способно сократить финансовые расходы на электроэнергию.
Коррекция «косинуса фи» в нужную сторону повышает пропускную способность электросистемы, оптимизируя энергопотери. Стабилизация энергопотребления предотвращает нежелательные падения напряжения в электросети, а значит, и критические сбои в работе оборудования. Кроме того, улучшение отношений мощностей способно сократить финансовые расходы на электроэнергию.
Разновидности коррекции
Непосредственной целью корректировки cos φ является приближение показателя значению 1. Это достигается с помощью компенсирующих устройств или путем сглаживания неравномерного потребления нагрузки. Процедура обязательно выполняется для цепей с импульсными стабилизаторами напряжения и трехфазных сетей, чтобы не допускать перегрузки нейтральной проводящей части.
Метод компенсации реактивной мощности предполагает включение в сеть реактивных компонентов обратного действия. Типичным корректирующим устройством при этом является конденсатор. Данный метод часто применяется на производственных предприятиях, использующих асинхронные электродвигатели. В целом, компенсационные мероприятия позволяют:
Данный метод часто применяется на производственных предприятиях, использующих асинхронные электродвигатели. В целом, компенсационные мероприятия позволяют:
- снизить нагрузку на электропередающие линии, трансформаторы и коммутаторы;
- уменьшить искажение формы напряжения;
- повысить качество электрической энергии в электроприборах;
- сэкономить на плате за электроэнергию.
Индуктивные устройства являются обязательным оборудованием в промышленности. Одно из их электродинамических свойств — сохранение тока в неизменном состоянии. Так как такое действие провоцирует расхождение циклов U и I, оно должно компенсироваться емкостными устройствами, стремящимися сохранить напряжение. На производствах эту роль выполняют целые блоки конденсаторов (БК), а также синхронные двигатели различной конструкции.
Применение конденсаторных установок снижает потери действительной мощности до 0,3%. БК обладает рядом преимуществ, включая несложную регулировку мощностных параметров под изменяющиеся условия работы, надежную стабилизацию напряжения, простоту эксплуатации и недорогое обслуживание. Конденсаторные установки бывают разного типа, в зависимости от своего назначения. Высоковольтные компенсаторы (6-35 кВ) применяются на распределительных подстанциях, низковольтные батареи конденсаторов (0,4-0,6 кВ) служат для корректировки тока на нагрузках от производственных устройств. Высокое быстродействие БК позволяет компенсировать не только постоянное фазовое смещение, но и нелинейную мощность от индуктивных элементов.
Конденсаторные установки бывают разного типа, в зависимости от своего назначения. Высоковольтные компенсаторы (6-35 кВ) применяются на распределительных подстанциях, низковольтные батареи конденсаторов (0,4-0,6 кВ) служат для корректировки тока на нагрузках от производственных устройств. Высокое быстродействие БК позволяет компенсировать не только постоянное фазовое смещение, но и нелинейную мощность от индуктивных элементов.
Реактивная часть энергии также может уменьшаться за счет ее потребления синхронной машиной. Будучи подключенным к электросети, аппарат работает с опережающим cos φ, вырабатывая те параметры электроэнергии, которые нужны для поддержки напряжения в конкретный момент.
Помимо коррекции реактивной энергии, идущей от индуктивных аппаратов, также выполняется корректировка нелинейного потребления электрического тока. В случае непостоянных нагрузок в электросети реализуется схема активной или пассивной нормализации «косинуса фи». Для этого может быть использован «электрический реактор», представляющий собой обмотку с высокой степенью индуктивности. Такая катушка сглаживает неровное потребление энергии и выделяет необходимые для работы электроприборов гармоники.
Для этого может быть использован «электрический реактор», представляющий собой обмотку с высокой степенью индуктивности. Такая катушка сглаживает неровное потребление энергии и выделяет необходимые для работы электроприборов гармоники.
Понравилась статья? Расскажите друзьям:
Оцените статью, для нас это очень важно:
Проголосовавших: 1 чел.
Средний рейтинг: 5 из 5.
Как найти отрицательный косинус
Все математические ресурсы ACT
14 диагностических тестов
767 практических тестов
Вопрос дня
Карточки
Learn by Concept
ACT Math Help »
Тригонометрия »
косинус »
Как найти отрицательный косинус
Если и , каково значение ?
Возможные ответы:
Правильный ответ:
Объяснение:
На основе этих данных мы можем составить небольшой треугольник, который выглядит так:
Это потому, что .
Теперь это означает, что должно быть равно. (Напомним, что функция косинуса во втором квадранте отрицательна.) Теперь ищем:
или . Это косинус опорного угла:
Глядя на наш маленький треугольник выше, мы видим, что косинус равен .
Сообщить об ошибке
Чему равен косинус угла, образованного между началом и точкой, если этот угол образован с одной стороной угла, начинающейся на оси, а затем вращающейся против часовой стрелки до ? Округлить до сотых.
Возможные ответы:
Правильный ответ:
Объяснение:
Вспомните, что когда вы вычисляете тригонометрическую функцию для такого тупого угла, вы всегда используете -ось в качестве исходной точки для вашего угла. (Поэтому он называется «угол отсчета».)
Теперь проще всего представить это так, будто вы рисуете маленький треугольник в третьем квадранте декартовой плоскости. Это будет выглядеть так:
Это будет выглядеть так:
Итак, сначала нужно вычислить гипотенузу. Это можно сделать с помощью теоремы Пифагора, , где и – длины катетов треугольника и длина гипотенузы. Преобразовав уравнение для решения, вы получите:
Подставив полученные значения:
Итак, косинус угла равен:
или, для ваших данных, .
Это примерно . Округление, это . Однако, поскольку находится в третьем квадранте, ваше значение должно быть отрицательным: .
Сообщить об ошибке
Чему равен косинус угла, образованного между началом и точкой, если этот угол образован с одной стороной угла, начинающейся на оси, а затем вращающейся против часовой стрелки до ? Округлить до сотых.
Возможные ответы:
Правильный ответ:
Объяснение:
Вспомните, что когда вы вычисляете тригонометрическую функцию для такого тупого угла, вы всегда используете -ось в качестве исходной точки для вашего угла. (Поэтому он называется «угол отсчета».) Теперь проще всего думать об этом, как будто вы рисуете маленький треугольник во втором квадранте декартовой плоскости. Это будет выглядеть так:
(Поэтому он называется «угол отсчета».) Теперь проще всего думать об этом, как будто вы рисуете маленький треугольник во втором квадранте декартовой плоскости. Это будет выглядеть так:
Итак, сначала нужно вычислить гипотенузу:
Итак, косинус угла равен:
или, для ваших данных, .
Это примерно . Округление, это . Однако, поскольку находится во втором квадранте, ваше значение должно быть отрицательным: .
Сообщить об ошибке
Чему равен косинус угла между началом и точкой с точностью до ? Допустим вращение против часовой стрелки.
Возможные ответы:
Правильный ответ:
Объяснение:
Если нужно достичь точки , то мы можем представить себе прямоугольный треугольник со сторонами и , и гипотенузой . Теорема Пифагора говорит нам об этом, поэтому мы подключаем и находим, что:
Таким образом,
Теперь SOHCAHTOA говорит нам об этом, поэтому мы знаем, что:
Таким образом, наш косинус приблизительно равен . Однако, поскольку мы находимся в третьем квадранте, косинус должен быть отрицательным! Следовательно, наш истинный косинус равен .
Однако, поскольку мы находимся в третьем квадранте, косинус должен быть отрицательным! Следовательно, наш истинный косинус равен .
Сообщить об ошибке
Чему равен косинус угла, образованного на сетке между линией от начала координат до и осью x?
Возможные ответы:
Правильный ответ:
Объяснение:
Если нужно достичь точки , то мы можем представить себе прямоугольный треугольник со сторонами и , и гипотенузой . Теорема Пифагора говорит нам об этом, поэтому мы подключаем и находим, что:
Таким образом, .
Теперь SOHCATOA говорит нам об этом, поэтому мы знаем, что:
Таким образом, наш косинус приблизительно равен . Однако, поскольку мы находимся во втором квадранте, косинус должен быть отрицательным! Следовательно, наш истинный косинус равен .
Сообщить об ошибке
Уведомление об авторских правах
Все математические ресурсы ACT
14 Диагностические тесты
767 практических тестов
Вопрос дня
Карточки
Learn by Concept
Тригонометрия
— Почему $\cos(-\theta)$ дает положительные значения, а в случае синуса — отрицательные?
$\begingroup$
Почему $\cos(-\theta)$ дает положительные значения, а в случае синуса отрицательные?
Я имею в виду
$\cos(-\theta) = +\cos(\theta)$
$\sin(-\theta) = -\sin(\theta)$
$\tan(-\ theta) = -\tan(\theta)$
и, пожалуйста, объясните общие углы в простых мирах?
- тригонометрия
$\endgroup$
11
$\begingroup$
Изменение знака $\theta$ соответствует обходу в другом направлении. Поскольку $\theta$ отсчитывается от положительной оси $x$, все, что нужно сделать, это перевернуть конечную точку по оси $x$, как показано ниже.
Поскольку $\theta$ отсчитывается от положительной оси $x$, все, что нужно сделать, это перевернуть конечную точку по оси $x$, как показано ниже.
Поскольку косинус — это $x$-компонента $P$, а синус — это $y$-компонента, переворот по оси $x$ сведет на нет $\sin\theta$, но не $\cos\ тета$. Надеюсь, это проясняет, почему синус и косинус ведут себя именно так. 95/5!\pm…$
Обратите внимание, что изменение знака для cos не имеет значения (поскольку у нас есть все четные степени x), но изменение знака для sin имеет значение (поскольку у нас есть все нечетные степени x ).
Также $\tan (-\theta)=\frac {sin (-\theta)}{cos (-\theta)}\frac {-sin (\theta)}{cos (\theta)}=-tan (\тета)$.
$\endgroup$
$\begingroup$
Функция $f(x)$ называется четной, если $f(-x) = f(x)$. С другой стороны, функция $g(x)$ называется нечетной, если $g(-x) = -g(x)$. Таким образом, мы хотим знать, почему $cos(x)$ — четная функция, а $sin(y)$ — нечетная.
Теперь мы можем представить, как синус и косинус зависят от угла тета ($θ$), используя единичный круг в декартовых координатах. Нарисуйте любой радиус единичной окружности, образуя угол $θ$ с положительной половиной оси x. Точка на окружности, где пересекается этот радиус, будет иметь координаты x и y как $\cos(θ)$ и $\sin(θ)$ соответственно. Это естественное следствие того, что гипотенуза соответствующего прямоугольного треугольника равна 1 (любой радиус единичного круга по определению будет равен 1).
Радиус единичной окружности как гипотенуза прямоугольного треугольника
Теперь при изменении угла $\theta$ мы получаем различные значения $sinθ$ и $cosθ$. Они были нанесены на следующий график:
Графики $\cos(x)$ и $\sin(y)$
Как видите, график косинуса симметричен относительно оси y, что означает, что для каждого $x$ $\cos(x) = \cos(-x)$. Сделать косинус четной функцией. С другой стороны, если вы посмотрите на график синуса, вы заметите, что $|\sin(x)|$ = $|\sin(-x)|$, но знак противоположный. То есть абсолютное значение совпадает с пересечением оси $y$, но с обратным направлением. Сделать синус нечетной функцией.
То есть абсолютное значение совпадает с пересечением оси $y$, но с обратным направлением. Сделать синус нечетной функцией.
$\endgroup$
$\begingroup$
Ну косинус принимает значения от 1 до -1 в интервале $[0,\pi]$, а синус принимает значения от 0 до 1.
Я не знаю, что вы имеете в виду под общими углами простыми словами. 92-2bc\cos\альфа.
$$
Аналогичное рассуждение, основанное на законе синусов, дает понять, что синус тупого угла должен быть таким же, как и синус дополнительного угла.
Синусы и косинусы позже были определены для любого угла; расширение можно обосновать тригонометрическим кругом, и стало ясно, что их нужно определить так, чтобы
$$
\sin(-\alpha)=-\sin\alpha,\qquad \cos(-\alpha)=\cos\alpha
$$
просто глядя на тригонометрический круг.
$\endgroup$
92-2bc\cos\альфа. $$ Аналогичное рассуждение, основанное на законе синусов, дает понять, что синус тупого угла должен быть таким же, как и синус дополнительного угла.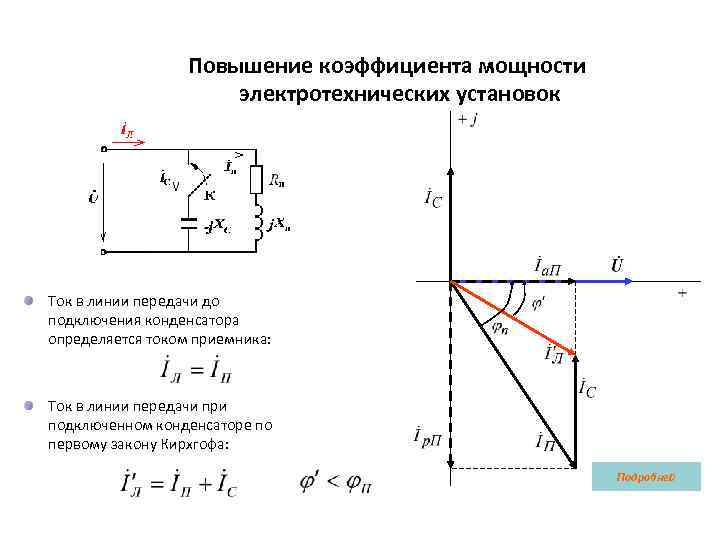
Синусы и косинусы позже были определены для любого угла; расширение можно оправдать тригонометрическим кругом, и стало ясно, что их нужно определить так, чтобы $$ \sin(-\alpha)=-\sin\alpha,\qquad \cos(-\alpha)=\cos\ alpha $$ просто взглянув на тригонометрический круг.
$\endgroup$
$\begingroup$
$\cos(-\theta)=\cos(0-\theta)=\cos0\cos\theta+\sin0\sin\theta=\cos(\theta)$.
$\sin(-\theta)=\sin(0-\theta)=\sin0\cos\theta-\cos0\sin\theta=-\sin(\theta)$.
$\tan(-\theta)=\frac {\sin(-\theta)}{\cos(-\theta)}=-\tan(\theta)$. (Используя два приведенных выше равенства.)
$\endgroup$
$\begingroup$
Помните, что углы отсчитываются от положительной оси $x$. Нарисуйте линию, образующую угол $\theta$ с положительной осью $x$. Эта прямая пересекает единичную окружность в точке $(\cos\theta,\sin\theta)$ и имеет уравнение $y=x\tan\theta$.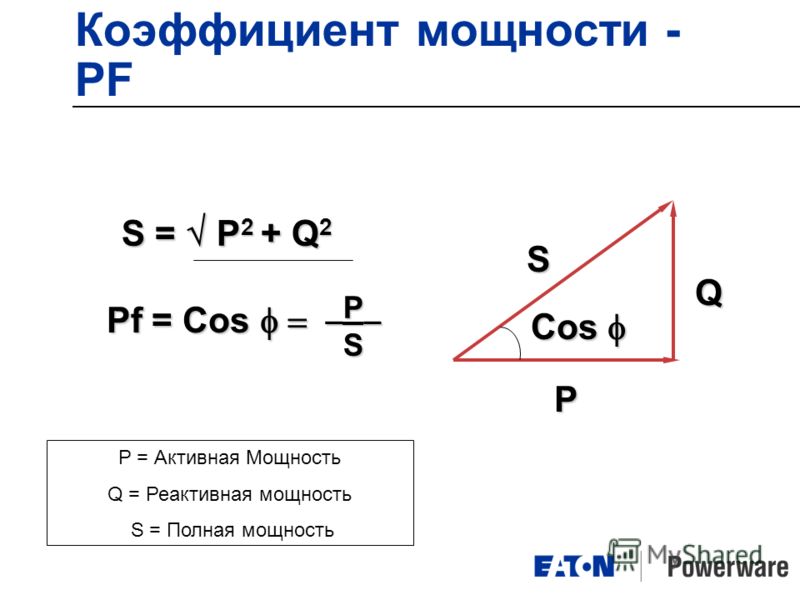
 08.2008
08.2008 ..
.. 04.2007
04.2007 11.2010 13:21
11.2010 13:21 03.2008
03.2008 11.2010 13:40
11.2010 13:40 11.2009
11.2009
 замеряют до сотен всяких параметров, определяют «качество» электроэнергии.
замеряют до сотен всяких параметров, определяют «качество» электроэнергии. 04.2007
04.2007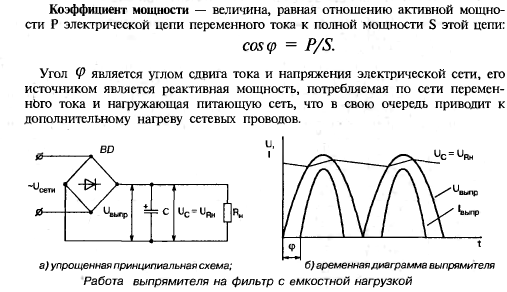 11.2010 15:01
11.2010 15:01 03.2008
03.2008 Посколько косинус функция четная, то при углах от меньше 90 по модулю он положителен.
Посколько косинус функция четная, то при углах от меньше 90 по модулю он положителен.