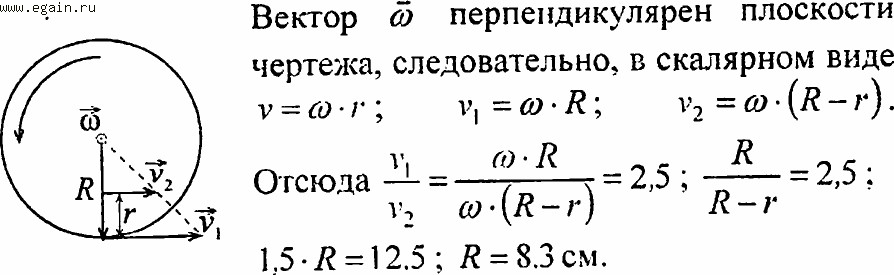Простая физика — EASY-PHYSIC

Задача 1. За промежуток времени с тело прошло половину окружности радиусом 100 см. Найти среднюю путевую скорость и модуль средней скорости .

Решение: средней путевой скоростью называется средняя скорость прохождения пути, которую мы с вами вычисляем, деля весь путь (длину траектории) на все время. Модуль средней скорости еще называют средней скоростью по перемещению. Ее можно определить, разделив перемещение на время. Тогда длина пути – это длина половины окружности, а перемещение – длина диаметра.

Ответ: средняя путевая скорость – 0,314 м/с, средняя скорость по перемещению – 0,2 м/с

Задача 2. Однородный диск радиусом 0,5 м катится без проскальзывания со скоростью 2 м/с. Найти скорость точек диска . Найти геометрическое место всех точек диска,  скорость которых 2 м/с. Угол .

Скорость точек окружности

Решение:

Точка A – центр вращения. Поэтому ее скорость относительно поверхности, по которой катится диск, равна 0. Поскольку в условии сказано, что диск катится со скоростью 2 м/с, то это означает, что с такой скоростью относительно поверхности будет передвигаться его центр: м/с. Поэтому точка А относительно центра будет передвигаться с точно такой же скоростью – со скоростью 2 м/с, и это и будет линейная скорость вращения диска, то есть скорость всех точек, лежащих на его краю, относительно центра м/с.  Линейные скорости показаны для  точек оранжевыми стрелками. Эти стрелки показывают, какой была бы скорость данной точки, если бы диск не катился, а вращался бы, например, на оси, проходящей через его центр. Но наш диск катится. Поэтому к линейной скорости вращения каждой точки необходимо еще прибавить скорость движения диска относительно опоры. То есть к каждой рыжей стрелке прибавим (векторно) скорость точки О – центра диска – черную стрелку. Тогда-то и становится понятным, почему у точки скорость равна 0 – линейная скорость вращения направлена влево, а скорость качения – вправо, и поскольку они равны, то гасят друг друга: .  В точке C скорости, напротив, сложатся, поскольку они сонаправлены: м/с.

Определим теперь скорости точек и . Понятно, что они будут равны численно, но направлены в разные стороны.

Осталось разобраться с точкой . Сделаем еще один рисунок. Линейная скорость вращения всегда направлена по касательной, то есть перпендикулярно радиусу . Углы, которые образуются между векторами, показаны на рисунке, в том числе угол . Тогда в параллелограмме угол , а так как

, то все углы в треугольнике равны и он равносторонний, то есть м/с. Также можно было найти длину этого вектора скорости по теореме косинусов или складывая проекции векторов. Можно догадаться, что точка, симметричная точке E относительно A также имеет скорость, равную 2 м/с. Вообще точки, лежащие на одном и том же расстоянии от центра вращения A будут иметь равные скорости, линии равных скоростей (геометрические места точек с равными скоростями) показаны на рисунке различного цвета дугами: единственная точка (точка C) будет иметь скорость 4 м/с, точки, лежащие на рыжей дуне, будут иметь скорости, равные , точки, лежащие на синей дуге, будут иметь скорости, равные 2 м/с, как у точки E.

Пробуксовывание

Задача 3. Колесо, пробуксовывая, катится по ровной, горизонтальной дороге. Найти скорость центра колеса , если известно, что скорость нижней точки м/c, а верхней — м/c.

Решение:

Если колесо пробуксовывает, то это означает, что скорость его нижней точки не равна нулю, то есть его центр вращения – не точка касания поверхности, центр вращения будет расположен выше. Но центр вращения находится и не в центре колеса. Найти его можно, если провести вертикальный диаметр, построить вектора скоростей в масштабе, а затем, соединив концы векторов скоростей прямой линией, отметить точку пересечения этой линии с диаметром. У нас на рисунке это точка О. Точка К – центр колеса, его скорость нам и нужно найти. Из подобия треугольников и запишем отношения сходственных сторон:

Тогда

Тогда

Теперь обратимся к подобным треугольникам и . Для них отношение сходственных сторон равно:

Откуда м/с.

Ну а более простым решение было бы, если бы мы просто нашли среднее арифметическое скоростей, ведь точка, про которую нас спрашивают, лежит по центру между точками приложения векторов скоростей и , при этом не забываем о векторном сложении скоростей, берем скорость со знаком «минус»:

м/с.

Ответ: 4 м/с.

Проскальзывание

Задача 4. Обруч, проскальзывая, катится по горизонтальной ровной поверхности. В некоторый момент скорость верхней точки А м/с, а нижней точки  B м/с. Определить скорость концов диаметра , перпендикулярного к , для того же момента времени. Под какими углами они направлены к горизонту?

Решение:

Проскальзывание – это ситуация, когда скорость нижней точки (точки касания обручем земли) не нулевая, но направлена она в сторону качения. В этом случае центр вращения, так же, как и в случае пробуксовки, не совпадает с центром колеса. Более того, центр вращения даже не внутри колеса – он снаружи (точка О). Как и в предыдущей задаче, можно найти его таким же способом – проведя линию через концы скоростей и найдя ее пересечение с продолжением вертикального диаметра. И, точно так же, как в предыдущей задаче, можно определить скорость центра колеса как среднее арифметическое, только обе скорости направлены у нас теперь в одну сторону, поэтому ставим знак «плюс» перед обеими:

м/с.

Так как скорость точки есть результат векторного сложения линейной скорости вращения колеса и скорости поступательного движения центра колеса , то можем из этого сделать вывод, что линейная скорость вращения равна 2 м/с – ровно на столько скорость центра колеса, найденная нами, отличается от скорости точки , данной в условии задачи. Линейную скорость на рисунке не показывала, или показывала не везде. Скорости точек и равны численно, но направлены по-разному. Их скорости – также результат векторного сложения линейной скорости вращения колеса и скорости поступательного движения центра, а, так как эти две скорости перпендикулярны друг другу, то результат их сложения может быть найден по Пифагору:

Понятно, что раз скорости перпендикулярны друг другу, то являются катетами некоторого прямоугольного треугольника, и связывает их между собой функция тангенса, поэтому угол наклона к горизонту скорости точки можно найти как

Ответ: ,

Шарик катится по двум линейкам

Задача 5. Шарик радиусом см катится равномерно и без проскальзывания по двум параллельным линейкам, расстояние между которыми равно см, и за время с проходит см. С какими скоростями движутся верхняя и нижняя точки шарика?

На рисунке изображено, как двигается шарик, при этом для удобства показан как вид спереди, так и вид сбоку. Поскольку скорость шарика равна м/с, то эта скорость – скорость поступательного движения его центра масс – точки А. Центр вращения шарика находится в точке О – на уровне края линеек. Определим положение точки О – определим длину отрезка . Это легко сделать, зная радиус шарика и рассмотрев рисунок, из треугольника . Центр вращения в данный момент неподвижен, а точка А двигается относительно него со скоростью 0,6 м/с. Поэтому скорость нижней точки   будет

Таким же способом определяем скорость верхней точки :

Ответ: скорость нижней точки 0,15 м/c, скорость верхней 1,35 м/c.

Задача 6.  Автомобиль движется по закругленному шоссе, имеющему радиус кривизны м. Закон движения автомобиля имеет вид: , где м, м/с, м/с. Найти скорость автомобиля , его тангенциальное  , нормальное и полное ускорения в момент времени с.

Решение.

Путь:

Производная пути – линейная скорость:

Вторая производная – тангенциальное ускорение:

Нормальное ускорение:

Полное ускорение:

Задача7. Угол поворота диска радиусом см  изменяется со временем по закону . Определить зависимости от времени угловой скорости, углового ускорения и линейной скорости точек диска.

Решение: угловая скорость – производная угла:

Угловое ускорение – производная угловой скорости:

Линейная скорость:

Задача 8.  Точка движется по окружности с постоянным угловым ускорением рад/. Найти угол между скоростью и ускорением  через 1 с после начала движения. Начальная скорость точки равна 0.

Решение: так как тангенциальное ускорение и линейная скорость совпадают по направлению, то определим обе составляющие ускорения: как нормальную, так и тангенциальную. Угол между полным ускорением и его тангенциальной составляющей можно тогда будет найти через функцию тангенса.

Известно, что нормальное ускорение  , тангенциальное ускорение . При этом , или . Тогда

Искомый угол:

Ответ:

Два концентрических колеса

Задача 9. Два концентрических колеса радиусами см и см вращаются с угловыми скоростями рад/c и рад/с соответственно. Между ними зажато третье колесо так, как показано на рисунке. Какова угловая скорость этого колеса вокруг собственной оси?  Проскальзывания нет.

Решение: определим радиус маленького (третьего) колеса, м:

Определим линейную скорость точек первого колеса:

Определим линейную скорость точек второго колеса:

Найдем угловую скорость маленького колеса, зная, что линейная скорость его точек равна линейной скорости больших колес, так как проскальзывания нет:

Ответ: 20 рад/с

Задача 10. Гайку закручивают на болт за время . Длина болта , резьба составляет угол с плоскостью гайки. Найдите угловую скорость гайки, если радиус болта равен .

Скорость вращения гайки по ходу завинчивания на болт

Решение: при закручивании гайка не только вращается, но и движется вдоль болта поступательно, например, спускается вниз. Поэтому точка, взятая на ребре гайки, будет обладать двумя составляющими скорости: скорость, с которой она будет двигаться вниз вдоль болта (назовем ее ) и скорость, с которой эта точка вращается – это уже знакомая нам линейная скорость (). Тогда .

Из рисунка видно, что

С другой стороны, так как длина болта , а гайка спускается по нему за время , то

Тогда

И можно определить :

Тогда

Ответ:

Физические основы механики

Рассмотрим теперь плоское движение твердого тела, то есть движение, при котором точки тела описывают траектории, лежащие в параллельных плоскостях. Пример такого движения — вращение колеса автомобиля при его движении по прямой. Можно взять любую точку 0 тела и мысленно провести через нее ось вращения перпендикулярно плоскостям, в которых лежат траектории точек тела. Тогда ось вращения будет двигаться поступательно, оставаясь все время параллельной самой себе.

Видео 7.2. Плоское движение твердого тела в однородном поле тяжести. Полет плоской картонной фигуры

Соответственно, скорость элементарной массы твердого тела складывается из скорости поступательного движения точки 0 и линейной скорости вращения вокруг связанной с ней (мысленно проведенной) оси:

где — радиус-вектор, определяющий положение элементарной массы по отношению к точке 0.

Кинетическая энергия элементарной массы равна тогда:

Векторное произведение

имеет модуль, равный , где — расстояние массы от оси вращения. Следовательно, третье слагаемое в скобках равно . Второе слагаемое, представляющее собой смешанное произведение векторов, не меняется при циклической перестановке сомножителей:

В результате получим для кинетической энергии элемента твердого тела следующее выражение

Для нахождения кинетической энергии тела просуммируем по всем элементарным массам:

Сумма элементарных масс

есть масса твердого тела. Выражение

где — радиус-вектор центра масс тела относительно точки 0.

Наконец,

— есть момент инерции тела относительно оси вращения. Поэтому для кинетической энергии твердого тела можно записать формулу:

Поскольку выбор мысленной оси вращения всецело в нашей власти, мы упростим полученное выражение, взяв в качестве точки 0 центр масс тела. Тогда = 0 и кинетическая энергия тела при плоском движении равна

Здесь — скорость движения центра масс, a — момент инерции относительно оси, проходящей через центр масс и ортогональной плоскости, где лежат траектории точек тела. Таким образом, кинетическая энергия твердого тела при плоском движении слагается из энергии поступательного движения со скоростью, равной скорости центра масс и энергии вращения вокруг оси, проходящей через центр масс тела.

Движение твердого тела определяется действующими на тело внешними силами и моментами этих сил

Индекс в обозначениях для момента внешней силы означает проекцию момента на ось вращения.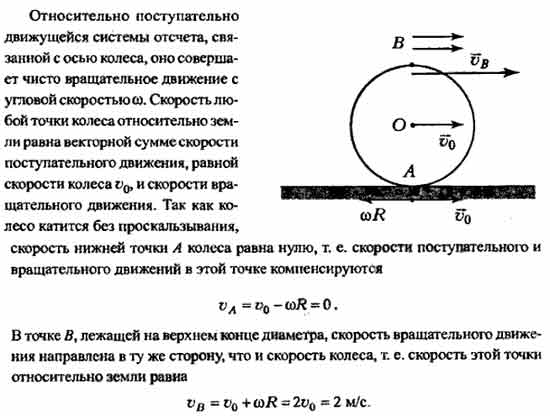

В следующих примерах мы имеем дело с плоским движением.

Видео 7.3. Зависимость поведения цилиндров на наклонной плоскости от характера распределение массы по их объему

Пример 1. Круглое однородное тело (обруч, цилиндр, шар) радиусом и массой скатывается без скольжения по наклонной плоскости под углом к горизонту с высоты (рис. 7.12). Начальная скорость тела равна нулю. Найдем скорость центра масс каждого тела в конце спуска.

Рис. 7.12. Скатывание тела с наклонной плоскости

Рассмотрение данной задачи можно вести двумя способами.

1-й способ. По условию тело катится без проскальзывания. Это условие используется у нас дважды. Сила трения между телом и плоскостью действует в точке соприкосновения и в отсутствие скольжения не превышает своего максимального значения:

где — коэффициент трения скольжения.

Оси координат удобно направить следующим образом: ось х — вдоль движения, ось у — перпендикулярно наклонной плоскости. Тело движется под действием трех сил: силы тяжести , силы трения и силы нормального давления , так что уравнение поступательного движения центра инерции тела имеет вид:

Вдоль оси у тело не движется. Проецируя уравнение движения центра масс на ось у, получаем для силы нормального давления соотношение:

Проекция уравнения движения на ось х дает:

Так как линейная скорость точек соприкосновения цилиндра с наклонной плоскостью равна нулю (опять используем условие отсутствия проскальзывания), то скорость (ускорение) поступательного движения связаны с угловой скоростью (угловым ускорением) тела обычными соотношениями:

Кроме поступательного движения, тело еще и вращается. Вращение удобно описывать относительно оси z, проходящей через центр масс цилиндра.

Выбор этот обусловлен тем, что линии действия силы тяжести и силы нормального давления плоскости проходят через ось вращения и, следовательно, моменты этих сил равны нулю. Таким образом, цилиндр вращается только под действием силы трения, и уравнение вращательного движения имеет вид:

Таким образом, получается система 4-х уравнений, описывающих поступательное и вращательное движение с дополнительным неравенством, выражающим закон трения. Решая систему уравнений, находим:

Чем больше момент инерции относительно оси, проходящей через центр масс, тем меньше ускорение тела. Мы уже получили ответ на один из вопросов задачи: шар будет двигаться быстрее цилиндра, а цилиндр — быстрее обруча. Подставляя решение для силы трения в неравенство, выражающее закон трения, находим условие, при котором будет отсутствовать проскальзывание:

Смысл этого условия прост: наклон не должен быть слишком крут.

Итак, центр масс тела движется вдоль плоскости с постоянным ускорением a, так что зависимость пройденного пути и скорости от времени имеет вид:

Отсюда следует связь скорости и пройденного пути:

К концу спуска тело проходит путь

так что его скорость достигает величины

Подставляя сюда моменты инерции обруча (), цилиндра () и шара (), находим соответственно:

2-й способ.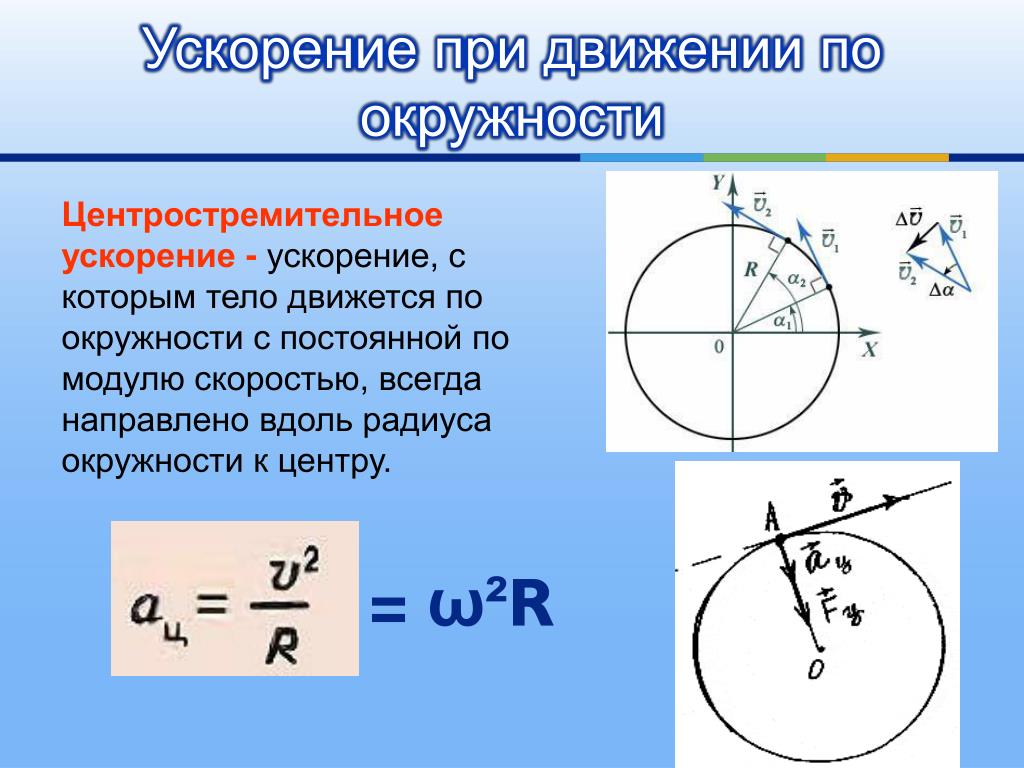 Используем закон сохранения полной энергии. В конце спуска тело приобретает кинетическую энергию

Эта кинетическая энергия приобретена за счет потенциальной энергии . Отсюда следует найдено выше выражение для скорости тела в конце спуска. Такой способ намного короче, но он не позволяет узнать детали процесса: действующие на тело силы и т.п.

В рассмотренном выше примере мы считали примере мы имели дело со случаем, когда проскальзывание отсутствовало. Это позволило утверждать простую связь () между угловой и линейной скоростями тела и его радиусом. Сила трения покоя находилась при этом в результате решения уравнений движения. В случае, когда тело движется с проскальзыванием, заранее известной связи между линейной и угловой скоростями нет. Зато мы заранее знаем силу трения: раз точка соприкосновения тела с поверхностью скользит по поверхности, сила трения есть сила трения скольжения,модуль которой связан с силой нормального давления законом Амонтона — Кулона.

Силы трения, как уже говорилось, направлены так, чтобы препятствовать относительному проскальзыванию соприкасающихся тел. Часто путают это возможное проскальзывание с осуществляемым поступательным движением. Необходимо четко понимать, что не редки случаи, когда сила трения не тормозит, но ускоряет тело, то есть направлена по его движению. Самый известный пример — трогание автомобиля с места. Колеса начинают вращаться и проскальзывают по земле назад. Соответственно, сила трения направлена вперед, и именно она заставляет автомобиль трогаться. Чтобы ближе познакомиться с подобными случаями, рассмотрим пример.

Пример 2. Цирковой артист бросает на арену обруч массой и радиусом , который начинает катиться в горизонтальном направлении со скоростью (рис. 7.13). При этом обручу придано обратное вращение с угловой скоростью . Найдем, при какой угловой скорости обруч после остановки покатится назад к артисту, а также конечную скорость поступательного движения обруча.

Рис. 7.13. Движение обруча с обратным вращением

При обратном вращении обруча точка его касания с ареной движется вперед как из-за вращения, так и из-за поступательного движения обруча. Поэтому неизбежно существует проскальзывание и, значит, сила трения достигает своего максимального значения. Она тормозит как поступательное движение, так и вращение обруча. Может случиться так, что поступательное движение обруча будет остановлено в тот момент, когда он еще сохраняет обратное вращение. Далее сила трения начнет ускорять обруч по направлению к артисту. Ускорение это прекратится, когда исчезнет тенденция к проскальзыванию, после чего обруч покатится назад равномерно с некоторой установившейся скоростью . Может, однако, случиться и так, что раньше будет остановлено обратное вращение, и тогда обруч сохранит поступательное движение вперед, изменив направление вращения на прямое. Чтобы различить эти два случая, качественных рассуждений недостаточно, и мы обратимся к формулам.

Направим ось ОХ направо (в направлении красной стрелки на рис. 7.13), ось вращения ОZ направим на нас (см. следующий пример, там эту ось удобнее направить от нас, то есть за чертеж), то есть в направлении «обратного» вращения, ось OY направим как обычно, вверх. Плоское движение обруча представим как суперпозицию его поступательного движения вместе с центром масс (геометрическим центром, поскольку обруч предполагается однородным). Спроектируем линейные и угловые скорости на соответствующие оси. Тогда, до тех пор, пока сила трения есть сила трения скольжения и направлена она налево, уравнения движения имеют вид

(7.3.1)

(7.3.2)

Уравнение (7.3.1) описывает движение центра масс обруча, а уравнение (7.3.2) его вращение вокруг оси проходящей через центр масс в той системе отсчета, в которой она покоится (системе центра масс). В (7.3.2) учтено, что момент инерции однородного обруча относительно его оси симметрии равен . После элементарного интегрирования получаем

(7.3.3)

(7.3.4)

Поступательное движение прекратится, то есть станет равным нулю, в момент времени

(7.3.5)

Вращение прекратится, то есть станет равным нулю,в момент времени

(7.3.6)

Их отношение

(7. 3.7)

может быть любым ввиду независимости начальных скоростей поступательного и вращательного движений.

Для дальнейшего анализа введем в рассмотрение скорость нижней точки обруча — той его точки, которая касается поверхности арены. Отметим уже здесь, что условием исчезновения проскальзывания является обращение в ноль скорости именно этой точки, потому что скорость соответствующей точки на поверхности арены (той, которой касается обруч) очевидным образом в нашей системе отсчета, где арена неподвижна, равна нулю. Отсутствие проскальзывания это и есть неподвижность этих двух точек относительно друг друга. При выбранном направлении осей OZ и OX, имеем

(7.3.8)

Если , то первым прекратится поступательное движение обруча. В момент времени скорости (7.3.3) и (7.3.8) будут иметь значения

Нижняя точка обруча, за счет продолжающегося вращения, будет по-прежнему скользить относительно арены направо (направо на рисунке 7.13), сила трения скольжения сохранит свою величину и направление налево. Соответственно, центр обруча начнет ускорятся налево, то есть станет меньше нуля и начнет расти по модулю, вращение против часовой стрелки (на рисунке 7.13) будет продолжать замедлятся. Другими словами, при обруч в момент времени (7.3.5) начинает возвращаться к бросившему его артисту.

Как следует из (7.3.8), в момент времени

(7.3.9)

скорость нижней точки обруча из (7.3.8) обращается в ноль, проскальзывание прекращается, сила трения скольжения скачком сменяется равной нулю силой трения покоя (силой трения качения пренебрегаем) и обруч начинает катится к артисту с постоянной скоростью движения центра масс

(7.3.10)

вращаясь против часовой стрелки с постоянной угловой скоростью

(7.3.11)

Если , то первым, в момент времени (7.3.6), прекратится вращение обруча. В момент времени скорость (7.3.8) нижней точки обруча будет равна скорости его центра и положительна:

(7.3.12)

Скольжение остается, сила трения скольжения сохраняет свою величину и направление налево, но обруч под действием этой силы трения скольжения начинает вращаться по часовой стрелке (напоминаем: налево, направо, по или против часовой стрелки — на рисунке 10). В результате этого скорость центра масс (центра обруча) будет уменьшаться, скорость вращения увеличиваться, в момент времени

(7.3.13)

проскальзывание обруча прекратится и обруч начнет равномерно удаляться от артиста со скоростью центра (7.3.10) и угловой скоростью вращения (7.3.11). Напомним, что в этом случае , так что а

Таким образом, ответ на вопрос: «Вернется обруч или укатится?» определяется начальными условиями, а конкретнее величиной параметра , который имеет простой физический смысл: это отношение модуля

скорости любой точки обруча за счет его поступательного движения вместе с центром масс к модулю скорости той же точки за счет вращения обруча вокруг оси, проходящей через его центр масс, в начальный момент времени.

Пример 3. Описать движение обруча (см. предыдущий пример), если ему придано прямое вращение (рис. 7.14). Поскольку обруч вращается теперь на рис. 7.14 по часовой стрелке, направим ось вращения OZ от нас, то есть за чертеж — в отличие от предыдущего случая.

Рис. 7.14. Движение обруча с прямым вращением: 1 – ; 2 –

Начальная скорость нижней точки обруча складывается из скорости поступательного движения и линейной скорости за счет вращения, направленной в противоположную сторону. В связи с этим надо различать два случая.

1 случай или . Тогда начальная скорость нижней точки обода положительна, то есть, направлена в ту же сторону, что и скорость . Значит, сила трения f направлена в противоположную сторону, как показано на рис. 11–1. В связи с изменением положительного направления оси вращения необходимо лишь изменить знак перед вторым слагаемым в уравнении (7.3.4). Решение уравнений движения в рассматриваемом случае имеют вид

(7.3.14)

(7.3.15)

При новом выборе направления оси вращения скорость нижней точки обруча записывается в виде

(7.3.16)

Момент исчезновения проскальзывания определится из того же соотношения равенства нулю скорости нижней точки обруча или равенства по модулю противоположно направленных скоростей этой точки за счет поступательного движения вместе с центром масс и вращательного движение вокруг оси, проходящей через центр масс:

откуда находим:

Скорость поступательного движения обруча в этот момент становится равной

и остается потом неизменной. Эта скорость меньше начальной скорости поступательного движения обруча.

2 случай или . В этом случае скорость нижней точки обода отрицательна, направлена против скорости . Значит, сила трения направлена по (см. рис.11-2).

Соответственно, в уравнениях движения и их решениях (7.3.14) и (7.3.15) надо изменить знаки на противоположные перед вторыми слагаемыми, содержащими изменившую направление силу трения, получаем:

(7.3.17)

(7.3.18)

Соответственно, выражение для скорости нижней точки обруча приобретает вид:

(7.3.19)

Момент прекращения проскальзывания определяется аналогично и оказывается равным:

а для скорости установившегося движения получается вновь выражение

но в данном случае она будет больше () начальной скорости поступательного движения.

Объединяя оба случая в один, записываем окончательный результат:

Дополнительная информация

http://www. plib.ru/library/book/14978.html Сивухин Д.В. Общий курс физики, том 1, Механика Изд. Наука 1979 г. — стр. 256 (§ 48, задача 9): рассмотрено движение маятника Максвелла, включая силу натяжения нитей подвеса в нижней точке.

http://kvant.mirror1.mccme.ru/pdf/1997/04/kv0497khorozov.pdf — журнал «Квант» — решение задачи об отскоке вращающегося мяча от плоской стенки (С. Хорозов).

http://kvant.mirror1.mccme.ru/pdf/1998/04/kv0498chernoutsan.pdf — журнал «Квант» — применение законов динамики твердого тела в задаче о падении вертикальной палочки на горизонтальный стол (А. Черноуцан).

http://kvant.mirror1.mccme.ru/pdf/1999/02/kv0299chernoutsan.pdf — журнал «Квант» — продолжение задачи о падении вертикальной палочки на горизонтальный стол (А. Черноуцан).

Формула линейной скорости (вращающийся объект)

Главная > Формулы > Формулы физики > Формула линейной скорости (вращающийся объект)

Формула линейной скорости (вращающийся объект)

Линейная скорость точки на вращающемся объекте зависит от его расстояния от центра вращения. Угловая скорость – это угол, на который движется объект за определенное время. Угловая скорость измеряется в радианах в секунду (рад/с). В полном круге 2π радиан. На расстоянии r от центра вращения точка объекта имеет линейную скорость, равную угловой скорости, умноженной на расстояние r. Единицы линейной скорости – метры в секунду, м/с.

линейная скорость = угловая скорость x радиус вращения

v = ωr

v = линейная скорость (м/с)

ω = угловая скорость (радиан/с)

r = радиус вращения ( m)

Формула линейной скорости (вращающийся объект) Вопросы:

1) Электродрель включена и вращается со скоростью 10,0 оборотов в секунду (об/с). Диаметр сверла 4,00 мм. Какова линейная скорость точки на поверхности сверла в метрах в секунду?

Ответ: Первым шагом является определение угловой скорости сверла. Обороты в секунду должны быть преобразованы в радианы в секунду. В полном круге 2π радиан.

ω = 10,0 об/с

Расстояние между центром вращения и точкой на поверхности сверла равно радиусу. Диаметр сверла указан в миллиметрах. Радиус в метрах

∴r = 0,002 м

Используя формулу v = ωr, линейная скорость точки на поверхности бурового долота равна )

Линейная скорость точки на поверхности сверла составляет примерно 0,126 м/с. Радианы являются единицей-заполнителем, поэтому они не включаются при записи решенного значения линейной скорости.

2) Еще вопрос.

Внутри колеса автомобиля подключен датчик, который измеряет линейную скорость. Датчик находится на расстоянии 0,080 м от центра вращения. В этом положении датчик считывает, что линейная скорость колеса составляет 8,00 м/с. Если радиус колеса равен 0,220 м, какова линейная скорость на внешней кромке колеса?

Ответ: Линейная скорость различна на разных расстояниях от центра вращения, но угловая скорость одинакова везде на колесе. Чтобы решить эту задачу, сначала найдите угловую скорость, используя линейную скорость в положении датчика, 0,080 м. Формулу v = ωr можно преобразовать для определения угловой скорости ω:

Это также угловая скорость на внешней кромке колеса, где радиус r = 0,220 м. Формулу v = ωr можно снова использовать для определения линейной скорости на этом радиусе:

v = ωr

v = (100 рад/с)(0,220 м)

∴v = 22,0 м/с

Линейная скорость колеса автомобиля на внешней кромке равна 22,0 м/с.

Формула линейной скорости (вращающийся объект)

Что такое линейная скорость (Видео)

Стенограмма

Привет, добро пожаловать в это видео о линейной скорости!

Представьте, что вы бежите вперед и прыгаете на вращающуюся карусель. Сначала вы бежите по прямой, но когда приземляетесь, ваше движение меняется, и вы начинаете вращаться. Как ваша скорость бега связана со скоростью вращения? Давай выясним!

Во-первых, напомним, что скорость — это расстояние, пройденное за определенный промежуток времени. В автомобилях есть спидометр, который сообщает нам скорость автомобиля в милях в час — мили в качестве единиц расстояния и часы в качестве единиц времени. Линейная скорость говорит нам, как быстро движется точка на вращающемся объекте. Расстояние, которое проходит точка, зависит от того, насколько далеко она находится от центра вращения. Точка, находящаяся дальше от центра вращения, перемещается дальше, чем точка, расположенная ближе к центру вращения. Время – это время, за которое объект совершает один оборот.

Мы вычисляем линейную скорость точки, используя несколько различных методов. Во-первых, нам нужно найти расстояние, пройденное точкой, а для этого нам нужно знать, как далеко точка находится от центра вращения; это радиус круга, который объект создает при вращении. Назовем это р. Далее нам нужно измерить, насколько далеко повернулась точка. Это угол , через который прошел объект, θ, который измеряется в радианах или градусах. Получив эти два измерения, мы вычисляем длину дуги, то есть расстояние, пройденное точкой. Мы называем это расстояние s и используем уравнение s=rθ. Теперь, когда у нас есть пройденное расстояние, мы измеряем время, необходимое для прохождения этого расстояния, t, и находим линейную скорость: v = s/t = rθ/t.

Иногда мы знаем, как быстро что-то вращается, и мы хотим рассчитать линейную скорость. Обычно мы знаем, сколько оборотов в минуту делает объект, поэтому давайте соединим RPM и линейную скорость.

Напомним, что угол можно измерять двумя разными единицами измерения: радианами или градусами. Полный оборот составляет 2π радиан или 360 градусов. При преобразовании между скоростью вращения и линейной скоростью единицы, которые мы используем, зависят от окончательного ответа, который мы хотим. Сначала воспользуемся радианами.

Предположим, у нас есть колесо, вращающееся со скоростью ω об/мин с радиус р метров. Какова линейная скорость в метрах в секунду точки на самом внешнем краю шины?

Мы можем использовать простой модульный анализ, чтобы найти ответ! Во-первых, мы знаем, что наше колесо вращается на 2π радиан за один оборот. Но как мы соотносим радианы с длиной в метрах? Представьте, что наше колесо обмотано веревкой. Эта струна делает один оборот вокруг нашего колеса. Он «измеряет» 2π радиан. Теперь давайте возьмем этот кусок веревки, разложим его и измерим линейкой его длину. Найдем длину 2πr метров. Таким образом, за каждый оборот наше колесо проходит 2πr метров. Чтобы перевести минуты в секунды, вспомните, что в одной минуте 60 секунд. Итак, мы видим,

В общем случае используется формула v = 2πrω, где r — расстояние от точки вращения до центра вращения, а ω — скорость вращения объекта. Давайте рассмотрим пример задачи:

Земля совершает один оборот вокруг Солнца за один год. Это примерно 93 миллиона миль от Солнца. Какова линейная скорость Земли в милях в час? Воспользуемся формулой v=2r с некоторыми изменениями единиц. У нас есть ω в единицах оборотов в год. Мы можем следовать модульному анализу, чтобы найти линейную скорость. В одном году 365,25 дня (каждые четыре года бывает високосный год, что эквивалентно добавлению к каждому году одной четверти дня), а в одном дне 24 часа. Тогда один оборот равен 2πr, где r равно 9.3 миллиона миль. Итак, мы видим, что Земля движется со скоростью 66 ТЫСЯЧ миль в час!

Но что, если мы используем градусы для измерения угла, а не радианы? Наше колесо с радиусом r теперь вращается со скоростью 60 градусов в минуту, и мы хотели бы знать линейную скорость в футах в секунду. Самый простой способ — добавить еще одно преобразование единиц измерения: преобразовать градусы в обороты! Затем вы можете использовать те же шаги, чтобы найти линейную скорость!

В общем случае используется формула v = 2πrω/180, где r — расстояние от вращающегося объекта до центра вращения, а ω — скорость вращения объекта в градусах в секунду.

Давайте посмотрим на другой пример:

Колесо обозрения Centennial на морском пирсе Чикаго поднимает пассажиров почти на 200 футов в высоту. Одна поездка длится примерно 15 минут, и вы можете объехать 3 раза. Какова ваша средняя линейная скорость в футах в секунду?

Во-первых, нам дан диаметр колеса обозрения, а не радиус. Напомним, что диаметр круга в 2 раза больше радиуса, поэтому r = 100 футов.