Содержание
Касательная сила — тяга — Большая Энциклопедия Нефти и Газа, статья, страница 1
Cтраница 1
Касательная сила тяги FK зависит от двух групп величин. В первую группу входят величины nv d, S, D, рк, характеризующие размеры основных элементов паровоза и, следовательно, являющиеся в условиях эксплоата-ции постоянными для данного паровоза.
[1]
Величину касательной силы тяги, ограничиваемой по первому фактору, можно выразить для различных локомотивов через мощность двигателя N или создаваемый им момент.
[2]
| Межосевой дифференциал автомобилей КамАЗ.
[3] |
Изменение касательной силы тяги у колес одной из ведущих осей вызывает соответствующее изменение касательной силы тяги колес другой оси. В частности, если колеса одной из осей попадают в неблагоприятные условия сцепления с дорогой и их касательная сила тяги уменьшается, го это приводит к снижению касательной силы тяги, развиваемой колесами другой оси, даже при хорошем сцеплении с дорогой. В этом случае межосевой дифференциал блокируют, как и межколесный.
В этом случае межосевой дифференциал блокируют, как и межколесный.
[4]
Отношение касательной силы тяги, реализуемой при отсутствии боксования осек электровоза, к его сцепному весу называют коэффициентом тяги.
[5]
| Примерные значения расчетных форсировок гм.
[6] |
Величина касательной силы тяги паровоза определяется и ограничивается тремя основными элементами: котлом, машиной и сцепным весом. В соответствии с этим различают силу тяги и ограничение ее по котлу, силу тяги и ограничение ее по машине, силу тяги и ограничение ее по сцепному весу.
[7]
Рк — касательная сила тяги, равная Мвеа / гк; Mjh — приведенный к ведущим колесам инерционный момент, возникающий при разгоне ( замедлении) машины и зависящий от инерционных моментов маховика двигателя, деталей трансмиссии и ведущих колес; Mf /, — момент сопротивления качению ведущих колес.
[8]
| Схема для определения необходимой силы тяги.
[9] |
Следовательно, касательная сила тяги Рк состоит из двух слагаемых, первое из которых Т идет на преодоление полезных сопротивлений и называется свободной силой тяги, а второе GK / — на перекатывание ведущего колеса — эту величину называют силой сопротивления качению.
[10]
| Примерные значения расчетных форсировок гм.
[11] |
В дальнейшем рассматривается только касательная сила тяги, как общепринятая в тяговых расчетах.
[12]
Для определения значения касательных сил тяги на забегающей и отстающей гусеницах разделим в формуле (31.3) оба уравнения на В.
[13]
Суммарное сопротивление преодолевается касательной силой тяги.
[14]
Расчет и построение зависимостей касательной силы тяги F и касательной мощности NK от скорости движения и не отличаются от расчета и построения тех же зависимостей для тепловоза с электрической передачей.
[15]
Страницы:
1
2
3
4
5
Расчёт касательной силы тяги автомобиля тягача ЗИЛ-4331. Определение расчётной массы автопоезда
Другие предметы \
Теория лесотранспорта
Страницы работы
6
страниц
(Word-файл)
Посмотреть все страницы
Скачать файл
Содержание работы
1. Расчёт касательной силы
тяги автомобиля тягача ЗИЛ-4331.
, [Н];
где: Ne – максимальная
мощность двигателя, кВт;
η =0,85 – КПД силовых агрегатов;
γ = 0,95 – коэффициент на внешние агрегаты;
β = 0,97 – коэффициент на эксплуатационные условия;
VII – скорость
движения тягача на второй передаче по гравийной дороге на iрук;
Н;
2. Определение
Определение
расчётной массы автопоезда.
, [т];
где: ω = 170 + 12,5 ∙ Vр, [Н/т] –
основное удельное сопротивление движению автопоезда;
ω = 170 + 12,5 ∙ 11,1 =
308,75 Н/т;
т;
3. Расход силы тяги,
расходуемой для движения автомобиля с грузом.
, [Н];
Н;
4. Расчёт силы тяги на
крюке автопоезда.
, [Н];
Н;
5. Расчёт полезной
нагрузки на прицеп автопоезда (расчётная величина).
, [т];
т;
6. Выбор марки прицепа
по его технической характеристике.
;
, [т];
т;
Выбираем марку прицепного состава автопоезда-сортиментовоза SISU.
Технические
характеристики прицепа: Pпр = 4,5 т; qпр = 12,5 т; bк = 2,0 м; hст = 2,25 м.
7. Расчёт полезной
нагрузки на автопоезд-сортиментовоз (расчётная величина).
, [м3];
где: qa –
грузоподъёмность тягача, т;
qпр –
грузоподъёмность прицепа, т;
м3;
8. Расчёт полезной
нагрузки на автопоезд-сортиментовоз (нормативная величина).
, [м3];
где: Lасорт, Lпрсорт –
соответственно номинальные длины сортиментов на тягач и прицеп, м;
bак, bпрк – внутренняя
ширина коника, м;
hаст, hпрст –
соответственно полезная высота стоек тягача и прицепа, м;
Kапд, Kпрпд – коэффициенты
полнодревесности;
м3;
так как 23,26 < 25,76, следовательно условие выполнено.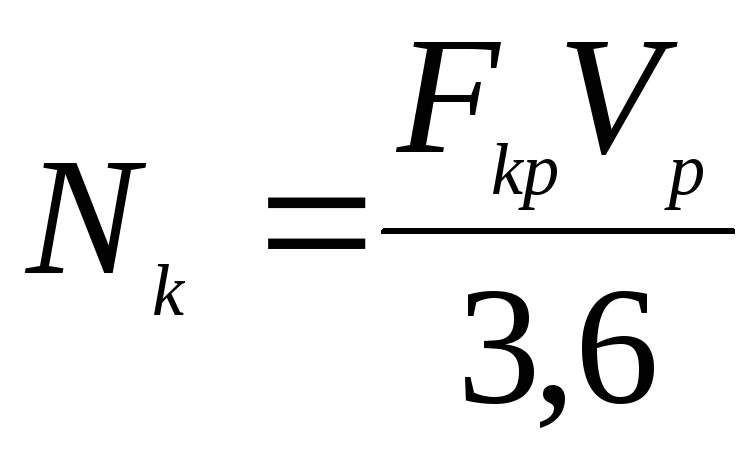
9. Схема выбранного
автопоезда-сортиментовоза ЗИЛ-4331 + прицеп SISU.
Рис. 1. Схема автопоезда-сортиментовоза
ЗИЛ-4331 + прицеп SISU.
10. Окончательный объём
полезной нагрузки на автопоезд-сортиментовоз.
м3;
11. Определение сменной
производительности автопоезда-сортиментовоза.
, [м3];
где: Kв = 0,85;
Vср – среднетехническая
скорость движения автопоезда, м/с;
, [мин]; мин;
м3;
12. Определение
коэффициента удельного расхода топлива.
;
;
где: Ki, K0 –
коэффициенты, учитывающие дополнительный расход горючего;
K1 = 15% — в
зимний период;
K2 = 20% -
движение по веткам и усам;
K0 = 1,005 –
внутригаражный расход;
Н1, Н2 – нормы расхода топлива на тягач и груз;
; ;
м3; км;
кг/м3;
;
13.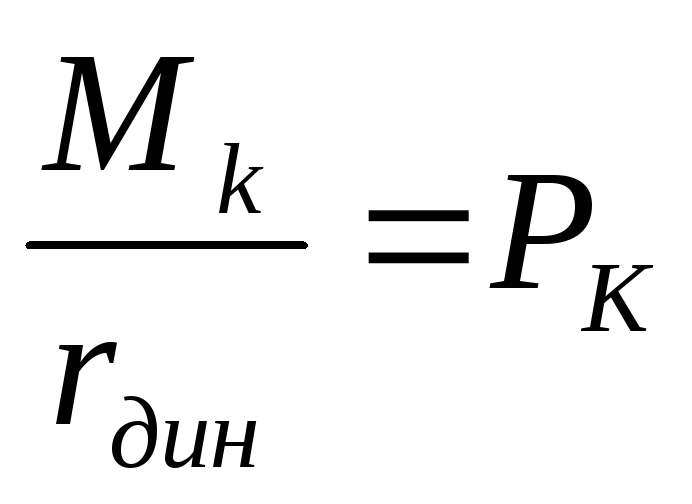 Мероприятия по
Мероприятия по
улучшению эксплуатации подвижного состава на вывозке лесоматериалов.
При повышении сменной производительности за счёт снижении времени простоев;
повышения среднетехнической скорости движения автопоезда за счёт повышения
эксплуатационных свойств дорожной одежды; снижения объёмной плотности древесины
– всё это позволяет уменьшить число линейных автопоездов, число прицепов,
количество водителей, расход ТСМ и прочее.
; ;
шт; шт;
коэффициент технической готовности Ктг = 0,85;
;
шт;
Число водителей автопоездов:
;
чел;
Количество прицепного состава:
;
где: Kпр = 1,2 –
коэффициент, учитывающий резервный прицепной состав;
шт;
Количество шин на период работы автопоезда:
;
так как колёсная формула УРАЛ-375 6 х 6, тогда понадобится:
шт;
а так как автомобилей 7, то следовательно понадобится Nобщ = 34 ∙ 5 = 170
шины.
Вывод:
для повышения сменной производительности на 55% против расчётно-нормативной
необходимо снижать влажность древесины до 63% и увеличивать коэффициент использования
рабочего времени до 0,90 и увеличивать среднетехническую скорость движения
автопоезда до 8,6 м/с.
Мероприятия по уменьшению времени простоев и являются желаемыми, но не
обязательными.
Однако, при выполнении всех вышеперечисленных мероприятий сменную
производительность теоретически можно увеличить до 78,32 м3, что
видно из распечатки расчётов на ЭВМ и по графику (Рис.2).
Тогда возникает необходимость в пересчёте показателей при максимальной
теоретической сменной производительности равной 78,32 м3.
шт;
шт;
шт;
чел;
шт;
шт;
Таким образом, становится понятным, что повышение сменной производительности
является выгодным для лесозаготовительного предприятия так, как при этом
понижается количество автопоездов-сортиментовозов на вывозке древесины и,
соответственно, затраты на их содержание, ТСМ, закупку новых шин и прочее.
Похожие материалы
Информация о работе
Скачать файл
Векторы тяги
Введение
Ссылка:
http://commons.wikimedia.org/wiki/File:stress_vector.svg
Вектор тяги , \({\bf T}\), это просто вектор силы
на поперечном сечении, деленном на площадь этого поперечного сечения.
\[
{\bf T} = {{\bf F} \over \text{Область}}
\]
Итак, \({\bf T}\) имеет единицы измерения напряжения, такие как МПа , но это абсолютно
вектор, а не тензор напряжений. Так что все обычные правила для векторов
применить к нему. Например, скалярные произведения, перекрестные произведения и координатные
могут быть применены преобразования.
92 \right) \text{4000}\,{\bf i}\,\text{N} = 8,66 \, {\bf i} \, \text{МПа}
\]
Обратите внимание, что направление вектора тяги всегда совпадает с вектором внутренней силы.
С изменением угла среза меняется только его величина.
Нормальные напряжения и напряжения сдвига
Нормальные и касательные напряжения — это просто компоненты вектора тяги.
которые являются нормальными и параллельными поверхности области, как показано на рисунке.
Используя \({\bf n}\) для единичного вектора нормали к поверхности, и
\({\bf s}\) для единичного вектора, параллельного ему, означает, что
\[
\sigma = {\bf T} \cdot {\bf n} \qquad \text{and} \qquad \tau = {\bf T} \cdot {\bf s}
\]
Очень важно понимать, что \(\sigma\) и \(\tau\) здесь
каждое скалярное значение, а не полные тензоры. Это естественный результат
операции скалярного произведения с участием \({\bf T}\), \({\bf n}\) и
\({\bf с}\). (Скалярные произведения дают скалярные результаты.)
Значения нормального напряжения и напряжения сдвига здесь являются скалярами, а не тензорами, поскольку
это всего лишь две отдельные компоненты полного тензора напряжений.
9\круг,\; 0) = -4,33 \, \text{МПа}
\]
Тензоры напряжений и векторы тяги
Зависимость вектора тяги от напряженного состояния при
точка получается непосредственно из задания суммы
силы на объект, равные нулю, т.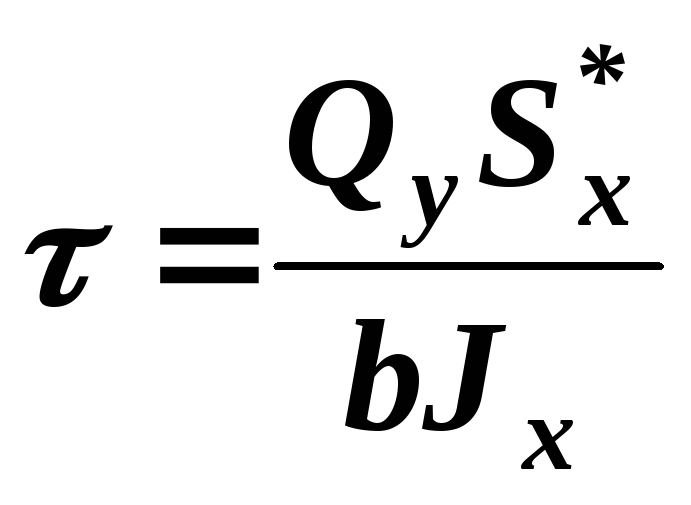 е. устанавливающие равновесие.
е. устанавливающие равновесие.
\[
\sigma_{xx} \, A \, \cos \theta + \tau_{xy} \, A \, \sin \theta = T_x \, A
\]
\[
\tau_{xy} \, A \, \cos \theta + \sigma_{yy} \, A \, \sin \theta = T_y \, A
\]
Область, \(A\), отменяется с обеих сторон, оставляя
\[
\sigma_{xx} \, \cos\theta + \tau_{xy} \, \sin\theta = T_x
\]
\[
\tau_{xy} \, \cos\theta + \sigma_{yy} \, \sin\theta = T_y
\]
, но \(\cos\theta\) и \(\sin\theta\) являются
компоненты устройства, нормальные к поверхности,
\({\bf n} = (\cos\theta, \sin\theta)\), что
\({\bf T}\) действует.
Замена \(\cos \theta\) и \(\sin \theta\) на \(n_x\) и \(n_y\) дает
\[
\sigma_{xx} \, n_x + \tau_{xy} \, n_y = T_x
\]
\[
\tau_{xy} \, n_x + \sigma_{yy} \, n_y = T_y
\]
Оба уравнения можно резюмировать как
\[
{\bf T} = \boldsymbol{\sigma} \cdot {\bf n}
\]
или в тензорной записи как
\[
T_i = \sigma_{ij} \, n_j
\]
Приведенные выше уравнения очень полезны, компактны, имеют матричные и тензорные обозначения.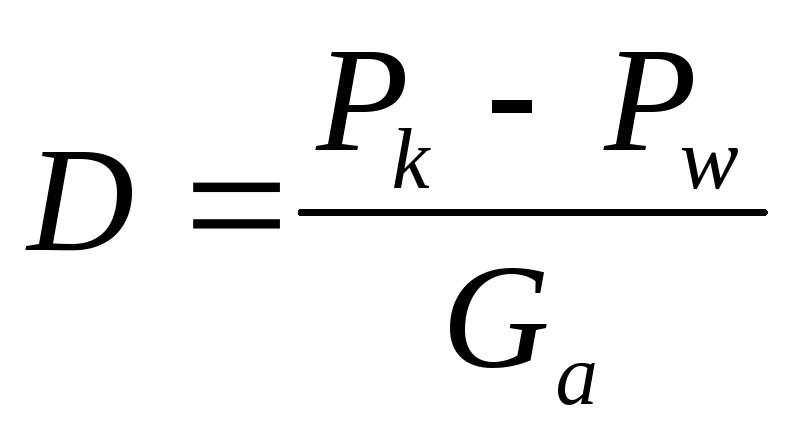
представления уравнений равновесия. Полные уравнения в 3-D,
являются
\[
\sigma_{xx} \, n_x + \tau_{xy} \, n_y + \tau_{xz} \, n_z = T_x
\]
\[
\tau_{yx} \, n_x + \sigma_{yy} \, n_y + \tau_{yz} \, n_z = T_y
\]
\[
\tau_{zx} \, n_x + \tau_{zy} \, n_y + \sigma_{zz} \, n_z = T_z
\]
Термин тензорной записи, \(\sigma_{ij} \, n_j\), приводит к
девять отдельных компонентов напряжения. Например, оба \(\sigma_{xz}\)
и \(\sigma_{zx}\) присутствуют выше, и оба всегда равны.
Фактически это характерно для всех уравнений, включающих напряжение и деформацию.
Вектор тяги из тензора напряжений
С учетом тензора напряжений (в МПа)
\[
\boldsymbol{\сигма} =
\слева[ \матрица{
50 и 10 и 30 \\
10 и 95 и 20\
30 и 20 и 15 }
\верно]
\]
Рассчитать вектор тяги на поверхности с единичной нормалью
\({\bf n} = (0,400, \, 0,600, \, 0,693)\).
\[
\слева\{ \матрица{
Т_х\Т_у\Т_з}
\верно\}
«=»
\слева[ \матрица{
50 и 10 и 30 \\
10 и 95 и 20\
30 и 20 и 15 }
\верно]
\слева\{ \матрица{
0,400\0,600\0,693}
\верно\}
«=»
\слева\{ \матрица{
46,79\74,86\34,40}
\верно\}
\]
Итак, \({\bf T} = 46,79 \, {\bf i} + 74,86 \, {\bf j} + 34,40 \, {\bf k} \, \text{МПа}\).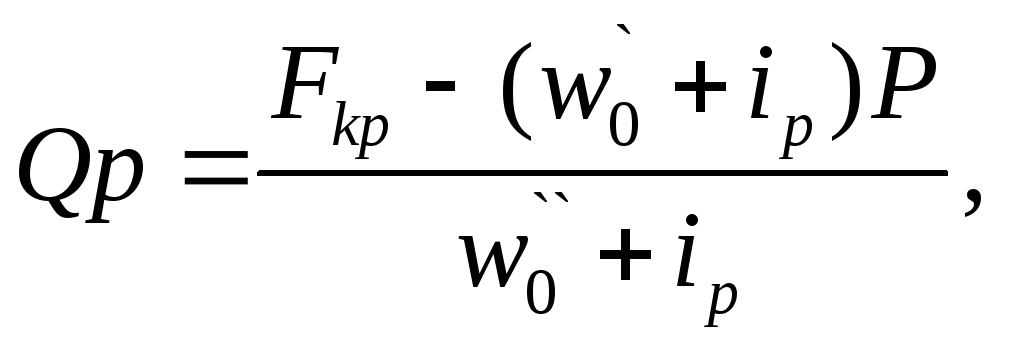
Если площадь равна 100 мм 2 , то сила на ней будет
\({\bf F} = 4679 \, {\bf i} + 7486 \, {\bf j} + 3440 \, {\bf k} \, \text{N}\).
Трансформация напряжения
В этом разделе вводится аспект координатных преобразований тензоров напряжений.
это подмножество общего случая, который будет рассмотрен позже. Это делается с помощью
объединение различных уравнений, включающих вектор тяги.
Напомним, что нормальные и касательные напряжения на поверхности связаны
к вектору тяги на
\[
\sigma = {\bf T} \cdot {\bf n} \qquad \text{and} \qquad \tau = {\bf T} \cdot {\bf s}
\]
Напомним, что нормальные и касательные напряжения здесь — просто скалярные величины на поверхности,
не полный тензор напряжений.
Но мы также видели, что вектор тяги связан с полным тензором напряжений соотношением
\[
{\bf T} = \boldsymbol{\sigma} \cdot {\bf n}
\]
Подстановка этого уравнения для \({\bf T}\) в приведенные выше дает
\[
\sigma = {\bf n} \cdot \boldsymbol{\sigma} \cdot {\bf n} \qquad \text{and} \qquad
\ тау = {\ bf s} \ cdot \boldsymbol {\ sigma} \ cdot {\ bf n}
\]
В тензорной записи уравнения
\[
\sigma = \sigma_{ij} \, n_i \, n_j \qquad \text{and} \qquad
\тау = \sigma_{ij} \, s_i \, n_j
\]
Они представляют собой очень полезные соотношения между тензором напряжений в глобальной
система координат и компоненты нормального напряжения и напряжения сдвига в любой другой
ориентация.
Пример преобразования напряжения
Напомним приведенный выше тензор напряжений
\[
\boldsymbol{\сигма} =
\слева[ \матрица{
50 и 10 и 30 \\
10 и 95 и 20\\
30 и 20 и 15 }
\верно]
\]
Мы рассчитали вектор тяги на поверхности с единичной нормалью
\({\bf n} = (0,400, \, 0,600, \, 0,693)\). На этот раз рассчитайте
нормальные и касательные напряжения на этой поверхности.
Нормальное напряжение на поверхности
\[
\begin{выравнивание}
\сигма
& \; «=» &
\матрица{
\влево\{ 0,400 \;\; 0,600 \;\; 0,693 \справа\} \\
\\
\\
}
\слева[ \матрица{
50 и 10 и 30 \\
10 и 95 и 20\
30 и 20 и 15 }
\верно]
\слева\{ \матрица{
0,400\0,600\0,693 }
\верно\}
\\
\\
«=»
87,47 \text{ МПа}
\end{эквнаррай}
\]
Для того, чтобы вычислить напряжение сдвига, нам сначала нужен конкретный из бесконечного
число единичных векторов, параллельных поверхности. Давайте выберем
\({\bf s} = (-0,832, \, 0,555, \, 0,000)\). Скалярный продукт подтвердит, что
этот вектор перпендикулярен \({\bf n}\).
\[
\begin{выравнивание}
\тау
& \; «=» &
\матрица{
\слева\{ -0,832 \;\; 0,555 \;\; 0.000 \справа\} \\
\\
\\
}
\слева[ \матрица{
50 и 10 и 30 \\
10 и 95 и 20\\
30 и 20 и 15 }
\верно]
\слева\{ \матрица{
0,400\0,600\0,693}
\верно\}
\\
\\
«=»
2,62 \text{ МПа}
\end{эквнаррай}
\]
Таким образом, на этой грани очень небольшой сдвиг в заданном s направлении .
Но это не значит, что на лице вообще нет сдвига. Чтобы увидеть это, выберите
второе направление параллельно поверхности и перпендикулярно первому s .
Получите это путем пересечения единичного вектора нормали с первым касательным вектором.
\[
\begin{выравнивание}
{\bf n} \times {\bf s} \; «=» (0,400 \, {\bf i} + 0,600 \, {\bf j} + 0,693 \, {\bf k})
\times (-0,832 \, {\bf i} + 0,555 \, {\bf j} + 0,000 \, {\bf k}) \\
\\
«=»
-0,385 \, {\bf i} — 0,576 \, {\bf j} + 0,721 \, {\bf k} \\
\end{эквнаррай}
\]
Таким образом, сдвиг в направлении, перпендикулярном первому, равен
\[
\begin{выравнивание}
\тау
& \; «=» &
\матрица{
\left\{ \text{-}0,385 \;\; \text{-}0,576 \;\; 0,721 \справа\} \\
\\
\\
}
\слева[ \матрица{
50 и 10 и 30 \\
10 и 95 и 20\\
30 и 20 и 15 }
\верно]
\слева\{ \матрица{
0,400\0,600\0,693}
\верно\}
\\
\\
«=»
-36,33 \text{ МПа}
\end{эквнаррай}
\]
Таким образом, в этом перпендикулярном направлении имеется значительное напряжение сдвига.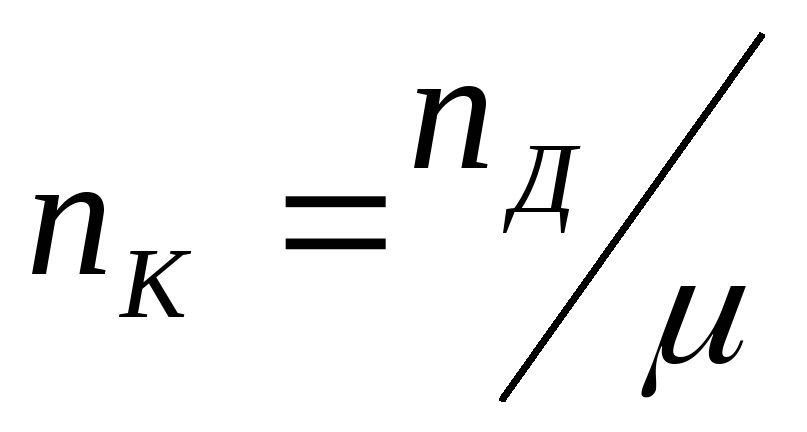 T\)
T\)
как и в случае с тензорами деформации.
Но верно и обратное. Тензор напряжений можно заменить на
тензор деформации, чтобы получить
\[
\epsilon_{\text{нормальный}} \; «=» {\bf n} \cdot \boldsymbol{\epsilon} \cdot {\bf n} \qquad \text{and} \qquad
\гамма/2\; «=» {\bf s} \cdot \boldsymbol{\epsilon} \cdot {\bf n}
\]
Или в тензорной записи как
\[
\epsilon_{\text{нормальный}} \; «=» \epsilon_{ij} \, n_i \, n_j \qquad \text{and} \qquad
\гамма/2\; «=» \epsilon_{ij} \, s_i \, n_j
\]
Это работает, потому что, поскольку и напряжение, и деформация являются тензорами, то любое
математическая операция, применимая к одному, также применима и к другому.
\[
\тау\; «=» {\bf s} \cdot \boldsymbol{\sigma} \cdot {\bf n} \; «=»
\boldsymbol{\sigma} : ({\bf s} \otimes {\bf n})
\]
(То же самое можно сделать и для вычисления нормального напряжения.)
Этот диадический продукт сдвига так часто возникает в пластичности металла, что
обозначается одной буквой \({\bf p}\) и называется
тензор Шмидта по имени инженера, изучавшего пластичность металлов
в начале 1900-х.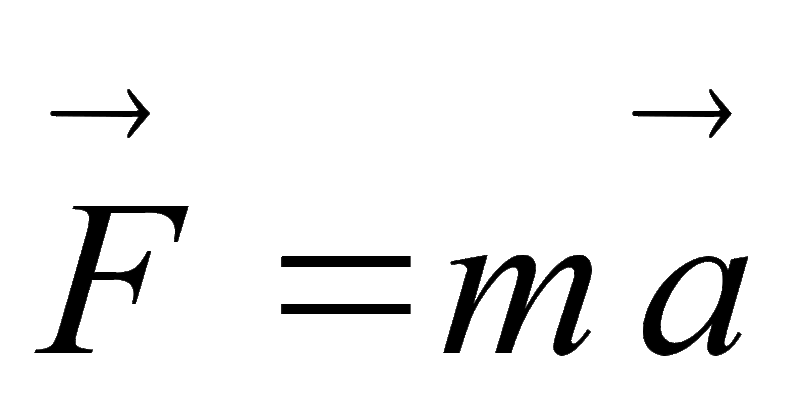
\[
{\ бф р} \; «=» {\bf s} \otimes {\bf n} \; «=»
\слева[ \матрица{
s_1 n_1 & s_1 n_2 & s_1 n_3 \\
s_2 n_1 & s_2 n_2 & s_2 n_3 \\
s_3 n_1 и s_3 n_2 и s_3 n_3 }
\верно]
\]
\[
{\ бф F} \; «=» \int {\bf T} \, дА \; «=» \int \boldsymbol{\sigma} \cdot {\bf n} \, дА
\]
Обе формы часто встречаются в литературе.
Уравнение силы тяги шин и калькулятор
Связанные ресурсы: калькуляторы
Уравнение и калькулятор силы тяги в шинах
Проектирование и разработка силовой трансмиссии
Приложения для проектирования и проектирования
Уравнение и калькулятор силы тяги в шинах
Родственные: 9 0005
Уравнение отрыва и калькулятор сцепления шин
Сцепление шин Сила или тяговая сила — это сила, используемая для создания движения между автомобилем или грузовиком и дорогой или касательной поверхностью.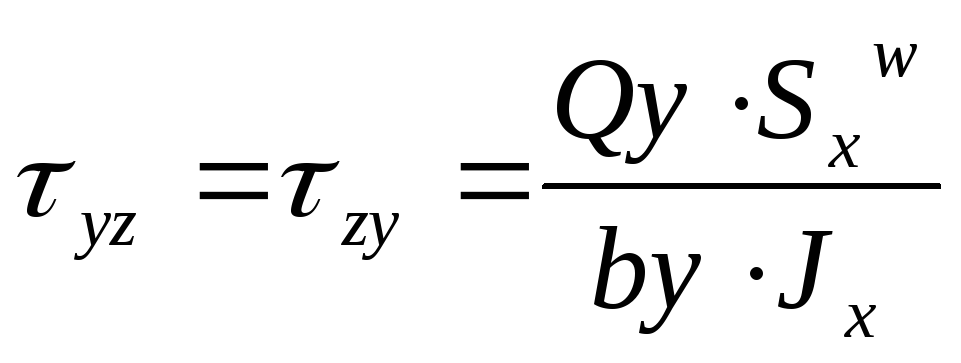
Сцепление с шиной может также относиться к максимальному тяговому усилию между телом и поверхностью, ограниченному доступным трением; в этом случае тяговое усилие часто выражается как отношение максимальной тяговой силы к нормальной силе и называется коэффициентом тягового усилия .
Приложенная тяговая сила на основе уравнения крутящего момента двигателя:
F z = [ 2 · π · M mot · η · i G 9 0226 · я v · i A ] / U
Где ,
F z = Тяговое усилие в Н
M mot = крутящий момент двигателя в Нм
η = общий КПД силовой передачи (см. таблицу ниже)
i G = Передаточное отношение)
i v = Передаточное число ведущего моста
i A = Конечная передача ведущей(их) оси(ей)
U = Окружность качения шины = 2 · π · r в м
r = радиус шины в м
Общий КПД трансмиссии
| Количество ведущих осей | η |
| Одна ось | 0,95 |
| Две оси | 0,90 |
| Три оси | 0,85 |
| Четыре оси | 0,80 |
Коэффициент сцепления : Коэффициент сцепления определяется как полезная сила тяги, деленная на вес ходовой части (колеса, гусеницы и т. д.).
д.).
полезное сцепление = коэффициент сцепления x нормальная сила
Факторы, влияющие на коэффициент сцепления
Сцепление шины между двумя поверхностями зависит от нескольких факторов:
- Состав материала каждой поверхности.
- Макроскопическая и микроскопическая форма (текстура; макротекстура и микротекстура)
- Нормальная сила, прижимающая контактные поверхности друг к другу.
- Загрязнения на границе материала, включая смазочные материалы и клеи.
- Относительное движение трущихся поверхностей — скользящий объект (один в кинетическом трении) имеет меньшее сцепление, чем нескользящий объект (один в статическом трении).
- Направление сцепления относительно некоторой системы координат — например, доступное сцепление шины часто различается при прохождении поворотов, ускорении и торможении.
- Для поверхностей с низким коэффициентом трения, таких как бездорожье или лед, сцепление можно увеличить за счет использования тяговых устройств, которые частично проникают в поверхность; эти устройства используют прочность на сдвиг подстилающей поверхности, а не полагаются исключительно на сухое трение (например, агрессивный протектор для бездорожья или цепи противоскольжения).
 …
…
Максимально допустимое тяговое усилие или сила, которая может быть приложена к колесам, определяется двумя факторами: весом автомобиля и коэффициентом сцепления между шиной и поверхностью дороги.
Чем больше вес и коэффициент сцепления, тем больше тягового усилия можно приложить к колесам, не вызывая пробуксовки между шинами и дорогой.
При проектировании колесных или гусеничных транспортных средств высокое сцепление колес с грунтом более желательно, чем низкое, поскольку оно обеспечивает более высокое ускорение (включая прохождение поворотов и торможение) без проскальзывания колес. Одним заметным исключением является техника дрифта в автоспорте, при которой сцепление задних колес намеренно теряется при прохождении поворотов на высокой скорости.
В некоторых приложениях существует сложный набор компромиссов при выборе материалов. Например, мягкая резина часто обеспечивает лучшее сцепление с дорогой, но также быстрее изнашивается и имеет более высокие потери при изгибе, что снижает расход топлива и эффективность качения.
 …
…