Часто эксперты автомобильных изданий, рассказывая о выдающейся динамике машины, в первую очередь превозносит огромный крутящий момент двигателя, оставляя мощности роль второго плана. Мол, благодаря именно моменту машина ровно и напористо разгоняется в широком диапазоне оборотов и скоростей. Особенно востребовано это качество на высших передачах, – ведь тяговые силы и ускорения на них в любом случае не столь велики, как на первой или второй передаче. А для безаварийного движения в потоке транспорта возможность быстро прибавить скорость зачастую играет судьбоносную роль. Ездить на таком автомобиле даже психологически легче. И все же, когда нужно быстрей разогнаться, что важней – мощность или крутящий момент?Сразу отметим: чаще всего эти два параметра «конфликтуют»… в головах журналистов, охотно повторяющих признанные публикой «истины» без какого-либо их анализа. На самом же деле смешно рассматривать мощность в отрыве от крутящего момента и наоборот. Первая показывает энергию, ежесекундно вырабатываемую двигателем, тогда как крутящий момент – всего лишь силовой фактор, показывающий, как нагружен при работе коленчатый вал. Крутящий момент может существовать и сам по себе, без мощности. Например, при неожиданной остановке перегруженного двигателя на крутом подъеме, в песке, при буксировке тяжелого прицепа в какой-то миг момент еще есть, а движения уже нет. А в некоторых механизмах можно обнаружить и длительно действующий на какой-нибудь вал момент, удерживающий его от поворота. Например, в рулевом механизме, когда мы лишь удерживаем управляемые колеса в нужных положениях, тогда как дорога пытается их нарушить. А самый типичный пример: пытаясь открутить «прикипевший» болт, ключ удлинили метровой трубой, – а болт ни с места. Момент огромный, а работа не идет. А коли нет работы – то нет и мощности.
Тут впору вспомнить школьную физику. Нарисуйте круг радиуса R – это будет сечение вала – и приложите к нему «касательную» силу F. Крутящий момент этой силы М = F • R. За один оборот вала сила F пройдет путь 2πR – и выполнит работу: А = F • R • 2π = М • 2π. А работа за n оборотов: А = М • 2π • n. Если n – число оборотов в минуту, то работа за одну секунду – то есть, мощность – составит N = М • 2πn /60.Выражение 2π n /60 = 0,1047 n = ω – угловая скорость вала. Итак, N = М • 0,1047 n (Формула [1]). Но мы имеем дело не только с вращающимися деталями, но и движущимися линейно. В этом случае в формуле (1) момент М заменим силой F, а угловую скорость ω – линейной v. Получим: N = F • v (Формула [2]). Эти формулы равноправны. Замерив, например, тяговую силу колес, умножим на достигнутую машиной скорость – и найдем затрачиваемую мощность. Но если крутящий момент на ведущей оси умножить на угловую скорость колес, получим то же самое. Итак, мощность – это работа (или энергия) израсходованная или произведенная за 1 секунду. Конечно, о «законе сохранения энергии» знает каждый. Говоря по пионерски, она «не возникает из ничего», но и не исчезает, не оставив следа. Так, лишь около четверти тепловой энергии, получаемой двигателем от сгорания топлива, превращается в механическую, соответствующая мощность (эффективная) тратится на движение машины. Большая же часть полученной в цилиндрах двигателя теплоты идет на «обогрев» окружающего нас мира. Эффективная мощность тоже доходит до ведущих колес не вся – до 15 % ее может рассеять в виде тепла трение в узлах и агрегатах трансмиссии. Но для нас важней другое: если при открытом дросселе (или при полной подаче топлива в дизель) двигатель выдает на колеса сколько-то киловатт, то это – его «потолок». Никакими простыми механизмами вроде коробок передач, редукторов и т. п. превысить эту величину невозможно – этого «закон сохранения» не допустит. Итак, крутящий момент – это удобный для нас «инструмент», связывающий процессы в двигателе с трансмиссией машины и ведущими колесами. Но не более того! Ракетчики, например, запрягают пламя напрямую, получают гигантские тяги и мощности, но о крутящих моментах вспоминают лишь в расчетах турбонасосных агрегатов, – да и то, если двигатели не твердотопливные! Из формулы (1) видно, что для получения достаточной мощности вовсе не обязателен огромный крутящий момент, ведь в произведении два сомножителя. Почему бы, например, не увеличивать мощность при постоянном моменте, наращивая угловую скорость в каком-то диапазоне оборотов? При этом мощность растет по оборотам линейно. А постоянство момента в заданном диапазоне – не чудо, которым некоторые почему-то восторгаются, а всего лишь признак постоянства тяговых сил. Если пренебречь сопротивлением воздуха (к примеру, на первой передаче оно невелико), то и ускорение машины в этом диапазоне постоянное. Это довольно удобно для водителя. Но спросим себя: если бы в начале диапазона момент был таким же, а ближе к пресловутым «верхам» стал больше, стал бы с таким «подхватом» автомобиль хуже? – Вряд ли. Разве только что-нибудь нарушилось бы в смысле экологии. Мощность можно менять и при постоянных оборотах. Пример: мы ехали со скоростью 90 км/ч по горизонтальному шоссе, а с началом подъема, дабы сохранить скорость, пришлось больше открыть дроссель. Это увеличение момента в чистом виде. Итак, имеем дело с формулой (1). К примеру, перед нами скромный двигатель грузовика с моментом 35 кгм при оборотах 3000 в минуту. Какова мощность? Тут отметим, что в расчетах всегда важен правильный выбор единиц измерений параметров. Угловую скорость измеряют в 1/сек. А момент? – В старых единицах это кгм. Получаем: N = 35 кгм . 0,1047 . 3000 1/сек = 10993 кгм/сек ≈ 146,6 л.с. А в современной системе СИ: 35 кгм = 343,35 Нм. Тогда N = 343,45 Нм • 0,1047 • 3000 1/сек ≈ 107846 Вт. На всякий случай напомним, что 1 лс = 75 кгм/сек = 75 • 9,81 Нм/сек = 735,75 Вт. Поэтому 107846 Вт ≈ 146,6 л.с. А теперь прикинем мощность «формульного» двигателя с таким же скромным моментом, но при оборотах 18 тысяч! Результат – 880 л.с. (647 кВт), которые обеспечивают машине роскошную динамику. Никакого чуда нет: чем больше циклов совершит наш «моментик» за одну секунду, тем больше и совершенная им работа. Еще пример. В авиатехнике ныне практически господствуют газотрубинные двигатели. Повторив наш расчет для небольшого двигателя, с оборотами свободной турбины 40 тысяч в минуту, получим мощность около 1950 л.с. или 1438 кВт. Момент турбины невелик, но ведь воздушный винт приводится от нее не напрямую, а через редуктор, – а уж «мощи» ему хватает! Но вернемся к автомобилю. Как уже сказано, любому комфортней ездить на машине, у которой под капотом достаточно и мощности, и момента. Но многим приходится ездить на скромных авто, возможности коих, как нынче говорят, «очень бюджетные»! Всякий, кто не умеет вовремя переключать передачи, с ними испытывает неприятности. Значит, надо учиться, друзья. Ну а что делать владельцу авто с АКП? На смену недовольству двигателем зачастую приходят претензии к автомату. Нередко – справедливые, ведь у АКПП тоже случаются специфические болячки, требующие ремонта. Но часто они оказываются не обоснованными: современный автомобиль, насыщенный электроникой и настроенный изготовителем на строгое выполнение жестких экологических норм, вовсе не обязан подстраиваться под любую российскую лихость! Гусеничному трактору дернуться и оборвать сцепку – плевое дело. Это похоже на выстрел из ружья – можно на миг и «формулу I» опередить. А дольше – никак. Ружье от ракеты отличается принципиально: последняя сохраняет нужное ускорение достаточно долго. В свое время, при стартах к Луне гигант «Сатурн 5» массой свыше 3100 т отделялся от пускового устройства мягко, как пассажирский поезд, – с ускорением чуть больше 1 м/сек2. А минут через пять, по мере выгорания топлива, настолько «терял в весе», что его скорость перед выключением первой ступени составляла 3 км/сек. Низшая передача бульдозера крайне «коротка»: чуть «перекрутил» – тяга упала. А другие не лучше, – вон и «формула» уже растворилась за горизонтом, так что для серьезных игрищ «мощи» на гусеницах маловато.Если пренебречь разницей в КПД передач (она невелика), то на любой передаче машину движут одни и те же киловатты. Но движут по-разному. Момент и тяговая сила на ведущих колесах подчиняются «золотому правилу»: сколько процентов выиграешь в скорости, столько потеряешь в силе. Это показывают рис. 1 и 2. Если двигатель заведомо слаб, с ним сильно не разгонишься.
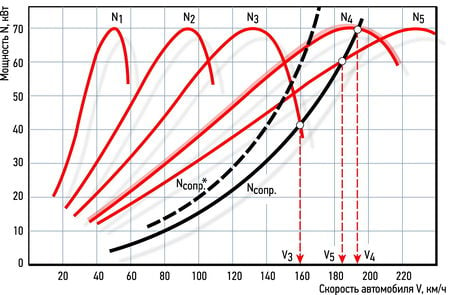
Рис. 1. Величины мощности N1 ... N5 на ведущей оси не зависят от включенной передачи. Точки пересечения кривой Nсопр с кривыми N3, N4 и N5 дают информацию о максимальных скоростях автомобиля на этих передачах. Здесь самая скоростная на горизонтальной дороге в безветрие – четвертая.
Вся история современной транспортной техники – это непрерывная борьба за большие мощности. У наиболее знаменитых ракетоносителей они давно превысили 100 миллионов кВт. Это не ошибка - именно 100 000 000 000 Вт, или 100 ГигаВатт. И хотя притязания автомобилиста не столь велики, «прохватить» на динамичной машине всякий не прочь. Главные враги любителя скорости – не гаишники, а силы, тормозящие движение, – от этих не откупишься! Мощность сопротивления воздуха вкупе с мощностью шинных потерь показаны на рис. 1 линией Nсопр. (Желающие посчитать, могут воспользоваться следующими формулами. Nсопр. = Nw + Nf. Мощность аэродинамических потерь Nw для автомобиля весом 15000 Н при плотности воздуха 1,25 кг/м3, Сх = 0,3 и лобовой площади S = 2 • м2 составляет: Nw = (0,3 • 2 • 1,25)/2 • v3 = 0,375 v3 Вт. А мощность шинных потерь Nf = 0,015 • 15000 • v = 225 v Вт. При 100 км/ч Nсопр составляет лишь 14,5 кВт. А при 200 км/ч – 77 кВт. Разница впечатляет?)Колеса автомобиля, борясь с мощностями сил сопротивления, при максимальной скорости полностью расходуют мощность, получаемую от двигателя. Но ее характеристика (например, показанная кривой N4 на рис.1) при полностью открытом дросселе похожа на гору с округлой макушкой, тогда как характеристика мощности сопротивлений Nсопр. поднимается как крутая парабола. Чтобы полностью использовать арсенал мощности двигателя – и получить максимум скорости V4 (на горизонтальной трассе, без ветра), передаточное число трансмиссии и размер шин подбирают так, чтобы кривая Nсопр пересекла кривую N4 возле вершины. Максимальные скорости на третьей и пятой передачах (V3 и V5) существенно ниже. Но на спуске или с ветром вдогон выгодней может стать пятая передача, а на подъеме или с ветром в лоб – третья.Другие враги скорости – подъем дороги и встречный ветер. Подъем с углом всего 1,5% добавит к потерям в шинах еще столько же. Но еще коварней ветер. Его скорость сложится со скоростью машины относительно дороги, – и уже эту сумму в расчете затрат мощности надо возвести в куб! При скорости по спидометру 36 км/ч (10 м/сек) и ровном встречном ветре 5 м/сек мощность Nсопр вырастет лишь на 0,9 кВт, а вот при 180 км/ч (50 м/сек) – аж на 15,5 кВт. Но придуманный нами автомобиль так ехать не может… Маловато мощи! Максимальная скорость снизится почти на 20 км/ч.
Рис. 2 - Так зависит крутящий момент (М1….М5) или тяговая сила (Fтяг 1 …Fтяг 5) на ведущей оси от включенной передачи. При коэффициенте сцепления шин с дорогой 0,7 ведущая ось, нагруженная половиной веса машины (Gавтом = 15000 н), может создать реальную тяговую силу не больше Fмакс. доп. = 5250 Н.
На рис.2 величины крутящего момента М1…М5, а заодно и теоретические тяговые силы F1…F5 на ведущей оси, показаны одними и теми же кривыми, – ведь тяговые силы пропорциональны моментам. Величины сил – на вертикальной оси справа. Но тут важно учесть следующее. Разгоняет машину не вся тяговая сила, а лишь избыточная – то есть разница между полной тяговой силой колес и сопротивлением воздуха. Отношение этой силы к весу машины академик Чудаков назвал динамическим фактором D. На первой передаче сопротивление воздуха мало, его можно не учитывать – считать, что машину разгоняет полная сила Fтяг.1. Но отталкиваться от дороги сильней, чем позволяет сцепление шин, невозможно! Если, например, ведущая ось несет половину веса машины – 7500 Н, то при коэффициенте сцепления φ = 0,7 тяговая сила не может превысить 35% ее веса. Это неплохо согласуется с такой официальной характеристикой любого автомобиля как предельно возможный угол подъема. С «моноприводом» трудно получить больше. Правда, у машины с задним приводом на подъемах ведущие колеса несколько догружаются весом машины, а вот передний тут невыгоден. Лучшая схема, но сложная и дорогая, – полный привод (конечно, не с такой скромной мощностью, как у «Нивы» или УАЗа!). Если избыточная сила (на первой передаче, например) слишком велика, машина «шлифует» дорогу. Дело нелепое, нужно перейти на следующую передачу. А вот при разработке нового авто конструктор учитывает высокую мощность двигателя и ее следствие – тяговые силы в передаточных числах трансмиссии. Передачи проектируются как достаточно «длинные», расширяющие диапазон скоростей при достаточных ускорениях. А это значит, что и при более высоких скоростях действуют нужные тяговые силы (или моменты) на колесах. Иначе говоря, реализуется весь арсенал мощности! Значит, она все же важнее.
Споры на тему влияния мощности-момента ведутся давно, и конца им не видно. Вроде бы сто раз уже объясняли самыми разными способами, что тут к чему, а воз и ныне там. Вызывает неподдельный интерес, откуда все же берется заблуждение и почему оно такое устойчивое?Причин видится две. Одна из них в том, что мощность есть функция от момента. Зависимость мощности от момента стоит барьером, который преодолеть оказывается непросто. Что странно. Поскольку очевидность того, что мощность есть функция не только от момента, но и от оборотов, не оспаривается, и тот факт, что у разных двигателей бывает весьма большой разброс по соотношению мощности к моменту, также не подвергается сомнению. То есть существует молчаливое согласие с тем, что мощность есть функция от двух аргументов - оборотов и момента, но при этом зависимость от оборотов как бы игнорируется. Почему?А в этом и есть вторая, главная причина заблуждения. И ключевая фраза здесь: "Человек совершенно может не иметь понятие про мощность.А вот разницу в ускорении на 3 и 4 передаче он вполне способен почувствовать." Ясно, что на динамику автомобиля оказывают большое влияние и передаточные числа КПП. На графике 1 видны кривые мощности двигателя, смещенные в зависимости от разных передаточных чисел и кривая сопротивлений. Видно, что с ростом передаточного числа динамика резко возрастает. Это очевидно и вопросов не вызывает. Странно, что не менее очевидный факт, что бОльшая часть времени при разгоне приходится вовсе не на 1 и 2 передачи, а на 3-4, при этом упускается из виду.При разгоне здравомыслящий водитель пользуется всеми четырьмя передачами и весьма широким диапазоном частот вращения двигателя. При этом редко задумывается о том, что динамика разгона на высокой скорости мала и плохо ощущается, но именно на нее и приходится львиная доля времени разгона (по той простой причине, повторю, что на высших передачах динамика хуже и потому занимает больше времени). Хорошо ощущается динамика разгона на низших передачах, в диапазоне низких и средних оборотов (дальше водитель двигатель раскручивает редко). И что выходит? А выходит, что "низовой", моментный двигатель дает ощущение уверенного и бодрого разгона по той простой причине, что легко и весело страгивает и начинает разгонять автомобиль. А по достижении скорости ощущения становятся слабыми, и оценить разницу в разгоне 100- и 120 сильного моторов на 4-5 передачах, способен не каждый. Потому и кажется, что момент определяет динамику. По ощущениям. А ощущениям человек склонен верить очень сильно, даже вопреки логике и здравому смыслу.
Проповедующие формулировку "скорость определяется мощностью, а динамика разгона - моментом двигателя" могут убедиться в своем заблуждении, решив простую задачу.Вводные1. Равномерный подъем на некоторую высоту равносилен равномерному ускорению, поскольку увеличивает потенциальную энергию тела mgh*. (что можно объяснить - чем с большей высоты упадет, тем сильней ударится).2. Поднимаем равномерно груз весом 75 кг на высоту 1 м за 1 с.3. Имеется черный ящик, в котором спрятан мотор неизвестной природы и, возможно, редуктор с КПД=1.Вопросы.1. Какая мощность должна быть в моторе, спрятанном внутри черного ящика?2. Какой момент должен быть в моторе, спрятанном внутри черного ящика?
Подъем указанного груз на нужную высоту за время аналогичен разгону по горизонтали той же массы с ускорением g0.5.Если ускорение определяется моментом - просто назовите цифруЕсли ускорение определяется мощностью - тоже просто назовите цифруЕсли цифру назвать не удается, значит параметр может быть самым разным и роли не играет.Вы можете разгонять тело с заданным ускорением (или поднимать его вверх), меняя крутящий момент по своей прихоти (и устанавливая каждый раз соответствующий редуктор). Вы можете отталкиваться от параметров редуктора, и всякий раз требуемый момент будет меняться и зависеть от передаточного отношения этого редуктора. Но всегда мощность будет оставаться одной и той же, неизменной величиной - для подъема груза 75 кг на 1 м за 1с понадобится ровно одна лошадиная сила или 0,73549875 кВт
Можно поступить и следующим образом.Берите любой момент, который причина разгона, берите любой редуктор и разгоните тело 75 кг до скорости 3.13 м/c за 1 с.Ограничение только по мощности - она не должна превышать 0.9 л.с.Есть ли решение у этой задачи? Если нет - то почему?Ответ.Задача не имеет решения по той простой причине, потому что невозможно обеспечить заданную динамику - для нее не хватит мощности. Каким бы ни был момент.Вывод. Момент двигателя для разгонной динамики не имеет значения, все решает мощность.
* Пояснение Вы поднимаете 75 кг получаете от этого энергию mgh. Она преобразуется так:поскольку a = V2 / 2h, а ускорение а у нас равно g, то V = (2hg)0.5.Кинетическая энергия тела E = mV2/2 = m2hg/2 = mgh.
Смотри также главу Как движется автомобиль
wiki.zr.ru
Мощность — выражается как отношению работы, выполняемой за некоторый промежуток времени, к промежутку времени
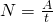
Из формулы следует, что в системе СИ единицей мощности является 1 Дж/с (джоуль в секунду). Эту единицу иначе называют ватт (Вт), 1 Вт= 1 Дж/с.
Мощность показывает, какая работа совершается за единицу времени
Если на движущееся тело действует сила, то эта сила совершает работу. Мощность в этом случае равна скалярному произведению вектора силы на вектор скорости, с которой движется тело:
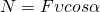
Формула показывает связь между мощностью и скоростью при равномерном движении. Так же формула справедлива и для переменного движения, если под N понимать мгновенную мощность, а под V — мгновенную скорость). Если направление силы совпадает с направлением перемещения, то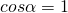 
и N=Fv.Тогда следует, что
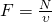
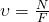
Из этих формул видно, что при постоянной мощности двигателя скорость движения обратно пропорциональна силе тяги и наоборот. На этом основан принцип действия коробки скоростей (коробки перемены передач) различных транспортных средств.
В формуле мы использовали :
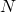— Мощность
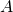— Выполненная работа
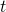— Время, за которое выполнялась работа
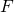— Сила, приложенная к телу
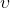— Скорость тела
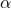— Угол между силой и скоростью
xn--b1agsdjmeuf9e.xn--p1ai
Основой для электрической машины является правило электроиндукции с магнитной индукцией. Такой прибор включает в себя статор или как его называют константной частью (характерно для асинхронных, синхронных машин изменяющегося тока) или индуктора (для приборов константного тока) и ротора, его называют активной или движущейся частью (для асинхронных и синхронных машин изменяющегося тока) или якоря (приборов константного тока). В роли константной части для машин тока с малой мощью активно применяются магниты (неизменного состояния).
Электрическая мощность – это физическая величина, которая характеризуется скоростью преобразования ну или передачи электрической энергии. Чтобы облегчить понимание движение тока электрики представляют, как передвижение жидкости по трубе, а напряжение – с разницей положения ярусов этой жидкости. Электричество, так же, осуществляя работу, передвигается от высокой возможности к низкой, как и жидкость. Значит мощь электрики это количество работы, некая совершается за 1 секунду, или быстрота выполнения самой работы. Сумма тока электрики, которая прокладывается сквозь поперечный разрез цепи на протяжении одной секунды, это и есть сила тока в самой цепи.
Отсюда вытекает, что мощность электрическая равна в пропорции напряжению и силе тока в цепи. Для определения мощи тока принята единица – ватт, сокращенно - Вт.Для физических подсчетов принято было применять стандартную формулу N=A/t, где N – мощность, A – работа, t – время.Существует много вариантов данной формулы с разными буквенными обозначениями.
Если вы постоянно используете электромашины, то часто натыкались на шильдики в которых, по сути, указанно все характеристики, в том числе и варианты мощности. Если посмотреть изображение шильдика, то среди разных параметров можно увидеть и значение мощности. Как видно, против надписи максимальная мощность стоит значение 1000 Вт. Но это не его электрическая мощность, как часто думает потребитель.
На изображённом ниже шильдике показана максимально допустимая мощность электротока. Часто пишут на шильдике рекомендуемую мощность и обозначают её киловаттами.
Итак, как же возможно рассчитать используемую мощность определенного двигателя из собственной электрической сети. Для этого нужно смотреть и на другие показатели на том же шильдике исследуемого прибора - это КПД и cosφ. Где КПД, бывает обозначают аббревиатурой КПД, или буквой η. Сначала нужно учитывать связь полезной мощности механики на валу и КПД. Имея данные значения можно легко рассчитать мощность потребляемую двигателем из электрической сети. Узнаем по соотношению: Ра=Р/η. Но это еще не результаты. Нужно помнить, электроприборы потребляют из сети как активную, так и реактивную энергию. При расчётах используемой движком полной мощи, необходимо получить соотношение из треугольника мощностей.
Для того что бы просчитать мощность определенного электродвижка потребуется не мало: источник тока (сеть), линейка (штангенциркуль), динамометр, амперметр, табличка «зависимости неизменной движка С от количества полюсов».
Итак, перейдем к вариантам действий. А именно, для определения мощности электродвигателя:
Обратите внимание! Для каждого двигателя предназначена сеть на определенное количество фаз. Примером выступает трехфазный двигатель, который предназначен только для питания от трёхфазной сети переменного тока.
ogodom.ru
Электрические двигатели сегодня используются в различных технических средствах и оборудовании, потому многих пользователей интересует, как определить мощность и ток электродвигателя? Производители двигателей оснащают свои товары специальными таблицами, устанавливаемыми на корпусах устройств. Эти таблички содержат в себе исчерпывающую информацию о технических характеристиках устройства: марка, номинальный рабочий ток, мощность, частота вращения, КПД, тип двигателя и т.д. Все эти данные содержатся также в технической документации на электродвигатели.
Из всех характеристик двигателей, для пользователей наибольшее значение имеют потребляемый ток и мощность. Эти данные позволяют определить сечение и пропускную способность электрических кабелей, которые необходимо использовать для подключения оборудования, выбрать подходящие по номиналам устройства безопасности – УЗО и автомат.
Несмотря на то, что в большинстве случаев с поиском технических характеристик двигателей не возникает никаких проблем, иногда техническая документация и таблички на устройствах отсутствуют. Подобные проблемы вынуждают пользователей искать другие варианты определения мощности, тока и других параметров работы электродвигателя.
Существуют различные формулы расчета, позволяющие определить точную мощность электродвигателя. Для использования некоторых формул пользователю придется измерить размеры статора двигателя, для других формул – нужно знать величину тока или КПД двигателя. Многие специалисты используют эти формулы на практике, но существует и гораздо более простая, удобная методика определения мощности двигателя – практические измерения. С помощью установленного счетчика потребления электрической энергии в бытовой электросети можно узнать мощность любого оборудования.
Для проведения таких измерений нужно будет отключить от питания все бытовые электрические устройства, чтобы ни один прибор не потреблял электрическую энергию и счетчик «не крутился». Освещение также необходимо отключить, так как даже одна включенная лампочка может навредить испытаниям.
Особенности определения мощности зависят от того, какой именно счетчик потребления электроэнергии у вас установлен. Если на вводе электричества на объект установлен счетчик «Меркурий», достаточно просто включить электродвигатель на полной мощности на 3-5 минут. В процессе работы двигателя счетчик будет показывать величину нагрузки, измеряемую в кВт.
Провести такие измерения можно и с помощью стандартного индукционного счетчика потребления, но нужно помнить, что такие устройства ведут учет в Квт/ч. Итак, сначала нужно записать точные показателя счетчика до начала исследования, затем нужно включить двигатель ровно на 10 минут, не допуская никаких погрешностей. Лучше всего засекать время с помощью секундомера, позволяющего вовремя включить и выключить двигатель. После выключения двигателя нужно снять показания с индукционного счетчика, отнять из показаний записанную перед измерениями величину. Теперь показатели умножаем на 6. Полученные в ходе этих простых измерений и вычислений результаты будут точно отображать активную мощность двигателя в кВт.
Сложнее определить технические характеристики маломощных двигателей, но и их мощность можно рассчитать, хотя это потребует больших усилий. Легче всего определить мощность двигателя путем подсчета полных оборотов диска за единицу времени. К примеру, на счетчике указано, что 1200 оборотов равняется 1 кВт/ч. Если в течение одной минуты счетчик сделает 10 оборотов, то в этом случае 10 нужно умножить на 60 (число минут в часе) и получаем 600 оборотов в час. Делим 1200 на 600 и получаем мощность электродвигателя. Важно отметить, что на точность напрямую влияет продолжительность измерений. Чем дольше измерять показания, тем точнее можно определить мощность двигателя.
Для эксплуатации электродвигателя пользователю требуются различные параметры его работы. Второй по важности характеристикой такого устройства является величина потребляемого тока. Методика расчета тока зависит от числа фаз в двигателе и величине потребляемого напряжения. Проще всего рассчитать величину тока для трехфазных двигателей, подключаемых от электрических сетей напряжением 380 В. Величина потребляемого тока для таких устройств равняется умноженной на 2 мощности. К примеру, трехфазный двигатель мощностью 2 кВт умножаем на 2 и получаем потребляемый ток двигателя, равный 4 Ампер.
Величина тока электродвигателя в момент времени может зависеть от вида запуска. Зависимость величины тока от вида запуска представлена на графике ниже.
Это точная формула, однако, требующая определенных дополнений. Обязательно нужно учитывать, что результат таких расчетов – это величина потребляемого тока при номинальной нагрузке. Двигатель на холостом ходу будет иметь куда меньшую величину потребляемого тока.
Для расчета тока трехфазного асинхронного двигателя можно также использовать формулу:
Iн = 1000 Pн / √3 * (ηн * Uн * cosφн),
В этой формуле:
Потребляемый ток однофазными двигателями рассчитывается по другой формуле. В этом случае для определения тока пользователю нужно будет разделить мощность двигателя на напряжение в электросети. Уровень напряжения в месте подключения двигателя необходимо измерить перед проведением расчетов, так как уровень напряжения при включенном устройстве в месте ввода будет снижаться.
Таким образом, если мощность мотора равняется 2 кВт или 2000 Вт, а напряжение в сети равняется 220 В, то 2000 следует разделить на 220. Получаем величину в 9 А, которая и принимается за величину потребляемого тока электродвигателем.
podvi.ru
Для того, чтобы перетащить 10 мешков картошки с огорода, расположенного в паре километров от дома, вам потребуется целый день носиться с ведром туда-обратно. Если вы возьмете тележку, рассчитанную на один мешок, то справитесь за два-три часа.
Ну а если закинуть все мешки в телегу, запряженную лошадью, то через полчаса ваш урожай благополучно перекочует в ваш погреб. В чем разница? Разница в быстроте выполнения работы. Быстроту совершения механической работы характеризуют физической величиной, изучаемой в курсе физики седьмого класса. Называется эта величина мощностью. Мощность показывает, какая работа совершается за единицу времени. То есть, чтобы найти мощность, надо совершенную работу разделить на затраченное время.
И в таком случае, формула расчета мощности принимает следующий вид: мощность= работа/время , или
N=A/t,
где N – мощность,A – работа,t – время.
Единицей мощности является ватт (1 Вт). 1 Вт – это такая мощность, при которой за 1 секунду совершается работа в 1 джоуль. Единица эта названа в честь английского изобретателя Дж. Уатта, который построил первую паровую машину. Любопытно, что сам Уатт пользовался другой единицей мощности – лошадиная сила, и формулу мощности в физике в том виде, в котором мы ее знаем сегодня, ввели позже. Измерение мощности в лошадиных силах используют и сегодня, например, когда говорят о мощности легкового автомобиля или грузовика. Одна лошадиная сила равна примерно 735,5 Вт.
Мощность является важнейшей характеристикой любого двигателя. Различные двигатели развивают совершенно разную мощность. Это могут быть как сотые доли киловатта, например, двигатель электробритвы, так и миллионы киловатт, например, двигатель ракеты-носителя космического корабля. При различной нагрузке двигатель автомобиля вырабатывает разную мощность, чтобы продолжать движение с одинаковой скоростью. Например, при увеличении массы груза, вес машины увеличивается, соответственно, возрастает сила трения о поверхность дороги, и для поддержания такой же скорости, как и без груза, двигатель должен будет совершать большую работу. Соответственно, возрастет вырабатываемая двигателем мощность. Двигатель будет потреблять больше топлива. Это хорошо известно всем шоферам. Однако, на большой скорости свою немалую роль играет и инерция движущегося транспортного средства, которая тем больше, чем больше его масса. Опытные водители грузовиков находят оптимальное сочетание скорости с потребляемым бензином, чтобы машина сжигала меньше топлива.
Предыдущая тема: Механическая работа: определение и формула Следующая тема:   Простые механизмы и их применение: рычаг, равновесие сил на рычагеВсе неприличные комментарии будут удаляться.
www.nado5.ru
Разделы: Физика
Цели урока:
Ход урока
«И вечный бой! Покой нам только снится Сквозь кровь и пыль… Летит, летит степная кобылица И мнет ковыль… И нет конца! Мелькают вёрсты, кручи… Останови! …Покоя нет! Степная кобылица несется вскачь!»
А.Блок «На поле Куликовом» (июнь 1908 г). ( Слайд 1).
Урок сегодня я хочу начать с вопросов к вам. (Слайд 2).
1. Как вы думаете, имеет ли какое-то отношение лошадь к физике?
2. С какой физической величиной связана лошадь?
Мощность – правильно, это и есть тема нашего урока. Запишем ее в тетрадь.
Действительно, мощность двигателей автомобилей, транспортных средств до сих пор измеряют в лошадиных силах. Сегодня на уроке мы с вами узнаем всё о мощности с точки зрения физики. Давайте подумаем вместе и определим, что мы должны знать о мощности, как о физической величине.
Существует план изучения физических величин: ( Слайд 3).
Этот план и будут целью нашего урока.
Начнем с примера из жизни. Вам необходимо набрать бочку воды для полива растений. Вода находится в колодце. У вас есть выбор: набрать при помощи ведра или при помощи насоса. Напомню, что в обоих случаях механическая работа, совершенная при этом будет одинаковой. Конечно же, большинство из вас выберут, насос.
Вопрос: В чем разница при выполнении одной и той же работы?
Ответ: Насос выполнит эту работу быстрее, т.е. затратит меньшее время.
1) Физическая величина, характеризующая быстроту выполнения работы, называют мощностью. ( Слайд 4).
2) Скаляр, т.к. не имеет направления.
3) N.
4) 
5) [N] = [ 1 Дж/с] = [1Вт ]
Название этой единицы мощности дано в честь английского изобретателя паровой машины (1784г) Джеймса Уатта. ( Слайд 5).
6) 1 Вт = мощности, при которой за время 1 с совершается работа в 1 Дж. ( Слайд 6).
Самолеты, автомобили, корабли и другие транспортные средства движутся часто с постоянной скоростью. Например, на трассах автомобиль достаточно долго может двигаться со скоростью 100 км/ч. ( Слайд 7).
Вопрос: от чего зависит скорость движения таких тел?
Оказывается, она напрямую зависит от мощности двигателя автомобиля.
Зная, формулу мощности мы выведем еще одну, но для этого давайте вспомним основную формулу для механической работы.
Учащийся выходит к доске для вывода формулы. ( Слайд 8).
Пусть сила совпадает по направлению со скоростью тела. Запишем формулу работы этой силы.
1.
2.При постоянной скорости движения , тело проходит путь определяемой формулой
Подставляем в исходную формулу мощности:
, получаем
-
мощность.
У нас получилась еще одна формула для расчета мощности, которую мы будем использовать при решении задач.
Эта формула показывает ( Слайд 9), что при постоянной мощности двигателя, изменением скорости можно менять силу тяги автомобиля и наоборот, при изменении скорости автомобиля можно менять силу тяги двигателя.
При N = const
v > , F <.
v < , F >.
Вопрос. Когда нужна большая сила тяги?
Ответ:
а)При подъеме в гору. Правильно, тогда водитель снижает скорость.
б) При вспашке земли тракторист движется с малой скоростью, чтобы была большая сила тяги. Для этого водитель, тракторист, машинист, токарь, фрезеровщик часто используют коробку передач, которая позволяет менять скорость. ( Слайд 10).
Мощность всегда указывают в паспорте технического устройства. И в современных технических паспортах автомобилей есть графа:
Мощность двигателя: кВт / л.с.
Следовательно, между этими единицами мощности существует связь.
Вопрос: А откуда взялась эта единица мощности? ( Слайд 11).
Дж. Уатту принадлежит идея измерять механическую мощность в «лошадиных силах». Предложенная им единица мощности была весьма популярна, но в 1948 г. Генеральной конференцией мер и весов была введена новая единица мощности в международной системе единиц – ватт. ( Слайд 12).
1 л.с. = 735,5 Вт.
1 Вт = ,00013596 л.с.
Эта единица мощности была изъята из обращения с 1 января 1980 г.
Примеры мощностей современных автомобилей. ( Слайд 13,14).
Различные двигатели имеют разные мощности.
Учебник, страница 134, таблица 5. [1]
Вопрос: А какова мощность человека?
Текс учебника, § 54. Мощность человека при нормальных условиях работы в среднем составляет 70-80 Вт. Совершая прыжки, взбегая по лестнице, человек может развивать мощность до 730 Вт, а в отдельных случаях и большую.[1]
Вопрос: А чем «живые двигатели» отличаются от механических? ( Слайд 15).
Ответ: Тем, что «живые двигатели» могут изменять свою мощность в несколько раз.
Закрепление материала.
1.Расскажите все, что вы знаете о мощности. Ответ по плану изучения физической величины.
2. Упр. 29, задача №6. ( Слайд 16).
| Дано: | СИ | Решение: |
| m = 125кг | N = A / t | |
| h = 70 см | 0,7 м | A = F s s = h |
| t = 0,3 с | F = P = mg | |
| N = mgh / t | ||
| N - ? | N = 125 кг · 9,8 Н/ кг · 0,7 м / 0,3 с= 2858,3 Вт ≈ 2,9 кВт |
Ответ : N ≈ 2,9 кВт.
Домашнее задание: ( Слайд 17).
Литература:
xn--i1abbnckbmcl9fb.xn--p1ai
| Мощность и среднее индикаторное давление двигателя можно выразить через параметры, влияющие на их значение. Количество тепла, вносимого топливом в двигатель в течение часа, равно
Соответственно подведенному теплу индикаторная мощность двигателя будет равна (уравнение индикаторной мощности)
Приравнивая выражения индикаторной мощности (126) и (156), найдем новое выражение среднего индикаторного давления:
Уравнения эффективной мощности и среднего эффективного давления соответственно будут иметь вид:
Полученные уравнения показывают, что при работе двигателя могут изменяться ?i/?, ?н, ?т, п и метеорологические условия, влияющие на развитие им эффективной мощности. Отношение Qн / L0 при работе двигателя остается постоянным и для всех жидких сортов топлива практически одинаково (20 000—20 200 ккал/моль). При изменении числа оборотов и нагрузки двигателя, как это было изложено ранее, изменяется ?т, ?н, ? и, следовательно, ?i. Причем для развития двигателем как можно большей мощности важно не столько ?i, сколько значение отношения ?i/?, которое должно быть наибольшим. Таким образом, отношение ?i/? является критерием совершенства рабочего цикла двигателя. При изменении метеорологических условий (давления и температуры наружного воздуха р0 и Т0), кроме непосредственного их влияния на мощность двигателя, что видно из формул (156) и (158), изменяется ? и, следовательно, ?i (если подача топлива за цикл остается неизменной. Отсюда следует сделать вывод, что при замере мощности двигателя должно быть всегда отмечено, при каких метеорологических условиях достигнута данная мощность. Из полученных выражений следует, что среднее индикаторное давление и, соответственно, индикаторная мощность дизеля в значительной мере зависят от плотности воздушного заряда. При работе дизеля с наддувом плотность воздушного заряда определяется не только давлением наддувочного воздуха, но и его температурой. Если сохранять неизменной величину ?i/? (путем увеличения цикловой подачи топлива), среднее индикаторное давление и индикаторная мощность пропорционально возрастают увеличению отношения pk / Tk. Опытные данные показывают, что снижение температуры наддувочного воздуха на каждые 20° (промежуточное охлаждение) позволяет повысить мощность дизеля на 5—6%. Промежуточное охлаждение наддувочного воздуха позволяет снизить среднюю температуру за цикл, температуру стенок цилиндра и удельный расход топлива. Оно осуществляется следующими способами: установкой воздуховодяного трубчатого холодильника; расширением воздуха как в цилиндре дизеля путем преждевременного закрытия впускного клапана, так и до поступления в цилиндр; расширением воздуха в турбине, приводящей в действие центробежный компрессор. Наибольшее применение получил способ охлаждения с использованием воздуховодяного холодильника. В последнее время были выполнены исследования эффективности испарительного охлаждения наддувочного воздуха. Впрыскиваемая в поток нагретого наддувочного воздуха вода (до поступления его в цилиндр) испаряется и одновременно охлаждает воздух. Исследования, восполненные на кафедре ДВС ЛИВТа, показывают, что при расходе воды до 1% по весу от расхода воздуха температура наддувочного воздуха снижается на 25°. При. этом температура поршня понижается на 8%, а скорость изнашивания деталей цилиндропоршневой группы при этом остается неизменной. Испарительное охлаждение является наиболее эффективным и приемлемым для судовых дизелей с малой степенью наддува. |
vdvizhke.ru
