|
КАТЕГОРИИ: Археология
ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрации Техника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Балочные системы. Определение реакций опор и моментов защемления
|
⇐ ПредыдущаяСтр 5 из 12Следующая ⇒ Принцип действия асинхронного двигателя, как указывалось, основан на взаимодействии вращающегося поля и тока, индуктированного этим полем в обмотке ротора. В результате взаимодействия магнитного потока Φ с током I2, протекающим в проводниках обмотки ротора, возникают электромагнитные силы, приводящие ротор во вращение. Поэтому вращающий момент, создаваемый на валу двигателя, зависит от величины тока ротора I2 и от магнитного потока Φ. Кроме того, на величину вращающего момента асинхронного двигателя влияет сдвиг фаз Ψ2 между током I2 и э.д.с. ротора. Для уяснения влияния cos Ψ2 рассмотрим картину электромагнитных сил, действующих на проводники ротора. Рассмотрим сначала случай, когда индуктивность обмотки ротора мала и поэтому сдвигом фаз между током и э. Рассмотрим второй случай, когда индуктивность обмотки ротора относительно велика. В этом случае сдвиг фаз между током ротора I2 и э.д.с. ротора будет также значительным. На рис. 255, б магнитное поле статора асинхронного двигателя по-прежнему показано в виде вращающихся по направлению часовой стрелки полюсов N и S. На рис. 255 показано направление индуктированных токов в отдельных проводниках ротора в рассматриваемый момент времени, а также направления отдельных электромагнитных сил, действующих на проводники. Если Ψ2 = 0, то все электромагнитные силы будут действовать согласованно. При большем Ψ2 часть электромагнитных сил создают вращающий момент, направленный по часовой стрелке, а остальные силы — против часовой стрелки. Магнитный поток Φ не зависит от скорости вращения ротора n. Следовательно, вращающий момент М пропорционален только активной составляющей тока ротора I2 cos Ψ2. Индуктивное сопротивление ротора Х2 = 2πfL2, а следовательно, и величина cos Ψ2 зависят от частоты тока ротора f2 и поэтому с изменением нагрузки на валу ротора изменяется не только величина тока I2, но и величина cos Ψ2. На основании математического анализа и экспериментального исследования можно построить график зависимости вращающего момента асинхронного двигателя М от скольжения S (рис. 256). Так как каждому значению S соответствует определенное значение n = n0 (1 — S), то указанный график можно представить и как зависимость вращающего момента от скорости n. Зависимость между вращающим моментом М и скольжением S называется механической характеристикой двигателя (рис. 256). На кривой А видно, что в начальный момент пуска, когда S = 1 и n = 0, вращающий пусковой момент двигателя относительно невелик. Это объясняется тем, что в момент пуска частота тока в обмотке ротора наибольшая и индуктивное сопротивление обмотки велико. При некотором скольжении S1, называемом критическим, вращающий момент двигателя будет иметь максимальное значение. При дальнейшем уменьшении скольжения (или, иначе говоря, при дальнейшем увеличении скорости вращения двигателя) вращающий момент будет быстро уменьшаться и при скольжении S = 0 момент двигателя будет равен нулю. Этот режим соответствует идеальному холостому ходу, когда двигатель не нагружен, а механическими потерями (на трение) можно пренебречь. Пусковой момент можно увеличить, если в момент пуска уменьшить сдвиг фаз между током и э.д.с. ротора. Если увеличить активное сопротивление цепи ротора, то угол Ψ2 уменьшится, что приведет к тому, что cos Ψ2 и вращающий момент двигателя станут больше. Этим пользуются на практике для увеличения пускового вращающего момента двигателя. Увеличение пускового момента приводит к тому, что максимальный вращающий момент двигателя получается при большем скольжении (точка S2 кривой В на рис. 256). Путем увеличения активного сопротивления цепи ротора при пуске можно добиться того, что максимальный вращающий момент будет в момент пуска (S = 1 кривой С). Вращающий момент, развиваемый асинхронным двигателем, как указывалось, зависит от величины магнитного потека Φ. При снижении приложенного напряжения U1 уменьшается магнитный поток Φ, а следовательно, и вращающий момент, развиваемый двигателем при данной скорости вращения. Теория и практика показывают, что вращающий момент асинхронного двигателя пропорционален квадрату напряжения, поэтому даже небольшое уменьшение напряжения сети сопровождается резким уменьшением момента. Кривая А называется естественной механической характеристикой, а кривые В и С — реостатными механическими характеристиками асинхронного двигателя. Работе двигателя с номинальной нагрузкой соответствует точка N на кривой A. При скольжении Sн двигатель развивает номинальный момент Mн. Ранее было указано, что путем увеличения активного сопротивления цепи роторной обмотки можно увеличить вращающий момент двигателя. Можно было бы сделать роторную обмотку большего сопротивления, но это вызвало бы значительный нагрев обмотки и уменьшение к.п.д. двигателя. Для улучшения пусковых характеристик асинхронных двигателей с короткозамкнутым ротором применяют двигатели с двумя короткозамкнутыми обмотками на роторе и двигатели с глубоким пазом. Двигатель с двумя клетками (короткозамкнутыми обмотками) был предложен Доливо-Добровольским. На роторе такого двигателя помещают две клетки (рис. 257): одну — пусковую, имеющую большое активное сопротивление и малое индуктивное сопротивление, и другую — рабочую, обладающую наоборот, малым активным сопротивлением и большим индуктивным сопротивлением. Стержни пусковой клетки изготовляют обычно из латуни. Материалом рабочей клетки служит медь. Сечение рабочей клетки делается больше сечения пусковой клетки. В результате подбора материала и сечения клеток активное сопротивление пусковой клетки получается в четыре — пять раз больше сопротивления рабочей клетки. Как видно на рис. 257, б, между стержнями пусковой и рабочей обмоток имеется узкая щель, размеры которой определяют индуктивность нижней рабочей клетки. Рассмотрим работу двуклеточного двигателя. Индуктивность рабочей клетки больше, так как она сцеплена с большим числом магнитных линий. В момент пуска двигателя, когда частота токов ротора равна частоте сети, индуктивное сопротивление этой клетки особенно велико. Благодаря этому сдвиг фаз между током рабочей клетки и э.д.с., индуктированной в ней, будет большим, а момент вращения, создаваемый клеткой, — малым. С увеличением скорости двигателя частота токов ротора уменьшается, индуктивное сопротивление клеток оказывает на работу двигателя все меньшее влияние и поэтому распределение токов в клетках определяется только их активным сопротивлением. Но, как было указано выше, активное сопротивление рабочей клетки в несколько раз меньше сопротивления пусковой клетки. Поэтому при нормальной работе двигателя большая часть тока проходит по рабочей клетке и вращающий момент получается преимущественно за счет рабочей клетки. На рис. 258 показана зависимость вращающего момента двигателя с двуклеточным ротором от величины скольжения. На диаграмме кривая 1 показывает изменение момента, создаваемого пусковой обмоткой, кривая 2 — изменение момента, создаваемого рабочей обмоткой. Более простым в изготовлении является ротор, у которого обе клетки заливают алюминием. На рис. 259 показаны внешний вид и частичный разрез ротора с двойной литой алюминиевой клеткой. Двуклеточный двигатель дороже асинхронного двигателя с короткозамкнутым ротором обычной конструкции на 20-30%. Наши заводы изготовляют двуклеточные двигатели от 5 до 2000 квт. Наряду с двуклеточным двигателем применяются двигатели с глубоким пазом (рис. 260). Отношение длины паза к ширине берется в пределах 10-12. Нижняя часть паза сцеплена с большим числом магнитных линий, чем верхняя часть паза. Вследствие этого индуктивное сопротивление нижней части паза больше, чем верхней, в особенности в момент пуска. Это приводит к вытеснению тока ротора в верхнюю часть стержней обмотки. В табл. 11 приведены пусковые характеристики двигателя с короткозамкнутым ротором нормального исполнения, двуклеточного двигателя и двигателя с глубоким пазом. Пусковые свойства даются в виде отношения пускового тока Iп к номинальному току Iн и в виде отношения пускового момента Мn к номинальному моменту Мн. Пуск асинхронных двигателей Пуск асинхронных двигателей можно производить при полном напряжении (прямой пуск) и при пониженном напряжении. Прямой пуск осуществляется при помощи рубильников, переключателей, магнитных пускателей и других пусковых аппаратов. При прямом пуске к двигателю подается полное напряжение сети. Недостатком этого способа пуска являются большие пусковые токи, которые в 2-7 раз больше номинальных токов двигателей. Наиболее простым является прямой пуск асинхронных двигателей с короткозамкнутым ротором. Пуск и остановка таких двигателей производятся включением или отключением рубильника (магнитного пускателя) и т. п. На рис. 261 показана схема прямого пуска асинхронного короткозамкнутого двигателя. Для уменьшения пусковых токов асинхронных двигателей с короткозамкнутым ротором уменьшают напряжение, подводимое к обмоткам статора двигателя. Рассмотрим подробнее способ пуска асинхронных двигателей при пониженном напряжении с помощью переключателя со звезды на треугольник. На рис. 262 дана принципиальная схема включения обмотки статора с переключателем со звезды на треугольник. На рис. 263, а схематически изображена обмотка статора, соединенная при пуске звездой. Пусть напряжение между линейными проводами двигателя равно 380 в, а следовательно, напряжение, приходящееся на фазу двигателя при пуске:
Если полное сопротивление фазной обмотки двигателя равно 10 ом, то ток фазы
При соединении звездой IлΥ = IфΥ. Поэтому ток, потребляемый двигателем из сети будет также равен 22 а. На рис. 263, б схематически показан тот же двигатель, если обмотка его соединена треугольником и включена на линейное напряжение 380 в. В том случае UлΔ = UфΔ, а поэтому ток фазы двигателя при пуске
Так как при соединении треугольником IлΔ = IфΔ√3, то двигатель в этом случае будет потреблять из сети линейный ток IлΔ = 38 ⋅ √3 = 66 а. Как видно из приведенного примера, при пуске линейный ток двигателя при соединении обмоток статора звездой в три раза меньше линейного тока двигателя, статорная обмотка которого соединена треугольником. По этому способу пуска двигателю в начальный момент подается напряжение в √3 раз меньше номинального. Так как момент вращения асинхронного двигателя пропорционален квадрату подводимого напряжения (М ≡ U21), то уменьшение напряжения в √3 раз вызовет уменьшение пускового момента в 3 раза. Поэтому этот способ пуска можно применять только в тех случаях, когда двигатели пускают вхолостую или слабо нагруженными. Само собой разумеется, что переключение обмотки статора со звезды на треугольник при пуске можно применять только для двигателей, нормально работающих по схеме треугольника. Уменьшить напряжение, подводимое к двигателю, а вместе с этим уменьшить пусковой ток двигателя можно также при помощи автотрансформатора. Пуск асинхронных двигателей с фазным ротором производится при помощи пускового реостата, подключаемого к обмотке ротора через кольца и щетки. Перед пуском двигателя нужно убедиться в том, что сопротивление пускового реостата полностью введено. ⇐ Предыдущая12345678910Следующая ⇒ Читайте также: Психологические особенности спортивного соревнования Приготовление дезинфицирующих растворов различной концентрации Занятость населения и рынок труда Социальный статус семьи и её типология | |||||||||||||||||||||||||||
|
|
Последнее изменение этой страницы: 2021-01-14; просмотров: 59; Нарушение авторского права страницы; Мы поможем в написании вашей работы!
infopedia.
|
Вращающий момент отсутствует. Уменьшенный вращающий момент
НЕДОСТАТОЧНЫЙ ВРАЩАЮЩИЙ МОМЕНТ ЭЛЕКТРОДВИГАТЕЛЯ
3. Вращающий момент отсутствует в некоторых положениях ротора
Эта неисправность характеризуется тем, что при включении электродвигателя в сеть ротор занимает устойчивое неподвижное положение. Возможны две причины этого явления: а) неблагоприятное соотношение между числами пазов статора и ротора для данного числа полюсов электродвигателя; б) задевание ротором статора вследствие одностороннего магнитного притяжения.
Первая причина вызывает, как правило, несколько устойчивых неподвижных положений ротора. Если установить ротор в другое положение и повторно включить электродвигатель в сеть, то в большинстве случаев происходит поворот ротора на небольшой угол до следующего устойчивого положения. Описанное явление наблюдается в электродвигателе с короткозамкнутой обмоткой ротора, если с целью получения другой скорости вращения произведена замена обмотки статора и не соблюдено благоприятное соотношение чисел пазов статора и ротора для необходимого числа полюсов. В новых электродвигателях этот недостаток не встречается, так как при изготовлении их подбирают необходимое число пазов статора и ротора или выполняют скос пазов таким образом, чтобы исключить местные силы притяжения между статором и ротором, вызывающие устойчивое неподвижное положение ротора. Устранение этой причины устойчивого неподвижного положения ротора является трудной и не всегда выполнимой задачей. В некоторых случаях удается восстановить удовлетворительные пусковые характеристики электродвигателя, если разрезать в нескольких местах короткозамыкающие кольца или же уменьшить сечение отдельных стержней беличьей клетки ротора. Для более подробных рекомендаций необходимо получить консультации специалиста по электрическим машинам.
Описанное явление наблюдается в электродвигателе с короткозамкнутой обмоткой ротора, если с целью получения другой скорости вращения произведена замена обмотки статора и не соблюдено благоприятное соотношение чисел пазов статора и ротора для необходимого числа полюсов. В новых электродвигателях этот недостаток не встречается, так как при изготовлении их подбирают необходимое число пазов статора и ротора или выполняют скос пазов таким образом, чтобы исключить местные силы притяжения между статором и ротором, вызывающие устойчивое неподвижное положение ротора. Устранение этой причины устойчивого неподвижного положения ротора является трудной и не всегда выполнимой задачей. В некоторых случаях удается восстановить удовлетворительные пусковые характеристики электродвигателя, если разрезать в нескольких местах короткозамыкающие кольца или же уменьшить сечение отдельных стержней беличьей клетки ротора. Для более подробных рекомендаций необходимо получить консультации специалиста по электрическим машинам.
Устойчивое неподвижное положение ротора вследствие одностороннего магнитного притяжения, как правило, вызывается нарушением равномерности зазора между статором и ротором (см. раздел 25).
4. Уменьшенный вращающий момент при низкой скорости вращения ротора
Эта неисправность чаще всего имеет место в асинхронных двигателях с короткозамкнутой обмоткой ротора. Устойчивая скорость вращения при пуске электродвигателя под нагрузкой получается в несколько раз меньше номинальной. В большинстве случаев она составляет 1/7 часть номинальной скорости вращения.
При пуске электродвигателя без нагрузки ротор обычно достигает номинальной скорости вращения и последующая нагрузка двигателя не осложняет его работы.
Указанные затруднения при пуске электродвигателя под нагрузкой обусловлены наличием тормозных моментов, вызванных высшими гармоническими магнитного потока в зазоре между статором и ротором. Кроме первой (основной) гармонической магнитного потока в зазоре имеются и его более высокие нечетные гармонические. В статоре трехфазной обмотки при симметричном трехфазном напряжении на зажимах электродвигателя третья и кратные трем гармонические (девятая, пятнадцатая и т. д.) отсутствуют. Из высших гармонических наибольшее влияние на работу электродвигателя оказывает пятая и седьмая. Пятая и первая гармонические вращаются в противоположные стороны, поэтому создаваемые ими электромагнитные моменты имеют противоположные направления. На рис. 5 электромагнитный момент первой гармонической показан линией 1 и пятой гармонической — линией 3. Седьмая гармоническая вращается в ту же сторону, что и первая гармоническая, но со скоростью в семь раз меньшей скорости вращения первой гармонической. Создаваемый ею электромагнитный момент показан линией 2.
В статоре трехфазной обмотки при симметричном трехфазном напряжении на зажимах электродвигателя третья и кратные трем гармонические (девятая, пятнадцатая и т. д.) отсутствуют. Из высших гармонических наибольшее влияние на работу электродвигателя оказывает пятая и седьмая. Пятая и первая гармонические вращаются в противоположные стороны, поэтому создаваемые ими электромагнитные моменты имеют противоположные направления. На рис. 5 электромагнитный момент первой гармонической показан линией 1 и пятой гармонической — линией 3. Седьмая гармоническая вращается в ту же сторону, что и первая гармоническая, но со скоростью в семь раз меньшей скорости вращения первой гармонической. Создаваемый ею электромагнитный момент показан линией 2.
Рис. 5. Механические характеристики для гармонических составляющих магнитного потока
Из приведенных механических характеристик для различных гармонических магнитного потока следует, что пятая гармоническая магнитного потока оказывает тормозное действие во всем диапазоне скоростей вращения ротора, а седьмая гармоническая увеличивает начальное значение пускового момента, но уменьшает вращающий момент электродвигателя в области скорости вращения ротора выше 1/7 номинальной. Эти тормозные моменты почти не влияют на величину максимального момента электродвигателя, так что нагрузка его при вращающемся роторе не нарушает нормальной работы.
Эти тормозные моменты почти не влияют на величину максимального момента электродвигателя, так что нагрузка его при вращающемся роторе не нарушает нормальной работы.
Так же как и устойчивое неподвижное положение ротора, устойчивая низкая скорость вращения его обычно наблюдается после замены обмотки статора с целью получения другой скорости вращения. Иногда эта неисправность может быть устранена уменьшением шага обмотки статора. Шаг катушки обмотки в этом случае должен быть близким к 0,86 полюсного давления.
В электродвигателях с фазной обмоткой ротора в некоторых случаях наблюдается устойчивая скорость вращения ротора, равная половине номинальной. Эта неисправность вызывается появлением тормозного момента вследствие обрыва одной фазы ротора. Обрыв может быть в обмотке ротора, в проводе, соединяющем щетки с реостатом, и в реостате. Однако более вероятным является нарушение целости соединений отдельных элементов цепи ротора, поэтому прежде всего следует проверить все контакты, в том числе и скользящие, в электродвигателе и в реостате. Место обрыва цепи можно установить одним из описанных ранее способов.
Место обрыва цепи можно установить одним из описанных ранее способов.
5. Уменьшенный вращающий момент
Уменьшение вращающего момента может иметь место у исправного электродвигателя и в случае повреждения одной из фазных обмоток статора при их соединении треугольником. Причины уменьшения вращающего момента у исправного электродвигателя обычно связаны с пониженным напряжением сети и иногда с большим сопротивлением цепи ротора (при фазной обмотке). В этом случае значение тока в линейных проводах одинаково, а уровень шума пониженный. При пониженном напряжении и номинальной нагрузке электродвигателя наблюдается повышенное нагревание его обмотки.
Вращающий момент электродвигателя пропорционален магнитному потоку и току в обмотке ротора. Одновременно с уменьшением напряжения на зажимах электродвигателя уменьшается магнитный поток. Если скорость вращения ротора остается неизменной, то э. д.с. и ток в обмотке ротора также уменьшается. В этих условиях вращающий момент электродвигателя зависит от напряжения во второй степени. Механические характеристики асинхронного двигателя для двух значений напряжения показаны на рис. 6 (1-для номинального, 2-для уменьшенного в 1,73 раза).
Механические характеристики асинхронного двигателя для двух значений напряжения показаны на рис. 6 (1-для номинального, 2-для уменьшенного в 1,73 раза).
Рис 6. Механические характеристики электродвигателя
Уменьшенное напряжение на обмотках электродвигателя может быть и при номинальном напряжении сети в случае ошибочного соединения фазных обмоток статора — звездой вместо треугольника. Например, если двигатель при соединении фазных обмоток треугольником предназначен для включения в сеть 220 В, то при соединении фазных обмоток звездой напряжение на зажимах электродвигателя должно быть 380 В и напряжение сети 220 В будет в 1,73 раза меньше необходимого. В рассмотренном примере максимальный и пусковой моменты электродвигателя уменьшаются в 3 раза и электродвигатель может работать только при значительно уменьшенной нагрузке, так как максимальный вращающий момент становится меньше номинального момента.
Обычно электродвигатель работает в таких условиях, когда нагрузка остается постоянной или мало изменяется, и тогда для создания номинального вращающего момента при пониженном напряжении на зажимах электродвигателя требуется больший ток ротора, увеличение которого происходит за счет уменьшения скорости вращения ротора. Это уменьшение скорости вызывается понижением напряжения сети и зависит от сопротивления цепи ротора. При малом сопротивлении (например, замкнутая накоротко фазная обмотка ротора) уменьшение скорости вращения ротора незначительно, а при большом сопротивлении (например, беличья клетка ротора электродвигателя небольшой мощности) становится очень заметным.
Это уменьшение скорости вызывается понижением напряжения сети и зависит от сопротивления цепи ротора. При малом сопротивлении (например, замкнутая накоротко фазная обмотка ротора) уменьшение скорости вращения ротора незначительно, а при большом сопротивлении (например, беличья клетка ротора электродвигателя небольшой мощности) становится очень заметным.
Увеличенному току в обмотке ротора соответствует увеличенный ток в обмотке статора. С увеличением тока происходит интенсивное преобразование электрической энергии в тепловую в обмотках и значительное повышение их температуры. Таким образом, повышенное нагревание обмоток и уменьшенная скорость вращения ротора при номинальной нагрузке являются косвенными признаками пониженного напряжения на зажимах электродвигателя.
Пониженное напряжение может быть следствием общей большой нагрузки электрической сети. Проверка напряжения производится непосредственным изменением его вольтметром на зажимах электродвигателя. Пределы допускаемого отклонения напряжения указаны в разделе 7.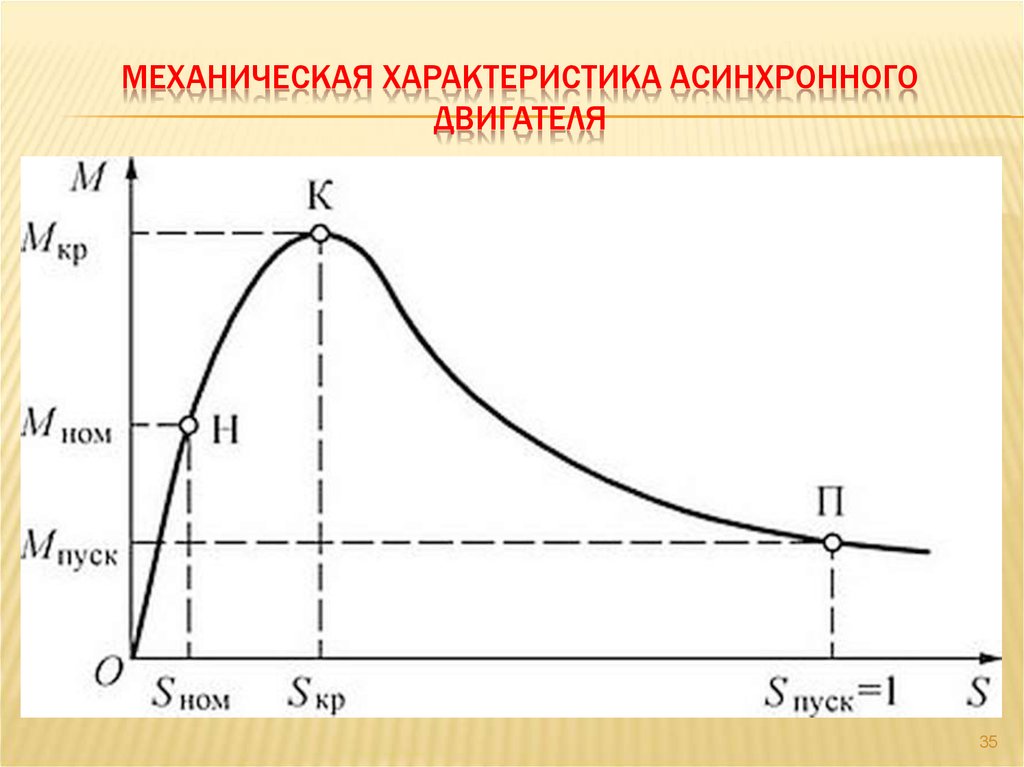
Рис. 7. Расположение выводов фазных обмоток статора и перемычек для соединения: а — звездой, б — треугольником
Если обмотка статора имеет шесть выводных концов, то по внешнему виду соединений фазных обмоток можно определить, звездой или треугольником выполнено соединение. В коробке зажимов выводы обмотки статора располагаются в два ряда, в одном ряду концы обмотки, в другом — их начала (рис. 7). Начала и концы отдельных фазных обмоток смешены относительно друг друга. Для соединения фазных обмоток звездой все зажимы нижнего ряда объединяют перемычками, а зажимы верхнего ряда включают в сеть (рис. 7, а).При соединении треугольником объединяют перемычками попарно зажимы верхнего и нижнего рядов и к общим точкам фазных обмоток подводят провода сети (рис. 7, б).
В некоторых электродвигателях выводы выполнены свободными гибкими проводами, пропущенными через два или три отверстия корпуса. В одном из двух отверстий размещаются начала фазных обмоток, в другом — их концы.
Для соединения Звездой следует объединить выводы одного отверстия в общую точку, а для соединения треугольником необходимо установить принадлежность выводов отдельным фазным обмоткам и соединить попарно выводы из обоих отверстий.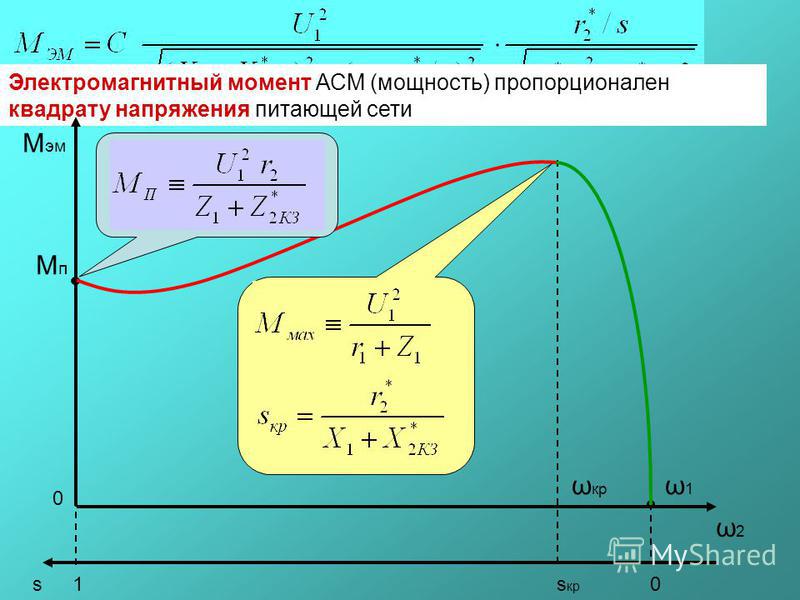 В каждом из трех отверстий размещаются начало и конец разных обмоток. Треугольник получается путем соединения попарно выводов каждого отверстия, а для соединения звездой необходимо установить принадлежность выводов отдельным фазным обмоткам и объединить в общую точку три вывода (по одному из каждого отверстия).
В каждом из трех отверстий размещаются начало и конец разных обмоток. Треугольник получается путем соединения попарно выводов каждого отверстия, а для соединения звездой необходимо установить принадлежность выводов отдельным фазным обмоткам и объединить в общую точку три вывода (по одному из каждого отверстия).
Для постоянной скорости вращения в устойчивой области механической характеристики (от нулевой нагрузки до максимального вращающего момента) при увеличенном активном сопротивлении обмотки ротора получается уменьшенный вращающий момент. Это объясняется тем, что в указанных условиях э.д.с. обмотки ротора остается постоянной и ток уменьшается. Если нагрузочный момент сохраняется постоянным, то при увеличении активного сопротивления цепи ротора должна уменьшаться скорость вращения ротора для сохранения тока неизменным в его обмотке.
Иногда эта закономерность используется для регулирования скорости вращения ротора с фазной обмоткой или для улучшения работы электропривода при кратковременных больших увеличениях нагрузки.
Если повышенное активное сопротивление цепи ротора не предусмотрено схемой электропривода, то вызываемое им уменьшение вращающего момента (или при постоянной нагрузке уменьшение скорости вращения ротора) снижает производительность приводимой электродвигателем машины.
Выявить причину уменьшения вращающего момента можно измерением сопротивления участка цепи ротора, состоящего из соединительных проводов между зажимами электродвигателя и реостатом и остающейся постоянно включенной частью реостата, или же измерением напряжения на этом участке роторной цепи. При измерении напряжения не требуется разъединять цепь ротора.
Для уменьшения сопротивления роторной цепи необходимо приблизить реостат к электродвигателю или увеличить сечение проводов между зажимами ротора и реостата.
Работа электродвигателя в случае обрыва в одной фазной обмотке статора при соединении треугольником сопровождается повышенным шумом и вибрацией. Величина тока в линейных проводах различна, ток в линейном проводе, присоединенном к неповрежденным обмоткам, значительно больше тока в других проводах. Так как энергия подводится только к двум фазным обмоткам, то при номинальной нагрузке электродвигателя ток в неповрежденных фазных обмотках будет больше номинального, что вызовет повышенное нагревание этих обмоток. Температура поврежденной фазной обмотки ниже температуры двух других обмоток, и это может быть использовано для ее выявления, так же как различие тока в линейных проводах. На рис 8, а показано включение электродвигателя в сеть при наличии обрыва в фазной обмотке С2-С5. В этом случае показания амперметров А2 и A3 будет в 1,73 раза меньше, амперметра А1.
Так как энергия подводится только к двум фазным обмоткам, то при номинальной нагрузке электродвигателя ток в неповрежденных фазных обмотках будет больше номинального, что вызовет повышенное нагревание этих обмоток. Температура поврежденной фазной обмотки ниже температуры двух других обмоток, и это может быть использовано для ее выявления, так же как различие тока в линейных проводах. На рис 8, а показано включение электродвигателя в сеть при наличии обрыва в фазной обмотке С2-С5. В этом случае показания амперметров А2 и A3 будет в 1,73 раза меньше, амперметра А1.
Рис. 8. Нахождение обрыва фазной обмотки при помощи: а — ампер метра, б — мегомметра
Проверку обмотки статора можно легко выполнить, если к зажимам электродвигателя выведены шесть концов фазных обмоток. Тогда путем проверки сопротивления отдельных фазных обмоток одним из известных способов, например мегомметром (рис. 8, б) или омметром, можно выявить поврежденную фазную обмотку. При наличии однофазного напряжения 220 В можно воспользоваться вольтметром или лампой накаливания. Если соединения фазных обмоток выполнены внутри электродвигателя, то обрыв можно обнаружить путем измерения сопротивления между зажимами. Из трех измерений две величины сопротивления будут одинаковы, а третья — между зажимами с поврежденной фазной обмоткой — вдвое больше. Можно также поочередно подводить через амперметр однофазное пониженное напряжение к двум из трех зажимов обмотки статора. Ток между зажимами с поврежденной обмоткой будет вдвое меньше тока между другими зажимами.
Если соединения фазных обмоток выполнены внутри электродвигателя, то обрыв можно обнаружить путем измерения сопротивления между зажимами. Из трех измерений две величины сопротивления будут одинаковы, а третья — между зажимами с поврежденной фазной обмоткой — вдвое больше. Можно также поочередно подводить через амперметр однофазное пониженное напряжение к двум из трех зажимов обмотки статора. Ток между зажимами с поврежденной обмоткой будет вдвое меньше тока между другими зажимами.
Если выявлена поврежденная фазная обмотка, то дальнейшее нахождение места обрыва производится, как указано в разделе 2 (см. рис. 4).
Как определить вращающий момент асинхронного двигателя
Содержание
- Механические и электрические характеристики асинхронных электродвигателей
- Вращающий момент электродвигателя
- РАБОЧИЙ ПРОЦЕСС АСИНХРОННОГО ДВИГАТЕЛЯ
- Мощность и вращающий момент электродвигателя. Что это такое?
- Мощность и вращающий момент электродвигателя
- Работа и мощность
- Потребляемая мощность электродвигателя
- Момент электродвигателя
- Нагрузка насосов и типы нагрузки электродвигателя
- Соответствие электродвигателя нагрузке
- Время пуска электрдвигателя
- Число пусков электродвигателя в час
- Мощность и КПД (eta) электродвигателя
- Видео
В данной статье осветим тему механических и электрических характеристик электродвигателей. На примере асинхронного двигателя рассмотрим такие параметры как мощность, работа, КПД, косинус фи, вращающий момент, угловая скорость, линейная скорость и частота. Все эти характеристики оказываются важными при проектировании оборудования, в котором электродвигатели служат в качестве приводных.
На примере асинхронного двигателя рассмотрим такие параметры как мощность, работа, КПД, косинус фи, вращающий момент, угловая скорость, линейная скорость и частота. Все эти характеристики оказываются важными при проектировании оборудования, в котором электродвигатели служат в качестве приводных.
Механические характеристики электродвигателя представляют собой зависимость угловой скорости ω от развиваемого им момента на валу, т.е. ω = f (M). Различают естественные и искусственные механические характеристики электродвигателя.
Естественная механическая характеристика соответствует работе электродвигателя с номинальными параметрами при нормальной схеме включения. Искусственная механическая характеристика соответствует работе электродвигателя с параметрами, отличающимися от номинальных, например, при введении сопротивления, изменении питающего напряжения, частоты и др.
Сегодня особенно широко распространены в промышленности именно асинхронные электродвигатели, поэтому на их характеристиках и остановимся.
Естественная механическая характеристика асинхронного двигателя
Для примера рассмотрим АИР80В2У3.
Номинальная механическая мощность асинхронного электродвигателя
На шильдике (на паспортной табличке) электродвигателя указывается всегда номинальная механическая мощность на валу данного двигателя. Это не та электрическая мощность, которую данный электродвигатель потребляет из сети.
Так, например, для двигателя АИР80В2У3, номинал в 2200 ватт соответствует именно механической мощности на валу. То есть в оптимальном рабочем режиме данный двигатель способен выполнять механическую работу 2200 джоулей каждую секунду. Обозначим эту мощность как P1 = 2200 Вт.
Номинальная активная электрическая мощность асинхронного электродвигателя
Чтобы определить номинальную активную электрическую мощность асинхронного электродвигателя, опираясь на данные с шильдика, необходимо принять в расчет КПД. Так, для данного электродвигателя КПД составляет 83%.
Что это значит? Это значит, что только часть активной мощности, подаваемой из сети на обмотки статора двигателя, и безвозвратно потребляемой двигателем, преобразуется в механическую мощность на валу. Активная мощность равна P = P1/КПД. Для нашего примера, по представленному шильдику видим, что P1 = 2200, КПД = 83%. Значит P = 2200/0,83 = 2650 Вт.
Номинальная полная электрическая мощность асинхронного электродвигателя
Полная электрическая мощность, подаваемая на статор электродвигателя от сети всегда больше механической мощности на валу и больше активной мощности, безвозвратно потребляемой электродвигателем.
Для нахождения полной мощности достаточно активную мощность разделить на косинус фи. Таким образом, полная мощность S = P/Cosφ. Для нашего примера P = 2650 Вт, Cosφ = 0,87. Следовательно полная мощность S = 2650/0,87 = 3046 ВА.
Номинальная реактивная электрическая мощность асинхронного электродвигателя
Часть полной мощности, подаваемой на обмотки статора асинхронного электродвигателя, возвращается в сеть. Это реактивная мощность Q.
Это реактивная мощность Q.
Реактивная мощность связана с полной мощностью через sinφ, и связана с активной и с полной мощностью через квадратный корень. Для нашего примера:
Реактивная мощность Q измеряется в ВАР — в вольт-амперах реактивных.
Теперь давайте рассмотрим механические характеристики нашего асинхронного двигателя: номинальный рабочий момент на валу, угловую скорость, линейную скорость, частоту вращения ротора и ее связь с частотой питания электродвигателя.
Частота вращения ротора асинхронного электродвигателя
На шильдике мы видим, что при питании переменным током частотой в 50 Гц, ротор двигателя совершает при номинальной нагрузке 2870 оборотов в минуту, обозначим эту частоту как n1.
Что это значит? Поскольку магнитное поле в обмотках статора создается переменным током частотой 50 Гц, то для двигателя с одной парой полюсов (коим является АИР80В2У3) частота «вращения» магнитного поля, синхронная частота n, оказывается равной 3000 оборотов в минуту, что тождественно 50 оборотам в секунду.
Значение s можно определить, разделив разность синхронной и асинхронной частот на синхронную частоту, и выразив это значение в процентах:
Для нашего примера s = ( (3000 – 2870)/3000 ) *100% = 4,3%.
Угловая скорость асинхронного двигателя
Угловая скорость ω выражается в радианах в секунду. Для определения угловой скорости достаточно частоту вращения ротора n1 перевести в обороты в секунду (f), и умножить на 2 Пи, поскольку один полный оборот составляет 2 Пи или 2*3,14159 радиан. Для двигателя АИР80В2У3 асинхронная частота n1 составляет 2870 оборотов в минуту, что соответствует 2870/60 = 47,833 оборотам в секунду.
Умножая на 2 Пи, имеем: 47,833*2*3,14159 = 300,543 рад/с. Можно перевести в градусы, для этого вместо 2 Пи подставить 360 градусов, тогда для нашего примера получится 360*47,833 = 17220 градусов в секунду. Однако подобные расчеты обычно ведут именно в радианах в секунду. Поэтому угловая скорость ω = 2*Пи*f, где f = n1/60.
Линейная скорость асинхронного электродвигателя
Линейная скорость v относится к оборудованию, на котором асинхронный двигатель установлен в качестве привода. Так, если на вал двигателя установлен шкив или, скажем, наждачный диск, известного радиуса R, то линейная скорость точки на краю шкива или диска может быть найдена по формуле:
Номинальный вращающий момент асинхронного двигателя
Каждый асинхронный электродвигатель характеризуется номинальным вращающим моментом Мн. Вращающий момент М связан с механической мощностью P1 через угловую скорость следующим образом:
Вращающий момент или момент силы, действующей на определенном расстоянии от центра вращения, для двигателя сохраняется, причем с ростом радиуса уменьшается сила, а чем радиус меньше, тем больше сила, поскольку:
Так, чем больше радиус шкива, тем меньшая сила действует на его краю, а наибольшая сила действует непосредственно на валу электродвигателя.
Для приведенного в качестве примера двигателя АИР80В2У3 мощность P1 равна 2200 Вт, а частота n1 равна 2870 оборотов в минуту или f = 47,833 оборота в секунду. Следовательно угловая скорость составляет 2*Пи*f, то есть 300,543 рад/с, и номинальный вращающий момент Мн равен P1/(2*Пи*f). Мн = 2200/(2*3,14159*47,833) = 7,32 Н*м.
Таким образом, исходя из данных, указанных на шильдике асинхронного электродвигателя, можно найти все основные электрические и механические его параметры.
Надеемся, что данная статья помогла вам разобраться в том, как связаны между собой угловая скорость, частота, вращающий момент, активная, полезная и полная мощность, а также КПД электродвигателя.
Источник
Вращающий момент электродвигателя
В двигателях постоянного тока вращающий момент определяется выражением М ≡ ФIя, т.е. он пропорционален потоку и току якоря. В асинхронном двигателе момент создается вращающимся потоком Ф и током ротора I2. Он может быть выражен
Он может быть выражен
Следовательно, момент пропорционален потоку и активной слагающей тока ротора I2 cos Ψ2, так как только активная слагающая тока определяет мощность, а значит и момент.
На рис. 10-20 представлена схема включения короткозамкнутого двигателя. Если пустить двигатель, включив рубильник 1, то в первый момент пуска, когда п2= 0, a s = 1, наведенная в роторе 2 э. д. с. Е2 и пусковой ток I2п максимальны. Однако, пусковой момент Мп не будет максимальным, а в 2—2,5 раза меньше максимального. Векторная диаграмма для цепи ротора (рис. 10-21), построенная подобно изображенной на рис. 9-9, показывает причину этого.
Рис 10-20. Схема включения короткозамкнутого асинхронного двигателя.
Обычно в роторе х2во много раз больше r2 и угол Ψ2, на который ток I2п отстает от э. д. с. Е2 велик. Поэтому активная слагающая тока I2п cos Ψ2, а значит и пусковой момент Мп малы. В современных асинхронных двигателях Мп/Мп = 1 — 1,5, хотя I2п/ Iн≈ 4,5—6,5.
д. с. Е2 велик. Поэтому активная слагающая тока I2п cos Ψ2, а значит и пусковой момент Мп малы. В современных асинхронных двигателях Мп/Мп = 1 — 1,5, хотя I2п/ Iн≈ 4,5—6,5.
Это же явление по другому объясняется на рис. 10-19 и 10-22.
Рис. 10-21. Векторная диаграмма в цепи ротора.
При описании принципа работы двигателя (рис. 10-19) было предположено, что ток I2 совпадает по фазе с э. д. с. Е2, т. е. что он активный ( Ψ2 = 0). На рис. 10-22 представлен момент пуска, когда направление э. д. с. в проводах ротора соответствует обозначенному на рис. 10-19, а ток показан отстающим от э. д. с. на угол Ψ2. Тогда шесть проводов ротора (три под полюсом N и три под полюсом S) создают усилия, действующие в направлении вращения потока, а два провода вызывают противодействующие усилия. В результате этого вращающий момент будет тем меньше, чем больше сдвиг фаз между током I2 и э. д. с. E2.
В результате этого вращающий момент будет тем меньше, чем больше сдвиг фаз между током I2 и э. д. с. E2.
Рис. 10-22. Ток в роторе двигателя в момент пуска.
По мере увеличения скорости вращения ротора реактивное сопротивление обмотки ротора x2s = x2s уменьшается, а вместе с этим уменьшается угол Ψ2, так как сопротивление r2≈ const. Наступает такое положение (рис 10-21), когда при некотором скольжении sм ≈ 0,1—0,15 реактивное сопротивление x2s становится равным активному r2, угол Ψ — 45° и э. д. с. E2s уравновешивает два равных падения напряжения I 2r2 и I2x2s.В это время активная слагающая тока I2 cos Ψ2 и вращающий момент М м становятся максимальными, несмотря на некоторое уменьшение тока I2.
Обычно Мм/Мм = 1,8—2,5 и называется способностью к перегрузкe.
При дальнейшем разгоне ротора x2s становится значительно меньшим, чем r2, им можно пренебречь и считать ток ротора активным (I2 ≈ I2 cos Ψ 2). Так как E2s= E2s тоже продолжает уменьшаться, то вместе с током I2 уменьшается и вращающий момент.
Рис. 10-23. Зависимость вращающего момента двигателя от скольжения.
Нормальная работа двигателя возможна только на участке кривой при скольжениях s от нуля до sм, так как в этом случае при увеличении тормозного момента и значит s вращающий момент возрастает. На участке от s = sм до s = 1 работа двигателя неустойчива. Номинальный момент Мн соответствует обычно номинальному скольжению sн = 1—6%.
Поток Ф пропорционален напряжению U1, подводимому к трансформатору. Сказанное остается в силе и для асинхронного двигателя. Так как М ≡ ФI2 cos Ψ 2, то можно написать, что
Отсюда можно сделать очень важный для асинхронных двигателей вывод
т. е. вращающий момент пропорционален квадрату подведенного к статору напряжения. Таким образом, падение напряжения в сети, например до 0,9 U1н, вызовет уменьшение момента до 0,9 • 0,9 Мн= 0,81 Мн и нагруженный двига тель может остановиться. Указанным обстоятельством и объясняется, частично, нормирование падения напряжения в распределительных сетях, питающих асинхронные двигатели.
В практике потребителя часто интересует механическая характеристика двигателя
Рис. 10-24. Механическая характеристика двигателя.
Эта характеристика получается простым перестроением рис, 10-23 и показана на рис. 10-24, где рабочая часть обозначена сплошной линией. Кривая 1 для двига телей нормального исполнения показывает, что асинхронный двигатель обладает жесткой характеристикой скорости, подобно двигателю постоянного тока параллельного возбуждения. Асинхронный двигатель с фазным ротором для регулирования скорости вращения, например для крановых и подъемных устройств, имеет более мягкую характеристику (кривая 2).
Кривая 1 для двига телей нормального исполнения показывает, что асинхронный двигатель обладает жесткой характеристикой скорости, подобно двигателю постоянного тока параллельного возбуждения. Асинхронный двигатель с фазным ротором для регулирования скорости вращения, например для крановых и подъемных устройств, имеет более мягкую характеристику (кривая 2).
РАБОЧИЙ ПРОЦЕСС АСИНХРОННОГО ДВИГАТЕЛЯ
рону н. с. со скоростью n2. Тогда скорость вращения н. с F2 относительно статора равна:
Таким образом, обе н. с. F1 и F2 вращаются с одной скоростью n1, друг относительно друга неподвижны и создают сообща вращающийся магнитный поток Ф. Следовательно, все приведенное на рис. 9-8 и 9-9 справедливо и для асинхронного двигателя.
Следует отметить, что благодаря воздушному зазору между ротором и статором ток холостого хода (рис. 9-7) двигателя очень велик (20—40)% I1Н. Поэтому для улучшения cos φ1 сети двигатель необходимо нагружать полностью.
Поэтому для улучшения cos φ1 сети двигатель необходимо нагружать полностью.
Статья на тему Вращающий момент электродвигателя
Источник
Мощность и вращающий момент электродвигателя
Данная глава посвящена вращающему моменту: что это такое, для чего он нужен и др. Мы также разберём типы нагрузок в зависимости от моделей насосов и соответствие между электродвигателем и нагрузкой насоса.
Вы когда-нибудь пробовали провернуть вал пустого насоса руками? Теперь представьте, что вы поворачиваете его, когда насос заполнен водой. Вы почувствуете, что в этом случае, чтобы создать вращающий момент, требуется гораздо большее усилие.
А теперь представьте, что вам надо крутить вал насоса несколько часов подряд. Вы бы устали быстрее, если бы насос был заполнен водой, и почувствовали бы, что потратили намного больше сил за тот же период времени, чем при выполнении тех же манипуляций с пустым насосом. Ваши наблюдения абсолютно верны: требуется большая мощность, которая является мерой работы (потраченной энергии) в единицу времени. Как правило, мощность стандартного электродвигателя выражается в кВт.
Как правило, мощность стандартного электродвигателя выражается в кВт.
Работа и мощность
Если мы говорим о вращении, мощность выражается как вращающий момент (T), умноженный на частоту вращения (w).
Частота вращения объекта определяется измерением времени, за которое определённая точка вращающегося объекта совершит полный оборот. Обычно эта величина выражается в оборотах в минуту, т.е. мин-1 или об/мин. Например, если объект совершает 10 полных оборотов в минуту, это означает, что его частота вращения: 10 мин-1 или 10 об/мин.
Итак, частота вращения измеряется в оборотах в минуту, т.е. мин-1.
Приведем единицы измерения к общему виду.
Для наглядности возьмём разные электродвигатели, чтобы более подробно проанализировать соотношение между мощностью, вращающим моментом и частотой вращения. Несмотря на то, что вращающий момент и частота вращения электродвигателей сильно различаются, они могут иметь одинаковую мощность.
Например, предположим, что у нас 2-полюсный электродвигатель (с частотой вращения 3000 мин-1) и 4-полюсной электродвигатель (с частотой вращения 1500 мин-1). Мощность обоих электродвигателей 3,0 кВт, но их вращающие моменты отличаются.
Таким образом, вращающий момент 4-полюсного электродвигателя в два раза больше вращающего момента двухполюсного электродвигателя с той же мощностью.
Как образуется вращающий момент и частота вращения?
Теперь, после того, как мы изучили основы вращающего момента и скорости вращения, следует остановиться на том, как они создаются.
В электродвигателях переменного тока вращающий момент и частота вращения создаются в результате взаимодействия между ротором и вращающимся магнитным полем. Магнитное поле вокруг обмоток ротора будет стремиться к магнитному полю статора. В реальных рабочих условиях частота вращения ротора всегда отстаёт от магнитного поля. Таким образом, магнитное поле ротора пересекает магнитное поле статора и отстает от него и создаёт вращающий момент. Разницу в частоте вращения ротора и статора, которая измеряется в %, называют скоростью скольжения.
Разницу в частоте вращения ротора и статора, которая измеряется в %, называют скоростью скольжения.
Скольжение является основным параметром электродвигателя, характеризующий его режим работы и нагрузку. Чем больше нагрузка, с которой должен работать электродвигатель, тем больше скольжение.
Помня о том, что было сказано выше, разберём ещё несколько формул. Вращающий момент индукционного электродвигателя зависит от силы магнитных полей ротора и статора, а также от фазового соотношения между этими полями. Это соотношение показано в следующей формуле:
Сила магнитного поля, в первую очередь, зависит от конструкции статора и материалов, из которых статор изготовлен. Однако напряжение и частота тока также играют важную роль. Отношение вращающих моментов пропорционально квадрату отношения напряжений, т.е. если подаваемое напряжение падает на 2%, вращающий момент, следовательно, уменьшается на 4%.
Потребляемая мощность электродвигателя
Ток ротора индуцируется через источник питания, к которому подсоединён электродвигатель, а магнитное поле частично создаётся напряжением. Входную мощность можно вычислить, если нам известны данные источника питания электродвигателя, т.е. напряжение, коэффициент мощности, потребляемый ток и КПД.
Входную мощность можно вычислить, если нам известны данные источника питания электродвигателя, т.е. напряжение, коэффициент мощности, потребляемый ток и КПД.
В Европе мощность на валу обычно измеряется в киловаттах. В США мощность на валу измеряется в лошадиных силах (л.с.).
Если вам необходимо перевести лошадиные силы в киловатты, просто умножьте соответствующую величину (в лошадиных силах) на 0,746. Например, 20 л.с. равняется (20 • 0,746) = 14,92 кВт.
И наоборот, киловатты можно перевести в лошадиные силы умножением величины в киловаттах на 1,341. Это значит, что 15 кВт равняется 20,11 л.с.
Момент электродвигателя
Мощность [кВт или л.с.] связывает вращающий момент с частотой вращения, чтобы определить общий объём работы, который должен быть выполнен за определённый промежуток времени.
Рассмотрим взаимодействие между вращающим моментом, мощностью и частотой вращения, а также их связь с электрическим напряжением на примере электродвигателей Grundfos. Электродвигатели имеют одну и ту же номинальную мощность как при 50 Гц, так и при 60 Гц.
Электродвигатели имеют одну и ту же номинальную мощность как при 50 Гц, так и при 60 Гц.
Это влечёт за собой резкое снижение вращающего момента при 60 Гц: частота 60 Гц вызывает 20%-ное увеличение числа оборотов, что приводит к 20%-ному уменьшению вращающего момента. Большинство производителей предпочитают указывать мощность электродвигателя при 60 Гц, таким образом, при снижении частоты тока в сети до 50 Гц электродвигатели будут обеспечивать меньшую мощность на валу и вращающий момент. Электродвигатели обеспечивают одинаковую мощность при 50 и 60 Гц.
Графическое представление вращающего момента электродвигателя изображено на рисунке.
Иллюстрация представляет типичную характеристику вращающий момент/частота вращения. Ниже приведены термины, используемые для характеристики вращающего момента электродвигателя переменного тока.
Пусковой момент (Мп): Механический вращающий момент, развиваемый электродвигателем на валу при пуске, т.е. когда через электродвигатель пропускается ток при полном напряжении, при этом вал застопорен.
Минимальный пусковой момент (Ммин): Этот термин используется для обозначения самой низкой точки на кривой вращающий момент/частота вращения электродвигателя, нагрузка которого увеличивается до полной скорости вращения. Для большинства электродвигателей Grundfos величина минимального пускового момента отдельно не указывается, так как самая низкая точка находится в точке заторможенного ротора. В результате для большинства электродвигателей Grundfos минимальный пусковой момент такой же, как пусковой момент.
Вращающий момент при полной нагрузке (Мп.н.): Вращающий момент, необходимый для создания номинальной мощности при полной нагрузке.
Нагрузка насосов и типы нагрузки электродвигателя
Выделяют следующие типы нагрузок:
Постоянная мощность
Термин «постоянная мощность» используется для определённых типов нагрузки, в которых требуется меньший вращающий момент при увеличении скорости вращения, и наоборот. Нагрузки при постоянной мощности обычно применяются в металлообработке, например, сверлении, прокатке и т. п.
п.
Постоянный вращающий момент
Переменный вращающий момент и мощность
Вся остальная часть данного раздела будет посвящена исключительно переменному вращающему моменту и мощности.
Определив, что для центробежных насосов типичным является переменный вращающий момент, мы должны проанализировать и оценить некоторые характеристики центробежного насоса. Использование приводов с переменной частотой вращения обусловлено особыми законами физики. В данном случае это законы подобия, которые описывают соотношение между разностями давления и расходами.
Во-первых, подача насоса прямо пропорциональна частоте вращения. Это означает, что если насос будет работать с частотой вращения на 25% больше, подача увеличится на 25%.
Во-вторых, напор насоса будет меняться пропорционально квадрату изменения скорости вращения. Если частота вращения увеличивается на 25%, напор возрастает на 56%.
В-третьих, что особенно интересно, мощность пропорциональна кубу изменения скорости вращения. Это означает, что если требуемая частота вращения уменьшается на 50%, это равняется 87,5%-ному уменьшению потребляемой мощности.
Это означает, что если требуемая частота вращения уменьшается на 50%, это равняется 87,5%-ному уменьшению потребляемой мощности.
Итак, законы подобия объясняют, почему использование приводов с переменной частотой вращения более целесообразно в тех областях применения, где требуются переменные значения расхода и давления. Grundfos предлагает ряд электродвигателей со встроенным частотным преобразователем, который регулирует частоту вращения для достижения именно этой цели.
Так же как подача, давление и мощность, потребная величина вращающего момента зависит от скорости вращения.
Это можно проиллюстрировать на примере характеристики вращающий момент/частота вращения, которую мы использовали ранее, когда рассказывали о вращающем моменте электродвигателя:
Когда электродвигатель набирает скорость от нуля до номинальной скорости, вращающий момент может значительно меняться. Величина вращающего момента, необходимая при определённой нагрузке, также изменяется с частотой вращения. Чтобы электродвигатель подходил для определённой нагрузки, необходимо чтобы величина вращающего момента электродвигателя всегда превышала вращающий момент, необходимый для данной нагрузки.
Чтобы электродвигатель подходил для определённой нагрузки, необходимо чтобы величина вращающего момента электродвигателя всегда превышала вращающий момент, необходимый для данной нагрузки.
В примере, центробежный насос при номинальной нагрузке имеет вращающий момент, равный 70 Нм, что соответствует 22 кВт при номинальной частоте вращения 3000 мин-1. В данном случае насосу при пуске требуется 20% вращающего момента при номинальной нагрузке, т.е. приблизительно 14 Нм. После пуска вращающий момент немного падает, а затем, по мере того, как насос набирает скорость, увеличивается до величины полной нагрузки.
Очевидно, что нам необходим насос, который будет обеспечивать требуемые значения расход/напор (Q/H). Это значит, что нельзя допускать остановок электродвигателя, кроме того, электродвигатель должен постоянно ускоряться до тех пор, пока не достигнет номинальной скорости. Следовательно, необходимо, чтобы характеристика вращающего момента совпадала или превышала характеристику нагрузки на всём диапазоне от 0% до 100% скорости вращения. Любой «избыточный» момент, т.е. разница между кривой нагрузки и кривой электродвигателя, используется как ускорение вращения.
Любой «избыточный» момент, т.е. разница между кривой нагрузки и кривой электродвигателя, используется как ускорение вращения.
Соответствие электродвигателя нагрузке
Если нужно определить, отвечает ли вращающий момент определённого электродвигателя требованиям нагрузки, Вы можете сравнить характеристики скорости вращения/вращающего момента электродвигателя с характеристикой скорости вращения/ вращающего момента нагрузки. Вращающий момент, создаваемый электродвигателем, должен превышать потребный для нагрузки вращающий момент, включая периоды ускорения и полной скорости вращения.
Характеристика зависимости вращающего момента от скорости вращения стандартного электродвигателя и центробежного насоса.
Когда двигатель приближается к своему номинальному значению скорости вращения, ток снижается. Как и следовало ожидать, во время начального периода пуска потери на электродвигателе высоки, поэтому этот период не должен быть продолжительным, чтобы не допустить перегрева.
Очень важно, чтобы максимальная скорость вращения достигалась как можно точнее. Это связано с потребляемой мощностью: например, увеличение скорости вращения на 1% по сравнению со стандартным максимумом приводит к 3%-ному увеличению потребляемой мощности.
Потребляемая мощность пропорциональна диаметру рабочего колеса насоса в четвертой степени.
Уменьшение диаметра рабочего колеса насоса на 10% приводит к уменьшению потребляемой мощности на (1- (0.9 * 0.9 * 0.9 * 0.9)) * 100 = 34%, что равно 66% номинальной мощности. Эта зависимость определяется исключительно на практике, так как зависит от типа насоса, конструкции рабочего колеса и от того, насколько вы уменьшаете диаметр рабочего колеса.
Время пуска электрдвигателя
Если нам необходимо подобрать типоразмер электродвигателя для определённой нагрузки, например для центробежных насосов, основная наша задача состоит в том, чтобы обеспечить соответствующий вращающий момент и мощность в номинальной рабочей точке, потому что пусковой момент для центробежных насосов довольно низкий. Время пуска достаточно ограниченно, так как вращающий момент довольно высокий.
Время пуска достаточно ограниченно, так как вращающий момент довольно высокий.
Нередко для сложных систем защиты и контроля электродвигателей требуется некоторое время для их пуска, чтобы они могли замерить пусковой ток электродвигателя. Время пуска электродвигателя и насоса рассчитывается с помощью следующей формулы:
tпуск = время, необходимое электродвигателю насоса, чтобы достичь частоты вращения при полной нагрузке
n = частота вращения электродвигателя при полной нагрузке
Iобщ = инерция, которая требует ускорения, т.е. инерция вала электродвигателя, ротора, вала насоса и рабочих колёс.
Момент инерции для насосов и электродвигателей можно найти в соответствующих технических данных.
Мизб = избыточный момент, ускоряющий вращение. Избыточный момент равен вращающему моменту электродвигателя минус вращающий момент насоса при различных частотах вращения.
Мизб можно рассчитать по следующим формулам:
Как видно из приведённых вычислений, выполненных для данного примера с электродвигателем мощностью 4 кВт насоса CR, время пуска составляет 0,11 секунды.
Число пусков электродвигателя в час
Современные сложные системы управления электродвигателями могут контролировать число пусков в час каждого конкретного насоса и электродвигателя. Необходимость контроля этого параметра состоит в том, что каждый раз, когда осуществляется пуск электродвигателя с последующим ускорением, отмечается высокое потребление пускового тока. Пусковой ток нагревает электродвигатель. Если электродвигатель не остывает, продолжительная нагрузка от пускового тока значительно нагревает обмотки статора электродвигателя, что приводит к выходу из строя электродвигателя или сокращению срока службы изоляции.
Обычно за количество пусков, которое может выполнить электродвигатель в час, отвечает поставщик электродвигателя. Например, Grundfos указывает максимальное число пусков в час в технических данных на насос, так как максимальное количество пусков зависит от момента инерции насоса.
Мощность и КПД (eta) электродвигателя
Существует прямая связь между мощностью, потребляемой электродвигателем от сети, мощностью на валу электродвигателя и гидравлической мощностью, развиваемой насосом.
При производстве насосов используются следующие обозначения этих трёх различных типов мощности.
Р3 (кВт) Входная мощность насоса = P2, при условии, что соединительная муфта между валами насоса и электродвигателя не рассеивает энергию.
Источник
Видео
4 5 Электромагнитный момент и механическая характеристика асинхронного двигателя
как определить число полюсов асинхронного двигателя или шпинделя чпу
Электрические машины, часть 4. Характеристики асинхронных двигателей
Крутящий момент. Что это такое и зависит ли от мощности?
Определение начала и конца обмоток трехфазного электродвигателя (простой способ)
Асинхронный двигатель. Определение полюсов. Лекция №11
Определение схемы обмоток и рабочего напряжения асинхронного электродвигателя
Обрыв стержней ротора асинхронного двигателя.mp4
Принцип работы асинхронного электродвигателя
Как найти начало и конец обмоток асинхронного электродвигателя. Определить полярность обмоток.
Как рассчитать крутящий момент электродвигателя
- Полезное
- Справочная информация
- Крутящий момент электродвигателя – расчет, формула, таблица
Крутящий момент электродвигателя – это сила вращения его вала. Именно момент вращения определяет мощность Вашего двигателя. Измеряется в ньютонах на метр Н*м или в килограмм-силах на метр кгс*м.
Виды крутящих моментов:
- Номинальный – значение момента при стандартном режиме работы и стандартной номинальной нагрузке на двигатель.
- Пусковой – это табличное значение. Сила вращения, которую в состоянии развивать электродвигатель при пуске. При подборе электродвигателя убедитесь, что данный параметр выше, чем статический момент Вашего оборудования — насоса, либо вентилятора и т.д. В противном случае электродвигатель не сможет запуститься, что чревато перегревом и перегоранием обмотки.

- Максимальный – предельное значение, по достижении которого нагрузка уравновесит двигатель и остановит его.
В данной таблице собраны крутящие моменты наиболее распространенных в Украине электродвигателей АИР, а также требуемый при пуске – пусковой, максимально допустимый для данного типа электродвигателя – максимальный крутящий момент и момент инерции двигателей АИР (усилие важное при подборе электромагнитного тормоза, например)
Мощности асинхронных электродвигателей:
| Двигатель | кВт/об | Мном, Нм | Мпуск, Нм | Ммакс, Нм | Минн, Нм |
| АИР56А2 | 0,18/2730 | 0,630 | 1,385 | 1,385 | 1,133 |
| АИР56В2 | 0,25/2700 | 0,884 | 1,945 | 1,945 | 1,592 |
| АИР56А4 | 0,12/1350 | 0,849 | 1,868 | 1,868 | 1,528 |
| АИР56В4 | 0,18/1350 | 1,273 | 2,801 | 2,801 | 2,292 |
| АИР63А2 | 0,37/2730 | 1,294 | 2,848 | 2,848 | 2,330 |
| АИР63В2 | 0,55/2730 | 1,924 | 4,233 | 4,233 | 3,463 |
| АИР63А4 | 0,25/1320 | 1,809 | 3,979 | 3,979 | 3,256 |
| АИР63В4 | 0,37/1320 | 2,677 | 5,889 | 5,889 | 4,818 |
| АИР63А6 | 0,18/860 | 1,999 | 4,397 | 4,397 | 3,198 |
| АИР63В6 | 0,25/860 | 2,776 | 6,108 | 6,108 | 4,442 |
| АИР71А2 | 0,75/2820 | 2,540 | 6,604 | 6,858 | 4,064 |
| АИР71В2 | 1,1/2800 | 3,752 | 8,254 | 9,004 | 6,003 |
| АИР71А4 | 0,55/1360 | 3,862 | 8,883 | 9,269 | 6,952 |
| АИР71В4 | 0,75/1350 | 5,306 | 13,264 | 13,794 | 12,733 |
| АИР71А6 | 0,37/900 | 3,926 | 8,245 | 8,637 | 6,282 |
| АИР71В6 | 0,55/920 | 5,709 | 10,848 | 12,560 | 9,135 |
| АИР71В8 | 0,25/680 | 3,511 | 5,618 | 6,671 | 4,915 |
| АИР80А2 | 1,5/2880 | 4,974 | 10,943 | 12,932 | 8,953 |
| АИР80В2 | 2,2/2860 | 7,346 | 15,427 | 19,100 | 13,223 |
| АИР80А4 | 1,1/1420 | 7,398 | 16,275 | 17,755 | 12,576 |
| АИР80В4 | 1,5/1410 | 10,160 | 22,351 | 24,383 | 17,271 |
| АИР80А6 | 0,75/920 | 7,785 | 16,349 | 17,128 | 12,457 |
| АИР80В6 | 1,1/920 | 11,418 | 25,121 | 26,263 | 20,553 |
| АИР80А8 | 0,37/680 | 5,196 | 10,393 | 11,952 | 7,275 |
| АИР80В8 | 0,55/680 | 7,724 | 15,449 | 16,221 | 10,814 |
| АИР90L2 | 3/2860 | 10,017 | 23,040 | 26,045 | 17,030 |
| АИР90L4 | 2,2/1430 | 14,692 | 29,385 | 35,262 | 29,385 |
| АИР90L6 | 1,5/940 | 15,239 | 30,479 | 35,051 | 28,955 |
| АИР90LА8 | 0,75/700 | 10,232 | 15,348 | 20,464 | 15,348 |
| АИР90LВ8 | 1,1/710 | 14,796 | 22,194 | 32,551 | 22,194 |
| АИР100S2 | 4/2850 | 13,404 | 26,807 | 32,168 | 21,446 |
| АИР100L2 | 5,5/2850 | 18,430 | 38,703 | 44,232 | 29,488 |
| АИР100S4 | 3/1410 | 20,319 | 40,638 | 44,702 | 32,511 |
| АИР100L4 | 4/1410 | 27,092 | 56,894 | 65,021 | 43,348 |
| АИР100L6 | 2,2/940 | 22,351 | 42,467 | 49,172 | 35,762 |
| АИР100L8 | 1,5/710 | 20,176 | 32,282 | 40,352 | 30,264 |
| АИР112М2 | 7,5/2900 | 24,698 | 49,397 | 54,336 | 39,517 |
| АИР112М4 | 5,5/1430 | 36,731 | 73,462 | 91,827 | 58,769 |
| АИР112МА6 | 3/950 | 30,158 | 60,316 | 66,347 | 48,253 |
| АИР112МВ6 | 4/950 | 40,211 | 80,421 | 88,463 | 64,337 |
| АИР112МА8 | 2,2/700 | 30,014 | 54,026 | 66,031 | 42,020 |
| АИР112МВ8 | 3/700 | 40,929 | 73,671 | 90,043 | 57,300 |
| АИР132М2 | 11/2910 | 36,100 | 57,759 | 79,419 | 43,320 |
| АИР132S4 | 7,5/1440 | 49,740 | 99,479 | 124,349 | 79,583 |
| АИР132М4 | 11/1450 | 72,448 | 173,876 | 210,100 | 159,386 |
| АИР132S6 | 5,5/960 | 54,714 | 109,427 | 120,370 | 87,542 |
| АИР132М6 | 7,5/950 | 75,395 | 150,789 | 165,868 | 120,632 |
| АИР132S8 | 4/700 | 54,571 | 98,229 | 120,057 | 76,400 |
| АИР132М8 | 5,5/700 | 75,036 | 135,064 | 165,079 | 105,050 |
| АИР160S2 | 15/2940 | 48,724 | 97,449 | 155,918 | 2,046 |
| АИР160М2 | 18,5/2940 | 60,094 | 120,187 | 192,299 | 2,884 |
| АИР180S2 | 22/2940 | 71,463 | 150,071 | 250,119 | 4,288 |
| АИР180М2 | 30/2940 | 97,449 | 214,388 | 341,071 | 6,821 |
| АИР200М2 | 37/2950 | 119,780 | 275,493 | 383,295 | 16,769 |
| АИР200L2 | 45/2940 | 146,173 | 380,051 | 584,694 | 19,003 |
| АИР225М2 | 55/2955 | 177,750 | 408,824 | 710,998 | 35,550 |
| АИР250S2 | 75/2965 | 241,568 | 628,078 | 966,273 | 84,549 |
| АИР250М2 | 90/2960 | 290,372 | 784,003 | 1161,486 | 116,149 |
| АИР280S2 | 110/2960 | 354,899 | 887,247 | 1171,166 | 212,939 |
| АИР280М2 | 132/2964 | 425,304 | 1233,381 | 1488,563 | 297,713 |
| АИР315S2 | 160/2977 | 513,268 | 1231,844 | 1693,786 | 590,259 |
| АИР315М2 | 200/2978 | 641,370 | 1603,425 | 2116,521 | 962,055 |
| АИР355SMA2 | 250/2980 | 801,174 | 1281,879 | 2403,523 | 2163,171 |
| АИР160S4 | 15/1460 | 98,116 | 186,421 | 284,538 | 7,457 |
| АИР160М4 | 18,5/1460 | 121,010 | 229,920 | 350,930 | 11,375 |
| АИР180S4 | 22/1460 | 143,904 | 302,199 | 402,932 | 15,110 |
| АИР180М2 | 30/1460 | 196,233 | 470,959 | 588,699 | 27,276 |
| АИР200М4 | 37/1460 | 242,021 | 532,445 | 847,072 | 46,952 |
| АИР200L4 | 45/1460 | 294,349 | 647,568 | 941,918 | 66,229 |
| АИР225М4 | 55/1475 | 356,102 | 997,085 | 1317,576 | 145,289 |
| АИР250S4 | 75/1470 | 487,245 | 1218,112 | 1559,184 | 301,605 |
| АИР250М4 | 90/1470 | 584,694 | 1461,735 | 1871,020 | 467,755 |
| АИР280S4 | 110/1470 | 714,626 | 2072,415 | 2429,728 | 578,847 |
| АИР280М4 | 132/1485 | 848,889 | 1697,778 | 2886,222 | 1612,889 |
| АИР315S4 | 160/1487 | 1027,572 | 2568,931 | 3802,017 | 2363,416 |
| АИР315М4 | 200/1484 | 1287,062 | 3217,655 | 4247,305 | 3603,774 |
| АИР355SMA4 | 250/1488 | 1604,503 | 3690,356 | 4492,608 | 8985,215 |
| АИР355SMВ4 | 315/1488 | 2021,673 | 5054,183 | 5862,853 | 12534,375 |
| АИР355SMС4 | 355/1488 | 2278,394 | 5012,466 | 6151,663 | 15493,078 |
| АИР160S6 | 11/970 | 108,299 | 205,768 | 314,067 | 12,021 |
| АИР160М6 | 15/970 | 147,680 | 339,665 | 443,041 | 20,675 |
| АИР180М6 | 18,5/970 | 182,139 | 400,706 | 546,418 | 29,324 |
| АИР200М6 | 22/975 | 215,487 | 517,169 | 711,108 | 50,209 |
| АИР200L6 | 30/975 | 293,846 | 617,077 | 881,538 | 102,846 |
| АИР225М6 | 37/980 | 360,561 | 721,122 | 1081,684 | 186,050 |
| АИР250S6 | 45/986 | 435,852 | 784,533 | 1307,556 | 440,210 |
| АИР250М6 | 55/986 | 532,708 | 1012,145 | 1811,207 | 633,922 |
| АИР280S6 | 75/985 | 727,157 | 1454,315 | 2326,904 | 1090,736 |
| АИР280М6 | 90/985 | 872,589 | 1745,178 | 2792,284 | 1657,919 |
| АИР315S6 | 110/987 | 1064,336 | 1809,372 | 2873,708 | 4044,478 |
| АИР315М6 | 132/989 | 1274,621 | 2166,855 | 3696,400 | 5735,794 |
| АИР355МА6 | 160/993 | 1538,771 | 2923,666 | 3539,174 | 11848,540 |
| АИР355МВ6 | 200/993 | 1923,464 | 3654,582 | 4423,968 | 17118,832 |
| АИР355MLA6 | 250/993 | 2404,330 | 4568,228 | 5529,960 | 25485,901 |
| AИР355MLB6 | 315/992 | 3032,510 | 6065,020 | 7278,024 | 40029,133 |
| АИР160S8 | 7,5/730 | 98,116 | 156,986 | 235,479 | 13,246 |
| АИР160М8 | 11/730 | 1007,329 | 1712,459 | 2417,589 | 181,319 |
| АИР180М8 | 15/730 | 196,233 | 333,596 | 529,829 | 41,994 |
| АИР200М8 | 18,5/728 | 242,685 | 509,639 | 606,714 | 67,952 |
| АИР200L8 | 22/725 | 289,793 | 579,586 | 724,483 | 88,966 |
| АИР225М8 | 30/735 | 389,796 | 701,633 | 1052,449 | 214,388 |
| АИР250S8 | 37/738 | 478,794 | 861,829 | 1196,985 | 481,188 |
| АИР250М8 | 45/735 | 584,694 | 1052,449 | 1520,204 | 695,786 |
| АИР280S8 | 55/735 | 714,626 | 1357,789 | 2143,878 | 1071,939 |
| АИР280М8 | 75/735 | 974,490 | 1754,082 | 2728,571 | 1851,531 |
| АИР315S8 | 90/740 | 1161,486 | 1509,932 | 2671,419 | 4413,649 |
| АИР315М8 | 110/742 | 1415,768 | 2265,229 | 3964,151 | 6370,957 |
| АИР355SMA8 | 132/743 | 1696,635 | 2714,616 | 3902,261 | 12215,774 |
| AИР355SMB8 | 160/743 | 2056,528 | 3496,097 | 4935,666 | 18097,443 |
| AИР355MLA8 | 200/743 | 2570,659 | 4627,187 | 6940,781 | 26991,925 |
| AИР355MLB8 | 250/743 | 4498,654 | 7647,712 | 10796,770 | 58032,638 |
Расчет крутящего момента – формула
Габариты электродвигателей АИР:
Примечание: при расчете стоит учесть коэффициент проскальзывания асинхронного двигателя. Номинальное количество оборотов двигателя не совпадает с реальным. Точное количество оборотов вы сможете найти, зная маркировку, в таблице выше.
Номинальное количество оборотов двигателя не совпадает с реальным. Точное количество оборотов вы сможете найти, зная маркировку, в таблице выше.
Где, Р — мощность электродвигателя в киловаттах (кВт). N — количество оборотов вала в минуту.
71013
28.01.2019
Вернуться к списку новостей
Пусковой момент электродвигателя
В процессе перехода механизма из состояния статики в состояние активности, на обмотки мотора начинает поступать номинальное напряжение, имеющее стандартную частоту. Именно тогда асинхронник может потребить наибольший объем энергии.
Под пусковым крутящим моментом мотора понимается момент его вращения в то время, как ротор остается статичным, а частота и напряжение переменного тока остаются номинальными. ПМ электромотора называется процесс развития повышенного вращающего момента.
Чтобы выявить показатель пускового момента, существует формула, которая предполагает использование кратности пм. Эта величина указывается в паспорте устройства. Чтобы определить величину пм асинхронника, нужно применить формулу:
Эта величина указывается в паспорте устройства. Чтобы определить величину пм асинхронника, нужно применить формулу:
Повышенных цифр на индикаторах пускового тока лучше не допускать в процессе запуска мотора, поскольку это может способствовать недостатку энергии, требующейся для корректной работы всех прочих систем и механизмов. Чтобы свести к минимуму значение тока пуска рационально применять пм по типу звезда и треугольник. Такие схемы более всего распространены при подключении электрических моторов.
Пусковой момент АЭД с фазным ротором обусловлен показателями по активному сопротивлению регулируемых резисторов, оказавшихся выведенными в роторную цепь. У асинхронников с короткозамкнутым ротором пусковой момент характеризуется наибольшим показателем. Но при этом существенно снижается показатель пускового тока.
Проверка электродвигателя по пусковому моменту проводится, учитывая динамическую нагрузку от маховых масс конструкции и дополнительного момента, который создается при помощи силы трения.
Короткозамкнутые асинхронные двигатели с повышенным пм имеют особенную конструкцию ротора. Эти свойства характерны для двигателей, имеющих двухклеточные и глубокопазные роторы.
Пусковой момент АЭД при уменьшении напряжения в 2 раза тоже уменьшается. Это подходит для конструкций, где произвести запуск можно с минимальной нагрузкой.
Что считать пусковым моментом
Многие задаются вопросом о том, как понимать кратность пускового момента АЭД. Ничего сложного здесь нет, поскольку сведения указываются в сертификате, паспорте или другом сопроводительном документе на электронный мотор. Под пусковым моментом понимается вращающий момент, который инициируется механическим способом. Его развивает мотор на валу непосредственно при запуске аккурат в то время, когда ток проходит через двигатель.
Иными словами, ПМ – вращающий момент, проявляющийся на валу, когда ток имеет устоявшееся значение, а скорость вращения нулевая, а обмотки электродвигателя имеют номинальное по частоте и напряжению значение.
Способы определения пускового момента
Чтобы узнать, как определить максимальный пусковой момент АЭД, потребуется воспользоваться специальной формулой:
Она помогает понять, за счет чего удастся повысить показатель. Стоит сказать о том, что пусковой момент обусловлен напряжением, которое подводится к обмотке статора. Чем оно ниже, тем дольше запускается двигатель и, соответственно, пусковой ток увеличивается, как и рабочий.
Расчет пускового момента
Он определяется по определенной формуле. Величина кратности может варьироваться в промежутке от 1.5 до 6. Важно соблюдать правило, в соответствии с которым статический момент всегда должен оказываться меньше пускового. Без этого невозможно добиться корректной работы мотора.
Чтобы понять, как определяется кратность ПМ асинхронника, нужно разобраться в самом механизме работы устройства. Непосредственно при запуске электрический мотор будет потреблять пусковой ток, показатель его существенно выше, чем у рабочего. Именно величина, которая обозначает разницу между указанными токами, обозначается как кратность, ее принято учитывать, как коэффициент. Но номинальный и рабочий токи – это разные обозначения, которые не стоит путать. Кратность тока обусловлена мощностью мотора. Если мощность невелика, то пусковой ток высокий.
Именно величина, которая обозначает разницу между указанными токами, обозначается как кратность, ее принято учитывать, как коэффициент. Но номинальный и рабочий токи – это разные обозначения, которые не стоит путать. Кратность тока обусловлена мощностью мотора. Если мощность невелика, то пусковой ток высокий.
Как определить пусковой момент электродвигателя и как определить пусковой момент асинхронного двигателя? Существует формула пусковой момент АЭД для расчета. Можно воспользоваться методом электрических измерений или воспользоваться специальными таблицами.
Увеличение пускового момента
Пусковой момент удастся увеличить за счет частотного преобразователя. Если сменить показатель сопротивления пускового реостата, удастся достичь большего пускового момента.
Но что произойдет, если уменьшить напряжение пускового момента вдвое? Он резко упадет. Изменение первичного тока определяется загрузкой электрического двигателя. При большой нагрузке асинхронного двигателя уменьшение напряжения на его зажимах приводит к перегрузке обмоток двигателя токами со всеми вытекающими отсюда последствиями. Наоборот, пусковой момент асинхронного двигателя при введении реостата в фазный ротор увеличивается.
Наоборот, пусковой момент асинхронного двигателя при введении реостата в фазный ротор увеличивается.
Существуют правила, в соответствии с которыми должен проводиться запуск асинхронного электродвигателя. При каком способе пуска увеличивается пусковой момент асинхронного двигателя? Соединение ротора с реостатом во время включения подойдет для включения в работу моторов с разным ротором. Если в цепь входит реостат, то уровень сопротивления увеличивается. Это обеспечивает увеличение пускового момента.
Асинхронные моторы, обладающие повышенным пусковым моментом созданы специально для приводов механизмов, характеризующихся высокими нагрузками на момент запуска. А вот моторы с повышенным показателем скольжения используют для оборудования, имеющего неравномерные ударные характеристики нагрузки и высокую частоту запусков и реверсов.
Как повысить пусковой момент? Нужно использовать АЭД с высоким ПМ. Его дальнейшее увеличение можно произвести, если использовать двигатели с обмоткой ротора по типу двойной «беличьей клетки», паз обязательно должен быть глубоким. У такого АЭД на роторе будет присутствовать пара короткозамкнутых обмоток. Одна из них пусковая, а другая рабочая. Чтобы повысить ПМ обмотка для запуска должна обладать большим активным сопротивлением, нежели рабочая.
У такого АЭД на роторе будет присутствовать пара короткозамкнутых обмоток. Одна из них пусковая, а другая рабочая. Чтобы повысить ПМ обмотка для запуска должна обладать большим активным сопротивлением, нежели рабочая.
Вычисление пускового момента однофазного АЭД при включенной и отключенной обмотке
ПМ для ротора однофазного мотора соответствует нулю, потому что одна обмотка создает два одинаковых по амплитуде магнитных поля только противоположных по направлению, и сумма их векторов будет равна 0.
Пусковым моментом однофазного АЭД называется вращающий момент, развивающийся на валу АЭД, когда ротор статичен, а статор тока закреплен на обмотках.
Ключевыми элементами каждого асинхронника можно по праву считать ротор (вращающийся элемент) и статор (неподвижная часть). За счет статора обеспечивается магнитное поле для вращения ротора.
ПМ однофазного АЭД без пусковой обмотки соответствует 1/2 максимального момента.
Пусковой момент двигателя. Вращающий момент асинхронного двигателя.
 Вывод формулы. Номинальный, критический и пусковой моменты
Вывод формулы. Номинальный, критический и пусковой моменты
Вращающий момент, развиваемый на валу асинхронного электродвигателя в условиях нулевой скорости вращения ротора (когда ротор еще неподвижен) и установившегося в обмотках статора тока, — называется пусковым моментом асинхронного двигателя.
Пусковой момент иногда называют еще моментом трогания или начальным моментом. При этом подразумевается, что напряжение и частота питающего напряжения приближены к номиналу, причем соединение обмоток выполнено правильно. В номинальном режиме работы данный двигатель будет работать именно так, как предполагали разработчики.
Пусковой момент вычисляется по приведенной формуле. В паспорте электродвигателя (паспорт предоставляется производителем) указана кратность пускового момента.
Обычно значение величины кратности лежит в пределах от 1,5 до 6, в зависимости от типа двигателя. И при выборе электродвигателя для своих нужд, важно убедиться, что пусковой момент окажется больше статического момента планируемой проектной нагрузки на валу. Если это условие не соблюсти, то двигатель попросту не сможет развить рабочий момент при вашей нагрузке, то есть не сможет нормально стартонуть и разогнаться до номинальных оборотов.
Если это условие не соблюсти, то двигатель попросту не сможет развить рабочий момент при вашей нагрузке, то есть не сможет нормально стартонуть и разогнаться до номинальных оборотов.
Давайте рассмотрим еще одну формулу для нахождения пускового момента. Она будет вам полезной для теоретических расчетов. Здесь достаточно знать мощность на валу в киловаттах и номинальные обороты, — все эти данные указаны на табличке (на шильдике). P2-номинальная мощность, F1-номинальные обороты. Итак, вот эта формула:
Для нахождения P2 применяют следующую формулу. Здесь необходимо учесть скольжение, пусковой ток и напряжение питания, все эти данные указаны на шильдике. Как видите, все довольно просто. Из формулы очевидно, что пусковой момент в принципе можно повысить двумя путями: увеличением стартового тока или повышением питающего напряжения.
Попробуем, однако, пойти наиболее простым путем, и рассчитаем значения пусковых моментов для трех двигателей серии АИР. Воспользуемся параметрами кратности пускового момента и величинами номинального момента, то есть пользоваться будем самой первой формулой. Результаты расчетов приведены в таблице:
Результаты расчетов приведены в таблице:
| Тип двигателя | Номинальный момент, Нм | Отношение пускового момента к номинальному моменту | Пусковой момент, Нм |
| АИРМ132М2 | 36 | 2,5 | 90 |
| АИР180S2 | 72 | 2 | 144 |
| АИР180М2 | 97 | 2,4 | 232,8 |
Роль пускового момента асинхронного электродвигателя (пусковой ток)
Часто двигатели включают напрямую в сеть, осуществляя коммутацию магнитным пускателем: на обмотки подается линейное напряжение, создается вращающееся магнитное поле статора, оборудование начинает работать.
Бросок тока в момент старта в данном случае неизбежен, и он превышает номинальный ток в 5-7 раз, причем длительность превышения зависит от мощности двигателя и от мощности нагрузки: более мощные двигатели стартуют дольше, их обмотки статора дольше принимают токовую перегрузку.
Маломощные двигатели (до 3 кВт) легко переносят данные броски, и сеть так же легко выдерживает эти незначительные кратковременные всплески мощности, ибо у сети всегда есть некоторый мощностный резерв. Вот почему небольшие насосы и вентиляторы, станки и бытовые электроприборы обычно включают напрямую, не заботясь особо о токовых перегрузках. Как правило обмотки статоров двигателей оборудования такого рода соединяются по схеме «звезда» из расчета на трехфазное напряжение 380 вольт или «треугольник» — для 220 вольт.
Если же вы имеете дело с мощным двигателем на 10 и более кВт, то включать напрямую такой двигатель в сеть нельзя. Бросок тока в момент пуска необходимо ограничить, иначе сеть испытает значительную перегрузку, что может привести к опасной «нештатной просадке напряжения».
Пути ограничения пускового тока
Наиболее простой способ ограничения пускового тока — пуск при пониженном напряжении. Обмотки просто переключаются с треугольника на звезду в момент пуска, а затем, когда двигатель набрал какие-то обороты — обратно на треугольник. Переключение осуществляется через несколько секунд после старта с помощью реле времени, например.
Переключение осуществляется через несколько секунд после старта с помощью реле времени, например.
В таком решении пусковой момент также понижается, причем зависимость квадратичная: при снижении напряжения в будет в 1,72 раза, момент снизится в 3 раза. По этой причине пуск при пониженном напряжении подходит для такого оборудования, где пуск возможен с минимальной нагрузкой на валу асинхронного двигателя (например пуск многопильного станка).
Мощным нагрузкам, например ленточному конвейеру, необходим другой способ ограничения пускового тока. Здесь лучше подойдет реостатный метод, позволяющий снизить пусковой ток без уменьшения крутящего момента.
Такой способ очень подходит асинхронным двигателям с фазным ротором, где реостат удобно включается в цепь обмотки ротора, и регулировка рабочего тока осуществляется ступенчато, получается очень плавный пуск. С помощью реостата тут же можно регулировать и рабочую скорость двигателя (не только в момент запуска).
Но наиболее эффективным способом безопасного пуска асинхронных двигателей является все же пуск посредством . Величину напряжения и частоту регулирует сам преобразователь автоматически, создавая оптимальные условия двигателю. Обороты получаются стабильными, при этом броски тока принципиально исключены.
Величину напряжения и частоту регулирует сам преобразователь автоматически, создавая оптимальные условия двигателю. Обороты получаются стабильными, при этом броски тока принципиально исключены.
Для каждого асинхронного двигателя может быть определен номинальный режим, т. е. режим длительной работы, при котором двигатель не перегревается сверх установленной температуры. Момент М ном, соответствующий номинальному режиму, называется. номинальным моментом. Соответствующее ему номинальное скольжение составляет для асинхронных двигателей средней мощности s H0M = 0,02…0,06, т.е. номинальная скорость n иом находится в пределах
n ном =
n 0 (1 — s 0)= (0,94…0,98) п 0 .
Отношение максимального момента к номинальному к м = = Mmах/M ном называется перегрузочной способностью асинхронного двигателя. Обычно к т = 1,8.. .2,5.
При пуске в ход, т. е. при трогании с места и при разгоне, асинхронный двигатель находится в условиях, существенно отличающихся от условий нормальной работы. Момент, развиваемый двигателем, должен превышать момент сопротивления нагрузки, иначе двигатель не сможет разгоняться. Таким образом, с точки зрения пуска двигателя важную роль играет его пусковой момент.
Момент, развиваемый двигателем, должен превышать момент сопротивления нагрузки, иначе двигатель не сможет разгоняться. Таким образом, с точки зрения пуска двигателя важную роль играет его пусковой момент.
Отношение пускового момента М п развиваемого двигателем в неподвижном состоянии, т. е. при n = 0, к номинальному моменту k п = М п /М ном называется кратностью пускового момента.
Максимальный момент М тах называется критическим моментом асинхронной машины. Работа машины с моментом, превышающим номинальный, возможна лишь кратковременно, в противном случае срок службы машины сокращается из-за ее перегрева.
В результате взаимодействия вращающегося магнитного потока с токами, индуктированными им в проводниках роторной обмотки, возникают силы, действующие на эти проводники в тангенциальном направлении. Найдем значение момента, создаваемого этими силами на валу машины.
Электромагнитная мощность, передаваемая ротору вращающимся магнитным полем, ровна:
где М эм — электромагнитный момент действующий на ротор.
В соответствии со схемой замещения одной фазы машины:
Из этих выражений найдем:
Учитывая действующий ток ротора, ЭДС, индуктивное сопротивление получим:
Введем постоянную и пренебрегая моментом трения, представим выражение момента на валу в виде:
Если магнитный поток Ф выражен в веберах, ток I 2
— в амперах, то вращающий момент получится в ньютон-метрах (Нм).
Вращающий момент машины зависит от изменяющихся при нагрузке ф, I 2
и, но его можно представить в виде функции однойпеременной. В качестве такой переменной для асинхронного двигателя наиболее удобно выбрать скольжениеs.
Полагая, что частота сети неизменна введем
Получим следующее выражение для вращающего момента:
42. Энергетическая диаграмма АД.
В электрической машине часть энергии теряется в виде тепла в различных частях — потери в обмотках, в стали, механические потери.
На диаграмме: Р 1
— мощность, подводимая из сети. Основная часть её за вычетом потерь в статоре, передаётся электромагнитным путём на ротор через зазор; Р эм
Основная часть её за вычетом потерь в статоре, передаётся электромагнитным путём на ротор через зазор; Р эм
называется электромагнитной мощностью.
Потери в статоре складываются из потерь в обмотке и в стали:
Рис. 42. Энергетическая диаграмма АД.
р с1 и р с2 . р с1
теряется на вихревые токи и перемагничивание сердечника. Потери в стали имеются и в сердечнике ротора, но они невелики и их можно не учитывать, т.к. n 0 во много раз больше скорости магнитного потока относительно ротора n 0 — n
, если n
соответствует устойчивой части естественной механической характеристики.
Механическая мощность, развиваемая на валу ротора, меньше Р эм
на значение р об2
потерь в обмотке ротораР мх = Р эм — р об2
Мощность на валу Р 2 = Р мх — р мх,
где р мх
— мощность механических потерь, равная сумме потерь на трение в подшипниках, на трение о воздух и трение щеток о кольца.
Электромагнитная и механическая Р
равныР эм = ω 0 М, Р мх = ωМ
, где ω
0 и ω
— скорости синхронная и ротора, М
— момент, развиваемый двигателей, т. е. момент, с которым вращающееся поле действует на ротор.
е. момент, с которым вращающееся поле действует на ротор.
Добавочные потери обусловлены зубчатостью ротора и статора, вихревыми токами в различных узлах и другими причинами. При полной нагрузке потери Рд принимаются равными 0,5% его номинальной мощности.
К.п.д. двигателя: h = P 2 /P 1 = / Р 1 .
Т.к. общие потери зависят от нагрузки, то и КПД является функцией нагрузки. Машина конструируется так, чтобы максимум ее коэффициента полезного действия h
имел место при нагрузке, несколько меньше номинальной. Для большинства двигателей к.п.д. равен 80-90%, а для мощных двигателей 90-96%.
43. Устройство синхронного двигателя. Схема замещения, уравнения энергетического состояния фазы обмотки статора, векторная диаграмма синхронного дв.
Основными частями статора являются неподвижный пакет магнитопровода и трехфазная обмотка. Пакет магнитопровода изготовлен в виде полого цилиндра, набранного, так же как и магнитопровод трансформатора, из тонких листов электротехнической стали. Листы имеют форму колец с пазами, симметрично расположенными вдоль внутренней окружности. В пазы пакета статора уложены стороны многовитковых мягких катушек, образующих три фазы обмотки. Пакет статора с обмоткой запрессован в алюминиевый или чугунный корпус-оболочку, неподвижно закрепляемый при установке машины на фундаментной плите. С корпусом прочно соединены два боковых литых щита со сквозными центральными отверстиями для подшипников, в которых вращается вал ротора.
Листы имеют форму колец с пазами, симметрично расположенными вдоль внутренней окружности. В пазы пакета статора уложены стороны многовитковых мягких катушек, образующих три фазы обмотки. Пакет статора с обмоткой запрессован в алюминиевый или чугунный корпус-оболочку, неподвижно закрепляемый при установке машины на фундаментной плите. С корпусом прочно соединены два боковых литых щита со сквозными центральными отверстиями для подшипников, в которых вращается вал ротора.
Начала и концы фаз обмотки статора присоединены к зажимам, расположенным в коробке выводов, укрепленной на корпусе. Большинство машин имеет коробку выводов с шестью зажимами, что позволяет соединять фазы обмотки треугольником или звездой.
Применяются два типа роторов синхронных машин — неявнопо-люсный, или с неявно выраженными полюсами, и ротор явнополюс-ный, или с явно выраженными полюсами. В первом случае сердечник ротора представляет массивное цилиндрическое тело из стали (бочка ротора), вдоль его поверхности выфрезерованы пазы, в которых закладывается обмотка возбуждения. Пазы и обмотка возбуждения размещаются так, чтобы получить по возможности синусоидальное распределение индукции в зазоре между сердечниками ротора и статора. Общий вид неявнополюсного ротора показан на рис.
Пазы и обмотка возбуждения размещаются так, чтобы получить по возможности синусоидальное распределение индукции в зазоре между сердечниками ротора и статора. Общий вид неявнополюсного ротора показан на рис.
Явнополюсный ротор состоит из массивного стального колеса, посаженного на вал. К его ободу по внешней поверхности крепятся стальные сердечники полюсов. Последние, а иногда и обод выполняются из листовой стали. Для малых машин и при не слишком большом числе полюсов вместо колеса на вал насаживается стальная втулка, к которой крепятся полюса. Обмотка возбуждения в виде катушек размещается на сердечниках полюсов. Такая конструкция ротора позволяет разместить на нем большое число полюсов, что необходимо для машин с небольшой скоростью вращения.
44. Регулирование реактивной мощности синхронного двигателя
осуществляется изменением тока возбуждения Iв
1) Номинальный режим Iв= Iв ном. cosφ=1.
2) Iв
реактивная составляющая увеличивается, носит индуктивный характер-режим работы АСД
3) Iв> Iв ном cos φ
ток якоря увеличивается,Емкостной характер
При этом способе реактивная мощность отдается в сеть,что является большим плюсом.
Изменяя ток возбуждения меняем ток якоря.
45. Регулирование активной мощности синхронного двигателя
осуществляется изменением угла согласования. При увеличении нагрузки угол увеличивается, при уменьшении- уменьшается. Угол рассогласования определяет перегрузочную способность двигателя.
Отношение максимального момента к номинальному:
46. Устройство, принцип действия двигателя постоянного тока. Способы возбуждения. ЭДС обмотки якоря и электромагнитный момент
Устройство и принцип действия двигателя постоянного тока Двигатель постоянного тока состоит из неподвижной части -статора и вращающейся части — якоря, разделенных воздушным зазором. К внутренней поверхности статора крепятся главные в добавочные полюсы. Главные полюсы с обмотками возбуждения служат для создания в машине основного магнитного потока Ф, а добавочные — для уменьшение искрения.
Якорь состоит из вала, сердечника, обмотки и коллектора. Коллектор содержит изолированные друг от друга медные пластины, которые соединяются с секциями обмотки якоря. На коллектор накладываются неподвижные щётки; соединяющие обмотку якоря с внешней электрической цепью. В результата взаимодействия тока якоря Iя И магнитного потока Ф создается вращающий момент, М=СмФIя, где См- постоянная момента, зависящая от конструктивных данных машины. Вращающий момент М, двигателя уравновешивается моментом сопротивления Мс рабочей машины. При вращении якоря с частотой n его обмотка пересекает магнитный поток Ф и в ней, согласно закону электромагнитной индукции, наводится противо-ЭДС E =СеФп, где Се _ конструктивная постоянная.
На коллектор накладываются неподвижные щётки; соединяющие обмотку якоря с внешней электрической цепью. В результата взаимодействия тока якоря Iя И магнитного потока Ф создается вращающий момент, М=СмФIя, где См- постоянная момента, зависящая от конструктивных данных машины. Вращающий момент М, двигателя уравновешивается моментом сопротивления Мс рабочей машины. При вращении якоря с частотой n его обмотка пересекает магнитный поток Ф и в ней, согласно закону электромагнитной индукции, наводится противо-ЭДС E =СеФп, где Се _ конструктивная постоянная.
Напряжение на эажимаx якоря U равно сумме ЭДС и падения напряжения на сопротивлении якорной цепи U=E +RяIя=CеФn, откуда ток якоря Iя=(U-CеФn)/Rя, а частота вращения n=(U- RяIя)/ CеФ/
В зависимости от способа питания обмотки возбуждения генераторы постоянного тока бывают:
| а) б) в) г) |
Рис. 50. Возбуждение генератора: а — независимое, б — параллельное, в — последовательное, г — смешанное.
При независимом возбуждении ОВ питается от постороннего источника. Применяется в случаях, когда необходимо в широких пределах регулировать ток возбуждения I в и напряжение U на зажимах машины. Ток якоря равен току нагрузки I я = I н (рис. 50, а)
Генераторы с самовозбуждением имеют ОВ, питаемые от самого генератора.
При включении ОВ параллельно с обмоткой якоря имеем генератор с параллельным возбуждением (рис. 50, б), у которого I я = I н + I в. У мощных машин нормального исполнения I в обычно составляет 1-3%, а у малых машин — до нескольких десятков % от тока якоря. У генератора с последовательным возбуждением (рис. 50, в) ОВП включён последовательно с якорем, т.е.
I я = I н = I в.
Генераторы со смешанным возбуждением имеют две обмотки возбуждения, ОВ включёна параллельно якорю, а другая ОВП — последователь но (рис. 50, г). Основной обычно является ОВ. ОВП подмагничивает машину при увеличении тока нагрузки, чем компенсируется падение напряжения U в обмотке якоря и размагничивающее влияние реакции якоря.
47. Нагрузочный режим двигателя постоянного тока с параллельным возбуждением. Механическая характеристика.
Подадим на зажимы неподвижного якоря напряжение. Напряжение вызовет ток в цепи якоря. При этом возникает электромагнитным момент. Этот момент начнёт вращать якорь, совершая механическую работу. Машина начнет работать в режиме электродвигателя. Чтобы преодолеть сопротивление механической нагрузки на валу, электродвигателя должен потреблять энергию из внешнего источника.
48. Способы пуска двигателя постоянного тока.
Нормальная машина постоянного тока имеет цилиндрический ротор с обмоткой, называемый якорем, который вращается в неподвижном магнитном поле. В витках 1-3 и 2-4 обмотки якоря индуктируются переменные ЭДС и для получения постоянного направления тока i
в сопротивлении нагрузки r, применяется коллектор К, состоящий из медных изолированных друг от друга пластин, образующих цилиндр, по которому скользят щетки а — B
. Наличие коллектора, к пластинам которого присоединяются начала и концы витков обмотки якоря, является отличительной особенностью м. п. т. В положении на рисунке стороны 1-3 витка пересекают магнитные линии перпендикулярно, поэтому между щетками будет Е мах.
п. т. В положении на рисунке стороны 1-3 витка пересекают магнитные линии перпендикулярно, поэтому между щетками будет Е мах.
Рис. 47. Схема генератора постоянного тока с двумя витками и четырьмя коллекторными пластинами.
Конец работы —
Эта тема принадлежит разделу:
Собственная и примесная электропроводность полупроводников
Выпрямителем называется устройство предназначенное для преобразования переменного тока в постоянный Основ ным элементом выпрямителей является…
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
Для каждого асинхронного двигателя может быть определен номинальный режим, т. е. режим длительной работы, при котором двигатель не перегревается сверх установленной температуры. Момент М ном, соответствующий номинальному режиму, называется. номинальным моментом. Соответствующее ему номинальное скольжение составляет для асинхронных двигателей средней мощности s H0M = 0,02…0,06, т.е. номинальная скорость n иом находится в пределах
номинальным моментом. Соответствующее ему номинальное скольжение составляет для асинхронных двигателей средней мощности s H0M = 0,02…0,06, т.е. номинальная скорость n иом находится в пределах
n ном =
n 0 (1 — s 0)= (0,94…0,98) п 0 .
Отношение максимального момента к номинальному к м = = Mmах/M ном называется перегрузочной способностью асинхронного двигателя. Обычно к т = 1,8.. .2,5.
При пуске в ход, т. е. …
при трогании с места и при разгоне, асинхронный двигатель находится в условиях, существенно отличающихся от условий нормальной работы. Момент, развиваемый двигателем, должен превышать момент сопротивления нагрузки, иначе двигатель не сможет разгоняться. Таким образом, с точки зрения пуска двигателя важную роль играет его пусковой момент.
Отношение пускового момента М п развиваемого двигателем в неподвижном состоянии, т. е. при n = 0, к номинальному моменту k п = М п /М ном называется кратностью пускового момента.
Максимальный момент М тах называется критическим моментом асинхронной машины. Работа машины с моментом, превышающим номинальный, возможна лишь кратковременно, в противном случае срок службы машины сокращается из-за ее перегрева.
Работа машины с моментом, превышающим номинальный, возможна лишь кратковременно, в противном случае срок службы машины сокращается из-за ее перегрева.
В результате взаимодействия вращающегося магнитного потока с токами, индуктированными им в проводниках роторной обмотки, возникают силы, действующие на эти проводники в тангенциальном направлении. Найдем значение момента, создаваемого этими силами на валу машины.
Электромагнитная мощность, передаваемая ротору вращающимся магнитным полем, ровна:
где М эм — электромагнитный момент действующий на ротор.
В соответствии со схемой замещения одной фазы машины:
Из этих выражений найдем:
Учитывая действующий ток ротора, ЭДС, индуктивное сопротивление получим:
Введем постоянную и пренебрегая моментом трения, представим выражение момента на валу в виде:
Если магнитный поток Ф выражен в веберах, ток I 2
— в амперах, то вращающий момент получится в ньютон-метрах (Нм).
Вращающий момент машины зависит от изменяющихся при нагрузке ф, I 2
и , но его можно представить в виде функции однойпеременной. В качестве такой переменной для асинхронного двигателя наиболее удобно выбрать скольжениеs.
В качестве такой переменной для асинхронного двигателя наиболее удобно выбрать скольжениеs.
Тогда
Полагая, что частота сети неизменна введем
Получим следующее выражение для вращающего момента:
42. Энергетическая диаграмма АД.
В электрической машине часть энергии теряется в виде тепла в различных частях — потери в обмотках, в стали, механические потери.
На диаграмме: Р 1
— мощность, подводимая из сети. Основная часть её за вычетом потерь в статоре, передаётся электромагнитным путём на ротор через зазор; Р эм
называется электромагнитной мощностью.
Потери в статоре складываются из потерь в обмотке и в стали:
Рис. 42. Энергетическая диаграмма АД.
р с1 и р с2 . р с1
теряется на вихревые токи и перемагничивание сердечника. Потери в стали имеются и в сердечнике ротора, но они невелики и их можно не учитывать, т.к. n 0 во много раз больше скорости магнитного потока относительно ротора n 0 — n
, если n
соответствует устойчивой части естественной механической характеристики.
Механическая мощность, развиваемая на валу ротора, меньше Р эм
на значение р об2
потерь в обмотке ротораР мх = Р эм — р об2
Мощность на валу Р 2 = Р мх — р мх,
где р мх
— мощность механических потерь, равная сумме потерь на трение в подшипниках, на трение о воздух и трение щеток о кольца.
Электромагнитная и механическая Р
равныР эм = ω 0 М, Р мх = ωМ
, где ω
0 и ω
— скорости синхронная и ротора, М
— момент, развиваемый двигателей, т.е. момент, с которым вращающееся поле действует на ротор.
Добавочные потери обусловлены зубчатостью ротора и статора, вихревыми токами в различных узлах и другими причинами. При полной нагрузке потери Рд принимаются равными 0,5% его номинальной мощности.
К.п.д. двигателя: h = P 2 /P 1 = / Р 1 .
Т.к. общие потери зависят от нагрузки, то и КПД является функцией нагрузки. Машина конструируется так, чтобы максимум ее коэффициента полезного действия h
имел место при нагрузке, несколько меньше номинальной. Для большинства двигателей к.п.д. равен 80-90%, а для мощных двигателей 90-96%.
Для большинства двигателей к.п.д. равен 80-90%, а для мощных двигателей 90-96%.
43. Устройство синхронного двигателя. Схема замещения, уравнения энергетического состояния фазы обмотки статора, векторная диаграмма синхронного дв.
Основными частями статора являются неподвижный пакет магнитопровода и трехфазная обмотка. Пакет магнитопровода изготовлен в виде полого цилиндра, набранного, так же как и магнитопровод трансформатора, из тонких листов электротехнической стали. Листы имеют форму колец с пазами, симметрично расположенными вдоль внутренней окружности. В пазы пакета статора уложены стороны многовитковых мягких катушек, образующих три фазы обмотки. Пакет статора с обмоткой запрессован в алюминиевый или чугунный корпус-оболочку, неподвижно закрепляемый при установке машины на фундаментной плите. С корпусом прочно соединены два боковых литых щита со сквозными центральными отверстиями для подшипников, в которых вращается вал ротора.
Начала и концы фаз обмотки статора присоединены к зажимам, расположенным в коробке выводов, укрепленной на корпусе. Большинство машин имеет коробку выводов с шестью зажимами, что позволяет соединять фазы обмотки треугольником или звездой.
Большинство машин имеет коробку выводов с шестью зажимами, что позволяет соединять фазы обмотки треугольником или звездой.
Применяются два типа роторов синхронных машин — неявнопо-люсный, или с неявно выраженными полюсами, и ротор явнополюс-ный, или с явно выраженными полюсами. В первом случае сердечник ротора представляет массивное цилиндрическое тело из стали (бочка ротора), вдоль его поверхности выфрезерованы пазы, в которых закладывается обмотка возбуждения. Пазы и обмотка возбуждения размещаются так, чтобы получить по возможности синусоидальное распределение индукции в зазоре между сердечниками ротора и статора. Общий вид неявнополюсного ротора показан на рис.
Явнополюсный ротор состоит из массивного стального колеса, посаженного на вал. К его ободу по внешней поверхности крепятся стальные сердечники полюсов. Последние, а иногда и обод выполняются из листовой стали. Для малых машин и при не слишком большом числе полюсов вместо колеса на вал насаживается стальная втулка, к которой крепятся полюса. Обмотка возбуждения в виде катушек размещается на сердечниках полюсов. Такая конструкция ротора позволяет разместить на нем большое число полюсов, что необходимо для машин с небольшой скоростью вращения.
Обмотка возбуждения в виде катушек размещается на сердечниках полюсов. Такая конструкция ротора позволяет разместить на нем большое число полюсов, что необходимо для машин с небольшой скоростью вращения.
44. Регулирование реактивной мощности синхронного двигателя
осуществляется изменением тока возбуждения Iв
1) Номинальный режим Iв= Iв ном. cosφ=1.
2) Iв
реактивная составляющая увеличивается, носит индуктивный характер-режим работы АСД
3) Iв> Iв ном cos φ
ток якоря увеличивается,Емкостной характер
При этом способе реактивная мощность отдается в сеть,что является большим плюсом.
Изменяя ток возбуждения меняем ток якоря.
45. Регулирование активной мощности синхронного двигателя
осуществляется изменением угла согласования. При увеличении нагрузки угол увеличивается, при уменьшении- уменьшается. Угол рассогласования определяет перегрузочную способность двигателя.
Отношение максимального момента к номинальному:
46. Устройство, принцип действия двигателя постоянного тока. Способы возбуждения. ЭДС обмотки якоря и электромагнитный момент
Устройство, принцип действия двигателя постоянного тока. Способы возбуждения. ЭДС обмотки якоря и электромагнитный момент
Устройство и принцип действия двигателя постоянного тока Двигатель постоянного тока состоит из неподвижной части -статора и вращающейся части — якоря, разделенных воздушным зазором. К внутренней поверхности статора крепятся главные в добавочные полюсы. Главные полюсы с обмотками возбуждения служат для создания в машине основного магнитного потока Ф, а добавочные — для уменьшение искрения.
Якорь состоит из вала, сердечника, обмотки и коллектора. Коллектор содержит изолированные друг от друга медные пластины, которые соединяются с секциями обмотки якоря. На коллектор накладываются неподвижные щётки; соединяющие обмотку якоря с внешней электрической цепью. В результата взаимодействия тока якоря Iя И магнитного потока Ф создается вращающий момент, М=СмФIя, где См- постоянная момента, зависящая от конструктивных данных машины. Вращающий момент М, двигателя уравновешивается моментом сопротивления Мс рабочей машины. При вращении якоря с частотой n его обмотка пересекает магнитный поток Ф и в ней, согласно закону электромагнитной индукции, наводится противо-ЭДС E =СеФп, где Се _ конструктивная постоянная.
При вращении якоря с частотой n его обмотка пересекает магнитный поток Ф и в ней, согласно закону электромагнитной индукции, наводится противо-ЭДС E =СеФп, где Се _ конструктивная постоянная.
Напряжение на эажимаx якоря U равно сумме ЭДС и падения напряжения на сопротивлении якорной цепи U=E +RяIя=CеФn, откуда ток якоря Iя=(U-CеФn)/Rя, а частота вращения n=(U- RяIя)/ CеФ/
В зависимости от способа питания обмотки возбуждения генераторы постоянного тока бывают:
| а) б) в) г) |
Рис. 50. Возбуждение генератора: а — независимое, б — параллельное, в — последовательное, г — смешанное.
При независимом возбуждении ОВ питается от постороннего источника. Применяется в случаях, когда необходимо в широких пределах регулировать ток возбуждения I в и напряжение U на зажимах машины. Ток якоря равен току нагрузки I я = I н (рис. 50, а)
Генераторы с самовозбуждением имеют ОВ, питаемые от самого генератора.
При включении ОВ параллельно с обмоткой якоря имеем генератор с параллельным возбуждением (рис. 50, б), у которого I я = I н + I в. У мощных машин нормального исполнения I в обычно составляет 1-3%, а у малых машин — до нескольких десятков % от тока якоря. У генератора с последовательным возбуждением (рис. 50, в) ОВП включён последовательно с якорем, т.е.
50, б), у которого I я = I н + I в. У мощных машин нормального исполнения I в обычно составляет 1-3%, а у малых машин — до нескольких десятков % от тока якоря. У генератора с последовательным возбуждением (рис. 50, в) ОВП включён последовательно с якорем, т.е.
I я = I н = I в.
Генераторы со смешанным возбуждением имеют две обмотки возбуждения, ОВ включёна параллельно якорю, а другая ОВП — последователь но (рис. 50, г). Основной обычно является ОВ. ОВП подмагничивает машину при увеличении тока нагрузки, чем компенсируется падение напряжения U в обмотке якоря и размагничивающее влияние реакции якоря.
47. Нагрузочный режим двигателя постоянного тока с параллельным возбуждением. Механическая характеристика.
Подадим на зажимы неподвижного якоря напряжение. Напряжение вызовет ток в цепи якоря. При этом возникает электромагнитным момент. Этот момент начнёт вращать якорь, совершая механическую работу. Машина начнет работать в режиме электродвигателя. Чтобы преодолеть сопротивление механической нагрузки на валу, электродвигателя должен потреблять энергию из внешнего источника.
48. Способы пуска двигателя постоянного тока.
Нормальная машина постоянного тока имеет цилиндрический ротор с обмоткой, называемый якорем, который вращается в неподвижном магнитном поле. В витках 1-3 и 2-4 обмотки якоря индуктируются переменные ЭДС и для получения постоянного направления тока i
в сопротивлении нагрузки r, применяется коллектор К, состоящий из медных изолированных друг от друга пластин, образующих цилиндр, по которому скользят щетки а — B
. Наличие коллектора, к пластинам которого присоединяются начала и концы витков обмотки якоря, является отличительной особенностью м. п. т. В положении на рисунке стороны 1-3 витка пересекают магнитные линии перпендикулярно, поэтому между щетками будет Е мах.
Рис. 47. Схема генератора постоянного тока с двумя витками и четырьмя коллекторными пластинами.
Уравнение крутящего момента трехфазного асинхронного двигателя
by Electrical4U
Крутящий момент трехфазного асинхронного двигателя зависит от следующих трех факторов:
Во-первых, величина тока ротора, во-вторых поток, который взаимодействует с ротором трехфазного асинхронного двигателя и отвечает за создание ЭДС в роторной части асинхронного двигателя, наконец, коэффициент мощности ротора трехфазного асинхронного двигателя.
Объединяя все эти факторы, мы получаем уравнение крутящего момента как-
Где, T — крутящий момент, создаваемый асинхронным двигателем,
φ — поток, ответственный за создание ЭДС индукции,
I 2 — ток ротора,
cosθ 2 – коэффициент мощности цепи ротора.
Поток φ, создаваемый статором, пропорционален ЭДС статора E 1 .
т. е. φ ∝ E 1
Мы знаем, что коэффициент трансформации K определяется как отношение вторичного напряжения (напряжение ротора) к первичному напряжению (напряжение статора).
Ток ротора I 2 определяется как отношение ЭДС ротора в рабочем состоянии sE 2 к полному сопротивлению Z 2 со стороны ротора,
и полному сопротивлению Z 2 со стороны ротора определяется как ,
Подставляя это значение в приведенное выше уравнение, мы получаем,
с = скольжение асинхронного двигателя
Мы знаем, что коэффициент мощности определяется как отношение сопротивления к импедансу. Коэффициент мощности цепи ротора равен 9.0009
Подставляя значения потока φ, тока ротора I 2 , коэффициента мощности cosθ 2 в уравнение крутящего момента получаем,
Комбинируя аналогичные члены получаем,
Удалив константу пропорциональности получаем,
9 , n
s — синхронная скорость в об/мин. п. s, n s = N s / 60. Итак, наконец, уравнение крутящего момента принимает вид
Вывод K в уравнении крутящего момента.
В случае трехфазного асинхронного двигателя в роторе возникают потери в меди. Эти потери в меди ротора выражаются как
P c = 3I 2 2 R 2
Мы знаем, что ток ротора,
Подставим это значение I 2 в уравнение потерь меди ротора, P c . Итак, получаем
Отношение P 2 : P c : P m = 1 : s : (1 – s)
Где, P 2 вход ротора,
P c
6 – потери в меди ротора,
P м – развиваемая механическая мощность.
Подставляем значение Pc в вышеприведенное уравнение, получаем
При упрощении получаем
Развиваемая механическая мощность P м = Tω,
Подставляя значение P м
Мы знаем, что скорость ротора N = N s (1 – s)
Подставляя это значение скорости ротора в приведенное выше уравнение, мы получаем,
N s — скорость в оборотах в минуту (об/мин) и n s — скорость в оборотах в секунду ( rps), а отношение между ними равно
Подставим это значение N на в приведенное выше уравнение и упростим его, получим
Сравнив оба уравнения, получим константу K = 3 / 2πn с
Принцип работы трехфазного асинхронного двигателя – Видео
Уравнение пускового момента трехфазного асинхронного двигателя
Пусковой момент — это крутящий момент, создаваемый асинхронным двигателем при запуске. Мы знаем, что в начале скорость вращения ротора N равна нулю.
Мы знаем, что в начале скорость вращения ротора N равна нулю.
Итак, уравнение пускового момента легко получить, просто подставив значение s = 1 в уравнение момента трехфазного асинхронного двигателя,
Пусковой крутящий момент также известен как пусковой крутящий момент.
Условия максимального крутящего момента для трехфазного асинхронного двигателя
В уравнении крутящего момента
Сопротивление ротора, индуктивное сопротивление ротора и синхронная скорость асинхронного двигателя остаются постоянными. Напряжение питания трехфазного асинхронного двигателя обычно номинальное и остается постоянным, поэтому ЭДС статора также остается постоянной. Мы определяем коэффициент трансформации как отношение ЭДС ротора к ЭДС статора. Таким образом, если ЭДС статора остается постоянной, то ЭДС ротора также остается постоянной.
Если мы хотим найти максимальное значение некоторой величины, то мы должны продифференцировать эту величину по какому-то переменному параметру и затем приравнять ее к нулю. В этом случае мы должны найти условие максимального крутящего момента, поэтому мы должны дифференцировать крутящий момент относительно некоторой переменной величины, которой является скольжение, т.к. в этом случае все остальные параметры в уравнении крутящего момента остаются постоянными.
В этом случае мы должны найти условие максимального крутящего момента, поэтому мы должны дифференцировать крутящий момент относительно некоторой переменной величины, которой является скольжение, т.к. в этом случае все остальные параметры в уравнении крутящего момента остаются постоянными.
Итак, чтобы крутящий момент был максимальным
Теперь продифференцируем приведенное выше уравнение, используя правило дифференцирования деления. Продифференцировав и приравняв члены к нулю, получим
Пренебрегая отрицательным значением скольжения, получаем
Итак, при скольжении s = R 2 / X 2 крутящий момент будет максимальным и это скольжение называется максимальным скольжением Sm и определяется как отношение ротора сопротивление равно реактивному сопротивлению ротора.
ПРИМЕЧАНИЕ. При пуске S = 1, поэтому максимальный пусковой момент возникает, когда сопротивление ротора равно реактивному сопротивлению ротора.
Уравнение максимального крутящего момента
Уравнение крутящего момента:
Крутящий момент будет максимальным, когда скольжение s = R 2 / X 2
Подставив значение этого проскальзывания в приведенное выше уравнение, мы получим максимальное значение крутящего момента как постепенно по мере увеличения скорости двигателя.
Заключение
Из приведенного выше уравнения следует, что
- Максимальный крутящий момент прямо пропорционален квадрату ЭДС ротора в состоянии покоя.
- Максимальный крутящий момент обратно пропорционален реактивному сопротивлению ротора.
- Максимальный крутящий момент не зависит от сопротивления ротора.
- Скольжение, при котором возникает максимальный крутящий момент, зависит от сопротивления ротора, R 2 . Таким образом, изменяя сопротивление ротора, можно получить максимальный крутящий момент при любом требуемом скольжении.
Хотите учиться быстрее? 🎓
Каждую неделю получайте электротехнические товары на свой почтовый ящик.
Кредитная карта не требуется — это абсолютно бесплатно.
О Electrical4U
Electrical4U посвящен обучению и распространению всего, что связано с электротехникой и электроникой.
…
[№. 24] Синхронные моменты в асинхронных двигателях
Рис. 1
1
На рис. 1 показаны два типа неравномерности характеристики скорость/момент асинхронного двигателя — падение крутящего момента асинхронного и падение крутящего момента синхронного . Их иногда называют «бугорками» или «крючками». Если характеристика скорости/крутящего момента нагрузки пересекается с кривой двигателя в области провала, двигатель может работать со скоростью, составляющей часть его нормальной скорости («медленно» или «зубчато»), и не сможет нормально запуститься. Обычно это состояние очень шумное. Двигатель может даже не запуститься («блокировка в состоянии покоя»).
С этими проблемами столкнулись в первые дни разработки асинхронного двигателя. Были разработаны эмпирические правила, часто основанные на практическом опыте, особенно в отношении комбинации номеров пазов ротора и статора. Некоторые компании построили и испытали десятки двигателей с разным количеством слотов, разной степенью перекоса и даже разным количеством фаз; но опубликованные данные очень редко встречаются в литературе. Даже сегодня проблема не имеет однозначного предписывающего решения, и различные авторитеты не достигли полного согласия. Остается много искусства, и тестирование остается важным.
Даже сегодня проблема не имеет однозначного предписывающего решения, и различные авторитеты не достигли полного согласия. Остается много искусства, и тестирование остается важным.
На рис. 1 показан только один провал асинхронного момента из-за 7 -й -й пространственной гармоники MMF статора, который вращается вперед на 1/7 синхронной скорости. Этот конкретный провал происходит исключительно из-за гармоники MMF и не зависит от слотирования. В трехфазном двигателе гармоника 5 th MMF может иметь сравнимый эффект, но она вращается в обратном направлении (со скоростью 1/5 синхронной скорости) и, следовательно, не создает проблем при нормальной работе двигателя. Хотя эффекты обычно уменьшаются с увеличением порядка гармоники, провалы асинхронного крутящего момента более высокого порядка могут возникать из-за взаимодействия с гармониками пермеанса.
Синхронный крутящий момент или «блокирующий крутящий момент» представляет собой нониусный реактивный крутящий момент, связанный с прорезями на обеих сторонах воздушного зазора, который имеет тенденцию стягивать зубья статора и ротора вместе группами. Эффект эквивалентен верньерному реактивному двигателю, встроенному в основной двигатель (Lee [1963]), и действительно, некоторые анализы, касающиеся номеров слотов, очень похожи на те же соображения, касающиеся шаговых двигателей и переключаемых реактивных двигателей.
Эффект эквивалентен верньерному реактивному двигателю, встроенному в основной двигатель (Lee [1963]), и действительно, некоторые анализы, касающиеся номеров слотов, очень похожи на те же соображения, касающиеся шаговых двигателей и переключаемых реактивных двигателей.
Рис. 2
Рис. 3
С 1920-х годов анализ паразитных крутящих моментов в значительной степени полагался на ряды Фурье (, а не БПФ!), чтобы найти пространственные гармоники распределения обмотки и пазов. Это хорошо работает, но вопрос о «безопасной» комбинации номеров пазов статора и ротора может быть потерян в математике, особенно для синхронных моментов.
На рис. 2 показан двигатель с 24 пазами и 26 стержнями ротора: \(Z_S = 24\) и \(Z_R = 26\). На левой диаграмме зуб ротора идеально совмещен с зубом статора на 9.0206 x — ось: зуб 1 на 0° и зуб 13 на 180°. В этих положениях преобладает «выровненное» состояние, обозначенное \(\mathsf{A}\) на более подробном изображении на рис. 3. Любая пространственно-гармоническая МДС статора, ориентированная вдоль оси x , заблокирует ротор в этом «фиксированном» положении. Термины «фиксированное положение» и «фиксирующий крутящий момент» являются стандартными терминами, связанными с верньерными реактивными двигателями и шаговыми двигателями, и их полезно позаимствовать здесь.
Любая пространственно-гармоническая МДС статора, ориентированная вдоль оси x , заблокирует ротор в этом «фиксированном» положении. Термины «фиксированное положение» и «фиксирующий крутящий момент» являются стандартными терминами, связанными с верньерными реактивными двигателями и шаговыми двигателями, и их полезно позаимствовать здесь.
Также на левой схеме показаны зубья статора 7 и 19.на ±90° точно выровнены с центральной линией паза ротора . В этих положениях мы находим состояние «невыравнивания», обозначенное \(\mathsf{U}\) на рис. 3. ротор в ближайшую совмещенную позицию. Этот принцип также хорошо известен в теории реактивных двигателей с нониусом.
В совмещенном положении перекрытие между зубьями статора и зубьями ротора максимальное, тогда как в несоосном состоянии зубец статора находится посередине между двумя зубьями ротора. Зубец статора имеет одинаковое перекрытие с обоими этими зубьями ротора, но любое вращение от этого положения создает крутящий момент повторного выравнивания, который имеет тенденцию увеличивать перекрытие с одним зубом ротора и уменьшать перекрытие с другим. Перекрытия заштрихованы на рис. 2, чтобы помочь визуализировать это поведение.
Перекрытия заштрихованы на рис. 2, чтобы помочь визуализировать это поведение.
На правой диаграмме рис. 2 ротор переместился на половину шага паза ротора, т. е. 0,5 × 360/26 = 6,923°. Выровненное состояние теперь обнаруживается при ±90° (зубья 7 и 19), а несоосное состояние обнаруживается при зубцах 1 и 13 (0 и 180°). Во время этого вращения на половину шага прорези ротора представьте, что основная волна МДС вращается в том же направлении на 90°. Положение «фиксация» теперь составляет 90°. При непрерывном вращении стопорный момент продвигает ротор вперед с «нониусной» или субсинхронной скоростью, которая составляет точно 6·923/90 = 1/13 синхронной скорости поля.
На самом деле существует шесть выровненных условий, возникающих в 90°, которые мы рассматривали. Они происходят последовательно на соседних зубьях статора и соседних зубцах ротора. За время, необходимое для того, чтобы поле продвинулось на один шаг паза статора, \(2 \pi / Z_S\), вращение ротора представляет собой только разность между шагами паза, то есть \(2\pi /Z_S – 2\pi / Z_R\). Если синхронная скорость равна \(n_S\) об/сек, а \(n_R\) — скорость ротора, то приравнивая времена, затрачиваемые на соответствующие обороты, получаем
Если синхронная скорость равна \(n_S\) об/сек, а \(n_R\) — скорость ротора, то приравнивая времена, затрачиваемые на соответствующие обороты, получаем
\(\НАИБОЛЬШИЙ \frac{2\pi/Z_S – 2\pi/Z_R}{n_R} = \frac{2\pi/Z_S}{n_S} ,\)(1)
из которых
\ (\LARGE \frac{n_R}{n_S} = \frac{Z_R – Z_S}{Z_R} ·\) (2)
Когда может возникнуть это условие?
На рис. 2 показана картина выравниваний, возникающих в симметричных группах, и это кажется неизбежным, когда \(\vert Z_S – Z_R \vert = 2\). Однако нетрудно представить себе 4-полюсную или 6-полюсную схему выравнивания. Это означает, что разрешающим условием является \(\vert Z_S — Z_R \vert = 2p\), где \(p\) — количество пар полюсов. Другой способ выразить это
\(\LARGE \frac{Z_R}{2p} = \frac{Z_S}{2p} \pm 1 , \) (3)
, форма, данная некоторыми авторами. Если \(Z_R > Z_S\) ротор вращается в том же направлении, что и МДС, но если \(Z_R
Еще одно «запирающее» состояние возникает в состоянии покоя, если \(Z_S = Z_R\), когда каждый зубец статора совмещен с зубцом ротора. В этом случае фиксирующий момент огромен, и двигатель не запустится. Многие другие комбинации пазов могут вызвать проблемы с синхронными блокирующими моментами, но рассмотренные здесь, безусловно, являются одними из самых важных.
В этом случае фиксирующий момент огромен, и двигатель не запустится. Многие другие комбинации пазов могут вызвать проблемы с синхронными блокирующими моментами, но рассмотренные здесь, безусловно, являются одними из самых важных.
На практике мы ожидаем, что синхронные запирающие моменты будут значительно снижены из-за перекоса и/или когда отверстия в пазах ротора малы или равны нулю. Это помогает объяснить, почему правила, основанные на ур. (3) и другие часто ломаются. Тем не менее, нет простого рецепта для оптимальной величины перекоса, потому что перекос может быть необходим для компенсации других эффектов, таких как асинхронные крутящие моменты, возникающие из-за щелевых гармоник МДС статора. Более того, даже там, где доступен «точный» гармонический анализ, эффекты перекоса могут стать непредсказуемыми из-за межстержневых токов, протекающих через пластины ротора, и из-за изменений уровня насыщения по длине. Возможности для дальнейшего анализа? Много!
Дополнительная литература — Lee CH, Vernier Motor and its Design , IEEE Transactions on Power Apparatus and Systems, 82 (66), pp. 343-349, 1963. асинхронные электроприводы — обзор | Защита и управление современными энергосистемами
343-349, 1963. асинхронные электроприводы — обзор | Защита и управление современными энергосистемами
Современные методы совершенствования прямого управления моментом асинхронных приводов – обзор
Скачать PDF
Скачать PDF
- Обзор
- Открытый доступ
- Опубликовано:
- Наджиб Эль Уанджли
ORCID: orcid.org/0000-0001-7775-7747 1 , - Азиз Деруич 1 ,
- Абдельазиз Эль Гизаль 1 ,
- SAAD MOTAHHIR 1 ,
- ALI CHEBABHI 2 ,
- Youness El Mourabit 1 и
- …
- Mohammed Taoussi 3
99999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999ня- .
 ..
..- .
, i r(α,β) : αβ components of the stator and rotor currentsЗащита и управление современными энергосистемами
том 4 , номер статьи: 11 (2019)
Процитировать эту статью15 тыс. обращений
46 цитирований
Сведения о показателях
Abstract
Обычное прямое управление крутящим моментом (DTC) является одной из превосходных стратегий управления, доступных для управления крутящим моментом асинхронной машины (IM). Однако низкая частота переключения DTC вызывает сильные пульсации потока и крутящего момента, что приводит к акустическому шуму, который ухудшает характеристики управления, особенно на низких скоростях.
 Появилось множество методов прямого управления крутящим моментом, чтобы решить эти проблемы, сосредоточив внимание конкретно на крутящем моменте и потоке. В этой статье представлен обзор различных современных методов повышения эффективности управления DTC. Цель состоит в том, чтобы провести критический анализ этих методов с точки зрения уменьшения пульсаций, скорости отслеживания, потерь при переключении, сложности алгоритма и чувствительности к параметрам. Кроме того, предполагается, что информация, представленная в этом обзорном документе, станет ценным источником информации для академических и промышленных исследователей.
Появилось множество методов прямого управления крутящим моментом, чтобы решить эти проблемы, сосредоточив внимание конкретно на крутящем моменте и потоке. В этой статье представлен обзор различных современных методов повышения эффективности управления DTC. Цель состоит в том, чтобы провести критический анализ этих методов с точки зрения уменьшения пульсаций, скорости отслеживания, потерь при переключении, сложности алгоритма и чувствительности к параметрам. Кроме того, предполагается, что информация, представленная в этом обзорном документе, станет ценным источником информации для академических и промышленных исследователей.Введение
В промышленности более половины всей производимой электроэнергии потребляется электродвигателями [1]. Среди нескольких типов электродвигателей видное место занимают трехфазные асинхронные машины (АД). Действительно, не менее 80% промышленных систем управления используют асинхронные двигатели [2], которые постепенно вытеснили машины постоянного тока благодаря своим хорошим характеристикам: надежности, простоте конструкции, дешевизне и простоте обслуживания [3, 4].
 Однако эти многочисленные достоинства не лишены неудобств, динамическое поведение машины часто бывает очень сложным [5, 6], так как при ее моделировании получается система нелинейных уравнений, сильно связанных и многомерных. Кроме того, некоторые его переменные состояния, такие как поток, не поддаются измерению [7]. Эти ограничения требуют более совершенных алгоритмов управления для управления крутящим моментом и магнитным потоком этих машин в режиме реального времени [8]. В течение нескольких лет академические и промышленные исследования проводились для решения проблемы управления АД и разработки надежных и эффективных средств управления [9].].
Однако эти многочисленные достоинства не лишены неудобств, динамическое поведение машины часто бывает очень сложным [5, 6], так как при ее моделировании получается система нелинейных уравнений, сильно связанных и многомерных. Кроме того, некоторые его переменные состояния, такие как поток, не поддаются измерению [7]. Эти ограничения требуют более совершенных алгоритмов управления для управления крутящим моментом и магнитным потоком этих машин в режиме реального времени [8]. В течение нескольких лет академические и промышленные исследования проводились для решения проблемы управления АД и разработки надежных и эффективных средств управления [9].].В этом контексте скалярное управление является первым методом, который был разработан для управления электрическими машинами. Эта стратегия управления состоит в поддержании постоянного значения V/f для поддержания постоянного потока в машине [10, 11]. Он характеризуется простотой реализации, простой структурой, в основе которой лежит управление потоком статора [12].
 Однако при пуске или изменении направления вращения машины поток сильно колеблется с большими амплитудами, а его модуль в переходных режимах изменяется [13, 14]. Эти колебания будут влиять на качество крутящего момента и скорость, тем самым ухудшая характеристики в переходном состоянии машины. Поэтому этот тип управления используется только для приложений, где изменение скорости невелико, например, в насосной или вентиляционной системе [15, 16].
Однако при пуске или изменении направления вращения машины поток сильно колеблется с большими амплитудами, а его модуль в переходных режимах изменяется [13, 14]. Эти колебания будут влиять на качество крутящего момента и скорость, тем самым ухудшая характеристики в переходном состоянии машины. Поэтому этот тип управления используется только для приложений, где изменение скорости невелико, например, в насосной или вентиляционной системе [15, 16].Впоследствии для управления переходным крутящим моментом был разработан метод полевого управления (FOC) [5]. Это управление обеспечивает поведение АД, аналогичное поведению машины постоянного тока, с развязкой между крутящим моментом и потоком машины [17,18,19], эта развязка обеспечивает очень быструю реакцию крутящего момента, большой диапазон регулирования скорости и высокая эффективность в широком диапазоне нагрузок. Однако этот контроль также имеет высокую чувствительность к параметрическим изменениям машины, особенно к резисторам, значение которых существенно изменяется с температурой [20, 21, 22].
 Любая разница между параметрами, используемыми алгоритмом ВОК, и реальными параметрами машины транслируется ошибками в выходных значениях потока и момента, что приводит к увеличению потерь в машине и снижению производительности управляемой системы. 23].
Любая разница между параметрами, используемыми алгоритмом ВОК, и реальными параметрами машины транслируется ошибками в выходных значениях потока и момента, что приводит к увеличению потерь в машине и снижению производительности управляемой системы. 23].В середине 1980-х годов была введена система прямого контроля крутящего момента (DTC), призванная конкурировать с обычными системами управления. Этот метод был представлен TAKAHASHI [24] и DEPENBROCK [25]. Он обладает замечательными динамическими характеристиками, а также хорошей устойчивостью к изменениям параметров машины. Его принцип основан на прямом определении управляющих импульсов, подаваемых на ключи инвертора напряжения [26,27,28]. Однако возникают два основных недостатка: (i) частота переключения сильно варьируется и (ii) амплитуда волнистости крутящего момента и потока статора плохо контролируются во всем диапазоне скоростей предполагаемой операции [29].,30,31]. Следует отметить, что пульсации крутящего момента создают дополнительный шум и вибрации и, следовательно, вызывают возмущения во вращающемся валу [32].

В настоящее время многие исследователи пытались решить эти проблемы. Термин «управление искусственным интеллектом» (ИИ) появился в последние годы и занимает большое место в современных областях исследований. Нечеткая логика, нейронные сети и генетические алгоритмы — основные семейства, составляющие ИИ. В [29, 33] авторы предлагают методы искусственного интеллекта для улучшения динамических характеристик управления DTC, эти методы управления могут обеспечить оптимизацию производительности при различных условиях эксплуатации, направленную на снижение пульсаций крутящего момента и потока, снижение THD, повышение эффективности, экономию энергии. и др.
Из опубликованной литературы разные работы, рассматривающие схемы ДТК для асинхронных двигателей, но эти схемы критически не рассматриваются. Наш вклад в эту работу заключается в рассмотрении различных современных методов улучшения характеристик прямого управления крутящим моментом; цель состоит в том, чтобы дать идею исследователям, которые интересуются современным состоянием стратегии DTC и работают над новыми направлениями исследований.

Обзорная статья организована следующим образом: В разделе 2 представлена трехфазная математическая модель АД и ее преобразование в двухфазной системе. Представление в виде состояния выводится из физических законов, управляющих его работой при подаче на машину напряжения. В разделе 3 обсуждается классический метод DTC, основанный на таблице переключений и гистерезисных контроллерах, а также основные проблемы, возникающие при использовании этой стратегии управления. В разделе 4 обсуждаются некоторые методы улучшения обычных DTC, кратко упоминаются некоторые типичные методы и рассматриваются современные методы, основанные на искусственном интеллекте. В разделе 5 представлено сравнительное исследование представленных методов улучшения, в конце этой статьи представлена таблица, обобщающая сравнение, которая призвана помочь в выборе подходящей команды для конкретного приложения, а в разделе 6 обобщаются выводы исследования. бумага.
Динамическая модель асинхронной машины
Наиболее подходящей моделью для исследования динамического поведения и разработки алгоритмов управления трехфазной АД является двухфазная модель, выраженная ссылкой (α,β) [34, 35].
 Эта модель снижает сложность трехфазного представления (a, b, c) машины.
Эта модель снижает сложность трехфазного представления (a, b, c) машины.Электромагнитные уравнения асинхронной машины в системе отсчета (α, β) имеют вид [36, 37]:
$$ \frac{d}{dt}\left[\begin{array}{l} {i}_{s\alpha}\\ {}{i}_{s\beta}\\ {}{\psi}_{s\alpha}\\ {}{\psi}_{s\beta} \end{массив}\right]=\left[\begin{array}{c}-\frac{1}{\sigma}\left(\frac{1}{\tau_s}+\frac{1}{\ tau_r}\right)\\ {}\begin{array}{c}{\omega}_r\\ {}\begin{array}{c}-{R}_s\\ {}0\end{array}\ конец {массив} \ конец {массив} \ kern0.5em \ begin {массив} {c} — {\ omega} _r \\ {} \ begin {массив} {c} — \ frac {1} {\ sigma} \ влево(\frac{1}{\tau_s}+\frac{1}{\tau_r}\right)\\ {}\begin{array}{c}0\\ {}-{R}_s\end{массив }\end{массив}\end{массив}\kern0.5em \begin{массив}{cc}\begin{массив}{c}\frac{1}{\sigma {L}_s{\tau}_r}\ \ {}\begin{array}{c}-\frac{\omega_r}{\sigma {L}_s}\\ {}\begin{array}{c}0\\ {}0\end{массив}\ конец {массив}\конец{массив}& \begin{массив}{c}\begin{массив}{c}\begin{массив}{c}\frac{\omega_r}{\sigma {L}_s}\\ {}\frac{1}{\sigma {L}_s{\tau}_r}\end{массив}\\ {}0\end{массив}\\ {}0\end{массив}\end{массив} \право лево [\begin{array}{l}{i}_{s\alpha}\\ {}{i}_{s\beta}\\ {}{\psi}_{s\alpha}\\ {}{}{ \psi}_{s\beta}\end{массив}\right]+\left[\begin{массив}{cc}\begin{массив}{c}\frac{1}{\sigma {L}_s} \\ {}\begin{array}{c}0\\ {}1\\ {}0\end{массив}\end{массив}& \begin{массив}{c}\begin{массив}{c} \begin{array}{c}0\\ {}\frac{1}{\sigma {L}_s}\end{array}\\ {}0\end{array}\\ {}1\end{array }\end{массив}\right].
 \left[\begin{массив}{l}{V}_{s\alpha}\\ {}{V}_{s\beta}\end{массив}\right ] $$ 92}{L_s{L}_r}\kern0.5em {\tau}_s=\frac{R_s}{L_s}\kern0.5em {\tau}_r=\frac{R_r}{L_r} $$
\left[\begin{массив}{l}{V}_{s\alpha}\\ {}{V}_{s\beta}\end{массив}\right ] $$ 92}{L_s{L}_r}\kern0.5em {\tau}_s=\frac{R_s}{L_s}\kern0.5em {\tau}_r=\frac{R_r}{L_r} $$уравнения электромагнитного момента и движения задаются следующими выражениями:
$$ {T}_{em}=p\left({\psi}_{s\alpha}{i}_{s\alpha}- {\psi}_{s\beta}{i}_{s\beta}\right) $$
(2)
$$ J.\frac{d\Omega}{dt}+f.\Omega ={T}_{em}-{T}_r $$
(3)
Переход трехфазного эталона (a, b, c) к двухфазному эталону (α, β) может быть достигается преобразованием, называемым Concordia [38], это преобразование определяется как:
$$ \left[\begin{array}{l}{X}_{\alpha}\\ {}{X}_{\beta}\end{array}\right]=\sqrt{\frac{ 2}{3}}.\left[\begin{массив}{c}\begin{массив}{l}1\\ {}\end{массив}\\ {}0\end{массив}\kern0.5em \begin{array}{cc}\begin{array}{c}-\frac{1}{2}\\ {}\frac{\sqrt{3}}{2}\end{array}& \begin{ array}{c}-\frac{1}{2}\\ {}-\frac{\sqrt{3}}{2}\end{массив}\end{массив}\right].\left[\begin {array}{l}{X}_a\\ {}{X}_b\\ {}{X}_c\end{array}\right] $$
(4)
С: X может быть текущим , напряжение или поток машины.

Прямое управление крутящим моментом
Прямое управление крутящим моментом (DTC) для асинхронных машин было предложено в середине 1980-х годов Такахаши [24] и Депенброком [25]. По сравнению с векторным управлением оно менее чувствительно к параметрическим изменениям машины [18, 39], его алгоритм управления прост из-за отсутствия широтно-импульсной модуляции (ШИМ), регуляторов тока и преобразований парка [40, 41]. . Он не использует контуры ПИ-регулирования, что априори должно улучшить его динамические навыки и устранить проблемы, связанные с насыщением ПИ-регуляторов. Управление DTC обеспечивает высокую эффективность работы и обеспечивает точную и быструю динамику крутящего момента. Принцип DTC основан на прямом применении управляющей последовательности к переключателям инвертора напряжения (состояния переключения), расположенным перед машиной [42,43,44,45]. Выбор этой последовательности осуществляется за счет использования коммутационной таблицы и двух гистерезисных регуляторов, роль которых заключается в контроле и регулировании электромагнитного момента и потока машины без связи.
 На рис. 1 показана простая структура управления DTC. Электромагнитный момент управляется компаратором с трехуровневым гистерезисом. В то время как поток статора контролируется с помощью компаратора с двухуровневым гистерезисом. Выходы этих компараторов, а также информация о векторе потока используются для определения таблицы переключения.
На рис. 1 показана простая структура управления DTC. Электромагнитный момент управляется компаратором с трехуровневым гистерезисом. В то время как поток статора контролируется с помощью компаратора с двухуровневым гистерезисом. Выходы этих компараторов, а также информация о векторе потока используются для определения таблицы переключения.Рис. 1
Краткая схема управления DTC асинхронной машины
Изображение в полный размер
В DTC точность оценки электромагнитного момента и потока статора очень важна для обеспечения удовлетворительной работы [34, 46]. Таким образом, необходимо определить несколько параметров, ток статора измеряется, а напряжение статора зависит от состояния переключения (S a , S b и S c ), создаваемого таблицей переключения и напряжением звена постоянного тока U 92} $$
(5)
$$ {T}_{em}=p.\left({\hat{\psi}}_{s\alpha}.{i}_{s\beta} -{\hat{\psi}}_{s\beta}.{i}_{s\alpha}\right) $$
(6)
Угол θ s вычисляется из:
$ $ {\ theta} _s = arctg \ left (\ frac {{\ hat {\ psi}} _ {s \ beta}} {{\ hat {\ psi}} _ {s \ alpha}} \ right) $ $
(7)
С компонентами потока статора в эталоне (α, β):
$$ \left\{\begin{array}{c}{\hat{\psi}}_{s\ alpha}=\underset{0}{\overset{t}{\int }}\left({v}_{s\alpha}-{R}_s.
 {i}_{s\alpha}\right). dt \\ {}{\ hat{\psi}}_{s\beta}=\underset{0}{\overset{t}{\int}}\left({v}_{s\beta}-{ R}_s.{i}_{s\beta}\right). дт\конец{массив}\право. $$
{i}_{s\alpha}\right). dt \\ {}{\ hat{\psi}}_{s\beta}=\underset{0}{\overset{t}{\int}}\left({v}_{s\beta}-{ R}_s.{i}_{s\beta}\right). дт\конец{массив}\право. $$(8)
Затем оценочные значения электромагнитного момента Test и потока статора ψ est сравниваются соответственно с их эталонными значениями T em* и ψ s* , результаты формы сравнения входы гистерезисных компараторов [48]. Выбор соответствующего вектора напряжения осуществляется на основе контрольной таблицы [10] (таблица 1). Входными данными этой таблицы являются номер сектора потока и выходные данные двух гистерезисных компараторов.
Таблица 1 Таблица переключений
Полноразмерная таблица
Несмотря на свою простоту, надежность и скорость, управление DTC имеет существенные недостатки. Использование гистерезисных регуляторов вызывает сильные пульсации потока и электромагнитного момента, которые вызывают механические вибрации и нежелательные акустические шумы и, следовательно, ухудшение характеристик машины [34, 49], таким образом, переменная частота коммутации и искажения тока, которые могут ухудшить качество выходной мощности [50, 51].
 Пренебрежение сопротивлением статора вызывает проблемы на низкой скорости. Кроме того, практическая реализация нелинейных элементов гистерезисного типа требует довольно малого периода дискретизации и, следовательно, высокой частоты вычислений, что приводит к ограничивающим архитектурам [52].
Пренебрежение сопротивлением статора вызывает проблемы на низкой скорости. Кроме того, практическая реализация нелинейных элементов гистерезисного типа требует довольно малого периода дискретизации и, следовательно, высокой частоты вычислений, что приводит к ограничивающим архитектурам [52].В последние годы появилось множество стратегий прямого управления, позволяющих преодолеть проблемы обычного DTC. Эти стратегии основаны на одном и том же принципе мгновенного регулирования крутящего момента и потока статора, а также на прямом определении управляющих сигналов инвертора из таблицы коммутации. В целом, эти методы контроля можно разделить на две категории: типовые и современные методы. К ним относятся: векторная пространственная модуляция (SVM) [53], DTC на основе скользящего режима, DTC с прогнозированием моделей и искусственный интеллект (нечеткая логика, нейронная сеть и генетический алгоритм) [54, 55]. На рис. 2 показана классификация методов, используемых для улучшения контроля DTC асинхронной машины.

Рис. 2
Классификация методов улучшения прямого управления крутящим моментом
Увеличенное изображение
Улучшение методов прямого управления крутящим моментом
Типовые методы улучшения прямого управления крутящим моментом
Несколько авторов использовали Модуляцию пространственного вектора (SVM) метод управления инвертором напряжения для улучшения DTC [56,57,58]. Принцип этой методики состоит в наложении соответствующего вектора напряжения через векторную модуляцию пространства, чтобы перейти к прогнозирующему регулированию крутящего момента и потока. Алгоритм управления для этого метода более сложен, но колебания потока и момента уменьшаются, а средняя частота коммутации инвертора становится постоянной [59].]. Как и любой метод прогнозирования, DTC-SVM имеет некоторую погрешность статического крутящего момента для управления без контура скорости во время практической реализации. Действительно, эта ошибка связана со временем вычислений, необходимым для предсказания управляющего напряжения.

Авторы [56] разработали метод, позволяющий получить постоянную частоту переключения. Эта стратегия характеризуется отказом от таблицы выбора Такахаши и компараторов с гистерезисом. В этом контексте метод ШИМ используется для генерации выходного вектора управления. Целью этой стратегии является реализация прямого управления вектором потока статора в системе отсчета (α, β), связанной со статором. Компоненты проекции желаемого вектора напряжения статора на два соседних вектора напряжения кадра (α, β) позволяют вычислить желаемое время переключения.
В [60, 61] предложен метод прямого управления моментом АД на основе широтно-импульсной модуляции (ШИМ) с постоянной частотой переключения. Предлагаемый метод управления разработан в дискретном времени, чтобы его можно было реализовать на микроконтроллерах или платах DSP. Авторы используют моделирование и экспериментальные тесты для проверки предложенного метода. В [62, 63] авторы показали, что обычный ДТК имеет малое количество векторов напряжения, прикладываемых к машине, что вызывает нежелательные колебания крутящего момента, потока и тока.
 Эта работа показывает, что улучшенная производительность может быть достигнута за счет использования нового алгоритма DTC, основанного на применении SVM для фиксированных интервалов времени. Таким образом, дискретная пространственно-векторная модуляция (DSVM) использует пятиуровневый компаратор крутящего момента для получения более высокого числа вектора напряжения. Численное моделирование и экспериментальные испытания показывают улучшенные характеристики крутящего момента и магнитного потока при фиксированной частоте переключения.
Эта работа показывает, что улучшенная производительность может быть достигнута за счет использования нового алгоритма DTC, основанного на применении SVM для фиксированных интервалов времени. Таким образом, дискретная пространственно-векторная модуляция (DSVM) использует пятиуровневый компаратор крутящего момента для получения более высокого числа вектора напряжения. Численное моделирование и экспериментальные испытания показывают улучшенные характеристики крутящего момента и магнитного потока при фиксированной частоте переключения.Некоторые авторы адаптировали ДТК для управления машинами, питаемыми от инверторов разноуровневых типов напряжения [64], действительно, большее количество векторов управления способствует минимизации результирующих пульсаций в установившемся режиме. В [64, 65] к ДТК применен трехуровневый инвертор для уменьшения пульсаций крутящего момента, но недостатком такой схемы является высокая стоимость. Они очень полезны, особенно при управлении высокой мощностью.

Современные методы усовершенствования прямого управления крутящим моментом
DTC на основе скользящего режима
Управление скользящим режимом (SMC) — это класс управления переменной структурой (VSC), введенный Уткиным [66], он в основном известен своей устойчивостью к внутренним неопределенностям (изменениям параметров машины), внешним неопределенности (возмущение из-за нагрузки) и явления, которые не учитывались при моделировании [67, 68]. Основная особенность СМК проявляется в модифицированном законе управления прерывистым образом [69]. Однако он имеет определенные недостатки: появление явления дребезжания, вызванного прерывистой частью управления, что может оказать пагубное влияние на машины [70], в каждый момент времени система подвергается высокому контролю для обеспечения ее сближение с желаемым и это нежелательно.
Методика SMC была изучена для улучшения DTC для ИМ [68, 71, 72]. Эти методы улучшают характеристики в установившемся режиме и сохраняют преимущества переходного режима [73].
 В [68, 73] авторы начинают использовать стратегию управления скользящим режимом с дискретным временем, чтобы крутящий момент и поток были устойчивыми к изменению параметров машины. Контроллеры подают опорные напряжения (V sa , V sb ) для подачи на IM, и ток контроллера не используется. Однако, в отличие от большинства методов скользящего режима, вектор опорного напряжения рассчитывается векторной системой ШИМ, и используется фиксированная частота переключения. Моделирование и экспериментальные результаты представлены, чтобы показать эффективность предложенной стратегии.
В [68, 73] авторы начинают использовать стратегию управления скользящим режимом с дискретным временем, чтобы крутящий момент и поток были устойчивыми к изменению параметров машины. Контроллеры подают опорные напряжения (V sa , V sb ) для подачи на IM, и ток контроллера не используется. Однако, в отличие от большинства методов скользящего режима, вектор опорного напряжения рассчитывается векторной системой ШИМ, и используется фиксированная частота переключения. Моделирование и экспериментальные результаты представлены, чтобы показать эффективность предложенной стратегии.На рис. 3 показана общая схема конструкции прямого управления крутящим моментом и потоком на основе скользящего режима асинхронной машины (DTC-SMC), управляемой по скорости. Это каскадная команда для управления электромагнитным моментом, квадратичной нормой потока и скоростью. Таким образом, существуют алгоритмы управления скользящими режимами, которые необходимо реализовать в структуре управления для регулировки крутящего момента, потока и скорости.
 Блок «оценщика» состоит из средства оценки потока и крутящего момента, в котором используются только измерения напряжений и токов статора в эталоне (α, β). Эта схема управления является быстрой и надежной. Однако контролируемая величина представляет нежелательную вибрацию.
Блок «оценщика» состоит из средства оценки потока и крутящего момента, в котором используются только измерения напряжений и токов статора в эталоне (α, β). Эта схема управления является быстрой и надежной. Однако контролируемая величина представляет нежелательную вибрацию.Рис. 3
Синоптическая схема DTC-SMC управления асинхронной машиной
Изображение в полный размер
В других работах использовался надежный наблюдатель скользящего режима [74], чтобы сделать оценку потока менее чувствительной к шуму измерения.
Упреждающий код неисправности модели
Упреждающий контроль — это усовершенствованный метод автоматического управления. Его целью является управление сложными промышленными системами. Принцип этой методики основан на расчете будущего поведения системы на основе динамической модели процесса внутри контроллера реального времени, чтобы иметь возможность использовать эту информацию для расчета оптимальных значений параметров настройки.
 [75]. Применение модели прогнозирующего управления (MPC) в области цифрового управления дало хорошие результаты с точки зрения скорости и точности [76].
[75]. Применение модели прогнозирующего управления (MPC) в области цифрового управления дало хорошие результаты с точки зрения скорости и точности [76].В последнее время стратегия прогнозирующего управления для DTC привлекла значительное внимание, в частности, из-за ее способности минимизировать частоту коммутации инвертора напряжения, питающего машину, и уменьшить пульсации крутящего момента и магнитного потока. В DTC-MPC традиционная таблица переключения DTC заменена алгоритмом онлайн-оптимизации [77,78,79]. Принцип выбора вектора в прогнозирующем управлении основан на оценке определенной функции стоимости [80, 81]. Прогностическая модель с потоком статора, крутящим моментом и угловой скоростью используется для прогнозирования будущего поведения контролируемых переменных. Упрощенная схема DTC-MPC представлена на рис. 4.
Рис. 4
Блок-схема DTC-MPC
Полноразмерное изображение
Выполнение алгоритма прогнозирования может быть выполнено в три основных этапа:
Оценка неизмеримых переменных.

Предсказание будущего поведения системы.
Оптимизация управляющих выходов в соответствии с ранее определенной функцией стоимости.
Эти шаги повторяются на каждом временном шаге дискретизации с учетом новых измерений. Управление с обратной связью достигается путем обратной связи на основе измерений, используемых для прогнозирования и принятия решения о мерах, принимаемых для уменьшения значения функции стоимости F. На рис. 5 показана блок-схема DTC-MPC.
Рис. 5
Блок-схема DTC-MPC
Полноразмерное изображение
Прогнозирующее управление имеет много преимуществ, концепция MPC очень проста и интуитивно понятна, ее легко реализовать, ограничения и нелинейности управляемых систем могут быть включены в управление и в случае многопараметрических систем.
 можно принять во внимание [34]. Однако этот тип управления требует большого количества онлайн-вычислений по сравнению с обычным DTC.
можно принять во внимание [34]. Однако этот тип управления требует большого количества онлайн-вычислений по сравнению с обычным DTC.В [82, 83] была представлена стратегия прогнозирующего управления, основанная на оптимизации функции стоимости, определенной на горизонте, чтобы гарантировать подавление возмущений и повысить устойчивость к изменениям параметров и сделать систему более эффективной. Также в [45, 77,78,79,80,81, 84] авторы предлагают методику улучшения динамических характеристик DTC с помощью предиктивного управления, они показали, что DTC-MPC обеспечивает лучшую производительность с точки зрения динамики, оцениваемой быстро, снижения пульсаций крутящего момента и потока и улучшения текущей формы.
Прямое управление крутящим моментом на основе искусственного интеллекта
В последнее время в литературе представлена еще одна категория управления на основе искусственного интеллекта. Эти методы улучшают динамические характеристики управления DTC либо путем адаптации полосы гистерезиса [85, 86], либо путем замены таблицы переключения Такахаши, а также гистерезиса интеллектуальными регуляторами [87,88,89].
 ,90,91,92]. Искусственный интеллект, такой как нечеткая логика, нейронная сеть и генетический алгоритм, познал большие успехи не только в моделировании, но и в управлении электрическими системами, в частности в управлении АД. Этот успех связан с тем, что искусственный интеллект может легко приблизиться к контрольному поведению человека-эксперта, который часто работает в плохо определенных средах. Поэтому в этом разделе мы рассмотрим различные подходы искусственного интеллекта к управлению DTC.
,90,91,92]. Искусственный интеллект, такой как нечеткая логика, нейронная сеть и генетический алгоритм, познал большие успехи не только в моделировании, но и в управлении электрическими системами, в частности в управлении АД. Этот успех связан с тем, что искусственный интеллект может легко приблизиться к контрольному поведению человека-эксперта, который часто работает в плохо определенных средах. Поэтому в этом разделе мы рассмотрим различные подходы искусственного интеллекта к управлению DTC.DTC на основе нечеткой логики
Нечеткая логика, или, в более общем смысле, обработка неопределенностей, является одним из классов искусственного интеллекта [93], он введен для улучшения характеристик различных классических стратегий управления, применяемых к приводам с регулируемой скоростью.
В [94, 95] авторы предлагают метод нечеткого прямого управления крутящим моментом (FDTC) для улучшения динамических характеристик обычного управления DTC. Они разработали новую таблицу выбора на основе контроллера с нечеткой логикой (FLC) для замены таблицы переключения и гистерезисных компараторов, чтобы генерировать векторное напряжение, которое оптимальным образом приводит поток и крутящий момент к их опорным значениям.
 На рис. 6 показана общая структура команды FDTC, применяемой к асинхронной машине.
На рис. 6 показана общая структура команды FDTC, применяемой к асинхронной машине.Рис. 6
Синоптическая схема DTC-нечеткого управления асинхронной машиной выходами являются состояния переключения плеч инвертора (S a , S b , S c ) [96,97,98]. Каждый вход и выход делится на определенное количество нечетких наборов, чтобы иметь лучший контроль с использованием минимума правил.
Правила вывода написаны таким образом, что различия между уставками потока и крутящего момента и их оценочными значениями могут быть скорректированы. Шесть лингвистических переменных используются для представления области угла вектора потока статора. Три лингвистические переменные (N: отрицательная, Z: ноль и P: положительная) используются для фаззификации речевой вселенной ε Tem . И две лингвистические переменные (N: отрицательная и P: положительная) используются для фаззификации речевой вселенной ε ψ .
 Вселенная дискурса каждого выхода делится на два нечетких множества (ноль и единица). Функции принадлежности, принятые для составления нечеткой таблицы, и правила вывода показаны на рис. 7.
Вселенная дискурса каждого выхода делится на два нечетких множества (ноль и единица). Функции принадлежности, принятые для составления нечеткой таблицы, и правила вывода показаны на рис. 7.Рис. 7
Структура нечеткой таблицы переключений стратегия, основанная на нечеткой логике. Целью работы является улучшение характеристик управления DTC при минимизации крутящего момента на малых скоростях. Они имеют встроенный нечеткий регулятор скорости, который позволяет динамически регулировать коэффициент интегрирования k i и коэффициент пропорциональности k p в зависимости от ошибки и изменений скорости. Кроме того, гистерезис потока и крутящего момента заменен нечетким регулятором для оптимизации выбора вектора напряжения. Экспериментальные результаты показывают, что предлагаемая система нечеткого управления может обеспечить быстрое реагирование и высокую точность установившейся скорости, а также заметное уменьшение пульсаций крутящего момента даже на низких скоростях.

Кроме того, нечеткая логика используется для управления пределами полосы гистерезиса электромагнитного момента [99], что влечет за собой минимизацию волнистости крутящего момента, а также улучшение динамических характеристик. В том же контексте Uddin Nasir et al. [86] предложили нечеткий регулятор для регулировки полосы гистерезиса в реальном времени. Эта регулировка основана на наклонах изменения расчетного крутящего момента и тока статора, где нечеткий регулятор выбирает оптимальную полосу пропускания гистерезиса крутящего момента. Результаты моделирования модели, разработанной в среде Matlab/Simulink, а также экспериментальные результаты, реализованные с помощью платы DSP, подтверждают характеристики, полученные этим нечетким контроллером. Сравнительное исследование DTC на основе предложенного нечеткого регулятора и обычного DTC показывает, что пульсации крутящего момента предлагаемого управления были значительно уменьшены.
В [100] стратегия нечеткой логики используется для изучения влияния изменения параметров на производительность DTC посредством использования контрольных таблиц, разработанных с помощью нечеткой логики.
 Работоспособность предложенного метода подтверждена результатами моделирования. Нечеткая логика может справиться с неопределенностью параметров. Однако основными проблемами этого метода являются сложность настройки параметров нечеткой логики и сложность реализации; поскольку нечеткий контроллер использует множество баз правил, проведите обширные эксперименты.
Работоспособность предложенного метода подтверждена результатами моделирования. Нечеткая логика может справиться с неопределенностью параметров. Однако основными проблемами этого метода являются сложность настройки параметров нечеткой логики и сложность реализации; поскольку нечеткий контроллер использует множество баз правил, проведите обширные эксперименты.DTC на основе нейронной сети
Искусственная нейронная сеть (ИНС) широко используется во многих областях применения технологий и научных исследований. Этот метод можно использовать в случаях сложных задач, которые не могут быть описаны с помощью точных математических подходов, когда ими очень сложно управлять [101]. Области применения этих нейронных сетей очень широки: классификация, обработка изображений и речи, оценка, идентификация процессов [102, 103] и управление электрическими системами [104, 105]. В [106] авторы интегрировали искусственные нейронные сети в управление асинхронной машиной; они отметили, что в некоторых случаях, когда динамика системы изменяется во времени и/или в зависимости от условий эксплуатации, снижается эффективность ПИ-регулятора и ухудшается качество настройки.
 Чтобы преодолеть эти проблемы и обеспечить хорошую работу команды, авторы интегрировали искусственные нейронные сети в управление скоростью. Было смоделировано несколько тестов для оценки вклада ИНС. Полученные результаты позволяют утверждать об улучшении характеристик и надежности управления АД.
Чтобы преодолеть эти проблемы и обеспечить хорошую работу команды, авторы интегрировали искусственные нейронные сети в управление скоростью. Было смоделировано несколько тестов для оценки вклада ИНС. Полученные результаты позволяют утверждать об улучшении характеристик и надежности управления АД.В нескольких исследованиях было предложено применение метода ИНС для выбора состояний переключателей инвертора напряжения, используемых для питания АД, управляемого DTC [107, 108, 109, 110, 111, 112]. Идея всегда состоит в том, чтобы заменить обычную таблицу коммутации, определяющую состояния инвертора, нейронным селектором, способным таким же образом управлять управляющими сигналами. На рис. 8 показана блок-схема прямого нейронного управления крутящим моментом (DTNC). Архитектура включает в себя многослойную нейронную сеть, позволяющую заменить как гистерезисные компараторы, так и таблицу выбора. Эта нейронная сеть состоит из входного слоя, двух скрытых слоев и выходного слоя. Входной слой состоит из трех нейронов, обозначенных соответственно ошибкой крутящего момента, ошибкой потока и угловым положением (θ) вектора потока статора.
 Каждый из двух скрытых слоев состоит из десяти нейронов. Выходной слой состоит из трех нейронов, которые производят опорное напряжение, которое должно быть приложено к АД через инвертор напряжения.
Каждый из двух скрытых слоев состоит из десяти нейронов. Выходной слой состоит из трех нейронов, которые производят опорное напряжение, которое должно быть приложено к АД через инвертор напряжения.Рис. 8
Синоптическая схема управления DTC-ANN асинхронной машины
Изображение в натуральную величину значительное снижение пульсаций крутящего момента и скорости гармоник токов по сравнению с другими традиционными методами [107]. Кроме того, он очень устойчив к различным неопределенностям параметров двигателя [111]. Однако этот предлагаемый способ имеет недостаток, заключающийся в более сложной внутренней структуре.
Генетический алгоритм на основе DTC
Генетические алгоритмы (ГА) представляют собой довольно богатое и интересное семейство алгоритмов стохастической оптимизации, основанных на методах, полученных из естественной эволюции и генетики [113]. Принцип этих алгоритмов заключается в стохастическом поиске в большом пространстве и в совокупности псевдорешений [114].
 Устойчивость к параметрическим вариациям — одна из основных характеристик генетических алгоритмов; они позволяют предоставить одно или несколько качественных решений для самых разнообразных задач, требуя относительно небольших инвестиций (времени и вычислительной мощности) [115]. Однако он имеет недостаток выбора параметров, так как выбор этих параметров сильно зависит от изучаемой проблематики и знаний пользователя об этой проблеме.
Устойчивость к параметрическим вариациям — одна из основных характеристик генетических алгоритмов; они позволяют предоставить одно или несколько качественных решений для самых разнообразных задач, требуя относительно небольших инвестиций (времени и вычислительной мощности) [115]. Однако он имеет недостаток выбора параметров, так как выбор этих параметров сильно зависит от изучаемой проблематики и знаний пользователя об этой проблеме.В последнее время генетический алгоритм используется для улучшения динамических характеристик системы управления DTC; он хорошо приспособлен для оптимизации значений усиления регулятора скорости [116, 117].
В [116] к ДТК применена методика оптимизации (ГА), авторы используют ПИ-регулятор, оптимизированный генетическим алгоритмом (ПИ-ГА). состояний, многие преимущества которых были подтверждены, связанные с пульсациями крутящего момента и потока, уменьшением перерегулирования и временем отклика.
В [118] авторы предложили новую стратегию DTC, используя генетический алгоритм для оптимизации PI-нечеткого регулятора.
 В этой стратегии в зависимости от ошибки скорости и ее производной по времени регулировка интегрального коэффициента k i и пропорционального k p осуществляется в реальном времени адаптивным регулятором PI-fuzzy скорости. Нечеткие параметры уточняются генетическим алгоритмом для улучшения самоадаптации скорости. Кроме того, гистерезисные регуляторы были заменены другим нечетким регулятором для улучшения выбора вектора напряжения. Наконец, автор представил сравнительное исследование обычного DTC Такахаши, PI-нечеткого регулятора и предложенной стратегии. Это исследование доказало значительное уменьшение пульсаций на уровне крутящего момента, потока и тока. А также повышение точности и скорости отслеживания.
В этой стратегии в зависимости от ошибки скорости и ее производной по времени регулировка интегрального коэффициента k i и пропорционального k p осуществляется в реальном времени адаптивным регулятором PI-fuzzy скорости. Нечеткие параметры уточняются генетическим алгоритмом для улучшения самоадаптации скорости. Кроме того, гистерезисные регуляторы были заменены другим нечетким регулятором для улучшения выбора вектора напряжения. Наконец, автор представил сравнительное исследование обычного DTC Такахаши, PI-нечеткого регулятора и предложенной стратегии. Это исследование доказало значительное уменьшение пульсаций на уровне крутящего момента, потока и тока. А также повышение точности и скорости отслеживания.Критический анализ
В таблице 2 представлен критический анализ предлагаемых методов улучшения характеристик прямого управления крутящим моментом в асинхронной машине. Этот анализ направлен на то, чтобы выделить идею для исследователей, которые заинтересованы в технике DTC.
 Оценка этих методов проводится с точки зрения пульсаций крутящего момента и потока, частоты коммутации, чувствительности к параметрам, стационарного и динамического отклика и сложности алгоритма. Следует отметить, что оценка не имеет абсолютно абсолютного значения, так как очень трудно найти несколько работ, выполненных в одинаковых условиях и на одном и том же типе станка, но основные недостатки и преимущества должны быть одинаковыми для каждого способа контроля. .
Оценка этих методов проводится с точки зрения пульсаций крутящего момента и потока, частоты коммутации, чувствительности к параметрам, стационарного и динамического отклика и сложности алгоритма. Следует отметить, что оценка не имеет абсолютно абсолютного значения, так как очень трудно найти несколько работ, выполненных в одинаковых условиях и на одном и том же типе станка, но основные недостатки и преимущества должны быть одинаковыми для каждого способа контроля. .Таблица 2 Критический анализ методов улучшения прямого управления крутящим моментом [29, 34, 53,54,55, 73, 116, 118,119,120,121]
Полноразмерная таблица
самая простая структура среди других стратегий управления с низкой частотой переключений, которая является основной проблемой DTC. Для преодоления этих проблем и получения достаточно низких пульсаций крутящего момента частота дискретизации обязательно должна быть высокой. Методы искусственного интеллекта и прогнозирующая модель DTC могут обеспечить меньшую пульсацию крутящего момента и частоту переключения, чем прямое управление крутящим моментом при той же частоте дискретизации, но сложность методов ИИ существенно повышается.
 Поэтому его можно использовать для высокоточного управления в приложениях большой мощности. Кроме того, методы SVM и SMC могут быть решениями для улучшения DTC, но они имеют ограничения, такие как чувствительность и явление вибрации.
Поэтому его можно использовать для высокоточного управления в приложениях большой мощности. Кроме того, методы SVM и SMC могут быть решениями для улучшения DTC, но они имеют ограничения, такие как чувствительность и явление вибрации.Предпочтительным подходом к решению проблемы сложности является упрощение алгоритма управления без увеличения вычислительной мощности микропроцессора. С другой стороны, можно повысить производительность привода DTC и получить недорогую систему, разработав гибридную стратегию управления путем объединения двух или более современных технологий.
Заключение
В этой статье рассматриваются несколько современных методов улучшения прямого управления крутящим моментом для асинхронного двигателя. Целью этого усовершенствования является минимизация пульсаций пары и потока АД, с одной стороны, и уменьшение частоты коммутации инвертора, с другой стороны. Представлены классификация и сравнение этих стратегий по уменьшению пульсаций, скорости слежения, коммутационным потерям, сложности алгоритма и чувствительности к параметрам.
 Очень сложно сделать вывод, какое решение является лучшим для улучшения характеристик DTC. Выбор метода зависит от применения, стоимости, наличия оборудования, надежности и точности системы. Ожидается, что этот обзор станет очень полезным инструментом для всех отраслей промышленности и исследователей, работающих в области управления электрическими машинами.
Очень сложно сделать вывод, какое решение является лучшим для улучшения характеристик DTC. Выбор метода зависит от применения, стоимости, наличия оборудования, надежности и точности системы. Ожидается, что этот обзор станет очень полезным инструментом для всех отраслей промышленности и исследователей, работающих в области управления электрическими машинами.Номенклатуры
V S (α, β) , V R (α, β) : αβ -компоненты статера и ротора. β)
ψ s(α,β) , ψ r( α,β) : компоненты αβ потока статора и ротора
S 1 , S 2 , S 3 : Switching states
R s , R r Stator and rotor resistances
L S , L R : индуктивность статора и ротора
M: взаимная индуктивность
τ S , τ R : Статор и ротор.
 0007
0007ω s , ω r : Stator and rotor pulsations
Ω: Mechanical pulsation
T r : Load torque
T em : Electromagnetic torque
Ω: Rotation speed of the machine
Дж: Момент инерции
f: Коэффициент вязкого трения
U c : Напряжение шины постоянного тока
θ с : Положение потока статора
H
0007
H ψs : Hysteresis band of stator flux
K i , K p : Integral and proportional gains
ε Ai : Error of the magnitude Ai
Abbreviations
- ANN:
Искусственные нейронные сети
- DSVM:
Дискретная пространственная векторная модуляция
- Код неисправности:
Прямое управление крутящим моментом
- DTNC:
Прямое нейронное управление крутящим моментом
- ФЛЦ:
Контроллер с нечеткой логикой
- ФОК:
Полевой контроль
- Джорджия:
Генетический алгоритм
- IM:
Индукционная машина
- ПДК:
Модель прогнозирующего управления
- ИП:
Пропорциональный интеграл
- ШИМ:
Широтно-импульсная модуляция
- SMC:
Управление скользящим режимом
- SVM:
Модуляция пространственного вектора
- ТГД:
Общее гармоническое искажение
- ВСК:
Управление переменной структурой
Ссылки
- «>
Хаджиан, М., Араб Маркаде, Г. Р., Солтани, Дж., и Хосейнния, С. (2009). Энергооптимизированное скользящее управление бездатчиковыми асинхронными двигателями. Преобразование энергии и управление, 50 , 2296–2306.
Артикул
Google ученый
- .
Сараванан, К., Сатисвар, Дж., и Раджа, С. (2012). Характеристики трехфазного асинхронного двигателя с модифицированной обмоткой статора. Международный журнал компьютерных приложений, 46 , 1–4.
Google ученый
Коста, Б.Л.Г., Грасиола, К.Л., Анджелико, Б.А., Гедтель, А., и Кастольди, М.Ф. (2018). Метаэвристическая оптимизация применительно к настройке ПИ-контроллеров привода DTC-SVM для трехфазных асинхронных двигателей. Прикладные программные вычисления, 62 , 776–788.
Траоре, Д., Леон, Д., и Глюмино, А. (2012). Адаптивная конструкция управления обратным шагом на основе наблюдателя межсоединений для бездатчикового асинхронного двигателя.
 Automatica, 48 , 682–687.
Automatica, 48 , 682–687.MathSciNet
МАТЕМАТИКА
СтатьяGoogle ученый
Карагианнис Д., Астольфи А., Ортега Р. и Илерет М. (2009). Нелинейный контроллер слежения для асинхронных двигателей, питаемых напряжением, с неопределенным крутящим моментом нагрузки. IEEE Transactions on Control Systems Technology, 17 , 608–619.
Артикул
Google ученый
Сен, ПК (1990). Приводы и управление электродвигателями — прошлое, настоящее и будущее. IEEE Transactions on Industrial Electronics, 37 , 562–575.
Артикул
Google ученый
Трабелси, Р., Хедер, А., Мимуни, М. Ф., и М’сахли, Ф. (2012). Пошаговое управление асинхронным двигателем с помощью адаптивного наблюдателя потока скользящего ротора. Исследование систем электроснабжения, 93 , 1–15.

Артикул
Google ученый
Заафури, А., Регая, К.Б., Азза, Х.Б., и Чаари, А. (2016). Адаптивный обратный шаг на основе DSP с использованием ошибок отслеживания для высокопроизводительного бездатчикового управления скоростью привода асинхронного двигателя. ISA Transactions, 60 , 333–347.
Артикул
Google ученый
Алсофьяни, И. М., и Идрис, Н. Р. Н. (2013). Обзор бессенсорных методов обеспечения устойчивой надежности и эффективности частотно-регулируемых приводов асинхронных двигателей. Обзоры возобновляемых и устойчивых источников энергии, 24 , 111–121.
Артикул
Google ученый
Деруич А. и Лагриуи А. (2014). Моделирование в реальном времени и анализ характеристик асинхронных машин, работающих при постоянном потоке. Международный журнал Advanced Computer Science and Applications, 5 , 59–64.

Артикул
Google ученый
Джаннати, М., Анбаран, С.А., Асгари, С.Х., Гох, В.Ю., Монади, А., Джунаиди, М.А.А., и Идрис, Н.Р.Н. (2017). Обзор методов регулирования скорости для эффективного управления однофазными асинхронными двигателями: эволюция, классификация, сравнение. Обзоры возобновляемых и устойчивых источников энергии, 75 , 1306–1319.
Артикул
Google ученый
Дос Сантос, Т. Х., Гедтель, А., Да Силва, С. А. О., и Суэтаке, М. (2014). Скалярное управление асинхронным двигателем с использованием нейронной бездатчиковой техники. Исследование систем электроснабжения, 108 , 322–330.
Артикул
Google ученый
Леонхард, В. (1994). Управление машинами с помощью микроэлектроники. В Третий симпозиум IFAC по управлению силовой электроникой и электроприводами (стр.
 35–58).
35–58).Google ученый
Перерам, К., Блобьерг, Ф., и Педерсен, Дж. (2003). Безсенсорный, стабильный метод управления V/F для приводов с синхронными двигателями с постоянными магнитами. IEEE Transactions on Industry Applications, 39 , 783–791.
Артикул
Google ученый
Хабби, Х.М.Д., Ажил, Х.Дж., и Инаам, И.А. (2016). Управление скоростью асинхронного двигателя с помощью скалярных векторных контроллеров PI и V/F. Международный журнал компьютерных приложений, 151 , 36–43.
Артикул
Google ученый
Мартинс, К.А., и Карвалью, А.С. (2001). Технологические направления в электроприводах асинхронных двигателей. В Протокол IEEE Porto Power Tech (Том 2).
Google ученый
«>Эль Уанджли, Н., Деруич, А., Эль Гзизал, А., Чебаби, А., и Таусси, М. (2017). Сравнительное исследование управления FOC и DTC асинхронного двигателя с двойным питанием (DFIM). В Международная конференция по электрическим и информационным технологиям: IEEE .
Google ученый
Мехаззем Ф., Неммур А. Л. и Реама А. (2017). Реализация обратного многоскалярного управления в режиме реального времени для асинхронного двигателя, питаемого от инвертора источника напряжения. Международный журнал водородной энергетики, 42 , 17965–17975.
Артикул
Google ученый
«>Профумо Ф., Дедонкер Р., Феррарис П. и Пасторелли М. (1995). Сравнение универсальных полевых (UFO) контроллеров в разных системах отсчета. IEEE Transactions on Power Electronics, 10 , 205–213.
Артикул
Google ученый
Робинс, Б., Бертеро, Ф., Отье, Ж.-П., и Буйз, Х. (2000). Мультимодельная ориентация поля на основе нечеткой логики в непрямом ВОК асинхронного двигателя. IEEE Transactions on Industrial Electronics, 47 , 380–388.
Артикул
Google ученый
«>Такахаши И. и Ногучи Т. (1986). Новая быстродействующая и высокоэффективная стратегия управления асинхронным двигателем. IEEE Transactions on Industry Applications, IA-22 (5), 820–827.
Артикул
Google ученый
Депенброк, М. (1988). Прямое самоуправление (DSC) асинхронной машины с инверторным питанием. Транзакции IEEE по силовой электронике, 3 , 420–429.
Артикул
Google ученый
Ваез-Заде С. и Джалали Э. (2007). Метод комбинированного векторного управления и прямого управления крутящим моментом для высокопроизводительных асинхронных двигателей. Преобразование энергии и управление, 48 , 3095–3101.

Артикул
Google ученый
Эль Уанджли, Н., Деруич, А., Эль Гзизаль, А., Эль Мурабет, Ю., Боссуфи, Б., и Таусси, М. (2017). Вклад в повышение производительности асинхронной машины с двойным питанием, работающей в двигательном режиме, за счет управления DTC. Международный журнал Power Electronics and Drive System, 8 , 1117–1127.
Google ученый
Хедхер, А., и Мимуни, М.Ф. (2010). Бессенсорно-адаптивный DTC асинхронного двигателя с двойной звездой. Преобразование энергии и управление, 51 , 2878–2892.
Артикул
Google ученый
Реза, К.М.Ф.С., Ислам, М.Д., и Мехилеф, С. (2014). Обзор надежных и энергоэффективных асинхронных приводов с прямым регулированием момента. Обзоры возобновляемых и устойчивых источников энергии, 37 , 919–932.

Артикул
Google ученый
Кадир, А., Мехилеф, С., и Пинг, Х.В. (2007). Привод синхронного двигателя с постоянными магнитами с прямым управлением крутящим моментом и асимметричным многоуровневым инверторным питанием. В Седьмая международная конференция по силовой электронике (ICPE): IEEE (стр. 1196–1201).
Google ученый
Наик, В. Н., Панда, А., и Сингх, С. П. (2016). Трехуровневый нечеткий код неисправности 2 привода асинхронного двигателя с использованием SVPW. IEEE Transactions on Industrial Electronics, 63 , 1467–1479.
Артикул
Google ученый
Абош, А. Х., Чжу, З. К., и Рен, Ю. (2017). Уменьшение пульсаций крутящего момента и потока при прямом управлении крутящим моментом асимметричной синхронной машины с постоянными магнитами на основе пространственно-векторной модуляции.
 IEEE Transactions on Power Electronics, 32 , 2976–2986.
IEEE Transactions on Power Electronics, 32 , 2976–2986.Артикул
Google ученый
Гоэль, Н., Патель, Р. Н., и Чакко, С. (2016). Уменьшение пульсаций крутящего момента привода DTC IM с использованием искусственного интеллекта. В Международная конференция по электроэнергетике и энергетическим системам .
Google ученый
Сутикно, Т., Идрис, Н.Р.Н., и Джидин, А. (2014). Обзор прямого управления крутящим моментом асинхронных двигателей для обеспечения устойчивой надежности и энергоэффективности приводов. Обзоры возобновляемых и устойчивых источников энергии, 23 , 548–558.
Артикул
Google ученый
Панчаде, В. М., Чили, Р. Х., и Патре, Б. М. (2013). Обзор стратегий управления скользящим режимом для асинхронных двигателей.
 Ежегодные обзоры в управлении, 37 , 289–307.
Ежегодные обзоры в управлении, 37 , 289–307.Артикул
Google ученый
Бужа Г., Касадей Д. и Серра Г. (1997). Прямое управление крутящим моментом асинхронных двигателей. В Материалы международного симпозиума IEEE по промышленной электронике .
Google ученый
Слемон, Г. Р. (1989). Моделирование асинхронных машин для электроприводов. IEEE Transactions on Industry Applications, 25 , 1126–1131.
Артикул
Google ученый
Хафиз, М., Уддин, М.Н., Рахим, Н.А., и Хью, В.П. (2014). Самонастраивающаяся схема DTC на основе NFC и адаптивного гистерезиса крутящего момента для асинхронного привода. IEEE Transactions on Industry Applications, 50 , 1410–1420.
Артикул
Google ученый
«>Йен-Шин, Л., и Цзянь-Хо, К. (2001). Новый подход к прямому управлению крутящим моментом асинхронных двигателей для обеспечения постоянной частоты коммутации инвертора и уменьшения пульсаций крутящего момента. IEEE Transactions on Energy Conversion, 6 , 220–227.
Артикул
Google ученый
Пуччи, М. (2012). Прямое полеориентированное управление линейными асинхронными двигателями. Исследование систем электроснабжения, 89 , 11–22.
Артикул
Google ученый
«>Эль Мурабит, Ю., Деруич, А., Эль Гзизал, А., Эль Уанджли, Н., и Замзум, О. (2017). DTC-SVM Control для синхронного генератора с постоянными магнитами на основе ветряной турбины с регулируемой скоростью. Международный журнал силовой электроники и систем привода, 8 , 1732–1743.
Google ученый
Талаизаде В., Кианинежад Р., Сейфоссадат С. Г. и Шаянфар Х. А. (2010). Прямое управление моментом шестифазных асинхронных двигателей с использованием трехфазного матричного преобразователя. Преобразование энергии и управление, 51 , 2482–2491.
Артикул
Google ученый
«>Локрити, А., Салхи, И., и Дубаби, С. (2015). Прямое управление крутящим моментом с помощью асинхронного двигателя без искажения потока и статической ошибки крутящего момента. ISA Transactions, 59 , 256–267.
Артикул
Google ученый
Сингх, А.К., Редди, К.У., Прабхакар, К.К., и Правин, К. (2015). Реализация ПЛИС прямого управления крутящим моментом асинхронного двигателя с уменьшенными пульсациями крутящего момента и потока. В IEEE международная конференция по электрификации транспорта .
Google ученый
«>Сутикно, Т., Никидрис, Н. Р., Жидин, А., и Кирстя, М. Н. (2013). Улучшенная реализация ПЛИС прямого управления крутящим моментом для асинхронных машин. IEEE Transactions on Industrial Informatics, 9 (3), 1280–1290.
Джузеппе, С. Б., и Казмерковски, М. П. (2004). Прямое управление крутящим моментом двигателей переменного тока с ШИМ-управлением инвертором — обзор. IEEE Transactions on Industrial Electronics, 51 , 744–757.
Артикул
Google ученый
Аммарн, А., Боурек, А., и Бенакча, А. (2017). Нелинейный SVM-DTC для привода асинхронного двигателя с использованием линеаризации обратной связи по входу-выходу и управления скользящим режимом высокого порядка.
 ISA Transactions, 67 , 428–442.
ISA Transactions, 67 , 428–442.Артикул
Google ученый
Касадей Д., Профумо Ф., Серра Г. и Тани А. (2002). FOC и DTC: две жизнеспособные схемы управления крутящим моментом асинхронных двигателей. IEEE Transactions on Power Electronics, 17 , 779–787.
Артикул
Google ученый
Аммар А., Бенакча А. и Бурек А. (2017). SVM-DTC с обратной связью по крутящему моменту на основе надежного регулятора скорости вращения для асинхронного двигателя с оптимизацией эффективности. Международный журнал водородной энергетики, 42 , 17940–17952.
Артикул
Google ученый
Гаду, С. М., Джаурис, Д., и Финч, Дж. В. (2009). Управление скоростью асинхронных двигателей DTC на основе искусственного интеллекта — сравнительное исследование.
 Исследование систем электроснабжения, 79 , 210–219.
Исследование систем электроснабжения, 79 , 210–219.Артикул
Google ученый
Гдаим С., Мтибаа А. и Мимуни М. Ф. (2010). Прямое управление крутящим моментом асинхронной машины на основе интеллектуальных методов. Международный журнал компьютерных приложений, 10 , 0975–8887.
Артикул
Google ученый
Белкасем, С., Насери, Ф., и Абдессемед, Р. (2011). Улучшение DTC-SVM приводов переменного тока с использованием нового надежного адаптивного алгоритма управления. Международный журнал управления, автоматизации и систем, 9 , 267–275.
Артикул
Google ученый
Родригес, Дж., Понт, Дж., Сильва, К., Куро, С., и Миранда, Х. (2004). Новая схема прямого управления крутящим моментом для асинхронных машин с модуляцией пространственного вектора.
 В Ежегодная конференция специалистов по силовой электронике IEEE (стр. 1392–1397).
В Ежегодная конференция специалистов по силовой электронике IEEE (стр. 1392–1397).Google ученый
Абделли Р., Рекиуа Д. и Рекиуа Т. (2011). Повышение производительности и минимизация пульсаций крутящего момента для асинхронной машины с питанием VSI с прямым управлением крутящим моментом. ISA Transactions, 50 , 213–219.
Артикул
Google ученый
Эль-Саадави, М., и Хатата, А. (2017). Новая схема защиты обмоток статора синхронных генераторов на основе SVM. Защита и управление современными энергосистемами, 2 (1), 24.
Статья
Google ученый
Пиццо, А.Д., Марино, П., и Вишано, Н. (2002). Гармоническое и интергармоническое влияние асинхронных двигателей на основе DTC на трехпроводную сеть. На международной конференции промышленной электроники IEEE .

Google ученый
Мэйс, Дж., и Мелкебек, Дж. (1998). Прямое управление крутящим моментом асинхронных двигателей с дискретным временем с использованием измерения противо-ЭДС. В Тридцать третьем ежегодном собрании IAS отраслевых приложений конференции .
Google ученый
Касадей Д., Серра Г. и Тани А. (2000). Реализация алгоритма прямого управления моментом для асинхронных двигателей на основе модуляции дискретного пространственного вектора. Транзакции IEEE по силовой электронике, 15 , 769–777.
Артикул
Google ученый
Кейхани, Х. Р., Золгадри, М. Р., и Хомайфар, А. (2004). Расширенное и улучшенное прямое управление крутящим моментом с дискретной пространственно-векторной модуляцией для асинхронных двигателей. В Ежегодная конференция специалистов по силовой электронике IEEE .

Google ученый
Дель Торо, X. Г., Ариас, А., Джейн, М. Г., Виттинг, П. А., Сала, В. М., и Ромераль, Дж. Л. (2005). Новая схема управления DTC для асинхронных двигателей с трехуровневым инвертором. Автоматика, 46 , 73–81.
Google ученый
Кё-Бем, Л., Джун-Хо, С., Чой, И., и Джи-Юн, Ю. (2002). Уменьшение пульсаций крутящего момента в DTC асинхронного двигателя, приводимого в действие трехступенчатым инвертором с низкой частотой коммутации. Транзакции IEEE по силовой электронике, 17 , 255–264.
Артикул
Google ученый
Уткин И.В. (1993). Принципы проектирования управления скользящим режимом и приложения к электроприводам. IEEE Transactions on Industrial Electronics, 40 , 23–36.
Артикул
Google ученый
«>Танвир, А., Бейг, А.Р., и Аль-Хосани, К. (2013). DTC на основе скользящего режима асинхронного двигателя с трехуровневым инверторным питанием с использованием таблицы векторов переключения. В Азиатская конференция по управлению .
Google ученый
Айярао, Т. С. (2019). Модифицированная ветроэнергетическая система DFIG с векторным управлением, основанная на адаптивном скользящем режиме барьерной функции. Защита и управление современными энергосистемами, 4 (1), 4.
Статья
Google ученый
Родич, М.
 , и Езерник, К. (2002). Плавное регулирование крутящего момента асинхронного двигателя без датчика скорости. IEEE Transactions on Industrial Electronics, 49 , 87–95.
, и Езерник, К. (2002). Плавное регулирование крутящего момента асинхронного двигателя без датчика скорости. IEEE Transactions on Industrial Electronics, 49 , 87–95.Артикул
Google ученый
Мехмет, Д. (2005). Бездатчиковый скользящий режим прямого управления крутящим моментом (DTC) асинхронного двигателя. В Материалы международного симпозиума IEEE по промышленной электронике .
Google ученый
Шир-Куан, Л., и Чжи-Синг, Ф. (2001). Скользящее прямое управление крутящим моментом асинхронного двигателя. В Ежегодная конференция общества промышленной электроники IEEE (стр. 2171–2177).
Google ученый
Ласку, К., Болдеа, И., и Блобьерг, Ф. (2004). Прямое управление крутящим моментом безсенсорных асинхронных двигателей: скользящий подход.
 IEEE Transactions on Industry Applications, 40 , 582–590.
IEEE Transactions on Industry Applications, 40 , 582–590.Артикул
Google ученый
Детиан, С. (2010). Прямое управление крутящим моментом в скользящем режиме для асинхронного двигателя с надежным датчиком магнитного потока статора. В Международная конференция по интеллектуальным вычислительным технологиям и автоматизации .
Google ученый
Камачо, Э. Ф. (1993). Ограниченное обобщенное прогностическое управление. IEEE Transactions on Automatic Control, 38 (2), 327–332.
MathSciNet
МАТЕМАТИКА
СтатьяGoogle ученый
Камачо, Э. Ф., и Бордонс, К. (2007). Модель Прогностическое управление. Расширенные учебники по управлению и обработке сигналов , Springer-Verlag: Лондон.
«>Зейнали, Ю., Гейер, Т., и Эгардт, Б. (2011). Методы расширения траектории для прямого управления крутящим моментом с предсказанием модели. 26-я ежегодная конференция и выставка прикладной силовой электроники IEEE (APEC) (стр. 1667–1674).
Google ученый
Папафотиу, Г., Клей, Дж., Пападопулос, К.Г., Борен, П., и Морари, М. (2009). Прямое управление крутящим моментом с прогнозированием модели — Часть II: Реализация и экспериментальная оценка. IEEE Transactions on Industrial Electronics, 56 , 1906–1915.
Артикул
Google ученый
«>Ван, Ф., Чжан, З., Мэй, X., Родригес, Дж., и Кеннел, Р. (2018). Усовершенствованные стратегии управления асинхронной машиной: управление, ориентированное на поле, прямое управление крутящим моментом и управление с прогнозированием модели. Энергия, 11 (1), 120.
Артикул
Google ученый
Гейер, Т., Папафотиу, Г., и Морари, М. (2009). Прямое управление крутящим моментом с прогнозированием модели — Часть I: Концепция, алгоритм и анализ. IEEE Transactions on Industrial Electronics, 56 , 6.
Статья
Google ученый
«>Пакас, М., и Вебер, Дж. (2005). Прогнозирующее прямое управление крутящим моментом для синхронной машины с постоянными магнитами. IEEE Transactions on Industrial Electronics, 52 , 5.
Статья
Google ученый
Окумус, Х.И., и Мустафа Актас, М. (2010). Адаптивное управление полосой гистерезиса для постоянной частоты коммутации в приводах асинхронных машин DTC. Турецкий журнал электротехники и компьютерных наук, 18 , 59–69.
Google ученый
Уддин, М. Н., и Хафиз, М. (2012). Схема DTC на основе FLC для улучшения динамических характеристик привода IM.
 IEEE Transactions on Industry Applications, 48 , 823–831.
IEEE Transactions on Industry Applications, 48 , 823–831.Артикул
Google ученый
Цзиньлянь Д. и Ту Л. (2006). Улучшение низкоскоростных характеристик прямого управления крутящим моментом с использованием метода нечеткой логики. В Международная конференция IEEE по мехатронике и автоматизации .
Google ученый
Туфути, Р., Мезиан, С., и Беналла, Х. (2007). Прямое управление крутящим моментом асинхронного двигателя с использованием интеллектуальных методов. Журнал теоретических и прикладных информационных технологий, 3 , 35–44.
Google ученый
Гдаим С., Мтибаа А. и Мимуни М. Ф. (2015). Проектно-экспериментальная реализация ДТК асинхронной машины на основе нечеткого логического управления на ПЛИС. Транзакции IEEE в нечетких системах, 23 , 644–655.

Артикул
Google ученый
Зегай, М.Л., Бенджеббар, М., Бельхадри, К., Думбия, М.Л., Хамане, Б., и Кумба, П.М. (2015). Прямое управление крутящим моментом асинхронного двигателя на основе искусственных нейронных сетей. Управление скоростью с помощью MRAS и нейронного ПИД-регулятора. В конференции IEEE по электроэнергетике и энергетике (EPEC) .
Google ученый
Юань, Г., Цзинькуань, В., и Синьюнь, К. (2011). Улучшение производительности системы DTC при нечетком управлении. Procedia Environmental Sciences, 10 , 589–594.
Артикул
Google ученый
Чжао, Т., Фэнхун, X., Цзяньпин, В., Чжан, Г., и Цзяньлинь, М. (2014). Исследование бессенсорного прямого нечеткого управления крутящим моментом асинхронных двигателей. В Международная конференция по электронике и системам связи .

Google ученый
Клемент, Э. П., и Слани, В. (1997). Нечеткая логика в искусственном интеллекте. В книге : Энциклопедия компьютерных наук и технологий, глава (стр. 34) Доп. 19.
Google ученый
Венугопал, К. (2010). DTC на основе нечеткой логики для управления скоростью асинхронного двигателя с питанием от матричного преобразователя. В 2010 Международная конференция IEEE по энергетике и энергетике (стр. 753–758). IEEE.
Эль Уанджли, Н., Деруич, А., Эль Гзизал, А., Чебаби, А., Таусси, М., и Боссуфи, Б. (2018). Стратегия прямого управления крутящим моментом, основанная на нечетком логическом контроллере для асинхронного двигателя с двойным питанием. В серии конференций IOP: Науки о Земле и окружающей среде (том 161, № 1, стр. 012004). Издательство ИОП.
«>Мир С.А., Зингер Д.С. и Эльбулук Э. (1993). Нечеткая реализация прямого саморегулирования асинхронных машин. В конференции IEEE на ежегодном собрании общества отраслевых приложений .
Google ученый
Джагадиш, Х. П., и Кодад, С. Ф. (2009 г.). Прямое нечеткое управление крутящим моментом привода переменного тока. На международной конференции IEEE , посвященной достижениям в области вычислений, управления и телекоммуникационных технологий .
Google ученый
«>Эль Уанджли, Н., Таусси, М., Деруич, А., Чебаби, А., Эль Гзизал, А., и Боссуфи, Б. (2018). Высокоэффективное прямое управление крутящим моментом с двойной подачей с использованием нечеткой логики. Научный журнал Университета Гази, 31 (2), 532–542.
Google ученый
Мондал, С.К., Пинто, Дж.О., и Бимал, К.Б. (2002). ШИМ-контроллер пространственного вектора на основе нейронной сети для трехуровневого инверторного асинхронного двигателя с питанием от напряжения. IEEE Transactions on Industry Applications, 38 , 660–669.
Артикул
Google ученый
«>Алессандро Гедтель, А., Да-Сильва, И. Н., и Амарал, С. П. Дж. (2007). Идентификация момента нагрузки в асинхронном двигателе с использованием метода нейронных сетей. Исследование систем электроснабжения, 77 , 35–45.
Артикул
Google ученый
Сингх, Б., Прадип, Дж., Миттал, А.П., и Гупта, Дж.Р.П. (2006). Нейросетевой привод DTC IM для силовой установки электромобиля. На конференции IEEE по электрическим и гибридным автомобилям .
Google ученый
Берраба Ф., Салах С.
 и Чебабхи А. (2016). Метод SVM, основанный на бездатчиковом управлении DTC, оптимизированном с помощью ИНС, применяется к асинхронной машине с двойным статором, питаемой от трехуровневого шестифазного инвертора. Средиземноморский журнал измерений и контроля, 12 , 571–579.
и Чебабхи А. (2016). Метод SVM, основанный на бездатчиковом управлении DTC, оптимизированном с помощью ИНС, применяется к асинхронной машине с двойным статором, питаемой от трехуровневого шестифазного инвертора. Средиземноморский журнал измерений и контроля, 12 , 571–579.Google ученый
Хаммуми, А., Массум, А., Меруфель, А., и Вира, П. (2012). Приложение де Réseaux де Neurones для ла Commande де ла Machine Asynchrone sans capteur mécanique. Acta Electrotehnica, 53 , 99–104.
Google ученый
Земмит А., Мессальти С. и Харраг А. (2016). Инновационное улучшенное прямое управление крутящим моментом асинхронной машины с двойной подачей (DFIM) с использованием искусственной нейронной сети (ANN-DTC). Международный журнал прикладной инженерии, 11 , 9099–9105.
Google ученый
«>Гжесяк, Л. М., и Уфнальский, Б. (2005). Привод DTC с оценщиком потока статора на основе ANN. Европейская конференция по силовой электронике и приложениям .
Google ученый
Боссуфи, Б., Карим, М., Сильвиу, С., и Лагриуи, А. (2011). Искусственная нейронная сеть на основе DTC Control для высокопроизводительного привода PMSM. Журнал теоретических и прикладных информационных технологий, 33 , 165–176.
Google ученый
Гжесяк Л.М., Меганк В.
 , Соболевский Дж. и Бартломей У. (2006). Обучаемый в режиме онлайн нейронный контроллер скорости с переменным периодом обновления веса для привода переменного тока с прямым управлением крутящим моментом. В 12-я международная конференция по силовой электронике и управлению движением (стр. 1127–1132).
, Соболевский Дж. и Бартломей У. (2006). Обучаемый в режиме онлайн нейронный контроллер скорости с переменным периодом обновления веса для привода переменного тока с прямым управлением крутящим моментом. В 12-я международная конференция по силовой электронике и управлению движением (стр. 1127–1132).Google ученый
Кумар Р., Гупта Р., Бхангале С. и Готвал Х. (2007). Прямое управление крутящим моментом асинхронных двигателей на основе искусственной нейронной сети. В Международная конференция IET-UK по информационным и коммуникационным технологиям в электротехнике (стр. 361–367).
Google ученый
Лин, Ф.Дж., Чоу, В.Д., и Хуанг, П.К. (2003). Адаптивный скользящий регулятор на основе генетического алгоритма реального времени для сервопривода асинхронного двигателя. В материалах IEE — заявки на электроэнергию (стр.
 1–13).
1–13).Google ученый
Мма, Массачусетс, и Уолкотт, Б.Л. (1996). Устойчивость и оптимальность в контроллерах генетических алгоритмов. На международном симпозиуме IEEE по интеллектуальному управлению .
Google ученый
Нареш, Б., Кумар, М. В., и Ядайя, Н. (2011). Настройка ПИ-регулятора на основе ГА. В IEEE последние достижения в области интеллектуальных вычислительных систем .
Google ученый
Земмит, А., Мессальти, С., и Харраг, А. (2017). Новый улучшенный DTC асинхронной машины с двойной подачей, использующей ПИ-регулятор на основе GA. Инженерный журнал Айн-Шамс, 9 (4), 1877–1885 гг.
Гаду, С. М., Джаурис, Д., и Финч, Дж. В. (2007). Генетический алгоритм оптимизировал PI и нечеткий скользящий режим управления скоростью для приводов DTC.
 В Труды Всемирного конгресса по машиностроению .
В Труды Всемирного конгресса по машиностроению .Google ученый
Хао, Л., Цююн, М., и Жилин, З. (2010). Исследование прямого управления крутящим моментом асинхронного двигателя на основе генетического алгоритма и нечеткого адаптивного ПИ-регулятора. В Международная конференция по измерительной технике и автоматизации мехатроники .
Google ученый
Трипати, С. М., Тивари, А. Н., и Сингх, Д. (2015). Системы преобразования энергии ветра на основе синхронных генераторов с постоянными магнитами, интегрированные в сеть: обзор технологий. Renewable and Sustainable Energy Reviews, 51 , 1288–1305.
Артикул
Google ученый
Кумар, Р. Х., Икбал, А., и Ленин, Н. К. (2017). Обзор последних достижений в области прямого управления крутящим моментом в приводах асинхронных двигателей — десятилетний прогресс.
 ИЭТ Силовая электроника, 11 (1), 1–15.
ИЭТ Силовая электроника, 11 (1), 1–15.Артикул
Google ученый
Ниу Ф., Ван Б., Бабель А. С., Ли К. и Странгас Э. Г. (2016). Сравнительная оценка стратегий прямого управления крутящим моментом для синхронных машин с постоянными магнитами. IEEE Transactions on Power Electronics, 31 (2), 1408–1424.
Артикул
Google ученый
Лаборатория технологии производства, энергетики и устойчивого развития, Высшая школа технологий, Университет Сиди Мохамед Бен Абделла, Фес, Марокко
Najib El Ouanjli, Aziz Derouich, Abdelaziz El Ghzizal, Saad Motahhir & Youness El Mourabit
Faculty of Sciences and Technology, University of Bordj Bou Arreridj, Bordj Bou Arreridj, Algeria
Ali Chebabhi
Laboratory of Системная интеграция и передовые технологии, Факультет естественных наук Дхар Эль Махраз, Университет Сиди Мохамед Бен Абделла, Фес, Марокко
Мохаммед Таусси
- Najib El Ouanjli
Просмотр публикаций автора
Вы также можете искать этого автора в
PubMed Google Scholar - Aziz Derouich
Просмотр публикаций автора
Вы также можете искать этого автора в
PubMed Google Scholar - Abdelaziz El Ghzizal
Просмотр публикаций автора
Вы также можете искать этого автора в
PubMed Google Scholar - Saad Motahhir
Просмотр публикаций автора
Вы также можете искать этого автора в
PubMed Google Scholar - Ali Chebabhi
Просмотр публикаций автора
Вы также можете искать этого автора в
PubMed Google Scholar - Youness El Mourabit
Просмотр публикаций автора
Вы также можете искать этого автора в
PubMed Google Scholar - Мохаммед Таусси
Просмотр публикаций автора
Вы также можете искать этого автора в
PubMed Google Scholar - Конструкция трехфазного асинхронного двигателя
- Вращающееся магнитное поле в трехфазном асинхронном двигателе
- Принцип работы трехфазного асинхронного двигателя
- Скольжение асинхронного двигателя
- Характеристики проскальзывания крутящего момента асинхронного двигателя
- Потери в асинхронном двигателе
- Испытания асинхронных двигателей
- Способы пуска асинхронного двигателя
- Асинхронный двигатель с короткозамкнутым ротором
- Регулятор скорости трехфазного асинхронного двигателя
- Что такое частотно-регулируемый привод?
- Принцип работы стартера автотрансформатора
- Тепловое реле перегрузки работает
- Эквивалентная схема асинхронного двигателя
- Линейный асинхронный двигатель | Приложения
E. Levi, R. Bojoi, F. Profumo, H. A. Toliyat и S. Williamson, «Многофазные асинхронные двигатели — обзор состояния технологии», IET Electric Power Applications , vol. 1, нет. 4, стр. 489–516, 2007 г.
Посмотреть по адресу:
Сайт издателя | Google Scholar
Р. Юань и З. К. Чжу, «Улучшение характеристик в установившемся режиме в двойных трехфазных синхронных приводах с постоянным магнитом и прямым управлением крутящим моментом с модифицированной таблицей переключения», IEEE Transactions on Industrial Electronics , vol.
 62, нет. 6, стр. 3338–3350, 2015.
62, нет. 6, стр. 3338–3350, 2015.Посмотреть по адресу:
Сайт издателя | Google Scholar
M. Abdellatif, M. Debbou, I. Slama-Belkhodja и M. Pietrzak-David, «Простой низкоскоростной двойной DTC без датчика для привода асинхронной машины с двойной подачей», IEEE Transactions on Industrial Electronics , том. 61, нет. 8, стр. 3915–3922, 2014.
Посмотреть по адресу:
Сайт издателя | Академия Google
К. Д. Хоанг, М. Фостер, З.-К. Чжу и Ю. Рен, «Модифицированная стратегия таблицы коммутации для уменьшения гармоник тока в двух-трехфазных синхронных приводах с постоянными магнитами с прямым управлением крутящим моментом», IET Electric Power Applications , vol. 9, нет. 1, стр. 10–19, 2015 г.
Посмотреть по адресу:
Сайт издателя | Google Scholar
Х.
 Х. Х. Муса, А.-Р. Юссеф и Е.Е.М. Мохамед, «Модель прогнозирующего управления скоростью пятифазной системы ветрогенерации на основе синхронного генератора с постоянными магнитами посредством оценки скорости ветра», Международные сделки по электроэнергетическим системам , vol. 29, ID статьи e2826, 2019.
Х. Х. Муса, А.-Р. Юссеф и Е.Е.М. Мохамед, «Модель прогнозирующего управления скоростью пятифазной системы ветрогенерации на основе синхронного генератора с постоянными магнитами посредством оценки скорости ветра», Международные сделки по электроэнергетическим системам , vol. 29, ID статьи e2826, 2019.Посмотреть по адресу:
Сайт издателя | Google Scholar
К. А. Чинмая и Г. К. Сингх, «Экспериментальный анализ различных методов пространственно-векторной широтно-импульсной модуляции (SVPWM) для привода сдвоенного трехфазного асинхронного двигателя», International Transactions on Electrical Energy Systems , vol. 29, нет. 1, ID статьи e2678, 2019.
Посмотреть по адресу:
9Сайт издателя 1905 года | Google Scholar
X. Чжэн и Д. Ван, «Регулирование крутящего момента многофазных асинхронных двигателей в условиях симметричной неисправности», IEEJ Transactions on Electrical and Electronic Engineering , vol.
 12, нет. 2, стр. 284–291, 2017.
12, нет. 2, стр. 284–291, 2017.Посмотреть по адресу:
Сайт издателя | Google Scholar
К. Хатуа и В. Т. Ранганатан, «Схемы прямого управления крутящим моментом для двухфазной асинхронной машины», IEEE Transactions on Industry Applications , том. 41, нет. 5, стр. 1243–1254, 2005.
Посмотреть по адресу:
Сайт издателя | Google Scholar
А. Тахери, А. Рахмати и С. Каболи, «Энергооптимизация шестифазного асинхронного двигателя, ориентированного на поле», Advanced in Electrical and Computer Engineering , vol. 11, нет. 2, стр. 107–112, 2011 г.
Посмотреть по адресу:
Сайт издателя | Google Scholar
А. Тахери, А. Рахмати и С. Каболи, «Сжатие эффективности для различных таблиц переключения в приводе DTC шестифазного асинхронного двигателя», Журнал силовой электроники , том.
 12, нет. 1, стр. 128–135, 2012 г.
12, нет. 1, стр. 128–135, 2012 г.Посмотреть по адресу:
Сайт издателя | Google Scholar
А. Тахери, А. Рахмати и С. Каболи, «Повышение эффективности DTC шестифазной асинхронной машины с помощью адаптивного градиентного спуска потока», IEEE Transactions on Power Electronics , vol. 27, нет. 3, стр. 1552–1562, 2012.
Посмотреть по адресу:
Сайт издателя | Google Scholar
М. Х. Холакуи, М. Оджаги и А. Тахери, «Наблюдатель Люенбергера полного порядка, основанный на нечетком логическом управлении для бездатчикового ориентированного на поле управления односторонним линейным асинхронным двигателем», ISA Transactions , vol. 60, стр. 96–108, 2016.
Посмотреть по адресу:
Сайт издателя | Google Scholar
M.
 H. Holakooie, M. Ojaghi, and A. Taheri, «Модифицированный DTC шестифазного асинхронного двигателя с оценкой скорости на основе MRAS со скользящим режимом второго порядка», IEEE Transactions on Power Electronics , том. 34, нет. 1, стр. 600–611, 2019 г.
H. Holakooie, M. Ojaghi, and A. Taheri, «Модифицированный DTC шестифазного асинхронного двигателя с оценкой скорости на основе MRAS со скользящим режимом второго порядка», IEEE Transactions on Power Electronics , том. 34, нет. 1, стр. 600–611, 2019 г.Посмотреть по адресу:
Сайт издателя | Google Scholar
Х. Масумхани и А. Тахери, «Управление рабочим циклом на основе ПИ-регулятора для уменьшения пульсаций крутящего момента и потока в DTC шестифазного асинхронного двигателя», IEEE Journal of Emerging and Selected Topics in Power Electronics , 2018.
Посмотреть по адресу:
Сайт издателя | Google Scholar
M. H. Holakooie, M. Ojaghi, and A. Taheri, «Прямое управление крутящим моментом шестифазного асинхронного двигателя с новым устройством оценки сопротивления статора на основе MRAS», IEEE Transactions on Industrial Electronics , vol.
 65, нет. 10, стр. 7685–7696, 2018.
65, нет. 10, стр. 7685–7696, 2018.Посмотреть по адресу:
Сайт издателя | Академия Google
C. M. Verrelli, A. Savoia, M. Mengoni, R. Marino, P. Tomei, and L. Zarri, «Оперативная идентификация сопротивления обмоток и момента нагрузки в асинхронных машинах», IEEE Transactions on Control Systems Technology , том. 22, нет. 4, стр. 1629–1637, 2014.
Посмотреть по адресу:
Сайт издателя | Google Scholar
Р. Антонелло, Л. Ортомбина, Ф. Тинацци и М. Зиглиотто, «Онлайн-отслеживание сопротивления статора для реактивных и внутренних синхронных двигателей с постоянными магнитами», IEEE Transactions on Industry Applications , vol. 54, нет. 4, стр. 3405–3414, 2018.
Посмотреть по адресу:
Сайт издателя | Google Scholar
C.
 P. Salomon, WC Sant’Ana, L. E. Borges da Silva et al., «Оценка эффективности асинхронного двигателя с использованием новой концепции сопротивления статора», IEEE Transactions on Instrumentation and Measurement , vol. 64, нет. 11, стр. 2908–2917, 2015.
P. Salomon, WC Sant’Ana, L. E. Borges da Silva et al., «Оценка эффективности асинхронного двигателя с использованием новой концепции сопротивления статора», IEEE Transactions on Instrumentation and Measurement , vol. 64, нет. 11, стр. 2908–2917, 2015.Посмотреть по адресу:
Сайт издателя | Академия Google
Ю. Сангсефиди, С. Зиаейнежад, А. Мехризи-Сани, Х. Пайродин-Наби и А. Шулайе, «Оценка сопротивления статора в синхронных двигателях с прямым управлением крутящим моментом», IEEE Transactions on Energy Conversion , том. 30, нет. 2, стр. 626–634, 2015 г.
Посмотреть по адресу:
Сайт издателя | Google Scholar
Ф. Банейра, А. Г. Йепес, О. Лопес и Дж. Доваль-Гандой, «Метод оценки температуры обмотки статора для сдвоенных трехфазных машин на основе подачи сигнала постоянного тока», IEEE Transactions on Power Electronics , vol.
 31, нет. 7, стр. 5141–5148, 2016.
31, нет. 7, стр. 5141–5148, 2016.Посмотреть по адресу:
Сайт издателя | Google Scholar
Z. Yin, G. Li, Y. Zhang и J. Liu, «Бессенсорное управление асинхронными двигателями на основе симметричного сильного отслеживания с расширенным фильтром Калмана для уменьшения ошибок моделирования», IEEE Transactions on Industrial Informatics , vol. 15, нет. 2, стр. 650–662, 2019.
Посмотреть по адресу:
Сайт издателя | Академия Google
М. Барут, Р. Демир, Э. Зердали и Р. Инан, «Реализация в реальном времени оценки на основе фильтра Калмана с расширенным вводом Bi для бессенсорного управления асинхронными двигателями», IEEE Transactions on Промышленная электроника , том. 59, нет. 11, стр. 4197–4206, 2012.
Посмотреть по адресу:
Сайт издателя | Google Scholar
Алонге Ф.
 , Кангеми Т., Д’Ипполито Ф., Фаджолини А., Сферлацца А., «Анализ сходимости расширенного фильтра Калмана для бездатчикового управления асинхронным двигателем», IEEE Transactions on Industrial Electronics , vol. 62, нет. 4, стр. 2341–2352, 2015.
, Кангеми Т., Д’Ипполито Ф., Фаджолини А., Сферлацца А., «Анализ сходимости расширенного фильтра Калмана для бездатчикового управления асинхронным двигателем», IEEE Transactions on Industrial Electronics , vol. 62, нет. 4, стр. 2341–2352, 2015.Посмотреть по адресу:
Сайт издателя | Google Scholar
Сюй Донг, С. Чжан и Дж. Лю, «Управление СДПМ на очень низкой скорости на основе оценки EKF с оптимизированными параметрами с обратной связью», ISA Transactions , vol. 52, нет. 6, стр. 835–843, 2013 г.
Посмотреть по адресу:
Сайт издателя | Google Scholar
О. Айдогмус и С. Зюнтер, «Реализация бездатчиковой приводной системы на основе EKF с использованием СДПМ с векторным управлением, питаемого от матричного преобразователя», Международный журнал электрических и энергетических систем , том.
 43, нет. 1, стр. 736–743, 2012 г.
43, нет. 1, стр. 736–743, 2012 г.Посмотреть по адресу:
Сайт издателя | Google Scholar
Алонге Ф., ДюИпполито Ф., Фаджолини А. и Сферлацца А., «Расширенный комплексный фильтр Калмана для бездатчикового управления асинхронным двигателем», Control Engineering Practice , vol. 27, стр. 1–10, 2014 г.
Посмотреть по адресу:
Сайт издателя | Google Scholar
H. Al-Ghossini, F. Locment, M. Sechilariu, L. Gagneur, and C. Forgez, «Адаптивная настройка расширенного фильтра Калмана, используемого для управления небольшим ветровым генератором», Возобновляемые источники энергии , том. 85, стр. 1237–1245, 2016.
Посмотреть по адресу:
Сайт издателя | Google Scholar
А. Тахери и М. Мохаммадбейги, «Бессенсорная оценка скорости и прогнозное управление шестифазным асинхронным двигателем с использованием расширенного фильтра Калмана», в Трудах 5-й ежегодной международной конференции по силовой электронике, приводным системам и Конференция по технологиям (PEDSTC 2014) , стр.
 13–18, Тегеран, Италия, февраль 2014 г.
13–18, Тегеран, Италия, февраль 2014 г.Посмотреть по адресу:
Сайт издателя | Google Scholar
С. К. Принц, К. П. Панда и Г. Панда, «Вариант интеллектуального управления фильтром Калмана для улучшения качества электроэнергии в фотоэлектрической системе фильтрации активной мощности», International Transactions on Electrical Energy Systems , vol. 30, нет. 3, ID статьи e12239, 2019.
Посмотреть по адресу:
Сайт издателя | Google Scholar
М. Хинкканен, Л. Харнефорс и Дж. Луоми, «Наблюдатели потока пониженного порядка с адаптацией сопротивления статора для приводов асинхронных двигателей без датчиков скорости», IEEE Transactions on Power Electronics , vol. 25, нет. 5, стр. 1173–1183, 2010.
Посмотреть по адресу:
Сайт издателя | Google Scholar
Р.
 Цао, Н. Цзян и М. Лу, «Бессенсорное управление линейным двигателем с постоянными магнитами с переключением потока на основе расширенного фильтра Калмана», IEEE Transactions on Industrial Electronics , vol. 67, нет. 7, стр. 5971–5979, 2020.
Цао, Н. Цзян и М. Лу, «Бессенсорное управление линейным двигателем с постоянными магнитами с переключением потока на основе расширенного фильтра Калмана», IEEE Transactions on Industrial Electronics , vol. 67, нет. 7, стр. 5971–5979, 2020.Посмотреть по адресу:
Сайт издателя | Google Scholar
Э. Зердали и М. Барут, «Сравнения оптимизированных расширенных фильтров Калмана для бездатчикового управления асинхронными двигателями», IEEE Transactions on Industrial Electronics , vol. 64, нет. 6, стр. 4340–4351, 2017.
Посмотреть по адресу:
Сайт издателя | Google Scholar
C. You, J. Lu и P. Tsiotras, «Нелинейная оценка параметров водителя и анализ поведения водителя для ADAS с использованием данных полевых испытаний», IEEE Transactions on Human-Machine Systems , vol. 47, нет.
 5, стр. 686–699, 2017.
5, стр. 686–699, 2017.Посмотреть по адресу:
Сайт издателя | Академия Google
А. Тахери, «Моделирование EKF управляемого поля шестифазного асинхронного двигателя», IEICE Electronics Express , vol. 9, нет. 7, стр. 642–647, 2012 г.
Посмотреть по адресу:
Сайт издателя | Google Scholar
X. Sun, Z. Nie, J. Zhu, Y. Han, and J. Sun, «Стратегия бездатчикового управления скоростью шестифазного линейного асинхронного двигателя на основе двойных последовательных расширенных фильтров Калмана уменьшенной размерности». », IET Power Electronics , vol. 12, нет. 14, стр. 3758–3766, 2019 г..
Посмотреть по адресу:
Сайт издателя | Google Scholar
А. Тахери, Х.-П. Ren и MH Holakooie, «Управление моделью потерь без датчика шестифазного асинхронного двигателя во всем диапазоне скоростей с помощью расширенного фильтра Калмана», IEEE Access , vol.
 8, стр. 118741–118750, 2020.
8, стр. 118741–118750, 2020.Посмотреть по адресу:
Сайт издателя | Google Scholar
С. Ван, В. Динавахи и Дж. Сяо, «Многоскоростная оценка параметров на основе модели в реальном времени и идентификация состояния для асинхронных двигателей», Электроэнергетические приложения ИЭТ , том. 7, нет. 1, стр. 77–86, 2013 г.
Посмотреть по адресу:
Сайт издателя | Google Scholar
C.-J. Чан, Ю.-К. Ван и В.-Т Ченг, «Оценка сопротивления ротора и статора на основе EKF при бездатчиковом управлении скоростью асинхронных двигателей», в Proceedings of the American Control Conference (ACC) , стр. 1174–1179, Монреаль, Канада, Июнь 2012 г.
Посмотреть по адресу:
Сайт издателя | Академия Google
Р. Демир, М.
 Барут, Р. Йилдиз, Р. Инан и Э. Зердали, «Оценка сопротивления ротора и статора на основе EKF для прямого управления крутящим моментом асинхронных двигателей», в Труды Международной конференции по оптимизации электрического и электронного оборудования (OPTIM) и Международная Эгейская конференция по электрическим машинам и силовой электронике (ACEMP) 2017 г. , стр. 376–381, Брашов, Румыния, май 2017 г.
Барут, Р. Йилдиз, Р. Инан и Э. Зердали, «Оценка сопротивления ротора и статора на основе EKF для прямого управления крутящим моментом асинхронных двигателей», в Труды Международной конференции по оптимизации электрического и электронного оборудования (OPTIM) и Международная Эгейская конференция по электрическим машинам и силовой электронике (ACEMP) 2017 г. , стр. 376–381, Брашов, Румыния, май 2017 г.Посмотреть по адресу:
Сайт издателя | Академия Google
М. Барут, С. Богосян и Г. Метин, «Переключение метода EKF для оценки сопротивления ротора и статора при бездатчиковом управлении скоростью АД», Energy Conversion and Management , vol. 48, нет. 12, стр. 3120–3134, 2007.
Посмотреть по адресу:
Сайт издателя | Google Scholar
Амескита-Брукс, Л., Лисеага-Кастро, Э., Лисеага-Кастро, Дж., и Угальде-Лоо, К.Э. (2015). Анализ перекрестной связи потока и крутящего момента схем FOC: новые характеристики подавления возмущений. ISA Transactions, 52 , 446–461.
МАТЕМАТИКА
Статья
Google ученый
Чихи А., Джаралла М. и Чих К. (2010). Сравнительное исследование управления с ориентацией поля и управлением прямым крутящим моментом асинхронными двигателями с использованием адаптивного наблюдателя потока. Сербский журнал электротехники, 7 , 41–55.
Артикул
Google ученый
Новотный, Д. В., и Липо, Т. А. (1996). Векторное управление и динамика приводов переменного тока . Оксфорд: Кларендон.
Google ученый
Каземия М.В., Морадиб М. и Каземич Р.В. (2012). Минимизация пульсаций мощности DFIG с прямым управлением мощностью с помощью нечеткого регулятора и улучшенной модуляции дискретного пространственного вектора. Исследование систем электроснабжения, 89 , 23–30.
Артикул
Google ученый
Бонне, Ф., Поль-Этьен, В., и Петшак-Дэвид, М. (2007). Двойное прямое управление крутящим моментом асинхронной машины с двойной подачей. IEEE Transactions on Industrial Electronics, 54 , 2482–2490.
Артикул
Google ученый
Бертен, Дж., Вервеккен, Дж., и Дризен, Дж. (2010). Прогнозирующее прямое управление крутящим моментом для уменьшения пульсаций потока и крутящего момента. IEEE Transactions on Industrial Electronics, 57 , 404–412.
Артикул
Google ученый
Джоннала, Р. Б., и Бабу, К. С. (2018). Модифицированный многополосный управляемый гистерезисом DTC асинхронной машины с 27-уровневым асимметричным CHB-MLI с модуляцией NVC. Инженерный журнал Айн Шамс, 9 , 15–29.
Артикул
Google ученый
Бубзизи С., Абид Х. и Чаабане М. (2018). Сравнительное исследование трех типов контроллеров для DFIG в системе преобразования энергии ветра. Защита и управление современными энергосистемами, 3 (1), 21.
Статья
Google ученый
Гейер, Т., Папафотиу, Г., и Морари, М. (2009). Прямое управление крутящим моментом с прогнозированием модели — Часть I: Концепция, алгоритм и анализ. IEEE Transactions on Industrial Electronics, 56 , 1894–1905.
Артикул
Google ученый
Эзеонвумелу, И., Шинде, А.М., и Гадираджу, В.М. (2007). Оценка эффективности методов DTC, MPDTC и DDTC для привода ВППМ. Американский научно-исследовательский журнал инженерии, технологий и наук (ASRJETS), 35 (1), 201–214.
Google ученый
Миранда, Х., Кортес, П., и Юз, Дж. (2009). Прогнозирующее управление крутящим моментом асинхронных машин на основе моделей в пространстве состояний. Транзакции IEEE по промышленной электронике, 56 , 6.
Артикул
Google ученый
Тлемкани, А., Бухида, О., Бенмансур, К., Бодана, Д., и Бушерит, М.С. (2009). Стратегия прямого управления крутящим моментом (DTC) на основе контроллера с нечеткой логикой для привода синхронной машины с постоянными магнитами. Журнал электротехники и технологий, 4 , 66–78.
Артикул
Google ученый
Хафиз М., Уддин М. Н. и Ребейро Р. С. (2010). Адаптация полосы гистерезиса на основе FLC для оптимизации пульсаций крутящего момента и потока статора асинхронного привода на основе DTC. На конференции IEEE по электроэнергетике и энергетике .
Google ученый
Фаа-Дженг, Л., Джи-Чян, Ю., и Мао-Шенг, Т. (2001). Бездатчиковый асинхронный привод шпинделя с использованием контроллера скорости на основе нечеткой нейронной сети. Исследование систем электроснабжения, 58 , 187–196.
Артикул
Google ученый
Джадхав, С., Киранкумар, Дж., и Чаудхари, Б. (2012). Интеллектуальное управление приводом асинхронного двигателя на основе ИНС с DTC, модулируемым пространственным вектором. На международной конференции IEEE Power Electronic, Drives Energy Systems (PEDES) (стр. 1–6).
Google ученый
Скачать ссылки
Благодарности
Авторы хотели бы поблагодарить анонимных рецензентов за их полезные и конструктивные комментарии, которые в значительной степени способствовали улучшению окончательной версии статьи. Они также хотели бы поблагодарить редакторов за их щедрые комментарии и поддержку в процессе рецензирования.
Финансирование
Работа не поддерживается никаким финансирующим агентством. Это собственная исследовательская работа авторов.
Доступность данных и материалов
Совместное использование данных неприменимо к этой статье, поскольку в ходе текущего исследования наборы данных не создавались и не анализировались.
Информация об авторе
Авторы и организации
Авторы
Вклады
NE, SM и AD выполнили исследование методов улучшения прямого управления крутящим моментом, соответствующих AE и AC, участвовали в изменении статьи и представили ее в PCMP. SM, MT и YM проверили грамматику и написание статьи. Все авторы прочитали и одобрили окончательный вариант рукописи.
SM, MT и YM проверили грамматику и написание статьи. Все авторы прочитали и одобрили окончательный вариант рукописи.
Автор, ответственный за переписку
Связь с
Наджиб Эль Уанджли.
Заявление об этике
Конкурирующие интересы
Авторы заявляют, что у них нет конкурирующих интересов.
Права и разрешения
Открытый доступ Эта статья распространяется в соответствии с условиями международной лицензии Creative Commons Attribution 4.0 (http://creativecommons.org/licenses/by/4.0/), которая разрешает неограниченное использование, распространение, и воспроизведение на любом носителе, при условии, что вы укажете автора(ов) оригинала и источник, предоставите ссылку на лицензию Creative Commons и укажете, были ли внесены изменения.
Перепечатка и разрешения
Об этой статье
Уравнение крутящего момента асинхронного двигателя
Полная нагрузка Уравнение крутящего момента асинхронного двигателя выглядит следующим образом:
Пусковой крутящий момент двигателя – это крутящий момент, который он создает при пуске. Он обозначается T st и соответствует s = 1. Таким образом, подставляя s = 1 в приведенное выше выражение, мы получаем выражение для пускового момента. Поэтому формула пускового момента для асинхронного двигателя выглядит следующим образом:
Он обозначается T st и соответствует s = 1. Таким образом, подставляя s = 1 в приведенное выше выражение, мы получаем выражение для пускового момента. Поэтому формула пускового момента для асинхронного двигателя выглядит следующим образом:
Максимальный крутящий момент при старте
Состояние для максимального крутящего момента составляет
S = R 2 /x 2 или R 2 = SX 2 ,
9 9009 R 2 2 2 = SX 2 ,
9 9009 R 2 2 2 = SX 2 ,
9 9009 R 2 2 = SX 2 ,
9 2 = SX 2 ,
9 2 . = X 2 (поскольку при пуске s = 1)
Таким образом, для получения максимального крутящего момента при пуске значение сопротивления ротора должно быть равно реактивному сопротивлению ротора в состоянии покоя.
Однако нормальное сопротивление ротора довольно мало по сравнению с реактивным сопротивлением, иначе потери в роторе будут высокими, а КПД двигателя будет низким.
Следовательно, для получения максимального (более высокого) значения при пуске в цепь ротора добавляется некоторое внешнее сопротивление, что возможно только в случае асинхронных двигателей с контактными кольцами. Как только двигатель набирает скорость, это внешнее сопротивление уменьшается до нуля, и токосъемные кольца замыкаются накоротко.
Для получения более высокого пускового момента в случае асинхронного двигателя с короткозамкнутым ротором на ротор накладывается другая клетка, и двигатель называется двигателем с двойной клеткой.
Формула максимального крутящего момента для асинхронного двигателя
Максимальный крутящий момент обозначается T m и возникает при s = R 2 /X 2 . Значение проскальзывания, соответствующее максимальному крутящему моменту, обозначается как s m . Таким образом, подставив s = R 2 /X 2 в выражение крутящего момента при полной нагрузке, мы получим выражение для максимального крутящего момента. Поэтому формула максимального крутящего момента для асинхронного двигателя выглядит следующим образом:
Поэтому формула максимального крутящего момента для асинхронного двигателя выглядит следующим образом:
Приведенное выше выражение показывает, что максимальный крутящий момент T m не зависит от значения сопротивления ротора R 2 .
Хотя T м не зависит от R 2 , значение скольжения s м , при котором возникает T м , прямо пропорционально сопротивлению ротора R 2 .
При этом максимальный крутящий момент T м обратно пропорционален реактивному сопротивлению ротора в состоянии покоя X 2 . Поэтому для достижения более высокого значения максимального крутящего момента реактивное сопротивление рассеяния ротора должно поддерживаться минимальным.
Это достигается размещением проводников ротора очень близко к внешней периферии ротора и уменьшением воздушного зазора между статором и ротором до минимально возможного значения.
Максимальный крутящий момент T м , полученный при s м , также называется тяговым крутящим моментом или разрушающим крутящим моментом. Если момент нагрузки превышает момент отрыва, то асинхронный двигатель будет перемещен в нестабильную область и, наконец, остановится.
Влияние изменения напряжения питания на крутящий момент
В выражении крутящего момента при полной нагрузке, как написано выше, E 2 ЭДС, индуцированная ротором, пропорциональна E 1 , т. е. напряжению питания статора.
Следовательно, T α sE 1 2
Таким образом, крутящий момент на любой скорости пропорционален квадрату напряжения питания статора . Следовательно, когда напряжение питания изменяется, он также изменяет крутящий момент Т нагрузки в рабочем состоянии.
При снижении напряжения питания крутящий момент резко уменьшается, и для поддержания того же крутящего момента увеличивается скольжение или снижается скорость. Следовательно, двигатель потребляет дополнительный ток от сети питания.
Следовательно, двигатель потребляет дополнительный ток от сети питания.
Спасибо, что прочитали о Уравнение крутящего момента асинхронного двигателя .
Трехфазный асинхронный двигатель | Все сообщения
© //www. yourelectricalguide.com/ Формула крутящего момента асинхронного двигателя.
yourelectricalguide.com/ Формула крутящего момента асинхронного двигателя.
ПОИСК В ЭТОМ БЛОГЕ
Ищи:
КАТЕГОРИИ
КАТЕГОРИИвыбрать категориюОсновы переменного тока (8)Основные понятия (14)Аккумуляторы (8)Автоматические выключатели (9)Двигатели постоянного тока (8)Электроизмерительные приборы (14)Электромагнетизм (6)Электроника (12)Гостевой пост (4)Приборные трансформаторы ( 4)Контрольно-измерительные приборы (29)MCQ (99)Электростанции (11)Однофазные двигатели (5)Синхронные машины (7)Трехфазный асинхронный двигатель (18)Трансформатор (23)Система передачи (19)Без категорий (21)Использование электрической энергии (10)
СВЯЖИТЕСЬ С НАМИ
[адрес электронной почты защищен]
БЫСТРЫЕ ССЫЛКИ
Главная
О нас
Подача гостевых сообщений
Скачать бесплатные книги в формате PDF
Грамматика английского языка 4 Все
E Notes 4U
сообщить об этом объявлении
Бездатчиковое прямое управление крутящим моментом шестифазного асинхронного двигателя с помощью расширенного фильтра Калмана быстрого пониженного порядка
На этой странице0007
В этой статье предлагается простой расширенный контроллер фильтра Калмана (EKF) для прямого управления крутящим моментом (DTC) шестифазной асинхронной машины во всех диапазонах скоростей. Целью данной статьи является сокращение времени выполнения EKF-моделирования шестифазного асинхронного двигателя. Предлагаемый метод является быстрым и может работать в режиме онлайн. Если параметры машины изменяются во время работы, активируется алгоритм EKF, чтобы найти параметры, используемые для управления двигателем. На низкой скорости затруднено не только измерение скорости двигателя, но и DTC машины. Модель EKF может оценивать скорость, магнитный поток, крутящий момент нагрузки и сопротивление статора на низкой скорости; таким образом, оптимизация может выполняться во всех диапазонах нагрузок и скоростей. Предлагаемый метод повышает точность DTC шестифазной асинхронной машины и снижает вычислительные затраты системы с использованием упрощенного алгоритма. Моделирование и экспериментальные результаты подтверждают эффективность и устойчивость предложенного метода к изменениям параметров.
Целью данной статьи является сокращение времени выполнения EKF-моделирования шестифазного асинхронного двигателя. Предлагаемый метод является быстрым и может работать в режиме онлайн. Если параметры машины изменяются во время работы, активируется алгоритм EKF, чтобы найти параметры, используемые для управления двигателем. На низкой скорости затруднено не только измерение скорости двигателя, но и DTC машины. Модель EKF может оценивать скорость, магнитный поток, крутящий момент нагрузки и сопротивление статора на низкой скорости; таким образом, оптимизация может выполняться во всех диапазонах нагрузок и скоростей. Предлагаемый метод повышает точность DTC шестифазной асинхронной машины и снижает вычислительные затраты системы с использованием упрощенного алгоритма. Моделирование и экспериментальные результаты подтверждают эффективность и устойчивость предложенного метода к изменениям параметров.
1. Введение
Шестифазные и пятифазные машины представляют собой два обычных типа многофазных машин, которые используются в нескольких приложениях [1–4]. Увеличение фаз машины дает некоторые преимущества, такие как более высокая избыточность и уменьшение пульсаций крутящего момента [5–7]. Методы ориентированного на поле управления (FOC) и прямого управления моментом (DTC) реализованы для управления скоростью шестифазных и пятифазных машин [8–11]. Эти методы не дают удовлетворительных результатов в низкоскоростных приложениях. В низкоскоростных приложениях требуется подходящий метод для оценки параметров и скорости. Метод DTC — это простой и надежный метод, позволяющий избежать изменений параметров. Этот метод имеет очень быстрый динамический отклик при изменении нагрузки. Таким образом, этот метод используется во многих промышленных приложениях. DTC — это мощный метод управления несколькими типами машин переменного тока. Этот метод хорошо себя зарекомендовал при управлении шестифазными и пятифазными асинхронными машинами [12]. Одна из основных ошибок метода DTC вызвана изменением сопротивления статора, которое более серьезно в условиях низкой скорости.
Увеличение фаз машины дает некоторые преимущества, такие как более высокая избыточность и уменьшение пульсаций крутящего момента [5–7]. Методы ориентированного на поле управления (FOC) и прямого управления моментом (DTC) реализованы для управления скоростью шестифазных и пятифазных машин [8–11]. Эти методы не дают удовлетворительных результатов в низкоскоростных приложениях. В низкоскоростных приложениях требуется подходящий метод для оценки параметров и скорости. Метод DTC — это простой и надежный метод, позволяющий избежать изменений параметров. Этот метод имеет очень быстрый динамический отклик при изменении нагрузки. Таким образом, этот метод используется во многих промышленных приложениях. DTC — это мощный метод управления несколькими типами машин переменного тока. Этот метод хорошо себя зарекомендовал при управлении шестифазными и пятифазными асинхронными машинами [12]. Одна из основных ошибок метода DTC вызвана изменением сопротивления статора, которое более серьезно в условиях низкой скорости. Сопротивление статора изменяется при изменении температуры двигателя. Если в методе DTC не учитывать изменение сопротивления статора, то это приводит к ошибке на выходе контроллера [13–16]. Таким образом, для повышения точности метода DTC необходим подходящий метод оценки сопротивления статора [14]. Для оценки сопротивления статора в литературе используется несколько методов. Антонелло и др. [17] предложили новый метод онлайн-оценки сопротивления статора, который подходит для анизотропных двигателей. Показано, что этот метод измеряет сопротивление статора без информации о параметрах двигателя, а отношение сигнал/шум (SNR) улучшается. Подходящий метод оценки сопротивления статора на основе механических потерь и крутящего момента предложен в исследовании Salomon et al. [18]. Этот метод подходит для автономной оценки сопротивления и в сервисных приложениях асинхронного двигателя. В этой статье используется алгоритм оптимизации роя частиц (PSO), основанный на уравнениях потока с минимизацией ошибки крутящего момента.
Сопротивление статора изменяется при изменении температуры двигателя. Если в методе DTC не учитывать изменение сопротивления статора, то это приводит к ошибке на выходе контроллера [13–16]. Таким образом, для повышения точности метода DTC необходим подходящий метод оценки сопротивления статора [14]. Для оценки сопротивления статора в литературе используется несколько методов. Антонелло и др. [17] предложили новый метод онлайн-оценки сопротивления статора, который подходит для анизотропных двигателей. Показано, что этот метод измеряет сопротивление статора без информации о параметрах двигателя, а отношение сигнал/шум (SNR) улучшается. Подходящий метод оценки сопротивления статора на основе механических потерь и крутящего момента предложен в исследовании Salomon et al. [18]. Этот метод подходит для автономной оценки сопротивления и в сервисных приложениях асинхронного двигателя. В этой статье используется алгоритм оптимизации роя частиц (PSO), основанный на уравнениях потока с минимизацией ошибки крутящего момента. Аналитический метод оценки сопротивления статора синхронного двигателя и DTC на основе этого метода предложен в исследовании Sangsefidi et al. [19]. Этот метод использует влияние ошибки сопротивления статора на расчетный угол между векторами потока статора и тока. Температура обмотки в двойной трехфазной машине оценивается с помощью подачи сигнала постоянного тока в исследовании Baneira et al. [20]. Этот сигнал вводится в подпространство для подавления пульсаций крутящего момента и потока в воздушном зазоре. Этот метод можно использовать только в многофазной машине с такой свободой моделирования. Задача идентификации в бессенсорном ИМ предложена в исследовании Yin et al. [21]. В этой статье используется аппроксимация первого порядка динамики ошибок в адаптивном наблюдателе. Асинхронный двигатель включал только известные сигналы; таким образом, этот метод осуществим. Оценка сопротивления статора на основе фазового компенсатора представлена в исследовании Barut et al. [22]. Этот метод отделен от средства оценки скорости коэффициентом компенсации отслеживания рабочей точки.
Аналитический метод оценки сопротивления статора синхронного двигателя и DTC на основе этого метода предложен в исследовании Sangsefidi et al. [19]. Этот метод использует влияние ошибки сопротивления статора на расчетный угол между векторами потока статора и тока. Температура обмотки в двойной трехфазной машине оценивается с помощью подачи сигнала постоянного тока в исследовании Baneira et al. [20]. Этот сигнал вводится в подпространство для подавления пульсаций крутящего момента и потока в воздушном зазоре. Этот метод можно использовать только в многофазной машине с такой свободой моделирования. Задача идентификации в бессенсорном ИМ предложена в исследовании Yin et al. [21]. В этой статье используется аппроксимация первого порядка динамики ошибок в адаптивном наблюдателе. Асинхронный двигатель включал только известные сигналы; таким образом, этот метод осуществим. Оценка сопротивления статора на основе фазового компенсатора представлена в исследовании Barut et al. [22]. Этот метод отделен от средства оценки скорости коэффициентом компенсации отслеживания рабочей точки.
Расширенный фильтр Калмана (EKF) является мощным средством оценки не только сопротивления статора, но также крутящего момента и магнитного потока машины [23–29]. Этот метод используется в ряде работ для оценки параметров машины. Этот метод подходит для оценки параметров машины с изменением нагрузки и параметров [25–28]. В настоящее время, с увеличением скорости обработки в DSP, возможен онлайн-эксперимент EKF. Асинхронный двигатель имеет стохастические свойства; таким образом, EKF можно легко использовать для его моделирования. Кроме того, его можно использовать для управления машиной, когда машина используется на низкой скорости или параметры машины меняются. Другие оценщики используются для оценки параметров асинхронных машин [30–33]. EKF используется для моделирования шестифазной асинхронной машины с мощными результатами [34, 35].
Предложен простой контроллер модели потерь (LMC) с расширенным фильтром Калмана (EKF) для повышения эффективности шестифазной асинхронной машины во всех диапазонах скоростей [36]. Предлагаемый метод является быстрым и может работать в режиме онлайн. Если параметры машины изменяются во время работы, активируется алгоритм EKF для определения параметров, обеспечивающих оптимальную эффективность работы. Модель EKF может оценивать скорость, нагрузку и КПД двигателя в диапазоне низких скоростей, так что оптимизация может выполняться во всех диапазонах нагрузок и скоростей. В отличие от обычного метода LMC, предлагаемый метод не зависит от вариаций параметров [36].
Предлагаемый метод является быстрым и может работать в режиме онлайн. Если параметры машины изменяются во время работы, активируется алгоритм EKF для определения параметров, обеспечивающих оптимальную эффективность работы. Модель EKF может оценивать скорость, нагрузку и КПД двигателя в диапазоне низких скоростей, так что оптимизация может выполняться во всех диапазонах нагрузок и скоростей. В отличие от обычного метода LMC, предлагаемый метод не зависит от вариаций параметров [36].
Предложен многоскоростной метод оценки параметров и состояний асинхронного двигателя на основе теории ЭКФ для оценки момента нагрузки асинхронного двигателя. Методы реализуются в режиме реального времени на узле кластера ПК, который действует как контроллер для экспериментальной установки асинхронного двигателя. Предложена эталонная адаптивная система многоскоростной модели (MRAS) для оценки постоянной времени ротора, чтобы гарантировать высокопроизводительное управление асинхронным двигателем [37].
Температурно-зависимое изменение сопротивлений статора и ротора, которое приводит к большой ошибке оценки скорости и магнитного потока, является критической проблемой для бессенсорного управления скоростью. Для оценки одновременных изменений сопротивлений статора и ротора при бездатчиковом управлении АД в различных условиях эксплуатации разработана оценка, основанная на методе расширенного фильтра Калмана (EKF). Для решения проблемы нестабильности одновременной оценки сопротивлений статора и ротора сопротивление статора оценивается с учетом его температурной зависимости и тепловой динамики обмоток статора, а сопротивление ротора оценивается как постоянное состояние [38]. DTC асинхронного привода с EKF для оценки составляющих неподвижной оси статора токов статора, потоков статора, сопротивлений статора и ротора с допущением доступных напряжений/токов статора и скорости ротора представлен в исследовании Демира и др. [39].]. Онлайн-оценки сопротивлений ротора и статора имеют хороший отклик при использовании одного алгоритма EKF и датчика скорости [39].
Подходящий оценщик EKF предлагается для точной оценки потока и скорости при очень низкой и нулевой скорости. Этот метод применяется с прямым векторным управлением без датчиков скорости и двумя алгоритмами EKF, путем переключения с одного алгоритма на другой в каждый момент выборки. Метод переключения требует точной и увеличенной оценки количества параметров. Оценка сопротивления ротора и статора в переходном и стационарном режимах является важной задачей в управлении АД без датчиков скорости, о чем сообщается в исследовании Barut et al. [40].
Целью данной статьи является сокращение времени выполнения EKF-моделирования шестифазного асинхронного двигателя. Предлагаемый метод повышает точность и снижает вычислительную стоимость системы. Кроме того, точность DTC шестифазной асинхронной машины повышается за счет оценки сопротивления статора. В предлагаемом методе используется подходящий алгоритм EKF для оценки потока и момента нагрузки. Точность метода DTC повышается с помощью онлайн-оценщика сопротивления статора. EKF-моделирование 6PIM является точным и устойчивым к изменениям параметров. В этом документе представлен соответствующий DTC 6PIM во всех диапазонах скоростей. Если нагрузка изменяется, алгоритм EKF быстро и точно оценивает нагрузку и скорость. Также представленный алгоритм отличается устойчивостью к изменению сопротивления. Оценка скорости является мощным инструментом расчета скорости во всех диапазонах скоростей, потому что расчет скорости двигателя на низкой и нулевой скорости чрезвычайно сложен и связан с ошибками.
EKF-моделирование 6PIM является точным и устойчивым к изменениям параметров. В этом документе представлен соответствующий DTC 6PIM во всех диапазонах скоростей. Если нагрузка изменяется, алгоритм EKF быстро и точно оценивает нагрузку и скорость. Также представленный алгоритм отличается устойчивостью к изменению сопротивления. Оценка скорости является мощным инструментом расчета скорости во всех диапазонах скоростей, потому что расчет скорости двигателя на низкой и нулевой скорости чрезвычайно сложен и связан с ошибками.
В этой статье сначала выводится моделирование шестифазного асинхронного двигателя и DTC 6PIM. EKF-моделирование 6PIM описано в следующем разделе. Описан подходящий код неисправности 6PIM, в котором использовалась оценка параметра EKF. Наконец, показаны результаты моделирования предложенных методов, а затем экспериментальные результаты подтверждают правильность предложенных методов во всех диапазонах скоростей.
2. Шестифазный асинхронный двигатель, модель
2.
 1. Моделирование и DTC шестифазного асинхронного двигателя
1. Моделирование и DTC шестифазного асинхронного двигателя
Метод декомпозиции векторного пространства (VSD) используется при моделировании 6PIM. С помощью этого метода и применения 66 матриц шестифазные уравнения напряжения, тока и потока преобразуются в три подпространства. Эти подпространства называются . Поток двигателя создается с помощью основных гармоник тока и напряжения, которые отображаются на подпространство. DTC 6PIM реализован в подпространстве, а другие текущие ссылки на подпространства установлены равными нулю. Потому что гармоники, отображаемые на единственные, производят потери и считаются нулевыми в различных методах управления. 6Моделирование PIM с помощью метода VSD показано в следующих уравнениях. Все обозначения двигателей указаны в таблице 1.
Динамическая модель шестифазного асинхронного двигателя в подпространстве может быть представлена как
X — вектор состояния системы, Y — измеряемый параметр двигателя, U — входной вектор в подпространстве. Все шумы системы , и измерительное оборудование в этом подпространстве .
Все шумы системы , и измерительное оборудование в этом подпространстве .
While
Весь шум приводной системы и измерительного оборудования в этом подпространстве моделируется с помощью . Для управления двигателем на основе цифровой обработки сигналов необходима подходящая дискретная модель двигателя. Дискретная модель 6PIM выводится путем дискретизации векторов состояния. Если время дискретизации равно , вектор дискретного состояния в подпространстве равен .
2.2. Уменьшенный порядок EKF Моделирование 6PIM
При низкой скорости качество датчиков скорости значительно снижается. EKF — это мощное средство оценки, которое можно использовать для повышения точности оценки. Выход EKF используется с обеими секциями с реакцией в реальном времени. Модель EKF шестифазного асинхронного двигателя может быть представлена рекурсивными уравнениями, как показано ниже: где
Три матрицы ковариации ( Q , R и ) используются для моделирования системы, измерения и входного шума система. Приведенные выше уравнения выполняются рекурсивно, чтобы уменьшить ошибку оценки. Поскольку приведенный выше алгоритм EKF требует большого времени для выполнения, модель EKF можно упростить следующим образом:0007
Приведенные выше уравнения выполняются рекурсивно, чтобы уменьшить ошибку оценки. Поскольку приведенный выше алгоритм EKF требует большого времени для выполнения, модель EKF можно упростить следующим образом:0007
Предлагаемое упрощенное моделирование EKF шестифазной асинхронной машины можно использовать для уменьшения времени выполнения моделирования EKF двигателя. В предлагаемом методе сокращается время выполнения, а также снижается сложность системы. Схема предлагаемого моделирования EKF (ROEKF) уменьшенного порядка DTC шестифазного асинхронного двигателя показана на рисунке 1.
Динамические характеристики EKF и ROEKF связаны с начальными значениями Q и R . При изменении этих параметров отклик фильтра Калмана несколько улучшится. Оценка EKF имеет большую первичную ошибку во времени начала, связанную с Q и R матрица и регулируется начальными значениями. Кроме того, если начальные значения матрицы состояния будут близки к реальным значениям, динамический отклик оценщика улучшится. В данной работе начальные значения параметров считаются неопределенными и оцениваются независимо от начальных значений.
В данной работе начальные значения параметров считаются неопределенными и оцениваются независимо от начальных значений.
В различных приложениях оценщик EKF часто настраивается на использование матриц с постоянными параметрами. В оценщике EKF Q количественно определяет неточности моделирования системы, а R определяет количество шумов измерения, преобладающих в системе. Низкое значение Q приводит к медленному переходному процессу, а высокое значение Q приводит к высокому уровню шума в оценках сопротивления в установившемся режиме. Согласно предложению рецензента, мы используем адаптивную настройку, которая изменяет матрицу Q в зависимости от ошибки оценки, посредством чего выбирается высокое значение Q в переходных процессах, низкое значение в устойчивом состоянии и линейное изменение обеспечивается между пределами. В литературе сообщается, что адаптивная настройка EKF реализуется с использованием различных механизмов адаптации для Q и R матрицы, основанные на снижении расчетных уровней шума. В этой статье мы используем простой механизм адаптации, подходящий для DTC машины. Другими словами, время установления наблюдателя должно быть меньше времени установления контроллера. В используемом адаптивном методе матрица Q изменяется до определенных предельных значений, что не влияет на сходимость фильтра и, следовательно, не оказывает отрицательного влияния на полосу пропускания контроллера.
В этой статье мы используем простой механизм адаптации, подходящий для DTC машины. Другими словами, время установления наблюдателя должно быть меньше времени установления контроллера. В используемом адаптивном методе матрица Q изменяется до определенных предельных значений, что не влияет на сходимость фильтра и, следовательно, не оказывает отрицательного влияния на полосу пропускания контроллера.
Эти параметры были выбраны на основе производительности замкнутого цикла и стоимости вычислений алгоритма. Значения параметров системы и элементов матрицы ковариации очень эффективны при оценке EKF. В данной работе во избежание вычислительной сложности ковариационная матрица системного шума Q выбрана в диагональном виде, также удовлетворяющем условию положительной определенности. Согласно теории КФ, Q и R матрицы должны быть получены путем рассмотрения стохастических свойств соответствующих шумов. Однако, поскольку Q и R обычно неизвестны, в большинстве случаев в качестве весовых коэффициентов или параметров настройки используются элементы ковариационной матрицы. В целом, в то время как настройка начальных значений (ковариационной матрицы ошибки оценки) и Q выполняется экспериментальным методом проб и ошибок для достижения быстрой начальной сходимости и желаемого поведения в переходном и установившемся режимах, Q и R определяются с учетом погрешностей измерения датчиков тока и напряжения и погрешностей квантования АЦП.
В целом, в то время как настройка начальных значений (ковариационной матрицы ошибки оценки) и Q выполняется экспериментальным методом проб и ошибок для достижения быстрой начальной сходимости и желаемого поведения в переходном и установившемся режимах, Q и R определяются с учетом погрешностей измерения датчиков тока и напряжения и погрешностей квантования АЦП.
При реализации метода фильтра Калмана некоторые вычисления только увеличивают время вычислений, хотя они не приводят к оценке параметров, в значительной степени учитывая объем вычислений ЦП. В предлагаемом методе требуемая память для кода несколько увеличивается, но требуемая память для данных уменьшается. Также сокращение времени вычислений повысит точность предлагаемого алгоритма и снизит стоимость реализации. При векторе состояния (4) в предыдущих методах EKF все размерности матрицы были бы выбраны равными шести. Например, матрица имеет 66 размерностей, но в предлагаемом методе размерность матрицы выбрана равной (16). Если вектор состояния имеет восемь переменных, предлагаемый метод сокращает время выполнения почти на четверть. Это означает уменьшение расчета на 75%. С уменьшением расчета EKF выбранное время выборки уменьшается.
Если вектор состояния имеет восемь переменных, предлагаемый метод сокращает время выполнения почти на четверть. Это означает уменьшение расчета на 75%. С уменьшением расчета EKF выбранное время выборки уменьшается.
3. Результаты моделирования и экспериментов
В этом разделе, во-первых, производительность ROEKF для оценки параметров в 6PIM показана на рисунках 2 и 3. В этих моделированиях эталонная скорость двигателя составляет 50 рад/сек и 2 рад/сек соответственно. . Алгоритм EKF активен и оценивает все состояния. Согласно этому рисунку сопротивление статора изменяется через 6 с, а нагрузка изменяется через 2 с, а затем через 5 с, но алгоритм EKF может очень хорошо оценить эти изменения. На рис. 2 показаны ток статора, поток, сопротивление статора, крутящий момент нагрузки и оценка скорости шестифазного асинхронного двигателя при 50 рад/сек. Согласно рисунку 2, крутящий момент нагрузки составляет 0,1 Нм в начальное время и изменяется до 4,5 Нм через 2 с. Согласно результатам, предложенный метод имеет хороший отклик, а ошибка оценки низкая.
На рис. 3 показаны результаты оценки параметров в ROEKF в условиях низкой скорости. На этом рисунке скорость двигателя составляет 1 рад/с, и предлагаемый метод может полностью оценить все параметры на низкой скорости. На рисунке 3 крутящий момент нагрузки составляет 0,1 Нм в начальное время и изменяется до 4,5 Нм через 2 с. На рис. 3 показаны ток и поток по осям (d-q), крутящий момент нагрузки, сопротивление статора, скорость двигателя и оценка фазного тока. Согласно результатам, предложенный метод ROEKF активен при изменении нагрузки и сопротивления статора и может быстро и точно оценивать реальные значения. Точность метода DTC тесно связана с точной оценкой сопротивления статора. Метод DTC сильно зависит от фактического значения сопротивления статора, и любая ошибка в расчете сопротивления приведет к сбою этого метода. Зависимость метода DTC от фактического значения сопротивления очень велика, особенно на малых скоростях. Любая ошибка в фактическом значении резистора статора вызовет ошибку в управлении и нестабильность системы.
Эта машина питается от шестифазного инвертора постоянного и переменного тока. Чтобы выполнить DTC с обратной связью 6PIM, токи шести фаз статора измеряются с помощью датчиков тока LEM. Четыре датчика тока используются для измерения фазных токов VSI. Выходы датчиков, используемые в качестве параметров, оцифровываются с помощью шести 12-битных аналого-цифровых преобразователей на плате TMS. Шестифазный асинхронный двигатель изготовлен из трехфазного асинхронного двигателя путем перемотки статора.
Экспериментальный результат предлагаемого метода в 50 рад/сек показан на рисунке 4. Параметры шестифазного асинхронного двигателя показаны в таблице 1. Скорость двигателя составляет 50 рад/сек, а нагрузка двигателя не нагружена и изменена на 1,5. Нм на t = 2,7 сек. Предлагаемый алгоритм EKF может оценивать все параметры точно так же, как и часть моделирования. Согласно результатам, предложенный алгоритм активен после изменения сопротивления статора и изменения нагрузки. К статору подключена коммутируемая решетка с шестью сопротивлениями 7,8 Ом. Одно реле переводило резисторы в состояние короткого замыкания. В этом состоянии сопротивление статора равно Rs. Задавая сопротивление коммутируемой матрицы, дополнительное сопротивление может быть добавлено или удалено к сопротивлению статора в указанное время.
К статору подключена коммутируемая решетка с шестью сопротивлениями 7,8 Ом. Одно реле переводило резисторы в состояние короткого замыкания. В этом состоянии сопротивление статора равно Rs. Задавая сопротивление коммутируемой матрицы, дополнительное сопротивление может быть добавлено или удалено к сопротивлению статора в указанное время.
Сравнение номеров математических операций в EKF и ROEKF показано в таблице 2. В этой таблице сравниваются различные функции, используемые в этих алгоритмах. В РОЭКФ уменьшено количество математических функций; таким образом, время выполнения алгоритма сокращается. Несмотря на сокращение времени выполнения, точность оценки алгоритма не изменилась. В предлагаемом методе это предотвращает ненужные вычисления, а это сокращает время расчета.
Также в предложенном методе было уменьшено байтовое пространство памяти. В таблице 3 показано сравнение объема памяти, используемого в методах EKF и ROEKF. Согласно таблицам 2 и 3, время выполнения алгоритма уменьшилось почти на 50%, а используемый объем памяти уменьшился на 35%. Обозначения двигателей, которые используются в этом документе, показаны в таблице 4.
Обозначения двигателей, которые используются в этом документе, показаны в таблице 4.
4. Выводы
EKF DTC шестифазного асинхронного двигателя, представленного в данной статье, способен управлять двигателем во всех диапазонах скоростей. Согласно результатам, предложенный метод активен при изменении нагрузки и изменении параметров. Если скорость двигателя низкая, предлагаемый метод точно оценивает скорость и сопротивление статора. Если сопротивление статора определено неверно, код неисправности имеет ошибку и, возможно, он нестабилен. Предлагаемый метод ROEKF имеет высокую скорость оценки. Предложенный алгоритм может быть реализован в недорогом микропроцессоре. В предлагаемом методе сокращается время выполнения, а также снижается сложность системы. Предлагаемый метод уменьшает время выполнения и предотвращает неиспользуемые вычисления в реализации DSP и FPGA. Работоспособность предлагаемого метода подтверждается моделированием и экспериментальными результатами.
Доступность данных
Данные файлов MATLAB, используемые для поддержки результатов этого исследования, можно получить у соответствующего автора по запросу.
Конфликт интересов
Авторы заявляют об отсутствии конфликта интересов.
Благодарности
Этот документ был частично поддержан Программой специальной поддержки провинции Шэньси для лидера инноваций в области науки и технологий и частично Shaanxi Industrial Key Project (2018GY-165). Открытый исследовательский фонд от Shaanxi Key Laboratory of Complex System Control и интеллектуальная обработка информации (2020CP01).
Ссылки
Copyright
Copyright © 2020 Asghar Taheri et al. Эта статья находится в открытом доступе и распространяется в соответствии с лицензией Creative Commons Attribution License, которая разрешает неограниченное использование, распространение и воспроизведение на любом носителе при условии надлежащего цитирования оригинальной работы.
Эта статья находится в открытом доступе и распространяется в соответствии с лицензией Creative Commons Attribution License, которая разрешает неограниченное использование, распространение и воспроизведение на любом носителе при условии надлежащего цитирования оригинальной работы.
Асинхронный двигатель
(Этот документ состоит из двух основных частей: принцип работы и характеристики асинхронного двигателя)
Асинхронные двигатели или асинхронные двигатели часто называют рабочими лошадками отрасли. Это результат множества преимуществ асинхронного двигателя перед другими технологиями. Двигатель требует минимального обслуживания. Единственные детали, которые могут изнашиваться, это подшипники. Если асинхронный двигатель не используется чрезмерно (высокое напряжение, ток или механическое воздействие), подшипники определяют срок службы асинхронного двигателя. В отличие от двигателя постоянного тока нет необходимости в угольных щетках для коммутации тока. Асинхронный двигатель можно легко изготовить, и при этом его цена относительно низка по сравнению с другими технологиями. Асинхронный двигатель не использует процесс сгорания для подачи энергии, поэтому нет необходимости (дозаправлять) топливом или воздухом. Охлаждение может быть интегрировано, чтобы асинхронный двигатель мог работать в герметично закрытой среде, например, под водой. Асинхронный двигатель имеет высокое отношение мощности к весу. Еще одним преимуществом является высокий пусковой крутящий момент, благодаря чему возможен запуск под нагрузкой. С момента разработки частотно-регулируемых приводов и систем векторного управления этот асинхронный двигатель также легко регулируется по скорости и крутящему моменту. Это дало массу возможностей в автоматизации процессов. В следующей статье объясняются принцип, характеристики и управление индукцией.
Асинхронный двигатель можно легко изготовить, и при этом его цена относительно низка по сравнению с другими технологиями. Асинхронный двигатель не использует процесс сгорания для подачи энергии, поэтому нет необходимости (дозаправлять) топливом или воздухом. Охлаждение может быть интегрировано, чтобы асинхронный двигатель мог работать в герметично закрытой среде, например, под водой. Асинхронный двигатель имеет высокое отношение мощности к весу. Еще одним преимуществом является высокий пусковой крутящий момент, благодаря чему возможен запуск под нагрузкой. С момента разработки частотно-регулируемых приводов и систем векторного управления этот асинхронный двигатель также легко регулируется по скорости и крутящему моменту. Это дало массу возможностей в автоматизации процессов. В следующей статье объясняются принцип, характеристики и управление индукцией.
Принцип работы асинхронного двигателя
Принцип действия асинхронного двигателя состоит в том, чтобы создать вращающееся магнитное поле в статоре и индуцировать ток в роторе, так что оба элемента вместе создают мощность на роторе, что приводит к круговому движению с определенной скоростью и крутящим моментом.
Статор
Теоретически статор представляет собой трехфазную обмотку, разделенную на цилиндрической поверхности, так что при приложении трехфазного напряжения индуцируется вращающееся магнитное поле. Обмотки уложены в металлическую цилиндрическую конструкцию, чтобы направлять линии магнитного поля и предотвращать перемещение обмоток. Эта конструкция изготовлена из ламинированных, перфорированных пластин. Это предотвращает циркуляцию сильных вихревых токов в статоре. Идеальной ситуацией является синусоидальное магнитное поле, но для объяснения принципов работы статора достаточно одной обмотки на фазу. Это показано на следующем рисунке.
Рисунок 1: Теоретическая конструкция статора с одной обмоткой на фазу
Рисунок 2: Трехфазный ток i s1 , i s2 и i s3 , который будет подключен к катушкам U, V и W
Здесь три обмотки сдвинуты на 120° так, чтобы они были симметричными. Обмотки часто называют пофазными; U 1 — U 2 , V 1 — V 2 и W 1 — W 2 . На этом рисунке есть два полюса на фазу. Три обмотки могут быть соединены по схеме звезда или треугольник. Это часто делается через перемычки вне асинхронного двигателя, потому что в зависимости от конфигурации такие характеристики, как ток, напряжение и направление вращения, изменяются.
На этом рисунке есть два полюса на фазу. Три обмотки могут быть соединены по схеме звезда или треугольник. Это часто делается через перемычки вне асинхронного двигателя, потому что в зависимости от конфигурации такие характеристики, как ток, напряжение и направление вращения, изменяются.
Рис. 3. Конфигурация «звезда-треугольник» с перемычками
Рисунок 4: Асинхронный двигатель в схеме звезды
На три обмотки подается трехфазное симметричное синусоидальное напряжение. Обмотки имеют определенную проводимость, так что через обмотки протекает трехфазный симметричный синусоидальный ток. Токи создают различные магнитные поля вокруг них. На рис. 5 показана эволюция этих магнитных полей за один период.
Рисунок 5: Магнитная обстановка в моменты времени с 1 по 7 (Рисунок 2)
Ток положительный, когда он течет со стороны 1 на сторону 2 (U 1 — U 2 , V 1 — V 2 и W 1 — W 2 ). Различные магнитные поля по фазам приводят к общему магнитному полю, показанному на рисунке mkl. Это магнитное поле вращается, в данном примере по часовой стрелке. Каждый период синуса напряжения магнитное поле совершает оборот на 360° через весь статор. Если разместить больше обмоток на фазу, так что будет создано 2*p полюсов на фазу, магнитные поля сделают оборот на 360°/p за период напряжения. Если частота системы напряжения f с , частота магнитного поля f с /p или количество оборотов в минуту
Различные магнитные поля по фазам приводят к общему магнитному полю, показанному на рисунке mkl. Это магнитное поле вращается, в данном примере по часовой стрелке. Каждый период синуса напряжения магнитное поле совершает оборот на 360° через весь статор. Если разместить больше обмоток на фазу, так что будет создано 2*p полюсов на фазу, магнитные поля сделают оборот на 360°/p за период напряжения. Если частота системы напряжения f с , частота магнитного поля f с /p или количество оборотов в минуту
n с = (60f с ) / p
Как упоминалось ранее, предыдущая ситуация с одной обмоткой на фазу на полюс является упрощенной моделью. Фактическое распределение содержит больше обмоток на щель в статоре. По фазам это распределение выполняется как синусоида. Если линию с севера на юг по наведенному магнитному полю от фазы назвать опорной линией статора, то оптимальное распределение N s проводов для одной фазной катушки определяется выражением:
n с = (N с / 2) sin α
Из этого выражения, в соответствии с выводом магнитной индукции в воздушном зазоре между статором и ротором, получается:
B δs1 (α) = (u 0 N s i s1 cos α) / 2δ
Также отсюда можно записать следующую формулу для эффективного значения магнитного поля в воздушном пространстве:
B δ = (3 N se u 0 I u ) / 4δ
Чтобы найти поток статора, индуктивность намагничивания и ЭДС индукции, воспользуйтесь предыдущими формулами и выражением для потока в одной обмотке. Итак, допустим один виток катушки U 1 — U 2 . Этот поворот составляет определенный угол α с базовой линией статора. Пусть статор имеет следующие характеристики: радиус r и осевую длину l. Тогда поток за один виток определяется по следующей формуле:
Итак, допустим один виток катушки U 1 — U 2 . Этот поворот составляет определенный угол α с базовой линией статора. Пусть статор имеет следующие характеристики: радиус r и осевую длину l. Тогда поток за один виток определяется по следующей формуле:
ф поворот = 2 В δ I r sin α
Из этого выражения можно найти максимум всего индукционного потока от катушки U 1 — U 2 , проинтегрировав его по всему распределению обмоток этой фазы:
Наведенный поток ф с1 пропорционален току намагничивания I u . Это включает в себя то, что поток и ток находятся в фазе. Отсюда можно определить индуктивность намагничивания как:
ЭДС индукции в одной катушке составляет:
Ротор
Ротор состоит из разных частей. Есть в основном два типа роторов. Асинхронные двигатели с фазным ротором имеют ротор, содержащий обычные трехфазные обмотки из изолированного провода. Другой тип, который будет использоваться далее в этой статье, — это асинхронный двигатель с короткозамкнутым ротором. Он имеет короткозамкнутый ротор. Для обоих типов кожух ротора состоит из перфорированных пластин. Они содержат прорези для трехфазных обмоток или короткозамкнутую клетку. Беличья клетка изготавливается из металлических (обычно медных или алюминиевых) стержней с соединением на обоих концах с короткозамкнутым металлическим кольцом. Вариации распространены, но принцип остается тем же. Процесс передачи крутящего момента в роторе основан на законе Фарадея и силе Лоренца. Объяснить процесс, происходящий в роторе. Представьте себе проводящую лестницу, состоящую из длинных металлических сторон и проводящих ступеней, как на рис. 6.9.2706
Есть в основном два типа роторов. Асинхронные двигатели с фазным ротором имеют ротор, содержащий обычные трехфазные обмотки из изолированного провода. Другой тип, который будет использоваться далее в этой статье, — это асинхронный двигатель с короткозамкнутым ротором. Он имеет короткозамкнутый ротор. Для обоих типов кожух ротора состоит из перфорированных пластин. Они содержат прорези для трехфазных обмоток или короткозамкнутую клетку. Беличья клетка изготавливается из металлических (обычно медных или алюминиевых) стержней с соединением на обоих концах с короткозамкнутым металлическим кольцом. Вариации распространены, но принцип остается тем же. Процесс передачи крутящего момента в роторе основан на законе Фарадея и силе Лоренца. Объяснить процесс, происходящий в роторе. Представьте себе проводящую лестницу, состоящую из длинных металлических сторон и проводящих ступеней, как на рис. 6.9.2706
Рисунок 6: Лестничный эквивалент ротора
Ступени имеют длину l. Перпендикулярно над плоскостью, образованной ступенями и проводящей стороной, размещен постоянный магнит. Затем магнит перемещается параллельно сторонам по ступеням лестницы, не касаясь их. Магнит имеет определенное магнитное поле B и скорость v согласно лестнице. Если этот воображаемый эксперимент провести достаточно быстро, можно будет заметить несколько событий. В соответствии с законом Фарадея будет индуцироваться ЭДС, приводящая к возникновению напряжения на проводнике прямо под магнитом.
Затем магнит перемещается параллельно сторонам по ступеням лестницы, не касаясь их. Магнит имеет определенное магнитное поле B и скорость v согласно лестнице. Если этот воображаемый эксперимент провести достаточно быстро, можно будет заметить несколько событий. В соответствии с законом Фарадея будет индуцироваться ЭДС, приводящая к возникновению напряжения на проводнике прямо под магнитом.
E = B.l.v
Это связано с тем, что проводник отсекает поток. Этот проводник образует вместе с боковинами лестницы и близлежащими проводящими ступенями замкнутый контур. Из-за напряжения на центральной ступени по этой петле будет протекать ток. Направление напряжения и тока таково, что противодействует изменению поля магнетита. В этом примере, если магнит движется вправо и его отрицательный полюс находится над лестницей, ток будет течь в центральном проводнике вперед и в соседних ступеньках назад.
Я = Э / Я
Где Z — импеданс, видимый потенциалом на центральном проводнике. Поскольку существует магнитное поле B, пересекающее ступеньку, и электрический ток, протекающий через ступеньку, на лестницу будет действовать сила Лоренца.
Поскольку существует магнитное поле B, пересекающее ступеньку, и электрический ток, протекающий через ступеньку, на лестницу будет действовать сила Лоренца.
Ф=БИ
Рисунок 7: Ротор с короткозамкнутым ротором
Эта сила действует в том же направлении, что и движение магнита, потому что это индуцированная сила, которая противодействует ее источнику!. Если лестница может двигаться свободно, она начнет ускоряться, чтобы уменьшить разницу скоростей между лестницей и магнитом. Когда разница скоростей уменьшается, ЭДС уменьшается, что приводит к снижению силы тока, силы и ускорения. Если лестница и магнит движутся с одинаковой скоростью, сила будет равна нулю. Чтобы сделать шаг к асинхронному двигателю с короткозамкнутым ротором, ротор с короткозамкнутым ротором эквивалентен лестнице, которая согнута в цилиндр, а движущийся магнит заменен вращающимся магнитным полем за счет трехфазных обмоток. Такой цилиндр показан на рисунке 7. На этом примере объясняется принцип работы асинхронного двигателя. Исходя из формулы ЭДС в одной катушке можно провести аналогию.
На этом примере объясняется принцип работы асинхронного двигателя. Исходя из формулы ЭДС в одной катушке можно провести аналогию.
E s1 = jw s ф s1 = jw s L 0 I u
Если пренебречь индуктивным и резистивным падением напряжения на катушке, ЭДС равна установленному напряжению U c1 . Вращающееся поле индуцирует ЭДС E r1-rest в обмотке ротора. Когда асинхронный двигатель не вращается, статор и ротор действуют как первичная и вторичная обмотки трансформатора. Обе частоты равны:
f r = f с
Обмотки связаны магнитным потоком, который действует как вращающееся поле. Как и в случае с реальным трансформатором, для асинхронного двигателя в этой ситуации без вращения можно определить коэффициент трансформации.
k = E s1 / E r1-остаток
Основное различие между асинхронным двигателем в этой ситуации и реальным трансформатором заключается в токе нулевой нагрузки. Из-за гораздо более высокого сопротивления асинхронного двигателя из-за воздушного зазора ток намагничивания и, тем самым, ток нулевой нагрузки значительно выше. В асинхронном двигателе этот ток составляет 20-50% от тока полной нагрузки, тогда как в реальном трансформаторе это лишь несколько процентов от тока полной нагрузки. Сила Лоренца, действующая на ротор, создает определенный крутящий момент на валу.
Из-за гораздо более высокого сопротивления асинхронного двигателя из-за воздушного зазора ток намагничивания и, тем самым, ток нулевой нагрузки значительно выше. В асинхронном двигателе этот ток составляет 20-50% от тока полной нагрузки, тогда как в реальном трансформаторе это лишь несколько процентов от тока полной нагрузки. Сила Лоренца, действующая на ротор, создает определенный крутящий момент на валу.
Этот крутящий момент максимален, когда ток ротора находится в фазе с магнитным потоком статора. Ток ротора сильно отстает от ЭДС ротора из-за его высокой собственной индуктивности.
tan φ = (wL r ) / R r
Это ситуация, когда ротор останавливается, например, когда асинхронный двигатель останавливается. Генерируемый крутящий момент на роторе вызовет ускорение. По мере увеличения скорости вращения ротора до скорости вращения магнитного поля, также называемой синхронной скоростью, ЭДС E r1 уменьшается так же, как частота напряжения ротора f r . Если асинхронный двигатель достигнет синхронной скорости, на ротор больше не будет действовать сила, поэтому это невозможно. Вот почему асинхронный двигатель также называют асинхронным двигателем. При увеличении нагрузки скорость уменьшается, а крутящий момент увеличивается. В ситуации с нагрузкой, например, при номинальной нагрузке, скорость асинхронного двигателя обозначается буквой n.
Если асинхронный двигатель достигнет синхронной скорости, на ротор больше не будет действовать сила, поэтому это невозможно. Вот почему асинхронный двигатель также называют асинхронным двигателем. При увеличении нагрузки скорость уменьшается, а крутящий момент увеличивается. В ситуации с нагрузкой, например, при номинальной нагрузке, скорость асинхронного двигателя обозначается буквой n.
Характеристики асинхронного двигателя
Слип
Из предыдущей главы ясно, что ротор никогда не может достичь той же скорости вращения, что и вращательное магнитное поле статора. Резюмируя: синхронная скорость потока статора n с зависит от частоты f с приложенного напряжения и числа пар полюсов p:
n с = (60f с ) / p
Поскольку ротор никогда не достигает этой скорости, определяется коэффициент, указывающий на относительную разницу между обеими скоростями. Этот фактор, скольжение g, определяется следующим образом:
Этот фактор, скольжение g, определяется следующим образом:
g = (n с — n) / n с
Скольжение часто указывается в процентах. При постановке на систему координат скольжение будет иметь направление, противоположное скорости вращения ротора. Скольжение будет равно нулю, когда скорость ротора равна синхронной скорости, будет равно единице, если асинхронный двигатель стоит на месте, будет отрицательной во время генерации и будет больше единицы, когда вращающееся магнитное поле приложено в направлении, противоположном направлению вращения. ротора. Это электрическое торможение.
Характеристики ротора
Частота ротора
Частота ЭДС в роторе зависит от разности скорости вращения ротора и скорости магнитного поля в статоре:
f r = p(n s — n) / 60 = pn s g / 60 = f s g
ЭДС ротора
Когда ротор стоял на месте, разница! в скорости ротора и магнитного поля статора равна синхронной скорости. В этой ситуации ЭДС E r1-остальное дано:
В этой ситуации ЭДС E r1-остальное дано:
E = бульвар с
При вращении ротора с определенной скоростью n ЭДС, зависящая от разности скоростей, будет меньше:
E = Bl(v s — v r ) = gBlv s
Таким образом, при заданном скольжении g ЭДС в роторе определяется как:
E r = gE r1-остаток
Скорость магнитного поля ротора
В роторе течет ток за счет наведенного напряжения. Этот ток дает, согласно закону Гопкинсона, магнитодвижущую силу. Эта сила создает магнитное поле, которое из-за вращательного характера текущей системы также будет вращаться. Ранее было показано, что частота системы напряжения ротора f r пропорциональна частоте статора f s с коэффициентом скольжения g:
f r = gf с
Таким образом, скорость вращения магнитного поля ротора w r определяется следующими формулами:
w r = gw s = 2πf r
Сам ротор вращается со скоростью
w = (2πn/60) рад/с
Таким образом, w определяется как
.
w = (1 — g)w с
Таким образом, когда скорость вращения ротора и его поле объединяются, результатом является магнитное поле ротора, которое вращается с той же синхронной скоростью в соответствии с опорной линией статора.
w s = w + w r
Мощность и крутящий момент
Поток активной мощности
Чтобы лучше понять электрические процессы в асинхронном двигателе, полезно рассмотреть эквивалентную схему асинхронного двигателя, как показано на рисунке 8. Таким образом, гальванически развязанные процессы статора и ротора объединяются в одну электрическую эквивалентную схему одной фазы. Индекс s указывает количество статора, индекс r количество ротора. Акценты используются там, где количество ротора относится к статору.
Рисунок 8: Эквивалентная схема асинхронного двигателя
Помимо всех электрических параметров асинхронного двигателя основное назначение заключается в передаче определенного крутящего момента на вал при определенной угловой скорости. Имея в виду электрические характеристики, можно рассмотреть блок-схему, показанную на рисунке 9. Напряжение U, приложенное к обмоткам, известно. В простых неуправляемых приложениях это напряжение сети. В процессах с частотным регулированием это напряжение, подаваемое преобразователем частоты. Асинхронный двигатель требует определенного тока I. Асинхронный двигатель имеет индуктивный характер из-за использования различных катушек. Это означает, что ток и напряжение в обмотках не совпадают по фазе. Хотя важно знать, какое приложенное напряжение влияет на изоляцию обмоток, напряжение для дальнейших отводов мощности не так важно.
Имея в виду электрические характеристики, можно рассмотреть блок-схему, показанную на рисунке 9. Напряжение U, приложенное к обмоткам, известно. В простых неуправляемых приложениях это напряжение сети. В процессах с частотным регулированием это напряжение, подаваемое преобразователем частоты. Асинхронный двигатель требует определенного тока I. Асинхронный двигатель имеет индуктивный характер из-за использования различных катушек. Это означает, что ток и напряжение в обмотках не совпадают по фазе. Хотя важно знать, какое приложенное напряжение влияет на изоляцию обмоток, напряжение для дальнейших отводов мощности не так важно.
Рис. 9: Поток мощности в асинхронном двигателе
Рис. 9 начинается с активной подводимой мощности к статору
P e = √3U l I l cos φ = 3U p I p cos φ
Где φ — угол между вектором напряжения и тока в векторном представлении. Индексы I и p указывают, является ли используемая величина линейной или фазовой величиной. Далее используются фазовые величины, поскольку они согласуются с величинами статора. Из активной мощности, поступающей в асинхронный двигатель, первая часть теряется на тепло в обмотках статора. Эта часть, называемая потерями в меди статора P js , зависит от сопротивления статора и тока:
Индексы I и p указывают, является ли используемая величина линейной или фазовой величиной. Далее используются фазовые величины, поскольку они согласуются с величинами статора. Из активной мощности, поступающей в асинхронный двигатель, первая часть теряется на тепло в обмотках статора. Эта часть, называемая потерями в меди статора P js , зависит от сопротивления статора и тока:
P js = 3I p 2 R s
Другая часть рассеивается в виде тепла в сердечнике статора. Эти потери представляют собой потери в стали из-за вихревых токов в сердечнике:
P f = 3V p 2 / R m ≈ 3V s 2 / R m
7
Оставшаяся часть мощности – это мощность зазора P r , который передается от статора к ротору через воздушный зазор:
P r = 3(I r ‘ ) 2 R s ‘/g
Часть мощности промежутка рассеивается в виде тепла в обмотках ротора, называемого потерями в меди ротора:
P jr = 3(I r ‘ ) 2 R s ‘ =gR r
Теперь остается механическая мощность мотора:
Р м = (1 — г) Р р
Часть механической мощности теряется из-за трения вращающихся и подвижных частей с воздухом и особенно неподвижных частей двигателя. Эта часть, обозначенная как P v , равна мощности без нагрузки:
Эта часть, обозначенная как P v , равна мощности без нагрузки:
P v = P без нагрузки
Из всех этих мощностей общий КПД асинхронного двигателя можно выразить как:
η = P из / P в = (P m — P v ) / (P m + P f + P js + P fr ) = P нагрузка
В таблице 1 приведены абсолютные и относительные значения нескольких величин асинхронных двигателей. Маленькие двигатели имеют мощность менее 11 кВт, большие двигатели — более 1100 кВт.
| Нагрузка | Текущий родственник | Относительный крутящий момент | Скольжение относительное | Абсолютная эффективность | Абсолютный коэффициент мощности | |||||
| Размер двигателя | Маленький | Большой | Маленький | Большой | Маленький | Большой | Маленький | Большой | Маленький | Большой |
| Полная загрузка | 1 | 1 | 1 | 1 | 0,03 | 0,004 | 0,7-0,9 | 0,96-0,98 | 0,8-0,85 | 0,87-0,9 |
| Без нагрузки | 0,5 | 0,3 | 0 | 0 | ~0 | ~0 | 0 | 0 | 0,2 | 0,05 |
| Заблокированный ротор | 5-9 | 4-6 | 1,5-3 | 0,5-1 | 1 | 1 | 0 | 0 | 0,4 | 0,1 |
Кривая зависимости крутящего момента от скорости
Когда крутящий момент рассчитывается из мощности зазора P r и синхронной угловой скорости w s , можно предпринять следующие шаги, чтобы найти общее выражение для крутящего момента в зависимости от скорости:
Где
X r ‘ = w s σ r ‘ L 0
— индуктивность рассеяния ротора относительно статора. С этого момента все упомянутые термины … r ‘ заменены терминами … R для сохранения ясности. С
С этого момента все упомянутые термины … r ‘ заменены терминами … R для сохранения ясности. С
U с1 ≈ E с1 = φ с1 w с
Крутящий момент становится:
T = (3PR R / W R ) φ S1 2 / ((R R / W R ) 2 + (σ R L 0 ) + 2 R L 0 ) 40074 40074 40074 + (σ R L 0 ) . )
Максимальный крутящий момент достигается, когда
dT / dw r = 0 (это происходит, когда w r = R R / σ R L 0 )
Когда это вводится в формулу крутящего момента, это дает выражение максимального крутящего момента или пробивного крутящего момента:
T = 3pφ s1 2 / 2σ R L 0
На рис. 10 хорошо представлена кривая зависимости крутящего момента от скорости.
10 хорошо представлена кривая зависимости крутящего момента от скорости.
Рисунок 10: Кривая зависимости крутящего момента от скорости асинхронного двигателя
На рисунке 10 также показано выражение для скорости, когда крутящий момент максимален. Как доказано ранее, пробивной момент достигается при частоте вращения ротора
w r = R R / σ Р Л 0
Скорость ротора дает разницу между синхронной скоростью и фактической скоростью. Таким образом, пробивной момент достигается при частоте вращения
w = w s — (1/p) R R / σ R L 0
или указано в оборотах в минуту RPM:
n b = n s — (30/πp) R R / σ R L 0
Скорость зависит от сопротивления ротора. Само значение пробивного момента не зависит от сопротивления ротора. Когда скорость ротора по эталонной линии статора выше синхронной скорости, значение скорости ротора w r становится отрицательным. Поток энергии будет от ротора к статору. Это происходит, когда ротор приводится в движение или асинхронная машина работает как генератор, а не двигатель. Необходимо учитывать, что крутящий момент, указанный в предыдущих выражениях, является крутящим моментом, поэтому потери ротора, потери на трение и потери на вентиляцию еще не учитываются. Теоретически асинхронный двигатель может передать максимальный крутящий момент нагрузке. В основном номинальный крутящий момент в 1,75-3 раза меньше. Это дает несколько эффектов. Номинальный ток будет ниже, рабочая точка, вероятно, будет намного более стабильной, номинальная скорость будет почти синхронной, а асинхронный двигатель будет поддерживать большой ускоряющий момент. На рисунке 11 визуализирована концепция ускоряющего момента.
Само значение пробивного момента не зависит от сопротивления ротора. Когда скорость ротора по эталонной линии статора выше синхронной скорости, значение скорости ротора w r становится отрицательным. Поток энергии будет от ротора к статору. Это происходит, когда ротор приводится в движение или асинхронная машина работает как генератор, а не двигатель. Необходимо учитывать, что крутящий момент, указанный в предыдущих выражениях, является крутящим моментом, поэтому потери ротора, потери на трение и потери на вентиляцию еще не учитываются. Теоретически асинхронный двигатель может передать максимальный крутящий момент нагрузке. В основном номинальный крутящий момент в 1,75-3 раза меньше. Это дает несколько эффектов. Номинальный ток будет ниже, рабочая точка, вероятно, будет намного более стабильной, номинальная скорость будет почти синхронной, а асинхронный двигатель будет поддерживать большой ускоряющий момент. На рисунке 11 визуализирована концепция ускоряющего момента.
Рисунок 11: Графический пример ускоряющего момента
Из состояния покоя нагрузка с противодействующим моментом T c1 будет ускоряться до точки P, где в каждый момент времени
T — T c1 = T α = J m dw/dt
Действительная причина этого последнего выражения будет объяснена далее в главе о механике. Если противодействующий момент 01f нагрузки следует курсу T c2 , асинхронный двигатель не может самостоятельно ускорить нагрузку. Чтобы получить более высокий пусковой и разгонный крутящий момент без использования асинхронного двигателя с завышенными характеристиками, решение состоит в том, чтобы иметь более высокое сопротивление ротора.
Если противодействующий момент 01f нагрузки следует курсу T c2 , асинхронный двигатель не может самостоятельно ускорить нагрузку. Чтобы получить более высокий пусковой и разгонный крутящий момент без использования асинхронного двигателя с завышенными характеристиками, решение состоит в том, чтобы иметь более высокое сопротивление ротора.
Это можно сделать вне асинхронного двигателя в случае асинхронного двигателя с фазным ротором или внутри двигателя при использовании асинхронного двигателя с двойной клеткой или роторных стержней с более высоким сопротивлением. Принцип обмотки ротора и стержня ротора с более высоким сопротивлением напрямую влияет на сопротивление ротора. Влияние на кривую зависимости крутящего момента от скорости показано на рис. 12.
Рис. 12: Крутящий момент в зависимости от скорости для различных значений сопротивления ротора
Опрокидывающий крутящий момент не изменяется, как было сказано ранее, только при действительно высоком сопротивлении. В фазном роторе с внешними зажимами сопротивления сопротивление можно регулировать, когда асинхронный двигатель работает на более высокой скорости, чтобы уменьшить скольжение. В двигателе с двойной клеткой две короткозамкнутые клетки установлены концентрично. Это показано на рис. 13. Внутренняя клетка содержит толстые стержни и почти полностью окружена железным сердечником.
В фазном роторе с внешними зажимами сопротивления сопротивление можно регулировать, когда асинхронный двигатель работает на более высокой скорости, чтобы уменьшить скольжение. В двигателе с двойной клеткой две короткозамкнутые клетки установлены концентрично. Это показано на рис. 13. Внутренняя клетка содержит толстые стержни и почти полностью окружена железным сердечником.
Обладает высокой индуктивностью и низким сопротивлением. Внешняя клетка состоит из более тонких стержней, расположенных близко к воздушному зазору между ротором и статором. Сопротивление выше, чем во внутренней клетке. Поток вокруг внешних стержней частично перекрывается в воздушном зазоре. Благодаря этому он имеет меньшую индуктивность. При запуске асинхронного двигателя скорость вращения ротора w r максимальна.
Рисунок 5.13: Принцип работы ротора с двойной клеткой
Важное значение имеет реактивное сопротивление ротора. Ток ротора будет высоким во внешней клетке и низким во внутренней клетке. Это клетка с более высоким сопротивлением, что означает более высокий момент ускорения. Когда асинхронный двигатель набирает обороты, скорость вращения ротора уменьшается и достигает небольшого значения (f r ~ от 1 до 4 Гц) . Реактивное сопротивление больше не так важно, и ток в основном будет течь во внутренней клетке, потому что ее сопротивление намного ниже, чем во внешней клетке. Сопротивление ротора адаптируется полностью электрически. В основном возможны три ситуации, как показано на рис. 14. Первая кривая дает асинхронный двигатель с низким сопротивлением ротора, меньшим пусковым моментом, но более высокой эффективностью. Вторая кривая иллюстрирует наиболее распространенный асинхронный двигатель с повышенным пусковым моментом. Третья кривая называется седловой кривой и используется, когда требуется действительно высокий пусковой момент, здесь пусковой момент может быть даже выше! пробивной крутящий момент.
Это клетка с более высоким сопротивлением, что означает более высокий момент ускорения. Когда асинхронный двигатель набирает обороты, скорость вращения ротора уменьшается и достигает небольшого значения (f r ~ от 1 до 4 Гц) . Реактивное сопротивление больше не так важно, и ток в основном будет течь во внутренней клетке, потому что ее сопротивление намного ниже, чем во внешней клетке. Сопротивление ротора адаптируется полностью электрически. В основном возможны три ситуации, как показано на рис. 14. Первая кривая дает асинхронный двигатель с низким сопротивлением ротора, меньшим пусковым моментом, но более высокой эффективностью. Вторая кривая иллюстрирует наиболее распространенный асинхронный двигатель с повышенным пусковым моментом. Третья кривая называется седловой кривой и используется, когда требуется действительно высокий пусковой момент, здесь пусковой момент может быть даже выше! пробивной крутящий момент.
Рисунок 5.14: Колебания крутящего момента ротора с двойной клеткой
Пусковой ток
Когда асинхронный двигатель запускается прямым подключением к сети, от сети требуется высокий пусковой ток.
 д.с. можно пренебречь (рис. 255, а). Вращающееся магнитное поле статора здесь заменено полем полюсов N и S, вращающимся, предположим, по направлению часовой стрелки. Пользуясь правилом «правой руки», определяем направление э.д.с. и токов в обмотке ротора. Токи ротора, взаимодействуя с вращающимся магнитным полем, создают момент вращения. Направления сил, действующих на проводники с током, определяются по правилу «левой руки». Как видно из чертежа, ротор под действием электромагнитных сил будет вращаться в ту же сторону, что и само вращающееся поле, т. е. по часовой стрелке.
д.с. можно пренебречь (рис. 255, а). Вращающееся магнитное поле статора здесь заменено полем полюсов N и S, вращающимся, предположим, по направлению часовой стрелки. Пользуясь правилом «правой руки», определяем направление э.д.с. и токов в обмотке ротора. Токи ротора, взаимодействуя с вращающимся магнитным полем, создают момент вращения. Направления сил, действующих на проводники с током, определяются по правилу «левой руки». Как видно из чертежа, ротор под действием электромагнитных сил будет вращаться в ту же сторону, что и само вращающееся поле, т. е. по часовой стрелке. Направление индуктированной в обмотке ротора э.д.с. остается таким же, как и на рис. 255, а, но вследствие запаздывания тока по фазе максимум тока I2 наступает позднее, чем максимум э.д.с.
Направление индуктированной в обмотке ротора э.д.с. остается таким же, как и на рис. 255, а, но вследствие запаздывания тока по фазе максимум тока I2 наступает позднее, чем максимум э.д.с.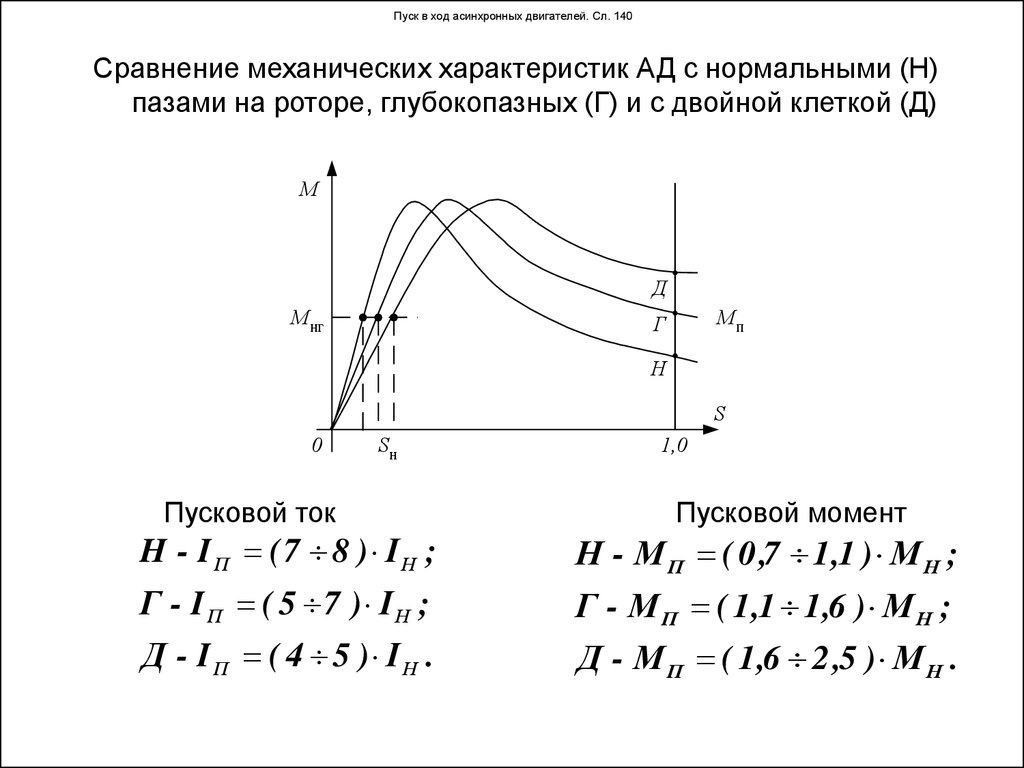 Таким образом, изменение вращающего момента, развиваемого двигателем, с изменением скорости вращения (и скольжения) определяется одновременно как изменением тока I2, так и изменением cos Ψ2.
Таким образом, изменение вращающего момента, развиваемого двигателем, с изменением скорости вращения (и скольжения) определяется одновременно как изменением тока I2, так и изменением cos Ψ2. Вследствие этого cos Ψ2 имеет малое значение (около 0,1-0,2). Поэтому, несмотря на большую величину пускового тока, пусковой вращающий момент будет наибольшим. По мере разгона двигателя скольжение уменьшается.
Вследствие этого cos Ψ2 имеет малое значение (около 0,1-0,2). Поэтому, несмотря на большую величину пускового тока, пусковой вращающий момент будет наибольшим. По мере разгона двигателя скольжение уменьшается. В момент пуска в цепь ротора вводят активное сопротивление (пусковой реостат), которое затем выводят по мере разгона двигателя.
В момент пуска в цепь ротора вводят активное сопротивление (пусковой реостат), которое затем выводят по мере разгона двигателя.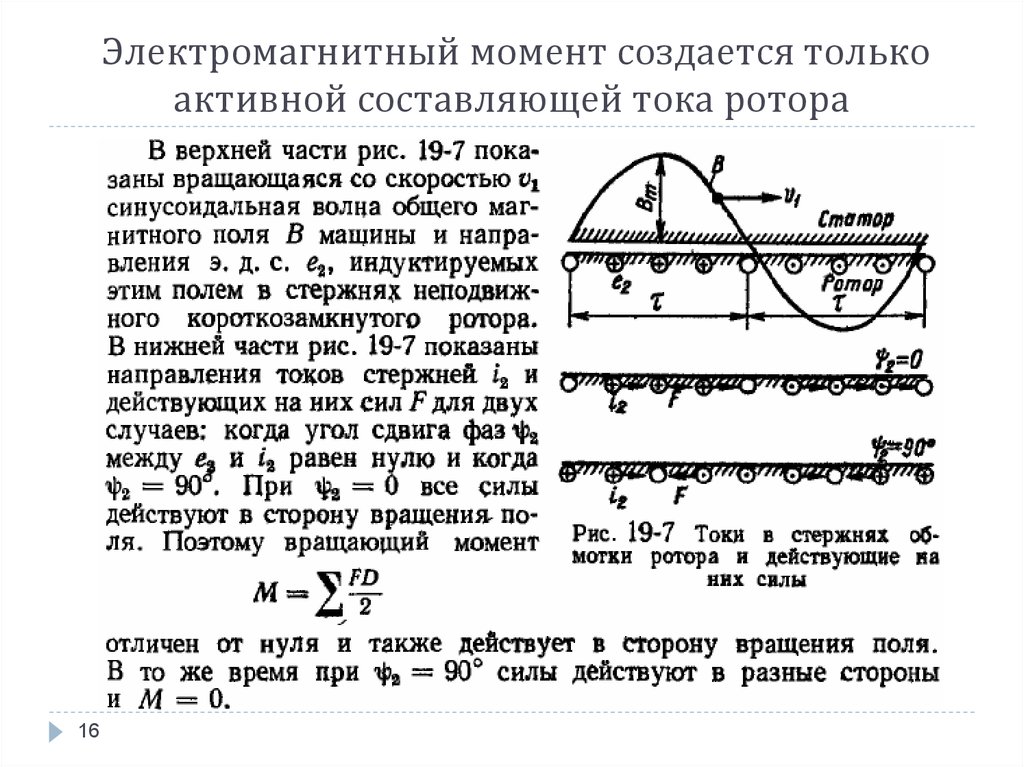
 257. Двуклеточный ротор: а — общий вид ротора с частичным разрезом, б — разрез паза; 1 — нижняя рабочая клетка, 2 — верхняя пусковая клетка
257. Двуклеточный ротор: а — общий вид ротора с частичным разрезом, б — разрез паза; 1 — нижняя рабочая клетка, 2 — верхняя пусковая клетка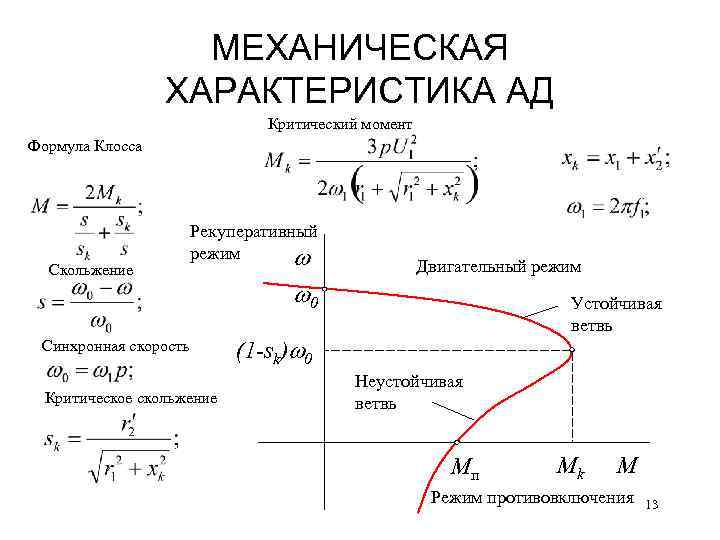 Ввиду большого активного сопротивления и малой индуктивности верхней пусковой клетки ток и э.д.с., индуктированные в ней, будут незначительно сдвинуты по фазе, и вращающий момент, развиваемый пусковой клеткой, будет большим. Следовательно, при пуске вращающий момент двигателя получается преимущественно за счет пусковой клетки.
Ввиду большого активного сопротивления и малой индуктивности верхней пусковой клетки ток и э.д.с., индуктированные в ней, будут незначительно сдвинуты по фазе, и вращающий момент, развиваемый пусковой клеткой, будет большим. Следовательно, при пуске вращающий момент двигателя получается преимущественно за счет пусковой клетки. Сумма мгновенных значений моментов двух обмоток дает кривую М момента двуклеточного двигателя.
Сумма мгновенных значений моментов двух обмоток дает кривую М момента двуклеточного двигателя.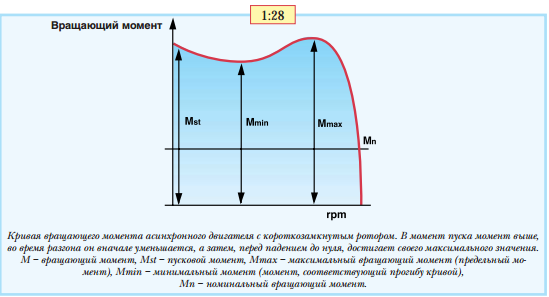 Плотность тока в верхних слоях стержня увеличивается, что равносильно уменьшению сечения стержней и увеличению активного сопротивления обмотки. Это, как известно, приводит к увеличению вращающего момента двигателя. Кроме того, увеличение индуктивного и активного сопротивления обмотки ротора вызывает уменьшение пускового тока. С увеличением скорости двигатель приобретает свойства, соответствующие его обычной конструкции.
Плотность тока в верхних слоях стержня увеличивается, что равносильно уменьшению сечения стержней и увеличению активного сопротивления обмотки. Это, как известно, приводит к увеличению вращающего момента двигателя. Кроме того, увеличение индуктивного и активного сопротивления обмотки ротора вызывает уменьшение пускового тока. С увеличением скорости двигатель приобретает свойства, соответствующие его обычной конструкции.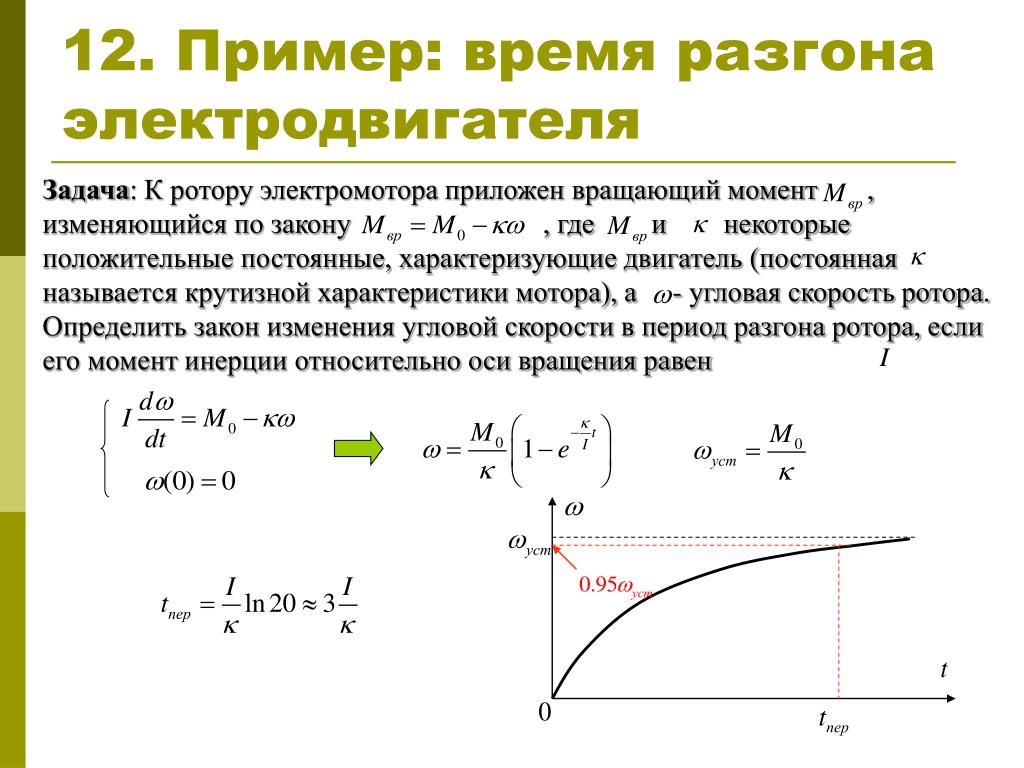
 При пуске обмотка статора с помощью рубильника соединяется звездой и, как только двигатель разовьет максимальную возможную скорость вращения, переключатель откидывается влево, обмотка статора оказывается включенной треугольником. При этом способе пуска двигателя пусковой ток уменьшается в три раза. Поясним это на примере.
При пуске обмотка статора с помощью рубильника соединяется звездой и, как только двигатель разовьет максимальную возможную скорость вращения, переключатель откидывается влево, обмотка статора оказывается включенной треугольником. При этом способе пуска двигателя пусковой ток уменьшается в три раза. Поясним это на примере.

 В конце пуска реостат плавно выводится и закорачивается. Наличие активного сопротивления в цепи ротора при пуске приводит к уменьшению пускового тока и увеличению пускового момента. На рис. 264 дана схема пуска асинхронного двигателя с фазным ротором.
В конце пуска реостат плавно выводится и закорачивается. Наличие активного сопротивления в цепи ротора при пуске приводит к уменьшению пускового тока и увеличению пускового момента. На рис. 264 дана схема пуска асинхронного двигателя с фазным ротором. su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 176.9.44.166 (0.017 с.)
su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 176.9.44.166 (0.017 с.)