1. Электромагнитные переходные процессы в обмотке возбуждения.
Исходное уравнение по IIзакону Кирхгофа:
; (1)
Рисунок 1
; (2) 
;
Получаем:
; (3)
;
;
; (4)
Если 
, то:
; (5)
Во времени график нарастания тока возбуждения выглядит как на рисунке 2.
Рисунок 2
Влияние скорости возбуждения.
Чтобы форсировать изменение Iв обмотке возбуждения генератора, надо:
1) параметрический способ за счет изменения параметров в цепи возбуждения генератора.
Добавим последовательно с обмоткой возбуждения добавочное сопротивление 
(рисунок 3).
Рисунок 3
Новое значение постоянной времени примет вид:
;
И будет иметь вид изображенный на рисунке 4
Рисунок 4
Значение коэффициента 
найдем из соотношения:
;
– коэффициент форсировки;
Но в этом случае чтобы Iв осталось неизменным, необходимоUв увеличить в
раз.
Уравнение (5) примет вид: 
. (6)
2) Форсировка отсечкой.
При данном способе форсируется подводимое напряжение к обмотке возбуждения в 
. Закон изменения тока в обмотке возбуждения в этом случае опишется уравнением: 
(7)
Так как в этом случае установившееся значение тока превосходит допустимое в 
раз, то по достижении током этого значения необходимо ограничить ток (отсечь). Этот способ называется форсировкой с отсечкой. Переходный процесс данного типа форсировки изображен на рисунке 5
Рисунок 5
Время переходного процесса 
(8)
График зависимости коэффициента форсировки от отношения времени переходного процесса к постоянной времени изображен на рисунке 6
Рисунок 6
Из этого графика следует что 
больше чем (3÷4) принимать нецелесообразно, так как на
практически не влияет.
2. Переходные процессы в двигатели постоянного тока независимого возбуждения.
Схема соединения двигателя изображена на рисунке 7.
Рисунок 7
; (9)
; (10)
; (11)
;
;
(12)
Подставляя (13), (10) и (12) в (9) получим:
(14)
или 
(15)
Разделим обе части уравнения (15) на С:
(16)
Обозначим 
– электромагнитная постоянная времени.
Составляющую 
умножим на
, получим:
где: 
– электромагнитная постоянная времени.
С учетом последнего выражения:
(17)
Уравнение (17) позволяет производить анализ поведения электродвигателя в переходных режимах.
В статическом (установившемся) режиме, при 
уравнение (17) будет выглядеть как:
(18)
– уравнение электромеханической характеристики, которая изображена на рисунке 8.
Рисунок 8
Переходные процессы будут вычисляться по выражению (рисунок 9):
Рисунок 9
Здесь 
.
Если считать что 
, то решение дифференциального уравнения для двигателя можно заменить на:
;
Данные графики изображены на рисунке 10.
Рисунок 10
3. Переходные процессы в системе Г-Д.
Схема системы Г-Д изображена на рисунке 11.
Рисунок 11
; (19)
; (20)
; (21)
; (22)
Из (21) 
; (24)
Подставив (23) и (24) в (20) получим
; (25)
или 
; (26)
;
При 
,
– можно принебречь, тогда
; (27)
Учитывая то что 
, из (27) определим:
; (28)
; (29)
Подставляя (28) и (29) в (26) получим:
(30)
; (31)
Его характеристическое уравнение:
В установившемся режиме:
; (32)
или 
;
где: 
.
Механическая характеристика (32) изображена на рисунке 12
Рисунок 12
Полное решение уравнения (31) имеет вид:
. (33)
studfiles.net
В большинстве случаев к.з. АД питается от сети с U1=const и f1=const. Поэтому нелинейность их механических характеристик проявляется полностью как в режимах пуска ,так и торможения. Магнитный поток в переходных режимах изменяется в широких пределах и на характер переходных процессов существенное влияние оказывает электромагнитная инерция. С учетом ее движение электропривода в переходном процессе пуска включением на сеть можно описать, если воспользоваться уравнениями динамической механической характеристики в комплексной форме в осях U, V и уравнением движения обобщенной машины, подставить в них вместо U2 - 0, т.к. двигатель короткозамкнутый. Уравнения в комплексной форме, полученные ранее, имеют вид
Если выразить векторы потокосцеплений через обобщенные векторы токов статора и
ротора т.е
и подставить в уравнения равновесия ЭДС, получим
Заменив р на 
, а вместоU2 подставив 0, будем иметь
Решить эту нелинейную систему уравнений можно только с помощью ЭВМ. Однако оценить влияние электромагнитной инерции в общем виде можно при анализе процесса включения двигателя на сеть при неизменной скорости ротора, т.е. эл=const .
На начальном этапе скорость двигателя еще не успела существенно измениться и можно принять эл=0. Анализировать такой процесс удобнее всего в осях и , принимая к=0.При этих условиях первые 2 уравнения системы запишутся так
Переходя к изображениям переменных по Карсону при нулевых начальных условиях и учитывая, что синусоидальное напряжение сети U1имеет изображение в виде
, получим
Найдя из второго уравнения i’2(p) и подставив в первое, а затем из второго же найдя i1(p) и подставив в первое получим после преобразований изображения токов
1) 
Если выразить L1, L2, L12 через индуктивные сопротивления
и учесть что 
и
, получим
где 
, ибо в нормальных АД 
и 
и величиной
можно пренебречь.
Здесь и - коэффициенты затухания, причем как видно из полученных соотношений , а их отношение 
.
Для нахождения оригиналов, т.е. действительных значений токов 
и 
, будем иметь в виду, что при обозначении р1=-и p2=-принимаются во внимание точные значения р1 и р2 , соответствующие выражению 1 . т.о.
Из этих выражений видно, что вектор каждого тока, кроме установившейся составляющей, изменяющейся с частотой 0эл, содержит 2 свободные составляющие, затухающие с коэффициентами затухания и .
Для вычисления момента двигателя необходимо найти комплексно-сопряженный вектор тока ротора 
. С этой целью в выражении для 
перед всеми
ставится знак минус. Подставив найденное значение 
и значение тока
в выражение электромагнитного момента, получим его составляющие, обусловленные взаимодействием составляющих токов. Если для примера найти установившееся значение пускового момента двигателя, пропорциональное мнимой части произведения первых членов уравнений для 
и 
, выразить индуктивности через индуктивные сопротивления, то имея в виду, что амплитудаU1M двухфазной машины связана с амплитудой U1M трехфазного напряжения коэффициентом 
, получим
Если сюда подставить значения и из выражения 1 и выполнить некоторые преобразования с учетом того, что 
и 
, получим значение пускового момента
Полное выражение пускового момента имеет вид
Здесь 7 составляющих момента.
Первая - установившийся для данной угловой скорости момент, соответствующий его статической механической характеристике. Следующие две составляющие – апериодические свободные составляющие. Следующие четыре составляющие - периодические составляющие, обусловленные взаимодействием затухающих апериодических (свободных) составляющих с принужденными токами, обусловленными действием напряжения сети. Поэтому они имеют угловую частоту напряжения сети 0эл. Апериодические (свободные) составляющие момента обусловлены взаимодействием свободных токов.
Поскольку, как показано ранее, , то характер изменения момента определяется главным образом переменными составляющими момента, затухающими с коэффициентом . Логарифмический декремент затухания для этих составляющих
т.к. 
Т.к. x1<x1+x на порядок, а Skp=0,1-0,5 , то 
для колебательной составляющей равен десятым долям единицы. Это значит, что за время затухания совершается десятки колебаний 
периодической составляющей момента, которая суммируясь с Муст, создает пики пускового момента, превышающие статический пусковой момент в несколько раз.
Для иллюстрации на рис. приведены кривые переходного процесса к.з. АД при пуске вхолостую, которые отражают рассмотренное влияние электромагнитной инерции, т.е. электромагнитных переходных процессов. Тут же приведена динамическая механическая характеристика двигателя (кривая 1), построенная на основе зависимостей M=f(t) и =f(t). Еще большие пики момента имеют место при противовключении двигателя с незатухающим полем. Т.о. электромагнитная инерция исключает возможность нарастания момента скачком и существенно ухудшает характер процесса пуска, вызывая большие и многократно повторяемые пики, ускоряющие износ самого двигателя и механического оборудования.
Исследования показывают, что к моменту выхода к.з. АД на устойчивую часть статической механической характеристики (S<Skp) электромагнитные переходные процессы, обусловленные подключением двигателя к сети, практически затухают. В этом случае дальнейший процесс увеличения скорости до (при Мс=0) протекает следующим образом. При S<Skp токи в обмотках 
статора машины, определяемые по статической электромеханической характеристике (см. рис. ) , резко меняются по величине с изменением скорости. Однако, в следствии влияния индуктивности обмоток токи ротора не успевают измениться в соответствии с данной характеристикой. Чем жестче рабочий участок статической механической характеристики и чем меньше приведенный момент инерции, тем в большей степени изменение токов будет отставать от изменения скорости. В результате при 0 в процессе пуска вхолостую токи могут быть не равными нулю, поэтому не будет равен 0 и момент. И ротор разгоняется до скорости, превышающей синхронную. Момент становится тормозным, скорость начнет уменьшаться и т.д. (см. кривую 1- динамическую характеристику). Поэтому в конце переходного процесса изменение и М двигателя имеет затухающий колебательный характер. Чем мягче рабочий участок статической механической характеристики и чем больше момент инерции ротора, тем меньше амплитуда этих колебаний. Практически эти колебания в конце переходного процесса возникают не всегда.
Рассмотренные особенности переходных процессов к.з. АД относятся к числу его существенных недостатков и снижают надежность его работы. Снижения переходных составляющих тока и момента можно достичь путем ограничения темпа нарастания напряжения, приложенного к двигателю при пуске, что осуществляется применением тиристорных регуляторов напряжения, тиристорных преобразователей частоты.
studfiles.net
Теория электропривода
В большинстве случаев к. з. АД питается от сети с U1=const и f1=const. Поэтому нелинейность их механических характеристик проявляется полностью как в режимах пуска, так и торможения. Магнитный поток в переходных режимах изменяется в широких пределах и на характер переходных процессов существенное влияние оказывает электромагнитная инерция. С учетом ее движение электропривода в переходном процессе пуска включением на сеть можно описать, если воспользоваться уравнениями динамической механической характеристики в комплексной форме в осях U, V и уравнением движения обобщенной машины, подставить в них вместо U2 - 0, т. к. двигатель короткозамкнутый. Уравнения в комплексной форме, полученные ранее, имеют вид
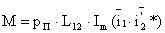
Если выразить векторы потокосцеплений через обобщенные векторы токов статора и
Ротора т. е
И подставить в уравнения равновесия ЭДС, получим
Заменив р на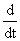 
, а вместо U2 подставив 0, будем иметь
Решить эту нелинейную систему уравнений можно только с помощью ЭВМ. Однако оценить влияние электромагнитной инерции в общем виде можно при анализе процесса включения двигателя на сеть при неизменной скорости ротора, т. е. wэл=const.
На начальном этапе скорость двигателя еще не успела существенно измениться и можно принять wэл=0. Анализировать такой процесс удобнее всего в осях a и b, принимая wк=0.При этих условиях первые 2 уравнения системы запишутся так
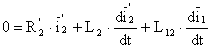
Переходя к изображениям переменных по Карсону при нулевых начальных условиях и учитывая, что синусоидальное напряжение сети U1 имеет изображение в виде
, получим
Найдя из второго уравнения i’2(p) и подставив в первое, а затем из второго же найдя i1(p) и подставив в первое получим после преобразований изображения токов
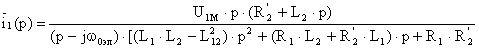
Производим и продаем частотные преобразователи: Цены на преобразователи частоты(21.01.16г.): Частотники одна фаза в три: Модель Мощность Цена CFM110 0.25кВт 2300грн CFM110 0.37кВт 2400грн CFM110 0.55кВт 2500грн CFM210 1,0 кВт 3200грн …
Обычно ДНВ работает при Ф=Фн если U=const или U=var. Необходимость ослабления потока возникает когда требуется получить скорость, превышающую основную (согласно требованиям технологического процесса ). Если бы поток изменялся мгновенно, то …
msd.com.ua
В большинстве случаев к.з. АД питается от сети с U1 = constиf1 = const.Поэтому нелинейность их механических характеристик проявляется полностью как в режимах пуска, так и торможения. Магнитный поток в переходных режимах изменяется в широких пределах и на характер переходных процессов существенное влияние оказывает электромагнитная инерция. С учетом ее движение электропривода в переходном процессе пуска включением на сеть можно описать, если воспользоваться уравнениями динамической механической характеристики в комплексной форме в осяхU, Vи уравнением движения обобщенной машины, подставить в них вместоU2 - 0, т.к. двигатель короткозамкнутый. Уравнения в комплексной форме, полученные ранее, имеют вид
;
;
.
Если выразить векторы потокосцеплений через обобщенные векторы токов статора и ротора т.е.
;
,
и подставить в уравнения равновесия ЭДС, получим
;
.
Заменив рна
, а вместоU2подставив 0, будем иметь
;
;
;
.
Решить эту нелинейную систему уравнений можно только с помощью ЭВМ. Однако, оценить влияние электромагнитной инерции в общем виде можно при анализе процесса включения двигателя на сеть при неизменной скорости ротора, т.е. эл=const.
На начальном этапе скорость двигателя еще не успела существенно измениться и можно принять эл= 0. Анализировать такой процесс удобнее всего в осяхи, принимаяк= 0. При этих условиях первые 2 уравнения системы запишутся так
;
.
Переходя к изображениям переменных по Карсону при нулевых начальных условиях и учитывая, что синусоидальное напряжение сети U1имеет изображение в виде
,
получим
;
.
Найдя из второго уравнения i’2(p) и подставив в первое, а затем из второго же найдяi1(p) и подставив в первое получим после преобразований изображения токов
;
.
Характер изменения свободных составляющих и их затухание определяются корнями p1иp2характеристического уравнения
1)
.
Корень 
определяет установившийся режим т.к. относится к изображению напряжения.
Если учесть, что 
, то
поэтому
.
Если выразить L1,L2,L12через индуктивные сопротивления
;
;
,
и учесть что 
и
, получим
;
,
где 
, ибо в нормальных АД 
и
и величиной
можно пренебречь.
Здесь и- коэффициенты затухания, причем как видно из полученных соотношений, а их отношение
.
Для нахождения оригиналов, т.е. действительных значений токов 
и 
, будем иметь в виду, что при обозначениир1= -иp2= -принимаются во внимание точные значенияр1ир2, соответствующие выражению 1 таким образом
;
.
Из этих выражений видно, что вектор каждого тока, кроме установившейся составляющей, изменяющейся с частотой 0эл, содержит 2 свободные составляющие, затухающие с коэффициентами затуханияи.
Для вычисления момента двигателя необходимо найти комплексно-сопряженный вектор тока ротора 
. С этой целью в выражении для 
перед всеми
ставится знак минус. Подставив найденное значение
и значение тока
в выражение электромагнитного момента, получим его составляющие, обусловленные взаимодействием составляющих токов. Если для примера найти установившееся значение пускового момента двигателя, пропорциональное мнимой части произведения первых членов уравнений для
и
, выразить индуктивности через индуктивные сопротивления, то, имея в виду, что амплитудаU1Mдвухфазной машины связана с амплитудойU1Mтрехфазного напряжения коэффициентом
, получим
Если сюда подставить значения ииз выражения 1 и выполнить некоторые преобразования с учетом того, что 
и
, получим значение пускового момента
.
Полное выражение пускового момента имеет вид
Здесь 7 составляющих момента.
Первая - установившийся для данной угловой скорости момент, соответствующий его статической механической характеристике. Следующие две составляющие – апериодические свободные составляющие. Следующие четыре составляющие - периодические составляющие, обусловленные взаимодействием затухающих апериодических (свободных) составляющих с принужденными токами, обусловленными действием напряжения сети. Поэтому они имеют угловую частоту напряжения сети 0эл. Апериодические (свободные) составляющие момента обусловлены взаимодействием свободных токов.
Поскольку, как показано ранее, , то характер изменения момента определяется главным образом переменными составляющими момента, затухающими с коэффициентом. Логарифмический декремент затухания для этих составляющих
т.к. 
Т.к. x1 < x1+ xна порядок, аskp= 0,1 - 0,5 , то
для колебательной составляющей равен десятым долям единицы. Это значит, что за время затухания совершается десятки колебаний
периодической составляющей момента, которая, суммируясь сМуст, создает пики пускового момента, превышающие статический пусковой момент в несколько раз.
Для иллюстрации на рис. приведены кривые переходного процесса к.з. АД при пуске вхолостую, которые отражают рассмотренное влияние электромагнитной инерции, т.е. электромагнитных переходных процессов. Тут же приведена динамическая механическая характеристика двигателя (кривая 1), построенная на основе зависимостей M = f(t)и = f(t). Еще большие пики момента имеют место при противовключении двигателя с незатухающим полем. Таким образом, электромагнитная инерция исключает возможность нарастания момента скачком и существенно ухудшает характер процесса пуска, вызывая большие и многократно повторяемые пики, ускоряющие износ самого двигателя и механического оборудования.
Исследования показывают, что к моменту выхода к.з. АД на устойчивую часть статической механической характеристики (s < skp) электромагнитные переходные процессы, обусловленные подключением двигателя к сети, практически затухают. В этом случае дальнейший процесс увеличения скорости до(приМс =0) протекает следующим образом. Приs<skpтоки в обмотках
статора машины, определяемые по статической электромеханической характеристике (см. рис.), резко меняются по величине с изменением скорости. Однако вследствие влияния индуктивности обмоток токи ротора не успевают измениться в соответствии с данной характеристикой. Чем жестче рабочий участок статической механической характеристики и чем меньше приведенный момент инерции, тем в большей степени изменение токов будет отставать от изменения скорости. В результате при0в процессе пуска вхолостую токи могут быть не равными нулю, поэтому не будет равен 0 и момент. И ротор разгоняется до скорости, превышающей синхронную. Момент становится тормозным, скорость начнет уменьшаться и т.д. (см. кривую 1- динамическую характеристику). Поэтому в конце переходного процесса изменениеи М двигателя имеет затухающий колебательный характер. Чем мягче рабочий участок статической механической характеристики и чем больше момент инерции ротора, тем меньше амплитуда этих колебаний. Практически эти колебания в конце переходного процесса возникают не всегда.
Рассмотренные особенности переходных процессов к.з. АД относятся к числу его существенных недостатков и снижают надежность его работы. Снижения переходных составляющих тока и момента можно достичь путем ограничения темпа нарастания напряжения, приложенного к двигателю при пуске, что осуществляется применением тиристорных регуляторов напряжения, тиристорных преобразователей частоты.
studfiles.net
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«БЕЛГОРОДСКАЯ ГОСУДАРСТВЕННАЯ СЕЛЬСКОХОЗЯЙСТВЕННАЯ АКАДЕМИЯ»
Расчетно–графическая работа
По дисциплине
«Электропривод и электрооборудование»
ТЕМА: «Переходные процессы при пуске и торможении трехфазного асинхронного двигателя»
Работу выполнил:
студент 45(И-Э) группы
Ребрищев И.
п. Майский, 2009 г.
Исходные данные для варианта № 39:
1. РАСЧЕТ ХАРАКТЕРИСТИК ДВИГАТЕЛЯ
1)Номинальная скорость вращения якоря
2)Номинальный вращающий момент
3)Номинальное сопротивление цепи якоря
4) Сопротивление цепи якоря
5) Скорость идеального холостого хода двигателя
6) Коэффициент пропорциональности между ЭДС и скоростью, а также электромагнитным моментом и током якоря в ДПТ НВ при неизменном магнитном потоке возбуждения
7) Уравнение естественной электромеханической характеристики
8) Уравнение естественной механической характеристики
2. РАСЧЕТ ПУСКОВОГО РЕОСТАТА
1) Определяем величины токов, при которых должно происходить переключение ступеней реостата. Принимаем
2) Задавшись значением тока
, определяем ток
с учетом заданного числа ступеней пускового реостата 
, из условия 
Отсюда
, значит: 
3) Сопротивление цепи якоря при пуске (первая ступень)
4) Отношение токов при пуске
5) Сопротивление цепи якоря на второй ступени
6) Сопротивление цепи якоря на третьей ступени
7) Величина добавочного резистора на последней ступени
8) Величина добавочного резистора на второй ступени
9) Величина добавочного резистора на первой ступени
3. РАСЧЕТ ВРЕМЕНИ ПУСКА
1) Строим электродинамические характеристики двигателя на всех участках и определяем значение скоростей вращения в точках переключения реостата (рис. 1 и рис. 2).
2) Время перехода от одной скорости вращения к другой, при динамическом моменте – описываемом линейной функцией
где:
значения ω находим по Рисунку 2, измеряя расстояния от начала координат, до требуемого значения скорости с учетом масштаба; ω1 =0.
2.1) Время перехода от 1 до 2:
2.2) Время перехода от 3 до 4:
2.3) Время перехода от 5 до 6:
2.4) Время перехода от 7 до b:
2.5) Время, требуемое для разгона двигателя от 0 до ωн :
На рис. 3 приведена схема включения пусковых резисторов.
mirznanii.com
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«БЕЛГОРОДСКАЯ ГОСУДАРСТВЕННАЯ СЕЛЬСКОХОЗЯЙСТВЕННАЯ АКАДЕМИЯ»
Расчетно–графическая работа
По дисциплине
«Электропривод и электрооборудование»
ТЕМА: «Переходные процессы при пуске и торможении трехфазного асинхронного двигателя»
Работу выполнил:
студент 45(И-Э) группы
Ребрищев И.
п. Майский, 2009 г.
Исходные данные для варианта № 39:
1. РАСЧЕТ ХАРАКТЕРИСТИК ДВИГАТЕЛЯ
1)Номинальная скорость вращения якоря
2)Номинальный вращающий момент
3)Номинальное сопротивление цепи якоря
4) Сопротивление цепи якоря
5) Скорость идеального холостого хода двигателя
6) Коэффициент пропорциональности между ЭДС и скоростью, а также электромагнитным моментом и током якоря в ДПТ НВ при неизменном магнитном потоке возбуждения
7) Уравнение естественной электромеханической характеристики
8) Уравнение естественной механической характеристики
2. РАСЧЕТ ПУСКОВОГО РЕОСТАТА
1) Определяем величины токов, при которых должно происходить переключение ступеней реостата. Принимаем
2) Задавшись значением тока , определяем ток с учетом заданного числа ступеней пускового реостата , из условия
Отсюда , значит:
3) Сопротивление цепи якоря при пуске (первая ступень)
4) Отношение токов при пуске
5) Сопротивление цепи якоря на второй ступени
6) Сопротивление цепи якоря на третьей ступени
7) Величина добавочного резистора на последней ступени
8) Величина добавочного резистора на второй ступени
9) Величина добавочного резистора на первой ступени
3. РАСЧЕТ ВРЕМЕНИ ПУСКА
Строим электродинамические характеристики двигателя на всех участках и определяем значение скоростей вращения в точках переключения реостата (рис. 1 и рис. 2).
Время перехода от одной скорости вращения к другой, при динамическом моменте – описываемом линейной функцией
где:
значения ω находим по Рисунку 2, измеряя расстояния от начала координат, до требуемого значения скорости с учетом масштаба; ω1 =0.
2.1) Время перехода от 1 до 2:
2.2) Время перехода от 3 до 4:
2.3) Время перехода от 5 до 6:
2.4) Время перехода от 7 до b:
2.5) Время, требуемое для разгона двигателя от 0 до ωн:
На рис. 3 приведена схема включения пусковых резисторов.
1
globuss24.ru
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«БЕЛГОРОДСКАЯ ГОСУДАРСТВЕННАЯ СЕЛЬСКОХОЗЯЙСТВЕННАЯ АКАДЕМИЯ»
Расчетно–графическая работа
По дисциплине
«Электропривод и электрооборудование»
ТЕМА: «Переходные процессы при пуске и торможении трехфазного асинхронного двигателя»
Работу выполнил:
студент 45(И-Э) группы
Ребрищев И.
п. Майский, 2009 г.
Исходные данные для варианта № 39:
1. РАСЧЕТ ХАРАКТЕРИСТИК ДВИГАТЕЛЯ
1)Номинальная скорость вращения якоря
2)Номинальный вращающий момент
3)Номинальное сопротивление цепи якоря
4) Сопротивление цепи якоря
5) Скорость идеального холостого хода двигателя
6) Коэффициент пропорциональности между ЭДС и скоростью, а также электромагнитным моментом и током якоря в ДПТ НВ при неизменном магнитном потоке возбуждения
7) Уравнение естественной электромеханической характеристики
8) Уравнение естественной механической характеристики
2. РАСЧЕТ ПУСКОВОГО РЕОСТАТА
1) Определяем величины токов, при которых должно происходить переключение ступеней реостата. Принимаем
2) Задавшись значением тока , определяем ток с учетом заданного числа ступеней пускового реостата , из условия
Отсюда , значит:
3) Сопротивление цепи якоря при пуске (первая ступень)
4) Отношение токов при пуске
5) Сопротивление цепи якоря на второй ступени
6) Сопротивление цепи якоря на третьей ступени
7) Величина добавочного резистора на последней ступени
8) Величина добавочного резистора на второй ступени
9) Величина добавочного резистора на первой ступени
3. РАСЧЕТ ВРЕМЕНИ ПУСКА
Строим электродинамические характеристики двигателя на всех участках и определяем значение скоростей вращения в точках переключения реостата (рис. 1 и рис. 2).
Время перехода от одной скорости вращения к другой, при динамическом моменте – описываемом линейной функцией
где:
значения ω находим по Рисунку 2, измеряя расстояния от начала координат, до требуемого значения скорости с учетом масштаба; ω1 =0.
2.1) Время перехода от 1 до 2:
2.2) Время перехода от 3 до 4:
2.3) Время перехода от 5 до 6:
2.4) Время перехода от 7 до b:
2.5) Время, требуемое для разгона двигателя от 0 до ωн:
На рис. 3 приведена схема включения пусковых резисторов.
1
doc4web.ru
