







36) Уравнение напряжения и тока асинхронного двигателя
2.5. Процессы в асинхронной машине
2.5.1. Цепь статора
а) ЭДС статора.
Магнитное поле, создаваемое обмоткой статора, вращается относительно неподвижного статора с частотой n0=60f)/p и будет наводить в обмотке статора ЭДС. Действующее значение ЭДС, наводимой этим полем в одной фазе обмотки статора определяется выражением:
E1=4,44w1k1fΦ,
где: k1=0.92÷0.98 – обмоточный коэффициент; f1=f – частота сети; w1 – число витков одной фазы обмотки статора; Φ – результирующее магнитное поле в машине.
б) Уравнение электрического равновесия фазы обмотки статора.
Это уравнение составлено по аналогии с катушкой с сердечником, работающей на переменном токе.
 .
.
Здесь Ú и Ú1 – напряжение сети и напряжение, подведённое к обмотке статора. R1 – активное сопротивление обмотки статора, связанное с потерями на нагрев обмотки. x1 – индуктивное сопротивление обмотки статора, связанное с потоком рассеяния. z1 – полное сопротивление обмотки статора. İ1 – ток в обмотке статора.
При анализе работы асинхронных машин часто принимают I1z1=0. Тогда можно записать:
U1≈E1=4,44w1k1fΦ.
Из этого выражения следует, что магнитный поток Φ в асинхронной машине не зависит от её режима работы, а при заданной частоте сети f зависит только от действующего значения приложенного напряжения U1. Аналогичное соотношение имеет место и в другой машине переменного тока – в трансформаторе.
2.5.2. Цепь ротора
а) Частота ЭДС и тока ротора.
При неподвижном роторе частота ЭДС f2 равна частоте сети f.
f2=f=(n0p)/60.
При вращающемся роторе частота ЭДС ротора зависит от частоты вращения магнитного поля относительно вращающегося ротора, которая определяется соотношением:
n'=n0−n.
Тогда частота ЭДС вращающегося ротора:
 .
.
Частота ЭДС ротора изменяется пропорционально скольжению и в режиме двигателя имеет наибольшее значение в момент пуска в ход.
Пусть при f=50Гц, номинальное скольжение Sн=2%. Тогда при номинальной частоте вращения ротора f2=f×Sн=1Гц.
Таким образом, в обмотке ротора асинхронной машины частота наводимой ЭДС зависит от частоты вращения ротора.
б) ЭДС ротора.
При неподвижном роторе f2=f и действующее значение ЭДС определяется по аналогии с E1.
E2=4,44w2k2fΦ,
где: w2 и k2 – соответственно число витков и обмоточный коэффициент обмотки ротора.
Если ротор вращается, то f2=f×Sн и ЭДС вращающегося ротора определяется соотношением:
E2S=4,44w2k2f2Φ=E2S.
ЭДС, наводимая в обмотке ротора, изменяется пропорционально скольжению и в режиме двигателя имеет наибольшее значение в момент пуска в ход.
Отношение ЭДС статора к ЭДС неподвижного ротора называется коэффициентом трансформации асинхронной машины.
| k= | E1 | = | w1k1 | . |
| E2 | w2k2 |
в) ток ротора.
Запишем уравнение равновесия для одной фазы короткозамкнутого ротора.
При неподвижном роторе.
 ,
,
где: x2=2πfL2 – индуктивное сопротивление обмотки неподвижного ротора, связанное с потоком рассеяния; R2 – активное сопротивление обмотки ротора, связанное с потерями на нагрев обмотки.
При вращающемся роторе.

где: x2S=2πf2L2=2πfL2S=x2S – индуктивное сопротивление обмотки вращающегося ротора.
Для тока ротора в общем случае можно получить такое соотношение:
 .
.
Отсюда следует, что ток ротора зависит от скольжения и возрастает при его увеличении, но медленнее, чем ЭДС.
г) поле ротора
Обмотка ротора, как и обмотка статора, является многофазной и при появлении в ней тока создаёт своё вращающееся магнитное поле. Обозначим через n2 частоту вращения магнитного поля ротора относительно ротора.
n2=(60f2)/p=(60fS)/p.
Здесь p – число пар полюсов обмотки ротора, оно всегда равно числу пар полюсов обмотки статора.
Относительно статора магнитное поле ротора вращается с частотой
 .
.
Из полученного соотношения следует, что магнитное поле ротора относительно статора вращается с той же частотой, что и магнитное поле статора. Таким образом, магнитные поля ротора и статора относительно друг друга неподвижны. Поэтому при анализе работы асинхронной машины можно применить те же соотношения, что и трансформаторе.
2.5.3. Ток статора
Так как результирующее магнитное поле асинхронной машины не зависит от её режима работы, можно составить для одной фазы уравнение магнитодвижущих сил, приравняв магнитодвижущую силу в режиме холостого хода к сумме магнитодвижущих сил в режиме нагрузки.
İ0w1k1=İ1w1k1+İ2w2k2
Отсюда İ1=İ0+İ'2.
Здесь I0 – ток в обмотке статора в режиме идеального холостого хода, I'2=−I2(w2k2)/(w1k1) – составляющая тока статора, которая компенсирует действие магнитодвижущей силы обмотки ротора. Полученное выражение для тока статора отражает свойство саморегулирования асинхронной машины. Чем больше ток ротора, тем больше ток статора. В режиме холостого хода ток статора минимальный. В режиме нагрузки ток статора возрастает. Ток реального холостого хода асинхронной машины I0=(20÷60)%I1н и значительно больше по сравнению с номинальным током, чем у трансформатора. Это объясняется тем, что величина тока I0 зависит от магнитного сопротивления среды, в которой создаётся магнитное поле. У асинхронной машины, в отличие от трансформатора, есть воздушный зазор, который создаст большое сопротивление магнитному полю.
3
studfiles.net
Электродвижущая сила в обмотке электрической машины индуктируется только при условии изменения потокосцепления магнитного поля с витками катушки, что находит отражение в известном соотношении:

отражающем закон электромагнитной индукции. Потокосцепление может изменяться под действием различных причин.
При вращении витка в магнитном поле или при перемещении магнитного поля относительно неподвижного витка в нем индуктируется ЭДС, которую называют ЭДС вращения. При изменении во времени потока, сцепленного с неподвижным витком, в нем индуктируется так называемая трансформаторная ЭДС. Во всех случаях величина и характер изменения индуктируемой ЭДС определяется величиной и характером изменения потокосцепления и также параметрами витка.
Определим ЭДС в одной катушке обмотки статора синхронного генератора, имеющей число витков Wк и диаметральный шаг (рис. 3).
Частота индуктируемой в витке ЭДС определяется скоростью вращения и числом пар полюсов ротора. Одному повороту двухполюсного ротора соответствует один период изменения ЭДС. Для того чтобы в двухполюсном СГ получить частоту ЭДС 50 Гц, необходимо вращать ротор со скоростью 50 оборотов в секунду или 3000 оборотов в минуту. При увеличении числа полюсов скорость вращения ротора будет пропорционально уменьшается. В общем случае, если ротор имеет 2р полюсов и вращается со скоростью n об/мин, то частота ЭДС равна:

Величину ЭДС вращения удобно определить по соотношению:
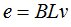
из которого ясно видна зависимость формы кривой ЭДС от характера распределения магнитной индукции на полюсном делении.
Одно из основных требований, предъявляемых к генераторам переменного тока, заключается в обеспечении синусоидальности изменения во времени ЭДС, индуктируемой в обмотке статора, т.е. в обеспечении зависимости:

Как отмечалось выше, в СГ это достигается за счет создания в воздушном зазоре между статором и ротором синусоидального (или близкого к синусоидальному) распределения магнитной индукции по ширине полюсного деления.
Практически распределение поля в зазоре всегда отличается от синусоидального, что связано как с несинусоидальностью распределения МДС (особенно в неявнополюсном роторе, так и с наличием зубцов на статоре, насыщением и т.д. Следовательно, и ЭДС в обмотках также несинусоидальна. Для упрощения расчетов и анализа физических процессов в электрических машинах несинусоидальную кривую магнитной индукции представляют в виде гармонического ряда синусоидальных кривых, в который кроме первой (основной) гармоники B1 входят высшие гармонические порядка 3, 5, 7 (В3, В5 В7) и т.д. (рис. 2) и считают, что каждая из этих гармоник индуктирует в обмотке синусоидальную ЭДС соответствующего порядка.
Рассмотрим величину ЭДС в проводнике от первой гармоники магнитной индукции:

где в соответствии с соотношением:

имеем
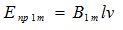
Полный магнитный поток от 1-й гармоники магнитной индукции равен (рис. 2 ,а) :

откуда получаем:

Окружная скорость вращения ротора равна:

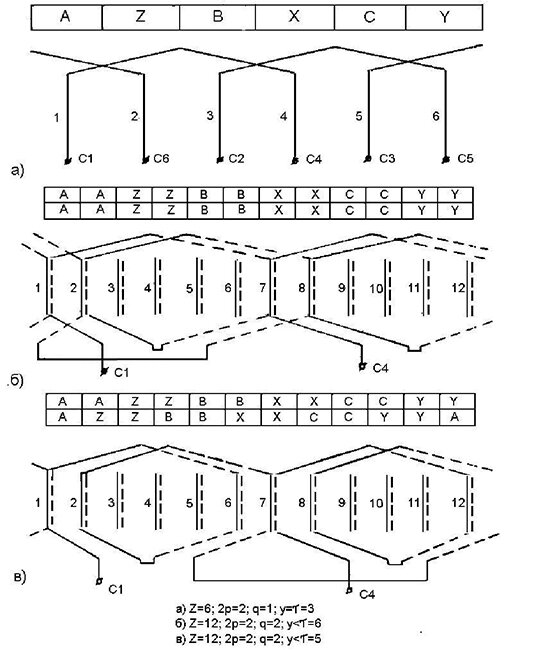
Рис. 1 — Принцип построения трехфазных обмоток машин переменного тока: а,б) – двухполюсная обмотка с диаметральным шагом; в) – двухполюсная обмотка с укороченным шагом
Подставляя:

и

в
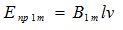
получаем:

Практический интерес представляет действующее значение ЭДС первой гармоники:

ЭДС для витка с диаметральным шагом (рис. 2 ,б) складывается из ЭДС двух проводников, находящихся под полюсами разной полярности:

а ЭДС катушки с диаметральным шагом равна:

ЭДС, индуктируемые в катушке высшими гармониками магнитной индукции, рассчитываются по аналогичным соотношениям:

где ν — порядок пространственной гармоники.
Магнитный поток Фνm определяется из соотношения:

Для пространственных гармоник магнитного поля fν = f1.
Для катушки с укороченным шагом (как на рис. 1, в) ЭДС уменьшается, что связано с уменьшением магнитного потока Фm (рис.2 ,в). Коэффициент укорочения ку определяется отношением геометрической суммы ЭДС двух проводников (рис.2 ,в) :

к арифметической сумме, определяемой по :
 т.е.
т.е.

Где выражение :

характеризует относительный шаг обмотки.
Следовательно, ЭДС катушки с укороченным шагом рассчитывается по формуле:
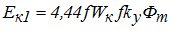
Укорочение обмотки помимо экономии обмоточных материалов позволяет существенно уменьшить действие высших гармоник магнитной индукции, что показано на рис. 2,в.
Выбирая, например, укорочение :

можно добиться полного устранения действия пятой гармоник магнитной индукции, т.к. ЭДС в противоположных проводниках витка от этой гармоники поля равны по величине, но направлены навстречу друг другу.

Рис. 2 - Распределение магнитной индукции под полюсом: а – разложение индукции на гармонические; б – ЭДС витка с диаметральным шагом; в – ЭДС витка с укороченным шагом.
На практике чаще всего применяют укорочение:

что позволяет существенно уменьшить одновременно и пятую, и седьмую гармоники, наиболее проявленные в общей кривой ЭДС.
ЭДС катушечной группы, состоящей из q последовательно соединенных и расположенных в соседних пазах катушек определяется как геометрическая сумма векторов ЭДС отдельных катушек, сдвинутых в пространстве на угол:
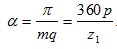
Например, при q=3, 2р=2 и z =18, угол α составляет 20°. На рис. 3 эти ЭДС показаны тремя векторами, каждый из которых представляет собой действующее значение ЭДС одной катушки.

Рис. 3 - ЭДС катушечной группы
Из построения следует, что геометрическая сумма рассматриваемых ЭДС, равная:
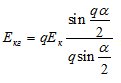
меньше арифметической суммы ЭДС отдельных катушек qЕк. Таким образом, распределение катушек, составляющих фазу обмотки, по пазам приводит к уменьшению результирующей ЭДС, что учитывается коэффициентом распределения, равным:

Выражение для ЭДС фазы обмотки статора (для первой гармоники) записывается в виде:

где члены выражения:

— обмоточный коэффициент для первой гармоники;

- число последовательно соединенных витков фазы.
Для определения высших гармоник ЭДС фазы используют соотношение:

где член выражения:

Результирующая ЭДС фазы с учетом высших гармония определяется из соотношения:

Как отмечалось выше высшие гармоники искажают ЭДС и форма напряжения на зажимах СГ становится несинусоидальной. Это отрицательно сказывается как на работе самого генератора, так и потребителей электроэнергии — асинхронных двигателей, систем управления, вычислительных комплексов, навигационных приборов и т.д. Снижаются КПД и коэффициент мощности потребителей, увеличиваются потери энергии, появляются погрешности в измерениях, повышаются шумы и вибрации электрических машин.
Поэтому коэффициент несинусоидальности кривой напряжения судовых СГ, под которым понимают отношение:

не должен превышать 10 %.
Укорочение шага обмотки, ее распределение по пазам способствуют улучшению формы кривой ЭДС и напряжения. Кроме того, для этих же целей часто применяют скос пазов на статоре (или на роторе) на одно зубцовое деление.
На форму кривой ЭДС также оказывает влияние способ соединения фаз — «звезда» (Y), или «треугольник» (Δ). В трехфазных системах первые гармоники ЭДС отдельных фаз сдвинуты на 120°относительно друг друга, а ЭДС третьих и кратных трем гармоник — на 360°, т.е. совладают по фазе и при соединении фаз в «звезду» в линейных напряжениях эти гармоники отсутствуют. При соединении фаз обмотки в «треугольник» ЭДС этих гармоник по контуру «треугольника» складываются и создают ток тройной частоты. В линейных напряжениях и в этом случае гармоник, кратных трем, не содержится.
Все эти особенности необходимо учитывать при эксплуатации электрических машин.
www.radioingener.ru
Асинхронный двигатель работает посредством индукции токов и напряжений в цепи ротора через цепь статора. Это фактически действие трансформации и потому эквивалентная схема асинхронной электрической машины будет аналогичной схеме замещения (equivalent circuit) трансформатора.
Эквивалентная схема асинхронного трёхфазного двигателя как трансформатора относительно фазного напряжения показана ниже.

Модель асинхронного двигателя, имеющего ротор и статор, или же идеального трансформатора, связана соотношением трансформации aeff (соотношением витков).
Как и в любом трансформаторе, есть первичная обмотка, которая имеет определённое активное сопротивление и собственную индуктивность. Для асинхронного двигателя это обмотка статора. На схеме её активное сопротивление обозначено как R1, а собственная индуктивность показана как реактивное сопротивление X1.
Кроме того, как и у любого трансформатора с железным сердечником, магнитный поток в асинхронной машине связан с интегралом от приложенного напряжения E1. На графике можно увидеть, две кривые зависимости между магнитодвижущей силой (МДС)(MMF) и магнитным потоком Ф. Одна кривая для асинхронной машины, а другая аналогичная кривая для трансформатора.

Наклон кривой связи МДС (MMF) и магнитного потока асинхронного двигателя меньше, чем наклон кривой хорошего трансформатора. Это потому, что в асинхронном двигателе имеется воздушный зазор, что значительно ухудшает путь магнитного потока и тем самым уменьшает связь между первичными и вторичными обмотками.
Более высокое магнитное сопротивление при наличии воздушного зазора означает, более высокий ток намагничивания, который необходимый для получения заданного уровня магнитного потока. Таким образом, реактивное сопротивление намагничивания XM в эквивалентной схеме будет иметь гораздо меньшее значение, чем это было бы в трансформаторе.
Напряжение на первичной обмотке, то есть на статоре E1 связанно с напряжением ER на вторичной обмотке, то есть роторе. Эта связь для идеального трансформатора выражается эффективным коэффициентом витков aeff. Довольно трудно увидеть соотношение витков на роторе и статоре, потому как ротор является короткозамкнутым. Дело в том, что нет чётких витков на роторе, как это можно увидеть в обмотке статора, но коэффициент витков aeff существует, потому как существует магнитная связь и происходит трансформация за счёт индукции.
Электродвижущая сила ER в роторе производит электрический ток, потому как вторичная цепь находится в состоянии короткого замыкания. Цепь ротора является вторичной обмоткой трансформатора.
Полное сопротивление (импеданс) и ток намагничивания первичной цепи асинхронного двигателя, которая представлена статором, очень похожи на аналогичные элементы первичной цепи эквивалентной схемы трансформатора (схема замещения).
Когда к обмоткам статора приложено напряжение, в обмотке ротора индуцируется ЭДС. Чем больше относительное движение магнитного поля между ротором и статором, тем большее ЭДС индуцируется в роторе и тем больше частота вращения ротора. Самое большое относительное движение магнитного поля происходит тогда, когда ротор находится в неподвижном состоянии. Такое состояние называется заторможенным ротором (locked-rotor) или состояние блокированного ротора (blocked-rotor). В этом состоянии максимальное ЭДС и максимальная частота вращающегося магнитного поля, которое проходит сквозь обмотку ротора. Наименьшее ЭДС и частота вращающегося магнитного поля, которое проходит сквозь ротор соответствует движению ротора с той же скоростью, что и скорость магнитного поля статора.
Здесь необходимо рассматривать генерацию ЭДС в роторе относительно движения ротора и магнитного потока. Если относительно ротора магнитное поле не движется, а значит, нет изменения магнитного потока, проходящего через витки ротора, тогда и ЭДС не возникает и потому ток в роторе отсутствует.
Величина и частота ЭДС, которая индуцируется в роторе при любой скорости ротора, между этими двумя крайностями, прямо пропорциональна скольжению ротора. Таким образом, если величину ЭДС ротора при условиях заторможенного ротора обозначается как ER0, то величина ЭДС ротора при любом скольжении определяется следующим выражением:

А также частота вращения ротора при любом скольжении:

Это ЭДС индуцируется в роторе, которое содержит как активное, так и реактивное сопротивления. Активное сопротивление ротора RR является постоянным и не зависит от скольжения, в то время как на реактивное сопротивление ротора скольжение оказывает сложное влияние.
Реактивное сопротивление ротора асинхронного двигателя зависит от индуктивности ротора, а также от частоты тока в роторе и от величины напряжения на обмотке ротора. При индуктивности ротора LR, его реактивное сопротивление определяется уравнением:

В результате эквивалентная схема ротора приобретает следующий вид:

Ток в цепи ротора определяется следующим уравнением:

Таким образом, общий импеданс (общее сопротивление) ротора с учётом его скольжения в итоге будет равен:

В этом случае, с учётом преобразования, эквивалентная схема цепи ротора приобретает следующий вид:

В этой эквивалентной схеме, ЭДС ротора постоянное ER0, а общее сопротивление ротора ZR,EQ имеет зависимость от скольжения (s) ротора. Из приведённого выше уравнения видно, что при малом скольжении активное сопротивление ротора во много раз больше по величине, чем реактивное сопротивление XR0. При больших значениях скольжения, XR0 будет значительно больше, чем активное сопротивление ротора.
Для получения конечной фазной эквивалентной схемы асинхронного двигателя, необходимо совместить часть модели ротора с частью модели статора. В обычном трансформаторе такие характеристики как напряжения, токи и сопротивления, в цепи вторичной обмотки, можно соотнести к характеристикам цепи в первичной обмотке. Для этого надо использовать коэффициент трансформации трансформатора.
Точно такие же преобразования можно сделать и для асинхронного двигателя, где первичная обмотка (цепь) – обмотка статора, а вторичная обмотка (цепь) – обмотка короткозамкнутого ротора. Если использовать коэффициент эффективных витков асинхронного двигателя aeff, то напряжение в цепи ротора выражено через уравнение:

Ток в цепи ротора определяется как:

Общее сопротивление цепи ротора (импеданс) равно:

Приняв во внимание следующие соотношения:

Эквивалентная схема асинхронного трёхфазного двигателя с короткозамкнутым ротором, относительно фазного напряжения питания, примет следующий вид.

Теорема Тевенина утверждает, что любая линейная цепь, в которой можно выделить отдельную часть от всей схемы, может быть заменена одним источником напряжения в совокупности с эквивалентным сопротивлением.
Эквивалентная схема с выделенной частью согласно теореме Тевенина представлена ниже:

Эквивалентное сопротивление ZM равно:

Далее преобразовав схему, получим новое значение источника питания (напряжения) VTH и новое эквивалентное значение общего сопротивления ZTH согласно теореме Тевенина.
Схема после преобразования Тевенина:

Уравнения для расчёта эквивалентных сопротивления ZTH и напряжения VTH:

В итоге, зная все значения сопротивлений и напряжение источника питания, мы можем рассчитать ток в цепи, а также падения напряжений. Эти расчёты нужны для дальнейшего определения рабочих параметров двигателя, для расчёта потерь мощности и её преобразования, а также для расчёта крутящего момента и пусковых характеристик двигателя.
Дата: 26.01.2016
© Valentin Grigoryev (Валентин Григорьев)
Тег статьи: Асинхронные двигатели
Все теги раздела Электротехника:Электричество Закон Ома Электрический ток Электробезопасность Устройства Биоэлектричество Характеристики Физические величины Электролиз Электрические схемы Асинхронные двигатели
www.electricity-automation.com
ЭДС обмотки статора. ЭДС обмотки статора e1наводится вращающимся магнитным потоком. По аналогии с трансформатором можно написать, что ЭДС фазы обмотки статора определяется формулой:
 , (3.6)
, (3.6)
где w1 – число витков обмотки статора;kоб1 - обмоточный коэффициент, который учитывает укорочение шага обмотки, ее распределение по нескольким пазам и скос пазов.
 3.8.2. ЭДС обмотки ротора. По аналогии с трансформатором можно написать выражение (3.6) для ЭДС неподвижного ротора (3.7)
3.8.2. ЭДС обмотки ротора. По аналогии с трансформатором можно написать выражение (3.6) для ЭДС неподвижного ротора (3.7)
В неподвижном роторе частота ЭДС f2 = f1, т. е. такая же как у ЭДС обмотки статора. Во вращающемся роторе частота ЭДС равна f2 . В этом случае из (3.7) наводимая ЭДС
 (3.8)
(3.8)
Индекс s относится к вращающемуся ротору.

 Учитывая,
Учитывая,
что , получаем

Подставив (3.5) в (3.8) находим связь между ЭДС вращающегося и неподвижного роторов
(3.9)
 Из (3.9) следует, что ЭДС в обмотке вращающегося ротора составляет s % ЭДС неподвижного ротора, т. е. Легко показать, что связь между индуктивными сопротивлениями неподвижного ротора X2 вращающегося ротора X2sаналогична (3.9): для вращающегося ротора
Из (3.9) следует, что ЭДС в обмотке вращающегося ротора составляет s % ЭДС неподвижного ротора, т. е. Легко показать, что связь между индуктивными сопротивлениями неподвижного ротора X2 вращающегося ротора X2sаналогична (3.9): для вращающегося ротора
 ,
,
а для неподвижного
 ,
,
electrono.ru
Для привода механизмов подъемно-транспортных машин применяются электродвигатели с параллельным, последовательным и смешанным возбуждением постоянного тока, а также асинхронные переменного тока. Основной величиной, характеризующей работу электродвигателя, является вращающий момент, развиваемый электродвигателем на валу. Обычно номинальный вращающий момент указывается в паспорте электродвигателя. Он может быть определен по формуле

где Мн — номинальный вращающий момент, кГм;
Рн — номинальная мощность, квт;
пн — номинальное число оборотов в минуту.
Как указывалось, вращающий момент электродвигателей постоянного тока создается за счет взаимодействия магнитного поля полюсов с током в обмотке якоря, т. е. он пропорционален току Iя и потоку возбуждения Ф:

где к — постоянный коэффициент, зависящий от конструкции машины;
Iя —ток в обмотке якоря;
Ф — магнитный поток электродвигателя.

где р —число пар полюсов машины;
а — число пар параллельных ветвей обмотки якоря;
N — число проводников обмотки якоря.
Вращающий момент асинхронного электродвигателя образуется в результате взаимодействия магнитного поля статора с токами роторной цепи и равен

где Ф1 — магнитный поток статора;
I2 —ток в обмотке ротора;
cos ?2 — коэффициент мощности роторной цепи.
По законам электромагнитной индукции в обмотке якоря работающего электродвигателя наводится э. д. c., которая часто называется встречной э. д. с. (или противоэлектродвижущей силой), так как при работе машины в двигательном режиме она направлена навстречу приложенному напряжению. Известно, что индуктируемая в обмотке э. д. с. зависит от числа оборотов и магнитного потока и определяется по выражению

где с — постоянный для данной машины коэффициент;
n —число оборотов в минуту;
Ф —магнитный поток электродвигателя.

где р — число пар полюсов машины;
N — число проводников обмотки якоря;
а —число пар параллельных .ветвей обмотки якоря.
vdvizhke.ru