В современной электроэнергетике почти повсеместно переменный ток вытесняет постоянный. Это объясняется многими преимуществами машин переменного тока в сравнении с машинами постоянного тока. В частности, у машин переменного тока вес, габариты и стоимость меньше, а к. п. д. выше; они проще в обслуживании, долговечнее и надежнее машин постоянного тока. Правда, электродвигатели переменного тока хуже поддаются регулировке, они развивают значительно меньшие пусковые моменты. Поэтому, если от электродвигателей требуются высокие регулировочные качества и повышенные пусковые моменты, применяют электродвигатели постоянного тока.
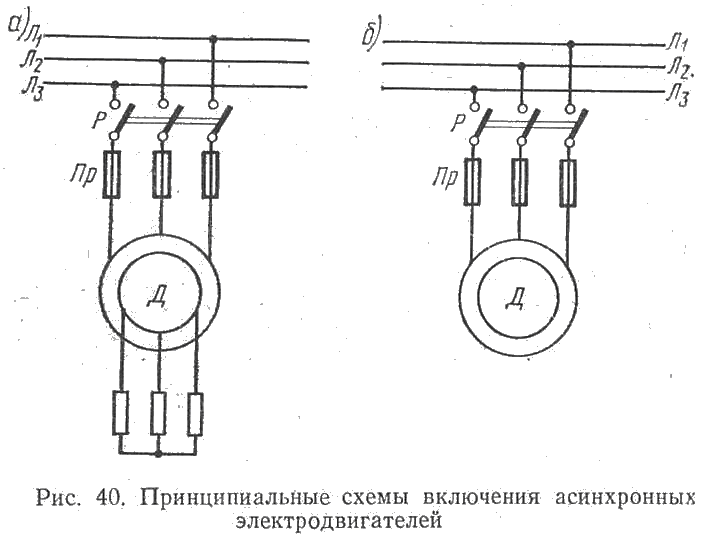
Привод механизмов портовых подъемно-транспортных машин чаще всего осуществляется асинхронными электродвигателями трехфазного переменного тока, получившими наибольшее распространение в электроэнергетике. Зависимости от исполнения ротора, различают асинхронные электродвигатели с короткозамкнутым ротором и с фазным ротором (с контактными кольцами). Принципиальная схема включения этих электродвигателей приведена на рис. 40..
Из курса электротехники известно, что принцип действия асинхронных электродвигателей основан на использовании так называемого вращающегося магнитного поля. При подаче трехфазного тока в обмотке статора создается магнитное поле, вращающееся со скоростью
где f— частота тока в обмотке статора;
р — число пар полюсов обмотки статора.
Эта скорость называется синхронной. Магнитное поле статора, (пересекая обмотку ротора, наводит в ней э. д. с., которая создает в цепи ротора ток. Последний, взаимодействуя с магнитным полем статора, образует вращающий момент, заставляющий ротор вращаться в ту же сторону, что и магнитное поле статора. При нормальной работе асинхронного электродвигателя его ротор вращается со скоростью п2<п1. Если бы скорость вращения ротора была равна скорости, с которой вращается магнитное поле статора, то последнее относительно ротора было бы неподвижным. В этом случае э. д. с. и ток в обмотке ротора были бы равны нулю и никакого вращающего момента не возникло бы.
Величиной, характеризующей работу асинхронного электродвигателя, является скольжение s:
где n1—синхронная скорость;
n2 — скорость вращения ротора.
Зная скольжение, нетрудно определить скорость вращения электродвигателя
При работе электродвигателя без нагрузки скорость его близка к синхронной, а скольжение очень мало.
Двигательный режим асинхронного электродвигателя имеет место при скольжениях, изменяющихся в пределах от 0 до 1, при этом число оборотов ротора изменяется от n1 до 0. Номинальная величина скольжения асинхронного электродвигателя составляет 0,03—0,1, причем первая цифра относится к более мощным, а вторая — к менее мощным электродвигателям (до 10—20 квт).
Очевидно, s = 0 в том случае, когда ротор вращается с синхронной скоростью n1. Можно считать, что на холостом ходу электродвигателя его ротор вращается с этой скоростью, если не учитывается трение.
Величина скольжения s =1, когда ротор электродвигателя не вращается при включенной обмотке статора. Этот режим называют режимом короткого замыкания электродвигателя (или режимом стоянки под током). Получить режим короткого замыкания можно, искусственно затормозив ротор или перегрузив электродвигатель до полной остановки его. Пуск асинхронного электродвигателя также начинается именно с этого режима.
Выражение (81) показывает, что скольжение может изменяться гораздо в больших пределах, чем указано выше. Действительно, ротор электродвигателя под действием постороннего источника механической энергии (например, под действием опускающегося груза) может вращаться со скоростью больше синхронной. В этом случае скольжение будет отрицательным (s<0). Отрицательное скольжение имеет место при работе асинхронного электродвигателя в генераторном режиме, когда, например, под действием опускающегося груза ротор вращается в ту же сторону, что и магнитное поле статора со скоростью n2>n1.
Можно также представить, что ротор электродвигателя под действием опускающегося груза вращается в направлении, противоположном направлению вращения магнитного поля статора. В этом случае s>1, так как в выражение (81) величину п2 нужно подставить с отрицательным знаком. Такой режим называется режимом противовключения.
Таким образом, теоретически скольжение асинхронного электродвигателя может изменяться в пределах от —? до + ?. Практически же скольжение асинхронного электродвигателя при работе последнего в двигательном и тормозных режима« изменяется в пределах от —2 до +2.
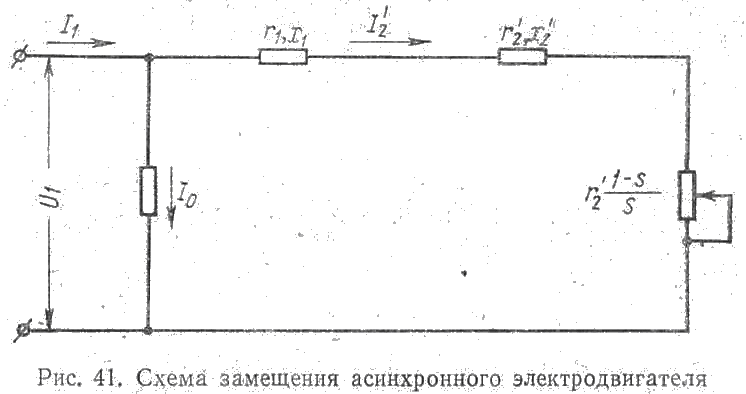
Из курса электрических машин известно, что для асинхронного электродвигателя может быть составлена схема замещения, с помощью которой производится анализ работы электродвигателя и исследуются режимы его работы. На рис. 41 приведена упрощенная схема замещения асинхронного электродвигателя, в которой приняты следующие обозначения:
U1 — фазное напряжение обмотки статора, в;
I1 — фазный ток обмотки статора, а;
I0 — фазный ток холостого хода электродвигателя, а;
I2 — приведенный фазный ток обмотки ротора, а;
r1 и х1 — активное и индуктивное сопротивления фазы обмотки статора, ом;
r2’ и х2‘ — приведенные активное и индуктивное сопротивления фазы обмотки ротора, ом.
Для приведенных величин могут быть выведены следующие соотношения:
где т1 и т2 — число фаз обмоток статора и ротора;
к = U1н / E2н — коэффициент трансформации э. д. с. (U1н — номинальное фазное напряжение обмотки статора; E2н — фазная э. д. с. обмотки ротора при разомкнутых контактных кольцах).
Мощность Р1 забираемая электродвигателем из сети, определяется напряжением сети U1, током статора I1 зависящим от нагрузки, и коэффициентом мощности cos? т.е.
Мощность на валу электродвигателя зависит от его к. п. д.? и может быть вычислена по формуле
Если пренебречь механическими и вентиляционными потерями, которые незначительны, то можно считать, что механическая мощность асинхронного электродвигателя (мощность на валу) равна, потерям мощности в сопротивлении 
схемы замещения, приведенной на рис. 41, т. е.
где т2 = т1 — приведенное число фаз обмотки ротора.
Между токами асинхронного электродвигателя, согласно схеме замещения, существует зависимость
Ток статора асинхронных электродвигателей I1 очень велик даже при отсутствии нагрузки на валу. Это объясняется тем, что намагничивающий ток этих электродвигателей составляет 50—70% номинального тока статора.
vdvizhke.ru
Для оценки свойств асинхронного двигателя прибегают к построению механической характеристики.
Механическая характеристика асинхронного двигателя выражает зависимость между электромагнитным моментом и частотой вращения, либо скольжением. Скольжение – это величина, которая показывает, насколько частота вращения магнитного поля опережает частоту вращения ротора.
Благодаря механической характеристике, появляется возможность определить к какому типу установки больше подходит двигатель, на каком участке сохраняется его устойчивая работа, перегрузочную способность и другое.
Построим механическую характеристику для двигателя 4A90L4У3.
Паспортные данные двигателя:
n1 = 1500 об/мин
Pн = 2.2 КВт
nн = 1425 об/мин
η = 80 %
cos φ = 0.83
Mmax/Mн = λ = 2,2
Для построения нам необходимо произвести расчет номинального момента и скольжения.
Рассчитаем критическое скольжение и момент, для этого необходимо знать коэффициент λ.
Итак, мы определили основные точки характеристики, но для её построения их недостаточно. Поэтому с помощью упрощенной формулы Клосса, рассчитаем моменты для других значений скольжений.
Упрощенная формула Клосса выглядит следующим образом
Для удобства составим таблицу.
|
s |
0 |
sн | sкр/2 | sкр |
0.2 |
0.3 |
0.4 |
0.5 |
0.6 |
0.7 |
0.8 |
0.9 |
1 |
|
M |
0 |
14.61 |
25.94 |
32.43 |
32,39 |
30.47 |
26.69 |
23.16 |
20.22 |
17.85 |
15.93 |
14.35 |
13.05 |
|
n |
1500 |
1425 |
1342.5 |
1185 |
1200 |
|
900 |
750 |
600 |
450 |
300 |
150 |
0 |
Рассчитаем для каждого значения скольжения момент и частоту вращения. Например, для значения 0.2
Частоту вращения выразим из формулы для определения скольжения
Подобным образом рассчитываются остальные значения.
Так как формула упрощенная, значения могут несколько отличаться от действительных, что не критично для расчетов.
Теперь на основании расчетов мы можем построить саму механическую характеристику.
Зависимость момента от скольжения M = f(s)
Зависимость частоты оборотов от момента n = f(M)
Спасибо за внимание!
Рекомендуем - механическая характеристика электропривода
electroandi.ru
Схема подключения двигателя к сети показана на рис. 7.3, а. В отличие от электродвигателя с короткозамкнутым ротором, двигатель с, фазным ротором имеет фазную обмотку на роторе, концы которой выведены на кольца, закрепленные на валу ротора. При замыкании колец накоротко двигатель работает как короткозамкнутый.
Если между кольцами обмотки ротора включить дополнительное активное сопротивление R (как показано на рис. 7.2, а), то механическая характеристика станет более мягкой (рис. 7.2, б, кривая 2), при сохранении той же величины М,(. Чем больше по величине сопротивление R, тем при большем значении s двигатель будет иметь максимальный (критический) момент Мк. При этом изменится и величина пускового момента в сторону увеличения его.
Можно подобрать такое значение R, при котором пусковой момент станет равен критическому. Если в процессе работы сопротивление R не будет выведено, то двигатель будет работать при моменте сопротивления, равном номинальному моменту, с частотой вращения ni и скольжением S. При этом пх будет меньше лном (соответственно Si sHom)- Если для данного случая построить скоростную характеристику, то окажется, что при сопротивлении в цепи ротора Rpnт + R пусковой ток меньше, чем при работе двигателя только с сопротивлением R&л (т. е. при работе двигателя с короткозамкнутым ротором). Таким образом, включая в цепь ротора асинхронного двигателя с фазным ротором различные по величине дополнительные сопротивления, можно увеличить пусковой момент, одновременно уменьшая величину пускового тока, а также получать различную частоту вращения при заданном моменте сопротивления.
Указанные особенности асинхронного двигателя с фазным ротором дают возможность применять его в установках, где требуется большой пусковой момент, небольшой пусковой ток и регулирование частоты вращения.
Асинхронный двигатель с фазным ротором имеет ограниченное применение потому, что у него коэффициент мощности меньше, чем у таких же двигателей с коротко- замкнутым ротором, включение дополнительного сопротивления в цепь ротора вызывает неоправданные потери электрической энергии (на нагрев реостата), двигатель имеет искрящие части.
alyos.ru
Механическая характеристика асинхронного двигателя - зависимость частоты оборота ротора от момента вала n = f (M2). Потому что, во время нагрузки момент холостого хода не велик, то M2 ≈ M и механические свойства отображаются отношением n = f (M). Если принимать во внимание связь s = (n1 - n) / n1, поэтому механические свойства можно извлечь, построив ее графическое соотношение в положении n и М.
Механическая естественная характеристика асинхронного двигателя соответствует паспортной схеме его активации и номинальным параметрам напряжения. Неестественные характеристики создаются, если работают какие-либо второстепенные элементы: реакторы, резисторы, конденсаторы. При включении в сеть генератора не номинальным напряжением характеристики различаются от механической естественной характеристики.
Механические характеристики - полезный и удобный инструмент для анализа динамических и статических режимов электропривода.
Расчет механической характеристики асинхронного электродвигателя.Асинхронный трехфазный двигатель с короткозамкнутым ротором подключен в сеть с напряжением 380 В и частотой 50 Гц. Параметры двигателя cosφн= 0,85, nн= 960 об/мин, ηн= 0,88, Pн= 14 кВт, кратность наибольшего момента 1,8.Требуется найти: количество пар полюсов, номинальный ток в фазе обвивки статора, номинальное скольжение, критический момент, критическое скольжение, номинальный валовый момент, составить механическую характеристику двигателя.Расчет. Значение номинальной мощности, которая питается из сети:P1н =Pн / ηн = 16 кВт.Показатель номинального тока, питающегося из сети:
Количество пар полюсовp = 60 f / n1 = 3Значение номинального скольженияsн = (n1 - nн) / n1 = 0,04Номинальный валовый момент:
Показатель критического момента:Мк = kм х Мн =250,7 Н•мПоказатель критического скольжения:
Чтобы построить механическую характеристику асинхронного двигателя, требуется найти точки: отметка холостого хода s = 0, n = 1000 об/мин, М = 0, отметка критического режима sк = 0,132, nк = 868 об/мин, Мк =250,7 Н•м, отметка номинального режима sн = 0,04, nн = 960 об/мин, Мн = 139,3 Н•м.Для отметки пускового режима n = 0, sп = 1:
| 1.jpg | 6.56 КБ |
| 2.jpg | 3.68 КБ |
| 3.jpg | 4.11 КБ |
| 4.jpg | 4.95 КБ |
| 5.jpg | 4.08 КБ |
44kw.com
Рабочие характеристики асинхронного двигателя представляют собой графически выраженные зависимости частоты вращения 
, КПД 
, полезного момента (момента на валу) 
, коэффициента мощности 
и тока статора 
от полезной мощности 
при 
и 
.
Скоростная характеристика 
. Частота вращения ротора асинхронного двигателя
Рис. 62. Рабочие характеристики асинхронного двигателя
Скольжение по (13.5) 
, (13.24) т. е. скольжение двигателя, а следовательно, и его частота вращения определяются отношением электрических потерь в роторе к электромагнитной мощности 
. Пренебрегая электрическими потерями в роторе в режиме холостого хода, можно принять 
, а поэтому 
и 
. По мере увеличения нагрузки на валу двигателя отношение (13.24) растет, достигая значений 0,01-0,08 при номинальной нагрузке. В соответствии с этим зависимость представляет собой кривую, слабо наклоненную к оси абсцисс. Однако при увеличении активного сопротивления ротора 
угол наклона этой кривой увеличивается. В этом случае изменения частоты вращения при колебаниях нагрузки возрастают. Объясняется это тем, что с увеличением возрастают электрические потери в роторе [см. (13.3)].
Зависимость 
. Зависимость полезного момента на валу двигателя от полезной мощности Р2 определяется выражением
, (13.25)
где: – полезная мощность, Вт; 
– угловая частота вращения ротора.
Рис. 63. Векторная диаграмма асинхронного двигателя при большой нагрузке
Из этого выражения следует, что если 
, то график 
представляет собой прямую линию. Но в асинхронном двигателе с увеличением нагрузки частота вращения ротора уменьшается, а поэтому полезный момент на валу с увеличением нагрузки возрастает несколько быстрее нагрузки, а следовательно, график имеет криволинейный вид.
Зависимость 
. В связи с тем что ток статора имеет реактивную (индуктивную) составляющую, необходимую для создания магнитного поля в статоре, коэффициент мощности асинхронных двигателей меньше единицы. Наименьшее значение коэффициента мощности соответствует режиму х.х. Объясняется это тем, что ток х.х. 
при любой нагрузке остается практически неизменным. Поэтому при малых нагрузках двигателя ток статора невелик и в значительной части является реактивным 
. В результате сдвиг по фазе тока статора 
относительно напряжения 
получается значительным 
, лишь немногим меньше 90° (рис. 63). Коэффициент мощности асинхронных двигателей в режиме х.х. обычно не превышает 0,2.
Рис. 64. Зависимость , от нагрузки при соединении обмотки статора
звездой (1) и треугольником (2)
При увеличении нагрузки на валу двигателя растет активная составляющая тока и коэффициент мощности возрастает, достигая наибольшего значения (0,80—0,90) при нагрузке, близкой к номинальной. Дальнейшее увеличение нагрузки сопровождается уменьшением , что объясняется возрастанием индуктивного сопротивления ротора 
за счет увеличения скольжения, а следовательно, и частоты тока в роторе. В целях повышения коэффициента мощности асинхронных двигателей чрезвычайно важно, чтобы двигатель работал всегда или по крайней мере значительную часть времени с нагрузкой, близкой к номинальной. Это можно обеспечить лишь при правильном выборе мощности двигателя. Если же двигатель работает значительную часть времени недогруженным, то для повышения целесообразно подводимое к двигателю напряжение 
уменьшить. Например, в двигателях, работающих при соединении обмотки статора треугольником, это можно сделать пересоединив обмотки статора в звезду, что вызовет уменьшение фазного напряжения в 
раз. При этом магнитный поток статора, а следовательно, и намагничивающий ток уменьшаются примерное раз. Кроме того, активная составляющая тока статора несколько увеличивается. Все это способствует повышению коэффициента мощности двигателя. На рис. 64 представлены графики зависимости асинхронного двигателя от нагрузки при соединении обмоток статора звездой (кривая 1) и треугольником (кривая 2).
poznayka.org
Рабочие характеристики асинхронного двигателя представляют собой графически выраженные зависимости частоты вращения n2, КПД асинхронного двигателя η, полезного момента (момента на валу) М2, коэффициента мощности cos φ, и тока статора I1 от полезной мощности Р2 при U1 = const f1 = const.
Скоростная характеристика n2 = f(P2). Частота вращения ротора асинхронного двигателя n2 = n1(1 — s).
Скольжение s = Pэ2/Pэм, то есть скольжение асинхронного двигателя, а следовательно, и его частота вращения определяются отношением электрических потерь в роторе к электромагнитной мощности. Пренебрегая электрическими потерями в роторе в режиме холостого хода, можно принять Рэ2 = 0, а поэтому s ≈ 0 и n2 ≈ n1.
По мере увеличения нагрузки на валу асинхронного двигателя отношение s = Pэ2/Pэм растет, достигая значений 0,01 — 0,08 при номинальной нагрузке. В соответствии с этим зависимость n2 = f(P2) представляет собой кривую, слабо наклоненную к оси абсцисс. Однако при увеличении активного сопротивления ротора двигателя r2′ угол наклона этой кривой увеличивается. В этом случае изменения частоты асинхронного двигателя n2 при колебаниях нагрузки Р2 возрастают. Объясняется это тем, что с увеличением r2′ возрастают электрические потери в роторе.
Зависимость М2 = f(P2). Зависимость полезного момента на валу асинхронного двигателя М2 от полезной мощности Р2 определяется выражением M2 = Р2/ω2 = 60 P2/(2πn2) = 9,55Р2/n2, где Р2 — полезная мощность, Вт; ω2 = 2πf2/60 — угловая частота вращения ротора.
Из этого выражения следует, что если n2 = const, то график М2 = f2(Р2) представляет собой прямую линию. Но в асинхронном двигателе с увеличением нагрузки Р2 частота вращения ротора уменьшается, а поэтому полезный момент на валу М2 с увеличением нагрузки возрастает не сколько быстрее нагрузки, а следовательно, график М2 = f (P2) имеет криволинейный вид.
Зависимость cos φ1 = f (P2). В связи с тем что ток статора асинхронного двигателя I1 имеет реактивную (индуктивную) составляющую, необходимую для создания магнитного поля в статоре, коэффициент мощности асинхронных двигателей меньше единицы. Наименьшее значение коэффициента мощности соответствует режиму холостого хода. Объясняется это тем, что ток холостого хода электродвигателя I0 при любой нагрузке остается практически неизменным. Поэтому при малых нагрузках двигателя ток статора невелик и в значительной части является реактивным (I1 ≈ I0). В результате сдвиг по фазе тока статора относительно напряжения получается значительным (φ1 ≈ φ0), лишь немногим меньше 90°.
Коэффициент мощности асинхронных двигателей в режиме холостого хода обычно не превышает 0,2. При увеличении нагрузки на валу двигателя растет активная составляющая тока I1 и коэффициент мощности возрастает, достигая наибольшего значения (0,80 — 0,90) при нагрузке, близкой к номинальной. Дальнейшее увеличение нагрузки на валу двигателя сопровождается уменьшением cos φ1 что объясняется возрастанием индуктивного сопротивления ротора (x2s) за счет увеличения скольжения, а следовательно, и частоты тока в роторе.
В целях повышения коэффициента мощности асинхронных двигателей чрезвычайно важно, чтобы двигатель работал всегда или по крайней мере значительную часть времени с нагрузкой, близкой к номинальной. Это можно обеспечить лишь при правильном выборе мощности двигателя. Если же двигатель работает значительную часть времени недогруженным, то для повышения cos φ1, целесообразно подводимое к двигателю напряжение U1 уменьшить. Например, в двигателях, работающих при соединении обмотки статора треугольником, это можно сделать пересоединив обмотки статора в звезду, что вызовет уменьшение фазного напряжения в раз. При этом магнитный поток статора, а следовательно, и намагничивающий ток уменьшаются примерно в раз. Кроме того, активная составляющая тока статора несколько увеличивается. Все это способствует повышению коэффициента мощности двигателя.
www.mtomd.info
Анализ работы асинхронного электродвигателя удобно проводить на основе его механических характеристик, представляющих собой графически выраженную зависимость вида п = f(М). Скоростными характеристиками в этих случаях пользуются весьма редко, так как для асинхронного электродвигателя скоростная характеристика представляет собой зависимость числа оборотов от тока ротора, при определении которого встречается ряд трудностей, особенно, в случае асинхронных электродвигателей с короткозамкнутым ротором.
Для асинхронных электродвигателей, так же как и для электродвигателей постоянного тока, различают естественные и искусственные механические характеристики. Асинхронный электродвигатель работает на естественной механической характеристике в том случае, если его статорная обмотка подключена к сети трехфазного тока, напряжение и частота тока которой соответствует номинальным значениям, и если в цепь ротора не включены какие-либо дополнительные сопротивления.
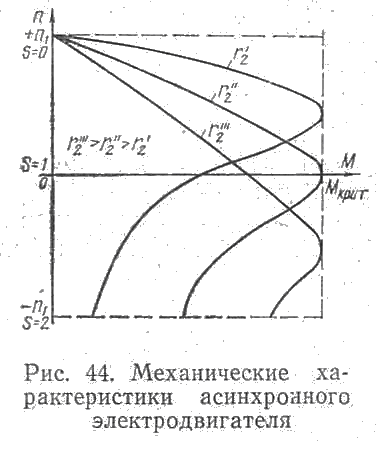
На рис. 42 была приведена зависимость М = f(s), которая позволяет легко перейти к механической характеристике n = f(M), так как, согласно выражению (82), от величины скольжения зависит скорость вращения ротора.
Подставив формулу (81) в выражение (91) и решив полученное уравнение относительно п2 получим следующее уравнение механических характеристик асинхронного электродвигателя
Член r1s опущен, ввиду его малости. Механические характеристики, соответствующие этому уравнению, приведены на рис. 44.
Для практических построений уравнение (95) неудобно, поэтому на практике обычно пользуются упрощенными уравнениями. Так, в случае работы электродвигателя на естественной характеристике при вращающем моменте, не превышающем 1,5 его номинального значения, скольжение обычно не превышает 0,1. Поэтому для указанного случая в уравнении (95) можно пренебречь членом x2 s2 /kr’2·M , в результате чего получим следующее упрощенное уравнение естественной характеристики:
являющееся уравнением прямой линии, наклоненной к оси абсцисс.
Хотя уравнение (97) является приближенным, опыт показывает, что при изменениях момента в пределах от М = 0 до М=1,5Мн характеристики асинхронных электродвигателей действительно прямолинейны и уравнение (97) дает результаты, хорошо согласующиеся с опытными данными.
При введении в цепь ротора дополнительных сопротивлений характеристику п = f(М) с достаточной для практических целей точностью также можно считать прямолинейной в указанных пределах для вращающего момента и производить ее построение по уравнению (97).
Таким образом, механические характеристики асинхронного электродвигателя в диапазоне от М = 0 до М = 1,5 Мн при различных сопротивлениях роторной цепи представляют семейство прямых, пересекающихся в одной точке, соответствующей синхронному числу оборотов (рис. 45). Как показывает уравнение (97), наклон каждой характеристики к оси абсцисс определяется величиной активного сопротивления роторной цепи r’2. Очевидно, чем больше сопротивление, введенное в каждую фазу ротора, тем больше наклонена к оси абсцисс характеристика.
Как указывалось, обычно на практике скоростными характеристиками асинхронных электродвигателей не пользуются. Расчет же пусковых и регулировочных сопротивлений производят с помощью уравнения (97). Построение естественной характеристики можно выполнить по двум точкам — по синхронной скорости n1= 60f /р при нулевом моменте и по номинальной скорости при номинальном моменте.
Следует иметь в виду, что для асинхронных электродвигателей зависимость момента от тока ротора I2 носит более сложный характер, чем зависимость момента от тока якоря для
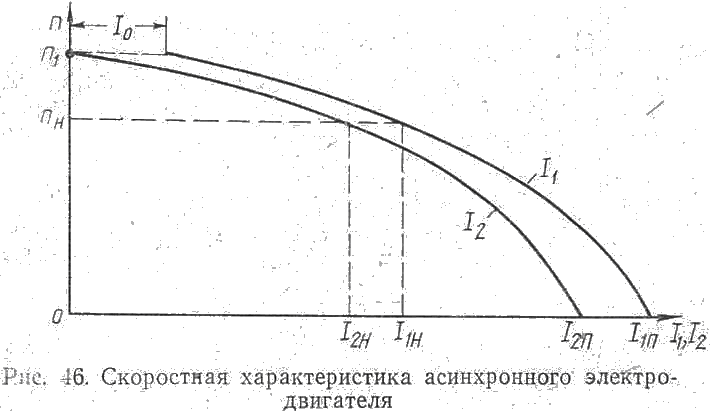
электродвигателей постоянного тока. Поэтому скоростная характеристика асинхронного двигателя неидентична механической характеристике. Характеристика п = f(I2) имеет вид, показанный на рис. 46. Там же дана характеристика n = f (I1).
vdvizhke.ru
