Содержание
Основные режимы движения машины.
Процесс
движения машины в общем случае состоит
из трех фаз: разбега, установившегося
режима и выбега (рис. 7.2). Разбег (режимI
и II)
и выбег (режимы IV
и V)
относятся к неустановившемуся режиму,
который характеризуется непериодическими,
т. е. неповторяющимися, изменениями
скорости главного вала машины (начального
звена). Такой процесс движения называют
переходным.
Рис. 7.2
При
установившемся режиме III
скорость главного вала изменяется
периодически. В частном случае скорость
может быть постоянной. В установившемся
режиме работает большинство энергетических
и технологических машин. Часто
установившееся движение чередуется
с разгонами (при повышениях скоростного
режима II)
и торможениями (при понижениях
скоростного режима IV).
Так работают, например, автомобильный
двигатель и различные другие транспортные
машины. Многие механизмы в установившемся
режиме вообще не работают. Это особенно
характерно для целого ряда приборов
(реле,
контакторы и т. п.). Их механизм во время
п.). Их механизм во время
срабатывания (режим VI)
переходит из одного положения в другое,
не совершая замкнутого повторяющегося
кинематического цикла.
Неустановившийся режим движения машины
имеет место тогда, когда ее пускают в
ход и она, набирая скорость, выходит на
установившийся режим, а также тогда,
когда для остановки машины ее двигатель
выключают и она продолжает двигаться
за счет накопленного запаса кинетической
энергии; при этом машина постепенно
теряет скорость из-за действия сил
трения или каких-либо других сил
сопротивления, в том числе и специальных
тормозных сил. В этих случаях необходимо
знать, насколько быстро происходят
переход из неподвижного состояния в
рабочее и обратный переход до полной
остановки. Применительно к транспортным
машинам изучение обратного перехода
особенно важно для надежного расчета
длины тормозного пути. Исследование
неустановившегося режима движения
дает возможность определить время
срабатывания механизма, что абсолютно
необходимо для проектирования многих
приборов, таких, как фотозатворы, средства
автоматической защиты и др.
Разгоны (разбеги)
и торможения могут происходить с большим
ускорением. Это вызывает значительное
динамическое нагружение механизма,
что, в свою очередь, может привести к
перенапряжениям и даже к поломкам.
Во время разбега
и выбега угловая скорость многих машин
проходит через критическую (резонансную)
зону. Во избежание динамической перегрузки
механизма и возможной аварии проход
этой зоны должен быть достаточно быстрым,
что надо обеспечить при проектировании,
сделав расчет обеих фаз неустановившегося
режима. Решение многих других динамических
задач также связано с исследованием
этого режима.
Таким образом,
изучение неустановившихся (переходных)
процессов весьма существенно для
грамотного динамического проектирования
механизма, машины или прибора.
Для определения
закона движения механизма при
неустановившемся режиме должны быть
известны следующие исходные данные:
кинематическая схема механизма;
характеристики геометрии масс всех
подвижных звеньев; механические
характеристики сил и моментов; начальные
условия движения. Последнее важно для
Последнее важно для
исследования именно неустановившегося
режима.
Рассмотрим
механизм, нагруженный силами и моментами,
которые являются функциями только
перемещения своих точек приложения.
Пусть приведенный момент инерции
рассматриваемого механизма имеет
переменную величину
.
Требуется определить зависимость
скорости начального звена от его угла
поворота, т. е..
Подобная задача является весьма
распространенной. В качестве примеров
можно привести механизмы дизель-компрессоров,
буровых станков и подъемных кранов с
приводом от двигателей внутреннего
сгорания, различных устройств с
пневмоприводом, приборов с пружинными
двигателями и др.
КАТЕГОРИИ: Главная Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748) | Краткое содержание: Установившийся режим движения машины.
Установившийся режим движения машины.
Установившийся режим движения машины наступает тогда, когда работа внешних сил за цикл не изменяет ее энергии, то есть суммарная работа внешних сил за цикл движения равна нулю.
Период изменения скорости начального звена (обобщенной скорости механизма) называется циклом установившегося движения или сокращенно циклом. Время цикла равно или кратно периоду действия сил. Поэтому при установившемся режиме сумма работ всех сил за цикл равна нулю, а так как работа сил тяжести за цикл равна нулю, то это равенство будет выполняться, если работа движущих сил за цикл равна работе всех сил сопротивления за цикл (по модулю):
Установившееся движение где
и — соответственно работа за цикл движущих сил и сил сопротивления,
— начальное значение обобщенной координаты,
— приращение обобщенной координаты за цикл.
Неравномерность движения и методы ее регулирования.
Уравнение работ является основным энергетическим уравнением установившегося режима. Из него вытекает, что приращения кинетической энергии механизма за цикл не происходит и, следовательно, угловая скорость начального звена в начале и в конце цикла одинакова, однако в пределах цикла текущее значение суммарной работы не равно нулю. Работа может быть то положительной, то отрицательной. При положительной величине работы машина увеличивает свою кинетическую энергию за счет увеличения скорости, то есть разгоняется. На участках, где суммарная работа отрицательна, кинетическая энергия и скорость машины уменьшается, машина притормаживается. В установившемся режиме величины увеличения скорости на участках разгона и снижения на участках торможения за цикл равны, поэтому средняя скорость движения постоянна, где — частота вращения начального звена агрегата .
В машинах, приведенный момент инерции которых зависит от обобщенной координаты, на неравномерность движения оказывает влияние величина изменения приведенного момента инерции.
Дата добавления: 2014-01-07; Просмотров: 509; Нарушение авторских прав?; Мы поможем в написании вашей работы! Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет |
4.12: Стационарное приближение — Химия LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 35450
Цели обучения
- Объяснить устойчивое состояние и стационарное приближение .

- Получить закон скорости, когда задан механизм, но шаг, определяющий скорость, не указан.
- Получите общее выражение закона скорости, используя стационарное приближение.
- Сделайте соответствующие предположения, чтобы полученный закон скорости согласовывался с наблюдаемым законом скорости.
- Приведите выражения для скорости производства промежуточного продукта.
- Дайте выражения для потребления курс промежуточного звена.
- Выразите концентрацию промежуточного продукта через концентрацию реагентов.
- Исключите концентрации промежуточных продуктов, используя концентрации реагентов.
- Выведите закон скорости из множества элементарных шагов.
- Обсудить полученный закон скорости .
Приближение стационарного состояния
Когда механизм реакции имеет несколько стадий с сопоставимыми скоростями, стадия, определяющая скорость, часто не очевидна. Однако на некоторых этапах есть промежуточное звено. 9Промежуточное соединение 0027 представляет собой вещество, которое не является ни одним из реагентов, ни одним из продуктов. Аппроксимация стационарного состояния — это метод, используемый для получения закона скорости. Метод основан на предположении, что один промежуточный продукт в механизме реакции расходуется так же быстро, как и образуется. Его концентрация остается неизменной в течение всей реакции.
Однако на некоторых этапах есть промежуточное звено. 9Промежуточное соединение 0027 представляет собой вещество, которое не является ни одним из реагентов, ни одним из продуктов. Аппроксимация стационарного состояния — это метод, используемый для получения закона скорости. Метод основан на предположении, что один промежуточный продукт в механизме реакции расходуется так же быстро, как и образуется. Его концентрация остается неизменной в течение всей реакции.
Определение: Промежуточные продукты
Промежуточный продукт представляет собой вещество, которое не является ни одним из реагентов, ни одним из продуктов. Он временно существует в ходе реакции.
Когда в реакции участвует одно или несколько промежуточных соединений, концентрация одного из них остается постоянной на некоторой стадии реакции. Таким образом, система достигла стационарного состояния . Концентрация одного из промежуточных соединений, \([Int]\), изменяется с 90 039 по 90 040, как показано на рисунке \(\PageIndex{1}\). В начале и в конце реакции [Int] изменяется со временем.
В начале и в конце реакции [Int] изменяется со временем.
\[ \dfrac{d[Int]}{dt}= 0 \nonumber \]
Рисунок \(\PageIndex{1}\): Пример, когда промежуточное состояние можно аппроксимировать как стационарное.
Когда механизм реакции состоит из нескольких стадий с сопоставимыми скоростями, стадия, определяющая скорость, не очевидна. Однако на некоторых этапах есть промежуточное звено. Стационарное приближение подразумевает, что вы выбираете промежуточное соединение в механизме реакции и рассчитываете его концентрацию, предполагая, что оно потребляется так же быстро, как и образуется. Ниже приводится пример, показывающий, как работает метод стационарной аппроксимации.
Пример \(\PageIndex{1}\)
Используйте стационарное приближение, чтобы вывести закон скорости для этой реакции
\[\ce{2 N2O5 \rightarrow 4 NO2 + O2}\nonumber \]
, предполагая, что она следует следующему трехступенчатому механизму:
\ [\begin{align} \ce{N_2O_5} &\underset{\Large{k_{\textrm b}}}{\overset{\Large{k_{\textrm f}}}\rightleftharpoons} \ce{NO_2 + NO_3 } \tag{шаг 1} \\[4pt] \ce{NO3 + NO2} &\ce{->[\large{k_2}] NO + NO2 + O2} \tag{шаг 2} \\[4pt] \ ce{NO3 + NO} & \ce{->[\Large{k_3}] 2 NO2} \tag{шаг 3} \end{align} \]
Решение
На этих стадиях \(\ce{NO}\) и \(\ce{NO3}\) являются промежуточными продуктами. У вас есть
У вас есть
\(\ce{производство\: скорость\: of\: NO} = k_2 \ce{[NO3] [NO2]}\)
\(\ce{потребление\: норма\: of\: NO } = k_3 \ce{[NO3] [NO]}\)
Стационарный подход использует предположение, что скорость производства промежуточного продукта равна скорости его потребления. Таким образом, мы имеем
\(k_2 \ce{[NO3] [NO2]} = k_3 \ce{[NO3] [NO]}\)
и решение для \(\ce{[NO]}\) дает результат,
\(\ce{[NO]} = \dfrac{k_2 \ce{[NO3] [NO2]}}{k_3 \ce{[NO3]}} \tag{1}\)
Для других промежуточных продуктов \(\ce{NO3}\),
\(\ce{производство\: норма\: of\: NO3} = k_{\ce f} \ce{[N2O5]}\)
\(\ce{ расход\: норма\: из\: NO3} = k_2\ce{[NO3] [NO2]} + k_3\ce{[NO3] [NO]} + k_{\ce b}\ce{[NO3] [NO2 ]}\)
Применение стационарного предположения дает:
\(k_{\ce f} \ce{[N2O5]} = k_2\ce{[NO3] [NO2]} + k_3\ce{[NO3 ] [NO]} + k_{\ce b}\ce{[NO3] [NO2]}\)
Таким образом,
\(\ce{[NO3]} = \dfrac{k_{\ce f} \ce{[N2O5]}}{k_2\ce{[NO2]} + k_3\ce{[NO]} + k_{\ce b}\ce{[NO2]}}\tag{2}\)
Рассмотрим три уравнения (шага) в механизме:
Шаг i. находится в равновесии и поэтому не может дать выражение скорости.
находится в равновесии и поэтому не может дать выражение скорости.
Шаг II. приводит к образованию некоторых продуктов, а активные частицы \(\ce{NO}\) вызывают дальнейшую реакцию на стадии iii. Это соображение привело к выражению скорости из шага ii. как:
\(\ce{\dfrac{d[O2]}{dt}} = k_2 \ce{[NO3] [NO2]} \tag{3}\)
Подстановка (1) в (2), а затем в (3) дает
\(\ce{\dfrac{d[O2]}{dt}}= \dfrac{k_{\ce f} k_2 \ce{ [N2O5]}}{k_{\ce b} + 2 k_2} = \ce{k [N2O5]}\)
, где \(\ce{k} = \dfrac{k_{\ce f} k_2}{ k_{\ce b} + 2 k_2}\).
Это дифференциальный закон скорости, и он согласуется с экспериментальными результатами. Вышеописанную манипуляцию проведите самостоятельно на листе бумаги. Простое прочтение вышеизложенного еще не приведет к основательному обучению.
На этой странице приведен еще один пример, иллюстрирующий технику вывода законов скорости с использованием стационарного приближения. Здесь рассматривается реакция между газами \(\ce{h3}\) и \(\ce{I2}\).
Пример \(\PageIndex{1}\)
Для реакции:
\(\ce{H_{2\large{(g)}} + I_{2\large{(g)}} \rightarrow 2 HI_{\large{(g)}}}\)
Какие механизмы могут быть подходящими? Выведите закон скорости из предложенного механизма.
Решение
Что ж, на этот вопрос нет простого ответа, и нет способа доказать одно над другим на его достоверность. Начинающим студентам-химикам не будет предложено предложить механизм, но вас попросят вывести закон скорости из предложенного механизма.
Прежде всего, вы должны быть в состоянии выразить скорость реакции через изменение концентрации,
\(скорость = — \ce{\dfrac{d[h3]}{dt}} = — \ce{ \dfrac{ d[I2]}{dt}} = \ce{\dfrac{1}{2}\dfrac{d[HI]}{dt}}\)
Еще раз посмотрите на общее уравнение реакции, чтобы увидеть его отношение и скорость выражения.
Предложение механизма
Чтобы предложить механизм, применим следующие рассуждения. Поскольку связь между \(\ce{I-I}\) слабая, мы ожидаем, что \(\ce{I2}\) диссоциирует на атомы или радикалы. Эти радикалы активны и реагируют с \(\ce{h3}\) с образованием продуктов. Таким образом, мы предлагаем трехэтапный механизм:
Эти радикалы активны и реагируют с \(\ce{h3}\) с образованием продуктов. Таким образом, мы предлагаем трехэтапный механизм:
- \(\ce{I_{2\large{(g)}}} \xrightarrow{\Large{k_1}} \ce{2 I_{\large{(g)}}}\)
- \(\ce{2 I_{\large{(g)}}} \xrightarrow{\Large{k_2}} \ce{I_{2\large{(g)}}}\)
- \(\ce{H_{2\large{(g)}} + 2 I _{\large{(g)}}} \xrightarrow{\Large{k_3}} \ce{2 HI_{\large{(g) )}}}\)
Какой шаг вы бы использовали, чтобы написать закон дифференциальной ставки?
Поскольку только шаг iii. дает реальные продукты, мы ожидаем, что вы признаете этот шаг iii. намекает на закон скорости: 92}\) в выражение rate , у вас есть
\(\begin{align}
rate &= k_3 \ce{[h3]} \dfrac{k_1 \ce{[I2]}}{k_2 + k_3 \ce{[h3]}}\\
&= \dfrac{k_1 k_3 \ce{[h3] [I2]}}{k_2 + k_3 \ce{[h3]}}
\end{align}\)
Обсуждение
Если шаг III. медленно, то \(k_3\) и \(k_2 >> k_3 \ce{[h3]}\). Закон скорости сводится к
Закон скорости сводится к
\(\ce{скорость} = \ce{k [h3] [I2]}\),
, где \(\ce{k} = \dfrac{k_1 k_3}{k_2}\). (Проработайте это на бумаге самостоятельно; чтение приведенного выше вывода не приведет к обучению.)
Поскольку закон скорости имеет первый порядок по отношению к обоим реагентам, можно утверждать, что закон скорости также поддерживает одношаговый механизм,
\(\ce{H_{2\large{(g)}} + I_{2\large{(g)}} \rightarrow 2 HI}\)
Эта элементарная стадия аналогична общей реакции.
Предположим, мы используем большое количество \(\ce{h3}\) по сравнению с \(\ce{I2}\), тогда изменение \(\ce{[h3]}\) незначительно. Например, если \(\mathrm{[H_2] = 10}\) и \(\mathrm{[I_2] = 0,1}\) первоначально, \(\ce{[h3]}\) остается по существу 10 (9.9 только с одной значащей цифрой). Другими словами, \(\ce{[h3]}\) почти не изменилось, когда реакция закончилась. Таким образом,
\(k_3 \ce{[h3]} >> k_3\)
и закон скоростей принимает вид:
\(rate = k_1 \ce{[I2]}\).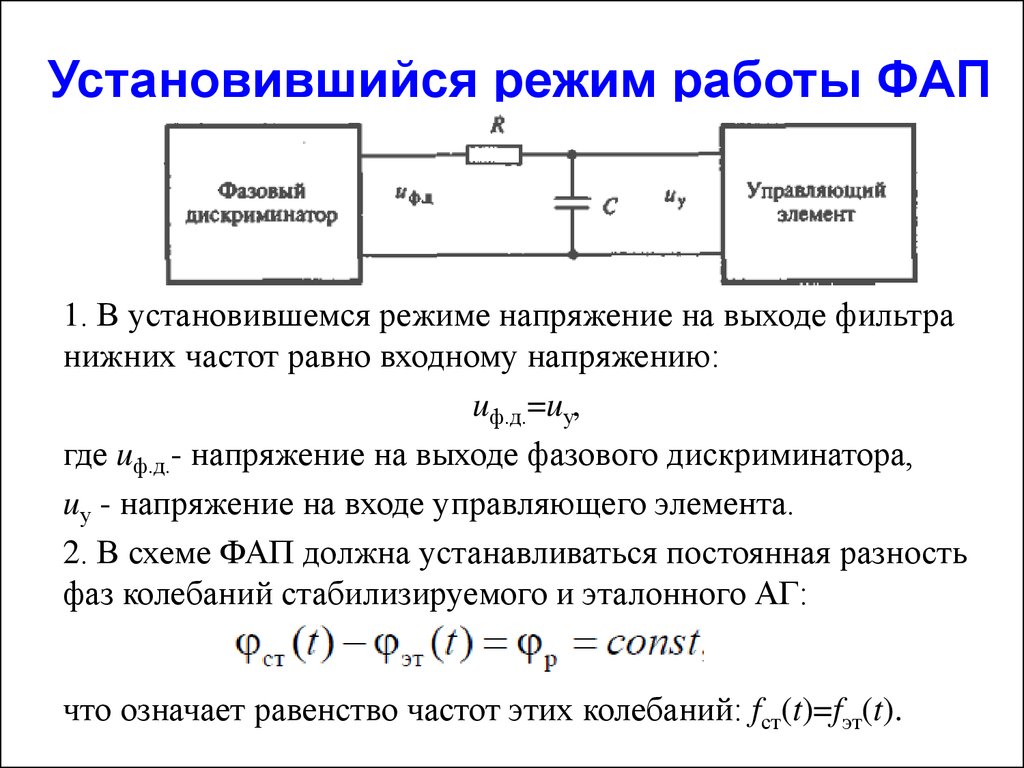
Таким образом, реакция является реакцией псевдопервого порядка из-за большого количества одного реагента. Результаты предполагают iii. быстрый шаг (из-за большого количества \(\ce{h3}\)), и i. этап определения скорости.
Авторы и авторство
4.12: Steady-State Approximation распространяется под лицензией CC BY-NC-SA 4.0 и был создан, изменен и/или курирован LibreTexts.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Лицензия
- CC BY-NC-SA
- Версия лицензии
- 4,0
- Показать страницу TOC
- № на стр.

- Теги
- стационарное приближение
3.2.6: Приближение стационарного состояния — Химия LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 1420
Приближение стационарного состояния — это метод, используемый для оценки общей скорости многостадийной реакции. Предполагается, что скорость изменения концентрации промежуточного продукта в многостадийной реакции постоянна. Этот метод можно применять только тогда, когда первая стадия реакции значительно медленнее, чем последующая стадия в последовательной реакции с образованием промежуточного продукта.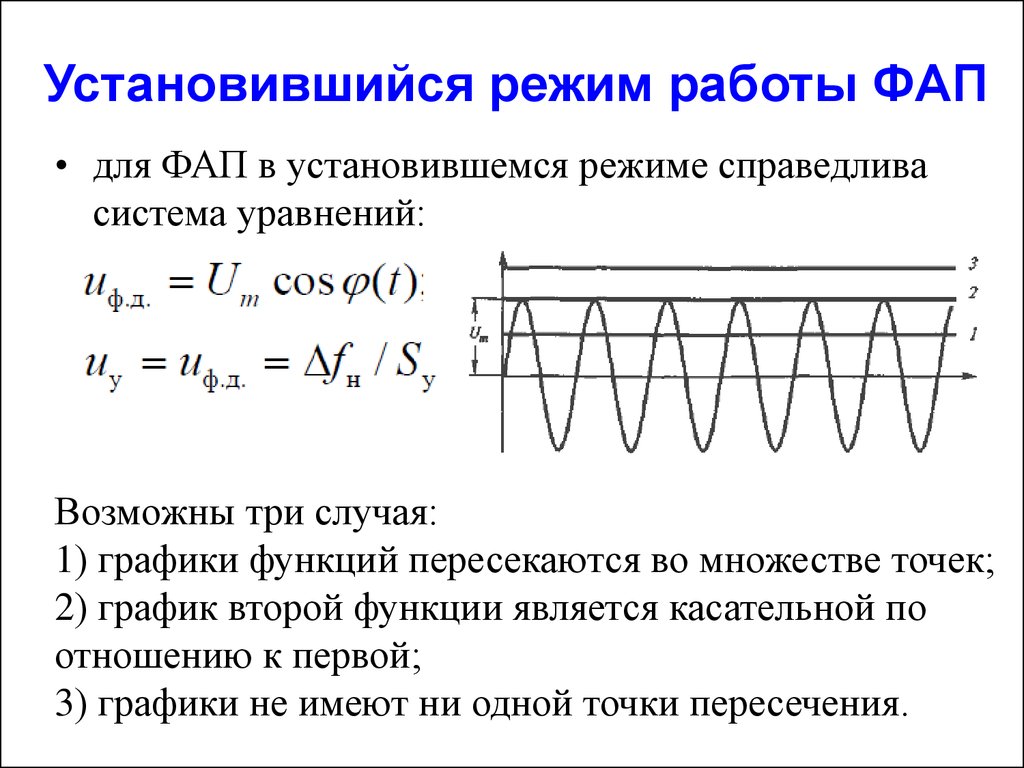
Введение
Прежде чем обсуждать аппроксимацию стационарного состояния, необходимо понять, что аппроксимация получена для упрощения кинетического выражения для концентрации продукта [продукт]. Рассмотрим следующую последовательную реакцию:
\[A \xrightarrow[]{k_1} B \xrightarrow {k_2} C \nonumber \]
Расчет [продукта] зависит от всех констант скорости на каждом шаге. Например, если бы кинетический метод использовался для определения концентрации C, [C] в момент времени t в вышеуказанной реакции, выражение было бы 9{-k_2t})}{k_1 — k_2}\right) \label{1} \]
При более сложных механизмах кинетическое выражение становится труднее вывести. Чтобы упростить этот расчет, мы часто используем одно из двух приближений для определения общих скоростей последовательных реакций: приближение стационарного состояния и приближение предравновесного состояния. Эта статья касается стационарного приближения.
Приближение установившегося состояния
Приближение установившегося состояния применяется к последовательной реакции с медленной первой стадией и быстрой второй стадией (\(k_1 \ll k_2\)). Если первая стадия очень медленная по сравнению со второй стадией, накопления промежуточного продукта, такого как продукт B в приведенном выше примере, не происходит. 9{-k_1t}) \label{5} \]
Если первая стадия очень медленная по сравнению со второй стадией, накопления промежуточного продукта, такого как продукт B в приведенном выше примере, не происходит. 9{-k_1t}) \label{5} \]
Уравнение \(\ref{5}\) вывести намного проще, чем уравнение \(\ref{1}\), особенно с более сложной многостадийной реакцией механизмы.
Пример \(\PageIndex{1}\)
Рассмотрим реакцию:
\[A + 2B \xrightarrow[]{} C \nonumber \]
- Каков ожидаемый закон скоростей согласно предложенному ниже многоступенчатый механизм в приближении стационарного состояния с \(k_2 \gg k_{-1}\)) для следующего механизма: \[A + B \ce{<=>[k_1][k_{-1}]} I \tag{Медленно} \] \[I + B \xrightarrow[]{k_2} C \tag{Быстро} \]
- Если \(х\) — порядок реакции по \(А\), \(у\) — порядок реакции по \(В\), а \(п\) — общий порядок реакции. Каковы значения \(x\), \(y\) и \(n\)?
Решение
a: Сначала мы используем аппроксимацию установившегося состояния для промежуточного звена (т.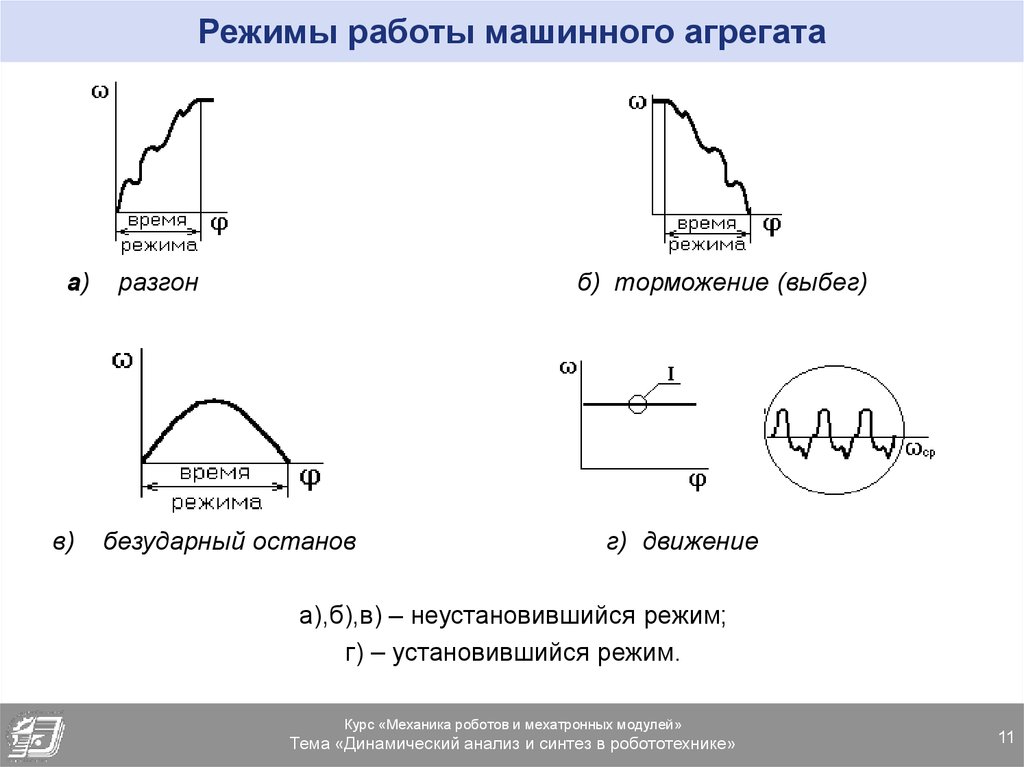 е. уравнение \ref{2})
е. уравнение \ref{2})
\[\dfrac{d[I]}{dt} = k_1[A][B] — k_{-1}[I] — k_2[I][B] = 0 \nonumber \]
затем находим (стационарную) концентрацию промежуточного соединения
\[[I] = \dfrac{k_1[A][B]}{ k_{-1} +k_2[B]} \nonumber \]
Поскольку второй шаг намного быстрее первого, то \(k_2 \gg k_{-1}\), затем \(k_{-1} \приблизительно 0\) для этого приближения, и приведенное выше уравнение можно упростить до
\[[I] = \dfrac{k_1[A ]}{k_2} \нон. \nonumber \]
Закон скорости производства \([C]\) может быть построен непосредственно на втором этапе, и когда добавляется стационарная концентрация \(I\), окончательное выражение закона скорости имеет вид полученный.
\[ \begin{align*}\dfrac{d[C]}{dt} & = k_2[I][B] \\[4pt] &= \dfrac{k_1k_2[A][B]}{k_2 } \\[4pt] &= k_1[A][B] \end{align*} \]
b: Прямая проверка окончательного закона скорости, полученного выше, дает следующие параметры:
- \(x = 1\)
- \(у = 1\)
- \(n = 2\)
Использование аппроксимации стационарного состояния в кинетике ферментов
В 1925 году Джордж Э.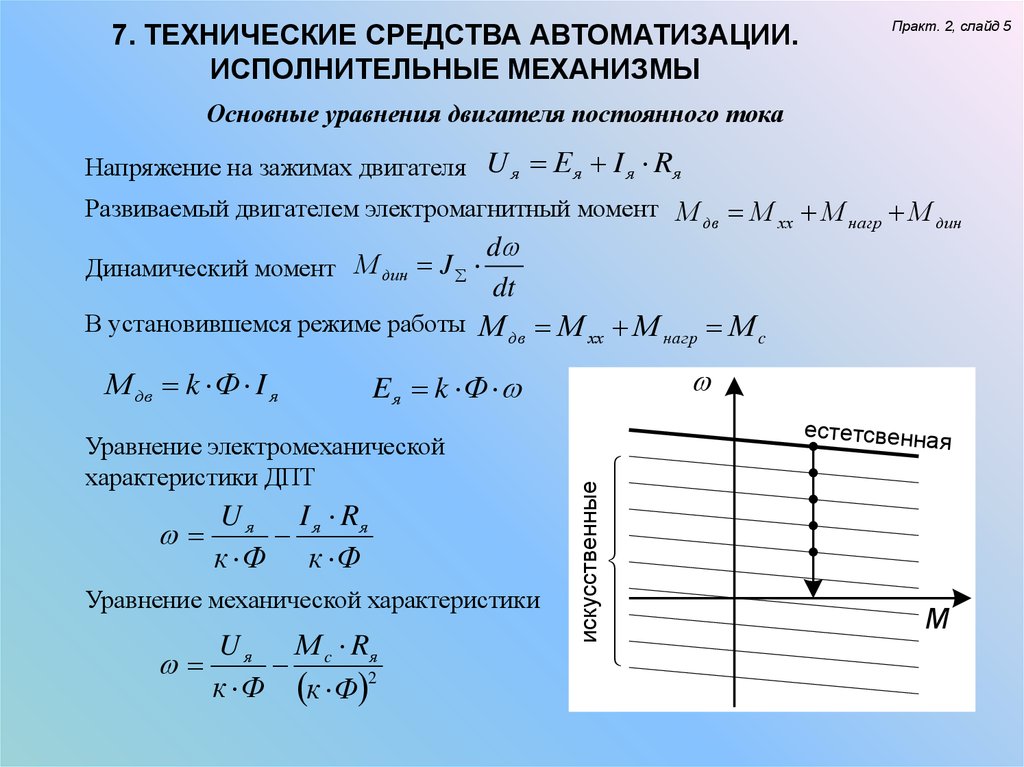 Бриггс и Джон Б. С. Холдейн применили метод аппроксимации стационарного состояния для определения закона скорости реакции, катализируемой ферментом (рис. 1). Были сделаны следующие предположения:
Бриггс и Джон Б. С. Холдейн применили метод аппроксимации стационарного состояния для определения закона скорости реакции, катализируемой ферментом (рис. 1). Были сделаны следующие предположения:
- Константа скорости первого шага должна быть меньше, чем константа скорости второго шага (\(k_1 \ll k_2\)), поэтому \[\dfrac{d[ES]}{dt} = 0 \nonumber \]
- Концентрация фермента должна быть значительно ниже концентрации субстрата, чтобы первый этап был медленнее, чем второй.
Рисунок 1: Стационарная динамика ферментов
Это дает следующее: dfrac{d[ES]}{dt} = 0 = k_1[E][S] — k_{-1}[ES] — k_2[ES] \label{7} \]
Поскольку
\[[S] \gg [E] \label{8} \]
Используя второе предположение и тот факт, что концентрация фермента равна исходной концентрации фермента за вычетом концентрации промежуточного соединения фермент-субстрат,
\[[E] = [E]_o — [ES] \label{9} \]
Получается следующее уравнение:
\[k_1[E]_o[S] = k_{-1}[ ES] + k_2[ES] + k_1[ES][S] \label{10} \]
Из этого уравнения можно найти концентрацию промежуточного продукта ES:
\[[ES] = \dfrac{k_1[E]_o[S]}{(k_{-1} + k_2) + k_1[S]} \label{11} \]
Подставьте это в уравнение \ (\ref{6}\) дает,
\[\dfrac{d[P]}{dt} = \dfrac{k_2[E]_0[S]}{[(k_1+k_2)/k_1]+[ S]} = \dfrac{k_2[E]_0[S]}{K_M+[S]} \label{12} \]
, где
\[K_M = \dfrac{k_{-1}+k_{2 }}{k_1} \label{13} \]
Поскольку в большинстве случаев для определения скорости образования продукта измеряется только начальное \(d[P]/dt\), уравнение \ref{12} можно переписать как:
\[v_o = \dfrac{d[P]_0}{dt} = \dfrac{k_2[E]_0[S]}{K_M+[S]} \label{14} \]
Поскольку \([ E]_o = v_{max}/k_2\). Уравнение \(\ref{14}\) становится следующим:
Уравнение \(\ref{14}\) становится следующим:
\[ \begin{align} v_0 &= \dfrac{d[P]_o}{dt} \\[4pt] &= \dfrac{(k_2 /k_2)v_{max}[S]}{K_M+[S]} \label{15} \\ &= \dfrac{v_{max}[S]}{K_M+[S]} \label{16} \end {align} \]
Это уравнение является полезным инструментом для расчета \(v_{max}\) и \(K_M\) ( константа Михаэлиса ) фермента с использованием графика Лайнуивера-Берка (1/ [S] против 1/v 0 ) или график Иди-Хофсти (v 0 /[S] против v 0 ).
Задачи
Учитывая реакцию \(A \xrightarrow[]{k_1} B \xrightarrow[]{k_2} C\)
где k 1 = 0,2 M -1 с -1 , k 2 = 2000 с -1
- Запишите скорости реакций для А, В и С.
- Это стационарная реакция?
- Напишите выражение для d[C]/dt, используя аппроксимацию установившегося состояния
- Рассчитать d[C]/dt, если [A] = 1M
- Рассчитать [C] при t = 3 с и [A] 0 = 2M
Растворы
1) d[A]/dt = -k 1 [A]; d[B]/dt = k 1 [A] — k 2 [B]; d[C]/dt = k 2 [B]
2) Поскольку k 1 намного больше, чем k 2 , это стационарная реакция.
3) d[C]/dt = k 2 [B]
где d[B]/dt = k 1 [A] — k 2 [B] = 0
Итак, [B] = k 1 [A]/k 2
Подставим это в d[C]/dt
d[C]/dt = k 1 [A]
1 ) d[C]/dt = 0,2M -1 с -1 (1M) = 0,2 с -1
5) [C] = [A] 0 (1-e -k 1 t ) = 2M(1-e -0,2(3) ) = 0,9 M
Ссылки:
- Chang, Raymond. Физическая химия для биологических наук . Саусалито: Университетские научные книги, 2005. 368–370.
- Гарретт, Реджинальд Х., Чарльз М. Гришэм. Биохимия . 4 -е изд. Бостон: Brooks/Cole Cengage Learning, 2010. 389–397.
- Сегель, Ирвин Х. Биохимические расчеты . 2 и изд. Нью-Джерси: John Wiley and Sons, Inc., 1976. 216–218.
3.2.6: Approximation Steady State Approximation распространяется под лицензией CC BY-NC-SA 4.
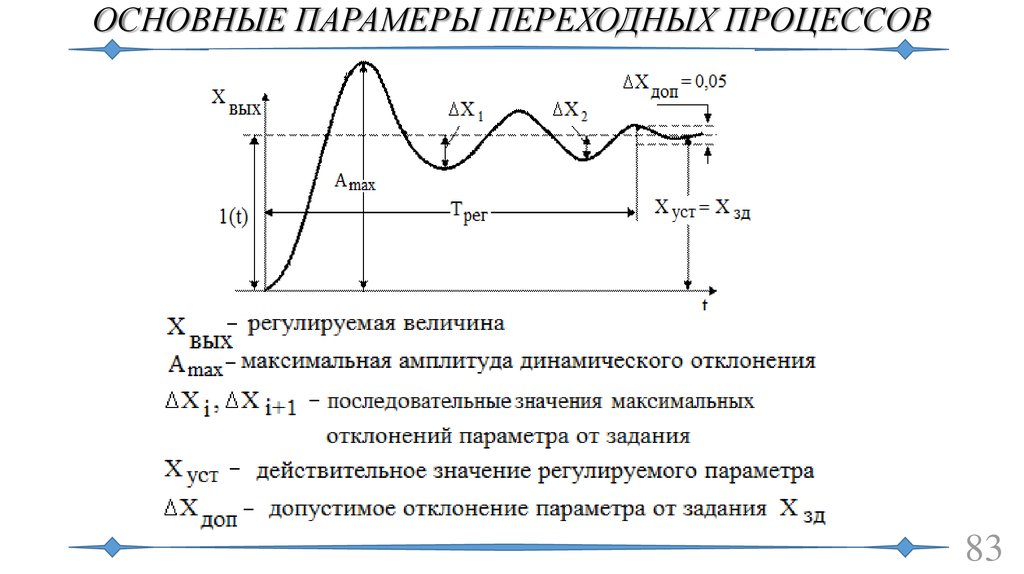 Неравномерность движения и методы ее регулирования. Коэффициент неравномерности. Маховик и его назначение. Определение момента инерции первой группы звеньев. Определение момента инерции дополнительной маховой массы (маховика). Решение задачи регулирования хода машины по методу Н.И.Мерцалова. Определение закона движения начального звена механизма при установившемся режиме движения.
Неравномерность движения и методы ее регулирования. Коэффициент неравномерности. Маховик и его назначение. Определение момента инерции первой группы звеньев. Определение момента инерции дополнительной маховой массы (маховика). Решение задачи регулирования хода машины по методу Н.И.Мерцалова. Определение закона движения начального звена механизма при установившемся режиме движения.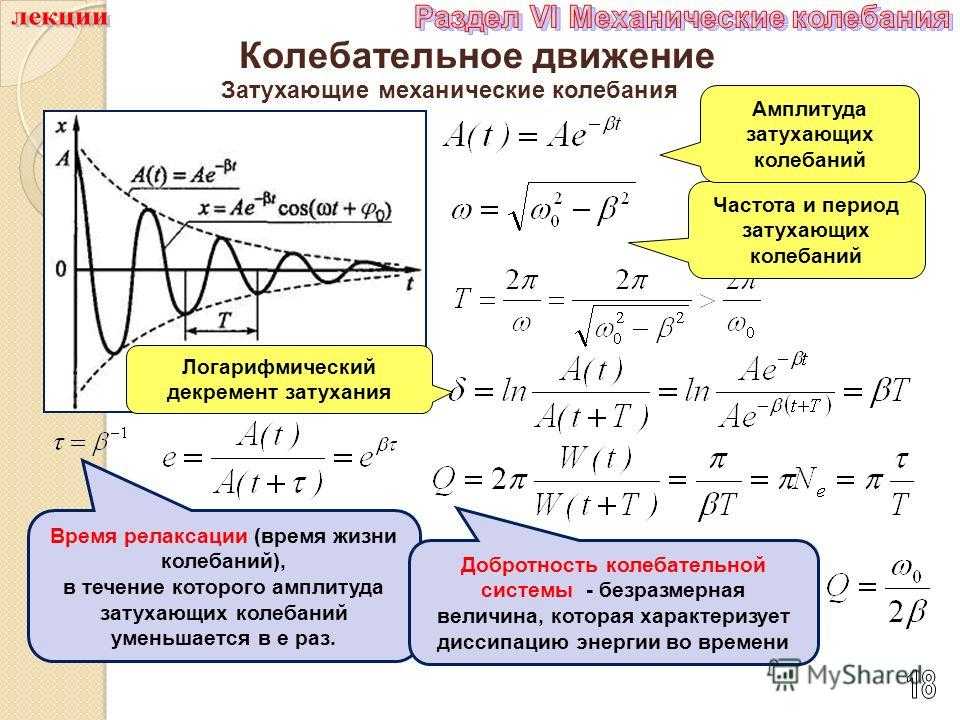
 Колебания скорости изменения обобщенной координаты машины не оказывают прямого влияния на фундамент машины. Поэтому эти колебания и вызывающие их причины определяют, так называемую, внутреннюю виброактивность машины.
Колебания скорости изменения обобщенной координаты машины не оказывают прямого влияния на фундамент машины. Поэтому эти колебания и вызывающие их причины определяют, так называемую, внутреннюю виброактивность машины.
