Установившийся режим движения машины

Моделирование в электроэнергетике — Способы представления нагрузочных узлов при расчете установившегося режима работы

Режим работы электрической системы непрерывно изменяются в режиме реального времени, но эти изменения, происходящие около некоторого среднего значения, могут быть настолько малыми, что режим работы электрической системы практически не изменяется. Режим работы электрической системы, при котором параметры режима (напряжение, токи, мощности, частота) остаются практически неизменными, называют установившимся режимом работы.

Перед выполнением расчета установившегося режима работы электрической системы необходимо составить схему замещения электрической системы. Схема замещения электрической системы представляет собой электрическую схему, в которой все реальные элементы заменены максимально близкими по функциональности цепями из идеальных элементов. Схема замещения электрической системы является связанным графом и состоит из ветвей и узлов.

В состав типовой ветви расчетной схемы замещения входит активное, индуктивное и емкостное сопротивление. В зависимости от моделируемого элемента ветвь расчетной схемы представляется как продольными, так и поперечными элементами электрической цепи. На способах моделирования элементов электрической системы (воздушных и кабельных линий, трансформаторного и реакторного оборудования)  останавливаться не будем, так как они были рассмотрены в предыдущих статьях.

В данной статье остановимся на способах представления генерирующего оборудования и электроустановок потребителя при расчете установившегося режима работы сети. Узлы расчетной схемы замещения представляют собой:

— точки соединения нескольких ветвей;

— нагрузочные узлы;

— генерирующие узлы.

В зависимости от способа задания нагрузок и генераторов уравнения установившегося режима линейны и нелинейны. Способы представления нагрузочных узлов при выполнении расчетов установившихся режимов работы зависят от вида сети и целей расчета.

2.1. Представление нагрузки в виде осветительной нагрузки при расчете установившихся режимов работы

Осветительная нагрузка, которая состоит из ламп накаливания, содержит только активное сопротивление R_н и не потребляет реактивной мощности. Активная мощность не зависит от частоты и пропорционально квадрату напряжения:

2.2. Представление нагрузки в виде асинхронного двигателя при расчете установившихся режимов работы

Нагрузка в виде асинхронных двигателей при расчете установившихся режимов работы представляется статической характеристикой активной и реактивной мощности от напряжения (,).  Зависимости изменения активной и реактивной мощности асинхронного двигателя от напряжения представлены на рис.1.

Независимыми параметрами в данном случае являются модуль и угол напряжения в узле (, ).

Рис.1. Характеристика изменения активной и реактивной мощности асинхронного двигателя от напряжения

∙ В установившемся режиме работы асинхронного двигателя на ротор и полюсы статора действуют вращающие/тормозящие моменты, одинаковые по величине, но направленные в противоположные стороны:

— электромагнитный момент двигателя ()

— механический момент сопротивления на валу двигателя (или статический момент) , включающий момент сопротивления механизма и момент от всех механических потерь в системе, в том числе и от механических потерь в двигателе.

— момент на валу двигателя (полезный нагрузочный момент)

— момент холостого хода двигателя

Электромагнитный момент связан с активной мощностью, затрачиваемой на приведение в действие механизма следующим образом:

 — угловая синхронная скорость вращения ротора асинхронного двигателя.

∙ Определим зависимости изменения активной и реактивной мощности от напряжения, для этого рассмотрим упрощенную схему замещения асинхронного двигателя. Схема замещения представляет собой параллельное соединение двух ветвей: ветви с сопротивлением намагничивания X_μ и ветви с сопротивлением рассеяния X_s. и активным сопротивлением обмотки статора и обмотки ротора, приведенное к напряжению обмотки статора.  

Рис.2. Упрощенная схема замещения асинхронного двигателя.

Активная мощность определяется функцией от напряжения и скольжения в соответствии со схемой замещения:

Зависимость изменения электромагнитного момента асинхронного двигателя от скольжения M(s) при различных значениях напряжения, а также зависимость скольжения от напряжения s(U) представлены на рис.2.

Рис.3. Зависимость электромагнитного момента асинхронного двигателя от скольжения при различных значениях подведенного напряжения

При заданном механическом моменте на валу двигателя  М_мех  каждому значению напряжения  соответствуют два значения s, т. е. два режима, при которых активная мощность двигателя равна механической мощности  на валу. Следует отметить, что точки 1,2,3 на участке механической характеристики соответствуют устойчивому режиму работы электродвигателя, в которых выполняется условие , а точки 5,6,7 на участке механической характеристики соответствуют неустойчивому режиму работы электродвигателя. Таким образом, устойчивая работа асинхронного двигателя возможна при скольжениях меньше критического (s < s_кр).

При снижении напряжения на выводах асинхронного двигателя происходит изменения значения скольжения асинхронного двигателя, при сохранении неизменным электромагнитного момента . При дальнейшем снижении напряжения ниже критического значения (U_кр) режим работы двигателя не возможен, так как его электромагнитный момент меньше механического момента на валу двигателя  (М_эм < М_мех). Физически при снижении напряжения  ниже критического значения вращающийся двигатель будет тормозиться, ток и реактивная мощность будут резко расти, а затем двигатель остановится – опрокинется. Обычно двигатели работают с большим запасом устойчивости, поэтому опрокидывание двигателя возникает только в случае большого снижения напряжения – до 20-40% от U_ном.

Таким образом, при снижении напряжения на зажимах асинхронного двигателя происходит увеличение скольжение (, где  — частота сети,  — скорость вращения ротора асинхронного двигателя) из-за снижения скорости вращения ротора асинхронного двигателя. Снижение скорости вращения асинхронного двигателя приводит к снижению потребления активной мощности асинхронного двигателя от сети, что отражено на рис.1.

Реактивная мощность асинхронного двигателя Q определяется суммой двух составляющих: намагничивающей реактивной мощности Q_μ, связанной с намагничивающим токов, и мощностью рассеивания Q_s.

Намагничивающей реактивной мощности Q_μ зависит от квадрата напряжения:

Реактивная мощность рассеивания Q_s пропорциональна квадрату тока:

Потребляемая асинхронным двигателем реактивная мощность намагничивания  Qµ и рассеяния Qs также зависят от напряжения, соответственно суммарная потребляемая реактивная мощность Q имеет сложную зависимость от напряжения (см. рис.4).

Рис.4. Зависимость изменения реактивной мощности от напряжения

Значение критического напряжения составляет для разных узлов нагрузки Uкр=(0,6-0,85)∙Uном, и если напряжение на шинах нагрузки снижается до такого значения, то появляются условия для возникновения лавины напряжения, т.е. лавинообразного снижения напряжения вследствие нарастающего дефицита реактивной мощности. В таком случае рост потребляемой реактивной мощности приводит к увеличению потери напряжения  в сети, к которой подключена нагрузка, и напряжение снова снижается. Если в течение нескольких секунд не повысить напряжение в центре питания, то двигатели начинают тормозиться и отключаться (саморазгрузка). После отключения двигательной нагрузки напряжение повышается, так как в сети исчезают перетоки реактивной мощности из-за отключившейся двигательной нагрузки.

2.3. Представление нагрузки в виде синхронного двигателя при расчете установившихся режимов работы

Нагрузка в виде синхронных двигателей при расчете установившихся режимов работы представляется постоянной по величине значением активной мощностью и статической характеристикой реактивной мощности от напряжения (, ).   Зависимости изменения активной и реактивной мощности асинхронного двигателя от напряжения представлены на рис.5. Кривые 1,2,3 – это зависимости  синхронного двигателя с независимым возбуждениям от напряжения при разных сопротивлениях .

Независимыми параметрами в данном случае являются модуль и угол напряжения в узле (, ).

Рис.5. Характеристика изменения активной и реактивной мощности синхронного двигателя от напряжения

∙ В установившемся режиме работы синхронного двигателя на ротор и полюсы статора действуют вращающие/тормозящие моменты, одинаковые по величине, но направленные в противоположные стороны:

— электромагнитный момент двигателя (),

— механический момент сопротивления на вале двигателя (или статический момент) , включающий момент сопротивления механизма и момент от всех механических потерь в системе, в том числе и от механических потерь в двигателе.

— момент на валу двигателя (полезный нагрузочный момент)

— момент холостого хода двигателя

Электромагнитный момент связан с активной мощностью, затрачиваемой на приведение в действие механизма следующим образом:

 — угловая синхронная скорость вращения ротора асинхронного двигателя.

Механическая характеристика  синхронного двигателя (при Mс < Mmax) абсолютно жесткая и частота вращения ротора синхронного двигателя не зависит от момента сопротивления (). Частота вращения ротора синхронного двигателя соответствует частоте системы. В связи с этим при неизменном механическом моменте на валу двигателя  М_мех  потребляемая активная мощность от сети будет также постоянной.

∙ Определим зависимости изменения активной и реактивной мощности от напряжения, для этого рассмотрим упрощенную схему замещения неявнополюсного синхронного двигателя, в которой не учитывают потери активной мощности в статоре.

Рис.6. Упрощенная схема замещения неявнополюсного синхронного двигателя

Активная и реактивная мощность синхронной машины определяется по следующим формулам:

Рис.7. Векторная диаграмма синхронного двигателя, работающего с перевозбуждением (а) и недовозбуждением (б)

Следует отметить, что в двигательном режиме вектор синхронной ЭДС   отстает от вектора напряжения статора  на угол  (другими словами ось поля ротора отстает от оси поля статора).

Зависимость изменения угловой характеристики мощности (электромагнитного момента) асинхронного двигателя от угла нагрузки  при различных значениях напряжения представлена на рис. При неявнополюсной машине зависимость  представляет собой синусоиду, симметричную относительно осей координат. В явнополюсной машине угловая характеристика несколько отличается от синусоиды из-за наличия реактивного момента, возникающего вследствие неодинаковой магнитной проводимости по продольной и поперечной осям.

Рис.8. Зависимость электромагнитного момента синхронного двигателя от угла δ при различных значениях подведенного напряжения

При заданном механическом моменте на валу двигателя  М_мех  каждому значению напряжения  соответствуют два значения угла δ, т.е. два режима, при которых активная мощность двигателя равна механической мощности  на валу. Следует отметить, что точки 1,2,3 на участке механической характеристики соответствуют устойчивому режиму работы электродвигателя, в которых выполняется условие , а точки 5,6,7 на участке механической характеристики соответствуют неустойчивому режиму работы электродвигателя. Таким образом, устойчивая работа асинхронного двигателя возможна при угле δ от 0 градусов до 90 градусов.

При заданном механическом моменте на валу двигателя  М_мех  в случае снижения напряжения будет изменяться угловая характеристика мощности с ростом угла . Изменение угла  и напряжение статора  вызовет изменение реактивной мощности. Характеристика изменения реактивной мощности от напряжения синхронного двигателя представлена на рис.5.

Достоинства синхронного двигателя в сравнении с асинхронным:

а) Синхронные двигатели имеют возбуждение от независимого источника постоянного тока, что позволяют двигателем работать как в режиме потребления реактивной мощности, так и в режиме выработки реактивной мощности.

б)   вращающий момент синхронного двигателя пропорционален напряжению сети. Поэтому при понижении напряжения в сети синхронный двигатель сохраняет большую перегрузочную способность, чем асинхронный, и, следовательно, обладает большей надёжностью.

в) постоянство частоты вращения независимо от механической нагрузки на валу.

Недостатки синхронного двигателя в сравнении с асинхронным:

а)  сложность конструкции;

б)  сравнительная сложность пуска синхронных двигателей. Синхронные двигатели должны иметь источник постоянного тока (специальный возбудитель или выпрямитель), пуск у них протекает сложнее, чем у асинхронных.

в)  трудности с регулированием частоты вращения, которое возможно только путем изменения частоты питающего напряжения. Частотное регулирование является единственным способом регулирования угловой частоты вращения ротора синхронного двигателя.

2.4. Представление нагрузки в виде синхронного компенсатора при расчете установившихся режимов работы

В рассматриваемом способе генерирующий узел представляется постоянной по величине значением активной мощности и модулем напряжения в узле (; ). Независимыми параметрами в данном случае являются значение реактивной мощности угол напряжения в узле  (; ).

При таком способе задания генерирующего узла реактивная мощность вырабатываемая/потребляемая синхронным компенсатором зависит от напряжения в узле. Величина реактивной мощности синхронного компенсатора меняется в заданном диапазоне: .

В случае достижения граничного значения по выработки/потребления реактивной мощности в узле, то модель синхронного компенсатора превращается в PQ-модель. Другими словами в узле осуществляется фиксация граничного значения реактивной мощности и независимыми (свободными) параметрами электроэнергетического режима становятся модуль и угол напряжения (; )..

Следует отметить, что такие узлы называют балансирующими по ре­активной мощности. Задание постоянного модуля напряжения соответствует реальным условиям работы генераторов с установленными регуляторами напряжения.

2.5. Представление обобщенной нагрузки в виде постоянного источника тока.

В рассматриваемом способе узел нагрузки представляется постоянным источником тока, который может быть задан значением тока по модулю и фазе или действующей и мнимой составляющей тока ().  Независимыми параметрами в данном случае являются модуль и угол напряжения в узле (, ).

Такая форма представления генераторов и нагрузки потребителей в расчетной схеме в виде постоянного источника тока позволяет установившийся режим работы описать системой линейных алгебраических уравнений, что в свою очередь упрощает выполнение аналитических расчетов. Таким образом, данная форма представления генерирующих узлов может использоваться при всех расчетах распределительных сетей низкого напряжения до 1 кВ.

2.6. Представление обобщенной нагрузки в виде постоянного значения мощности

В рассматриваемом способе узел нагрузки представляется постоянной по величине значением активной и реактивной мощностью (,).  Независимыми параметрами в данном случае являются модуль и угол напряжения в узле (, ). Следует отметить, что в рассматриваемом способе мощность в узле нагрузки не зависит от значения напряжения в узле и является постоянным значением.

Этот способ задания нагрузки является достаточно точным для электрических систем, полностью обеспеченных устройствами регулирования напряжения. В этих условиях при изменениях режима напряжение на нагрузке практически не меняется и полная мощность нагрузки остается постоянной. Подержание постоянного напряжения в узлах расчетной схемы может обеспечиваться следующими устройствами:

—           регулированием РПН и ПБВ трансформаторов и автотрансформаторов;

—           оснащением нерегулируемых трансформаторов на существующих подстанциях линейными регулировочными трансформаторами;

—           средствами компенсации реактивной мощностью (управляемые батареи конденсаторов, синхронные двигатели и т.д.).

В действительности у потребителей не обеспечивается поддержание постоянного по модулю напряжения. В этом случае задание постоянной мощности нагрузки потребителей приводит к ошибкам при расчетах установившихся режимов питающих сетей. Величина ошибки тем больше, чем больше отличаются напряжения потребителей от номинального значения.

2.7. Представление обобщенной нагрузки в виде постоянного значения проводимости или постоянного значения сопротивления.

В рассматриваемом способе узел нагрузки представляется постоянной величиной проводимостью с параллельным соединением элементов и постоянным сопротивлением с последовательным соединением элементов.

Независимыми параметрами в данном случае являются модуль и угол напряжения в узле  (, ), а также значения активной и реактивной мощности, которые являются функцией от напряжения в узле (,).

Рис.9. Схемы замещения нагрузки.

Моделирование нагрузки постоянным сопротивлением дает обратную квадратичную зависимость от напряжения:

;  

где и — параметры, которые вычислены при номинальном напряжении

Моделирование нагрузки постоянной проводимостью дает зависимость пропорционально квадрату напряжения:

; ,

где и — параметры, которые вычислены при номинальном напряжении

Следует отметить, что представление нагрузки в виде постоянного значения проводимости используется при расчете электромеханических переходных процессов.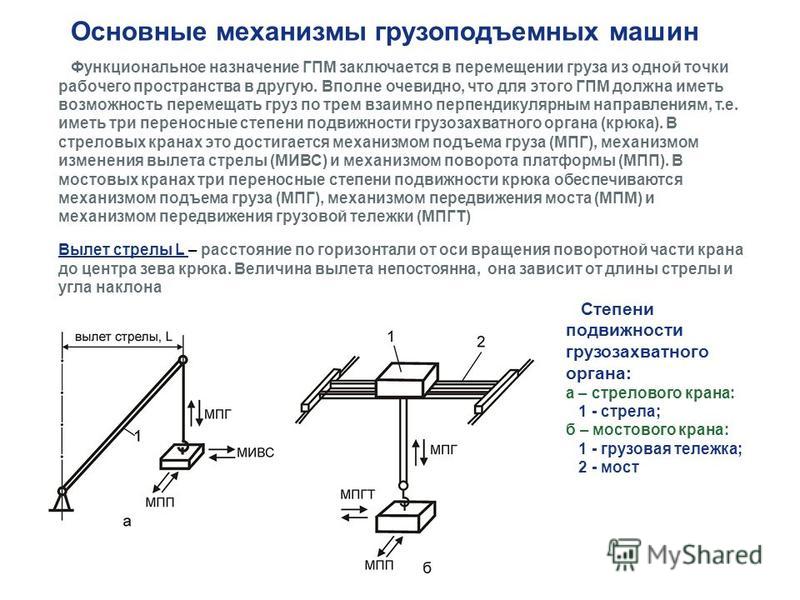 Данная модель хорошо согласуется с моделью статической характеристики реактивной мощности нагрузки, поэтому для представления реактивной мощности вполне приемлема. При представлении активной мощности нагрузки часто пользуются линейной зависимостью:

; 

Характеристика изменения активной и реактивной нагрузки от напряжения представлены ниже: сплошной линии показаны  действительные статические характеристики нагрузки, а пунктирной линией показаны характеристики нагрузки, которая представлена в виде  постоянного значения проводимости.

Рис.10. Характеристика изменения действительной нагрузки и моделируемой нагрузки

2.8. Представление обобщенной нагрузки в виде статических характеристик по напряжению.

Под понятием «статическая характеристика элемента» понимается зависимость установившихся значений выходной величины от значения величины на входе системы.

Независимыми параметрами в данном случае являются модуль и угол напряжения в узле  (, ), а также значения активной и реактивной мощности, которые являются функцией от напряжения в узле (,).

Статические характеристики для каждого типа электрической нагрузки и их совокупностей могут быть получены экспериментально. Однако в каждом конкретном случае это затруднительно и чаще всего пользуются так называемыми типовыми характеристиками. В общем случае статические характеристики нагрузки по напряжению могут быть представлены в виде:

;

;

где  и — активная и реактивная мощности при номинальном напряжении;

, ,  И , ,  — коэффициенты (параметры) моделей, полученные в результате обработки экспериментальных данных.

Моделирование электрических нагрузок статическими характеристиками по напряжению в расчетах установившихся режимов считается наиболее точным способом учета потребляемой мощности нагрузки. Однако для получения действительных статических характеристик требуются экспериментальные исследования, а для подбора типовых статических характеристик должен быть известен состав нагрузки, который может сильно изменяться во времени. Кроме того, в этом случае в расчетах непременно следует учитывать действие регуляторов напряжения, что значительно усложняет подготовку данных и требует знания законов регулирования.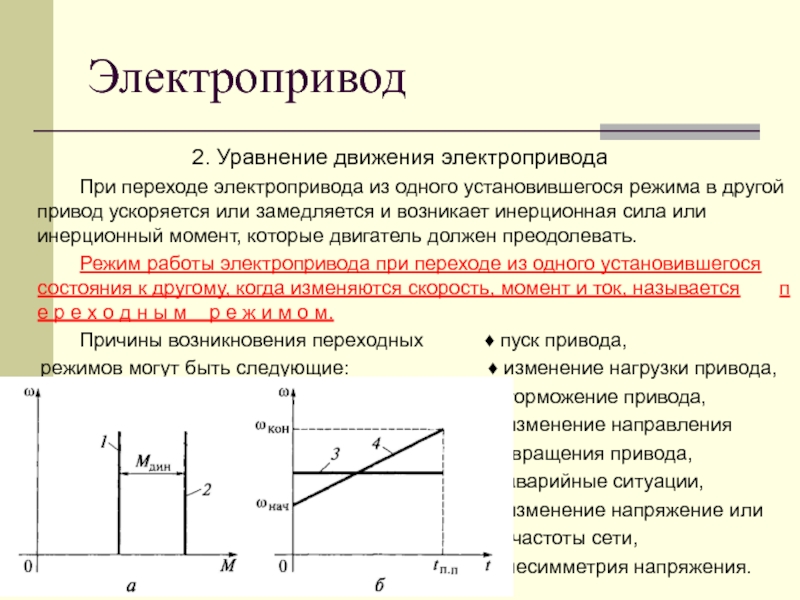

Обычно при расчетах принимается понятие «Средние статические характеристики», которые соответствуют следующему составу нагрузки, %:

Мелкие асинхронные двигатели – 35 %

Крупные асинхронные двигатели – 15 %

Освещение и бытовая нагрузка – 22 %

Печи и ртутные выпрямители – 11 %

Крупные синхронные двигатели – 9 %

Потери в сетях – 8 %

Следует отметить, что коэффициенты для представления статической характеристики нагрузки различны.

Например, в случае преобладании крупных промышленных предприятий в узле нагрузки статические характеристики нагрузки моделируется следующим образом:

; .

В случае отсутствия крупных промышленных предприятий в узле нагрузки статические характеристики нагрузки моделируется следующим образом:

; .

            В соответствии с другим источником (В.И. Идельчик «Электрические системы и сети») для задания обобщенной типовой нагрузки, используются следующие коэффициенты уравнения:

— нагрузка представляется на напряжении 110 кВ:

; .

— нагрузка представляется на напряжении 35 кВ:

; .

4.12: Стационарное приближение — Химия LibreTexts

1. Последнее обновление

2. Сохранить как PDF

Цели обучения

• Объяснить устойчивое состояние и стационарное приближение .
• Получить закон скорости, когда задан механизм, но шаг, определяющий скорость, не указан.
• Получите общее выражение закона скорости, используя стационарное приближение.
• Сделайте соответствующие предположения, чтобы полученный закон скорости согласовывался с наблюдаемым законом скорости.
• Приведите выражения для скорости производства промежуточного продукта.
• Дайте выражения для потребления курс промежуточного звена.
• Выразите концентрацию промежуточного продукта через концентрацию реагентов.
• Исключите концентрации промежуточных продуктов, используя концентрации реагентов.
• Выведите закон скорости из множества элементарных шагов.
• Обсудить полученный закон скорости .

Приближение стационарного состояния

Когда механизм реакции имеет несколько стадий с сопоставимыми скоростями, стадия, определяющая скорость, часто не очевидна. Однако на некоторых этапах есть промежуточное звено. 9Промежуточное соединение 0027 представляет собой вещество, которое не является ни одним из реагентов, ни одним из продуктов. Аппроксимация стационарного состояния — это метод, используемый для получения закона скорости. Метод основан на предположении, что один промежуточный продукт в механизме реакции расходуется так же быстро, как и образуется. Его концентрация остается неизменной в течение всей реакции.

Определение: Промежуточные продукты

Промежуточный продукт представляет собой вещество, которое не является ни одним из реагентов, ни одним из продуктов. Он временно существует в ходе реакции.

Когда в реакции участвует один или несколько промежуточных продуктов, концентрация одного из них остается постоянной на некоторой стадии реакции. Таким образом, система достигла стационарного состояния . Концентрация одного из промежуточных соединений, \([Int]\), изменяется с 90 039 по 90 040, как показано на рисунке \(\PageIndex{1}\). В начале и в конце реакции [Int] изменяется со временем.

\[ \dfrac{d[Int]}{dt}= 0 \nonumber \]

Рисунок \(\PageIndex{1}\): Пример, когда промежуточное состояние можно аппроксимировать как стационарное.

Когда механизм реакции состоит из нескольких стадий с сопоставимыми скоростями, стадия, определяющая скорость, не очевидна. Однако на некоторых этапах есть промежуточное звено. Стационарное приближение подразумевает, что вы выбираете промежуточное соединение в механизме реакции и рассчитываете его концентрацию, предполагая, что оно потребляется так же быстро, как и образуется. Ниже приводится пример, показывающий, как работает метод стационарной аппроксимации.

Пример \(\PageIndex{1}\)

Используйте стационарное приближение, чтобы вывести закон скорости для этой реакции

\[\ce{2 N2O5 \rightarrow 4 NO2 + O2}\nonumber \]

, предполагая, что она следует следующему трехступенчатому механизму:

\ [\begin{align} \ce{N_2O_5} &\underset{\Large{k_{\textrm b}}}{\overset{\Large{k_{\textrm f}}}\rightleftharpoons} \ce{NO_2 + NO_3 } \tag{шаг 1} \\[4pt] \ce{NO3 + NO2} &\ce{->[\large{k_2}] NO + NO2 + O2} \tag{шаг 2} \\[4pt] \ ce{NO3 + NO} & \ce{->[\Large{k_3}] 2 NO2} \tag{шаг 3} \end{align} \]

Решение

На этих стадиях \(\ce{NO}\) и \(\ce{NO3}\) являются промежуточными продуктами. У вас есть

\(\ce{производство\: скорость\: of\: NO} = k_2 \ce{[NO3] [NO2]}\)
\(\ce{потребление\: норма\: of\: NO } = k_3 \ce{[NO3] [NO]}\)

Стационарный подход использует предположение, что скорость производства промежуточного продукта равна скорости его потребления. Таким образом, мы имеем

\(k_2 \ce{[NO3] [NO2]} = k_3 \ce{[NO3] [NO]}\)

и решение для \(\ce{[NO]}\) дает результат,

\(\ce{[NO]} = \dfrac{k_2 \ce{[NO3] [NO2]}}{k_3 \ce{[NO3]}} \tag{1}\)

Для других промежуточных продуктов \(\ce{NO3}\),

\(\ce{производство\: норма\: of\: NO3} = k_{\ce f} \ce{[N2O5]}\)
\(\ce{ расход\: норма\: из\: NO3} = k_2\ce{[NO3] [NO2]} + k_3\ce{[NO3] [NO]} + k_{\ce b}\ce{[NO3] [NO2 ]}\)

Применение стационарного предположения дает:

\(k_{\ce f} \ce{[N2O5]} = k_2\ce{[NO3] [NO2]} + k_3\ce{[NO3 ] [NO]} + k_{\ce b}\ce{[NO3] [NO2]}\)

Таким образом,

\(\ce{[NO3]} = \dfrac{k_{\ce f} \ce{[N2O5]}}{k_2\ce{[NO2]} + k_3\ce{[NO]} + k_{\ce b}\ce{[NO2]}}\tag{2}\)

Рассмотрим три уравнения (шага) в механизме:
Шаг i. находится в равновесии и поэтому не может дать выражение скорости.
Шаг II. приводит к образованию некоторых продуктов, а активные частицы \(\ce{NO}\) вызывают дальнейшую реакцию на стадии iii. Это соображение привело к выражению скорости из шага ii. как:

\(\ce{\dfrac{d[O2]}{dt}} = k_2 \ce{[NO3] [NO2]} \tag{3}\)

Подстановка (1) в (2), а затем в (3) дает

\(\ce{\dfrac{d[O2]}{dt}}= \dfrac{k_{\ce f} k_2 \ce{ [N2O5]}}{k_{\ce b} + 2 k_2} = \ce{k [N2O5]}\)

, где \(\ce{k} = \dfrac{k_{\ce f} k_2}{ k_{\ce b} + 2 k_2}\).

Это дифференциальный закон скорости, и он согласуется с экспериментальными результатами. Вышеописанную манипуляцию проведите самостоятельно на листе бумаги. Простое прочтение вышеизложенного еще не приведет к основательному обучению.

На этой странице приведен еще один пример, иллюстрирующий технику вывода законов скорости с использованием стационарного приближения. Здесь рассматривается реакция между газами \(\ce{h3}\) и \(\ce{I2}\).

Пример \(\PageIndex{1}\)

Для реакции:

\(\ce{H_{2\large{(g)}} + I_{2\large{(g)}} \rightarrow 2 HI_{\large{(g)}}}\)

Какие механизмы могут быть подходящими? Выведите закон скорости из предложенного механизма.

Решение

Что ж, на этот вопрос нет простого ответа, и нет способа доказать одно над другим на его достоверность. Начинающим студентам-химикам не будет предложено предложить механизм, но вас попросят вывести закон скорости из предложенного механизма.

Прежде всего, вы должны быть в состоянии выразить скорость реакции через изменение концентрации,

\(скорость = — \ce{\dfrac{d[h3]}{dt}} = — \ce{ \dfrac{ d[I2]}{dt}} = \ce{\dfrac{1}{2}\dfrac{d[HI]}{dt}}\)

Еще раз посмотрите на общее уравнение реакции, чтобы увидеть его отношение и скорость выражения.

Предложение механизма

Чтобы предложить механизм, применим следующие рассуждения. Поскольку связь между \(\ce{I-I}\) слабая, мы ожидаем, что \(\ce{I2}\) диссоциирует на атомы или радикалы. Эти радикалы активны и реагируют с \(\ce{h3}\) с образованием продуктов. Таким образом, мы предлагаем трехэтапный механизм:

1. \(\ce{I_{2\large{(g)}}} \xrightarrow{\Large{k_1}} \ce{2 I_{\large{(g)}}}\)
2. \(\ce{2 I_{\large{(g)}}} \xrightarrow{\Large{k_2}} \ce{I_{2\large{(g)}}}\)
3. \(\ce{H_{2\large{(g)}} + 2 I _{\large{(g)}}} \xrightarrow{\Large{k_3}} \ce{2 HI_{\large{(g) )}}}\)

Какой шаг вы бы использовали, чтобы написать закон дифференциальной ставки?

Поскольку только шаг iii. дает реальные продукты, мы ожидаем, что вы признаете этот шаг iii. намекает на закон скорости: 92}\) в выражение rate , у вас есть

\(\begin{align}
rate &= k_3 \ce{[h3]} \dfrac{k_1 \ce{[I2]}}{k_2 + k_3 \ce{[h3]}}\\
&= \dfrac{k_1 k_3 \ce{[h3] [I2]}}{k_2 + k_3 \ce{[h3]}}
\end{align}\)

Обсуждение

Если шаг III. медленно, то \(k_3\) и \(k_2 >> k_3 \ce{[h3]}\). Закон скорости сводится к

\(\ce{скорость} = \ce{k [h3] [I2]}\),

, где \(\ce{k} = \dfrac{k_1 k_3}{k_2}\). (Проработайте это на бумаге самостоятельно; чтение приведенного выше вывода не приведет к обучению.)

Поскольку закон скорости имеет первый порядок по отношению к обоим реагентам, можно утверждать, что закон скорости также поддерживает одношаговый механизм,

\(\ce{H_{2\large{(g)}} + I_{2\large{(g)}} \rightarrow 2 HI}\)

Эта элементарная стадия аналогична общей реакции.

Предположим, мы используем большое количество \(\ce{h3}\) по сравнению с \(\ce{I2}\), тогда изменение \(\ce{[h3]}\) незначительно. Например, если \(\mathrm{[H_2] = 10}\) и \(\mathrm{[I_2] = 0,1}\) первоначально, \(\ce{[h3]}\) остается по существу 10 (9.9 только с одной значащей цифрой). Другими словами, \(\ce{[h3]}\) почти не изменилось, когда реакция закончилась. Таким образом,

\(k_3 \ce{[h3]} >> k_3\)

и закон скоростей принимает вид:

\(rate = k_1 \ce{[I2]}\).

Таким образом, реакция является реакцией псевдопервого порядка из-за большого количества одного реагента. Результаты предполагают iii. быстрый шаг (из-за большого количества \(\ce{h3}\)), и i. этап определения скорости.

Авторы и авторство

4.12: Steady-State Approximation распространяется под лицензией CC BY-NC-SA 4.0 и был создан, изменен и/или курирован LibreTexts.

1. Наверх

• Была ли эта статья полезной?

1. Тип изделия

   Раздел или Страница

   Лицензия

   CC BY-NC-SA

   Версия лицензии

   4,0

   Показать страницу TOC

   № на стр.

2. Теги

   1. стационарное приближение

3.2.6: Приближение стационарного состояния — Химия LibreTexts

1. Последнее обновление

2. Сохранить как PDF

Приближение стационарного состояния — это метод, используемый для оценки общей скорости многостадийной реакции. Предполагается, что скорость изменения концентрации промежуточного продукта в многостадийной реакции постоянна. Этот метод можно применять только тогда, когда первая стадия реакции значительно медленнее, чем последующая стадия в последовательной реакции с образованием промежуточного продукта.

Введение

Прежде чем обсуждать аппроксимацию стационарного состояния, необходимо понять, что аппроксимация получена для упрощения кинетического выражения для концентрации продукта, [продукт]. Рассмотрим следующую последовательную реакцию:

\[A \xrightarrow[]{k_1} B \xrightarrow {k_2} C \nonumber \]

Расчет [продукта] зависит от всех констант скорости на каждом шаге. Например, если бы кинетический метод использовался для определения концентрации C, [C] в момент времени t в вышеуказанной реакции, выражение было бы 9{-k_2t})}{k_1 — k_2}\right) \label{1} \]

При более сложных механизмах кинетическое выражение становится труднее вывести. Чтобы упростить этот расчет, мы часто используем одно из двух приближений для определения общих скоростей последовательных реакций: приближение стационарного состояния и приближение предравновесного состояния. Эта статья касается стационарного приближения.

Приближение установившегося состояния

Приближение установившегося состояния применяется к последовательной реакции с медленной первой стадией и быстрой второй стадией (\(k_1 \ll k_2\)). Если первая стадия очень медленная по сравнению со второй стадией, накопления промежуточного продукта, такого как продукт B в приведенном выше примере, не происходит. 9{-k_1t}) \label{5} \]

Уравнение \(\ref{5}\) вывести намного проще, чем уравнение \(\ref{1}\), особенно с более сложной многостадийной реакцией механизмы.

Пример \(\PageIndex{1}\)

Рассмотрим реакцию:

\[A + 2B \xrightarrow[]{} C \nonumber \]

1. Каков ожидаемый закон скоростей согласно предложенному ниже многоступенчатый механизм в приближении стационарного состояния с \(k_2 \gg k_{-1}\)) для следующего механизма: \[A + B \ce{<=>[k_1][k_{-1}]} I \tag{Медленно} \] \[I + B \xrightarrow[]{k_2} C \tag{Быстро} \]
2. Если \(х\) — порядок реакции по \(А\), \(у\) — порядок реакции по \(В\), а \(п\) — общий порядок реакции. Каковы значения \(x\), \(y\) и \(n\)?

Решение

a: Сначала мы используем аппроксимацию установившегося состояния для промежуточного звена (т. е. уравнение \ref{2})

\[\dfrac{d[I]}{dt} = k_1[A][B] — k_{-1}[I] — k_2[I][B] = 0 \nonumber \]

затем находим (стационарную) концентрацию промежуточного соединения

\[[I] = \dfrac{k_1[A][B]}{ k_{-1} +k_2[B]} \nonumber \]

Поскольку второй шаг намного быстрее первого, то \(k_2 \gg k_{-1}\), затем \(k_{-1} \приблизительно 0\) для этого приближения, и приведенное выше уравнение можно упростить до

\[[I] = \dfrac{k_1[A ]}{k_2} \нон. \nonumber \]

Закон скорости производства \([C]\) может быть построен непосредственно на втором этапе, и когда добавляется стационарная концентрация \(I\), окончательное выражение закона скорости имеет вид полученный.

\[ \begin{align*}\dfrac{d[C]}{dt} & = k_2[I][B] \\[4pt] &= \dfrac{k_1k_2[A][B]}{k_2 } \\[4pt] &= k_1[A][B] \end{align*} \]

b: Прямая проверка окончательного закона скорости, полученного выше, дает следующие параметры:

• \(x = 1\)
• \(у = 1\)
• \(n = 2\)

Использование аппроксимации стационарного состояния в кинетике ферментов

В 1925 году Джордж Э. Бриггс и Джон Б. С. Холдейн применили метод аппроксимации стационарного состояния для определения закона скорости реакции, катализируемой ферментом (рис. 1). Были сделаны следующие предположения:

1. Константа скорости первого шага должна быть меньше, чем константа скорости второго шага (\(k_1 \ll k_2\)), поэтому \[\dfrac{d[ES]}{dt} = 0 \nonumber \]
2. Концентрация фермента должна быть значительно ниже концентрации субстрата, чтобы первый этап был медленнее, чем второй.

Рисунок 1: Стационарная динамика ферментов

Это дает следующее: dfrac{d[ES]}{dt} = 0 = k_1[E][S] — k_{-1}[ES] — k_2[ES] \label{7} \]

Поскольку

\[[S] \gg [E] \label{8} \]

Используя второе предположение и тот факт, что концентрация фермента равна исходной концентрации фермента за вычетом концентрации промежуточного соединения фермент-субстрат,

\[[E] = [E]_o — [ES] \label{9} \]

Получается следующее уравнение:

\[k_1[E]_o[S] = k_{-1}[ ES] + k_2[ES] + k_1[ES][S] \label{10} \]

Из этого уравнения можно найти концентрацию промежуточного продукта ES:

\[[ES] = \dfrac{k_1[E]_o[S]}{(k_{-1} + k_2) + k_1[S]} \label{11} \]

Подставьте это в уравнение \ (\ref{6}\) дает,

\[\dfrac{d[P]}{dt} = \dfrac{k_2[E]_0[S]}{[(k_1+k_2)/k_1]+[ S]} = \dfrac{k_2[E]_0[S]}{K_M+[S]} \label{12} \]

, где

\[K_M = \dfrac{k_{-1}+k_{2 }}{k_1} \label{13} \]

Поскольку в большинстве случаев для определения скорости образования продукта измеряется только начальное \(d[P]/dt\), уравнение \ref{12} можно переписать как:

\[v_o = \dfrac{d[P]_0}{dt} = \dfrac{k_2[E]_0[S]}{K_M+[S]} \label{14} \]

Поскольку \([ E]_o = v_{max}/k_2\). Уравнение \(\ref{14}\) становится следующим:

\[ \begin{align} v_0 &= \dfrac{d[P]_o}{dt} \\[4pt] &= \dfrac{(k_2 /k_2)v_{max}[S]}{K_M+[S]} \label{15} \\ &= \dfrac{v_{max}[S]}{K_M+[S]} \label{16} \end {align} \]

Это уравнение является полезным инструментом для расчета \(v_{max}\) и \(K_M\) ( константа Михаэлиса ) фермента с использованием графика Лайнуивера-Берка (1/ [S] против 1/v ₀ ) или график Иди-Хофсти (v ₀ /[S] против v ₀ ).

Задачи

Учитывая реакцию \(A \xrightarrow[]{k_1} B \xrightarrow[]{k_2} C\)

где k ₁ = 0,2 M ^-1 с ^-1 , к ₂ = 2000 с ^-1

1. Запишите скорости реакций для А, В и С.
2. Это стационарная реакция?
3. Напишите выражение для d[C]/dt, используя аппроксимацию установившегося состояния
4. Рассчитать d[C]/dt, если [A] = 1M
5. Рассчитать [C] при t = 3 с и [A] ₀ = 2M

Растворы

1) d[A]/dt = -k ₁ [A]; d[B]/dt = k ₁ [A] — k ₂ [B]; d[C]/dt = k ₂ [B]

2) Поскольку k ₁ намного больше, чем k ₂ , это стационарная реакция.

3) d[C]/dt = k ₂ [B]

где d[B]/dt = k ₁ [A] — k ₂ [B] = 0

Итак, [B] = k ₁ [A]/k ₂

Подставим это в d[C]/dt

d[C]/dt = k ₁ [A]

4 ) d[C]/dt = 0,2M ^-1 с ^-1 (1M) = 0,2 с ^-1

5) [C] = [A] ₀ (1-e ^{-k ₁ t} ) = 2M(1-e ^-0,2(3) ) = 0,9 M

Ссылки:

1. Chang, Raymond. Физическая химия для биологических наук . Саусалито: Университетские научные книги, 2005. 368–370.
2. Гарретт, Реджинальд Х., Чарльз М. Гришэм. Биохимия . 4 ^{-е изд.} Бостон: Brooks/Cole Cengage Learning, 2010. 389–397.
3. Сегель, Ирвин Х. Биохимические расчеты . 2 ^и изд. Нью-Джерси: John Wiley and Sons, Inc., 1976. 216–218.

3.2.6: Approximation Steady State Approximation распространяется под лицензией CC BY-NC-SA 4.