Содержание
4 способа расчета угловой скорости колеса барабана
Пример решения задачи по определению угловой скорости колеса заданного радиуса и приводимого в движение приложенным моментом из состояния покоя, которое посредством невесомой нити двигает груз по шероховатой поверхности.
Задача
Однородное колесо 1 массой M и радиусом r1 приводится в движении из состояния покоя приложенным моментом mвр. Груз 2 массой m посредством невесомой нити, намотанной на колесо барабана, движется по шероховатой поверхности, коэффициент трения скольжения которой равен f (рисунок 3.6).
Рисунок 3.6
Определить угловую скорость колеса в 4 случаях:
- а) mвр=A;
- б) mвр=a∙t, где a – постоянная, t – время;
- в) mвр=b∙φ, где b – постоянная, φ – угол поворота барабана;
- г)
где c – постоянная,
– угловая скорость колеса.
Другие примеры решений >
Помощь с решением задач >
Пример решения
Механическая система состоит из двух тел: барабана 1, вращающегося вокруг оси x, и груза 2, движущегося поступательно.
Выделим все силы, действующие на систему:
P1 = M∙g – сила тяжести барабана;
R1 и R2 – составляющие реакции колеса по осям Oz и Oy;
mвр – вращающий момент;
P2 = M∙g – сила тяжести груза;
N – нормальная реакция плоскости;
Fтр = f∙N = f∙m∙g – сила трения при скольжении груза о плоскость.
Согласно теореме об изменении момента количества движения механической системы относительно оси
где
Kx – кинетический момент системы.
Кинетический момент системы определяется по формуле
где kб – кинетический момент барабана;
kгр – кинетический момент груза;
Тогда
Итак,
Окончательно получим
Решим последнее соотношение относительно угловой скорости колеса в четырех случаях, указанных в условии задачи.
Случай (а) mвр=A (A = const).
Для удобства в выражении (3.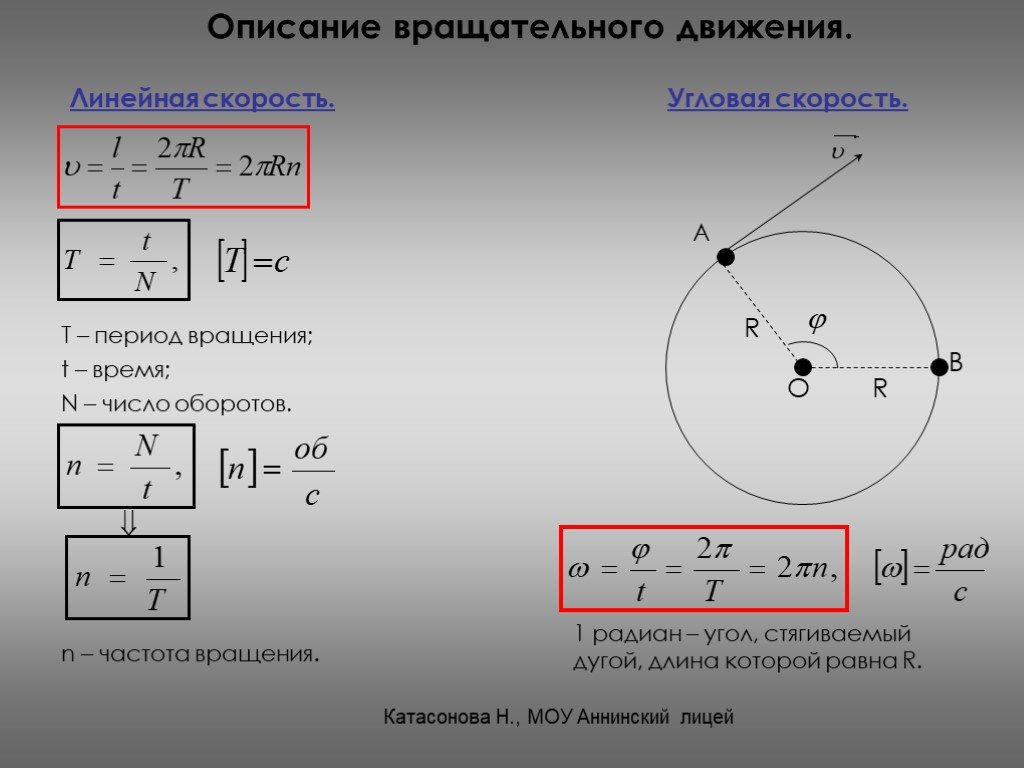 15) введем для момента инерции системы обозначение
15) введем для момента инерции системы обозначение
Тогда
Разделив переменные и проинтегрировав обе части уравнения, получим
Окончательно будем иметь
Случай (б) mвр = a∙t.
Разделив переменные и проинтегрировав обе части этого уравнения
получим
Случай (в) mвр = b∙φ.
Так как правая часть зависит от угла поворота φ и прямого разделения переменных совершить невозможно, произведем замену переменной t:
тогда
Разделим переменные и проинтегрируем полученное уравнение
откуда
Случай (г)
Разделив переменные, проинтегрируем и определим угловую скорость
Другие примеры решения задач >
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
Стоимость мы сообщим в течение 5 минут
на указанный вами адрес электронной почты.
Если стоимость устроит вы сможете оформить заказ.
НАБОР СТУДЕНТА ДЛЯ УЧЁБЫ
На нашем сайте можно бесплатно скачать:
— Рамки A4 для учебных работ
— Миллиметровки разного цвета
— Шрифты чертежные ГОСТ
— Листы в клетку и в линейку
Сохранить или поделиться с друзьями
Заказать решение
Поиск формул и решений задач
Угловая скорость
1. 54 Найти угловую скорость вращения электрона вокруг ядра
В первом приближении можно считать, что электрон в атоме водорода движется по круговой орбите с линейной скоростью v. Найти угловую скорость ω вращения электрона вокруг ядра и его нормальное ускорение аn.
1. 55 Найти для точек на ободе колеса угловую скорость
Колесо радиусом R = 10 см вращается с угловым ускорением ε = 3,14 рад/с2.
1. 60 Найти через время после начала движения угловую скорость
Колесо радиусом R = 0,1 м вращается так, что зависимость угла поворота радиуса колеса от времени дается уравнением φ=А+B+Ct2, где В = 2 рад/с и С = 1 рад/с3.
1. 41 Найти угловую скоростью суточного вращения Земли
Найти угловую скоростью ω: а) суточного вращения Земли; б) часовой стрелки на часах; в) минутной стрелки на часах; г) искусственного спутника Земли, движущегося по круговой орбите с периодом вращения Т = 88 мин.
1. 46 Найти угловое ускорение колеса
Колесо, вращаясь равноускоренно, достигло угловой скорости ω = 20 рад/с через N = 10 об после начала вращения. Найти угловое ускорение ε колеса.
469 Определить максимальную мощность необходимую для вращения…
Проволочный контур площадью \(S = 500\) см2 и сопротивлением \(R = 0,1\) Ом равномерно вращается в однородном магнитном поле (\(B = 0,5\) Тл). Ось вращения лежит в плоскости кольца и перпендикулярна линиям магнитной индукции.
422 Определить магнитный момент при вращении диска…
Диск радиусом \(R = 8\) см несет равномерно распределенный по поверхности заряд (\(\sigma = 100\) нКл/м2). Определить магнитный момент \({P_m}\), обусловленный вращением диска, относительно оси, проходящей через его центр и перпендикулярной плоскости диска.
Определить магнитный момент \({P_m}\), обусловленный вращением диска, относительно оси, проходящей через его центр и перпендикулярной плоскости диска.
425 Найти магнитный момент обусловленный вращением…
Тонкое кольцо радиусом \(R = 10\) см несет равномерно распределенный заряд \(Q = 80\) нКл. Кольцо вращается с угловой скоростью \(\omega = 50\) рад/с относительно оси, совпадающей с одним из диаметров кольца. Найти магнитный момент \({P_m}\), обусловленный вращением кольца.
426 Найти магнитный момент обусловленный вращением стержня…
Заряд \(Q = 0,1\) мкКл равномерно распределен по стержню длиной \(L = 50\) см. Стержень вращается с угловой скоростью \(\omega = 20\) рад/с относительно оси, перпендикулярной стержню и проходящей через его середину. Найти магнитный момент \({P_m}\), обусловленный вращением стержня.
429 Определить магнитный момент P…
По поверхности диска радиусом \(R = 15\) см равномерно распределен заряд \(Q = 0,2\) мкКл. Диск вращается с угловой скоростью \(\omega = 30\) рад/с относительно оси, перпендикулярной плоскости диска и проходящей через его центр.
152 С какой угловой скоростью будет вращаться скамья…
На скамье Жуковского стоит человек и держит в руках стержень вертикально по оси скамьи. Скамья с человеком вращается с угловой скоростью ω = 4 рад/с.
153 С какой угловой скоростью будет вращаться платформа…
Платформа в виде диска диаметром D = 3 м и массой m1 = 180 кг может вращаться вокруг вертикальной оси.
155 С какой скоростью станет вращаться скамья…
На скамье Жуковского стоит человек и держит в руке за ось велосипедное колесо, вращающееся вокруг своей оси с угловой скоростью ω = 25 рад/с. Ось колеса расположена вертикально и совпадает с осью скамьи Жуковского.
158 С какой угловой скоростью начнет вращаться скамья…
На краю неподвижной скамьи Жуковского диаметром D = 0,8 м и массой m1 = 6 кг стоит человек массой m2 = 60 кг.
159 С какой угловой скоростью начнет вращаться платформа. ..
..
Горизонтальная платформа массой M = 150 кг вращается вокруг вертикальной оси, проходящей через центр платформы, с частотой ν2 = 8 мин-1. Человек массой m = 70 кг стоит при этом на краю платформы.
168 Определить линейную и угловую скорости спутника…
Определить линейную и угловую скорости спутника Земли, обращающегося по круговой орбите на высоте r = 1000 км. Ускорение свободного падения g у поверхности Земли и ее радиус Rз считать известными.
107 Во сколько раз путь будет больше модуля перемещения…
Материальная точка движется по окружности с постоянной угловой скоростью ω = π/6 рад/с. Во сколько раз путь ΔS, пройденный точкой за время T = 4 с, будет больше модуля ее перемещения Δr ?
109 Каково наибольшее ускорение движения человека…
По краю равномерно вращающейся с угловой скоростью ω = 1 рад/с платформы идет человек и обходит платформу за время t = 9,9 с. Каково наибольшее ускорение а движения человека относительно Земли? Принять радиус платформы R = 2 м.
Каково наибольшее ускорение а движения человека относительно Земли? Принять радиус платформы R = 2 м.
143 Определить момент инерции маховика…
На обод маховика диаметром D = 60 см намотан шнур, к концу которого привязан груз массой m = 2 кг.
6.1 Угол поворота и угловая скорость
Цели обученияУгол вращенияУгловая скорость
Цели обучения
К концу этого раздела вы сможете делать следующее:
- Определение длины дуги, угла поворота, радиуса кривизны и угловой скорости
- Рассчитать угловую скорость вращения колеса автомобиля
В кинематике мы изучали движение по прямой и ввели такие понятия, как перемещение, скорость и ускорение. Двумерная кинематика имеет дело с движением в двух измерениях. Движение снаряда — это частный случай двумерной кинематики, в котором объект проецируется в воздух, подвергаясь действию силы гравитации, и приземляется на расстоянии. В этой главе мы рассмотрим ситуации, когда объект не приземляется, а движется по кривой. Начнем изучение равномерного кругового движения с определения двух угловых величин, необходимых для описания вращательного движения.
В этой главе мы рассмотрим ситуации, когда объект не приземляется, а движется по кривой. Начнем изучение равномерного кругового движения с определения двух угловых величин, необходимых для описания вращательного движения.
Угол поворота
Когда объекты вращаются вокруг некоторой оси — например, когда компакт-диск (CD) на рис. 6.2 вращается вокруг своего центра — каждая точка объекта следует дуге окружности. Рассмотрим линию от центра компакт-диска к его краю. Каждая яма, используемая для записи звука вдоль этой линии, проходит под одним и тем же углом за одно и то же время. Угол поворота представляет собой величину поворота и аналогичен линейному расстоянию. Определяем угол поворота
Размер ΔθΔθ 12{Δθ} {} должен быть отношением длины дуги к радиусу кривизны.
6.1 Δθ=Δср.Δθ=Δср. размер 12{Δθ= {{Δs} над {r} } } {}
Рис. 6.2 Все точки на компакт-диске движутся по дугам окружности. Ямки вдоль линии от центра к краю все перемещаются на один и тот же угол ΔθΔθ размер 12{Δθ} {} за время ΔtΔt размер 12{Δt} {}.
Рисунок 6.3 Радиус окружности поворачивается на угол ΔθΔθ величиной 12{Δθ} {}. Длина дуги ΔsΔs размером 12{Δs} {} описана на окружности.
Длина дуги ΔsΔs размер 12{Δs} {} — это расстояние, пройденное по круговому пути, как показано на рис. 6.3. Обратите внимание, что rr размер 12{r} {} — это радиус кривизны кругового пути.
Мы знаем, что для одного полного оборота длина дуги равна длине окружности радиуса rr размера 12{r} {}. Длина окружности равна 2πr2πr размера 12{2πr} {}. Таким образом, за один полный оборот угол поворота равен
.
6.2 Δθ=2πrr=2π.Δθ=2πrr=2π. size 12{Δθ= {{2πr} over {r} } =2π».»} {}
Этот результат является основой для определения единиц, используемых для измерения углов поворота, ΔθΔθ size 12{Δθ} {} в радианах (рад), определяемый таким образом, что
6,3 2πрад = 1 оборот. 2πрад = 1 оборот. размер 12{2π» рад «=» 1 оборот.»} {}
Сравнение некоторых полезных углов, выраженных как в градусах, так и в радианах, показано в таблице 6. 1.
1.
| Градусы | Измерение в радианах |
|---|---|
| 30º30º размер 12{«30″°} {} | π6π6 размер 12{ { {π} больше {6} } } {} |
| 60º60º размер 12{«60″°} {} | π3π3 размер 12{ { {π} над {3} } } {} |
| 90º90º размер 12{«90″°} {} | π2π2 размер 12{ { {π} более {2} } } {} |
| 120º120º размер 12{«120″°} {} | 2π32π3 размер 12{ { {2π} более {3} } } {} |
| 135º135º размер 12{«135″°} {} | 3π43π4 размер 12{ { {3π} больше {4} } } {} |
| 180º180º размер 12{«180″°} {} | ππ размер 12{π} {} |
Таблица 6. 1 Сравнение угловых единиц
1 Сравнение угловых единиц
Рисунок 6.4 Точки 1 и 2 поворачиваются на один и тот же угол (ΔθΔθ размер 12{Δθ} {}), но точка 2 перемещается по дуге большей длины ΔsΔs размер 12{ влево (Δs вправо )} {}, потому что она находится на большем расстояние от центра вращения (r)(r) размер 12{ \( r \) } {}.
Если Δθ=2πΔθ=2π размер 12{Δθ=2π} {} рад, то компакт-диск совершил один полный оборот, и каждая точка на компакт-диске вернулась в исходное положение. Поскольку в круге или одном обороте есть 360º360º размера 12{«360″°} {}, соотношение между радианами и градусами, таким образом, равно
6,4 2πrad=360º2πrad=360º размер 12{2π» рад»=»360″ rSup { размер 8{ circ } } } {}
так что
6,5 1rad=360º2π≈57,3 º,1 рад=360º2π≈57,3º . размер 12{1″ рад»= {{«360″ rSup {размер 8{круг} } } более {2π} } =»57» «.» 3 rSup { size 8{ circ } } «.»} {}
Угловая скорость
Как быстро вращается объект? Определим угловую скорость ωω величиной 12{ω} {} как скорость изменения угла. В символах это
В символах это
6,6 ω=ΔθΔt,ω=ΔθΔt, размер 12{ω= {{Δθ} над {Δt} } «,»} {}
где угловой поворот ΔθΔθ размер 12{Δθ} {} происходит за время ΔtΔt размер 12{Δt} {}. Чем больше угол поворота за данный промежуток времени, тем больше угловая скорость. Единицами угловой скорости являются радианы в секунду (рад/с).
Угловая скорость ωω размера 12{ω} {} аналогична линейной скорости vv размера 12{v} {}. Чтобы получить точное соотношение между угловой и линейной скоростью, мы снова рассмотрим ямку на вращающемся компакт-диске. Эта яма перемещается по дуге длиной ΔsΔs размером 12{Δs} {} за время ΔtΔt размером 12{Δt} {}, поэтому она имеет линейную скорость
6,7 v=ΔsΔt.v=ΔsΔt. size 12{v= {{Δs} над {Δt} } «.»} {}
Из Δθ=ΔsrΔθ=Δsr size 12{Δθ= {{Δs} над {r} } } {} мы видим, что Δs= rΔθΔs=rΔθ размер 12{Δs=rΔθ} {}. Подстановка этого выражения в выражение для размера vv 12{v} {} дает
6,8 v=rΔθΔt=rω.v=rΔθΔt=rω. size 12{v= {{rΔθ} над {Δt} } =rω».»} {}
Мы запишем это отношение двумя разными способами и получим два разных понимания
6,9 v=rω или ω=vr. v=rω или ω=vr. размер 12{v=rω«»или «ω= { {v} над {r} } «.»} {}
v=rω или ω=vr. размер 12{v=rω«»или «ω= { {v} над {r} } «.»} {}
Первое соотношение в v=rω или ω=vrv=rω или ω=vr size 12{v=rω«»или «ω= { {v} over {r} } } {} утверждает, что линейная скорость vv размер 12{v} {} пропорционален расстоянию от центра вращения, поэтому он является наибольшим для точки на ободе (наибольший размер rr 12{r} {}), как и следовало ожидать. Мы также можем назвать эту линейную скорость vv размером 12{v} {} точки на ободе тангенциальной скоростью . Второе соотношение в v=rω или ω=vrv=rω или ω=vr size 12{v=rω«» или «ω= {{v} over {r}}} {} можно проиллюстрировать, рассмотрев шину движущаяся машина. Обратите внимание, что скорость точки на ободе шины такая же, как скорость vv размера 12{v} {} автомобиля. (см. рис. 6.5). Таким образом, чем быстрее движется автомобиль, тем быстрее вращается шина — большой размер vv 12{v} {} означает большой размер ωω 12{ω} {}, потому что v=rωv=rω размер 12{v=rω} {}. Точно так же шина большего радиуса, вращающаяся с той же угловой скоростью (ωω размер 12{ω} {}), будет производить большую линейную скорость (vv размер 12{v} {}) для автомобиля.
Рисунок 6.5 Автомобиль, движущийся со скоростью vv размера 12{v} {} вправо, имеет шину, вращающуюся с угловой скоростью ωω размера 12{ω} {}. Скорость протектора шины относительно оси равна vv размер 12{v}{}, такой же, как если бы автомобиль был на домкрате. Таким образом, автомобиль движется вперед с линейной скоростью v=rωv=rω размер 12{v=rω} {}, где rr размер 12{r} {} — радиус шины. Большая угловая скорость шины означает большую скорость автомобиля.
Пример 6.1 Как быстро вращается автомобильная шина?
Рассчитайте угловую скорость автомобильной шины радиусом 0,300 м, когда автомобиль движется со скоростью 15,0 м/с15,0 м/с Размер 12{«15» «.» 0`»м/с»} {} (около 54 км/ч54км/ч размер 12{«54″`»км/ч»} {}) (см. рис. 6.5.
Стратегия
Поскольку линейная скорость обод шины такой же, как и скорость автомобиля, мы имеем
v=15,0 м/с. v=15,0 м/с. размер 12 {v} {}
Радиус шины принимается равным
r=0,300 м. r=0,300 м. размер 12{r} {} Зная
vv size 12{v} {} и rr size 12{r} {}, мы можем использовать второе соотношение в v=rω, ω=vrv=rω, ω=vr size 12{v=rω,«ω= { {v} над {r} } } {} для вычисления угловой скорости.
Решение
Для расчета угловой скорости воспользуемся следующим соотношением
6.10 ω=vr.ω=vr. размер 12{ω= { {v} над {r} } «.»} {}
Подстановка известных,
6,11 ω=15,0м/с0,300м=50,0рад/с.ω=15,0м/с0. 300 м = 50,0 рад/с. размер 12{ω= {{«15» «.» 0″ м/с»} более {0 «.» «300»» м»} } =»50″ «.» 0″ рад/с.»} {}
Обсуждение
Когда мы исключаем единицы измерения в приведенном выше расчете, мы получаем 50,0/с. Но угловая скорость должна иметь единицы рад/с. Поскольку радианы на самом деле безразмерны, поскольку определяются как отношение расстояния, мы можем просто вставить их в ответ для угловой скорости. Также обратите внимание, что если бы землеройная машина с гораздо большими шинами, скажем, радиусом 1,20 м, двигалась с той же скоростью 15,0 м/с, ее шины вращались бы медленнее. Они будут иметь угловую скорость
6,12 ω=(15,0 м/с)/(1,20 м)=12,5 рад/с. ω=(15,0 м/с)/(1,20 м)=12,5 рад/с. размер 12{ω= \(«15» «.» 0`»м/с» \) / \( 1 «.» «20»`м \) =»12″ «.» 5`»рад/с.»} {}
размер 12{ω= \(«15» «.» 0`»м/с» \) / \( 1 «.» «20»`м \) =»12″ «.» 5`»рад/с.»} {}
Оба ωω размера 12{ω} {} и vv размера 12{v} {} имеют направления, следовательно, они являются угловой и линейной скоростями , соответственно. Угловая скорость имеет только два направления относительно оси вращения — либо по часовой стрелке, либо против часовой стрелки. Линейная скорость касается траектории, как показано на рис. 6.6.
Эксперимент на вынос
Привяжите предмет к концу веревки и раскачивайте его по горизонтальному кругу над головой (покачивая на запястье). Поддерживайте постоянную скорость при раскачивании объекта и измеряйте угловую скорость движения. Какова примерная скорость объекта? Определите точку рядом с вашей рукой и выполните соответствующие измерения, чтобы рассчитать линейную скорость в этой точке. Определите другие круговые движения и измерьте их угловые скорости.
Рис. 6.6 Поскольку объект движется по кругу, здесь муха на краю старомодной виниловой пластинки, ее мгновенная скорость всегда касается окружности. Направление угловой скорости в этом случае – по часовой стрелке.
Направление угловой скорости в этом случае – по часовой стрелке.
Исследования PhET: революция божьей коровки
Рисунок 6.7. Революция божьей коровки
Присоединяйтесь к божьей коровке в исследовании вращательного движения. Вращайте карусель, чтобы изменить ее угол, или выберите постоянную угловую скорость или угловое ускорение. Узнайте, как круговое движение связано с ошибкой x,y — положение, скорость и ускорение с использованием векторов или графиков.
- Печать
- Поделиться
Угловая и линейная скорость и число оборотов в минуту
Секторы, площади и задачи ArcsWord
Purplemath
По какой-то причине учебники довольно часто обращаются к вопросам угловой скорости, линейной скорости и оборотов в минуту (об/мин).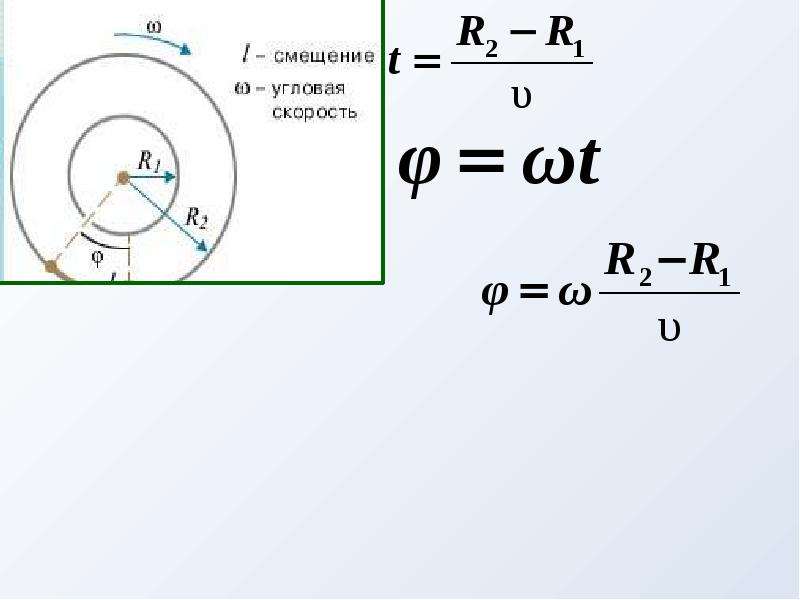 вскоре после объяснения секторов круга, их площадей и длин дуг.
вскоре после объяснения секторов круга, их площадей и длин дуг.
Длина дуги — это расстояние, пройденное частично по окружности; а линейное расстояние, пройденное, скажем, велосипедом, связано с радиусом велосипедных шин. Если вы отметите одну точку на передней шине велосипеда (скажем, место напротив вентиля шины) и подсчитаете количество оборотов колеса, вы сможете найти количество окружностей окружности, которые прошла отмеченная точка.
Содержание продолжается ниже
MathHelp.com
Если вы «развернете» эти окружности, чтобы получить прямую линию, то вы найдете расстояние, которое проехал велосипед. Я думаю, что такая связь между различными показателями является причиной того, что эта тема часто возникает на этом этапе исследований.
Во-первых, нам нужны некоторые технические термины и определения.
«Угловая скорость» является мерой поворота в единицу времени. Он говорит вам размер угла, под которым что-то вращается в данный промежуток времени. Например, если колесо вращается шестьдесят раз за одну минуту, то его угловая скорость составляет 120 π радиан в минуту. Тогда угловая скорость измеряется в радианах в секунду, в качестве ее названия часто используется строчная греческая омега (ω).
Например, если колесо вращается шестьдесят раз за одну минуту, то его угловая скорость составляет 120 π радиан в минуту. Тогда угловая скорость измеряется в радианах в секунду, в качестве ее названия часто используется строчная греческая омега (ω).
«Линейная скорость» является мерой расстояния в единицу времени. Например, если колесо в предыдущем примере имеет радиус 47 сантиметров, то каждый проход по окружности составляет 94π см, или около 295 см. Так как колесо совершает шестьдесят таких оборотов за одну минуту, то общая пройденная длина составляет 60 × 94&pi = 5640π см, или около 177 метров, за одну минуту. (Это около 10,6 км/ч, или около 6,7 миль/ч.)
«Обороты в минуту», обычно сокращенно обозначаемые как «об/мин», — это мера оборотов в единицу времени, но единицей времени является , всегда одна минута. И вместо того, чтобы указывать меру угла поворота, он просто дает количество поворотов. Когда вы смотрите на тахометр на приборной панели автомобиля, вы смотрите на текущие обороты двигателя автомобиля. В приведенном выше примере число оборотов в минуту было бы просто «60».
В приведенном выше примере число оборотов в минуту было бы просто «60».
«Частота» f — это мера вращения (или вибрации) в единицу времени, но единицей времени всегда является одна секунда. Единицей частоты является «герц», который обозначается как Гц.
Связь между частотой f (в Гц), об/мин и угловой скоростью ω (в радианах) показана ниже (все элементы в любой строке эквивалентны):
Однако вы можете обнаружить, что «угловая скорость» используется взаимозаменяемо (но только неофициально, а не учеными) с оборотами в минуту или частотой. Кроме того, некоторые (например, физики) считают, что «угловая скорость» — это векторная величина, а ω — скалярная величина, называемая «угловой частотой».
Пожалуйста, не утруждайте себя запоминанием этих возможных смешений и не беспокойтесь о том, что такое «векторы» или «скаляры». Я говорю вам об этом для того, чтобы предупредить вас, что вы должны уделять очень пристальное внимание тому, как ваш конкретный учебник и ваш конкретный преподаватель определяют различные термины для этого конкретного класса. И знайте, что на следующем уроке термины и определения вполне могут быть другими.
И знайте, что на следующем уроке термины и определения вполне могут быть другими.
Колесо диаметром 100 сантиметров. Если колесо поддерживает тележку, движущуюся со скоростью 45 километров в час, то какова скорость вращения колеса с точностью до целого числа оборотов в минуту?
«Об/мин» — это количество оборотов колеса в минуту. Чтобы вычислить, сколько раз это колесо вращается за одну минуту, мне нужно найти расстояние (по прямой или по прямой линии), пройденное (в минуту) при движении со скоростью 45 км/ч. Затем мне нужно найти окружность колеса и разделить общее расстояние в минуту (линейное) на это расстояние «один раз вокруг». Количество окружностей, вписывающихся в общее расстояние, равно количеству оборотов колеса за этот период времени.
Во-первых, я переведу (линейную) скорость тележки из километров в час в «сантиметры в минуту», используя то, что я узнал о преобразовании единиц измерения. (Почему «сантиметры в минуту»? Потому что я ищу «обороты в минуту», так что минуты — лучшая единица измерения времени, чем часы. Кроме того, диаметр дается в сантиметрах, так что это лучшая единица измерения длины, чем километры. )
(Почему «сантиметры в минуту»? Потому что я ищу «обороты в минуту», так что минуты — лучшая единица измерения времени, чем часы. Кроме того, диаметр дается в сантиметрах, так что это лучшая единица измерения длины, чем километры. )
Таким образом, расстояние, пройденное за одну минуту, равно 75 000 сантиметров. Диаметр колеса 100 см, поэтому радиус равен 50 см, а длина окружности 100π см. Сколько из этих окружностей (или оборотов колеса) умещается в пределах 75 000 см? Другими словами, если бы я снял гусеницу этого колеса с тележки и разложил ее горизонтально, расстояние до нее составило бы 100π см. Сколько из этих длин укладывается во все расстояние, пройденное за одну минуту? Чтобы узнать, сколько (этого) вписывается в столько-то (того), я должен разделить (это) на (это), так что:
Тогда, округляя до ближайшего целого оборота (то есть округляя ответ до целого числа), мой ответ:
239 об/мин
Примечание: Эта скорость не так высока, как может показаться: она чуть ниже четыре оборота в секунду. Вы можете сделать это на своем велосипеде, не вспотев. Вот еще одно примечание: источник, из которого я получил свою структуру для вышеупомянутого упражнения, использовал «угловую скорость» и «ω» для «количества оборотов в минуту». Да, в учебнике по алгебре использовались неправильные единицы измерения.
Вы можете сделать это на своем велосипеде, не вспотев. Вот еще одно примечание: источник, из которого я получил свою структуру для вышеупомянутого упражнения, использовал «угловую скорость» и «ω» для «количества оборотов в минуту». Да, в учебнике по алгебре использовались неправильные единицы измерения.
Предыдущее упражнение дало скорость автомобиля и информацию о колесе. Отсюда мы нашли число оборотов в минуту. Мы можем пойти и другим путем; мы можем начать с оборотов в минуту (плюс информация о колесе) и найти скорость автомобиля.
Велосипедное колесо имеет диаметр 78 см. Если колесо вращается со скоростью 120 оборотов в минуту, какова линейная скорость велосипеда в километрах в час? Округлите ответ до одного десятичного знака.
Линейная скорость — это расстояние по прямой, которое велосипед проходит за определенный период времени. Они дали мне количество оборотов колеса в минуту. Неподвижная точка на шине (скажем, камешек в протекторе шины) перемещается на длину окружности за каждый оборот. Развернув это расстояние на землю, велосипед будет двигаться по земле на такое же расстояние, по одной окружности за каждый оборот. Итак, этот вопрос просит меня найти длину окружности, а затем использовать ее, чтобы найти общее расстояние, пройденное за минуту.
Неподвижная точка на шине (скажем, камешек в протекторе шины) перемещается на длину окружности за каждый оборот. Развернув это расстояние на землю, велосипед будет двигаться по земле на такое же расстояние, по одной окружности за каждый оборот. Итак, этот вопрос просит меня найти длину окружности, а затем использовать ее, чтобы найти общее расстояние, пройденное за минуту.
Так как диаметр равен 78 см, то длина окружности равна C = 78π см. Раскручивая путь шины по прямой линии на земле, это означает, что велосипед перемещается на 78π см вперед за каждый оборот шины. Таких оборотов в минуту 120, поэтому:
(78π см/об) × (120 об/мин) = 9360π см/мин
Теперь мне нужно преобразовать это из сантиметров в минуту в километры в минуту. час:
Велосипед движется со скоростью около 17,6 км/ч.
…или примерно одиннадцать миль в час.
Предположим, что орбита Земли круговая с радиусом 93 000 000 миль, и пусть «один год» равен 365,25 дня.
 В этих условиях найти линейную скорость Земли в милях в секунду. Округлите ответ до одного десятичного знака.
В этих условиях найти линейную скорость Земли в милях в секунду. Округлите ответ до одного десятичного знака.
Скорость будет равна (линейному или эквивалентному прямолинейному) расстоянию, пройденному за одну секунду, деленному на одну секунду. Они дали мне информацию за один год, так что я начну оттуда. Окружность круга с r = 93 000 000 миль будет линейным расстоянием, которое Земля проходит за один год.
C = 2π (93 000 000 миль)/год = 186 000 000π миль/год
Это количество миль, пройденных за один год, но мне нужно количество миль, пройденных всего за одну секунду. В сутках двадцать четыре часа, в часе шестьдесят минут, а в минуте шестьдесят секунд, поэтому общее количество секунд в этом году равно:
Тогда линейная скорость, равная общему линейному расстоянию, деленному на общее время и выраженное в единицах скорости, составляет:
Тогда, округлив до одного десятичного знака, линейная скорость Земли составит:
18,5 миль в секунду
«Эй!» Я слышу, как ты плачешь. «Когда мы собираемся использовать угловые меры для чего-либо?» Хотя многие («большинство»?) упражнений в вашей книге, вероятно, будут похожи на приведенные выше, иногда вы можете столкнуться с реальными радианами и градусами.
«Когда мы собираемся использовать угловые меры для чего-либо?» Хотя многие («большинство»?) упражнений в вашей книге, вероятно, будут похожи на приведенные выше, иногда вы можете столкнуться с реальными радианами и градусами.
«Кривая радиусом 3000 футов» означает, что если бы я попытался вписать окружность внутри кривой, лучше всего вписался бы окружность с радиусом r = 3000 футов. Другими словами, я могу использовать круговые факты, чтобы ответить на этот вопрос.
Поскольку радиус кривой измеряется в футах и мне нужно найти угол, пройденный за одну минуту, я начну с преобразования скорости в милях в час в футы в секунду:
(10 миль /ч)(5280 футов/миль)(1 час/60 мин) = 880 футов/мин
Длина изогнутого пути, который проходит поезд, также является частью окружности круга. Итак, эти 880 футов — это длина дуги, и теперь мне нужно найти стягиваемый угол (подразумеваемого) сектора круга:
Но это значение в радианах (поскольку это то, что использует формула длины дуги), и мне нужно, чтобы мой ответ был в градусах, поэтому мне нужно преобразовать:
Поезд поворачивает на угол примерно:
17 °
Представьте, что вы стоите в центре этого воображаемого круга (то есть в трех тысячах футов от кривой, более чем в полумиле) и смотрите, как поезд движется по кривой.
 В этих условиях найти линейную скорость Земли в милях в секунду. Округлите ответ до одного десятичного знака.
В этих условиях найти линейную скорость Земли в милях в секунду. Округлите ответ до одного десятичного знака.