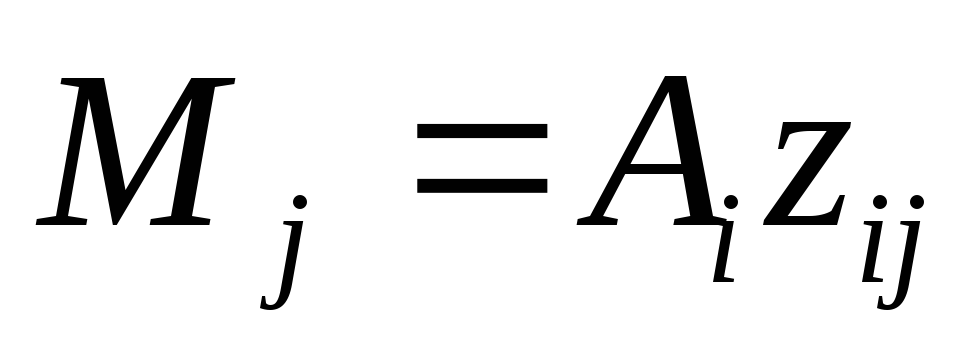Содержание
2.2.4. Коэффициент тяги
Задается
соотношением
.
Коэффициент
тяги показывает увеличение тяги двигателя
вследствие наличия сопла. Иногда КТ
называют
безразмерной тягой. Теоретическое
значение КТ
рассчитывается по полученному из формулы
тяги выражению
.
(2.9)
Условно
коэффициент тяги можно представить в
виде
,
где
— коэффициент прироста тяги за счет
дозвуковой части сопла;
—
коэффициент
прироста тяги за счет сверхзвуковой
части сопла. При
γ=1.15
и
=
1 (сопло без сверхзвуковой части) КТ
имеет
значение КТ
= 1.235.
При наличии сверхзвуковой части сопла
со степенью расширения
= 6.5
(стандартные условия: рк
=4МПа, ра
=0. 1МПа) КТ
1МПа) КТ
имеет значение КТ
=
1.709, что означает увеличение тяги на
70.9%, из которых на сверхзвуковую часть
сопла приходится 47.4%. В пределе, когда
→∞,
получается KTMAX
=
2,9 для
=1,1.
Для
анализа удобнее использовать коэффициент
тяги в пустоте
.
Расчетное
выражение для КТП
получается
из (2.9)
при pн
=0
(2.10)
Очевидно,
что КТП
не
зависит ни от работы камеры сгорания,
ни от внешних условий (рн)
и
является характеристикой, определяющей
только работу сопла камеры.
Коэффициенты
КТ
и
КТП
связаны
между собой зависимостью
В
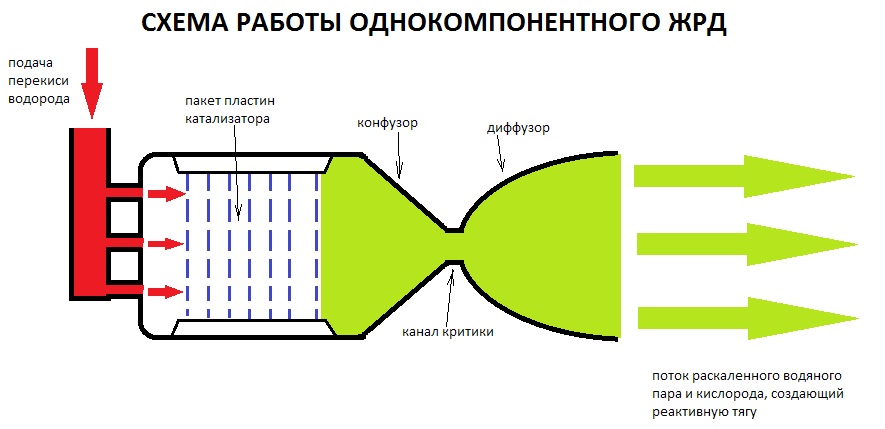
заключение следует отметить, что для
определения
и
,
можно
использовать следующие выражения:
.
Также:
2.2.5. Геометрическая степень расширения сопла
Эта
величина не только определяет размеры
сопла, но и характеризует основные
параметры работы сопла:
(или скорость
).
Связь между основными параметрами
определяется известными из газовой
динамики соотношениями:
Таким
образом, РД
имеет 5 основных показателей,
нужных для создания ракеты:
тяга,
импульс
тяги
,
удельный
импульс тяги
,
расходный
комплекс
,
коэффициент
тяги
.
2.2.6. Удельная масса ракетного двигателя
Также
существует такой важный для любой
подсистемы ЛА показатель, как масса
конструкции РД.
Удельной массой двигателя называют
отношение его массы в рабочем состоянии
к развиваемой наибольшей тяге на основном
режиме работы. Это определение справедливо
только для ЖРД, так как массу РДТТ трудно
отделить от массы ракеты.
Рабочим
считают состояние ЖРД, при котором
магистрали и агрегаты двигателя заполнены
компонентами топлива, и масса двигателя
составляет МД.
По определению
,кг/Н.
У
лучших ЖРД с тягой Р > 1000 кН
значение
удельной массы может составлять 0,8 кг/кН
—
на 1 кг массы РД
развивается
усилие более 1000 Н!
Массовое
совершенство РДДТ характеризуют
коэффициентом качества
,
показывающим отношение массы конструкции
двигателя к
массе
топлива. Для лучших РДТТ значение
коэффициента массового совершенства
не превышает 0.07, а коэффициент объемного
заполнения корпуса двигателя
.
2. Генерация рабочего тела
ЛЕКЦИЯ
3
3.1. Оценка эффективности ракетного двигателя
Очевидно,
что эффективность РД можно оценивать
только с позиций ЛА, т.е. критерии качества
РД должны вытекать из целей ЛА как
объекта высшего уровня иерархии.
Из курса ОУЛА известно, что критерием
эффективности УБР является конечная
скорость
ступени или Л А в момент окончания
активного участка: чем больше значение
,
тем больше будет дальность полета при
фиксированной полезной нагрузке.
Идеальное значение конечной скорости
в конце активного участка полета
(действует только сила тяги ДУ, нет
атмосферы и поля тяготения Земли)
определяет формула К.Э.Циолковского:
, (3.1)
где
— массовое
число;
—
конечная
масса в момент окончания АУТ;
—
соответственно
массы топлива, конструкции ракеты и
полезной нагрузки;
—
эффективная скорость истечения рабочего
тела.
Отсюда
ясно, что необходимо увеличивать значение
удельного импульса
(),
увеличивать
мaccу
топлива на борту и снижать массу
конструкции двигательной установки.
Создавать
двигатели сложно, но сущест-вует
экзогенность целей, т.е. их наперед
ясность разработчикам.
Из
(3.1)
следует,
что конечная скорость линейно зависит
от удельного импульса при постоянном
массовом числе
.
Неизбежные потери скорости на преодоление
силы тяжести, сопротивление атмосферы
и противодавление атмосферы (уменьшение
удельного импульса) при вариации
удельного импульса в связи с рассмотрением
различных топлив меняются по разному
в зависимости от ограничений по нагрузке
на тягу, массу топлива, и собственно
тягу. Влияние удельного импульса
Влияние удельного импульса
возрастает с увеличением
дальности полета. Для УБР с дальностью
12 000 км и удельным импульсом в пустоте
2500 м/с увеличение
на
1% приводит к росту дальности на 600 км.
Для УБР средней
дальности (L=2500
км) с тем же значением удельного импульса
увеличение
на
1% приводит к росту дальности всего на
70 км.
Степень
влияния массы конструкции двигательной
установки на конечную скорость ЛА
зависит от того, на какой ступени он
установлен. Для первой ступени масса
ракеты существенно больше массы
конструкции ДУ и поэтому влияние
изменения массы конструкции ДУ на
конечную
скорость последней ступени незначительно.
А масса конструкции двигателя последней
ступени вносит свой вклад в значения
и
оказывает существенное влияние на
конечную
скорость
ЛА.
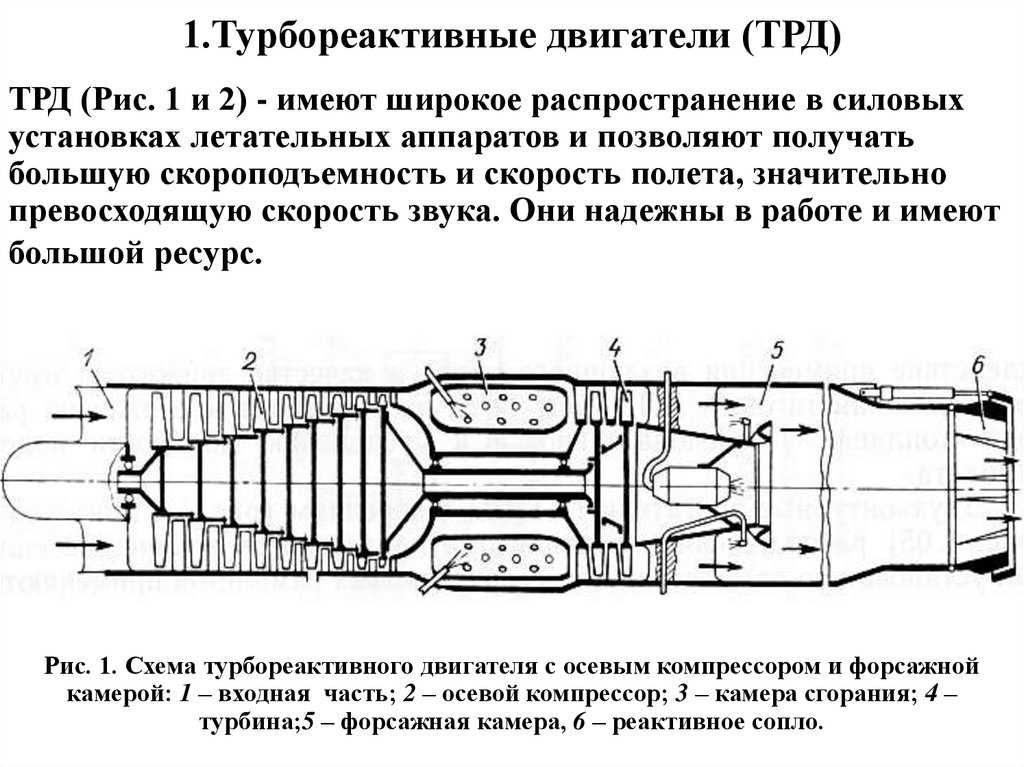
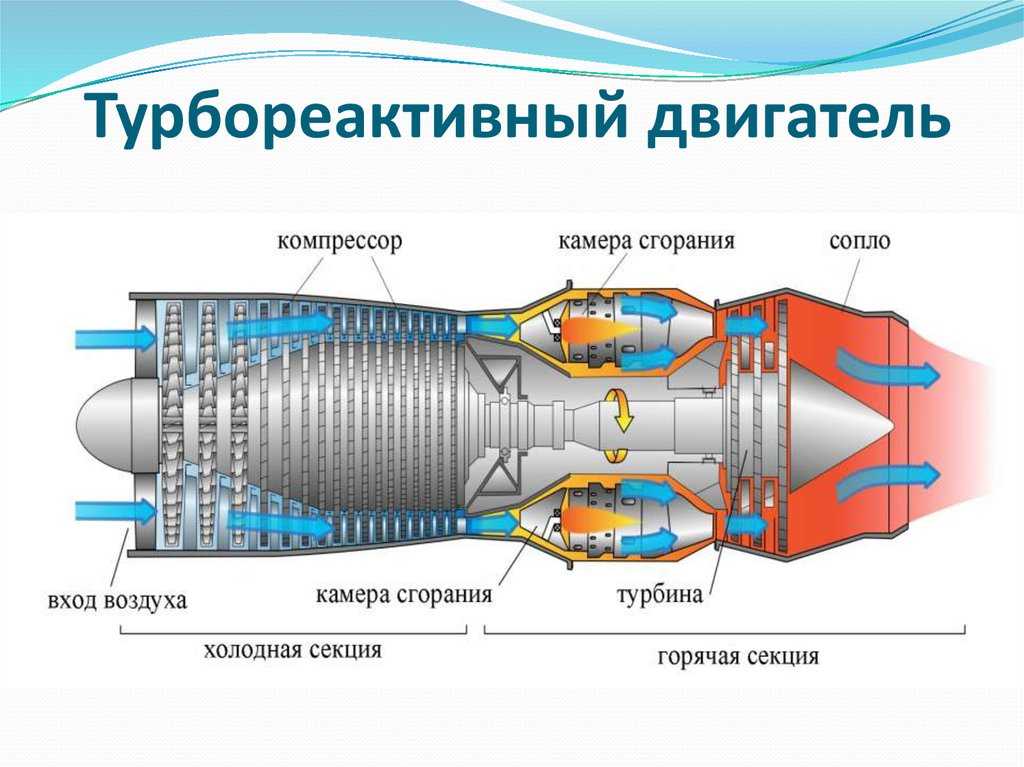
Реактивная тяга или как устроен ионный реактивный двигатель / Habr
Не секрет, что все реактивные двигатели работают за счёт закона сохранения импульса. Именно из него вытекает, что реактивная тяга — это произведение массового расхода на скорость выхода рабочего тела из сопла.
Эту скорость принято называть удельным импульсом реактивного двигателя. Давайте для примера найдём реактивную тягу при стрельбе из автомата Калашникова, которая является основной составляющей отдачи. Пусть масса пули будет 0,016 кг, начальная скорость пули 700 м/с, а скорострельность 10 выстр./с. Тогда отдача F=700∙0,016∙10=112 Н (или 11 кгс). Большая отдача, но тут приведена техническая скорострельность 600 выстр./мин. В реальности стрельба ведётся очередями или одиночными и составляет ≈50 выстр./мин.
Выстрел из АК
Вернёмся к реальным реактивным двигателям, в которых вместо пуль обычно используются потоки выходящего с гиперзвуковой скоростью газа. Химические реактивные двигатели являются самыми распространёнными, но не единственными.
В этой статье, с большим предисловием, я хочу рассказать об ионных реактивных двигателях (далее ИРД). ИРД используют в качестве рабочего тела заряженные частицы — ионы.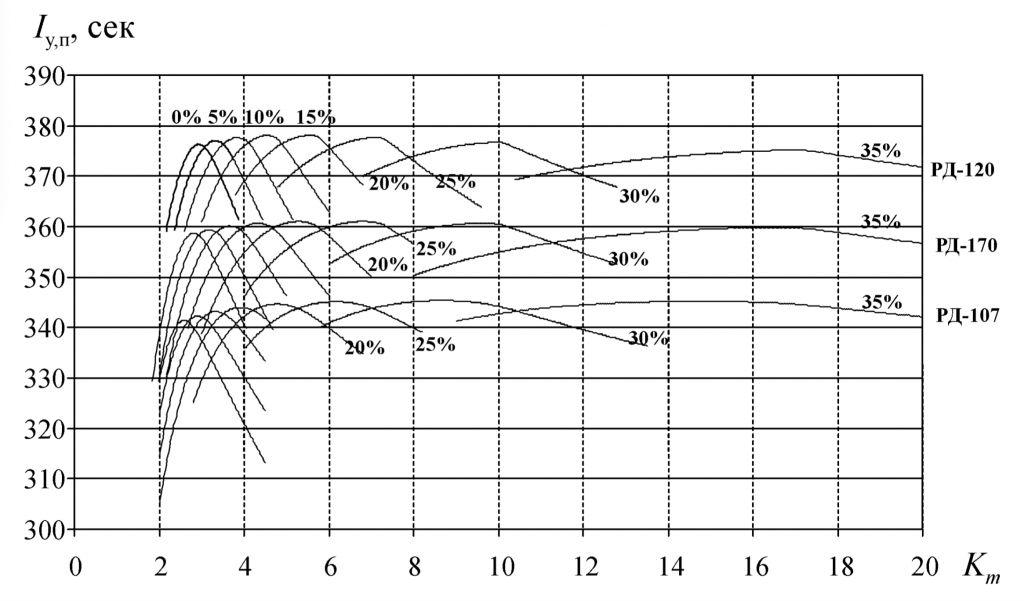 Ионы имеют массу, и если их разогнать электрическим полем, то можно создать реактивную тягу. Это всё в теории, а теперь подробнее. ИРД имеет некоторый запас газа, который ионизируют (т.е. нейтрально-заряженные атомы газа разбивают на отрицательные электроны и положительные ионы) с помощью газового разряда. Далее ионы разгоняются электрическим полем с помощью специальной системы сеток, и эта же система сеток блокирует движение электронов. После того, как положительные ионы вылетели из сопла, их нейтрализуют отрицательными электронами (в результате этого происходит рекомбинация и газ начинает светиться), чтобы ионы не притягивались обратно к двигателю, и тем самым не снижали его тяги.
Ионы имеют массу, и если их разогнать электрическим полем, то можно создать реактивную тягу. Это всё в теории, а теперь подробнее. ИРД имеет некоторый запас газа, который ионизируют (т.е. нейтрально-заряженные атомы газа разбивают на отрицательные электроны и положительные ионы) с помощью газового разряда. Далее ионы разгоняются электрическим полем с помощью специальной системы сеток, и эта же система сеток блокирует движение электронов. После того, как положительные ионы вылетели из сопла, их нейтрализуют отрицательными электронами (в результате этого происходит рекомбинация и газ начинает светиться), чтобы ионы не притягивались обратно к двигателю, и тем самым не снижали его тяги.
Почему ксенон?
Обычно в ИРД в качестве рабочего тела используется газ ксенон, так как он имеет наименьшую энергию ионизации среди инертных газов.
Удельный импульс ионных реактивных двигателей достигает 50 км/с, что в 150 раз превышает скорость звука! Увы, но тяга таких двигателей составляет около 0,2 Н. Почему же так? Ведь удельный импульс очень большой. Дело в том, что масса ионов очень маленькая и массовый расход получается небольшим. Для чего тогда такие двигатели нужны, если они ничего не смогут сдвинуть с места? На Земле может быть не смогут, а вот в космосе, где нет сил сопротивления, они достаточно эффективные. Существует такое понятие как полный импульс — произведение тяги на время или произведение удельного импульса на массу топлива, который у ИРД является достаточно большим.
Почему же так? Ведь удельный импульс очень большой. Дело в том, что масса ионов очень маленькая и массовый расход получается небольшим. Для чего тогда такие двигатели нужны, если они ничего не смогут сдвинуть с места? На Земле может быть не смогут, а вот в космосе, где нет сил сопротивления, они достаточно эффективные. Существует такое понятие как полный импульс — произведение тяги на время или произведение удельного импульса на массу топлива, который у ИРД является достаточно большим.
Решим следующую задачу. Пусть жидкостный ракетный двигатель имеет удельный импульс 5 км/с, а у нашего ИРД он будет 50 км/с. И давайте масса рабочего тела (в ЖРД она равна массе топлива) у обоих двигателей будет 50 кг. Примем массу космического аппарата равной 100 кг.
Найдём по формуле Циолковского конечную скорость аппарата (т.е. когда в нём закончится рабочая масса).
И что получается, если ионный и химический реактивные двигатели будут иметь одинаковую массу топлива, то ИРД сможет разогнать космический аппарат до больших скоростей, нежели химический РД.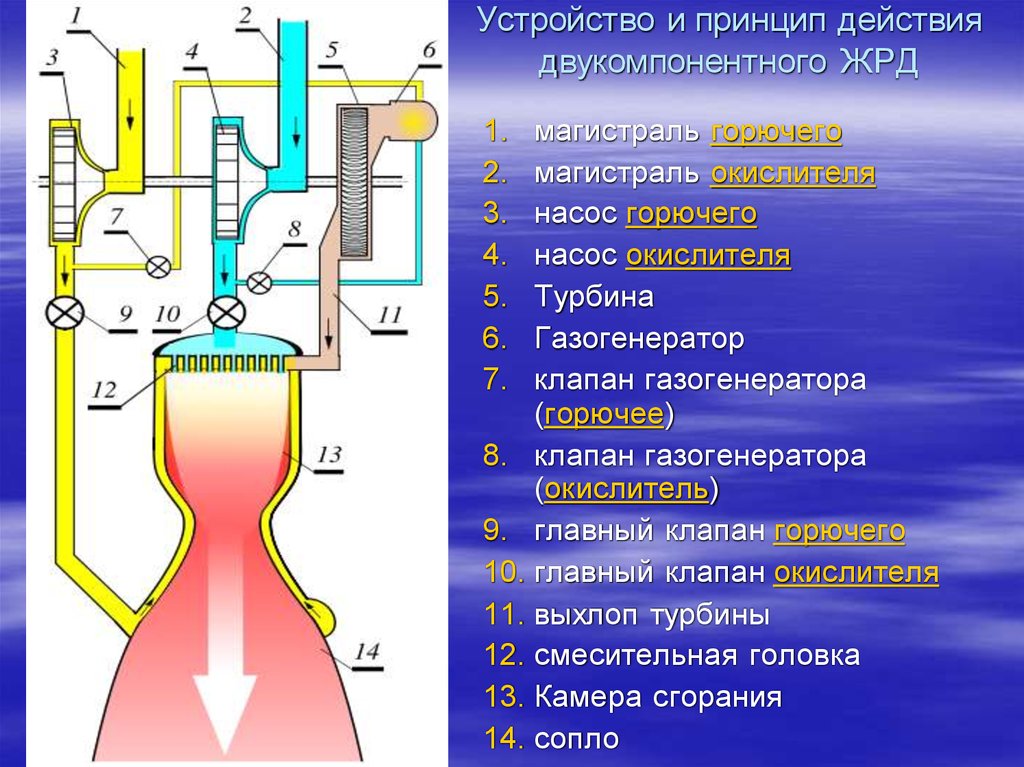 -16 Кл.
-16 Кл.
Напряжение — это работа по переносу заряда, т.е. на выходе из сопла ион будет иметь кинетическую энергию равную произведению напряжения на заряд иона. Из кинетической энергии выражаем скорость (удельный импульс). Найдём массовый расход из определения тока, электрический ток — это проходящий заряд во времени. Получается, что массовый расход — это произведение массы иона и тока, делённое на заряд иона. Перемножая удельный импульс и массовый расход, получаем тягу равную 0,1 Н.
Подводя итог, хочу сказать, что существуют плазменные реактивные двигатели, у которых схожее устройство, но которые имеют намного больший массовый расход рабочего тела. Кто знает, может быть уже завтра на таких двигателях человечество будет летать на Марс и Луну.
Раздел 3.3 — Ракетная тяга
‹ Предыдущий раздел Следующий раздел ›
‹‹ Предыдущий раздел Следующий раздел ››
Уравнение реактивной тяги
Тяга ракеты может быть рассчитана по следующей формуле:
$T = {\dot m}V_e + (p_e — p_a)A_e$
$T = $ тяга
${\dot m} = $ массовый расход
$V_e = $скорость выхлопа
$p_e = $ давление выхлопа на выходе из сопла
$p_a = $ давление окружающей среды на выходе из сопла
$A_e = $область выхода сопла
Обратите внимание, что справа от знака равенства есть два члена: ${\dot m}V_e$ и $(p_e — p_a)A_e$.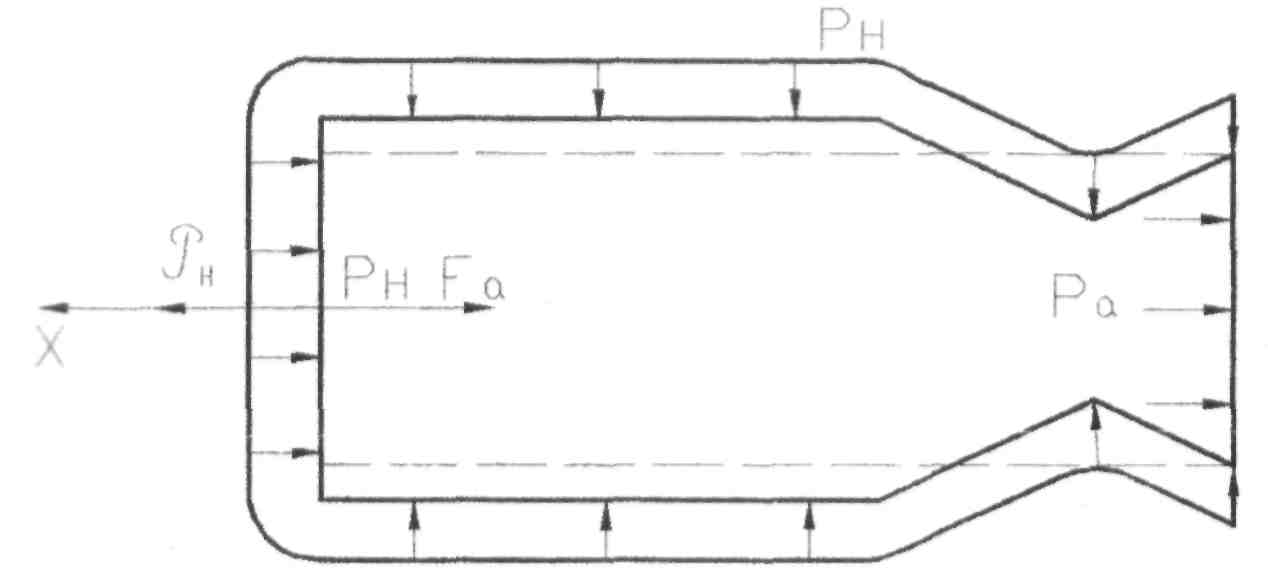 По сути, это говорит нам о том, что тяга создается двумя факторами
По сути, это говорит нам о том, что тяга создается двумя факторами
- Импульсом, создаваемым выхлопом, выходящим из сопла (который намного больше по величине)
- Разность давлений между выхлопом и атмосферным давлением в районе сопла. Думайте об этом как о естественной диффузии газа из области высокого давления в область низкого давления, немного увеличивая тягу 92$. Кроме того, проблема говорит нам, что двигатель работает в вакууме, поэтому $p_a = 0$
.
Оптимальное давление выхлопаИсходя из уравнения тяги ракеты, у нас может возникнуть соблазн сделать $p_e$ как можно большим по отношению к $p_a$, чтобы выжать некоторую дополнительную тягу. На самом деле инженеры хотят, чтобы давление выхлопных газов было равно давлению окружающей среды ($p_e = p_a$) для оптимальной эффективности. Почему? Рассмотрим варианты:
Слева: недорасширенный | Центр: Оптимизировано | Справа: перерасширено - Недорасширенное сопло ($p_e > p_a$): это сопло не так эффективно, как могло бы быть, потому что часть выхлопных газов направлена под углом, а не прямо вниз
- Перерасширенная форсунка ($p_e < p_a$): эта форсунка опасна, поскольку в обведенных местах может произойти отрыв потока и вызвать разрушительные вибрации, которые могут привести к разрушению конструкции
Итак, мы решили попробовать установить $p_e = p_a$.
 Вот в чем проблема: давление окружающей среды постоянно меняется (давление уменьшается по мере того, как ракета достигает все большей и большей высоты), поэтому невозможно всегда соответствовать $p_a$. Лучшее, что мы можем сделать, это найти золотую середину: сопло ракеты должно быть слегка расширено на уровне моря, а по мере подъема оно будет становиться все более и более недорасширенным и терять эффективность. Постановка ракеты также может помочь решить эту проблему, так как каждая ступень имеет свой набор ракетных двигателей, которые можно оптимизировать для разных высот (подробнее о постановке позже) 9.0004
Вот в чем проблема: давление окружающей среды постоянно меняется (давление уменьшается по мере того, как ракета достигает все большей и большей высоты), поэтому невозможно всегда соответствовать $p_a$. Лучшее, что мы можем сделать, это найти золотую середину: сопло ракеты должно быть слегка расширено на уровне моря, а по мере подъема оно будет становиться все более и более недорасширенным и терять эффективность. Постановка ракеты также может помочь решить эту проблему, так как каждая ступень имеет свой набор ракетных двигателей, которые можно оптимизировать для разных высот (подробнее о постановке позже) 9.0004Для получения дополнительной информации о конструкции ракетных двигателей и других темах ракетостроения этот веб-сайт, безусловно, лучший из тех, что я нашел для не-инженеров, которым все же нужны технические знания: http://www.
 braeunig.us/space/. Более технический, чем то, что у меня есть здесь, но определенно стоит попробовать!
braeunig.us/space/. Более технический, чем то, что у меня есть здесь, но определенно стоит попробовать!‹ Предыдущий раздел Следующий раздел ›
‹‹ Предыдущий блок Следующий блок ››
Калькулятор реактивной тяги
Создано Davide Borchia
Последнее обновление: 08 сентября 2022 г.
Содержание:
- …ракетостроение! Физика работы ракеты и уравнение ракетной тяги.
- Уравнение тяги ракеты
- Влияние изменения массы в формуле тяги ракеты
- Давление в уравнении тяги ракеты
- Использование уравнения тяги ракеты: пример из жизни
Ракеты двигали нас до звезды — почти: с нашим инструментом вы научитесь рассчитывать тягу ракеты. Вы познакомитесь с уравнением, узнаете, как рассчитать тягу ракеты и ее элемента, важность давления, массы и скорости на характеристики ракеты, а также пример применения уравнения тяги ракеты. Вскоре вы окажетесь на стартовой площадке для своего путешествия в области ракетостроения! Ведь это же.
 ..
..… ракетостроение! Физика работы ракеты и уравнение ракетной тяги.
Человечество использует ракеты примерно с XVI века: рудиментарное самоходное оружие, но со всем, что заставляет вас идентифицировать их как ракеты. Только в конце XIX века мы получили математическое описание принципов их работы, а еще позже — твердое понимание, которое позволило нам отправлять людей на орбиту и дальше.
Ракеты концептуально просты: их действие полностью зависит от Третий закон движения Ньютона . По закону силы всегда парные: на каждую силу можно найти другую с такой же величиной и противоположным направлением. Ракета выбрасывает свой выхлоп с заданной силой сзади; следовательно, ракета испытывает движение вперед 90 108, движущую силу 90 109 .
Уравнение тяги ракеты
Формула тяги ракеты учитывает множество фундаментальных факторов, влияющих на характеристики ракеты. Давайте сначала посмотрим уравнение для тяги ракеты, а затем проанализируем его составляющие.

F=dmdt⋅ve+A⋅(Pe−Pamb)F = \frac{\text{d}m}{\text{d}t}\cdot v_{\text{e}}+A\cdot( P_{\text{e}}-P_{\text{amb}})F=dtdm⋅ve+A⋅(Pe–Pamb)
Где:
- FFF — расчетная тяга ракеты ;
- dm/dt\text{d}m/\text{d}tdm/dt — изменение массы ракеты во времени ;
- VeV _{\text{e}}Ve — скорость выхлопа в сопле ;
- AAA — Зона форсунки ;
- PeP _ {\ text {e}} Pe — статическое давление на выхлопе ракеты ; и
- PambP _{\text{amb}}Pamb — давление среды, в которой движется ракета .
🙋 Давление часто измеряют в мегапаскалях , хотя для этой величины существует много разных единиц измерения: научитесь переключаться между ними с помощью нашего конвертера давления!
Уравнение тяги ракеты не простое: здесь играет роль множество переменных с разными ролями и эффектами.
Уравнение тяги ракеты теоретически можно использовать для расчета ускорения ракеты с использованием второго закона Ньютона.
 Однако, поскольку масса ракеты уменьшается, нам нужно рассуждать несколько иначе.
Однако, поскольку масса ракеты уменьшается, нам нужно рассуждать несколько иначе.Влияние изменения массы в формуле тяги ракеты
Ракета становится легче по мере подъема: эта особенность является фундаментальной при расчетах уравнения тяги ракеты, и мы подробно говорили о ней в нашей калькулятор уравнения ракеты.
В формулу тяги ракеты, которую мы использовали в нашем инструменте, вы можете либо вставить скорость потери массы , либо рассчитать это значение по изменению массы за заданный промежуток времени.
Давление в уравнении тяги ракеты
Ракета — это мощная машина, способная подниматься от уровня моря до глубины космоса. Хотя история более сложная, в целом верно то, что ракеты спроектированы так, чтобы работать при различных давлениях. Вот причина существования член давления в уравнении тяги ракеты.
Умножаем разницу между давлением внутри сопла и давлением окружающей среды на поверхность сопла: граница между ракетой и внешним миром.
 Чем выше перепад давления, тем выше тяга: ракеты более эффективны на больших высотах.
Чем выше перепад давления, тем выше тяга: ракеты более эффективны на больших высотах.Использование уравнения тяги ракеты: пример из жизни
Выберите свою ракету — мы выбрали Delta IV тяжелая ракета — и следуйте дальнейшим шагам!
- Соберите данные для уравнения тяги ракеты:
- Изменение массы: dm=200 400 кг\text{d}m =200 400\ \text{kg}dm=200 400 кг в dt=328 s\text{d}t = 328\ \text{s}dt=328 s ;
- Скорость истечения: ve=5 130 м/с _{\text{e}} = 5 130\ \text{м}/\text{s}ve=5 130 м/с
- Давление в сопле: Pe=10,26 МПаP_{\text{e}} = 10,26\ \text{МПа}Pe=10,26 МПа;
- Давление окружающей среды зависит от высоты. Проверим уравнение тяги ракеты при давлении на уровне моря: Pamb=0,1012 MPaP_{\text{amb}} = 0,1012\ \text{MPa}Pamb=0,1012 MPa; 92\!\cdot\!(10,26-0,1012)\ \text{МПа}\\
&\!=3,137\ \text{кН}
\end{align*}F=dtdm⋅ve+A⋅(Pe−Pamb)=328 с200 400 кг⋅5,13 см+4,68 м2⋅(10,26-0,1012) МПа=3,137 кНРС-68А имеет одну из самых высоких тяг в мире.

 Вот в чем проблема: давление окружающей среды постоянно меняется (давление уменьшается по мере того, как ракета достигает все большей и большей высоты), поэтому невозможно всегда соответствовать $p_a$. Лучшее, что мы можем сделать, это найти золотую середину: сопло ракеты должно быть слегка расширено на уровне моря, а по мере подъема оно будет становиться все более и более недорасширенным и терять эффективность. Постановка ракеты также может помочь решить эту проблему, так как каждая ступень имеет свой набор ракетных двигателей, которые можно оптимизировать для разных высот (подробнее о постановке позже) 9.0004
Вот в чем проблема: давление окружающей среды постоянно меняется (давление уменьшается по мере того, как ракета достигает все большей и большей высоты), поэтому невозможно всегда соответствовать $p_a$. Лучшее, что мы можем сделать, это найти золотую середину: сопло ракеты должно быть слегка расширено на уровне моря, а по мере подъема оно будет становиться все более и более недорасширенным и терять эффективность. Постановка ракеты также может помочь решить эту проблему, так как каждая ступень имеет свой набор ракетных двигателей, которые можно оптимизировать для разных высот (подробнее о постановке позже) 9.0004 braeunig.us/space/. Более технический, чем то, что у меня есть здесь, но определенно стоит попробовать!
braeunig.us/space/. Более технический, чем то, что у меня есть здесь, но определенно стоит попробовать! ..
..
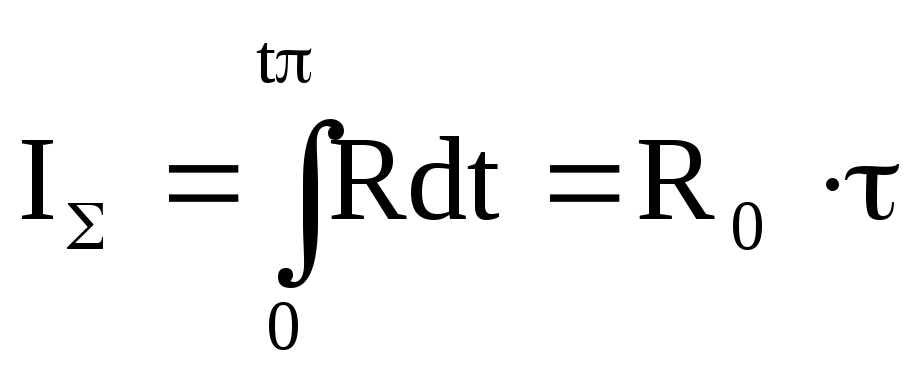 Однако, поскольку масса ракеты уменьшается, нам нужно рассуждать несколько иначе.
Однако, поскольку масса ракеты уменьшается, нам нужно рассуждать несколько иначе. Чем выше перепад давления, тем выше тяга: ракеты более эффективны на больших высотах.
Чем выше перепад давления, тем выше тяга: ракеты более эффективны на больших высотах.