\circ\) C, \(T_2-?\)

Решение задачи:

Для начала запишем уравнение Клапейрона (объединённый газовый закон) для начального и конечного состояния воздуха в сосуде:

\[\frac{{{p_1}{V_1}}}{{{T_1}}} = \frac{{{p_2}{V_2}}}{{{T_2}}}\]

Выразим из уравнения конечную температуру \(T_2\):

\[{T_2} = {T_1}\frac{{{p_2}{V_2}}}{{{p_1}{V_1}}}\;\;\;\;(1)\]

Объем, занимаемый газом в каждом состоянии, можно найти как произведение площади основания \(S\) на высоту, на которой находится поршень, поэтому:

\[\left\{ \begin{gathered}
{V_1} = Sh \hfill \\
{V_2} = S\left( {h – \Delta h} \right) \hfill \\
\end{gathered} \right.\]

Теперь разберемся с давлением. Запишем условие равновесия поршня (первый закон Ньютона) при начальном и конечном состоянии газа:

\[\left\{ \begin{gathered}
{p_1}S = {p_0}S + {m_п}g \hfill \\
{p_2}S = {p_0}S + {m_п}g + mg \hfill \\
\end{gathered} \right.\]

Здесь \(m_п\) – масса поршня, \(p_0\) – атмосферное давление. \circ\;C \]

Ответ: 67,87° C.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

4.2.99 Воздушный шар объемом 1000 м3 наполнен гелием при температуре окружающего воздуха
4.2.101 В сосуд, на дне которого лежит твердый шар, нагнетают воздух при температуре 27 C
4.2.102 В закрытом с обоих концов цилиндре длиной 2 м поршень соединён с днищами пружинами

34. Влажность: задачи по физике с ответами без решений

(Все задачи по молекулярно-кинетической теории и ответы к ним находятся в zip-архиве (290 кб), который можно скачать и открыть на своем компьютере. Попробуйте решить задачи самостоятельно и только потом сравнивать свои ответы с нашими. Желаем успехов!)

34.1.   Температура воздуха 18° С, а его точка росы 10° С. Найти относительную влажность при 18° С. Плотность насыщенного водяного пара при 18° С равна 15,4 г/м³, а при 10° С — 9,4 г/м³.   [60 %]

34.2.   При температуре 25° С относительная влажность воздуха равна 70 %. Сколько влаги выделится из каждого м³ при понижении температуры до 16° С? Плотность насыщенного пара при 25° С равна 23 г/м³, при 16° С — 13,6 г/см³.   [2,5 г/см³]

34.3.   В закрытом сосуде находится воздух при температуре 100° С и относительной влажности 3,5 %. Какой станет относительная влажность воздуха, если сосуд остудить до температуры 29 С? Давление насыщенного пара при 29° С равно 30 мм рт. ст.   [72 %]

34.4.   Какое количество воды может испариться в помещении размером 10 × 8 × 4,5 м³, если температура воздуха 22° С, а относительная влажность 70%. Плотность насыщенного пара при 22° С равна 19,4 г/м³.   [2,1 кг]

34.5.   В помещение нужно подать V = 20000 м³ воздуха при температуре t₁ = 18° С и относительной влажности φ₁ = 50 %. Воздух забирается с улицы, где температура t₂ = 10° С, а влажность φ₂ = 60%. Сколько воды нужно дополнительно испарить? Плотность насыщенного пара при 18° С равна 15,4 г/м³, а при 10° С — 9,4 г/м³.   [41,2 кг]

34.6.   В закрытом сосуде объёмом V = 1,1 л находится m = 100 г воды и пар при температуре t = 100° С. Воздуха в сосуде нет. Найти массу пара в сосуде.   [0,6 г]

34.7.   В закрытом горизонтальном цилиндре объёмом V = 2 л находится подвижный поршень. В цилиндр вводится с одной стороны m₁ = 2 г воды, а с другой — m₂ = 1 г азота. Какую часть объёма цилиндра будет занимать азот при температуре t = 100° С.   [ ≅ 0.55 ]

34.8.   При температуре t = 20° С и давлении p = 10⁵ Па воздух имеет влажность 100 %. На сколько процентов он легче сухого воздуха при тех же температуре и давлении? Давление насыщенного пара при 20° С равно p_н = 2330 Па.   [ ≅ 0.88% ]

34.9.   В сосуде объёмом V = 0,4 л находится пар при давлении p = 60 мм рт. ст. и температуре t₁ = 150° С. Какое количество росы выделится при охлаждении сосуда до температуры t₂ = 22° С? Давление насыщенного пара при 22° С равно p_н = 19 мм рт. ст.   [ ≅ 8.9×10⁻³ г ]

34.10.   Смешали V₁ = 1 м³ воздуха с влажностью φ₁ = 20% и V₂ = 2 м³ воздуха с влажностью φ₂ = 30 %. Температура одинакова, объём смеси V = 3 м³. Определить относительную влажность смеси.   [ ≅ 27% ]

34.11.   В цилиндре под поршнем находится воздух при температуре t₁ = 100° C с относительной влажностью φ = 40 %. Объём воздуха при этом V₁ = 100 см³. Цилиндр охлаждается до температуры t₂ = 20° С. На сколько надо изменить объём воздуха, чтобы не выпала роса? Давление насыщенного пара при 20° С равно p_н = 17,5 мм рт.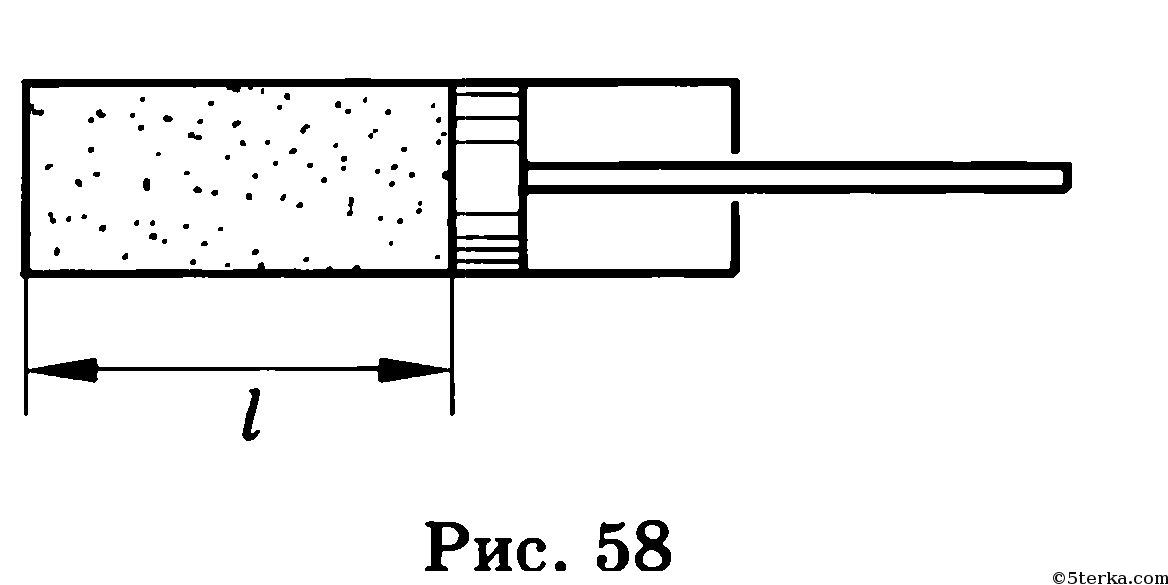 ст.   [ ≅ 1300 см³ ]

34.12.   В сосуд объёмом V = 10 л, наполненный сухим воздухом при давлении p = 1 атм. и температуре t = 0° С, вводят m = 3 г воды. Определить давление в сосуде при его нагревании до t₁ = 100° С.   [ ≅ 1.88 атм.]

34.13.   Какова была влажность воздуха под поршнем при температуре 20° С и давлении 1 атм, если при температуре 100° С конденсация пара началась при давлении 60 атм? Давление насыщенного пара при 20° С равно 17,5 мм рт. ст.   [72 %]

34.14.   Смешали 1 м³ пара с влажностью 20 % при температуре 20° С и 2 м³ пара с влажностью 30 % при температуре 50° С. Объём смеси 3 м³. Найти влажность смеси, если система теплоизолирована.   [21 %]

34.15. На рис. представлена изотерма влажного воздуха. Найти относительную влажность воздуха в точках A, B и C.   [смотрите ответ в общем файле темы]

34. 16.   При изотермическом сжатии m = 9 г водяного пара при температуре T = 373 K его объём уменьшился в 3 раза, а давление увеличилось в 2 раза. Найти начальный объём пара.   [ ≅ 3.1×10⁻² м³ ]

34.17.   В газовом баллоне объёмом V = 5 л может поместиться не более m = 2,2 кг пропана (С₃Н₈) под давлением 16 атм. и температуре t = 27° С. Какая масса газообразного пропана будет находиться в баллоне, если из полного баллона израсходовать 80 % пропана? Давление насыщенного пара пропана при 27° С равно p_н = 16 атм.   [смотрите ответ в общем файле темы]

34.18.   Насыщенный водяной пар находится при температуре t = 100° С в цилиндре под невесомым поршнем. При медленном изотермическом вдвигании поршня небольшая часть пара массой Δm = 0,7 г сконденсировалась. Какая работа была при этом совершена? Объёмом жидкости пренебречь.   [1.2 Дж]

34. 19.   Пространство под поршнем в цилиндре занимает водяной пар с относительной влажностью φ = 50 % при температуре t = 100° С. Какая масса воды получится при изотермическом уменьшении объёма под поршнем от V₁ = 5 л до V₂ = 1 л?   [ ≅ 0.87 г ]

34.20.   Закрытый цилиндр делится лёгким подвижным поршнем на две равные части. В одной из них находится воздух, а в другой – вода и пар. При медленном нагревании всего сосуда поршень начинает двигаться и в некоторый момент останавливается. В этот момент он делит сосуд на части в отношении 1:3. Определить отношение массы воды к массе пара в начальном состоянии. Объёмом воды пренебречь.   [2]

34.21.   В цилиндре под легким подвижным поршнем находится смесь воздуха и равных по массе количеств воды и водяного пара. При медленном изотермическом уменьшении давления на поршень от p_o до 2p_o/3 вся вода испаряется. Найти давление пара в условиях опыта. Объемом воды пренебречь.   [ p_o/3 ]

Далее: поверхностное натяжение.   |   Вернуться к списку разделов молекулярно-кинетической теории.

(i) Горизонтальный цилиндр снабжен гладким подвижным поршнем. В баллоне находится идеальный газ. Газ нагревается медленно, так что поршень постепенно выдвигается. Отойдя на некоторое расстояние, поршень наталкивается на идеальную пружину и при движении сжимает ее. Нарисуйте P-V-диаграмму для всего процесса. (ii) Один моль идеального газа изотермически расширяется при температуре T0, увеличивая его объем вдвое с V0 до 2V0. Начертите график зависимости объема (V) газа от количества подведенного к нему тепла (Q).

Вопрос

Обновлено:26/04/2023

АРИХАНТ-ПЕРВЫЙ ЗАКОН ТЕРМОДИНАМИКИ-Уровень 3

7 видео

РЕКЛАМА

Текст Решение

Ответ 9 0003

Правильный ответ: (i) (##IJAPHYV02C04E01009_A01# #)

Ответить

Пошаговое решение, разработанное экспертами, чтобы помочь вам в сомнениях и получить отличные оценки на экзаменах.

Ab Padhai каро бина объявления ке

Khareedo DN Pro и дехо сари видео бина киси объявление ки rukaavat ке!

Видео по теме

Газ находится в металлическом цилиндре, снабженном поршнем. Поршень внезапно перемещается, чтобы сжать газ, и удерживается в этом положении. С течением времени давление газа в цилиндре

9544241

Два моля двухатомного газа при температуре 300 К заключены в цилиндр, как показано на рисунке. Поршень легкий. Найдите количество теплоты, отдаваемое газу при медленном нагревании газа до 400 К в следующих трех случаях. (i) Поршень свободно перемещается (ii) Если поршень не движется (iii) Если поршень тяжелый и подвижный

14162610

Вертикальный цилиндр с теплопроводящими стенками закрыт снизу и снабжен гладким легким поршнем. Он содержит один моль идеального газа. Температура газа всегда равна температуре окружающей среды T0. Поршень медленно перемещают вверх, чтобы увеличить объем газа в η раз. Что из следующего неверно?

15635158

Текст Решение

Вертикальный цилиндр с теплопроводными стенками закрыт снизу и снабжен гладким легким поршнем. Он содержит один моль идеального газа. Температура газа всегда равна температуре окружающей среды, T _ (0). Поршень медленно перемещается вверх, чтобы увеличить объем газа в эта раз. Что из перечисленного неверно?

205980404

Два цилиндра А и В, снабженные поршнями, содержат одинаковое количество молей идеального одноатомного газа при температуре 400 К. Поршень A может свободно двигаться, в то время как поршень B зафиксирован. В каждом цилиндре газу передается одинаковое количество тепловой энергии. Если повышение температуры газа в А равно 42 К, то повышение температуры газа в В равно

233493781

Один моль идеального газа содержится в вертикальном цилиндре под безмассовым поршнем, движущимся без трения. Поршень медленно поднимают так, чтобы при температуре Т0 = 300 К газ изотермически расширился. Найти работу, совершаемую при увеличении объема в η=2 раза. Внешнее давление атмосферное.

256693975

Газ находится в металлическом цилиндре, снабженном поршнем. Поршень внезапно перемещается для сжатия газа и удерживается в этом положении. С течением времени давление газа в цилиндре

642596617

Два цилиндра А и В, снабженные поршнями, содержат одинаковое количество молей идеального одноатомного газа при температуре 400 К. Поршень A может свободно двигаться, в то время как поршень B зафиксирован. В каждом цилиндре газу передается одинаковое количество тепловой энергии. Если повышение температуры газа в точке А равно 42 К, то повышение температуры газа в точке В равно

642708895

Два цилиндра А и В, снабженные поршнями, содержат одинаковое количество молей идеального одноатомного газа при температуре 400К. Поршень А может свободно двигаться, а поршень В зафиксирован. В каждом цилиндре газу передается одинаковое количество теплоты. Если повышение температуры газа в A равно 42K, то повышение температуры газа в B равно (γ=5/3)

642728898

Text Solution

Два цилиндра A и B, снабженные поршнями, содержат одинаковые число молей идеального одноатомного газа при 400 К. Поршень A может свободно двигаться, в то время как поршень B зафиксирован. В каждом цилиндре газу передается одинаковое количество тепловой энергии. Если повышение температуры газа в точке А равно 42 К, то повышение температуры газа в точке В равно

642731269

Газ находится в металлическом цилиндре с поршнем. Поршень внезапно перемещается для сжатия газа и удерживается в этом положении. С течением времени давление газа в цилиндре

643108082

Текст Решение

Газ находится в металлическом цилиндре, снабженном поршнем. Поршень внезапно перемещается для сжатия газа и удерживается в этом положении. С течением времени давление газа в цилиндре

643140992

Газ находится в металлическом цилиндре, снабженном поршнем. Поршень внезапно перемещается для сжатия газа и удерживается в этом положении. С течением времени давление газа в цилиндре

643183719

Два моля двухатомного газа при температуре 300 К заключены в цилиндр, как показано на рисунке. Поршень легкий. Найдите количество теплоты, отдаваемое газу при медленном нагревании газа до 400 К в следующих трех случаях. (i) Поршень свободно перемещается (ii) Если поршень не движется (iii) Если поршень тяжелый и подвижный

644525193

Газ находится в металлическом цилиндре, снабженном поршнем. Поршень внезапно перемещается для сжатия газа и удерживается в этом положении. С течением времени давление газа в цилиндре

644525343

Поршень может свободно перемещаться внутри закрытого с обоих концов горизонтального цилиндрического сосуда. Первоначально поршень разделяет внутреннее пространство цилиндра на две равные части объемом ${V_0}$ каждая при одинаковом давлении ${P_0}$ и всегда при одной и той же температуре. Какую работу необходимо совершить, чтобы изотермически увеличить объем одной части газа в $\eta$ раз по сравнению с объемом другой при медленном перемещении поршня?

Подсказка: Поскольку в задаче речь идет о газах в закрытом цилиндре, существует давление и соответствующая сила, связанная с ним. Уравнение, основанное на концепции равновесия, применяется для определения сил, действующих на поршень со стороны газов, а также сил, действующих со стороны агента. Формула для работы, выполненной с точки зрения силы и перемещения, применяется вместе с концепцией идеальных газов и уравнением идеального газа.

Полный пошаговый ответ:
Вышеупомянутая задача связана с концепцией идеальных газов внутри закрытого цилиндра. Чтобы узнать работу, совершаемую при перемещении поршня, нам сначала нужно узнать концепцию идеальных газов, запертых внутри закрытого цилиндра. Когда поршень помещается внутрь цилиндра, который закрыт с обоих концов, поршень разделяет воздух или газ внутри цилиндра, так что некоторое количество газа присутствует с обеих сторон поршня. Отсюда появляется понятие давления, потому что молекулы частиц газа, присутствующие по обе стороны от поршня, должны оказывать силу на поршень, потому что давление называется силой, прикладываемой газом к единице площади.

Точно так же будет сила, которая действует агентом на перемещение поршня, чтобы сделать объем одной стороны равным \[\eta \], умноженному на объем другой стороны поршня, как указано в вопросе. Следовательно, для уравновешивания этих сил, создаваемых молекулами газа, присутствующими в левой части поршня, и силой, создаваемой агентом, будет эквивалентна сила, создаваемая молекулами газа, присутствующими в правой части поршня, как показано на рис. фигура. Именно здесь появляется понятие равновесия.

Следовательно, применяя понятие равновесия, мы получаем уравнение:
${P_1}A + {F_{агент}} = {P_2}A$
Где, ${P_1}$ указывает давление молекул газа, присутствующих на с левой стороны поршня, а ${P_2}$ указывает на давление молекул газа, присутствующих на правой стороне поршня, а ${F_{агент}}$ представляет собой силу, действующую на агент. Поскольку используется один и тот же поршень, площадь поршня везде одинакова, что обозначено как $A$
. Переставляя члены так, чтобы ${F_{агент}}$ был субъектом, мы получаем:
$ \Rightarrow {F_{агент}} = {P_2}A — {P_1}A$
Вычитая общие члены, получаем:
$ \Rightarrow {F_{агент}} = \left( {{P_2} — { P_1}} \right)A$ ———($1$)

Когда к поршню приложена определенная внешняя сила, перемещающая его на определенное смещение $x$, как показано на диаграмме мы знаем, что при перемещении поршня совершается некоторая работа. Следовательно, формула для проделанной работы применяется к небольшому перемещению $dx$.
$ \Rightarrow dW = {F_{агент}}dx$ ———($2$)
Теперь подставим уравнение ($1$) в уравнение ($2$), чтобы получить:
$dW = \left( {{P_2} — {P_1}} \right)A \times dx$
Переставляя члены, мы получаем:
$dW = \left( {{P_2} — {P_1}} \right)\left( {Adx} \right)$

Теперь применим формулу для объема. Математически мы знаем, что объем эквивалентен произведению площади на высоту. Здесь высота будет смещением поршня, и поэтому говорят, что объем $V$ равен произведению площади на смещение. Поскольку $V = A \times dx$, мы заменяем значение в приведенном выше уравнении, чтобы получить: 9V {\left( {{P_2} — {P_1}} \right)dV} $ ————($3$)

Мы предположили, что газы внутри цилиндра являются идеальными газами и следовательно, проявляют свойства идеальных газов. Следовательно, теперь мы применяем уравнение идеального газа для молекул газа, находящихся внутри цилиндра.
$PV = nRT$
Где $P$ и $V$ — давление и объем соответственно. В вопросе упоминается, что температура постоянна, то есть температура остается неизменной во все времена, а также, поскольку одинаковое число молекул газа, находящихся по обе стороны от поршня, одинаково, указанное число молей на $n$ также постоянно. Универсальная газовая постоянная $R$ тоже постоянна. Следовательно, приведенное выше уравнение идеального газа принимает вид:
$PV = константа$

Когда поршень перемещается на определенное перемещение, говорят, что происходит изменение значений давления и объема, и, следовательно, в соответствии с приведенным выше уравнением мы получаем другое уравнение:
${P_1}{V_1 } = {P_2}{V_2}$
Указывает на изменение объемов и давления после перемещения поршня.
Теперь рассмотрим изменение громкости. Когда поршень перемещается к правой стороне поршня, так что объем газа в левой части увеличивается в $\eta $ раз по сравнению с правой стороной, мы видим, что объем в левой части увеличивается, а объем газа в левой части увеличивается. объем в правой части соответственно уменьшается.

Поскольку ${V_0}$ указывает первоначальный объем, изменение объема с левой стороны будет увеличено на величину $Ax$ (относительно смещения поршня вправо) и изменится в объеме справа уменьшится на величину $Ax$. Количество, смещенное влево, будет таким же, как количество, смещенное в правую сторону.
Следовательно, уравнения принимают вид:
${P_1}\left( {{V_0} + Ax} \right) = {P_0}{V_0}$
$ \Rightarrow {P_2}\left( {{V_0} — Ax} \ справа) = {P_0}{V_0}$

Мы составили два уравнения для определения изменения давления и объемов по обе стороны от поршня. Первое уравнение для левой части, второе уравнение для правой. Переставляя члены приведенных выше уравнений, мы получаем:
${P_1} = \dfrac{{{P_0}{V_0}}}{{\left( {{V_0} + Ax} \right)}}$ — —-($4$)
$ \Rightarrow {P_2} = \dfrac{{{P_0}{V_0}}}{{\left( {{V_0} — Ax} \right)}}$ —- —($5$)
Теперь вычтем уравнение ($5$) из ($4$), чтобы получить:
${P_1} — {P_2} = \dfrac{{{P_0}{V_0}}}{{\left( {{V_0} + Ax} \right)}} — \dfrac{{{P_0}{V_0} }}{{\left( {{V_0} — Ax} \right)}}$
Теперь возьмем НОК уравнений, чтобы получить:
${P_1} — {P_2} = \dfrac{{{P_0}{ V_0}\left( {{V_0} — Ax} \right) — {P_0}{V_0}\left( {{V_0} + Ax} \right)}}{{\left( {{V_0} + Ax} \ right)\left( {{V_0} — Ax} \right)}}$
Выбрасывая общие члены, получаем:
${P_1} — {P_2} = {P_0}{V_0}\left[ {\dfrac{ {\left( {{V_0} — Ax} \right) — \left( {{V_0} + Ax} \right)}}{{\left( {{V_0} + Ax} \right)\left( {{ V_0} — Ax} \right)}}} \right]$

При дальнейшем упрощении получаем:
${P_1} — {P_2} = {P_0}{V_0}\left[ {\dfrac{{{V_0} — Ax — {V_0} — Ax}}{{\left( {{V_0} + Ax} \right)\left( {{V_0} — Ax} \right)}}} \right]$
Сокращая общие члены, получаем:
${P_1} — {P_2} = {P_0}{V_0}\left[ {\dfrac{{ — 2Ax}}{{\left( {{V_0} + Ax} \right)\left( {{V_0} — Ax} \right)}}} \ right]$
Теперь мы меняем знак обеих частей уравнения, чтобы получить:
${P_2} — {P_1} = {P_0}{V_0}\left[ {\dfrac{{2Ax}}{{\left( {{V_0} + Ax} \right)\left( {{V_0} — Ax} \right)}}} \right]$ 92}}} \right]$ ————($7$)

Определим теперь зависимость между изменениями объемов двух сторон поршня.