несколько подходов и примеры задач —

В статье обсуждаются несколько подходов к вычислению скорости по силе и массе, а также решенные проблемы. 

Чтобы вычислить скорость, мы должны понять, насколько далеко уходит масса объекта при приложении силы. Скорость объекта — это не что иное, как величина его вектора скорости. Вот почему мы можем рассчитать скорость по силе и массе, используя законы Ньютона, кинематическое уравнение движения и формулы работы-энергии.

Подробнее о том, как рассчитать массу по силе и расстоянию.

Как рассчитать скорость по силе и массе, используя второй закон Ньютона?

Давайте вычислим скорость по силе и массе, используя второй закон движения Ньютона. 

Второй закон Ньютона связывает скорость изменения скорости или ускорение с приложенной силой и массой. Вычислять скорость из второго закона Ньютона, нам сначала нужно понять разницу между скоростью и скоростью, а затем вычислить значение скорости из скорости изменения скорости.  

Согласно Второй закон Ньютона,

F = ma

]

F=m*[(vv₀)/(тт₀)

В то время как v₀ — начальная скорость, v — конечная скорость.

Прежде чем рассчитывать скорость по закону Ньютона, давайте разберемся в разнице между скоростью и скоростью.Как рассчитать скорость
от силы и массы

Разница между скоростью и скоростью

Скорость	Скорость
Это скалярная величина, связанная с расстоянием.	Это векторная величина, связанная со смещением.
Это ненулевая величина, которая всегда положительна.	Может быть нулевым, положительным и отрицательным.
Это может не быть равным скорости.	Разные скорости одного и того же объекта обладают одинаковой скоростью.
Единица СИ — метр в секунду (м / сек).	Единица СИ — километр / час (км / час).

Скорость против скорости
(Кредит: Shutterstock)

Когда автомобиль проехал определенное расстояние d за время t, мы называем его скорость v.

v=d/t

Как вы знаете, иногда нам нужно изменить направление во время движения из-за пробок или по другим причинам; в этом случае мы измеряем смещение вместо расстояния d в интервале времени t.

Уравнение (*) превращается в скорость v как,

Смещение — это кратчайшее расстояние между конечным и начальным расстоянием, но его величина меньше или равна общему расстоянию d. Расстояние против смещения
(Кредит: Shutterstock)

Поскольку скорость не равна нулю или никогда не уменьшается со временем, величина скорости становится значением скорости, когда время приближается к нулю. 

Это означает скорость v говорит нам, насколько быстро машина.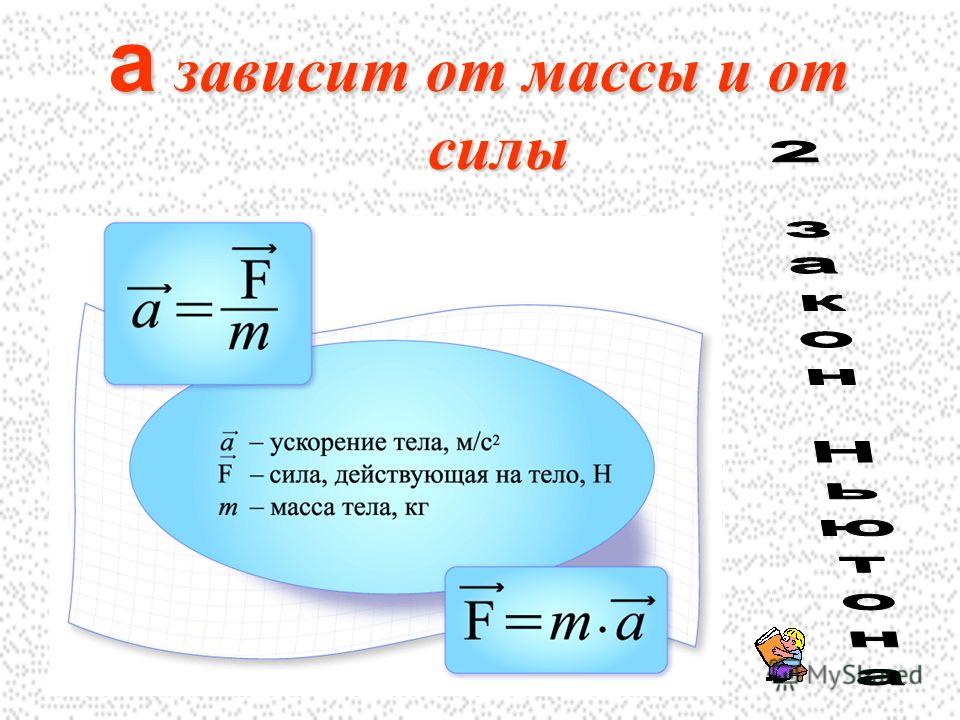 В то время как скорость v говорит нам как о скорости автомобиля, так и о его направлении. Поэтому мы назвали скорость величиной вектора скорости. 

Узнать больше об относительном движении.

Автомобиль массой 1000 кг в состоянии покоя проехал около 1 часа при силе 6 х 10

⁴ Применяется N. Рассчитайте скорость автомобиля.

Данный:

F = 6 х 10⁴ N

m = 1000 кг

t = 1 час

Найти: v=?

Формула:

F = ma

Решение:

Скорость автомобиля рассчитывается с использованием Второй закон движения Ньютона.

F = ма

F=m*[(vv₀)/(тт₀)

Поскольку автомобиль изначально находится в состоянии покоя, v₀ = 0 и t₀ = 0

Следовательно,

Подставляя все значения,

Преобразуем скорость в скорость в метрах в секунду.

1 км = 1000 м

1 час = 3600 секунд

v=60*(1000/3600)

v = 60000/3600

v = 16. 6

Автомобиль движется со скоростью 16.6 м / сек.

Подробнее о том, как рассчитать ускорение свободного падения.

Как рассчитать скорость по силе и массе, используя кинематическое уравнение движения?

Давайте вычислим скорость по силе и массе, используя второе кинематическое уравнение движения. 

Второе кинематическое уравнение движения связывает общее пройденное расстояние объекта с начальной скоростью и ускорением. Когда мы внедрили формулу ускорения из второго закона Ньютона в кинематическое уравнение, мы получили формулу, которая рассчитывала скорость на основе приложенной силы и ее массы. 

Второе кинематическое уравнение движения:

Как рассчитать скорость по силе и массе с помощью кинематического уравнения

Узнать больше о кинематических уравнениях движения.

Парашютист массой 60 кг выпрыгивает из самолета и за 1 минуту достигает земли. Если сила, воздействующая на парашютиста по воздуху, составляет 800 Н, какова скорость парашютиста?

Данный:

m = 60 кг

t = 1 минута = 60 секунд

F = 800 Н

Найти: v =?

Формула:

Решения:

Скорость парашютиста рассчитывается с помощью второе кинематическое уравнение движения.

а=Ф/м

Но

Поскольку парашютист изначально находится в состоянии покоя относительно плоскости, следовательно, d₀ = 0 и v₀ = 0.

d=(1/2)*(Ф/м)*t²

С скорость v= d / t

vt=(1/2)*(Ф/м)*t²

v=фут/2м

Подставляем все значения

v=(800*60)/(2*60)

v = 48000/120

V = 400

Скорость парашютиста 400 м / сек.

Подробнее о преобразовании потенциала в кинетическую энергию.

Как рассчитать скорость по силе и массе, используя формулу работы-энергии?

Давайте вычислим скорость по силе и массе, используя формулу работы-энергии. 

Когда покоящийся объект перемещается на определенное расстояние при приложении силы, он выполняет работу. Приложенная сила преобразует накопленную потенциальную энергию неподвижного объекта в кинетическую энергию для выполнения работы. Вот почему используется формула работы-энергии; мы можем вычислить скорость по силе и массе.  

Компания формула работы является,

W = Fd

Поскольку работа, совершаемая телом, есть приобретение им кинетической энергии KE=(1/2)mv²

(1/2)мв² =Fд

Узнать больше о выполненной работе.

Мужчина имеет горки массой 80 кг со скоростью 30 км / ч за 2 секунды, когда к нему прилагается сила 200 Н, когда он толкает горку на игровой площадке. Рассчитайте скорость скольжения человека. 

Данный:

F = 200 Н

m = 80 кг

v=30км/ч=30*(1000/3600)

t = 2 часа

Найти: v=?

Формула:

(1/2)мв²=Fд

Решения:

Скорость скольжения человека рассчитывается с помощью формула работы-энергии в виде,

(1/2)мв²=Fд

Но скорость v = d / t

(1/2)мв²=Fdt

v=мв²/2 фута

Используя формулу работы и энергии, мы можем вычислить скорость в терминах силы, массы и скорости.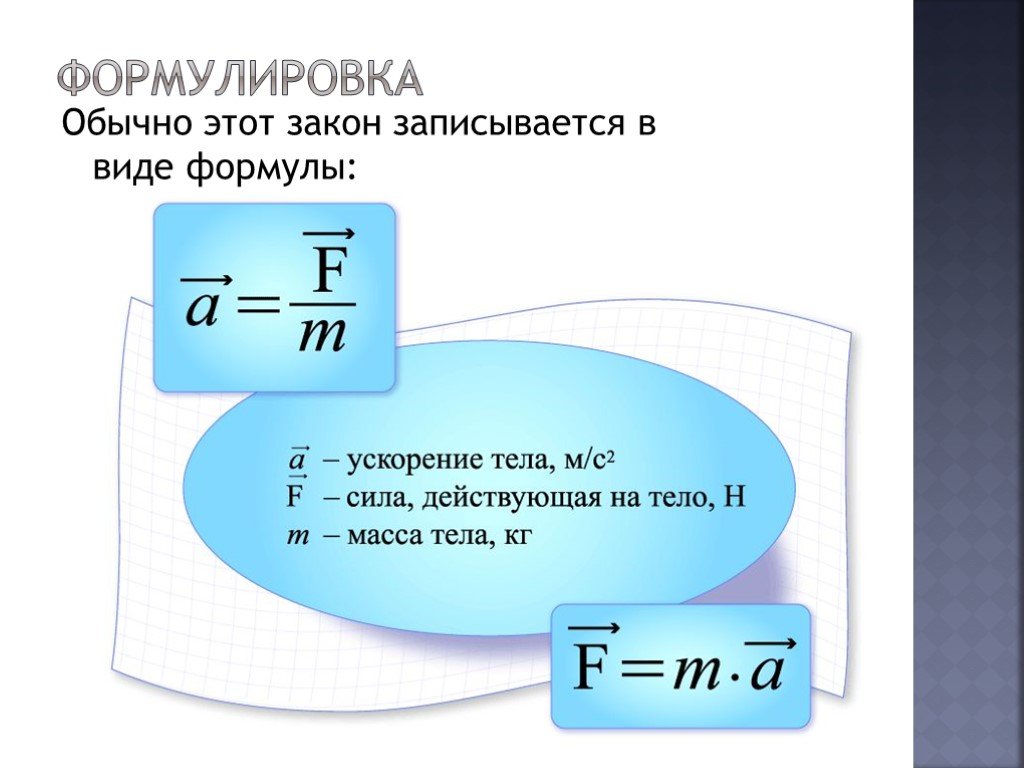

Подставляя все значения,

v=(72*10⁶)/(28.8*10⁵)

v = 25

Скорость скольжения человека 25 м / сек.

Узнайте больше о проделанной работе на уклоне.

Как рассчитать скорость по силе и массе с помощью формулы мощности?

Давайте рассчитаем скорость по силе и массе, используя формулу мощности. 

Мощность любого объекта измеряется количеством его работы, выполненной за единицу времени. Поскольку проделанная работа объекта является произведением приложенной силы и пройденного расстояния. Следовательно, используя формулу мощности, мы можем рассчитать скорость объекта непосредственно из приложенной силы и ее мощности.  

Компания формула мощности является,

P=Вт/т

W = Fd

Но работа сделана

P=Fd/т

v=d/t

Поскольку скорость

Р=Fv

Как рассчитать скорость по силе и массе с помощью формулы мощности
(Кредит: Shutterstock)

Узнать больше о Power.  

Если номинальная мощность двигателя составляет 500 Вт, он может выполнять работу при приложении силы 80 Н. Какая скорость у мотора?

Данный:

P = 500 Вт

1Вт=1кг.м²/s³

F = 80 Н

1Н=1кг.м²/s²

Найти: v=?

Формула:

P=Вт/т

Решения:

Скорость рассчитывается с использованием формула мощности,

P = Fv

v=П/Ф

Подставляя все значения,

В=500Вт/80Н

v = 40 м / сек

Скорость двигателя 40 м / сек.

Формула силы в физике

Содержание:

• Определение и формула силы
• Второй закон Ньютона
• Единицы измерения силы
• Примеры решения задач

Определение и формула силы

Определение

Силой называют векторную величину, которая характеризует взаимодействия тел. Ее модуль определяет «степень»
(интенсивность) воздействия. {n} \bar{F}_{i}=\frac{d \bar{p}}{d t}(1)$$

где $\bar{p}=m \bar{v}$ — импульс тела, m–масса рассматриваемого тела,
$\bar{v}$ — скорость. Надо отметить, что уравнение (1) строго применимо только относительно
материальной точки. Если рассматривается протяженное тело, то под скоростью понимают скорость движения центра масс тела.

Если масса материальной точки (m)не изменяется во времени, то формула, определяющая результирующую силу, приложенную к ней
(второй закон Ньютона) можно представить в виде:

$$\bar{F}=m \frac{d \bar{v}}{d t}=m \bar{a}(2)$$

где $\bar{a}$ – ускорение, которое материальная точка приобретает в результате
воздействия на нее силы. Выражение (2) показывает то, что если
$\bar{F}$=0, то тело (материальная точка) движется равномерно и прямолинейно или покоится.

Если сила, приложенная к телу, является постоянной (по модулю и направлению), то формулу для нее можно представить в виде:

$$F=\frac{\Delta p}{\Delta t}=\frac{m\left(v_{2}-v_{1}\right)}{t_{2}-t_{1}}$$

Единицы измерения силы

Основной единицей измерения момента силы в системе СИ является: [F]=Н=(кг•м)/с²

В СГС: [F]=дин

1Н=10⁵ дин

Примеры решения задач

Пример

Задание. {2}}(1.4)$$

то, учитывая выражения (1.2) и (1.3), получаем:

$a = 6 \alpha t (1.5)$

Так как a_y=0, то получаем, что сила, которая действует на нашу точку, направлена по оси X, так как направление ускорение
и силы совпадают, а мы получили:

$$\bar{a}=6 \alpha t \cdot \bar{i}(1.6)$$

где $\bar{i}$ – единичный вектор, направленный по оси X.

Исходя из второго закона Ньютона, имеем:

$$F=m \cdot 6 \alpha t, \bar{F}=m 6 \alpha t \cdot \bar{i}$$

Ответ. Так как $F=m \cdot 6 \alpha t$, то с течением времени сила увеличивается по модулю.

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Пример

Задание. Два параллелепипеда лежат на горизонтальной поверхности. Они соприкасаются. Данные тела могут
скользить по поверхности опоры без трения. {\prime}}=\left(m_{1}+m_{2}\right) \bar{a}(2.3)$$

В проекции на ось X уравнение (2.3) примет вид:

$$F_{0}=\left(m_{1}+m_{2}\right) a(2.4)$$

Из уравнения (2.4) выразим ускорение:

$$a=\frac{F_{0}}{m_{1}+m_{2}}$$

Подставим правую часть выражения (2.5) в (2.2) вместо ускорения:

$$F=F_{0}-m_{1} \cdot \frac{F_{0}}{m_{1}+m_{2}}$$

Ответ. $F=F_{0}-m_{1} \cdot \frac{F_{0}}{m_{1}+m_{2}}$

Читать дальше: Формула сопротивления.

Сила, масса и ускорение: второй закон движения Ньютона

При покупке по ссылкам на нашем сайте мы можем получать партнерскую комиссию. Вот как это работает.

У побережья Пусана, Южная Корея, 7 июля 1999 г. — F/A-18 Hornet, приписанный к эскадрилье ударных истребителей One Five One (VFA-151), преодолевает звуковой барьер в небе над Тихим океаном. VFA-151 развернут на борту USS Constellation (CVN 64).
(Изображение предоставлено: фото ВМС США, сделанное энсином Джоном Гэем)

Первый закон движения Исаака Ньютона гласит: «Тело в состоянии покоя останется в покое, а тело в движении останется в движении, если на него не действует внешняя сила». Что же происходит с телом при приложении к нему внешней силы? Эта ситуация описывается вторым законом движения Ньютона.

Согласно НАСА, этот закон гласит: «Сила равна изменению импульса на изменение во времени. Для постоянной массы сила равна массе, умноженной на ускорение». Это записывается в математической форме как F = м a

F — сила, м — масса и a — ускорение. Математика этого довольно проста. Если вы удвоите силу, вы удвоите ускорение, но если вы удвоите массу, вы сократите ускорение вдвое.

Ньютон опубликовал свои законы движения в 1687 году в своей основополагающей работе «Philosophiæ Naturalis Principia Mathematica» («Математические принципы натуральной философии»), в которой он формализовал описание того, как массивные тела движутся под действием внешних сил.

Ньютон расширил более раннюю работу Галилео Галилея, который разработал первые точные законы движения масс, по словам Грега Ботуна, профессора физики Орегонского университета. Эксперименты Галилея показали, что все тела ускоряются с одинаковой скоростью независимо от размера или массы. Ньютон также подверг критике и расширил работу Рене Декарта, который также опубликовал свод законов природы в 1644 году, через два года после рождения Ньютона. Законы Декарта очень похожи на первый закон движения Ньютона.

Ускорение и скорость

Второй закон Ньютона гласит, что когда на массивное тело действует постоянная сила, она заставляет его ускоряться, т. е. изменять свою скорость с постоянной скоростью. В простейшем случае сила, приложенная к покоящемуся объекту, заставляет его ускоряться в направлении действия силы. Однако, если объект уже находится в движении или если эта ситуация рассматривается из движущейся инерциальной системы отсчета, может показаться, что это тело ускоряется, замедляется или меняет направление в зависимости от направления силы и направлений, в которых движется объект. и система отсчета движутся относительно друг друга.

Жирные буквы F и a в уравнении указывают на то, что сила и ускорение являются векторными величинами, что означает, что они имеют как величину, так и направление. Сила может быть одиночной силой или комбинацией нескольких сил. В этом случае мы запишем уравнение как ∑ F = м a

Большая Σ (греческая буква сигма) представляет векторную сумму всех сил, или результирующую силу, действующую на тело.

Довольно сложно представить приложение постоянной силы к телу в течение неопределенного времени. В большинстве случаев силы можно прикладывать только в течение ограниченного времени, производя так называемый импульс . Для массивного тела, движущегося в инерциальной системе отсчета без действующих на него других сил, таких как трение, определенный импульс вызовет определенное изменение его скорости. Тело может ускориться, замедлиться или изменить направление, после чего тело продолжит движение с новой постоянной скоростью (если, конечно, импульс не заставит тело остановиться).

Однако есть одна ситуация, когда мы сталкиваемся с постоянной силой — силой гравитационного ускорения, которая заставляет массивные тела воздействовать на Землю с силой, направленной вниз. В этом случае постоянное ускорение свободного падения записывается как г , а второй закон Ньютона принимает вид F = мг . Обратите внимание, что в данном случае F и g обычно не записываются как векторы, потому что они всегда указывают в одном и том же направлении, вниз.

Произведение массы на ускорение свободного падения, мг , известно как вес , что является просто другим видом силы. Без гравитации массивное тело не имеет веса, а без массивного тела гравитация не может создавать силу. Чтобы преодолеть гравитацию и поднять массивное тело, вы должны создать восходящую силу м a , которая больше, чем направленная вниз сила тяжести мг .

Второй закон Ньютона в действии

Ракеты, путешествующие в космосе, подчиняются всем трем законам движения Ньютона.

Если ракете необходимо замедлиться, ускориться или изменить направление, для ее толкания используется сила, обычно исходящая от двигателя. Величина силы и место, где она обеспечивает толчок, могут изменить либо скорость (величину ускорения), либо направление, либо обе скорости.

Теперь, когда мы знаем, как ведет себя массивное тело в инерциальной системе отсчета, когда на него действует внешняя сила, например, как двигатели создают толчковый маневр ракеты, что происходит с телом, на которое воздействует эта сила? Эта ситуация описывается третьим законом движения Ньютона.

Дополнительный отчет Рэйчел Росс, автора Live Science.

См. также:

• Законы движения Ньютона
• Инерция и первый закон движения Ньютона

Дополнительные ресурсы 9000 3

• Гиперфизика: Законы Ньютона
• Кабинет физики: Законы Ньютона
• НАСА: Законы движения Ньютона

Будьте в курсе последних научных новостей, подписавшись на нашу рассылку Essentials.

Свяжитесь со мной, чтобы сообщить новости и предложения от других брендов FutureПолучайте электронные письма от нас от имени наших надежных партнеров или спонсоров

Джим Лукас — автор статей для Live Science. Он охватывает физику, астрономию и инженерное дело. Джим окончил Университет штата Миссури, где получил степень бакалавра наук в области физики, а также астрономию и техническое письмо. После окончания университета он работал в Лос-Аламосской национальной лаборатории системным администратором, техническим писателем-редактором и специалистом по ядерной безопасности. Помимо написания статей, он редактирует статьи в научных журналах по различным тематическим направлениям.

1. 1

   Редкая и смертоносная кобра-альбинос заползла в дом во время сильного ливня

2. 2

   Apple Watch Series 8 снова удешевили на Amazon, поэтому на них стоит обратить внимание

9 0089

3

Неандертальцы прошли

3. 4

   Современные люди возникли после скрещивания двух различных групп в Африке на протяжении десятков тысяч лет

4. 5

   Акула совершила 3 ​​нападения на серфера в Австралии, что привело к смертельной и «нетипичной» встрече

1. 1

   ливень

2. 2

   носорог

3. 3

   5400-летняя гробница, обнаруженная в Испании, точно отражает дату летнего солнцестояния

4. 4

   Давно вымерший тасманийский тигр, возможно, все еще жив и бродит по пустыне, утверждают ученые 3

Второй закон движения Ньютона

Первый закон движения Ньютона предсказывает поведение объектов, для которых все существующие силы уравновешены. Первый закон, иногда называемый законом инерции, гласит, что если силы, действующие на объект, уравновешены, то ускорение этого объекта будет равно 0 м/с/с. Объекты на равновесие (состояние, при котором все силы уравновешены) не будет ускоряться. Согласно Ньютону, объект будет ускоряться только в том случае, если на него действует чистая или неуравновешенная сила. Наличие неуравновешенной силы ускоряет объект, изменяя его скорость, направление или и скорость, и направление.

Второй закон Ньютона относится к поведению объектов, для которых все существующие силы не уравновешены. Второй закон гласит, что ускорение объекта зависит от двух переменных — общей силы, действующей на объект, и массы объекта. Ускорение объекта напрямую зависит от чистой силы, действующей на объект, и обратно пропорционально массе объекта. Когда сила, действующая на объект, увеличивается, ускорение объекта увеличивается. По мере увеличения массы объекта ускорение объекта уменьшается.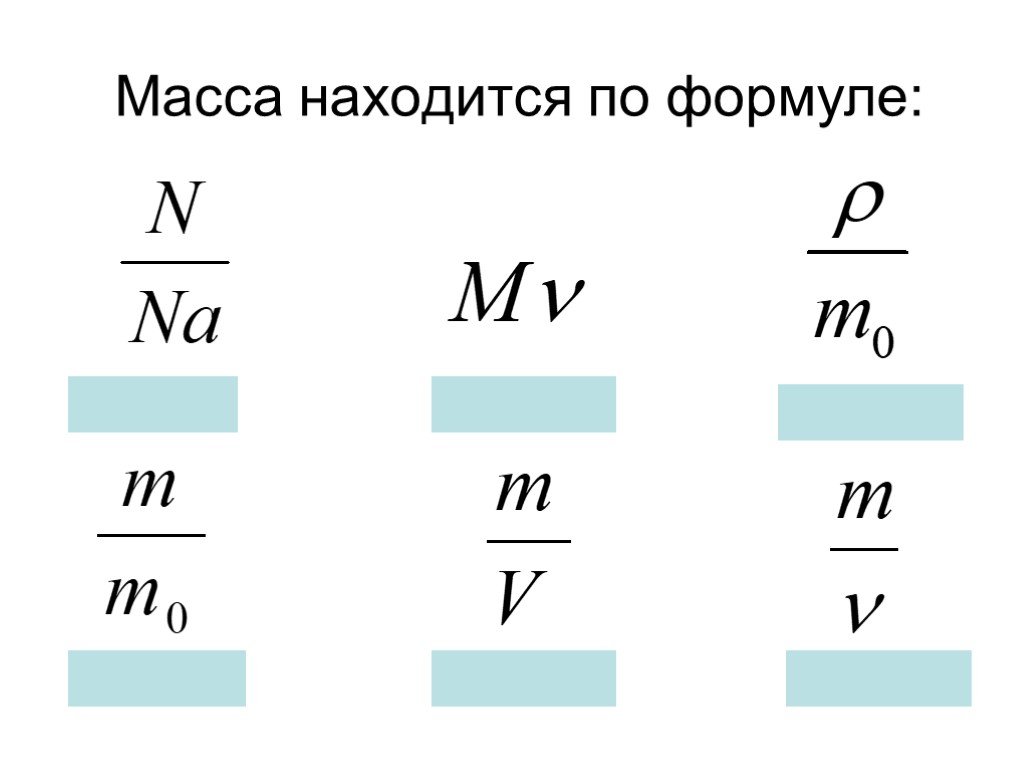

БОЛЬШОЕ Уравнение

Второй закон движения Ньютона можно формально сформулировать следующим образом:

Ускорение объекта, вызванное результирующей силой, прямо пропорционально величине результирующей силы в том же направлении, что и результирующая сила, и обратно пропорционально массе объекта.

Это словесное утверждение может быть выражено в виде уравнения следующим образом:

Приведенное выше уравнение часто преобразуется в более знакомую форму, как показано ниже. Чистая сила равна произведению массы на ускорение.

Во всем этом обсуждении акцент делался на net force . Ускорение прямо пропорционально чистой силе ; результирующая сила равна массе, умноженной на ускорение; ускорение в том же направлении, что и чистая сила ; ускорение производится результирующей силой . ЧИСТАЯ СИЛА. Важно помнить об этом различии. Не используйте значение просто «любой «старой силы» в приведенном выше уравнении. Это чистая сила, связанная с ускорением. Как обсуждалось в предыдущем уроке, результирующая сила представляет собой векторную сумму всех сил. Если известны все отдельные силы, действующие на объект, то можно определить результирующую силу. При необходимости повторите этот принцип, вернувшись к практическим вопросам урока 2.

В соответствии с приведенным выше уравнением единица силы равна единице массы, умноженной на единицу ускорения. Подставив стандартные метрические единицы силы, массы и ускорения в приведенное выше уравнение, можно записать следующую единицу эквивалентности.

Стандартная метрическая единица силы определяется приведенным выше уравнением. Один ньютон определяется как количество силы, необходимой для придания массе 1 кг ускорения 1 м/с/с.

Ваша очередь практиковаться

Сеть F = m • уравнение часто используется при решении алгебраических задач. Приведенную ниже таблицу можно заполнить, подставив в уравнение и найдя неизвестную величину. Попробуйте сами, а затем используйте кнопки для просмотра ответов.

	Чистая сила (Н)	Масса (кг)	Ускорение (м/с/с)
1.	10	2
2.	20	2
3.	20	4
4.		2	5
5.	10		10

Второй закон Ньютона как руководство к размышлению

Числовая информация в приведенной выше таблице демонстрирует некоторые важные качественные соотношения между силой, массой и ускорением. Сравнивая значения в строках 1 и 2, можно увидеть, что удвоение чистой силы приводит к удвоению ускорения (если масса сохраняется постоянной). Точно так же сравнение значений в строках 2 и 4 показывает, что деление вдвое чистой силы приводит к уменьшение вдвое ускорения (если масса остается постоянной). Ускорение прямо пропорционально чистой силе.

Кроме того, качественную связь между массой и ускорением можно увидеть путем сравнения числовых значений в приведенной выше таблице. Заметьте из строк 2 и 3, что удвоение массы приводит к уменьшению вдвое ускорения (если сила сохраняется постоянной). Точно так же строки 4 и 5 показывают, что уменьшение вдвое массы на приводит к удвоению ускорения (если сила сохраняется постоянной). Ускорение обратно пропорционально массе.

Анализ табличных данных показывает, что такое уравнение, как F _net = m*a, может служить руководством к размышлению о том, как изменение одной величины может повлиять на другую величину. Каково бы ни было изменение результирующей силы, такое же изменение произойдет с ускорением. Удвойте, утройте или учетверите результирующую силу, и ускорение сделает то же самое. С другой стороны, какое бы изменение ни производилось в массе, противоположное или обратное изменение будет происходить с ускорением. Удвойте, утройте или учетверите массу, и ускорение составит половину, треть или четверть первоначального значения.

Направление чистой силы и ускорения

Как указано выше, направление чистой силы совпадает с направлением ускорения. Таким образом, если известно направление ускорения, то известно и направление результирующей силы. Рассмотрим две диаграммы падения масла ниже для ускорения автомобиля. По диаграмме определите направление чистой силы, действующей на автомобиль. Затем нажмите кнопки, чтобы просмотреть ответы. (При необходимости просмотрите ускорение по сравнению с предыдущим блоком.)

В заключение, второй закон Ньютона дает объяснение поведения объектов, на которые силы не уравновешиваются. Закон гласит, что неуравновешенные силы заставляют объекты ускоряться с ускорением, которое прямо пропорционально результирующей силе и обратно пропорционально массе.

Мы хотели бы предложить …

Иногда недостаточно просто прочитать об этом. Вы должны взаимодействовать с ним! И это именно то, что вы делаете, когда используете один из интерактивных материалов The Physics Classroom. Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашего Force Interactive. Вы можете найти его в разделе Physics Interactives на нашем сайте. Force Interactive позволяет учащимся исследовать влияние изменений приложенной силы, результирующей силы, массы и трения на ускорение объекта.

Посетите: Force

Ракетостроение!

Ракеты НАСА (и другие) ускоряются вверх от стартовой площадки, сжигая огромное количество топлива. По мере того, как топливо сгорает и расходуется для приведения ракеты в движение, масса ракеты изменяется. Таким образом, одна и та же движущая сила может привести к увеличению значений ускорения с течением времени. Используйте ракетную науку ниже, чтобы изучить этот эффект.

1.