Содержание
Вращательное движение
Страница 1 из 3
Существует большое количество расчетных задач, которые моделируют явления, происходящие в различных вращающихся агрегатах или около них. При постановке подобной численной задачи важно выбрать способ описания вращения в численной модели, который будет корректен с точки зрения физики и оптимален с точки зрения производительности вычислений. FlowVision позволяет задавать вращение различными способами: с помощью вращающейся локальной системы координат; с помощью подвижных тел; с помощью скользящих поверхностей. С целью помочь пользователю разобраться с постановкой такого типа задач, рассмотрены примеры задач разного типа, начиная с физико-математических основ.
1. Кинематика вращательного движения
1.1. Вращательное движение материальной точки
Вращательное движение материальной точки (м.т.) вокруг неподвижной оси – это движение материальной точки по окружности радиуса R, центр которой лежит на неподвижной относительно данной системы отсчета прямой (ось вращения), перпендикулярной плоскости, в которой лежит траектория точки.
Рис.1.
Вращательное движение тела вокруг неподвижной оси — движение тела, при котором все его точки, двигаясь в параллельных плоскостях, описывают окружности с центрами, лежащими на одной неподвижной прямой, называемой осью вращения. Тело, совершающее вращательное движение, имеет одну степень свободы, и его положение относительно данной системы отсчёта определяется углом поворота φ между неподвижной полуплоскостью и полуплоскостью, жёстко связанной с телом, проведёнными через ось вращения.
Рис.2.
1.2. Угол поворота
Угол φ считается положительным, если он отложен от неподвижной плоскости в направлении против хода часовой стрелки (для наблюдателя, смотрящего с положительного конца оси Az), и отрицательным, если по ходу часовой стрелки. Чтобы знать положение в любой момент времени, надо знать зависимость угла φ от времени t, т.е. φ=f(t).
1.3. Основные кинематические характеристики вращательного движения
Основными кинематическими характеристиками вращательного движения являются угловая скорость и угловое ускорение .
Угловая скорость и угловое ускорение величины векторные. Вектор угловой скорости направлен вдоль оси вращения в ту сторону, откуда вращение видно происходящим против хода часовой стрелки (рис.3). Такой вектор определяет сразу и модуль угловой скорости, и ось вращения, и направление вращения вокруг этой оси. Аналогично углу поворота, когда вращение происходит против хода часовой стрелки (для наблюдателя, смотрящего с положительного конца оси Az) ω>0, а когда по ходу часовой стрелки, то ω<0. Таким образом, знак ωопределяет направление вращения.
а) б) в)
Рис.3
1.4. Прочие кинематические характеристики
Скорость точки M на расстоянии R от оси (рис.2):
Тангенциальная составляющая ускорения точки M (рис.3б):
Нормальная составляющая ускорения точки M (рис.3б):
Полное ускорение точки M (рис.3б):
Формула Эйлера (рис.3в):
2. Силы инерции, действующие на материальную точку во вращающейся системе отсчета
2.
 1. Материальная точка, покоящаяся во вращающейся системе отсчета
1. Материальная точка, покоящаяся во вращающейся системе отсчета
Если рассмотреть движение вращающейся точки M, то относительно неподвижной системы координат (СК) XYZ (рис.4а) силу, действующую на неё можно определить из второго закона Ньютона: . Относительно вращающейся системы координат X’Y’Z’ точка M неподвижна (рис.4б). Это обеспечивается тем, что равнодействующая сил уравновешивается инерциальной силой (центробежной): .
Рис.4 (а,б)
2.2. Материальная точка, движущаяся во вращающейся системе отсчета
Если же точка движется во вращающейся системе отсчета, то помимо центробежной силы на неё действует ещё одна сила инерции – сила Кориолиса (рис.5). Направление силы Кориолиса определяется правилом правого винта.
Рис. 5.
Таким образом, при переходе от основной неподвижной СК к локальной СК, которая является вращающейся системой отсчета, появляются дополнительные составляющие вектора силы, которые действуют на материальную точку: центробежная сила и сила Кориолиса .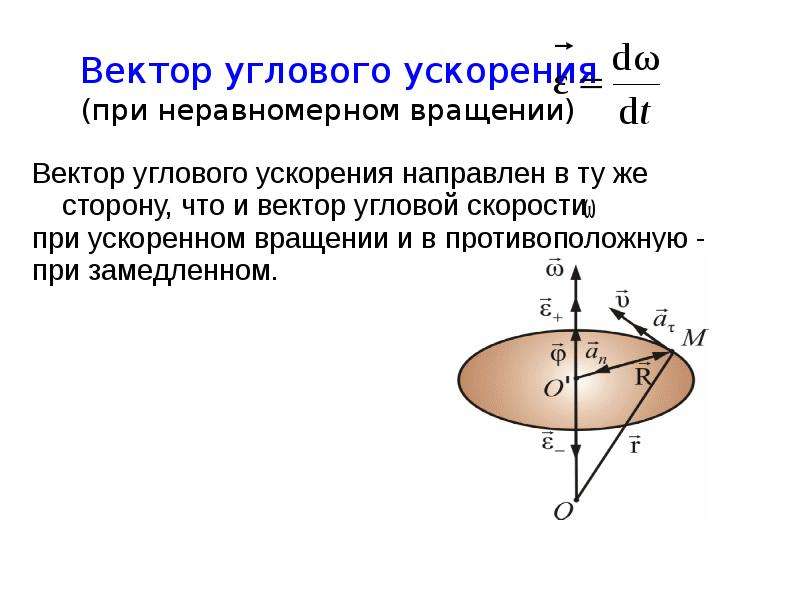
42. Как определить направление угловой скорости?
Углова́я
ско́рость —
векторная
физическая величина, характеризующая
скорость вращения тела. Вектор угловой
скорости по величине равен углу
поворота тела в единицу времени:
,
а
направлен по оси
вращения согласно правилу
буравчика, то есть, в ту сторону, в
которую ввинчивался бы буравчик
с правой резьбой, если бы вращался в ту
же сторону. Единица
измерения
угловой скорости, принятая в системах
СИ
и СГС) —
радианы
в секунду.
(Примечание: радиан,
как и любые единицы измерения угла, —
физически безразмерен, поэтому физическая
размерность угловой скорости —
просто [1/секунда]).Определим угловую
скорость как вектор, величина которого
численно равна угловой скорости, b
направленный вдоль оси вращения, причем,
если смотреть с конца этого вектора,
то вращение направлено против часовой
стрелки.
Исторически сложилось, что положительным
направлением вращения считается
вращение «против часовой стрелки»,
хотя, конечно, выбор этого направления
абсолютно условен. Для определения
Для определения
направления вектора угловой скорости
можно также воспользоваться «правилом
буравчика» (которое также называется
«правилом правого винта») — если
направление движения ручки буравчика
(или штопора) совместить с направлением
вращения, то направление движения всего
буравчика совпадет с направлением
вектора угловой скорости.
43.
Как
определить направление углового
ускарения? Угловое
ускорение
— векторная физическая величина,
характеризующая быстроту изменения
угловой скорости твёрдого тела.Угловое
ускорение
равно первой производной от угловой
скорости по времени.Формула угловой
скорости:
Единица
углового ускорения — радиан в секунду
в квадрате.
Углово́е
ускоре́ние —
псевдовекторная
физическая
величина, характеризующая быстроту
изменения угловой
скорости твёрдого
тела.
При
вращении
тела вокруг неподвижной оси,
угловое ускорение по модулю равно[1]:
Вектор
углового ускорения α
направлен вдоль оси вращения (в сторону
при
ускоренном вращении и противоположно
—
при замедленном).
При
вращении вокруг неподвижной точки
вектор углового ускорения определяется
как первая производная от вектора
угловой скорости ω
по времени[2],
то есть
,
и
направлен по касательной к годографу
вектора
в
соответствующей его точке.
44.
При
каком условии мы имеем право считать
в лабораторной работе №4 «Изучение
основного закона динамики вращательного
движения» линейное ускорение точек на
ободе щкива равным ускорению
поступательного движения груза?
Момент
сил создается грузом m, привязанным к
нити Н, которая навита на один из
шкивов. Если момент сил трения Mтр,
приложенный к оси маятника, мал по
сравнению с моментом силы натяжения
нити, то проверка уравнения
не представляет труда. Действительно,
измеряя время t,
в течение которого груз из состояния
покоя опустится на расстояние h,
можно легко найти ускорение груза
а, в проекции на координатную ось,
совпадающую с направлением движения:
, которое
связано с угловым ускорением
(при отсутствии проскальзывания
нити относительно обода шкива) очевидным
соотношением
, где
r
— радиус шкива.