Содержание
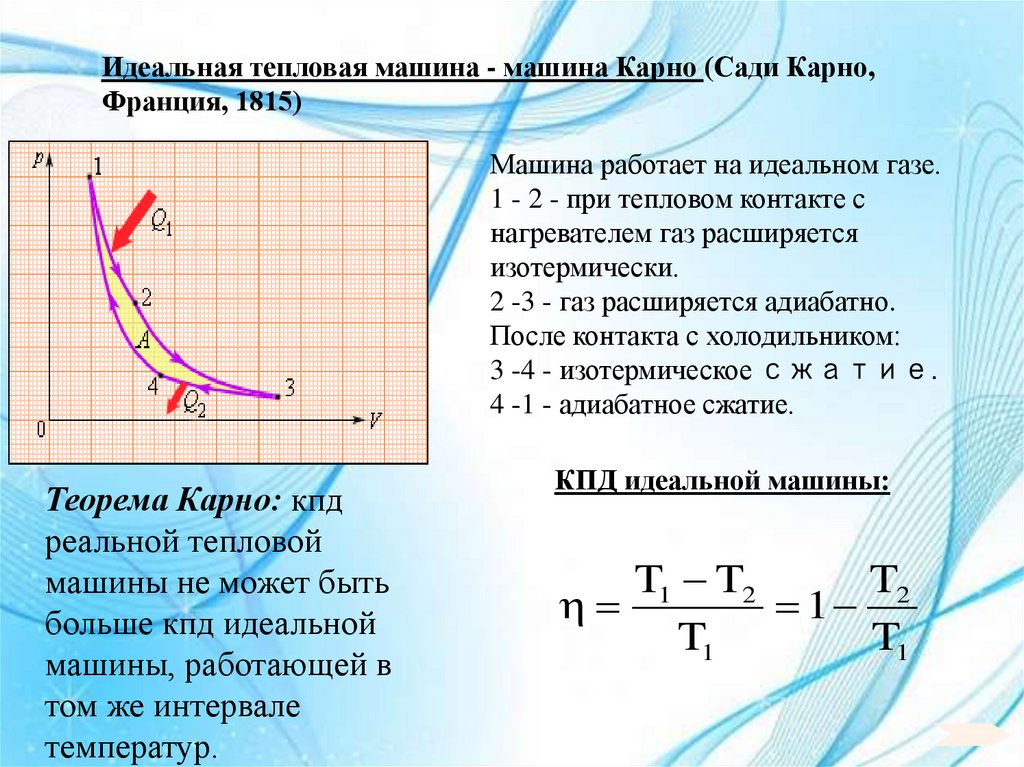
23)Цикл Карно. Расчет кпд идеальной тепловой машины, работающей по прямому обратимому циклу Карно. Теоремы Карно. Способы повышения кпд тепловых машин.
В
1824 г. С. Карно предложил и исследовал
идеальный тепловой цикл, названный в
последствии циклом
Карно. Этот цикл
состоит из двух изотерм и двух адиабат
(рис). Карно также сформулировал две
теоремы, определяющие максимальное
значение КПД теплового двигателя.
1-2
изобарное сжатие
2-3
изотермическое расширение
3-4
адиабатическое расширение
4-1
изотермическое сжатие
«Коэффициент
полезного действия тепловой машины,
работающей по циклу Карно, зависит
только от температур Т1
и Т2
нагревателя и холодильника, но не зависит
от устройства машины, а также от вида
используемого рабочего вещества».
«Коэффициент
полезного действия всякой тепловой
машины не может превосходить коэффициента
полезного действия идеальной машины,
работающей по циклу Карно с теми же
самыми температурами нагревателя и
холодильника».
Наибольшим
КПД при заданных температурах нагревателя
Tнагр
и холодильника Tхол
обладает тепловой двигатель, где рабочее
тело расширяется и сжимается по циклу
Карно
(рис. 2), график которого состоит из двух
изотерм (2–3 и 4–1) и двух адиабат (3–4 и
1–2).
Теорема
Карно
доказывает, что КПД такого двигателя
не зависит от используемого рабочего
тела, поэтому его можно вычислить,
используя соотношения термодинамики
для идеального газа:
Великое
прозрение Карно состоит в том, что он
показал, что ни один тепловой двигатель,
работающий при двух заданных температурах,
не может быть эффективнее идеального
двигателя Карно (это утверждение называют
теоремой
Карно). В
противном случае мы столкнулись бы с
нарушением второго
начала термодинамики,
поскольку такой двигатель отбирал бы
тепло от менее нагретого резервуара и
передавал бы его более нагретому. (На
самом деле, второе начало термодинамики
является следствием теоремы Карно. )Теорема
)Теорема
Карно 1)КПД
тепловой машины, работающей с данными
нагревателя и холодильником по прямому
обратному циклу карно, не зависит от
рода вещества, а определяется лишь Тн
и Тх.
2)КПД тепловой машины, работающей по
прямому обратному циклу будет всегда
больше КПД тепловой машины, работающей
по не обратному циклу с тем же нагревателем
и холодильником.
коэффициент.
II закон термодинамики в формулировке
Клаузиуса.
Обратный
цикл – цикл проходящий против часовой
стрелки.
Холодильный
коэффициент — безразмерная величина
(обычно больше единицы), характеризующая
эффективность работы холодильной
машины. Она равна
отношению холодопроизводительности
к количеству энергии (работе), затраченной
в единицу времени на осуществление
холодильного цикла. Определяется типом
холодильного цикла, по котором у работает
машина, совершенством её основных
элементов и для одной и той же машины
зависит от температурных условий её
работы.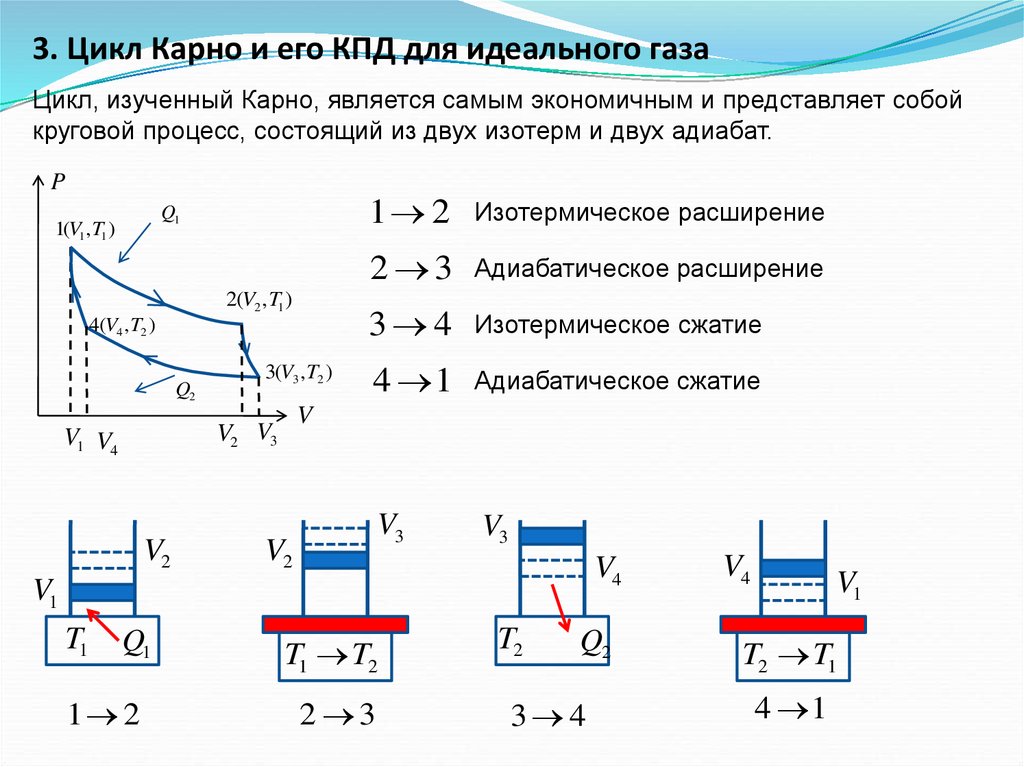 При заданной температуре
При заданной температуре
окружающей среды Т
на единицу полученного искусственного
холода затрачивается тем большая
энергия, чем ниже температура охлаждаемого
объекта.
Холодильная
машина — устройство,
служащее для отвода теплоты от охлаждаемого
тела при температуре более низкой, чем
температура окружающей среды. Х. м.
работают по принципу теплового
насоса
— отнимают теплоту от охлаждаемого
тела и с затратой энергии (механической,
тепловой и т.д.) передают её охлаждающей
среде, имеющей более высокую температуру,
чем охлаждаемое тело.
«Теплота
не может самопроизвольно переходить
от тела менее нагретого к телу более
нагретому».Рудольф Клаузиус.
Второе
начало термодинамики не только установило
границы преобразования тепла в работу,
но и позволило построить рациональную
шкалу температур (термодинамическая
шкала температур) и установить направление
процессов, происходящих в теплоизолированных
системах.
Х. м.
м.
– устройство, которое
работает по обратному циклу, передовая
теплоту от < нагретых к > нагретым
телам за счет А’
внешних сил. Основные компоненты: 1)
холодильник,
2)
рабочее тело, 3)нагреватель.
25)Приведенное
количество теплоты. Приведенное
количество теплоты в обратимых и
необратимых процессах – неравенство
Клаузиуса.
Рассматривая
процессы превращения тепла в работу,
Р. Клаузиус сформулировал термодинамическое
неравенство (неравенство
Клаузиуса): «Приведенное
количество тепла, полученное системой
в ходе произвольного кругового процесса,
не может быть больше нуля».
где
Q
– количество тепла, полученное системой
при температуре Т, Q1
количество тепла, получаемое системой
от участков окружающей среды с температурой
Т1,
Q2
– количество тепла, отдаваемое системой
участкам окружающей среды при температуре
Т2.
Неравенство Клаузиуса позволяет
установить верхний предел термического
КПД при переменных температурах
нагревателя и холодильника.
,
где
Т1 макс
– максимальная температура участка
среды, от которого система получает
тепло; Т2 мин –
минимальная температура участка среды,
которому система отдает тепло.
Из
выражения для обратимого цикла Карно
следует, что
или
,
т.е.
для обратимого цикла неравенство
Клаузиуса переходит в равенство. Это
означает, что приведенное количество
тепла, полученное системой в ходе
обратимого процесса, не зависит от вида
процесса, а определяется только начальным
и конечным состояниями системы. Поэтому
приведенное количество тепла, полученное
системой в ходе обратимого процесса,
служит мерой изменения функции состояния
системы, называемой энтропией.
26)
Энтропия термодинамических систем —
функция состояния. Изменение
Изменение
энтропии в замкнутых системах при
обратимых и необратимых процессах.
Закон возрастания энтропии. Примеры,
подтверждающие закон возрастания
энтропии.
Энтропия
системы – функция ее
состояния, определенная с точностью до
произвольной постоянной. Приращение
энтропии равно приведенному количеству
тепла, которое нужно сообщить системе,
чтобы перевести ее из начального
состояния в конечное по любому обратимому
процессу.
,
.
Важной
особенностью энтропии является ее
возрастание в изолированных системах
(закон возрастания энтропии): «Энтропия
теплоизолированной (адиабатической)
системы не может убывать; она возрастает,
если в системе идет необратимый процесс,
и остается постоянной при обратимом
процессе в системе».
Необратимые
процессы в системе приводят к установлению
равновесного состояния. В этом состоянии
энтропия изолированной системы достигает
максимума и в дальнейшем никакие
макроскопические процессы в системе
невозможны.
Изменение
энтропии при наличии теплообмена с
окружающей средой, может быть каким
угодно: как больше нуля, так и меньше
нуля.
Получим
выражение для приращения энтропии
идеального газа при переходе из состояния
с параметрами T1,
V1
в состояние с параметрами T2,
V2:
Из
выражения для приращения энтропии газа
следует, что энтропия является функцией
двух параметров
температуры и объема S=S(T,V).
Введение
энтропии позволяет объединить первое
и второе начала термодинамики в виде
термодинамического неравенства
,
где
знак равенства относится к обратимым
процессам, знак неравенства
к необратимым. Энтропия, как и внутренняя
энергия, связана с микроскопическим
строением системы и статистическим
характером теплового движения частиц
системы.
Тепловые машины. Цикл Карно. Школьный курс физики
Главная | Физика 10 класс | Тепловые машины. Цикл Карно
Цикл Карно
Тепловые двигатели.
Большая часть двигателей на Земле — тепловые машины, т. е. устройства, превращающие внутреннюю энергию тел в механическую энергию и обратно. По способу теплообмена и совершения механической работы тепловые машины разделяют на
тепловые двигатели и холодильные установки. К тепловым двигателям относят поршневые, роторные и реактивные, а к холодильным установкам — домашние холодильники и кондиционеры.
В силу необратимости процессов в природе существуют определённые ограничения на возможность использования внутренней энергии для совершения работы тепловыми двигателями. Так, ни один тепловой двигатель не может иметь КПД, равный единице.
Коэффициентом полезного действия (КПД) η теплового двигателя называют физическую величину, равную отношению совершённой двигателем работы А к количеству теплоты Q, полученному для этой цели.
При адиабатическом расширении газа в цилиндре работа совершается за счёт убыли его внутренней энергии без передачи количества теплоты другим телам. Согласно первому закону термодинамики, ΔU = А, A’ = -А = -ΔU. При изотермическом процессе всё передаваемое газу количество теплоты оказывается равным работе газа: А’ = Q. Однако как в первом, так и во втором процессе работа совершается при однократном расширении газа до давления, равного внешнему (например, атмосферному давлению). Тепловой двигатель же должен работать длительное время. Это возможно лишь в том случае, когда все части двигателя (поршни, клапаны и т. д.) совершают движения, повторяющиеся через определённые промежутки времени. Тем самым, двигатель должен периодически по прошествии одного рабочего цикла возвращаться в исходное состояние, или же в двигателе должен совершаться неизменный во времени (стационарный) процесс (например, непрерывное вращение турбины).
Для того чтобы возвратить газ в цилиндре в исходное состояние, его необходимо сжать. Для сжатия газа над ним следует совершить работу. Работа сжатия будет меньше работы, совершаемой самим газом при расширении, если газ сжимать при меньшей температуре, а значит, и при меньшем давлении, чем это происходило при расширении газа. Для этого до сжатия или в процессе сжатия газ охлаждают, передав некоторое количество теплоты другим телам (холодильнику).
Для сжатия газа над ним следует совершить работу. Работа сжатия будет меньше работы, совершаемой самим газом при расширении, если газ сжимать при меньшей температуре, а значит, и при меньшем давлении, чем это происходило при расширении газа. Для этого до сжатия или в процессе сжатия газ охлаждают, передав некоторое количество теплоты другим телам (холодильнику).
Принцип действия теплового двигателя.
Рабочим телом тепловых двигателей является газ или пар, который совершает работу при расширении. Обозначим начальную температуру рабочего тела через T1. Эту температуру в паровых турбинах или машинах приобретает пар в паровом котле. В двигателях внутреннего сгорания и газовых турбинах повышение температуры происходит при сгорании топлива внутри самого двигателя. Температуру T1 называют температурой нагревателя. По мере совершения работы газ теряет энергию и неизбежно охлаждается до некоторой температуры T2. Эта температура не может быть ниже температуры окружающей среды, так как в противном случае давление газа станет меньше атмосферного и двигатель не сможет работать.
Эта температура не может быть ниже температуры окружающей среды, так как в противном случае давление газа станет меньше атмосферного и двигатель не сможет работать.
Температуру T2 называют температурой холодильника. Холодильником являются атмосфера или специальные устройства для охлаждения и конденсации отработанного пара — конденсаторы. Таким образом, в двигателе рабочее тело при расширении не может отдать всю свою внутреннюю энергию на совершение работы. Часть энергии неизбежно передаётся атмосфере (холодильнику) вместе с отработанным паром или выхлопными газами двигателей внутреннего сгорания и газовых турбин. Эта часть внутренней энергии безвозвратно теряется.
Принципиальная схема теплового двигателя изображена на рисунке 7.20.
Рис. 7.20
Рабочее тело двигателя получает при сгорании топлива количество теплоты Q1, совершает работу А’ и передаёт холодильнику количество теплоты Q2 < Q1.
Согласно закону сохранения энергии работа, совершаемая двигателем, равна
А’ = Q1 — Q2.
Тогда КПД теплового двигателя будет равен
Так как у всех двигателей некоторое количество теплоты передаётся холодильнику, то η < 1.
Идеальная тепловая машина Карно.
Представляет большой интерес нахождение максимально возможного КПД теплового двигателя при использовании нагревателя и холодильника с заданными температурами. C целью решения этой важной для теплотехники задачи французский учёный и военный инженер Сади Карно (1796—1832) придумал идеальную тепловую машину. Все процессы в ней рассматриваются как равновесные (обратимые). В машине Карно осуществляется круговой процесс, или цикл, при котором система после ряда преобразований возвращается в исходное состояние.
Цикл Карно состоит из двух изотерм и двух адиабат (рис. 7.21).
Рис. 7.21
Кривые 1—2 и 3—4 — это изотермы, а 2—3 и 4—1 — адиабаты. Сначала газ расширяется изотермически при температуре нагревателя T1. При этом он получает от нагревателя количество теплоты Q1. Затем он адиабатически расширяется и не обменивается количеством теплоты с окружающими телами. Далее следует изотермическое сжатие газа при температуре холодильника T2. В этом процессе газ отдаёт холодильнику количество теплоты Q2. Наконец, газ сжимается адиабатически и возвращается в начальное состояние.
Сначала газ расширяется изотермически при температуре нагревателя T1. При этом он получает от нагревателя количество теплоты Q1. Затем он адиабатически расширяется и не обменивается количеством теплоты с окружающими телами. Далее следует изотермическое сжатие газа при температуре холодильника T2. В этом процессе газ отдаёт холодильнику количество теплоты Q2. Наконец, газ сжимается адиабатически и возвращается в начальное состояние.
При изотермическом расширении газ совершает работу A’1 > 0, равную количеству теплоты Q1. При адиабатическом расширении 2—3 положительная работа A’3 равна уменьшению внутренней энергии при охлаждении газа от температуры T1 до температуры T2: A’3 = -ΔU12 = U(T1)-U(T2).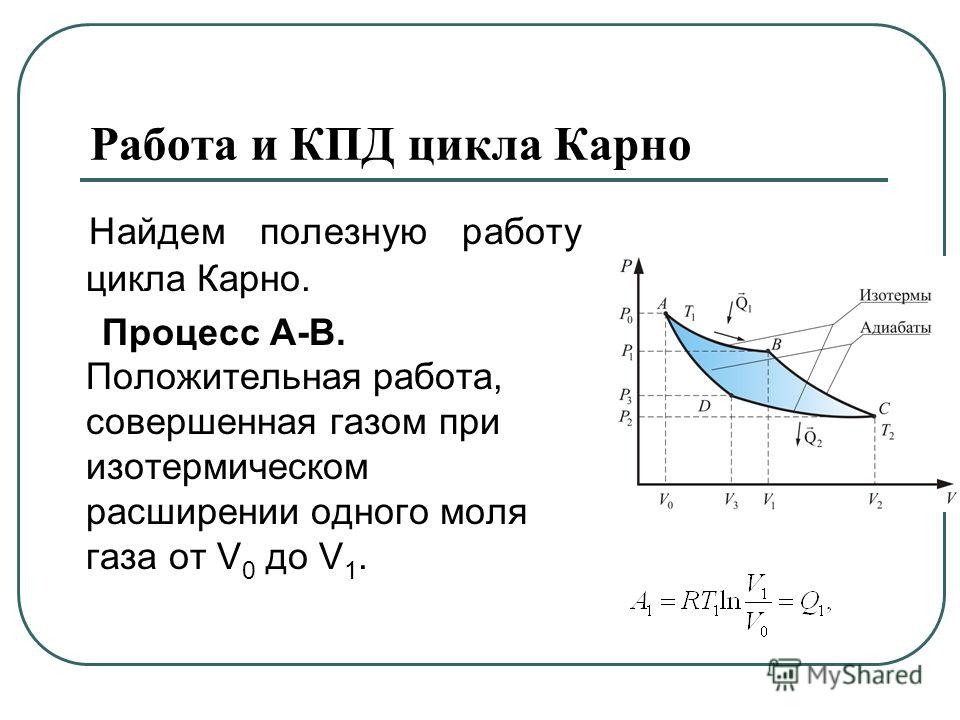
Изотермическое сжатие при температуре T2 требует совершения над газом работы A2. Газ совершает соответственно отрицательную работу A’2 = —A2 = Q2. Адиабатическое сжатие приводит к совершению над газом работы A4 = ΔU21. Работа самого газа A’4 = —A4 = — ΔU21 = U(T2)-U(T1). Поэтому суммарная работа газа при двух адиабатических процессах равна нулю.
Итак, за цикл Карно газ совершает работу:
Для вычисления КПД идеальной тепловой машины Карно нужно вычислить значения работ при изотермических процессах 1—2 и 3—4. Расчёты привели Карно к следующему результату:
Максимально возможный КПД тепловой машины, работающей по циклу Карно, всегда меньше единицы. КПД идеальной тепловой машины зависит от температур T1нагревателя и T2холодильника и не зависит от природы рабочего тела. В таком двигателе устранены любые потери энергии, кроме передачи энергии холодильнику. Но в реальных двигателях всегда существуют потери энергии, например из-за трения и рассеяния энергии в окружающую среду.
КПД идеальной тепловой машины зависит от температур T1нагревателя и T2холодильника и не зависит от природы рабочего тела. В таком двигателе устранены любые потери энергии, кроме передачи энергии холодильнику. Но в реальных двигателях всегда существуют потери энергии, например из-за трения и рассеяния энергии в окружающую среду.
Из формулы (1) следует, что для повышения КПД теплового двигателя необходимо повышать температуру нагревателя и понижать температуру холодильника.
Идеальная холодильная машина.
Цикл Карно обратим, поэтому его можно провести в обратном направлении. Тем самым, у нас получится идеальная холодильная машина. При этом процессы пойдут в обратном порядке, работа А совершается для приведения в действие машины.
Количество теплоты Q1 передаётся рабочим телом нагревателю более высокой температуры, а количество теплоты Q2 поступает к рабочему телу от холодильника (рис. 7.22).
7.22).
Рис. 7.22
Таким образом, количество теплоты передаётся от холодного тела к горячему, поэтому данную машину и называют холодильной. Но второму закону термодинамики это не противоречит: количество теплоты переходит не само собой, а за счёт совершения работы.
Эффективность холодильной машины характеризуют отношением ε = Q2/ A. Физическую величину ε называют холодильным коэффициентом. Для идеальной холодильной машины
Из формулы (2) следует, что холодильный коэффициент тем больше, чем меньше разность температур, и тем меньше, чем меньше температура того тела, которое отдаёт количество теплоты.
Очевидно, холодильный коэффициент может быть больше единицы. Для реальных холодильников ε > 3. Разновидностью холодильной машины является кондиционер, который забирает количество теплоты из комнаты и передаёт его окружающему воздуху.
Вопросы:
1. Опишите схему работы теплового двигателя.
2. Какую физическую величину называют КПД теплового двигателя?
3. Это представляет собой цикл Карно? Какие процессы происходят в цикле Карно?
4. Как можно определить КПД идеальной тепловой машины, работающей по циклу Карно?
5. Как можно повысить КПД теплового двигателя?
6. Какие процессы происходят в идеальной холодильной машине, работающей по циклу Карно?
Вопросы для обсуждения:
1. Что является рабочим телом, нагревателем и холодильником:
а) в ракетном двигателе;
б) в дизельном двигателе?
2. Древнегреческий учёный и изобретатель Герои Александрийский в трактате «Пневматика» описал различные пневматические устройства. Одним из них является эолипил — полый шар, укреплённый на оси (рис. 7.23).
Рис. 7.23
Шар снабжён двумя выступающими диаметрально противоположными изогнутыми трубками; под ним установлен сосуд, частично заполненный водой.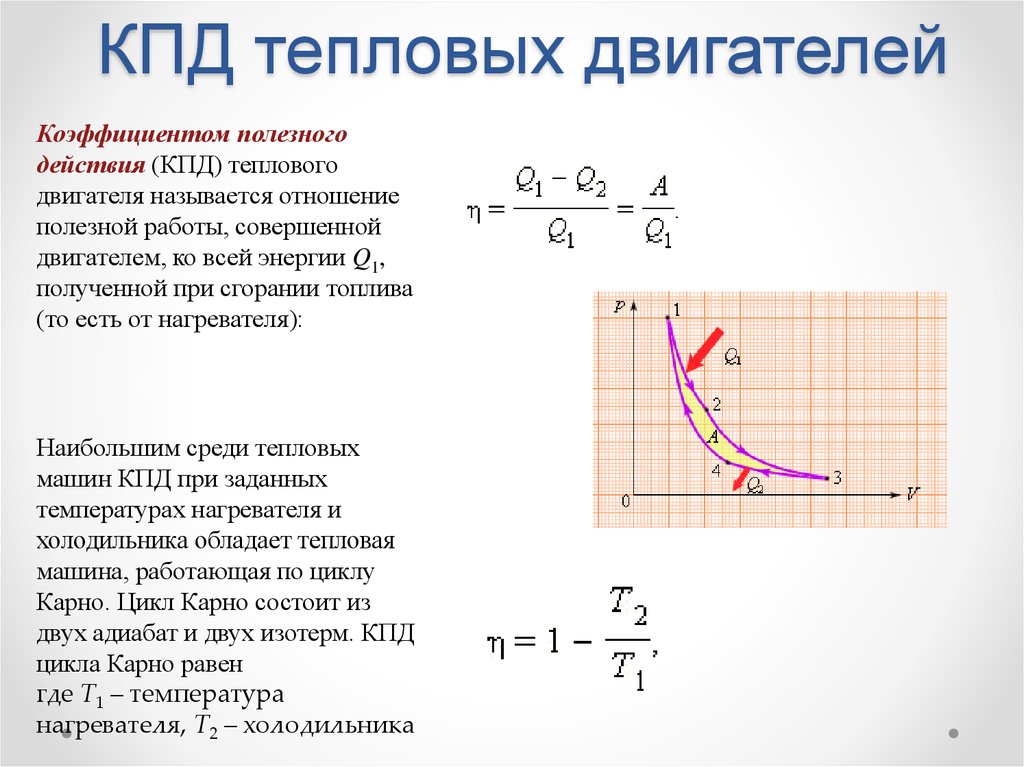 Когда под сосудом разводили огонь, вода в нём закипала, образующийся пар поступал во внутреннюю полость шара по пароотводам и вытекал из неё по изогнутым трубкам, вызывая вращение шара. Прообразом какого современного технического устройства стал эолипил Герона?
Когда под сосудом разводили огонь, вода в нём закипала, образующийся пар поступал во внутреннюю полость шара по пароотводам и вытекал из неё по изогнутым трубкам, вызывая вращение шара. Прообразом какого современного технического устройства стал эолипил Герона?
3. На рисунке 7.24 изображена схема устройства простейшей паровой турбины.
Рис. 7.24
На вал 1 насажен массивный диск 2. на котором укреплены лопасти 3. На лопасти поступает пар из сопел 4. Какие преобразования энергии происходят при работе паровой турбины?
Что является в паровой турбине:
а) нагревателем;
б) рабочим телом;
в) холодильником?
Какими преимуществами обладает паровая турбина по сравнению с двигателем внутреннего сгорания?
Пример решения задачи
КПД тепловой машины равен 40%. Каким станет КПД этой машины, если количество теплоты, получаемое машиной за цикл, увеличить на 20%, а количество теплоты, отдаваемое холодильнику, уменьшить на 10% ?
Ответ: η2 = 55%.
Упражнения:
1. Определите КПД теплового двигателя, работающего по циклу Карно, если температура нагревателя равна 400 К, а температура холодильника — 300 К.
2. В идеальной тепловой машине температура нагревателя в 3 раза больше температуры холодильника. Какую работу совершила машина, если она получила от нагревателя количество теплоты, равное 42 кДж?
3. Совершая замкнутый цикл, газ получил от нагревателя количество теплоты, равное 4130 Дж. Какую работу совершил газ в результате протекания всего цикла, если КПД цикла равен 17% ?
4. В идеальной тепловой машине 2/3 количества теплоты, полученного от нагревателя, рабочее тело отдаёт холодильнику. Температура холодильника равна 0 °C. Определите температуру нагревателя.
5. В идеальной тепловой машине за счёт каждого килоджоуля энергии, получаемой от нагревателя, совершается работа, равная 300 Дж. Определите КПД тепловой машины и температуру нагревателя, если температура холодильника равна 280 К.
Это любопытно…
Из истории развития физики и техники
К выводу о том, что тепловые процессы происходят при передаче количества теплоты от более нагретых тел к менее нагретым, впервые пришёл Карно. В книге «Размышления о движущей силе огня и о машинах, способных развивать эту силу» (1824) он на основе теории теплорода выполнил анализ существовавших в то время паровых машин и сформулировал условия, при которых КПД достигает максимального значения (в паровых машинах того времени КПД не превышал 2%). Оказалось, что только разность температур определяет КПД теплового двигателя, рабочее же тело не играет никакой роли (теорема Карно). Кроме того, Карно ввёл в обиход ряд терминов, которые до сих пор используются в термодинамике: идеальная тепловая машина, идеальный цикл, обратимость процесса и т. п. Карно вычислил КПД идеальной тепловой машины и доказал, что он является максимально возможным для любого реального теплового двигателя.
C. Карно
Спустя 10 лет после смерти Карно Клапейрон привлёк внимание научной общественности к его работам.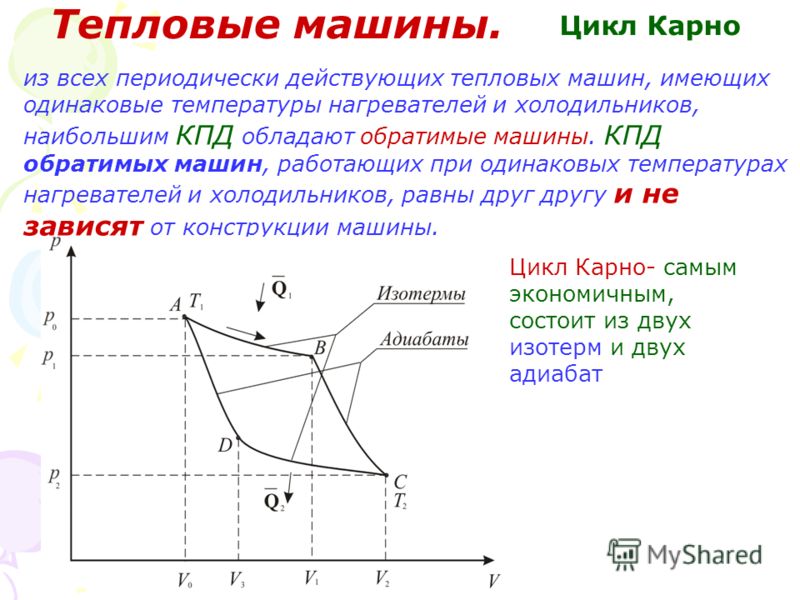 Благодаря Клапейрону идеи Карно стали широко известны и позволили Томсону, Клаузиусу и другим учёным разработать основы классической термодинамики.
Благодаря Клапейрону идеи Карно стали широко известны и позволили Томсону, Клаузиусу и другим учёным разработать основы классической термодинамики.
Более подробно на сайте «История техники»
Предыдущая страницаСледующая страница
Термодинамика
Термодинамика
Тепло
двигатели преобразуют внутреннюю энергию в механическую энергию.работу обратимой тепловой машины можно описать на ФВ
диаграмма.КПД обратимой тепловой машины зависит от
температуры, между которыми он работает.Мы
опишет тепловую машину с помощью такой диаграммы:Вопрос ч = Q с +
ВтКПД тепловой машины
описывает, насколько эффективно он превращает теплоту в работу.Сади Карно
Принцип Карно: An
необратимая тепловая машина, работающая между двумя тепловыми резервуарами при
постоянные температуры не могут иметь КПД больше, чем
обратимой тепловой машины, работающей между двумя
температуры.Следствие: Все обратимы
тепловые двигатели, работающие при одинаковых температурах, имеют
такая же эффективность .Цикл Карно:
Реверсивный «двигатель» Карно использует
изотермические и адиабатические процессы между двумя резервуарами тепла при
температуры Т ч (горячая) и Т с
(холодный).A Цикл Карно также может быть
представлен на диаграмме PV.Холодильник — это тепловая машина, обкатываемая в
реверс .Вт + Q с =
Q чДругой формой второго закона термодинамики является
чтоНевозможно сделать
тепловой двигатель, единственным действием которого является поглощение тепла от
области высоких температур и превратить все это тепло в
работа.
То есть нельзя
спроектировать тепловую машину, которая отдает , а не тепла отработавших газов.
среда.Или невозможно спроектировать
тепловой двигатель с КПД 1,00 или 100%.Если бы мы могли разработать такой 100%
эффективную тепловую машину, тогда мы могли бы использовать эту тепловую машину
для питания холодильника. И чистый результат этой комбинации
было бы заставить тепло течь от холодной температуры к высокой
температура.и , что возвращает нас к нашему
оригинальное утверждение Второго Закона
Термодинамика:
Секунда
ЗаконНастоящее тепло
ДвигателиВозврат в ToC, Нагрев
Трансфер(c) 2002 г.
, Дуг Дэвис; все права защищены
13.5: Второй закон термодинамики
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 18083
- Boundless (теперь LumenLearning)
- Boundless
- Сравните концепцию необратимости между Первым и Вторым законами термодинамики
- Обоснуйте, почему КПД является одним из важнейших параметров любой тепловой машины
- Проанализировать, почему двигатель Карно считается идеальным двигателем
- Объяснить, как компоненты теплового насоса вызывают передачу тепла от холодного резервуара к горячему
- Многие термодинамические явления, допускаемые первым законом термодинамики, никогда не происходят в природе.
- Многие процессы происходят самопроизвольно только в одном направлении, и второй закон термодинамики имеет дело с направлением самопроизвольных процессов.

- Согласно второму закону термодинамики, ни один процесс не может иметь единственным результатом передачу тепла от более холодного объекта к более горячему.
- Циклический процесс возвращает систему, например газ в цилиндре, в исходное состояние в конце каждого цикла. В большинстве тепловых двигателей, таких как поршневые двигатели и вращающиеся турбины, используются циклические процессы.
- Второй закон термодинамики можно выразить следующим образом: ни в какой системе теплопередача от резервуара не может полностью превратиться в работу в циклическом процессе, при котором система возвращается в исходное состояние.
- Эффективность тепловой машины (Eff) определяется как чистая мощность работы двигателя W, деленная на теплоотдачу двигателю: Eff=WQh=1−QcQhEff=WQh=1−QcQh, где Q c и Q h обозначает теплопередачу в горячий (двигатель) и холодный (окружающая среда) резервуар.
- Второй закон термодинамики указывает, что двигатель Карно, работающий между двумя заданными температурами, имеет максимально возможный КПД любой тепловой машины, работающей между этими двумя температурами.

- В необратимых процессах участвуют диссипативные факторы, что снижает КПД двигателя. Очевидно, что обратимые процессы лучше с точки зрения эффективности.
- Эффективность Карно, максимально достижимая эффективность тепловой машины, определяется как Effc=1−TcThEffc=1−TcTh.
- Задачей теплового насоса является передача тепла Qh в теплую среду, например, в дом зимой.
- Задача кондиционеров и холодильников заключается в передаче тепла Qc из прохладной среды, например, при охлаждении помещения или хранении продуктов при более низких температурах, чем температура окружающей среды.
- Тепловой насос можно использовать как для обогрева, так и для охлаждения помещения. По сути, это кондиционер и обогреватель в одном флаконе. Это стало возможным благодаря реверсированию потока его хладагента, изменению направления полезной теплопередачи.
- энтропия : Мера того, насколько равномерно энергия (или какое-либо аналогичное свойство) распределяется в системе.

- первый закон термодинамики : Вариант закона сохранения энергии, специализированный для термодинамических систем. Обычно выражается как ΔU=Q-W.
- тепловая энергия : Внутренняя энергия системы, находящейся в термодинамическом равновесии из-за ее температуры.
- внутренняя энергия : сумма всей энергии, присутствующей в системе, включая кинетическую и потенциальную энергию; эквивалентно энергии, необходимой для создания системы, за исключением энергии, необходимой для смещения ее окружения.
- второй закон термодинамики : Закон, утверждающий, что энтропия изолированной системы никогда не уменьшается, потому что изолированные системы самопроизвольно эволюционируют к термодинамическому равновесию — состоянию максимальной энтропии. Точно так же вечные двигатели второго рода невозможны.
- тепловая машина : Любое устройство, преобразующее тепловую энергию в механическую работу.

- CFC : Органическое соединение, обычно используемое в качестве хладагента. Больше не используется из-за эффекта разрушения озонового слоя.
- Курирование и пересмотр. Предоставлено : Boundless.com. Лицензия : CC BY-SA: Attribution-ShareAlike
- OpenStax College, College Physics. 17 сентября 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42234/latest…ol11406/latest . Лицензия : CC BY: Attribution
- первый закон термодинамики. Предоставлено : Википедия. Расположен по адресу : en.
 Wikipedia.org/wiki/the%20f…термодинамика . Лицензия : CC BY-SA: Attribution-ShareAlike
Wikipedia.org/wiki/the%20f…термодинамика . Лицензия : CC BY-SA: Attribution-ShareAlike - энтропия. Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/entropy . Лицензия : CC BY-SA: Attribution-ShareAlike
- Колледж OpenStax, Колледж физики. 13 февраля 2013 г. Предоставлено : OpenStaxCNX. Расположен по адресу : http://cnx.org/content/m42234/latest…ol11406/latest . Лицензия : CC BY: Attribution
- Термодинамика и тепловые двигатели. Расположен по адресу : http://www.youtube.com/watch?v=I4_AfJo17qQ . Лицензия : Общественное достояние: неизвестно Авторские права .
 Условия лицензии : Стандартная лицензия YouTube
Условия лицензии : Стандартная лицензия YouTube - Колледж OpenStax, Колледж физики. 17 сентября 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42234/latest…ol11406/latest . Лицензия : CC BY: Attribution
- Тепловая машина. Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Heat_engine . Лицензия : CC BY-SA: Attribution-ShareAlike
- Безграничный. Предоставлено : Безграничное обучение. Расположен по адресу : www.boundless.com//physics/de…nternal-energy . Лицензия : CC BY-SA: Attribution-ShareAlike
- Тепловая энергия.
 Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Thermal_energy . Лицензия : CC BY-SA: Attribution-ShareAlike
Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Thermal_energy . Лицензия : CC BY-SA: Attribution-ShareAlike - Колледж OpenStax, Колледж физики. 13 февраля 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42234/latest…ol11406/latest . Лицензия : CC BY: Attribution
- Термодинамика и тепловые двигатели. Расположен по адресу : http://www.youtube.com/watch?v=I4_AfJo17qQ . Лицензия : Общественное достояние: неизвестно Авторские права . Условия лицензии : Стандартная лицензия YouTube
- Термодинамика и тепловые двигатели. Расположен по адресу : http://www.
 youtube.com/watch?v=I4_AfJo17qQ . Лицензия : Общественное достояние: неизвестно Авторские права . Условия лицензии : Стандартная лицензия YouTube
youtube.com/watch?v=I4_AfJo17qQ . Лицензия : Общественное достояние: неизвестно Авторские права . Условия лицензии : Стандартная лицензия YouTube - Колледж OpenStax, Колледж физики. 13 февраля 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42234/latest…ol11406/latest . Лицензия : CC BY: Attribution
- Колледж OpenStax, Колледж физики. 17 сентября 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42235/latest…ol11406/latest . Лицензия : CC BY: Attribution
- Безграничный. Предоставлено : Безграничное обучение. Расположен по адресу : www.
 boundless.com//physics/de…thermodynamics . Лицензия : CC BY-SA: Attribution-ShareAlike
boundless.com//physics/de…thermodynamics . Лицензия : CC BY-SA: Attribution-ShareAlike - . Предоставлено : Викисловарь. Расположен по адресу : en.wiktionary.org/wiki/heat_engine . Лицензия : CC BY-SA: Attribution-ShareAlike
- Колледж OpenStax, Колледж физики. 13 февраля 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42234/latest…ol11406/latest . Лицензия : CC BY: Attribution
- Термодинамика и тепловые двигатели. Расположен по адресу : http://www.youtube.com/watch?v=I4_AfJo17qQ . Лицензия : Общественное достояние: неизвестно Авторское право .
 Условия лицензии : Стандартная лицензия YouTube
Условия лицензии : Стандартная лицензия YouTube - Термодинамика и тепловые двигатели. Расположен по адресу : http://www.youtube.com/watch?v=I4_AfJo17qQ . Лицензия : Общественное достояние: неизвестно Авторские права . Условия лицензии : Стандартная лицензия YouTube
- Колледж OpenStax, Колледж физики. 13 февраля 2013 г. Предоставлено : OpenStaxCNX. Расположен по адресу : http://cnx.org/content/m42234/latest…ol11406/latest . Лицензия : CC BY: Attribution
- Колледж OpenStax, Колледж физики. 16 января 2015 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42235/latest…ol11406/latest . Лицензия : CC BY: Attribution
- Колледж OpenStax, Колледж физики.
 17 сентября 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42236/latest…ol11406/latest . Лицензия : CC BY: Attribution
17 сентября 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42236/latest…ol11406/latest . Лицензия : CC BY: Attribution - Тепловой насос. Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Heat_pump . Лицензия : CC BY-SA: Attribution-ShareAlike
- Безграничный. Предоставлено : Безграничное обучение. Расположен по адресу : www.boundless.com//physics/definition/cfc . Лицензия : CC BY-SA: Attribution-ShareAlike
- Колледж OpenStax, Колледж физики. 13 февраля 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.
 org/content/m42234/latest…ol11406/latest . Лицензия : CC BY: Attribution
org/content/m42234/latest…ol11406/latest . Лицензия : CC BY: Attribution - Термодинамика и тепловые двигатели. Расположен по адресу : http://www.youtube.com/watch?v=I4_AfJo17qQ . Лицензия : Общественное достояние: неизвестно Авторские права . Условия лицензии : Стандартная лицензия YouTube
- Термодинамика и тепловые двигатели. Расположен по адресу : http://www.youtube.com/watch?v=I4_AfJo17qQ . Лицензия : Общественное достояние: неизвестно Авторские права . Условия лицензии : Стандартная лицензия YouTube
- Колледж OpenStax, Колледж физики. 13 февраля 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.
 org/content/m42234/latest…ol11406/latest . Лицензия : CC BY: Attribution
org/content/m42234/latest…ol11406/latest . Лицензия : CC BY: Attribution - Колледж OpenStax, Колледж физики. 16 января 2015 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42235/latest…ol11406/latest . Лицензия : CC BY: Attribution
- Колледж OpenStax, Колледж физики. 13 февраля 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42236/latest…ol11406/latest . Лицензия : CC BY: Attribution
901 97
цели обучения
Необратимость
Второй закон термодинамики касается направления самопроизвольных процессов. Многие процессы протекают самопроизвольно только в одном направлении, т. е. необратимы при данном наборе условий. Хотя необратимость наблюдается в повседневной жизни — например, разбитое стекло не возвращается в исходное состояние — полная необратимость — это статистическое утверждение, которое нельзя увидеть в течение жизни Вселенной.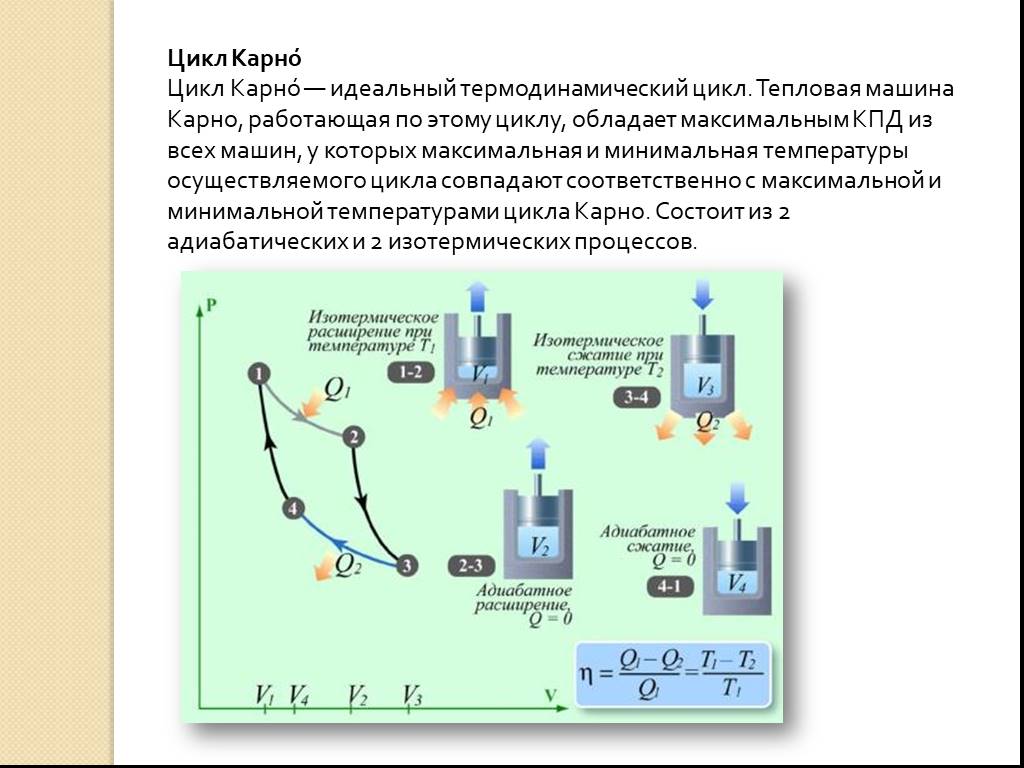 Точнее, необратимый процесс — это процесс, зависящий от пути. Если процесс может идти только в одном направлении, то обратный путь принципиально иной и процесс не может быть обратимым.
Точнее, необратимый процесс — это процесс, зависящий от пути. Если процесс может идти только в одном направлении, то обратный путь принципиально иной и процесс не может быть обратимым.
Например, теплота связана с передачей энергии от более высокой температуры к более низкой. Холодный объект при соприкосновении с горячим никогда не становится холоднее, передавая тепло горячему объекту и делая его горячее. Кроме того, механическая энергия, например кинетическая энергия, может быть полностью преобразована в тепловую энергию трения, но обратное невозможно. Горячий неподвижный объект никогда самопроизвольно не остывает и не приходит в движение. Еще одним примером является расширение струи газа, введенной в один из углов вакуумной камеры. Газ расширяется, заполняя камеру, но никогда не собирается в углу. Беспорядочное движение молекул газа могло бы привести их всех обратно в угол, но этого никогда не происходит.
Односторонняя обработка в природе : Примеры односторонней обработки в природе.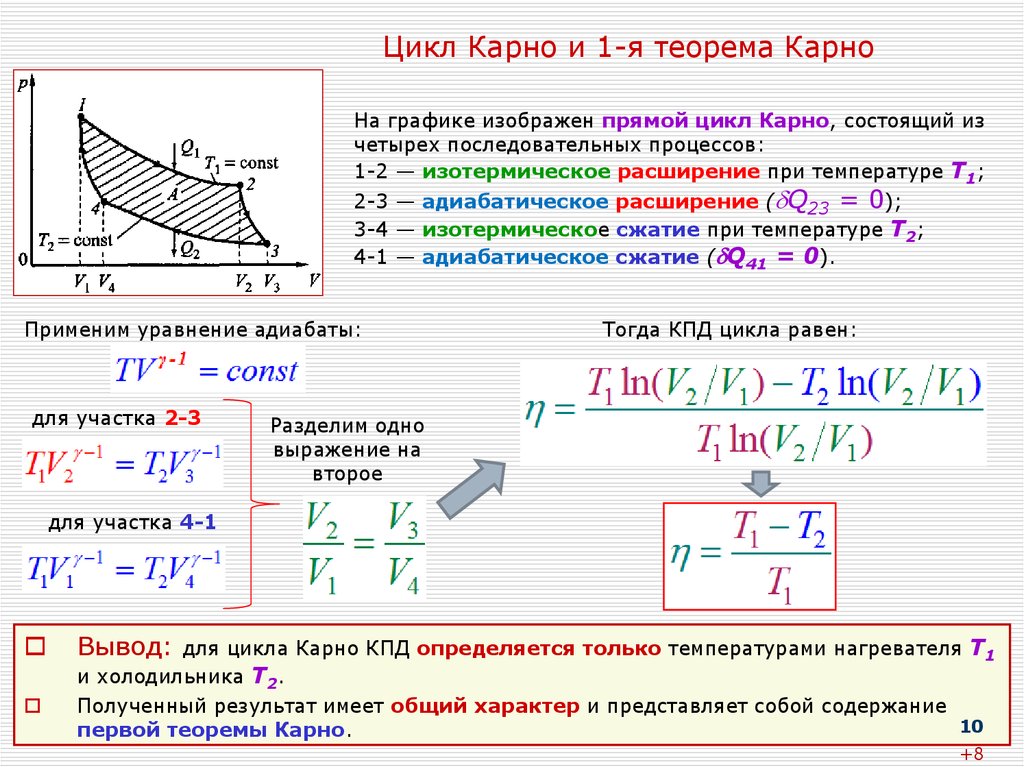 а) Теплопередача происходит самопроизвольно от горячего к холодному, а не от холодного к горячему. (b) Тормоза этого автомобиля преобразуют его кинетическую энергию в передачу тепла окружающей среде. Обратный процесс невозможен. (c) Выброс газа, впущенного в эту вакуумную камеру, быстро расширяется, чтобы равномерно заполнить все части камеры. Беспорядочные движения молекул газа никогда не вернут их в угол.
а) Теплопередача происходит самопроизвольно от горячего к холодному, а не от холодного к горячему. (b) Тормоза этого автомобиля преобразуют его кинетическую энергию в передачу тепла окружающей среде. Обратный процесс невозможен. (c) Выброс газа, впущенного в эту вакуумную камеру, быстро расширяется, чтобы равномерно заполнить все части камеры. Беспорядочные движения молекул газа никогда не вернут их в угол.
Второй закон термодинамики
Тот факт, что определенные процессы никогда не происходят, предполагает, что существует закон, запрещающий им происходить. Первый закон термодинамики допускает их возникновение — ни один из этих процессов не нарушает закон сохранения энергии. Закон, запрещающий эти процессы, называется вторым законом термодинамики. Мы увидим, что второй закон можно сформулировать разными способами, которые могут показаться разными, но на самом деле эти способы эквивалентны. Как и все законы природы, второй закон термодинамики дает представление о природе, и несколько его утверждений подразумевают, что он широко применим, коренным образом влияя на многие, казалось бы, несопоставимые процессы. Уже знакомое нам направление теплопередачи от горячего к холодному лежит в основе нашей первой версии второго закона термодинамики.
Уже знакомое нам направление теплопередачи от горячего к холодному лежит в основе нашей первой версии второго закона термодинамики.
Термодинамика и тепловые двигатели : Краткое введение в тепловые двигатели и термодинамические концепции, такие как двигатель Карно, для студентов.
Второй закон термодинамики (первое выражение): Теплопередача происходит самопроизвольно от тел с более высокой температурой к телам с более низкой температурой, но никогда самопроизвольно в обратном направлении.
Закон гласит, что ни один процесс не может иметь своим единственным результатом передачу тепла от более холодного объекта к более горячему. Позже мы выразим этот закон в других терминах, в первую очередь в терминах энтропии.
Тепловые двигатели
В термодинамике тепловой двигатель представляет собой систему, которая выполняет преобразование тепла или тепловой энергии в механическую работу.
цели обучения
В термодинамике тепловой двигатель представляет собой систему, которая выполняет преобразование тепла или тепловой энергии в механическую работу. Бензиновые и дизельные двигатели, реактивные двигатели и паровые турбины — все это тепловые двигатели, которые работают, используя часть теплопередачи из какого-либо источника. Теплоотдача от горячего объекта (или горячего резервуара) обозначается как Q h , а теплоотдача в холодный объект (или холодный резервуар) равна Q c , а работа двигателя равна W. Температуры горячего и холодного резервуаров равны T h и T c , соответственно.
Теплопередача : (a) Теплопередача происходит спонтанно от горячего объекта к холодному, в соответствии со вторым законом термодинамики. б) Тепловая машина, представленная здесь кружком, использует часть теплопередачи для совершения работы. Горячие и холодные объекты называются горячими и холодными резервуарами. Qh — теплоотдача из горячего резервуара, W — работа, Qc — теплопередача в холодный резервуар.
Горячие и холодные объекты называются горячими и холодными резервуарами. Qh — теплоотдача из горячего резервуара, W — работа, Qc — теплопередача в холодный резервуар.
Термодинамика и тепловые двигатели : Краткое введение в тепловые двигатели и термодинамические концепции, такие как двигатель Карно, для студентов.
Поскольку горячий резервуар нагревается снаружи, что требует больших затрат энергии, важно, чтобы работа выполнялась максимально эффективно. На самом деле хотелось бы, чтобы W было равно Q h , и чтобы не было передачи тепла в окружающую среду (Q c =0). К сожалению, это невозможно. Второй закон термодинамики (второе выражение) также утверждает относительно использования теплопередачи для выполнения работы: Ни в одной системе теплопередачи от резервуара невозможно полностью преобразовать в работу циклический процесс, при котором система возвращается в исходное состояние.
Циклический процесс возвращает систему, например газ в баллоне, в исходное состояние в конце каждого цикла. В большинстве тепловых двигателей, таких как поршневые двигатели и вращающиеся турбины, используются циклические процессы. Второй закон в его второй форме ясно утверждает, что в таких двигателях не может быть совершенного преобразования теплопередачи в совершаемую работу.
Эффективность
Циклический процесс возвращает систему в исходное состояние в конце каждого цикла. По определению внутренняя энергия такой системы U одинакова в начале и в конце каждого цикла, то есть \(\mathrm{ΔU=0}\). Первый закон термодинамики утверждает, что \(\mathrm{ΔU=Q−W}\), где Q — чистая теплопередача в течение цикла (\(\mathrm{W=Q_h−Q_c}\)) и W — чистая работа, выполненная системой. Поскольку \(\mathrm{ΔU=0}\) для полного цикла, мы имеем \(\mathrm{W=Q}\). Таким образом, чистая работа, совершаемая системой, равна чистой передаче тепла в систему, или
\(\mathrm{W=Q_h−Q_c}\) (циклический процесс),
, как схематично показано на (b).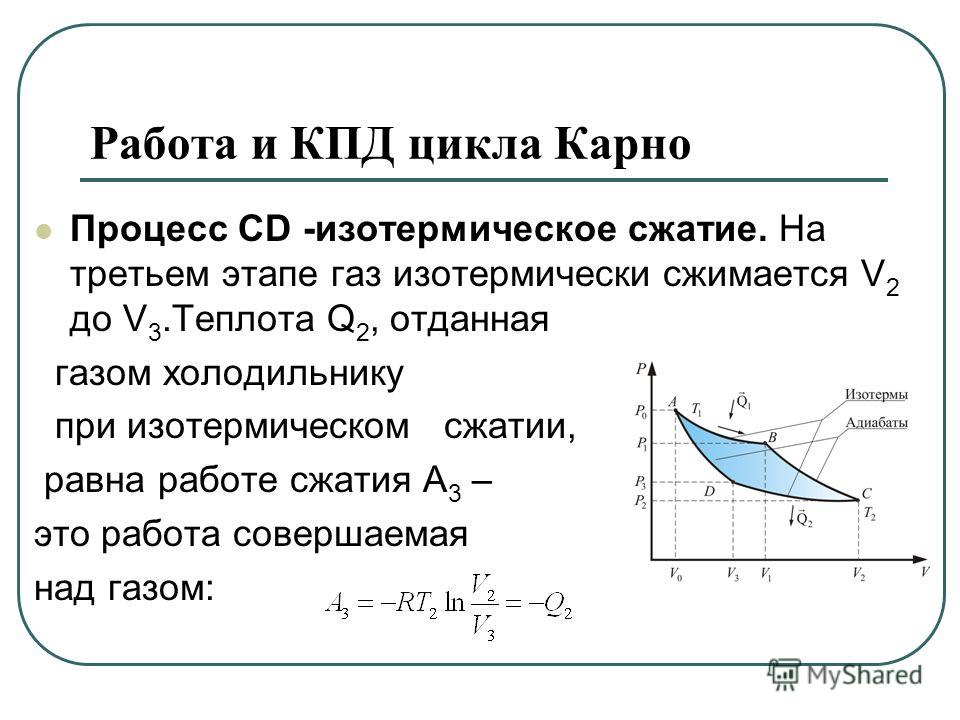
КПД – один из важнейших параметров любой тепловой машины. Проблема в том, что во всех процессах значительная часть тепла Q c теряется в окружающую среду. При преобразовании энергии в работу мы всегда сталкиваемся с проблемой того, что получаем меньше, чем вкладываем. Мы определяем КПД тепловой машины ( Eff ) как его чистую выходную мощность W, деленную на теплоотдачу к двигатель Q h:
\[\mathrm{E_{ff}=WQ_h.}\]
Поскольку \(\mathrm{W=Q_h−Q_c}\) в циклическом процессе, мы также можем выразить это как
\(\mathrm{Eff=\frac{Q_h−Q_c}{Q_h}=1−\frac{Q_c}{Q_h}}\) (для циклического процесса),
, чтобы было ясно, что эффективность 1 или 100 %, возможен только при отсутствии передачи тепла в окружающую среду (Q c =0).
Циклы Карно
Цикл Карно является наиболее эффективным из возможных циклических процессов, в нем используются только обратимые процессы.
цели обучения
Из второго закона термодинамики мы знаем, что тепловая машина не может быть КПД на 100 %, поскольку всегда должна иметь место теплопередача Q c в окружающую среду.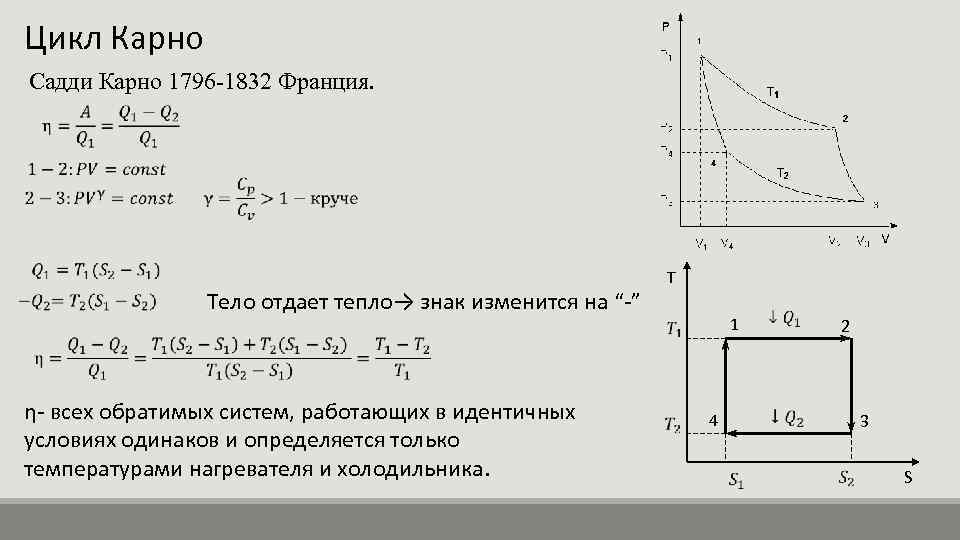 (См. наш атом в разделе «Тепловые двигатели».) Насколько эффективным может быть тогда тепловой двигатель? На этот вопрос на теоретическом уровне ответил молодой французский инженер Сади Карно (1796–1832) в 1824 г., изучая появившуюся в то время технологию теплового двигателя, решающую для промышленной революции. Он разработал теоретический цикл, теперь называемый циклом Карно, который является наиболее эффективным из возможных циклических процессов. Второй закон термодинамики можно переформулировать в терминах цикла Карно, и, таким образом, Карно на самом деле открыл этот фундаментальный закон. Любая тепловая машина, использующая цикл Карно, называется двигателем Карно.
(См. наш атом в разделе «Тепловые двигатели».) Насколько эффективным может быть тогда тепловой двигатель? На этот вопрос на теоретическом уровне ответил молодой французский инженер Сади Карно (1796–1832) в 1824 г., изучая появившуюся в то время технологию теплового двигателя, решающую для промышленной революции. Он разработал теоретический цикл, теперь называемый циклом Карно, который является наиболее эффективным из возможных циклических процессов. Второй закон термодинамики можно переформулировать в терминах цикла Карно, и, таким образом, Карно на самом деле открыл этот фундаментальный закон. Любая тепловая машина, использующая цикл Карно, называется двигателем Карно.
Для цикла Карно важно то, что используются только обратимые процессы. Необратимые процессы связаны с диссипативными факторами, такими как трение и турбулентность. Это увеличивает теплоотдачу Q c в окружающую среду и снижает КПД двигателя. Очевидно, что обратимые процессы предпочтительнее.
Второй закон термодинамики (третья форма): Двигатель Карно, работающий между двумя заданными температурами, имеет максимально возможный КПД любой тепловой машины, работающей между этими двумя температурами.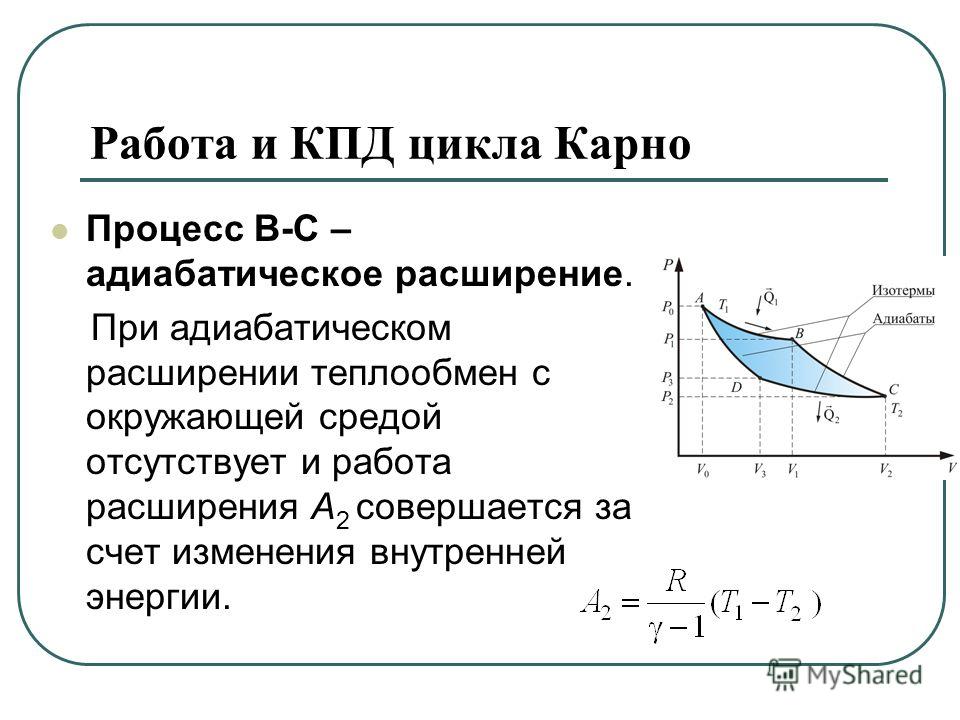 Кроме того, все двигатели, использующие только обратимые процессы, имеют одинаковую максимальную эффективность при работе в пределах одних и тех же заданных температур.
Кроме того, все двигатели, использующие только обратимые процессы, имеют одинаковую максимальную эффективность при работе в пределах одних и тех же заданных температур.
Эффективность
Цикл Карно состоит из двух изотермических и двух адиабатических процессов. Напомним, что и изотермические, и адиабатические процессы в принципе обратимы.
Диаграмма PV для цикла Карно : Диаграмма PV для цикла Карно, использующего только обратимые изотермические и адиабатические процессы. Теплопередача Qh в рабочее тело происходит по изотермическому пути AB, который протекает при постоянной температуре Th. Теплопередача Qc происходит от рабочего тела по изотермическому пути CD, который протекает при постоянной температуре Tc. Чистый выход W равен площади внутри пути ABCDA. Также показана схема двигателя Карно, работающего между горячим и холодным резервуарами при температурах Th и Tc.
Карно также определил КПД идеальной тепловой машины, то есть машины Карно. Всегда верно, что эффективность циклической тепловой машины определяется выражением: \(\mathrm{Eff=\frac{Q_h−Q_c}{Q_h}=1−\frac{Q_c}{Q_h}}\) .
Всегда верно, что эффективность циклической тепловой машины определяется выражением: \(\mathrm{Eff=\frac{Q_h−Q_c}{Q_h}=1−\frac{Q_c}{Q_h}}\) .
Карно обнаружил, что для идеальной тепловой машины отношение \(\mathrm{\frac{Q_c}{Q_h}}}\) равно отношению абсолютных температур тепловых резервуаров. То есть \(\mathrm{\frac{Q_c}{Q_h} = \frac{T_c}{T_h}}\) для двигателя Карно, так что максимальная эффективность или эффективность Карно Eff C определяется выражением \(\mathrm{Eff_c=1−\frac{T_c}{T_h}}\), где T h и T c в градусах Кельвина. (Вывод формулы немного выходит за рамки этого атома.) Никакая настоящая тепловая машина не может работать так же хорошо, как КПД Карно — фактический КПД около 0,7 от этого максимума обычно является лучшим, чего можно достичь.
Тепловые насосы и холодильники
Тепловой насос — это устройство, которое передает тепловую энергию от источника тепла к радиатору против градиента температуры.
цели обучения
Тепловые насосы, кондиционеры и холодильники используют передачу тепла от холодного к горячему. Теплопередача (Q c ) происходит из холодного резервуара в горячий. Для этого требуется затрата работы W, которая также преобразуется в теплопередачу. Таким образом, теплопередача в горячий резервуар равна Q ч = Q с +В. Задачей теплового насоса является передача тепла Q h в теплую среду, например, в дом зимой. Задача кондиционеров и холодильников заключается в передаче тепла Q c из прохладной среды, например, при охлаждении комнаты или хранении продуктов при более низких температурах, чем температура окружающей среды. На самом деле, тепловой насос можно использовать как для обогрева, так и для охлаждения помещения. По сути, это кондиционер и обогреватель в одном флаконе. В этом разделе мы сосредоточимся на его режиме нагрева.
Теплопередача (Q c ) происходит из холодного резервуара в горячий. Для этого требуется затрата работы W, которая также преобразуется в теплопередачу. Таким образом, теплопередача в горячий резервуар равна Q ч = Q с +В. Задачей теплового насоса является передача тепла Q h в теплую среду, например, в дом зимой. Задача кондиционеров и холодильников заключается в передаче тепла Q c из прохладной среды, например, при охлаждении комнаты или хранении продуктов при более низких температурах, чем температура окружающей среды. На самом деле, тепловой насос можно использовать как для обогрева, так и для охлаждения помещения. По сути, это кондиционер и обогреватель в одном флаконе. В этом разделе мы сосредоточимся на его режиме нагрева.
Тепловые насосы
В базовом тепловом насосе используется рабочая жидкость, такая как хладагент, не содержащий хлорфторуглеродов. Основными компонентами теплового насоса являются конденсатор, расширительный клапан, испаритель и компрессор.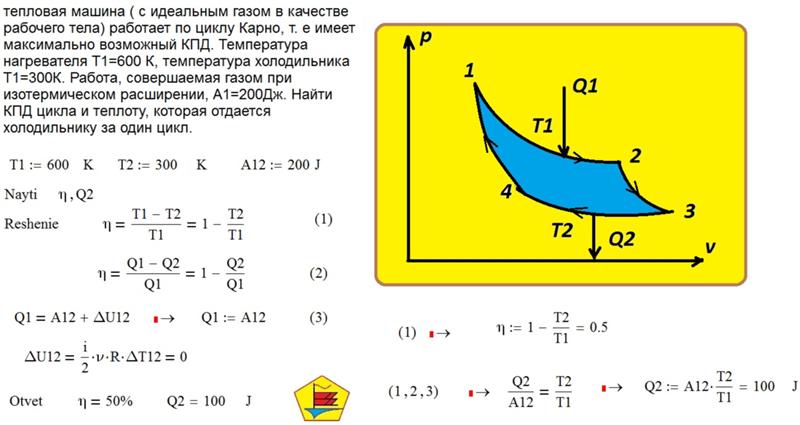 В наружных змеевиках (испарителях) теплообмен Q c происходит от холодного наружного воздуха к рабочему телу, превращая его в газ. Компрессор с электрическим приводом (рабочая мощность W) повышает температуру и давление газа и нагнетает его в змеевики конденсатора, находящиеся внутри отапливаемого помещения. Поскольку температура газа выше температуры внутри помещения, происходит передача тепла в помещение, и газ конденсируется в жидкость. Затем жидкость возвращается через редукционный клапан к наружным змеевикам испарителя, охлаждаясь за счет расширения. (В цикле охлаждения змеевики испарителя и конденсатора меняются ролями, и направление потока жидкости меняется на противоположное.)
В наружных змеевиках (испарителях) теплообмен Q c происходит от холодного наружного воздуха к рабочему телу, превращая его в газ. Компрессор с электрическим приводом (рабочая мощность W) повышает температуру и давление газа и нагнетает его в змеевики конденсатора, находящиеся внутри отапливаемого помещения. Поскольку температура газа выше температуры внутри помещения, происходит передача тепла в помещение, и газ конденсируется в жидкость. Затем жидкость возвращается через редукционный клапан к наружным змеевикам испарителя, охлаждаясь за счет расширения. (В цикле охлаждения змеевики испарителя и конденсатора меняются ролями, и направление потока жидкости меняется на противоположное.)
Простой тепловой насос : Простой тепловой насос состоит из четырех основных компонентов: (1) конденсатор, (2) расширительный клапан, (3) испаритель и (4) компрессор.
Коэффициент полезного действия
О качестве теплового насоса судят по тому, сколько тепла Q ч передается в теплое помещение по сравнению с тем, сколько работы W требуется. Мы определяем коэффициент полезного действия теплового насоса (COP л.с. ) равным
Мы определяем коэффициент полезного действия теплового насоса (COP л.с. ) равным
\[\mathrm{COP_{hp}=\dfrac{Q_h}{W}.}\]
Поскольку КПД тепловой машины равен Eff = W/Q h , мы видим, что COP л.с. = 1/ Eff . Поскольку КПД любой тепловой машины меньше 1, это означает, что КПД л.с. всегда больше 1, то есть теплопередача теплового насоса Q ч всегда больше, чем затраченная на него работа. Еще один интересный момент заключается в том, что тепловые насосы лучше всего работают при небольшой разнице температур. КПД совершенной машины (или машины Карно) равен 9.0004
\[\mathrm{Eff_C=1\dfrac{T_c}{T_h};}\]
Таким образом, чем меньше разность температур, тем меньше КПД и больше КПД л.с. .
Кондиционеры и холодильники
Кондиционеры и холодильники предназначены для охлаждения чего-либо в теплой среде. Как и в случае с тепловыми насосами, для передачи тепла от холодного к горячему требуется затрата работы. О качестве кондиционеров и холодильников судят по величине теплоотдачи Q c происходит из-за холода по сравнению с тем, сколько работы W требуется. То, что считается преимуществом в тепловом насосе, считается отходящим теплом в холодильнике. Таким образом, мы определяем коэффициент полезного действия (COP ref ) кондиционера или холодильника как
О качестве кондиционеров и холодильников судят по величине теплоотдачи Q c происходит из-за холода по сравнению с тем, сколько работы W требуется. То, что считается преимуществом в тепловом насосе, считается отходящим теплом в холодильнике. Таким образом, мы определяем коэффициент полезного действия (COP ref ) кондиционера или холодильника как
\[\mathrm{COP_{ref}=\dfrac{Q_c}{W}.}\]
Поскольку \( \mathrm{Q_h = Q_c + W}\) и \(\mathrm{COP_{hp} = \frac{Q_h}{W}}\), получаем, что
\[\mathrm{COP_{ref}=COP_ {л.с.}−1.}\]
Также из Q h >Q c мы видим, что кондиционер будет иметь более низкий коэффициент полезного действия, чем тепловой насос.
Ключевые моменты
Ключевые термины
ЛИЦЕНЗИИ И АВТОРСТВО
CC ЛИЦЕНЗИОННОЕ СОДЕРЖИМОЕ, ПРЕДОСТАВЛЕННОЕ РАНЕЕ
CC ЛИЦЕНЗИОННОЕ СОДЕРЖИМОЕ, КОНКРЕТНОЕ АВТОРСТВО
Тепловая машина
Эта страница под названием 13.5: Второй закон термодинамики распространяется по незаявленной лицензии и была создана, изменена и/или курирована Boundless.


 , Дуг Дэвис; все права защищены
, Дуг Дэвис; все права защищены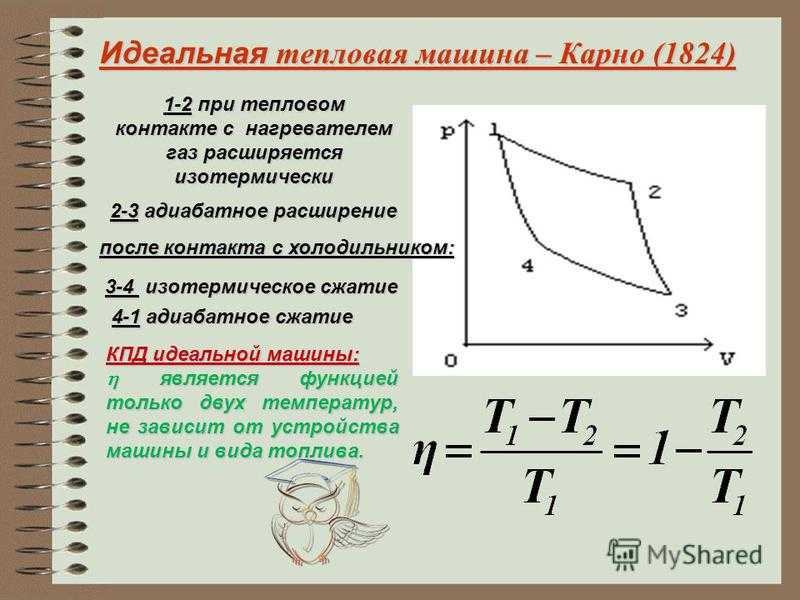


 Wikipedia.org/wiki/the%20f…термодинамика . Лицензия : CC BY-SA: Attribution-ShareAlike
Wikipedia.org/wiki/the%20f…термодинамика . Лицензия : CC BY-SA: Attribution-ShareAlike  Условия лицензии : Стандартная лицензия YouTube
Условия лицензии : Стандартная лицензия YouTube Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Thermal_energy . Лицензия : CC BY-SA: Attribution-ShareAlike
Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Thermal_energy . Лицензия : CC BY-SA: Attribution-ShareAlike  youtube.com/watch?v=I4_AfJo17qQ . Лицензия : Общественное достояние: неизвестно Авторские права . Условия лицензии : Стандартная лицензия YouTube
youtube.com/watch?v=I4_AfJo17qQ . Лицензия : Общественное достояние: неизвестно Авторские права . Условия лицензии : Стандартная лицензия YouTube boundless.com//physics/de…thermodynamics . Лицензия : CC BY-SA: Attribution-ShareAlike
boundless.com//physics/de…thermodynamics . Лицензия : CC BY-SA: Attribution-ShareAlike 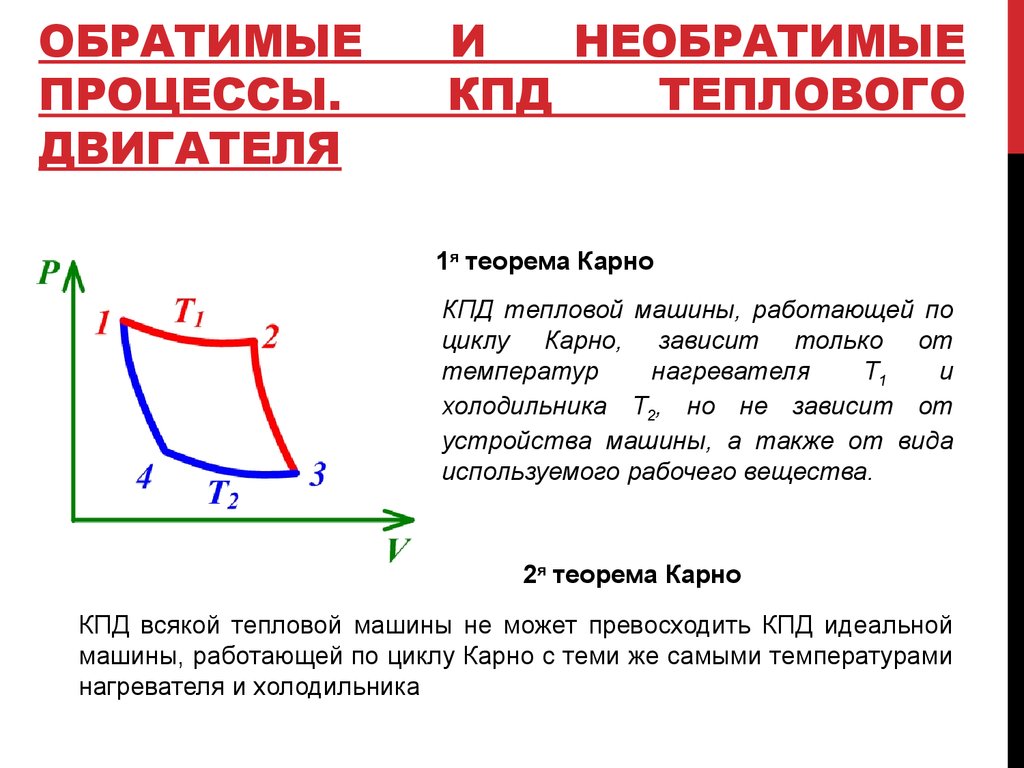 Условия лицензии : Стандартная лицензия YouTube
Условия лицензии : Стандартная лицензия YouTube 17 сентября 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42236/latest…ol11406/latest . Лицензия : CC BY: Attribution
17 сентября 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42236/latest…ol11406/latest . Лицензия : CC BY: Attribution  org/content/m42234/latest…ol11406/latest . Лицензия : CC BY: Attribution
org/content/m42234/latest…ol11406/latest . Лицензия : CC BY: Attribution  org/content/m42234/latest…ol11406/latest . Лицензия : CC BY: Attribution
org/content/m42234/latest…ol11406/latest . Лицензия : CC BY: Attribution