Сборник задач абитуриенту. ОСНОВЫ ТЕРМОДИНАМИКИ. Циклы. Тепловые машины. Тема 14-7

Опубликовано чт, 07/18/2019 — 11:04 пользователем fizportal.ru

ОСНОВЫ ТЕРМОДИНАМИКИ. Циклы. Тепловые машины. Тема 14-7

14.101. В идеальной тепловой машине за счет каждого килоджоуля энергии, получаемой от нагревателя, совершается работа A = 300 Дж. Определите КПД машины и температуру T₁ нагревателя, если температура холодильника T₂ = 280 К.

Ответ

0,3; 400 K

14.102. Совершая замкнутый цикл, газ получил от нагревателя 420 Дж теплоты. Какую работу совершил газ, если КПД цикла 10 %?

Ответ

14.103. В ходе цикла Карно рабочее вещество получает от нагревателя количество теплоты – 300 кДж. Температуры нагревателя и холодильника равны соответственно T₁ = 450 K и T₂ = 280 K. Определите работу A, совершаемую рабочим веществом за цикл.

Ответ

113 Дж

14.104. Тепловая машина совершает работу 200 Дж, при этом холодильнику передается 300 Дж энергии. Определите КПД (в процентах) тепловой машины.

Ответ

14.105. КПД тепловой машины 50 %. Какую работу совершает машина за один цикл, если холодильнику при этом передается 700 Дж теплоты?

Ответ

14.106. двигатель внутреннего сгорания имеет КПД $\eta$ = 28 % при температуре горения топлива t₁ = 927 °C и при температуре отходящих газов t₂ = 447 °C. На какую величину $\Delta \eta$ КПД идеальной тепловой машины, работающей при тех же температурах нагревателя и холодильника, превышает КПД данного двигателя?

Ответ

14.107. КПД идеальной тепловой машины, работающей по циклу Карно, равен 25 %. Какова температура (в °С) нагревателя, если температура холодильника 27 °С?

Ответ

14.108. Идеальная тепловая машина передает холодильнику 80 % теплоты, полученной от нагревателя.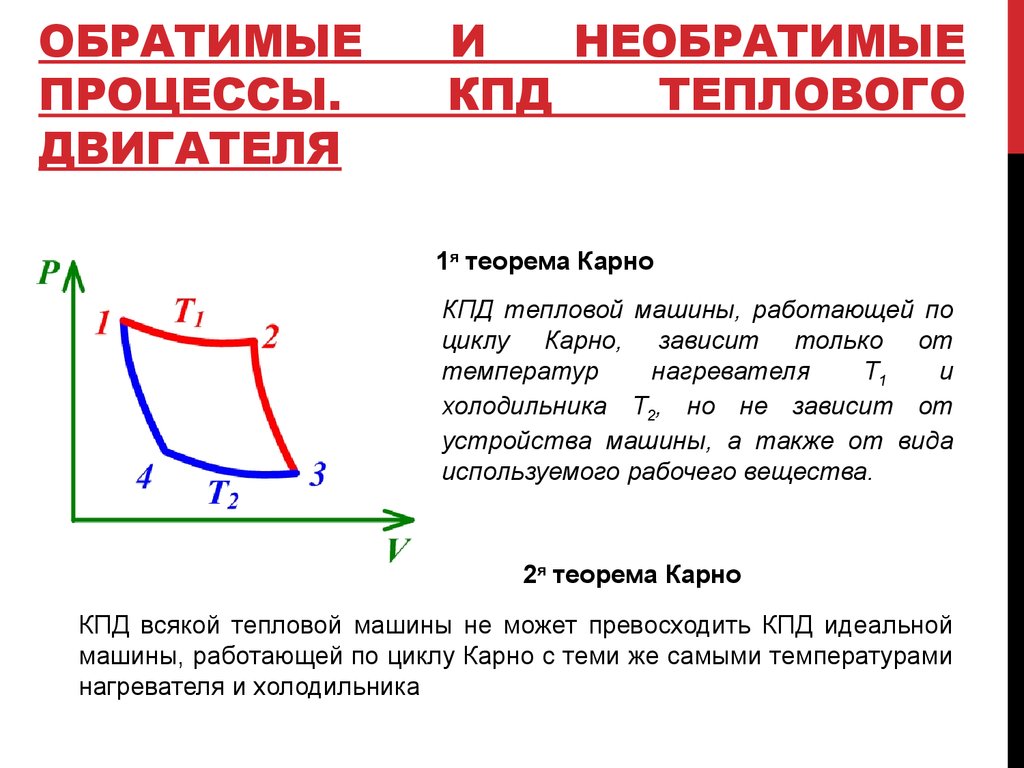 Найдите температуру (в Кельвинах) нагревателя, если температура холодильника 248 К.

Ответ

14.109. КПД идеальной тепловой машины, работающей по циклу Карно, равен 80 %. Во сколько раз абсолютная температура нагревателя больше абсолютной температуры холодильника?

Ответ

14.110. Идеальный газ работает по циклу Карно. Абсолютная температура нагревателя 400 К, холодильника 300 К. Во сколько раз увеличится КПД цикла, если абсолютную температуру нагревателя повысить на 200 К?

Ответ

14.111. Идеальный газ совершает цикл Карно. Абсолютная температура нагревателя в 4 раза больше абсолютной температуры холодильника. Определите долю (в процентах) теплоты, отдаваемой холодильнику.

Ответ

14.112. Идеальная тепловая машина, работающая по циклу Карно, совершает за один цикл работу 100 Дж. Температура нагревателя 100 °С, температура холодильника 0 °С. Найдите количество тепла, отдаваемое за один цикл холодильнику.

Ответ

14. 113. Рабочее тело тепловой машины, работающей по идеальному циклу Карно, в каждом цикле получает от нагревателя ΔQ = 8,4 кДж и k = 80 % из них передает холодильнику. Определите КПД η цикла и работу A, совершаемую машиной в каждом цикле.

Ответ

20 %; 1,67 Дж

14.114. В каком случае КПД цикла Карно возрастет больше: при увеличении температуры нагревателя на ΔT или при уменьшении температуры холодильника на такую же величину?

Ответ

Во втором случае

14.115. Водород совершает цикл Карно. Найдите КПД цикла, если при адиабатном расширении: а) объем газа увеличивается в n = 2 раза; б) давление увеличивается в n = 2 раза.

Ответ

0,25; 0,18

14.116. Найдите КПД η цикла, состоящего из двух изохор и двух адиабат, если в пределах цикла объем идеального газа изменяется в n = 10 раз. Рабочим веществом является азот.

Ответ

14.117. Один моль идеального газа находится в цилиндре под поршнем при температуре T₁. Газ при постоянном давлении нагревают до температуры T₂, затем при постоянном объеме нагревают до температуры T₃. Далее газ охлаждают при постоянном давлении, и его объем падает при этом до первоначального значения. Затем газ при постоянном объеме возвращают в начальное состояние. Какую работу совершил газ за цикл?

Ответ

A = νR(T₃ − T₂)(T₂ − T₁)/ T₂

14.118. На подъем груза весом 1000 кН на высоту 6 м пошло 80 % всей механической работы, полученной в результате работы идеальной тепловой машины, у которой разность температур нагревателя и холодильника равна 125 К, а отношение количества теплоты, полученной от нагревателя, к его абсолютной температуре равно 300 Дж/К. Сколько циклов было совершено за время подъема груза?

Ответ

14.119. Идеальный одноатомный газ совершает замкнутый цикл, состоящий из двух изохорных и двух изобарных процессов. При изохорном нагревании давление увеличивается в 2 раза, а при изобарном нагревании объем увеличивается на 70 %.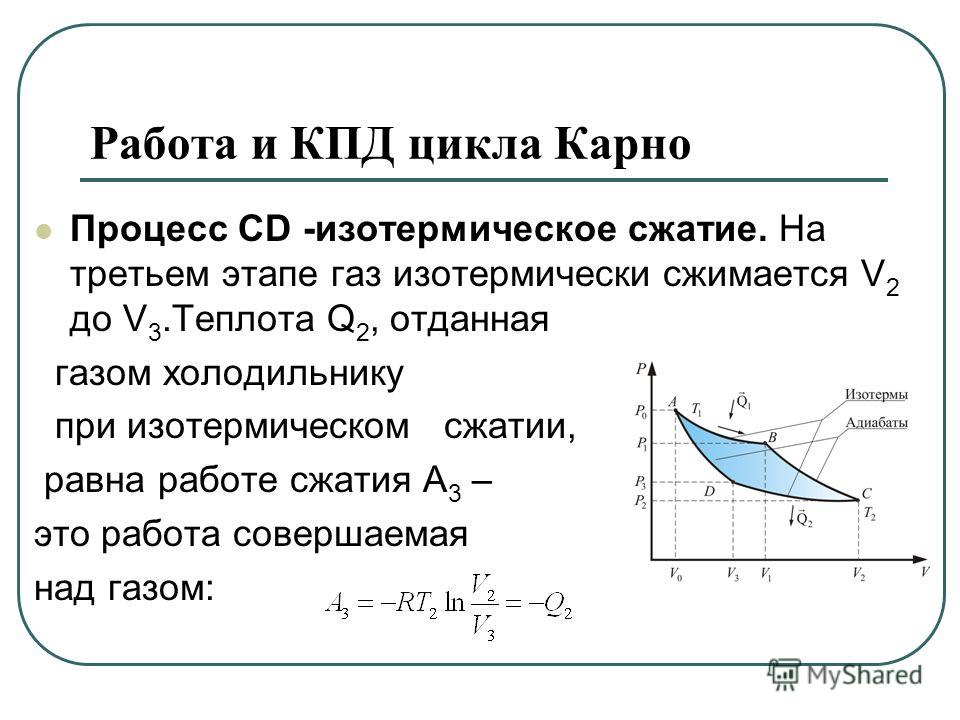 Найдите КПД (в процентах) цикла.

Ответ

14.120. Идеальный одноатомный газ совершает циклический процесс, состоящий из изохорного нагревания, при котором давление газа возрастает на 40 %, затем изобарного расширения и, наконец, возвращения в исходное состояние в процессе, в котором давление изменяется прямо пропорционально объему. Найдите КПД (в процентах) цикла.

Ответ

14.121. Идеальная холодильная машина, работающая по обратному циклу Карно, используется для замораживания воды при 0 °С. Теплота отдается окружающему воздуху, температура которого 27 °С. Сколько минут потребуется для превращения в лед 420 г воды, если холодильная машина потребляет от сети мощность 25 Вт? Удельная теплота плавления льда 330 кДж/кг.

Ответ

Tags: 

Абитуриенту

термодинамика

циклы

тепловые машины

КПД

Тепловые двигатели, цикл Карно, коэффициент полезного действия. Тест

Всего вопросов: 11

Вопрос 1.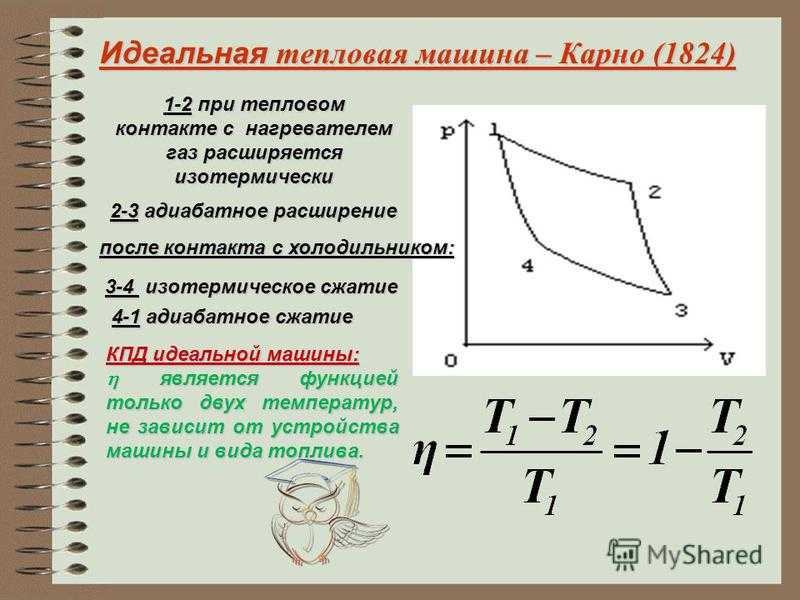 Газ, совершающий цикл Карно, 70% теплоты, полученной от нагревателя, отдает холодильнику. Температура нагревателя 430 К. Определите температуру (К) холодильника.

Вопрос 2. Определите КПД цикла тепловой машины, если известно, что за один цикл была совершена работа 3 кДж и холодильнику было передано 13,4 кДж теплоты.

Вопрос 3. Идеальная тепловая машина совершает за один цикл работу, равную 103 Дж. Чему равна равна температура холодильника, если температура нагревателя — 375К, максимальный КПД составляет 40%.

Вопрос 4. В идеальном тепловом двигателе абсолютная температура холодильника вдвое меньше температуры нагревателя. Если, не меняя температуры нагревателя, температуру холодильника понизить втрое, то во сколько раз увеличится КПД двигателя?

Вопрос 5. Идеальная тепловая машина, работающая по циклу Карно, получает от нагревателя с температурой 493⁰С количество теплоты 80 кДж. Холодильником является окружающий воздух с температурой 20⁰С. На какую максимальную высоту эта машина может поднять груз массой 500 кг?

Вопрос 6. Абсолютная температура нагревателя идеального теплового двигателя в 3 раза выше температуры холодильника. Какое количество теплоты (кДж) получает рабочее тело от нагревателя, если за один цикл двигатель поднимает поршень массой 5 кг на высоту 20 м и сжимает при этом пружину жесткостью 625 кН/м на 8 см?

Вопрос 7. Идеальная холодильная машина, работающая по обратному циклу Карно, использует в качестве холодильника тающий лед при температуре 0⁰С, а в качестве нагревателя – кипяток при 100⁰С. Холодильная машина получила от сети энергию 25 кДж. Определите массу (г) полученного льда, если удельная теплота плавления льда .

Вопрос 8. Тепловой двигатель, рабочим телом которого является идеальный газ, совершает цикл, изображенный на рисунке. Определите КПД двигателя.

Вопрос 9. Один моль одноатомного газа совершает цикл, состоящий из двух изохор и двух изобар. При этом его максимальное давление в 2 раза больше минимального, а максимальный объем в 3 раза больше минимального. Определите КПД цикла.

Вопрос 10. Одноатомный идеальный газ совершает цикл, состоящий из двух адиабат и двух изохор. Если в процессе адиабатного расширения 1-2 температура газа T₂=0,75T₁, а в процессе адиабатного сжатия 3-4 температура газа T₃=0,75T₄. Определите КПД цикла.

Вопрос 11. КПД тепловой машины в цикле 1-2-3-1, состоящем из изотермы 1-2, изохоры 2-3 и адиабаты 3-1, равен 50%. В цикле 1-3-4-1, состоящем из адиабаты 1-3, изотермы 3-4 и изохоры 4-1, КПД 20%. Рабочим телом является одноатомный идеальный газ. Определите КПД тепловой машины, работающей по циклу 1-2-3-4-1.

Второй закон термодинамики в новой редакции — College Physics: OpenStax

Глава 15 Термодинамика

Резюме

• Определение цикла Карно.
• Рассчитайте максимальный теоретический КПД ядерного реактора.
• Объясните, как диссипативные процессы влияют на идеальную машину Карно.

Рисунок 1. Эта новая игрушка, известная как пьющая птица, является примером двигателя Карно. Он содержит хлористый метилен (смешанный с красителем) в брюшной полости, который кипит при очень низкой температуре — около 100ºF . Для работы нужно намочить голову птицы. Когда вода испаряется, жидкость поднимается в голову, заставляя птицу утяжеляться и нырять вперед обратно в воду. Это охлаждает хлористый метилен в голове, и он перемещается обратно в брюшную полость, в результате чего низ птицы становится тяжелым, и она опрокидывается вверх. Если не считать очень небольшого вклада энергии — первоначального смачивания головы — птица становится своего рода вечным двигателем. (кредит: Arabesk.nl, Wikimedia Commons)

Из второго закона термодинамики мы знаем, что тепловая машина не может быть на 100 % эффективнее, поскольку всегда должна существовать некоторая теплопередача[латекс]\boldsymbol{Q _{\textbf{c} }}[/latex]в окружающую среду, которую часто называют отходящим теплом. Насколько эффективной может быть тепловая машина? На этот вопрос на теоретическом уровне ответил в 1824 г. молодой французский инженер Сади Карно (179 г.6–1832), в своем исследовании появившейся тогда технологии теплового двигателя, имеющей решающее значение для промышленной революции. Он разработал теоретический цикл, который теперь называется циклом Карно , который является наиболее эффективным из возможных циклических процессов. Второй закон термодинамики можно переформулировать в терминах цикла Карно, и, таким образом, Карно на самом деле открыл этот фундаментальный закон. Любая тепловая машина, использующая цикл Карно, называется двигателем Карно .

Важнейшее значение цикла Карно — и, по сути, его определение — заключается в том, что используются только обратимые процессы. Необратимые процессы связаны с диссипативными факторами, такими как трение и турбулентность. Это увеличивает передачу тепла[латекс]\boldsymbol{Q_{\textbf{c}}}[/латекс]в окружающую среду и снижает эффективность двигателя. Очевидно, что обратимые процессы предпочтительнее.

ДВИГАТЕЛЬ КАРНО

Сформулированный в терминах обратимых процессов, второй закон термодинамики имеет третью форму:

Двигатель Карно, работающий между двумя заданными температурами, имеет максимально возможный КПД любой тепловой машины, работающей между этими двумя температурами. Кроме того, все двигатели, использующие только обратимые процессы, имеют одинаковую максимальную эффективность при работе в пределах одних и тех же заданных температур.

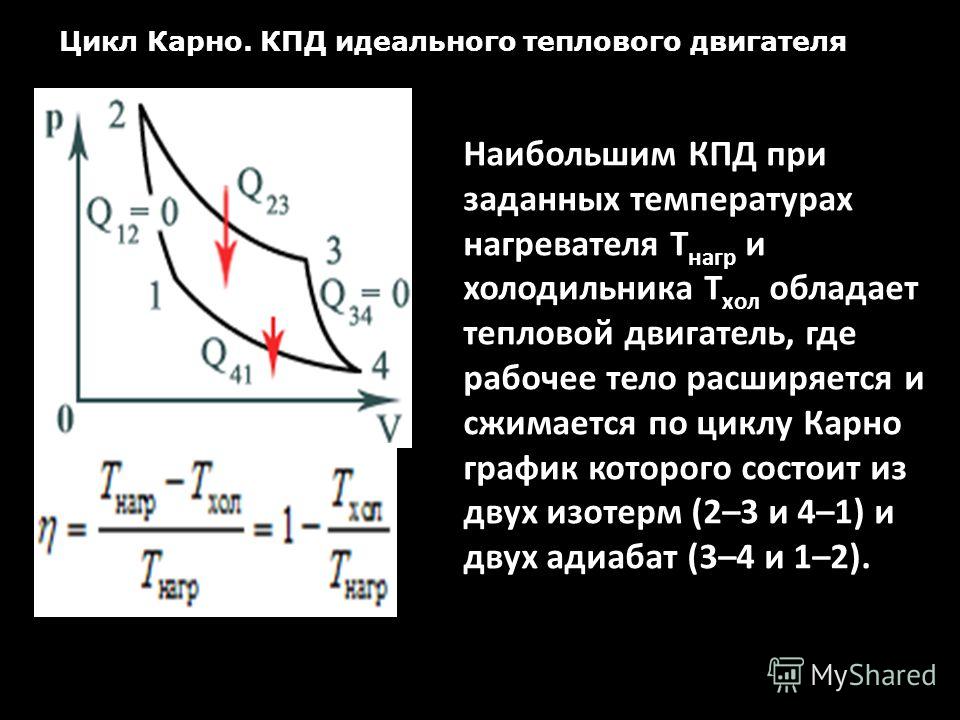
На рис. 2 показана диаграмма[latex]\boldsymbol{PV}[/latex]для цикла Карно. Цикл включает два изотермических и два адиабатических процесса. Напомним, что и изотермические, и адиабатические процессы в принципе обратимы.

Карно также определил КПД идеальной тепловой машины, то есть машины Карно. Всегда верно, что КПД циклической тепловой машины определяется выражением:

.

[латекс]\boldsymbol{Эфф\:=}[/латекс][латекс]\boldsymbol{\frac{Q _{\textbf{h}} -Q _{\textbf{c}}}{Q _{\textbf{h }}}}[/латекс][латекс]\boldsymbol{=1-}[/латекс][латекс]\boldsymbol{\frac{Q_{\textbf{c}}}{Q_{\textbf{h}}} }. [/латекс]

Карно обнаружил, что для идеальной тепловой машины отношение[latex]\boldsymbol{Q_{\textbf{c}}/Q_{\textbf{h}}}[/latex] равно отношению абсолютных температур тепловые резервуары. То есть [латекс]\boldsymbol{Q_{\textbf{c}}/Q_{\textbf{h}}=T_{\textbf{c}}/T_{\textbf{h}}}[/latex]для двигатель Карно, так что максимум или Эффективность Карно [латекс]\boldsymbol{Eff _{\textbf{C}}}[/латекс] определяется как

[латекс]\boldsymbol{Eff _{\textbf{C}}=1-}[/latex][латекс]\boldsymbol{\frac{T_{\textbf{c}}}{T_{\textbf{h}} }},[/латекс]

, где[latex]\boldsymbol{T_{\textbf{h}}}[/latex]и[latex]\boldsymbol{T_{\textbf{c}}}[/latex]в градусах Кельвина (или любая другая абсолютная температура шкала). Ни одна настоящая тепловая машина не может работать так же хорошо, как КПД Карно — фактический КПД около 0,7 от этого максимума обычно является лучшим, чего можно достичь. Но идеальный двигатель Карно, как и пьющая птица выше, хотя и является увлекательной новинкой, но имеет нулевую мощность. Это делает его нереальным для любых приложений.

Интересный результат Карно подразумевает, что 100% эффективность была бы возможна только в том случае, если[latex]\boldsymbol{T_{\textbf{c}}=0\textbf{K}}[/latex]—то есть, только если бы холодный резервуар был при абсолютном нуле, практическая и теоретическая невозможность. Но физический смысл таков: единственный способ заставить всю теплопередачу пойти на работу — это убрать всю тепловую энергию, а для этого требуется холодный резервуар при абсолютном нуле.

Также очевидно, что наибольшая эффективность достигается, когда соотношение [латекс]\жирный символ{Т_{\textbf{с}}/Т_{\текстbf{h}}}[/латекс] является как можно меньшим. Как обсуждалось для цикла Отто в предыдущем разделе, это означает, что эффективность максимальна при максимально возможной температуре горячего резервуара и минимально возможной температуре холодного резервуара. (Эта установка увеличивает площадь внутри замкнутого контура на диаграмме [латекс]\boldsymbol{PV}[/латекс]; кроме того, кажется разумным, что чем больше разница температур, тем легче направить теплопередачу на работу. ) Фактические температуры резервуара тепловой машины обычно связаны с типом источника тепла и температурой окружающей среды, в которую происходит передача тепла. Рассмотрим следующий пример.

Рис. 2. PV диаграмма цикла Карно, использующего только обратимые изотермические и адиабатические процессы. Теплопередача Q _h происходит в рабочее тело на изотермическом пути AB, который протекает при постоянной температуре Th. Теплообмен Q _c происходит вне рабочего тела по изотермическому пути CD, который происходит при постоянной температуре T _с . Чистый результат работы W равен площади внутри пути ABCDA. Также показана схема двигателя Карно, работающего между горячим и холодным резервуарами при температурах T _h и T _c .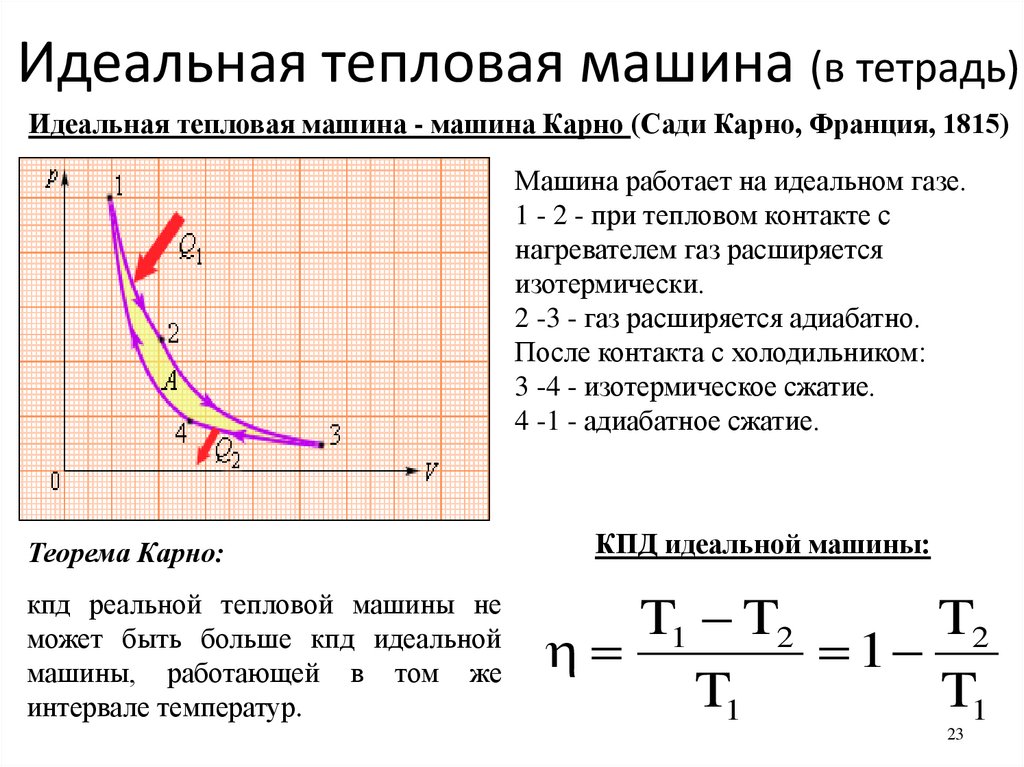 Любая тепловая машина, использующая обратимые процессы и работающая между этими двумя температурами, будет иметь такой же максимальный КПД, как и машина Карно.

Пример 1: Максимальная теоретическая эффективность ядерного реактора 9{\circ}\textbf{C}}[/latex], а затем снова нагревают, чтобы начать цикл заново. Рассчитайте максимальный теоретический КПД тепловой машины, работающей между этими двумя температурами.

Рисунок 3. Схематическая диаграмма ядерного реактора с водой под давлением и паровых турбин, преобразующих работу в электрическую энергию. Теплообмен используется для производства пара, отчасти для того, чтобы избежать загрязнения генераторов радиоактивностью. Две турбины используются, потому что это дешевле, чем работа одного генератора, который производит такое же количество электроэнергии. Пар конденсируется в жидкость перед возвратом в теплообменник, чтобы поддерживать низкое давление пара на выходе и способствовать прохождению пара через турбины (эквивалентно использованию холодного резервуара с более низкой температурой). Значительная энергия, связанная с конденсацией, должна рассеиваться в окружающей среде; в этом примере используется градирня, поэтому прямая передача тепла в водную среду отсутствует. (Обратите внимание, что вода, поступающая в градирню, не контактирует с паром, проходящим через турбины.) 9{\circ}\textbf{C}},[/latex] соответственно. Тогда в кельвинах [латекс]\boldsymbol{T_{\textbf{h}}=573\textbf{K}}[/latex]и[латекс]\boldsymbol{T_{\textbf{c}}=300\textbf { K}},[/latex], так что максимальная эффективность равна

[латекс]\boldsymbol{Eff _{\textbf{C}}=1-}[/latex][латекс]\boldsymbol{\frac{T_{ \textbf{c}}}{T_{\textbf{h}}}}.[/latex]

Таким образом,

[латекс]\begin{array}{lcl} \boldsymbol{Eff_{\textbf{C} }} & \boldsymbol{=} & \boldsymbol{1-\frac{300\textbf{ K}}{573\textbf{ K}}} \\ {} & \boldsymbol{=} & \boldsymbol{0.476\textbf {, или }47,6\%.} \end{массив}[/latex]

Обсуждение

Фактический КПД типичной атомной электростанции составляет около 35%, что немногим лучше, чем 0,7 раза от максимально возможного значения, что является данью превосходной инженерной мысли.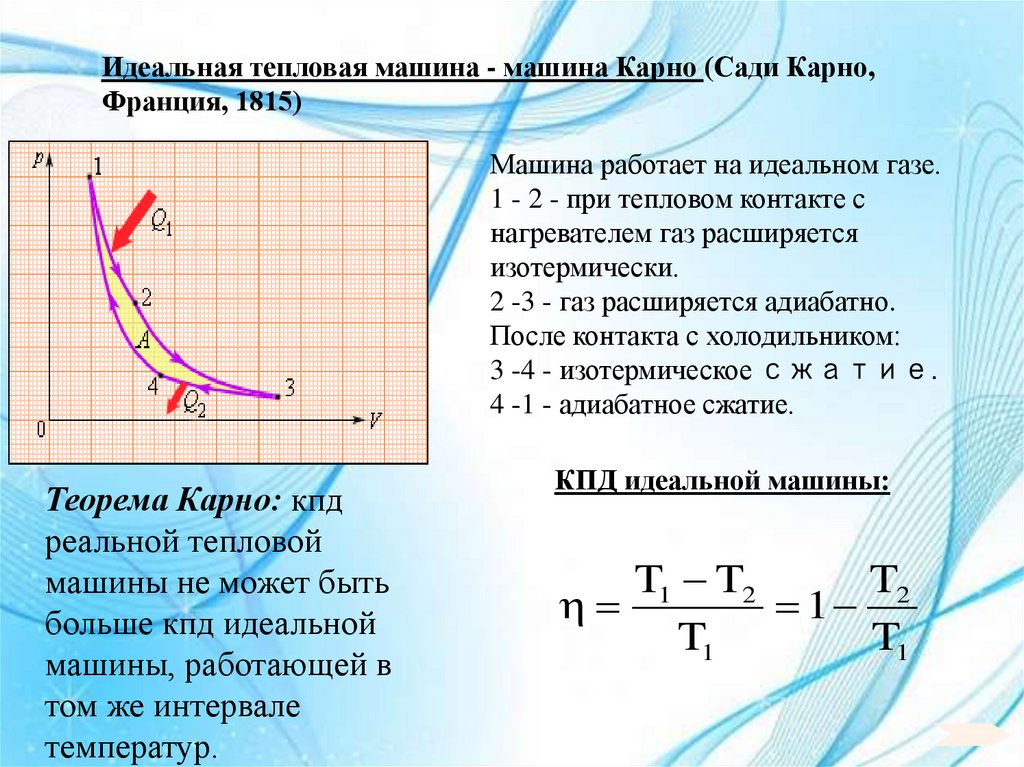 Электростанции, работающие на угле, нефти и природном газе, имеют больший фактический КПД (около 42%), потому что их котлы могут достигать более высоких температур и давлений. Температура холодного резервуара на любой из этих электростанций ограничена местными условиями. На рис. 4 показан (а) внешний вид атомной электростанции и (б) внешний вид угольной электростанции. У обоих есть градирни, в которые вода из конденсатора поступает в градирню в верхней части и распыляется вниз, охлаждаясь за счет испарения.

Рисунок 4. (а) Атомная электростанция (фото: BlatantWorld.com) и (б) угольная электростанция. Оба имеют градирни, в которых вода испаряется в окружающую среду, представляя Q _c . Ядерный реактор, поставляющий Q _h , расположен внутри куполообразной защитной оболочки. (Фото: Роберт и Михаэла Викол, publicphoto.org)

Поскольку все реальные процессы необратимы, реальный КПД тепловой машины никогда не может быть таким же большим, как у двигателя Карно, как показано на рис. 5(а). Даже при наличии наилучшей тепловой машины в периферийном оборудовании, таком как электрические трансформаторы или автомобильные трансмиссии, всегда присутствуют диссипативные процессы. Это еще больше снижает общую эффективность за счет преобразования части выходной мощности двигателя обратно в теплопередачу, как показано на рис. 5(b).

Рис. 5. Реальные тепловые двигатели менее эффективны, чем двигатели Карно. (а) В реальных двигателях используются необратимые процессы, уменьшающие передачу тепла на работу. Сплошные линии представляют реальный процесс; пунктирные линии — это то, что двигатель Карно сделал бы между теми же двумя резервуарами. б) Трение и другие диссипативные процессы в выходных механизмах тепловой машины преобразуют часть ее работы в теплопередачу окружающей среде.

• Цикл Карно — это теоретический цикл, который является наиболее эффективным из возможных циклических процессов. Любой двигатель, использующий цикл Карно, в котором используются только обратимые процессы (адиабатический и изотермический), известен как двигатель Карно.
• Любой двигатель, использующий цикл Карно, обладает максимальным теоретическим КПД.
• Хотя двигатели Карно являются идеальными двигателями, в действительности ни один двигатель не достигает теоретического максимального КПД Карно, поскольку определенную роль играют диссипативные процессы, такие как трение. Циклы Карно без потери тепла могут быть возможны при абсолютном нуле, но это никогда не наблюдалось в природе.

Цикл Карно

циклический процесс, в котором используются только обратимые процессы, адиабатические и изотермические процессы

Двигатель Карно

тепловой двигатель, использующий цикл Карно

Эффективность Карно

максимальный теоретический КПД тепловой машины

Тепловая эффективность — Энергетическое образование

Энергетическое образование

Меню навигации

ИСТОЧНИКИ ЭНЕРГИИ

ЭНЕРГЕТИЧЕСКОЕ ИСПОЛЬЗОВАНИЕ

ЭНЕРГЕТИЧЕСКОЕ ВОЗДЕЙСТВИЕ

ИНДЕКС

Поиск

Рис. 1. Количество работы, произведенной для данного количества тепла, определяет тепловую эффективность системы. ^[1]

Тепловые двигатели превращают тепло в работу. Тепловой КПД выражает долю тепла, которая превращается в полезную работу. Тепловой КПД обозначается символом [math]\eta[/math] и может быть рассчитан по уравнению:

Где:

[math]W[/math] — полезная работа и

[math]Q_H[/math] — общее количество подведенной тепловой энергии от горячего источника. ^[2]

Тепловые двигатели часто работают с эффективностью от 30% до 50% из-за практических ограничений. Тепловые двигатели не могут достичь 100% термического КПД ([математика]\эта = 1[/математика]) в соответствии со Вторым законом термодинамики. Это невозможно, потому что некоторое количество отработанного тепла всегда производится в тепловом двигателе, что показано на рисунке 1 термином [math]Q_L[/math]. Хотя полная эффективность тепловой машины невозможна, существует много способов повысить общую эффективность системы.

Пример

Если вводится 200 Дж тепловой энергии в виде тепла ([math]Q_H[/math]), а двигатель выполняет работу 80 Дж ([math]W[/math]), то КПД равен 80 Дж / 200 Дж, что составляет 40% КПД.

Тот же результат можно получить, измерив отработанное тепло двигателя. Например, если в двигатель вложено 200 Дж и наблюдается 120 Дж отходящего тепла, то должно быть выполнено 80 Дж работы, что дает КПД 40%.

Эффективность Карно

основной артикул

Существует максимально достижимая эффективность тепловой машины, которая была выведена физиком Сади Карно. Следуя законам термодинамики, уравнение для этого оказывается таким

Где

[math]T_L[/math] — температура холодной «раковины»
и

[math]T_H[/math] — температура теплового резервуара.

Описывает КПД идеализированного двигателя, которого в реальности достичь невозможно. ^[3] Согласно этому уравнению, чем ниже температура стока [math]T_L[/math] или выше температура источника [math]T_H[/math], тем больше работы доступно для тепловой машины.