Определите КПД идеальной тепловой машины, имеющей температуру нагревателя 480 °С, а температуру холодильника 30 °С. — вопрос №4281125 — Учеба и наука

Ответы

07. 04.21 Ответ понравился автору вопроса

Михаил Александров Читать ответы

Андрей Андреевич Читать ответы

Владимир Читать ответы

Посмотреть всех экспертов из раздела Учеба и наука > Физика

Похожие вопросы

Нормальная ли температура для GIGABYTE GeForce RTX 3070 Ti GAMING OC? Она держится на 80 градусов по цельсии, при этом корпус весь обдувается.

Решено

Появилась необходимость купить ультрабук. Бюджет 70к. НО Я ПРАКТИЧЕСКИ НЕ РАЗБИРАЮСЬ В ЖЕЛЕЗЕ.

Решено

Газ совершает цикл Карно. Температура нагревателя Т1=380 К, холодильника Т2=280 К. Во сколько раз увеличится коэффициент полезного действия цикла, если температуру нагревателя увеличить на ∆Т=200 К.

Психиатрия, неврология или инфектология? Повышенная температура в течение двух месяцев после ковида, ПА, тошнота, слабость…

600 p

Помогите пожалуйста с задачей по физике

Пользуйтесь нашим приложением

Второй закон термодинамики. Коэффициент полезного действия (КПД) теплового двигателя

Второе начало термодинамики – физический принцип, накладывающий ограничение на направление процессов передачи тепла между телами.

Второе начало термодинамики запрещает так называемые вечные двигатели второго рода, показывая, что коэффициент полезного действия не может равняться единице, поскольку для кругового процесса температура холодильника не может равняться абсолютному нулю (невозможно построить замкнутый цикл, проходящий через точку с нулевой температурой).

Второе начало термодинамики является постулатом, не доказываемым в рамках термодинамики. Оно было создано на основе обобщения опытных фактов и получило многочисленные экспериментальные подтверждения.

Существуют несколько эквивалентных формулировок второго начала термодинамики:

• Постулат Клаузиуса: «Невозможен процесс, единственным результатом которого являлась бы передача тепла от более холодного тела к более горячему» (такой процесс называется процессом Клаузиуса).

• Постулат Томсона (Кельвина): «Невозможен круговой процесс, единственным результатом которого было бы производство работы за счет охлаждения теплового резервуара» (такой процесс называется процессом Томсона).

Эквивалентность этих формулировок легко показать. В самом деле, допустим, что постулат Клаузиуса неверен, то есть существует процесс, единственным результатом которого была бы передача тепла от более холодного тела к более горячему. Тогда возьмем два тела с различной температурой (нагреватель и холодильник) и проведем несколько циклов тепловой машины, забрав тепло \(Q_1\) у нагревателя, отдав \(Q_2\) холодильнику и совершив при этом работу \(A=Q_1-Q_2\). После этого воспользуемся процессом Клаузиуса и вернем тепло \(Q_2\) от холодильника нагревателю. В результате получается, что мы совершили работу только за счет отъема теплоты от нагревателя, то есть постулат Томсона тоже неверен.

С другой стороны, предположим, что неверен постулат Томсона. Тогда можно отнять часть тепла у более холодного тела и превратить в механическую работу. Эту работу можно превратить в тепло, например, с помощью трения, нагрев более горячее тело. Значит, из неверности постулата Томсона следует неверность постулата Клаузиуса.

Таким образом, постулаты Клаузиуса и Томсона эквивалентны.

Другая формулировка второго начала термодинамики основывается на понятии энтропии:

• «Энтропия изолированной системы не может уменьшаться» (закон неубывания энтропии).

Такая формулировка основывается на представлении об энтропии как о функции состояния системы, что также должно быть постулировано.

Коэффицие́нт поле́зного де́йствия (КПД) – характеристика эффективности системы (устройства, машины) в отношении преобразования или передачи энергии. Определяется отношением полезно использованной энергии к суммарному количеству энергии, полученному системой; обозначается обычно \(\eta\) («эта»). \(\eta= \frac{W_{пол}}{W_{cyм}}\). КПД является безразмерной величиной и часто измеряется в процентах. Математически определение КПД может быть записано в виде:

\(\eta = \frac AQ \cdot 100\%\), где А – полезная работа, а \(Q\) – затраченная энергия. В силу закона сохранения энергии КПД всегда меньше единицы или равен ей, то есть невозможно получить полезной работы больше, чем затрачено энергии.

КПД теплово́го дви́гателя – отношение совершенной полезной работы двигателя, к энергии, полученной от нагревателя.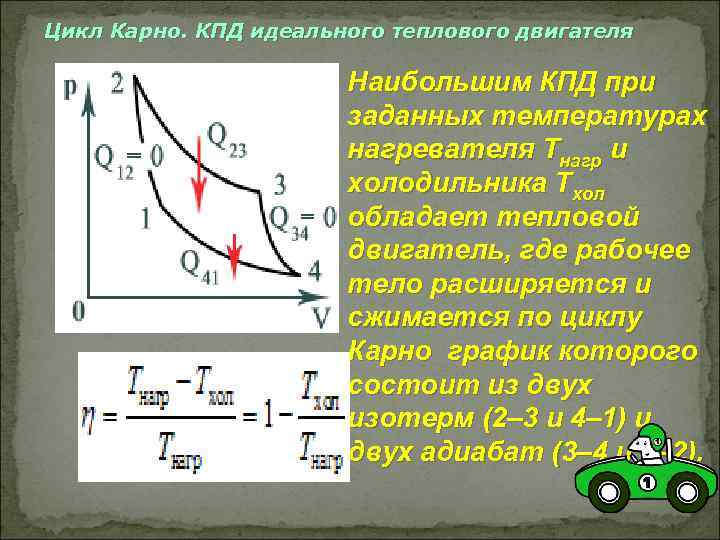 КПД теплового двигателя может быть вычислен по следующей формуле:

\(\eta = \frac{Q_1-Q_2}{Q_1}\cdot 100\%\),

где \(Q_1\) – количество теплоты, полученное от нагревателя, \(Q_2\) – количество теплоты, отданное холодильнику.

Наибольшим КПД среди циклических машин, оперирующих при заданных температурах горячего источника \(T_1\) и холодного \(T_2\), обладают тепловые двигатели, работающие по циклу Карно; этот предельный КПД равен

\(\eta =\frac {T_1-T_2}{T_1}.\)

Q4 Выберите правильную альтернативу a Для идеальной машины КПД 1 Больше единицы 2 Меньше t…

Перейти к

• Объективные вопросы
• Вопросы с короткими/длинными ответами
• Числа

• Иметь значение
• Физические величины и измерения
• Сила
• Простые машины
• Свет
• Магнетизм

Главная >

Селина Солюшнс
Класс 6
Физика
>

Глава 4. Простые машины
>

Упражнение:

Объективные вопросы
>
Вопрос 4

Вопрос 4 Объективные вопросы

Q4) Выберите правильную альтернативу

(a) Эффективность идеальной машины равна

1. Больше единицы

2. Меньше единицы

3. Равен единице

4. Зависит от значения нагрузки

(b) Механическое преимущество машины определяется как

1. Нагрузка x усилие

2. Нагрузка/усилие

3. Нагрузка + усилие

4. Усилие/нагрузка

(c) Механическое преимущество рычага равно

1. Погрузочный рычаг / рычаг усилия

2. Рычаг усилия/нагрузочный рычаг

3. Нагрузочный рычаг + рычаг усилия

4. Погрузочный рычаг — усилие

(d) Шкив используется, потому что он

1. Имеет механическое преимущество больше единицы

2. Имеет 100% КПД

3. Помогает приложить усилие в удобном направлении

4. Требуется больше усилий, чтобы поднять меньший груз.

(e) Колесо используется с осью, потому что

1. Трение скольжения меньше, чем трение скольжения

2. Трение качения меньше трения скольжения

3. Работают как наклонная плоскость

4. Они помогают нам изменить направление силы.

Ответ:

Решение:

(а) 3. Равен единице

(б) 2. Нагрузка/усилие

(в) 4. Нагрузочное плечо — усилие

(г) 3. Помогает приложить сила в удобном направлении

(e) 2. Трение качения меньше, чем трение скольжения

Стенограмма видео

«Здравствуйте, друзья, это Неха, и я приветствую вас сегодня на онлайн-сессии по решению домашних заданий. Мы рассмотрим следующий вопрос. В вопросе говорится: выберите правильный вариант. Итак, мы даем утверждение, и нам даны четыре варианта, из которых мы должны выбрать правильный вариант. Давайте посмотрим на утверждение один за другим. .Первый говорит за идеальную машину эффективную.Она больше Единицы или она меньше вас?Если или равна Единице или зависит от величины Господа, то для нас для идеальной машины разница в должна быть равна Единство, которое является опцией.. Номер три вверх.. Установить один следующий один механическое преимущество машины определяется как нагруженный предпочтительный много / фут на усилие процесса нагрузки на усилие, разделенное ниже. Итак, основная формула механического преимущества машины. Он загружен. / усилие по этому варианту номер два
Следующее механическое преимущество лямбды равно нагрузке мм/усилие слагаемое усилие, эм,/лаура или низкое рам + для более низкого — усилие вверх. Так что правильный вариант для этого нижнего рычага — усилие. Далее используется один шкив, потому что он имеет механическое преимущество больше, чем стопроцентный КПД. Она помогает приложить усилие в удобном направлении или требует больше усилий для поднятия склона. Таким образом, в основном используется шкив, потому что он помогает прикладывать усилие в направлении алюминия, что является правильным до третьего числа. Давайте посмотрим на последнее колесо
Те с абсолютным, потому что трение скольжения меньше, чем трение скольжения. Во-вторых, трение качения меньше, чем трение скольжения, в-третьих, работа по наклонной плоскости и вперед. Они помогают нам изменить направление силы. В основном колесо используется из-за того, что основное трение меньше, чем трение скольжения, которое является опцией. Во-вторых, друзья, вот как мы подходим к этому вопросу. Надеюсь, вы поняли решение, если вы так или иначе, пожалуйста, не стесняйтесь оставить комментарий ниже и подписаться на этот канал для регулярных обновлений. Спасибо.

Связанные вопросы

Q1) Укажите, верны ли следующие утверждения True или False.1. Мальчик работает, толкая стену…

Q2) Заполните пропуски 1. Полезная работа, совершаемая реальной машиной, всегда ____, чем работа, выполняемая…

Q3) Сопоставьте следующее

Фейсбук

WhatsApp

Копировать ссылку

Было ли это полезно? 100003

Сила

Простые машины

Свет

Магнетизм

Курсы

Быстрые ссылки

Условия и политика

Условия и политика

2022 © Quality Tutorials Pvt Ltd Все права защищены

9.3 Simple Machines | Техасский шлюз

Цели обученияПростые машиныРасчет механических преимуществ и эффективности простых машинУпражнения на выполнение задачПроверьте свое понимание

Цели обучения

К концу этого раздела вы сможете делать следующее:

• Описывать простые и сложные механизмы
• Расчет механического преимущества и эффективности простых и сложных машин

«>

Ключевые термины раздела

сложная машина	выход эффективности	идеальное механическое преимущество
наклонная плоскость	входная работа	рычаг
механическое преимущество	выходная работа	шкив
винт	простая машина	клин
колесо и ось

Простые машины

Простые машины облегчают работу, но не уменьшают ее объем. Почему простые машины не могут изменить объем выполняемой вами работы? Напомним, что в закрытых системах общее количество энергии сохраняется. Машина не может увеличить количество энергии, которую вы в нее вкладываете. Итак, чем полезна простая машина? Хотя она не может изменить объем выполняемой вами работы, простая машина может изменить величину силы, которую вы должны приложить к объекту, и расстояние, на котором вы прикладываете силу. В большинстве случаев для уменьшения силы, которую необходимо приложить для выполнения работы, используется простая машина. Обратной стороной является то, что вы должны приложить силу на большее расстояние, потому что произведение силы и расстояния, f d (что равно работе) не меняется.

Давайте посмотрим, как это работает на практике. На рис. 9.8(а) рабочий использует своего рода рычаг, чтобы приложить небольшое усилие на большом расстоянии, в то время как монтировка тянет гвоздь с большой силой на небольшом расстоянии. На рис. 9.8(b) показано, как математически работает рычаг. Сила усилия, приложенная к F _и , поднимает груз (сила сопротивления), который давит вниз в точке F _р . Треугольный стержень называется точкой опоры; часть рычага между точкой опоры и F _e является усилителем, L _e ; а часть слева — это рычаг сопротивления, L _r . Механическое преимущество — это число, которое говорит нам, во сколько раз простая машина увеличивает силу усилия. Идеальное механическое преимущество, IMA , представляет собой механическое преимущество совершенной машины без потери полезной работы, вызванной трением между движущимися частями. Уравнение для IMA показан на рис. 9.8(b).

Рисунок 9.8 (a) Монтировка представляет собой разновидность рычага. (b) Идеальное механическое преимущество равно длине плеча усилия, деленному на длину плеча сопротивления рычага.

В общем, IMA = сила сопротивления, F _r , деленная на силу усилия, F _e . IMA также равняется расстоянию, на котором прикладывается усилие, d _e , деленное на расстояние, которое проходит груз, d _r .

IMA=FrFe=dedrIMA=FrFe=dedr

Возвращаясь к сохранению энергии, для любой простой машины работа, вложенная в машину, Вт _i равна работе, производимой машиной, Вт _или . Объединив это с информацией из предыдущих абзацев, мы можем написать

.

Wi=WoFede=FrdrIf  FeFr, затем de>dr.Wi=WoFede=FrdrIf  FeFr, затем de>dr.

Уравнения показывают, как простая машина может производить тот же объем работы, уменьшая величину усилия за счет увеличения расстояния, на котором действует усилие.

Watch Physics

Введение в Mechanical Advantage

В этом видеоролике показано, как рассчитать IMA рычага тремя различными методами: (1) по силе усилия и силе сопротивления; (2) от длин плеч рычагов, и; (3) от расстояния, на котором приложена сила, и расстояния, на которое перемещается груз.

Проверка хватки

Двое детей разного веса катаются на качелях. Как они располагаются относительно точки опоры (точки опоры), чтобы сохранять равновесие?

1. Более тяжелый ребенок сидит ближе к точке опоры.
2. Более тяжелый ребенок сидит дальше от точки опоры.
3. Оба ребенка сидят на равном расстоянии от точки опоры.
4. Поскольку оба имеют разный вес, они никогда не будут сбалансированы.

Некоторые рычаги прикладывают большое усилие к короткому рычагу. Это приводит к тому, что на конце рычага сопротивления действует меньшая сила на большем расстоянии. Примерами этого типа рычага являются бейсбольные биты, молотки и клюшки для гольфа. В другом типе рычага точка опоры находится на конце рычага, а груз — посередине, как в конструкции тачки.

Простая машина, показанная на рис. 9.9, называется колесом и осью . На самом деле это форма рычага. Разница в том, что рычаг усилия может вращаться по полному кругу вокруг точки опоры, которая является центром оси. Сила, приложенная к внешней стороне колеса, вызывает большее усилие, приложенное к веревке, обернутой вокруг оси. Как показано на рисунке, идеальное механическое преимущество рассчитывается путем деления радиуса колеса на радиус оси. Любое устройство с кривошипным приводом является примером колеса и оси.

Рисунок 9.9 Сила, приложенная к колесу, действует на его ось.

Наклонная плоскость и клин — две формы одной и той же простой машины. Клин — это просто две наклонные плоскости, расположенные спиной к спине. На рис. 9.10 показаны простые формулы для расчета IMA s этих машин. Все наклонные мощеные поверхности для ходьбы или вождения представляют собой наклонные плоскости. Ножи и головки топоров являются примерами клиньев.

Рис. 9.10 Слева показана наклонная плоскость, справа — клин.

Винт, показанный на рис. 9.11, на самом деле представляет собой рычаг, прикрепленный к круглой наклонной плоскости. Шурупы по дереву (конечно) также являются примерами шурупов. Рычажная часть этих винтов представляет собой отвертку. В формуле для IMA расстояние между витками резьбы называется шагом и имеет символ P .

Рисунок 9.11 Показанный здесь винт используется для подъема очень тяжелых предметов, например, угла автомобиля или дома на небольшое расстояние.

На рис. 9.12 показаны три различные системы шкивов. Из всех простых машин механическое преимущество легче всего рассчитать для шкивов. Просто посчитайте количество канатов, поддерживающих груз. Это IMA . И снова мы должны применять силу на более длинном расстоянии, чтобы умножить силу. Чтобы поднять груз на 1 метр с помощью системы шкивов, вам нужно потянуть N метров веревки. Системы шкивов часто используются для подъема флагов и оконных жалюзи и являются частью механизма строительных кранов.

Рисунок 9.12 Здесь показаны три системы шкивов.

Watch Physics

Механические преимущества наклонных плоскостей и шкивов

В первой части этого видео показано, как рассчитать IMA систем шкивов. В последней части показано, как рассчитать IMA наклонной плоскости.

Нажмите, чтобы просмотреть содержание

Проверка захвата

Как можно использовать систему шкивов, чтобы поднять легкий груз на большую высоту?

1. Уменьшить радиус шкива.
2. Увеличить количество шкивов.
3. Уменьшите количество канатов, поддерживающих груз.
4. Увеличьте количество канатов, поддерживающих груз.

Сложная машина представляет собой комбинацию двух или более простых машин. Кусачки на рис. 9.13 сочетают в себе два рычага и два клина. Велосипеды включают в себя колеса и оси, рычаги, винты и шкивы. Автомобили и другие транспортные средства представляют собой комбинации многих машин.

Рис. 9.13 Кусачки для проволоки — обычное сложное оборудование.

Расчет механических преимуществ и эффективности простых машин

В общем, IMA = сила сопротивления, F _r , деленная на силу усилия, F _e . IMA также равно расстоянию, на которое прикладывается усилие, d _e , деленному на расстояние, которое проходит груз, d _r .

IMA=FrFe=dedrIMA=FrFe=dedr

Вернитесь к обсуждениям каждой простой машины для конкретных уравнений для IMA для каждого типа машины.

Никакие простые или сложные машины не обладают фактическими механическими преимуществами, рассчитанными по уравнениям IMA . В реальной жизни часть прикладной работы всегда заканчивается напрасной тратой тепла из-за трения между движущимися частями. Работа на входе ( W _i ) и на выходе ( W _o ) являются результатом действия силы, F , действующей на расстоянии, d .

Wi=Fidi     Wo=FodoWi=Fidi  and  Wo=Fodo

Выходная эффективность машины — это просто работа на выходе, деленная на работу на входе, и обычно умножается на 100, так что это выражается в процентах.

% эффективности=WoWi×100% эффективности=WoWi×100

Посмотрите на изображения простых машин и подумайте, какая из них будет иметь наибольшую эффективность. Эффективность связана с трением, а трение зависит от гладкости поверхностей и от площади соприкасающихся поверхностей. Как смазка повлияет на эффективность простой машины?

Рабочий пример

Эффективность рычага

Входная сила в 11 Н, действующая на плечо рычага, перемещается на 0,4 м, что поднимает груз массой 40 Н, опирающийся на плечо сопротивления, на расстояние 0,1 м. Каков КПД машины?

Стратегия

Составьте уравнение для эффективности простой машины, % эффективности = WoWi × 100, % эффективности = WoWi × 100, и рассчитайте Вт _o и Вт _i . _{Оба рабочих значения являются продуктом Fd .}

Решение

Wi=FidiWi=Fidi = (11)(0,4) = 4,4 Дж и Wo=FodoWo=Fodo = (40)(0,1) = 4,0 Дж, тогда % эффективности=WoWi×100=4,04,4×100 =91% % эффективность=WoWi×100=4,04.4×100=91% 

Обсуждение

КПД реальных машин всегда будет меньше 100 процентов из-за работы, которая преобразуется в недоступное тепло за счет трения и сопротивления воздуха. W _o и W _i всегда можно рассчитать как силу, умноженную на расстояние, хотя эти величины не всегда так очевидны, как в случае с рычагом.

Практические задачи

Какова IMA наклонной плоскости длиной 5 м и высотой 2 м?

1. 0,4
2. 2,5
3. 0,4 м
4. 2,5 м

Если система шкивов может поднять груз 200 Н с усилием 52 Н и имеет КПД почти 100 %, сколько канатов поддерживает груз?

1. Требуется 1 веревка, так как фактическое механическое преимущество равно 0,26.
2. Требуется 1 веревка, потому что фактическое механическое преимущество равно 3,80.
3. Требуется 4 веревки, потому что фактическое механическое преимущество составляет 0,26.
4. Требуется 4 веревки, потому что фактическое механическое преимущество составляет 3,80.