Содержание
Какую работу совершает газ при переходе из состояния 1 в состояние 3? Какое количество теплоты ему было передано при — вопрос №4683283 — Учеба и наука
Ответы | |||
|
| |||
| ||||||||||||
|
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука > Английский язык
| Похожие вопросы |
Деньги
Решено
тест3
Решено
мини сочинения 7-10 предложений не больше на английском
тема-рема
Решено
Help me. Please!
Please!
Пользуйтесь нашим приложением
Какую работу совершает газ при переходе из состояния 1 в состояние 3
Прочее › Находится › В сосуде находится некоторое количество идеального газа во сколько раз изменится температура газа
Какую работу совершает газ при переходе из состояния 1 в состояние 3? (Ответ дайте в килоджоулях.) Ответ: 8.
- При переходе газа из состояния 1 в состояние 3 он совершает работу, которая равна 8 килоджоулям.
- Работа, которую совершает газ, можно найти по формуле A = p (V2 — V1) = pΔV, где p — давление газа, V2 и V1 — объемы газа в конечном и начальном состояниях.
- При расширении газа при постоянном давлении 200 килопаскалей от объёма 1,6 л до 2,6 л, газ совершил работу в 200 Дж.
- Газ совершает работу, если он действует на поршень, сила которого равна pS, где p — давление газа, а S — площадь поршня.

- Если газ расширяется, то работа газа положительна, а если газ сжимается, то работа газа отрицательна.
- При расширении газа при постоянном давлении 304 килопаскалей от объёма 3 л до объёма 18 л, газ совершил работу в 4,56 килоджоуля.
- При уменьшении объёма газа его давление увеличивается, а при увеличении объёма — давление уменьшается (если масса и температура газа не изменяются).
- Работа, которую совершает газ при изохорном процессе с постоянным давлением 100 килопаскалей, равна 0.
- Газ совершает наибольшую работу в процессе 2-3.
- Как найти работу которую совершает газ
- Какую работу совершает газ расширяясь при постоянном давлении 200 Килопаскаль от объёма 1 6 л до 2 6 л
- Что значит газ совершает работу
- Как понять когда газ совершает отрицательную работу
- Какую работу совершит газ расширяясь при постоянном давлении 304 кпа от объема 3 л до объема 18 л
- Как зависит давление от объёма газа
- Чему равна работа газа при изохорном процессе с постоянным давлением 100 кпа *
- В каком из процессов газ совершает наибольшую работу
- В каком процессе работа газа равна нулю
- Когда работа над газом
- Какую работу совершает газ при переходе из состояния 1 в состояние 3 Ответ дайте в Килоджоулях ответ
- Какую работу совершает газ за один цикл
- Чему равна работа газа при Изохорном переходе системы
- Как определить работу по сжатию газа
- Как найти работу газа при расширении
- Как геометрически можно определить работу газа
- Как найти работу
Как найти работу которую совершает газ
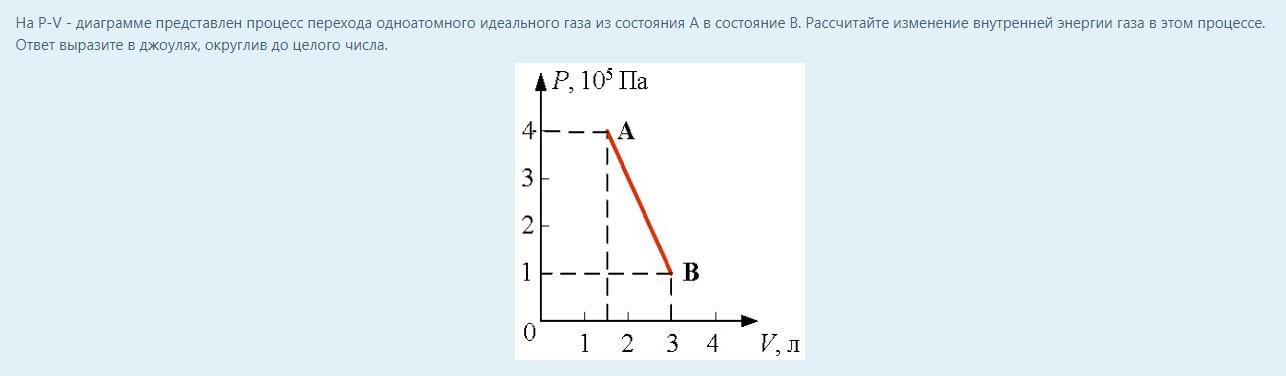
В изобарном процессе (p = const) работа, совершаемая газом, выражается соотношением: A = p (V2 — V1) = pΔV. В изотермическом процессе температура газа не изменяется, следовательно, не изменяется и внутренняя энергия газа, ΔU = 0.
В изотермическом процессе температура газа не изменяется, следовательно, не изменяется и внутренняя энергия газа, ΔU = 0.
Какую работу совершает газ расширяясь при постоянном давлении 200 Килопаскаль от объёма 1 6 л до 2 6 л
Ответ: Расширяясь, газ должен был выполнить работу в 200 Дж.
Что значит газ совершает работу
Газ, находящийся в сосуде под поршнем, действует на поршень с силой F = pS, где p давление газа, S площадь поршня. Если при этом поршень перемещается, то газ совершает работу.
Как понять когда газ совершает отрицательную работу
Очевидно, работа газа положительна, если газ расширяется, и отрицательна, если газ сжимается.
Какую работу совершит газ расширяясь при постоянном давлении 304 кпа от объема 3 л до объема 18 л
Решение: Работа газа определяется выражением: A = p · ∆ V = p · (V 2 − V 1) = 304 · 10 3 · (18 · 10 − 3 − 3 · 10 − 3) = 304 · 10 3 · 15 · 10 − 3 = 4560 = 4.56 кДж.
Как зависит давление от объёма газа
При уменьшении объёма газа его давление увеличивается, а при увеличении объёма — давление уменьшается (при условии, что масса и температура газа остаются неизменными).
Чему равна работа газа при изохорном процессе с постоянным давлением 100 кпа *
Ответ: Работа, совершенная газом в изобарном процессе, равна 200 Дж.
В каком из процессов газ совершает наибольшую работу
Поэтому в процессе 2-3 газ и совершает наибольшую по абсолютной величине (среди рассматриваемых процессов) работу (ответ 2.).
В каком процессе работа газа равна нулю
Изохорный процесс.
При изохорном нагревании или охлаждении (соответственно, прямые 1–2 и 1–3 на рис. 2.7) работа просто равна нулю, поскольку объем не меняется.
Когда работа над газом
Если нагревать газ, то он начинает увеличивать объем, а поршень от увеличения объема начинает отходить назад, следовательно ГАЗ СОВЕРШАЕТ работу.
Какую работу совершает газ при переходе из состояния 1 в состояние 3 Ответ дайте в Килоджоулях ответ
Какую работу совершает газ при переходе из состояния 1 в состояние 3? (Ответ дайте в килоджоулях.) Ответ: 8.
Какую работу совершает газ за один цикл
Работа газа за цикл численно равна площади фигуры, ограниченной графиком цикла на диаграмме pV.
Чему равна работа газа при Изохорном переходе системы
Изохорный процесс — это процесс, происходящий при постоянном объёме. То есть в этом процессе газ не расширяется и не сжимается, а значит не совершается работа ни газом, ни над газом, тогда Аг = 0 и первый закон термодинамики приобретает вид: ΔU = Q.
Как определить работу по сжатию газа
A = p * ΔV, где р — давление газа (Па), ΔV = (V₂ — V₁) — объём (м³). A = Q При изотермическом процессе.
Как найти работу газа при расширении
Работа изображается площадью криволинейной трапеции под графиком процесса (рис. 58). ΔA=P(V2–V1).
Как геометрически можно определить работу газа
Работу газа можно определить графически. Изобразим график зависимости давления газа от его объёма при р = const (рис. 68). Если процесс перехода газа из начального состояния в конечное является изобарным (АВ — изобара), то работа силы давления газа численно равна площади прямоугольника V1АВV2.
Как найти работу
Как искать работу: пять самых популярных способов:
- Знакомства Интересную работу в своей сфере можно найти через коллег.

- Кадровое агентство
- Объявления в соцсетях
- Сайты по поиску работы
- Профессиональные сообщества
- Биржа труда
Термодинамика
Термодинамика
ФИЗИКА 1151
Глава 18, Термодинамика
| ТУ,
Глава 18 | Курс
Календарь |
D18.1 Идеальный газ запечатан в жестком контейнере при 25°C и 1,0
банкомат Какой будет его температура при увеличении давления до 2,0 атм?
Каким будет его давление при повышении температуры до 50°С
Закон идеального газа
PV = nRTНаходясь в жестком контейнере, объем газа изменяется , а не ;
V = V или = константа. Это означает, что мы можем использовать закон идеального газа как.
Т/П = Т или /П илиили
T = P [T o /P o ] = [P/P o ]
Т илиПомните, эти температуры должны быть абсолютными температурами,
T o = 25°C = 302 K
T = [ P / P o ] T o = [ 2,0
атм / 1,0 атм ] [302
К] = [ 2 ] [ 302 К] = 604 КТ = 604 К = (604 — 273)°С = 331°С = Т
Или, хотя V = const, мы можем записать закон идеального газа как
П/Т = П или / Т илиили
P = T [P o / T o ] = [T / T o ]
Р илиПомните, эти температуры должны быть абсолютными температурами, измеренными
в Кельвинах, К.T o = 25°C = 302 K и T = 50°C = 327 K
P = [ T / T o
] P илиР = [ 327 К / 302
К ] (1 атм)P = 1,08 атм
Д18.
2 Газ на 1,5 атм расширяется от 2,5 литров
до 3,5 литров. Какую работу совершает газ?
Работа — это площадь под кривой на p-V диаграмме; для постоянного давления,
Это
Вт = p В
Вт = (1,5 атм)(1,0 л)
Вт = 1,5 атм-л = 1,5 л-атмХотя это, безусловно, верно, требуется преобразование в джоули,
1 л-атм = ( 10 — 3 м 3 ) (1,013 x 10 5 N / м 2)
= 1,013 x 10 2 Н-м = 101,3 ДжВт = 1,5 л-атм [ 101,3 Дж / 1
л-атм ] = 152 Дж = ВтВт = 152 Дж
D18.3 При постоянном давлении 1,5 атм газ
расширяется с 2,0 литров до 3,0 литров, при этом в него поступает 500 Дж энергии.
а) Какую работу совершает газ?
(б) Как изменится его внутренняя энергия?Часть (a) этого вопроса идентична вопросу 14.
17. Мы готовы
знать ответ на этот вопрос; работа, совершаемая газом, равна
Вт = 152 Дж
Поскольку газ совершает работу 152 Дж, он поглощает или получает 500 Дж энергии. Что
означает, что его чистое увеличение внутренней энергии равноE Интервал
= Q — Вт = 500 Дж — 152 Дж = 348 Дж
E инт
= 348 Дж
D18.4 При постоянном давлении 2,25 ат газ сжимают с 2,00
л до 1,50 л, при этом 375 Дж энергии уходит из газа.
а) Какую работу совершает газ ?
(б) Как изменится его внутренняя энергия?Работа — это площадь под кривой на p-V диаграмме; для постоянного давления,
этоВт = p В
Вт = (2,25 атм) (- 0,50 л)
Вт = — 1,125 л-атмВт = — 1,125 л-атм [ 101,3 Дж / 1
л-атм ] = — 114 Дж
Так как газ совершает работу W = -114 Дж (что эквивалентно 114 Дж
работы, выполненной на ), он также отдает 375 Дж энергии (что означает
Q = — 375 Дж).Это означает, что его чистое изменение внутренней энергии равно
.
Е интервал
= Q — W = — 375 Дж — (- 114 Дж)
E инт
= — 261 ДжD18.5 После 1,0 моль идеального газа первоначально при
0 °C и 1,0 атм расширяют изотермически до удвоенного исходного объема,
он сжимается изобарически обратно до исходного объема. Что
чистая работа, выполненная газом или над ним? Какова его конечная температура?
Для этого требуется диаграмма p-V.
Когда газ расширяется изотермически из состояния 1 в состояние 2 ,
работа, совершаемая газом, определяется уравнением 14.17,
W изотерма = n R T ln [V f / V i ]или
W изотерма = n R T ln [V 2 / V 1 ]Из условия задачи мы знаем
В 2 = 2 В 1Отсюда мы можем вычислить работу, совершенную газом,
Вт изотерма = (1,0 моль)(8,314 Дж / моль-К )
(273 К) лн [2 В 1 / В 1 ]
Вт изотерма = (1,0 моль)(8,314 Дж / моль-К
(273 К) ln [ 2 ]
Вт изотерма = (1,0 моль)(8,314 Дж / моль-К
) (273 К) 0,693Вт изотерма = 1,573 Дж
Это площадь под кривой от состояния 1 до состояния 2
При сжатии газа из состояния 2 в состояние 3 совершенная работа
это, как всегда, площадь под кривой.
Вт изобара = p В
= p (V o — 2 V o ) = — p V oМы должны найти p, давление для состояния 2 или состояния 3 . С
мы получили состояние 2 путем изотермического расширения из состояния 1 ,
мы знаем, что температура в состоянии 2 должна быть такой же, как и в состоянии 1 ;
T 1 = T 2 = 273 K. Тогда мы можем применить закон идеального газа
или, проще говоря, просто используйте
pV = константа (для постоянной T)
p 2 V 2 = p 1 V 1
p 2 = p 1 (V 1 / V 2 ) = (1,0 атм)
(V 1 / 2 V 1 ) = 0,5 атм = p 2
p 2 = p 1 ( 1 / 2
) = 0,5 атмЧтобы найти проделанную работу, W изобар = — pV o , нам нужна числовая
значение для V o , начальный объем.Мы могли бы также назвать это V 1 ,
том в состоянии 1 . Чтобы найти этот начальный объем V или или
V 1 , мы используем закон идеального газа,
pV = нРТОпять же, помните, что температура часто указывается в градусах Цельсия, потому что
это «удобно», но температуры в законе идеального газа должны
быть абсолютных температур или температур по шкале Кельвина!
pV = nRT
(1,0 атм) (V o ) = (1,0 моль) (8,314 Дж / моль-K )
(273 К)
(1,0 атм) [ (1,013 x 10 5 N / м 2)/атм.
] (V o ) = (1,0 моль) (8,314 Дж / моль-К
) (273 K)
[ 1,013 x 10 5 N / м 2
] (V o ) = (1,0 моль)(8,314 Дж / моль-К
) (273 K)
В o = 2,24 x 10 — 2 м 3
В 1 = V o = 2,24 x 10 — 2 м 3Теперь мы можем вернуться к вычислению работы, совершаемой газом,
W изобар = — p V o = — (0,5 атм)(2,24 x 10 — 2
m 3 )
W изобар = — p V o = — (0,5 x 1,013 x 10 5 N / m 2 )(2.24
x 10 — 2 м 3 )
Вт изобар = — 1,135 Дж
Теперь мы можем сложить эти два количества работы вместе для сети
работа выполнена.Вт нетто = Вт 12 + Вт 23
Вт нетто = Вт изотерма + Вт изобара
Вт нетто = 1,573 Дж + (-1,135 Дж)
Вт нетто = 438 ДжЭта работа net представляет собой область, показанную на графике выше.
D18.5 Тепловая машина поглощает 6 Дж от источника тепла и производит 2 Дж энергии
механическая работа. Какова его эффективность?
Эфф = Вт/Q ч
Eff = 2 Дж / 6 Дж = 0,33
Eff = 0,33
D19.6 Реверсивная тепловая машина с КПД
15 процентов совершают работу 180 Дж. Сколько тепла он поглощает от горячего
резервуар?
Eff = Вт / Q ч
Q ч = Вт / Eff
Q ч = 180 Дж / 0,15
Q ч = 1200 Дж
D18.
7 Двигатель Карно работает с горячим баком 650°C
при КПД 0,30. Какая должна быть температура, чтобы иметь КПД 0,35?
это водохранилище быть?Помните, что все эти температуры должны быть абсолютными температурами.
Это означает, что для нашего первоначального двигателя Карно
Т ч = 650°С = (650 + 273) К = 923 КСначала найдите T c температуру холодного резервуара. Что будет
оставаться прежним.
Eff = 1 — T c /T h = 0,30
T c /T h = 1 — 0,30 = 0,70
T c = 0,70 T 900 42 ч = (0,70) (923 К) = 646 K
( T c = 373°C )Теперь, при таком холодном резервуаре (T c = 646 K), какая температура
для горячего резервуара (T h = ?) даст КПД 0,35?
Eff = 1 — T c / T h = 0,35
T c / T h = 1 — 0,35 = 0,65
T h = T c /0,65Т ч = 646 К / 0,65
T h = 993 K
( T h = 620°C )
D18.
8 КПД бензинового двигателя 0,55. Оценить температуру
выхлопных газов, если выхлопные газы выходят из двигателя при температуре 125°C.до оценка работа реального двигателя, как
бензиновый двигатель, мы можем относиться к нему как к реверсивному двигателю или двигателю Карно.
Для такого двигателя Карно КПД равен.
Эфф = 1 — Т с / Т чВыхлопные газы уходят при холодной температуре Т c
= 125°С = 398 КT c / T h = 0,55
T c / T h = 1,0 — 0,55 = 0,45Т ч = 398 К / 0,45
T h = 884 K
( T h = 611°C )
| Возврат
в Календарь |
(с) 2000 г.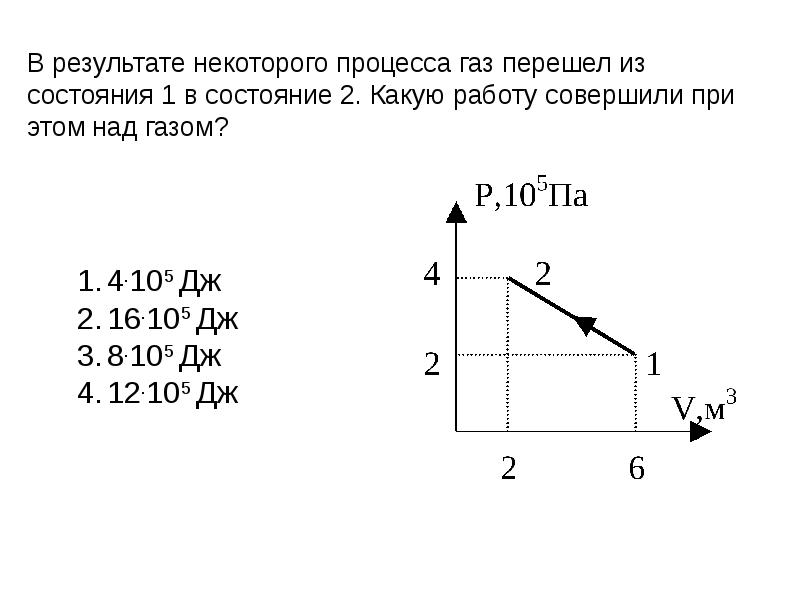 , Дуг Дэвис; все права защищены
, Дуг Дэвис; все права защищены
Работа, выполняемая газом — Исследовательский центр Гленна
Термодинамика — это раздел физики, изучающий энергию и работу системы. Термодинамика имеет дело только с крупномасштабной реакцией системы, которую мы можем наблюдать и измерять в экспериментах. Как аэродинамиков, нас больше всего интересует термодинамика двигательных установок, которые создают тягу за счет ускорения газа. Чтобы понять, как создается тяга, полезно изучить основы термодинамики газов.
Состояние газа определяется значениями некоторых измеримых свойств, таких как давление, температура и объем , который занимает газ. Значения этих переменных и состояние газа могут быть изменены процессами . На этом рисунке мы показываем газ, заключенный в голубой банке, в двух различных состояниях. Слева в состоянии 1 газ находится под более высоким давлением и занимает меньший объем, чем в состоянии 2 справа. Мы можем представить состояние газа на графике зависимости давления от объема, как показано справа. Чтобы изменить состояние газа из состояния 1 в состояние 2, мы должны изменить условия в банке, либо нагревая газ, либо физически изменяя объем, перемещая поршень, либо изменяя давление, добавляя или удаляя грузы из сосуда. поршень. При некоторых из этих изменений мы совершаем работу (или совершаем работу) над газом, при других изменениях мы добавляем (или удаляем) тепло. Термодинамика помогает нам определить количество работы и количество тепла, необходимое для изменения состояния газа.
Чтобы изменить состояние газа из состояния 1 в состояние 2, мы должны изменить условия в банке, либо нагревая газ, либо физически изменяя объем, перемещая поршень, либо изменяя давление, добавляя или удаляя грузы из сосуда. поршень. При некоторых из этих изменений мы совершаем работу (или совершаем работу) над газом, при других изменениях мы добавляем (или удаляем) тепло. Термодинамика помогает нам определить количество работы и количество тепла, необходимое для изменения состояния газа.
Ученые определяют работу (W) как произведение силы, действующей на расстоянии. Для газа работа есть произведение давления (p) и объема (V) при изменении объема.
дельта W = p * дельта V
«Дельта» указывает на изменение переменной. Мы можем выполнить быструю проверку единиц измерения, чтобы увидеть, что давление (сила/площадь), умноженное на объем, дает единицы силы, умноженные на длину, которые являются единицами работы (джоулями или футо-фунтами). Чтобы над газом была совершена работа, его объем должен измениться; должно быть какое-то движение, связанное с заменой переменных. Увеличение давления при сохранении постоянного объема не работает. В общем случае при изменении состояния изменяется как объем, так и давление. Поэтому правильнее определить работу как произведение интегрированного (суммированного) переменного давления на изменение объема из состояния 1 в состояние 2, определяемое интегральным уравнением. На графике зависимости давления от объема работа выполняется за область под кривой , которая описывает, как состояние изменяется с состояния 1 на состояние 2.
Увеличение давления при сохранении постоянного объема не работает. В общем случае при изменении состояния изменяется как объем, так и давление. Поэтому правильнее определить работу как произведение интегрированного (суммированного) переменного давления на изменение объема из состояния 1 в состояние 2, определяемое интегральным уравнением. На графике зависимости давления от объема работа выполняется за область под кривой , которая описывает, как состояние изменяется с состояния 1 на состояние 2.
Как упоминалось выше, существует несколько вариантов изменения состояния газа из одного состояния в другое. Таким образом, мы могли бы ожидать, что количество работы, выполненной над газом (или им), может различаться в зависимости от того, как именно изменяется состояние. В качестве примера на графике на рисунке мы показываем изогнутую черную линию от состояния 1 до состояния 2 нашего ограниченного газа. Эта линия представляет собой изменение, вызванное удалением грузов (уменьшением давления) и возможностью регулировки объема в соответствии с законом Бойля без подвода тепла.
 03.22
03.22


 2 Газ на 1,5 атм расширяется от 2,5 литров
2 Газ на 1,5 атм расширяется от 2,5 литров 17. Мы готовы
17. Мы готовы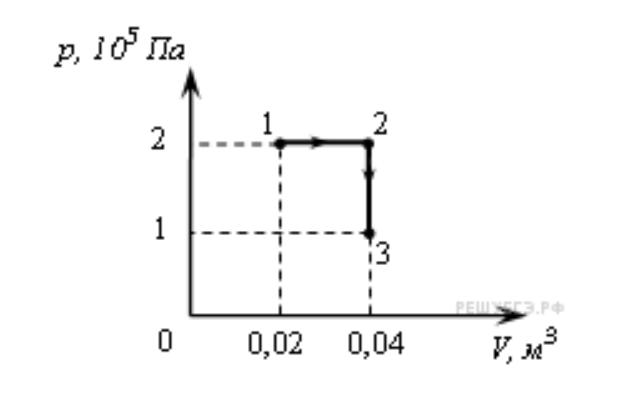 Это означает, что его чистое изменение внутренней энергии равно
Это означает, что его чистое изменение внутренней энергии равно
 Мы могли бы также назвать это V 1 ,
Мы могли бы также назвать это V 1 ,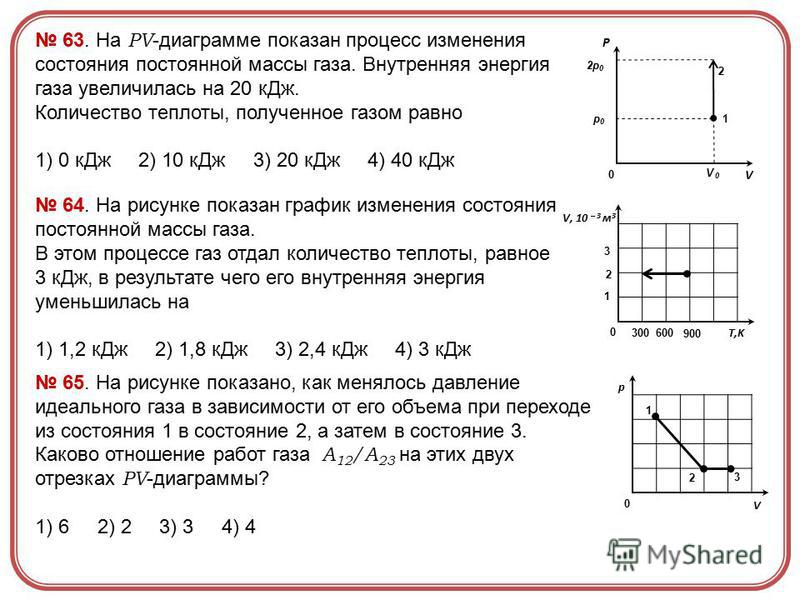 24
24 7 Двигатель Карно работает с горячим баком 650°C
7 Двигатель Карно работает с горячим баком 650°C 8 КПД бензинового двигателя 0,55. Оценить температуру
8 КПД бензинового двигателя 0,55. Оценить температуру