Передаточное число: расчет, формула, определение

Любое подвижное соединение, передающее усилие и меняющее направление движения, имеет свои технические характеристики. Основным критерием, определяющим изменение угловой скорости и направления движения, является передаточное число. С ним неразрывно связано изменение силы – передаточное отношение. Оно вычисляется для каждой передачи: ременной, цепной, зубчатой при проектировании механизмов и машин.

Перед тем как узнать передаточное число, надо посчитать количество зубьев на шестернях. Затем разделить их количество на ведомом колесе на аналогичный показатель ведущей шестерни. Число больше 1 означает повышающую передачу, увеличивающую количество оборотов, скорость. Если меньше 1, то передача понижающая, увеличивающая мощность, силу воздействия.

Общее определение

Наглядный пример изменения числа оборотов проще всего наблюдать на простом велосипеде. Человек медленно крутит педали. Колесо вращается значительно быстрее. Изменение количества оборотов происходит за счет 2 звездочек, соединенных в цепь. Когда большая, вращающаяся вместе с педалями, делает один оборот, маленькая, стоящая на задней ступице, прокручивается несколько раз.

Передачи с крутящим моментом

В механизмах используют несколько видов передач, изменяющих крутящий момент. Они имеют свои особенности, положительные качества и недостатки. Наиболее распространенные передачи:

• ременная;
• цепная;
• зубчатая.

Ременная передача самая простая в исполнении. Используется при создании самодельных станков, в станочном оборудование для изменения скорости вращения рабочего узла, в автомобилях.

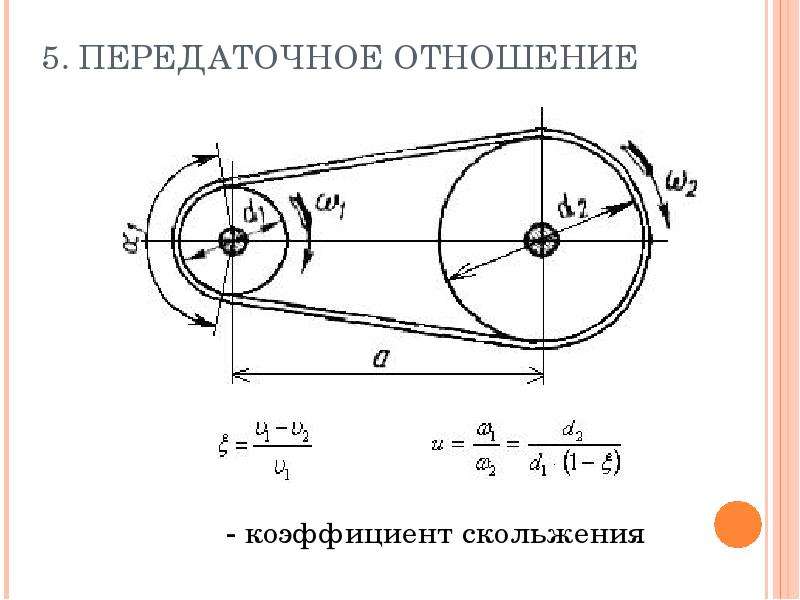
Ремень натягивается между 2 шкивами и передает вращение от ведущего в ведомому. Производительность низкая, поскольку ремень скользит по гладкой поверхности. Благодаря этому, ременной узел является самым безопасным способом передавать вращение. При перегрузке происходит проскальзывание ремня, и остановка ведомого вала.

Передаваемое количество оборотов зависит от диаметра шкивов и коэффициента сцепления. Направление вращения не меняется.

Переходной конструкцией является ременная зубчатая передача.

На ремне имеются выступы, на шестерне зубчики. Такой тип ремня расположен под капотом автомобиля и связывает звездочки на осях коленвала и карбюратора. При перегрузе ремень рвется, так как это самая дешевая деталь узла.

Цепная состоит из звездочек и цепи с роликами. Передающееся число оборотов, усилие и направление вращения не меняются. Цепные передачи широко применяются в транспортных механизмах, на конвейерах.

Характеристика зубчатой передачи

В зубчатой передаче ведущая и ведомая детали взаимодействуют непосредственно, за счет зацепления зубьев. Основное правило работы такого узла – модули должны быть одинаковыми. В противном случае механизм заклинит. Отсюда следует, что диаметры увеличиваются в прямой зависимости от количества зубьев. Одни значения можно в расчетах заменить другими.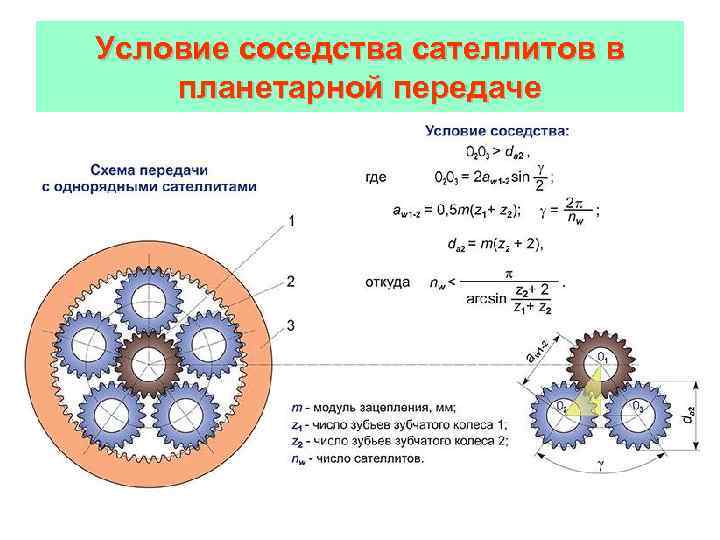

Модуль – размер между одинаковыми точками двух соседних зубьев.

Например, между осями или точками на эвольвенте по средней линии Размер модуля состоит из ширины зуба и промежутка между ними. Измерять модуль лучше в точке пересечения линии основания и оси зубца. Чем меньше радиус, тем сильнее искажается промежуток между зубьями по наружному диаметру, он увеличивается к вершине от номинального размера. Идеальные формы эвольвенты практически могут быть только на рейке. Теоретически на колесе с максимально бесконечным радиусом.

Деталь с меньшим количеством зубьев называют шестерней. Обычно она ведущая, передает крутящий момент от двигателя.

Зубчатое колесо имеет больший диаметр и в паре ведомое. Оно соединено с рабочим узлом. Например, передает вращение с необходимой скоростью на колеса автомобиля, шпиндель станка.

Обычно посредством зубчатой передачи уменьшается количество оборотов и увеличивается мощность. Если в паре деталь, имеющая больший диаметр, ведущая, на выходе шестерня имеет большее количество оборотов, вращается быстрее, но мощность механизма падает. Такие передачи называют понижающими.

Зачем нужна паразитка

При взаимодействии шестерни и колеса происходит изменение сразу нескольких величин:

• количества оборотов;
• мощности;
• направление вращения.

Только в планетарных узлах с нарезкой зубьев по внутреннему диаметру венца сохраняется направление вращения. При наружном зацеплении ставится две одинаковые шестерни подряд. Их взаимодействие не меняет ничего, кроме направления движения. В этом случае обе зубчатые детали называются шестернями, колеса нет. Вторая, промежуточная, получила название «паразитка», поскольку в вычислениях не участвует, меняет только знак.

Виды зубчатых соединений

Зубчатое зацепление может иметь различную форму зуба на деталях. Это зависит от исходной нагрузки и расположения осей сопрягаемых деталей. Различают виды зубчатых подвижных соединений:

• прямозубая;
• косозубая;
• шевронная;
• коническая;
• винтовая;
• червячная.

Самое распространенное и простое в исполнении прямозубое зацепление. Наружная поверхность зуба цилиндрическая. Расположение осей шестерни и колеса параллельное. Зуб расположен под прямым углом к торцу детали.

Когда нет возможности увеличить ширину колеса, а надо передать большое усилие, зуб нарезают под углом и за счет этого увеличивают площадь соприкосновения. Расчет передаточного числа при этом не изменяется. Узел становится более компактным и мощным.

Недостаток косозубых зацеплений в дополнительной нагрузки на подшипники. Сила от давления ведущей детали действует перпендикулярно плоскости контакта. Кроме радиального, появляется осевое усилие.

Компенсировать напряжение вдоль оси и еще больше увеличить мощность позволяет шевронное соединение. Колесо и шестерня имеют 2 ряда косых зубьев, направленных в разные стороны. Передающее число рассчитывается аналогично прямозубому зацеплению по соотношению количества зубьев и диаметров. Шевронное зацепление сложное в исполнении. Оно ставится только на механизмах с очень большой нагрузкой.

В конической зубчатой передачи оси расположены под углом. Рабочий элемент нарезается по конической плоскости. Передаточное число таких пар может равняться 1, когда надо только изменить плоскость действия силы. Для увеличения мощности нарезается полукруглый зуб. Передающееся количество оборотов считается только по зубу, диаметр в основном используется при расчетах габаритов узла.

Винтовая передача имеет зуб, нарезанный под углом 45⁰. Это позволяет располагать оси рабочих элементов перпендикулярно в разных плоскостях. У червячной передачи нет шестерни, ее заменяет червяк. Оси деталей не пересекаются. Они расположены перпендикулярно в пространстве, но разных плоскостях. Передаточное число пары определяется количеством заходов резьбы на червяке.

Кроме перечисленных производят и другие виды передач, но они встречаются крайне редко и к стандартным не относятся.

Многоступенчатые редукторы

Как подобрать нужное передаточное число. Двигатель обычно выдает несколько тысяч оборотов в минуту. На выходе – колесах автомобиля и шпинделе станка, такая скорость вращения приведет к аварии. Мощности исполняющего механизма не хватит, чтобы рабочий инструмент мог резать металл, а колеса сдвинули автомобиль. Одна пара зубчатого зацепления не сможет обеспечить требуемое понижение или ведомая деталь должна иметь огромные размеры.

Создается многоступенчатый узел с несколькими парами зацеплений. Передаточное число редуктора считается как произведение чисел каждой пары.

U_р = U₁×U₂ × … ×U_n;

Где:

U_р – передаточное число редуктора;

U_1,2,n – каждой из пар.

Перед тем как подобрать передаточное число редуктора, надо определиться с количеством пар, направлением вращения выходного вала, и делать расчет в обратном порядке, исходя из максимально допустимых габаритов колес.

В многоступенчатом редукторе все зубчатые детали, находящиеся между ведущей шестерней на входе в редуктор и ведомым зубчатым венцом на выходном валу, называются промежуточными. Каждая отдельная пара имеет свое передающееся число, шестерню и колесо.

Редуктор и коробка скоростей

Любая коробка скоростей с зубчатым зацеплением является редуктором, но обратное утверждение неверно.

Коробка скоростей представляет собой редуктор с подвижным валом, на котором расположены шестерни разного размера. Смещаясь вдоль оси, он включает в работу то одну, то другую пару деталей. Изменение происходит за счет поочередного соединения различных шестерен и колес. Они отличаются диаметром и передающимся количеством оборотов. Это дает возможность изменять не только скорость, но и мощность.

Трансмиссия автомобиля

В машине поступательное движение поршня преобразуется во вращательное коленвала. Трансмиссия представляет собой сложный механизм с большим количеством различных узлов, взаимодействующих между собой. Ее назначение — передать вращение от двигателя на колеса и регулировка количества оборотов – скорости и мощности автомобиля.

В состав трансмиссии входит несколько редукторов. Это, прежде всего:

• коробка передач – скоростей;
• дифференциал.

Коробка передач в кинематической схеме стоит сразу за коленвалом, изменяет скорость и направление вращения.

Посредством переключения – перемещения вала, шестерни на валу соединяются поочередно с разными колесами. При включении задней скорости, через паразитку меняется направление вращения, автомобиль в результате движется назад.

Дифференциал представляет собой конический редуктор с двумя выходными валами, расположенными в одной оси напротив друг друга. Они смотрят в разные стороны. Передаточное число редуктора – дифференциала небольшое, в пределах 2 единиц. Он меняет положение оси вращения и направление. Благодаря расположению конических зубчатых колес напротив друг друга, при зацеплении с одной шестерней они крутятся в одном направлении относительно положения оси автомобиля, и передают вращательный момент непосредственно на колеса. Дифференциал изменяет скорость и направление вращения ведомых коничек, а за ними и колес.

Как рассчитать передаточное число

Шестерня и колесо имеют разное количество зубов с одинаковым модулем и пропорциональный размер диаметров. Передаточное число показывает, сколько оборотов совершит ведущая деталь, чтобы провернуть ведомую на полный круг. Зубчатые передачи имеют жесткое соединение. Передающееся количество оборотов в них не меняется. Это негативно сказывается на работе узла в условиях перегрузок и запыленности. Зубец не может проскользнуть, как ремень по шкиву и ломается.

Расчет без учета сопротивления

В расчете передаточного числа шестерен используют количество зубьев на каждой детали или их радиусы.

u₁₂ = ± Z₂/Z₁ и u₂₁ = ± Z₁/Z₂,

Где u₁₂ – передаточное число шестерни и колеса;

Z₂ и Z₁ – соответственно количество зубьев ведомого колеса и ведущей шестерни.

Знак «+» ставится, если направление вращения не меняется. Это относится к планетарным редукторам и зубчатым передачам с нарезкой зубцов по внутреннему диаметру колеса. При наличии паразиток – промежуточных деталей, располагающихся между ведущей шестерней и зубчатым венцом, направление вращения изменяется, как и при наружном соединении. В этих случаях в формуле ставится «–».

При наружном соединении двух деталей посредством расположенной между ними паразитки, передаточное число вычисляется как соотношение количества зубьев колеса и шестерни со знаком «+». Паразитка в расчетах не участвует, только меняет направление, и соответственно знак перед формулой.

Обычно положительным считается направление движения по часовой стрелке. Знак играет большую роль при расчетах многоступенчатых редукторов. Определяется передаточное число каждой передачи отдельно по порядку расположения их в кинематической цепи. Знак сразу показывает направление вращения выходного вала и рабочего узла, без дополнительного составления схем.

Вычисление передаточного числа редуктора с несколькими зацеплениями – многоступенчатого, определяется как произведение передаточных чисел и вычисляется по формуле:

u₁₆ = u₁₂×u₂₃×u₄₅×u₅₆ = z₂/z₁×z₃/z₂×z₅/z₄×z₆/z₅ = z₃/z₁×z₆/z₄

Способ расчета передаточного числа позволяет спроектировать редуктор с заранее заданными выходными значениями количества оборотов и теоретически найти передаточное отношение.

Зубчатое зацепление жесткое. Детали не могут проскальзывать относительно друг друга, как в ременной передаче и менять соотношение количества вращений. Поэтому на выходе обороты не изменяются, не зависят от перегруза. Верным получается расчет скорости угловой и количества оборотов.

КПД зубчатой передачи

Для реального расчета передаточного отношения, следует учитывать дополнительные факторы. Формула действительна для угловой скорости, что касается момента силы и мощности, то они в реальном редукторе значительно меньше. Их величину уменьшает сопротивление передаточных моментов:

• трение соприкасаемых поверхностей;
• изгиб и скручивание деталей под воздействием силы и сопротивление деформации;
• потери на шпонках и шлицах;
• трение в подшипниках.

Для каждого вида соединения, подшипника и узла имеются свои корректирующие коэффициенты. Они включаются в формулу. Конструктора не делают расчеты по изгибу каждой шпонки и подшипника. В справочнике имеются все необходимые коэффициенты. При необходимости их можно рассчитать. Формулы простотой не отличаются. В них используются элементы высшей математики. В основе расчетов способность и свойства хромоникелевых сталей, их пластичность, сопротивление на растяжение, изгиб, излом и другие параметры, включая размеры детали.

Что касается подшипников, то в техническом справочнике, по которому их выбирают, указаны все данные для расчета их рабочего состояния.

При расчете мощности, основным из показателей зубчатых зацепления является пятно контакта, оно указывается в процентах и его размер имеет большое значение. Идеальную форму и касание по всей эвольвенте могут иметь только нарисованные зубья. На практике они изготавливаются с погрешностью в несколько сотых долей мм. Во время работы узла под нагрузкой на эвольвенте появляются пятна в местах воздействия деталей друг на друга. Чем больше площадь на поверхности зуба они занимают, тем лучше передается усилие при вращении.

Все коэффициенты объединяются вместе, и в результате получается значение КПД редуктора. Коэффициент полезного действия выражается в процентах. Он определяется соотношением мощности на входном и выходном валах. Чем больше зацеплений, соединений и подшипников, тем меньше КПД.

Передаточное отношение зубчатой передачи

Значение передаточного числа зубчатой передачи совпадает передаточным отношением. Величина угловой скорости и момента силы изменяется пропорционально диаметру, и соответственно количеству зубьев, но имеет обратное значение.

Чем больше количество зубьев, тем меньше угловая скорость и сила воздействия – мощность.

При схематическом изображении величины силы и перемещения шестерню и колесо можно представить в виде рычага с опорой в точке контакта зубьев и сторонами, равными диаметрам сопрягаемых деталей. При смещении на 1 зубец их крайние точки проходят одинаковое расстояние. Но угол поворота и крутящий момент на каждой детали разный.

Например, шестерня с 10 зубьями проворачивается на 36°. Одновременно с ней деталь с 30 зубцами смещается на 12°. Угловая скорость детали с меньшим диаметром значительно больше, в 3 раза. Одновременно и путь, который проходит точка на наружном диаметре имеет обратно пропорциональное отношение. На шестерне перемещение наружного диаметра меньше. Момент силы увеличивается обратно пропорционально соотношению перемещения.

Крутящий момент увеличивается вместе с радиусом детали. Он прямо пропорционален размеру плеча воздействия – длине воображаемого рычага.

Передаточное отношение показывает, насколько изменился момент силы при передаче его через зубчатое зацепление.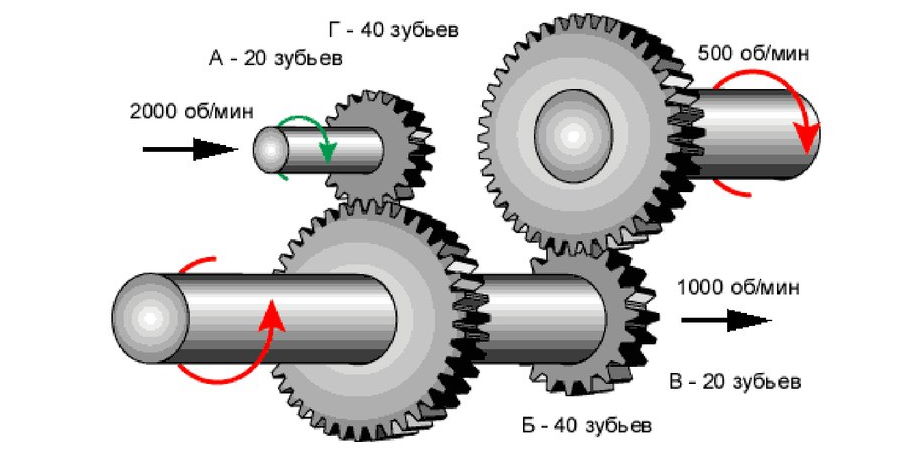 Цифровое значение совпадает с переданным числом оборотов.

Передаточное отношение редуктора вычисляется по формуле:

U₁₂ = ±ω₁/ω₂=±n₁/n₂

где U₁₂ – передаточное отношение шестерни относительно колеса;

ω₁ и ω₂ – угловые скорости ведущего и ведомого элемента соединения; n₁ и n₂ – частота вращения.

Отношение угловых скоростей можно считать через число зубьев. При этом направление вращения не учитывается и все цифры с положительным знаком.

Зубчатая передача имеет самый высокий КПД и наименьшую защиту от перегруза – ломается элемент приложения силы, приходится делать новую дорогостоящую деталь со сложной технологией изготовления.

Передаточное число редуктора

Передаточное отношение — это соотношение угловых скоростей или крутящих моментов валов (в зависимости от строения механизма).
Передачи применяются для того, чтобы передать вращающий момент от электродвигателя к исполнительному устройству. Почему это необходимо? Дело в том, что сам мотор обычно не может передать требуемый вращающий момент, кроме того, частота вращения вала электродвигателя оказывается слишком велика, поэтому её надо понизить. Для этого и сконструированы понижающие передачи, редукторы. Таким образом удаётся изменить сразу и частоту вращения вала, и крутящий момент.

Передачи с крутящим моментом

Механизм передачи крутящего момента — редуктор — имеет входной и выходной валы.
Существует два способа передачи вращающего момента: жёсткий (момент передается жесткими звеньями, например, шестернями) и фрикционный (момент передается силами трения, работающих на поверхностях вала, например, ременная передача). Также есть возможность совмещать эти способы передачи.
Характеристика зубчатой передачи редуктора
Зубчатая передача редуктора – это механизм, состоящих из отдельных звеньев для передачи мощности через вращение зубчатых колёс. Такую зубчатую передачу используют в механических редукторах для преобразования движения.
Зубчатые редукторы очень часто задействуют в машиностроении. Именно их выбирают благодаря большому количеству преимуществ: высокому КПД, долгому сроку службы механизма, маленьким габаритам, постоянству передаточного отношения, простой и надёжной конструкции.
Также у этих редукторов есть и недостатки. К ним относят шум при больших скоростях и большие размеры редукторов, если передаточные отношения велики. Тем не менее, плюсов их использования гораздо больше, чем минусов, что и определяет итоговую востребованность.

Многоступенчатые редукторы

Как известно, современные электродвигатели выдают частоту ведущего вала примерно в районе полутора тысячи (1500) оборотов в минуту. А конечным потребителям в цепочке передачи движения обычно требуется куда меньшая частота. Стоит рассмотреть для лучшего понимания на конкретном примере. Возьмём, скажем, ленту транспортёра. Она движется медленно. Как же сделать так, чтобы надежно передать вращающий момент от электродвигателя к конечному устройству?
Здесь на помощь как раз и придут многоступенчатые редукторы.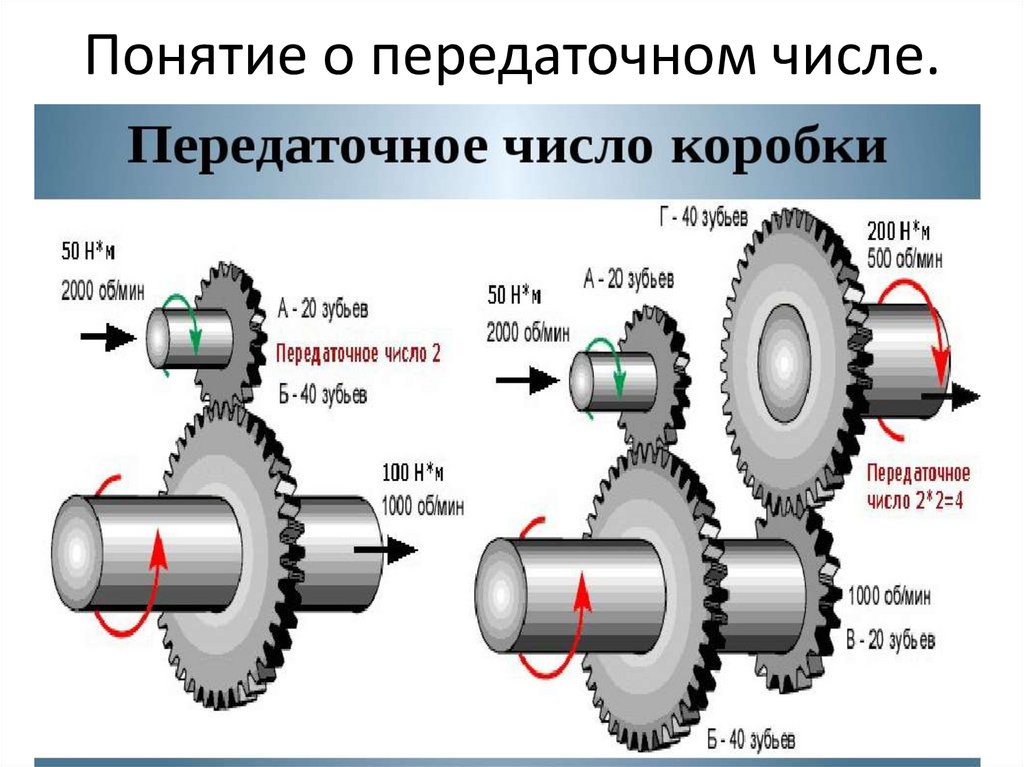 Наличие нескольких ступеней позволяет сделать компактное устройство, значительно снижающее частоту вращения вала.

Как правильно рассчитать передаточное число

Передаточное число многоступенчатого редуктора вычисляется как произведение передаточных чисел каждой ступени. Пример. В редукторе четыре зубчатые пары, передаточные отношения каждой из которых тоже равны 4. Общее передаточное число тогда будет равно 4х4х4х4 = 256.
В общем случае общее передаточное отношение редуктора равно отношению частоты вращения входного (ведущего) вала и частоты вращения ведомого (выходного) вала. Отсюда следует, что если выходной вал вращается медленнее входного, то передаточное отношение будет больше единицы. Такие передачи называют понижающими. Если же скорость выходного вала будет выше скорости входного вала, то передаточное число будет меньше единицы. В этом случае говорят о повышающей передаче или мультипликаторе.
При передаче движения всегда соответственно меняется и крутящий момент: если передача понижающая, то момент увеличивается, если повышающая, то уменьшается.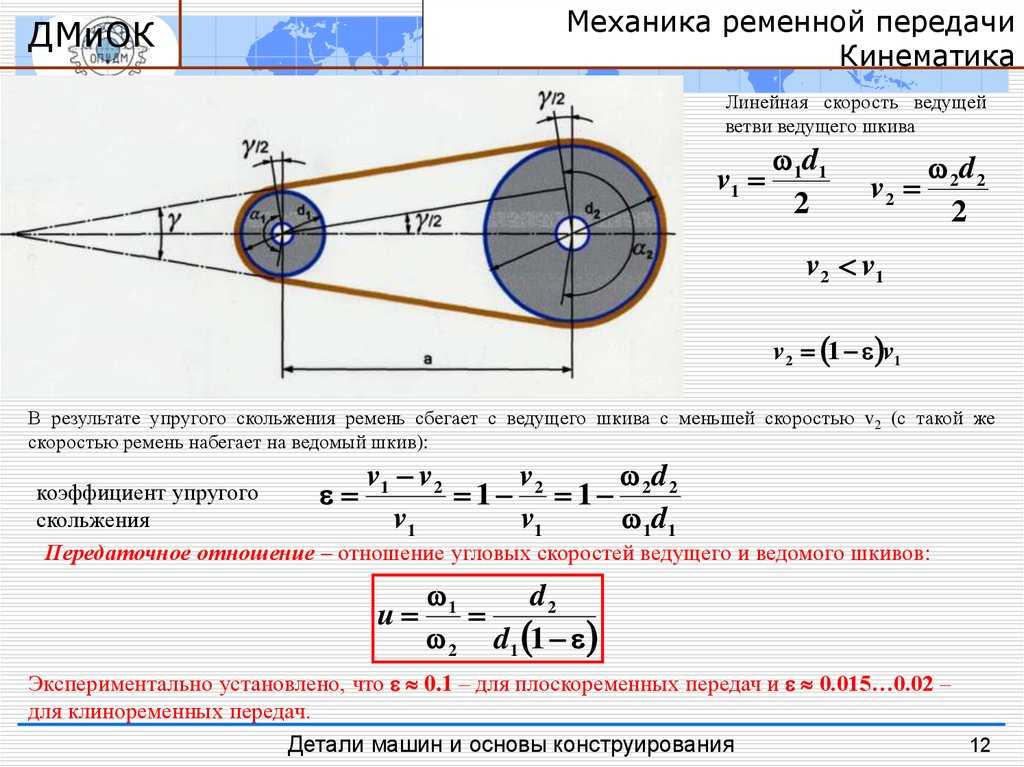 Поэтому передаточное число можно представить как отношение крутящего момента на выходе к крутящему моменту на входе в редуктор.

Расчёт без учета сопротивления

Любой редуктор состоит из зубчатых пар. Чтобы рассчитать передаточное число каждой пары, надо разделить количество зубьев ведущего колеса на количество зубьев ведомого колеса.

Важно! При этом надо смотреть, меняется ли направление вращения шестеренки. Если меняется, то передаточное отношение принимается со знаком минус, если не меняется, то плюс. Направление вращения не меняется, если у колеса нарезка зубьев сделана внутри колеса.

Если в передаче участвует так называемая паразитка, то она в расчете передаточного отношения не участвует, так как ее задача лишь менять направление движения.
Также при расчете передаточных отношений можно использовать наружный диаметр шестерни. Иногда это удобно, если посчитать число зубьев затруднительно. Важно: зубчатая передача жесткая, здесь нет проскальзывания, как в ременной передаче, поэтому передаточное число всегда можно рассчитать с абсолютной точностью.
Если в редукторе применен червячный редуктор, то его передаточное отношение определяется как отношение числа зубьев ведущего колеса к числу заходов (витков) червяка. Чаще всего у червяка один заход, поэтому ясно: передаточное отношение червячной пары огромно, а вращающий момент может повышаться в десятки раз.

КПД зубчатой передачи

Преимуществами данной передачи считаются:

1. Большая и неограниченная мощность.
2. Небольшая масса и габариты.
3. Большой коэффициент полезного действия (приблизительно 0,95-0,99).
4. Надёжны, но нуждаются в большой точности изготовления.

КПД определяется как отношение реально полученной энергии к потребленной. Чем выше КПД механизма, тем больше энергии преобразовывается на полезные цели, тем меньше потери, тем эффективнее механизм.
Учёные всего мира постоянно ведут борьбу именно за сокращение непроизводительных потерь. Чтобы обеспечить хорошую работу машины с большим КПД, можно использовать масла с различными свойствами при больших изменениях температуры среды. При экспериментах с различными видами масла совместно с допустимой нагрузочной способности зубчатых передач на рабочих поверхностях зубьев не обнаружили развитие процесса разрушения, что обеспечивает отличные технико-экономические показатели машины.

Важно! КПД зубчатой передачи сильно зависит от точности изготовления зубчатых колес. В случае грубых нарушений геометрии в редукторе будут большие расходы энергии, он будет нагреваться, его КПД значительно упадёт. Поэтому редукторы следует приобретать только у проверенных производителей.

Постоянное и переменное передаточное отношение редуктора

Передаточное отношение может быть как постоянным, так и переменным. При переменном случае оно может меняться бесступенчато или ступенчато. В промышленности нашли применение обе эти схемы. Если передаточное число меняется плавно, то такое устройство называют вариатором. Эти устройства дороги и требуют точной сборки и квалифицированного обслуживания. Но всё это оправдывается конечным результатом — их полезность уже проверена временем.

Калькулятор передаточного отношения

Этот калькулятор передаточного отношения определяет механическое преимущество, которое дает установка с двумя передачами в машине . Передаточное число дает нам представление о том, насколько ускоряется или замедляется выходная передача или сколько крутящего момента теряется или увеличивается в системе. Мы оснастили этот калькулятор уравнением передаточного числа и уравнением передаточного отношения , чтобы вы могли быстро определить передаточное число ваших передач.

Продолжайте читать, чтобы узнать больше о расчете передаточного числа и о том, как он важен при создании простых (и даже сложных) машин.

Предпочитаете смотреть , а не читать? Узнайте все, что вам нужно, за 90 секунд с помощью этого видео , которое мы сделали для вас :

Посмотрите это на YouTube

Что такое снаряжение?

Шестерня представляет собой зубчатое колесо, которое может изменять направление, крутящий момент и скорость приложенного к нему вращательного движения. Зубчатые колеса бывают разных форм и размеров (даже если наиболее распространенными являются эвольвентные зубчатые колеса — см. Калькулятор эвольвентных функций), и эти различия описывают поступательное движение или передачу вращательного движения. Передача движения происходит, когда две или более шестерни в системе зацепляются друг с другом во время движения. Мы называем эту систему передач зубчатая передача .

В зубчатой ​​передаче вращение одной шестерни приводит к вращению других шестерен. Шестерня, которая изначально получает вращающее усилие либо от мотора, либо просто вручную (или ногой в случае велосипеда), называется входной шестерней . Мы также можем назвать его ведущей шестерней, поскольку она инициирует движение всех остальных шестерен в зубчатой ​​передаче. Последняя передача, на которую влияет входная шестерня, известна как выходная шестерня . В системе с двумя передачами мы можем назвать эти передачи 9-ю.0003 ведущая шестерня и ведомая шестерня соответственно.

Результирующее движение выходной шестерни может быть в том же направлении, что и входной шестерни, но может быть и в другом направлении или осях вращения в зависимости от типа шестерни в зубчатой ​​передаче. Чтобы помочь вам визуализировать это, вот иллюстрация различных типов зубчатых колес и их соотношения между входом и выходом:

Вам также может понравиться наш калькулятор длины цепи и калькулятор шестерни спидометра.

Что такое передаточное число и как рассчитать передаточное число

Передаточное отношение — это отношение длины окружности входной шестерни к окружности выходной шестерни в зубчатой ​​передаче. Передаточное отношение помогает нам определить количество зубьев, необходимых каждой шестерне для получения желаемой выходной скорости/угловой скорости или крутящего момента (см. калькулятор крутящего момента).

Рассчитываем передаточное отношение между двумя шестернями по , разделив длину окружности входной шестерни на длину окружности выходной шестерни . Мы можем определить длину окружности конкретной шестерни так же, как вычисляем длину окружности. В виде уравнения это выглядит так:

передаточное число = (π × диаметр входной шестерни)/(π × диаметр выходной шестерни)

Упрощая это уравнение, мы также можем получить передаточное отношение, когда только шестерни учитываются диаметры или радиусы:

передаточное отношение = (диаметр входной шестерни)/(диаметр выходной шестерни)

передаточное отношение = (радиус входной шестерни)/(радиус выходной шестерни)

Точно так же мы можем рассчитать передаточное число, учитывая количество зубьев на входной и выходной шестернях. Это похоже на рассмотрение окружностей шестерен. Мы можем выразить окружность шестерни, умножив сумму толщины зуба и расстояния между зубьями на количество зубьев шестерни:

передаточное число = (количество входных зубьев шестерни × (толщина шестерни + расстояние между зубьями)) / ( число зубьев выходной шестерни × (толщина шестерни + расстояние между зубьями))

Но, поскольку толщина и расстояние между зубьями зубчатой ​​передачи должны быть одинаковыми для плавного зацепления шестерен, мы можем отменить множитель толщины шестерни и расстояния между зубьями в приведенном выше уравнении, оставив нам следующее уравнение:

Передаточное число = число зубьев входной шестерни / число зубьев выходной шестерни

Передаточное число, как и любое другое передаточное число, может быть выражено как:

Дробь или частное – где, если возможно, мы упрощаем дробь, разделив числитель и знаменатель на их наибольший общий множитель.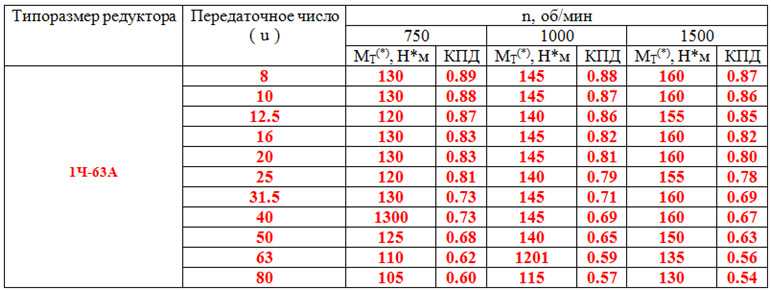

Десятичное число – выражение передаточного числа в виде десятичного числа дает нам быстрое представление о том, насколько нужно повернуть входную шестерню, чтобы выходная шестерня совершила один полный оборот.

Упорядоченная пара чисел , разделенных двоеточием, например 2:5 или 1:14 . При этом мы можем увидеть наименьшее количество оборотов, необходимых для того, чтобы как входная, так и выходная шестерни вернулись в исходное положение одновременно.

С другой точки зрения, если мы возьмем обратную величину передаточного отношения в дробной форме и упростим ее до десятичного числа, мы получим значение механического преимущества (или недостатка), которое имеет наша зубчатая передача или система зубчатых передач.

Понимание передаточного отношения и значений механического преимущества

Передаточные числа довольно легко понять, и теперь, когда мы знаем, как рассчитать передаточное число, не лучше ли узнать, как оно влияет на сами шестерни? Чтобы лучше объяснить передаточные числа, давайте рассмотрим двухступенчатую систему, в которой входная и выходная шестерни имеют десять и сорок зубьев соответственно:

Следуя нашему уравнению передаточного числа, мы можем сказать, что эта зубчатая передача имеет передаточное число 10:40, 10/40 или просто 1/4 (или 0,25). Это передаточное число означает, что выходная шестерня будет вращаться только на 1/4 полного оборота после того, как входная шестерня завершит полный оборот . Продолжая в том же духе и сохраняя постоянную входную скорость, мы видим, что скорость выходной шестерни также составляет 1/4 скорости входной передачи. Другими словами, скорость входной шестерни в четыре раза превышает скорость выходной шестерни, как видно на анимированном изображении ниже:

В то время как эта установка демонстрирует редуктор с точки зрения скорости, взамен она дает нам на выходе больший крутящий момент по сравнению с входом. Обратная величина его передаточного отношения составляет 4/1, поэтому мы можем сказать, что мы получаем четырехкратное механическое преимущество, когда речь идет о крутящем моменте.

Важное замечание по промежуточным шестерням

Цилиндрическая шестерня с любым количеством зубьев между ведущей и ведомой шестернями не изменяет общего передаточного числа зубчатой ​​передачи.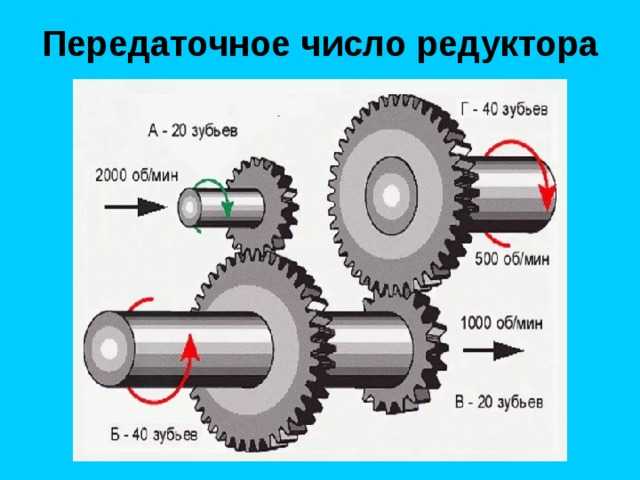 Однако эта шестерня (или шестерни) может изменять направление выходной шестерни. Мы называем это промежуточной передачей промежуточная шестерня . В качестве примера, вот редуктор 1:2,5 с дополнительной промежуточной шестерней:

Без промежуточной шестерни, вот та же зубчатая передача. Обратите внимание, что направление выходной шестерни обратное:

Реальные простые машины с шестернями

Мы видим шестерни в нашей повседневной жизни, и чтобы лучше понять передаточные числа, вот несколько реальных примеров простых машины с зубчатыми колесами:

Механическое преимущество по скорости

Ручные дрели, хотя они и кажутся менее популярными в настоящее время, являются прекрасным примером простой машины, демонстрирующей механическое преимущество с точки зрения скорости. При повороте рукоятки сверло будет вращаться с высокой скоростью.

Механическое преимущество по крутящему моменту

Ехать в гору на велосипеде легче, если вы находитесь на тихоходной передаче . Это приводит к лучшему крутящему моменту, обеспечивая большую мощность при движении в гору. Это может означать, что нам придется больше крутить педали, но наш подъем будет намного легче. Механизм велосипедной звездочки и цепи очень похож на зубчатую рейку. Цепь действует как зубчатая рейка, напрямую передавая движение задней звездочке велосипеда (см. калькулятор велосипедной передачи).

Часто задаваемые вопросы

Что такое шестерня?

Шестерня представляет собой круглую деталь машины, которая передает крутящий момент , когда входит в зацепление со своим аналогом. Шестерни обычно являются жизненно важной частью любой машины с движущимися частями, например, наручных часов или автомобиля.

Какие существуют типы шестерен?

Существуют различные типы передач в зависимости от угла передачи мощности. Для параллельной передачи к ним относятся прямозубые, косозубые, шевронные и планетарные передачи. Конические и спирально-конические шестерни используются для перпендикулярной передачи.

Какое передаточное число?

Передаточное отношение определяется как отношение длины окружности двух шестерен , которые входят в зацепление для передачи мощности. Этот параметр определяет, будет ли увеличиваться или уменьшаться количество передаваемой мощности.

Как рассчитать передаточное число?

Для расчета передаточного числа:

1. Найдите количество зубьев или диаметр 1-й (ведущей) шестерни.

2. Найдите количество зубьев или диаметр 2-й (ведомой) шестерни.

3. Разделите номер ведущей шестерни на номер ведомой шестерни, чтобы найти передаточное отношение.

В качестве альтернативы можно также узнать передаточное число, разделив скорость 1-й передачи на 2-ю передачу.

Шаги для расчета передаточного числа – Блог CLR больше всего из своих преимуществ.

Одним из ключевых понятий для их адекватного использования является передаточное число (r _t ). Правильный выбор передаточного отношения важен для того, чтобы:

• Шестерня могла выдерживать больший крутящий момент , сводя к минимуму ошибки
• Движение могло создаваться таким образом, чтобы крутящий момент шестерни двигателя превышал инерцию шестерни.

Ниже мы познакомимся с необходимыми формулами для расчета передаточного числа , и что вы должны иметь в виду для этого расчета.

Передаточное отношение необходимо для движения и для того, чтобы шестерня могла выдерживать крутящий момент без ошибок

Что такое передача движения?

Передаточное отношение в трансмиссии — это соотношение между скоростями вращения двух зацепляющихся шестерен.

Поскольку каждое зубчатое колесо имеет разный диаметр, каждая из осей вращается с разной скоростью, когда они обе зацеплены. Изменение передаточного отношения эквивалентно изменению крутящего момента , который применяется.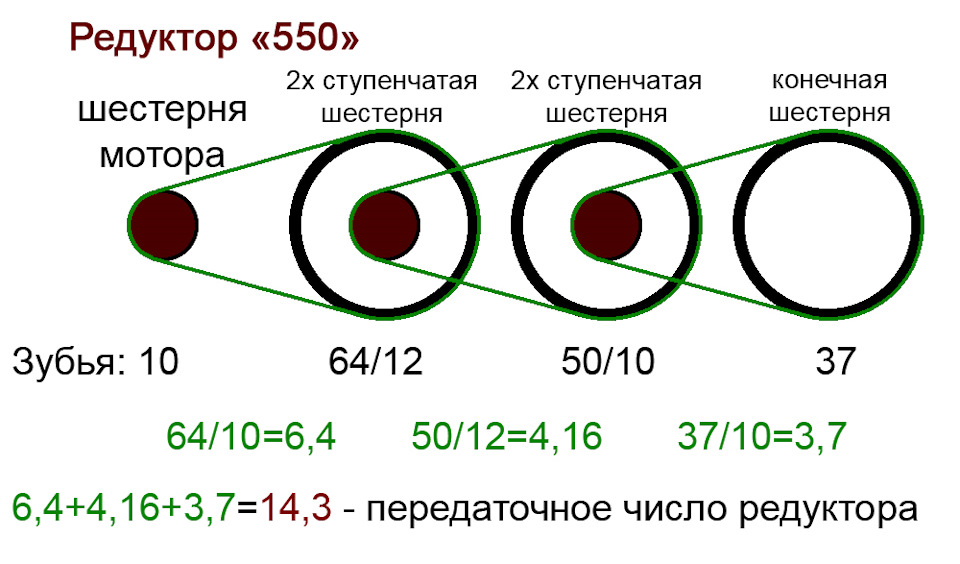

Передаточное отношение рассчитывается путем деления выходной скорости на входную скорость (i= Ws/We) или путем деления числа зубьев ведущей шестерни на число зубьев ведомой шестерни (i= Ze/ Зс).

i = Ws/We

i = Ze/Zs

Преимущества редукторных трансмиссий

Редукторная трансмиссия имеет ряд преимуществ по сравнению с другими трансмиссиями. Во-первых, они предлагают высокая производительность при передаче сил и движений , с длительным сроком службы и высокой надежностью.

Но что выделяет их, так это поразительная точность их передаточного числа, что означает, что они могут быть использованы в точном оборудовании .

Передаточные числа в зубчатых передачах очень точные, что делает эти передачи идеальными для прецизионного оборудования

В отличие от других механизмов, таких как цепи или шкивы, их размер мал , а это значит, что их можно устанавливать как в маленькие, так и в большие машины и помещения, а также в труднодоступные места.

Кроме того, их простота обслуживания делает редукторную трансмиссию одной из самых распространенных систем в основных отраслях промышленности, таких как автомобилестроение.

Параметры для проектирования зубчатой ​​передачи

При проектировании зубчатой ​​передачи необходимо учитывать следующие параметры:

Закон зацепления

Закон зубчатого зацепления определяет ситуацию, при которой точка контакта между двумя зубьями всегда будет пересекать точку O , если это позволяет ее профиль.

Эта точка O должна располагаться на линии, соединяющей центр вращения одной из шестерен и центр вращения другой .

Кроме того, радиусы шага и расстояния между точкой O и соответствующими центрами должны совпадать.

Передаточное число

Передаточное число ( r _t ) представляет собой передаточное отношение между скоростями вращения двух сопряженных шестерен .

More specifically, it is the quotient of the input and output speeds ( r _t  = ω _s  / ω _e ).

Система может вызвать снижение , если передаточное число меньше 1, или умножение на , если оно больше 1.

Вас может заинтересовать: Преобразователи частоты: все, что вам нужно знать о редукторах

Коэффициент контакта

среднее количество зубов в постоянном контакте .

Наилучшее передаточное отношение должно быть больше 1,2, чтобы обеспечить возможность передачи высоких нагрузок , обеспечить жесткость трансмиссии и обеспечить бесшумную и равномерную работу.

Как рассчитать передаточное число

Рассчитать передаточное число можно несколькими способами. Например:

Расчет передаточного отношения конических шестерен

При обращении к коническим шестерням нужно учитывать, что оно будет эквивалентно количеству зубьев ведущей шестерни, деленному на количество зубьев ведомой шестерни ( РТ = Z1 / Z2 ).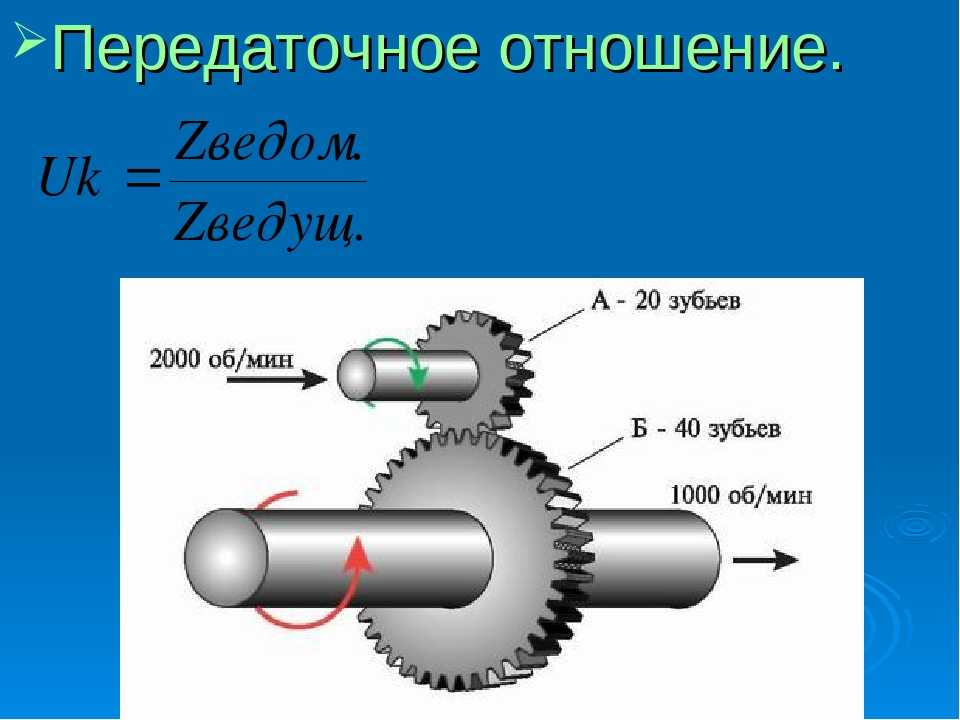

Вас может заинтересовать: Расчет передач: повысьте эффективность ваших трансмиссий.

Расчет передаточного числа зубчатой ​​передачи

В случае зубчатой ​​передачи с двумя шестернями нам необходимо выполнить следующие шаги:

1. Подсчитать количество зубьев . Сначала нам нужно будет посчитать количество зубьев ведущей шестерни и количество зубьев ведомой шестерни.
2. Разделить количество зубьев ведомой шестерни на количество зубьев ведущей шестерни . Полученное число будет числом раз, которое ведомая меньшая шестерня должна повернуть, чтобы большая совершила один полный оборот.

Передаточное число будет равно количеству зубьев ведущей шестерни, деленному на количество зубьев ведомой шестерни.

В случае зубчатой ​​передачи с более чем двумя шестернями нам потребуется выполнить следующие шаги:

1. Определить, какая шестерня является ведущей, а какая ведомой, и разделить количество зубьев бывший и последний .