Содержание

что это такое, в чем измеряется, как найти через скорость и время, формулы


Содержание:


  • Что такое ускорение


    • Единица измерения


  • Как рассчитать ускорение: формулы


    • Для прямолинейного движения


    • Для равноускоренного движения


    • Для равнозамедленного движения


    • Нахождение ускорения через массу и силу


  • Мгновенное ускорение


  • Максимальное ускорение


  • Среднее ускорение


  • Проекция ускорения


Содержание


  • Что такое ускорение


    • Единица измерения


  • Как рассчитать ускорение: формулы


    • Для прямолинейного движения


    • Для равноускоренного движения


    • Для равнозамедленного движения


    • Нахождение ускорения через массу и силу


  • Мгновенное ускорение


  • Максимальное ускорение


  • Среднее ускорение


  • Проекция ускорения



Что такое ускорение

Ускорение \(\overrightarrow а\) — векторная величина в физике, характеризующая быстроту изменения скорости тела. 2}{2S}\)

Где \(a\) — достигнутое ускорение тела, \(S\) — пройденный путь (расстояние), \(t\) — затраченное время.

Время отсчитывается от начала движения тела.

При прямолинейном равномерном движении ускорение по модулю равняется нулю.

Для равноускоренного движения

Равноускоренное движение — прямолинейное движение с постоянным положительным ускорением (разгон).

При таком виде движения ускорение определяется по формуле: \(a\;=\;\frac{V-V_0}t\), где \(V_0\) и \(V\) начальная и конечная скорости соответственно, \(a\) — достигнутое ускорение тела, \(t\) — затраченное время.

Для равнозамедленного движения

Равнозамедленное движение — прямолинейное движение с постоянным отрицательным ускорением (замедление).

При таком виде движения ускорение находим по формуле: \(a\;=-\;\frac{V-V_0}t\), где V0 и V начальная и конечная скорости соответственно, a — достигнутое ускорение тела, t — затраченное время.

Нахождение ускорения через массу и силу

Принцип инерции Галилея:

Если не действовать на тело, то его скорость не будет меняться.

Система отсчета (СО) — система координат, точка отсчета и указание начала отсчета времени.

Инерциальная система отсчета (ИСО) — это СО, в которой наблюдается движение по инерции (соблюдается принцип инерции).

II закон Ньютона:

В инерциальных системах отсчёта ускорение, приобретаемое материальной точкой, прямо пропорционально вызывающей его силе, совпадает с ней по направлению и обратно пропорционально массе материальной точки.

или

\(\overrightarrow a=\frac{\overrightarrow F}m\)

Мгновенное ускорение

Мгновенное ускорение тела (материальной точки) в данный момент времени — это физическая величина, равная пределу, к которому стремится среднее ускорение при стремлении промежутка времени к нулю. Другими словами — это ускорение, которое развивает тело за максимально короткий отрезок времени.

Выражается по формуле:

\( \overrightarrow a=\lim_{t\rightarrow0}\frac{\triangle\overrightarrow V}{\triangle t}\)

Максимальное ускорение

\(a_{max}=\omega v_{max},\) где \(a_{max}\) — максимальное ускорение, \(\omega\) — круговая (угловая, циклическая) частота, \(v_{max}\) — максимальная скорость.

Среднее ускорение

Среднее ускорение — это отношение изменения скорости к промежутку времени, за который это изменение произошло.

\(\overrightarrow{a_{ср}}=\frac{\triangle\overrightarrow V}{\triangle t}\), где \(\overrightarrow{a_{ср}}\) — среднее ускорение, \(\triangle\overrightarrow V\) — изменение скорости, \( \triangle t\) — изменение времени.

Проекция ускорения

Определение проекции ускорения на ось \(х\):

\(a_x=\frac{V_x-V_{0x}}t\), где где \(a_x\) — проекция ускорения на ось \(х\), \(V_x\) — проекция текущей скорости на ось \(х\), \(V_{0x}\) — проекция начальной скорости на ось \(х\), \(t\) или \(\triangle t\) — промежуток времени, за который произошло изменение проекции скорости.


Насколько полезной была для вас статья?

Рейтинг: 1.94 (Голосов: 35)

Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»

Поиск по содержимому

исчерпывающие подходы и факты —

Как рассчитать ускорение с помощью силы и массы — это известный вопрос, на который нужно ответить. Мы знаем ускорение, которое действует на тело, где сила и масса существенно влияют на него.

Ускорение измеряет, насколько скорость изменяется в данный момент времени. Скорость — это фактическая скорость, с которой объект изменяется в соответствии с системой отсчета. Скорость зависит от того, какая сила перемещает объект вперед или назад.

Ускорение, действующее на тело, в основном зависит от силы и массы, и как рассчитать ускорение с помощью силы и массы — это то, что мы обсудим далее. Когда неуравновешенная сила не равна нулю, действие на тело будет иметь большее ускорение, когда чистая сила не равна нулю.

Когда равнодействующая сила действующее на тело больше, ускорение, действующее на тело, также будет больше. Еще один момент, который следует помнить, это то, что масса также влияет на ускорение. Чем меньше масса, тем больше ускорение.

Как мы все знаем, законы Ньютона были применены к нескольким открытиям, а для ускорения мы используем Второй закон Ньютона. Это удобно, когда мы используем его для расчета ускорения любого движущегося тела.

Согласно второму закону Ньютона сила, действующая на тело, пропорциональна массе, постоянной во всем и изменяющейся скорости. Формула имеет вид F = ма. Мы получаем ускорение как а = Ф / м.

В этом контексте мы рассматриваем заставить быть сетью сила. Потому что на тело действует несколько сил, поддерживающих его движение, например, нормальная сила, сила трения и так далее. Следовательно, мы считаем, что полная сила, действующая на тело, является равнодействующей силой.

Как найти ускорение по чистой силе и массе

Во-первых, нам нужно понять, как сила и масса влияют на ускорение движущегося тела. Масса — это вес движущегося тела, а сила — это не что иное, как чистая сила, действующая на тело, которая запускает его движение.

Все это возможно только благодаря одной формуле, которая подчиняется Второму закону Ньютона и выводится из него. Формула выглядит так: а = Ф / м.

Здесь сила имеет разные случаи; сила может быть нормальной, силой трения, силой натяжения, силой тяжести, Равнодействующая сила, и чистая сила. Здесь, в этом случае, мы рассматриваем силу как результирующую силу. И эта конкретная сила случается с неуравновешенной силой.

При воздействии на тело эта неуравновешенная сила заставляет тело менять свое положение покоя, из которого оно начинает двигаться. Тогда у тела не будет другого выбора, кроме как совершить движение.

Простые примеры, иллюстрирующие, как найти ускорение с помощью силы и массы

Когда прикладываемая масса меньше, ускорение больше и наоборот. Возьмем небольшой пример мяча массой 10 кг, катящегося под гору с силой 40 Н. Поэтому мы также должны учитывать направление, в котором движется мяч. Пусть она будет перпендикулярна зоне, по которой движется.

Согласно уравнению Второго закона Ньютона, f = mxa

Итак, a = F / m

а = 40/10

a = 4 мс-2

Давайте также проиллюстрируем другой пример для лучшего понимания. В деревне был холм, на котором мало кто пользовался, потому что на нем было слишком много камней и мелких камней, которые могли скатиться и поранить пешеходов.

«горные породы» by стебул под лицензией CC BY 2.0

Однажды из-за проливных дождей скала и камни больше не оставались неподвижными и начали быстро катиться с холма. Теперь давайте посчитаем ускорение большого камня массой 500 кг, который скатывается с силой 1500 Н.

По формуле a = F / m

а = 15000/500

a = 30 мс-2

Помимо ускорения с силой и массой, есть еще один решающий фактор: сила тяжести. Кроме того, в этом разделе мы подробно рассмотрим реальный пример того, как вычислить ускорение с помощью силы и массы.

Группа мальчиков приехала в деревню на летние каникулы. Один из мальчишек из деревни очаровал своего друга рекой, имеющей прыгающий конец. Следовательно, все мальчики захотели попробовать. Один за другим прыгали в реку с прыжковой точки.

Теперь посчитайте ускорение мальчика весом 30 кг, который прыгает в реку с силой 120 Н. Мы знаем формулу, а = Ф / м. Следовательно, a = 120/30, a = 3 мс-2.

Ускорение с силой и массой в повседневной жизни

Всегда есть любопытство по поводу того, как все работает и воплощается в реальность. Точно так же мы обычно видим движение транспортного средства, но задумывались ли мы, как физики, о физике, лежащей в основе этой причины?

Каждый день то, что мы видим, воспринимаем физику, но не осознаем ее. Как было сказано ранее, мы видим машину, движущуюся или даже едущую в ней; мы никогда не замечаем науки, стоящей за этим процессом. Поэтому главное, что нужно делать, — это замечать и признавать их в нашей повседневной жизни.

Ускорение движения тела и выводы — это то, что мы рассмотрим в этом разделе. Итак, с этого момента, где бы и когда бы мы ни увидели движущийся автомобиль или автобус, мы немедленно должны знать, что ускорение способствует такому процессу.

Во-первых, нам нужно увидеть, какое отношение масса имеет к ускорению. Масса — это вес того конкретного тела, который связан с ускорением. Когда масса мала, ускорение больше. Следовательно, вот как рассчитать ускорение с силой и массой.

Это просто здравый смысл; когда предмет тяжелый, его сложно переместить с одного места на другое. Когда масса легкая, ее можно быстро мобилизовать. Следовательно, масса имеет прямую связь с ускорением.

«Автомобиль N Motion» by TheBusyBrain под лицензией CC BY 2.0

Задачи о том, как рассчитать ускорение с помощью силы и массы

1 задачи:

Кафе находится на углу города. Каждое утро несколько велосипедистов проезжают по городу и пересекают кафе. Скамейки кафе вынесены на улицу, поэтому вид улучшается, так как это пляжное кафе.

Однажды один из велосипедистов ехал слишком быстро, двинулся и слегка задел гигантскую статую, расположенную рядом. Эта статуя из-за своего тяжелого веса медленно упала на землю. Теперь посчитайте, с каким ускорением статуя весом 800 кг обладает силой тяжести 1100 Н.

Решение:

а = Ф / м

а = 1100/800

a = 1.375 мс-2

2 задачи:

В данный момент объект неподвижен. Когда чистая сила 175 Н действует на этот объект весом 50 кг, какое ускорение он будет использовать, чтобы выйти из своего исходного положения?

Решение:

а = Ф / м

а = 175/50

a = 3.5 мс-2

Часто задаваемый вопрос

Какие несколько примеров ускорения в повседневной деятельности?

Ускорение — это скорость, с которой объект движется в данный момент времени. Это зависит от изменения скорости с заданным временем.

  • Когда объект движется на юг на 10N м / с с постоянной скоростью, он остается в том же темпе до тех пор, пока не будет приложена сила. Таким образом, при приложении силы он будет двигаться со скоростью 2 мс-15. Теперь объект называется ускоряющимся.
  • Девушка идет на север со скоростью 10 мс-2. Говорят, что у девушки постоянная скорость, а значит, и ускорение равно нулю.
  • Когда мяч катится с холма, он ускоряется при приложении силы. Если мяч весит меньше, ускорение больше, а если мяч весит больше, ускорение со временем становится меньше.
  • Когда мальчик прыгает со скалы с приложенной к нему силой, он будет ускоряться еще больше, а затем, наконец, остановится под действием силы тяжести. Но величина необходимого ускорения будет зависеть от прилагаемой силы: если сила увеличивается, то ускорение увеличивается; если сила уменьшается, ускорение уменьшается.  
  • Мальчик движется на север с ускорением 9 мс.-2. Постепенно на мальчика действует другая сила, и теперь размер меняется на 15 мс.-2. Теперь говорят, что мальчика ускоряют за счет действующей на него чистой силы.

3 формулы, которые вам нужны

«Вау, вы действительно перешли от нуля к шестидесяти!»

Вы когда-нибудь слышали, чтобы кто-то использовал идиому «от нуля до шестидесяти», как это сделал я в приведенном выше примере? Когда кто-то говорит, что что-то изменилось с «ноля до шестидесяти», на самом деле он имеет в виду, что все ускорилось очень быстро. Ускорение — это величина, на которую изменяется скорость чего-либо за установленный период времени.

В этой статье мы поговорим об ускорении: что это такое и как его рассчитать. Пристегнитесь!

 

Что такое ускорение?

Ускорение — это скорость изменения скорости за заданный период времени. Для расчета ускорения необходимо знать скорость и время.

Многие путают ускорение со скоростью (или скоростью). Во-первых, скорость — это просто скорость с указанием направления, поэтому эти два понятия часто используются взаимозаменяемо, даже если между ними есть небольшие различия. Ускорение — это скорость изменения скорости, означающая, что что-то становится быстрее или медленнее.

 

Что такое формула ускорения?

Вы можете использовать уравнение ускорения для расчета ускорения. Вот наиболее распространенная формула ускорения:

$$a = {Δv}/{Δt}$$

, где $Δv$ — изменение скорости, а $Δt$ — изменение времени.

Вы также можете записать уравнение ускорения следующим образом:

$$a = {v(f) — v(i)}/{t(f) — t(i)}$$

В этом уравнении ускорения $v(f)$ — конечная скорость, а $v(i)$ — начальная скорость. $T(f)$ — конечное время, а $t(i)$ — начальное время.

Некоторые другие вещи, которые следует учитывать при использовании уравнения ускорения:

  • Вам нужно вычесть начальную скорость из конечной скорости. Если вы поменяете их местами, вы неправильно поймете направление ускорения.
  • Если у вас нет времени начала, вы можете использовать «0».
  • Если конечная скорость меньше начальной скорости, ускорение будет отрицательным, что означает, что объект замедлился.

Теперь давайте разберем уравнение ускорения шаг за шагом на реальном примере.

 

 

Как рассчитать ускорение: пошаговая разбивка

Теперь мы шаг за шагом разберем формулу ускорения на реальном примере.

Гоночный автомобиль разгоняется с 15 м/с до 35 м/с за 3 секунды. Каково его среднее ускорение?

Сначала напишите уравнение ускорения.

$$a = {v(f) — v(i)}/{t(f) — t(i)}$$

Затем определите свои переменные. 92$$

Давайте попробуем другой пример.

Велосипедист, движущийся со скоростью 23,2 м/с, полностью останавливается через 1,5 $s$. Каково было ее замедление?

Сначала напишите уравнение ускорения.

$$a = (v(f) — v(i)) ÷ (t(f) — t(i))$$

Затем определите свои переменные.

a = то, что мы решаем для

$$V(f) = 0 м/с$$

$$V(i) = 23,2 м/с$$

$$T(f) = 1,4 с $$

$$T(i) = 0 s$$

Теперь подставьте свои переменные в уравнение и решите: 92}$$

 

2 Другие распространенные формулы ускорения

Хотите узнать, как рассчитать ускорение по другой формуле? Есть несколько других распространенных формул ускорения.

 

Формула углового ускорения

Угловое ускорение — это скорость изменения углового ускорения вращающегося объекта во времени.

Вот уравнение углового ускорения:

$$a = {\change \in\угловая\скорость}/{\change\in\time}$$ 92}/r$$

$a(c) $= ускорение, центростремительное

$v$ = скорость

$r$ = радиус

 

Ключевые выводы

Ускорение – это скорость изменения скорости в течение установить период времени.

Ускорение рассчитывается путем деления изменения скорости на изменение времени.

 

Что дальше?

Ищете другие научные объяснения? Разбираем электрическую энергию и как определить различных типов облаков с нашими опытными гидами.

Работаете над исследовательской работой, но не знаете, с чего начать? Тогда ознакомьтесь с нашим руководством, в котором мы собрали множество высококачественных тем для исследований, которые вы можете использовать бесплатно.

Нужна помощь в изучении английского языка — особенно в определении литературных приемов в текстах, которые вы читаете? Тогда вам определенно стоит взглянуть на наше исчерпывающее объяснение самых важных литературных приемов 9.0177 и как они используются.

 

Нужна дополнительная помощь по этой теме? Проверьте Tutorbase!

Наша база данных проверенных преподавателей включает в себя ряд опытных преподавателей, которые могут помочь вам отшлифовать эссе по английскому языку или объяснить, как производные работают для исчисления. Вы можете использовать десятки фильтров и критериев поиска, чтобы найти идеального человека для ваших нужд.

{{cta(‘21006efe-96ea-47ea-9553-204221f7f333’)}}

 

Есть друзья, которым тоже нужна помощь в подготовке к экзаменам? Поделись этой статьей!

Хейли Миллиман

Об авторе

Хейли Миллиман — бывшая учительница, ставшая писателем и ведущая блоги об образовании, истории и технологиях. Когда она была учителем, ученики Хейли регулярно набирали 99-й процентиль благодаря ее страсти к тому, чтобы делать темы удобоваримыми и доступными. В дополнение к своей работе для PrepScholar, Хейли является автором Путеводителя Museum Hack по самым свирепым женщинам в истории.

Калькулятор ускорения | Определение | Формула

Создано Матеушем Мухой и Домиником Черниа, доктором философии

Отзыв от Bogna Szyk и Jack Bowater

Последнее обновление: 02 февраля 2023 г.

Содержание:

  • Что такое ускорение? — определение ускорения
  • Как найти ускорение? – калькулятор ускорения
  • Формула ускорения – три уравнения ускорения
  • Единицы ускорения
  • Примеры ускорения
  • Часто задаваемые вопросы

Наш калькулятор ускорения – это инструмент, который поможет вам узнать насколько быстро меняется скорость объекта . Он работает тремя различными способами, основанными на:

  1. Разнице между скоростями в два разных момента времени.
  2. Расстояние, пройденное при ускорении.
  3. Масса ускоряющегося тела и сила, действующая на него.

Если вы спрашиваете себя, что такое ускорение, какова формула ускорения или каковы единицы измерения ускорения, продолжайте читать, и вы узнаете, как найти ускорение. Ускорение строго связано с движением объекта, и каждый движущийся объект обладает определенной энергией.

Чтобы было понятнее, мы также подготовили несколько примеров ускорения, которые часто встречаются в физике. Вы можете найти там:

  1. Центростремительное ускорение и тангенциальное ускорение.
  2. Угловое ускорение.
  3. Ускорение под действием силы тяжести.
  4. Ускоритель частиц.

Ускорение всегда происходит всякий раз, когда на объект действует ненулевая результирующая сила. Вы можете почувствовать это в лифте, когда вы становитесь немного тяжелее (ускоряясь) или легче (замедляясь), или когда вы спускаетесь по крутому склону на санях по снегу. Более того, из общей теории относительности мы знаем, что вся Вселенная не только расширяется, но даже является ускоренным расширением! Это означает, что расстояние между двумя точками постоянно становится все больше и больше, но мы не можем чувствовать это каждый день, потому что все масштабы в мире тоже расширяются.

Что такое ускорение? — определение ускорения

Ускорение – скорость изменения скорости объекта; другими словами, это то, как быстро меняется скорость. Согласно второму закону Ньютона ускорение прямо пропорционально сумме всех сил, действующих на объект, и обратно пропорционально его массе. В этом есть здравый смысл — если на объект толкают несколько разных сил, вам нужно вычислить, к чему они в сумме (они могут действовать в разных направлениях), а затем разделить результирующую результирующую силу на массу вашего объекта.

Это определение ускорения говорит, что ускорение и сила, по сути, одно и то же. При изменении силы изменяется и ускорение, но величина его изменения зависит от массы объекта (подробнее см. наш калькулятор величины ускорения). Это неверно в ситуации, когда изменяется и масса, например, при ракетной тяге, когда из сопла ракеты выходит сгоревшее топливо. См. наш калькулятор тяги ракеты, чтобы узнать больше.

Мы можем измерить ускорение объекта напрямую с помощью акселерометр . Если вы повесите объект на акселерометр, он покажет ненулевое значение. Почему это? Ну, это из-за гравитационных сил, которые действуют на каждую частицу, имеющую массу. А где результирующая сила, там и ускорение. Таким образом, акселерометр в состоянии покоя измеряет ускорение свободного падения, которое на поверхности Земли составляет около 31,17405 футов/с² (9,80665 м/с²) . Другими словами, это ускорение свободного падения, которое получает любой объект в вакууме.

Говоря о пылесосах, вы когда-нибудь смотрели «Звездные войны» или другой фильм, действие которого происходит в космосе? Эпические сражения космических кораблей, звуки бластеров, двигателей и взрывов. Что ж, это ложь. Космос — это вакуум, и звука там не слышно (звуковым волнам для распространения требуется материя). Эти бои должны быть беззвучными! В космосе никто не услышит твой крик.

Как найти ускорение? – калькулятор ускорения

Калькулятор ускорения на этом сайте учитывает только ситуацию, в которой объект имеет равномерное (постоянное) ускорение. В этом случае уравнение ускорения по определению представляет собой соотношение изменения скорости за определенное время.

Здесь вы можете узнать, как найти ускорение еще двумя способами. Давайте посмотрим, как пользоваться нашим калькулятором (вы можете найти уравнения ускорения в следующем разделе):

  • В зависимости от того, какие данные у вас есть, вы можете рассчитать ускорение тремя различными способами. Прежде всего, выберите соответствующее окно (#1, #2 или #3),
  • [если вы выбрали #1] — Введите начальную v_i и конечную v_f скорости объекта и сколько времени Δt потребовалось для изменения скорости (при необходимости см. наш калькулятор скорости).
  • [если вы выбрали #2] — Введите начальную скорость v_i , пройденное расстояние Δd и время Δt пройденное во время ускорения. Здесь вам не нужно знать конечную скорость.
  • [если вы выберете #3] — Введите массу m объекта и результирующую силу F , действующую на этот объект. Это совершенно другой набор переменных, вытекающий из второго закона Ньютона (еще одно определение ускорения).
  • Считать результирующее ускорение из последнего поля. Вы также можете выполнить расчеты другим способом, если знаете, что такое ускорение, например, для оценки расстояния Δd . Просто укажите остальные параметры в этом окне.

Формула ускорения – три уравнения ускорения

В 17 веке сэр Исаак Ньютон , один из самых влиятельных ученых всех времен, опубликовал свою знаменитую книгу Principia . В ней он сформулировал закон всемирного тяготения, гласящий, что любые два объекта, обладающих массой, будут притягиваться друг к другу с силой, экспоненциально зависящей от расстояния между этими объектами (в частности, она обратно пропорциональна квадрату расстояния). Чем тяжелее объекты, тем больше сила гравитации. Это объясняет, например, почему планеты вращаются вокруг очень плотного Солнца.

В Principia Ньютон также включает три закона движения, которые занимают центральное место в понимании физики нашего мира. Калькулятор ускорения основан на трех различных уравнениях ускорения, где третье получено из работы Ньютона:

  1. а = (v_f - v_i) / Δt ;
  2. а = 2 × (Δd - v_i × Δt) / Δt² ;
  3. а = Ф/м ;

где:

  • a – Ускорение;
  • v_i и v_f — соответственно начальная и конечная скорости;
  • Δt – Время разгона;
  • Δd – Расстояние, пройденное при разгоне;
  • F – Суммарная сила, действующая на объект, который ускоряется; и
  • м – Масса этого объекта.

Теперь вы знаете, как рассчитать ускорение! В следующем абзаце мы обсудим единицы ускорения (SI и Imperial).

Единицы ускорения

Если вы уже знаете, как рассчитать ускорение, давайте сосредоточимся на единицах ускорения. Вы можете вывести их из уравнений, которые мы перечислили выше. Все, что вам нужно знать, это то, что скорость выражается в футах в секунду (имперская/американская система) или в метрах в секунду (система СИ), а время — в секундах. Следовательно, если разделить скорость на время (как мы делаем в первой формуле ускорения), то получим единицу ускорения 9.0289 фут/с² или м/с² в зависимости от используемой системы.

В качестве альтернативы можно использовать третье уравнение. В этом случае нужно разделить силу (фунты в США и ньютоны в СИ) на массу (фунты в США и килограммы в СИ), получив пдл/фунт или Н/кг . Оба они представляют одно и то же, так как фунт равен пдл = фунт·фут/с² , а ньютон равен Н = кг·м/с² . Когда вы подставите его и уменьшите единицы измерения, вы получите (фунт·фут/с²) / фунт = фут/с² или (кг·м/с²) / кг = м/с² .

Есть и третий вариант, который, кстати, широко используется. Вы можете выразить ускорение через стандартное ускорение , вызванное гравитацией вблизи поверхности Земли, которое определяется как г = 31,17405 фут/с² = 9,80665 м/с² . Например, если вы говорите, что лифт движется вверх с ускорением 0,2g , это означает, что он ускоряется примерно с 6,2 фут/с² или 2 м/с² (т. е. 0,2 × г ). Мы округлили приведенные выше выражения до двух значащих цифр с помощью правил значащих цифр, которые вы можете найти в нашей математической категории.

Примеры ускорения

Центростремительное ускорение и тангенциальное ускорение

Ускорение, как правило, представляет собой вектор, поэтому его всегда можно разложить на составляющие. Обычно у нас есть две части, перпендикулярные друг другу: центростремительная и тангенциальная . Центростремительное ускорение изменяет направление скорости и, следовательно, форму трека, но не влияет на значение скорости. С другой стороны, тангенциальное ускорение всегда перпендикулярно траектории движения. Он изменяет только значение скорости , а не ее направление.

В круговом движении (крайний левый рисунок ниже), когда объект движется по окружности круга, присутствует только центростремительная составляющая. Объект будет поддерживать свою скорость на постоянном уровне; подумайте о Земле, которая имеет центростремительное ускорение из-за гравитации Солнца (на самом деле ее скорость немного меняется в течение года).

Когда оба компонента присутствуют, траектория объекта выглядит как на картинке справа. Что произойдет, если есть только тангенциальное ускорение? Затем происходит прямолинейное движение. Это похоже на то, когда вы нажимаете на педаль газа в автомобиле на прямом участке автострады.

Угловое ускорение

Угловое ускорение играет жизненно важную роль в описании вращательного движения. Однако не путайте его с ранее упомянутыми центростремительным или тангенциальным ускорениями. Эта физическая величина соответствует скорости изменения угловой скорости. Другими словами, он сообщает вам, насколько быстро ускоряется вращение объекта — объект вращается все быстрее и быстрее (или все медленнее и медленнее, если угловое ускорение меньше нуля). Ознакомьтесь с нашим калькулятором углового ускорения для получения дополнительной информации.

Знаете ли вы, что мы можем найти аналогию между этим и законом динамики Ньютона во вращательном движении? В его втором законе, если вы можете поменять местами ускорение с угловым ускорением, силу с крутящим моментом и массу с моментом инерции, вы получите уравнение углового ускорения. Вы могли заметить, что некоторые физические законы, подобные этому, универсальны, что делает их очень важными в физике.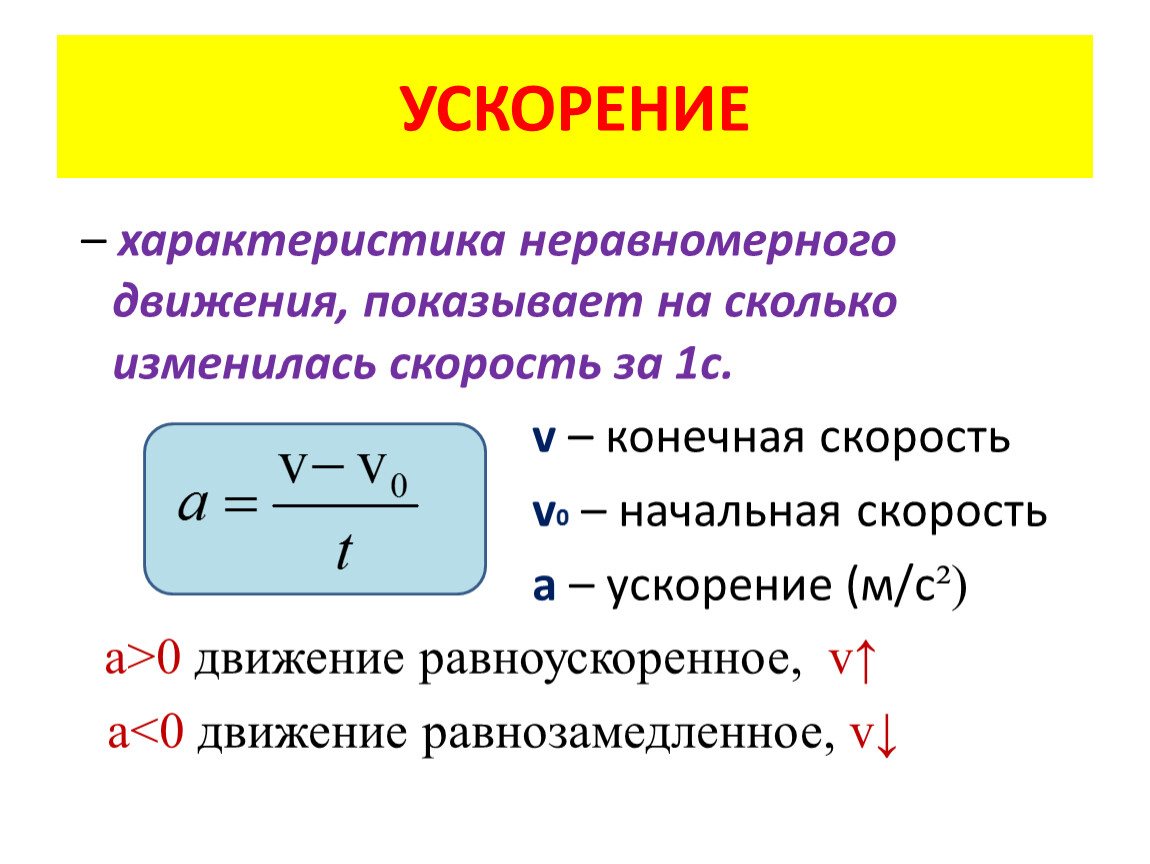

Гравитационное ускорение

Ранее мы упоминали ускорение свободного падения несколько раз. Оно возникает из-за гравитационной силы, которая существует между любыми двумя объектами, имеющими массу (обратите внимание, что уравнение гравитации не зависит от объема объекта — здесь важна только масса). Сначала это может показаться странным, но, согласно третьему закону движения Ньютона, вы действуете на Землю с такой же силой, как Земля действует на вас . Однако масса Земли намного больше массы человека (в ~10²² раз больше), поэтому наше влияние на Землю практически равно нулю. Это аналогично всем бактериям (примерно в 10¹⁸ раз легче человека), живущим на вашей руке; их даже не замечаешь! С другой стороны, мы можем чувствовать влияние нашей планеты, а именно ускорение под действием силы тяжести.

Стандартная гравитация по определению равна 31,17405 фут/с² (90,80665 м/с²), поэтому, если человек весит 220 фунтов (около 100 кг), он подвергается гравитационной силе около 7000 пдл (1000 Н). Введем это значение в окно №3 нашего калькулятора вместе с массой Земли (1,317 × 10²⁵ фунтов или 5,972 × 10²⁴ кг в экспоненциальном представлении). Каково расчетное ускорение? Это , настолько маленькое , что наш калькулятор считает его равным нулю . Мы ничто по сравнению с планетой!

Ускоритель частиц

Поговорив об огромных объектах в космосе, давайте перейдем к микроскопическому миру частиц. Хотя мы не можем видеть их глазами, мы научились использовать высокоэнергетические частицы, такие как электроны и протоны, и регулярно используем их в ускорителях частиц; распространены в физике, химии и медицине. Мы используем их, чтобы убивать раковые клетки, не затрагивая окружающие здоровые ткани, или исследовать структуру материала в атомном масштабе. В последнее время рак является одной из болезней изобилия, которая, вероятно, является результатом увеличения благосостояния в обществе.

Вы, наверное, знаете о Большом адронном коллайдере (ЦЕРН), самом мощном ускорителе частиц в мире. Это позволяет нам сделать шаг вперед, чтобы понять, как работает Вселенная, и разработать технологии, которые в будущем могут иметь множество важных применений. Однако для достижения таких высоких энергий мы должны разгонять частицы до скоростей, близких к скорости света. Короче говоря, мы можем сделать это с помощью магнитных или электрических полей.

Часто задаваемые вопросы

Является ли ускорение вектором?

Да , ускорение является вектором , поскольку имеет как величину , так и направление . Величина — это то, как быстро объект ускоряется, а направление — это ускорение в направлении движения объекта или против него. Это ускорение и замедление соответственно.

Как масса влияет на ускорение?

Если сила, с которой толкается объект, остается неизменной, ускорение будет уменьшаться по мере увеличения массы . Это связано с тем, что F/m = a, поэтому по мере увеличения массы фракция становится все меньше и меньше.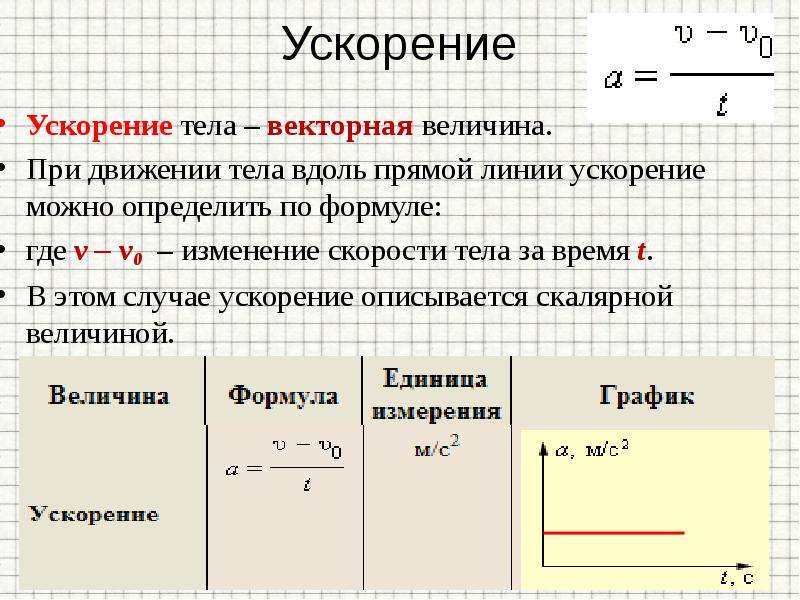

Может ли ускорение быть отрицательным?

Да , ускорение может быть отрицательным, известно как замедление . Два объекта, которые имеют одинаковое, но противоположное ускорение, будут ускоряться на одинаковую величину, только в двух противоположных направлениях.

Как найти среднее ускорение?

  1. Рассчитайте изменение скорости за заданное время.
  2. Рассчитайте изменение во времени для рассматриваемого периода.
  3. Разделите изменение скорости на изменение во времени.
  4. Результатом является среднее ускорение за этот период.

Как найти величину ускорения?

  1. Преобразуйте величину силы в ньютоны.
  2. Изменить массу объекта на килограммы.
  3. Умножьте оба значения на , чтобы найти ускорение в м/с².

В чем разница между ускорением и скоростью?

Скорость — это скорость, с которой объект движется в определенном направлении, а ускорение — это то, как скорость этого объекта изменяется со временем.

Posted inПопулярное