Содержание
Кинематический расчет привода — практическая работа
ПРАКТИЧЕСКАЯ РАБОТА № 1 КИНЕМАТИЧЕСКИЙ РАСЧЕТ ПРИВОДА
Цель работы:
1. Изучить последовательность выполнения кинематического расчета привода.
2. Ознакомиться с примером кинематического расчета привода.
3. Выполнить кинематический расчет привода для индивидуального задания.
Порядок выполнения кинематического расчета привода. Проектирование машины любого типа начинается с расчета привода, который начинают с выбора двигателя по потребной мощности, кинематической схеме привода и условиям эксплуатации, указанным в задании на разработку машины. Требуемую мощность двигателя определяют на основании исходных данных – рабочих характеристик машины.
Если указана мощность () на выходном валу привода, то расчетная мощность на входном валу привода определяется по зависимости:
, (1)
где — коэффициент полезного действия (КПД) привода, который равный произведению частных КПД элементов привода
, (2)
где — КПД отдельных звеньев кинематической цепи привода, ориентировочные значения, которых приведены в таблице 1. 1.
1.
С учетом расчетной мощности на входном валу привода определяется мощность двигателя привода из условия .
Если на выходном валу указаны вращающий момент () и его угловая скорость (), то мощность привода
. (3)
Если на выходном валу указаны тяговое усилие ()и его скорость (), то мощность на входном валу привода
. (4)
Таблица 1.1. Средние значения коэффициентов полезного действия элементов привода
|
Элемент привода
|
|
Элемент привода
|
|
|
Закрытая зубчатая:
с цилиндрическими колесами
с коническими колесами
Открытая зубчатая:
с цилиндрическими колесами
с коническими колесами
Закрытая червячная при числе
заходов червяка
|
0,97…0,98
0,96…0,97
0,92…0,94
0,91…0,93
0,70…0,75
0,80…0,85
0,90…0,95
|
Цепная:
закрытая
открытая
Ременная передача:
с плоским ремнем
с клиновым и зубчатым
Подшипники:
качения (одна пара)
скольжения (одна пара)
Муфта компенсирующая
|
0,95…0,97
0,90…0,95
0,96…0,98
0,95…0,97
0,99…0,995
0,99…0,995
0,985…0,995
|
В большинстве стационарных машин в качестве двигателя принимается трехфазный асинхронный электродвигатель, характерной особенностью которого является синхронная частота вращения, которая в зависимости от числа пар полюсов может быть 3000;1500;1000;750;600; 500 об/мин. Для обеспечения заданной скорости на выходном валу привода его передаточное отношение
Для обеспечения заданной скорости на выходном валу привода его передаточное отношение
(5)
Передаточное отношение привода равно произведению передаточных отношений всех передач привода:
, (6)
где — передаточное отношение отдельных передач кинематической цепи привода.
Передаточные отношения для различных видов механических передач приведены в таблице 1.2.
Таблица 1.2. Средние значения передаточных отношений механических передач
|
Передача
|
Передаточное отношение
|
|
Зубчатая:
с цилиндрическими колесами
с коническими колесами
Червячная:
с однозаходным червяком
с двухзаходным червяком
с четырехзаходным червяком
Цепная
Ременная
|
3…6
2…5
28…80
14…40
7…20
3…6
2…4
|
При кинематическом расчете привода принята нумерация валов начиная от вала приводного двигателя. Для каждого вала определяется мощность, момент и его угловая скорость (частота вращения) с учетом КПД передач и их передаточного отношения.
Для каждого вала определяется мощность, момент и его угловая скорость (частота вращения) с учетом КПД передач и их передаточного отношения.
Мощность на том валу привода
. (7)
Угловая скорость на том валу привода
. (8)
Момент том валу привода
. (9)
2. Пример расчета. Определить мощность привода ленточного транспортера, представленного на рис. 1.1. Рассчитать мощность, момент и угловую скорость на каждом валу привода.
Исходные данные. Тяговое усилие на ленте 10 кН, скорость движения ленты . 1 м/с. Электродвигатель с синхронной частотой вращения 1500 об/мин. Диаметр приводного барабана транспортера 800 мм. Передаточные отношения ременной, зубчатой и цепной передач: 3,45; 5,6;3,25.
Рис.1.1. Кинематическая схема привода: 1 – двигатель, 2 – клиноременная передача, 3 – закрытая зубчатая передача, 4 – цепная передача, 5 – барабан ленточного конвейера.
РЕШЕНИЕ
1. Принимаем КПД элементов привода по таблице 1. 1:
1:
0,97 — КПД ременной передачи,
0,97 – КПД зубчатой передачи,
0,92 – КПД цепной передачи,
0,99 –КПД пары опорных подшипников.
2. Общий КПД привода по формуле (2):
0,84.
3. Частота вращения приводного барабана:
23,9 об/мин.
4. Передаточное отношение привода по формуле (5):
62,8.
Проверка передаточного отношения для заданных передаточных отношений передач по формуле (6)
62,8.
5. Расчетная мощность на валу двигателя привода определяется по формуле (1)
11900 Вт = 11,9 кВт.
6. Угловые скорости, мощности и крутящие моменты на валах привода:
I вал – вал двигателя:
157 1/с,
кВт,
.
II вал – входной вал редуктора:
45,5 1/с,
11,4 кВт,
III вал – выходной вал редуктора:
8,1 1/с,
10,9 кВт,
IV вал – вал барабана:
2,5 1/с,
10 кВт,
.
Проверка тягового усилия на ленте конвейера:
н = 10 кН.
3. Индивидуальные задания для выполнения кинематического расчета привода.
Индивидуальные задания по практической работе выполняются для кинематической схемы, представленной на рис.1.1. с исходными данными приведенными в таблицах 1.3,1.4.
Необходимо определить мощность привода ленточного транспортера, представленного на рис. 1.1. Рассчитать мощность, момент и угловую скорость на каждом валу привода.
Таблица 1.3. Исходные данные для кинематической схемы рис.1.1.
|
№
варианта
|
Мощность на выходном валу привода, кВт
|
Синхронная частота вращения двигателя, об/мин
|
Частота вращения вала барабана, об/мин
|
Передаточное отношение передачи
| |
|
ременной
|
зубчатой
| ||||
|
1
|
4
|
3000
|
90
|
2,8
|
6,3
|
|
2
|
7,5
|
3000
|
100
|
2,5
|
5,6
|
|
3
|
12
|
3000
|
110
|
2,0
|
6,3
|
|
4
|
15
|
3000
|
120
|
1,8
|
5,6
|
|
5
|
18
|
3000
|
150
|
2,0
|
5,0
|
|
6
|
4
|
3000
|
80
|
2,24
|
4,0
|
|
7
|
7,5
|
3000
|
90
|
3,15
|
6,3
|
|
8
|
12
|
3000
|
100
|
2,8
|
5,6
|
|
9
|
15
|
3000
|
110
|
2,5
|
5,0
|
|
10
|
18
|
3000
|
120
|
3,15
|
4,5
|
|
11
|
4
|
1500
|
150
|
2,24
|
5,0
|
|
12
|
7,5
|
1500
|
80
|
2,0
|
4,0
|
|
13
|
12
|
1500
|
90
|
3,15
|
3,15
|
|
14
|
15
|
1500
|
100
|
1,4
|
2,8
|
|
15
|
18
|
1500
|
110
|
1,6
|
3,15
|
|
16
|
4
|
1500
|
120
|
2,8
|
2,8
|
|
17
|
7,5
|
1500
|
150
|
2,5
|
2,5
|
|
18
|
12
|
1500
|
80
|
2,0
|
2,0
|
|
19
|
15
|
1500
|
90
|
3,55
|
3,15
|
|
20
|
18
|
1500
|
100
|
3,15
|
3,55
|
|
21
|
4
|
1000
|
110
|
2,8
|
2,8
|
|
22
|
7,5
|
1000
|
120
|
2,24
|
2,24
|
|
23
|
12
|
1000
|
70
|
2,5
|
2,5
|
|
24
|
15
|
1000
|
60
|
1,6
|
2,0
|
|
25
|
18
|
1000
|
50
|
2,0
|
3,15
|
|
26
|
4
|
1000
|
80
|
3,55
|
3,55
|
|
27
|
7,5
|
1000
|
75
|
2,8
|
2,8
|
|
28
|
12
|
1000
|
65
|
2,24
|
2,24
|
|
29
|
15
|
1000
|
55
|
3,15
|
3,15
|
|
30
|
18
|
1000
|
70
|
1,6
|
2,24
|
|
31
|
12
|
750
|
60
|
2,5
|
1,8
|
|
32
|
15
|
750
|
50
|
2,0
|
2,0
|
ПРИМЕЧАНИЕ. При кинематическом расчете необходимо из общего передаточного отношения по заданным значениям определить передаточное отношение для цепной передачи.
При кинематическом расчете необходимо из общего передаточного отношения по заданным значениям определить передаточное отношение для цепной передачи.
Таблица 1.4. Исходные данные для кинематической схемы рис.1.1.
|
№
варианта
|
Мощность на выходном валу привода, кВт
|
Синхронная частота вращения двигателя, об/мин
|
Частота вращения вала барабана, об/мин
|
Передаточное отношение передачи
| |
|
ременной
|
зубчатой
| ||||
|
1
|
4
|
3000
|
110
|
4,0
|
5,6
|
|
2
|
7,5
|
3000
|
120
|
4,0
|
5,0
|
|
3
|
12
|
3000
|
130
|
3,6
|
5,6
|
|
4
|
15
|
3000
|
140
|
3,6
|
5,0
|
|
5
|
18
|
3000
|
170
|
2,5
|
4,0
|
|
6
|
4
|
3000
|
100
|
2,5
|
4,5
|
|
7
|
7,5
|
3000
|
110
|
4,1
|
6,3
|
|
8
|
12
|
3000
|
120
|
4,1
|
5,6
|
|
9
|
15
|
3000
|
130
|
3,7
|
5,0
|
|
10
|
18
|
3000
|
140
|
3,7
|
6,3
|
|
11
|
4
|
1500
|
130
|
2,5
|
4,5
|
|
12
|
7,5
|
1500
|
60
|
2,5
|
4,0
|
|
13
|
12
|
1500
|
70
|
2,0
|
3,15
|
|
14
|
15
|
1500
|
80
|
2,1
|
2,8
|
|
15
|
18
|
1500
|
90
|
1,9
|
3,15
|
|
16
|
4
|
1500
|
100
|
3,6
|
5,6
|
|
17
|
7,5
|
1500
|
130
|
2,5
|
2,5
|
|
18
|
12
|
1500
|
60
|
2,5
|
2,0
|
|
19
|
15
|
1500
|
70
|
2,1
|
3,55
|
|
20
|
18
|
1500
|
80
|
2,1
|
3,15
|
|
21
|
4
|
1000
|
90
|
3,7
|
2,8
|
|
22
|
7,5
|
1000
|
100
|
2,3
|
2,24
|
|
23
|
12
|
1000
|
50
|
2,5
|
2,5
|
|
24
|
15
|
1000
|
40
|
2,5
|
2,0
|
|
25
|
18
|
1000
|
30
|
2,1
|
4,0
|
|
26
|
4
|
1000
|
60
|
2,1
|
3,55
|
|
27
|
7,5
|
1000
|
55
|
3,7
|
2,8
|
|
28
|
12
|
1000
|
45
|
2,3
|
2,24
|
|
29
|
15
|
1000
|
35
|
1,9
|
3,15
|
|
30
|
18
|
1000
|
50
|
3,6
|
2,6
|
|
31
|
12
|
750
|
30
|
2,5
|
2,5
|
|
32
|
15
|
750
|
20
|
2,5
|
2,0
|
ПРИМЕЧАНИЕ.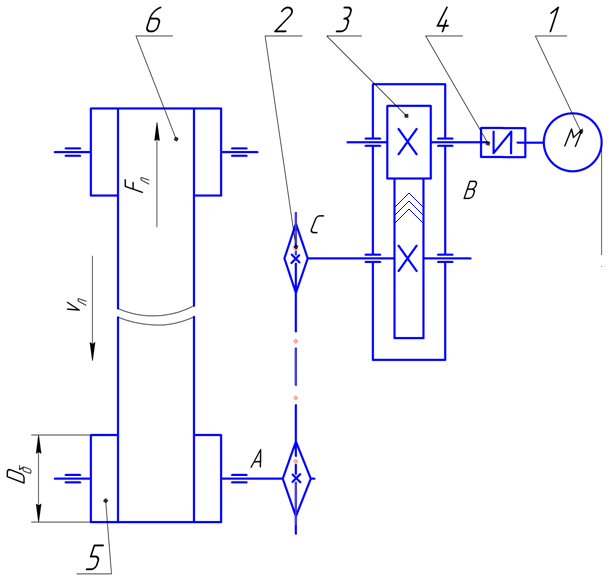 При кинематическом расчете необходимо из общего передаточного отношения по заданным значениям определить передаточное отношение для цепной передачи.
При кинематическом расчете необходимо из общего передаточного отношения по заданным значениям определить передаточное отношение для цепной передачи.
Кинематический расчет привода — практическая работа — 2.6 out of
5
based on
24 votes
Учебные материалы
Для преподавателей
Работы студентов
Справочная и техническая литература
Статьи по темам
- Механизмы и технологи
- Практические работы
- Кинематический расчет привода — практическая работа
3.
 4.3 Кинематические схемы и кинематические расчеты оборудования,
4.3 Кинематические схемы и кинематические расчеты оборудования,
используемого
при изготовлении детали
В настоящем
разделе расчетно-пояснительной записки
курсового проекта приводятся кинематические
схемы и описание работы станков по
представленной схеме для каждого из
них, а также производятся кинематические
расчеты основных узлов станка. На рисунке
2 представлена в качестве примера
кинематическая схема фрезерно-обрезного
станка Ц3Д-7Ф с необходимыми обозначениями
элементов и данных для их расчетов.
В кинематических
расчетах необходимо определить основные
скоростные и мощностные показатели
станка: скорость резания, скорость
подачи, частоту вращения инструмента,
мощность, затрачиваемую на резание и
подачу заготовки в зону резания.
Полученные данные необходимо сравнить
с данными технической характеристики
станка на правильность выполненных
расчетов.
Для выполнения
кинематических расчетов на схеме должны
быть указаны характеристики двигателей
(мощность, частота вращения), параметры
передач (число зубьев на звездочках и
зубчатых колесах, число заходов червяка,
диапазон регулирования вариатора,
передаточное число редуктора, диаметры
шкивов, вальцов, режущего инструмент и
пр.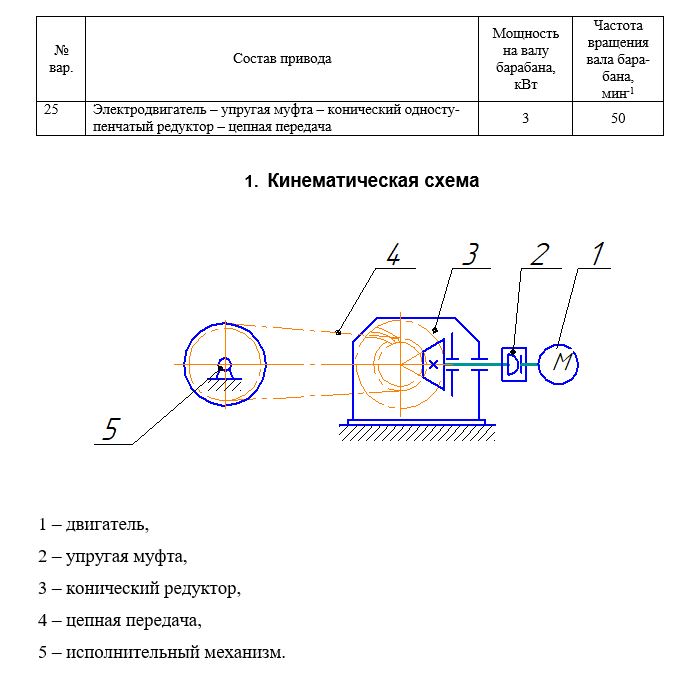 )
)
В зависимости
от конструкции режущего инструмента и
станка, скорость резания для основных
механизмов определяется по двум формулам,
V,
м/с:
— для механизмов
с вращательным движением режущего
инструмента:
V
= π
*Dn
/ (60*1000)
(1)
— для механизмов
с возвратно-поступательным перемещением
режущего инструмента:
Vср
= 2Н*n
/ 60 = 4Rn
/ 60
(2)
где Н – ход пильной
рамки (суппорта станка), м; R
– радиус кривошипа, м; n
– частота вращения коленчатого вала,
мин-1.
Диаметр режущего
инструмента определяется расчетами из
заданных параметров обрабатываемой
заготовки или из паспортных данных
станка.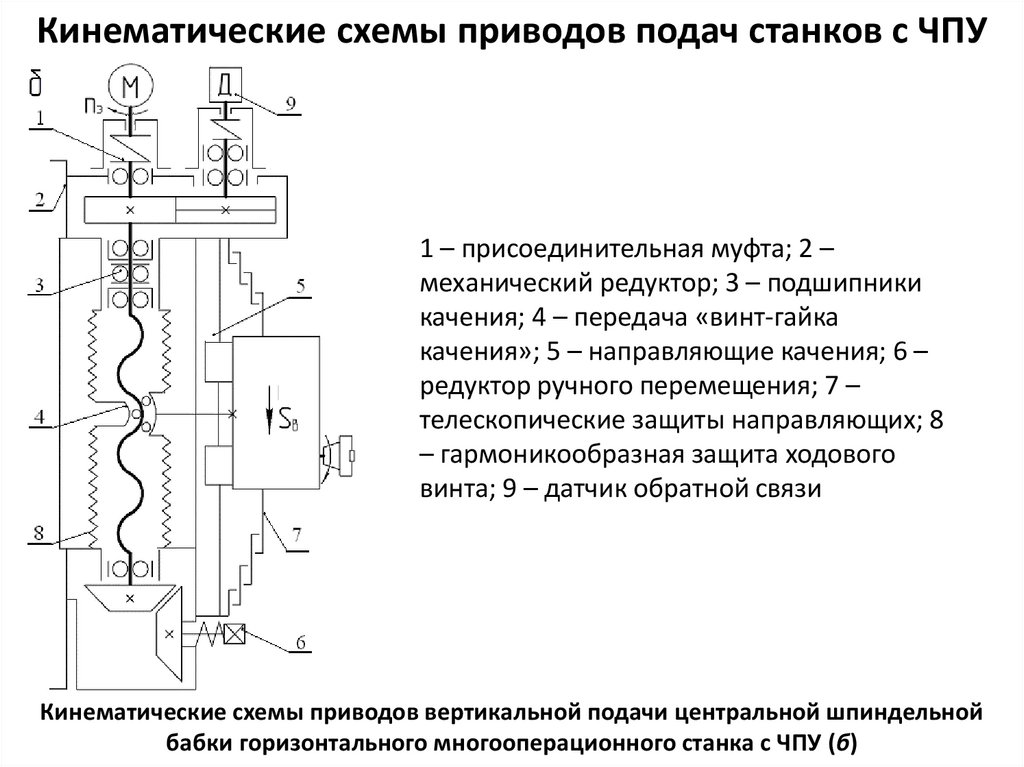 Величина хода пильной рамки
Величина хода пильной рамки
(суппорта станка) или радиус приводятся
в технической характеристике станка.
Частота вращения
находится кинематическим расчетом.
Причем, необходимо учитывать общее
передаточное число (отношение) в
передаточном механизме, U:
n
= nдв
/ U
(3)
где – U
передаточное число (отношение) всех
передач от двигателя до вала режущего
инструмента или кривошипа. Передаточное
число (отношение) рассчитывается по
параметрам кинематической схемы.
Рисунок 2 –
Кинематическая схема обрезного станка
Ц3Д-7Ф
представленные
в настоящих методических указаниях
Механизм резания
(рисунок 3а) состоит из двигателя 1, шкивов
2 и 4, клиноременной передачи 3 и ножевого
вала 5.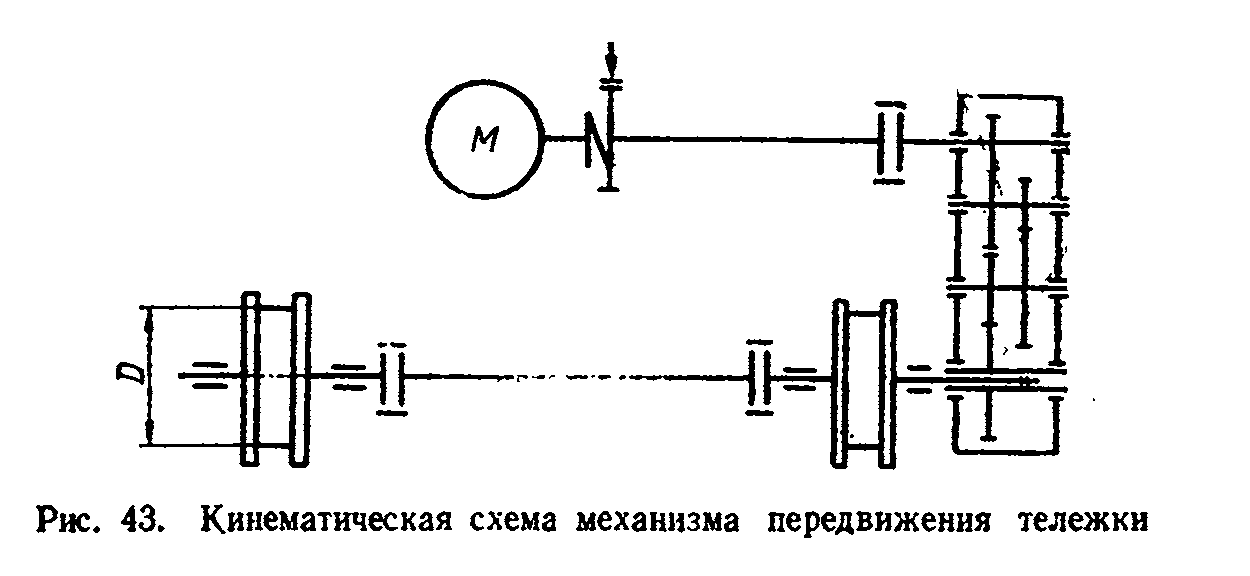 Необходимо определить скорость
Необходимо определить скорость
резания и к.п.д. механизма. Диаметры
шкивов D1 =
150 мм; D2
= 100 мм; диаметр окружности резания Dн
= 150 мм; частота вращения электродвигателя
n
= 3000 мин-1 ;
частота вращения ножевого вала 5 – n.
Определяется:
n
= nдв
* U;
U
= Uр
= D1
/ D2
= 150/100 = 1,5
n
= 3000* 1,5 = 4500
V
= π*D*n
/ 60*1000 = (3,14*150*4500) / (60*1000) = 35,3
Коэффициент
полезного действия механизма резания:
ήмех.р.
= ήр.п.*
ήп.
= 0,96*0,99 = 0,95
Значения к.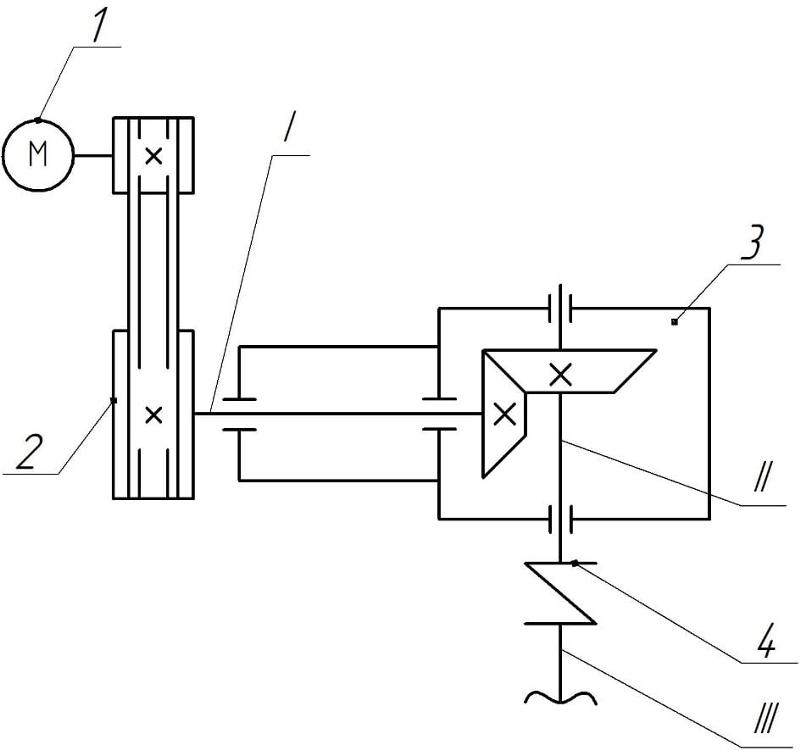 п.д.
п.д.
основных кинематических элементов
представлены таблицей 2.
Мощность на
ножевом валу, N,
кВт:
Nрез
= Nдв.*
ήмех.р.=
4,5*0,95 = 4,27 (4)
Механизм подачи
конвейерного типа состоит из
электродвигателя 1, вариатора 2 с
диапазоном регулирования 1…16; редуктора
с передаточным числом Uр
= 10 и
цепного подающего
конвейера 4 (рисунок 3б).
Представленный
механизм позволяет обеспечить
бесступенчатое регулирования скорости
подачи, Vs,
м/мин, в диапазоне от Vmin
до Vmax
за счет изменения передаточного числа
вариатора от 1до 16.
Vsmin
= (z * t * nmin)
/ 1000
(5)
Vsmax
= (z * t * nmax)
/ 1000
(6)
Частота вращения
приводной звездочки определяется:
nmin
= nдв
/
Umax
(7)
nmax=
nдв
/
Umin
(8)
где nдв
= 1440 мин-1
– частота вращения двигателя; Umin
и Umax
— минимальное
и максимальное передаточное число
механизма подачи.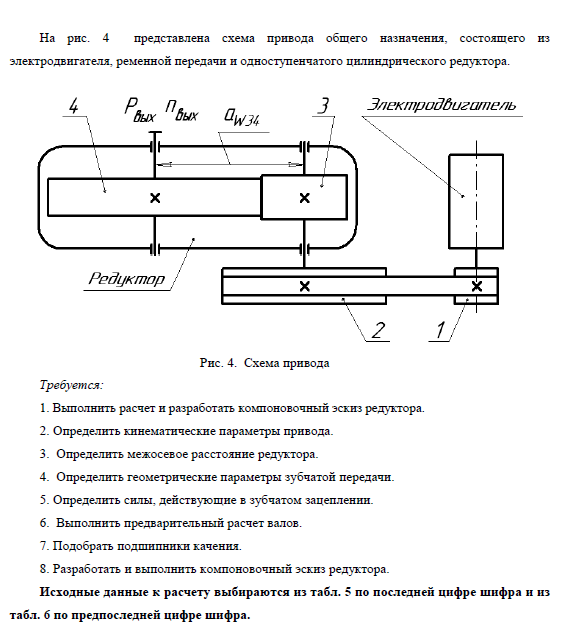
Umax
= Uвmax
* Uр
= 14*10 = 140 (9)
Umin
= Uвmin
* Uр
= 1*10 = 10
(10)
Соответственно:
nmin
= 1400 / 140 = 10 (11)
nmax=
1400 / 10 = 140 (12)
Следовательно:
Vsmin
=
(12*25,4*10) / 1000 = 3,04
(13)
Vsmax
=
(12*25,4*140) / 1000 = 42,7 (14)
Коэффициент
полезного действия механизма подачи:
ήмех. п.
п.
= ήв.*
ήр *
ήп.
=
0,85*0,9*0,99 = 0,76
(15)
где — ήв.
– к.п.д.
вариатора,
ήр
— цилиндрического
редуктора,
ήп.
–
подшипников качения соответственно
(таблица 2).
Таблица 2 — коэффициент
полезного действия элементов кинематических
цепей
Наименование | Численное |
1 | 2 |
Передачи: Плоскоременная Клиноременная Цепная Зубчатая Зубчатая Червячная Фрикционная Пара подшипников: Качения Скольжения Вариаторы Редуктор Редуктор Редуктор червячный | 0,97 0,96 0,96 0,98 0,97 0,3 …0,5 0,7 …0,85 0,99 0,93 0,8 … 0,9 0,85 …0,95 0,8 … 0,9 0,7 |
Рисунок
3 – Кинематические схемы: а – механизма
резания; б – механизма подачи
Мощность привода
механизма подачи можно определить:
Nдв
= (ΣW * Vs)
/ (60*1000)* ήмех. п.
п.
(16)
где ΣW
– суммарное
сопротивление подаче, определяемое
расчетами.
Кинематические уравнения и кинематические графики
Урок 4 этого раздела в классе физики был посвящен использованию графиков скорость-время для описания движения объектов. В этом Уроке подчеркивалось, что наклон линии на графике скорость-время равен ускорению объекта, а площадь между линией и осью времени равна смещению объекта. Таким образом, графики зависимости скорости от времени можно использовать для определения числовых значений и отношений между величинами перемещения (d), скорости (v), ускорения (a) и времени (t). В Уроке 6 основное внимание уделялось использованию четырех кинематических уравнений для описания движения объектов и предсказания численных значений одного из четырех параметров движения — смещения (d), скорости (v), ускорения (a) и время (т). Таким образом, теперь есть два метода решения задач, связанных с числовыми соотношениями между перемещением, скоростью, ускорением и временем. В этой части Урока 6 мы исследуем отношения между этими двумя методами.
В этой части Урока 6 мы исследуем отношения между этими двумя методами.
Пример задачи — графическое решение
Рассмотрим объект, который движется с постоянной скоростью +5 м/с в течение 5 секунд, а затем ускоряется до конечной скорости +15 м/с в течение следующих 5 секунд. секунды. Такое словесное описание движения может быть представлено графиком скорость-время. График показан ниже.
Горизонтальная часть графика изображает движение с постоянной скоростью, что соответствует словесному описанию. Участок графика с положительным наклоном (т. е. с наклоном вверх) изображает положительное ускорение, соответствующее словесному описанию объекта, движущегося в положительном направлении и ускоряющегося с 5 м/с до 15 м/с. Наклон линии можно вычислить, используя коэффициент подъема относительно пробега. Между 5 и 10 секундами скорость линии увеличивается с 5 м/с до 15 м/с и продолжается от 5 до 10 с. Это общий подъем +10 м/с и общий пробег 5 с. Таким образом, уклон (соотношение подъем/спуск) равен (10 м/с)/(5 с) = 2 м/с 2 . По графику скорость-время определено ускорение объекта, равное 2 м/с 2 в течение последних пяти секунд движения объекта. Смещение объекта также можно определить с помощью графика зависимости скорости от времени. Площадь между линией на графике и осью времени представляет смещение; эта область принимает форму трапеции. Как обсуждалось в Уроке 4, площадь трапеции можно приравнять к площади треугольника, лежащего на вершине площади прямоугольника. Это показано на диаграмме ниже.
Это общий подъем +10 м/с и общий пробег 5 с. Таким образом, уклон (соотношение подъем/спуск) равен (10 м/с)/(5 с) = 2 м/с 2 . По графику скорость-время определено ускорение объекта, равное 2 м/с 2 в течение последних пяти секунд движения объекта. Смещение объекта также можно определить с помощью графика зависимости скорости от времени. Площадь между линией на графике и осью времени представляет смещение; эта область принимает форму трапеции. Как обсуждалось в Уроке 4, площадь трапеции можно приравнять к площади треугольника, лежащего на вершине площади прямоугольника. Это показано на диаграмме ниже.
Общая площадь равна площади прямоугольника плюс площадь треугольника. Расчет этих площадей показан ниже.
| Прямоугольник | Треугольник |
|---|---|
| Площадь = основание * высота Площадь = (10 с) * (5 м/с) Площадь = 50 м | Площадь = 0,5 * основание * высота Площадь = 0,5 * (5 с) * (10 м/с) Площадь = 25 м |
Общая площадь (прямоугольник плюс треугольник) равна 75 м.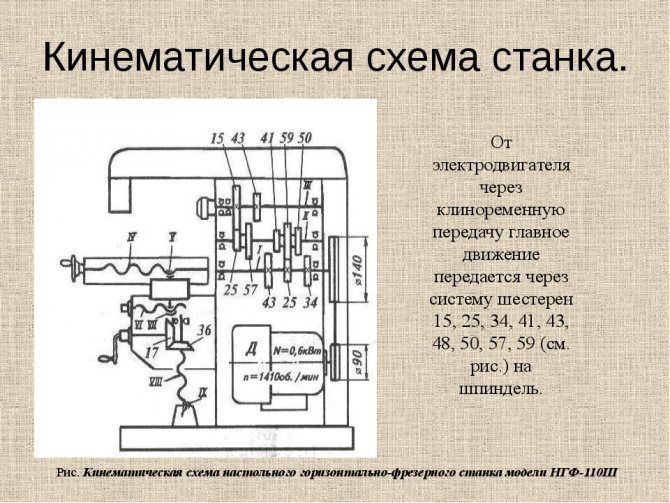 кв. Таким образом, перемещение объекта за 10 секунд движения составляет 75 метров.
кв. Таким образом, перемещение объекта за 10 секунд движения составляет 75 метров.
Приведенное выше обсуждение иллюстрирует, как графическое представление движения объекта может использоваться для извлечения числовой информации об ускорении и смещении объекта. После построения график зависимости скорости от времени можно использовать для определения скорости объекта в любой момент времени в течение 10 секунд движения. Например, скорость объекта в 7 секунд может быть определена путем считывания значения координаты y в координате x 7 секунд. Таким образом, графики скорость-время могут быть использованы для выявления (или определения) числовых значений и взаимосвязей между величинами смещения (d), скорости (v), ускорения (a) и времени (t) для любого заданного движения.
Пример задачи — решение с использованием кинематического уравнения
Теперь рассмотрим то же словесное описание и соответствующий анализ с использованием кинематического уравнения. Вербальное описание движения было следующим:
Вербальное описание движения было следующим:
Объект, который движется с постоянной скоростью +5 м/с в течение 5 секунд, а затем ускоряется до конечной скорости +15 м/с в течение следующих 5 секунд
Кинематические уравнения могут быть применены к любому движению, для которого ускорение является постоянным. Поскольку это движение имеет две отдельные стадии ускорения, любой кинематический анализ требует, чтобы параметры движения для первых 5 секунд не смешивались с параметрами движения для последних 5 секунд. В таблице ниже перечислены заданные параметры движения.
| t = 0 с — 5 с | т = 5 с — 10 с |
|---|---|
| v i = 5 м/с v f = 5 м/с t = 5 с a = 0 м/с 2 | v i = 5 м/с v f = 15 м/с t = 5 с |
Обратите внимание, что ускорение в течение первых 5 секунд указано как 0 м/с 2 , несмотря на то, что это явно не указано. Фраза постоянная скорость указывает на движение с нулевым ускорением. Ускорение объекта за последние 5 секунд можно рассчитать с помощью следующего кинематического уравнения.
Фраза постоянная скорость указывает на движение с нулевым ускорением. Ускорение объекта за последние 5 секунд можно рассчитать с помощью следующего кинематического уравнения.
v f = v i + a*t
Здесь показаны подстановка и алгебра.
15 м/с = 5 м/с + а*(5 с)
15 м/с — 5 м/с = a*(5 с)
10 м/с = a*(5 с)
(10 м/с)/(5 с) = a
a = 2 м /с 2
Это значение ускорения объекта за время от 5 с до 10 с согласуется со значением, определяемым по наклону линии на графике скорость-время.
Смещение объекта за все 10 секунд также можно рассчитать с помощью кинематических уравнений. Поскольку эти 10 секунд включают в себя два совершенно разных интервала ускорения, расчеты для каждого интервала необходимо выполнять отдельно. Это показано ниже.
| t = 0 с — 5 с | т = 5 с — 10 с |
|---|---|
| d = v i *t + 0,5*a*t 2 d = (5 м/с)*(5 с) +0,5*(0 м/с 2 )*(5 с) 2 d = 25 м + 0 м д = 25 м | d = ((v i + v f )/2)*t d = ((5 м/с + 15 м/с)/2)*(5 с) d = (10 м/с)*(5 с) д = 50 м |
Общее перемещение за первые 10 секунд движения составляет 75 метров, что соответствует значению, определенному по площади под линией на графике скорость-время.
Анализ этого простого движения иллюстрирует значение этих двух представлений движения — графика скорость-время и кинематических уравнений. Каждое представление можно использовать для извлечения числовой информации о неизвестных величинах движения для любого заданного движения. Приведенные ниже примеры предоставляют полезную возможность для тех, кому требуется дополнительная практика.
Проверьте свое понимание
1. Rennata Gas движется по городу со скоростью 25,0 м/с и начинает ускоряться с постоянной скоростью -1,0 м/с 2 . В конце концов Ренната полностью останавливается.
а. Представьте ускоренное движение Реннаты, нарисовав график зависимости скорости от времени. Используйте график зависимости скорости от времени, чтобы определить это расстояние.
б. Используйте кинематические уравнения для расчета расстояния, которое проходит Ренната при замедлении.
См. график и ответ
2. Отто Эмиссионс едет на своей машине со скоростью 25,0 м/с. Отто ускоряется со скоростью 2,0 м/с 2 в течение 5 секунд. Затем Отто поддерживает постоянную скорость еще 10,0 секунд.
Отто Эмиссионс едет на своей машине со скоростью 25,0 м/с. Отто ускоряется со скоростью 2,0 м/с 2 в течение 5 секунд. Затем Отто поддерживает постоянную скорость еще 10,0 секунд.
а. Представьте 15 секунд движения Отто Эмиссион, нарисовав график зависимости скорости от времени. Используйте график, чтобы определить расстояние, пройденное Отто за все 15 секунд.
б. Наконец, разбейте движение на два сегмента и используйте кинематические уравнения для расчета общего расстояния, пройденного за все 15 секунд.
См. график и ответ
3. Люк Отбелоу, человек, мастер по стрельбе из пушечного ядра, был сброшен с края обрыва с начальной восходящей скоростью +40,0 м/с. Люк ускоряется с постоянным нисходящим ускорением -10,0 м/с 2 (приблизительное значение ускорения свободного падения).
а. Нарисуйте график зависимости скорости от времени для первых 8 секунд движения Люка.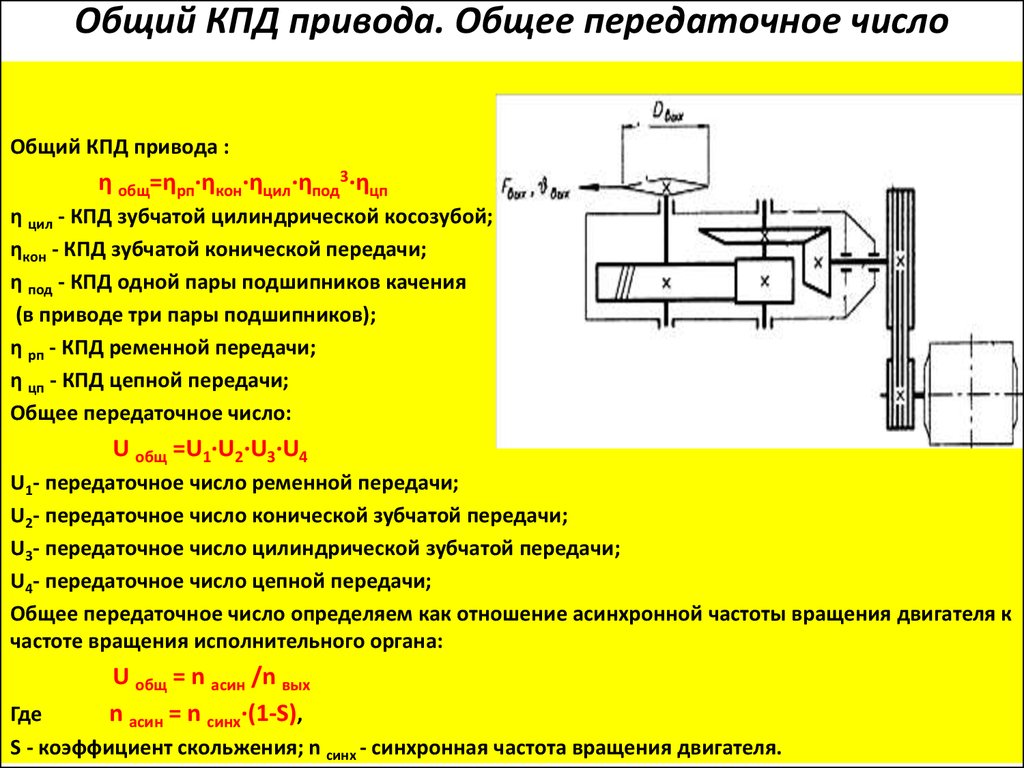
б. Используйте кинематические уравнения, чтобы определить время, необходимое Люку Отбело, чтобы вернуться на исходную высоту скалы. Укажите это время на графике.
См. график и ответ
4. Чак Вагон движется с постоянной скоростью 0,5 мили/мин в течение 10 минут. Затем Чак замедляется со скоростью -0,25 мили/мин 2 в течение 2 минут.
а. Нарисуйте график скорости во времени для движения Чака Вагона. Используйте график зависимости скорости от времени, чтобы определить общее расстояние, пройденное Чаком Вагоном за 12 минут движения.
б. Наконец, разбейте движение на два сегмента и используйте кинематические уравнения, чтобы определить общее расстояние, пройденное Чаком Вагоном.
См. график и ответ
5. Вера Сайд мчится по межштатной автомагистрали со скоростью 45,0 м/с. Вера смотрит вперед и наблюдает за аварией, в результате которой посреди дороги образовалась авария. К моменту, когда Вера бьет по тормозам, она находится в 50,0 м от пайлапа. Она замедляется со скоростью -10,0 м/с 2 .
К моменту, когда Вера бьет по тормозам, она находится в 50,0 м от пайлапа. Она замедляется со скоростью -10,0 м/с 2 .
а. Постройте график зависимости скорости от времени для движения Веры Сайд. Используйте график, чтобы определить расстояние, которое Вера преодолела бы до полной остановки (если бы она не столкнулась с нагромождением).
б. Используйте кинематические уравнения, чтобы определить расстояние, которое Вера Сайд преодолела бы до полной остановки (если бы она не столкнулась с нагромождением). Столкнется ли Вера с машинами в толпе? То есть проедет ли Вера больше 50,0 метров?
См. график и ответ
6. Эрл Э. Берд движется со скоростью 30,0 м/с за 10,0 секунд. Затем он ускоряется со скоростью 3,00 м/с 2 в течение 5,00 секунд.
a.Построить график зависимости скорости от времени для движения Эрла Э. Бёрда. Используйте график, чтобы определить общее пройденное расстояние.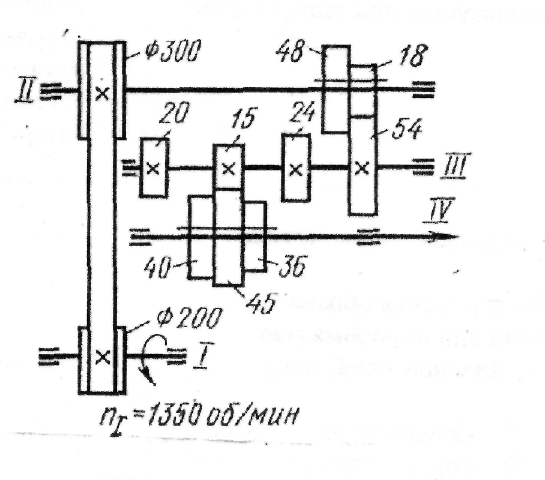
б. Разделите движение Earl E. Bird на два временных сегмента и используйте кинематические уравнения для расчета полного смещения.
См. график и ответ
Ответы на вышеуказанные вопросы
Ответ на вопрос 1
а. График скорость-время для движения:
Пройденное расстояние можно определить путем вычисления площади между линией на графике и осью времени.
Площадь = 0,5*b*h = 0,5*(25,0 с)*(25,0 м/с)
Площадь = 313 м
б. Пройденное расстояние можно рассчитать с помощью кинематического уравнения. Решение показано здесь.
Дано:
| Найти: д = ?? |
v f 2 = v i 2 + 2*a*d
(0 м/с) 2 = (25,0 м/с) 2 + 2 * (-1,0 м/с 2 )*д
0,0 м 2 /с 2 = 625,0 м 2 /с 2 + (-2,0 м/с 2 )*d
0,0 м 2 /с 2 — 625,0 м 2 /с 2 = (-2,0 м/с 2 )*d
(-625,0 м 2 /с 2 )/(-2,0 м/с 2 ) = d
313 м = д
Вернуться к вопросу 1
Ответ на вопрос 2
а. График скорости во времени для движения:
График скорости во времени для движения:
Пройденное расстояние можно определить путем вычисления площади между линией на графике и осью времени. Эта площадь будет равна площади треугольника плюс площадь прямоугольника 1 плюс площадь прямоугольника 2.
Площадь = 0,5*b tri *h tri + b rect1 *h rect1 + b rect2 *h rect2
Площадь = 0,5*(5,0 с)*(10,0 м/с) + (5,0 с)*(25,0 м/с) + (10,0 с)*(35,0 м/с)
Площадь = 25 м + 125 м + 350 м
Площадь = 500 м
б. Пройденное расстояние можно рассчитать с помощью кинематического уравнения. Решение показано здесь.
Сначала найдите d за первые 5 секунд:
Дано:
| Найти: д = ?? |
d = v i *t + 0,5*a*t 2
d = (25,0 м/с)*(5,0 с) + 0,5*(2,0 м/с 2 )*(5,0 с) 2
d = 125 м + 25,0 м
д = 150 м
Теперь найдите d за последние 10 секунд:
Дано:
| Найти: д = ?? |
(Примечание: скорость на 5-й секунде можно найти, зная, что автомобиль ускоряется с 25,0 м/с до +2,0 м/с 2 на 5 секунд.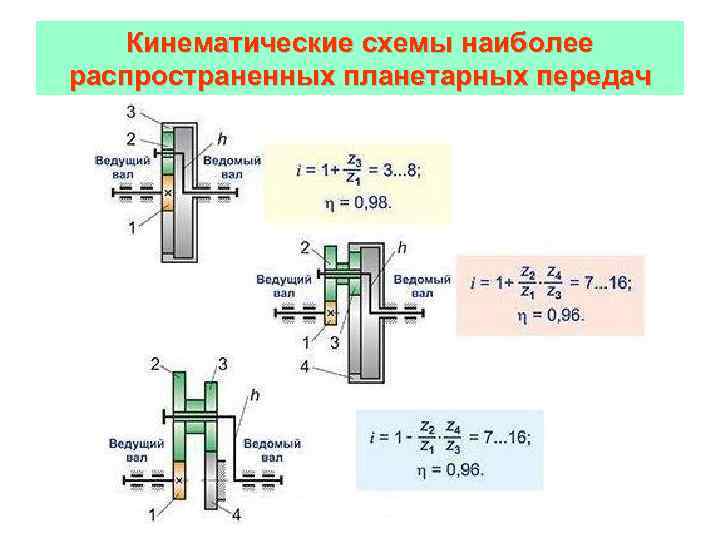 Это приводит к изменению скорости a*t = 10 м/с и, следовательно, к скорости 35,0 м/с.)
Это приводит к изменению скорости a*t = 10 м/с и, следовательно, к скорости 35,0 м/с.)
d = v i *t + 0,5*a*t 2
d = (35,0 м/с)*(10,0 с) + 0,5*(0,0 м/с 2 )*(10,0 с) 2
d = 350 м + 0 м
d =350 м
Общее расстояние за 15 секунд движения равно сумме этих двух расчетов расстояния (150 м + 350 м):
расстояние = 500 м
Вернуться к вопросу 2
Ответ на вопрос 3
а. График скорость-время для движения:
б. Время подъема и падения на исходную высоту в два раза превышает время подъема на пик. Таким образом, решение заключается в том, чтобы найти время, чтобы подняться до пика, а затем удвоить его.
Дано:
| Найти: т до = ?? 2*t вверх = ?? |
v f = v i + a*t вверх
0 м/с = 40 м/с + (-10 м/с2)*t вверх
(10 м/с 2 )*t до = 40 м/с
t up = (40 м/с)/(10 м/с 2 )
т до = 4,0 с
2*t до = 8,0 с
Вернуться к вопросу 3
Ответ на вопрос 4
а. График скорость-время для движения:
График скорость-время для движения:
Пройденное расстояние можно определить путем вычисления площади между линией на графике и осью времени. Эта площадь будет равна площади прямоугольника плюс площадь треугольника.
Площадь = b прямоугольная *h прямоугольная + 0,5*b тройная *h тройная
Площадь = (10,0 мин)*(0,50 мили/мин) + 0,5*(2,0 мин)*(0,50 мили/мин)
Площадь = 5 миль + 0,5 мили
Площадь = 5,5 мили
б. Пройденное расстояние можно рассчитать с помощью кинематического уравнения. Решение показано здесь.
Сначала найдите d за первые 10 минут:
Дано:
| Найти: д = ?? |
d = v i *t + 0,5*a*t 2
d = (0,50 миль/мин)*(10,0 мин) + 0,5*(0,0 миль/мин 2 )*(10,0 мин) 2
d = 5,0 миль + 0 миль
d = 5,0 миль
Теперь найдите d за последние 2 минуты:
Дано:
| Найти: д = ?? |
d = v i *t + 0,5*a*t 2
d = (0,50 миль/мин)*(2,0 мин) + 0,5*(-0,25 м/с 2 )*(2,0 мин) 2
d = 1,0 мили + (-0,5 мили)
d = 0,5 мили
Общее расстояние за 12 минут движения равно сумме этих двух расчетов расстояния (5,0 миль + 0,5 мили):
расстояние = 5,5 мили
Вернуться к вопросу 4
Ответ на вопрос 5
а.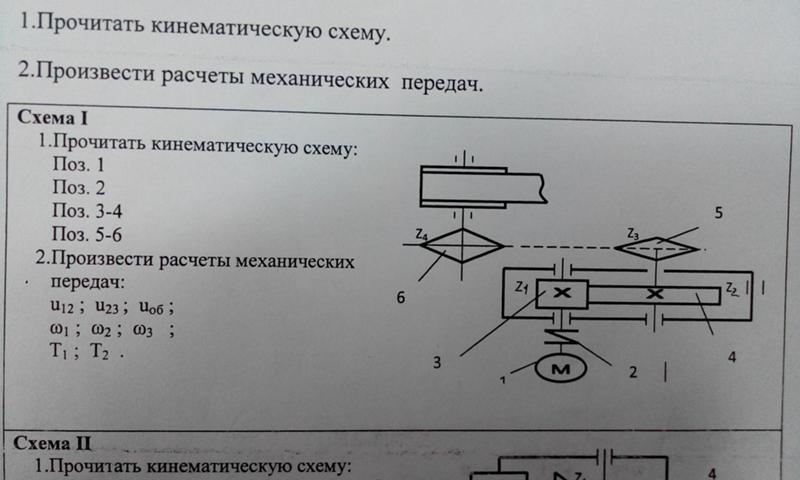 График скорость-время для движения:
График скорость-время для движения:
Пройденное расстояние можно определить путем вычисления площади между линией на графике и осью времени.
Площадь = 0,5*b*h = 0,5*(4,5 с)*(45,0 м/с)
Площадь = 101 м
б.
Дано:
| Найти: д = ?? |
v f 2 = v i 2 + 2*a*d
(0 м/с) 2 = (45,0 м/с) 2 + 2 * (-10,0 м/с 2 )*d
0,0 м 2 /с 2 = 2025,0 м 2 /с 2 + (-20,0 м/с 2 )*d
0,0 м 2 /с 2 — 2025,0 м 2 /с 2 = (-20,0 м/с 2 )*d
(-2025,0 м 2 /с 2 )/(-20,0 м/с 2 ) =d
101 м =d
Так как место аварии находится менее чем в 101 м от Веры, она действительно врежется в нагромождение перед полной остановкой (если не отклонится в сторону).
Вернуться к вопросу 5
Ответ на вопрос 6
а. График скорость-время для движения:
Пройденное расстояние можно определить путем вычисления площади между линией на графике и осью времени. Эта площадь будет равна площади треугольника плюс площадь прямоугольника 1 плюс площадь прямоугольника 2.
Площадь = 0,5*b tri *h tri + b 1 *ч 1 + б 2 *ч 2
Площадь = 0,5*(5,0 с)*(15,0 м/с) + (10,0 с)*(30,0 м/с) + (5,0 с)*(30,0 м/с)
Площадь = 37,5 м + 300 м + 150 м
Площадь = 488 м
б. Пройденное расстояние можно рассчитать с помощью кинематического уравнения. Решение показано здесь.
Сначала найдите d за первые 10 секунд:
Дано:
| Найти: д = ?? |
d = v i *t + 0,5*a*t 2
d = (30,0 м/с)*(10,0 с) + 0,5*(0,0 м/с 2 )*(10,0 с) 2
d = 300 м + 0 м
d =300 м
Теперь найдите d за последние 5 секунд:
Дано:
| Найти: д = ?? |
d = v i *t + 0,5*a*t 2
d = (30,0 м/с)*(5,0 с) + 0,5*(3,0 м/с 2 )*(5,0 с) 2
d = 150 м + 37,5 м
д = 187,5 м
Общее расстояние за 15 секунд движения равно сумме этих двух расчетов расстояния (300 м + 187,5 м):
расстояние = 488 м
Вернуться к вопросу 6
Как рассчитать переднюю кинематику робота за 5 простых шагов
Расчет прямой кинематики часто является первым шагом к использованию нового робота. Но как начать?
Но как начать?
Несмотря на то, что в Интернете доступно несколько хороших руководств, до сих пор не было простого пошагового руководства для расчета прямой кинематики.
Вот простое руководство по расчету кинематики любого робота-манипулятора.
[С тех пор, как я впервые опубликовал эту статью в 2015 году, она стала одной из наших самых популярных статей! С тех пор я обновил и улучшил его, но основная простота осталась прежней..]
Вычисление кинематики является краеугольным камнем для инженеров-робототехников. Но кинематика иногда может быть проблемой (например, понимание разницы между прямой и обратной кинематикой).
Когда я впервые начал заниматься исследованиями в области робототехники, мне часто говорили: «иди и посчитай переднюю кинематику этого робота». По сути, эта фраза является сокращением для исследования робототехники для «иди и познакомься с этим роботом».
Расчет прямой кинематики является жизненно важным первым шагом при использовании любого нового робота в исследованиях, особенно для манипуляторов.
Несмотря на то, что я изучил теорию кинематики в университете, только когда я рассчитал различные кинематические решения для нескольких реальных роботов, весь процесс стал интуитивно понятным. Даже тогда, поскольку я не рассчитывал кинематику каждый день, мне приходилось возвращаться к своим заметкам, чтобы напоминать себе, как это сделать, каждый раз, когда я сталкивался с новым роботом.
Было бы очень полезно иметь пошаговое руководство по этапам прохождения. Таким образом, мне не пришлось бы читать сотни страниц академически написанных уравнений в учебниках.
Что-то вроде «шпаргалки» по кинематике было бы полезно.
Этот пост как раз и есть шпаргалка.
В первую очередь я сосредоточусь на подходе Деванита-Хартенберга (DH) к прямой кинематике, поскольку он является наиболее распространенным.
Надеюсь, вам понравится!
Шаг 1: возьмите карандаш и бумагу
При запуске нового робота может возникнуть соблазн сразу же перейти к компьютеру. Однако, даже если робот выглядит как «стандартный» манипулятор 6R (наиболее распространенный тип робота), я всегда сажусь с карандашом и бумагой, чтобы нарисовать кинематическую схему.
Однако, даже если робот выглядит как «стандартный» манипулятор 6R (наиболее распространенный тип робота), я всегда сажусь с карандашом и бумагой, чтобы нарисовать кинематическую схему.
Эта простая задача заставляет вас тщательно рассмотреть реальную физическую конфигурацию робота, избегая ложных предположений, которые могут нанести ущерб позже во время кодирования.
Существуют различные способы рисования кинематической цепи. Выберите любой стиль, который вы предпочитаете.
Я предпочитаю простые цилиндры для поворотных соединений и линии для звеньев, как показано на рисунке. Выполните поиск картинок в Google по запросу «кинематическая диаграмма» и просмотрите несколько доступных стилей.
Во время рисования определите, в каком направлении движется каждый сустав, и нарисуйте это движение в виде двусторонних стрелок на диаграмме.
Шаг 2: Нарисуйте оси
Следующим важным шагом является нанесение осей на каждый сустав. Подход DH назначает разные оси каждому подвижному суставу.
Если правильно настроить оси, то работать с роботом будет легко. Настройте их неправильно, и вы будете страдать бесчисленными головными болями. Эти оси потребуются симуляторам, решателям обратной кинематики и вашим коллегам в вашей команде (никто не хочет решать решение прямой кинематики, если это уже сделал кто-то другой).
Посмотрите это видео, чтобы узнать, как их настроить:
Две важные оси для работы:
- Ось Z — Ось Z должна лежать на оси вращения для вращательное соединение или ось расширения для призматического соединения.
- Ось X — Ось X должна лежать вдоль «общей нормали», которая является кратчайшей ортогональной линией между предыдущей осью Z и текущей осью Z (серьезно, посмотрите видео).
- Ось Y — После того, как вы рассчитали две другие, эта ось должна встать на место, следуя «правилу правой руки» (см.
 ниже).
ниже).
Лично я рисую оси, используя следующую раскраску: ось z (синяя) , ось x (красная) и ось y (зеленая) . Кстати, это цветовая схема, которая используется в визуализаторе RViz от ROS, которую я широко использовал во время работы над диссертацией.
Еще когда я был студентом, наш лектор посоветовал нам сделать ось «скульптуру» из трех цветных соломинок, вставленных в шарик из синей канвы, чтобы объяснить нам теорию. Хотя это может показаться немного «игровой школой», это может быть очень полезно, поскольку вы можете расположить скульптуру рядом с физическим роботом, чтобы убедиться, что оси указывают в правильном направлении. Чтобы получить виртуальную версию, воспользуйтесь этим интерактивным инструментом.
В качестве альтернативы вы можете использовать «правило правой руки».
Правило правой руки
Быстрый и простой способ запомнить направление оси Y — следовать правилу правой руки. Это мнемоника (помощь для запоминания), широко используемая в физике для запоминания ориентации трехмерной оси.
Это мнемоника (помощь для запоминания), широко используемая в физике для запоминания ориентации трехмерной оси.
Чтобы использовать его, вытяните правую руку перед собой, вытянув большой, указательный и средний пальцы под углом 90 градусов друг к другу. Каждый палец соответствует оси:
- Большой палец = ось Z.
- Указательный палец = ось X.
- Средний палец = ось Y.
Направляя большой и указательный пальцы по осям z и x шарнира робота, ваш средний палец естественным образом попадает в направлении оси y.
Шаг 3: Запомните свой концевой эффектор
Цель расчета прямой кинематики состоит в том, чтобы иметь возможность рассчитать положение конечного эффектора по положению суставов.
В большинстве учебных пособий по прямой кинематике конечный эффектор рассматривается как одно расстояние от конечного сустава. Это нормально для простого захвата «открыть-закрыть». Однако, поскольку современные захваты часто более сложны, стоит рассмотреть, как работает концевой эффектор.
Однако, поскольку современные захваты часто более сложны, стоит рассмотреть, как работает концевой эффектор.
Например, 3-пальцевый адаптивный захват Robotiq имеет несколько различных режимов захвата. Каждый режим будет соответствовать немного отличающемуся желаемому положению конечного эффектора. Если вы хотите зажать объект между его пальцами, для этого потребуется другое расстояние, чем если бы вы хотели обхватить объект пальцами.
При разработке кинематической модели всегда следует тщательно учитывать концевой зажим.
Шаг 4: Расчет параметров DH
Параметры Denavit-Hartenberg (DH) часто требуются для ввода модели робота в симулятор и начала выполнения любого анализа на ней.
Лучший способ визуализировать параметры DH — посмотреть видео, которое я уже включил выше.
Параметры DH разбивают каждое соединение робота на четыре параметра, каждый из которых берется относительно предыдущего соединения. Они рассчитываются относительно «общей нормы», описанной выше. Обратите внимание, что если предыдущая ось z пересекает текущую ось z, что часто бывает, общая нормаль имеет нулевую длину.
Обратите внимание, что если предыдущая ось z пересекает текущую ось z, что часто бывает, общая нормаль имеет нулевую длину.
- d — расстояние между предыдущей осью x и текущей осью x, по предыдущей оси z.
- θ — угол вокруг оси z между предыдущей осью x и текущей осью x.
- a (или r) — длина общей нормали, которая представляет собой расстояние между предыдущей осью z и текущей осью z
- α — угол вокруг общей нормали между предыдущей осью z и текущей осью z.
Просмотрите все соединения на чертеже и запишите параметры DH для каждого соединения. Каждое соединение должно иметь одно значение, которое является переменной, представляющей приводимое в действие соединение.
Для получения более подробного объяснения и некоторых примеров я рекомендую этот раздаточный материал Питера Корка или эту главу из Введение в робототехнику.
Альтернативы параметрам DH
Подход DH является наиболее распространенным подходом к прямой кинематике, но он не идеален. Одним из его недостатков является то, что он не очень элегантно обрабатывает параллельные оси Z. Существуют различные альтернативы, включая представления теории винтов, Хаяти-Робертса и другие геометрические модели (см. эту статью для сравнения). Это могут (или не могут) быть лучшие подходы. Однако большинство кинематических библиотек принимают параметры DH, и по этой причине это разумный подход для начала.
Одним из его недостатков является то, что он не очень элегантно обрабатывает параллельные оси Z. Существуют различные альтернативы, включая представления теории винтов, Хаяти-Робертса и другие геометрические модели (см. эту статью для сравнения). Это могут (или не могут) быть лучшие подходы. Однако большинство кинематических библиотек принимают параметры DH, и по этой причине это разумный подход для начала.
Шаг 5. Объединение параметров в робота целиком
Последний шаг — объединение всех параметров DH в робота целиком. Есть два способа сделать это, сложный и простой:
Трудный путь: Создайте свой собственный решатель
«Чистый» метод использования параметров DH состоит в том, чтобы «свернуть свой собственный» решатель Forward Kinematic, используя ваш любимый язык программирования. Я сам использовал этот подход в прошлом, хотя, вероятно, в наши дни я бы не стал этого делать.
Когда у вас есть параметры DH для каждого соединения, вы можете использовать этот метод для кодирования их в решателе прямой кинематики:
- Найдите библиотеку на вашем языке программирования, которая позволяет выполнять матричное умножение.
 Кроме того, напишите свой собственный код, используя методы из этого списка.
Кроме того, напишите свой собственный код, используя методы из этого списка. - Для каждого соединения робота заполните новую матрицу 4 x 4 следующими значениями:
- Перемножьте все матрицы вместе, начиная с первого сустава и заканчивая концевым эффектором.
- Окончательный вектор T будет содержать положение концевого эффектора. Матрица R будет содержать ориентацию концевого зажима.
Если вы просто хотите попробовать это с некоторыми значениями, не кодируя свой собственный решатель, вы можете использовать этот удобный онлайн-инструмент, чтобы создать рабочий пример полного робота из его параметров DH.
По моему опыту, создание собственного решателя не дает больше преимуществ, чем использование существующей библиотеки. Тем не менее, это хорошее упражнение для обучения.
Простой способ: используйте существующие библиотеки
Гораздо более эффективный способ расчета прямой кинематики, если у вас есть параметры DH, — использовать существующую библиотеку.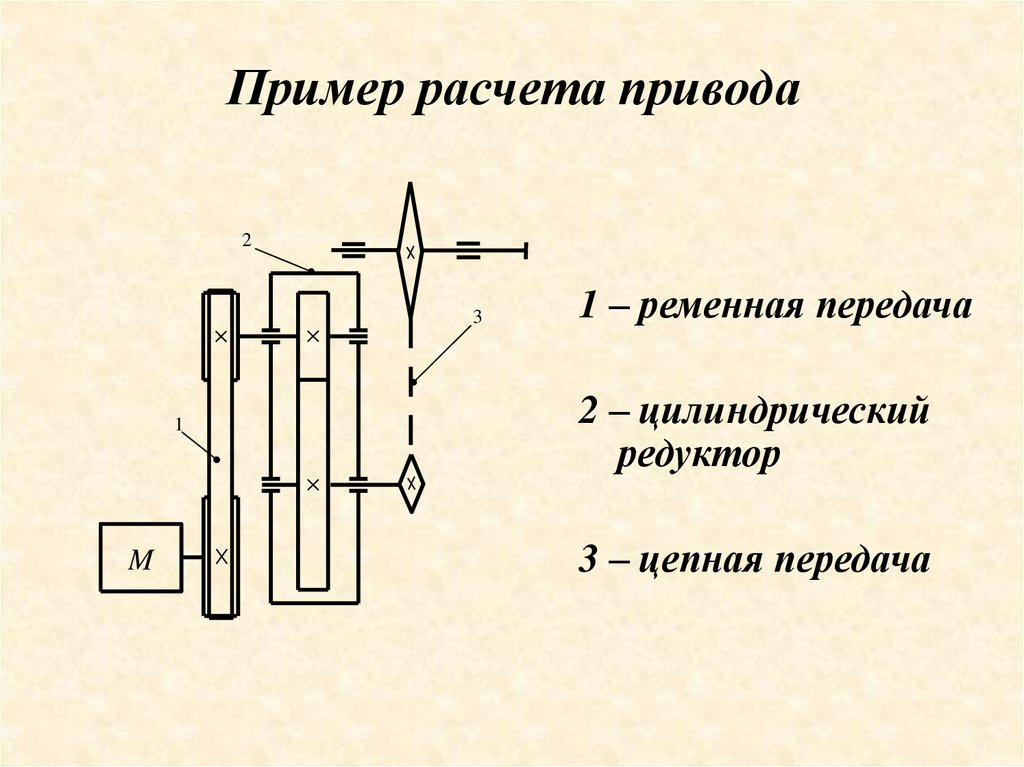
 ниже).
ниже). Кроме того, напишите свой собственный код, используя методы из этого списка.
Кроме того, напишите свой собственный код, используя методы из этого списка.