что это, как рассчитать, формулы и примеры

Автор Andrey Ku На чтение 4 мин Опубликовано 20.10.2021

Трансформатор, как элемент радиотехники и электротехники, работает на основе электромагнитной индукции. Говоря об индуктивности трансформатора, имеют в виду индуктивность обмоток и взаимоиндукцию между ними.

Каждая из обмоток представляет некоторое количество витков провода, намотанных на ферромагнитный сердечник, то есть обыкновенную катушку индуктивности.

Трудность в определении параметров катушки заключается в том, что они изменяются в зависимости от нескольких параметров и их сочетания:

• токи в обмотках;
• уровень намагниченности магнитопровода;
• магнитные характеристики сердечника;
• взаимодействие между соседними обмотками;
• наличия постоянной составляющей тока.

Содержание

1. Конструкция и принцип действия силового трансформатора
2. Физическое понятие индуктивности обмоток
3. Формулы и измерение
4. Как измерить в домашних условиях
5. Пример расчета

Конструкция и принцип действия силового трансформатора

В основе конструкции любого трансформатора находятся следующие элементы:

1. Сердечник из ферромагнитного материала.
2. Первичная и вторичные обмотки. В случае автотрансформатора одна обмотка выполняет обе функции.

В сетях переменного тока промышленной частоты (50 или 60Гц) в качестве ферромагнитного материала используется сталь, обработанная по специальной технологии. На высоких частотах часто делаются трансформаторы без сердечника, поскольку для нормальной работы достаточно взаимосвязи межу катушками.

Принцип работы:

• в первичной обмотке, подключенной в цепь питания, создается переменное электрическое поле;
• под действием поля первичной катушки в сердечнике создается переменное магнитное поле;
• в силу электромагнитной индукции во всех обмотках наблюдается ЭДС индукции.

ЭДС индукции в первичной обмотке направлена противоположно поданному напряжению, поэтому они взаимно компенсируются. В результате, при отсутствии нагрузки через первичную обмотку протекает сравнительно небольшой ток холостого хода.

Наличие тока вторичной цепи аналогично вызывает дополнительный магнитный поток, а он – ЭДС самоиндукции в первичное катушке. В результате компенсация первичного напряжения снижается и растет ток в первичной цепи.

Физическое понятие индуктивности обмоток

Индуктивность представляет собой коэффициент пропорциональности между током, создаваемым замкнутым электрическим контуром, и магнитным потоком, который создается этим контуром.

Более понятной формулировкой будет та, которая говорит о величине ЭДС самоиндукции в замкнутом контуре, которая возникает при изменении силы тока за единицу времени. То есть, понятие индуктивности справедливо для изменяющегося тока.

При постоянном токе говорить об индуктивности бессмысленно.

В идеальном трансформаторе все электромагнитное поле, создаваемое обмотками, замкнуто в магнитном сердечнике. В реальных конструкциях существует поле рассеяния, величина которого зависит от способа выполнения катушки и конструктивных особенностей сердечника. Чем больше толщина намотки, тем большая часть электромагнитного поля замыкается вне магнитопровода.

Этому способствует также качество сборки магнитопровода. Зазоры между пластинами способствуют резкому увеличению рассеивания. В связи с этим наилучшими свойствами обладают О-образные сердечники.

Формулы и измерение

Формулы для расчета индуктивности катушек довольно сложны и имеет различный вид для различных типов исполнения обмоток:

• линейный проводник;
• одновитковая катушка;
• плоская катушка;
• соленоидальная обмотка;
• тороидальная форма.

Наибольшие сложности возникают при расчетах многовитковых многослойных катушек, то есть тех, которые составляют обмотку трансформаторов.

В подавляющем большинстве случаев точный расчет невозможен, поэтому приходится использовать примерные данные и уточнять их после проведения измерений.

Формулы  для расчета индуктивности трансформатора основаны на расчетах соленоида:

L=µ₀µN²S/l, где

µ0 – магнитная постоянная;

µ – магнитная проницаемость сердечника;

N – количество витков;

S – площадь одного витка;

l – длина обмотки.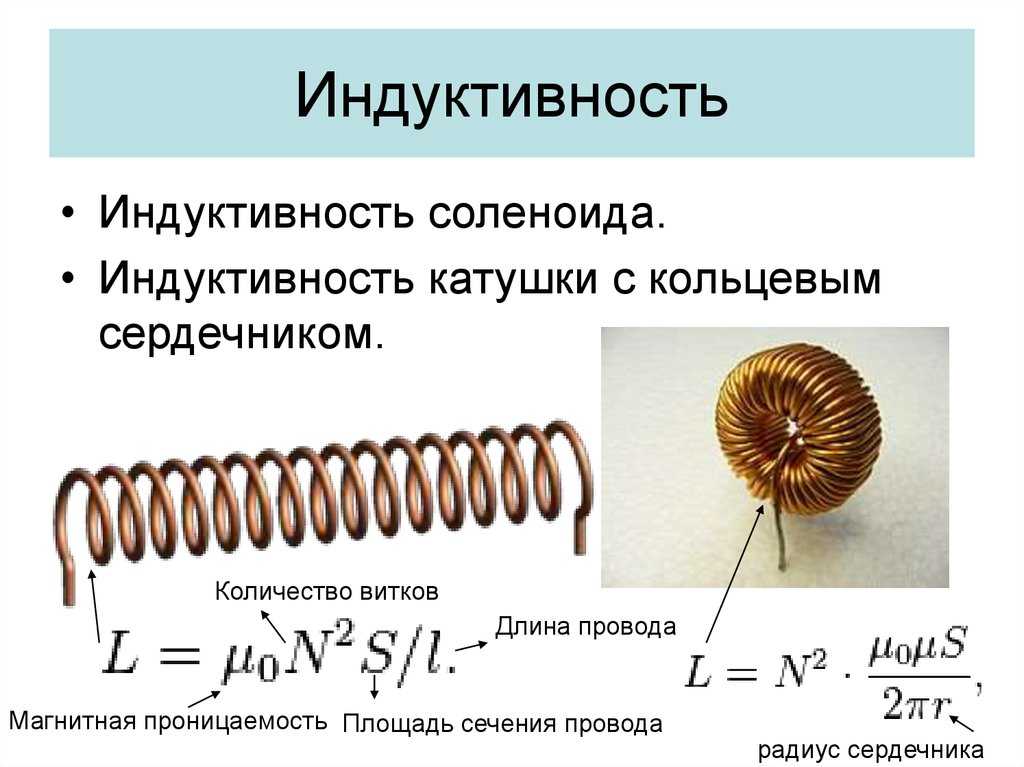

Для измерения индуктивности существует несколько методик и приборов, созданных на их основе. В большинстве случаев измерение производится путем вычислений индуктивного сопротивления катушки при подаче образцового напряжения заданной частоты и измеренного значения тока через обмотку.

В специализированных приборах вычисления производятся автоматически, и пользователь только считывает показания шкалы прибора, выраженные в единицах индуктивности – Гн, мГн или мкГн.

Как измерить в домашних условиях

Приборы для непосредственного измерения индуктивности имеют высокую стоимость и редко используются в домашних условиях. С приемлемой точностью результаты можно получить, используя обычные приборы для измерения переменного тока: амперметр и вольтметр. Также необходим омметр.

Порядок действий следующий:

1. При помощи омметра определяют активное сопротивление обмотки R.
2. Подключают трансформатор последовательно с амперметром в сеть.
3. Параллельно обмотке подключают вольтметр.
4. По показаниям приборов определяют полное сопротивление трансформатора: Z=U/I
5. Индуктивное сопротивление находят, вычитая из полного сопротивления активное: X_L=Z-R
6. Индуктивность определяется по формуле: L=X_L/(2πf), где π – число пи 3.14, f – частота измерений.

Как правило, активное сопротивление намотки значительно (на несколько порядков) меньше индуктивного, поэтому можно его не учитывать. Именно поэтому, включение трансформатора в цепь постоянного напряжения вызывает короткое  замыкание. Ток обмотки при этом будет ограничиваться только активным сопротивлением.

Пример расчета

К примеру, требуется рассчитать индуктивность первичной обмотки трансформатора питания. Путем измерений определено:

1. Сопротивление обмотки 3 Ом.
2. Напряжение сети 220 В.
3. Частота питающего напряжения 50 Гц.
4. Ток холостого хода 05 А.

Полное сопротивление:

Z=U/I=220/0. 05=4400 Ом

Активное сопротивление меньше полного в 10000 раз и его можно не учитывать.

Определяем индуктивность:

L=X_L/(2πf) =4400/ (2∙3.14∙50) =14 Гн.

KSD-FT2319-h493 Синфазный дроссель KSD-FT2319-h493 | ООО «KODO TRANS»

9.2: Расчет индуктивности обмоток — Engineering LibreTexts

1. Последнее обновление

2. Сохранить как PDF

• Идентификатор страницы

  57008

• Джеймс Киртли
• Массачусетский технологический институт через MIT OpenCourseWare

Цель этого раздела — показать, как можно рассчитать индуктивность обмоток в машинах с круглым ротором и узкими воздушными зазорами. Мы имеем дело только с идеализированными магнитными полями воздушного зазора и не рассматриваем пазовые, лобовые, периферийные или косые реактивные сопротивления. Однако мы рассматриваем пространственные гармоники магнитодвижущей силы обмотки (МДС).

Для начала рассмотрим МДС полношаговой сосредоточенной обмотки. Предполагая, что обмотка имеет в общей сложности \(\N\) витков на \(\p\) пар полюсов, МДС равна: 9{\ infty} \ frac {\ mu_ {0}} {g} \ frac {4} {n \ pi} \ frac {N I} {2 p} \ sin n p \ phi \\
&\ text { nodd }
\конец{выровнено}\)

Обратите внимание, что реальная обмотка, которая, скорее всего, не будет полной и сосредоточенной, будет иметь коэффициент намотки, который является произведением коэффициентов шага и ширины, что будет обсуждаться позже.

Теперь предположим, что имеется многофазная обмотка, состоящая более чем из одной фазы (мы будем использовать три фазы), питаемая одним из двух видов тока. Первый из них балансный, ток:

\(\ \begin{align}
I_{a} &=I \cos (\omega t) \\
I_{b} &=I \cos \left(\omega t-\frac{2 \pi} {3}\right) \\
I_{c} &=I \cos \left(\omega t+\frac{2 \pi}{3}\right)
\end{aligned}\label{1}\)

И наоборот, мы могли бы рассмотреть токи нулевой последовательности:

\(\ I_{a}=I_{b}=I_{c}=I \cos \omega t\)

Тогда можно выразить плотность магнитного потока для двух различных случаев. {\infty} B_{r n} \sin (n p \phi \mp \omega t)\) 9{\infty} \frac{B_{r n}}{n p} \cos (\omega t)\)

Это позволяет нам рассчитать собственную и взаимную индуктивность, поскольку поток обмотки равен:

\(\ \лямбда=N \фи\)

Конец этого набора выражений для различных индуктивностей. Следует отметить, что в реальном мире большинство обмоток не имеют полного шага и не сосредоточены. К счастью, эти недостатки можно компенсировать за счет использования коэффициентов обмотки.

Простейшим и, возможно, лучшим определением коэффициента обмотки является отношение потока, связанного с фактической обмоткой, к потоку, который был бы связан с полношаговой концентрированной обмоткой с тем же числом витков. То есть:

\(\ k_ {w} = \ frac {\ lambda _ {\ text {фактическое}}} {\ lambda _ {\ text {полный шаг}}} \)

Относительно легко показать, используя аргументы взаимности, что коэффициенты обмотки также являются отношением эффективной МДС, создаваемой фактической обмоткой, к МДС, которая была бы произведена той же обмоткой, если бы она была полной и концентрированной. Аргумент звучит так: взаимная индуктивность между любой парой обмоток обратна. То есть, если обмотки обозначены один и два, взаимная индуктивность есть поток, индуцируемый в первой обмотке током во второй обмотке, а во второй обмотке также поток, индуцируемый током в первой обмотке. Поскольку каждая обмотка имеет коэффициент обмотки, влияющий на ее поток связи, и поскольку взаимная индуктивность должна быть обратной, один и тот же коэффициент обмотки должен влиять на МДС, создаваемую обмоткой.

Коэффициенты обмотки часто выражаются для каждой пространственной гармоники, хотя иногда, когда коэффициент обмотки упоминается без ссылки на номер гармоники, имеется в виду пространственный коэффициент для пространственной основной гармоники.

Для обычных обычных обмоток обычно указываются два коэффициента обмотки. Их обычно называют факторами шага и ширины, отражая тот факт, что часто обмотки не имеют полного шага, что означает, что отдельные витки не охватывают полное π электрических радианов и что обмотки занимают диапазон или ширину пазов в фазовом поясе. Коэффициенты широты представляют собой отношения потока, связанного с данной обмоткой, к потоку, который был бы связан с этой обмоткой, если бы она была полной и концентрированной. Эти два фактора обмотки обсуждаются более подробно ниже. Что интересно отметить, хотя мы и не доказываем это здесь, так это то, что коэффициент обмотки любой данной обмотки является произведением коэффициентов шага и ширины: 9{2}} \cos (n p \theta) \\
& \text {nodd}
\end{выровнено}\)

Теперь обратим внимание на вычисление коэффициентов намотки для простых, регулярных схем намотки. Мы не доказываем, а только утверждаем, что коэффициент намотки для регулярных схем намотки может быть выражен как произведение коэффициента шага и коэффициента ширины, каждый из которых может быть оценен отдельно.

Коэффициент шага определяется с учетом потока, связанного с обмоткой с меньшим шагом. Рассмотрим ситуацию, в которой плотность радиального магнитного потока равна: 9{\ frac {\ pi} {2 p} + \ frac {\ alpha} {2 p}} B_ {n} \ sin (n p \ phi- \ omega t) R d \ phi \)

Шаг \(\ \alpha\) относится к угловому смещению между сторонами катушки, выраженному в электрических радианах. {j\left(\omega t-n \xi_{i}\right)}\right)\) 9{-j n \gamma}}\)

Теперь коэффициент ширины найден:

\(\ k_{b n}=\frac{\sin \frac{n m \gamma}{2}}{m \sin \frac{n \gamma}{2}}\)

---

Эта страница под названием 9.2: Расчет индуктивности обмотки распространяется под лицензией CC BY-NC-SA 4.0 и была создана, изменена и/или курирована Джеймсом Киртли (MIT OpenCourseWare) посредством исходного содержимого, которое было отредактировано в соответствии со стилем и стандартами. платформы LibreTexts; подробная история редактирования доступна по запросу.

1. Наверх
• Была ли эта статья полезной?

1. Тип изделия

   Раздел или Страница

   Автор

   Джеймс Киртли

   Лицензия

   CC BY-NC-SA

   Версия лицензии

   4,0

   Программа OER или Publisher

   MIT OpenCourseWare

   Показать оглавление

   нет

2. Теги

   1. source@https://ocw. mit.edu/courses/6-061-introduction-to-electric-power-systems-spring-2011

Emetor — Глоссарий — Индуктивность рассеяния лобовой обмотки

Внимание! Emetor лучше всего работает с включенным JavaScript. Включите JavaScript в настройках браузера и повторите попытку.

Индуктивность рассеяния витков обмотки.

---

Индуктивность рассеяния лобовой обмотки, как правило, довольно мала и зависит от фактической формы и расположения концевых витков. Поэтому сложно подсчитать в общем виде. В Emetor предполагается, что концевые витки имеют форму полукруга, см. рис. 1. Это допущение позволяет с достаточной точностью аппроксимировать индуктивность рассеяния лобовой обмотки. 92}{2}\ln\left(\frac{\tau_p\sqrt{\pi}}{\sqrt{2A}}\right)$$ в зависимости от шага катушки $\tau_p$, числа витков на виток $N$, а площадь витка $A$ показана на рис. 1. Для однослойной обмотки площадь витка соответствует площади пазов, а для двухслойной обмотки площадь витка составляет только половину площади пазов.