Примеры решения задач — ЗФТШ, МФТИ

1) Для ответа на первый вопрос задачи необходимо определить знак количества теплоты для каждого участка цикла.

Процесс $$ 1–2$$ – изохорный процесс, идущий с увеличением давления. В этом процессе внутренняя энергия газа увеличивается:

$$ $$ $$ \Delta {U}_{1-2}={\displaystyle \frac{i}{2}}{V}_{12}({p}_{23}-{p}_{14})>0$$ $$ $$

(здесь и далее двойной индекс означает равенство данной величины в двух состояниях (двух точках на диаграмме) $$ {V}_{12}={V}_{1}={V}_{2}$$ или $$ {p}_{23}={p}_{2}={p}_{3}$$), а работа газа равна нулю: $$ {A}_{1-2}=0$$, т. к. объём газа не изменяется. Следовательно, на изохоре $$ 1–2$$ газ получает теплоту: $$ \Delta {Q}_{1-2}=(\Delta {U}_{1-2}+{A}_{1-2})>0$$.

Процесс $$ 2–3$$ изобарный, идущий с увеличением объёма. В этом процессе внутренняя энергия газа увеличивается: $$ \Delta {U}_{1-2}={\displaystyle \frac{i}{2}}{p}_{2-3}({V}_{34}-{V}_{12})>0$$, а работа газа при увеличении объёма положительна: $$ {A}_{2-3}={p}_{23}({V}_{34}-{V}_{12})>0$$.  Следовательно, на изобаре $$ 2–3$$ газ получает теплоту:  

$$ \Delta {Q}_{2-3}=(\Delta {U}_{2-3}+{A}_{2-3})>0$$.

Процесс $$ 3–4$$ – изохорный процесс, идущий с уменьшением давления.

В этом процессе внутренняя энергия газа уменьшается:

`DeltaU_(1-2)=i/2 V_(34)(p_(14)-p_(23))<0`, а работа газа равна нулю: $$ {A}_{3-4}=0$$, т. к. объём газа не изменяется. Следовательно, на изохоре $$ 3–4$$ газ отдаёт теплоту: $$ΔQ_{3-4} < 0$$.

Процесс $$ 4–1$$ изобарный, идущий с уменьшением объёма. В этом процессе внутренняя энергия газа уменьшается: `DeltaU_(1-2)=i/2 p_(14)(V_(12)-V_(34)<0`, а работа газа при уменьшении объёма отрицательна: $$ {A}_{4-1}={p}_{14}({V}_{12}-{V}_{34})$$. Следовательно, на изобаре $$ 4–1$$ газ отдаёт теплоту: $$ΔQ_{4-1} = (ΔU_{4-1} + A_{4-1}) < 0 $$.

2) Второй вопрос требует от нас анализа итогового изменения внутренней энергии. Так как цикл замкнутый, то термодинамическая система возвращается в исходное состояние, следовательно, внутренняя энергия не изменяется (внутренняя энергия, являясь функцией состояния, определяется только температурой.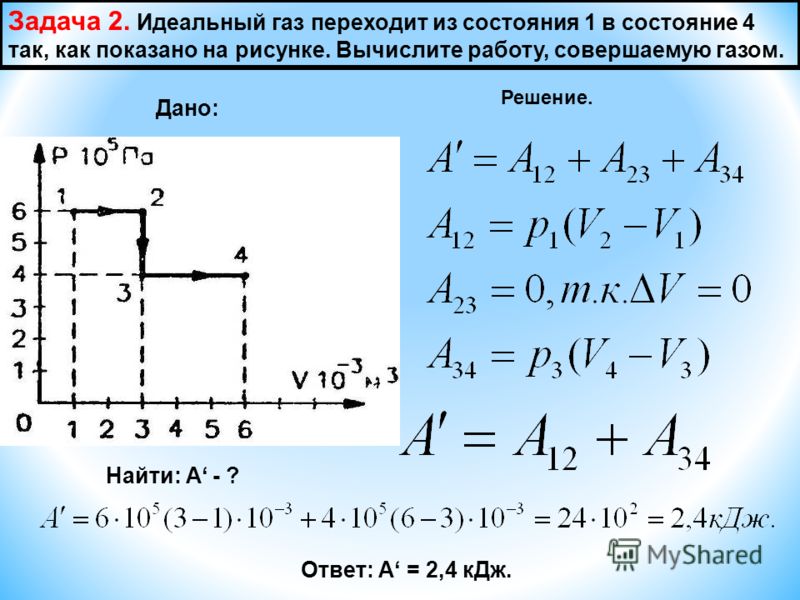 Температура же после совершения замкнутого цикла примет первоначальное значение). Следовательно,

$$ \Delta {U}_{1-2-3-4-1}=0$$.

3) Работа за цикл равна сумме работ в отдельных процессах:

$$ {A}_{1-2-3-4-1}={A}_{1-2}+{A}_{2-3}+{A}_{3-4}+{A}_{4-1}={A}_{2-3}+{A}_{4-1}=$$

$$ ={p}_{23}({V}_{34}-{V}_{12})+{p}_{14}({V}_{12}-{V}_{34})=({p}_{23}-{p}_{14})({V}_{34}-{V}_{12})$$.

На $$ pV$$-диаграмме это есть площадь фигуры, ограниченной графиками процессов, составляющих цикл.

Для нахождения работы за цикл можно складывать не работы, а количества теплоты, потраченные в отдельных процессах цикла. Докажем это:

$$ {A}_{1-2-3-4-1}= \Delta {Q}_{1-2}+ \Delta {Q}_{2-3}+ \Delta {Q}_{3-4}+ \Delta {Q}_{4-1}=$$

$$ =(\Delta {U}_{1-2}+{A}_{1-2})+(\Delta {U}_{2-3}+{A}_{2-3})+ (\Delta {U}_{3-4}+{A}_{3-4})+ (\Delta {U}_{4-1}+{A}_{4-1}=$$

$$ =(\Delta {U}_{1-2}+ \Delta {U}_{2-3}+ \Delta {U}_{3-4}+ \Delta {U}_{4-1})+({A}_{1-2}+{A}_{2-3}+{A}_{3-4}+{A}_{4-1})=$$

$$ ={A}_{1-2}+{A}_{2-3}+{A}_{3-4}+{A}_{4-1}$$.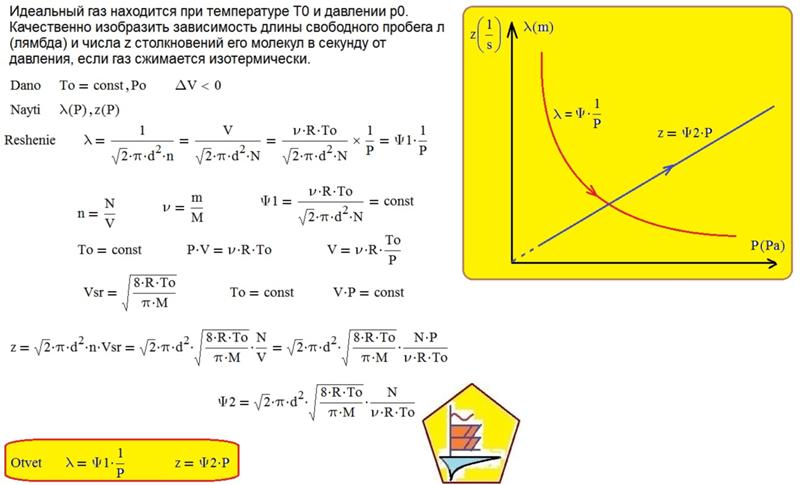 {\text{‘}}=-\Delta \nu R{T}_{1}+ \Delta \nu R{T}_{2}= \Delta \nu R({T}_{2}-{T}_{1})$$,

С учётом вышеизложенного перепишем первой закон термодинамики для рассматриваемой ситуации:

$$ N \Delta T={\displaystyle \frac{i}{2}} \Delta \nu R({T}_{2}-{T}_{1})+\Delta \nu R({T}_{2}-{T}_{1})=({\displaystyle \frac{i}{2}}+1) \Delta \nu R({T}_{2}-{T}_{1})$$.

Любопытно заметить, что процесс нагрева воздуха проходит так, что его описание совпадает с процессом изобарного нагрева.

Теперь подробнее остановимся на массовом расходе воздуха $$ {m}_{\tau }$$.

$$ {m}_{\tau }={\displaystyle \frac{\Delta m}{ \Delta t}}={\displaystyle \frac{\Delta \nu M}{ \Delta t}}$$, тогда $$ \Delta \nu ={m}_{\tau }{\displaystyle \frac{\Delta t}{M}}$$,

$$ N·\Delta t=({\displaystyle \frac{i}{2}}+1) \Delta \nu R({T}_{2}-{T}_{1})=({\displaystyle \frac{i}{2}}+1){m}_{\tau }{\displaystyle \frac{\Delta t}{M}}R({T}_{2}-{T}_{1})$$.

Откуда получаем ответ:

$$ N=({\displaystyle \frac{i}{2}}+1){\displaystyle \frac{{m}_{\tau }}{M}}R({T}_{2}-{T}_{1})=$$

$$ =\left(\mathrm{3,5}\right){\displaystyle \frac{720\mathrm{кг}}{360с \mathrm{0,029}\frac{\mathrm{кг}}{\mathrm{моль}}}}\mathrm{8,31}{\displaystyle \frac{\mathrm{Дж}}{\mathrm{моль}·\mathrm{К}}}5 \mathrm{K} \approx 1000 \mathrm{Вт}$$.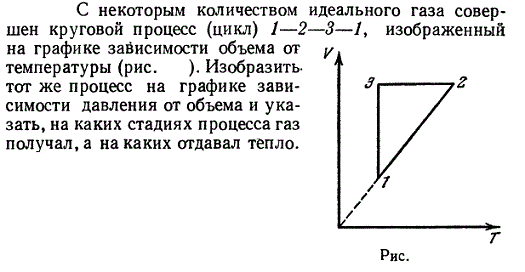

Термодинамика

Программированное
контрольное задания № 6

Укажите
номера (табл. 30) правильных ответов на
вопросы.

В а р и а н т 1

1. Как
выглядит математическая запись первого
начала термодинамики применительно к
изохорическому процессу?

2. В
каком процессе изменение внутренней
энергии идеального газа численно равно
работе, совершаемой газом?

3. Чему равна
работа, совершаемая идеальным газом в
изобарном процессе?

4. Как
будет меняться внутренняя энергия
данной массы идеального газа (u)
при изотермическом расширении?

5. Чему равна
теплоемкость газа в изотермическом
процессе?

6. Газ
из состояния 1 сначала адиабатически
расширяется, а затем изотермически
сжимается до первоначального объема
(состояние 2). Укажите график такого
перехода из состояния 1 в состояние 2.

7. Сколько
степеней свободы имеет двухатомная
молекула?

В а р и а н т 2

1. Как
выглядит математическая запись первого
начала термодинамики применительно к
изотермическому процессу?

2. В
каком процессе изменение внутренней
энергии газа равно количеству переданной
газу теплоты?

3. Чему
численно равна работа, совершаемая
идеальным газом в адиабатном процессе?

4. Каково
изменение внутренней энергии данной
массы идеального газа u
при ее изобарическом сжатии?

5. Чему
равна молярная теплоемкость идеального
газа в адиабатном процессе?

6. Газ
сначала из состояния 1 изотермически
расширяется, а затем адиабатически
сжимается до первоначального объема
(состояние 2). Укажите график перехода
системы из состояния 1 в состояние 2.

7.
Сколько степеней свободы имеет
многоатомная молекула (число атомов
более трех)?

В а р и а н т 3

1. Как
выглядит математическая запись первого
начала термодинамики применительно к
изобарическому процессу?

2. В
каком процессе количество переданной
газу теплоты равно изменению внутренней
энергии газа?

3. Чему
равна работа, совершаемая идеальным
газом в изотермическом процессе?

4. Каково
изменение внутренней энергии данной
массы идеального газа при ее адиабатическом
расширении?

5. Чему
равна молярная теплоемкость идеального
газа в изохорическом процессе?

6. Газ
из состояния 1 сначала изотермически
сжимается, а затем адиабатически
расширяется до первоначального объема
(состояние 2). Укажите график перехода
системы из состояния 1 в состояние 2.

7. Сколько
степеней свободы имеет трехатомная
молекула?

Таблица 30

	1	2	3	4	5
1	Q = A	Q = U + A	U = – A	Q = U
2	В адиабатическом	В изохорическом	В изобарическом	В изотермическом	В любом
3	PV				0
4	U > 0	U < 0	U = 0		–
P P P P P 2 1 1 1 2 2 1 2 1 2 V1 V V1 V V1 V V1 V V1 V 5			0
6

Таблица
31

Р1 1	P 1 2 P1 3 V1 V2 V	P 1(P1) Q=0 . 3 2(P2) V1 V2 V	P 2(P2) T=const 1(P1) 3 V1 V	P 2(P2) Q=0 1 V2 V1 V	P 2 3 Q=0 1 V2 V1 V
2			PV = const	PV = const	—
3	1  2	2  3	3  1	—	—
4				0
5			0	P2V2 – P1V1	—
6	P(V2 – V1)		Q1 – Q2	U	Q1 – U
7					—

В а р и а н т
4

1. Как
выглядит математическая запись первого
начала термодинамики применительно к
адиабатическому процессу?

2. В
каком процессе количество переданной
газу теплоты равно работе, совершенной
газом?

3. Чему
равна работа, совершаемая идеальным
газом в изохорическом процессе?

4. Каково изменение
внутренней энергии данной массы
идеального газа при ее адиабатическом
сжатии?

5. Чему равна
молярная теплоемкость идеального газа
в изобарическом процессе?

6. Газ
сначала из состояния 1 адиабатически
сжимается, а затем изотермически
расширяется до первоначального объема
(состояние 2). Укажите график перехода
системы из состояния 1 в состояние 2.

7. Сколько
степеней свободы имеет одноатомная
молекула?

В а р и а н т 5

1. Как
выглядит математическая запись первого
начала термодинамики в общем случае?

2. В каком процессе
работа, совершаемая газом, равна
количеству полученной газом теплоты?

3. Чему равна
работа, совершаемая газом при изобарическом
нагревании?

4. Как будет
меняться внутренняя энергия газа при
изохорическом уменьшении давления?

5. Чему равна
молярная теплоемкость газа в адиабатном
процессе?

6. Газ
из состояния 1 сначала изотермически
расширяется, а затем адиабатически
сжимается до первоначального объема
(состояние 2). Укажите график перехода
системы из состояния 1 в состояние 2.

7. Сколько
степеней свободы имеет трехатомная
молекула линейной структуры

?

Программированное
контрольное задание № 7

На
вопросы, поставленные к каждому из
рассматриваемых в вариантах 1-5 циклов,
выберите номера правильных ответов из
табл. 31.

В а р и а н т 1

Идеальный
газ из состояния 1 с параметрами P₁,
V₁, T₁
сначала адиабатически расширяется,
затем изобарически сжимается до
первоначального объема после чего
изохорически возвращается в исходное
состояние.

1. Укажите в
табл. 31 график данного кругового процесса.

2. Укажите
уравнение, которому подчиняется в данном
цикле переход газа из состояния 2 в
состояние 3.

3. На каких этапах
рассматриваемого цикла газ получает
тепло из окружающей среды? Газ получает
тепло в процессе…

4. Чему равно
количество тепла, отданное газом за
цикл?

Q₂=…

5. Каково изменение
внутренней энергии за цикл? U
=…

6. Чему равна
работа газа за цикл? A =…

7. По какой
формуле можно подсчитать КПД данного
цикла? 
=…

8. Какому состоянию
газа в данном цикле соответствует
минимальное значение внутренней энергии?

В а р и а н т 2

Идеальный
газ, находящийся в состоянии 1 с параметрами
P₁, V₁,
T₁ нагревается при
постоянном объеме до давления P₂,
затем изотермически расширяется до
начального давления, после чего
изобарически возвращается в исходное
состояние.

1. Укажите в
табл. 31 график данного цикла.

2. Укажите
уравнение, которому подчиняется в данном
цикле переход газа из состояния 1 в
состояние 2.

3. На каких этапах
рассматриваемого цикла газ получает
тепло из окружающей среды? Газ получает
тепло в процессах…

4. Чему равно
количество тепла, отданное газом за
цикл?

Q₂
=…

5. Каково изменение
внутренней энергии газа за цикл? U
=…

6. Чему равна
работа газа за цикл в рассматриваемом
цикле? A =…

7. По какой
формуле можно посчитать КПД данного
цикла? 
=…

8. Какому
состоянию газа в данном цикле соответствует
максимальное значение внутренней
энергии газа?

В а р и а н т 3

Идеальный
газ из состояния 1 с параметрами P₁,
V₁, T₁
расширяется при постоянном давлении
до объема V₂, затем
изохорически охлаждается до прежней
температуры, после чего возвращается
в исходное состояние.

1. Укажите в
табл. 31 график рассматриваемого цикла.

2.
Укажите уравнение, которому подчиняется
в рассматриваемом цикле переход из
состояния 2 в состояние 3.

3. На каких этапах
рассматриваемого цикла газ отдает тепло
в окружающую среду? Газ отдает тепло в
процессах…

4. Чему равно
количество тепла, полученного газом в
данном цикле?

Q₁
=…

5. Каково изменение
внутренней энергии газа за цикл? U
=…

6. Чему равна
работа газа за цикл в данном цикле? A
=…

7. По какой
формуле можно посчитать КПД данного
цикла? 
=…

8. Какому
состоянию газа в данном цикле соответствует
максимальное значение внутренней
энергии газа?

В а р и а н т 4

Идеальный
газ из состояния 1 с параметрами P₁,
V₁, T₁,
сначала адиабатически сжимается до
объема V₂, затем
изобарически расширяется до первоначального
объема, после чего изохорически
возвращается в исходное состояние.

1. Укажите в
табл. 31 график данного цикла.

2.
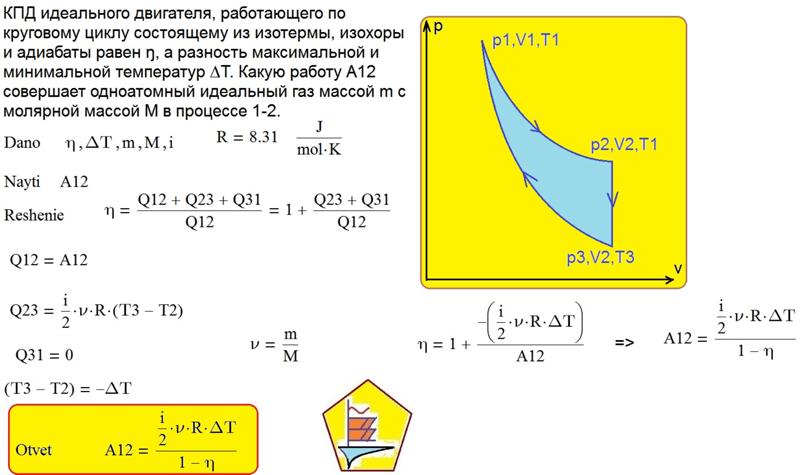
Укажите уравнение, которому подчиняется
в рассматриваемом цикле переход газа
из состояния 1 в состояние 2.

3. На
каких этапах рассматриваемого цикла
газ отдает тепло в окружающую среду?

4. Чему равно
количество тепла, полученное газом в
данном цикле? Q₁ =…

5. Каково изменение
внутренней энергии за цикл? U
=…

6. Чему равна в
данном случае работа газа за цикл? A
=…

7. По какой
формуле можно посчитать КПД ()
данного цикла?

 = …

8. Какому
состоянию газа в данном цикле соответствует
максимальное значение внутренней
энергии газа?

В а р и а н т 5

Газ из
состояния 1 с параметрами P₁,
V₁, T₁,
сначала адиабатически сжимается до
объема V₂, после чего
изотермически расширяется до
первоначального объема, а затем
изохорически возвращается в исходное
состояние.

1. Укажите в
табл. 31 график рассматриваемого цикла.

2. Укажите
уравнение, которому подчиняется в данном
цикле переход 1-2.

3. На
каких этапах рассматриваемого цикла
газ получает тепло из окружающей среды?

4. Чему равно
количество тепла, отданное газом за
цикл? Q₂ =…

5. Каково изменение
внутренней энергии газа за цикл? U
=…

6. Чему равна в
рассматриваемом случае работа газа за
цикл? A =…

7. По какой
формуле можно посчитать КПД ()
данного цикла? 
=…

8. Какому состоянию
газа в данном цикле соответствует
минимальное значение внутренней энергии
газа?

Термодинамические процессы

Термодинамические процессы

Часто система, из которой мы
хотят извлечь теплоту, чтобы сделать работу, является газом. Когда газ расширяется, как
какую работу он производит над своим окружением?

Рассмотрим идеальный газ в цилиндре с подвижным поршнем.
газ занимает объем V, температура T, давление
P. Предположим, что поршень имеет площадь поперечного сечения A. Предположим, что
газ расширяется на небольшую величину, а поршень выдвигается на небольшую
сумма ды. Газ действует на поршень с силой F = PA и
следовательно, поршень работает dW = Fdy.

dW = Fdy = PAdy = PdV

dV — изменение объема газа. dV положителен, потому что
газ расширяется. (Если газ сжимается, то dV равно
отрицательный и над газом совершается работа.)

Если объем газа изменится с V ₁ на V ₂ , то общее
работа, совершенная газом, равна

.

ΔW = lim _ΔV—>0 ∑ _j P _j ΔV _д
= ∫ _V1 ^V2 PdV.

Суммируем работу, проделанную за большое количество малых изменений громкости. Работа
зависит от того, как именно изменяется давление при расширении
процесс. Если известны давление и объем на каждом шаге
процесс расширения, то работу можно представить в виде площади
под кривой на диаграмме PV.

Проблема:

Газ в баллоне находится при давлении 1,5 атм и объеме 4 м ³ .
Какую работу совершит газ, если при постоянном давлении он расширится до удвоенного своего первоначального объема?

Решение:

• Обоснование:
  Процесс изобарический. Для изобарического процесса W = P(V ₂ — V ₁ ).
• Детали расчета:
  W = P(V ₂ — V ₁ ) = P(2V ₁ — V ₁ )
  = PV ₁ = 151500 Па*4 м ³
  = 606000 Дж.
  (Работа — это площадь под кривой на диаграмме PV.  ΔV положителен, потому что
  газ расширяется, поэтому работа W, совершаемая газом, равна
  положительный.)

Проблема:

Газ в баллоне при давлении 1,5 атм и объеме 4 м ³ .
Какую работу совершит газ, если его сжать при постоянном давлении до 1/4 первоначального объема?

Решение:

• Обоснование:
  Процесс изобарический. Для изобарического процесса W = P(V ₂ — В ₁ ).
• Детали расчета:
  Вт = P(0,25 В ₁ — В ₁ ) = -0,75 PV ₁
  = -454500 Дж.
  (Работа — это площадь под кривой на диаграмме PV.  ΔV равно
  отрицательно, так как газ сжат, и поэтому работа W, совершаемая
  газ отрицательный. )

Проблема:

Газ в баллоне при давлении 1,5 атм и объеме 4 м ³ .
Какую чистую работу совершит газ, если он совершит следующий цикл?

(i) Газ расширяется при постоянном давлении 1,5 атм до объема
4 м ³ .
(ii) При постоянном объеме 4 м ³ давление снижается
до 1 атм.
(iii) Газ сжимают при постоянном давлении 1 атм до
объем 4 м ³ .
(iv) При постоянном объеме 4 м ³ давление равно
увеличилось до 1,5 атм.

Решение:

• Обоснование:
  Процессы (i) и (iii) являются изобарными. W = PΔV.
  Процессы (i) и (iii) изометричны. Вт = 0,
• Детали расчета:
  (i) W = PΔV _{= 151500 Па*4 м ³
  = 606000 Дж.
  (ii) W = 0, поскольку ΔV = 0. (без смещения <--> без работы).
  (iii) W = PΔV = -101000 Па*4 м ³
  = -404000 Дж.
  (iv)  W = 0.
  Чистая работа, совершаемая газом:  Вт нетто = 606000 Дж — 404000 Дж =
  202000 Дж.}

Чистая работа, совершаемая газом за один цикл процесса, возвращающего
газа до его начального состояния – это площадь внутри замкнутого контура в PV
диаграмма. Если цикл проходится за по часовой стрелке направление сети
работа положительная . Если петля проходится в против часовой стрелки
направление сети отрицательное .

• При расширении газ совершает положительную работу. Он упирается в стену
  контейнер и стенка контейнера перемещаются наружу. Имеем ∆W =
  F*∆r = (F/A)*A*∆r = P *∆V. Здесь А — площадь стенки контейнера.
  который сместился, а ∆r — насколько он сместился наружу.
• Когда объем газа уменьшается, газ совершает отрицательную работу. ∆W =
  -P*∆V. Газ по-прежнему выталкивается наружу, к стене, но стена движется.
  внутрь.
• Когда объем не меняется, газ не работает, независимо от
  значение давления.
• Итак, когда у вас есть диаграмма P-V (вертикальная ось P, горизонтальная ось V)
  показывая замкнутый цикл, вы можете разбить цикл на маленькие шаги, которые
  либо увеличьте, либо уменьшите громкость, либо не изменяйте ее.
  Любое положительное ∆V (в сторону большего V) означает, что газ совершает положительную работу P*∆V,
  и любое отрицательное ∆V (в сторону меньшего V) означает, что газ совершает отрицательную работу
  -P*∆V.
• Сложив все это, вы обнаружите, что работа, выполненная газом, равна площади
  внутри петли на диаграмме PV. Работа положительна, если давление
  больше при расширении, чем при сжатии, а работа
  отрицательное (работа совершается над газом), если давление меньше во время
  расширение, чем при сжатии.

Проблема:

Рассчитайте чистую выходную мощность тепловой машины по пути ABCDA в
рисунок справа.

Решение:

• Обоснование:
  Путь представляет собой замкнутый контур на диаграмме PV.
  Чистая проделанная работа — это площадь внутри замкнутого контура на диаграмме PV.
• Детали расчета:
  Вт = (1,5 * 3)*(10 ⁶ Н/м ² )(10 ^-3 м ³ )
  = 4,5*10 ³ Дж,
  с использованием площади = средняя высота * ширина.
  или
  область внутри цикла =
  площадь центрального прямоугольника + площадь верхнего треугольника — площадь нижнего треугольника
  = (1*3 + 0,6*3/2
  — 0,4*3/2)*(10 ⁶ Н/м ² )(10 ^-3
  м ³ ) = 4,5*10 ³ Дж.

Проблема:

Газ сжимают при постоянном давлении 0,8 атм из 9 литров в 2 литра.
(1 литр = 10 ^-3
м ³ )  При этом из газа уходит 400 Дж тепловой энергии.
(а)  Какую работу совершает газ?
(б) Как изменится его внутренняя энергия?

Решение:

• Обоснование:
  Для изобарического процесса W = P(V ₂ — V ₁ ).
  Энергосбережение: ΔU = ΔQ — ΔW.
• Детали расчета:
  (a) W = P(V ₂ — V ₁ ) = -80800 Па*7*10 ^-3
  м ³ = -565,6 Дж. (На газе совершается работа.)
  (б) ΔU = -400 Дж + 565,6 Дж = 165,6 Дж.

Проблема:

Один моль идеального газа совершает над окружающей средой работу 3000 Дж.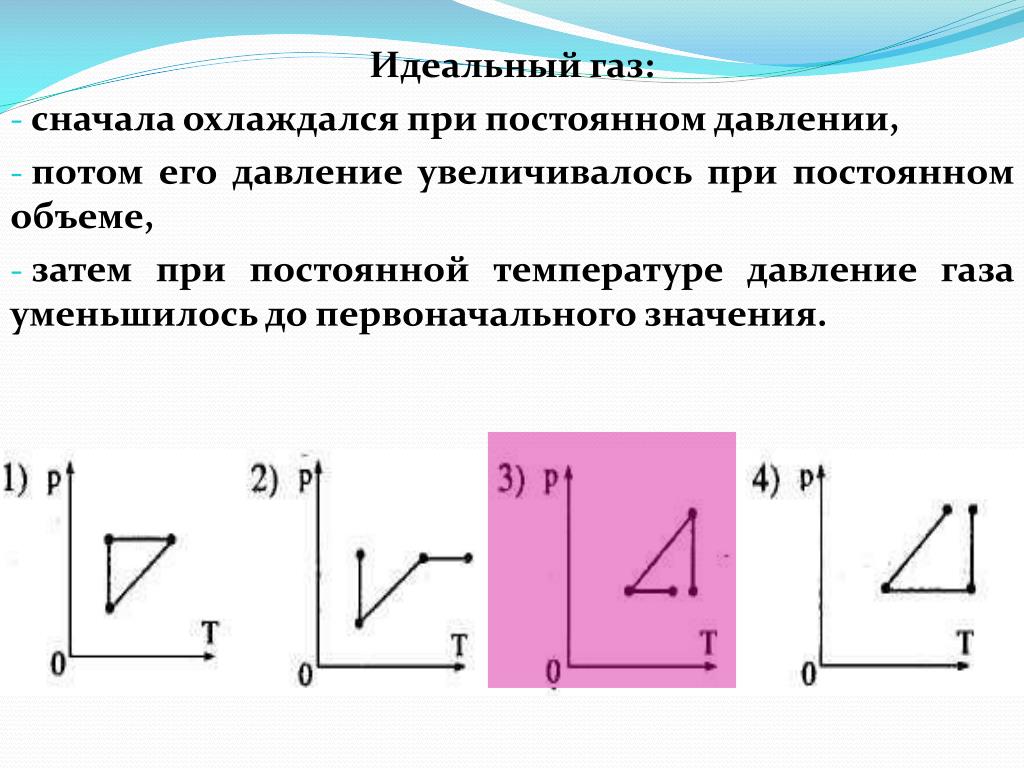
изотермически расширяется до конечного давления 1 атм и объема 25 л.
Определить
(а) начальный объем и
(б) температуру
газ.

Решение:

---

Велосипед Эргометр представляет собой устройство,
напоминает велосипед и используется для измерения количества работы, выполненной человеком
крутя педали, чтобы вращать большой маховик, обычно переднее колесо
стационарный велосипед, против силы трения. Проделанная работа по преодолению
сила трения преобразуется в тепловую энергию, которая вызывает температуру
маховика и других компонентов, контактирующих с системой, увеличиться.
Нейлоновый ремень, натянутый и намотанный на колесо, может обеспечить
сила трения. Натяжение можно измерить калиброванной пружиной.
работа W, совершаемая человеком на эргометре, является произведением силы,
натяжение F ремня, умноженное на расстояние, на котором действует эта сила.
сила касается обода колеса. Таким образом, расстояние в 2π раз
радиус маховика r, умноженный на число оборотов N, совершаемых маховиком.
колесо. Имеем W = NF2πr. Для эргометра имеем из первого закона
термодинамика ΔU = ΔQ — ΔW. ΔW положителен, если система работает на своем
окружающей среды и является отрицательным, если в системе выполняется работа. Здесь ΔW
отрицательно, так как человек работает на эргометре. ΔW = -W. ΔQ – это
тепло, поступающее в систему или отводимое из нее. Имеем ∆U — ∆Q = NF2πr. Если мы
теплоотдачей системы в окружающую среду пренебречь и положить ΔQ = 0, тогда
увеличение тепловой энергии системы равно ΔU = NF2πr. Температура
маховика поэтому увеличивается на ΔT = ΔU/mc, где m — масса
маховика, c – его удельная теплоемкость.
Эргометр преобразует полезную работу в тепловую энергию. По анализу воздуха
выдыхаемый человеком, крутящим педали эргометра, скорость, с которой тело использует
можно измерить химическую энергию. Зная, сколько химической энергии в организме
использует в покое и сколько он использует при вращении педалей, эффективность тела в
можно определить превращение химической энергии в полезную работу.

---

Встроенный вопрос 1

Внутренняя энергия идеального газа не меняется.
изотермический процесс, так как внутренняя энергия зависит только от температуры.
Поэтому правильно ли говорить, что изотермический процесс — это то же самое, что и
адиабатический процесс для идеального газа? Поясните свой ответ.

Обсудите это со своими однокурсниками на дискуссионном форуме!

12.2 Первый закон термодинамики: тепловая энергия и работа

Цели обученияДавление, объем, температура и закон идеального газаРабота давления–объемаПервый закон термодинамикиРешение задач, связанных с первым законом термодинамикиПрактические задачиПроверьте свое понимание

Цели обучения

К концу этого раздела вы сможете выполнять следующее:

• Описать, как давление, объем и температура связаны друг с другом и работают на основе закона идеального газа
• Опишите работу давление-объем
• Опишите первый закон термодинамики словесно и математически
• Решить задачи, связанные с первым законом термодинамики

The first row reads Boltzmann constant, first law of thermodynamics, ideal gas law. The second row reads internal energy, pressure.»>

Основные термины раздела

Постоянная Больцмана	первый закон термодинамики	закон идеального газа
внутренняя энергия	давление

Давление, объем, температура и закон идеального газа

Перед рассмотрением первого закона термодинамики важно понять связь между давлением, объемом и температурой. Давление, P , определяется как

12.1P=FA,P=FA,

, где F — сила, приложенная к площади A , которая перпендикулярна силе.

В зависимости от области, на которую она воздействует, данная сила может иметь существенно различный эффект, как показано на рисунке 12.3.

Рис. 12.3 (а) Хотя человек, которого тыкают пальцем, может испытывать раздражение, сила не имеет длительного эффекта.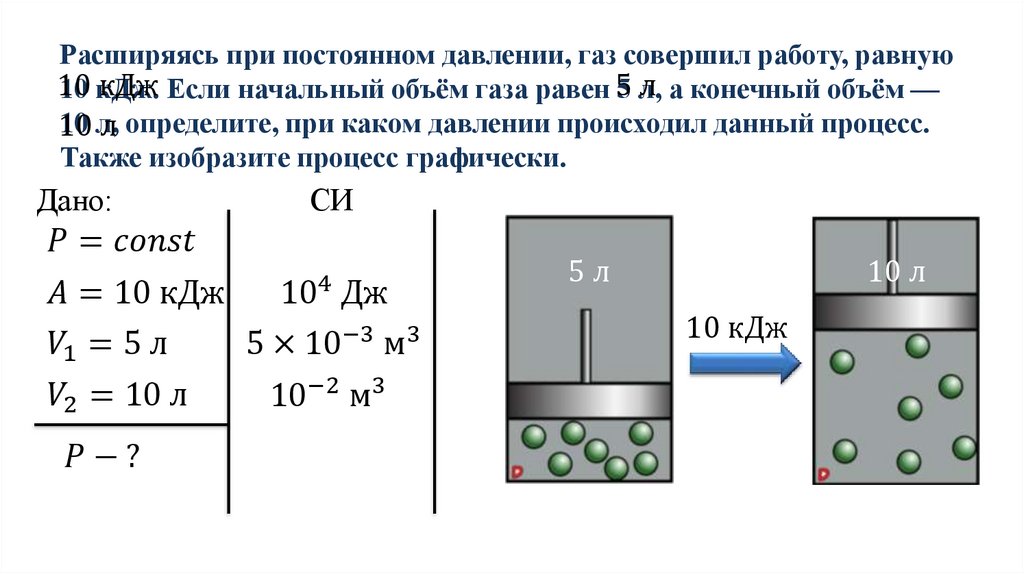 (b) Напротив, та же самая сила, приложенная к участку размером с острый конец иглы, достаточно велика, чтобы повредить кожу.

Единицей измерения давления в системе СИ является паскалей , где 1 Па=1 Н/м2,1 Па=1 Н/м2.

Давление определяется для всех состояний вещества, но особенно важно при обсуждении жидкостей (например, воздуха). Вы, наверное, слышали, что слово давление используется по отношению к крови (высокое или низкое кровяное давление) и по отношению к погоде (погодные системы высокого и низкого давления). Это только два из многих примеров давлений в жидкостях.

Связь между давлением, объемом и температурой идеального газа определяется законом идеального газа. Газ считается идеальным при низком давлении и достаточно высокой температуре, и силами между составляющими его частицами можно пренебречь. Закон идеального газа гласит, что

12.2PV=NkT.PV=NkT.

, где P — давление газа, V — занимаемый им объем, N — число частиц (атомов или молекул) в газе, а T — его абсолютная температура. Константа k называется постоянной Больцмана и имеет значение k=1,38×10−23 Дж/К, k=1,38×10−23 Дж/К. газовый закон. Вместо этого нам важно заметить из уравнения, что для данной массы газа верно следующее:

• Когда объем постоянный, давление прямо пропорционально температуре.
• Когда температура постоянна, давление обратно пропорционально объему.
• Когда давление постоянно, объем прямо пропорционален температуре.

Этот последний пункт описывает тепловое расширение — изменение размера или объема данной массы при изменении температуры. Что является основной причиной теплового расширения? Повышение температуры означает увеличение кинетической энергии отдельных атомов. Газы особенно подвержены тепловому расширению, хотя жидкости расширяются в меньшей степени при аналогичном повышении температуры, и даже твердые тела имеют незначительное расширение при более высоких температурах. Вот почему железнодорожные пути и мосты имеют компенсаторы, которые позволяют им свободно расширяться и сужаться при изменении температуры.

Чтобы получить некоторое представление о том, как связаны друг с другом давление, температура и объем газа, представьте, что происходит, когда вы накачиваете воздух в спущенную шину. Объем шины сначала увеличивается прямо пропорционально количеству впрыскиваемого воздуха без значительного увеличения давления в шине. Как только шина расширяется почти до своего полного размера, стенки ограничивают объемное расширение. Если вы продолжите накачивать воздух в шину (которая теперь имеет почти постоянный объем), давление будет увеличиваться с повышением температуры (см. рис. 12.4).

Рисунок 12.4 (а) Когда воздух нагнетается в спущенную шину, ее объем сначала увеличивается без значительного увеличения давления. (b) Когда шина заполнена до определенной точки, стенки шины сопротивляются дальнейшему расширению, и давление увеличивается по мере добавления воздуха. (c) Когда шина полностью накачана, давление в ней увеличивается с температурой.

Давление-Объем Работа

Работа давление-объем — это работа, совершаемая при сжатии или расширении жидкости. Всякий раз, когда происходит изменение объема, а внешнее давление остается постоянным, происходит работа давление-объем. При сжатии уменьшение объема увеличивает внутреннее давление в системе при совершении работы на система. Во время расширения (рис. 12.5) увеличение объема снижает внутреннее давление в системе, поскольку система выполняет работу .

Рис. 12.5 Расширение газа требует передачи энергии для поддержания постоянного давления. Поскольку давление постоянно, совершаемая работа равна P∆VP∆V.

Напомним, что формула работы W=Fd.W=Fd. Мы можем изменить определение давления, P=FA,P=FA, чтобы получить выражение для силы через давление.

12.3F=ПАФ=ПА

Подставляя это выражение для силы в определение работы, получаем

12.4W=PAd.W=PAd.

Поскольку площадь, умноженная на смещение, представляет собой изменение объема, W=PΔVW=PΔV , математическое выражение для работы «давление-объем» равно

.

12,5W=PΔV.W=PΔV.

Точно так же, как мы говорим, что работа — это сила, действующая на расстоянии, для жидкостей мы можем сказать, что работа — это давление, действующее через изменение объема. Для работы давление-объем давление аналогично силе, а объем аналогичен расстоянию в традиционном определении работы.

Watch Physics

Работа с расширением

В этом видео описывается работа с расширением (или работа давление-объем). Сал комбинирует уравнения W=P∆VW=P∆V и ∆U=Q-W∆U=Q-W, чтобы получить ∆U=Q-P∆V∆U=Q-P∆V.

Воспроизвести видео «Работа из дополнения».

Проверка захвата

Если объем системы увеличивается, а давление остается постоянным, является ли значение работы, выполненной системой Вт , положительной или отрицательной? Приведет ли это к увеличению или уменьшению внутренней энергии системы?

1. Положительный; внутренняя энергия уменьшится
2. Положительный; внутренняя энергия увеличится
3. Отрицательный; внутренняя энергия уменьшится
4. Отрицательный; внутренняя энергия увеличится

 

Первый закон термодинамики

Теплота ( Q ) и работа ( W ) — два способа добавления или удаления энергии из системы. Процессы очень разные. Тепло вызывается разницей температур, а работа связана с силой, действующей на расстоянии. Тем не менее, теплота и работа могут давать одинаковые результаты. Например, оба могут вызвать повышение температуры. Тепло передает энергию в систему, например, когда солнце нагревает воздух в велосипедной шине и повышает температуру воздуха. Точно так же над системой может совершаться работа, например, когда велосипедист накачивает воздух в шину. После того, как произошло повышение температуры, невозможно сказать, было ли оно вызвано теплом или работой. И теплота, и работа представляют собой энергию в пути — ни одна из них не хранится как таковая в системе. Однако оба могут изменять внутреннюю энергию, У , системы.

Внутренняя энергия представляет собой сумму кинетической и потенциальной энергий атомов и молекул системы. Ее можно разделить на множество подкатегорий, таких как тепловая и химическая энергия, и она зависит только от состояния системы (т. система.

Чтобы понять взаимосвязь между теплом, работой и внутренней энергией, мы используем первый закон термодинамики. Первый закон термодинамики применяет принцип сохранения энергии к системам, в которых теплота и работа являются методами передачи энергии в системы и из них. Его также можно использовать для описания того, как энергия, передаваемая теплом, преобразуется и снова передается за счет работы.

Советы для достижения успеха

Вспомним, что принцип сохранения энергии гласит, что энергия не может быть создана или уничтожена, но ее можно преобразовать из одной формы в другую.

Первый закон термодинамики гласит, что изменение внутренней энергии замкнутой системы равно чистой передаче тепла в систему минус сетевая работа, выполненная на систему. В форме уравнения первый закон термодинамики равен

.

12,6ΔU=Q−W.ΔU=Q−W.

Здесь ΔUΔU — изменение внутренней энергии , U , системы. Как показано на рис. 12.6, Q — это полезного тепла, переданного в систему , то есть Q — это сумма всех теплопередач в систему и из нее. W — чистая работа, выполненная системой — то есть Вт — это сумма всей работы, проделанной системой или над ней. По соглашению, если Q положительное, то в систему поступает чистый теплообмен; если Вт положительно, то система совершает чистую работу. Таким образом, положительное Q добавляет в систему энергию за счет теплоты, а положительное W забирает энергию у системы за счет работы. Обратите внимание, что если тепло передает в систему больше энергии, чем та, которая совершается за счет работы, разница запасается в виде внутренней энергии.

Рис. 12.6 Первый закон термодинамики — это принцип сохранения энергии, сформулированный для системы, где теплота и работа — это методы передачи энергии в систему и из нее. Q представляет чистую теплопередачу — это сумма всех передач энергии в виде тепла в систему и из нее. Q положителен для чистой теплопередачи в систему. WoutWout — это работа, проделанная на системой, а WinWin — это проделанная работа на система. Вт — это общая работа, выполненная в системе или на . W является положительным, когда на система выполняет больше работы, чем на на ней. Изменение внутренней энергии системы ΔUΔU связано с выделением тепла и работой согласно первому закону термодинамики: ΔU=Q−W. ΔU=Q−W.

Из этого также следует, что отрицательное Q указывает на то, что энергия передается от из системы за счет тепла и, таким образом, уменьшает внутреннюю энергию системы, тогда как отрицательное Вт это работа над системой, увеличивающая внутреннюю энергию.

Watch Physics

Первый закон термодинамики/Внутренняя энергия

В этом видео объясняется первый закон термодинамики, сохранение энергии и внутренняя энергия. В нем рассматривается пример преобразования энергии между кинетической энергией, потенциальной энергией и теплопередачей из-за сопротивления воздуха.

Воспроизвести видео «Первый закон термодинамики».

Проверка захвата

Рассмотрим пример подбрасывания мяча при наличии сопротивления воздуха. Что, по вашему мнению, произойдет с конечной скоростью и конечной кинетической энергией мяча по мере увеличения сопротивления воздуха? Почему?

1. Оба будут уменьшаться. Энергия передается воздуху за счет тепла из-за сопротивления воздуха.
2. Оба будут увеличиваться. Энергия передается от воздуха к мячу за счет сопротивления воздуха.
3. Конечная скорость увеличится, но конечная кинетическая энергия уменьшится. Энергия передается в виде тепла воздуху от мяча за счет сопротивления воздуха.
4. Конечная скорость уменьшится, но конечная кинетическая энергия увеличится. Энергия передается теплом от воздуха к мячу за счет сопротивления воздуха.

Смотреть физику

Подробнее о внутренней энергии

В этом видео более подробно рассказывается о внутренней энергии и о том, как использовать уравнение ΔU=Q−W.ΔU=Q−W. Обратите внимание, что Сал использует уравнение ΔU=Q+WΔU=Q+W , где Вт — это работа, проделанная над системой, тогда как мы используем W для представления работы, выполненной на системой.

Проиграть видео «Внутренняя энергия».

Проверка захвата

Если 5 Дж отводится теплом из системы, и система совершает 5 Дж работы, как изменится внутренняя энергия системы?

1. −10 Дж
2. 0Дж
3. 10Дж
4. 25Дж

 

Решение задач, связанных с первым законом термодинамики

Рабочий пример

Расчет изменения внутренней энергии

Предположим, что 40,00 Дж энергии передается системе в виде тепла, а система совершает 10,00 Дж работы. Далее из системы передается 25,00 Дж теплоты, а за счет работы над системой совершается 4,00 Дж. Каково чистое изменение внутренней энергии системы?

СТРАТЕГИЯ

Сначала необходимо рассчитать полезное тепло и чистую работу. Затем, используя первый закон термодинамики ΔU=Q−W, ΔU=Q−W, найдите изменение внутренней энергии.

Решение

Чистая теплота представляет собой передачу тепла в систему минус передачу тепла из системы, или

12,7Q=40,00 Дж-25,00 Дж=15,00 Дж. Q=40,00 Дж-25,00 Дж=15,00 Дж.

Полная работа – это работа, выполненная системой, за вычетом работы, выполненной системой, или

12,8 Вт=10,00 Дж−4,00 Дж=6,00 Дж. Вт=10,00 Дж−4,00 Дж=6,00 Дж.

Изменение внутренней энергии определяется первым законом термодинамики.

12,9ΔU=Q−W=15,00 Дж−6,00 Дж=9,00 ДжΔU=Q−W=15,00 Дж−6,00 Дж=9.00 Дж

Обсуждение

Другой способ решения этой задачи состоит в том, чтобы найти изменение внутренней энергии для каждого из двух шагов в отдельности, а затем сложить два изменения, чтобы получить общее изменение внутренней энергии. Этот подход будет выглядеть следующим образом:

Для 40,00 Дж тепла и 10,00 Дж работы изменение внутренней энергии равно W1=40,00 Дж−10,00 Дж=30,00 Дж.

Для 25,00 Дж тепловыделения и 4,00 Дж работы изменения внутренней энергии равно

12,11ΔU2=Q2-W2=-25,00 Дж-(-4,00 Дж)=-21,00 Дж. ΔU2=Q2-W2=-25,00 Дж-(-4,00 Дж)=-21,00 Дж.

Общее изменение равно

12,12ΔU=ΔU1+ΔU2=30,00 Дж+(−21,00 Дж)=9,00 Дж. ΔU=ΔU1+ΔU2=30,00 Дж+(−21,00 Дж)=9,00 Дж. на ступени изменение внутренней энергии одинаково.

Рабочий пример

Расчет изменения внутренней энергии: одно и то же изменение

U производится двумя разными процессами

Как изменится внутренняя энергия системы, если в общей сложности 150,00 Дж передано теплотой от системы и 159,00 Дж произведена работой над системой?

СТРАТЕГИЯ

Чистое тепло и работа уже даны, поэтому просто используйте эти значения в уравнении ΔU=Q−W.ΔU=Q−W.

Решение

Здесь чистая теплота и полная работа задаются непосредственно как Q=-150,00 Дж и W=-159,00 Дж, Q=-150,00 Дж и W=-159,00 Дж, так что

12,13ΔU=Q- Вт=-150,00 Дж-(-1590,00 Дж)=9,00 Дж.ΔU=Q-W=-150,00 Дж-(-159,00 Дж)=9,00 Дж.

Обсуждение

Рис. 12.8. Два разных процесса вызывают одно и то же изменение в системе. (а) Всего в систему поступает 15,00 Дж теплоты, а работа отнимает всего 6,00 Дж. Изменение внутренней энергии равно ΔU = Q – W = 9,00 Дж. (б) Теплопередачей отводится 150,00 Дж из система при работе вкладывает в нее 159,00 Дж, производя увеличение внутренней энергии на 9,00 Дж. Если система начинается в одном и том же состоянии в (а) и (б), она в конечном итоге окажется в одном и том же конечном состоянии в любом случае — ее конечное состояние связано с внутренней энергией, а не с тем, как эта энергия была приобретена.

Совершенно другой процесс во втором рабочем примере приводит к тому же изменению внутренней энергии на 9,00 Дж, что и в первом рабочем примере. Обратите внимание, что изменение в системе в обеих частях связано с ΔUΔU, а не с отдельными задействованными Q или W . В обеих задачах система оказывается в том же состоянии , что и . Обратите внимание, что, как обычно, на рис. 12.8 выше WoutWout — это работа, выполненная 90 299 на 90 300 системе, а WinWin — это работа, выполненная 90 299 на 90 300 системе.

 

Практические задачи

Какова работа давления и объема, совершаемая системой, если давление 20 Па вызывает изменение объема 3,0 м3?

1. 0,15 Дж
2. 6,7 Дж
3. 23Дж
4. 60Дж

Какова чистая теплота, выделяемая системой, если 25 Дж передается теплом в систему, а 45 Дж передается из нее?

1. −70 Дж
2. −20 Дж
3. 20Дж
4. 70Дж

Проверьте свое понимание

Упражнение 3

Что такое давление?

1. Давление равно силе, деленной на длину.
2. Давление — это сила, деленная на площадь.
3. Давление равно силе, деленной на объем.
4. Давление равно силе, деленной на массу.

Упражнение 4

Что такое единица СИ для давления?

1. паскаль или Н/м ³
2. кулон
3. ньютона
4. паскаль или Н/м ²

Упражнение 5

Что такое работа давление-объем?

1. Работа, совершаемая при сжатии или расширении жидкости.
2. Это работа, совершаемая силой над объектом для получения определенного перемещения.
3. Это работа, совершаемая поверхностными молекулами жидкости.
4. Это работа, которую совершают высокоэнергетические молекулы жидкости.

Упражнение 6

Когда считается, что работа давление-объем совершается В системе?

1. При увеличении как объема, так и внутреннего давления.
2. При снижении как объема, так и внутреннего давления.
3. При снижении объема и повышении внутреннего давления.
4. При увеличении объема и снижении внутреннего давления.

Упражнение 7

Каковы способы добавления или удаления энергии из системы?

1. Передача энергии с помощью тепла — единственный способ добавления энергии в систему или удаления энергии из нее.
2. Выполнение работы сжатия — единственный способ добавить энергию в систему или убрать ее из системы.
3. Выполнение работ по расширению — единственный способ добавить или убрать энергию из системы.
4. Передача энергии с помощью тепла или выполнения работы — это способы добавления энергии в систему или удаления энергии из нее.

Упражнение 8

Что такое внутренняя энергия?

1. Это сумма кинетических энергий атомов и молекул системы.