Содержание
Режимы работы (двигательный, генераторный, торможение) двигателя постоянного тока ДПТ
В двигателях параллельного возбуждения при неизменном токе в обмотке возбуждения (IВ = const) магнитный поток изменяется при нагрузке весьма незначительно, поэтому с некоторым приближением можно принять Ф = const. В этом случае электромагнитный момент [см. (25.24)] пропорционален току в цепи якоря и механическая характеристика n = f(M) может быть представлена зависимостью n = f(Ia) (рис. 29.8). Если эту характеристику продолжить в обе стороны за пределы осей координат (прямая 1), то можно показать, что электрическая машина в зависимости от величины и знака внешнего момента, действующего на ее вал со стороны связанного с ним механизма, может работать в трех режимах: двигательном, тормозном и генераторном.
При работе двигателя без нагрузки ток в цепи якоря Ia0небольшой. При этом частота вращения n = n0 (точка А). Затем с появлением на валу двигателя нагрузочного момента, противодействующего вращающему, ток в цепи якоря возрастает, а частота вращения уменьшается. Если увеличить противодействующий момент до значения, при котором якорь двигателя остановится (точка В), то ЭДС Ea = 0 и ток двигателя достигает значения
Затем с появлением на валу двигателя нагрузочного момента, противодействующего вращающему, ток в цепи якоря возрастает, а частота вращения уменьшается. Если увеличить противодействующий момент до значения, при котором якорь двигателя остановится (точка В), то ЭДС Ea = 0 и ток двигателя достигает значения
Если двигатель применяют для привода механизма, нагрузочный момент которого может быть больше вращающегося (например, привод барабана, на который наматывается трос с грузом), то при последующем увеличении нагрузочного момента этого механизма якорь машины вновь начнет вращаться, но теперь уже в другую сторону. Теперь момент, действующий на вал электрической машины со стороны нагрузочного механизма, будет вращающим, а электромагнитный момент машины — тормозящим, т. е. электрическая машина перейдет в тормозной режим. При работе машины в этом режиме ЭДС якоря действует согласованно с напряжением, т. е.
.
При использовании машины в тормозном режиме необходимо принять меры для ограничения тока якоря. С этой целью в цепь якоря включают добавочное сопротивление, величина которого обеспечивает получение искусственной характеристики двигателя, пересекающейся с осью абсцисс при токе якоря (штриховая прямая).
С этой целью в цепь якоря включают добавочное сопротивление, величина которого обеспечивает получение искусственной характеристики двигателя, пересекающейся с осью абсцисс при токе якоря (штриховая прямая).
Если при работе двигателя в режиме х.х. к его валу приложить момент, направленный в сторону вращения якоря, то частота вращения, а следовательно, и ЭДС Ea начнут возрастать. Когда ЭДС Ea = U, машина не будет потреблять тока из сети (точка С) и частота вращения якоря достигает значения, называемого пограничной частотой вращения nxx
Рис. 29.8. Режимы работы машины постоянного тока:
1 — с параллельным (независимым) возбуждением;
2 — со смешанным возбуждением;
3 — с последовательным возбуждением
При дальнейшем увеличении внешнего момента на валу машины ЭДС Ea станет больше напряжения, а в цепи якоря опять возникает ток, но другого направления. При этом машина перейдет в генераторный режим: механическая энергия, затрачиваемая на вращение якоря, будет преобразовываться в электрическую и поступать в сеть.
При этом машина перейдет в генераторный режим: механическая энергия, затрачиваемая на вращение якоря, будет преобразовываться в электрическую и поступать в сеть.
Перевод машины из двигательного в генераторный режим используют для торможения двигателя, так как в генераторном режиме электромагнитный момент является тормозящим (рекуперативное торможение).
19.10.2014
Электрические машины,Машины постоянного тока,Двигатель постоянного тока,ДПТ,ДПТ НВ,Режимы работы электродвигателей
Электрические машины постоянного тока
Принцип действия двигателя постоянного тока
Хотя в современном электроприводе преобладают машины переменного тока (асинхронные электродвигатели), двигатели постоянного тока все еще используют и не только в предыдущих решениях.
Устройство простейшего электродвигателя постоянного тока
На рисунке ниже приведена простейшая машина постоянного тока:
Рисунок 1
Схематическое отображение электродвигателя постоянного тока в осевом направлении показано ниже:
Рисунок 2
Неподвижная часть двигателя постоянного тока называется индуктором или статором.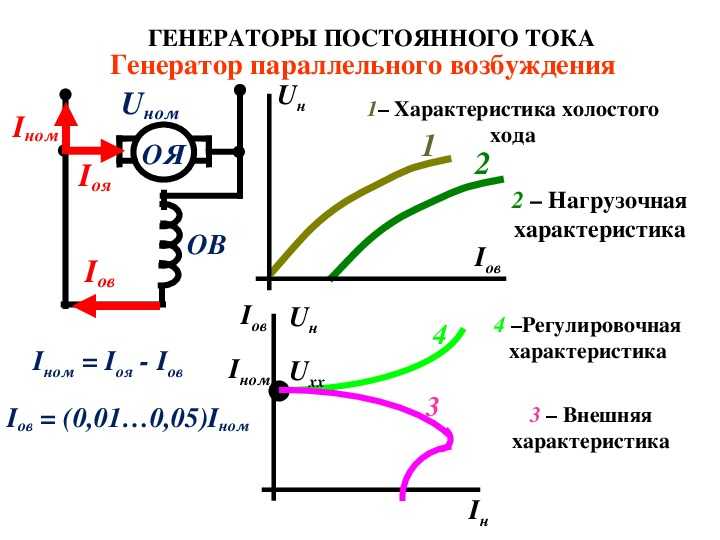 Состоит он из полюсов и круглого стального ярма, к которому крепятся полюса. Главным назначением индуктора является генерация постоянного (основного) магнитного потока машины. Индуктор простейшей машины, отображенный выше, имеет два полюса 1 (ярмо индуктора не показано).
Состоит он из полюсов и круглого стального ярма, к которому крепятся полюса. Главным назначением индуктора является генерация постоянного (основного) магнитного потока машины. Индуктор простейшей машины, отображенный выше, имеет два полюса 1 (ярмо индуктора не показано).
Вращающаяся часть машины состоит из цилиндрического якоря 2, укрепленного на валу, и коллектора 3. Якорь состоит из набранного из листов электротехнической стали сердечника и обмотки, укрепленной на сердечника якоря. Обмотка якоря в показанном на рисунке простейшем двигателе имеет один виток. Концы витка соединяются с изолированными
от вала медными пластинами коллектора, число которых в рассматриваемом случае равно двум. Две неподвижные щетки 4 налегают на коллектор. С помощью щеток обмотка якоря соединяется с внешней цепью.
Основной магнитный поток в электродвигателях постоянного тока создается обмоткой возбуждения, которая запитывается постоянным напряжением и располагается на сердечниках полюсов. Магнитный поток «идет» через якорь от северного полюса N к южному полюсу S, а от него через ярмо снова к северному. Ярмо и сердечники полюсов также изготавливаются из ферромагнитных материалов.
Ярмо и сердечники полюсов также изготавливаются из ферромагнитных материалов.
Рисунок 3
Генераторный режим двигателя постоянного тока
Предположим, что в нашем случае якорь электрической машины (рисунок 1 и рисунок 2 а)) движется по часовой стрелке. Тогда в проводниках обмотки якоря будет индуцироваться ЭДС, направление которой можно определить используя правило правой руки (рисунок 3 а)), что и показано на рисунках 1 и 2а). Поскольку поток полюсов является неизменным, то ЭДС сможет индуцироваться только в случае вращения якоря электродвигателя постоянного тока и называется ЭДС вращения.
Величина индуктируемой в проводнике обмотки якоря ЭДС будет равна:
Где: B – магнитная индукция воздушного зазора между якорем и полюсом в месте расположения проводника; l – активная длина проводника с током, то есть это длина, на протяжении которой проводник расположен в магнитном поле; υ – скорость движения проводника в магнитном поле (линейная).
В обоих проводниках из-за симметрии индуктируются одинаковые ЭДС, которые складываются по контуру витка, и поэтому полная ЭДС якоря двигателя постоянного тока будет равна:
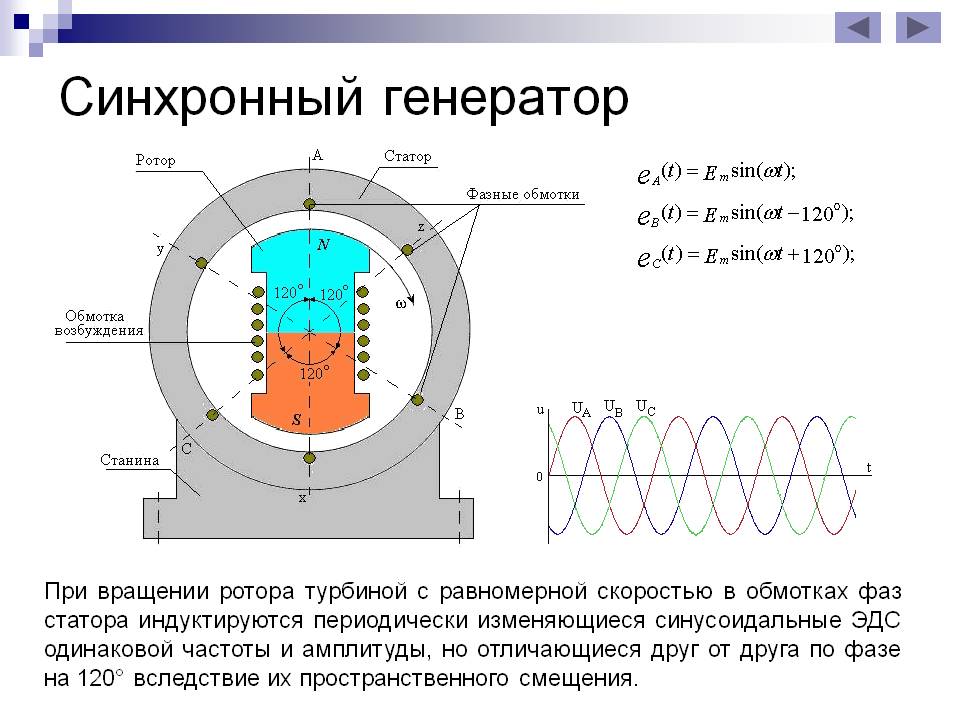
ЭДС Еа является величиной переменной, так как проводники якорной обмотки попеременно проходят под южным и северным полюсами, в результате чего направление ЭДС в проводниках изменяется. Кривая ЭДС проводника по форме повторяет кривую распределения индукции B вдоль воздушного зазора в зависимости от времени t (рисунок 4 а)).
Кривая ЭДС проводника по форме повторяет кривую распределения индукции B вдоль воздушного зазора в зависимости от времени t (рисунок 4 а)).
Рисунок 4
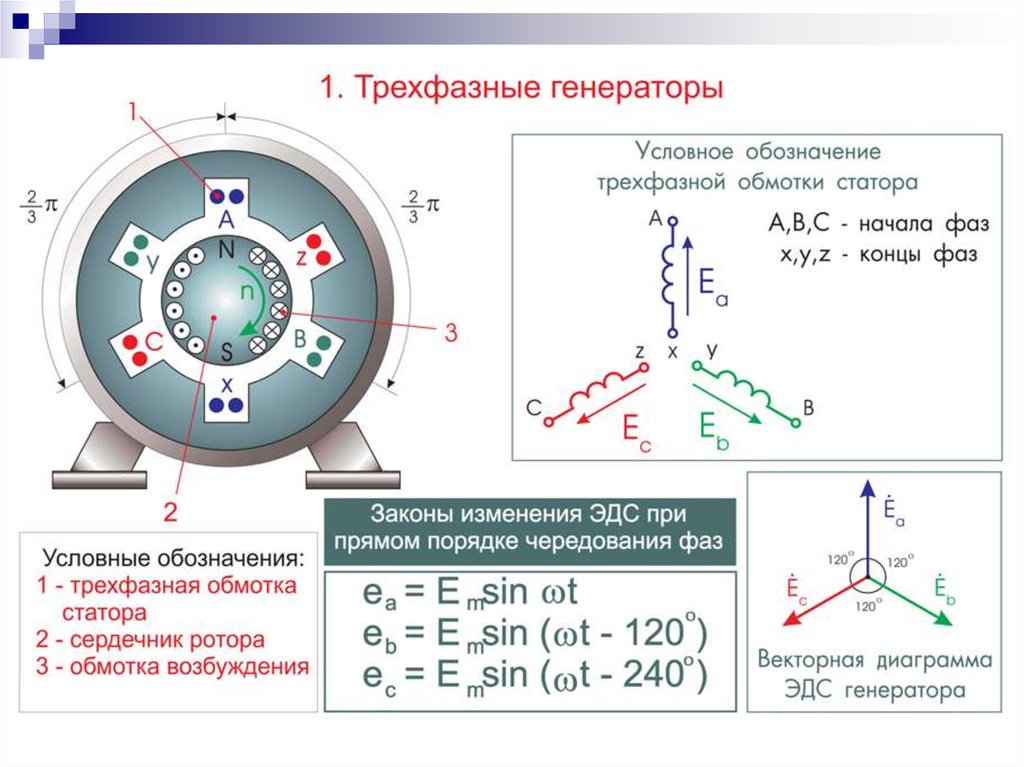
В двухполюсной машине частота ЭДС f равна скорости вращения якоря n, выраженной в оборотах в секунду: f = n. А вот в общем случае, когда двигатель постоянного тока имеет p пар полюсов с чередующеюся полярностью:
Обмотка якоря с помощью щеток замыкается через внешнюю цепь и, соответственно, в этой цепи начинает протекать ток Ia. В обмотке якоря будет протекать переменный ток и его кривая аналогична кривой ЭДС (рисунок 4). Однако во внешней цепи протекает постоянный ток, это объясняется действием коллектора. При повороте коллектора и якоря на 900 (рисунок 1) происходит смена коллекторных пластин под щетками и изменение направления ЭДС в проводниках. Вследствие чего под верхней щеткой всегда будет находиться пластина соединенная с проводником северного полюса, а под нижней щеткой пластина соединенная с проводником южного полюса. В результате такого соединения направление тока и полярность щеток для внешней цепи остаются неизменными.
В результате такого соединения направление тока и полярность щеток для внешней цепи остаются неизменными.
Таким образом, коллекторный узел является механическим
выпрямителем, который преобразовывает переменный ток якоря в постоянный ток внешней цепи.
Изменив знак второго полупериода кривой на рисунке 4 а), получим форму кривой напряжения и тока внешней цепи (рисунок 4 б)). Пульсирующий ток внешней цепи малопригоден для практических целей. Для избавления от пульсаций применяют более сложные по своему устройству коллектор и якорь двигателя постоянного напряжения, однако основные свойства машины постоянного тока могут быть рассмотрены на примере рассматриваемого нами простейшего двигателя постоянного тока.
Постоянное напряжение на зажимах якоря генератора будет меньше Еа на величину падения напряжения в сопротивлении обмотки якоря ra:
Поскольку проводники якоря находятся в магнитном поле и через них протекает ток Ia, то на них будут действовать электромагнитные силы (рисунки 1, 2 а)):
Направление этих сил определяют с помощью правила левой руки (рисунок 3 б)). Данные силы и создают электромагнитный вращающий момент, который будет равен:
Данные силы и создают электромагнитный вращающий момент, который будет равен:
Здесь Da это диаметр якоря машины. Из рисунков 1-2 а) можно увидеть, что в генераторном режиме данный момент действует против направления вращения якоря и является тормозящим.
Режим двигателя
Простейший двигатель постоянного напряжения может работать не только в режиме генератора, но и в режиме двигателя, если к обмотке якоря подвести напряжение от внешнего источника. На проводники обмотки якоря будут действовать электромагнитные силы Fпр в результате чего создается электромагнитный момент Мэм. Как и для режима генератора, величины Fпр и Мэм вычисляются из равенств (4) и (5). При достаточной величине Мэм якорь
электрической машины придет в движение и будет развивать механическую мощность. Момент Мэм в таком случае будет являться движущим, и приводить в движение якорь в направлении вращения.
Если мы хотим, чтобы при той же полярности полюсов направление вращения генератора (рисунок 1-2 а)) и двигателя (рисунок 1-2 б)) были одинаковы, то направление действия Мэм, а также тока Iа у электродвигателя постоянного напряжения должны быть обратными по сравнению с генератором (рисунок 1-2 б)).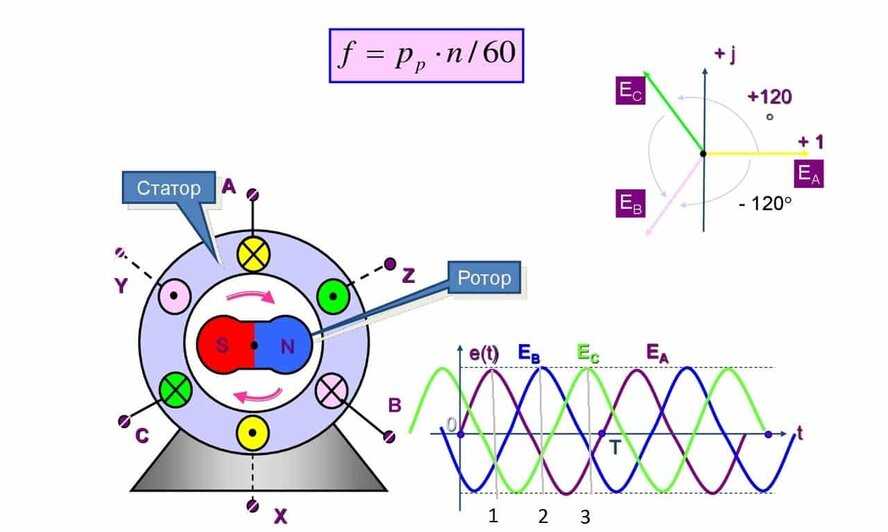
Коллектор превращает постоянный ток из внешней цепи в переменный ток якоря в режиме двигателя, что смело можно назвать механическим
инвертором тока.
Проводники обмотки якоря электрической машины тоже вращаются в магнитном поле, из-за чего в обмотке якоря двигателя индуцируется ЭДС Еа, величину которой можно определить из формулы (1). В электродвигателе направление этой ЭДС (рисунок 1-2 б)) такое же, как и в генераторе (рисунок 1-2 а)). Таким образом, ЭДС якоря Еа в двигателе направлена против тока Ia и приложенного напряжения Ua к зажимам якоря. Поэтому довольно часто ЭДС якоря называют противоэлектродвижущей силой.
Напряжение, приложенное к якорю электрической машины, уравновешивается падением напряжения на обмотке якоря и ЭДС Еа:
Если сравнить уравнения (3) и (6) можно увидеть одну очень важную особенность – в режиме генератора Ua < Ea, в режиме двигателя Ua > Ea.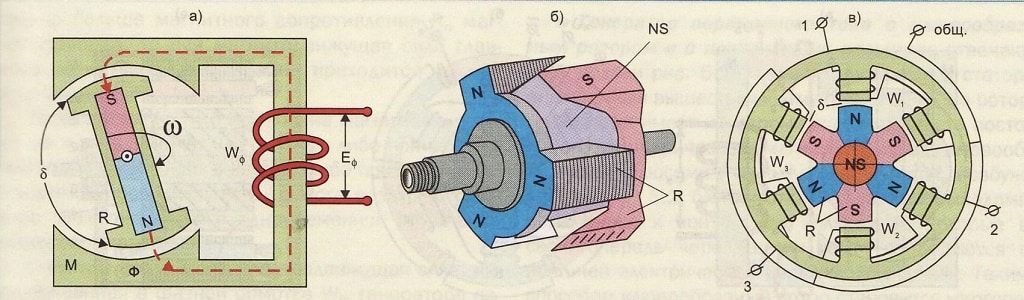
Принцип обратимости электродвигателя
Из изложенных выше формул и описаний следует вывод, что каждая машина постоянного тока (и не только постоянного) может работать как в режиме двигателя, так и в режиме генератора. Такое свойство имеют все электрические машины, и оно носит название обратимость.
Для перехода двигателя постоянного тока из режима генератора в режим двигателя и обратно при неизменной полярности щеток и полюсов, а также при неизменном направлении вращения необходимо всего лишь изменить направление тока в обмотке якоря (что сейчас легко делается с помощью тиристорных преобразователей и других управляемых выпрямителей).
В современных системах такой переход осуществляется автоматически.
Преобразование энергии в двигателе постоянного тока
На рисунке 5 показаны направления действия электрических и механических величин в якоре двигателя и генератора постоянного тока.
Рисунок 5
В соответствии с первым законом Ньютона в применении к вращающемуся телу, действующие на это тело тормозящие и вращающие моменты уравновешивают друг друга. Поэтому в установившемся режиме работы генератора электромагнитный момент будет равен:
Поэтому в установившемся режиме работы генератора электромагнитный момент будет равен:
Здесь Мв – момент на валу генератора, который развивает приводной двигатель, Мтр – момент трения на коллекторе электрической машины и в подшипниках, а также сопротивления воздуха, Мс – тормозящий момент, вызываемый потерями на вихревые токи и гистерезис в сердечнике якоря. Данные потери мощности возникают вследствие вращения сердечника якоря в неподвижном магнитном поле
полюсов. Электромагнитные силы, возникающие при вращении ротора электрической машины постоянного тока, оказывают на ротор тормозящее действие и в таком представлении ведут себя подобно силам трения.
Электромагнитный момент двигателя постоянного тока в установившемся режиме работы будет равен:
Здесь Мв – развиваемый рабочей машиной (насос, тележка, кран…) тормозящий момент на валу электродвигателя.
В режиме генератора электромагнитный момент Мэм является движущем, а в режиме двигателя наоборот, тормозящим. При этом в обеих случаях Мв и Мэм противоположны по направлению.
При этом в обеих случаях Мв и Мэм противоположны по направлению.
Электромагнитная мощность Рэм, развиваемая электромагнитным моментом Мэм, будет равна:
Где:
В данном случае ω – это угловая скорость машины постоянного тока.
Подставив значения Мэм и ω в формулу (8) из формул (5) и (9) и учтем, что линейная скорость на окружности якоря:
Или же на основании выражения (1):
Под действием тока Ia и ЭДС Еа в обмотке якоря развивается внутренняя электрическая мощность:
Исходя из формул (10) и (11), Рэм = Ра, то есть внутренняя электрическая мощность якоря равна электромагнитной мощности, которую развивает электромагнитный момент, что довольно наглядно демонстрирует процесс преобразования электрической энергии в механическую в режиме двигателя, и процесс преобразования механической энергии в электрическую в режиме генератора.
Умножив соотношения (3) и (6) на Ia получим следующие выражения для генератора:
Левые части приведенных выше формул представляют собой электрическую мощность на зажимах якоря, первые члены первых частей электромагнитную мощность все того же якоря, и последние выражение мощность потерь в якорной цепи.
Хотя полученные формулы приведены для простейшей машины постоянного тока (рисунок 1), они все равно будут действовать и в более сложной обмотке якоря, так как моменты отдельных проводников и ЭДС складываются. Данные формулы являются выражением закона сохранения энергии и отражают процесс преобразования энергии в машине постоянного тока.
Подведем итоги
Развиваемая на валу генератора приводным электродвигателем механическая мощность, за вычетом магнитных и механических потерь, превращается в электрическую мощность (с вычетом потерь в обмотке) и передается во внешнюю цепь. В режиме двигателя электрическая мощность, подающаяся на якорь электрической машины, частично расходуется на потери, а остальная ее часть преобразуется в мощность электромагнитного поля – потом в механическую мощность, которая после вычета потерь в стали якоря и сил трения с помощью вала передается рабочей машине (лифт, станок, тяговый привод электротранспорта и другие).
Общие закономерности превращения энергии для двигателей постоянного тока также актуальны и для двигателей переменного
тока.
13.7: Электрогенераторы и обратная ЭДС
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 4433
- OpenStax
- OpenStax
Цели обучения
К концу этого раздела вы сможете:
- Объяснить, как работает электрический генератор
- Определить ЭДС индукции в петле в любой момент времени, вращающейся с постоянной скоростью в магнитном поле
- Показать, что вращающиеся катушки имеют ЭДС индукции; в двигателях это называется обратной ЭДС, потому что она противодействует входу ЭДС двигателя
Множество важных явлений и устройств можно понять с помощью закона Фарадея. В этом разделе мы рассмотрим два из них. 9о\)) за 15,0 мс. Круглая катушка из 200 витков имеет радиус 5,00 см и находится в однородном магнитном поле 0,80 Тл. Какая ЭДС наведена?
В этом разделе мы рассмотрим два из них. 9о\)) за 15,0 мс. Круглая катушка из 200 витков имеет радиус 5,00 см и находится в однородном магнитном поле 0,80 Тл. Какая ЭДС наведена?
Рисунок \(\PageIndex{1}\): Когда эта генераторная катушка поворачивается на четверть оборота, магнитный поток \(\Phi_m\) изменяется от своего максимума до нуля, индуцируя ЭДС.
Стратегия
Для нахождения ЭДС индукции используется закон индукции Фарадея: в примере 13.4.3. Согласно диаграмме, проекция вектора нормали к поверхности \(\hat{n}\) на магнитное поле изначально равна \(cos\, \theta\), и это вставляется определением скалярного произведения. Величина магнитного поля и площадь петли фиксируются во времени, что упрощает интегрирование. ЭДС индукции записывается по закону Фарадея: 9{-3} s} = 131 \, V.\]
Значение
Это практическое среднее значение, аналогичное 120 В, используемому в домашнем хозяйстве.
ЭДС, рассчитанная в примере \(\PageIndex{1}\), представляет собой среднее значение за одну четвертую оборота. Чему равна ЭДС в каждый момент времени? Оно изменяется в зависимости от угла между магнитным полем и перпендикуляром к катушке. Мы можем получить выражение для ЭДС как функции времени, рассматривая ЭДС движения на вращающейся прямоугольной катушке шириной w и высота l в однородном магнитном поле, как показано на рисунке \(\PageIndex{2}\).
Чему равна ЭДС в каждый момент времени? Оно изменяется в зависимости от угла между магнитным полем и перпендикуляром к катушке. Мы можем получить выражение для ЭДС как функции времени, рассматривая ЭДС движения на вращающейся прямоугольной катушке шириной w и высота l в однородном магнитном поле, как показано на рисунке \(\PageIndex{2}\).
Рисунок \(\PageIndex{2}\): Генератор с одной прямоугольной катушкой, вращающейся с постоянной угловой скоростью в однородном магнитном поле, создает ЭДС, которая изменяется синусоидально во времени. Обратите внимание, что генератор похож на двигатель, за исключением того, что вал вращается для создания тока, а не наоборот.
Заряды в проводах петли испытывают магнитную силу, потому что они движутся в магнитном поле. На заряды в вертикальных проводах действуют силы, параллельные проводу, вызывающие токи. Но находящиеся в верхнем и нижнем сегментах ощущают силу, перпендикулярную проводу, которая не вызывает тока. Таким образом, мы можем найти ЭДС индукции, рассматривая только боковые провода. ЭДС движения равна \(\epsilon = Blv\), где скорость v перпендикулярно магнитному полю B . Здесь скорость составляет угол \(\theta\) с B , так что ее составляющая, перпендикулярная B , равна v sin \(\theta\) (см. рисунок \(\PageIndex{2}\) ). Таким образом, в этом случае ЭДС, индуцированная с каждой стороны, равна \(\эпсилон = Blv \, sin \, \theta\), и они имеют одинаковое направление. Полная ЭДС вокруг контура тогда равна
Таким образом, мы можем найти ЭДС индукции, рассматривая только боковые провода. ЭДС движения равна \(\epsilon = Blv\), где скорость v перпендикулярно магнитному полю B . Здесь скорость составляет угол \(\theta\) с B , так что ее составляющая, перпендикулярная B , равна v sin \(\theta\) (см. рисунок \(\PageIndex{2}\) ). Таким образом, в этом случае ЭДС, индуцированная с каждой стороны, равна \(\эпсилон = Blv \, sin \, \theta\), и они имеют одинаковое направление. Полная ЭДС вокруг контура тогда равна
\[\epsilon = 2 Blv \, sin \, \theta.\]
Это выражение верно, но оно не дает ЭДС как функцию времени. Чтобы найти зависимость ЭДС от времени, предположим, что катушка вращается с постоянной угловой скоростью \(\omega\). Угол \(\theta\) связан с угловой скоростью соотношением \(\theta = \omega t\), так что \[\epsilon = 2 Blv \, sin (\omega t).\]
Теперь линейная скорость v связана с угловой скоростью \(\omega\) соотношением \(v = r\omega\). Здесь \(r = \omega/2\), так что \(v = (\omega/2)\omega\), и
Здесь \(r = \omega/2\), так что \(v = (\omega/2)\omega\), и
\[\epsilon = 2Bl \frac{\omega}{2} \omega \, sin \, \omega t = (l\omega) Bw \, sin \, \omega t.\]
Учитывая, что площадь петли равна \(A = l\omega\), и учитывая N витков, находим, что
\[\epsilon = NBAw \, sin \, (\omega t).\]
Это ЭДС наведенная в катушке генератора N витков и площадь A вращающихся с постоянной угловой скоростью \(ω\) в однородном магнитном поле B . Это также может быть выражено как
\[\epsilon = \epsilon_0 \, sin \, \omega t,\], где
\[\epsilon_0 = NAB\omega\]
— пиковая ЭДС, поскольку максимальное значение из \(sin (\omega t) = 1\). Обратите внимание, что частота колебаний равна \(f = \omega/2\pi\), а период равен \(T = 1/f = 2\pi /\omega\). На рисунке \(\PageIndex{3}\) показан график ЭДС как функции времени, и теперь кажется разумным, что переменное напряжение является синусоидальным.
Рисунок \(\PageIndex{3}\): ЭДС генератора передается на лампочку с показанной системой колец и щеток. На графике показана ЭДС генератора как функция времени, где \(\epsilon_0\) — пиковая ЭДС. Период равен \(T = 1/f = 2\pi /\omega\), где f — частота.
Тот факт, что пиковая ЭДС равна \(\epsilon_0 = NBA\omega\), имеет смысл. Чем больше количество катушек, тем больше их площадь, и чем сильнее поле, тем больше выходное напряжение. Интересно, что чем быстрее раскручивается генератор (больше ω), тем больше ЭДС. Это заметно на велосипедных генераторах, по крайней мере, на более дешевых.
На рисунке \(\PageIndex{4}\) показана схема, с помощью которой генератор может производить импульсы постоянного тока. Более сложное расположение нескольких катушек и разъемных колец может обеспечить более плавный постоянный ток, хотя для создания постоянного тока без пульсаций обычно используются электронные, а не механические средства.
Рисунок \(\PageIndex{4}\): Разъемные кольца, называемые коммутаторами, в этой конфигурации создают импульсную ЭДС постоянного тока.
В реальной жизни электрические генераторы сильно отличаются от рисунков в этом разделе, но принцип тот же. Источником механической энергии, вращающей катушку, может быть падающая вода (гидроэнергия), пар, образующийся при сжигании ископаемого топлива, или кинетическая энергия ветра. На рисунке \(\PageIndex{5}\) показан вид паровой турбины в разрезе; пар движется по лопастям, соединенным с валом, который вращает катушку внутри генератора. Генерация электрической энергии из механической энергии является основным принципом всей энергии, которая передается через наши электрические сети в наши дома.
Рисунок \(\PageIndex{5}\): Паровая турбина/генератор. Пар, образующийся при сжигании угля, воздействует на лопатки турбины, вращая вал, соединенный с генератором.
Генераторы, показанные в этом разделе, очень похожи на двигатели, показанные ранее. Это не случайно. Фактически двигатель становится генератором, когда его вал вращается. Некоторые ранние автомобили использовали свой стартер в качестве генератора. В следующем разделе мы дополнительно исследуем действие двигателя в качестве генератора.
В следующем разделе мы дополнительно исследуем действие двигателя в качестве генератора.
Back Emf
Генераторы преобразуют механическую энергию в электрическую, тогда как двигатели преобразуют электрическую энергию в механическую. Таким образом, неудивительно, что двигатели и генераторы имеют одинаковую общую конструкцию. Двигатель работает, посылая ток через петлю провода, расположенную в магнитном поле. В результате магнитное поле оказывает крутящий момент на петлю. Это вращает вал, тем самым извлекая механическую работу из электрического тока, подаваемого изначально. (Обратитесь к разделу «Сила и крутящий момент в токовой петле» для обсуждения двигателей, которые помогут вам больше узнать о них, прежде чем продолжить.)
Когда катушка двигателя вращается, магнитный поток через катушку изменяется, и возникает ЭДС (в соответствии с законом Фарадея). Таким образом, двигатель действует как генератор всякий раз, когда его катушка вращается. Это происходит независимо от того, вращается ли вал от внешнего источника, например, от ременной передачи, или от действия самого двигателя. То есть, когда двигатель совершает работу и его вал вращается, возникает ЭДС. Закон Ленца говорит нам, что ЭДС противодействует любому изменению, так что входная ЭДС, питающая двигатель, противостоит ЭДС, создаваемой самим двигателем, называемой 9.0048 противоЭДС двигателя (рисунок \(\PageIndex{6}\)).
То есть, когда двигатель совершает работу и его вал вращается, возникает ЭДС. Закон Ленца говорит нам, что ЭДС противодействует любому изменению, так что входная ЭДС, питающая двигатель, противостоит ЭДС, создаваемой самим двигателем, называемой 9.0048 противоЭДС двигателя (рисунок \(\PageIndex{6}\)).
Рисунок \(\PageIndex{6}\): Катушка двигателя постоянного тока представлена на этой схеме в виде резистора. Обратная ЭДС представлена как переменная ЭДС, которая противодействует ЭДС, приводящей в движение двигатель. Обратная ЭДС равна нулю, когда двигатель не вращается, и увеличивается пропорционально угловой скорости двигателя.
Выходная мощность генератора двигателя представляет собой разницу между напряжением питания и противо-ЭДС. Обратная ЭДС равна нулю при первом включении двигателя, а это означает, что катушка получает полное управляющее напряжение, а двигатель потребляет максимальный ток, когда он включен, но не вращается. По мере того, как двигатель вращается быстрее, обратная ЭДС растет, всегда противодействуя ЭДС возбуждения, и снижает как напряжение на катушке, так и количество потребляемого ею тока. Этот эффект заметен во многих распространенных ситуациях. При первом включении пылесоса, холодильника или стиральной машины свет в той же цепи ненадолго гаснет из-за 92R)\), возможно, даже выжечь. С другой стороны, если на двигатель нет механической нагрузки, он увеличивает свою угловую скорость ω до тех пор, пока противо-ЭДС не станет почти равной движущей ЭДС. Тогда двигатель использует ровно столько энергии, сколько необходимо для преодоления трения.
Этот эффект заметен во многих распространенных ситуациях. При первом включении пылесоса, холодильника или стиральной машины свет в той же цепи ненадолго гаснет из-за 92R)\), возможно, даже выжечь. С другой стороны, если на двигатель нет механической нагрузки, он увеличивает свою угловую скорость ω до тех пор, пока противо-ЭДС не станет почти равной движущей ЭДС. Тогда двигатель использует ровно столько энергии, сколько необходимо для преодоления трения.
Вихревые токи в железных сердечниках двигателей могут привести к значительным потерям энергии. Их обычно минимизируют за счет изготовления сердечников из тонких электроизолированных листов железа. На магнитные свойства сердечника практически не влияет ламинирование изоляционного листа, в то время как резистивный нагрев значительно снижается. Рассмотрим, например, катушки двигателя, представленные на рисунке \(\PageIndex{6}\). Катушки имеют эквивалентное сопротивление \(0,400 Ом, Омега\) и приводятся в действие ЭДС 48,0 В. Вскоре после включения они потребляют ток 92R = 5,76 \, кВт\) энергии в виде теплопередачи.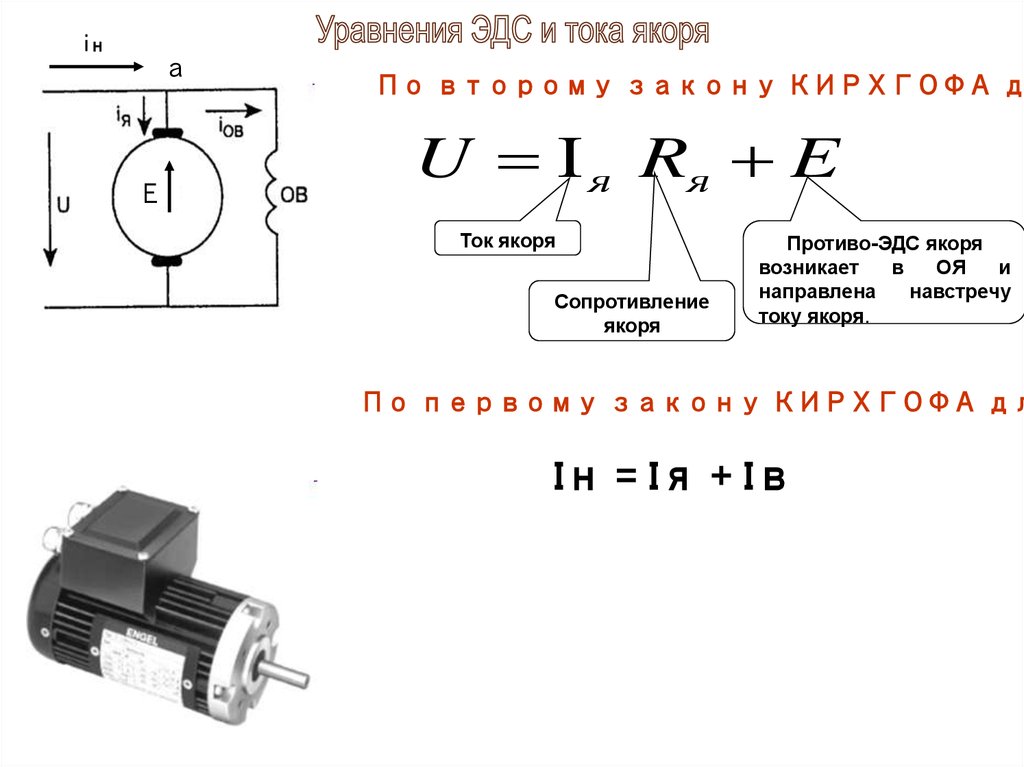 При нормальных условиях работы этого двигателя предположим, что противо-ЭДС равна 40,0 В. Тогда при рабочей скорости общее напряжение на катушках составляет 8,0 В (48,0 В минус противо-ЭДС 40,0 В), а потребляемый ток равен
При нормальных условиях работы этого двигателя предположим, что противо-ЭДС равна 40,0 В. Тогда при рабочей скорости общее напряжение на катушках составляет 8,0 В (48,0 В минус противо-ЭДС 40,0 В), а потребляемый ток равен
\[ I = V/R = (8,0 Ом, В)/(0,400 Ом, Омега) = 20 Ом, А.\]
Тогда при нормальной нагрузке рассеиваемая мощность равна \(P = IV = (20 Ом, А)(8,0 л, В) = 160 л, Вт\). Это не создает проблем для этого двигателя, в то время как прежние 5,76 кВт сожгли бы катушки, если бы они продолжались.
Двигатель с последовательным возбуждением в работе
Общее сопротивление \((R_f + R_a)\) двигателя постоянного тока с последовательным возбуждением составляет \(2,0 \, \Omega\) (Рисунок \(\PageIndex{7}\ )). При подключении к источнику 120 В \((\epsilon_S)\) двигатель потребляет 10 А при работе с постоянной угловой скоростью. (a) Чему равна противо-ЭДС, индуцируемая во вращающейся катушке \(\epsilon_i\)? б) Какова механическая мощность двигателя? в) Какая мощность рассеивается на сопротивлении катушек? г) Какова выходная мощность источника 120 В? (e) Предположим, что нагрузка на двигатель увеличивается, что приводит к его замедлению до точки, когда он потребляет 20 А. Ответьте на пункты с (a) по (d) для этой ситуации.
Ответьте на пункты с (a) по (d) для этой ситуации.
Рисунок \(\PageIndex{7}\): Представление схемы двигателя постоянного тока с последовательной обмоткой.
Стратегия
ПротивоЭДС рассчитывается на основе разницы между подаваемым напряжением и потерями от тока через сопротивление. Мощность каждого устройства рассчитывается по одной из формул мощности на основе предоставленной информации.
Решение
- Обратная ЭДС равна \[\epsilon_i = \epsilon_S — I(R_f + RE_a) = 120 \, V — (10 \, A)(2,0 \, \Omega) = 100 \, V .\] 92 \, Вт.\]
Эта страница под названием 13.7: Electric Generators and Back Emf распространяется под лицензией CC BY 4.0 и была создана, изменена и/или курирована OpenStax с использованием исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- ОпенСтакс
- Лицензия
- СС BY
- Версия лицензии
- 4,0
- Программа OER или Publisher
- ОпенСтакс
- Показать оглавление
- нет
- Теги
- задняя ЭДС
- Электрогенератор
- пиковая ЭДС
- источник@https://openstax.
 org/details/books/university-physics-volume-2
org/details/books/university-physics-volume-2
Электрогенераторы | Физика
Цели обучения
К концу этого раздела вы сможете:
- Рассчитать ЭДС, индуцируемую в генераторе.
- Рассчитайте пиковую ЭДС, которая может быть наведена в конкретной генераторной системе.
Электрические генераторы индуцируют ЭДС, вращая катушку в магнитном поле, как кратко описано в ЭДС индукции и магнитном потоке. Теперь мы рассмотрим генераторы более подробно. Рассмотрим следующий пример.
Пример 1. Расчет ЭДС, наведенной в катушке генератора
Катушка генератора, показанная на рисунке 1, поворачивается на четверть оборота (от θ = 0º до θ = 90º) за 15,0 мс. Круглая катушка из 200 витков имеет радиус 5,00 см и находится в однородном магнитном поле 1,25 Тл. Чему равна средняя ЭДС индукции?
Рис. 1. Когда катушка этого генератора поворачивается на четверть оборота, магнитный поток Φ изменяется от своего максимума до нуля, индуцируя ЭДС.

Стратегия
Мы используем закон индукции Фарадея, чтобы найти среднюю ЭДС, индуцированную за время Δ t :
[латекс]\text{emf}=-N\frac{\Delta\Phi}{\Delta t}\\[/latex].
Мы знаем, что Н = 200 и Δ t = 15,0 мс, поэтому мы должны определить изменение потока Δ Φ , чтобы найти ЭДС.
Решение
Поскольку площадь петли и напряженность магнитного поля постоянны, мы видим, что
[латекс]\Delta\Phi =\Delta\left(BA\cos\theta\right)=AB\ Дельта\влево(\cos\тета\вправо)\\[/латекс].
Теперь, Δ (cos 9{-3}\text{ s}}=131\text{ V}\\[/latex].
Обсуждение
Это практическое среднее значение, аналогичное 120 В, используемому в домашнем хозяйстве.
ЭДС, рассчитанная в приведенном выше примере 1 , представляет собой среднее значение за одну четвертую оборота. Чему равна ЭДС в каждый момент времени? Оно изменяется в зависимости от угла между магнитным полем и перпендикуляром к катушке.
 Мы можем получить выражение для ЭДС как функции времени, рассматривая ЭДС движения на вращающейся прямоугольной катушке шириной w и высотой ℓ в однородном магнитном поле, как показано на рисунке 2.
Мы можем получить выражение для ЭДС как функции времени, рассматривая ЭДС движения на вращающейся прямоугольной катушке шириной w и высотой ℓ в однородном магнитном поле, как показано на рисунке 2.Рисунок 2. Генератор с одной прямоугольной катушкой, вращающейся с постоянной угловой скоростью в однородном магнитном поле, создает ЭДС, которая изменяется синусоидально во времени . Обратите внимание, что генератор похож на двигатель, за исключением того, что вал вращается для создания тока, а не наоборот.
Заряды в проводах петли испытывают магнитную силу, так как движутся в магнитном поле. На заряды в вертикальных проводах действуют силы, параллельные проводу, вызывающие токи. Но находящиеся в верхнем и нижнем сегментах ощущают силу, перпендикулярную проводу, которая не вызывает тока. Таким образом, мы можем найти ЭДС индукции, рассматривая только боковые провода. ЭДС движения принимается равной ЭДС = 9.0280 Bℓv , где скорость v перпендикулярна магнитному полю B .
 Здесь скорость составляет угол θ с B , так что ее составляющая, перпендикулярная B , равна v sin θ (см. рис. 2). Таким образом, в этом случае ЭДС, индуцированная с каждой стороны, равна ЭДС = Bℓv sin θ , и они имеют одинаковое направление. Суммарная ЭДС вокруг петли тогда равна
Здесь скорость составляет угол θ с B , так что ее составляющая, перпендикулярная B , равна v sin θ (см. рис. 2). Таким образом, в этом случае ЭДС, индуцированная с каждой стороны, равна ЭДС = Bℓv sin θ , и они имеют одинаковое направление. Суммарная ЭДС вокруг петли тогда равна[латекс]\текст{ЭДС}=2{B\ell v}\sin\theta\\[/латекс].
Это выражение верно, но оно не дает ЭДС как функцию времени. Чтобы найти зависимость ЭДС от времени, предположим, что катушка вращается с постоянной угловой скоростью ω . Угол θ связан с угловой скоростью соотношением θ = ωt , так что
[латекс]\текст{ЭДС}=2{B\ell v}\sin\omega t\\[/ латекс].
Теперь линейная скорость v связана с угловой скоростью ω соотношением v = rω . Здесь r = w /2, так что v = ( w /2) ω , и
[латекс]\text{emf}=2 B\ell \frac }{2}\omega\sin\omega t=\left(\ell w\right)B\omega\sin\omega t\\[/latex].

Заметив, что площадь петли равна A = ℓ w , и учитывая N петель, мы находим, что
[латекс]\text{emf}=NAB\omega\sin\omega t\\[/latex]
— ЭДС , индуцированная в катушке генератора N витков и площадь A вращающаяся с постоянной угловой скоростью ω в однородном магнитном поле B . Это также может быть выражено как
[латекс]\text{emf}={\text{emf}}_{0}\sin\omega t\\[/latex],
, где
[латекс]{\ text{emf}}_{0}=NAB\omega\\[/latex]
— максимальная (пиковая) emf . Обратите внимание, что частота колебаний равна f = ω /2π , а период равен T = 1/ f = 2π/ ω . На рис. 3 показан график зависимости ЭДС от времени, и теперь кажется разумным, что переменное напряжение является синусоидальным.
Рис. 3. ЭДС генератора подается на лампочку с показанной системой колец и щеток.
 На графике показана зависимость ЭДС генератора от времени. emf0 — пиковая эдс. Период T = 1/ f = 2π/ω, где f — частота. Обратите внимание, что буква E означает emf.
На графике показана зависимость ЭДС генератора от времени. emf0 — пиковая эдс. Период T = 1/ f = 2π/ω, где f — частота. Обратите внимание, что буква E означает emf.Тот факт, что пиковая ЭДС, ЭДС 0 = NABω , имеет смысл. Чем больше количество катушек, тем больше их площадь, и чем сильнее поле, тем больше выходное напряжение. Интересно, что чем быстрее раскручивается генератор (больше ω ), тем больше ЭДС. Это заметно на велосипедных генераторах, по крайней мере, на более дешевых. Один из авторов, будучи подростком, находил забавным ехать на велосипеде достаточно быстро, чтобы сжечь его фары, пока однажды темной ночью ему не пришлось ехать домой без света. На рисунке 4 показана схема, с помощью которой можно сделать генератор для получения импульсного постоянного тока. Более сложное расположение нескольких катушек и разъемных колец может обеспечить более плавный постоянный ток, хотя для создания постоянного тока без пульсаций обычно используются электронные, а не механические средства.

Рис. 4. Разъемные кольца, называемые коммутаторами, в этой конфигурации создают на выходе импульсную ЭДС постоянного тока.
Пример 2. Расчет максимальной ЭДС генератора
Вычислить максимальную ЭДС, ЭДС 0 , генератора, рассмотренного в Примере 1. , определено, по ЭДС 0 = NABω можно найти ЭДС 0 . Все остальные величины известны.
Решение
Угловая скорость определяется как изменение угла в единицу времени:
[латекс]\omega =\frac{\Delta\theta}{\Delta t}\\[/latex].
Одна четвертая оборота составляет π/2 радиана, а время составляет 0,0150 с; таким образом,
[латекс]\begin{array}{lll}\omega & =& \frac{\pi /2\text{rad}}{0,0150 \text{s}}\\ & =& 104,7\text{ рад/с}\end{массив}\\[/latex].
104,7 рад/с — это ровно 1000 об/мин. Подставляем это значение на 9{2}\right)\left(1.25\text{ T}\right)\left(104.7 \text{ рад/с}\right)\\ & =& 206\text{ V}\end{массив}\\ [/латекс].

Обсуждение
Максимальная ЭДС больше, чем средняя ЭДС 131 В, найденная в предыдущем примере, как и должно быть.
В реальной жизни электрические генераторы выглядят совсем иначе, чем на рисунках в этом разделе, но принцип тот же. Источником механической энергии, вращающей катушку, может быть падающая вода (гидроэнергия), пар, образующийся при сжигании ископаемого топлива, или кинетическая энергия ветра. На рис. 5 показан вид в разрезе паровой турбины; пар движется по лопастям, соединенным с валом, который вращает катушку внутри генератора.
Рис. 5. Паровая турбина/генератор. Пар, образующийся при сжигании угля, воздействует на лопатки турбины, вращая вал, соединенный с генератором. (кредит: Nabonaco, Wikimedia Commons)
Генераторы, показанные в этом разделе, очень похожи на двигатели, показанные ранее. Это не случайно. Фактически двигатель становится генератором, когда его вал вращается. Некоторые ранние автомобили использовали свой стартер в качестве генератора.
 В разделе «Обратная ЭДС» мы дополнительно исследуем работу двигателя как генератора.
В разделе «Обратная ЭДС» мы дополнительно исследуем работу двигателя как генератора.Резюме раздела
- Электрический генератор вращает катушку в магнитном поле, индуцируя ЭДС, определяемую как функция времени
[латекс]\text{emf}=2{B\ell v}\sin\omega t\\[/latex],
, где A – площадь витковой катушки Н , вращаемой с постоянной угловой скоростью ω в однородном магнитном поле B .
- Пиковая ЭДС ЭДС 0 генератора равна
эдс 0 = NABω
Концептуальные вопросы
- Используя RHR-1, покажите, что ЭДС на сторонах контура генератора на рисунке 4 одинаковы, и, таким образом, добавьте.
- Источником электрической энергии генератора является работа, совершаемая для вращения его катушек. Как работа, необходимая для поворота генератора, связана с законом Ленца?
Задачи и упражнения
1. Рассчитайте пиковое напряжение генератора, который вращает свою 200-витковую катушку диаметром 0,100 м со скоростью 3600 об/мин в поле 0,800 Тл.

2. При какой угловой скорости в об/мин пиковое напряжение генератора составит 480 В, если его 500-витковая катушка диаметром 8,00 см вращается в поле 0,250 Тл?
3. Какова пиковая ЭДС, создаваемая вращением катушки диаметром 20,0 см из 1000 витков в магнитном поле Земли 5,00 × 10 −5 Тл, если плоскость катушки первоначально перпендикулярна полю Земли и поворачивается параллельно полю за 10,0 мс?
4. Какова пиковая ЭДС, создаваемая катушкой радиусом 0,250 м, состоящей из 500 витков, которая поворачивается на четверть оборота за 4,17 мс, первоначально имея плоскость, перпендикулярную однородному магнитному полю. (Это 60 об/с.)
5. (a) Велосипедный генератор вращается со скоростью 1875 рад/с, производя пиковую ЭДС 18,0 В. Он имеет прямоугольную катушку размером 1,00 на 3,00 см в поле 0,640 Тл. Сколько витков в катушке? (b) Практично ли такое количество витков провода для катушки размером 1,00 на 3,00 см?
6. Интегрированные понятия Эта задача относится к велосипедному генератору, рассмотренному в предыдущей задаче.
 Он приводится в движение колесом диаметром 1,60 см, которое катится по внешнему ободу велосипедной шины. а) Какова скорость велосипеда, если угловая скорость генератора равна 1875 рад/с? б) Какова максимальная ЭДС генератора, когда велосипед движется со скоростью 10,0 м/с, учитывая, что в первоначальных условиях она составляла 18,0 В? (c) Если сложный генератор может изменять свое собственное магнитное поле, какая напряженность поля ему потребуется при скорости 5,00 м/с, чтобы произвести 90,00 В максимальная ЭДС?
Он приводится в движение колесом диаметром 1,60 см, которое катится по внешнему ободу велосипедной шины. а) Какова скорость велосипеда, если угловая скорость генератора равна 1875 рад/с? б) Какова максимальная ЭДС генератора, когда велосипед движется со скоростью 10,0 м/с, учитывая, что в первоначальных условиях она составляла 18,0 В? (c) Если сложный генератор может изменять свое собственное магнитное поле, какая напряженность поля ему потребуется при скорости 5,00 м/с, чтобы произвести 90,00 В максимальная ЭДС?7. (a) Автомобильный генератор вращается со скоростью 400 об/мин, когда двигатель работает на холостом ходу. Его 300-витковая прямоугольная катушка размером 5,00 на 8,00 см вращается в регулируемом магнитном поле, так что она может создавать достаточное напряжение даже при низких оборотах. Какая напряженность поля необходима для создания пиковой ЭДС 24,0 В? (b) Обсудите, как эта требуемая напряженность поля соотносится с напряженностью поля, доступной для постоянных и электромагнитов.

8. Покажите, что если катушка вращается с угловой скоростью ω , период ее выхода переменного тока равен 2π/ ω .
9. Катушка диаметром 10,0 см из 75 витков вращается с угловой скоростью 8,00 рад/с в поле 1,25 Тл, начиная с плоскости катушки, параллельной полю. а) Чему равна пиковая ЭДС? б) В какой момент времени достигается максимальная ЭДС? в) В какой момент ЭДС достигает своего максимального отрицательного значения? (d) Каков период выходного напряжения переменного тока?
10. а) Если ЭДС катушки, вращающейся в магнитном поле, равна нулю при t = 0 и возрастает до своего первого максимума при t = 0,100 мс, какова угловая скорость катушки? б) В какое время произойдет ее следующий максимум? в) Каков период выпуска продукции? (d) Когда объем выпуска составляет первую четверть своего максимума? (e) Когда она составляет следующую четверть своего максимума?
11. Необоснованные результаты 500-витковая катушка площадью 0,250 м 2 вращается в поле Земли 5,00 × 10 −5 Тл, производя максимальную ЭДС 12,0 кВ.
 а) С какой угловой скоростью должна вращаться катушка? б) Что неразумного в этом результате? (c) Какое предположение или предпосылка являются ответственными?
а) С какой угловой скоростью должна вращаться катушка? б) Что неразумного в этом результате? (c) Какое предположение или предпосылка являются ответственными?Глоссарий
- электрогенератор:
- Устройство для преобразования механической работы в электрическую энергию; он индуцирует ЭДС, вращая катушку в магнитном поле
- ЭДС, индуцированная в катушке генератора:
- EMF = NAB Ом SIN ωT , где A -это площадь N -Терн, вращающаяся на постоянной угловой Velocity ω в ANIFOR времени т
- пиковая ЭДС:
- ЭДС 0 = NABω
Избранные решения задач и упражнений
1. 474 В
3. 0,247 В
5. (а) 50 (б) да
7. (а) 0,477 Тл (б) Эта напряженность поля достаточно мала, чтобы ее можно было получить с помощью постоянного магнит или электромагнит.
9. (а) 5,89 В (б) При т = 0 (в) 0,393 с (г) 0,785 с
11.

 org/details/books/university-physics-volume-2
org/details/books/university-physics-volume-2
 Мы можем получить выражение для ЭДС как функции времени, рассматривая ЭДС движения на вращающейся прямоугольной катушке шириной w и высотой ℓ в однородном магнитном поле, как показано на рисунке 2.
Мы можем получить выражение для ЭДС как функции времени, рассматривая ЭДС движения на вращающейся прямоугольной катушке шириной w и высотой ℓ в однородном магнитном поле, как показано на рисунке 2.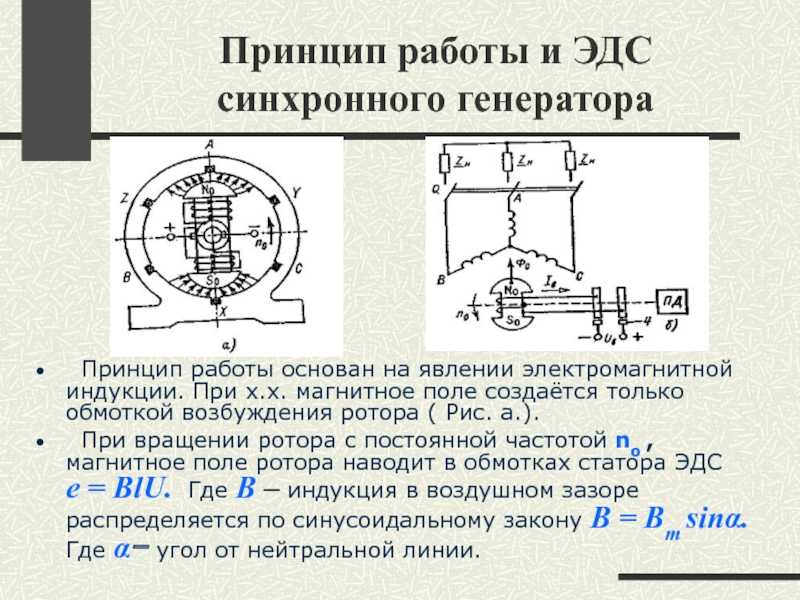 Здесь скорость составляет угол θ с B , так что ее составляющая, перпендикулярная B , равна v sin θ (см. рис. 2). Таким образом, в этом случае ЭДС, индуцированная с каждой стороны, равна ЭДС = Bℓv sin θ , и они имеют одинаковое направление. Суммарная ЭДС вокруг петли тогда равна
Здесь скорость составляет угол θ с B , так что ее составляющая, перпендикулярная B , равна v sin θ (см. рис. 2). Таким образом, в этом случае ЭДС, индуцированная с каждой стороны, равна ЭДС = Bℓv sin θ , и они имеют одинаковое направление. Суммарная ЭДС вокруг петли тогда равна
 На графике показана зависимость ЭДС генератора от времени. emf0 — пиковая эдс. Период T = 1/ f = 2π/ω, где f — частота. Обратите внимание, что буква E означает emf.
На графике показана зависимость ЭДС генератора от времени. emf0 — пиковая эдс. Период T = 1/ f = 2π/ω, где f — частота. Обратите внимание, что буква E означает emf.
 В разделе «Обратная ЭДС» мы дополнительно исследуем работу двигателя как генератора.
В разделе «Обратная ЭДС» мы дополнительно исследуем работу двигателя как генератора.
 Он приводится в движение колесом диаметром 1,60 см, которое катится по внешнему ободу велосипедной шины. а) Какова скорость велосипеда, если угловая скорость генератора равна 1875 рад/с? б) Какова максимальная ЭДС генератора, когда велосипед движется со скоростью 10,0 м/с, учитывая, что в первоначальных условиях она составляла 18,0 В? (c) Если сложный генератор может изменять свое собственное магнитное поле, какая напряженность поля ему потребуется при скорости 5,00 м/с, чтобы произвести 90,00 В максимальная ЭДС?
Он приводится в движение колесом диаметром 1,60 см, которое катится по внешнему ободу велосипедной шины. а) Какова скорость велосипеда, если угловая скорость генератора равна 1875 рад/с? б) Какова максимальная ЭДС генератора, когда велосипед движется со скоростью 10,0 м/с, учитывая, что в первоначальных условиях она составляла 18,0 В? (c) Если сложный генератор может изменять свое собственное магнитное поле, какая напряженность поля ему потребуется при скорости 5,00 м/с, чтобы произвести 90,00 В максимальная ЭДС?
 а) С какой угловой скоростью должна вращаться катушка? б) Что неразумного в этом результате? (c) Какое предположение или предпосылка являются ответственными?
а) С какой угловой скоростью должна вращаться катушка? б) Что неразумного в этом результате? (c) Какое предположение или предпосылка являются ответственными?