3.8.Преобразование треугольника сопротивлений в эквивалентную звезду и обратное преобразование

При расчете разветвленных цепей и,
особенно, при определении их входных
сопротивлений может возникнуть вопрос
о преобразовании треугольника
сопротивлений в эквивалентную звезду
или обратного преобразования. Такая
процедура становится возможной при
условии неизменности потенциалов на
зажимах преобразуемого участка цепи.

Рассмотрим
участок цепи, соединенный треугольником
(Рис. 3 .48).

Составим
уравнения по первому и второму законам
Кирхгофа для «треугольника».

Рис.3.48. Взаимное
преобразование «треугольника» в «звезду»

По
первому закону Кирхгофа

«1 узел»:

;

«2 узел»:

.

По
второму закону Кирхгофа

.

Решим
эту систему уравнений, например,
относительно тока

Определим
напряжение

:

в схеме
«треугольник»

;

в схеме
«звезда»

Причем,
должно выполняться такое равенство:

.
Приравнивая эти выражения, получим
формулы перехода от соединения
сопротивлений «треугольником» к
сопротивлениям «звезды»

.86(3.83)

Покажем
на примере применимость данного
преобразования.

Рис.3.49. Преобразование
«треугольника»
сопротивлений в
«звезду»

Рис.3.50. Преобразование
«звезды»
сопротивлений в «треугольник»

Обратное
преобразование из «звезды» в «треугольник»
выполняется по формулам перехода

87(3.84)

Все методы, рассмотренные ранее,
предполагали расчет токов одновременно
во всех ветвях цепи. Однако в ряде случаев
бывает необходимым контролировать ток
в одной отдельно взятой ветви. В этом
случае применяют для расчета метод
эквивалентного генератора.

Пусть дана некоторая электрическая
цепь, которую представим активным
двухполюсником (Рис. 3 .51). Необходимо
рассчитать ток в ветви ab:

1) введем в ветвь ab два
источника ЭДС

и

,
одинаковые по величине и противоположно
направленные

;

Рис. 3.51. Преобразование
исходного двухполюсника
в сумму двух
цепей

2) используя принцип наложения, данную
цепь представим суммой двух цепей. В
первой оставим все источники активного
двухполюсника и источник ЭДС
.
Вторая цепь представляет собой пассивный
двухполюсник и источник ЭДС

.

На
основании принципа наложения ток ветви
ab,

;

;

.

Поскольку

– любые по величине, то подберем их
значения такими, чтобы ток

был равен нулю. Для этого выберем

.

Напряжение
на зажимах источника в режиме холостого
хода численно равна его ЭДС. Тогда
активный двухполюсник с источником

может быть представлен в виде:

Рис.3.52. Схема замещения
активного двухполюсника

В этой схеме эквивалентная ЭДС активного
двухполюсника

и
следовательно, ток

.

Таким
образом, ток в ветви ab

.
88(3.85)

Пусть дана цепь (рис.2.12), рассчитаем ток

методом эквивалентного генератора.

Рис.3.53. Исходная цепь

Последовательность
расчета:

1.
Разомкнем ветвь с сопротивлением Z₁
или примем Z₁
=  .

2. Зададим положительное направление

и для произвольно выбранных положительных
направлений токов, например, первого
контура, запишем уравнение по второму
закону Кирхгофа

.

3. Токи

и

в преобразованной схеме (рис. 3.13)
рассчитываем любым известным методом,
например, методом контурных токов

Тогда

;

.

Рис.3.54. Преобразованная
цепь

4. Определим эквивалентное сопротивление
пассивного двухполюсника. Для этого
мысленно закоротим все источники ЭДС
исходной цепи, оставляя для реальных
источников их внутренние сопротивления.

Рис.3.55. Схема пассивного
двухполюсника

В образовавшейся схеме пассивного
двухполюсника невозможно определить
эквивалентное сопротивление относительно
зажимов a—b,
так как нет последовательно-параллельного
соединения приемников, поэтому необходимо
выполнить преобразование какого-либо
участка цепи из «треугольника» в «звезду»
или выполнить обратное преобразование.

Заменим, например, треугольник
сопротивлений Z₂ –
Z₃ – Z₅
в звезду Z₂₃ – Z₂₅
– Z₃₅. При этом
получится схема с последовательно-параллельным
соединением приемников (Рис. 3 .55).

Сопротивления
этой схемы

и эквивалентное сопротивление

.

Окончательно

.

Преобразование треугольник/звезда: что за сценой?

Добавлено 17 июня 2019 в 12:15

Преобразования треугольник/звезда позволяют нам заменить часть схемы другой схемой, которая, хотя и эквивалентна в поведении, но может значительно упростить анализ общей схемы. Здесь мы узнаем, откуда берутся эти преобразования.

Зачем?

Когда мы начали изучать электронику, резисторы были соединены либо последовательно, либо параллельно, и мы научились заменять такие комбинации их эквивалентными сопротивлениями, часто с целью уменьшения всей сети сопротивлений до единственного эквивалентного сопротивления, видимого из источника питания. После этого появились схемы (рисунок 1), которые содержали резисторы, которые не были ни последовательными, ни параллельными, но их всё же можно было убрать, тщательно определяя и сокращая фрагменты схемы в правильном порядке. Обратите внимание, что R₁ не параллелен и не последователен ни с R₂, ни с R₃, но путем объединения R₂ последовательно с R₄, и объединяя R₃ последовательно с R₅, мы можем затем объединить эти два эквивалентных сопротивления параллельно и, наконец, объединив результат последовательно с R₁, получить полное сопротивление, видимое источнику питания, которое, используя закон Ома, поможет получить общий ток источника питания.

Рисунок 1

Но теперь мы подошли к схемам (рисунок 2), где нет никаких пар резисторов, которые включены последовательно или параллельно, – похоже, мы зашли в тупик. Одним из способов анализа этой схемы является использование закона напряжений Кирхгофа (второй закон) и закона токов Кирхгофа (первый закон) для получения алгебраических уравнений, которые мы можем решить для напряжений и токов. Хотя этот подход будет работать всегда (для этой и большинства других типов схем), он может быть довольно громоздким. Мы могли бы смириться с этим как с ценой возможности анализа этих более сложных схем, но иногда мы можем избежать оплаты этого счета, изменяя или «преобразовывая» фрагменты схемы, чтобы превратить ее в нечто, что мы можем уменьшить, используя только правила последовательного/параллельного объединения.

Рисунок 2

Для простоты мы будем рассматривать только цепи постоянного тока с резисторами, но эти принципы применимы к любой линейной системе переменного или постоянного тока. Кроме того, чтобы сфокусировать обсуждение на преобразованиях, мы найдем только общий ток, поставляемый источником напряжения, что означает, что мы стремимся свести всю сеть резисторов в единое эквивалентное сопротивление.

Давайте рассмотрим эти две схемы немного подробнее (рисунок 3). Мы видим, что единственная разница между ними заключается в том, что находится внутри пунктирных окружностей. В каждом случае цепь в окружности имеет три контакта, которые пересекают окружность для взаимодействия с остальной частью схемы. В левой цепи (рисунок 3(a)) резисторы подключены к контактам в конфигурации «треугольник» (в англоязычной литературе, конфигурация «delta», «дельта», названная в честь заглавной греческой буквы Δ). А в правой цепи резисторы подключены в конфигурации «звезда» (в англоязычной литературе, конфигурация «wye», «уай», названная в честь заглавной английской буквы Y, хотя в схеме она перевернута).

Рисунок 3

Теперь представьте, что резисторы внутри пунктирной окружности в левой цепи помещены в черный ящик, этот ящик удален из схемы и заменен другим черным ящиком, который заставляет схему вести себя точно так же. Далее представьте, что, когда вы открываете, этот новый ящик он содержит три резистора, расположенных как в правой цепи.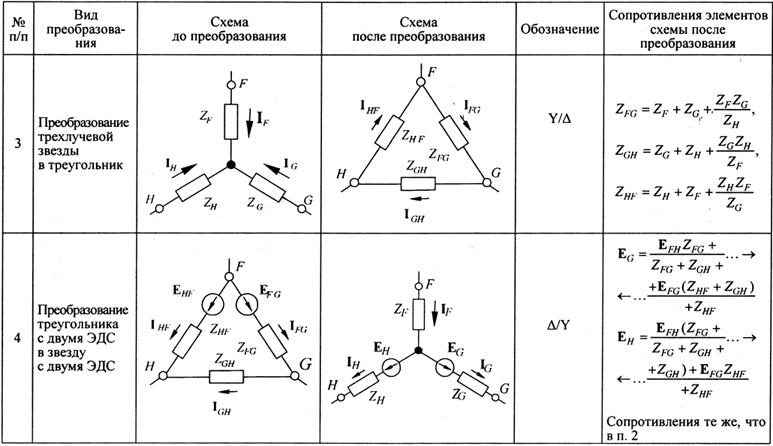 Кто бы ни придумал второй черный ящик, он очень тщательно выбрал значения резисторов так, чтобы эти два блока были неразличимы для остальной части схемы: мы знаем, как анализировать правую схему, и теперь мы знаем, что когда мы это делаем, результаты можно применить к левой схеме, потому что они эквивалентны. Вот зачем выполнять преобразования «треугольник→звезда» и «звезда→треугольник».

Основные соотношения

Чтобы определить уравнения, связывающие резисторы в цепи, соединенной треугольником, с резисторами в цепи, соединенной звездой, нам ничего не нужно, кроме наших надежных формул для последовательных/параллельных соединений (и немного алгебры). Идея заключается в выравнивании эквивалентных сопротивлений между соответствующими парами контактов при отключенном оставшемся контакте (рисунок 4)

Рисунок 4

Выполнив это для эквивалентного сопротивления между контактами B-C, мы получим:

\[R_B + R_C = \frac{R_{BC} \left( R_{AB} + R_{AC} \right) }{R_{AB} + R_{BC} + R_{AC}}\]

Если мы повторим этот процесс для каждой другой пары контактов по очереди, мы получим еще два аналогичных уравнения, и любое из них даст нам необходимую нам информацию (при условии, что мы распознаем задействованную симметрию).

Частный случай: симметричные схемы

Если сопротивления в каждом плече цепи, соединенной треугольником или звездой, равны, такая цепь считается «симметричной». Это означает, что

\[R_∆ = R_{AB} = R_{BC} = R_{AC}\]

\[R_Y = R_A = R_B = R_C\]

Комбинация этого условия с соотношением из предыдущего раздела сразу приводит к уравнению преобразования для случая симметрии.

\[2R_Y = \frac{R_∆(2R_∆)}{3R_∆}\]

\[R_Y = \frac{R_∆}{3}\]

\[R_∆ = 3R_Y\]

Это гораздо более значительный результат, чем может показаться на первый взгляд, и причина довольно проста – когда инженеры проектируют схемы с соединениями треугольник или звезда, они часто стараются сделать эти схемы симметричными. Хотя, конечно, это не всегда возможно, и поэтому мы должны иметь возможность разобраться с общим случаем, когда схема не симметрична.

Общий случай преобразования треугольник→звезда

Для преобразования треугольник/звезда нам дана известная схема, соединенная треугольником, и мы хотим найти значения для эквивалентной схемы, соединенной звездой, – поэтому мы пытаемся найти {R_A, R_B, R_C} для заданных {R_AB, R_BC, R_AC}.

Мы начнем с того, что запишем наши основные соотношения из первоначального вида в несколько более компактной форме, определив новую величину, R_ΔS, которая равна сумме сопротивлений всех резисторов в цепи, соединенной треугольником.

\[R_{ΔS}=R_{AB}+R_{BC}+R_{AC}\]

Затем мы делаем перестановку нашего соотношения для получения вида линейного алгебраического уравнения с неизвестными {R_A, R_B, R_C}.

\[(0)R_A+(R_{ΔS})R_B+(R_{ΔS})R_C=R_{AB}R_{BC}+R_{BC}R_{AC}\]

Поскольку у нас есть три неизвестных, нам нужно еще два уравнения. Они получаются из эквивалентных сопротивлений, видимых при рассмотрении двух других пар контактов. Выполнив это (или используя симметрию) мы получаем

\[(R_{ΔS})R_A+(0)R_B+(R_{ΔS})R_C=R_{AB}R_{AC}+R_{BC}R_{AC}\]

\[(R_{ΔS})R_A+(R_{ΔS})R_B+(0)R_C=R_{AB}R_{AC}+R_{AB}R_{BC}\]

Сложив эти два уравнения вместе и вычтя наше первое уравнение, мы получим

\[2(R_{ΔS})R_A=2R_{AB}R_{AC}\]

\[R_A= {R_{AB}R_{AC} \over R_{ΔS}}\]

Мы можем решить систему уравнению для двух других неизвестных сопротивлений (или использовать симметрию), чтобы получить

\[R_B= {R_{AB}R_{BC} \over R_{ΔS}}\]

\[R_C= {R_{AC}R_{BC} \over R_{ΔS}}\]

Эти отношения могут быть обобщены очень компактно. Сопротивление, подключенное к каждому узлу в эквивалентной цепи, соединенной звездой, равно произведению сопротивлений, подключенных к соответствующему узлу в цепи, соединенной треугольником, деленному на сумму сопротивлений всех резисторов в треугольнике. Обычно это выражается формулой, такой как

\[R_N= {R_{N1}R_{N2} \over R_{ΔS}}\]

где

• R_N – резистор, подключенный к контакту N в схеме «звезда»;
• R_N1 и R_N2 – резисторы, подключенные к контакту N в схеме «треугольник»

Общий случай преобразования звезда→треугольник

Для преобразования звезда→треугольник нам дана известная схема, соединенная звездой, и мы хотим найти значения для эквивалентной схемы, соединенной треугольником. Следовательно, мы пытаемся найти {R_AB, R_BC, R_AC} для заданных {R_A, R_B, R_C}.

Это не так просто, как в случае преобразования треугольник→звезда потому, что неизвестные сопротивления перемножаются вместе, делая результирующие уравнения нелинейными. К счастью, мы можем обойти это неудобство, рассмотрев отношения сопротивлений резисторов в каждой цепи. Например, взяв отношение R_A к R_B, мы получаем

\[{R_A \over R_B} = { R_{AB}R_{AC} \over R_{AB}R_{BC} } = {R_{AC} \over R_{BC} }\]

Другими словами, отношение сопротивлений резисторов, подключенных к любым двум контактам в схеме звезда, равно отношению сопротивлений резисторов, соединяющих те же самые два контакта с третьим контактом в схеме треугольник. Следовательно, два других соотношения будут следующими

\[{R_B \over R_C} = {R_{AB} \over R_{AC} }\]

\[{R_A \over R_C} = {R_{AB} \over R_{BC} }\]

Вооружившись этим, мы могли бы вернуться к нашим основным соотношениям и продолжить работу с ними, но в качестве отправной точки проще использовать одно из отношений из общего случая преобразования треугольник→звезда.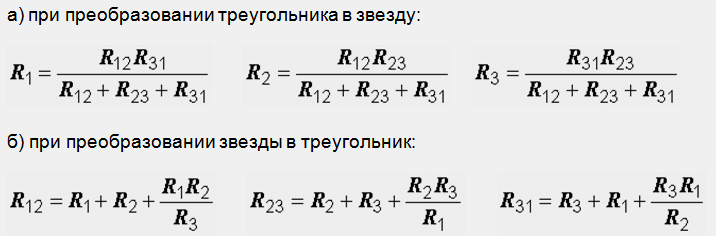

\[R_A= {R_{AB}R_{AC} \over R_{AB} + R_{BC}+R_{AC} }\]

\[R_{AB}R_{AC} = R_A (R_{AB} + R_{BC}+R_{AC})\]

\[R_{AB} = R_A \left( {R_{AB} + R_{BC}+R_{AC} \over R_{AC} } \right)\]

\[R_{AB} = R_A \left( {R_{AB} \over R_{AC}} + {R_{BC} \over R_{AC} } + 1 \right)\]

\[R_{AB} = R_A \left( {R_{B} \over R_{C}} + {R_{B} \over R_{A} } + 1 \right)\]

\[R_{AB} = R_A + R_B + {R_AR_B \over R_C } \]

Два других выражения получаются аналогично (или согласно симметрии):

\[R_{BC} = R_B + R_C + {R_B R_C \over R_A } \]

\[R_{AC} = R_A + R_C + {R_A R_C \over R_B } \]

Эти выражения могут быть обобщены очень компактно. Сопротивление, подключенное между каждой парой узлов в эквивалентной схеме, соединенной треугольником, равно сумме сопротивлений двух резисторов, подключенных к соответствующим узлам в схеме, соединенной звездой, плюс произведение сопротивлений этих двух резисторов, деленное на сопротивление третьего резистора.

Общий способ выразить это состоит в том, чтобы поместить правую часть под общим знаменателем, а затем отметить, что числитель в каждом выражении является суммой произведений каждой пары сопротивлений в цепи, соединенной звездой, а знаменатель – это сопротивление, подключенное к третьему контакту.

\[R_{AB}={R_P \over R_C}\]

\[R_P = R_A R_B + R_B R_C + R_A R_C\]

Пример

Рисунок 5

Давайте поработаем с задачей, показанной на рисунке 5. Прежде чем мы начнем, давайте определим ожидаемый ответ, чтобы у нас была хорошая проверка того, является ли наш окончательный ответ правильным. Для этого рассмотрим роль мостового резистора 150 Ом. Этот резистор служит для уменьшения общего сопротивления, обеспечивая путь между левой и правой сторонами цепи. Следовательно, самое высокое эффективное сопротивление будет иметь место, если этот резистор будет удален полностью, и в этом случае полное сопротивление будет равно параллельной комбинации левой и правой сторон, что приведет к

\[R_{экв.max}=(100 +220)||(470+330)=228,6 \; Ом\]

С другой стороны, наименьшее общее сопротивление было бы получено путем уменьшения мостового резистора до прямого короткого замыкания, и в этом случае общее сопротивление было бы равно параллельной комбинации двух верхних резисторов, включенной последовательно с параллельной комбинацией двух нижних резисторов, что приведет к

\[R_{экв. min}=(100||470)+(220||330)=214,5 \; Ом\]

Теперь мы ЗНАЕМ, что наш ответ ДОЛЖЕН быть между этими двумя предельными значениями. Во многих случаях простой анализ границ, такой как этот, приводит к ответу, который «достаточно хорошо» подходит для данной цели, но давайте предположим, что это не так. Используя приведенные выше уравнения преобразования треугольник→звезда, мы сначала определяем сумму сопротивлений резисторов треугольника.

\[R_{ΔS}=100+150+470=720 \; Ом\]

А затем находим значение R₁, перемножив сопротивления двух резисторов, которые подключены к верхнему контакту, и разделив это произведение на сумму всех трех сопротивлений.

\[R_1={100⋅470 \over 720}=65,28 \; Ом\]

Повторим это же для R₂.

\[R_2={100⋅150 \over 720}=20,83 \; Ом\]

Мы могли бы повторить это еще раз для R₃, но давайте, вместо этого, определим R₃, используя свойства отношений.

\[{R_3 \over R_1}={150 \over 100}⇒R_3=1,5R_1=97,92 \; Ом\]

Теперь, когда у нас есть все сопротивления для эквивалентной схемы звезда, мы можем очень легко определить общее сопротивление.

\[R_{экв.}=R_1+[(R_2+220)||(R_3+330)]=219,4 \; Ом\]

Поскольку это значение находится между нашими минимальной и максимальной границами, мы полностью уверены, что это правильный ответ, или, даже если мы допустили ошибку, наш ответ довольно близок к правильному. Поэтому суммарный ток равен

\[I={12\; В \over 219,4 \; Ом}=54,7 \; мА\]

Заключение

Теперь мы увидели, что преобразования треугольник/звезда полезны, и, что более важно, увидели, как их можно легко выполнить, используя не более чем концепцию эквивалентных сопротивлений с использованием последовательных/параллельных комбинаций резисторов. Это может хорошо вам помочь, поскольку дает вам возможность вывести эти формулы на лету, если когда-нибудь возникнет в них необходимость, и у вас не будет подходящего справочного материала. Но что еще более важно, это должно служить для более прочного закрепления фундаментальных понятий в наборе инструментов, который хранится у вас в голове, позволяя вам использовать в своей работе еще более эффективные навыки анализа цепей.

В конце мы должны принять к сведению распространенное заблуждение, заключающееся в том, что преобразования треугольник↔звезда являются ЕДИНСТВЕННЫМ способом анализа цепей, которые нельзя уменьшить другими способами. В действительности, хотя эти преобразования могут сделать нашу жизнь проще, они не обязательны, поскольку ЛЮБОЙ контур, который можно проанализировать с их помощью, также можно проанализировать с помощью правил Кирхгофа, либо напрямую, либо с помощью одного из более формализованных методов их применения, включая метод контурных токов или метод узловых напряжений, а также с методиками, такими как эквивалентная схема Тевенина.

Оригинал статьи:

• William Bahn. Delta/Wye Transforms: Behind the Scenes

Теги

Анализ цепейТреугольник-звезда

Теория и исследование преобразования «Дельта-звезда»

Существуют схемы, которые имеют дифференцированную топологию и которые не могут быть
решая их с помощью обычных последовательных и параллельных схем.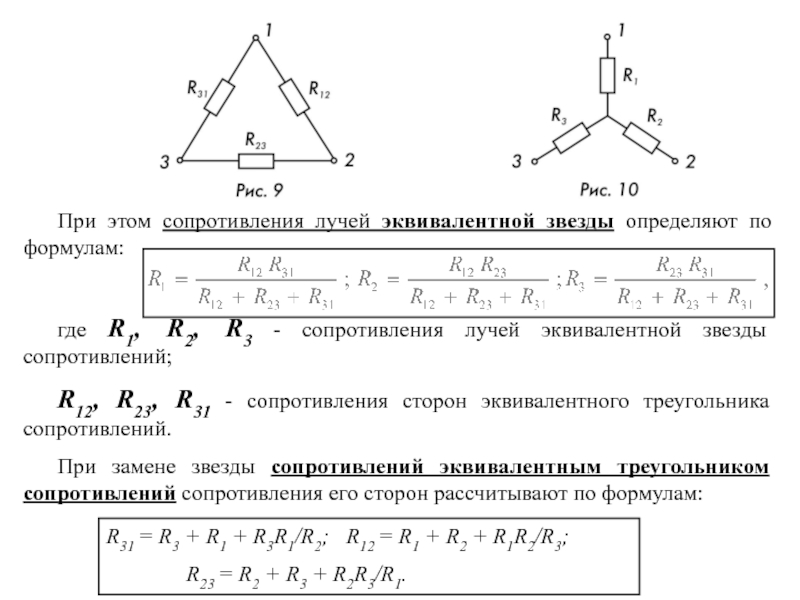 Те
цепи, в зависимости от их строения, называются
«Дельта-схемы (или треугольник, или пи)»
и  «Звездные цепи (или T, или Y )».

Однако есть возможность трансформировать Дельту
в цепи звезды и наоборот, как мы изучим позже. мы увидим, что
этот инструмент разрешения схемы незаменим для тех, кто хочет большего
углубление в изучении электрических схем.

2. Цепи Delta

На рисунке 05-01 мы видим топологию схемы треугольник или треугольник.
На рисунке 05-02 представлена ​​топология схемы Pi. Обратите внимание, что
две схемы идентичны, меняется только способ их прорисовки и номинал.

Рисунок 05-01                            Рисунок 05-02

3. Звездные схемы

На рисунке 05-03 мы видим топологию схемы звезда.
На рисунке 05-04 представлена ​​топология схемы T. Опять же, обратите внимание, что
две схемы идентичны, меняется только способ их прорисовки и номинал.

Рисунок 05-03                            Рисунок 05-04

4. Эквивалентность цепей Delta-Star

Давайте изучим, как мы можем преобразовать схему треугольника или треугольника в схему
Звезда или Y. Обратите внимание, что после использования формул преобразования схема треугольника или треугольника заменяется схемой звезды или Y, то есть мы заменили схему, показанную на рисунке 05-05, схемой, показанной на
Рисунок 05-06.

Рисунок 05-05                            Рисунок 05-06

Уравнения для преобразования схемы «треугольник» или «треугольник» в схему «звезда» или «Y»
показаны ниже.

экв. 05-01

экв. 05-02

экв. 05-03

Обратите внимание, что знаменатели трех уравнений идентичны, то есть это сумма трех
резисторы, из которых состоит цепь. Числитель образован произведением двух
резисторы, рядом с которыми мы хотим вычислить их значение.

5. Эквивалентность цепей звезда и треугольник

Теперь давайте посмотрим, как мы можем преобразовать схему звезды или Y в схему
Дельта или треугольник. Обратите внимание, что после использования формул преобразования схема «Звезда» или «Y» заменяется схемой «Треугольник» или «Треугольник», то есть мы заменили схему, показанную на рисунке 05-07, схемой, показанной на рисунке 05-08.

Рисунок 05-07                            Рисунок 05-08

Уравнения, позволяющие преобразовать схему звезды (или Y ) в
Треугольник (или Дельта) показаны ниже.

экв. 05-04

экв. 05-05

экв. 05-06

Обратите внимание, что числители трех уравнений идентичны, то есть это сумма произведения
резисторов, составляющих цепь, два к двум. Знаменатель формируется
только на значение сопротивления, которое находится на стороне, противоположной нужному нам сопротивлению
рассчитать его значение.
Другими словами, если мы хотим вычислить значение R ₁ , мы должны
заметьте, что на противоположной стороне у нас есть точка с, и в этой точке она
связан с сопротивлением R _c .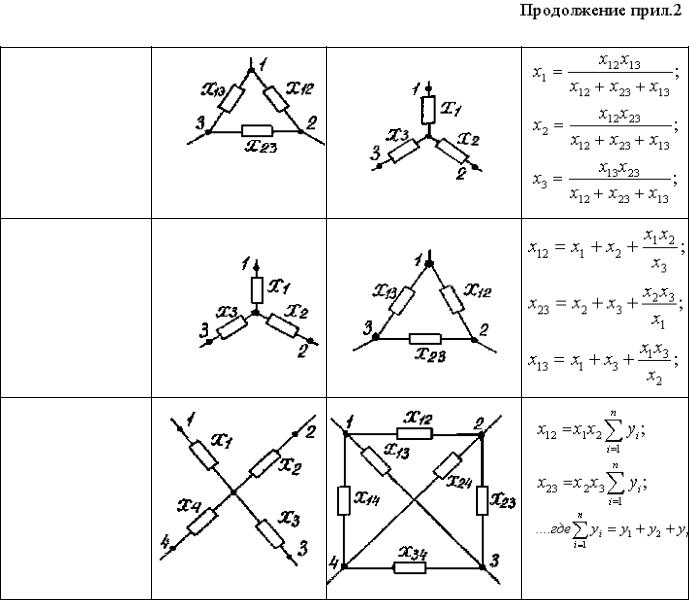 Поэтому мы должны использовать
R _c в знаменателе. Для расчета других сопротивлений
мы используем те же рассуждения, которые облегчают запоминание.

6.     Эквивалентность цепей треугольник-звезда     для конденсаторов

Когда у нас есть схемы треугольник-звезда с конденсаторами, мы используем тот же принцип, что и
используем для резисторов, только сделав замену в уравнениях R
по 1/с.
См. рисунок 05-09.преобразованная схема и ее уравнения для расчета
стоимость конденсаторов.

Рисунок 05-09

Это уравнение можно обработать алгебраически, чтобы получить более простую форму.
См. ниже уже преобразованные три уравнения.

экв. 05-07

экв. 05-08

экв. 05-09

Обратите внимание, что эти уравнения аналогичны тем, которые используются с сопротивлениями для случая преобразования
Звезда-Треугольник.

7.     Эквивалентность цепей звезда-треугольник
для конденсаторов

Для схемы Звезда-Треугольник используется тот же принцип, что и в предыдущем пункте.
На рисунке 05-10 мы видим преобразованную схему и соответствующие уравнения для расчета
конденсаторы.

Рисунок 05-10

Это уравнение можно обработать алгебраически, чтобы получить более простую форму.
См. ниже уже преобразованные три уравнения. Уравнения, аналогичные тем, которые используются для сопротивлений
в преобразовании Треугольник-Звезда.

экв. 05-10

экв. 05-11

экв. 05-12

---


Наверх


Предыдущая глава


Следующая глава


---

Объяснение преобразования звезда-треугольник с советами по запоминанию формул звезда и мы делаем
это когда наши резисторы не соединены параллельно или последовательно.



Этот метод весьма полезен, но в большинстве случаев учащиеся забывают формулу для быстрого использования, но,
в
В этом разделе я дам вам наглядный совет, чтобы никогда не забывать об этом, так что давайте начнем.

Способ соединения треугольника и звезды проиллюстрирован ниже в сравнении с последовательностью и последовательностью.
параллельное соединение резисторов.

Дельта может быть структурирована двумя способами как треугольник
форму или форму пирога, в то время как звезда имеет
звезда или Т-образная форма, поэтому обязательно обратите внимание на это.

Маленький самородок

Звезду иногда называют звездой, а дельту — буквой Пи.

Преобразование или преобразование из треугольника в звезду

Пока мы будем решать схемы, иногда мы сталкиваемся с резисторами, соединенными в форме, которая
не легче работать, за исключением того, что мы преобразуем его в другую форму, а затем решаем, поэтому мы
выполнить это преобразование.

Итак, чтобы преобразовать дельту в звезду, это делается следующим образом, хотя формула указана как —

Формула преобразования дельты в звезду

Как запомнить формулу преобразования дельты в звезду

Итак, давайте вспомним эту формулу начиная с R ₁ .

Глядя на R ₁ , мы видим, что узел в верхней части R ₁ имеет два резистора.
из дельта сети,
связаны или привязаны к нему. Таким образом, в этом случае мы говорим, что есть 2 ноги, влияющие на R ₁ , которые
R _и и
Р _б .

Затем, поскольку дельта является нашим источником преобразования и также соединены последовательно (помните в
резисторы, соединенные последовательно, значения складываются и через них протекает одинаковый ток) поэтому,
суммируем (R _a + R _b + R _c ), а затем разделить на наш первый результат
это R _a и R _b (помните, что нам нужно
умножить _{рэндов на} и _{рэндов b на} , поскольку они влияют на _{рэндов 1} ).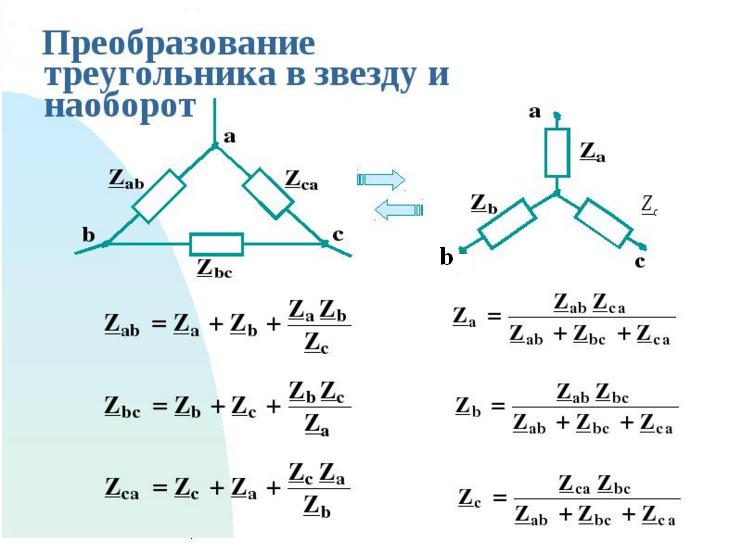

Таким образом, преобразование дает R ₁ = (R _a R _b ) / (R _a +
R _b + R _c ).

Проделав то же самое для R ₂ , получим
Р ₂ = (Р _a Р _c ) / (R _a + R _b + R _c )
а за R ₃ что будет если сделать самому не глядя в ответ.

Если вы получили ответ
правильно, это хорошо и по существу видно, это только ножка, привязанная к нашему резистору в фокусе
имеет значение, поскольку нижняя часть (R _a + R _b + R _c ) одинакова для
R ₁ , R ₂ и R ₃ .

Преобразование или преобразование из звезды в треугольник

Во-первых, в этом преобразовании мы должны найти R _a , R _b и R _c как
напротив последнего раздела, где мы должны найти R ₁ , R ₂ и R ₃ .

Формула записана как

R _a = (R ₁ R ₂ + R ₂ R ₃ +
Р ₃ Р ₁ ) / Р ₃ ,
Р _б = (Р ₁ Р ₂ + Р ₂ Р ₃ +
Р ₃ Р ₁ ) / Р ₂ и
Р _с = (Р ₁ Р ₂ + Р ₂ Р ₃ +
R ₃ R ₁ ) / R ₁

Формула преобразования звезда в треугольник

Как запомнить формулу преобразования звезда в треугольник

Теперь вспомним формулу, используя нашу подсказку. Прежде всего, вы можете видеть, что R _и затронуты
по R ₁ и R ₂ . А это Р ₁ и R ₂ также объединены в
средней точки друг к другу с R ₃ , поэтому в этом случае мы не можем просто применить то же правило, что и
предыдущий мы сделали для преобразования из дельты в звезду.

Но что нам нужно сделать, так это то, что R ₁ и R ₂ привязаны к R _a , а также
R ₁ и R ₂ соединены в узле с R ₃ , тогда мы просто умножаем
R ₁ R ₂ и затем добавить R ₂ R ₃ и в последнюю очередь добавить
R ₃ R ₁ что дает это.

Этот шаг может показаться немного запутанным, но просто повторите его еще раз, пока не поймете, что к чему.
этого.

Подсказка

Если вы посмотрите на два предыдущих изображения, вы обнаружите, где показан шаблон — это также может помочь вспомнить формулу.

Затем после этого мы делим наш первый результат, который равен (R ₁ R ₂ + R ₂ R ₃ + R ₃ R ₁ ) за ногу, противоположную нашей R _a
это R ₃ , или мы можем сказать, что ветвь не связана напрямую с R _a .

Аналогично, R _b = (R ₁ R ₂ + R ₂ R ₃ + R ₃ R _{1 9009 1 ) / Р 2 .}

Примечание

Поскольку верхняя сторона одинакова для всех случаев, а меняется только нижняя, вспомните нижнюю часть как ножку
напротив искомого резистора. И в этом случае R _b и противоположная сторона R ₂ .

Теперь ваша очередь сделать R _c и позже проверить свой ответ.

Наконец, давайте попробуем резюмировать все, что мы только что обсудили, решив несколько примеров.

Пример преобразования треугольника в звезду

Пример 1.