Содержание
конструкция с короткозамкнутым ротором, работа трёхфазного варианта
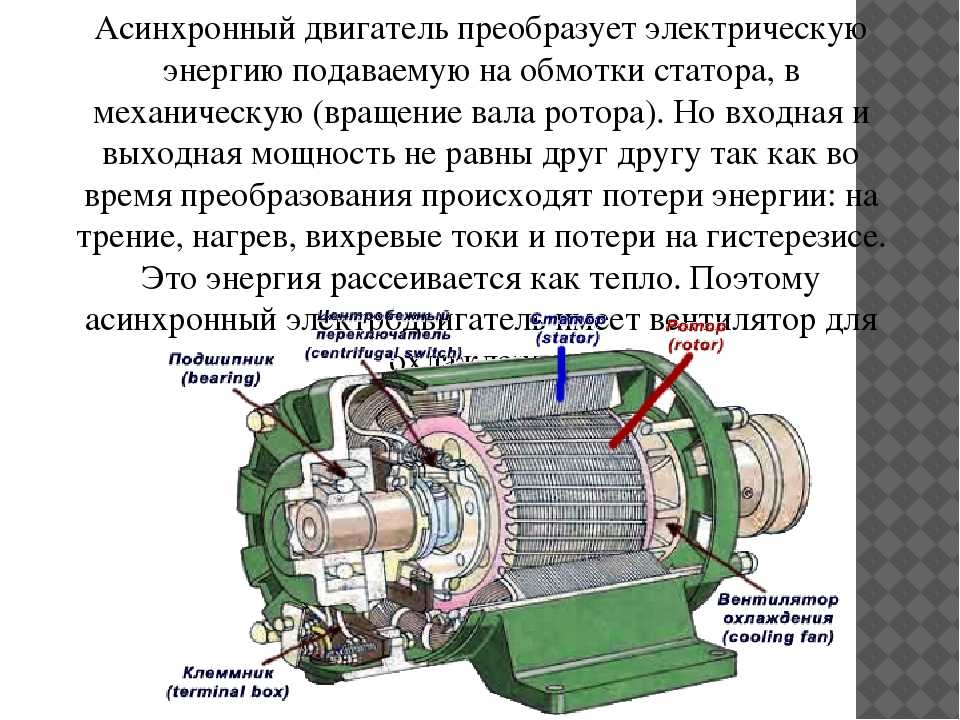
Сегодня трудно встретить механическое электрооборудование без использования асинхронного двигателя с короткозамкнутым ротором. Изобретение позапрошлого века до сих пор активно применяется и совершенствуется. В любой машине есть такое устройство. Благодаря ему жизнь людей вышла на новый уровень. Она стала немыслимой без электромоторов. Не удивительно, что многие желают узнать, как всё это работает.
- Немного истории
- Основное устройство
- Принцип работы
Немного истории
В конце позапрошлого века итальянский учёный Г. Феррарис написал статью с теоретическими выкладками асинхронного электродвигателя. В то же время в 1988 году американский учёный с австро-венгерскими корнями Н. Тесла запатентовал это устройство. А на следующий год российский изобретатель М. О. Доливо-Добравольский придумал и создал первый асинхронный двигатель с короткозамкнутым ротором.
Принцип действия этого устройства до наших дней является основополагающим в работе всех электродвигателей. Сам Михаил Осипович первым применил своё изобретение в деле. В Новороссийске была построена первая электросеть с использованием устройства на трёхфазном асинхронном двигателе. Местный элеватор был оборудован трансформаторами и машинами новой, по тем временам, технологии.
В наши дни трудно представить электромеханику без изобретения Доливо-Добровольского. На разработанных им принципах работают все современные электродвигатели. Вот основные ключи успеха данного изобретения:
- невероятная простота и лёгкость в изготовлении;
- коммерческая выгода. Малые затраты и большой спрос на такие изделия;
- большая эффективность и надёжность — всегда привлекают и обеспечивают постоянный спрос;
- лёгкость в эксплуатации и большой диапазон сфер применения.
Судя уже по этим ключам, спрос на подобные изделия будет большим ещё долгие годы.
К тому же прогресс не стоит на месте, многие изобретатели продолжают усовершенствовать конструкцию двигателя.
Основное устройство
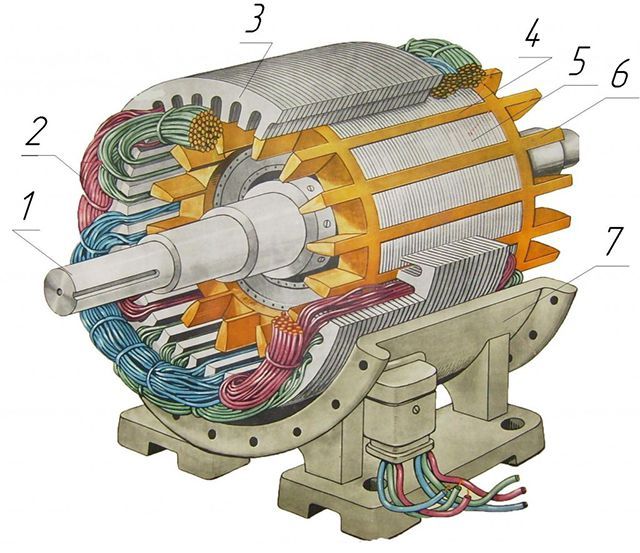
Если внимательно рассмотреть схему асинхронного двигателя, то сразу станет заметным наличие в ней двух основных деталей.
Без статора и ротора этот агрегат просто немыслим. Благодаря им образуется электромагнитное поле и вырабатывается электроток.
Статор обычно имеет статическое положение. Он всегда цилиндрической формы. Делают его из стали. Внутри имеются пазы с уложенной в них обмоткой. Применяют угол в 120 градусов для смещения обмоток относительно друг друга. Соединяют концы обмоток звездой или треугольником — это зависит от подаваемого на прибор напряжения.
Ротор — вращающаяся часть. Он тоже имеет пазы и обмотку. Они бывают двух видов: фазные и короткозамкнутые. Фазные обмотаны как статоры и подсоединяются так же, а короткозамкнутые имеют алюминевый заливной сердечник. «Беличье колесо» — так его называют со времён изобретения.
«Беличье колесо» — так его называют со времён изобретения.
Кроме основных деталей, имеются вспомогательные. Они могут различаться по строению и конструкции, но чаще всего присутствуют на всех двигателях подобного вида. Вот эти детали:
- основной вал, на который крепится ротор;
- подшипники. Без этих деталей просто невозможно сегодня представить подвижные механизмы с быстрым вращением;
- щиты для крепления подшипников;
- лапы для крепления двигателя на месте работы;
- основной кожух, срывающий внутренности двигателя;
- кожух вентилятора. Служит для укрытия лопастей;
- крыльчатка вентилятора. Её основное предназначение — не давать двигателю перегреваться;
- коробка для клемм вывода. Место подсоединения электродвигателя к электропроводке.
В зависимости от модели, устройство трёхфазного асинхронного двигателя может выглядеть по-разному, но, как правило, основные узлы в них присутствуют.
Более современные модели оснащают электронными датчиками и другими приборами, улучшающими удобство их эксплуатации.
Принцип работы
Простота присуща этому двигателю во всём. В том числе и в принципе действия. Трёхфазный асинхронный двигатель использует закон электромагнитной индукции. Как видно из устройства электродвигателя, он состоит из двух электромагнитов. По закону ЭМЭ при вращении возникает движущая сила, которая по закону Ампера будет поддерживать вращение ротора в статере и продолжать вырабатывать ток.
Частоту вращения магнитного поля в статоре вычисляют, поделив частоту переменного тока (умноженную на 60 минут) на число пар полюсов трёхфазной обмотки. Имея эту величину, вычисляют скольжение электродвигателя. Для этого вычитают из частоты вращения ЭМП частоту вращения ротора и делят разность на частоту вращения ЭМП.
На холостом ходу скольжение равно 0, а в фазе короткого замыкания и полной остановки равно 1 или 100%. Чем больше механическая нагрузка на вал вращения, тем выше показатель скольжения. Для электродвигателей определяется номинальное скольжение. Для малых и средних мощностей этот показатель варьируется в пределах от 8 до 2%.
Чем больше механическая нагрузка на вал вращения, тем выше показатель скольжения. Для электродвигателей определяется номинальное скольжение. Для малых и средних мощностей этот показатель варьируется в пределах от 8 до 2%.
Сфера применения электродвигателей настолько обширна, что трудно представить, что станет с жизнью человека, если исчезнут все такие устройства. Однако, они не только не исчезают, но и наоборот, их становиться всё больше. Это способствует дальнейшему научному прогрессу человечества.
§76. Асинхронный двигатель с короткозамкнутым ротором
Асинхронный двигатель с короткозамкнутым ротором (рис. 249 и 250) состоит из следующих основных частей: статор с трехфазной обмоткой, ротор с короткозамкнутой обмоткой и остов. Обмотка ротора выполнена бесконтактной (она не соединена ни с какой внешней цепью), что определяет высокую надежность такого двигателя.
Магнитная система. Асинхронная машина в отличие от машины постоянного тока не имеет явно выраженных полюсов. Такую магнитную систему называют неявнополюсной. Число полюсов в машине определяется числом катушек в обмотке статора и схемой их соединения. В четырехполюсной машине (рис. 251) магнитная система состоит из четырех одинаковых ветвей, по каждой из которых проходит половина магнитного потока Фп одного полюса, в двухполюсной машине таких ветвей две, в шестиполюсной — шесть и т. д. Так как через все элементы магнитной системы проходит переменный магнитный поток, то не только ротор 1, но
Рис. 249. Асинхронный двигатель с короткозамкнутым ротором: 1 — остов; 2 — статор; 3 — ротор; 4 — стержни обмотки ротора; 5 — подшипниковый щит; 6 — вентиляционные лопатки ротора; 7 — вентилятор; 8 — коробка выводов
Рис. 250. Электрическая схема асинхронного двигателя с короткозамкнутым ротором (а) и его условное графическое изображение (б): 1 — статор; 2 — ротор
Рис. 251. Магнитное поле четырехполюсной асинхронной машины
251. Магнитное поле четырехполюсной асинхронной машины
Рис. 252. Листы ротора (а) и статора (б)
Рис. 253. Пакет собранного статора (а) и статор с обмоткой (б)
и статор 2 выполняют из листов электротехнической стали (рис. 252), изолированных один от другого изоляционной лаковой пленкой, окалиной и пр. В результате этого уменьшается вредное действие вихревых токов, возникающих в стали статора и ротора при вращении магнитного поля. Листы статора и ротора имеют пазы открытой, полузакрытой или закрытой формы, в которых располагаются проводники соответствующих обмоток. В статоре чаще всего применяют полузакрытые пазы прямоугольной или овальной формы, в машинах большой мощности — открытые пазы прямоугольной формы.
Сердечник статора 1 (рис. 253, а) запрессовывают в литой остов 3 и укрепляют стопорными винтами. Сердечник ротора напрессовывают на вал ротора, который вращается в шариковых подшипниках, установленных в двух подшипниковых щитах. Воздушный зазор между статором и ротором имеет минимальный размер, допускаемый с точки зрения точности сборки и механической жесткости конструкции. В двигателях малой и средней мощности воздушный зазор обычно составляет несколько десятых миллиметра. Такой зазор обеспечивает уменьшение магнитного сопротивления магнитной цепи машины, а следовательно, и уменьшение намагничивающего тока, требуемого для создания в двигателе магнитного потока. Снижение намагничивающего тока позволяет повысить коэффициент мощности двигателя.
Воздушный зазор между статором и ротором имеет минимальный размер, допускаемый с точки зрения точности сборки и механической жесткости конструкции. В двигателях малой и средней мощности воздушный зазор обычно составляет несколько десятых миллиметра. Такой зазор обеспечивает уменьшение магнитного сопротивления магнитной цепи машины, а следовательно, и уменьшение намагничивающего тока, требуемого для создания в двигателе магнитного потока. Снижение намагничивающего тока позволяет повысить коэффициент мощности двигателя.
Обмотка статора. Она выполнена в виде ряда катушек из проволоки круглого или прямоугольного сечения. Проводники, находящиеся в пазах, соединяются, образуя ряд катушек 2 (рис. 253,б). Катушки разбивают на одинаковые группы по числу фаз, которые располагают симметрично вдоль окружности статора (рис. 254, а) или ротора. В каждой такой группе все катушки электрически соединяются, образуя одну фазу обмотки, т. е. отдельную электрическую цепь. При больших значениях фазного тока или при необходимости переключения отдельных катушек фазы могут иметь несколько параллельных ветвей. Простейшим элементом обмотки является виток (рис. 254,б), состоящий из двух проводников 1 и 2, размещенных в пазах, находящихся друг от друга на неко-
Простейшим элементом обмотки является виток (рис. 254,б), состоящий из двух проводников 1 и 2, размещенных в пазах, находящихся друг от друга на неко-
Рис. 254. Расположение катушек трехфазной обмотки на статоре асинхронного двигателя (а) и виток из двух проводников (б)
тором расстоянии у. Это расстояние приблизительно равно одному полюсному делению т, под которым понимают длину дуги, соответствующую одному полюсу.
Обычно витки, образованные проводниками, лежащими в одних и тех же пазах, объединяют в одну или две катушки. Иногда их называют секциями. Их укладывают таким образом, что в каждом пазу размещается одна сторона катушки или две стороны — одна над другой. В соответствии с этим различают одно- и двухслойные обмотки. Основным параметром, определяющим распределение обмотки по пазам, является число пазов q на полюс и фазу.
В обмотке статора двухполюсного двигателя (см. рис. 254, а) каждая фаза (А-Х; B-Y; C-Z) состоит из трех катушек, стороны которых расположены в трех смежных пазах, т. е. q = 3. Обычно q > 1, такая обмотка называется распределенной.
е. q = 3. Обычно q > 1, такая обмотка называется распределенной.
Наибольшее распространение получили двухслойные распределенные обмотки. Их секции 1 (рис. 255, а) укладывают в пазы 2 статора в два слоя. Проводники обмотки статора укрепляют в пазах текстолитовыми клиньями 5 (рис. 255,б), которые закладывают у головок зубцов.
Стенки паза покрывают листовым изоляционным материалом 4 (электрокартоном, лакотканью и пр.). Проводники, лежащие в пазах, соединяют друг с другом соответствующим образом с торцовых сторон машины. Соединяющие их провода называют лобовыми частями. Так как лобовые части не принимают участия в индуцировании э. д. с, их выполняют как можно короче.
Отдельные катушки обмотки статора могут соединяться «звездой» или «треугольником». Начала и концы обмоток каждой фазы выводят к шести зажимам двигателя.
Обмотка ротора. Обмотка ротора выполнена в виде беличьей клетки (рис. 256,а). Она сделана из медных или алюминиевых стержней, замкнутых накоротко с торцов двумя кольцами (рис. 256,б). Стержни этой обмотки вставляют в пазы ротора без какой-либо изоляции, так как напряжение в короткозамкну-
256,б). Стержни этой обмотки вставляют в пазы ротора без какой-либо изоляции, так как напряжение в короткозамкну-
Рис. 255. Двухслойная обмотка статора асинхронного двигателя: 1 — секция; 2 — паз; 3 — проводник; 4 — изоляционный материал; 5 — клин; 6 — зубец
Рис. 256. Короткозамкнутый ротор: а — беличья клетка; б — ротор с беличьей клеткой из стержней; в — ротор с литой беличьей клеткой; 1 — короткозамыкающие кольца; 2— стержни; 3— вал; 4 — сердечник ротора; 5 — вентиляционные лопасти; 6 — стержни литой клетки
той обмотке ротора равно нулю. Пазы короткозамкнутого ротора обычно выполняют полузакрытыми, а в машинах малой мощности — закрытыми (паз имеет стальной ободок, отделяющий его от воздушного зазора). Такая форма паза позволяет хорошо укрепить проводники обмотки ротора, хотя и несколько увеличивает ее индуктивное сопротивление.
В двигателях мощностью до 100 кВт стержни беличьей клетки обычно получают путем заливки расплавленного алюминия в пазы сердечника ротора (рис. 256, в). Вместе со стержнями беличьей клетки отливают и соединяющие их торцовые короткозамыкающие кольца.
256, в). Вместе со стержнями беличьей клетки отливают и соединяющие их торцовые короткозамыкающие кольца.
Для этой цели пригоден алюминий, так как он обладает малой плотностью, достаточно высокой электропроводностью и легко плавится.
Обычно двигатели имеют вентиляторы, насаженные на вал ротора. Они осуществляют принудительную вентиляцию нагретых частей машины (обмоток и стали статора и ротора), позволяя получить от двигателя большую мощность. В двигателях с короткозамкнутым ротором лопасти вентилятора часто отливают совместно с боковыми кольцами беличьей клетки (см. рис. 256, в).
Асинхронные двигатели с короткозамкнутым ротором просты по конструкции, надежны в эксплуатации. Их широко применяют для привода металлообрабатывающих станков и других устройств, которые начинают работать без нагрузки. Однако сравнительно малый пусковой момент у этих двигателей и большой пусковой ток не позволяют использовать их для привода таких машин и механизмов, которые должны пускаться в ход сразу под большой нагрузкой (с большим пусковым моментом). К таким машинам относятся грузоподъемные устройства, компрессоры и др.
К таким машинам относятся грузоподъемные устройства, компрессоры и др.
Увеличить пусковой момент и уменьшить пусковой ток можно при выполнении беличьей клетки с повышенным активным сопротивлением. При этом двигатель будет иметь увеличенное скольжение и большие потери мощности в обмотке ротора. Такие двигатели называют двигателями с повышенным скольжением (обозначаются АС). Их можно использовать для привода машин, работающих сравнительно небольшое время. На э. п. с. переменного тока эти двигатели (со скольжением до 10%) применяют для привода компрессоров, которые работают периодически в течение коротких промежутков времени при уменьшении давления в воздушных резервуарах ниже определенного предела.
Двигатели с повышенным пусковым моментом. Короткозамкнутые асинхронные двигатели с повышенным пусковым моментом имеют специальную конструкцию ротора (обозначаются АП). К ним относятся двигатели с двойной беличьей клеткой и двигатели с глубокими пазами.
Ротор 3 (рис. 257,а) двигателя с двойной беличьей клеткой имеет две короткозамкнутые обмотки. Наружная клетка 1 является пусковой. Она обладает большим активным и малым реактивным сопротивлениями. Внутренняя клетка 2 является основной обмоткой ротора; она, наоборот, обладает незначительным активным и большим реактивным сопротивлениями. В начальный момент пуска ток проходит, главным образом, по наружной клетке, которая создает значительный вращающий момент. По мере увеличения частоты вращения ток переходит во внутреннюю клетку, и по окончании процесса пуска машина работает как обычный короткозамкнутый двигатель с одной (внутренней) клеткой. Вытеснение тока в наружную клетку в начальный момент пуска объясняется действием, э. д. с. самоиндукции, индуцируемой в проводниках ротора. Чем ниже расположен в пазу проводник, тем большим магнитным потоком рассеяния 6 он охватывается и тем большая э. д. с. самоиндукции в нем индуцируется (рис. 257, в), следовательно, тем большее он будет иметь индуктивное сопротивление.
257,а) двигателя с двойной беличьей клеткой имеет две короткозамкнутые обмотки. Наружная клетка 1 является пусковой. Она обладает большим активным и малым реактивным сопротивлениями. Внутренняя клетка 2 является основной обмоткой ротора; она, наоборот, обладает незначительным активным и большим реактивным сопротивлениями. В начальный момент пуска ток проходит, главным образом, по наружной клетке, которая создает значительный вращающий момент. По мере увеличения частоты вращения ток переходит во внутреннюю клетку, и по окончании процесса пуска машина работает как обычный короткозамкнутый двигатель с одной (внутренней) клеткой. Вытеснение тока в наружную клетку в начальный момент пуска объясняется действием, э. д. с. самоиндукции, индуцируемой в проводниках ротора. Чем ниже расположен в пазу проводник, тем большим магнитным потоком рассеяния 6 он охватывается и тем большая э. д. с. самоиндукции в нем индуцируется (рис. 257, в), следовательно, тем большее он будет иметь индуктивное сопротивление.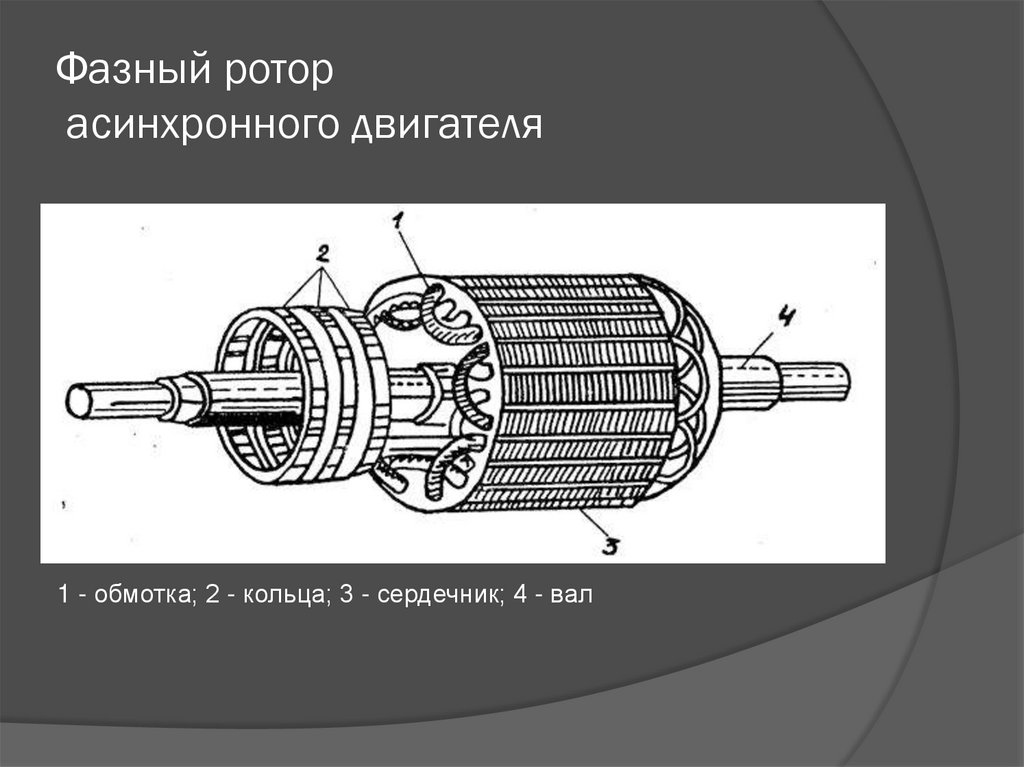
Вытеснение тока в верхние проводники ротора сильно сказывается при неподвижном роторе, когда частота тока, индуцируемого в обеих клетках ротора, велика. При этом индуктивные
Рис. 257. Конструкция роторов асинхронных двигателей с повышенным пусковым моментом: с двойной беличьей клеткой (а), с глубокими пазами (б) и разрезы их пазов (в и г)
сопротивления обеих клеток значительно больше активных и ток распределяется между ними обратно пропорционально их индуктивным сопротивлениям, т. е. проходит в основном по наружной клетке с большим активным сопротивлением. По мере возрастания частоты вращения ротора частота тока в нем будет уменьшаться (вращающееся магнитное поле будут пересекать проводники ротора с меньшей частотой), и ток начнет проходить по обеим клеткам в соответствии с их активными сопротивлениями, т. е., главным образом, через внутреннюю клетку.
Таким образом, процесс пуска двигателя с двойной беличьей клеткой имеет сходство с процессом пуска асинхронного двигателя с фазным ротором, когда в начале пуска в цепь обмотки ротора вводится добавочное активное сопротивление (пусковой реостат), а по мере разгона это сопротивление выводится. Точно так же и в рассматриваемом двигателе ток в начале пуска проходит по наружной клетке с большим активным сопротивлением, а затем по мере разгона постепенно переходит во внутреннюю клетку с малым активным сопротивлением.
Точно так же и в рассматриваемом двигателе ток в начале пуска проходит по наружной клетке с большим активным сопротивлением, а затем по мере разгона постепенно переходит во внутреннюю клетку с малым активным сопротивлением.
Для повышения активного сопротивления пусковой клетки стержни ее изготовляют из маргацовистой латуни или бронзы. Стержни рабочей клетки выполняют из меди, обладающей малым удельным сопротивлением, причем площадь поперечного сечения их больше, чем у пусковой клетки. В результате этого активное сопротивление пусковой клетки увеличивается в 4—5 раз по сравнению с рабочей. Между стержнями обеих клеток имеется узкая щель 5, размеры которой определяют индуктивность рабочей клетки. Двухклеточный двигатель на 20—30% дороже коротко-замкнутого двигателя обычной конструкции. Для упрощения технологии изготовления ротора двухклеточные двигатели небольшой и средней мощности выполняют с литой алюминиевой клеткой.
Действие двигателей с глубокими пазами (рис. 257, б) также основано на использовании явления вытеснения тока.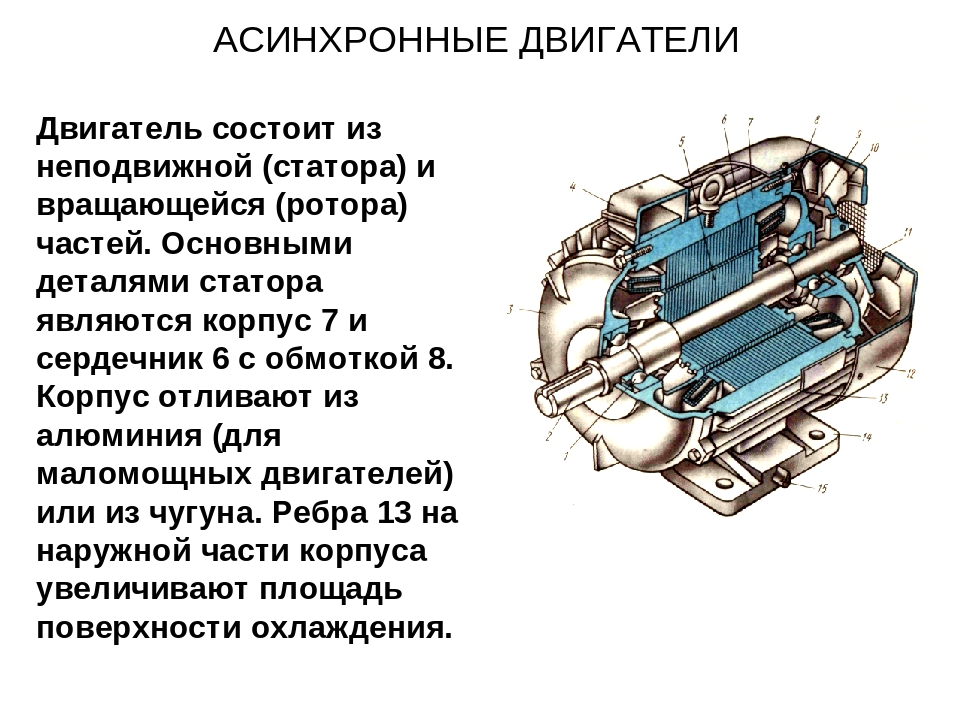 В этих двигателях стержни 4 беличьей клетки выполнены в виде узких медных шин, заложенных в глубокие пазы ротора 3 (высота паза в 10— 12 раз больше его ширины). Нижние слои стержней, расположенные дальше от поверхности ротора, охватываются значительно большим числом магнитных линий потока рассеяния 6, чем верхние (рис. 257,г), поэтому они имеют во много раз большую индуктивность. В начале пуска в результате увеличенного индуктивного сопротивления нижних частей стержней ток проходит, главным образом, по их верхним частям. При этом используется только небольшая часть поперечного сечения каждого стержня, что приводит к увеличению его активного сопротивления, а следовательно, и к возрастанию активного сопротивления всей обмотки ротора.
В этих двигателях стержни 4 беличьей клетки выполнены в виде узких медных шин, заложенных в глубокие пазы ротора 3 (высота паза в 10— 12 раз больше его ширины). Нижние слои стержней, расположенные дальше от поверхности ротора, охватываются значительно большим числом магнитных линий потока рассеяния 6, чем верхние (рис. 257,г), поэтому они имеют во много раз большую индуктивность. В начале пуска в результате увеличенного индуктивного сопротивления нижних частей стержней ток проходит, главным образом, по их верхним частям. При этом используется только небольшая часть поперечного сечения каждого стержня, что приводит к увеличению его активного сопротивления, а следовательно, и к возрастанию активного сопротивления всей обмотки ротора.
При увеличении частоты вращения ротора вытеснение тока в верхние части стержней уменьшается (по той же причине, что и в двигателе с двойной беличьей клеткой), и после окончания пуска ток равномерно распределяется по площади их поперечного сечения.
Типы ротора трехфазного асинхронного двигателя
следующий → Существует два типа роторов асинхронных двигателей:
Ротор с короткозамкнутым ротором:Двигатель с короткозамкнутым ротором работает по принципу Электромагнетизм . Он состоит из ротора, статора и других частей, таких как подшипники, цилиндрический многослойный сердечник, вал и т. д. Функция подшипников в двигателе с короткозамкнутым ротором заключается в уменьшении трения между вращающимися и неподвижными частями машины. Ротор двигателя состоит из цилиндрического многослойного сердечника с параллельными пазами для несущих проводников ротора. Проводники ротора не являются проводами, а состоят из тяжелых стержней из меди, алюминия или сплава. Вал используется в двигателе для передачи механической энергии от машины или к машине. Статор – это внешняя неподвижная часть двигателя. Рисунок: ротор с клеткой Преимущества перекоса проводников короткозамкнутого ротора:
Ротор с обмоткой или ротор с контактными кольцами:Раневой ротор состоит из якоря с прорезями. Изолированные жилы вставлены в пазы и соединены в трехфазную двухслойную распределенную обмотку, аналогичную обмотке статора. Обмотки ротора соединены в звезду. Обмотки ротора распределены равномерно и обычно соединены в звезду с выводами, выведенными из машины через контактные кольца, установленные на валу. Токосъемные кольца нарезаются с помощью медных угольных щеток. Конструкция ротора с обмоткой обычно используется для машин большого размера, где требования к пусковому крутящему моменту являются строгими. Внешнее сопротивление может быть добавлено в цепь ротора через токосъемное кольцо для уменьшения пускового тока и одновременно пускового момента. Рисунок: Асинхронный двигатель с контактными кольцами Разница между ротором с клеткой и ротором с обмоткой:Преимущества короткозамкнутого ротора:
Преимущества фазных роторов:
Next Topic Тест без нагрузки и блокировки ротора ← предыдущая |
Для видео Присоединяйтесь к нашему каналу Youtube: Присоединяйтесь сейчас
Обратная связь
- Отправьте свой отзыв на [email protected]
Помогите другим, пожалуйста, поделитесь
Изучите последние учебные пособия
Подготовка
Современные технологии
Б.
 Тех / МСА
Тех / МСА
Поле-ориентированное управление ротором (RFOC) асинхронной машины
Содержание
В этом техническом примечании представлена возможная реализация роторного поля-ориентированного управления (RFOC) асинхронной машины (IM) с короткозамкнутым ротором.
Во-первых, в примечании представлены общие принципы работы RFOC. Затем объясняется, как электрическая скорость и положение статора могут быть оценены по механической скорости ротора.
Наконец, представлена практическая реализация управления, нацеленная на B-Box RCP или B-Board PRO с ACG SDK на Simulink. Обратите внимание, что компания imperix предлагает готовую к использованию систему привода двигателя для разработки и тестирования методов управления двигателем. Более подробную информацию можно найти в кратком руководстве Motor Testbench.
Программные ресурсы
Пример кода готов к использованию с Motor Testbench. В него входят:
- асинхронная машина с управлением по полю ротора и регулятором скорости
- синхронная машина с постоянными магнитами для нагрузки АД.

Машины смоделированы с помощью Simscape Electrical. Для запуска моделей в режиме симуляции требуется Matlab R2022a (или более поздней версии).
TN139_Motor_TB_RFOCЗагрузить
Общие принципы управления полем ротора
В техническом примечании TN111 представлены принципы управления полем (FOC) для синхронной машины с постоянными магнитами (PMSM). В случае асинхронной машины с короткозамкнутым ротором [1] общая идея та же: поток и крутящий момент контролируются независимо в эталонной вращающейся системе координат (RRF) с помощью, соответственно, компонентов d и q тока статора. .
Однако между СДПМ и АД есть два ключевых отличия [2]: ротор АД механически не синхронен с потоком статора. Более того, АД не имеет постоянных магнитов на роторе: вместо этого ротор намагничивается от статора. Следовательно, FOC от PMSM должен быть адаптирован с учетом этих ключевых отличий.
Выбор ориентации
Как упоминалось выше, ротор не обязательно вращается с той же скоростью, что и статор (с точки зрения механики). Следовательно, в отличие от PMSM (TN111), существует несколько способов ориентации RRF для IM. Раздельное управление величинами крутящего момента и потока может быть достигнуто путем ориентации RRF на поток статора, поток ротора или поток воздушного зазора [3]. В этой заметке Полево-ориентированное управление ротором (RFOC) выбрано из-за его простоты и более высокой динамики крутящего момента [3].
Следовательно, в отличие от PMSM (TN111), существует несколько способов ориентации RRF для IM. Раздельное управление величинами крутящего момента и потока может быть достигнуто путем ориентации RRF на поток статора, поток ротора или поток воздушного зазора [3]. В этой заметке Полево-ориентированное управление ротором (RFOC) выбрано из-за его простоты и более высокой динамики крутящего момента [3].
В асинхронной машине частота потока ротора представляет собой сумму механической частоты и частоты скольжения [4]. Механическую частоту можно измерить, но проскальзывание должно быть оценено, как описано в разделе , посвященном ориентации RRF.
Моделирование на уровне системы
Независимое управление \(I_{ds}\) и \(I_{qs}\) может состоять из двух ПИ-регуляторов с развязывающей сетью, как и любая стратегия векторного управления [1]. Алгоритм FOC обычно генерирует опорное напряжение, которое ШИМ-модулятор преобразует в стробирующие сигналы для инвертора источника напряжения. В настоящей реализации измерение положения ротора производится с помощью инкрементного энкодера. На рисунке ниже показана полная блок-схема реализации с ШИМ-модулятором на основе несущей и модулем кодера/декодера. Обратите внимание, что в качестве альтернативы можно использовать модуляцию пространственного вектора для улучшения использования шины постоянного тока.
В настоящей реализации измерение положения ротора производится с помощью инкрементного энкодера. На рисунке ниже показана полная блок-схема реализации с ШИМ-модулятором на основе несущей и модулем кодера/декодера. Обратите внимание, что в качестве альтернативы можно использовать модуляцию пространственного вектора для улучшения использования шины постоянного тока.
Блок-схема управления по полю ротора
В этом примечании все скорости и углы выражены в виде электрических величин.
- \(\omega _m\) : механическая скорость ротора (неподвижная система отсчета)
- \(\omega _r\) : скорость потока ротора (неподвижная система отсчета)
- \(\omega _s \) : скорость потока статора (стационарная система отсчета)
- \(\omega _{slip} = \omega _r – \omega _m\) : скорость потока ротора (система отсчета ротора)
Соответствующие углы затем получаются путем интегрирования.
Моделирование асинхронной машины
Теперь, когда мы выбрали ориентацию RRF, нам нужно установить модель машины в этом кадре.
Уравнение цепи статора [4]:
$$\displaystyle (1) \qquad \underline{V}_{dqs} = R_s \underline{I}_{dqs} + \frac{d \ underline{\Psi}_{dqs}}{dt} + j \omega _r \underline{\Psi}_{dqs}$$
Уравнение цепи ротора [4]:
$$\displaystyle (2) \qquad 0 = R_r \underline{I}_{dqr} + \frac{d \underline{\Psi}_{dqr}}{dt} + j (\omega _r – \ omega _m)\underline{\Psi}_{dqr}$$
Затем потоки связываются с токами [4] по формуле:
$$\displaystyle (3) \qquad \underline{\Psi}_{dqs } = L_s \underline{I}_{dqs} + L_m \underline{I}_{dqr} \\ \displaystyle (4) \qquad \underline{\Psi}_{dqr} = L_r \underline{I}_ {dqr} + L_m \underline{I}_{dqs}$$
Наконец, крутящий момент равен [4]:
$$\displaystyle (5) \qquad T_{em} = \frac{3}{2 } p (\Psi _{ds} I_{qs} – \Psi _{qs} I_{ds})$$
В литературе [4] уравнения (1) – (4) обычно используются для создания эквивалентной схемы машины в установившемся режиме, как показано на рисунке ниже. Обратите внимание, что сопротивлением железа часто пренебрегают, потому что I_fe намного меньше других токов.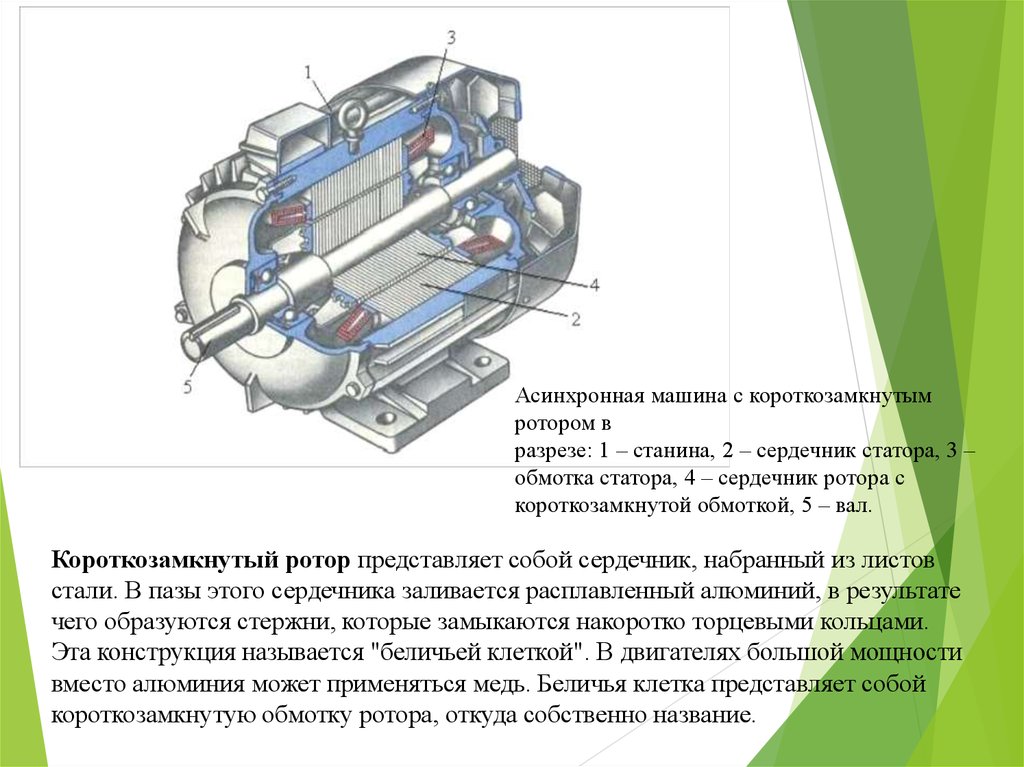
Установившаяся схема замещения асинхронной машины с короткозамкнутым ротором
| Параметр | Обозначение | |
|---|---|---|
| Сопротивление статора | \(R_s1) | |
| Индуктивность статора | \ (L_S \) | |
| Индуктивность утечки статора | \ (L {{\ Gamma S} \) | |
Mutual Inductinab| Parameter | Symbol | |
| Rotor resistance * | \(R_r\) | |
| Rotor inductance * | \(L_r\) | |
| Rotor leakage inductance * | \ (l _ {\ gamma r} \) | |
| Железный сопротивление | \ (r_ {Fe} \) |
* Переменные роттор. 4) ток ротора можно выразить следующим образом:
$$\displaystyle (6) \qquad \underline{I} _{dqr} = \frac{1}{L_r} (\underline{\Psi} _{dqr } – L_m \underline{I}_{dqs})$$
В асинхронной машине с короткозамкнутым ротором нет доступа к цепи ротора.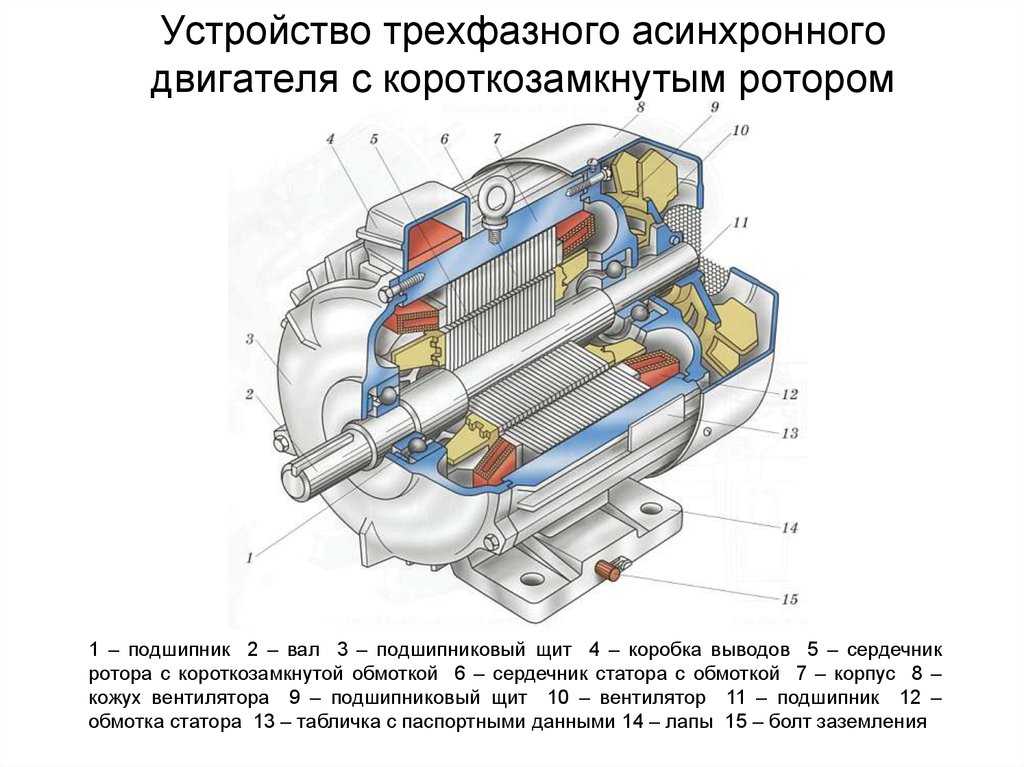 Следовательно, ток ротора \(\underline{I} _r\) не может быть измерен и должен быть исключен из предыдущих выражений. 92}{L_r}$$
Следовательно, ток ротора \(\underline{I} _r\) не может быть измерен и должен быть исключен из предыдущих выражений. 92}{L_r}$$
Аналогичным образом можно исключить \(\underline{I} _r\) из уравнения цепи ротора (2):
$$\displaystyle (8) \qquad \frac{ d \underline{\Psi} _{dqr}}{dt} = \frac{L_m}{T_r} \underline{I} _{dqs} – \left(j (\omega _r – \omega _m) + \frac {1}{T_r}\right) \underline{\Psi} _{dqr} \qquad \text{with} \space T_r = \frac{L_r}{R_r}$$
Управление потоком ротора
Следующий шаг заключается в том, чтобы установить, как управлять потоком ротора. В асинхронной машине с короткозамкнутым ротором нет доступа к цепи ротора и нет постоянных магнитов. Следовательно, ротор должен намагничиваться от статора.
Уравнение (8) предполагает, что потоком ротора можно управлять током статора. Предполагая, что RRF правильно ориентирован на поток ротора, разделим уравнение (8) на его действительную и мнимую части:
$$\displaystyle (9) \qquad \frac{d \Psi _r}{dt} = \ frac{L_m}{T_r} I_{ds} – \frac{1}{T_r} \Psi _r \\ \displaystyle (10) \qquad 0 = \frac{L_m}{T_r} I_{qs} – (\omega _r – \omega _m) \Psi _r$$
Из (9) поток ротора прямо пропорционален току статора по оси d в установившемся режиме:
$$\displaystyle (11) \qquad \Psi _r = L_m I_{ds}$$
Управление крутящим моментом
После намагничивания ротора машина может создавать крутящий момент.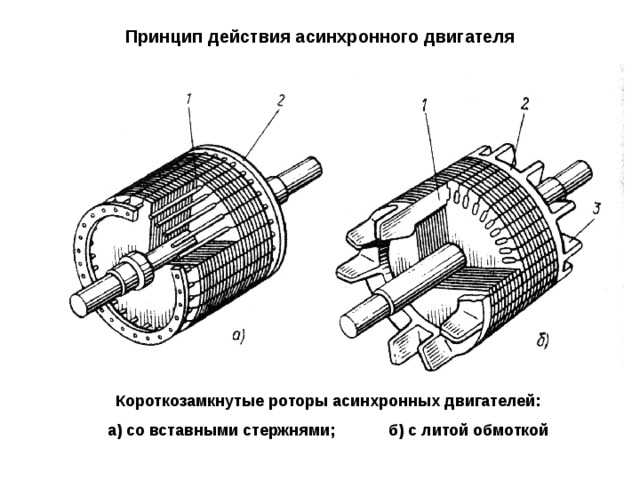 Уравнение (5) описывает крутящий момент как функцию потока и тока статора. Однако в предыдущем разделе мы видели, как управлять потоком ротора, а не потоком статора. К счастью, уравнение (7) описывает связь между потоками статора и ротора.
Уравнение (5) описывает крутящий момент как функцию потока и тока статора. Однако в предыдущем разделе мы видели, как управлять потоком ротора, а не потоком статора. К счастью, уравнение (7) описывает связь между потоками статора и ротора.
Давайте еще раз предположим, что RRF правильно выровнен по потоку ротора. В этом случае уравнение (7) принимает вид:
$$(12) \qquad \left\{ \begin{array}{ll} \displaystyle \Psi _{ds} &= L_{\sigma} I_{ds} + \frac{L_m}{L_r} \ Psi _r \\ \displaystyle \Psi _{qs} &= L_{\sigma} I_{qs} \end{array}\right.$$
Подставляя (12) в (5), можно выразить крутящий момент в зависимости от потока ротора и составляющей тока по оси q.
$$\displaystyle (13) \qquad T_{em} = \frac{3}{2} p \frac{L_m}{L_r} \Psi _r I_{qs}$$
Если поток ротора сохраняется постоянный, крутящий момент тогда прямо пропорционален составляющей тока статора по оси q.
В отличие от СДПМ, составляющая тока АД по оси d также способствует созданию крутящего момента.
Регулятор тока
Как объяснялось в предыдущем разделе, поток ротора и крутящий момент прямо пропорциональны, соответственно, компонентам d и q тока статора. Поэтому ими можно управлять с помощью регулятора тока статора.
Цепь статора описывается (1). Подставив (7) в (1), можно заменить поток статора потоком ротора, которым мы умеем управлять.
$$\displaystyle (14) \qquad \underline{V}_{dqs} = R_s \underline{I}_{dqs} + L_{\sigma} \frac{d \underline{I}_{dqs} }{dt} + j \omega _r L_{\sigma} \underline{I}_{dqs} + \frac{L_m}{L_r} \frac{d \underline{\Psi}_{dqr}}{dt} + j \omega _r \frac{L_m}{L_r} \underline{\Psi}_{dqr}$$
В предположении, что RRF правильно выровнен по потоку ротора, действительная и мнимая части (14) равны:
$$(15) \qquad \left\{ \begin{array}{ll} \displaystyle V_{ds} &= R_s I_{ds} + L_{\sigma} \cfrac{d I_{ds}}{ dt} – \omega _r L_{\sigma} I_{qs} + \cfrac{L_m}{L_r} \cfrac{d \Psi_{r}}{dt} \\ V_{qs} &= R_s I_{qs} + L_{\sigma} \cfrac{d I_{qs}}{dt} + \omega _r L_{\sigma} I_{ds} + \omega _r \cfrac{L_m}{L_r} \Psi_{r} \end {массив}\право.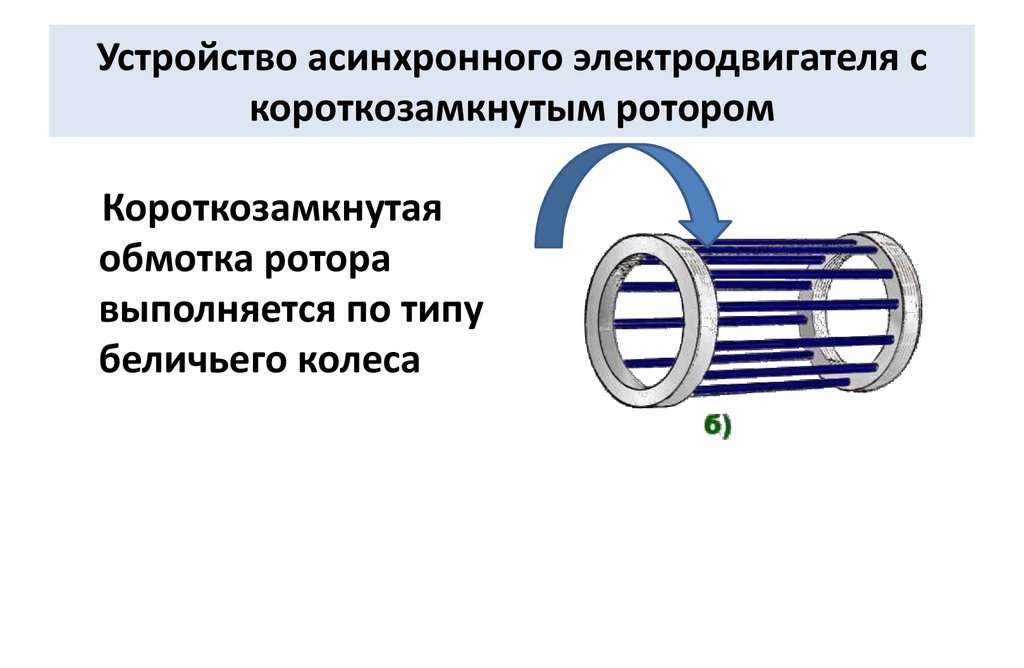 $$
$$
Первые два члена уравнений (15) выражают связь между напряжением и током на статоре. Это соотношение можно переформулировать как передаточную функцию: оно одинаково на обеих осях:
$$(16) \qquad H_d(s) = H_q(s) = \frac{I_{s}(s)}{V_ {s}(s)} = \frac{1/R_s}{1 + s \space L_{\sigma}/R_s} = \frac{K_1}{1 + s \space T_1}$$
Передаточная функция в (16) выражает, как ток реагирует на изменение входного напряжения, генерируемого инвертором. Таким образом, с помощью ПИ-регулятора можно управлять токами на статоре. Настройка PI рассматривается в следующем разделе.
Третий член уравнений в (15) соответствует сопряжению осей. TN106 объясняет, как можно использовать развязывающую сеть, чтобы обеспечить действительно независимое управление осями d и q.
Последний член соответствует влиянию потока ротора на цепь статора. Как объяснялось ранее, желательно поддерживать постоянный поток ротора, чтобы упростить управление крутящим моментом. Следовательно, поскольку \(d \Psi _r/dt = 0\), поток ротора влияет только на ось q. Термин \(\omega_r \frac{L_m}{L_r} \Psi_r\) может быть рассчитан системой управления и добавлен к опорному напряжению по оси q.
Термин \(\omega_r \frac{L_m}{L_r} \Psi_r\) может быть рассчитан системой управления и добавлен к опорному напряжению по оси q.
Поначалу наличие \(\omega_r\) в (15) может сбить с толку. Ведь регулятор тока работает на стороне статора. Следовательно, это должно быть \(\omega_s\). Однако потоки статора и ротора имеют одинаковую скорость в стационарной системе отсчета, поэтому \(\omega _r = \omega _s\).
Настройка контроллера
Как описано в [5], критерий оптимального значения является подходящим способом настройки PI, когда передаточная функция объекта имеет ту же форму, что и в (16). Параметры контроллера:
$$(17) \qquad \left\{ \begin{array}{ll} T_n &= T_1\\ T_i &= 2 K_1 T_d \\ K_p &= T_n / T_i \\ K_i &= 1 / T_i\ end{array}\right.$$
Параметр \(T_d\) представляет собой сумму всех малых задержек в системе. В примечании к продукту PN142 объясняется, как определить общую задержку системы.
Текущие ссылки
Чтобы использовать машину в номинальных условиях, поток ротора должен быть номинальным.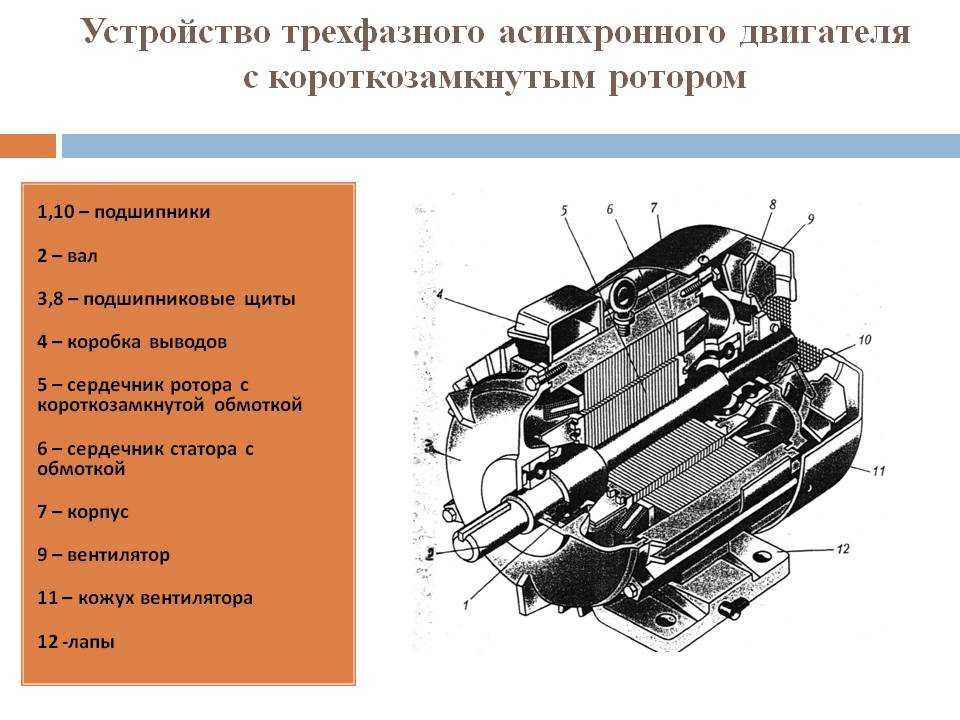
Из (11) поток ротора задается опорным током по оси d: 9*}{\cfrac{3}{2} p \cfrac{L_m}{L_r} \Psi _r}$$
Однако есть небольшое неудобство при запуске: машина не может намагничиться мгновенно. Таким образом, когда поток \(\Psi_r\) еще нарастает, потребление тока согласно (19) будет большим.
Если вас беспокоит потребление тока при запуске, поток можно считать постоянным и равным его номинальному значению. В этом случае машина не может создать задание крутящего момента, потому что поток ротора завышен. Однако это происходит только во время переходного процесса запуска. Таким образом, влияние на эффективность управления минимально.
Оценка \(\Psi_r\) объясняется позже в разделе ориентации RRF.
Расчет номинального тока по оси d
Если номинальный поток ротора неизвестен в (18), номинальный ток по оси d можно рассчитать из номинального напряжения, номинального тока и эквивалентной схемы машина.
Из эквивалентной схемы:
$$\displaystyle (20) \qquad \underline{V}_{s} = R_s \underline{I}_s + j \omega _s (L_s – L_m) \underline{I} _s + \underline{V}_m$$
Принимая \(\arg( \underline{V}_s) = 0 \,\text{rad}\) в качестве эталонной фазы, тогда действительная и мнимая части \(\underline{V}_m\) равны:
$$(21) \qquad \left\{ \begin{array}{l} \displaystyle \text{Re}\{\underline{V}_m\} = V_s – R_s I_s \cos\phi + \omega _s (L_s – L_m) I_s \sin\phi \\ \\ \displaystyle \text{Im}\{ \underline{V}_m\} = – R_s I_s \sin\phi – \omega _s (L_s – L_m) I_s \cos\phi \end{array}\right. $$
$$
с \(\cos \phi\) коэффициентом мощности машины. 92} = \omega _s L_m I_m = \omega _s L_m \frac{I_{ds}}{\sqrt{2}}$$
Из (22) ток по оси d равен:
$$\ displaystyle (23) \qquad I_{ds} = \frac{\sqrt{2} V_m}{\omega _s L_m}$$
Номинальный ток статора по оси d находится путем решения уравнений (21)–(23) используя номинальное напряжение \(V_{sn}\) и ток \(I_{sn}\) АД. Коэффициент мощности обычно указан в паспорте машины.
Динамическое насыщение
Выход регулятора тока представляет собой опорное напряжение для генерации с помощью инвертора источника напряжения (VSI). Однако максимальное выходное напряжение VSI ограничено напряжением на шине постоянного тока. В RRF этот предел насыщения соответствует кругу радиуса \(V_{dc}/\sqrt{3}\). Рисунок справа иллюстрирует ситуацию в одном квадранте: пока опорное напряжение находится внутри круга, оно может генерироваться VSI. 9*\) являются допустимыми ссылками, даже если они находятся за пределами границ \(\pm V_{dc}/\sqrt{6}\). 2} \end{массив}\right.$$ 92}{3}\right)} \end{array}\right.$$
2} \end{массив}\right.$$ 92}{3}\right)} \end{array}\right.$$
Ориентация RRF
В предыдущих разделах предполагалось, что RRF ориентирован на поток ротора. Тогда вопрос: как правильно ориентировать РРФ? Чтобы выровнять RRF по потоку ротора, нам сначала нужно знать положение потока. В [6] и [7] авторы представляют вариант FOC под названием Indirect Field-Oriented Control (IFOC) . Этот метод является косвенным , потому что поток ротора оценивается по модели машины.
Предположим, что RRF действительно ориентирован на поток ротора. В этом случае из (9) поток ротора можно оценить по току оси d:
$$ (26) \qquad \Psi _r = \cfrac{L_m}{s \space T_r + 1} I_{ ds}$$
Согласно (10) частота скольжения рассчитывается по току оси q:
$$(27) \qquad \omega _{slip} = \omega _r – \omega _m = \frac {L_m}{T_r \Psi _r} I_{qs}$$
Тогда, переставляя члены в (27):
$$(28) \qquad \omega _r = \omega _m + \omega _ {промах}$$ 9t \omega _r \space dt $$
Поскольку RFOC выравнивает RRF по потоку ротора, для преобразования Парка необходимо использовать угол \(\theta _r\). Даже если \(\omega _r = \omega _s\), \(\theta _r \neq \theta _s\) из-за разности фаз между потоками статора и ротора.
Даже если \(\omega _r = \omega _s\), \(\theta _r \neq \theta _s\) из-за разности фаз между потоками статора и ротора.
Реализация B-Box/B-Board управления полем ротора
Simulink-модель реализованного алгоритма RFOC можно загрузить в верхней части этой страницы. Основные блоки описаны ниже.
Оценка угла потока ротора
Косвенный метод ориентации вращающейся системы отсчета использует уравнения (26-29), и его реализация показана ниже. Он вычисляет угол потока ротора \(\theta_r\), который используется для преобразования токов статора в кадре dq .
Регулятор тока статора
Регулятор тока статора в RRF ротора показан ниже. Сеть развязки использует скорость потока ротора \(\omega_r\), оцененную вышеописанным косвенным методом. Задание тока по оси d вычисляется с помощью уравнения (23) и задает номинальный поток ротора. Задание тока по оси q получается из задания крутящего момента с использованием уравнения (19). Наконец, пределы динамического насыщения регуляторов по осям d и q вычисляются с использованием уравнения (25).
Контроллер скорости
Контроллер скорости такой же, как в TN114, и вычисляет необходимое задание момента для каскадного контроллера момента (т. е. тока). В настоящей реализации интегральная составляющая регулятора скорости (внешний контур) сохраняется в состоянии сброса, когда регулятор тока (внутренний контур) достигает насыщения, чтобы избежать накопления больших ошибок.
Экспериментальные результаты управления полем ротора
Экспериментальная установка состоит из асинхронной машины, соединенной с синхронной машиной с постоянными магнитами (СДПМ). СДПМ используется для приложения крутящего момента к АД. Каждая машина питается от инвертора источника напряжения, состоящего из 3 модулей фаз PEB 8032. Код управления каждой машиной реализован в Simulink с использованием библиотеки ACG SDK, и оба алгоритма работают на одном контроллере B-Box RCP.
В этой конфигурации оба инвертора используют одну и ту же шину постоянного тока. Дополнительную информацию об этой топологии см. в PN180: Как построить преобразователь частоты.
в PN180: Как построить преобразователь частоты.
Все следующие экспериментальные результаты экспортированы из регистратора данных программного обеспечения BB Control (теперь замененного на Cockpit) и обработаны с помощью MATLAB.
Параметры машины
Параметры индукционной машины приведены в таблице ниже. PMSM (Control Techniques 115UMC300CACAA) был выбран для работы примерно в тех же номинальных условиях.
| Модель: Leroy-Somer 2P LSES 100 л 3 кВт | |||
| Параметр | Символ | Значение | Блок |
| . | 1 | — | |
| Фазовое напряжение | \ (v_ {sn} \) | 230 | V |
| Отскол ) | 6.1 | A | |
| . | |||
| Rated power factor | \(\cos \phi\) | 0.88 | – |
| Stator resistance | \(R_s\) | 1. 5 5 | Ω |
| Stator inductance | \( Л_с\) | 307 | mH |
| Rotor resistance* | \(R_r\) | 1.4 | Ω |
| Rotor inductance* | \(L_r\) | 313 | mH |
| Mutual inductance | \(L_m\) | 295 | mH |
| Moment of inertia (IM only) | \(J_m\) | 0.0036 | kg m 2 |
* The переменные ротора относятся к стороне статора.
СДПМ из этого эксперимента имеет только номинальный крутящий момент 9,5.
Отслеживание скорости
Эффективность отслеживания регулятора скорости была проверена экспериментально путем применения шага задания скорости от 0 до 2870 об/мин. В то же время СДПМ прикладывал момент нагрузки, пропорциональный скорости. В итоге АД работал на номинальной частоте вращения и с нагрузкой 9,5 Нм в установившемся режиме.
Поскольку регулятор скорости настраивается с использованием симметричного критерия оптимальности [8], к заданию скорости был применен ограничитель скорости для ограничения перерегулирования. Использование ограничителя скорости подробно описано в TN114. Во время экспериментальной проверки ускорение было ограничено до 2870 об/мин. Таким образом, АД может достичь своей номинальной скорости за ~1 с практически без перерегулирования.
Результаты экспериментов представлены ниже. Обратите внимание, что в самом начале ротор не двигается сразу, что приводит к плохим характеристикам отслеживания. Такое поведение связано с отсутствием намагниченности, как подробно описано в следующем разделе.
Поскольку это асинхронная машина, механическая скорость ротора \(\omega_m\) меньше, чем поток ротора \(\omega_r\) под нагрузкой (см. ниже слева). Напомним определение относительного скольжения [4]:
$$(30) \qquad s = \frac{\omega _r – \omega_m}{\omega_r}$$
При запуске скольжение равно 1, так как ротор остановлен. Однако машина быстро переходит в стабильную рабочую точку с малым проскальзыванием, как показано ниже (справа). В установившемся режиме относительное скольжение составляет приблизительно \(s\приблизительно 0,023\).
Однако машина быстро переходит в стабильную рабочую точку с малым проскальзыванием, как показано ниже (справа). В установившемся режиме относительное скольжение составляет приблизительно \(s\приблизительно 0,023\).
Подавление помех
Ранее было показано, что регулятор скорости может отслеживать задание скорости. Однако он также должен быть способен подавлять помехи (например, момент нагрузки).
Для проверки подавления помех скорость АД была увеличена до 2870 об/мин без нагрузки. Затем шаг от 0 до 9.5 Нм было применено PMSM (см. ниже слева). На рисунке ниже (справа) видно, что регулятору тока удалось одновременно поддерживать постоянный поток (через \(I_{ds}\)) и адаптировать крутящий момент (через \(I_{qs}\)) . Это стало возможным благодаря независимому управлению токами статора по осям d и q. Обратите внимание, что регулятор скорости достигает своего верхнего предела насыщения, который был установлен на 110% от номинального крутящего момента.
В то же время регулятор скорости должен адаптировать задание крутящего момента, чтобы поддерживать постоянную механическую скорость ротора. Поскольку скольжение увеличивается с нагрузкой (см. ниже справа), частота потока ротора должна быть увеличена, чтобы сохранить постоянную механическую скорость. Во время переходного процесса механическая скорость падает на ~ 5,2% ниже опорной, и для восстановления после скачка нагрузки требуется ~ 150 мс.
Поскольку скольжение увеличивается с нагрузкой (см. ниже справа), частота потока ротора должна быть увеличена, чтобы сохранить постоянную механическую скорость. Во время переходного процесса механическая скорость падает на ~ 5,2% ниже опорной, и для восстановления после скачка нагрузки требуется ~ 150 мс.
Сравнение управления по полю ротора и управления V/f
Как упоминалось в теоретической части данной технической заметки, RFOC относится к семейству методов векторного управления. Однако управление V/f асинхронной машины (TN138) представляет собой гораздо более простой метод, называемый управлением V/f, который представляет собой скалярный метод управления. В чем тогда смысл реализации (довольно сложного) RFOC вместо алгоритма V/f? Чтобы ответить на этот вопрос, одна и та же асинхронная машина использовалась для проведения одних и тех же испытаний в технических примечаниях к V/f и RFOC.
Отслеживание скорости
На приведенном ниже рисунке для целей сравнения экспериментальные характеристики отслеживания скорости V/f и RFOC наложены друг на друга.
Отслеживающие характеристики V/f и RFOC фактически неразличимы в большинстве диапазонов скоростей. Единственная существенная разница заключается в низкоскоростном диапазоне, здесь V/f имеет мертвую зону, тогда как RFOC не имеет таких ограничений. Помните, что после намагничивания АД RFOC может работать на любой скорости без каких-либо искажений. Таким образом, V/f-управление является привлекательным вариантом, если не требуется работа на низкой скорости.
Давайте теперь посмотрим на скольжение: даже если и RFOC, и V/f с обратной связью поддерживают одинаковую механическую скорость ротора, скольжение больше при V/f. Это связано с небольшой разницей в намагниченности машины: при V/f норма потока статора поддерживается постоянной и равной его номинальному значению. Таким образом, норма потока ротора также должна оставаться постоянной. Однако при рассмотрении этого потока в RRF, ориентированном на поток ротора, только Компонент оси d намагничивает станок. Поскольку V/f — это только скалярный метод, нет явного управления компонентой потока ротора по оси d. Напротив, RFOC имеет явное управление этим компонентом оси d. Следовательно, RFOC поддерживает составляющую оси d потока ротора до ее номинального значения вместо нормы вектора. Небольшая разница в потоке ротора приводит к разным характеристикам скольжения крутящего момента для каждого метода и, таким образом, к разному скольжению при одной и той же нагрузке.
Поскольку V/f — это только скалярный метод, нет явного управления компонентой потока ротора по оси d. Напротив, RFOC имеет явное управление этим компонентом оси d. Следовательно, RFOC поддерживает составляющую оси d потока ротора до ее номинального значения вместо нормы вектора. Небольшая разница в потоке ротора приводит к разным характеристикам скольжения крутящего момента для каждого метода и, таким образом, к разному скольжению при одной и той же нагрузке.
Согласно результатам эксперимента, при нагрузке 95,5% от номинального момента проскальзывание составляет ~0,023 при ВЧХ и ~0,027 при V/f с обратной связью. Теоретически, чем ниже скольжение, тем лучше, поскольку машина работает дальше от своего пробуксовывания [4]. Однако это вызывает беспокойство только в том случае, если АД должен работать с очень высоким крутящим моментом, близким к его пробивному крутящему моменту.
Подавление помех
На приведенном ниже рисунке для целей сравнения экспериментальные характеристики подавления помех V/f и RFOC наложены друг на друга.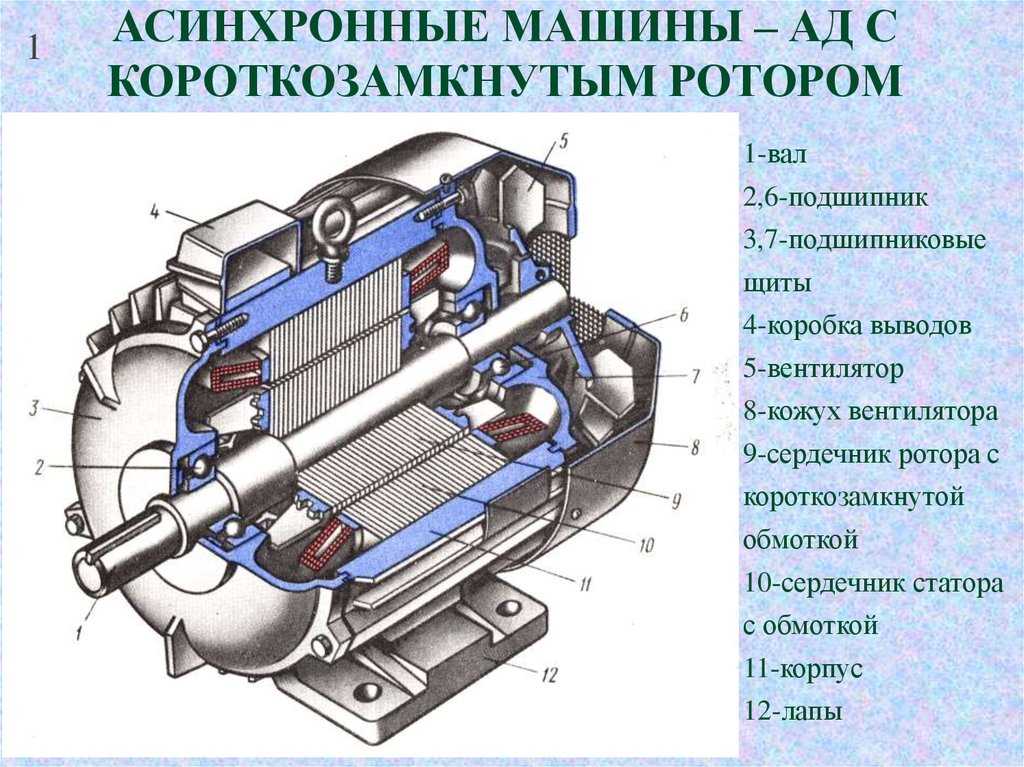
Существует принципиальное различие в оценке проскальзывания (см. ниже справа) между двумя методами: с одной стороны, RFOC оценивает проскальзывание по модели ИМ. Таким образом, оценка достаточно точна даже во время быстрых переходных процессов. С другой стороны, оценка скольжения по методу V/f зависит от PI регулятора скорости (см. раздел отслеживания скорости в V/f-управлении асинхронной машины (TN138)). Это означает, что если скольжение изменяется резко из-за внезапного изменения нагрузки, оценка скольжения будет меняться медленно из-за интегрального действия ПИ-регулятора. Экспериментально замкнутому контуру V/f требуется ~1750 мс для восстановления после возмущения, что почти в 12 раз дольше, чем для RFOC (~150 мс). Это существенная разница в производительности между двумя методами.
Академические ссылки
[1] Б. Робинс, Б. Франсуа, П. Дегобер, Ж. П. Отье, «Векторное управление асинхронными машинами», Springer, 2012.
[2] Нгуен Фунг Куанг, Йорг-Андреас Диттрих, «Векторное управление трехфазными машинами переменного тока», Springer, 2015, ISBN 978-3-662-46914-9
.
 К тому же прогресс не стоит на месте, многие изобретатели продолжают усовершенствовать конструкцию двигателя.
К тому же прогресс не стоит на месте, многие изобретатели продолжают усовершенствовать конструкцию двигателя. Более современные модели оснащают электронными датчиками и другими приборами, улучшающими удобство их эксплуатации.
Более современные модели оснащают электронными датчиками и другими приборами, улучшающими удобство их эксплуатации.