Содержание
Двигатели постоянного тока момент характеристика
Аналитическое выражение механической характеристики двигателя постоянного тока можно получить из уравнения равновесия напряжений якорной цепи (при установившемся режиме)
где U — напряжение на зажимах двигателя, В; 1Я — ток в цепи якоря, A; Rя — сопротивление цепи якоря, Ом; Ф — магнитный поток двигателя, Вб; ω — угловая скорость якоря, рад/с; сд — коэффициент, зависящий от конструктивных данных двигателя. Решив уравнение (3.1) относительно угловой скорости, получим уравнение скоростной характеристики двигателя
Электромагнитный вращающий момент двигателя (Н • м) пропорционален магнитному потоку и току якоря:
Из уравнения (3.3) ток якоря
Подставив в уравнение (3.2) значение тока, выраженное уравнением (3.4), получим уравнение механической характеристики двигателей постоянного тока независимо от способа возбуждения
Рассмотрим механические характеристики двигателей постоянного тока в зависимости от способа возбуждения.
Двигатели постоянного тока параллельного возбуждения. Схема включения двигателя постоянного тока параллельного возбуждения приведена на рис. 3.1, а. Обмотка возбуждения ОВ может быть подключена к той же сети, что и якорь, или к отдельному источнику тока (независимое возбуждение).
В том и другом случае ток возбуждения не зависит от процессов, происходящих в якоре двигателя и при постоянном напряжении сети магнитный поток можно считать постоянным Ф = const. Обозначив сдФ=kд и подставив его в уравнение (3.
5), получим уравнение механической характеристики двигателя постоянного тока параллельного возбуждения
При М=0 угловая скорость якоря
называется скоростью идеального холостого хода.
Второй член уравнения (3.6) определяет изменение угловой скорости двигателя при изменении момента
Величина Δω зависит не только от момента, но и от сопротивления цепи якоря. С увеличением Rя величина Δω увеличивается. С учетом уравнений (3.7) и (3.8) уравнение (3.6) можно записать в виде
С увеличением Rя величина Δω увеличивается. С учетом уравнений (3.7) и (3.8) уравнение (3.6) можно записать в виде
Из уравнений (3.6) и (3-.9) видно, что механическая характеристика двигателя параллельного возбуждения является прямой линией, тангенс угла наклона которой определяется величиной Rя/kд2
На рис. 3.1,6 приведены естественная и искусственные механические характеристики, полученные введением в цепь якоря реостата. Такие искусственные характеристики используются при пуске и торможении двигателя.
Двигатели постоянного тока последовательного возбуждения. Схема включения двигателя последовательного возбуждения приведена на рис. 3.2, а. Обмотка возбуждения ОВ включена последовательно с якорем и по ней протекает ток якоря.
Следовательно, магнитный поток двигателя является функцией тока якоря. Эта зависимость выражается графически в виде кривой намагничивания, которая является нелинейной функцией и не имеет аналитического выражения.
Поэтому нельзя получить аналитическую зависимость для механической характеристики.
Характерной особенностью двигателей последовательного возбуждения является то, что изменение магнитного потока с изменением тока якоря оказывает большое влияние на скорость двигателя. Это хорошо видно из уравнения скоростной характеристики
- которое показывает, что с изменением магнитного потока скорость двигателя может изменяться в широких пределах.
- Если для упрощения предположить, что магнитная цепь двигателя не насыщена и поток пропорционален току
- Ф = сф/Я,
- то момент двигателя
где k = cд / сф.
Подставив в уравнение скоростной характеристики значение Ф = Сф/я, получим
где R — внутреннее сопротивление цепи якоря, равное сумме сопротивлений обмоток якоря и возбуждения (Rя + rя).
Заменив в уравнении ток якоря его выражением из (3.10), получим уравнение механической характеристики
Уравнение (3.12) представляет собой уравнение кривой, для которой ось ординат является асимптотой. Подобная характеристика представлена на рис. 3.2,6. Уравнение (3.12) дает лишь общее представление о механической характеристике двигателя.
Подобная характеристика представлена на рис. 3.2,6. Уравнение (3.12) дает лишь общее представление о механической характеристике двигателя.
При расчетах им пользоваться нельзя, так как аналитически учесть намагничивание стали невозможно. Как видно на рис. 3.2,6, механическая характеристика двигателя последовательного возбуждения — мягкая.
При уменьшении нагрузки угловая скорость резко возрастает, а при М = 0 она стремится к бесконечности.
В реальных двигателях ток при холостом ходе не может быть равен нулю вследствие потерь в стали и механических потерь, но угловая скорость может достигнуть опасных по условиям механической прочности значений, равных (5÷6)ωном. Поэтому холостой ход для двигателей последовательного возбуждения недопустим.
Двигатели постоянного тока смешанного возбуждения. Двигатели смешанного возбуждения имеют две обмотки возбуждения (рис. 3.3). Магнитный поток двигателя определяется суммой потоков параллельной ОВпар и последовательной ОВпос обмоток:
Вследствие нелинейной зависимости магнитного потока от тока якоря аналитическое выражение механической характеристики, так же как и для двигателя последовательного возбуждения, получить нельзя.
В зависимости от соотношения магнитных потоков обмоток возбуждения механические характеристики имеют различную жесткость. Чем больше доля магнитного потока последовательной обмотки, тем мягче характеристика. На рис. 3.
3 приведены две естественные характеристики с различным соотношением магнитных потоков обмоток возбуждения.
Обмотка параллельного возбуждения создает поток Фпар независимый от тока якоря, поэтому двигатель может работать вхолостую со скоростью
Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
Электродвигатель постоянного тока: устройство, принцип работы, типы, управление
Эра электродвигателей берёт своё начало с 30-х годов XIX века, когда Фарадей на опытах доказал способность вращения проводника, по которому проходит ток, вокруг постоянного магнита.
На этом принципе Томасом Девенпортом был сконструирован и испытан первый электродвигатель постоянного тока.
Изобретатель установил своё устройство на действующую модель поезда, доказав тем самым работоспособность электромотора.
Практическое применение ДПТ нашёл Б. С. Якоби, установив его на лодке для вращения лопастей. Источником тока учёному послужили 320 гальванических элементов. Несмотря на громоздкость оборудования, лодка могла плыть против течения, транспортируя 12 пассажиров на борту.
Лишь в конце XIX столетия синхронными электродвигателями начали оснащать промышленные машины. Этому способствовало осознание принципа преобразования электродвигателем постоянного тока механической энергии в электричество.
То есть, используя электродвигатель в режиме генератора, удалось получать электроэнергию, производство которой оказалось существенно дешевле от затрат на выпуск гальванических элементов.
С тех пор электродвигатели совершенствовались и стали завоёвывать прочные позиции во всех сферах нашей жизнедеятельности.
Устройство и описание ДПТ
Конструктивно электродвигатель постоянного тока устроен по принципу взаимодействия магнитных полей.
Самый простой ДПТ состоит из следующих основных узлов:
- Двух обмоток с сердечниками, соединенных последовательно.
 Данная конструкция расположена на валу и образует узел, называемый ротором или якорем.
Данная конструкция расположена на валу и образует узел, называемый ротором или якорем. - Двух постоянных магнитов, повёрнутых разными полюсами к обмоткам. Они выполняют задачу неподвижного статора.
- Коллектора – двух полукруглых, изолированных пластин, расположенных на валу ДПТ.
- Двух неподвижных контактных элементов (щёток), предназначенных для передачи электротока через коллектор до обмоток возбуждения.
Рисунок 1. Схематическое изображение простейшего электродвигателя постоянного тока.
Рассмотренный выше пример – это скорее рабочая модель коллекторного электродвигателя. На практике такие устройства не применяются. Дело в том, что у такого моторчика слишком маленькая мощность. Он работает рывками, особенно при подключении механической нагрузки.
Статор (индуктор)
В моделях мощных современных двигателях постоянного тока используются статоры, они же индукторы, в виде катушек, намотанных на сердечники. При замыкании электрической цепи происходит образование линий магнитного поля, под действием возникающей электромагнитной индукции.
Для запитывания обмоток индуктора ДПТ могут использоваться различные схемы подключения:
- с независимым возбуждением обмоток;
- соединение параллельно обмоткам якоря;
- варианты с последовательным возбуждением катушек ротора и статора;
- смешанное подсоединение.
Схемы подключения наглядно видно на рисунке 2.
Рисунок 2. Схемы подключения обмоток статора ДПТ
У каждого способа есть свои преимущества и недостатки. Часто способ подключения диктуется условиями, в которых предстоит эксплуатация электродвигателя постоянного тока. В частности, если требуется уменьшить искрения коллектора, то применяют параллельное соединение.
Для увеличения крутящего момента лучше использовать схемы с последовательным подключением обмоток. Наличие высоких пусковых токов создаёт повышенную электрическую мощность в момент запуска мотора. Данный способ подходит для двигателя постоянного тока, интенсивно работающего в кратковременном режиме, например для стартера.
В таком режиме работы детали электродвигателя не успевают перегреться, поэтому износ их незначителен.
Ротор (якорь)
В рассмотренном выше примере примитивного электромотора ротор состоит из двухзубцового якоря на одной обмотке, с чётко выраженными полюсами. Конструкция обеспечивает вращение вала электромотора.
В описанном устройстве есть существенный недостаток: при остановке вращения якоря, его обмотки занимают устойчивое. Для повторного запуска электродвигателя требуется сообщить валу некий крутящий момент.
Этого серьёзного недостатка лишён якорь с тремя и большим количеством обмоток. На рисунке 3 показано изображение трёхобмоточного ротора, а на рис. 4 – якорь с большим количеством обмоток.
Рисунок 3. Ротор с тремя обмотками
Рисунок 4. Якорь со многими обмотками
Подобные роторы довольно часто встречаются в небольших маломощных электродвигателях.
Для построения мощных тяговых электродвигателей и с целью повышения стабильности частоты вращения используют якоря с большим количеством обмоток. Схема такого двигателя показана на рисунке 5.
Схема такого двигателя показана на рисунке 5.
Рисунок 5. Схема электромотора с многообмоточным якорем
Коллектор
Если на выводы обмоток ротора подключить источник постоянного тока, якорь сделает пол-оборота и остановится. Для продолжения процесса вращения необходимо поменять полярность подводимого тока. Устройство, выполняющее функции переключения тока с целью изменения полярности на выводах обмоток, называется коллектором.
Самый простой коллектор состоит из двух, изолированных полукруглых пластин. Каждая из них в определённый момент контактирует со щёткой, с которой снимается напряжение. Одна ламель всегда подсоединена к плюсу, а вторая – к минусу. При повороте вала на 180º пластины коллектора меняются местами, вследствие чего происходит новая коммутация со сменой полярности.
Такой же принцип коммутации питания обмоток используются во всех коллекторах, в т. ч. и в устройствах с большим количеством ламелей (по паре на каждую обмотку). Таким образом, коллектор обеспечивает коммутацию, необходимую для непрерывного вращения ротора.
В современных конструкциях коллектора ламели расположены по кругу таким образом, что каждая пластина соответствующей пары находится на диаметрально противоположной стороне. Цепь якоря коммутируется в результате изменения положения вала.
Принцип работы
Ещё со школьной скамьи мы помним, что на провод под напряжением, расположенный между полюсами магнита, действует выталкивающая сила. Происходит это потому, что вокруг проволоки образуется магнитное поле по всей его длине. В результате взаимодействия магнитных полей возникает результирующая «Амперова» сила:
F=B×I×L, где B означает величину магнитной индукции поля, I – сила тока, L – длина провода.
Вектор «Амперовой» всегда перпендикулярен до линий магнитных потоков между полюсами. Схематически принцип работы изображён на рис. 6.
Рис. 6. Принцип работы ДПТ
Если вместо прямого проводника возьмём контурную рамку и подсоединим её к источнику тока, то она повернётся на 180º и остановится в в таком положении, в котором результирующая сила окажется равной 0. Попробуем подтолкнуть рамку. Она возвращается в исходное положение.
Попробуем подтолкнуть рамку. Она возвращается в исходное положение.
Поменяем полярность тока и повторим попытку: рамка сделала ещё пол-оборота. Логично припустить, что необходимо менять направление тока каждый раз, когда соответствующие витки обмоток проходят точки смены полюсов магнитов. Именно для этой цели и создан коллектор.
Схематически можно представить себе каждую якорную обмотку в виде отдельной контурной рамки. Если обмоток несколько, то в каждый момент времени одна из них подходит к магниту статора и оказывается под действием выталкивающей силы. Таким образом, поддерживается непрерывное вращение якоря.
Типы ДПТ
Существующие электродвигатели постоянного тока можно классифицировать по двум основным признакам: по наличию или отсутствию в конструкции мотора щеточно-коллекторного узла и по типу магнитной системы статора.
Рассмотрим основные отличия.
По наличию щеточно-коллекторного узла
Двигатели постоянного тока для коммутации обмоток, которых используются щёточно-коллекторные узлы, называются коллекторными. Они охватывают большой спектр линейки моделей электромоторов. Существуют двигатели, в конструкции которых применяется до 8 щёточно-коллекторных узлов.
Они охватывают большой спектр линейки моделей электромоторов. Существуют двигатели, в конструкции которых применяется до 8 щёточно-коллекторных узлов.
Функции ротора может выполнять постоянный магнит, а ток от электрической сети подаётся непосредственно на обмотки статора. В таком варианте отпадает надобность в коллекторе, а проблемы, связанные с коммутацией, решаются с помощью электроники.
В таких бесколлекторных двигателях устранён один из недостатков –искрение, приводящее к интенсивному износу пластин коллектора и щёток. Кроме того, они проще в обслуживании и сохраняют все полезные характеристики ДПТ: простота в управлении связанном с регулировкой оборотов, высокие показатели КПД и другие. Бесколлекторные моторы носят название вентильных электродвигателей.
По виду конструкции магнитной системы статора
В конструкциях синхронных двигателей существуют модели с постоянными магнитами и ДПТ с обмотками возбуждения. Электродвигатели серий, в которых применяются статоры с потоком возбуждения от обмоток, довольно распространены.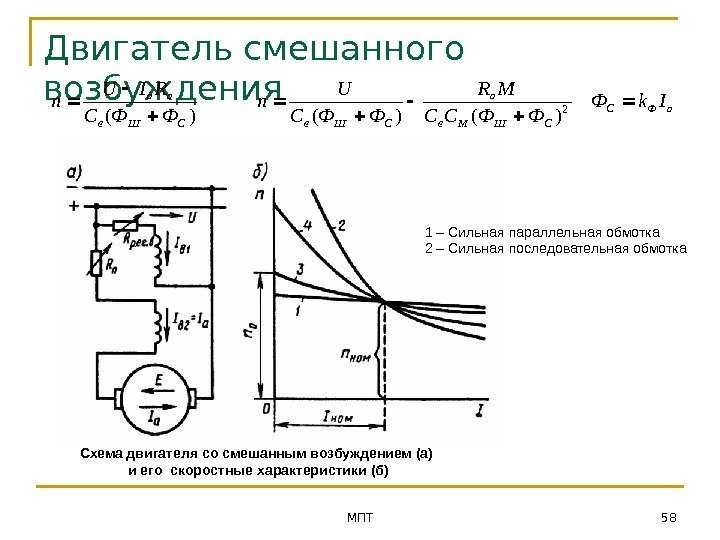 Они обеспечивают стабильную скорость вращения валов, высокую номинальную механическую мощность.
Они обеспечивают стабильную скорость вращения валов, высокую номинальную механическую мощность.
О способах подключения статорных обмоток шла речь выше. Ещё раз подчеркнём, что от выбора схемы подключения зависят электрические и тяговые характеристики двигателей постоянного тока. Они разные в последовательных обмотках и в катушках с параллельным возбуждением.
Управление
Не трудно понять, что если изменить полярность напряжения, то направление вращения якоря также изменится. Это позволяет легко управлять электромотором, манипулируя полярностью щеток.
Механическая характеристика
Рассмотрим график зависимости частоты от момента силы на валу. Мы видим прямую с отрицательным наклоном. Эта прямая выражает механическую характеристику электродвигателя постоянного тока. Для её построения выбирают определённое фиксированное напряжение, подведённое для питания обмоток ротора.
Примеры механических характеристик ДПТ независимого возбуждения
Регулировочная характеристика
Такая же прямая, но идущая с положительным наклоном, является графиком зависимости частоты вращения якоря от напряжения питания.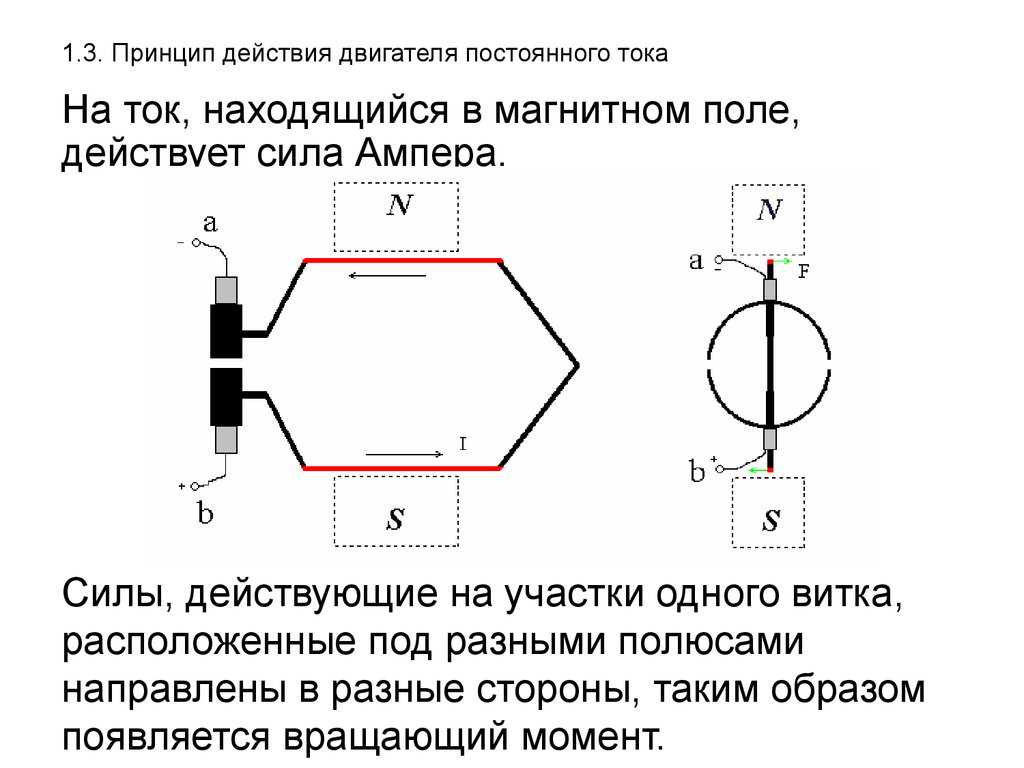 Это и есть регулировочная характеристика синхронного двигателя.
Это и есть регулировочная характеристика синхронного двигателя.
Построение указанного графика осуществляется при определённом моменте развиваемом ДПТ.
Пример регулировочных характеристик двигателя с якорным управлением
Благодаря линейности характеристик упрощается управление электродвигателями постоянного тока. Поскольку сила F пропорциональна току, то изменяя его величину, например переменным сопротивлением, можно регулировать параметры работы электродвигателя.
Регулирование частоты вращения ротора легко осуществляется путём изменения напряжения.
В коллекторных двигателях с помощью пусковых реостатов добиваются плавности увеличения оборотов, что особенно важно для тяговых двигателей. Это также один из эффективных способов торможения.
Мало того, в режиме торможения синхронный электродвигатель вырабатывает электрическую энергию, которую можно возвращать в энергосеть.
Области применения
Перечислять все области применения электродвигателей можно бесконечно долго. Для примера назовём лишь несколько из них:
Для примера назовём лишь несколько из них:
- бытовые и промышленные электроинструменты;
- автомобилестроение – стеклоподъёмники, вентиляторы и другая автоматика;
- трамваи, троллейбусы, электрокары, подъёмные краны и другие механизмы, для которых важны высокие параметры тяговых характеристик.
Преимущества и недостатки
К достоинствам относится:
- Линейная зависимость характеристик электродвигателей постоянного тока (прямые линии) упрощающие управление;
- Легко регулируемая частота вращения;
- хорошие пусковые характеристики;
- компактные размеры.
У асинхронных электродвигателей, являющихся двигателями переменного тока очень трудно достичь таких характеристик.
Недостатки:
- ограниченный ресурс коллектора и щёток;
- дополнительная трата времени на профилактическое обслуживание, связанное с поддержанием коллекторно-щёточных узлов;
- ввиду того, что мы пользуемся сетями с переменным напряжением, возникает необходимость выпрямления тока;
- дороговизна в изготовлении якорей.

По перечисленным параметрам из недостатков в выигрыше оказываются модели асинхронных двигателей. Однако во многих случаях применение электродвигателя постоянного тока является единственно возможным вариантом, не требующим усложнения электрической схемы.
Видео в дополнение к написанному
Электродвигатели постоянного тока. Свойства и механические характеристики
Электродвигатель постоянного тока состоит из неподвижной части
(индуктора) с электромагнитами, на полюсах которых расположена обмот-ка возбуждения, и вращающегося якоря, обмотка которого соединена с коллектором.
При подведении напряжения постоянного тока через коллек-тор к обмотке якоря одновременно подается напряжение и в обмотку возбуждения электромагнитов.
При этом в магнитной системе индуктора возникает магнитный поток, взаимодействие которого с магнитным полем якоря приводит к образованию вращающегося момента, вызывающего вращения якоря.
- В зависимости от принятой схемы питания обмоток возбуждения машины постоянного тока подразделяются:
- — на двигатели с последовательным возбуждением;
- — на двигатели с параллельным возбуждении
- — на двигатели со смешанным возбуждением.

- а — с последовательным возбуждением;
- б – с параллельным возбуждением;
- с – со смешанным возбуждением.
- ОВ – обмотка возбуждения; RП – реостат пусковой; RВ – реостат возбуждения.
- Рабочие параметры электродвигателей постоянного тока регулируются при помощи реостатов (RП и RВ) в цепи ротора и в цепи возбуждения ОВ. Подводимое к электродвигателю постоянного тока напряжение U урав-новешивается с индуцируемой в машине ЭДС Е и с падением напряжения в цепи якоря на его сопротивление R при прохождении тока I
Индуцируемая в якоре ЭДС
- Где С – коэффициент пропорциональности, зависящий от конструкции машины; Ф – магнитный поток, Вб; n – частота вращения якоря.

- Механическая мощность развиваемая машиной Р
- E∙I, Вт
- Вращающий момент (Н∙м)
- М=С∙Ф∙I
- Откуда
- I=
- И
Это уравнение является уравнением механической характеристики электродвигателя постоянного тока.
Механические характеристики электродвигателей постоянного тока с различным возбуждением имеют различную форму.
- Рис. Механические характеристики электродвигателей постоянного тока:
- 1 – с последовательным возбуждением;
- 2 – со смешанным возбуждением;
- 3 – с параллельным возбуждением
- Частота вращения якоря двигателя с последовательным возбуждением (кривая 1) резко изменяется с изменением нагрузки.
- Двигатель может преодолеть большой момент сопротивления при сильном снижении частоты вращения и наоборот, при резком снижении нагрузки частота вращения может возрасти до опасных пределов (воз-можность разноса).

- Механическая характеристика двигателя постоянного тока с параллельным возбуждением (кривая 3) подобна характеристике асинх-ронного двигателя в области устойчивой работы: при изменении нагрузки частота вращения ротора меняется незначительно.
- Характеристика двигателя со смешанным возбуждением (кривая 2) имеет промежуточную форму между вышеуказанными харак-теристиками, приближаясь к той или иной в зависимости от соотношения ампер-витков обмоток.
- При пуске электродвигателя пусковые токи достигают высоких значений.
В период пуска n=0; E=0; I= U/R максимально (превышает номинальное значение в 8 – 15 раз). Для ограничения пусковых токов в цепь якоря вводят реостат RП, обеспечивающий превышение пускового тока над номинальным не более чем в 2 раза.
В период пуска реостат в цепи якоря должен быть введен, а в цепи возбуждения реостат RП – выведен, при последовательном возбуждении – введен. При этих условиях пусковой ток имеет минимальное значение.
По мере разгона пусковой реостат выводится из цепи.
- Частоту вращения электродвигателей постоянного тока можно регулировать тремя способами:
- — изменением сопротивления в цепи якоря R;
- — изменением магнитного потока;
- — изменением величины подводимого напряжения.
Введение в цепь якоря сопротивления снижает его частоту вращения. При этом наклон кривых (механических характеристик двигателя) с ростом сопротивления увеличиваются и все они проходят ниже естественной характеристики. Но при таком способе проиходит значительная потеря энергии в реостате, значительное смягчение характеристик и необходимость иметь громоздкий реостат.
Частоту вращения можно регулировать с помощью специальных устройств, позволяющих изменять напряжение в якоре в необходимых пределах. К таким устройствам относятся система генератор – двигатель (Г –Д) или управляемые выпрямители, выполняемые на базе различных элементов.
Электрическое торможение двигателей постоянного тока произ-водится теми же способами, что торможение синхронных двигателей, т. е . возвратом энергии в сеть, электродинамическим способом и противо-током.
е . возвратом энергии в сеть, электродинамическим способом и противо-током.
Реверсирование двигателей достигается изменением полярности питающих проводов на клеммах обмотки якоря или обмотки воз-буждения.
Преимущества двигателей постоянного тока. Возможность плавного регулирования частоты вращения в широком диапазоне.
Недостатки двигателей постоянного тока. Необходимость иметь преобразовательные устройства, более сложная конструкция по сравнению с асинхронным двигателем, меньшая надежность в работе и меньший К.П.Д.
Электродвигатель постоянного тока
Постоянная ЭДС
Направление ЭДС определяется по правилу правой руки. Направление наводимой ЭДС противоположно направлению протекающего в проводнике тока.
Наведенная ЭДС последовательно изменяется по направлению из-за перемещения проводников в магнитном поле. Суммарная ЭДС, равная сумме ЭДС в каждой катушке, прикладывается к внешним выводам двигателя.
Это и есть противо-ЭДС. Направление противо-ЭДС противоположно приложенному к двигателю напряжению.
Значение противо-ЭДС пропорционально частоте вращения и определяется из следующего выражения: [1]
- где — электродвижущая сила, В,
- – постоянная ЭДС, В∙с/рад,
- — угловая частота, рад/с
Постоянные момента и ЭДС в точности равны между собой KT = KE. Постоянные KT и KE равны друг другу, если они определены в единой системе едениц.
Постоянная электродвигателя
Одним из основных параметров электродвигателя постоянного тока является постоянная электродвигателя Kм. Постоянная электродвигателя определяет способность электродвигателя преобразовывать электрическую энергию в механическую.
- где — постоянная электродвигателя, Нм/√Вт,
- R — сопротивление обмоток, Ом,
- – максимальный момент, Нм,
- — мощность потребляемая при максимальном моменте, Вт
Справка: Постоянная электродвигателя вместе с размерами электродвигателя являются основными параметрами для инженера при выборе электродвигателя с лучшим соотношением мощность / объем.
Постоянная электродвигателя не зависит от соединения обмоток, при условии, что используется один и тот же материал проводника. Например, обмотка двигателя с 6 ветками и 2 параллельными проводами вместо 12 одиночных проводов удвоят постоянную ЭДС, при этом постоянная электродвигателя останется не изменой.
Жесткость механической характеристики двигателя
- где — жесткость механической характеристики электродвигателя постоянного тока
Напряжение электродвигателя
- Уравнение баланса напряжений на зажимах двигателя постоянного тока имеет вид (в случае коллекторного двигателя не учитывается падение напряжения в щеточно-коллекторном узле):
- ,
- Уравнение напряжения выраженное через момент двигателя будет выглядеть следующим образом:
Соотношение между моментом и частотой вращения при двух различных напряжениях питания двигателя постоянного тока неизменно. При увеличении частоты вращения момент линейно уменьшается. Наклон этой функции KTKE/R постоянный и не зависит от значения напряжения питания и частоты вращения двигателя.
Наклон этой функции KTKE/R постоянный и не зависит от значения напряжения питания и частоты вращения двигателя.
Благодаря таким характеристикам упрощается управление частотой вращения и углом поворота двигателей постоянного тока. Это характерно для коллекторных и вентильных двигателей постоянного тока, что нельзя сказать о двигателях переменного тока и шаговых двигателях [1].
Мощность электродвигателя постоянного тока
Упрощенная модель электродвигателя выглядит следующим образом:
- где I – сила тока, А
- U — напряжение, В,
- M — момент электродвигателя, Н∙м
- R — сопротивление токопроводящих элементов, Ом,
- L — индуктивность, Гн,
- Pэл — электрическая мощность (подведенная), Вт
- Pмех — механическая мощность (полезная), Вт
- Pтеп — тепловые потери, Вт
- Pинд — мощность затрачиваемая на заряд катушки индуктивности, Вт
- Pтр — потери на трение, Вт
Механическая постоянная времени
Механическая постоянная времени — это время, отсчитываемое с момента подачи постоянного напряжения на электродвигатель, за которое частота вращения ненагруженного электродвигателя достигает уровня в 63,21% (1-1/e) от своего конечного значения.
,
- где — механическая постоянная времени, с
Смотрите также
5. Основные расчетные характеристики двигателей постоянного тока [1989 Михайлов О.П., Орлова Р.Т., Пальцев А.В. — Гибкие производственные системы, промышленные роботы, робототехнические комплексы. Практическое пособие. Книга 14. Современный электропривод станков с ЧПУ и промышленных роботов]
НОВОСТИ БИБЛИОТЕКА КАРТА САЙТА ССЫЛКИ О ПРОЕКТЕ
Кратко рассмотрим основные параметры двигателей постоянного тока.
Номинальный ток якоря — длительно допустимый ток по условиям нагрева электродвигателя. Номинальный ток зависит от класса изоляции обмотки, условий охлаждения, материала коллектора и щеток, габаритных размеров и других конструктивных особенностей машины. При питании двигателя пульсирующим напряжением номинальному току соответствует эффективное значение (среднеквадратичное).
Максимальный ток — кратковременно допустимый по условиям коммутации или размагничивания ток якоря двигателя. Максимальный ток зависит от скорости, наличия дополнительных полюсов, степени компенсации реакции якоря, материала и конструкции щеточно-коллекторного узла, индуктивности коммутируемой секции обмотки якоря и т. д. Для высокомоментных двигателей максимальному току соответствует ток якоря неподвижного двигателя, не вызывающий существенного (более чем на 10 %) размагничивания полюсов. Его обозначают Обычно максимально допустимый по условиям размагничивания ток составляет (10÷20) Iн.
Максимальный ток зависит от скорости, наличия дополнительных полюсов, степени компенсации реакции якоря, материала и конструкции щеточно-коллекторного узла, индуктивности коммутируемой секции обмотки якоря и т. д. Для высокомоментных двигателей максимальному току соответствует ток якоря неподвижного двигателя, не вызывающий существенного (более чем на 10 %) размагничивания полюсов. Его обозначают Обычно максимально допустимый по условиям размагничивания ток составляет (10÷20) Iн.
При питании двигателя пульсирующим напряжением за максимальный ток принимается его амплитудное значение.
Номинальный магнитный поток — магнитный поток, характеризующий магнитное поле в рабочем воздушном зазоре двигателя при нормальной скорости. Номинальный магнитный поток в воздушном зазоре сохраняется при регулировании скорости изменением напряжения на якоре. Магнитный поток зависит от тока в обмотке возбуждения, числа витков обмотки, числа полюсов и степени насыщения магнитной системы двигателя.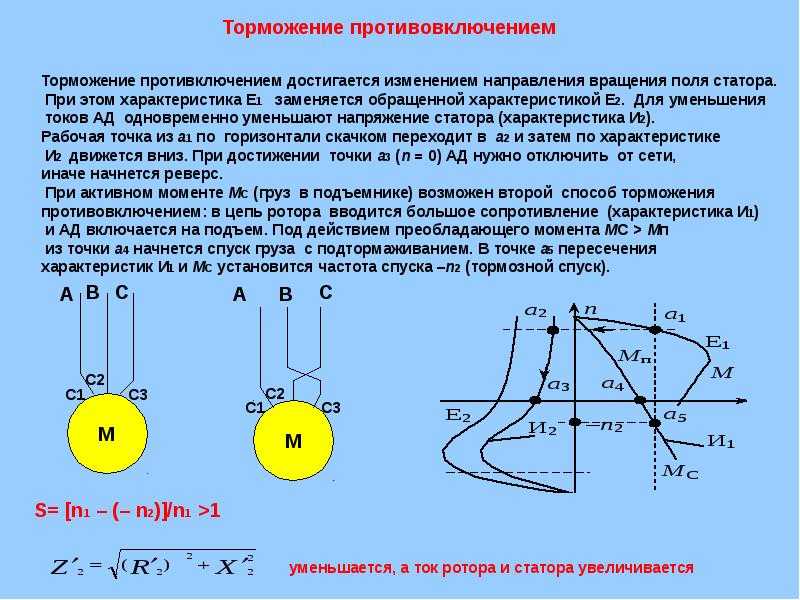 Для высокомоментных двигателей величина магнитного потока определяется как геометрией машины, так и параметрами постоянных магнитов.
Для высокомоментных двигателей величина магнитного потока определяется как геометрией машины, так и параметрами постоянных магнитов.
Номинальное напряжение якоря — длительно допустимое напряжение на якоре двигателя, соответствующее номинальной скорости. Номинальное напряжение зависит от активной длины проводника обмотки якоря, числа проводников в его пазу, величины магнитного потока, линейной скорости вращения.
Номинальное напряжения возбуждения — длительно допустимое напряжение на обмотке возбуждения, определяемое длительно допустимым по условиям нагрева током возбуждения. Номинальное напряжение возбуждения зависит от сопротивления и числа витков обмотки возбуждения. При многополюсной системе возбуждения зависит также от схемы включения обмоток.
Максимальное напряжение якоря — напряжение, соответствующее максимальной скорости. Максимальное напряжение лимитируется величиной напряжения между смежными пластинами коллектора, обеспечивающей приемлемую коммутацию.
- Номинальная скорость (об/мин) — скорость при номинальном напряжении на якоре, номинальном магнитном потоке и номинальном токе якоря.
- Максимальная скорость (об/мин) — максимальная скорость при максимальном напряжении на якоре и номинальном магнитном потоке
- Максимальная скорость (об/мин) — максимальная скорость при минимальном магнитном потоке и номинальном напряжении на якоре Uн.
- Номинальный момент — длительно допустимый момент на валу двигателя, соответствующий номинальному току якоря и номинальному магнитному потоку При питании двигателя пульсирующим напряжением номинальный момент соответствует среднему (среднеарифметическому) значению тока якоря.
- Максимальный момент — кратковременный момент на валу двигателя, соответствующий максимальному току в якоре и номинальному магнитному потоку Обычно кратность максимального момента меньше кратности максимального тока вследствие насыщения магнитной системы и размагничивающего действия реакции якоря.
 Для высокомоментных двигателей максимальный момент соответствует по условиям размагничивания максимальному току якоря при неподвижном двигателе
Для высокомоментных двигателей максимальный момент соответствует по условиям размагничивания максимальному току якоря при неподвижном двигателе - Номинальная мощность — мощность на валу двигателя при номинальном моменте и номинальной скорости: При уменьшении скорости мощность двигателя пропорционально снижается.
- Электрическая мощность — мощность, потребляемая двигателем из сети: Для высокомоментных двигателей номинальный ток равен номинальному току якоря.
Часовая мощность — мощность на валу двигателя, допустимая по условиям нагрева в течение 1 ч работы. Часовая мощность больше номинальной. Эта разница тем больше, чем больше тепловая постоянная времени двигателя.
Номинальный кпд η (%) — отношение номинальной мощности на валу двигателя к потребляемой:
- Момент инерции J (кг*м2) — конструктивный параметр двигателя, определяемый геометрическими размерами и материалом якоря.
- Максимальное теоретическое ускорение — ускорение, развиваемое двигателем без дополнительной инерционной массы при максимальном вращающем моменте.

- Коэффициент момента — момент, развиваемый двигателем на 1 А тока якоря при номинальном магнитном потоке:
- Коэффициент эдс — эдс двигателя, вращающегося со скоростью 1 рад/с (1 об/мин) при номинальном магнитном потоке
- где — сопротивление обмотки дополнительных полюсов.
- При размагничивании двигателя значения коэффициентов уменьшаются.
- Электромеханическая постоянная времени — время, необходимое для разгона двигателя до номинальной скорости при постоянном моменте короткого замыкания, развиваемом при прямом включении якоря двигателя на номинальное напряжение:
При апериодическом процессе разгона постоянная времени равна времени достижения 0,63 установившегося значения (рис. 17) заданного параметра.
Рис. 17. Кривая разгона двигателя
Электромагнитная постоянная времени — время, необходимое для нарастания тока в обмотке якоря до 0,63 номинального значения при подаче на заторможенный якорь двигателя ступенчатого напряжения:
где — индуктивности обмотки якоря и обмотки дополнительных полюсов.
Собственная частота — величина, характеризующая полосу пропускания (быстродействие) электродвигателя.
Коэффициент демпфирования дает представление о характере изменения скорости (колебательности) электродвигателей в переходных режимах. Он зависит от соотношения электромеханической и электромагнитной постоянных времени:
Тепловая постоянная времени — время нагрева обмотки якоря до значения 0,63 установившейся температуры. Тепловая постоянная зависит от материала, конструкции и геометрических размеров якоря и способа охлаждения двигателя.
- Крутизна напряжения тахогенератора — напряжение на якоре тахогенератора при скорости 1000 об/мин; она зависит от интенсивности магнитного поля, активной длины и числа проводников обмотки якоря тахогенератора.
- Минимальное сопротивление нагрузки — минимальное значение сопротивления, при котором тахогенератор сохраняет свои точностные параметры.
- Для наиболее полного использования двигателей в условиях, отличных от номинальных, целесообразно знать механические характеристики, представляющие собой зависимость между скоростью и вращающим моментом в длительном, повторно-кратковременном и кратковременном режимах работы.

- В зоне длительного режима двигатель может длительно работать при любом сочетании скорости и момента, не превышающем пределы длительного режима.
- В зоне повторно-кратковременного режима двигатель может работать только при допустимой продолжительности включения.
Крутящий момент двигателя постоянного тока Калькулятор
✖Постоянная двигателя постоянного тока — это постоянная величина, которую мы определяем для упрощения уравнения ЭДС машины постоянного тока.ⓘ Постоянная двигателя постоянного тока [K] | +10% -10% | ||
✖Ток якоря двигателя постоянного тока определяется как ток якоря, развиваемый в электрическом двигателе постоянного тока из-за вращения ротора.ⓘ Двигатель постоянного тока с током якоря [Ia] | AbampereАмперАттоамперБайотсантиамперСГС ЭМБлок ЭС СГСДециамперДекаампереEMU текущегоESU текущегоExaampereФемтоамперГигаамперГилбертгектоамперкилоамперМегаампермикроамперМиллиампернаноамперПетаамперПикоамперStatampereтераамперЙоктоампереЙоттаампереZeptoampereZettaampere | +10% -10% | |
✖Магнитный поток (Φ) — это количество силовых линий магнитного поля, проходящих через магнитный сердечник электрического двигателя постоянного тока. | Гаусс сантиметр²килолинЛинияКвант магнитного потокамаксвеллМегалайнМикровеберМилливеберТесла сантиметр²Тесла метр²блок полюсВольт-секундВебер | +10% -10% |
|
|
|
|
👎
Формула
сбросить
👍
Крутящий момент двигателя постоянного тока Решение
ШАГ 0: Сводка предварительного расчета
ШАГ 1. 2)*Сопротивление якоря)+Механические потери+Основные потери)/(Напряжение питания*(1-Общая электрическая эффективность))
2)*Сопротивление якоря)+Механические потери+Основные потери)/(Напряжение питания*(1-Общая электрическая эффективность))
Идти
ЭДС двигателя постоянного тока с использованием уравнения ЭДС
Наведенная противо-ЭДС = (Количество полюсов*Магнитный поток*Количество проводников*Скорость двигателя)/(60*Количество параллельных путей в машине постоянного тока)
Идти
Крутящий момент якоря с учетом электрического КПД двигателя постоянного тока
Крутящий момент якоря = Двигатель постоянного тока с током якоря*Напряжение питания*Электрическая эффективность/Угловая скорость
Идти
Напряжение при заданном электрическом КПД двигателя постоянного тока
Напряжение питания = Угловая скорость*Крутящий момент якоря/Двигатель постоянного тока с током якоря*Электрическая эффективность
Идти
Ток якоря с учетом электрического КПД двигателя постоянного тока
Двигатель постоянного тока с током якоря = Угловая скорость*Крутящий момент якоря/Напряжение питания*Электрическая эффективность
Идти
Шунтирующий ток возбуждения в двигателе постоянного тока
Шунтирующий ток возбуждения = Напряжение питания/Сопротивление шунтирующего поля
Идти
Крутящий момент якоря с учетом механического КПД двигателя постоянного тока
Крутящий момент якоря = Механическая эффективность*крутящий момент
Идти
Приведенный крутящий момент Механический КПД двигателя постоянного тока
крутящий момент = Крутящий момент якоря/Механическая эффективность
Идти
Обратная ЭДС для режима максимальной мощности двигателя постоянного тока
Наведенная противо-ЭДС = Напряжение источника/2
Идти
Крутящий момент двигателя постоянного тока формула
крутящий момент = Постоянная двигателя постоянного тока*Двигатель постоянного тока с током якоря*Магнитный поток
Τ = K*Ia*Φf
Каков принцип работы двигателя постоянного тока?
Работа двигателя постоянного тока основана на том принципе, что когда проводник с током помещается в магнитное поле, на проводник действует механическая сила.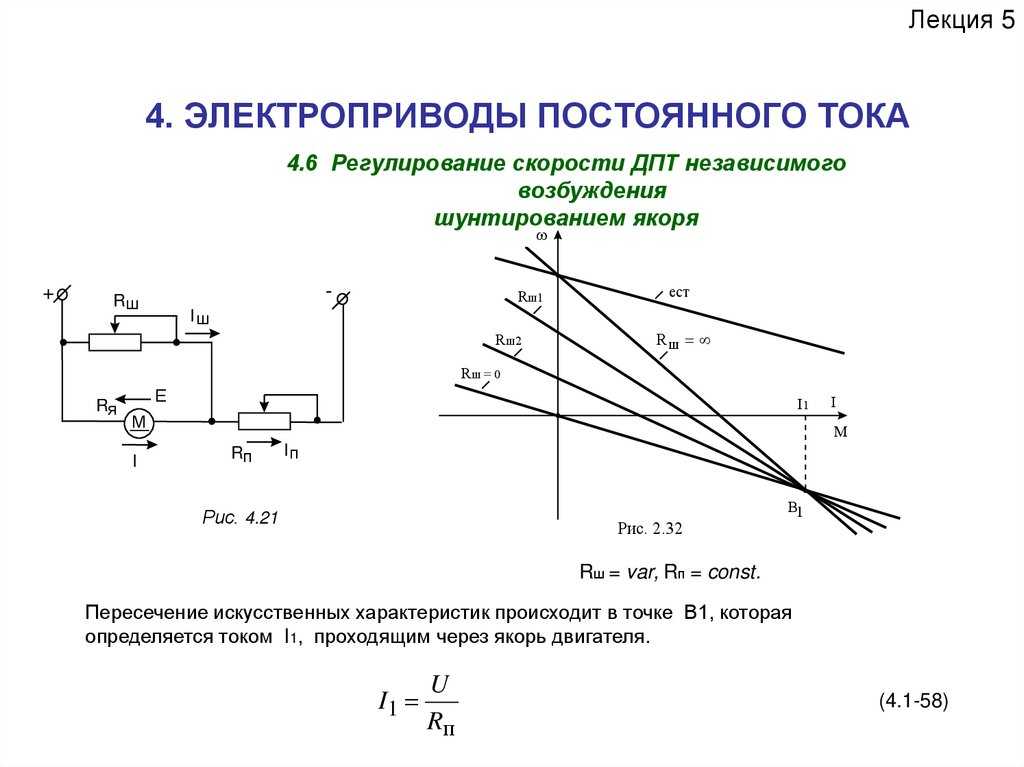 В принципе, конструктивных различий между двигателем постоянного тока и генератором постоянного тока нет.
В принципе, конструктивных различий между двигателем постоянного тока и генератором постоянного тока нет.
Share
Copied!
Как определить момент электродвигателя постоянного тока
Лошадиная сила – это математически полученное число, предназначенное для того, чтобы дать представление о том, сколько работы двигатель может произвести относительно лошади. Идея лошадиных сил довольно произвольна, и первоначально она была разработана Джеймсом Уаттом для продажи своего нового и улучшенного парового двигателя. В действительности средняя лошадь может производить около 15 лошадиных сил короткими очередями и около 5 лошадиных сил непрерывно. Одна лошадиная сила на самом деле ближе к выходу обезьяны среднего размера.
Расчет крутящего момента электродвигателя
Крутящий момент электродвигателя – это сила вращения его вала. Именно момент вращения определяет мощность Вашего двигателя. Измеряется в ньютонах на метр или в килограмм-силах на метр.
Измеряется в ньютонах на метр или в килограмм-силах на метр.
Виды крутящих моментов:
- Номинальный – значение момента при стандартном режиме работы и стандартной номинальной нагрузке на двигатель.
- Пусковой – это табличное значение. Сила вращения, которую в состоянии развивать электродвигатель при пуске. При подборе эл двигателя убедитесь, что данный параметр выше, чем статический момент Вашего оборудования — насоса, либо вентилятора и т.д. В противном случае электродвигатель не сможет запуститься, что чревато перегревом и перегоранием обмотки.
- Максимальный
– предельное значение, по достижении которого нагрузка уравновесит двигатель и остановит его.
Nascar или Formula1?
Сравнение двигателей Nascar и Formula1 это сравнение момента и мощности. Сравним наскаровский V8 и формульный V8 (с 2006 до 2013 года) двигатели. Оба атмосферные, бензиновые. Объем двигателей различается более чем в два раза — 5. 8 литров у Nascar против 2.4 литров у Formula1. Крутящий момент: Nascar — 706 (@7500) Н•м, Formula1 — 290 (@17000) Н•м. Однако максимальная мощность различается не столь существенно: 825 (@9000) и 755 (@19250) л.с. соответственно. За счет чего же формульный двигатель при более чем в два раза меньшем объеме выжимает сравнимую мощность? За счет максимальных оборотов. Формульный двигатель очень оборотистый — рабочие обороты доходят до 20000 оборотов в минуту, что позволяет ему имея малый момент иметь сравнительно большую мощность.
8 литров у Nascar против 2.4 литров у Formula1. Крутящий момент: Nascar — 706 (@7500) Н•м, Formula1 — 290 (@17000) Н•м. Однако максимальная мощность различается не столь существенно: 825 (@9000) и 755 (@19250) л.с. соответственно. За счет чего же формульный двигатель при более чем в два раза меньшем объеме выжимает сравнимую мощность? За счет максимальных оборотов. Формульный двигатель очень оборотистый — рабочие обороты доходят до 20000 оборотов в минуту, что позволяет ему имея малый момент иметь сравнительно большую мощность.
Таблица крутящих моментов электродвигателей
В данной таблице собраны крутящие моменты наиболее распространенных в Украине электродвигателей АИР, а также требуемый при пуске – пусковой, максимально допустимый для данного типа электродвигателя – максимальный крутящий момент и момент инерции двигателей АИР (усилие важное при подборе электромагнитного тормоза, например)
| Двигатель | кВт/об | Мном, Нм | Мпуск, Нм | Ммакс, Нм | Минн, Нм |
| АИР56А2 | 0,18/2730 | 0,630 | 1,385 | 1,385 | 1,133 |
| АИР56В2 | 0,25/2700 | 0,884 | 1,945 | 1,945 | 1,592 |
| АИР56А4 | 0,12/1350 | 0,849 | 1,868 | 1,868 | 1,528 |
| АИР56В4 | 0,18/1350 | 1,273 | 2,801 | 2,801 | 2,292 |
| АИР63А2 | 0,37/2730 | 1,294 | 2,848 | 2,848 | 2,330 |
| АИР63В2 | 0,55/2730 | 1,924 | 4,233 | 4,233 | 3,463 |
| АИР63А4 | 0,25/1320 | 1,809 | 3,979 | 3,979 | 3,256 |
| АИР63В4 | 0,37/1320 | 2,677 | 5,889 | 5,889 | 4,818 |
| АИР63А6 | 0,18/860 | 1,999 | 4,397 | 4,397 | 3,198 |
| АИР63В6 | 0,25/860 | 2,776 | 6,108 | 6,108 | 4,442 |
| АИР71А2 | 0,75/2820 | 2,540 | 6,604 | 6,858 | 4,064 |
| АИР71В2 | 1,1/2800 | 3,752 | 8,254 | 9,004 | 6,003 |
| АИР71А4 | 0,55/1360 | 3,862 | 8,883 | 9,269 | 6,952 |
| АИР71В4 | 0,75/1350 | 5,306 | 13,264 | 13,794 | 12,733 |
| АИР71А6 | 0,37/900 | 3,926 | 8,245 | 8,637 | 6,282 |
| АИР71В6 | 0,55/920 | 5,709 | 10,848 | 12,560 | 9,135 |
| АИР71В8 | 0,25/680 | 3,511 | 5,618 | 6,671 | 4,915 |
| АИР80А2 | 1,5/2880 | 4,974 | 10,943 | 12,932 | 8,953 |
| АИР80В2 | 2,2/2860 | 7,346 | 15,427 | 19,100 | 13,223 |
| АИР80А4 | 1,1/1420 | 7,398 | 16,275 | 17,755 | 12,576 |
| АИР80В4 | 1,5/1410 | 10,160 | 22,351 | 24,383 | 17,271 |
| АИР80А6 | 0,75/920 | 7,785 | 16,349 | 17,128 | 12,457 |
| АИР80В6 | 1,1/920 | 11,418 | 25,121 | 26,263 | 20,553 |
| АИР80А8 | 0,37/680 | 5,196 | 10,393 | 11,952 | 7,275 |
| АИР80В8 | 0,55/680 | 7,724 | 15,449 | 16,221 | 10,814 |
| АИР90L2 | 3/2860 | 10,017 | 23,040 | 26,045 | 17,030 |
| АИР90L4 | 2,2/1430 | 14,692 | 29,385 | 35,262 | 29,385 |
| АИР90L6 | 1,5/940 | 15,239 | 30,479 | 35,051 | 28,955 |
| АИР90LА8 | 0,75/700 | 10,232 | 15,348 | 20,464 | 15,348 |
| АИР90LВ8 | 1,1/710 | 14,796 | 22,194 | 32,551 | 22,194 |
| АИР100S2 | 4/2850 | 13,404 | 26,807 | 32,168 | 21,446 |
| АИР100L2 | 5,5/2850 | 18,430 | 38,703 | 44,232 | 29,488 |
| АИР100S4 | 3/1410 | 20,319 | 40,638 | 44,702 | 32,511 |
| АИР100L4 | 4/1410 | 27,092 | 56,894 | 65,021 | 43,348 |
| АИР100L6 | 2,2/940 | 22,351 | 42,467 | 49,172 | 35,762 |
| АИР100L8 | 1,5/710 | 20,176 | 32,282 | 40,352 | 30,264 |
| АИР112М2 | 7,5/2900 | 24,698 | 49,397 | 54,336 | 39,517 |
| АИР112М4 | 5,5/1430 | 36,731 | 73,462 | 91,827 | 58,769 |
| АИР112МА6 | 3/950 | 30,158 | 60,316 | 66,347 | 48,253 |
| АИР112МВ6 | 4/950 | 40,211 | 80,421 | 88,463 | 64,337 |
| АИР112МА8 | 2,2/700 | 30,014 | 54,026 | 66,031 | 42,020 |
| АИР112МВ8 | 3/700 | 40,929 | 73,671 | 90,043 | 57,300 |
| АИР132М2 | 11/2910 | 36,100 | 57,759 | 79,419 | 43,320 |
| АИР132S4 | 7,5/1440 | 49,740 | 99,479 | 124,349 | 79,583 |
| АИР132М4 | 11/1450 | 72,448 | 173,876 | 210,100 | 159,386 |
| АИР132S6 | 5,5/960 | 54,714 | 109,427 | 120,370 | 87,542 |
| АИР132М6 | 7,5/950 | 75,395 | 150,789 | 165,868 | 120,632 |
| АИР132S8 | 4/700 | 54,571 | 98,229 | 120,057 | 76,400 |
| АИР132М8 | 5,5/700 | 75,036 | 135,064 | 165,079 | 105,050 |
| АИР160S2 | 15/2940 | 48,724 | 97,449 | 155,918 | 2,046 |
| АИР160М2 | 18,5/2940 | 60,094 | 120,187 | 192,299 | 2,884 |
| АИР180S2 | 22/2940 | 71,463 | 150,071 | 250,119 | 4,288 |
| АИР180М2 | 30/2940 | 97,449 | 214,388 | 341,071 | 6,821 |
| АИР200М2 | 37/2950 | 119,780 | 275,493 | 383,295 | 16,769 |
| АИР200L2 | 45/2940 | 146,173 | 380,051 | 584,694 | 19,003 |
| АИР225М2 | 55/2955 | 177,750 | 408,824 | 710,998 | 35,550 |
| АИР250S2 | 75/2965 | 241,568 | 628,078 | 966,273 | 84,549 |
| АИР250М2 | 90/2960 | 290,372 | 784,003 | 1161,486 | 116,149 |
| АИР280S2 | 110/2960 | 354,899 | 887,247 | 1171,166 | 212,939 |
| АИР280М2 | 132/2964 | 425,304 | 1233,381 | 1488,563 | 297,713 |
| АИР315S2 | 160/2977 | 513,268 | 1231,844 | 1693,786 | 590,259 |
| АИР315М2 | 200/2978 | 641,370 | 1603,425 | 2116,521 | 962,055 |
| АИР355SMA2 | 250/2980 | 801,174 | 1281,879 | 2403,523 | 2163,171 |
| АИР160S4 | 15/1460 | 98,116 | 186,421 | 284,538 | 7,457 |
| АИР160М4 | 18,5/1460 | 121,010 | 229,920 | 350,930 | 11,375 |
| АИР180S4 | 22/1460 | 143,904 | 302,199 | 402,932 | 15,110 |
| АИР180М2 | 30/1460 | 196,233 | 470,959 | 588,699 | 27,276 |
| АИР200М4 | 37/1460 | 242,021 | 532,445 | 847,072 | 46,952 |
| АИР200L4 | 45/1460 | 294,349 | 647,568 | 941,918 | 66,229 |
| АИР225М4 | 55/1475 | 356,102 | 997,085 | 1317,576 | 145,289 |
| АИР250S4 | 75/1470 | 487,245 | 1218,112 | 1559,184 | 301,605 |
| АИР250М4 | 90/1470 | 584,694 | 1461,735 | 1871,020 | 467,755 |
| АИР280S4 | 110/1470 | 714,626 | 2072,415 | 2429,728 | 578,847 |
| АИР280М4 | 132/1485 | 848,889 | 1697,778 | 2886,222 | 1612,889 |
| АИР315S4 | 160/1487 | 1027,572 | 2568,931 | 3802,017 | 2363,416 |
| АИР315М4 | 200/1484 | 1287,062 | 3217,655 | 4247,305 | 3603,774 |
| АИР355SMA4 | 250/1488 | 1604,503 | 3690,356 | 4492,608 | 8985,215 |
| АИР355SMВ4 | 315/1488 | 2021,673 | 5054,183 | 5862,853 | 12534,375 |
| АИР355SMС4 | 355/1488 | 2278,394 | 5012,466 | 6151,663 | 15493,078 |
| АИР160S6 | 11/970 | 108,299 | 205,768 | 314,067 | 12,021 |
| АИР160М6 | 15/970 | 147,680 | 339,665 | 443,041 | 20,675 |
| АИР180М6 | 18,5/970 | 182,139 | 400,706 | 546,418 | 29,324 |
| АИР200М6 | 22/975 | 215,487 | 517,169 | 711,108 | 50,209 |
| АИР200L6 | 30/975 | 293,846 | 617,077 | 881,538 | 102,846 |
| АИР225М6 | 37/980 | 360,561 | 721,122 | 1081,684 | 186,050 |
| АИР250S6 | 45/986 | 435,852 | 784,533 | 1307,556 | 440,210 |
| АИР250М6 | 55/986 | 532,708 | 1012,145 | 1811,207 | 633,922 |
| АИР280S6 | 75/985 | 727,157 | 1454,315 | 2326,904 | 1090,736 |
| АИР280М6 | 90/985 | 872,589 | 1745,178 | 2792,284 | 1657,919 |
| АИР315S6 | 110/987 | 1064,336 | 1809,372 | 2873,708 | 4044,478 |
| АИР315М6 | 132/989 | 1274,621 | 2166,855 | 3696,400 | 5735,794 |
| АИР355МА6 | 160/993 | 1538,771 | 2923,666 | 3539,174 | 11848,540 |
| АИР355МВ6 | 200/993 | 1923,464 | 3654,582 | 4423,968 | 17118,832 |
| АИР355MLA6 | 250/993 | 2404,330 | 4568,228 | 5529,960 | 25485,901 |
| AИР355MLB6 | 315/992 | 3032,510 | 6065,020 | 7278,024 | 40029,133 |
| АИР160S8 | 7,5/730 | 98,116 | 156,986 | 235,479 | 13,246 |
| АИР160М8 | 11/730 | 1007,329 | 1712,459 | 2417,589 | 181,319 |
| АИР180М8 | 15/730 | 196,233 | 333,596 | 529,829 | 41,994 |
| АИР200М8 | 18,5/728 | 242,685 | 509,639 | 606,714 | 67,952 |
| АИР200L8 | 22/725 | 289,793 | 579,586 | 724,483 | 88,966 |
| АИР225М8 | 30/735 | 389,796 | 701,633 | 1052,449 | 214,388 |
| АИР250S8 | 37/738 | 478,794 | 861,829 | 1196,985 | 481,188 |
| АИР250М8 | 45/735 | 584,694 | 1052,449 | 1520,204 | 695,786 |
| АИР280S8 | 55/735 | 714,626 | 1357,789 | 2143,878 | 1071,939 |
| АИР280М8 | 75/735 | 974,490 | 1754,082 | 2728,571 | 1851,531 |
| АИР315S8 | 90/740 | 1161,486 | 1509,932 | 2671,419 | 4413,649 |
| АИР315М8 | 110/742 | 1415,768 | 2265,229 | 3964,151 | 6370,957 |
| АИР355SMA8 | 132/743 | 1696,635 | 2714,616 | 3902,261 | 12215,774 |
| AИР355SMB8 | 160/743 | 2056,528 | 3496,097 | 4935,666 | 18097,443 |
| AИР355MLA8 | 200/743 | 2570,659 | 4627,187 | 6940,781 | 26991,925 |
| AИР355MLB8 | 250/743 | 4498,654 | 7647,712 | 10796,770 | 58032,638 |
Расчет крутящего момента – формула
Примечание: при расчете стоит учесть коэффициент проскальзывания асинхронного двигателя. Номинальное количество оборотов двигателя не совпадает с реальным. Точное количество оборотов вы сможете найти, зная маркировку, в таблице выше.
Номинальное количество оборотов двигателя не совпадает с реальным. Точное количество оборотов вы сможете найти, зная маркировку, в таблице выше.
Расчет онлайн
Для расчета крутящего момента электродвигателя онлайн введите значение мощности ЭД и реальную угловую скорость (количество оборотов в минуту)
тут будет калькулятор
После расчета крутящего момента, посмотрите схемы подключения асинхронных электродвигателей звездой и треугольником на сайте «Слобожанского завода»
Источник
Основные параметры электродвигателя постоянного тока
- Постоянная момента
- Постоянная ЭДС
- Постоянная электродвигателя
- Жесткость механической характеристики
Постоянная момента
- где M — момент электродвигателя, Нм,
- – постоянная момента, Н∙м/А,
- I — сила тока, А
Постоянная ЭДС
Направление ЭДС определяется по правилу правой руки. Направление наводимой ЭДС противоположно направлению протекающего в проводнике тока.
Наведенная ЭДС последовательно изменяется по направлению из-за перемещения проводников в магнитном поле. Суммарная ЭДС, равная сумме ЭДС в каждой катушке, прикладывается к внешним выводам двигателя. Это и есть противо-ЭДС. Направление противо-ЭДС противоположно приложенному к двигателю напряжению. Значение противо-ЭДС пропорционально частоте вращения и определяется из следующего выражения: [1]
- где — электродвижущая сила, В,
- – постоянная ЭДС, В∙с/рад,
- — угловая частота, рад/с
Постоянные момента и ЭДС в точности равны между собой KT = KE. Постоянные KT и KE равны друг другу, если они определены в единой системе едениц.
Постоянная электродвигателя
Одним из основных параметров электродвигателя постоянного тока является постоянная электродвигателя Kм. Постоянная электродвигателя определяет способность электродвигателя преобразовывать электрическую энергию в механическую.
- где — постоянная электродвигателя, Нм/√ Вт ,
- R — сопротивление обмоток, Ом,
- – максимальный момент, Нм,
- — мощность потребляемая при максимальном моменте, Вт
Постоянная электродвигателя не зависит от соединения обмоток, при условии, что используется один и тот же материал проводника.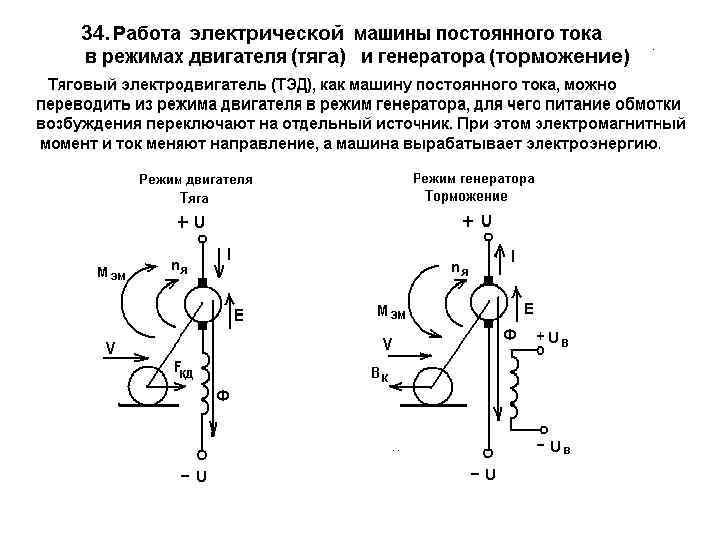 Например, обмотка двигателя с 6 ветками и 2 параллельными проводами вместо 12 одиночных проводов удвоят постоянную ЭДС, при этом постоянная электродвигателя останется не изменой.
Например, обмотка двигателя с 6 ветками и 2 параллельными проводами вместо 12 одиночных проводов удвоят постоянную ЭДС, при этом постоянная электродвигателя останется не изменой.
Жесткость механической характеристики двигателя
- где — жесткость механической характеристики электродвигателя постоянного тока
Напряжение электродвигателя
Уравнение баланса напряжений на зажимах двигателя постоянного тока имеет вид (в случае коллекторного двигателя не учитывается падение напряжения в щеточно-коллекторном узле):
- где U — напряжение, В.
Уравнение напряжения выраженное через момент двигателя будет выглядеть следующим образом:
Соотношение между моментом и частотой вращения при двух различных напряжениях питания двигателя постоянного тока неизменно. При увеличении частоты вращения момент линейно уменьшается. Наклон этой функции KTKE/R постоянный и не зависит от значения напряжения питания и частоты вращения двигателя.
Благодаря таким характеристикам упрощается управление частотой вращения и углом поворота двигателей постоянного тока. Это характерно для коллекторных и вентильных двигателей постоянного тока, что нельзя сказать о двигателях переменного тока и шаговых двигателях [1].
Это характерно для коллекторных и вентильных двигателей постоянного тока, что нельзя сказать о двигателях переменного тока и шаговых двигателях [1].
Мощность электродвигателя постоянного тока
Упрощенная модель электродвигателя выглядит следующим образом:
- где I – сила тока, А
- U — напряжение, В,
- M — момент электродвигателя, Н∙м
- R — сопротивление токопроводящих элементов, Ом,
- L — индуктивность, Гн,
- Pэл — электрическая мощность (подведенная), Вт
- Pмех — механическая мощность (полезная), Вт
- Pтеп — тепловые потери, Вт
- Pинд — мощность затрачиваемая на заряд катушки индуктивности, Вт
- Pтр — потери на трение, Вт
Механическая постоянная времени
Механическая постоянная времени — это время, отсчитываемое с момента подачи постоянного напряжения на электродвигатель, за которое частота вращения ненагруженного электродвигателя достигает уровня в 63,21% (1-1/e) от своего конечного значения.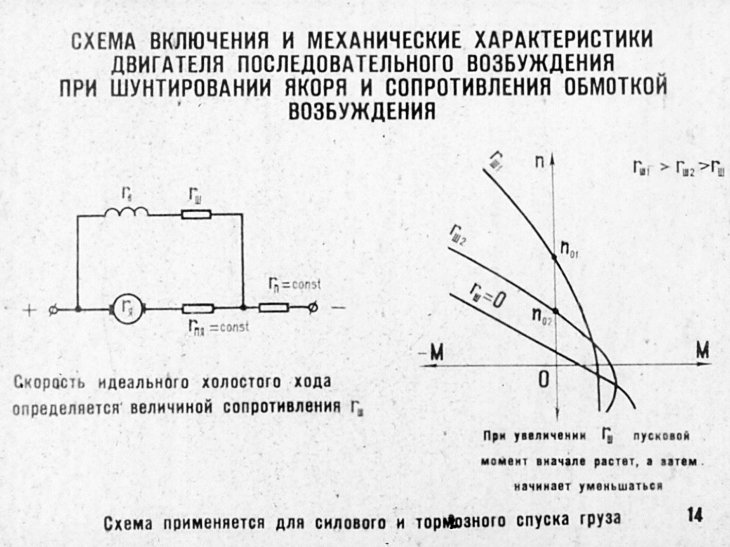
- где — механическая постоянная времени, с
Источник
Максимальная мощность и максимальный момент
Что же означает максимальная мощность и когда она доступна. Все наверняка знают какую максимальную мощность, которую выдает их двигатель. И при сравнении разных авто количество кобыл под капотом является если не основным, то весьма существенным фактором. Возьмем, к примеру, бензиновый двухлитровый двигатель от Mazda Skyactiv. Мотор имеет мощность 155 л.с., правда на 6000 оборотах в минуту.
А как часто вы раскручиваете мотор до таких оборотов? Каков при этом будет расход топлива? Взяв «городской» диапазон оборотов 3-4 тыс. об/мин, с этого мотора можно снять мощность от 75 до 110 л.с., что в полтора раза ниже максимальной. Зато в этот диапазон оборотов входит максимум момента. Получается, что максимальный момент в городском цикле реализуется гораздо чаще, чем максимальная мощность. Последняя понадобится если мы решим участвовать в гонках, ну или хотя-бы выедем на автобан без скоростных ограничений. Кстати, красная зона у этого мотора начинается с 6500 об/мин и характеризуется падением мощности и значительным провалом в моменте. Не говоря о вреде таких оборотов для двигателя, можно однозначно сказать что езда на таких оборотах крайне неэффективна.
Кстати, красная зона у этого мотора начинается с 6500 об/мин и характеризуется падением мощности и значительным провалом в моменте. Не говоря о вреде таких оборотов для двигателя, можно однозначно сказать что езда на таких оборотах крайне неэффективна.
Основные уравнения двигателя постоянного тока (ДПТ)
В этой статье описаны основные формулы, величины и их обозначения которые относятся ко всем двигателям постоянного тока.
В результате взаимодействия Iя тока якоря в проводнике L обмотки якоря с внешним магнитным полем возникает электромагнитная сила создающая электромагнитный момент М который приводит якорь во вращение с частотой n.
Резюмируя
В итоге имеем, что мощность это производная от момента. Двигатель развивает момент, а мощность характеризует скорость вращения вала при выдаваемом моменте. Мощность показывает максимальную скорость, которую сможет развить автомобиль. Момент же показывает «тяговитость», т. е. характеризует способность двигателя «тянуть» автомобиль, и чтобы понять насколько быстро двигатель тянет машину, вводят понятие мощности.
е. характеризует способность двигателя «тянуть» автомобиль, и чтобы понять насколько быстро двигатель тянет машину, вводят понятие мощности.
Мощность и момент на колесах (часть 2)
Использованные материалы: Характеристики ДВС Renault K7M Сравнение Nascar и Formula 1 Mazda Skyactiv Двигатель Opel Z13DTH
Противо ЭДС двигателя Eя
При вращении якоря пазовый проводник пресекает линии поля возбуждения с магнитной индукцией B и в соответствии с явлением электромагнитной индукции в проводнике наводится ЭДС Eя направленная навстречу Iя. Поэтому эта ЭДС называется противо ЭДС и она прямо пропорциональна Ф магнитному потоку и частоте вращения n.
Ce — постоянный коэффициент определяемой конструкцией двигателя.
Применив второй закон Кирхгофа получаем уравнение напряжения двигателя.
где ∑R — суммарное сопротивления обмотки якоря включающая сопротивление :
- обмотки якоря
- добавочных полюсов
- обмотки возбуждения (для двигателей с последовательным возбуждением)
Вращающий момент электродвигателя
В двигателях постоянного тока вращающий момент определяется выражением М
≡ Ф
I
я, т. е. он пропорционален потоку и току якоря. В асинхронном двигателе момент создается вращающимся потоком Ф и током ротора
е. он пропорционален потоку и току якоря. В асинхронном двигателе момент создается вращающимся потоком Ф и током ротора
I
2. Он может быть выражен
Следовательно, момент пропорционален потоку и активной слагающей тока ротора I
2 cos Ψ2, так как только активная слагающая тока определяет мощность, а значит и момент.
На рис. 10-20 представлена схема включения короткозамкнутого двигателя. Если пустить двигатель, включив рубильник 1, то в первый момент пуска, когда п
2
=
0, a
s
= 1, наведенная в роторе
2
э. д. с.
Е
2 и пусковой ток
I
2п максимальны. Однако, пусковой момент
М
п не будет максимальным, а в 2—2,5 раза меньше максимального. Векторная диаграмма для цепи ротора (рис. 10-21), построенная подобно изображенной на рис. 9-9, показывает причину этого.
Рис 10-20.
Схема включения короткозамкнутого асинхронного двигателя.
Обычно в роторе х2
во много раз больше
r
2 и угол Ψ2, на который ток
I
2п отстает от э. д. с.
д. с.
Е
2 велик. Поэтому активная слагающая тока
I
2п cos Ψ2, а значит и пусковой момент
М
п малы. В современных асинхронных двигателях
М
п/
М
п = 1 — 1,5, хотя
I
2п/
I
н≈ 4,5—6,5.
Это же явление по другому объясняется на рис. 10-19 и 10-22.
Рис. 10-21.
Векторная диаграмма в цепи ротора.
При описании принципа работы двигателя (рис. 10-19) было предположено, что ток I
2 совпадает по фазе с э. д. с.
Е
2, т. е. что он активный ( Ψ2 = 0). На рис. 10-22 представлен момент пуска, когда направление э. д. с. в проводах ротора соответствует обозначенному на рис. 10-19, а ток показан отстающим от э. д. с. на угол Ψ2. Тогда шесть проводов ротора (три под полюсом
N
и три под полюсом
S
) создают усилия, действующие в направлении вращения потока, а два провода вызывают противодействующие усилия. В результате этого вращающий момент будет тем меньше, чем больше сдвиг фаз между током
I
2 и э. д. с.
д. с.
E
2.
Рис. 10-22.
Ток в роторе двигателя в момент пуска.
По мере увеличения скорости вращения ротора реактивное сопротивление обмотки ротора x
2
s = x
2
s
уменьшается, а вместе с этим уменьшается угол Ψ2, так как сопротивление
r2
≈ const. Наступает такое положение (рис 10-21), когда при некотором скольжении
s
м ≈ 0,1—0,15 реактивное сопротивление
x
2
s
становится равным активному
r
2, угол Ψ — 45° и э. д. с.
E
2
s
уравновешивает два равных падения напряжения
I
2
r
2 и
I
2
x
2
s
.В это время активная слагающая тока
I
2 cos Ψ2 и вращающий момент
М
м становятся максимальными, несмотря на некоторое уменьшение тока
I
2.
Обычно М
м/
М
м = 1,8—2,5 и называется способностью к перегрузкe.
При дальнейшем разгоне ротора x2s становится значительно меньшим, чем r
2, им можно пренебречь и считать ток ротора активным (
I
2 ≈
I
2 cos Ψ 2). Так как
E
2
s= E
2
s
тоже продолжает уменьшаться, то вместе с током
I
2 уменьшается и вращающий момент.
Максимальная скоростьn
вращения будет при холостом ходе двигателя и тогда
n
2 ≈
n
1 , a s ≈ 0. Зависимость вращающего момента от скольжения
М =f
(
s
) представлена на рис. 10-23.
Рис. 10-23.
Зависимость вращающего момента двигателя от скольжения.
Нормальная работа двигателя возможна только на участке кривой при скольжениях s
от нуля до sм, так как в этом случае при увеличении тормозного момента и значит
s
вращающий момент возрастает. На участке от
s
=
s
м до
s
= 1 работа двигателя неустойчива. Номинальный момент Мн соответствует обычно номинальному скольжению
Номинальный момент Мн соответствует обычно номинальному скольжению
s
н = 1—6%.
Поток Ф пропорционален напряжению U
1, подводимому к трансформатору. Сказанное остается в силе и для асинхронного двигателя. Так как
М
≡ Ф
I
2 cos Ψ 2, то можно написать, что
Отсюда можно сделать очень важный для асинхронных двигателей вывод
т. е. вращающий момент пропорционален квадрату подведенного к статору напряжения. Таким образом, падение напряжения в сети, например до 0,9 U
1н, вызовет уменьшение момента до 0,9 • 0,9
М
н
=
0,81
М
н и нагруженный двига тель может остановиться. Указанным обстоятельством и объясняется, частично, нормирование падения напряжения в распределительных сетях, питающих асинхронные двигатели.
В практике потребителя часто интересует механическая характеристика двигателя
п
2
= f
(
М
) при
U
1
=
const и
f
1 = const. Для удобства пользования по осям откладывают (
Для удобства пользования по осям откладывают (
n
2/
n
1)100% и (
М
/
М
н)100%.
Рис. 10-24.
Механическая характеристика двигателя.
Эта характеристика получается простым перестроением рис, 10-23 и показана на рис. 10-24, где рабочая часть обозначена сплошной линией. Кривая 1 для двига телей нормального исполнения показывает, что асинхронный двигатель обладает жесткой характеристикой скорости, подобно двигателю постоянного тока параллельного возбуждения. Асинхронный двигатель с фазным ротором для регулирования скорости вращения, например для крановых и подъемных устройств, имеет более мягкую характеристику (кривая 2).
Бензин или Дизель?
Бензин, как известно, имеет большую температуру горения и выделяет при этом больше энергии. Кроме того, дизельный двигатель имеет более ограниченный диапазон оборотов, стало быть большой мощности с дизеля не снять. Поэтому дизель оптимизирован под момент (длинные шатуны и большой ход поршня). А чтобы он хоть как-то ехал на него обычно устанавливают турбину, ведь дизель не имеет проблем с детонацией при увеличении степени сжатия. Приведу в пример характеристики двигателя Opel Z13DTH (Astra-H, Corsa-D) — это турбо-дизель с объемом 1.3 литра.
А чтобы он хоть как-то ехал на него обычно устанавливают турбину, ведь дизель не имеет проблем с детонацией при увеличении степени сжатия. Приведу в пример характеристики двигателя Opel Z13DTH (Astra-H, Corsa-D) — это турбо-дизель с объемом 1.3 литра.
Двигатель имеет довольно малую мощность в 90 л.с. (на 4000 об/мин), но зато момент в 200 Нм. Тут будет уверенный подхват с низов, но малая максимальная скорость автомобиля (172 км/ч для Astra при 1250 кг массы). Малая мощность характеризуется резким падением момента на максимальных оборотах и, собственно, невысокими максимальными оборотами.
Как управляются двигатели постоянного тока? — Регулирование скорости двигателей постоянного тока
Двигатели постоянного тока питаются от постоянного тока. Они имеют широкий спектр применения в таких продуктах, как бытовая техника, транспортные средства и заводы. Можно сказать, что они играют жизненно важную роль в нашей жизни.
Однако многие пользователи выражают неуверенность в том, как управлять скоростью двигателей постоянного тока. На этой странице представлено простое введение в то, как это делается.
На этой странице представлено простое введение в то, как это делается.
Что такое двигатель постоянного тока?
Начнем с того, что электродвигатель — это машина, которая использует электричество для вращения вала, тем самым преобразуя электрическую энергию в механическую. Электродвигатели в целом делятся на следующие три типа.
- Двигатели постоянного тока
- Двигатели переменного тока
- Шаговые двигатели
Двигатели переменного тока приводятся в действие переменным током, а шаговые двигатели приводятся в действие импульсами электроэнергии. С другой стороны, двигатели постоянного тока питаются от постоянного тока и имеют следующие особенности.
- Высокий пусковой момент и возможность вращения на высоких скоростях
- Мощность двигателя пропорциональна приложенному напряжению
Двигатели постоянного тока подразделяются на щеточные двигатели постоянного тока и бесщеточные двигатели постоянного тока. Коллекторные двигатели постоянного тока имеют катушки в своем роторе и изменяют способ прохождения тока через катушки на основе механизма, использующего коммутаторы и щетки. Коллекторные двигатели постоянного тока создают электрические и акустические шумы и требуют частого обслуживания, поскольку их щетки и коллектор являются расходными частями. Но они также имеют простую конструкцию и могут работать без электронной схемы привода, если не требуется регулирование скорости.
Коллекторные двигатели постоянного тока имеют катушки в своем роторе и изменяют способ прохождения тока через катушки на основе механизма, использующего коммутаторы и щетки. Коллекторные двигатели постоянного тока создают электрические и акустические шумы и требуют частого обслуживания, поскольку их щетки и коллектор являются расходными частями. Но они также имеют простую конструкцию и могут работать без электронной схемы привода, если не требуется регулирование скорости.
Бесщеточный двигатель постоянного тока, напротив, не требует коммутатора и щеток, поскольку в роторе имеется постоянный магнит. Это, однако, означает, что им требуется схема привода. Они также отличаются низким уровнем обслуживания, бесшумной работой и длительным сроком службы.
Характеристики двигателей постоянного тока
В отличие от двигателей переменного тока, двигатели постоянного тока очень просты в использовании благодаря простоте изменения их скорости. Итак, как это достигается на практике? Следующее объяснение начинается с рассмотрения характеристик двигателя постоянного тока.
Характеристики двигателя постоянного тока представлены кривой крутящий момент-скорость, которая наклонена вниз вправо, с крутящим моментом в качестве горизонтальной оси и скоростью в качестве вертикальной оси. Скорость самая высокая, когда нет нагрузки, спадает вправо, пока не будет достигнут максимальный крутящий момент при нулевой скорости.
Крутящий момент и скорость изменяются в зависимости от нагрузки, как показано на этой кривой зависимости крутящего момента от скорости. Глядя на график ниже, давайте рассмотрим двигатель, вращающийся со скоростью ω0 с крутящим моментом T0. Если крутящий момент нагрузки затем увеличится до T1, скорость двигателя будет следовать за крутящим моментом до новой скорости ω1. Аналогичным образом, если момент нагрузки далее увеличивается до T2, скорость падает до ω2.
Крутящий момент и скорость двигателя постоянного тока
Взгляд на взаимосвязь между крутящим моментом и током показывает, что они пропорциональны друг другу.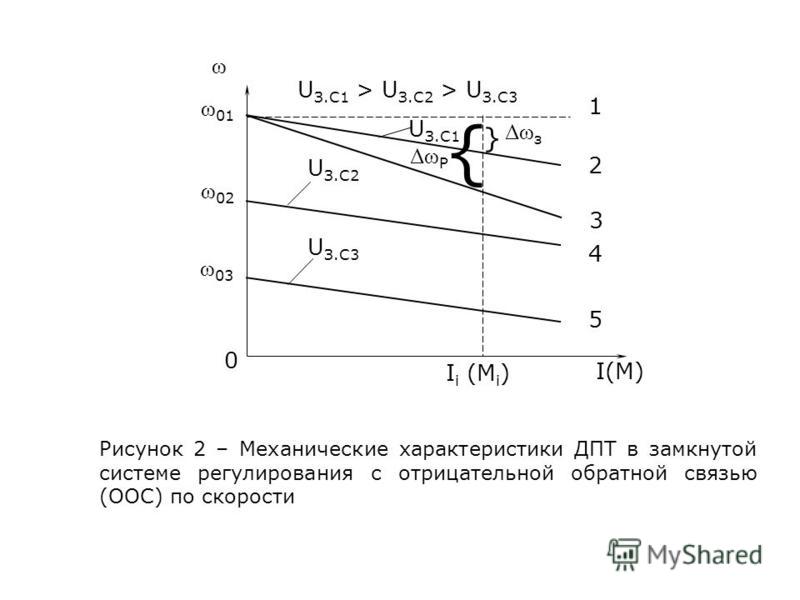 Соотношение между ними является постоянным для двигателя, при этом соотношение остается неизменным независимо от изменений скорости двигателя или напряжения привода. Это означает, что измерения тока двигателя достаточно для определения крутящего момента двигателя.
Соотношение между ними является постоянным для двигателя, при этом соотношение остается неизменным независимо от изменений скорости двигателя или напряжения привода. Это означает, что измерения тока двигателя достаточно для определения крутящего момента двигателя.
Момент-скорость двигателя постоянного тока и кривая момента-тока
Что происходит при изменении напряжения привода?
Итак, что происходит с кривой крутящий момент-скорость, когда изменяется напряжение, используемое для привода двигателя постоянного тока? На приведенном ниже графике показаны кривые крутящий момент-скорость для различных напряжений. Удвоение напряжения привода удваивает как скорость двигателя без нагрузки, так и пусковой момент (крутящий момент, когда двигатель зафиксирован). Другими словами, увеличение напряжения сдвигает кривую крутящий момент-скорость вверх, параллельно. Кривая крутящий момент-скорость для двигателя постоянного тока может быть скорректирована по желанию путем изменения напряжения, подаваемого на двигатель.
Напряжение привода двигателя и кривая крутящего момента
Как заставить двигатель постоянного тока вращаться с необходимой скоростью
Теперь, учитывая эти характеристики, как вы можете вращать двигатель с требуемой скоростью при любом заданном моменте нагрузки?
Кривая момент-скорость двигателя постоянного тока преобразуется в зависимости от изменения напряжения привода. Это означает, что указанная выше цель может быть достигнута простой регулировкой напряжения возбуждения. Если посмотреть на график ниже, если требуется вращение со скоростью ω1, когда момент нагрузки равен, например, T0, напряжение привода V4 слишком низкое, что приводит к скорости ω2. Напряжение возбуждения V0 слишком велико, что приводит к скорости ω0. Однако управление двигателем при промежуточном напряжении V3 как раз подходит для достижения желаемой скорости ω1.
Напряжение и скорость привода двигателя
Регулируя таким образом напряжение привода, можно заставить двигатель постоянного тока вращаться с желаемой скоростью независимо от крутящего момента нагрузки.
Методы управления напряжением привода
Два способа регулировки напряжения привода: линейное управление и ШИМ-управление.
Линейное управление работает путем включения переменного резистора последовательно с двигателем и регулировки сопротивления для изменения напряжения на двигателе. Хотя транзистор или другое полупроводниковое устройство можно использовать в качестве последовательно соединенного переменного резистора, этот подход имеет низкую эффективность из-за большого количества тепла, выделяемого сопротивлением (полупроводником), и поэтому в наши дни он используется редко.
Альтернативным методом является ШИМ-управление. Напряжение, подаваемое на двигатель, можно изменять, включая и выключая полупроводниковый переключатель (например, транзистор или полевой транзистор) на высокой скорости, при этом напряжение определяется шириной импульса включения и выключения. Высокая эффективность этого метода делает его наиболее распространенным в настоящее время.
Линейное управление
ШИМ-управление
Регулятор скорости двигателя
Использование этих методов позволяет гибко регулировать скорость двигателя постоянного тока. Однако для поддержания постоянной скорости вращения двигателя требуется дополнительное управление. Это связано с тем, что крутящий момент двигателя зависит от самой нагрузки, а также от других факторов, таких как температура, влажность и изменения во времени. Простое вождение двигателя с постоянным напряжением приведет к тому, что его скорость будет колебаться при изменении нагрузки.
Поддержание постоянной скорости, несмотря на переменную нагрузку, требует постоянной регулировки напряжения привода в ответ на эти изменения нагрузки. На приведенном ниже графике показан пример, когда момент нагрузки для двигателя, работающего со скоростью ω0, уменьшается с T1 до T0, и в этом случае снижение напряжения привода до V0 поддерживает скорость двигателя на уровне ω0. Если вместо этого крутящий момент увеличивается до T2, для поддержания постоянной скорости двигателя ω0 требуется, чтобы напряжение привода увеличилось до V2.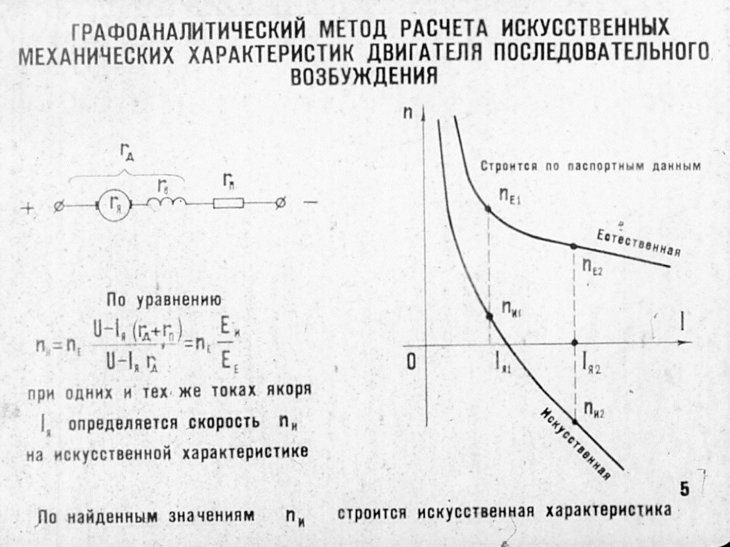
Контроль скорости
Скорость измеряется датчиком, прикрепленным к двигателю. Вычисляется разница между измеренной и требуемой скоростью двигателя (ошибка скорости), а напряжение привода регулируется таким образом, чтобы оно увеличивалось, если скорость была слишком низкой, и уменьшалась, если скорость была слишком высокой. При этом поддерживается постоянная скорость двигателя. В то время как в прошлом для управления напряжением возбуждения использовались операционные усилители или другие аналоговые схемы, в последние годы использование микрокомпьютеров стало нормой.
Схема управления скоростью двигателя постоянного тока
Схема управления скоростью бесщеточного двигателя постоянного тока
Датчик скорости
Выводит сигнал, указывающий скорость двигателя. К устройствам, используемым для этой цели, относятся датчики Холла, энкодеры и тахогенераторы.
Цепь определения скорости
Расчет скорости двигателя по сигналу датчика скорости.

Задание скорости
Выводит целевую скорость двигателя.
Компаратор
Вычисляет разницу между заданием скорости и измеренной скоростью.
Схема расчета напряжения привода
Вычисляет напряжение привода двигателя на основе расчетной ошибки скорости.
Цепь привода
Цепь, которая регулирует напряжение, подаваемое на двигатель, в соответствии с сигналом напряжения привода.
Двигатель постоянного тока может работать в устойчивом режиме, контролируя его скорость так, чтобы она оставалась постоянной независимо от изменений нагрузки. Эти двигатели также подходят для широкого спектра методов управления, которые могут быть реализованы с помощью микрокомпьютера. Двигатели постоянного тока находят применение во многих различных приложениях, в которых используется простота управления.
Двигатели постоянного тока: простые в использовании двигатели с простой регулировкой скорости
Двигатели постоянного тока питаются от постоянного тока, и, в отличие от двигателей переменного тока, их скорость легко регулируется. Характеристики двигателя постоянного тока представлены его кривой крутящий момент-скорость, в которой скорость и крутящий момент нагрузки обратно пропорциональны. Эта кривая крутящий момент-скорость преобразуется в зависимости от изменения напряжения привода. Соответственно, регулируя напряжение, подаваемое на двигатель постоянного тока, его можно заставить работать на любой скорости независимо от крутящего момента нагрузки.
Для изменения напряжения привода двигателя можно использовать линейное или ШИМ-управление. ШИМ-управление стало преобладать в последние годы из-за его превосходной эффективности. ШИМ-управление изменяет напряжение, включая и выключая полупроводниковый переключатель с высокой скоростью таким образом, что изменение ширины импульса включения и выключения изменяет напряжение.
Решение проблем с бесщеточными двигателями постоянного тока
ASPINA поставляет не только автономные бесщеточные двигатели постоянного тока, но и системные продукты, включающие системы привода и управления, а также механические конструкции. Они подкреплены всесторонней поддержкой, которая простирается от прототипирования до коммерческого производства и послепродажного обслуживания.
ASPINA может предложить решения, адаптированные к функциям и характеристикам, требуемым в различных отраслях промышленности, областях применения и потребительских продуктах, а также для ваших конкретных производственных схем.
ASPINA поддерживает не только клиентов, которые уже знают свои требования или спецификации, но и тех, кто сталкивается с проблемами на ранних стадиях разработки. Вы боретесь со следующими проблемами?
- Выбор двигателя
- У вас еще нет подробных спецификаций или проектных чертежей, но вам нужен совет по двигателям?
- У вас нет штатного специалиста по двигателям, и вы не можете определить, какой тип двигателя лучше всего подойдет для вашего нового продукта?
- Разработка двигателя и связанных с ним компонентов
- Хотите сосредоточить свои ресурсы на основных технологиях и заказать приводные системы и разработку двигателей?
- Хотите сэкономить время и силы на перепроектирование существующих механических компонентов при замене двигателя?
- Уникальное требование
- Вам нужен нестандартный двигатель для вашего продукта, но ваш обычный поставщик отказался?
- Не можете найти двигатель, который дает вам требуемый контроль, и почти теряете надежду?
Ищете ответы на эти вопросы? Свяжитесь с ASPINA, мы здесь, чтобы помочь.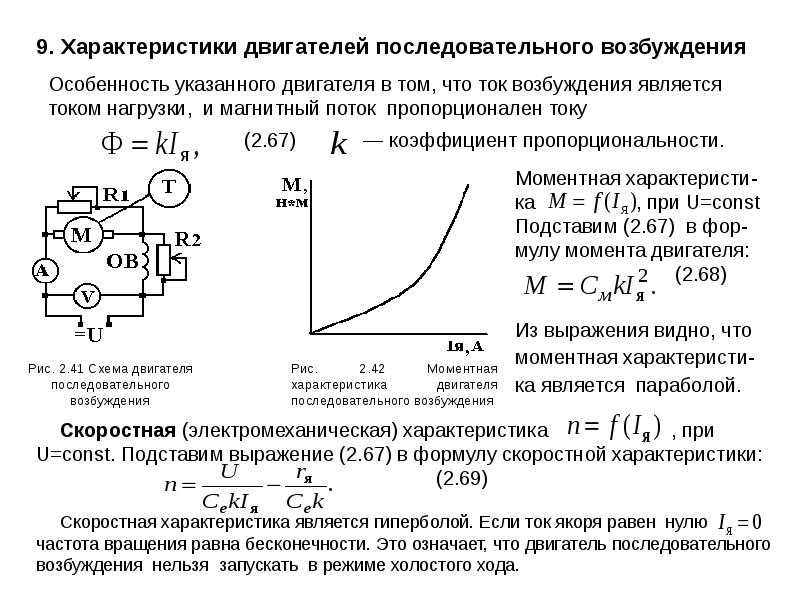
Ссылки на глоссарий и страницы часто задаваемых вопросов Выходная скорость против. Крутящий момент Двигатели постоянного тока – напряжение по сравнению с. Выходная скорость против. Крутящий момент
Взаимосвязь между напряжением, крутящим моментом и выходной скоростью является частой темой обсуждения между нашими клиентами и инженерами по продажам Precision Microdrives.
Целью следующей статьи является обсуждение и уточнение взаимосвязи между этими параметрами и методами их использования вместе с другими ресурсами, чтобы понять все возможности наших двигателей постоянного тока и мотор-редукторов.
Определения терминов, используемых в нашем техпаспорте, можно найти ниже со ссылками, щедро разбросанными по всей статье для дальнейшего чтения.
Крутящий момент и скорость
Крутящий момент можно определить как «крутящую силу», которая имеет тенденцию вращать объект вокруг точки опоры. Что касается двигателей постоянного тока и мотор-редукторов, мы обычно будем называть «номинальный крутящий момент» «номинальной нагрузкой», чтобы избежать путаницы в наших значениях. В конечном счете, эти два термина представляют одно и то же значение — вращательное усилие, приложенное к выходному валу.
В конечном счете, эти два термина представляют одно и то же значение — вращательное усилие, приложенное к выходному валу.
Говоря о скорости, мы обычно имеем в виду угловую скорость выходного вала наших двигателей постоянного тока и мотор-редукторов (обычно в оборотах в минуту). В зависимости от приложения этот параметр будет влиять на скорость выполнения конкретной функции и может существенно повлиять на общую производительность устройства.
Зачем менять крутящий момент?
Наиболее очевидным преимуществом изменения крутящего момента является поддержание постоянной скорости при изменении нагрузки двигателя с учетом взаимозависимого характера скорости, крутящего момента и напряжения.
Хотя этот пример может быть устаревшим, аудиокассеты — отличный способ объяснить, как в некоторых приложениях необходимо изменять крутящий момент, чтобы соответствовать изменяющейся нагрузке. По мере воспроизведения кассеты и перемещения аудиозаписи с одного шпинделя на другой нагрузка на приводной двигатель будет изменяться. Тем не менее, воспроизведение должно оставаться с постоянной скоростью, иначе это повлияет на высоту тона звука.
Тем не менее, воспроизведение должно оставаться с постоянной скоростью, иначе это повлияет на высоту тона звука.
Также бывают случаи, когда нагрузка двигателя резко меняется между операциями, а не медленно, как в примере с кассетой. Это часто происходит со шкивами и подъемниками: двигатель останавливается в крайнем случае, когда груз прикрепляется или снимается. Здесь поддержание постоянной скорости не так важно, как способность двигателя выдерживать различные крутящие нагрузки, поскольку для перемещения более тяжелого объекта требуется больший выходной крутящий момент, чем для легкого объекта или без нагрузки.
Все эти приложения имеют общую тему переменной нагрузки, прикрепленной к двигателю. Если ваше приложение предполагает фиксированную нагрузку, то, вероятно, вам будет интереснее варьировать скорость.
Свяжитесь с нами по телефону
Поговорите с членом нашей команды.
Каталог двигателей
Ищете нашу продукцию?
Надежные, экономичные миниатюрные механизмы и двигатели, отвечающие вашим требованиям.
Зачем менять скорость?
Возможность изменять скорость двигателя при поддержании постоянного крутящего момента важна для многих приложений по разным причинам.
Примером приложения, требующего переменной скорости и постоянного крутящего момента, является проигрыватель аудио компакт-дисков, поскольку обычно наблюдается, что в одних точках компакт-диск будет вращаться быстрее, чем в других. Это связано с тем, что информация хранится в спиральных круговых дорожках на диске, а длина/окружность дорожек прямо пропорциональна количеству хранимой на них информации. Это означает, что скорость должна быть уменьшена по мере того, как лазер считывает данные с крайних дорожек, потому что за один оборот поступает больше информации. И наоборот, скорость увеличивается по мере того, как лазер считывает самые внутренние дорожки, поскольку окружности спирали меньше и, следовательно, содержат меньше информации за один оборот.
Без возможности регулировать скорость двигателя (с напряжением) при поддержании этого постоянного крутящего момента было бы очень сложно считывать и воспроизводить эту информацию с постоянной скоростью.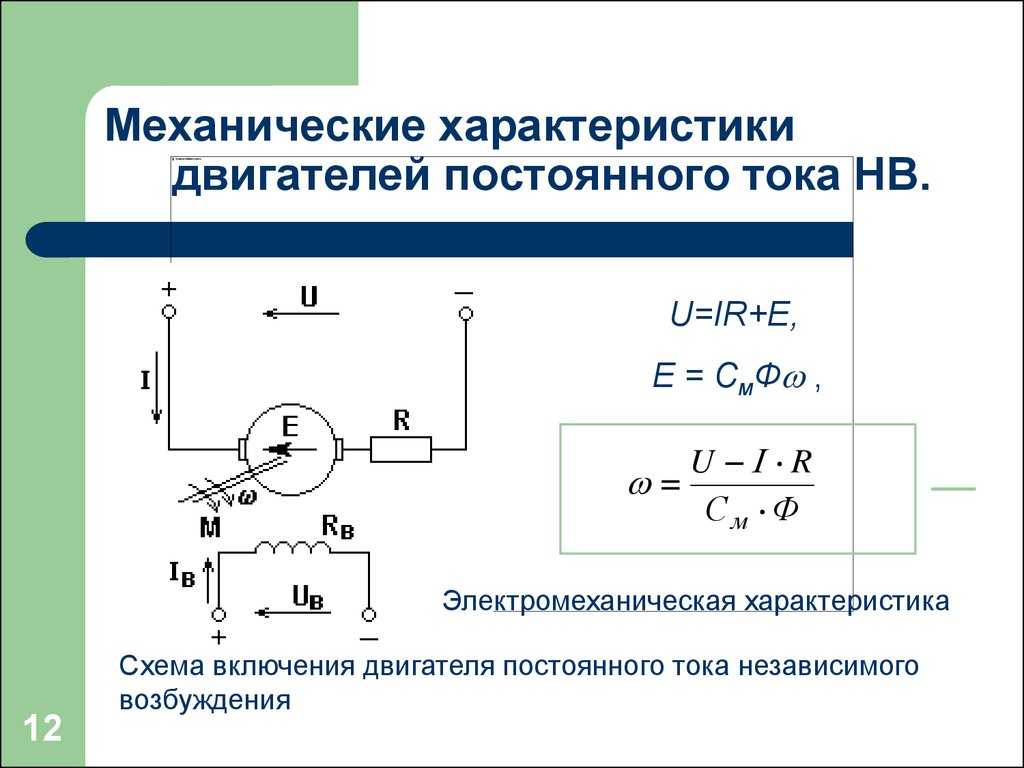
Этот же принцип может быть применен к большому количеству приложений и часто имеет решающее значение для их успешной работы. Многие из наших двигателей постоянного тока и мотор-редукторов могут работать при самых разных скоростях и нагрузках, что позволяет нашим клиентам изучить возможности своего проекта и, как правило, найти подходящее решение с одним двигателем.
Как читать типовую таблицу характеристик производительности
Таблица типичных рабочих характеристик находится на первой странице каждого из наших технических паспортов. Этот график является чрезвычайно полезным инструментом, иллюстрирующим типичное поведение отдельного двигателя.
Как мы уже обсуждали ранее, многие из наших клиентов ищут двигатель или мотор-редуктор, который будет работать с заданной скоростью и нагрузкой. Одним из лучших мест для поиска решения является наш онлайн-каталог, и мы всегда можем помочь порекомендовать подходящие двигатели и обсудить варианты настройки. Поскольку скорость двигателя в двигателях постоянного тока и редукторных двигателях в основном определяется нагрузкой и напряжением привода, значение «Номинальная скорость» в техпаспорте берется при «Номинальном напряжении» и «Номинальной нагрузке». Это означает, что значения скорости, указанные в технических характеристиках, берутся в контролируемых и конкретных условиях и не отражают всех возможностей какого-либо отдельного двигателя. Именно здесь типичная диаграмма производительности является полезным инструментом для просмотра более широкого диапазона возможностей двигателя.
Это означает, что значения скорости, указанные в технических характеристиках, берутся в контролируемых и конкретных условиях и не отражают всех возможностей какого-либо отдельного двигателя. Именно здесь типичная диаграмма производительности является полезным инструментом для просмотра более широкого диапазона возможностей двигателя.
108-106 Motor Performance Graph
Графики для наших двигателей постоянного тока и мотор-редукторов предполагают фиксированное напряжение и показывают, как потребляемый ток, мощность, КПД и скорость двигателя зависят от изменения нагрузки. Каждый из затронутых параметров имеет свою независимую линию производительности и соответствующую шкалу по оси Y.
Синяя линия на диаграмме типичных характеристик 108-106 (выше) показывает скорости, при которых двигатель будет работать от точки холостого хода до крутящего момента (около 0,725 мНм) и позволяет нам исследовать производительность двигателя, а также понять взаимосвязь между скоростью и крутящим моментом для отдельного двигателя.
Например; если клиенту требуется постоянная скорость и крутящий момент 1900 об/мин и 0,65 мНм соответственно, в разделе «ключевые характеристики» (выше) листа данных будет указано, что 108-106 не подходит, поскольку в нем указано:
.
Номинальная нагрузка – 0,15 мН·м
Номинальная скорость нагрузки – 12 600 об/мин
Однако после проверки диаграммы производительности при нагрузке 0,65 мНм по оси X синяя линия производительности (скорость) указывает на соответствующей оси Y, что скорость будет равна 1900 об/мин. Изображение выше иллюстрирует это и демонстрирует, что 108-106 действительно подходит для клиентов, исходя из их требований к фиксированной скорости и крутящему моменту. Эту диаграмму также можно расширить, чтобы проиллюстрировать диапазон возможностей двигателя, если он будет использоваться с динамической нагрузкой/скоростью.
Связь между скоростью, крутящим моментом и напряжением
Теперь, когда мы обсудили, как читать диаграмму производительности, мы можем взглянуть на взаимосвязь между скоростью и крутящим моментом. В этом разделе мы обрисуем взаимосвязь между скоростью и крутящим моментом и объясним пределы каждого из них, прежде чем рассматривать дальнейшее влияние напряжения на эти параметры.
В этом разделе мы обрисуем взаимосвязь между скоростью и крутящим моментом и объясним пределы каждого из них, прежде чем рассматривать дальнейшее влияние напряжения на эти параметры.
N/L скорость и момент опрокидывания на графиках рабочих характеристик двигателя
Если предположить, что двигатель приводится в действие при фиксированном напряжении, есть две точки, которые описывают пиковую производительность двигателя на каждом конце. «Холостой ход» (N/L) и «опрокидывающий момент»
- Момент остановки представляет собой точку, в которой двигатель достигает максимальной рабочей нагрузки. В этот момент вал больше не будет вращаться, и двигатель будет находиться в «заглохшем» состоянии. Обратите внимание, что двигатель не должен работать в режиме остановки, так как это почти наверняка приведет к преждевременному выходу из строя.
- Скорость холостого хода — это максимальная выходная скорость, которую двигатель достигает при заданном напряжении. В этот момент двигатель работает свободно и без внешней нагрузки
Наши двигатели постоянного тока и мотор-редукторы могут работать в любом диапазоне между этими пределами до остановки. Если мы посмотрим на синюю линию производительности, связь между скоростью и крутящим моментом довольно легко понять — крутящий момент обратно пропорционален скорости двигателя — начиная с точки холостого хода/полной скорости и, по мере увеличения нагрузки, скорость уменьшается пропорционально, пока двигатель не заглохнет.
Если мы посмотрим на синюю линию производительности, связь между скоростью и крутящим моментом довольно легко понять — крутящий момент обратно пропорционален скорости двигателя — начиная с точки холостого хода/полной скорости и, по мере увеличения нагрузки, скорость уменьшается пропорционально, пока двигатель не заглохнет.
Хотя диаграмма производительности показывает, как скорость влияет на применение различных нагрузок, она не указывает на то, что скорость наших двигателей постоянного тока также прямо пропорциональна приложенному напряжению. Теорию, лежащую в основе этого принципа, можно найти здесь. Короче говоря, это означает, что мы можем управлять скоростью двигателя независимо от крутящего момента, и это позволяет нам поддерживать постоянную скорость для переменной нагрузки, а также поддерживать постоянный крутящий момент при изменении скорости двигателя.
Этот принцип используется для обеспечения правильного воспроизведения нашего проигрывателя компакт-дисков и кассеты и, вероятно, будет включать систему обратной связи с обратной связью, которая будет измерять скорость двигателя и регулировать напряжение возбуждения, чтобы либо поддерживать постоянную скорость при переменной нагрузке, либо обеспечивать переменная скорость для фиксированной нагрузки.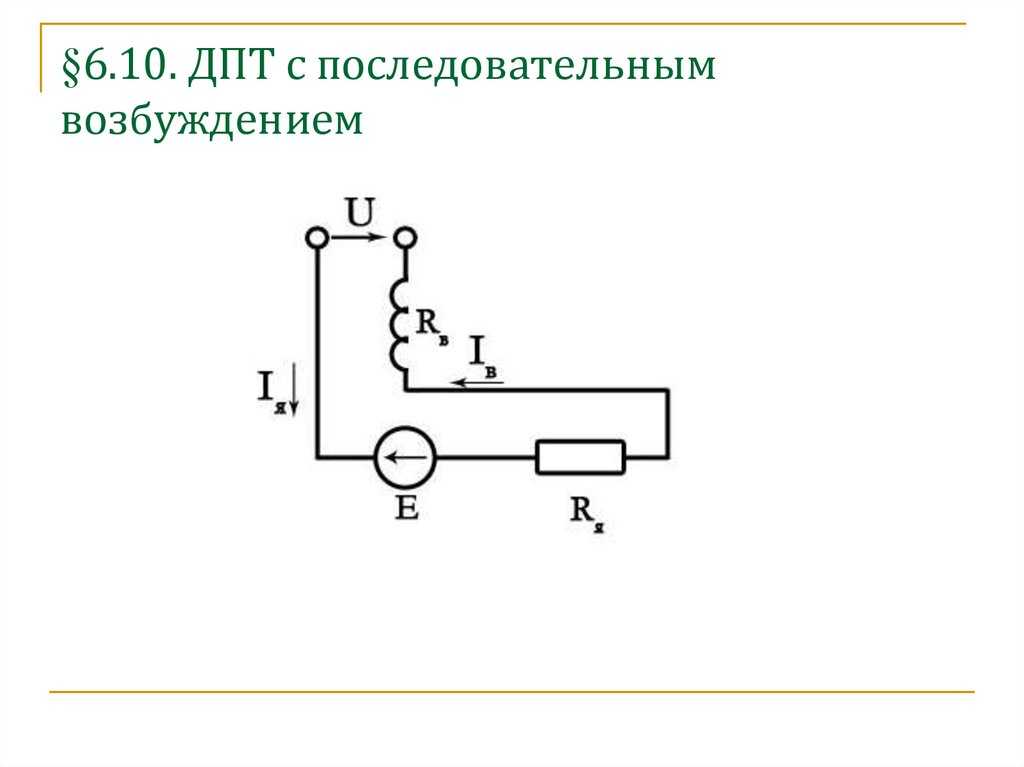
Как мы можем изменить производительность двигателя
Существует несколько методов настройки характеристик двигателя, будь то индивидуальное решение, адаптированное к потребностям клиента, или простая регулировка режима работы двигателя. Некоторые распространенные модификации перечислены ниже:
- Обмотки: Путем изменения количества витков в обмотках двигателя и/или площади поперечного сечения используемого провода можно управлять сопротивлением клемм, рабочим напряжением/током и индуктивностью клемм. Это означает, что как электрические, так и механические характеристики двигателя могут быть легко адаптированы к конкретной спецификации.
- Передаточные числа коробки передач: коробки передач являются эффективным методом точного изменения характеристик двигателя постоянного тока с использованием одной или нескольких ступеней редуктора. Несмотря на то, что мы поставляем мотор-редукторы со склада, многие из наших клиентов хотели бы разработать свой собственный набор шестерен.
 Если вы хотите поэкспериментировать со своими собственными зубчатыми цепями, простые уравнения для шестерен можно найти в AB-024. Тем не менее, мы можем предложить нестандартные редукторы и модификации стандартных деталей, поэтому, пожалуйста, не стесняйтесь обращаться к инженеру, если вы хотите обсудить ваши требования и варианты, которые мы можем предложить.
Если вы хотите поэкспериментировать со своими собственными зубчатыми цепями, простые уравнения для шестерен можно найти в AB-024. Тем не менее, мы можем предложить нестандартные редукторы и модификации стандартных деталей, поэтому, пожалуйста, не стесняйтесь обращаться к инженеру, если вы хотите обсудить ваши требования и варианты, которые мы можем предложить. - Управляющее напряжение: это может быть простой и экономичный способ управления производительностью наших двигателей. Есть несколько способов, которыми вы можете настроить управляющее напряжение для вашего двигателя, включая ШИМ и даже специальные микросхемы драйвера. Ранее мы обсуждали эти темы более подробно по следующим ссылкам – 1 и 2
- . Выбор материала. Используемые материалы могут существенно повлиять на общую производительность вашего мотор-редуктора. Некоторые из возможных вариантов здесь перечислены ниже
- Материал редуктора: общая точка отказа микроредукторов возникает на последней ступени редуктора.
 Это точка приложения наибольшей силы при приложении нагрузки к двигателю. В этом случае редуктор может выйти из строя задолго до того, как будет достигнут момент остановки двигателя, и потенциальные возможности не будут использованы полностью. В этом случае на последней ступени (ступенях) можно добавить более мощные шестерни, чтобы можно было достичь более высокого крутящего момента и более широкого диапазона производительности. На практике это использовалось с 206-108, который глохнет примерно на 17 мНм из-за отказа шестерни. На графике характеристик это характеризуется резкой остановкой на линии крутящий момент-скорость задолго до приближения к остановке (0 об/мин). Вставляя металлическую шестерню на последнем этапе, достигается крутящий момент примерно 34 мНм, что удваивает возможности двигателя по крутящему моменту и открывает более широкий спектр возможностей. Ему был присвоен номер детали 206-10C 9.0014
Это точка приложения наибольшей силы при приложении нагрузки к двигателю. В этом случае редуктор может выйти из строя задолго до того, как будет достигнут момент остановки двигателя, и потенциальные возможности не будут использованы полностью. В этом случае на последней ступени (ступенях) можно добавить более мощные шестерни, чтобы можно было достичь более высокого крутящего момента и более широкого диапазона производительности. На практике это использовалось с 206-108, который глохнет примерно на 17 мНм из-за отказа шестерни. На графике характеристик это характеризуется резкой остановкой на линии крутящий момент-скорость задолго до приближения к остановке (0 об/мин). Вставляя металлическую шестерню на последнем этапе, достигается крутящий момент примерно 34 мНм, что удваивает возможности двигателя по крутящему моменту и открывает более широкий спектр возможностей. Ему был присвоен номер детали 206-10C 9.0014 - Смазочные материалы: температура окружающей среды и рабочая температура в значительной степени влияют на эффективность редукторного двигателя и общую производительность, достигаемую на выходном валу.
 В то время как электрический КПД двигателя часто может увеличиваться при низких температурах, эффективность редуктора и эффективность смазки могут снижаться, что приводит к снижению общей производительности. Распространенным методом уменьшения этого эффекта является использование специальной низкотемпературной смазки. Это может повысить КПД редуктора и, следовательно, производительность двигателя на выходе. Это означает, что диапазон температур, указанный в техпаспорте, не является абсолютным пределом, и существует несколько способов его расширения. Если возникнут вопросы, инженеры Precision Microdrives будут рады помочь
В то время как электрический КПД двигателя часто может увеличиваться при низких температурах, эффективность редуктора и эффективность смазки могут снижаться, что приводит к снижению общей производительности. Распространенным методом уменьшения этого эффекта является использование специальной низкотемпературной смазки. Это может повысить КПД редуктора и, следовательно, производительность двигателя на выходе. Это означает, что диапазон температур, указанный в техпаспорте, не является абсолютным пределом, и существует несколько способов его расширения. Если возникнут вопросы, инженеры Precision Microdrives будут рады помочь - Энкодеры: если вам требуется больший контроль над мотор-редуктором или вы используете его в приводе позиционирования, вам может потребоваться энкодер. Это типичная модификация, которую мы можем предложить, начиная от простых тахометров для измерения скорости, инкрементных энкодеров для позиционирования по одному эталону и заканчивая абсолютными энкодерами для точного позиционирования выходного вала.
 Эти энкодеры также можно использовать в управлении с обратной связью для поддержания скорости при изменении крутящего момента, изменения скорости для постоянного крутящего момента или любой комбинации этих двух способов (примеры обсуждались ранее в этой статье). Пожалуйста, свяжитесь с инженером Precision Microdrives, если вам нужна дополнительная информация о том, что мы можем поставить
Эти энкодеры также можно использовать в управлении с обратной связью для поддержания скорости при изменении крутящего момента, изменения скорости для постоянного крутящего момента или любой комбинации этих двух способов (примеры обсуждались ранее в этой статье). Пожалуйста, свяжитесь с инженером Precision Microdrives, если вам нужна дополнительная информация о том, что мы можем поставить
Любая комбинация вышеперечисленного может быть использована вместе для достижения широкого диапазона мощностей наших мотор-редукторов. Таким образом, даже если вы не можете найти таблицу характеристик мотор-редуктора, соответствующую вашим требованиям, свяжитесь с нашими инженерами, поскольку мы можем найти множество способов удовлетворить ваши требования.
Ограничения
Как и все хорошее, есть ограничения на то, чего можно достичь. Целью этого раздела является описание некоторых связанных ограничений, возникающих при модификации мотор-редуктора.
- Обмотки: К сожалению, без значительных модификаций и затрат на разработку провода с определенной площадью поперечного сечения иногда трудно обеспечить точные характеристики при требуемом сопротивлении на клеммах, рабочем напряжении/токе и индуктивности на клеммах.
 В этом случае требования часто выполняются очень точно, и отклонения могут быть незначительными. Здесь также действуют ограничения по размерам, поскольку для обмоток имеется очень ограниченное пространство. На практике это означает, что определенные механические/электрические характеристики не могут быть достигнуты с данным двигателем из-за доступного пространства оболочки для обмоток и требуемой площади поперечного сечения/количества проводов обмотки. Разумеется, компания Precision Microdrives будет рада оценить осуществимость вашего запроса, поэтому, пожалуйста, не стесняйтесь обращаться к нам с вашими требованиями
В этом случае требования часто выполняются очень точно, и отклонения могут быть незначительными. Здесь также действуют ограничения по размерам, поскольку для обмоток имеется очень ограниченное пространство. На практике это означает, что определенные механические/электрические характеристики не могут быть достигнуты с данным двигателем из-за доступного пространства оболочки для обмоток и требуемой площади поперечного сечения/количества проводов обмотки. Разумеется, компания Precision Microdrives будет рада оценить осуществимость вашего запроса, поэтому, пожалуйста, не стесняйтесь обращаться к нам с вашими требованиями - Свойства материалов: Свойства материалов также являются ограничением при рассмотрении достижимых модификаций наших двигателей.
Как уже говорилось, смазочные материалы для низких температур можно использовать для улучшения характеристик материала при определенных температурах, однако существуют очевидные физические ограничения для конкретных материалов. К заметным ограничивающим свойствам относятся коэффициент теплового расширения, прочность материала, температуры плавления и многие другие. Если у вас есть какие-либо вопросы, связанные с этим, пожалуйста, свяжитесь с нами
Если у вас есть какие-либо вопросы, связанные с этим, пожалуйста, свяжитесь с нами
В этом разделе мы обсудили несколько очевидных ограничений, возникающих при модификации мотор-редуктора. Во многих случаях эти ограничения можно преодолеть, если менее важные параметры более гибкие. Поэтому, пожалуйста, обратитесь к нашим инженерам, чтобы оценить, что можно реализовать в вашем приложении.
Заключение
В этой статье мы обсудили некоторые причины, по которым пользователь может изменять скорость и крутящий момент двигателя, и рассмотрели конкретные примеры для каждой ситуации. Это побудило нас рассмотреть пределы скорости и крутящего момента для наших мотор-редукторов при постоянном напряжении. Здесь мы поняли, что при фиксированном напряжении наши двигатели могут работать в широком диапазоне скоростей и крутящих моментов между точкой холостого хода (полная скорость) и точкой максимальной нагрузки (опрокидывание).
Мы также обсудили, как читать «таблицу типичных рабочих характеристик», чтобы понять весь диапазон возможностей крутящего момента и скорости данного двигателя (при его номинальном напряжении).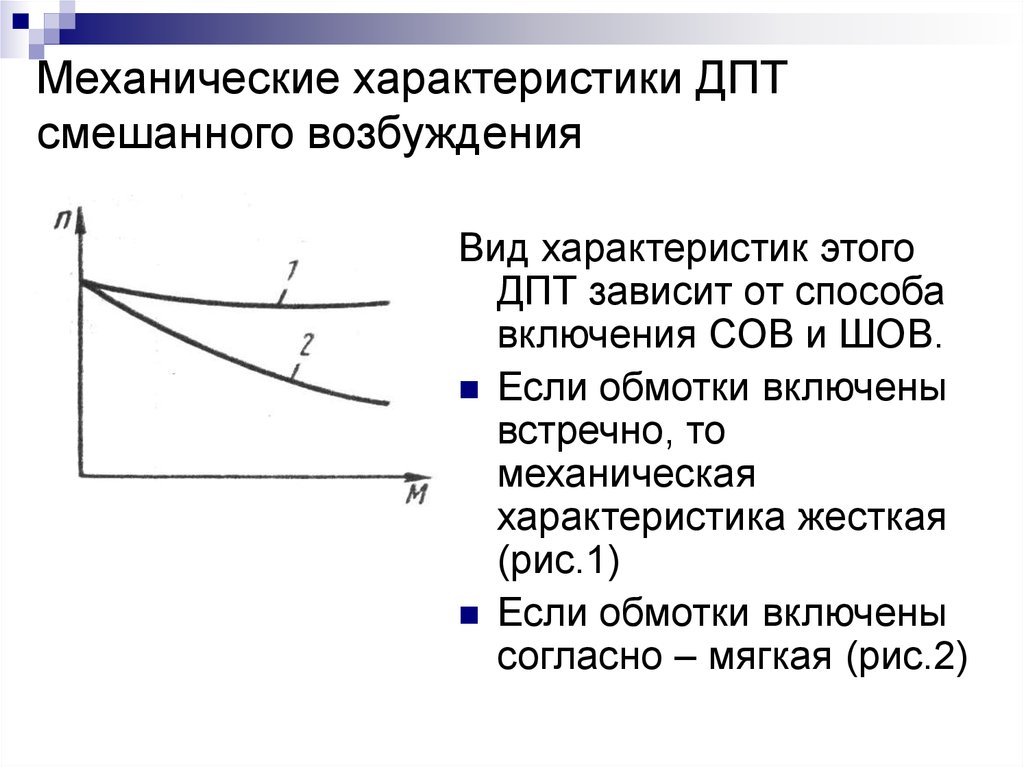 Отсюда мы увидели, что соотношение между скоростью и крутящим моментом обратно пропорционально от точки холостого хода до крутящего момента, и обсудили, как мы можем отрегулировать управляющее напряжение, чтобы поддерживать постоянную скорость или крутящий момент, когда другая переменная является динамической.
Отсюда мы увидели, что соотношение между скоростью и крутящим моментом обратно пропорционально от точки холостого хода до крутящего момента, и обсудили, как мы можем отрегулировать управляющее напряжение, чтобы поддерживать постоянную скорость или крутящий момент, когда другая переменная является динамической.
Последний раздел этого бюллетеня был посвящен описанию некоторых методов управления двигательной активностью. Некоторые из этих методов легко реализуются, и с ними можно экспериментировать при тестировании, в то время как другие являются постоянными модификациями, которые могут быть предусмотрены для конкретной спецификации. Если вы хотите рассмотреть варианты, которые у вас есть для вашего проекта, свяжитесь с одним из наших инженеров, чтобы обсудить ваши требования и варианты, которые мы можем вам предложить.
Информационный бюллетень
Подпишитесь на получение новых блогов, тематических исследований и ресурсов прямо на ваш почтовый ящик.
Зарегистрироваться
Имя
Первое
Последний
Электронная почта (обязательно)
Согласие с условиями (обязательно)
Я прочитал и согласен с Условиями и политикой конфиденциальности Precision Microdrives
Согласие на обсуждение (обязательно)
Я рад, что Precision Microdrives получил мои данные, чтобы мы могли обсудить мой запрос
Подробнее
Прецизионные микроприводы
Нужен ли вам компонент двигателя или полностью проверенный и испытанный сложный механизм — мы здесь, чтобы помочь. Узнайте больше о нашей компании.
Узнайте больше о нашей компании.
- Почему PMD
- О нас
- Двигатели
- Механизмы
- Карьера
Учебное пособие по двигателю постоянного тока
. Расчеты двигателей постоянного тока без сердечника
Ниже приведен метод определения параметров двигателя на примере двигателя постоянного тока без сердечника 2668W024CR. Сначала мы объясним более эмпирический подход, затем проведем теоретический расчет.
Одним из широко используемых методов графического отображения характеристик двигателя является использование кривых крутящий момент-скорость. Хотя использование кривых крутящий момент-скорость гораздо более распространено в технической литературе для более крупных машин постоянного тока, чем для небольших устройств без сердечника, этот метод применим в любом случае.
Обычно кривые крутящий момент-скорость строятся путем построения графика скорости двигателя, тока двигателя, механической выходной мощности и КПД в зависимости от крутящего момента двигателя. В следующем обсуждении будет описано построение набора кривых крутящий момент-скорость для типичного двигателя постоянного тока на основе серии измерений необработанных данных.
В следующем обсуждении будет описано построение набора кривых крутящий момент-скорость для типичного двигателя постоянного тока на основе серии измерений необработанных данных.
Номинальное напряжение 2668W024CR составляет 24 В. Если у вас есть несколько основных элементов лабораторного оборудования, вы можете измерить кривые крутящий момент-скорость для двигателя постоянного тока без сердечника серии 2668 CR в заданной рабочей точке.
Шаг 1: Измерьте основные параметры
Многие параметры можно получить непосредственно с помощью контроллера движения, например, одного из контроллеров движения FAULHABER MC3. Большинство производителей контроллеров предлагают программное обеспечение, такое как FAULHABER Motion Manager, которое включает в себя функцию записи кривой, отображающую напряжение, ток, положение, скорость и т. д. Они также могут предоставить точный моментальный снимок работы двигателя в мельчайших деталях. Например, контроллеры движения семейства MC3 (MC 5004, MC 5005 и MC 5010) могут измерять множество параметров движения. Это, вероятно, самый быстрый метод получения данных для построения кривой крутящий момент-скорость, но это не единственный метод.
Это, вероятно, самый быстрый метод получения данных для построения кривой крутящий момент-скорость, но это не единственный метод.
Если контроллер с возможностью записи трассировки недоступен, мы также можем использовать базовое лабораторное оборудование для определения характеристик двигателя в условиях останова, номинального состояния и без нагрузки. Используя источник питания, настроенный на 24 В, запустите 2668W024CR без нагрузки и измерьте скорость вращения с помощью бесконтактного тахометра (например, стробоскопа). Кроме того, измерьте ток двигателя в этом состоянии без нагрузки. Токовый пробник идеально подходит для этого измерения, так как он не добавляет сопротивления последовательно с работающим двигателем. Используя нагрузку с регулируемым крутящим моментом, такую как тормоз мелких частиц или динамометр с регулируемым гистерезисом, к валу двигателя может быть присоединена нагрузка.
Теперь увеличьте крутящий момент двигателя до точки, при которой происходит остановка. В остановленном состоянии измерьте крутящий момент от тормоза и ток двигателя. Для этого обсуждения предположим, что муфта не добавляет нагрузки к двигателю и что нагрузка от тормоза не включает неизвестные фрикционные компоненты. В этот момент также полезно измерить терминальное сопротивление двигателя. Измерьте сопротивление, прикоснувшись к клеммам двигателя омметром. Затем прокрутите вал двигателя и выполните еще одно измерение. Измерения должны быть очень близки по значению. Продолжайте вращать вал и сделайте не менее трех измерений. Это гарантирует, что измерения не проводились в точке минимального контакта с коммутатором.
В остановленном состоянии измерьте крутящий момент от тормоза и ток двигателя. Для этого обсуждения предположим, что муфта не добавляет нагрузки к двигателю и что нагрузка от тормоза не включает неизвестные фрикционные компоненты. В этот момент также полезно измерить терминальное сопротивление двигателя. Измерьте сопротивление, прикоснувшись к клеммам двигателя омметром. Затем прокрутите вал двигателя и выполните еще одно измерение. Измерения должны быть очень близки по значению. Продолжайте вращать вал и сделайте не менее трех измерений. Это гарантирует, что измерения не проводились в точке минимального контакта с коммутатором.
Теперь мы измерили:
N 0 = Скорость без нагрузки
I 0 = CURENCE
M H = STALLE
M H = STALLY M H = STALLE M H = STALLE M H = STALLY
M H = STAl
Шаг 2.
 Постройте график зависимости тока от крутящего момента и скорости от крутящего момента
Постройте график зависимости тока от крутящего момента и скорости от крутящего момента
Вы можете построить график с крутящим моментом двигателя по оси абсцисс (горизонтальная ось), скоростью по левой оси ординаты (вертикальная ось) и током по правой стороне ординаты. Масштабируйте оси на основе измерений, сделанных на первом шаге. Проведите прямую линию от левого начала графика (нулевой крутящий момент и нулевой ток) к току останова на правой стороне ординаты (момент останова и ток останова). Эта линия представляет собой график зависимости тока двигателя от крутящего момента двигателя. Наклон этой линии представляет собой текущую константу k I , которая представляет собой константу пропорциональности для отношения между током двигателя и крутящим моментом двигателя (в единицах тока на единицу крутящего момента или А/мНм). Обратная величина этого наклона представляет собой постоянную крутящего момента k M (в единицах крутящего момента на единицу тока или мНм/А).
Где:
k I = постоянная тока
k M = постоянная крутящего момента
Для целей данного обсуждения предполагается, что двигатель не имеет внутреннего трения. На практике момент трения двигателя M R определяется путем умножения постоянной крутящего момента k M двигателя на измеренный ток холостого хода I 0 . Линия крутящего момента в зависимости от скорости и линия крутящего момента в зависимости от тока затем начинаются не от левой вертикальной оси, а со смещением по горизонтальной оси, равным расчетному моменту трения.
Где:
M R = Момент трения
Шаг 3: График зависимости мощности от крутящего момента и эффективности от крутящего момента
В большинстве случаев можно добавить две дополнительные вертикальные оси для построения зависимости мощности и эффективности от крутящего момента. Вторая вертикальная ось обычно используется для эффективности, а третья вертикальная ось может использоваться для мощности. Для упрощения этого обсуждения КПД в зависимости от крутящего момента и мощность в зависимости от крутящего момента будут нанесены на тот же график, что и графики зависимости скорости от крутящего момента и тока от крутящего момента (пример показан ниже).
Вторая вертикальная ось обычно используется для эффективности, а третья вертикальная ось может использоваться для мощности. Для упрощения этого обсуждения КПД в зависимости от крутящего момента и мощность в зависимости от крутящего момента будут нанесены на тот же график, что и графики зависимости скорости от крутящего момента и тока от крутящего момента (пример показан ниже).
Составьте таблицу механической мощности двигателя в различных точках от холостого хода до момента остановки. Поскольку выходная механическая мощность — это просто произведение крутящего момента и скорости с поправочным коэффициентом для единиц измерения (см. раздел о расчете начальной требуемой мощности), мощность можно рассчитать, используя ранее построенную линию зависимости скорости от крутящего момента.
Пример таблицы расчетов для двигателя 2668W024CR показан в Таблице 1. Затем каждая расчетная точка для мощности наносится на график. Результирующая функция представляет собой параболическую кривую, как показано ниже на графике 1. Максимальная механическая мощность возникает примерно при половине крутящего момента срыва. Скорость в этот момент составляет примерно половину скорости холостого хода.
Максимальная механическая мощность возникает примерно при половине крутящего момента срыва. Скорость в этот момент составляет примерно половину скорости холостого хода.
Составьте таблицу КПД двигателя в различных точках от скорости холостого хода до крутящего момента. Задано напряжение, приложенное к двигателю, и нанесен ток при различных уровнях крутящего момента. Произведение тока двигателя и приложенного напряжения представляет собой потребляемую двигателем мощность. В каждой точке, выбранной для расчета, КПД η двигателя представляет собой выходную механическую мощность, деленную на потребляемую электрическую мощность. Опять же, примерная таблица для двигателя 2668W024CR показана в таблице 1, а примерная кривая — на графике 1. Максимальный КПД достигается примерно при 10% крутящего момента двигателя.
Определения графика
- Синий = скорость против крутящего момента ( N против M )
- Красный = ток против крутящего момента ( I против M )
- 74 против Greefice = Greefice = Greefice = Greefice = Greefice = Greefice = Greefice = Greefice = Greefiate vs.
 greeque = greecity vs. greeciate vs. greek r greeque = green green greeque. η по сравнению с M )
greeque = greecity vs. greeciate vs. greek r greeque = green green greeque. η по сравнению с M ) - Коричневый = мощность по отношению к крутящему моменту ( P по сравнению с M )
Характеристики двигателя
Примечание. Обратите внимание на изменение всех четырех сплошных графиков в результате увеличения сопротивления в медных обмотках и ослабления выходного крутящего момента из-за повышения температуры. Таким образом, ваши результаты могут немного отличаться в зависимости от того, холодный или теплый двигатель, когда вы строите графики.
| Load current | 2,79 A |
| Load voltage | 24,11 V |
| Motor winding temperature | 140,23 °C |
| Motor housing temperature | 105 , 03 ° C |
| Скорость двигателя | 7370 мин -1 |
| Требуется крутящий момент | 68 мН | 68 мН | 68 мН | 68 мН | 68 МНЕ0481 | Эффективность (общая) | 77,97 % |
Примечание. Из-за нехватки места показан пример расчета для одной точки.
Из-за нехватки места показан пример расчета для одной точки.
Теоретический расчет параметров двигателя
Другим полезным параметром при выборе двигателя является постоянная двигателя. Правильное использование этого показателя качества существенно сократит итерационный процесс выбора двигателя постоянного тока. Он просто измеряет внутреннюю способность преобразователя преобразовывать электрическую энергию в механическую.
Максимальный КПД достигается примерно при 10% крутящего момента двигателя. Знаменатель известен как резистивная потеря мощности. С помощью некоторых алгебраических преобразований уравнение можно упростить до:
Пожалуйста, имейте в виду, что k m (постоянная двигателя) не следует путать с k M (постоянная крутящего момента). Обратите внимание, что нижний индекс константы двигателя имеет строчную букву « m », а нижний индекс константы крутящего момента использует верхний регистр « M 9». 0374».
0374».
Для щеточного или бесщеточного двигателя постоянного тока относительно небольшого размера зависимости, управляющие поведением двигателя в различных обстоятельствах, могут быть получены из законов физики и характеристик самих двигателей. Правило напряжения Кирхгофа гласит: «Сумма повышений потенциала в контуре цепи должна равняться сумме падений потенциалов». Применительно к двигателю постоянного тока, соединенному последовательно с источником питания постоянного тока, правило напряжения Кирхгофа может быть выражено как «Номинальное напряжение питания от источника питания должно быть равно по величине сумме падения напряжения на сопротивлении обмоток и противо-ЭДС, создаваемой двигателем».
Где:
U = источник питания в V
I = ток в
R = сопротивление терминала в ω
U E = v Back-Emf-in v 903f-in v 903f-in v 903f-in v 903f-in v 903f-in v 903f-in v e . генерируемая двигателем, прямо пропорциональна угловой скорости двигателя. Константа пропорциональности – это константа противо-ЭДС двигателя.
генерируемая двигателем, прямо пропорциональна угловой скорости двигателя. Константа пропорциональности – это константа противо-ЭДС двигателя.
Где:
ω = угловая скорость двигателя
k E = постоянная противо-ЭДС двигателя
Таким образом, путем замены:
Константа противо-ЭДС двигателя обычно указывается производителем двигателя в В/об/мин или мВ/об/мин. Чтобы получить осмысленное значение противо-ЭДС, необходимо указать скорость двигателя в единицах, совместимых с заданной константой противо-ЭДС.
«Сумма повышений потенциала в контуре должна равняться сумме падений потенциалов».
(правило напряжения Кирхгофа)
Постоянная двигателя зависит от конструкции катушки, силы и направления силовых линий в воздушном зазоре. Хотя можно показать, что обычно указанные три константы двигателя (константа противо-ЭДС, константа крутящего момента и константа скорости) равны, если используются соответствующие единицы измерения, расчет облегчается заданием трех констант в общепринятых единицах измерения.
Крутящий момент, создаваемый ротором, прямо пропорционален току в обмотках якоря. Константа пропорциональности – это константа крутящего момента двигателя.
Где:
M m = крутящий момент, развиваемый двигателем
k M = постоянный крутящий момент двигателя крутящий момент двигателя плюс крутящий момент нагрузки (из-за внешней механической нагрузки):
Где:
M R = момент трения двигателя
M L = крутящий момент нагрузки сумма момента трения и момента нагрузки. Константа пропорциональности представляет собой наклон кривой крутящий момент-скорость. Производительность двигателя лучше, когда этот наклон имеет меньшее значение. Чем круче падение наклона, тем хуже производительность, которую можно ожидать от данного двигателя без сердечника. Это соотношение можно рассчитать по формуле:
Где:
ΔN = изменение скорости
ΔM = изменение крутящего момента
M H = Крутой следов
N 0 = Крутой для прила это значение для определения скорости, n :
С помощью исчисления мы дифференцируем обе части относительно M , что дает:
или
Хотя мы не показываем здесь отрицательный знак, подразумевается, что результат даст уменьшающийся (отрицательный) наклон.
Пример теоретического расчета двигателя
Давайте немного углубимся в теоретические расчеты. Двигатель постоянного тока без сердечника 2668W024CR должен работать с напряжением 24 В, подаваемым на клеммы двигателя, и с крутящим моментом 68 мН·м. Найдите результирующую постоянную двигателя, скорость двигателя, ток двигателя, КПД двигателя и выходную мощность. Из паспорта двигателя видно, что частота вращения двигателя на холостом ходу при 24 В составляет 7 800 мин -1 . Если крутящий момент не соединен с валом двигателя, двигатель будет работать на этой скорости.
Во-первых, давайте получим общее представление о работе двигателя, рассчитав постоянную двигателя k m . В этом случае мы получаем константу 28,48 мНм/А. «Согласно техпаспорту двигателя, электрическое сопротивление составляет 1,03 Ом в холодном состоянии для варианта 24 В».
Скорость двигателя под нагрузкой — это просто скорость холостого хода за вычетом снижения скорости из-за нагрузки. Константа пропорциональности для соотношения между скоростью двигателя и крутящим моментом двигателя представляет собой наклон кривой зависимости крутящего момента от скорости, определяемый отношением скорости холостого хода двигателя к крутящему моменту двигателя. В этом примере мы рассчитаем снижение скорости (без учета влияния температуры), вызванное крутящим моментом 68 мНм, путем исключения единиц мНм:
Константа пропорциональности для соотношения между скоростью двигателя и крутящим моментом двигателя представляет собой наклон кривой зависимости крутящего момента от скорости, определяемый отношением скорости холостого хода двигателя к крутящему моменту двигателя. В этом примере мы рассчитаем снижение скорости (без учета влияния температуры), вызванное крутящим моментом 68 мНм, путем исключения единиц мНм:
Теперь путем замены:
Скорость двигателя под нагрузкой должна быть приблизительно равна:
Ток двигателя под нагрузкой представляет собой сумму тока холостого хода и тока, возникающего под нагрузкой.
Константа пропорциональности, связывающая ток с нагрузкой крутящего момента, представляет собой константу крутящего момента ( k M ) . Это значение составляет 28,9 мНм/А. Принимая обратное значение, мы получаем постоянную тока k I , которая может помочь нам рассчитать ток при нагрузке. В этом случае нагрузка составляет 68 мН·м, а ток, вытекающий из этой нагрузки (без учета тепловыделения), примерно равен:
В этом случае нагрузка составляет 68 мН·м, а ток, вытекающий из этой нагрузки (без учета тепловыделения), примерно равен:
Общий ток двигателя можно приблизительно определить путем суммирования этого значения с током двигателя без нагрузки. В техническом описании ток холостого хода двигателя указан как 78 мА. После округления общий ток примерно равен:
Выходная механическая мощность двигателя представляет собой просто произведение скорости двигателя и крутящего момента с поправочным коэффициентом для единиц (при необходимости). Таким образом, выходная мощность двигателя будет приблизительно равна:
Механическая мощность, потребляемая двигателем, является произведением приложенного напряжения и полного тока двигателя в амперах. В этом приложении:
Так как эффективность η это просто выходная мощность, деленная на входную мощность, давайте рассчитаем ее в нашей рабочей точке:
Оценка температуры обмотки двигателя во время работы:
Ток I , протекающий через сопротивление R , приводит к потере мощности в виде тепла I 2 · R .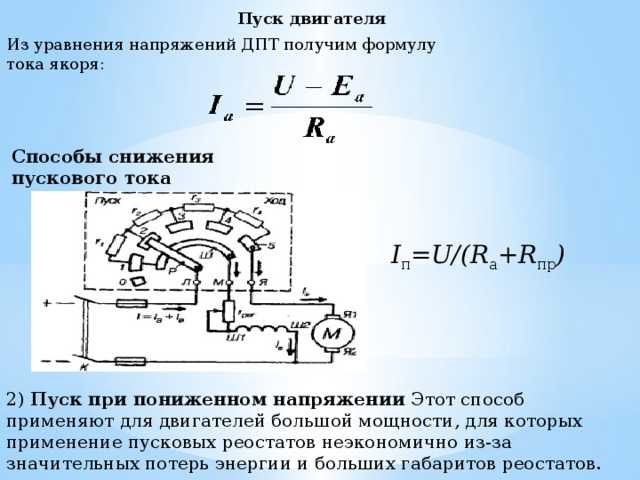 В случае двигателя постоянного тока произведение квадрата полного тока двигателя на сопротивление якоря представляет собой потери мощности в виде тепла в обмотках якоря. Например, если общий ток двигателя 0,203 А, а сопротивление якоря 14,5 Ом, потери мощности на тепло в обмотках составляют:
В случае двигателя постоянного тока произведение квадрата полного тока двигателя на сопротивление якоря представляет собой потери мощности в виде тепла в обмотках якоря. Например, если общий ток двигателя 0,203 А, а сопротивление якоря 14,5 Ом, потери мощности на тепло в обмотках составляют:
Тепло, возникающее в результате I 2 · R потерь в катушке, рассеивается за счет теплопроводности через компоненты двигателя и поток воздуха в воздушном зазоре. Легкость, с которой это тепло может быть рассеяно в двигателе (или любой системе), определяется тепловым сопротивлением.
Термическое сопротивление (которое является обратной величиной теплопроводности) показывает, насколько хорошо материал сопротивляется передаче тепла по определенному пути. Производители двигателей обычно указывают способность двигателя рассеивать тепло, обеспечивая тепловое сопротивление R й значений. Например, алюминиевая пластина большого сечения будет иметь очень низкое тепловое сопротивление, в то время как значения для воздуха или вакуума будут значительно выше.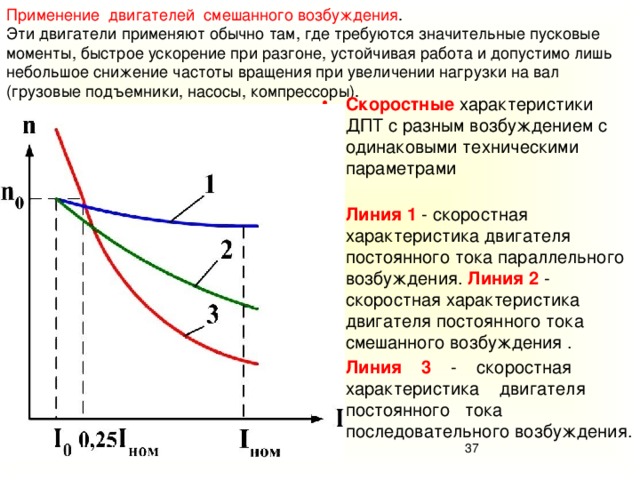 В случае двигателей постоянного тока существует тепловой путь от обмоток двигателя к корпусу двигателя и второй тепловой путь между корпусом двигателя и окружающей средой двигателя (окружающий воздух и т. д.). Некоторые производители двигателей указывают тепловое сопротивление для каждого из двух тепловых путей, в то время как другие указывают только их сумму как общее тепловое сопротивление двигателя. Значения термического сопротивления указаны в приросте температуры на единицу потерь мощности. Всего I 2 · R потери в катушке (источнике тепла) умножаются на тепловые сопротивления для определения установившейся температуры якоря. Повышение температуры двигателя в установившемся режиме ( T ) определяется как:
В случае двигателей постоянного тока существует тепловой путь от обмоток двигателя к корпусу двигателя и второй тепловой путь между корпусом двигателя и окружающей средой двигателя (окружающий воздух и т. д.). Некоторые производители двигателей указывают тепловое сопротивление для каждого из двух тепловых путей, в то время как другие указывают только их сумму как общее тепловое сопротивление двигателя. Значения термического сопротивления указаны в приросте температуры на единицу потерь мощности. Всего I 2 · R потери в катушке (источнике тепла) умножаются на тепловые сопротивления для определения установившейся температуры якоря. Повышение температуры двигателя в установившемся режиме ( T ) определяется как:
Где:
ΔT = изменение температуры в К
I = ток через обмотки двигателя в А обмотки двигателя в Ом
R th2 = Тепловое сопротивление от обмоток к корпусу в К/Вт
R th3 = Термическое сопротивление корпуса к окружающей среде в К/Вт
Продолжим наш пример, используя двигатель 2668W024CR, работающий с током 2,458 А в обмотках двигателя, с сопротивлением якоря 1,03 Ом, а тепловое сопротивление между обмоткой и корпусом 3 К/Вт и тепловое сопротивление между корпусом и окружающей средой 8 К/Вт. Повышение температуры обмоток определяется по приведенной ниже формуле; мы можем заменить Ploss на I 2 · R :
Повышение температуры обмоток определяется по приведенной ниже формуле; мы можем заменить Ploss на I 2 · R :
Поскольку шкала Кельвина использует тот же приращение единицы, что и шкала Цельсия, мы можем просто заменить значение Кельвина, как если бы оно было значением Цельсия. Если предположить, что температура окружающего воздуха составляет 22°C, то конечную температуру обмоток двигателя можно приблизительно представить как:
Где:
T теплый = температура обмотки
Важно убедиться, что конечная температура обмоток не превышает номинальное значение двигателя, указанное в паспорте. В приведенном выше примере максимально допустимая температура обмотки составляет 125°C. Поскольку расчетная температура обмотки составляет всего 90,4°C, тепловое повреждение обмоток двигателя не должно быть проблемой в этом приложении.
Подобные расчеты можно было бы использовать для ответа на вопрос другого типа. Например, приложение может потребовать, чтобы двигатель работал с максимальным крутящим моментом, в надежде, что он не будет поврежден в результате перегрева. Предположим, требуется запустить двигатель с максимально возможным крутящим моментом при температуре окружающего воздуха 22°C. Разработчик хочет знать, какой крутящий момент двигатель может обеспечить без перегрева. Опять же, в техническом описании двигателя постоянного тока без сердечника 2668W024CR указана максимальная температура обмотки 125°C. Таким образом, поскольку температура окружающей среды составляет 22°C, максимально допустимое повышение температуры ротора составляет: 125°C – 22°C = 103°C
Например, приложение может потребовать, чтобы двигатель работал с максимальным крутящим моментом, в надежде, что он не будет поврежден в результате перегрева. Предположим, требуется запустить двигатель с максимально возможным крутящим моментом при температуре окружающего воздуха 22°C. Разработчик хочет знать, какой крутящий момент двигатель может обеспечить без перегрева. Опять же, в техническом описании двигателя постоянного тока без сердечника 2668W024CR указана максимальная температура обмотки 125°C. Таким образом, поскольку температура окружающей среды составляет 22°C, максимально допустимое повышение температуры ротора составляет: 125°C – 22°C = 103°C
Теперь мы можем рассчитать увеличение сопротивления катушки из-за рассеяния тепловой мощности:
Где:
α Cu = Температурный коэффициент меди в единицах К нагрева катушки и магнита за счет рассеивания мощности от потерь I 2 · R сопротивление катушки увеличилось с 1,03 Ом до 1,44 Ом. Теперь мы можем пересчитать новую константу крутящего момента k M для наблюдения за влиянием повышения температуры на производительность двигателя:
Теперь мы можем пересчитать новую константу крутящего момента k M для наблюдения за влиянием повышения температуры на производительность двигателя:
Где:
α M = Температурный коэффициент магнита в единицах К Постоянная ЭДС k E и наблюдайте за результатами. Из формулы, которую мы вывели выше:
Как мы видим, константа крутящего момента ослабевает в результате повышения температуры, как и константа противо-ЭДС! Таким образом, сопротивление обмотки двигателя, постоянная крутящего момента и постоянная противо-ЭДС оказывают негативное влияние по той простой причине, что они являются функциями температуры.
Мы могли бы продолжить расчет дополнительных параметров из-за более горячих катушки и магнита, но наилучшие результаты дает выполнение нескольких итераций, что лучше всего делать с помощью количественного программного обеспечения. Поскольку температура двигателя продолжает расти, каждый из трех параметров будет изменяться таким образом, что ухудшаются характеристики двигателя и увеличиваются потери мощности. При непрерывной работе двигатель может даже достичь точки «теплового разгона», что потенциально может привести к повреждению двигателя, не подлежащему ремонту. Это может произойти, даже если первоначальные расчеты показали приемлемое повышение температуры (используя значения R и k M при температуре окружающей среды).
При непрерывной работе двигатель может даже достичь точки «теплового разгона», что потенциально может привести к повреждению двигателя, не подлежащему ремонту. Это может произойти, даже если первоначальные расчеты показали приемлемое повышение температуры (используя значения R и k M при температуре окружающей среды).
Обратите внимание, что максимально допустимый ток через обмотки двигателя можно увеличить, уменьшив тепловое сопротивление двигателя. Термическое сопротивление между ротором и корпусом R th2 в основном определяется конструкцией двигателя. Тепловое сопротивление корпус-окружающая среда R th3 можно значительно снизить за счет добавления радиаторов. Термическое сопротивление двигателя для небольших двигателей постоянного тока обычно указывается для двигателя, подвешенного на открытом воздухе. Поэтому обычно имеет место некоторый отвод тепла в результате простой установки двигателя в теплопроводящую раму или шасси.

 Данная конструкция расположена на валу и образует узел, называемый ротором или якорем.
Данная конструкция расположена на валу и образует узел, называемый ротором или якорем.


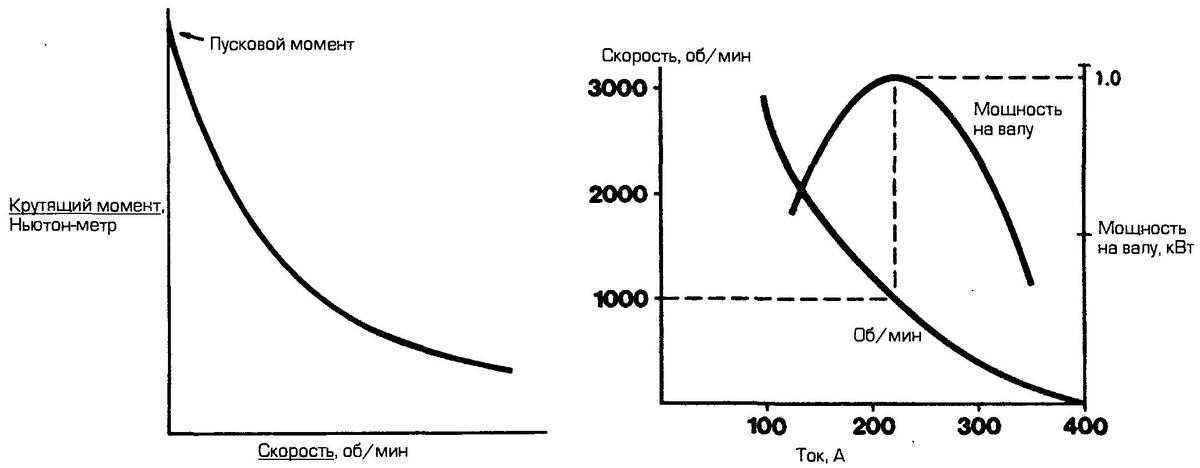 Для высокомоментных двигателей максимальный момент соответствует по условиям размагничивания максимальному току якоря при неподвижном двигателе
Для высокомоментных двигателей максимальный момент соответствует по условиям размагничивания максимальному току якоря при неподвижном двигателе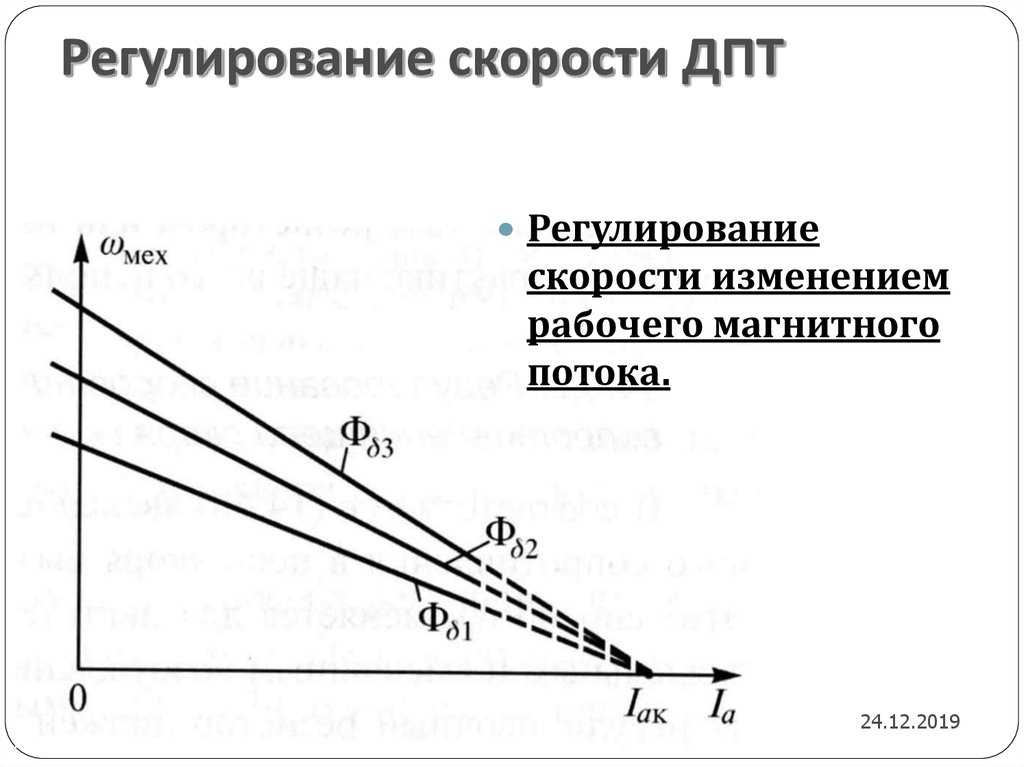
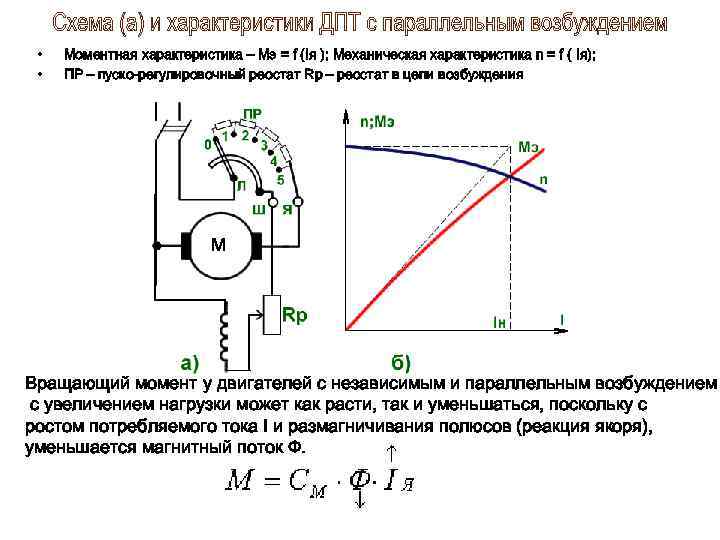
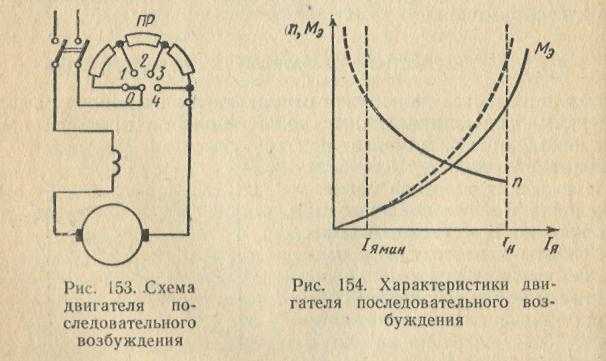 ⓘ Магнитный поток [Φf]
ⓘ Магнитный поток [Φf]
 Если вы хотите поэкспериментировать со своими собственными зубчатыми цепями, простые уравнения для шестерен можно найти в AB-024. Тем не менее, мы можем предложить нестандартные редукторы и модификации стандартных деталей, поэтому, пожалуйста, не стесняйтесь обращаться к инженеру, если вы хотите обсудить ваши требования и варианты, которые мы можем предложить.
Если вы хотите поэкспериментировать со своими собственными зубчатыми цепями, простые уравнения для шестерен можно найти в AB-024. Тем не менее, мы можем предложить нестандартные редукторы и модификации стандартных деталей, поэтому, пожалуйста, не стесняйтесь обращаться к инженеру, если вы хотите обсудить ваши требования и варианты, которые мы можем предложить. Это точка приложения наибольшей силы при приложении нагрузки к двигателю. В этом случае редуктор может выйти из строя задолго до того, как будет достигнут момент остановки двигателя, и потенциальные возможности не будут использованы полностью. В этом случае на последней ступени (ступенях) можно добавить более мощные шестерни, чтобы можно было достичь более высокого крутящего момента и более широкого диапазона производительности. На практике это использовалось с 206-108, который глохнет примерно на 17 мНм из-за отказа шестерни. На графике характеристик это характеризуется резкой остановкой на линии крутящий момент-скорость задолго до приближения к остановке (0 об/мин). Вставляя металлическую шестерню на последнем этапе, достигается крутящий момент примерно 34 мНм, что удваивает возможности двигателя по крутящему моменту и открывает более широкий спектр возможностей. Ему был присвоен номер детали 206-10C 9.0014
Это точка приложения наибольшей силы при приложении нагрузки к двигателю. В этом случае редуктор может выйти из строя задолго до того, как будет достигнут момент остановки двигателя, и потенциальные возможности не будут использованы полностью. В этом случае на последней ступени (ступенях) можно добавить более мощные шестерни, чтобы можно было достичь более высокого крутящего момента и более широкого диапазона производительности. На практике это использовалось с 206-108, который глохнет примерно на 17 мНм из-за отказа шестерни. На графике характеристик это характеризуется резкой остановкой на линии крутящий момент-скорость задолго до приближения к остановке (0 об/мин). Вставляя металлическую шестерню на последнем этапе, достигается крутящий момент примерно 34 мНм, что удваивает возможности двигателя по крутящему моменту и открывает более широкий спектр возможностей. Ему был присвоен номер детали 206-10C 9.0014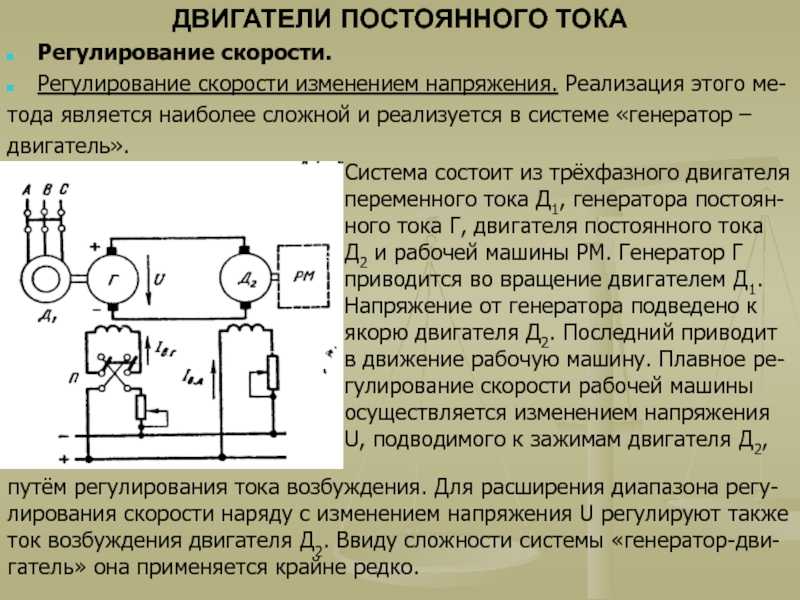 В то время как электрический КПД двигателя часто может увеличиваться при низких температурах, эффективность редуктора и эффективность смазки могут снижаться, что приводит к снижению общей производительности. Распространенным методом уменьшения этого эффекта является использование специальной низкотемпературной смазки. Это может повысить КПД редуктора и, следовательно, производительность двигателя на выходе. Это означает, что диапазон температур, указанный в техпаспорте, не является абсолютным пределом, и существует несколько способов его расширения. Если возникнут вопросы, инженеры Precision Microdrives будут рады помочь
В то время как электрический КПД двигателя часто может увеличиваться при низких температурах, эффективность редуктора и эффективность смазки могут снижаться, что приводит к снижению общей производительности. Распространенным методом уменьшения этого эффекта является использование специальной низкотемпературной смазки. Это может повысить КПД редуктора и, следовательно, производительность двигателя на выходе. Это означает, что диапазон температур, указанный в техпаспорте, не является абсолютным пределом, и существует несколько способов его расширения. Если возникнут вопросы, инженеры Precision Microdrives будут рады помочь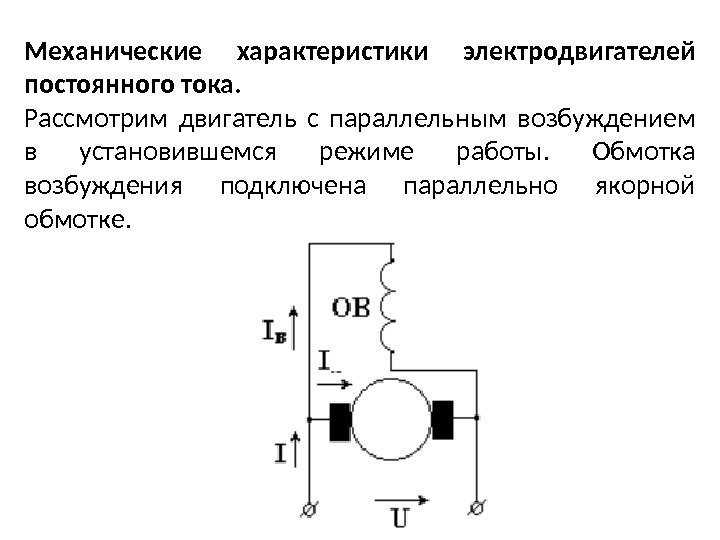 Эти энкодеры также можно использовать в управлении с обратной связью для поддержания скорости при изменении крутящего момента, изменения скорости для постоянного крутящего момента или любой комбинации этих двух способов (примеры обсуждались ранее в этой статье). Пожалуйста, свяжитесь с инженером Precision Microdrives, если вам нужна дополнительная информация о том, что мы можем поставить
Эти энкодеры также можно использовать в управлении с обратной связью для поддержания скорости при изменении крутящего момента, изменения скорости для постоянного крутящего момента или любой комбинации этих двух способов (примеры обсуждались ранее в этой статье). Пожалуйста, свяжитесь с инженером Precision Microdrives, если вам нужна дополнительная информация о том, что мы можем поставить В этом случае требования часто выполняются очень точно, и отклонения могут быть незначительными. Здесь также действуют ограничения по размерам, поскольку для обмоток имеется очень ограниченное пространство. На практике это означает, что определенные механические/электрические характеристики не могут быть достигнуты с данным двигателем из-за доступного пространства оболочки для обмоток и требуемой площади поперечного сечения/количества проводов обмотки. Разумеется, компания Precision Microdrives будет рада оценить осуществимость вашего запроса, поэтому, пожалуйста, не стесняйтесь обращаться к нам с вашими требованиями
В этом случае требования часто выполняются очень точно, и отклонения могут быть незначительными. Здесь также действуют ограничения по размерам, поскольку для обмоток имеется очень ограниченное пространство. На практике это означает, что определенные механические/электрические характеристики не могут быть достигнуты с данным двигателем из-за доступного пространства оболочки для обмоток и требуемой площади поперечного сечения/количества проводов обмотки. Разумеется, компания Precision Microdrives будет рада оценить осуществимость вашего запроса, поэтому, пожалуйста, не стесняйтесь обращаться к нам с вашими требованиями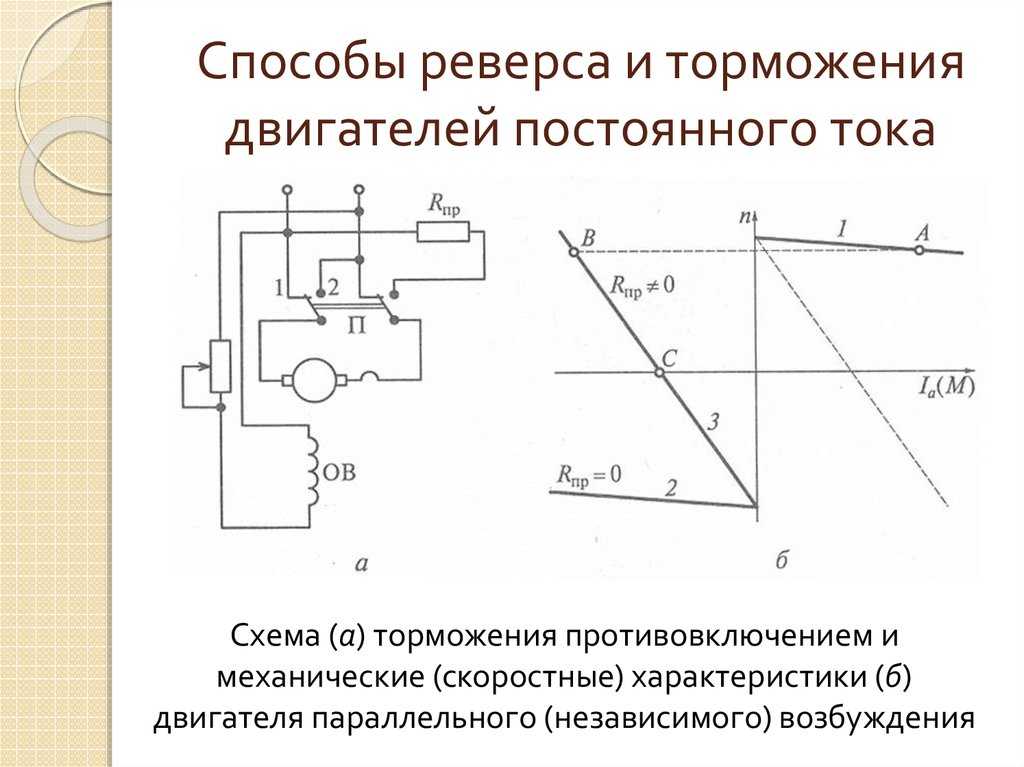 Если у вас есть какие-либо вопросы, связанные с этим, пожалуйста, свяжитесь с нами
Если у вас есть какие-либо вопросы, связанные с этим, пожалуйста, свяжитесь с нами greeque = greecity vs. greeciate vs. greek r greeque = green green greeque. η по сравнению с M )
greeque = greecity vs. greeciate vs. greek r greeque = green green greeque. η по сравнению с M )