Содержание
Что характеризует кпд электродвигателя. Кпд электродвигателей и что влияет на его значение
В электродвигателе при преобразовании электрической энергии в механическую часть энергии теряется в виде тепла, которое сразу рассеивается в различных частях мотора и частично – в окружающей среде. Все потери делятся на три вида: механические, обмоточные и потери в стали. Причем существуют еще и добавочные потери.
Расчет потерь в электрическом двигателе
- Для расчета потерь в электродвигателе используют специальные формулы. На диаграммах можно заметить, что часть мощности, которая подается к статору из электросети, передается на ротор через зазор. Рэм – это электромагнитная мощность.
- Потери мощности непосредственно в статоре – это слагаемое потерь на вихревые токи и на частичное перемагничивание сердечника самого статора. Если рассматривать потери в стали, они настолько незначительные, что редко принимаются во внимание. Объяснить такое можно достаточно просто.
 Скорость вращения самого статора электродвигателя значительно выше скорости, создаваемой магнитным потоком. Так происходит только в том случае, если скорость вращения ротора полностью соответствует техническим характеристикам электромотора, заявленным производителем.
Скорость вращения самого статора электродвигателя значительно выше скорости, создаваемой магнитным потоком. Так происходит только в том случае, если скорость вращения ротора полностью соответствует техническим характеристикам электромотора, заявленным производителем.
- Механическая мощность на валу ротора, как правило, меньше мощности Рэм ровно на количество потерь в обмотке. Механические потери в основном приходятся на определенное трение в подшипниках, а также на трение щеток, что характерно для электродвигателей с фазными роторами и на трение вращающихся частей, встречающих воздушную преграду.
- Добавочные потери в асинхронных электродвигателях обусловлены наличием зубчатости статора и ротора, вихревых потоков в разных узлах электродвигателя и иными потерями. При расчете такие потери уменьшают КПД электродвигателя на половину процента от номинальной мощности.
КПД электродвигателя в расчетах
Коэффициент полезного действия асинхронного электродвигателя уменьшается на суммарность потерь мощности, которые рассчитываются по формуле.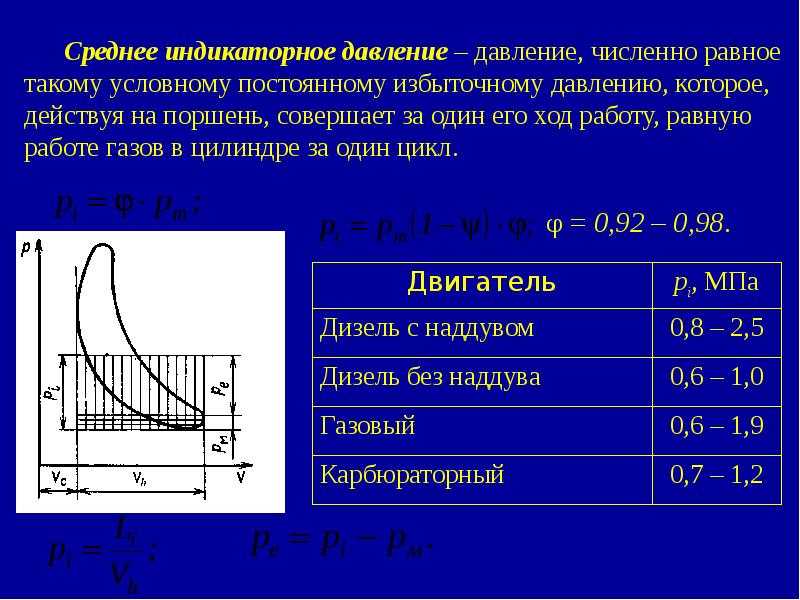 Общая же сумма потерь напрямую зависит от нагрузки электродвигателя. Чем выше нагрузка, тем больше потерь и меньше КПД.
Общая же сумма потерь напрямую зависит от нагрузки электродвигателя. Чем выше нагрузка, тем больше потерь и меньше КПД.
Конструирование асинхронного электродвигателя производится с учетом всех потерь при максимальной нагрузке. Поэтому данный диапазон может быть достаточно широким. Большинство асинхронных электромоторов имеет коэффициент полезного действия 80-90%. Мощные моторы выпускают с КПД от 90 до 96%.
Электрические двигатели имеют высокий коэффициент полезного действия (КПД), но все же он далек от идеальных показателей, к которым продолжают стремиться конструкторы. Все дело в том, что при работе силового агрегата преобразование одного вида энергии в другой проходит с выделение теплоты и неминуемыми потерями. Рассеивание тепловой энергии можно зафиксировать в разных узлах двигателя любого типа. Потери мощности в электродвигателях являются следствием локальных потерь в обмотке, в стальных деталях и при механической работе. Вносят свой вклад, пусть и незначительный, дополнительные потери.
Магнитные потери мощности
При перемагничивании в магнитном поле сердечника якоря электродвигателя происходят магнитные потери. Их величина, состоящая из суммарных потерь вихревых токов и тех, что возникают при перемагничивании, зависят от частоты перемагничивания, значений магнитной индукции спинки и зубцов якоря. Немалую роль играет толщина листов используемой электротехнической стали, качество ее изоляции.
Механические и электрические потери
Механические потери при работе электродвигателя, как и магнитные, относятся к числу постоянных. Они складываются из потерь на трение подшипников, на трение щеток, на вентиляцию двигателя. Минимизировать механические потери позволяет использование современных материалов, эксплуатационные характеристики которых совершенствуются из года в год. В отличие от них электрические потери не являются постоянными и зависят от уровня нагрузки электродвигателя. Чаще всего они возникают вследствие нагрева щеток, щеточного контакта. Падает коэффициент полезного действия (КПД) от потерь в обмотке якоря и цепи возбуждения. Механические и электрические потери вносят основной вклад в изменение эффективности работы двигателя.
Падает коэффициент полезного действия (КПД) от потерь в обмотке якоря и цепи возбуждения. Механические и электрические потери вносят основной вклад в изменение эффективности работы двигателя.
Добавочные потери
Добавочные потери мощности в электродвигателях складываются из потерь, возникающих в уравнительных соединениях, из потерь из-за неравномерной индукции в стали якоря при высокой нагрузке. Вносят свой вклад в общую сумму добавочных потерь вихревые токи, а также потери в полюсных наконечниках. Точно определить все эти значения довольно сложно, поэтому их сумму принимают обычно равной в пределах 0,5-1%. Эти цифры используют при расчете общих потерь для определения КПД электродвигателя.
КПД и его зависимость от нагрузки
Коэффициент полезного действия (КПД) электрического двигателя это отношение полезной мощности силового агрегата к мощности потребляемой. Этот показатель у двигателей, мощностью до 100 кВт находится в пределах от 0,75 до 0,9. для более мощных силовых агрегатов КПД существенно выше: 0,9-0,97. Определив суммарные потери мощности в электродвигателях можно достаточно точно вычислить коэффициент полезного действия любого силового агрегата. Этот метод определения КПД называется косвенным и он может применяться для машин различной мощности. Для маломощных силовых агрегатов часто используют метод непосредственной нагрузки, заключающийся в измерениях потребляемой двигателем мощности.
Определив суммарные потери мощности в электродвигателях можно достаточно точно вычислить коэффициент полезного действия любого силового агрегата. Этот метод определения КПД называется косвенным и он может применяться для машин различной мощности. Для маломощных силовых агрегатов часто используют метод непосредственной нагрузки, заключающийся в измерениях потребляемой двигателем мощности.
КПД электрического двигателя не является величиной постоянной, своего максимума он достигает при нагрузках около 80% мощности. Достигает он пикового значения быстро и уверенно, но после своего максимума начинает медленно уменьшаться. Это связывают с возрастанием электрических потерь при нагрузках, более 80% от номинальной мощности. Падение коэффициента полезного действия не велико, что позволяет говорить о высоких показателях эффективности электродвигателей в широком диапазоне мощностей.
Разработан электродвигатель нового типа
, обладающий значительно более высокой эффективностью, чем выпускающиеся сейчас. С возбуждением, от электромагнитов
С возбуждением, от электромагнитов
, или от постоянных магнитов
. Вариантов конструктивного исполнения может быть много.
Все находится в полном соответствии с известными законами физики и законами сохранения энергии. Дело в том, что в известных электродвигателях только очень малая часть потребляемой мощности используется для создания работы, а основная часть тратится на преодоление так называемой обратной(или генераторной) ЭДС, возникающей согласно закону Ленца во вращающемся роторе. Во всех руководствах по электротехнике утверждается, что КПД электродвигателя может достигать 80-98%, но проведя необходимые исследования, я убедился, что это не так, а истинный КПД электродвигателя не превышает 5-10%, поэтому имеются огромные резервы для его увеличения, и соответственно улучшения экономичности электродвигателя во много раз.
С тех пор, как в 1821 году Эрстед продемонстрировал возникновение магнитного поля
вокруг проводника с током, электротехника начала стремительно развиваться.
Уже через несколько лет были установлены основные законы электротехники, созданы мощные электромагниты
, а также первые электродвигатели. Но удивительное дело: электромагниты
, создающие большую статическую силу магнитного взаимодействия и потребляющие при этом небольшую мощность, при работе электродвигателя
, когда ротор начинал вращаться, теряли свою силу и требовали увеличения напряжения, а следовательно и мощности для того, чтобы электродвигатель
мог совершать механическую работу.
Правильное объяснение этому явлению дал русский физик Ленц. Сейчас это явление можно кратко назвать противоЭДС.
Суть этого явления в том, что при движении относительно друг друга проводников с током или магнита
и проводника с током, в проводнике возникает напряжение, которое всегда направлено встречно питающему обмотку двигателя
, поэтому и приходится, для поддержания мощности двигателя
, увеличивать напряжение его питания. Получается странная картина: с одной стороны — мощное магнитное поле
и огромная сила взаимодействия катушек с ферромагнитными сердечниками друг с другом, при малой потребляемой мощности, а с другой, при относительно медленном движении катушек относительно друг друга уже требуется значительно увеличивать напряжения питания для поддержания силы магнитного
взаимодействия. Поэтому возникла мысль, что если удастся найти способ нейтрализовать влияние закона Ленца в электродвигателе, то можно получить огромный выигрыш в получаемой механической мощности, относительно затраченной электрической. В результате проведенных исследований были теоретически найдены и подтверждены опытным путем несколько частных случаев, когда закон Ленца не оказывает своего влияния на процессы, происходящие в электродвигателе, или значительно ослабляется. Это дает возможность создавать электродвигатели, которые способны на единицу затраченной электрической мощности, произвести от двух до десяти и больше единиц механической работы. При этом все остается в полном соответствии с любыми известными законами физики! Я не могу открыто говорить о конструктивных особенностях подобных двигателей, скажу только, что основные варианты мало отличаются от уже известных конструкций. Другие варианты совершенно не похожи на любые известные электродвигатели. Я даже не ожидал, что задача имеет такое множество решений! А взяться за решение подобной задачи меня побудила заметка, что около 50-и лет назад, в СССР, один умелец ездил на автомобиле «Москвич» с электромотором целый день, на энергии обычного автомобильного аккумулятора.
Поэтому возникла мысль, что если удастся найти способ нейтрализовать влияние закона Ленца в электродвигателе, то можно получить огромный выигрыш в получаемой механической мощности, относительно затраченной электрической. В результате проведенных исследований были теоретически найдены и подтверждены опытным путем несколько частных случаев, когда закон Ленца не оказывает своего влияния на процессы, происходящие в электродвигателе, или значительно ослабляется. Это дает возможность создавать электродвигатели, которые способны на единицу затраченной электрической мощности, произвести от двух до десяти и больше единиц механической работы. При этом все остается в полном соответствии с любыми известными законами физики! Я не могу открыто говорить о конструктивных особенностях подобных двигателей, скажу только, что основные варианты мало отличаются от уже известных конструкций. Другие варианты совершенно не похожи на любые известные электродвигатели. Я даже не ожидал, что задача имеет такое множество решений! А взяться за решение подобной задачи меня побудила заметка, что около 50-и лет назад, в СССР, один умелец ездил на автомобиле «Москвич» с электромотором целый день, на энергии обычного автомобильного аккумулятора. Я сразу подумал о том, что его электромотор потреблял значительно меньшую мощность, чем развиваемая механическая и принял за аксиому, что раз было возможно тогда, то возможно и сейчас.
Я сразу подумал о том, что его электромотор потреблял значительно меньшую мощность, чем развиваемая механическая и принял за аксиому, что раз было возможно тогда, то возможно и сейчас.
Сравнение электродвигателя без противоЭДС с обычным, по мощности потребления
Для простоты анализа возьмем любой коллекторный или вентильный двигатель
. Он состоит из ротора и статора. Обмотки возбуждения могут быть как на роторе со статором, так и только на одном роторе или статоре (если используются постоянные магниты
возбуждения). При подаче напряжения на двигатель
, ротор и статор начинают двигаться относительно друг друга, при этом в обмотках якоря или статора (если ротор возбуждается постоянными магнитами
), индуцируется ЭДС, направленная всегда против напряжения внешнего источника питания. По мере увеличения числа оборотов ротора (действительной или кажущейся линейной скорости движения проводника относительно магнитного поля
возбуждения) ток в обмотках под действием этой ЭДС уменьшается, соответственно уменьшается, и вращающий момент.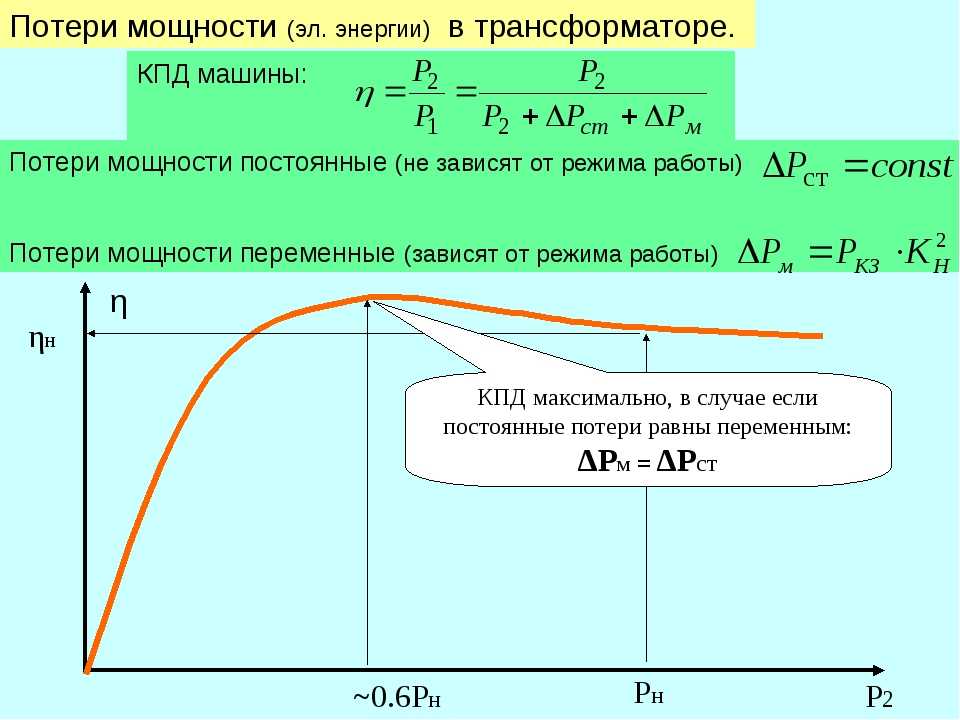 Для его увеличения приходится повышать напряжение (мощность) питания электродвигателя
Для его увеличения приходится повышать напряжение (мощность) питания электродвигателя
. В современных электродвигателях
практически вся мощность, подводимая для питания, расходуется на преодоление противодействующей ЭДС.
Например, серийный электродвигатель
постоянного тока типа 4ПН 200S имеет следующие характеристики:
мощность 60 кВт; напряжение 440 В; ток 149 А; частота вращения 3150/3500 об/мин; кпд 90,5%; длина статора 377 мм; диаметр ротора 250 мм, напряжение потерь 41,8 В; напряжение на преодоление индуцированной ЭДС 398,2 В; мощность на преодоление потерь 6228 Вт; вращающий момент (3500 об/мин) 164,6 Нм.
Получается, что если мы избавимся от противоЭДС, то для питания двигателя
нужен источник напряжения не 440 вольт, а только 42 вольта, при том же токе 150А. Поэтому потребляемая мощность при полной нагрузке составит 6300 ватт при механической выходной мощности 60 кВт. Регулировка выходной мощности двигателя
без противоЭДС может осуществляться изменением напряжения питания или импульсным регулированием.
В результате сравнительного анализа мы видим, что использование электродвигателя
без противоЭДС способно в корне изменить всю экономику человечества. Это один из способов навсегда отказаться от использования органического топлива для энергетических и транспортных потребностей человечества. В самом деле, подобные электродвигатели, возможно, соединить на одном валу с генераторами небольшой мощности и получить самопитаемую систему! Только для запуска требуется аккумулятор. А ведь есть еще и разработки безтопливных генераторов, которые могут использоваться совместно с электродвигателями данного типа. При этом возникает большая экономия, так как требуется генератор гораздо меньшей мощности. Совместное использование БТГ и описанных электродвигателей
позволит в ближайшем будущем выпускать абсолютно автономные электромобили, способные двигаться без всякого топлива до тех пор, пока не износятся механически. На таком принципе можно строить большинство известных сегодня транспортных средств. В том числе и самолеты, и даже космические аппараты, ведь есть варианты и электрических полевых устройств, создающих тягу без отбрасывания массы. Это совершенно новая эра в истории человечества и трудно даже предположить последствия применения подобных конструкций.
В том числе и самолеты, и даже космические аппараты, ведь есть варианты и электрических полевых устройств, создающих тягу без отбрасывания массы. Это совершенно новая эра в истории человечества и трудно даже предположить последствия применения подобных конструкций.
Двигатель
прост по конструкции и недорог.
Отличие от существующих двигателей
небольшое. Но при этом, предлагаемый двигатель
будет потреблять в несколько раз меньшую мощность, чем равный ему по характеристикам промышленный.
КПД двигателя
не превысит 100%
, это невозможно. Просто он гораздо эффективнее преобразует электрическую энергию в механическую. Обычные электродвигатели
, имеют самый высокий КПД только в узком диапазоне нагрузок, но и при этом он очень далек от указываемого производителем.
Проведенные практические опыты показали, что на единицу израсходованной электрической энергии, новый двигатель
, сможет выработать в несколько раз большую механическую мощность. Испытание макета двигателя
Испытание макета двигателя
полностью подтвердило теорию. Выходная, механическая мощность, в три раза превысила, потребляемую электрическую. Для эксперимента был изготовлен один из самых простых и неэффективных вариантов двигателя
. Данный двигатель
разместили на одной раме с автомобильным генератором от автомобиля «Жигули», соединив клиноременной передачей их шкивы. Двигатель
питался от сети 220 вольт. Для управления двигателем
был использован механический коммутатор, а не электронный, что также значительно снизило эффективность его работы. В качестве нагрузки генератора использовались автомобильные лампы. При этом потребляемая двигателем
мощность (по постоянному току) составила 140 ватт. Измерив мощность на выходе генератора на лампочках(тоже по постоянному току), получили 160 ватт электрической мощности. Известно, что автомобильные генераторы имеют КПД, не превышающий 60%, поэтому механическая мощность на валу двигателя
была значительно выше, чем электрическая на выходе генератора. К сожалению, не было возможности достать на 220 вольт необходимой мощности и проверить устройство в режиме самозапитки. А от того генератора, что использовался, это было невозможно. Но и в этом виде, испытания показали, что возможно получение большей механической мощности, чем затрачено электрической. Используя электронный Блок Управления двигателем
К сожалению, не было возможности достать на 220 вольт необходимой мощности и проверить устройство в режиме самозапитки. А от того генератора, что использовался, это было невозможно. Но и в этом виде, испытания показали, что возможно получение большей механической мощности, чем затрачено электрической. Используя электронный Блок Управления двигателем
, можно значительно улучшить параметры. Исследования на другом макете(электромагнитных взаимодействий) показало, что реально достичь отношения входная электрическая/выходная механическая мощность 1/20, а немного усложнив конструкцию, показатели можно улучшить в несколько раз.
Инструкция
Определение КПД
двигателя
внутреннего сгоранияНайдите в технической документации мощность данного двигателя
внутреннего сгорания . Залейте в него топливо, это может быть бензин или дизельное топливо, и заставьте проработать на максимальных оборотах некоторое время, которое замеряйте с помощью секундомера, в секундах . Слейте остатки и определите объем сгоревшего топлива, отняв от первоначального объема конечный. Найдите его массу, умножив объем, переведенный в м³, на его плотность в кг/ м³.
Слейте остатки и определите объем сгоревшего топлива, отняв от первоначального объема конечный. Найдите его массу, умножив объем, переведенный в м³, на его плотность в кг/ м³.
Для определения КПД
мощность двигателя
умножьте на время и поделите на произведение массы затраченного топлива на его удельную теплоту сгорания КПД
=P t/(q m). Чтобы получить результат в процентах , получившееся число умножьте на 100.
Если нужно измерить КПД
двигателя
автомобиля, а мощность его неизвестна, но известна масса, для определения полезной работы разгонитесь на нем из состояния покоя до скорости 30 м/с (если это возможно), измерив массу затраченного топлива. Затем массу автомобиля умножьте на квадрат его скорости, и поделите на удвоенное произведение массы затраченного топлива на удельную теплоту его сгорания КПД
=М v²/(2 q m).
Определение КПД
электродвигателя
Если известна мощность электродвигателя
, то подключите его к источнику тока с известным напряжением, добейтесь максимальных оборотов и тестером , измерьте ток в цепи. Затем мощность поделите на произведение силы тока и напряжения КПД
Затем мощность поделите на произведение силы тока и напряжения КПД
=P/(I U).
Если мощность двигателя
неизвестна, прикрепите к его валу шкив, и поднимите на известную высоту, груз известной массы. Измерьте тестером напряжение и силу тока на двигателе , а так же время подъема груза. Затем произведение массы груза на высоту подъема и число 9,81 поделите на произведение напряжения, силы тока и времени подъема в секундах КПД
=m g h/(I U t).
Обратите внимание
Во всех случаях КПД должен быть меньше 1 в дольных величинах или 100 %.
Чтобы найти коэффициент полезного действия любого двигателя
, нужно полезную работу поделить на затраченную и умножить на 100 процентов. Для теплового двигателя
найдите данную величину по отношению мощности, умноженной на длительность работы, к теплу, выделившемуся при сгорании топлива. Теоретически КПД
теплового двигателя
определяется по соотношению температур холодильника и нагревателя. Для электрических двигателей найдите отношение его мощности к мощности потребляемого тока.
Вам понадобится
- паспорт двигателя внутреннего сгорания (ДВС), термометр, тестер
Инструкция
Определение КПД
ДВС Найдите в технической документации данного конкретного двигателя
его мощность. Залейте в его бак некоторое количество топлива и запустите двигатель, чтобы он проработал некоторое время на полных оборотах, развивая максимальную мощность, указанную в паспорте. С помощью секундомера засеките время работы двигателя
, выразив его в секундах. Через некоторое время остановите двигатель, и слейте остатки топлива. Отняв от начального объема залитого топлива конечный объем, найдите объем израсходованного топлива. Используя таблицу , найдите его плотность и умножьте на объем, получив массу израсходованного топлива m=ρ V. Массу выразите в килограммах. В зависимости от вида топлива (бензин или дизельное топливо), определите по таблице его удельную теплоту сгорания. Для определения КПД
максимальную мощность умножьте на время работы двигателя
и на 100%, а результат последовательно поделите на его массу и удельную теплоту сгорания КПД
=P t 100%/(q m).
Для идеальной тепловой машины , можно применить формулу Карно. Для этого узнайте температуру сгорания топлива и измерьте температуру холодильника (выхлопных газов) специальным термометром. Переведите температуру, измеренную в градусах Цельсия в абсолютную шкалу, для чего к значению прибавьте число 273. Для определения КПД
от числа 1 отнимите отношение температур холодильника и нагревателя (температуру сгорания топлива) КПД
=(1-Тхол/Тнаг) 100%. Данный вариант расчета КПД
не учитывает механическое трение и теплообмен с внешней средой.
Определение КПД
электродвигателя
Узнайте номинальную мощность электродвигателя
, по технической документации. Подключите его к источнику тока, добившись максимальных оборотов вала, и с помощью тестера измерьте значение напряжения на нем и силу тока в цепи. Для определения КПД
заявленную в документации мощность, поделите на произведение силы тока на напряжение, результат умножьте на 100% КПД
=P 100%/(I U).
Видео по теме
Обратите внимание
Во всех расчетах КПД должен быть меньше 100%.
Некоторым автомобилистам со временем надоедает ездить на стоковом автомобиле. Поэтому они начинают тюнинговать своего железного, то есть вносить те или иные иные изменения в техническую конструкцию, чтобы таким образом увеличить возможности автомобиля. Однако после модернизации нужно знать, сколько мощности прибавилось. Как же измерить мощность двигателя?
Вам понадобится
- Компьютер, кабель, специальная программа, динамометрический стенд.
Инструкция
Есть несколько способов, как измерить мощность двигателя. Сразу же стоит отметить, что все являются неточными, то есть имеют некую погрешность. Можно установить специальное электронное оборудование, которое будет следить за параметрами работы вашего двигателя в режиме онлайн . Такое оборудование имеет среднюю погрешность. Однако у него есть минус — его большая стоимость. Также ноутбук . Загрузите программу. Необходим будет проехать несколько раз на разной скорости. Программа запомнит показатели, а потом автоматически вычислит мощность силового агрегата и укажет погрешность вычислений.
Необходим будет проехать несколько раз на разной скорости. Программа запомнит показатели, а потом автоматически вычислит мощность силового агрегата и укажет погрешность вычислений.
Самый точный способ измерить мощность двигателя — загнать автомобиль на динамометрический стенд. Для этого необходимо найти сервис, в котором имеется такая установка. Загоните ваш автомобиль на стенд передом к вентилятору. Колеса должны быть ровно между двух барабанов. Закрепите специальные ремни за несущую конструкцию авто. Подключите аппаратуру к машине через диагностический разъем. На выхлопную трубу наденьте гофрированный каркас, который будет выводить газы из бокса. Включите вентилятор, который будет имитировать сопротивление встречного воздуха. Теперь нужно максимально разогнать автомобиль. Параллельно следите за состоянием соединяющих ремней. Сделайте несколько попыток, чтобы исключить вероятность ошибки . После каждой попытки компьютер выдаст вам распечатку, где будет указана максимальная скорость и мощность.
Видео по теме
Решение задач на КПД теплового двигателя | 8 класс
Содержание
КПД теплового двигателя рассчитывается по формуле $\eta = \frac{A_п}{Q_1}$ или $\eta = \frac{Q_1 — Q_2}{Q_1} \cdot 100 \%$, где
$A_п$ — полезная работа,
$Q_1$ — количество теплоты, полученное от нагревателя,
$Q_2$ — количество теплоты, отданное холодильнику.
Когда говорят о коэффициенте полезного действия теплового двигателя, часто используют понятие мощности или полезной мощности: $N = \frac{A_п}{t}$. Эту величину в жизни использовать удобнее, чем говорить о полезной работе.
На данном уроке мы разберем решение задач, используя формулы, приведенные выше.
Для решения задач, в условиях которых, говорится о сжигании топлива ($Q = qm$), вам понадобятся табличные значения удельной теплоты сгорания топлива.
Задача №1
Какая работа совершена внешними силами при обработке железной заготовки массой $300 \space г$, если она нагрелась на $200 \degree C$?
Дано:
$m = 300 \space г$
$\Delta t = 200 \degree C$
$c = 460 \frac{Дж}{кг \cdot \degree C}$
СИ:
$m = 0. 6}{86 \space 400} = 25 \space сут$.
6}{86 \space 400} = 25 \space сут$.
Ответ: $t = 25 \space сут$.
5
Оценить урок
Поделиться уроком →
Войдите, чтобы оценивать уроки
Что нужно исправить?
Спасибо, что помогаете нам стать лучше!
Комментарии
Как определить кпд теплового двигателя » Драйв
Разделы: Физика
Класс: 10
Тип урока: Урок изучения нового материала.
Цель урока: Разъяснить принцип действия теплового двигателя.
Образовательные: познакомить учащихся с видами тепловых двигателей, развивать умение определять КПД тепловых двигателей, раскрыть роль и значение ТД в современной цивилизации; обобщить и расширить знания учащихся по экологическим проблемам.
Развивающие: развивать внимание и речь, совершенствовать навыки работы с презентацией.
Воспитательные: воспитывать у учащихся чувство ответственности перед последующими поколениями, в связи с чем, рассмотреть вопрос о влиянии тепловых двигателей на окружающую среду.
Оборудование: компьютеры для учащихся, компьютер учителя, мультимедийный проектор, тесты (в Excel), Физика 7-11 Библиотека электронных наглядных пособий. “Кирилл и Мефодий”.
Ход урока
1. Оргмомент
2. Организация внимания учащихся
Тема нашего урока: “Тепловые двигатели”. (Слайд 1)
Сегодня мы вспомним виды тепловых двигателей, рассмотрим условия их эффективной работы, поговорим о проблемах связанных с их массовым применением. (Слайд 2)
3. Актуализация опорных знаний
Прежде чем перейти к изучению нового материала предлагаю проверить как вы к этому готовы.
– Дайте формулировку первого закона термодинамики. (Изменение внутренней энергии системы при переходе ее из одного состояния в другое равно сумме работы внешних сил и количество теплоты, переданное системе. U=A+Q)
– Может ли газ нагреться или охладиться без теплообмена с окружающей средой? Как это происходит? (При адиабатических процессах.) (Слайд 3)
– Напишите первый закон термодинамики в следующих случаях: а) теплообмен между телами в калориметре; б) нагрев воды на спиртовке; в) нагрев тела при ударе.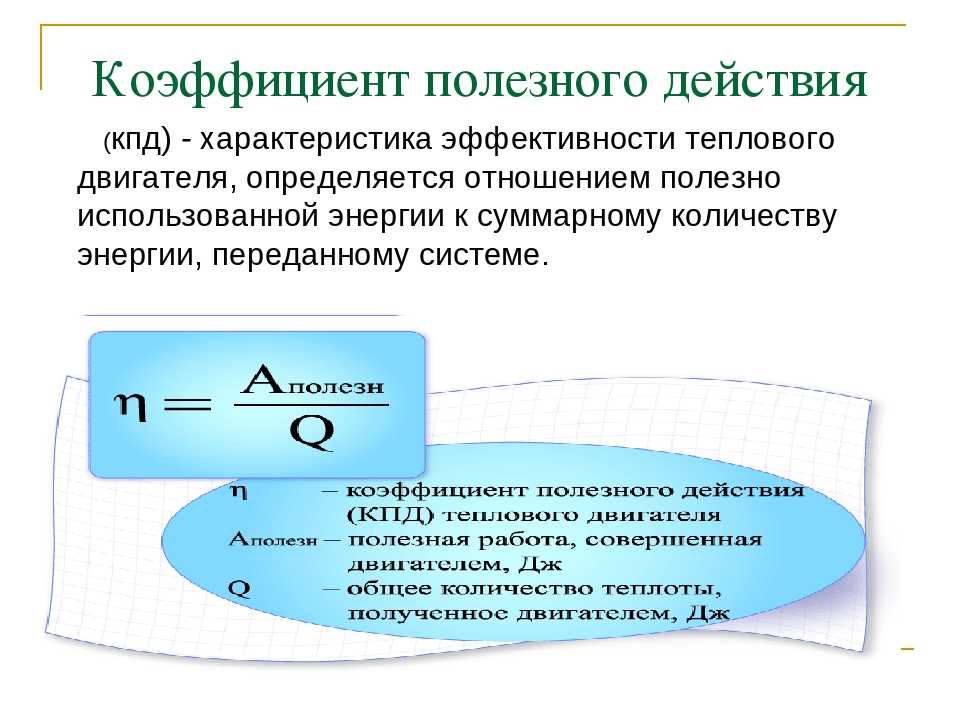 (а) А=0, Q=0, U=0; б) А=0, U= Q; в) Q=0, U=А)
(а) А=0, Q=0, U=0; б) А=0, U= Q; в) Q=0, U=А)
– На рисунке изображен цикл, совершаемый идеальным газом определенной массы. Изобразить этот цикл на графиках р(Т) и Т(р). На каких участках цикла газ выделяет теплоту и на каких – поглощает?
(На участках 3-4 и 2-3 газ выделяет некоторое количество теплоты, а на участках 1-2 и 4-1 теплота поглощается газом.) (Слайд 4)
4. Изучение нового материала
Все физические явления и законы находят применение в повседневной жизни человека. Запасы внутренней энергии в океанах и земной коре можно считать практически неограниченными. Но располагать этими запасами недостаточно. Необходимо за счет энергии уметь приводить в действие устройства, способные совершать работу. (Слайд 5)
Что является источником энергии? (различные виды топлива, энергия ветра, солнца, приливов и отливов)
Существуют различные типы машин, которые реализуют в своей работе превращение одного вида энергии в другой.
Тепловой двигатель – устройство, превращающее внутреннею энергию топлива в механическую энергию. (Слайд 6)
(Слайд 6)
Рассмотрим устройство и принцип работы теплового двигателя. Тепловая машина работает циклично.
Любая тепловая машина состоит из нагревателя, рабочего тела и холодильника. (Слайд 7)
КПД замкнутого цикла (Слайд 8)
Q1 – количество теплоты полученное от нагревания Q1>Q2
Для дошкольников и учеников 1-11 классов
Рекордно низкий оргвзнос 25 Р.
Описание презентации по отдельным слайдам:
Тема: Тепловые двигатели.Коэффициент полезного действия тепловых двигателей На уроке: ознакомитесь с принципом работы двигателя, научитесь расчитывать КПД двигателя. Ключевые понятия: тепловой двигатель, нагреватель, охладитель, рабочее тело, КПД двигателя. «Аксуский колледж черной металлургии» Преподаватель физики: Клопот Валентина Георгиевна
Джеймс Уатт Простейший тепловой двигатель был Изобретен в 17 веке Джеймсом Уаттом
Устройство, превращающее внутреннюю энергию топлива в механическую называют тепловым двигателем. Все гениальное – просто.
Все гениальное – просто.
Паровая машина Двигатель внутреннего сгорания Паровая и газовая турбины Реактивный двигатель
нагреватель рРррррр Рабочее тело (пар или газ) холодильник Q 1 Q 2 A
КПД теплового двигателя называют отношение работы, совершаемой двигателем, к количеству теплоты, полученному от нагревателя.
Сади Карно придумал тепловую машину с идеальным газом в качестве рабочего тела и рассчитал максимальный КПД. Реальный КПД всегда меньше идеального Температура нагревателя Температура холодильника
Паровая машина-10%-15% Двигатель внутреннего сгорания-20%-40% Паровая и газовая турбины-30%-40% Реактивный двигатель-10%-20%
Загрязнение окружающей среды Уменьшение запасов природных ископаемых(уголь, нефть, газ…) Парниковый эффект Накопление в земле тяжелых металлов . . . . . . . . . . . . . . . . . . . . .
Реши задачи Температура нагревателя 3000С, температура холодильника 2000С. Чему равен КПД этого двигателя? Температура холодильника идеального теплового двигателя равна 270 С, а температура нагревателя на 900 С больше. Каков КПД этого двигателя? Температура нагревателя в 2 раза больше температуры холодильника. Определить КПД двигателя.
Каков КПД этого двигателя? Температура нагревателя в 2 раза больше температуры холодильника. Определить КПД двигателя.
Использование солнечной энергии Использование энергии ветра Приливные электростанции Атомная энергетика(экология ) Электромобили
- Все материалы
- Статьи
- Научные работы
- Видеоуроки
- Презентации
- Конспекты
- Тесты
- Рабочие программы
- Другие методич. материалы
Объектом изучения в термодинамике является система – тело или группа тел, фактически или мысленно отделенных от окружающей среды. Системой можно назвать кристалл минерала, раствор любого вещества в какой-либо емкости, газ в баллоне и т.д.
Систему называют термодинамической, если между телами, ее составляющими, может происходить обмен теплотой, веществом и если система описывается полностью термодинамическими параметрами.
термодинамическими параметрами. Тепловой двигатель это система в которой происходит превращение энергии внутренней в механическую. КПД тепловых двигателей всегда меньше 100%.
Тепловой двигатель это система в которой происходит превращение энергии внутренней в механическую. КПД тепловых двигателей всегда меньше 100%.
- Клопот Валентина ГеоргиевнаНаписать 55 10.11.2020
Номер материала: ДБ-1477019
- Физика
- 10 класс
- Презентации
- 10.11.2020 0
- 09.11.2020 0
- 09.11.2020 0
- 09.11.2020 0
- 09.11.2020 0
- 09.11.2020 0
- 09.11.2020 0
- 08.11.2020 0
Не нашли то что искали?
Вам будут интересны эти курсы:
Оставьте свой комментарий
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Формулы, используемые на уроках «Задачи на КПД тепловых двигателей».
Название величины
Обозначение
Единица измерения
Формула
Масса топлива
Удельная теплота сгорания топлива
Полезная работа
Ап = ɳ Q
Затраченная энергия
Q = qm
КПД
Относится ли ружьё к тепловым двигателям? Да, так как при выстреле внутренняя энергия топлива превращается в механическую энергию.
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача № 1. Определите КПД двигателя автомобиля, которому для выполнения работы 110,4 МДж потребовалось 8 кг бензина.
Задача № 2. Определите КПД двигателя автомобиля, которому для выполнения работы 220,8 МДж потребовалось 16 кг бензина.
Задача № 3. Определите КПД двигателя автомобиля, которому для выполнения работы 27,6 МДж потребовалось 2 кг бензина.
Задача № 4. На теплоходе установлен дизельный двигатель мощностью 80 кВт с КПД 30%. На сколько километров пути ему хватит 1 т дизельного топлива при скорости движения 20 км/ч? Удельная теплота сгорания дизельного топлива 43 МДж/кг.
Задача № 5. Патрон травматического пистолета «Оса» 18 x 45 мм, содержит резиновую пулю массой 8,4 г. Определите КПД патрона, если пуля при выстреле приобрела скорость 140 м/с. Масса порохового заряда патрона составляет 0,18 г, удельная теплота сгорания пороха 3,8 • 10 6 Дж/кг.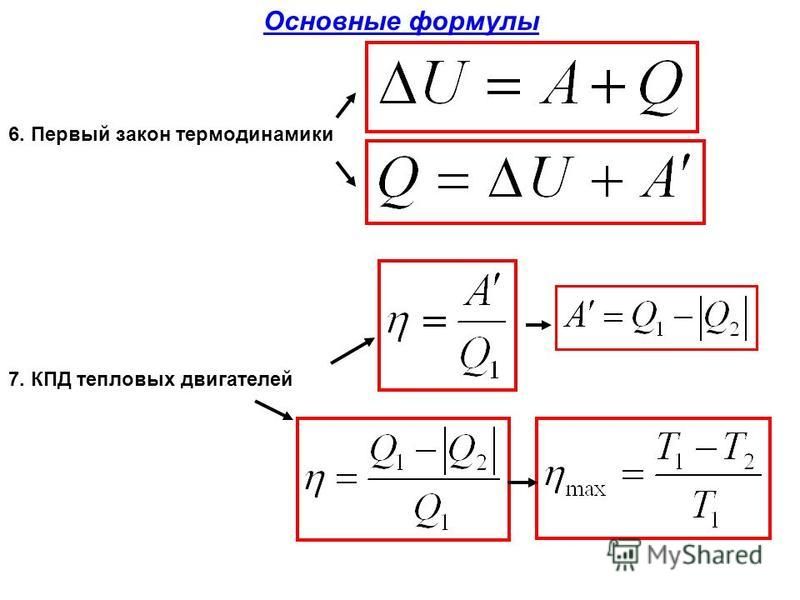
Задача № 6. Первый гусеничный трактор конструкции А. Ф. Блинова, 1888 г., имел два паровых двигателя. За 1 ч он расходовал 5 кг топлива, у которого удельная теплота сгорания равна 30 • 10 6 Дж/кг. Вычислите КПД трактора, если мощность двигателя его была равна около 1,5 кВт.
Задача № 7. Двигатель внутреннего сгорания совершил полезную работу, равную 2,3 • 10 4 кДж, и при этом израсходовал бензин массой 2 кг. Вычислите КПД этого двигателя.
Задача № 8. За 3 ч пробега автомобиль, КПД которого равен 25%, израсходовал 24 кг бензина. Какую среднюю мощность развивал двигатель автомобиля при этом пробеге?
Задача № 9. Двигатель внутреннего сгорания мощностью 36 кВт за 1 ч работы израсходовал 14 кг бензина. Определите КПД двигателя.
Задача № 10. ОГЭ Идеальная тепловая машина, работающая по циклу Карно, 80 % теплоты, полученной от нагревания, передаёт охладителю. Количество теплоты, получаемое рабочим телом за один цикл от нагревателя, Q1 = 6,3 Дж. Найти КПД цикла ɳ и работу А, совершаемую за один цикл.
Количество теплоты, получаемое рабочим телом за один цикл от нагревателя, Q1 = 6,3 Дж. Найти КПД цикла ɳ и работу А, совершаемую за один цикл.
Задача № 11. ЕГЭ Тепловая машина, работающая по циклу Карно, совершает за один цикл работу А = 2,94 кДж и отдаёт за один цикл охладителю количество теплоты Q2 = 13,4 кДж. Найти КПД цикла ɳ.
Задача № 12. Снегоуборочная машина мощностью 40 кВт за 1 час работы расходует примерно 5 л бензина. Каков КПД снегоуборочной машины? Удельная теплота сгорания бензина 46 МДж/кг, плотность бензина — 710 кг/м 3 .
Краткая теория для решения Задачи на КПД тепловых двигателей.
Это конспект по теме «ЗАДАЧИ на КПД тепловых двигателей». Выберите дальнейшие действия:
- Перейти к теме: ЗАДАЧИ на Закон Ома.
- Посмотреть конспект «Тепловые машины. ДВС. Удельная теплота сгорания».

- Вернуться к списку конспектов по Физике.
- Проверить свои знания по Физике.
Урок 40. Физика 10 класс ФГОС
Конспект урока «Коэффициент полезного действия тепловых двигателей»
На прошлом уроке мы с вами начали знакомство с тепловыми двигателями. Давайте вспомним, что так называется устройство, которое совершает механическую работу за счёт внутренней энергии топлива.
Простейший тепловой двигатель представляет собой цилиндрический сосуд, в котором находится газ под поршнем. При нагревании газа, его давление и объём увеличиваются, и поршень приходит в движение, поднимая груз на некоторую высоту.
Любой тепловой двигатель состоит из трёх основных элементов: нагревателя, рабочего тела (как правило, газ) и холодильника (чаще всего атмосфера или вода при температуре окружающей среды).
Энергия, выделяемая при сгорании топлива в нагревателе, передаётся рабочему телу путём теплопередачи. При расширении газа часть его внутренней энергии идёт на совершение работы. А некоторое количество теплоты неизбежно передаётся холодильнику. Таким образом, получается, что полное превращение внутренней энергии газа в работу невозможно. Это обусловлено необратимостью процессов в природе. Если бы тепло могло самопроизвольно возвращаться от холодильника к нагревателю, то внутренняя энергия могла бы быть полностью превращена в полезную работу с помощью любого теплового двигателя. Но второй закон термодинамики запрещает это: ведь невозможно создать вечный двигатель второго рода, то есть двигатель, который полностью превращал бы теплоту в механическую работу.
При расширении газа часть его внутренней энергии идёт на совершение работы. А некоторое количество теплоты неизбежно передаётся холодильнику. Таким образом, получается, что полное превращение внутренней энергии газа в работу невозможно. Это обусловлено необратимостью процессов в природе. Если бы тепло могло самопроизвольно возвращаться от холодильника к нагревателю, то внутренняя энергия могла бы быть полностью превращена в полезную работу с помощью любого теплового двигателя. Но второй закон термодинамики запрещает это: ведь невозможно создать вечный двигатель второго рода, то есть двигатель, который полностью превращал бы теплоту в механическую работу.
Баланс энергии за цикл можно получить на основе первого закона термодинамики.
Для идеального теплового двигателя изменение внутренней энергии равно нулю, так как рабочее тело вернулось в исходное состояние. Отсюда находим, что полезная работа, совершаемая тепловым двигателем, равна разности между количеством теплоты, полученной от нагревателя, и количеством теплоты, отданной холодильнику:
Отношение полезной работы к количеству теплоты, которое рабочее тело получило от нагревателя, называется коэффициентом полезного действия теплового двигателя (сокращённо, КПД):
Так как часть теплоты, полученной от нагревателя, передаётся холодильнику, то коэффициент полезного действия любого теплового двигателя всегда меньше единицы:
Для получения максимально возможного коэффициента полезного действия необходимо охладить рабочее тело перед сжатием.
Это можно сделать путём адиабатного расширения газа, при котором его температура понизится до температуры холодильника. Далее при изотермическом сжатии рабочее тело передаст холодильнику некоторое количество теплоты. А завершить цикл теплового двигателя эффективнее всего адиабатным сжатием газа до первоначальной температуры. Впервые этот цикл был предложен французским инженером Сади Карно, поэтому его ещё называют циклом Карно. Формулу для определения коэффициента полезного действия цикла Карно вы сейчас видите на экране:
КПД любого реального теплового двигателя не может превышать КПД идеального цикла Карно. Формула Карно даёт теоретический предел для максимального значения коэффициента полезного действия тепловых двигателей. Она показывает, что двигатель тем эффективней, чем больше разность температур нагревателя и холодильника.
А КПД идеального теплового двигателя мог бы быть равен единице только в том случае, если бы было возможно использовать холодильник с температурой, равной абсолютному нулю. Но, как известно, это невозможно даже теоретически, потому что абсолютного нуля температуры достичь нельзя.
Но, как известно, это невозможно даже теоретически, потому что абсолютного нуля температуры достичь нельзя.
Для закрепления нового материала, решим с вами задачу. Задача 1. Каждый из четырёх двигателей реактивного самолёта на 5000 км пути развивает среднюю силу тяги 0,11 МН. Определите объём керосина, израсходованного на этом пути, если коэффициент полезного действия двигателя равен 24 %. Плотность и удельная теплота сгорания керосина соответственно равны 800 кг/м 3 и 43 МДж/кг.
В заключение урока отметим, что изобретение паровой машины, а впоследствии и двигателя внутреннего сгорания французским инженером Этьеном Ленуаром в 1860 г. имело исключительно важное значение.
Сейчас трудно представить нашу жизнь без автомобилей, самолётов, кораблей и других устройств, в которых внутренняя энергия сжигаемого топлива частично преобразуется в механическую работу.
Наибольшее значение имеет использование тепловых двигателей в энергетике и на транспорте. Тепловые двигатели — паровые турбины — устанавливают на тепловых и атомных электростанциях, где энергия пара превращается в механическую энергию роторов генераторов электрического тока.
Тепловые двигатели — паровые турбины — устанавливают на тепловых и атомных электростанциях, где энергия пара превращается в механическую энергию роторов генераторов электрического тока.
Двигатели внутреннего сгорания устанавливают на автомобилях, мотоциклах, вертолётах и самолётах, тракторах и тяжёлых автомобилях. Создание реактивного двигателя позволило поднять самолёты на большую высоту, увеличить скорость и дальность их полётов.
Однако интенсивное использование тепловых двигателей в энергетике и на транспорте отрицательно влияет на окружающую среду. При работе тепловые двигатели выбрасывают в атмосферу огромное количество горячего пара или газа, что приводит к тепловому загрязнению атмосферы.
Широкое использование различных видов топлива влечёт за собой увеличение в атмосфере углекислого газа, который, соединяясь в атмосфере с водяными парами, образует угольную кислоту и выпадает в виде кислотных дождей.
Сжигание топлива на тепловых электростанциях ведёт к накоплению в атмосфере угарного газа, являющегося ядом для живых организмов. Например, при сгорании тонны бензина образуется около 60 кг оксида углерода.
Например, при сгорании тонны бензина образуется около 60 кг оксида углерода.
Решение проблем, возникающих при сжигании топлива учёные и конструкторы видят:
· в очистке газовых выбросов в атмосферу;
· увеличении коэффициента полезного действия тепловых двигателей, в частности, путём создания условий для наиболее полного сгорания топлива;
· замене тепловых двигателей на более экологически чистые двигатели, например, электрические;
· использование альтернативных источников энергии.
Любой тепловой двигатель превращает в механическую энергию только незначительную часть энергии, которая выделяется топливом. Большая часть энергии топлива не используется полезно, а теряется в окружающем пространстве.
Тепловой двигатель состоит из нагревателя, рабочего тела и холодильника. Газ или пар, который является рабочим телом, получает от нагревателя некоторое количество теплоты.
Рабочее тело, нагреваясь, расширяется и совершает работу за счёт своей внутренней энергии. Часть энергии передаётся атмосфере — холодильнику — вместе с отработанным паром или выхлопными газами.
Часть энергии передаётся атмосфере — холодильнику — вместе с отработанным паром или выхлопными газами.
Очень важно знать, какую часть энергии, выделяемой топливом, тепловой двигатель превращает в полезную работу. Чем больше эта часть энергии, тем двигатель экономичнее.
Для характеристики экономичности различных двигателей введено понятие коэффициента полезного действия двигателя — КПД.
Отношение совершённой полезной работы двигателя к энергии, полученной от нагревателя, называют коэффициентом полезного действия теплового двигателя.
Коэффициент полезного действия обозначают η (греч. буква «эта»).
КПД теплового двигателя определяют по формуле
где Ап — полезная работа, Q1 — количество теплоты, полученное от нагревателя, Q2 — количество теплоты, отданное холодильнику, Q1 — Q2 — количество теплоты, которое пошло на совершение работы. КПД выражается в процентах.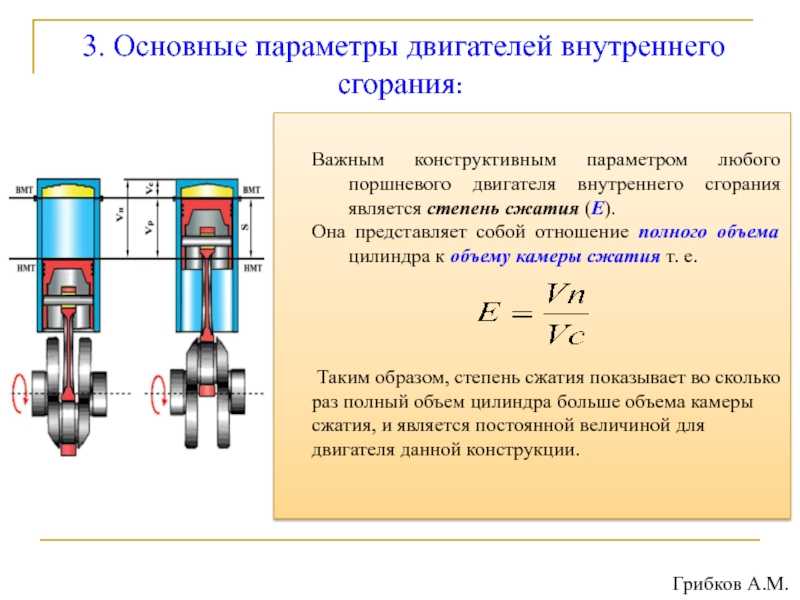
Например, двигатель из всей энергии, выделившейся при сгорании топлива, расходует на совершение полезной работы только одну четвёртую часть. Тогда коэффициент полезного действия двигателя равен ¼, или 25% .
КПД двигателя обычно выражают в процентах. Он всегда меньше единицы, т. е. меньше 100% . Например, КПД двигателей внутреннего сгорания 20—40%, паровых турбин — немногим выше 30%.
Вопросы
- Почему в тепловых двигателях только часть энергии топлива превращается в механическую энергию?
- Что называют КПД теплового двигателя?
- Почему КПД двигателя не может быть не только больше 100%, но и равен 100%?
- Какой такт работы двигателя внутреннего сгорания изображён на рисунке 29?
Упражнение 17
- Можно ли за счёт внутренней энергии тела, равной 200 Дж, совершить механическую работу в 200 Дж?
- Тепловая машина за цикл получает от нагревателя количество теплоты, равное 155 Дж, а холодильнику отдаёт количество теплоты, равное 85 Дж.
 Определите КПД машины.
Определите КПД машины. - Определите количество теплоты, отданное двигателем внутреннего сгорания холодильнику, если его КПД равен 30%, а полезная работа равна 450 Дж.
Задание
Подготовьте доклад на одну из тем (по выбору). История изобретения паровых машин.
- История изобретения турбин.
- Первые паровозы Стефенсона и Черепановых.
- Достижения науки и техники в строительстве паровых турбин.
- Использование энергии Солнца на Земле.
Любой тепловой двигатель превращает в механическую энергию только незначительную часть энергии, которая выделяется топливом. Большая часть энергии топлива не используется полезно, а теряется в окружающем пространстве.
Тепловой двигатель состоит из нагревателя, рабочего тела и холодильника. Газ или пар, который является рабочим телом, получает от нагревателя некоторое количество теплоты.
Рабочее тело, нагреваясь, расширяется и совершает работу за счёт своей внутренней энергии. Часть энергии передаётся атмосфере — холодильнику — вместе с отработанным паром или выхлопными газами.
Часть энергии передаётся атмосфере — холодильнику — вместе с отработанным паром или выхлопными газами.
Очень важно знать, какую часть энергии, выделяемой топливом, тепловой двигатель превращает в полезную работу. Чем больше эта часть энергии, тем двигатель экономичнее.
Для характеристики экономичности различных двигателей введено понятие коэффициента полезного действия двигателя — КПД.
Отношение совершённой полезной работы двигателя к энергии, полученной от нагревателя, называют коэффициентом полезного действия теплового двигателя.
Коэффициент полезного действия обозначают η (греч. буква «эта»).
КПД теплового двигателя определяют по формуле
где Ап — полезная работа, Q1 — количество теплоты, полученное от нагревателя, Q2 — количество теплоты, отданное холодильнику, Q1 — Q2 — количество теплоты, которое пошло на совершение работы. КПД выражается в процентах.
Например, двигатель из всей энергии, выделившейся при сгорании топлива, расходует на совершение полезной работы только одну четвёртую часть. Тогда коэффициент полезного действия двигателя равен ¼, или 25% .
КПД двигателя обычно выражают в процентах. Он всегда меньше единицы, т. е. меньше 100% . Например, КПД двигателей внутреннего сгорания 20—40%, паровых турбин — немногим выше 30%.
Вопросы
- Почему в тепловых двигателях только часть энергии топлива превращается в механическую энергию?
- Что называют КПД теплового двигателя?
- Почему КПД двигателя не может быть не только больше 100%, но и равен 100%?
- Какой такт работы двигателя внутреннего сгорания изображён на рисунке 29?
Упражнение 17
- Можно ли за счёт внутренней энергии тела, равной 200 Дж, совершить механическую работу в 200 Дж?
- Тепловая машина за цикл получает от нагревателя количество теплоты, равное 155 Дж, а холодильнику отдаёт количество теплоты, равное 85 Дж.
 Определите КПД машины.
Определите КПД машины. - Определите количество теплоты, отданное двигателем внутреннего сгорания холодильнику, если его КПД равен 30%, а полезная работа равна 450 Дж.
Задание
Подготовьте доклад на одну из тем (по выбору). История изобретения паровых машин.
- История изобретения турбин.
- Первые паровозы Стефенсона и Черепановых.
- Достижения науки и техники в строительстве паровых турбин.
- Использование энергии Солнца на Земле.
Степень совершенства преобразования теплоты в механическую работу в термодинамическом цикле двигателя оценивается термическим (или тепловым, или термодинамическим) коэффициентом полезного действия ηt .
Термический КПД Отношение работы, совершенной в прямом обратимом термодинамическом цикле, к теплоте, сообщенной рабочему телу от внешних источников.
где At – тепло, преобразованное в цикле в работу; Q1 – тепло, подведённое в цикле к рабочему телу; Q2 – тепло, отданное в цикле рабочим телом.
| Термический КПД |
|---|
| На индикаторной диаграмме это отношение площадей работы за цикл At (область заштрихованая «в клетку») и подведённой в цикле к рабочему телу теплоты Q1 (вся заштрихованная область). |
Термический КПД термодинамического цикла показывает, какое количество получаемой теплоты машина превращает в работу в конкретных условиях протекания идеального цикла. Чем больше величина ηt , тем совершеннее цикл и тепловая машина.
В качестве критерия оценки термодинамических циклов часто используют цикл Карно, потому что КПД тепловой машины Карно максимален в том смысле, что никакая тепловая машина с теми же температурами нагревателя и холодильника не может обладать бόльшим КПД [1]. Формула для расчёта термического КПД данного цикла общеизвестна
где T1 – абсолютная температура нагревателя; T2 – абсолютная температура холодильника.
Из анализа цикла Карно можно сделать следующие выводы:
- КПД любого термодинамического цикла тем больше, чем больше разница температур нагревателя T1 и холодильника T2 ;
- термический КПД никогда не достигает 100 %, потому что температура T2 в лучшем случае равна температуре окружающей среды;
Сегодня наибольшая разница температур достигнута в двигателях внутреннего сгорания, благодаря высокой температуре рабочего тела T1 . Температура газов в цилиндре поршневого ДВС достигает 2000 °C и более, а в газовой турбине порядка 900 – 1300 °C, что связано с необходимость обеспечить жаропрочность лопаток турбины. Для двигателей с внешним подводом теплоты такие значения температур рабочего тела остаются пока недостижимыми из-за высокого термического сопротивления на границе нагреватель-рабочее тело. Температура пара в современных паровой турбине или поршневом паровом двигателе находится в диапазоне от 300 до 600 °C.
Температура газов в цилиндре поршневого ДВС достигает 2000 °C и более, а в газовой турбине порядка 900 – 1300 °C, что связано с необходимость обеспечить жаропрочность лопаток турбины. Для двигателей с внешним подводом теплоты такие значения температур рабочего тела остаются пока недостижимыми из-за высокого термического сопротивления на границе нагреватель-рабочее тело. Температура пара в современных паровой турбине или поршневом паровом двигателе находится в диапазоне от 300 до 600 °C.
Стоит заметить, что высокий термический КПД не служит гарантией высокого эффективного КПД двигателя.
Читайте также
Использовать всю эффективную мощность двигателя на ведущих колесах не представляется возможным, поскольку она частично теряется при передаче ее трансмиссией.
Для движения по мягкому грунту шины должны соответствовать особым требованиям.
Подписка на рассылку
- ВКонтакте
- ok
- YouTube
- Яндекс.
 Дзен
Дзен - TikTok
Электрическими двигателями переменного или постоянного тока комплектуются приводы станков, насосов и вентиляторов, а также других механизмов, используемых на предприятиях тяжелой и легкой промышленности. Рентабельность производства напрямую зависит от себестоимости продукции, на которую в большой степени влияет эффективность эксплуатации оборудования, поэтому КПД и мощность электродвигателя являются основными параметрами, на основании которых выполняется подбор привода.
Определение КПД электродвигателя
Принцип работы любой электрической машины основан на преобразовании энергии тока, протекающего по обмоткам статора и создающего магнитное поле, во вращение ротора. Коэффициент полезного действия (КПД) электродвигателя определяется соотношением вырабатываемой им механической мощности на валу (p2) к полной мощности, потребляемой из сети (p1) и выражается в процентах:
Исходя из формулы, следует, что чем ближе этот параметр к единице, тем выше будет эффективность использования оборудования.
Факторы, влияющие на величину КПД
Коэффициент полезного действия никогда не может быть равным единице, так как существуют неизбежные потери, снижающие полезную мощность. Они делятся на три группы:
- электрические;
- магнитные;
- механические.
Электрические потери зависят от степени нагрузки двигателя и являются следствием нагрева обмоток статора, вызванного работой тока по преодолению электрического сопротивления проводников, из которых они выполнены. Поэтому максимальный КПД электродвигателя достигается, когда нагрузка на двигатель составляет 75% от максимальной расчетной величины.
Магнитные потери происходят из-за неизбежного перемагничивания активного железа статора и ротора, а также возникновения в нем вихревых токов.
Третья группа обусловлена наличием трения в подшипниках, на которых вращается вал, а также сопротивлением, оказываемым воздухом крыльчатке вентилятора и самому ротору (якорю). Из-за наличия щеточно-коллекторного узла КПД электродвигателя постоянного тока несколько ниже коэффициента полезного действия машин с короткозамкнутым ротором. Это также относится к асинхронным электродвигателям с фазным ротором из-за дополнительного трения щеток об контактные кольца.
Это также относится к асинхронным электродвигателям с фазным ротором из-за дополнительного трения щеток об контактные кольца.
Способы повысить КПД двигателя
Следует помнить, что реальный коэффициент полезного действия может несколько отличатся от паспортных величин, указанных на шильдике двигателя. Чтобы выполнить расчет КПД электродвигателя в реальных условиях эксплуатации, необходимо учитывать неравномерность распределения питающего напряжения в фазах. В зависимости от величины асимметрии падение полезной мощности может достигать 5-7%.
Увеличение КПД электрической машины возможно только за счет снижения потерь и контроля качества силовой сети.
Механические потери можно уменьшить благодаря более качественным подшипникам, установки крыльчатки вентилятора, выполненной из современных материалов для уменьшения сопротивлению воздуху. Нагрев обмоток можно уменьшить благодаря использованию обмоточных проводов, выполненных из очищенной меди, имеющих меньшее сопротивление.
Снизить потери на перемагничивание активного железа и минимизировать влияние вихревых токов можно используя для набора сердечника необходимо использовать качественную электромагнитную сталь с надежной изоляцией. Кроме того, ведутся работы по разработке наилучшей геометрии зубцов статора, благодаря которым будет увеличена концентрация магнитного поля.
В реальности КПД асинхронного электродвигателя можно несколько увеличить за счет использования частотного преобразователя, позволяющего оптимизировать расход электроэнергии. Следует помнить, что эффективность эксплуатации двигателя с КПД 98% сильно упадет, если его использовать для приведения в движения механизма, имеющего более низкий коэффициент полезного действия.
Данная презентация поможет при решениии задач по теме КПД в 8 классе
Просмотр содержимого документа
«КПД теплового двигателя. Решение задач. 8класс»
КПД теплового двигателя Решение задач 8класс
1. Тепловой двигатель за некоторое время получает от нагревателя количество теплоты, равное 230 кДж, а отдает холодильнику количество теплоты, равное 100 кДж. Определите полезную работу двигателя за это время.
Тепловой двигатель за некоторое время получает от нагревателя количество теплоты, равное 230 кДж, а отдает холодильнику количество теплоты, равное 100 кДж. Определите полезную работу двигателя за это время.
2. Тепловой двигатель за некоторое время получает от нагревателя количество теплоты, равное 120кДж, и совершает при этом полезную работу 20 кДж. Определите КПД такого двигателя.
3. КПД теплового двигателя равен 45%. Какую полезную работу совершит двигатель, если он получит от нагревателя количество теплоты, равное 600 кДж?
4. Количество теплоты, полученное от нагревателя тепловым двигателем, равно 10 кДж. За тоже время он отдает холодильнику количество теплоты, равное 5 кДж. Найдите работу, совершенную двигателем, и КПД этого двигателя.
5. На древесном угле массой 17г нагревают воду. Взяли 200г воды и нагрели от 15 0 С до 57 0 С. Найти КПД тепловой установки.
продолжение на следующем слайде
Для закрепления:
- Каков КПД двигателя, который совершил работу 50кДж, если при полном сгорании топлива выделилось бы энергия 200кДж.

- Израсходовано 70г бензина, тепловой двигатель совершил полезную работу 2,1 МДж. Каков КПД этого двигателя?
- Сколько природного газа необходимо для совершения полезной работы 110кДж, если КПД двигателя – 25%?
Лучший ответ по мнению автора | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука > Физика
| Похожие вопросы |
Электрический самовар потребляет силу тока 10 А. Какое количество теплоты выделится из его спирали за 0,5 ч, если он включён в цепь напряжением 220 В?
Какое количество теплоты выделится из его спирали за 0,5 ч, если он включён в цепь напряжением 220 В?
Вагонетка должна перевезти груз в…
Колебательный контур имеет индуктивность L=1.6 мГн
Решено
Задачи на ускорение
Решено
Задача
Что такое КПД двигателя? 3 фактора, влияющих на эффективность работы двигателя
Тепловой двигатель (машина) — это устройство, преобразующее внутреннюю энергию топлива в механическую работу, обмениваясь теплотой с окружающими телами. Большинство современных автомобильных, самолетных, судовых и ракетных двигателей сконструированы на принципах работы теплового двигателя. Работа производится за счет изменения объема рабочего вещества, а для характеристики эффективности работы любого типа двигателя используется величина, которая называется коэффициентом полезного действия (КПД).
Что такое КПД
Коэффициент полезного действия машины или механизма – это важная величина, характеризующая энергоэффективность данного устройства. Понятие используется и в повседневной жизни. Например, когда человек говорит, что КПД его усилий низкий, это значит, что сил затрачено много, а результата почти нет. Величина измеряет отношение полезной работы ко всей совершенной работе.
Понятие используется и в повседневной жизни. Например, когда человек говорит, что КПД его усилий низкий, это значит, что сил затрачено много, а результата почти нет. Величина измеряет отношение полезной работы ко всей совершенной работе.
Согласно формуле, чтобы найти величину, нужно полезную работу разделить на всю совершенную работу. Или полезную энергию разделить на всю израсходованную энергию. Этот коэффициент всегда меньше единицы. Работа и энергия измеряется в Джоулях. Поделив Джоули на Джоули, получаем безразмерную величину. КПД иногда называют энергоэффективностью устройства.
Если попытаться объяснить простым языком, то представим, что мы кипятим чайник на плите. При сгорании газа образуется определенное количество теплоты. Часть этой теплоты нагревает саму горелку, плиту и окружающее пространство. Остальная часть идет на нагревание чайника и воды в нем. Чтобы рассчитать энергоэффективность данной плитки, нужно будет разделить количество тепла, требуемое для нагрева воды до температуры кипения на количество тепла, выделившееся при горении газа.
Данная величина всегда ниже единицы. Например, для любой атомной электростанции она не превышает 35%. Причиной является то, что электростанция представляет собой паровую машину, где нагретый за счет ядерной реакции пар вращает турбину. Большая часть энергии идет на нагрев окружающего пространства. Тот факт, что η не может быть равен 100%, следует из второго начала термодинамики.
Асинхронные механизмы
Расшифровка термина «асинхронность» — несовпадение по времени. Понятие используется во многих современных машинах, которые являются электрическими и способны преобразовывать соответствующую энергию в механическую. Плюсы устройств:
- простое изготовление;
- низкая цена;
- надёжность;
- незначительные эксплуатационные затраты.
Чтобы рассчитать КПД, используется уравнение η = P2 / P1. Для расчёта Р1 и Р2 применяются общие данные потери энергии в обмотках мотора. У большинства агрегатов показатель находится в пределах 80−90%. Для быстрого расчёта используется онлайн-ресурс либо личный калькулятор. Для проверки возможного КПД у мотора внешнего сгорания, который функционирует от разных источников тепла, используется силовой агрегат Стирлинга. Он представлен в виде тепловой машины с рабочим телом в виде жидкости либо газа. Вещество движется по замкнутому объёму.
Для быстрого расчёта используется онлайн-ресурс либо личный калькулятор. Для проверки возможного КПД у мотора внешнего сгорания, который функционирует от разных источников тепла, используется силовой агрегат Стирлинга. Он представлен в виде тепловой машины с рабочим телом в виде жидкости либо газа. Вещество движется по замкнутому объёму.
Принцип его функционирования основан на постепенном нагреве и охлаждении объекта за счёт извлечения энергии из давления. Подобный механизм применяется на косметическом аппарате и современной подводной лодке. Его работоспособность наблюдается при любой температуре. Он не нуждается в дополнительной системе для запуска. Его КПД возможно расширить до 70%, в отличие от стандартного мотора.
Примеры расчета КПД
Пример 1. Нужно рассчитать коэффициент для классического камина. Дано: удельная теплота сгорания березовых дров – 107Дж/кг, количество дров – 8 кг. После сгорания дров температура в комнате повысилась на 20 градусов. Удельная теплоемкость кубометра воздуха – 1,3 кДж/ кг*град. Общая кубатура комнаты – 75 кубометров.
Общая кубатура комнаты – 75 кубометров.
Чтобы решить задачу, нужно найти частное или отношение двух величин. В числителе будет количество теплоты, которое получил воздух в комнате (1300Дж*75*20=1950 кДж ). В знаменателе – количество теплоты, выделенное дровами при горении (10000000Дж*8 =8*107 кДж). После подсчетов получаем, что энергоэффективность дровяного камина – около 2,5%. Действительно, современная теория об устройстве печей и каминов говорит, что классическая конструкция не является энергоэффективной. Это связано с тем, что труба напрямую выводит горячий воздух в атмосферу. Для повышения эффективности устраивают дымоход с каналами, где воздух сначала отдает тепло кладке каналов, и лишь потом выходит наружу. Но справедливости ради, нужно отметить, что в процессе горения камина нагревается не только воздух, но и предметы в комнате, а часть тепла выходит наружу через элементы, плохо теплоизолированные – окна, двери и т.д.
Пример 2. Автомобиль проделал путь 100 км. Вес машины с пассажирами и багажом – 1400 кг. При этом было затрачено14 литров бензина. Найти: КПД двигателя.
Вес машины с пассажирами и багажом – 1400 кг. При этом было затрачено14 литров бензина. Найти: КПД двигателя.
Для решения задачи необходимо отношение работы по перемещению груза к количеству тепла, выделившемуся при сгорании топлива. Количество тепла также измеряется в Джоулях, поэтому не придется приводить к другим единицам. A будет равна произведению силы на путь( A=F*S=m*g*S). Сила равна произведению массы на ускорение свободного падения. Полезная работа = 1400 кг x 9,8м/с2 x 100000м=1,37*108 Дж
Удельная теплота сгорания бензина – 46 МДж/кг=46000 кДж/кг. Восемь литров бензина будем считать примерно равными 8 кг. Тепла выделилось 46*106*14=6.44*108 Дж. В результате получаем η ≈21%.
От чего зависит величина КПД
Эта величина зависит от того, насколько общая совершенная работа может переходить в полезную. Прежде всего, это зависит от самого устройства механизма или машины. Инженеры всего мира бьются над тем, чтобы повышать КПД машин. Например, для электромобилей коэффициент очень высок – больше 90%.
А вот двигатель внутреннего сгорания, в силу своего устройства, не может иметь η, близкий к 100 процентам. Ведь энергия топлива не действует непосредственно на вращающиеся колеса. Энергия рассеивается на каждом передаточном звене. Слишком много передаточных звеньев, и часть выхлопных газов все равно выходит в выхлопную трубу.
Значения показателя
В 1824 году инженер Карно дал определение КПД идеального двигателя, когда коэффициент равен 100%. Для трактовки понятия была создана специальная машина со следующей формулой: η=(T1 — Т2)/ T1. Для расчёта максимального показателя применяется уравнение КПД макс = (T1-T2)/T1x100%. В двух примерах T1 указывает на температуру нагревателя, а T2 — температуру холодильника.
На практике для достижения 100% коэффициента потребуется приравнять температуру охладителя к нулю. Подобное явление невозможно, так как T1 выше температуры воздуха. Процедура повышения КПД источника тока либо силового агрегата считается важной технической задачей. Теоретически проблема решается путём снижения трения элементов двигателя и уменьшения теплопотери. В дизельном моторе подобное достигается турбонаддувом. В таком случае КПД возрастает до 50%.
Теоретически проблема решается путём снижения трения элементов двигателя и уменьшения теплопотери. В дизельном моторе подобное достигается турбонаддувом. В таком случае КПД возрастает до 50%.
Мощность стандартного двигателя увеличивается следующими способами:
- подключение к системе многоцилиндрового агрегата;
- применение специального топлива;
- замена некоторых деталей;
- перенос места сжигания бензина.
КПД зависит от типа и конструкции мотора. Современные учёные утверждают, что будущее за электродвигателями. На практике работа, которую совершает любое устройство, превышает полезную, так как определённая её часть выполняется против трения. Если используется подвижный блок, совершается дополнительная работа: поднимается блок с верёвкой, преодолеваются силы трения в блоке.
Мощность и КПД
Мощность механизма или устройства равна работе, совершаемой в единицу времени. Работа(A) измеряется в Джоулях, а время в системе Си – в секундах. Но не стоит путать понятие мощности и номинальной мощности. Если на чайнике написана мощность 1 700 Ватт, это не значит, что он передаст 1 700 Джоулей за одну секунду воде, налитой в него. Это мощность номинальная. Чтобы узнать η электрочайника, нужно узнать количество теплоты(Q), которое должно получить определенное количество воды при нагреве на энное количество градусов. Эту цифру делят на работу электрического тока, выполненную за время нагревания воды.
Но не стоит путать понятие мощности и номинальной мощности. Если на чайнике написана мощность 1 700 Ватт, это не значит, что он передаст 1 700 Джоулей за одну секунду воде, налитой в него. Это мощность номинальная. Чтобы узнать η электрочайника, нужно узнать количество теплоты(Q), которое должно получить определенное количество воды при нагреве на энное количество градусов. Эту цифру делят на работу электрического тока, выполненную за время нагревания воды.
Величина A будет равна номинальной мощности, умноженной на время в секундах. Q будет равно объему воды, умноженному на разницу температур на удельную теплоемкость. Потом делим Q на A тока и получаем КПД электрочайника, примерно равное 80 процентам. Прогресс не стоит на месте, и КПД различных устройств повышается, в том числе бытовой техники.
Напрашивается вопрос, почему через мощность нельзя узнать КПД устройства. На упаковке с оборудованием всегда указана номинальная мощность. Она показывает, сколько энергии потребляет устройство из сети. Но в каждом конкретном случае невозможно будет предсказать, сколько конкретно потребуется энергии для нагрева даже одного литра воды.
Но в каждом конкретном случае невозможно будет предсказать, сколько конкретно потребуется энергии для нагрева даже одного литра воды.
Например, в холодной комнате часть энергии потратится на обогрев пространства. Это связано с тем, что в результате теплообмена чайник будет охлаждаться. Если, наоборот, в комнате будет жарко, чайник закипит быстрее. То есть КПД в каждом из этих случаев будет разным.
Формула работы в физике
Для механической работы формула несложна: A = F x S. Если расшифровать, она равна приложенной силе на путь, на протяжении которого эта сила действовала. Например, мы поднимаем груз массой 15 кг на высоту 2 метра. Механическая работа по преодолению силы тяжести будет равна F x S = m x g x S. То есть, 15 x 9,8 x 2 = 294 Дж. Если речь идет о количестве теплоты, то A в этом случае равняется изменению количества теплоты. Например, на плите нагрели воду. Ее внутренняя энергия изменилась, она увеличилась на величину, равную произведению массы воды на удельную теплоемкость на количество градусов, на которое она нагрелась.
Решение примеров
Задача 1. Поезд на скорости 54 км/ч развивает мощность 720 кВт. Нужно вычислить силу тяги силовых агрегатов. Решение: чтобы найти мощность, используется формула N=F x v. Если перевести скорость в единицу СИ, получится 15 м/с. Подставив данные в уравнение, определяется, что F равно 48 kН.
Задача 2. Масса транспортного средства соответствует 2200 кг. Машина, поднимаясь в гору под уклоном в 0,018, проходит расстояние 100 м. Скорость развивается до 32,4 км/ч, а коэффициент трения соответствует 0,04. Нужно определить среднюю мощность авто при движении. Решение: вычисляется средняя скорость — v/2. Чтобы определить силу тяги мотора, выполняется рисунок, на котором отображаются силы, воздействующие на машину:
- тяжесть — mg;
- реакция опоры — N;
- трение — Ftr;
- тяга — F.
Первая величина вычисляется по второму закону Ньютона: mg+N+Ftr+F=ma. Для ускорения используется уравнение a=v2/2S. Если подставить последние значение и воспользоваться cos, получится средняя мощность. Так как ускорение считается постоянной величиной и равно 9,8 м/с2, поэтому v= 9 м/с. Подставив данные в первую формулу, получится: N= 9,5 kBt.
Так как ускорение считается постоянной величиной и равно 9,8 м/с2, поэтому v= 9 м/с. Подставив данные в первую формулу, получится: N= 9,5 kBt.
При решении сложных задач по физике рекомендуется проверить соответствие предоставленных в условиях единиц измерения с международными стандартами. Если они отличаются, необходимости перевести данные с учётом СИ.
Это интересно
Наукой обосновано, что коэффициент полезного действия любого механизма всегда меньше единицы. Это связано со вторым началом термодинамики.
Для сравнения, коэффициенты полезного действия различных устройств:
- гидроэлектростанций 93-95%;
- АЭС – не более 35%;
- тепловых электростанций – 25-40%;
- бензинового двигателя – около 20%;
- дизельного двигателя – около 40%;
- электрочайника – более 95%;
- электромобиля – 88-95%.
Наука и инженерная мысль не стоит на месте. постоянно изобретаются способы, как уменьшить теплопотери, снизить трение между частями агрегата, повысить энергоэффективность техники.
Глава 15. Работа газа в циклическом процессе. Тепловые двигатели. Цикл Карно
В программу школьного курса физики входит ряд вопросов, связанных с тепловыми двигателями. Школьник должен знать основные принципы работы теплового двигателя, понимать определение коэффициента полезного действия (КПД) циклического процесса, уметь находить эту величину в простейших случаях, знать, что такое цикл Карно и его КПД.
Тепловым двигателем (или тепловой машиной) называется процесс, в результате которого внутренняя энергия какого-то тела превращается в механическую работу. Тело, внутренняя энергия которого превращается двигателем в работу, называется нагревателем двигателя. Механическая работа в тепловых машинах совершается газом, который принято называть рабочим телом (или рабочим веществом) тепловой машины. При расширении рабочее тело и совершает полезную работу.
Для того чтобы сделать процесс работы двигателя циклическим, необходимо еще одно тело, температура которого меньше температуры нагревателя и которое называется холодильником двигателя. Действительно, если при расширении газ совершает положительную (полезную) работу (левый рисунок; работа газа численно равна площади «залитой» фигуры), то при сжатии газа он совершает отрицательную («вредную») работу, которая должна быть по абсолютной величине меньше полезной работы. А для этого сжатие газа необходимо проводить при меньших температурах, чем расширение, и, следовательно, газ перед сжатием необходимо охладить. На среднем рисунком показан процесс сжатия газа 2-1, в котором газ совершает отрицательную работу , абсолютная величина которой показана на среднем рисунке более светлой «заливкой». Чтобы суммарная работа газа за цикл была положительна, площадь под графиком расширения должна быть больше площади под графиком сжатия. А для этого газ перед сжатием следует охладить. Кроме того, из проведенных рассуждений следует, что работа газа за цикл численно равна площади цикла на графике
Действительно, если при расширении газ совершает положительную (полезную) работу (левый рисунок; работа газа численно равна площади «залитой» фигуры), то при сжатии газа он совершает отрицательную («вредную») работу, которая должна быть по абсолютной величине меньше полезной работы. А для этого сжатие газа необходимо проводить при меньших температурах, чем расширение, и, следовательно, газ перед сжатием необходимо охладить. На среднем рисунком показан процесс сжатия газа 2-1, в котором газ совершает отрицательную работу , абсолютная величина которой показана на среднем рисунке более светлой «заливкой». Чтобы суммарная работа газа за цикл была положительна, площадь под графиком расширения должна быть больше площади под графиком сжатия. А для этого газ перед сжатием следует охладить. Кроме того, из проведенных рассуждений следует, что работа газа за цикл численно равна площади цикла на графике
зависимости давления от объема, причем со знаком «плюс», если цикл проходится по часовой стрелке, и «минус» — если против.
Таким образом, двигатель превращает в механическую работу не всю энергию, взятую у нагревателя, а только ее часть; остальная часть этой энергии используется не для совершения работы, а передается холодильнику, т.е. фактически теряется для совершения работы. Поэтому величиной, характеризующей эффективность работы двигателя, является отношение
(15.1) |
где — работа, совершаемая газом в течение цикла, — количество теплоты, полученное газом от нагревателя за цикл. Отношение (15.1) показывает, какую часть количества теплоты, полученного у нагревателя, двигатель превращает в работу и называется коэффициентом полезного действия (КПД) двигателя.
Если в течение цикла рабочее тело двигателя отдает холодильнику количество теплоты (эта величина по своему смыслу положительна), то для работы газа справедливо соотношение . Поэтому существует ряд других форм записи формулы (15.1) для КПД двигателя
(15. |
Французский физик и инженер С. Карно доказал, что максимальным КПД среди всех процессов, использующих некоторое тело с температурой в качестве нагревателя, и некоторое другое тело с температурой ( ) в качестве холодильника, обладает процесс, состоящий из двух изотерм (при температурах нагревателя и холодильника ) и двух адиабат (см. рисунок).
Изотермам на графике отвечают участки графика 1-2 (при температуре нагревателя ) и 3-4 (при температуре холодильника ), адиабатам — участки графика 2-3 и 4-1. Этот процесс называется циклом Карно. КПД цикла Карно равен
(15.3) |
Теперь рассмотрим задачи. В задаче 15.1.1 необходимо использовать то обстоятельство, что работа газа в циклическом процессе численно равна площади цикла на графике зависимости давления от объема, причем со знаком «плюс», если цикл проходится по часовой стрелке, и «минус» — если против. Поэтому во втором цикле работа газа положительна, в третьем отрицательна. Первый цикл состоит из двух циклов, один из которых проходится по, второй — против часовой стрелки, причем, как следует из графика 1, площади этих циклов равны. Поэтому работа газа за цикл в процессе 1 равна нулю (правильный ответ — 2).
Поэтому во втором цикле работа газа положительна, в третьем отрицательна. Первый цикл состоит из двух циклов, один из которых проходится по, второй — против часовой стрелки, причем, как следует из графика 1, площади этих циклов равны. Поэтому работа газа за цикл в процессе 1 равна нулю (правильный ответ — 2).
Поскольку в результате совершения циклического процесса газ возвращается в первоначальное состояние (задача 15.1.2), то изменение внутренней энергии газа в этом процессе равно нулю (ответ 2).
Применяя в задаче 15.1.3 первый закон термодинамики ко всему циклическому процессу и учитывая, что изменение внутренней энергии газа равно нулю (см. предыдущую задачу), заключаем, что (ответ 3).
Поскольку работа газа численно равна площади цикла на диаграмме «давление-объем», то работа газа в процессе в задаче 15.1.4 равна (ответ 1). Аналогично в задаче 15.1.5 газ за цикл совершает работу (ответ 1).
Работа газа в любом процессе равна сумме работ на отдельных участках процесса. Поскольку процесс 2-3 в задаче 15.1.6 — изохорический, то работа газа в этом процессе равна нулю. Поэтому (ответ 3).
Поскольку процесс 2-3 в задаче 15.1.6 — изохорический, то работа газа в этом процессе равна нулю. Поэтому (ответ 3).
По определению КПД показывает, какую часть количества теплоты, полученного у нагревателя, двигатель превращает в работу (задача 15.1.7 — ответ 4).
Работа двигателя за цикл равна разности количеств теплоты, полученного от нагревателя и отданного холодильнику : . Поэтому КПД цикла есть
(задача 15.1.8 — ответ 3).
По формуле (15.3) находим КПД цикла Карно в задаче 15.1.9
(ответ 2).
Пусть температура нагревателя первоначального цикла Карно равна , температура холодильника (задача 15.1.10). Тогда по формуле (15.3) для КПД первоначального цикла имеем
Отсюда находим . Поэтому для КПД нового цикла Карно получаем
Поэтому для КПД нового цикла Карно получаем
(ответ 2).
В задаче 15.2.1 формулы (2), (3) и (4) представляют собой разные варианты записи определения КПД теплового двигателя (см. формулы (15.1) и (15.2)). Поэтому не определяет КПД двигателя только формула 1. (ответ 1).
Мощностью двигателя называется работа, совершенная двигателем в единицу времени. Поскольку работа двигателя равна разности полученного от нагревателя и отданного холодильнику количеств теплоты, имеем для мощности двигателя в задаче 15.2.2
(ответ 3).
По формуле (15.2) имеем для КПД двигателя в задаче 15.2.3
где — количество теплоты, полученное от нагревателя, — количество теплоты, отданное холодильнику (правильный ответ — 2).
Для нахождения КПД теплового двигателя в задаче 15.2.4 удобно использовать последнюю из формул (15.2). Имеем
где — работа газа, — количество теплоты, отданное холодильнику. Поэтому правильный ответ в задаче — 3.
Пусть газ совершает за цикл работу (задача 15.2.5). Поскольку количество теплоты, полученное от нагревателя равно ( — количество теплоты, отданное холодильнику), и работа составляет 20 % от этой величины, то для работы справедливо соотношение = 0,2 ( + 100). Отсюда находим = 25 Дж (ответ 1).
Поскольку работа теплового двигателя в задаче 15.2.6 равна 100 Дж при КПД двигателя 25 %, то двигатель получает от нагревателя количество теплоты 400 Дж. Поэтому он отдает холодильнику 300 Дж теплоты в течение цикла (ответ 4).
В задаче 15.2.7 газ получает или отдает теплоту только в процессах 1-2 и 3-1 (процесс 2-3 по условию адиабатический). |
Цикл, данный в задаче 15.2.8, состоит из двух изотерм 2-3 и 4-1 и двух изохор 1-2 и 3-4. Работа газа в изохорических процессах равна нулю. Сравним работы газа в изотермических процессах. Для этого удобно построить график зависимости давления от объема в рассматриваемом процессе, поскольку работа газа есть площадь под этим графиком. График зависимости давления от объема для заданного в условии процесса приведен на рисунке. Поскольку изотерме 2-3 соответствует бóльшая температура, чем изотерме 4-1, то она будет расположена выше на графике . Объем газа в процессе 2-3 увеличивается, в процессе 4-1 уменьшается. Таким образом, график процесса на графике проходится по часовой стрелке, и, следовательно, работа газа за цикл положительна (ответ 1). |
Для сравнения работ газа на различных участках процесса в задаче 15.2.9 построим график зависимости давления от объема. Этот график представлен на рисунке. Из рисунка следует, что работы газа в процессах 1-2 и 3-4 одинаковы по модулю (этим работам отвечают площади прямоугольников, «залитых» на рисунке светлой и темной «заливкой»). Работе газа на участке 4-1 отвечает площадь под графиком 4-1, которая меньше площади под графиком 1-2. Работе газа на участке 2-3 отвечает площадь под кривой 2-3 на рисунке, которая заведомо больше площади «залитых» прямоугольников. Поэтому в процессе 2-3 газ и совершает наибольшую по абсолютной величине (среди рассматриваемых процессов) работу (ответ 2.).
Согласно определению коэффициент полезного действия представляет отношение работы газа за цикл к количеству теплоты , полученному от нагревателя . Как следует из данного в условии задачи 15.2.10 графика, и в процессе 1-2-4-1 и в процессе 1-2-3-1 газ получает теплоту только на участке 1-2. Поэтому количество теплоты, полученное газом от нагревателя в процессах
Поэтому количество теплоты, полученное газом от нагревателя в процессах
1-2-4-1 и 1-2-3-1 одинаково. А вот работа газа в процессе 1-2-4-1 вдвое меньше (так площадь треугольника 1-2-4 как вдвое меньше площади треугольника 1-2-4-1). Поэтому коэффициент полезного действия процесса 1-2-4-1 вдвое меньше коэффициента полезного действия процесса 1-2-3-1 (ответ 1).
Общая физика II
Глава 22:
Вопросы 22:3, 4, 6, 16, 17
Задачи 22:1, 2, 6, 7, 8, 9, 11, 28, 31, 32, 41
Будьте уверены и сделайте
эти; делай не просто подожди
и смотреть мне делать их в
учебный класс!
Q22.3 Используйте первый закон термодинамики, чтобы объяснить, почему
полная энергия изолированной системы всегда постоянна.
Первый закон термодинамики
это просто переформулировка Энергосбережения.Если система
изолированы, над ним не совершается работа и теплота не передается ему или
от него. Энергия может передаваться от одной части системы
к другому, но полная энергия остается постоянной.
Q22.4 Можно ли преобразовать внутреннюю энергию в механическую
энергия?
Первый закон термодинамики касается именно этого.
Внутренняя энергия может быть использована для передачи энергии в
тепла или в виде работы.
Q22.6 В практических тепловых двигателях, над которыми у нас больше контроля, температура
горячего резервуара или температуры холодного резервуара? Объяснять.
Вероятно, низкая температура
будет температура окружающего воздуха — возможно,
температура охлаждающего пруда, реки или океана. Есть
мало контроля над любым из них. Горячая температура будет
температура горящего масла или угля или расщепления
Уран; это температура, которую мы можем контролировать.
Q22.16 Приведите пример природного процесса, который почти
обратимый.
Почти полное устранение трения
означает, что процесс почти обратим. Простой маятник это
обратимым до тех пор, пока мы не посмотрим на него достаточно внимательно, чтобы обнаружить
трение с воздуха. Медленное сжатие воздушного шара почти
обратимый.
Q22.17 Происходит термодинамический процесс, при котором энтропия
система изменяется на — 8,0 Дж/К. Согласно второму закону
термодинамики, какой вывод вы можете сделать об изменении энтропии
окружение?
Изменение энтропии
окружающая среда — окружающая среда, остальная часть Вселенной
вне нашей «системы» — должно быть +8,0 Дж/К или больше, чтобы
полная энергия Вселенной не уменьшается.
22.1 Тепловая машина поглощает 360 Дж тепловой энергии и работает
25 Дж работы в каждом цикле.
Найти (а) КПД двигателя
е = 25 Дж / 360 Дж
е = 0,069
e = 6,9%
и (b) тепловая энергия, выделяемая в каждом цикле.
1 — [Q c /Q h ] = e = 0,069
Q c /Q h = 1 — 0,069
Q с /Q ч = 0,931
Q c /Q h (0,931)
Q c = (360 Дж) (0,931)
Q c = 335 Дж
22.2 Тепловая машина совершает работу 200 Дж в каждом цикле и имеет
КПД 30%. За каждый цикл сколько тепловой энергии уходит
(а) поглощенные и
Q ч = Вт/е
Ом ч = 200 Дж/0,30
Q ч = 667 Дж
(б) исключен?
1 — [Q c /Q h ] = e = 0,30
Q c /Q h = 1 — 0,30
Q с /Q ч = 0,70
Q c = Q h (0,70)
Q c = (667 Дж) (0,70)
Q c = 467 Дж
22,6 Отдельный двигатель имеет выходную мощность 5,0 кВт и
КПД 25%. Если двигатель выделяет 8 000 Дж тепловой энергии
Если двигатель выделяет 8 000 Дж тепловой энергии
в каждом цикле найти
(a) теплота, поглощаемая в каждом цикле и
1 — [Q c /Q h ] = e = 0,25
Q c /Q h = 1 — 0,25
Q с /Q ч = 0,75
Q h = Q c /0,75
Q ч = 8000 Дж/0,75
Q ч = 10 667 Дж
(б) время каждого цикла.
Для каждого цикла
Вт = Q ч — Q c
Вт = 10 667 Дж — 8 000 ДжВт = 2 667 Дж = 2,667 кДж
Р = Вт/т
т
= Вт / Пт
= 2,667 кДж/5,0 кВтт
= 0,533 с
22.7 Двигатель поглощает 1600 Дж из горячего резервуара и выбрасывает
1 000 Дж в холодный резервуар в каждом цикле.
(а) Каков КПД двигателя?
е = 1 — [ 1000 Дж/1600 Дж]
е = 1 — 0,625
е = 0,375
е = 37,5%
(b) Какова выходная мощность двигателя, если каждый цикл длится
за 0,30 с?
Для каждого цикла
Вт = Q ч — Q c Вт = 1 600 Дж — 1 000 Дж
Вт = 600 Дж
Тогда мощность
P = Вт/т P = 600 Дж / 0,30 с
P = 2 000 Вт = 2 кВт
22.8 Тепловая машина работает между двумя резервуарами при
20 o C и 300 o C. Какова максимальная
возможный КПД для этого двигателя?
Из нашего исследования двигателей Карно мы знаем максимальное
эффективностьПомните, конечно, что эти температуры должны измеряться в
кельвины,Т с = 20°С = 293 К Т ч = 300°С = 573 К
е = 1 — [ 293 К/573 К]
е = 1 — 0,511
е = 0,489
е = 48,9%
22,9 Электростанция работает с КПД 32% в течение
летом, когда морская вода для охлаждения имеет температуру 20 o С.
завод использует пар 350 o C для привода турбин. Предполагая
эффективность установки изменяется в той же пропорции, что и идеальная
КПД, какова эффективность установки зимой, когда
морской воды в 10 или С?
Сначала рассчитайте КПД Карно для летнего периода.
и зима,е лето = 1 — [ 293
К / 623 К ]е лето = 1 — 0,470
е лето = 0,530
e зима = 1 — [283 К/623 К]
е зима = 1 — 0,454
e зима = 0,546
Соотношение = e Зима /e Лето
Соотношение = 0,546/0,530
Коэффициент = 1,03
То есть КПД Карно зимой в 1,03 раза
Эффективность Карно летом. Из-за более низких холодов
температуры эффективность Карно увеличивается на 3%.Если реальный
КПД изменяется на 3% — по сравнению с летним значением в 32% —
тогда мы ожидаем зимнюю эффективностьe зима /e лето = соотношение e зима /e лето = 1,03
e зима = 1,03 e лето
e зима = 1,03 (32%)
e зима = 33%
22.11 Предложена электростанция, которая будет использовать
температурный градиент в океане. Система должна работать
между 20 o C (температура поверхностной воды) и
5 o С (температура воды на глубине около 1 км).
(a) Какова максимальная эффективность такой системы?
Максимально возможная эффективность по методу Карно
эффективность,Т с = 5 о С = 278 К Т ч = 20 о С = 293 К
е = 1 — [ 278 К/293 К]
е = 1 — 0,949
е = 0,051
е = 5,1%
(b) Если выходная мощность станции составляет 75 МВт, сколько тепла
энергия поглощается в час?
Во-первых, сколько работы выполняется в час?
Вт = P т
Вт = (75 МВт) (1 час)
Вт = (75 x 10 6 Вт) [(Дж/с)/Вт] (1 час) [3 600
с/ч]
Вт = 2,7 x 10 12 Дж
Итак, сколько тепла необходимо для
обеспечить столько выходной работы?Q ч = Вт/Э
Ом ч = (2,7 х 10 12 Дж) / 0,051
Q h = 5,3 x 10 13 J
(c) Какой компенсирующий фактор сделал это предложение интересным
несмотря на значение КПД, рассчитанное в части (а)?Есть МНОГО морской воды! Температура
градиент в океане обеспечивает обильный источник энергии
хотя небольшой температурный градиент означает, что эффективность
очень низкий.22.14 Пар поступает в турбину при температуре 800 o С и
исчерпаны при 120 o С. Каков максимальный КПД
эта турбина?Т с = 120 о С = 393 К Т ч = 800 о С = 1073 К
е = 1 — [ 393 К/1073 К]
е = 1 — 0,366
е = 0,634
е = 63,4%
22.28 Как изменится энтропия, если 1 моль серебра (108
г) плавится при 961 o С?Сколько тепла потребуется, чтобы расплавить 108 г серебра?
Q = м лQ = (0,108 кг) (8,82 x 10 4 Дж/кг)
Q = 90,53 x 10 3 Дж
S = Q/T
Т = (273 + 961) К
Т = 1234 К
S = (9,53 x 10 3 Дж)/(1234 К)
S = 7,72 Дж/К
22.
31 Рассчитайте изменение энтропии 250 г нагретой воды.
медленно от 20 o С до 80 o С.(Подсказка: обратите внимание, что dQ = m c dT).
Это тепло добавляется при разных температурах, поэтому мы
должен брать интеграл,dQ = мк dT
22,32. Поднос содержит 500 г воды 0 O C.
изменение энтропии воды при ее полном и медленном замерзании при 0 o С.Сколько тепла требуется, чтобы заморозить 500 г воды
при 0°С?Q = м Lf
Q = (0,500 кг) (3,33 x 10 5 Дж/кг)
Q = 1,67 x 10 5 Дж
С
= Q/TС
= (1,67 х 10 5 Дж)/273 КС
= 610 Дж/К22,41 Кубик льда массой 18 г при 0,0 o С нагревают до
испаряется в виде пара.(а) Насколько увеличилась энтропия?
Сколько тепла требуется для растопить кубик льда
в воду при 0°С (или 273 К)?Q = м л f Q = (0,018 кг) (3,33 x 10 5 Дж/кг)
Q = 599 Дж
Это означает, что добавленная энтропия была
С
= Q/TС
= (599 Дж)/273 КС
= 2,2 Дж/КСколько энтропии добавляется при увеличении температуры от
0 o C до 100 o C (или 373 K)? Это как
задача 22.32, которую мы уже решили; это тоже из
конечно, требует интеграла.dQ = m c dT
Сколько теплоты требуется, чтобы испарить воду в
пара при 100 o С?
Q = м L vQ = (0,018 кг) (2,26 x 10 6 Дж/кг)
Q = 40 700 Дж
Это означает, что добавленная энтропия была
С =
К/ТТ = (100 + 273) К
С =
(40 700 Дж)/373 КС =
109 Дж/КСледовательно, общее изменение энтропии есть просто сумма
из этих частей:
С по
= [2,2 + 23,5 + 109] Дж/КС по
= 135 Дж/К(см.
Таблицу 20.2)
(b) Сколько энергии потребовалось, чтобы испарить кубик льда?
Мы уже сделали (почти) всю работу (т.е.
усилия) на этом, нам просто нужно собрать по кусочкамQ tot = Q расплавить + Q поднять
+ Q парQ поднять = m c T
Q поднять = (0,018 кг) (4186 Дж/кг-К) (100 К)
Ом поднять = 7535 Дж
Q tot = Q расплавить + Q поднять +
Q vapQ tot = 599 Дж + 7 535 Дж + 40 700 Дж
Q to = 48 834 Дж
Резюме
Ч33, Е-поля
Вернуться к
КП(с) Дуг Дэвис, 2002 г.
; все права защищены
Максимально возможная эффективность — Body Physics 2.0
Перейти к содержимому
Изменение энтропии для процесса с постоянной температурой можно рассчитать исходя из переданного тепла ( Q ) и температуры , при которой происходит перенос ( T ), как:
(1)
Обратите внимание, что нам определенно нужно использовать абсолютную шкалу температуры при работе с изменением уравнения, иначе мы можем обнаружить, что пытаемся делить на ноль! Что касается второго закона термодинамики, мы знаем, что для любого реального процесса сумма всегда должна быть больше нуля.
Повседневный пример: геотермальная тепловая машина
Давайте представим, что расплавленная порода из земной мантии частично проходит через земную мантию и поддерживает постоянную температуру в области 300 °C . Если бы скала была не слишком глубокой, мы могли бы проложить в скале трубы, а затем кипятить воду, пропуская ее по трубам. По сути, у нас была бы гигантская скороварка! Вместо того, чтобы готовить еду, мы могли бы выпускать сжатый пар, чтобы толкать поршень или вращать турбину. После сброса давления и некоторой работы у нас останется пар более низкого давления. Мы могли бы сконденсировать пар обратно в воду, пропуская его по трубам, открытым для 20 °C воздух над землей. Тепловая энергия будет передаваться от пара к воздуху в виде тепла выхлопных газов, пар сконденсируется в жидкую воду, и мы сможем начать все заново.
По сути, у нас была бы гигантская скороварка! Вместо того, чтобы готовить еду, мы могли бы выпускать сжатый пар, чтобы толкать поршень или вращать турбину. После сброса давления и некоторой работы у нас останется пар более низкого давления. Мы могли бы сконденсировать пар обратно в воду, пропуская его по трубам, открытым для 20 °C воздух над землей. Тепловая энергия будет передаваться от пара к воздуху в виде тепла выхлопных газов, пар сконденсируется в жидкую воду, и мы сможем начать все заново.
Цикл сухого пара из «Геотермальных электростанций» Energy Education, University of Calgary
Машины, подобные описанной, преобразующие тепловую энергию в механическую, называются тепловыми двигателями. Ваш автомобиль оснащен тепловым двигателем внутреннего сгорания. Давайте посмотрим, как Второй закон термодинамики определяет эффективность нашей геотермальной тепловой машины.
Сначала мы вычисляем изменение энтропии, когда 1000 Дж тепловой энергии передается от породы к воде для запуска двигателя, не забывая преобразовать температуру породы 300 °C в, добавив 273 К :
Если наш двигатель реален, то реальны и его процессы, а это означает, что работа двигателя должна увеличивать общую вселенную согласно второму закону термодинамики. Нам нужно выяснить, какое количество тепловой энергии должно быть передано от пара низкого давления в воздух при 20 °C (293 K ) для того, чтобы энтропия воздуха увеличилась по крайней мере на столько, на сколько уменьшилась энтропия горных пород (1,75 Дж/К ). Мы можем найти это, изменив уравнение изменения энтропии и подставив положительное изменение энтропии, равное по размеру отрицательному изменению, испытываемому горячим камнем:
Нам нужно выяснить, какое количество тепловой энергии должно быть передано от пара низкого давления в воздух при 20 °C (293 K ) для того, чтобы энтропия воздуха увеличилась по крайней мере на столько, на сколько уменьшилась энтропия горных пород (1,75 Дж/К ). Мы можем найти это, изменив уравнение изменения энтропии и подставив положительное изменение энтропии, равное по размеру отрицательному изменению, испытываемому горячим камнем:
только 487 J оригинала 1000 J входная энергия доступна для выполнения. Следовательно, максимально возможная эффективность нашего двигателя ограничена, независимо от того, насколько хорошо он спроектирован, даже если все механические неэффективности можно каким-то образом устранить. Максимальная теоретическая эффективность:
Умножив на 100 % , мы получим эффективность в процентах: 49 % .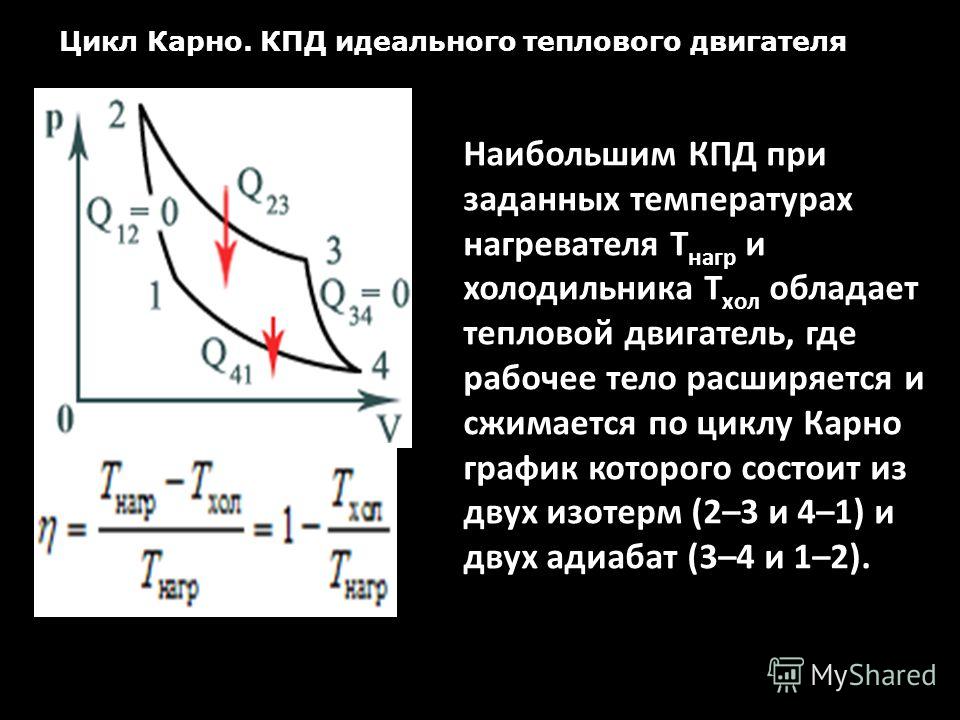 Это максимально возможная эффективность. Любой двигатель, который мы на самом деле построили, был бы менее эффективным.
Это максимально возможная эффективность. Любой двигатель, который мы на самом деле построили, был бы менее эффективным.
Первый закон термодинамики говорит нам, что вы не можете построить двигатель, который превышает 100 % эффективен, потому что энергия не может быть создана. Хуже того, второй закон говорит нам, что даже если нам удастся устранить все механические неэффективности, такие как , мы все равно не сможем достичь 100 % , потому что все двигатели должны расходовать некоторую энергию, чтобы в целом увеличить энтропию. Теоретический максимальный КПД, который всегда меньше 100 % , известен как ( e c ) и зависит только от высоких и низких рабочих температур (T H и T L ), как мы видели в предыдущем примере. Формула эффективности Карно ( e c ) эффективно воссоздает всю работу, которую мы проделали в предыдущем примере:
(2)
Теоретический двигатель, который мог бы обеспечить теоретически максимальную эффективность, известен как двигатель Карно. Принципы работы двигателя Карно хорошо известны, они были разработаны Николя Леонаром Сади Карно в 1824 году, но двигатель невозможно спроектировать или построить реалистично. [1]
Принципы работы двигателя Карно хорошо известны, они были разработаны Николя Леонаром Сади Карно в 1824 году, но двигатель невозможно спроектировать или построить реалистично. [1]
Дополнительное упражнение: КПД Карно
Убедитесь, что уравнение КПД Карно дает правильный максимальный КПД для нашего примера геотермальной тепловой машины.
Вы обнаружите, что этот двигатель более эффективен только потому, что горячая рабочая температура выше, хотя он по-прежнему работает так же, и больше ничего не изменилось. Эффективность увеличилась, потому что входная энергия вначале была более концентрированной и менее рассеянной (на что указывает более высокая температура), поэтому меньше этой энергии должно было быть рассеяно в окружающей среде, чтобы обеспечить увеличение энтропии на величину, достаточную для удовлетворения второго закона. Термодинамика. По этой причине говорят, что тепловая энергия, которая вначале более концентрирована (при высокой температуре), составляет более качественная энергия.
Упражнение с подкреплением:
- «Тепловая машина Карно» из Википедии ↵
Лицензия
Физика тела 2.0 Лоуренса Дэвиса находится под лицензией Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, если не указано иное.
Поделиться этой книгой
Поделиться в Твиттере
Эффективность двигателя
Aero: как далеко мы можем продвинуться? — ИННОВАЦИИ
8 января 2015 г., автор Andrea Bristot
Современные производители авиадвигателей испытывают растущее давление со стороны клиентов и государственных учреждений с целью снижения расхода топлива. Потребность авиакомпаний в минимизации эксплуатационных расходов в сочетании с общим стремлением иметь «более экологичные» двигатели (как четко указано в целях ACARE ЕС и FAA США) требует, чтобы отрасль авиационных двигателей была одной из самых передовых областей исследований в мире. инженерия. Высокая конкуренция между производителями еще больше расширяет возможности новых технологий для снижения расхода топлива, выбросов, шума и затрат на техническое обслуживание. Но как еще мы можем увеличить тепловой цикл реактивного двигателя, чтобы повысить эффективность?
Но как еще мы можем увеличить тепловой цикл реактивного двигателя, чтобы повысить эффективность?
Из законов термодинамики мы знаем, что для получения полезной работы от тепловой машины нам необходимо сжать рабочее тело (в нашем случае воздух), нагреть его, а затем преобразовать энергию горячих газов в механическую и кинетическую энергия. Другими словами: сосать, сжимать, сжигать и дуть.
Рисунок 1 – Упрощенный принцип работы газовой турбины
Насколько хорошо мы преобразовываем тепловую энергию горящей топливно-воздушной смеси в полезную энергию, будет определять эффективность нашей машины. Наш путь теперь разделяется между тем, что мы может получить топливо и что мы можем получить на самом деле.
Во-первых, еще раз: законы термодинамики в простой форме помогают нам. Для идеального цикла Брайтона, лежащего в основе принципа работы реактивных двигателей, мы обнаруживаем, что тепловой КПД увеличивается по мере увеличения отношения давлений между камерой сгорания и внешней атмосферой. Корреляция не является линейной, что означает, что увеличение коэффициента давления должно быть постепенно больше, чтобы сделать следующий шаг в повышении эффективности.
Корреляция не является линейной, что означает, что увеличение коэффициента давления должно быть постепенно больше, чтобы сделать следующий шаг в повышении эффективности.
Если мы добавим некоторые числа в наше уравнение, мы обнаружим, что для текущего значения коэффициента сжатия 50, достижимого в новейших коммерческих двигателях, идеальный тепловой КПД (например, соотношение между полезной мощностью работы и тепловложением) составляет порядка 67%. Чтобы достичь порога 70%, нам нужно подняться до значения степени сжатия 68. Это означает, что степень повышения давления на 36% выше для повышения эффективности на 3%, и подразумевает серьезные технические проблемы.
Теперь наша задача переходит ко второй части пути, то есть к реальный КПД двигателя. Этот параметр количественно определяет фактическую производительность машины по отношению к подводимому теплу. Следовательно, с практической точки зрения полезнее понять, насколько хорошо двигатель преобразует доступную энергию в полезную работу. Теперь в игру вступают многие другие параметры.
Теперь в игру вступают многие другие параметры.
Прежде всего, расход топлива двигателем во время полета будет зависеть от того, насколько хорошо мы преобразуем энергию газа в тягу, которая количественно определяется тяговой эффективностью. Максимальная тяговая эффективность достигается, когда выхлопные газы имеют ту же скорость, что и окружающий воздух, что, конечно, является идеальным условием. Мы можем повысить тяговую эффективность, увеличив размер вентилятора, что примерно эквивалентно оснащению аквалангиста более длинными ластами: массовый поток, проходящий через двигатель, будет больше, но выбрасывается с меньшей скоростью.
Произведение между реальным тепловым КПД и тяговым КПД дает желаемый результат, например. общий КПД двигателя, который выражается в скорости сжигания топлива. Поскольку параметров, влияющих на общую эффективность, несколько, были разработаны соответствующие программы для расчета ее значения. Один простой и полезный инструмент для количественной оценки влияния различных параметров на эффективность реактивного двигателя предоставляется НАСА и доступен здесь.
Испытание, проведенное с помощью этого инструмента с использованием актуальных входных данных, дало общую эффективность около 50% для самолета в крейсерском режиме. Это хороший результат, но он очень далек от идеальных 67%. Куда ушла оставшаяся энергия?
Часть его, как объяснялось выше, отсутствует из-за далекой от идеала тяговой эффективности. Следовательно, он теряется при смешении выбрасываемых двигателем газов с окружающим воздухом в результате турбулентных столкновений частиц воздуха.
Еще одна отсутствующая часть связана с эффективностью компонентов внутри двигателя, которая не так идеальна, как хотелось бы. На самом деле воздух трудно сжимать; он имеет тенденцию нагреваться и, следовательно, рассеивает часть подводимой энергии в виде тепла. Само сгорание приводит к потерям энергии, и хотя в настоящее время сгорает почти 100% топлива, небольшие его порции могут улетучиваться из камеры сгорания. Наконец, суровые условия в турбине приводят к необходимости систем охлаждения, что достигается ценой потерь энергии. Кроме того, все подсистемы внутри двигателя, такие как шестерни, электрические системы, пневматические системы и масляные системы, предполагают отбор мощности.
Кроме того, все подсистемы внутри двигателя, такие как шестерни, электрические системы, пневматические системы и масляные системы, предполагают отбор мощности.
Имея все это в виду, мы находим три варианта увеличения общего КПД двигателя:
- увеличение идеального теплового КПД, следовательно, верхний предел, который может быть достигнут
- увеличить эффективность тяги
- приближает реальный тепловой КПД к идеальному значению
Во-первых, все, что нам в идеале нужно сделать, это увеличить общую степень сжатия двигателя (OPR). Хотя это может показаться простым, связанные с этим технические проблемы значительны: чем больше мы сжимаем воздух, тем выше его температура. Это подразумевает высокое тепловыделение, что означает повышенные потери энергии в компрессоре. Более того, по мере уменьшения объема воздуха лопатки компрессора будут постепенно укорачиваться до точки, в которой зазор между лопаткой и стенками становится значительной частью длины лопатки, что приводит к недопустимым обратным потокам воздуха. Для решения этих проблем необходимо создать новую архитектуру, включающую промежуточные охладители и компрессоры малого диаметра.
Для решения этих проблем необходимо создать новую архитектуру, включающую промежуточные охладители и компрессоры малого диаметра.
Рисунок 2. Некоторые концепции двигателей с высоким OPR. Источник: NEWAC
Чтобы ответить на наш второй вопрос, т.е. с увеличением эффективности тяги, текущая тенденция заключается в переходе к более крупным вентиляторам, тем самым увеличивая их вклад в общую тягу. В этом случае задача состоит в том, чтобы позволить вентилятору и приводящей его турбине вращаться с оптимальной скоростью.
Возможность разделения скоростей вращения была недавно достигнута компанией Pratt & Whitney, которая разработала в сотрудничестве с Avio систему привода вентилятора, способную обрабатывать крутящий момент, создаваемый турбиной низкого давления, для своего семейства двигателей PurePower среднего диапазона. Учитывая осуществимость и обоснованность этой системы, компания Rolls-Royce недавно объявила, что она также применит силовую коробку передач в своей концепции двигателя дальнего действия UltraFan.
Последним из трех наших пунктов является повышение КПД компонентов, чтобы приблизить реальный тепловой КПД к соответствующему идеальному значению. Этого можно добиться за счет улучшения конструкции таких компонентов, как компрессор, камера сгорания и турбина, лучшего управления температурой ядра двигателя, инновационных материалов и рационализации отбора мощности. Для последней цели в отрасли была разработана тенденция к увеличению количества ядер электрических двигателей с целью упрощения архитектуры двигателя за счет удаления или, по крайней мере, уменьшения размеров пневматических, гидравлических и механических отводов. Значительная часть деятельности Университета Ноттингема в рамках его Исследовательской группы по силовой электронике, машинам и управлению направлена на изучение и разработку технологий для этой цели. Другие проекты, направленные на повышение эффективности ядра авиадвигателя, являются частью рабочего пакета 1 программы INNOVATE. Эти проекты касаются разработки технологий для улучшенных масляных систем и герметизации воздуха, а также предусматривают интеграцию нового электрического оборудования в активную зону.
В заключение следует отметить, что отрасль авиационных двигателей сталкивается с серьезными постоянными проблемами, связанными с разработкой более экономичных двигателей. Верхняя граница предела энергоэффективности устанавливается законами термодинамики, которые дают нам точное значение того, как далеко мы можем продвинуться с нашим текущим циклом двигателя.
На данный момент инвестиции направлены на повышение эффективности компонентов и подсистем двигателя, а также повышение эффективности тяги. Возможности для улучшения в этом смысле, хотя и ограничены, по-прежнему многообещающи и позволяют архитектуре авиационных двигателей развиваться постепенно, с небольшим количеством рискованных отклонений от хорошо зарекомендовавших себя, надежных базовых конструкций.
Однако с исследовательской точки зрения изучаются все концепции, которые могли бы дать значительный скачок в плане конструкции и эффективности использования топлива, так что в далеком будущем архитектура двигателей может значительно измениться, чтобы обеспечить более сложные, энергосберегающие эффективные циклы, включая промежуточное охлаждение и регенерацию.
Опубликовано в
Аэрокосмическая промышленностьINNOVATE
- Поделиться через фейсбук
- Поделиться в Твиттере
- Поделиться в Google+
- Поделиться в LinkedIn
КПД при максимальной мощности двигателя с пассивным поршнем | Успехи теоретической и экспериментальной физики
Журнальная статья
Томохико Г. Сано,
Томохико Г. Сано
*
† Текущий адрес: Факультет физики, Университет Рицумейкан, Кусацу, Сига 525-8577, Япония. Электронная почта: [email protected]
Ищите другие работы этого автора на:
Оксфордский академический
Google ученый
ОБЪЯВЛЕНИЯ
Хисао Хаякава
Хисао Хаякава
Ищите другие работы этого автора на:
Оксфордский академический
Google ученый
ОБЪЯВЛЕНИЯ
Примечания автора
Progress of Theoretical and Experimental Physics , Volume 2016, Issue 8, August 2016, 083A03, https://doi. org/10.1093/ptep/ptw103
org/10.1093/ptep/ptw103
Опубликовано:
29 августа 2016
История статьи
Получен:
15 марта 2016 г.
Полученная ревизия:
16 июня 2016 г.
Принято:
22 июня 2016 г.
Опубликовано:
29 августа 2016
Фильтр поиска панели навигации
Progress of Theoretical and Experimental PhysicsЭтот выпускA47 Другие темы равновесной статистической механикиA50Случайные процессы, стохастические модели и протеканияA56Нелинейные и неравновесные явленияA58Другие темы неравновесной статистической механикиJPS JournalsPhysicsBooksJournalsOxford Academic
Термин поиска мобильного микросайта
Закрыть
Фильтр поиска панели навигации
Progress of Theoretical and Experimental PhysicsЭтот выпускA47 Другие темы равновесной статистической механикиA50Случайные процессы, стохастические модели и протеканияA56Нелинейные и неравновесные явленияA58Другие темы неравновесной статистической механикиJPS JournalsPhysicsBooksJournalsOxford Academic
Термин поиска на микросайте
Advanced Search
Abstract
Теоретически исследуется КПД двигателя с пассивным поршнем без механического управления между двумя резервуарами при максимальной мощности (MP). Мы помещаем твердый газ, разделенный массивным поршнем, в контейнер с контролируемой температурой и анализируем эффективность при MP в соответствии с протоколом нагрева и охлаждения без контроля давления, действующего на поршень извне. Мы получаем следующие три результата: (i) эффективность при МП для разбавленного газа близка к эффективности Чамбадала–Новикова–Керзона–Альборна (CNCA), если мы можем пренебречь боковым трением и потерей энергии между газовой частицей и поршень, а (ii) эффективность для умеренно плотного газа становится меньше, чем эффективность CNCA, даже когда разница температур резервуаров мала. (iii) Вводя матрицу Онзагера для двигателя с пассивным поршнем, убеждаемся, что условие жесткой связи для матрицы разбавленного газа выполняется, а для умеренно плотного газа не выполняется из-за неизбежной утечки тепла. Мы подтверждаем достоверность этих результатов, используя моделирование молекулярной динамики и вводя эффективную модель, подобную среднему полю, которую мы называем стохастической моделью среднего поля.
Мы помещаем твердый газ, разделенный массивным поршнем, в контейнер с контролируемой температурой и анализируем эффективность при MP в соответствии с протоколом нагрева и охлаждения без контроля давления, действующего на поршень извне. Мы получаем следующие три результата: (i) эффективность при МП для разбавленного газа близка к эффективности Чамбадала–Новикова–Керзона–Альборна (CNCA), если мы можем пренебречь боковым трением и потерей энергии между газовой частицей и поршень, а (ii) эффективность для умеренно плотного газа становится меньше, чем эффективность CNCA, даже когда разница температур резервуаров мала. (iii) Вводя матрицу Онзагера для двигателя с пассивным поршнем, убеждаемся, что условие жесткой связи для матрицы разбавленного газа выполняется, а для умеренно плотного газа не выполняется из-за неизбежной утечки тепла. Мы подтверждаем достоверность этих результатов, используя моделирование молекулярной динамики и вводя эффективную модель, подобную среднему полю, которую мы называем стохастической моделью среднего поля.
1. Введение
Равновесная термодинамика раскрывает связь между работой и теплом, а также верхнюю границу для извлеченной работы из произвольного теплового цикла [1,2]. Вехой равновесной термодинамики является то, что термодинамическая эффективность для любого теплового цикла между двумя резервуарами, характеризуемого температурами TH и TL(TH>TL), ограничена эффективностью Карно: ηC≡1−TL/TH, достигаемой при квазистатической работе [3]. ]. Существует множество исследований эффективности двигателей, в том числе двигателей как внешнего, так и внутреннего сгорания. К первой категории относятся паровые двигатели и паровые турбины, идеальными циклами которых являются цикл Карно, цикл Стирлинга и т. д. [3,4]. Примерами последних являются дизельные и свободнопоршневые двигатели, а их идеальными циклами являются цикл Отто, цикл Брайтона и т. д. [5,6]. Также известно, что максимальный КПД идеальных двигателей внешнего сгорания равен ηC, а идеальных двигателей внутреннего сгорания обычно меньше ηC. С практической точки зрения двигатель с ηС бесполезен, так как его мощность равна нулю.
С практической точки зрения двигатель с ηС бесполезен, так как его мощность равна нулю.
Распространение термодинамики на операции с конечным временем, так называемая термодинамика с конечным временем, исследовалась многими авторами [7–35]. Шамбадал и Новиков независимо друг от друга предложили, а позже Керзон и Альборн заново открыли, что КПД при максимальной выходной мощности (MP) определяется эффективностью Чамбадала–Новикова–Керзона–Альборна (CNCA): ηCA≡1–TL/TH [7–13]. ]. Недавно было обнаружено, что Reitlinger первоначально предложил ηCA в 1929 году [7,8]. Справедливость эффективности CNCA вблизи равновесия была подтверждена линейной необратимой термодинамикой [17], молекулярной кинетикой [18,19] или предположение о низкой диссипации [20]. Считается, что эффективность CNCA — это, вообще говоря, только эффективность при МП, близких к равновесным ситуациям. Действительно, есть много ситуаций, которые превышают эффективность CNCA в идеализированных установках [18,20,22]. Хотя существует несколько исследований термодинамики с конечным временем, включая двигатели внешнего и внутреннего сгорания или флуктуационные тепловые двигатели [31–35], они в основном интересуются двигателями с силовым управлением [18,19,21–24,27–32,34,35]. ], где поршень или потенциал разделения управляются внешним агентом. С другой стороны, КПД при СД для двигателя, разделенного пассивным поршнем без внешнего силового управления, до настоящего времени подробно не изучался.
], где поршень или потенциал разделения управляются внешним агентом. С другой стороны, КПД при СД для двигателя, разделенного пассивным поршнем без внешнего силового управления, до настоящего времени подробно не изучался.
Целью данной статьи является уточнение КПД при МР для двигателя с пассивным поршнем, который представляет собой идеализированную модель двигателя внутреннего сгорания без механического управления. Рассмотрим газ с твердым ядром, заключенный массивным поршнем в камере, где поршень свободно перемещается в одном направлении за счет перепада давления (см. рис. 1). Мы используем молекулярно-динамическое (МД) моделирование твердых газов ядра, чтобы исследовать теоретически полученную эффективность в МП на основе эффективной модели, которую мы называем моделью стохастического среднего поля (СМП).
Рис. 1.
Открыть в новой вкладкеСкачать слайд
Схематическое изображение нашей установки, где N одинаковых частиц твердого ядра заключены в контейнер, разделенный адиабатическим поршнем массы M при x=Xˆ. Плотность nout и температура Tout для внешнего газа x>Xˆ поддерживаются постоянными. Температура Tbath тепловой стенки при x=0 регулируется внешним агентом, а термодинамические величины, такие как плотность nˆin и температура Tˆin, флуктуируют во времени.
Плотность nout и температура Tout для внешнего газа x>Xˆ поддерживаются постоянными. Температура Tbath тепловой стенки при x=0 регулируется внешним агентом, а термодинамические величины, такие как плотность nˆin и температура Tˆin, флуктуируют во времени.
Поскольку рассматриваемый нами двигатель является двигателем внутреннего сгорания, максимальный КПД меньше, чем КПД Карно. Наше исследование актуально по следующим двум причинам. Во-первых, мы можем найти много ситуаций, когда прямое механическое управление поршнем затруднено. Например, конструкция двигателей внутреннего сгорания обычно слишком сложна для обеспечения внутреннего механического управления [6]. Поэтому необходимо выяснить влияние неуправляемого движения поршня на КПД. Во-вторых, изучение двигателей с пассивными поршнями важно даже для термодинамики с конечным временем. При отсутствии механического управления поршнем или перегородкой, поток тепла при креплении тепловой перегородки неизбежен. Поскольку в традиционной термодинамике конечного времени тепловой поток из резервуара обычно не учитывается, важно проверить, остаются ли существующие теоретические результаты неизменными при наличии такого теплового потока [10–32]. Действительно, мы покажем, что обычные результаты справедливы для нашей системы только тогда, когда поток тепла пренебрежимо мал, как в разбавленных газах. Таким образом, мы считаем, что наше исследование для простейшего двигателя с пассивным поршнем с термодинамической точки зрения является важным.
Действительно, мы покажем, что обычные результаты справедливы для нашей системы только тогда, когда поток тепла пренебрежимо мал, как в разбавленных газах. Таким образом, мы считаем, что наше исследование для простейшего двигателя с пассивным поршнем с термодинамической точки зрения является важным.
Структура этого документа следующая. Мы объясняем нашу установку и протокол работы для температуры термостены Tbath в разд. 2. Мы вводим SMF в разд. 3 для анализа мощности и эффективности. Мы исследуем достоверность SMF в разд. 4, сравнивая временную эволюцию симуляции MD и SMF. В разд. 5, мы теоретически получаем КПД при МП для наших двигателей, содержащих разбавленные твердые газы, который близок к КПД CNCA в пределе массивного поршня. Мы также находим, что эффективность при МП для умеренно плотных газов меньше, чем эффективность CNCA даже в линейном неравновесном режиме. В разд. 6, для уточнения эффективности в линейном неравновесном режиме мы явно выводим матрицу Онзагера. Мы также разъясняем влияние конечной плотности на КПД и подчеркиваем важность теплового потока, когда связываем ванну при Tbath с эффективностью при MP. Мы обсуждаем разницу между нашими результатами и предыдущими результатами в разд. 7, и завершите статью некоторыми замечаниями в разд. 8. В Приложении A мы показываем часть вывода SMF. В Приложении B мы обсуждаем временную эволюцию температурного профиля после присоединения горячего резервуара. В Приложении C обсуждается определение работы и теплоты для нашей системы. В Приложении D изучается влияние массы поршня и неупругости поршня, а влияние трения о боковые стенки на поршень обсуждается в Приложении E. В этой статье переменные со знаком « ˆ» обозначают стохастические переменные.
Мы обсуждаем разницу между нашими результатами и предыдущими результатами в разд. 7, и завершите статью некоторыми замечаниями в разд. 8. В Приложении A мы показываем часть вывода SMF. В Приложении B мы обсуждаем временную эволюцию температурного профиля после присоединения горячего резервуара. В Приложении C обсуждается определение работы и теплоты для нашей системы. В Приложении D изучается влияние массы поршня и неупругости поршня, а влияние трения о боковые стенки на поршень обсуждается в Приложении E. В этой статье переменные со знаком « ˆ» обозначают стохастические переменные.
2. Установка
В нашей системе N частиц твердого ядра массой m и диаметром din заключены в трехмерный контейнер, разделенный адиабатическим поршнем массы M и площадью A справа от x- направление, диатермическая стена, прикрепленная к термальной ванне с левой стороны от направления x, и четыре адиабатических стенки в других направлениях (рис. 1). Существует постоянное давление, удовлетворяющее условию Pout=noutTout снаружи поршня (правая сторона поршня). Плотность nout и температура Tout для внешнего газа x>X поддерживаются постоянными. Будем считать, что адгезией между частицами и стенками контейнера, а также между частицами можно пренебречь. Предполагается, что поршень движется в одном направлении без трения о боковые стенки. Скорость после столкновения (v′,V′) и скорость до столкновения (v,V) в направлении x для сталкивающейся частицы и поршня связаны соотношением:
1). Существует постоянное давление, удовлетворяющее условию Pout=noutTout снаружи поршня (правая сторона поршня). Плотность nout и температура Tout для внешнего газа x>X поддерживаются постоянными. Будем считать, что адгезией между частицами и стенками контейнера, а также между частицами можно пренебречь. Предполагается, что поршень движется в одном направлении без трения о боковые стенки. Скорость после столкновения (v′,V′) и скорость до столкновения (v,V) в направлении x для сталкивающейся частицы и поршня связаны соотношением:
v′(v,V)=v−1mPv,
(1)
V′(v,V)=V+1MPv,
(2)
где вклад горизонтального движения частиц в стена аннулируется в результате статистического усреднения. Здесь Pv=Pv(V)≡M(V′−V)=(1+e)mM(v−V)/(m+M) представляет изменение импульса поршня из-за столкновения для частицы со скоростью v, где e — коэффициент восстановления между частицами и поршнем. Причина введения коэффициента реституции состоит в том, что стенка состоит из макроскопического числа частиц и часть импульса каждого столкновения может поглощаться стенкой как возбуждение внутренних колебаний.
Причина введения коэффициента реституции состоит в том, что стенка состоит из макроскопического числа частиц и часть импульса каждого столкновения может поглощаться стенкой как возбуждение внутренних колебаний.
Примем правило отражения Максвелла для столкновения частицы с диатермической стенкой, присоединенной к ванне при Тванн. Скорость после столкновения v′=(vx’,vy’,vz’) к стенке при x=0 выбирается как случайная величина, подчиняющаяся распределению
φwall(v’,Tbath)=12π(mTbath)2vx’ exp[−mv′22Tbath],
(3)
, область определения которого определяется как 0 Рассмотрим тепловой цикл для процессов нагрева Tванна=TH>Tвых и охлаждения Tванна=TL=Tвых (рис. 2). Первоначально замкнутый газ и газ снаружи находятся в состоянии механического равновесия, которое удовлетворяет условиям Pˆin=Pout и Tˆin=Tout=Tbath. При t=0 на диатермическую стенку прикрепляем тепловую баню при TH. Рис. 2. Открыть в новой вкладкеСкачать слайд Схематические рисунки протокола операции. К диатермической стенке при t=0 прикрепляем тепловую баню при TH. (a) При 0 Предположим, что частицы упруго сталкиваются друг с другом и с боковыми стенками. Правило столкновения между поршнем и частицей определяется уравнениями. (1) и (2). Мы вводим типичные масштабы длины и времени как Xini≡NTout/PoutA и t0≡XiniM/Tout для дальнейшего удобства. Количество частиц N=200 фиксировано на протяжении всей симуляции. Сила столкновения снаружи поршня моделируется Fˆout, как будет определено в уравнении. (6). Введем модель стохастического среднего поля (SMF) для описания динамики поршня и энергетического баланса нашей системы с использованием двух независимых стохастических переменных: флуктуирующей плотности nˆin(t)=N /AXˆ(t) и флуктуации температуры Tˆin(t). Причина, по которой мы называем нашу модель SMF, заключается в том, что поршень движется стохастическим образом из-за импульсов твердых частиц, и мы усредняем пространственную неоднородность газа. dnˆindt = −nˆinxˆvˆvˆ, (4) Mdvˆdt = fˆin+fˆout, (5) , где стохастическая сила fˆν (ν = in, Out) вводится как 9000 3 Fˆν=. (t|Vˆ,nˆν,Tˆν). (6) Здесь ξˆinv и ξˆoutv обозначают пуассоновские шумы единичной амплитуды, вероятности событий которых соответственно равны +4Φˆg0(Φˆ)} , (7) λoutv≡dv|v−Vˆ|Θ(Vˆ−v)noutφ0(v,Tout), (8) , где мы ввели радиальную функцию распределения на контакте g0 [36]. Символ «⋅» в уравнении (6) представляет собой стохастический продукт типа Ито [37–39]. Θ(x) — функция Хевисайда, удовлетворяющая Θ(x)=1 при x≥0 и Θ(x)=0 при x<0. Плотность и температура газа снаружи поддерживаются постоянными во времени, т. Pˆin=nˆinTˆin(1+4Φˆg0(Φˆ)). (9) Далее мы предлагаем временную эволюцию для Tˆin. Дифференциал внутренней энергии для газа uˆin 3ntˆin/2 определяется как duˆin = dqˆwall+deˆpis, (10) dqˆwall®dqˆ0+dqˆj, (11) dqˆ0dtinin −Tˆin)2Tˆinπm, (12) dEˆpisdt≡∑vm2{v′2(v,Vˆ)−v2}⋅ξˆinv(Vˆ,nˆin,Tˆin), (13) dQˆJ=−45π64JˆinAdt. (14) Здесь dQˆwall обозначает полный тепловой поток от термальной ванны при Tbath, dQˆJ обозначает тепловой поток от внутренней теплопроводности Jin, а dQˆ0 представляет остаточный тепловой поток dQˆ0=dQˆwall−dQˆJ [18]. ,19]. dEˆpis обозначает передачу кинетической энергии от поршня к газу. Таким образом, основная часть нашей модели SMF состоит из двух связанных уравнений: уравнения движения поршня (5) и уравнения энергии замкнутого газа (10). В приложении A мы выводим уравнения. (11), (12) и (14). Тепловой поток Jin оценивается из решения уравнения диффузии тепла для профиля температуры T=T(x,t): ∂T∂t−κn∂2T∂x2=0, (15) при условии, что теплопроводность κ и плотность nˆin=n являются постоянными в пространстве и времени, где положение поршня зафиксировано при Xˆ=L. Наложение граничных условий T(x,t=0)≡Tini, T(x=0,t)=Tbath и ∂xT(x=L,t)=0 на уравнение. (16) Предполагая, что Tini, L, κ и n изменяются во времени адиабатически, т. е. Tini→Tˆin(t), L→Xˆ(t), κ→κˆ(Φˆ(t) ,Tˆin(t)) [40,41] и n→nˆin(t), получаем приблизительный тепловой поток Jin=∫0L−κ∂xT(x,t)dx/L как Jˆin(t) =4κˆπXˆ(t)(Tbath−Tˆin(t))∑l=1∞sin(lπ/2)leexp[−(lπ2Xˆ(t))2κˆtnˆin], (17) где мы приняли выражения из работ . [40,41] для зависимости теплопроводности от плотности и температуры κˆ(Φ,T)=(75T/π/64mdin2g0(Φ))[{1+(12Φg0(Φ)/5)}2+(4608Φ2g0( Φ)/225π)]. Поскольку теплопроводность быстро релаксирует до стационарного состояния для разбавленного газа, мы можем упростить уравнение. (10) как dUˆin=dQˆ0+dEˆpis, (18) хотя теплопроводность существует. Рис. 3. Открыть в новой вкладкеСкачать слайд Сравнение SMF и SMF без теплопроводности (без конв.) для din/A=0,01 и tc/t0=1,60. Начальная объемная доля рассчитана как Φ=1,05×10-4. Сплошная линия и кресты представляют динамику температуры для СМЖ и разбавленной версии СМЖ соответственно. На вставке представлена подробная временная эволюция для 0 Численное интегрирование выполняется методом Адамса–Башфорта с dt/t0≡0,01ϵ и ϵ≡m/M. Чтобы проверить правильность модели SMF, мы сравним эволюцию во времени моделирования MD и SMF. Мы рассматриваем разбавленные и умеренно плотные газы в разд. 4.1 и 4.2 соответственно. Мы рассматриваем разбавленный газ диаметром din/A=0,01, что соответствует Φ=1,05×10−4 при t=0. Эволюция объема во времени (положение поршня) для TH/TL=5,0 представлена на рис. Рис. 4. Открыть в новой вкладкеСкачать слайд Временные эволюции установившихся циклов для TH/TL=5.0. Они подразделяются на два типа: демпфирующие колебательные для ϵ=0,01 (слева) и сверхдемпфирующие для ϵ=0,1 (справа). Эволюция во времени положения поршня [(a) и (b)], температуры [(c) и (d)] и скорости поршня [(e) и (f)] нанесена на график. Эволюция во времени соответствующих физических величин для МД-моделирования (сплошная линия) согласуется с таковой для модели SMF (штриховая линия). Поясним поведение системы, изображенной на рис. 4. Когда начинается процесс нагрева, объемный газ начинает расширяться, чтобы найти новую механическую равновесную плотность, определяемую условием Pˆвх=Pвых, поскольку давление для замкнутого газ становится больше, чем снаружи после нагрева. Точно так же газ сжимается, когда начинается процесс охлаждения. Следует подчеркнуть, что процессы нагрева (охлаждения) и расширения (сжатия) происходят одновременно. Эволюцию физических величин во времени можно разделить на два типа: (а) тип затухающих колебаний и (б) тип сверхдемпфирования, в зависимости от отношения масс ϵ≡m/M. Взяв среднее значение уравнения. (18) и предполагая, что поршень тяжелый ϵ≪1, изменение средней температуры во времени записывается как 19) а0≡πм2Тванн=ϵπМ2Тванн. (20) Предполагая, что смещение поршня мало, x/Xini≡(X−Xini)/Xini≪1, среднее из уравнения (5) записывается как dVdt=−PoutAMxXini−γ¯V, (21) где введены коэффициенты вязкого трения γ¯≡(γgas+a0PoutA)/M и γgas≡4(1+e)PoutAm/2πTout. Рассмотрим справедливость SMF для умеренно плотного газа. Мы принимаем din/A=0,1, что соответствует Φ=0,105 при t=0. На рис. 5 представлены результаты моделирования для MD, SMF и SMF без теплопроводности. Очевидно, что теплопроводность играет важную роль для умеренно плотного газа в отличие от разреженного (см. вставку к рис. 5). Хотя временная эволюция MD для малых t/t0 хорошо предсказывается SMF (см. вставку к рис. 5), согласие относительно плохое для 0,1 Рис. 5. Открыть в новой вкладкеСкачать слайд Сравнивается изменение температуры во времени для MD, SMF и разбавленного приближения SMF. Для режима нагрева t/t0<1,6 разбавленный СМП завышает теплоприток, при этом СМП работает лучше, чем разбавленный вариант, особенно при малых t/t0. На вставке представлена подробная временная эволюция для 0 В этом разделе мы обсуждаем КПД двигателя на МП. Мы показываем в разд. 5.1 следует, что КПД при МП для разбавленного газа соответствует КПД СНКА, если поршень достаточно массивен и упруг, а для газа средней плотности меньше КПД СНКА, как будет показано в разд. 5.2. Проиллюстрируем, что МП существует для нашего двигателя. Wˆtot≡∮1+e2(Pˆin−Pout)AdXˆ, (22) QˆH≡∫THdQˆ0, (23) где ∮ и ∫Tµ представляют собой интеграл по одному циклу баня при Tbath=Tμ (μ=H или L), соответственно, с определением в уравнении. (12). Следует отметить, что уравнение. (23) согласуется с предыдущими работами [18,19], и справедливость определения работы в формуле. (22) обсуждается в Приложении C. Эффективность для одного протокола операции [42] определяется как ηˆ≡WˆtotQˆH. (24) Введем также условный КПД, который определяется как η¯≡〈Wˆtot〉SC〈QˆH〉SC. (25) В этом разделе мы усредняем данные с 11-го по 110-й цикл. Зависимость мощности контакта от времени pˆw≡Wˆtot/2tc для недодемпфированного типа ϵ=0,01 (квадраты) и передемпфированного типа ϵ=0,1 (кружки) показаны на рис. Рис. 6. Открыть в новой вкладкеСкачать слайд График зависимости средней мощности от tc. По-видимому, существует tc для работы на максимальной мощности, которое соответствует необходимому времени для расширения газа до механического равновесия. Пунктирная кривая нарисована как направляющая линия, пропорциональная 1/tc. Обратите внимание, что полученная работа уравновешивается работой вязкого трения для газов. Умножение V в уравнение (21) и интегрируя по циклу, получаем Wtot=∮Mγ¯VdX>0, так как интеграл от левой части уравнения (21) равен нулю. Представлены результаты по КПД при МП (рис. 7) для массивного упругого поршня ϵ=0,01 и e=1,0. Мы обсуждаем влияние массы поршня и его неупругости в Приложении D. Незаштрихованные квадраты 〈ηˆ〉SC и треугольники η¯ представляют собой данные моделирования для SMF без теплопроводности, характеризуемого уравнением (18), а закрашенные — данные для соответствующего МД-моделирования. Хотя η¯ и 〈ηˆ〉SC — разные величины, они согласуются друг с другом. Для сравнения с предыдущими исследованиями построена диаграмма эффективности CNCA ηCA (пунктирные линии). Наша модель SMF правильно предсказывает эффективность при MP для моделирования MD для ϵ = 0,01. Отметим, что эффективность для нашей модели близка к эффективности CNCA. Рис. 7. Открыть в новой вкладкеСкачать слайд КПД при работе на максимальной мощности для разбавленных газов при ϵ=0,01. Наносим результат SMF (открытые треугольники). Здесь мы выводим полуаналитическое выражение для η¯ на основе SMF в пределе ϵ→0. В этом пределе Tˆin быстро релаксирует до температуры ванны сразу после переключения Tbath. Среднее значение работы Eq. (22) можно аппроксимировать 〈Wˆtot〉SC≃N(TH−TL)lnX˜(tc), (26) где введено изменение объема газа за цикл, X˜(tc)≡〈Xˆ (tc)〉SC〈Xˆ(0)〉SC, (27) и выберите e=1. Интегрируя уравнение сохранения энергии (18), получаем ΔUˆ=QˆH+Eˆpis(H), (28) , где мы ввели ΔUˆ=3N(TH−TL)/2 и Eˆpis(H)≡ ∫THdEˆpis. 〈QˆH〉SC=32N(TH−TL)+NTHlnX˜(tc)+O(ϵ), (29) , где мы не учитывали утечку тепла из-за колебаний поршня O(ϵ). Таким образом, эффективность η¯ определяется выражением η¯=TH−TLTH+32TH−TLlnX˜(tc)=ηC1+32ηClnX˜(tc). (30) Предполагая, что X˜(tcMP) зависит от мощности TH/TL с индексом мощности α, X˜(tcMP)=(THTL)α=(1−ηC)−α, (31) получаем аналитическое выражение для η¯ для МП: , которое показано на рис. 7 сплошными линиями. Показатель степени α оценивается из моделирования SMF, где α = 1,5 для ϵ = 0,01 (рис. 8). Физический смысл α будет объяснен в разд. 6. Как показано на рис. 7, уравнение. (32) согласуется с результатами МД для ϵ=0,01. Мы ожидаем, что показатель степени α уменьшится до α=3/2 в пределе ϵ→0 и e→1 следующим образом. η¯MP=ηC2+ηC28+5ηC396+O(ηC4). (33) Отметим, что уравнение. (33) идентично разложению ηCA до O(ηC2): ηCA=ηC2+ηC28+ηC316+O(ηC4). (34) Таким образом, мы можем заключить, что КПД двигателя с упругим пассивным поршнем, масса которого достаточно велика для удерживания разбавленных газов, является КПД CNCA. Рис. 8. Открыть в новой вкладкеСкачать слайд График изменения объема заключенного газа при MP X˜(tcMP) в зависимости от TH/TL для ϵ=0,01. Мы проанализировали эффективность для разбавленных газов в предыдущем подразделе. Здесь мы обсуждаем эффективность при MP для твердого газа средней плотности. Эффективность при MP представлена на основном рисунке рис. 9, где модель SMF почти правильно предсказывает результаты нашего моделирования MD. Данные для SMF при TH/TL=1,2, 1,3, 1,4 усреднены по 1,0×104 циклам после 10 циклов начальной релаксации для повышения их численной точности. Остальные данные усреднены с 11-го по 110-й цикл. Мы обнаружили, что эффективность компенсации теплового потока Jin для умеренно плотных твердых газов меньше, чем для разбавленных, как будет показано в следующем разделе. Рис. 9. Открыть в новой вкладкеСкачать слайд Основная цифра представляет собой КПД при MP для твердых газов средней плотности. В предыдущем разделе мы предположили, что эффективность на выходе МП для разбавленного газа может быть описана эффективностью CNCA в пределе ϵ→0 и e→1, а для умеренно плотного газа меньше, чем Эффективность ЦНК. В этом разделе мы покажем, что результаты в линейной неравновесной ситуации ηC→0 могут быть поняты соотношениями между токами Ji и термодинамическими силами Xi на основе принципа симметрии Кюри–Пригожина [43,44]: J1=L11X1+L12X2, (35) J2=L21X1+L22X2, (36) , где матрица Онзагера удовлетворяет условиям ≥0. Выведем матрицу Онзагера Lij в нашей установке для разбавленного газа, следуя работам [1]. [19,21]. Мы рассматриваем линейную неравновесную ситуацию как TH,L=T±ΔT/2, где T и ΔT — средняя температура T≡(TH+TL)/2 и разность температур ΔT=TH−TL соответственно , удовлетворяющий ΔT/T≪1. Здесь общее производство энтропии за единицу цикла Δσ=−QH/TH−QL/TL переписывается как Δσ=−WtotT+ΔTT2QH, (37) , где мы использовали Wtot=QH+QL и ΔT/ Т≪1. На основании соотношения Δσ2tc=J1X1+J2X2, (38) Ji и Xi соответственно равны J1=T2tc, J2=Qh3tc, (39) X1=−WtotT2, X2=ΔTT2=ηCT. (40) Найдем L11 и L21, взяв ηC=ΔT/T→0. Wtot записывается как Wtot≃NηCTlnX˜(tc)−2a0NT∫XLXHVdXX. (41) Первый член в правой части уравнения. (41) обращается в нуль в пределе ηC→0. Затем, из уравнений. (35), (39) и (40) получаем L11=T24tcN1E˜≥0, (42) E˜≡∫XLXHa0VdXX. (43) Здесь мы ввели E˜ как неизбежную диссипацию из-за конечной скорости поршня. Теперь теплота QH равна QH=32NΔTTT+N(T+ΔT2)lnX˜(tc)−N(T+ΔT2)a0∫XLXHVdXX, (44) , что можно переписать как Qh3tc=T24tclnX˜(tc) E˜E˜(−WtotT2)≃T24tclnX˜(tc)E˜X1, (45) L21=T24tcE˜lnX˜(tc), (46) в ведущем порядке Wtot/T и предел ηC→0. Wtot=NX2T2lnX˜(tc)−2NTE˜=0. (47) Тогда получаем взаимное соотношение L12=T24tcE˜lnX˜(tc)=L21. (48) Взяв члены, зависящие только от ΔT в уравнении (44) получаем , где мы проигнорировали член более высокого порядка, включая a0. Уравнения (42), (46), (48) и (50) являются явным выражением матрицы Онзагера. Здесь мы показываем, что α=3/2 соответствует пределу сильной связи матрицы Онзагера, где поток J1 пропорционален J2. Поскольку определитель легко вычисляется как (tc))22E˜}=T48tc2E˜(32+12lnX˜(tc)−lnX˜(tc)ηC)≃T48tc2E˜(32−α)≥0, (51) , где мы использовали уравнение (47) с уравнением. Подчеркнем, что КПД при МП двигателя на умеренно плотном газе значительно меньше КПД CNCA даже в линейно-неравновесном режиме ηC≪1, что является следствием неизбежной слабой связи матрицу Онзагера Lij* следующим образом. Решение среднего уравнения. (10) через Tin получаем Tin(t)=Tbath(1−a0*(t)V(t))+O(ϵ2), (52) a0*(t) ≡a01+4Φ(t)g0(Φ(t))+j˜in(t), (53) , где мы ввели масштабированный поток j˜in={Tbath/(Tbath−Tin)}dQJ/dt. Δσ=−Wtot*T+ΔTT2QH+1TQJ, (54) QH=32NΔTTT+N(T+ΔT2)lnX˜*(tc)+ QJH−N(T+∆T2)∫XLXHa0*(t)VdXX, (55) где введены , (57) Wtot*≡NηCTlnX˜*(tc)−2NT∫XLXHa0*VdXX, (58) X˜*(tc)≡〈Xˆ(tc)〉SC−4vex/A〈Xˆ( 0)〉SC−4vex/A. (59) Обратите внимание, что знаки QJH и QJL положительные и отрицательные соответственно, и они равны O(ΔT), тогда как QJ>0 равно O(ΔT2) [см. (14), (17) и (57)]. Мы учли влияние конечного исключенного объема vex≡Nπdin3/6 с точностью до O(Φ) для X˜*, где мы аппроксимировали уравнение (9) как Pin≃ninTin(1+4Φ)≃ninTin/(1−4Φ). L11*≡T24tcN1E˜*≥0, (60) L21*≡T24tcE˜*lnX˜*(tc)=L12*, (61) nNT3Xt+ L22* *(tc)+q˜)≥0, (62) где мы ввели E˜*≡∫XLXH(V/X)a0*(t)dX и q˜≡QJH/N∆T+QJT/N∆T2 >0. Обратите внимание, что были введены J1*≡T/2tc, J2*≡(QH+TQJ/∆T)/2tc, X1*≡−Wtot*/T и X2*≡ηC/T. Мы проверили, что положительный ток q˜ существует даже при TH~TL, поскольку q˜≃1,91 для работы МП с TH/TL=1,1 путем моделирования СМП. Найдем значение α* для условия сильной связи, detLij*=0. Вводя X˜*=(TH/TL)α* с помощью аргумента, параллельного выводу уравнения. (51) условие сильной связи для Lij* сводится к detLij*=(T48tc21E˜*)(32+12lnX˜*(tc)+q˜)−(T24tcE˜*lnX˜*(tc))2 ≃T48tc2E˜*(32−α*+q˜)=0. (63) Таким образом, мы получаем α* для условия сильной связи как α*=32+q˜. (64) Однако это условие не может быть удовлетворено, если конечный положительный ток q˜ существует, как наблюдается в нашем моделировании, потому что мы находим, что α*≃3/2 выполняется в нашем моделировании (вставка на рис. 9).). Таким образом, мы заключаем, что условие сильной связи для умеренно плотных газов не выполняется из-за q˜. Свойство слабой связи матрицы Онзагера можно переписать как утечку тепла из горячего резервуара тепла в холодный горячий резервуар: Jleak=J2*−(L22*J1*/L11*) [21]. Из наших соотношений (60)–(62) утечка тепла выражается как (65) Как указано в разд. 5.1 показатель степени α=3/2 для разбавленных газов такой же, как и для адиабатических процессов. Поэтому мы можем проверить, можно ли использовать такую идею даже в умеренно плотных газах. Как известно, соотношение Пуассона для умеренно плотного газа можно записать в виде: (Олово(2)Олово(1))3/2(X(2)−4vex/AX(1)−4vex/A)=1. (66) Следовательно, мы также имеем соотношение X˜*≃(TH/TL)3/2, т.е. α*=3/2 для квазистатических адиабатических процессов. Хотя это совпадение может быть случайным, поскольку в процессе существует утечка тепла, интересно выяснить причину, по которой соотношение Пуассона работает хорошо. Обсудим разницу между нашими результатами и предыдущими результатами. Здесь мы объясняем, что наш двигатель содержит изохорный и квазиадиабатический процессы нагрева/охлаждения, т. е. наш двигатель похож на двигатель Отто, но отличается от него. График давление-объем для ϵ=0,01 и TH/TL=5,0 показан на основном рисунке рис. давление (штриховая линия) при 0 Рис. 10. Открыть в новой вкладкеСкачать слайд На основном рисунке представлена зависимость давление-объем для ϵ=0,01,TH/TL=5,0. На вставке показано изменение во времени теплового потока от тепловой стенки (сплошная линия), положения поршня (штриховая линия) и давления замкнутого газа (штриховая линия) при 0 Поясним, почему тепловой поток dQJ для умеренно плотного газа имеет отношение к КПД при МП в отличие от традиционной термодинамики с конечным временем. В качестве контрпримера рассмотрим цикл Карно конечного времени, содержащий изотермические и адиабатические процессы. Для макроскопического поршня в пределе ϵ→0 одномерная модель передачи импульса [уравнения. (1) и (2)] слишком просты для реалистичного движения поршня, где должны учитываться трение о стенки [39,45], возбуждение атомов на поверхности поршня [46], наклон поршня и т.д. иметь отношение к реальному движению поршня. В Приложении E мы обсуждаем влияние трения о боковые стенки на эффективность нашего протокола и показываем, что трение о боковые стенки снижает эффективность. Модель, рассматриваемая в данной статье, может оказаться нереалистичной, если рассматривать газ как молекулярный, поскольку масса поршня должна быть много больше массы каждой молекулы, а сцепление между молекулами и стенками нельзя игнорировать в таком малом двигатель. В этой статье мы исследовали КПД при МР для двигателя с пассивным поршнем. Чтобы улучшить модель SMF, нам необходимо решить гидродинамические уравнения при движущейся границе, в отличие от рассмотрения в этой статье. Нам также необходимо исследовать нелинейную матрицу Онзагера, чтобы понять эффективность в нелинейном неравновесном режиме [20,21]. Наконец, поскольку термодинамические исследования двигателей без каких-либо силовых регуляторов пока малоизвестны, в ближайшем будущем ожидаются экспериментальные исследования. Мы благодарны за полезные обсуждения с Ю. Изумида, К. Канадзава, А. Пуглиси, Л. Серино, С. Ито, Э. Иода и Т. Сагава. Эта работа поддерживается стипендиатами Grants-in-Aid для Японского общества содействия науке (JSPS) (гранты № 26⋅2906) и JSPS KAKENHI (гранты № 25287098). Эта работа также частично поддерживается сквозной программой JSPS для неравновесной динамики мягкой материи и информации. Известно, что ФРВД для твердого газа под действием теплового потока Jˆin [40,41] определяется как A1) где мы ввели φ0(v)≡∏µ=x,y,zφ0(vµ,Tˆin). (A2) В ур. (A1), c(v) записывается как c(v)≡−45nˆinTˆin(mv22Tˆin−52). (A3) Потоки энергии dQˆ0/dt и dQˆJ/dt можно рассчитать следующим образом. Потоки тепла, выходящие qˆwallout и входящие qˆwallin через стенку, соответственно равны qˆwallout={∫−∞∞dvydvz∫−∞0dvxmv22(−vx)nˆinAφflux(v)}, (A4) qˆwallin={∫−∞∞∞dvydvz∫−xˆ0 )}{∫−∞∞dvydvz∫0∞dvxmv22φwall(v,Tbath)}. (A5) Подставляя уравнения. В этом приложении мы показываем, что изменение профиля температуры во времени сильно зависит от плотности окружающего газа. На рис. Б1 построены профили температуры с временным интервалом Δt=5,0×10–3 МА/Твых сразу после изменения Тванн. Здесь сплошная и пунктирная кривые представляют профиль температуры для плотного (din/A=0,1) и разбавленного (din/A=0,01) газа соответственно. Вертикальные сплошные и пунктирные линии показывают положение поршня, содержащего плотный и разреженный газ соответственно. Градиент температуры для разбавленных газов релаксирует значительно быстрее, чем для плотных газов. По мере увеличения значения din/A время релаксации градиента становится больше, что можно получить, введя dQJ, как в тексте. Рис. Б1. Открыть в новой вкладкеСкачать слайд Профили температуры с интервалом времени Δt=5. В тексте мы определяем работу как «изменение давления × объема», что не является тривиальным. В этом приложении мы обосновываем определение, т. е. разлагаем изменение кинетической энергии поршня на теплоту и работаем, рассматривая вероятность пути (Xˆ(t),Vˆ(t)) при Tˆin(t)=Tin . Обсуждение здесь является расширением Ref. [48] для случая, когда объем заключенного газа флуктуирует во времени. Рассмотрим вероятность пути для прямой эволюции P([Xˆ,Vˆ|τ) (Xˆ,Vˆ) в течение интервала τ от (Xˆ(0),Vˆ(0)) до (Xˆ(τ),Vˆ( τ)) и обратный P([Xˆ,Vˆ]†|τ) от (Xˆ(τ),−Vˆ(τ)) до (Xˆ(0),−Vˆ(0)), где n столкновений между поршень и частицы происходят в момент времени {ti}i=1n с 0=t0 Win(Vi ←Vi−1|Xi−1)≡nin(Xi−1)A∫−∞∞dv|v−Vi−1|Θ(v−Vi−1)φ(v,Tin) ×δ (Vi−Vi−1−Pv(Vi−1)M), (C1) Wout(Vi ←Vi−1)≡noutA∫−∞∞dv|v−Vi−1|Θ(Vi−1 −v)φ(v,Tout) ×δ(Vi−Vi−1−Pv(Vi−1)M), (C2) Wtot(Vi ←Vi−1|Xi−1)≡Win(Vi ←Vi−1|Xi−1)+Wout(Vi ←Vi−1). (C3) Скорость ухода в единицу времени κ(Vi−1|Xi−1) для (Xi−1,Vi−1) представлена как κ(Vi−1|Xi−1)=∫ −∞∞dV′Wtot(V′ ←Vi−1|Xi−1) =nin(Xi−1)A∫Vi−1∞|v−Vi−1|φ0(v,Tin)dv +noutA∫−∞ Vi−1|v−Vi−1|φ0(v,Tout)dv. (C4) Таким образом, P([X,V]|τ) и P([X,V]†|τ) представлены как P([X,V]|τ)=exp[− ∑i=0n−1∫titi+1κ(Vi|X(si))dsi][∏i=1nWtot(Vi ←Vi−1|Xi−1)], (C5) P([X, V]†|τ)=exp[−∑i=0n−1∫titi+1κ(−Vi|X(si))dsi][∏i=1nWtot(−Vi−1 ←−Vi|Xi−1)] . (C6) Здесь положение поршня в момент времени ti ∫titi+1{κ(Vi|Xsi)−κ(−Vi|Xsi)}dsi=−Nln(Xi+1Xi)+noutAVi(ti+1−ti)=−βin∫XiXi+1nin( X)TinAdX+βoutPoutAVj(ti+1−ti), (C7) ln{Wtot(V′ ←V|X)Wtot(−V ←−V′|X)}={βinm(v′2−v2)2≡βinΔEin(V′>V), βoutm(v′2−v2)2≡βout∆Eout(V′ (C8) Здесь мы ввели обратную температуру βν≡1/Tν и изменение энергии газа ν-стороны ΔEν за счет колебаний поршня (ν=in, out). Используя уравнения (С7) и (С8), получаем следующее выражение для определения работы: ΔSinel, (C9) ΔEin=ΔQin−∫XiniXτ1+e2ninTinAdX, (C10) ΔEOUT = ΔQOUT+1+E2Pouta∫xinixτDX, (C11) ΔSinel®1 — E2∫xinixτ {Nintin -pout} ADX, (C12) 99999999999999999999999999 год 99999999999999999 999999999 999999999 год 999999999999999 год 999999999999999 годы}. В этом приложении изучается влияние массы и неупругости поршня. Аналогично разд. 5, мы находим существование максимальной мощности для легких или неупругих поршней. Мы наносим эффективность при MP для (a) e = 1,0 и ϵ = 0,1, (b) e = 0,9 и ϵ = 0,01 и (c) e = 0,9 и ϵ = 0,1 на рис. D1. Наблюдаемый КПД для легких и неупругих поршней намного меньше, чем ηCA (штриховая линия). С помощью нашего моделирования мы находим α = 0,79 для e = 1,0 и ϵ = 0,1. Рис. D1. Открыть в новой вкладкеСкачать слайд КПД при работе на максимальной мощности для разбавленных газов для (a) e=1,0 и ϵ=0,1, (b) e=0,9 и ϵ=0,01, и (c) e=0,9 и ϵ=0,1. Светлые квадраты 〈ηˆ〉SC и светлые треугольники η¯ – данные моделирования для ОВС без теплопроводности. Наблюдаемый КПД для легких и неупругих поршней намного меньше, чем ηCA (штриховая линия). Мы также строим уравнение (32) сплошной линией на (а), что завышает результаты моделирования. В этом приложении мы обсуждаем влияние трения о боковые стенки на КПД двигателя с пассивным поршнем, которое существует для реальных ситуаций. MdVˆdt=Fˆin+Fˆout+Fˆfri. (E1) Предположим, что γ не зависит от ϵ и γ/γgas=O(1), где движение поршня становится сверхдемпфирующим, даже если поршень тяжелый. Поскольку боковое трение можно рассматривать как трение, связанное с ванной с нулевой температурой, мы определим КПД при трении [45], введя теплоту трения: Qˆfri≡∮γVˆ2dt, (E2) ηˆfri≡WˆtotQˆH+Qˆfri. (E3) Данные моделирования эффективности при СД с γ/γgas=2,0 и e=1,0 представлены на рис. E1. Асимптотическое поведение 〈ηˆ〉SC и 〈ηˆfri〉SC в пределе ϵ→0 для TH/TL=5,0 показано на рис. E1(a). На рис. Д1(б) изображена температурная зависимость 〈ηˆ〉СК и 〈ηˆfri〉СК при МП с ϵ=0,001, где КПД меньше, чем ηCA (см. рис. 7(а)). Рис. Д1. Открыть в новой вкладкеСкачать слайд Эффективность МП при боковом трении. Асимптотическое поведение эффективности в пределе ϵ→0 (а) и их температурная зависимость при ϵ=0,001 и γ/γгаз=2,0 (б). Трение о боковину снижает эффективность. [1] Callen H. , Термодинамика и введение в термостатистику ( Wiley , Нью-Йорк , 1985 ). [2] Landau L. D. Lifshitz E. , Statistical Physics, Part 1 ( Butterworth-Heinemann , Oxford , 1980 ). [3] Carnot S. , Размышления о мощи Motorice Du Feu et Sur Les Machines ( Политехническая школа , Париж , 1824 ). [4] West C. D. , Принципы и применение двигателей Stirling ( Van Nostrand-Reinhold , 99599, , 9959 9 , . [5] Magnasco M. O. , Phys. Преподобный Летт. 72 , 2656 ( 1994 ). 10.1103/PhysRevLett.72.2656 [6] Ganesan V. , Internal Combustion Engines ( Tata McGraw-Hill Education , New Delhi , 2012 ). [7] Vaudrey A. Lanzetta F. Feidt М. , Дж. Неравн. Термодин. 39 , 199 ( 2014 ). 10.1515/jnet-2014-0018 [8] Reitlinger H. B. , Sur lÚtilisation de la Chaleur dans les Machines á Feu ( Vaillant-Carmanne , Liége , 1929 ). [9] Ивон Дж. , , ( 1955 ). [10] Chambadal P. , Les Centrales Nucléaires ( Armand Colin , Paris , 1957 ). [11] Новиков И.И. , Ут. Энергия (Нью-Йорк) 3 , 1269 ( 1957 ). 10.1007/BF01507240 [12] Новиков I. , J. Nucl. Энергия 7 , 125 ( 1958 ). 10.1016/0891-3919(58)-4 [13] Curzon F. Ahlborn B. 90 0 Дж. Физ. 43 , 22 ( 1975 ). 10.1119/1.10023 [14] De Vos A. , Endoreversible Thermodynamics of Solar Energy Conversion ( Oxford University Press , Oxford , 1992 ). [15] Ягода Р. С. Казаков В. А. Сенютыч С. Шваст Z. Tsvilin A. M. , Thermodynamic Optimization of Finite Time Processes ( John Wiley & Sons , Chichester , 2000 ). [16] Salamon P. Nulton J. D. Siragusa G. Andersen T. R. Limon A. T. R. A. T. R. A. T. R. A. T. R. .0006 , Энергия 26 , 307 ( 2001 ). 10.1016/S0360-5442(00)00059-1 [17] Van den Broeck C. , Физ. Преподобный Летт. 95 , 1 ( 2005 ). 10.1103/PhysRevLett.95.1 [18] Изумида Ю. Окуда К. , Еврофиз. лат. 83 , 60003 ( 2008 ). 10.1209/0295-5075/83/60003 [19] Изумида Ю. Окуда К. , Физ Ред. E 80 , 021121 ( 2009 ). 10.1103/PhysRevE.80.021121 [20] Esposito M. Kawai R. Lindenberg K. Van den Broeck C. 6, 90 Phys. Преподобный Летт. 105 , 150603 ( 2010 ). 10.1103/PhysRevLett.105.150603 [21] Изумида Ю. Окуда К. При 0
При 0 3. Модель стохастического среднего поля
 Здесь nˆin(t) и Vˆ≡dXˆ/dt удовлетворяют стохастическим уравнениям:
Здесь nˆin(t) и Vˆ≡dXˆ/dt удовлетворяют стохастическим уравнениям: е. nˆout≡nout и Tˆout≡Tout. Мы ввели функцию распределения газа по скоростям (ФРС) как φ0(v,Tin)≡m/2πTinexp[−mv2/2Tin]. Следует отметить, что набор уравнений. (5) и (6) являются расширением нашего предыдущего исследования к газу с твердым ядром конечной плотности, когда плотность и температура изменяются во времени, и это причина, по которой мы принимаем произведение Ито в уравнении. (6) [39]. Примем уравнение состояния твердых ядерных газов с объемной долей Φˆ≡nˆinπdin3/6, данное [40]
е. nˆout≡nout и Tˆout≡Tout. Мы ввели функцию распределения газа по скоростям (ФРС) как φ0(v,Tin)≡m/2πTinexp[−mv2/2Tin]. Следует отметить, что набор уравнений. (5) и (6) являются расширением нашего предыдущего исследования к газу с твердым ядром конечной плотности, когда плотность и температура изменяются во времени, и это причина, по которой мы принимаем произведение Ито в уравнении. (6) [39]. Примем уравнение состояния твердых ядерных газов с объемной долей Φˆ≡nˆinπdin3/6, данное [40]
 (15), решение уравнения. (15) имеет вид
(15), решение уравнения. (15) имеет вид Мы численно подтверждаем, что градиент температуры для разбавленного газа релаксирует быстрее, чем для плотного газа в Приложении B. Действительно, мы сравниваем динамику температуры на рис. 3 для SMF и SMF без теплопроводности, используя уравнение. (18) — разница между двумя методами незначительна. Здесь мы приняли начальную объемную долю как Φ=1,05×10-4. Мы выбираем tc/t0=1,60, что достаточно для релаксации системы. Позже мы также покажем, что dQJ не влияет на эффективность при СД для разбавленного газа. Таким образом, мы используем уравнение (18) для разбавленного газа вместо уравнения (10).
Мы численно подтверждаем, что градиент температуры для разбавленного газа релаксирует быстрее, чем для плотного газа в Приложении B. Действительно, мы сравниваем динамику температуры на рис. 3 для SMF и SMF без теплопроводности, используя уравнение. (18) — разница между двумя методами незначительна. Здесь мы приняли начальную объемную долю как Φ=1,05×10-4. Мы выбираем tc/t0=1,60, что достаточно для релаксации системы. Позже мы также покажем, что dQJ не влияет на эффективность при СД для разбавленного газа. Таким образом, мы используем уравнение (18) для разбавленного газа вместо уравнения (10). При вычислении ξˆνv v и dv соответственно заменяются на vi и Δv, где vi=iΔv−vmax (i=1,2,…,600), vmax≡6,0kBTν/M (ν=in,out) и Δv≡vmax/300. Поскольку уравнение (10) оказывается неустойчивым, если теплопроводность в уравнении (14) больше, чем в уравнении. (12) мы налагаем условие dQJ=0, если dQJ>dQ0, благодаря численной устойчивости нашего моделирования. Данные моделирования усредняются в устойчивых циклах, где усредненная величина представлена 〈⋯〉SC.
При вычислении ξˆνv v и dv соответственно заменяются на vi и Δv, где vi=iΔv−vmax (i=1,2,…,600), vmax≡6,0kBTν/M (ν=in,out) и Δv≡vmax/300. Поскольку уравнение (10) оказывается неустойчивым, если теплопроводность в уравнении (14) больше, чем в уравнении. (12) мы налагаем условие dQJ=0, если dQJ>dQ0, благодаря численной устойчивости нашего моделирования. Данные моделирования усредняются в устойчивых циклах, где усредненная величина представлена 〈⋯〉SC. 4. Эволюция во времени
4.1. Разбавленный случай
 4(а) для ϵ=0,01, tc/t0=1,60 и (б) для ϵ=0,1, tc/ t0=8,0. Мы подтвердили, что это tc для каждого ϵ больше, чем время релаксации в соответствующее стационарное состояние. Данные моделирования усреднены с 11-го по 20-й цикл, где сплошная и пунктирная линии, соответственно, представляют данные для моделирования MD и данные для моделирования нашей модели SMF. Аналогично, рис. 4(c) и (d) — изменение температуры газа во времени, а рис. 4(e) и (f) — временная эволюция скорости поршня. Пунктирные линии представляют протокол работы Tbath. Примечательно, что наша модель SMF правильно предсказывает эволюцию МД во времени.
4(а) для ϵ=0,01, tc/t0=1,60 и (б) для ϵ=0,1, tc/ t0=8,0. Мы подтвердили, что это tc для каждого ϵ больше, чем время релаксации в соответствующее стационарное состояние. Данные моделирования усреднены с 11-го по 20-й цикл, где сплошная и пунктирная линии, соответственно, представляют данные для моделирования MD и данные для моделирования нашей модели SMF. Аналогично, рис. 4(c) и (d) — изменение температуры газа во времени, а рис. 4(e) и (f) — временная эволюция скорости поршня. Пунктирные линии представляют протокол работы Tbath. Примечательно, что наша модель SMF правильно предсказывает эволюцию МД во времени.
 Правая часть уравнения. (21) эквивалентно силе, действующей на гармонический осциллятор в вязкой среде. Если вязкое сопротивление достаточно мало, т. е. ϵ→0, то движение поршня носит затухающий колебательный характер [рис. 4(а)], а движение оказывается передемпфирующим, если ϵ не мало (рис. 4(б)].
Правая часть уравнения. (21) эквивалентно силе, действующей на гармонический осциллятор в вязкой среде. Если вязкое сопротивление достаточно мало, т. е. ϵ→0, то движение поршня носит затухающий колебательный характер [рис. 4(а)], а движение оказывается передемпфирующим, если ϵ не мало (рис. 4(б)]. 4.2. Умеренно плотный случай
5. Наличие максимальной мощности и ее КПД
5.1. Разбавленный случай
 Определим работу Wˆtot и тепло, затрачиваемое за цикл QˆH, как
Определим работу Wˆtot и тепло, затрачиваемое за цикл QˆH, как 6, где TH/TL= 5,0 и e=1,0 фиксированы, а p0≡Tout/t0. По-видимому, МП достигается за время tcМП, что соответствует необходимому времени для расширения газа в сторону механического равновесия. Заметим, что длительное нагревание или охлаждение разрушает мощность, потому что извлекаемая работа составляет, самое большее, N(TH−TL)ln(TH/TL). Таким образом, мощность уменьшается как функция tc: 〈pˆw〉SC∝1/tc при tc≫tcMP, что показано штриховой линией на рис. 6.9.0006
6, где TH/TL= 5,0 и e=1,0 фиксированы, а p0≡Tout/t0. По-видимому, МП достигается за время tcМП, что соответствует необходимому времени для расширения газа в сторону механического равновесия. Заметим, что длительное нагревание или охлаждение разрушает мощность, потому что извлекаемая работа составляет, самое большее, N(TH−TL)ln(TH/TL). Таким образом, мощность уменьшается как функция tc: 〈pˆw〉SC∝1/tc при tc≫tcMP, что показано штриховой линией на рис. 6.9.0006 Таким образом, полученная работа уравновешивается работой вязкого трения для газов.
Таким образом, полученная работа уравновешивается работой вязкого трения для газов. Светлые квадраты 〈ηˆ〉SC и светлые треугольники η¯ – данные моделирования для СМП без теплопроводности, а закрашенные – данные для соответствующего МД-моделирования. Наблюдаемая эффективность близка к ηCA (штриховая линия) и уравнению. (32)(сплошная линия).
Светлые квадраты 〈ηˆ〉SC и светлые треугольники η¯ – данные моделирования для СМП без теплопроводности, а закрашенные – данные для соответствующего МД-моделирования. Наблюдаемая эффективность близка к ηCA (штриховая линия) и уравнению. (32)(сплошная линия).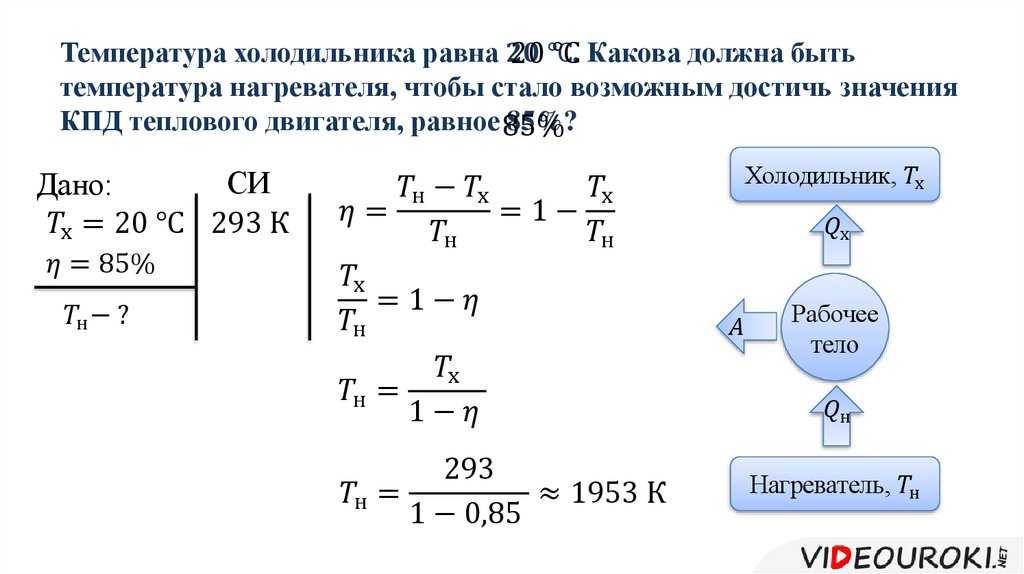 Усреднение уравнения (28) и разлагая по ϵ, получаем
Усреднение уравнения (28) и разлагая по ϵ, получаем Несмотря на то, что в процессе расширения существует крошечная утечка тепла, мы можем приблизительно игнорировать утечку, поскольку процесс нагревания является почти изохорным, как это будет обсуждаться в разд. 7. Вспоминая соотношение Пуассона для адиабатического процесса идеальных одноатомных газов между состояниями 1 и 2, (Tin(2)/Tin(1))3/2(X(2)/X(1))=1, где X (a) и Tin(a) (a=1,2) соответственно представляют положение поршня и температуру для состояния a, показатель степени α=3/2 согласуется с результатом моделирования. В разд. В разделе 6 мы докажем, что α=3/2 соответствует условию сильной связи для матрицы Онзагера в линейно-необратимой термодинамике. Подставив полученное значение α=3/2 для ε=0,01 в уравнение (32), получаем
Несмотря на то, что в процессе расширения существует крошечная утечка тепла, мы можем приблизительно игнорировать утечку, поскольку процесс нагревания является почти изохорным, как это будет обсуждаться в разд. 7. Вспоминая соотношение Пуассона для адиабатического процесса идеальных одноатомных газов между состояниями 1 и 2, (Tin(2)/Tin(1))3/2(X(2)/X(1))=1, где X (a) и Tin(a) (a=1,2) соответственно представляют положение поршня и температуру для состояния a, показатель степени α=3/2 согласуется с результатом моделирования. В разд. В разделе 6 мы докажем, что α=3/2 соответствует условию сильной связи для матрицы Онзагера в линейно-необратимой термодинамике. Подставив полученное значение α=3/2 для ε=0,01 в уравнение (32), получаем
5.2. Умеренно плотный корпус
 SMF почти правильно предсказывает эффективность моделирования МД. Отметим, что КПД значительно меньше, чем у CNCA, что обусловлено неизбежным тепловым потоком dQJ. На вставке показан коэффициент расширения X˜*, определенный в уравнении. (59) для умеренно плотных газов. Показатель степени α оценивается как α * ≃ 3/2 .
SMF почти правильно предсказывает эффективность моделирования МД. Отметим, что КПД значительно меньше, чем у CNCA, что обусловлено неизбежным тепловым потоком dQJ. На вставке показан коэффициент расширения X˜*, определенный в уравнении. (59) для умеренно плотных газов. Показатель степени α оценивается как α * ≃ 3/2 . 6. Линейно-необратимая термодинамика
 В дальнейшем мы предполагаем, что поршень упругий (e=1,0) и массивный (ϵ→0), и мы сокращаем среднее значение произвольной стохастической величины Aˆ как A=〈Aˆ〉SC. Мы исследуем разбавленный газ в разд. 6.1 и прояснить эффект конечной плотности в разд. 6.2.
В дальнейшем мы предполагаем, что поршень упругий (e=1,0) и массивный (ϵ→0), и мы сокращаем среднее значение произвольной стохастической величины Aˆ как A=〈Aˆ〉SC. Мы исследуем разбавленный газ в разд. 6.1 и прояснить эффект конечной плотности в разд. 6.2. 6.1. Разбавленный случай

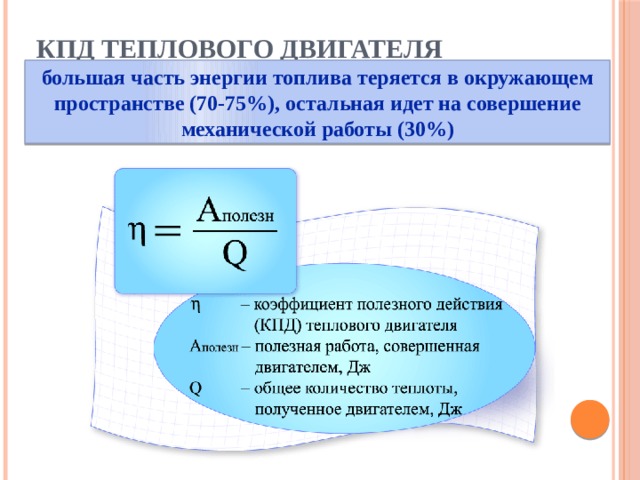 Из уравнения (20) мы использовали lnX˜(tc)≫E˜=O(ϵ) в пределе ϵ→0. Далее определим L12 и L22. L12 можно определить из условия Wtot=0, т. е. трудоемкого состояния:
Из уравнения (20) мы использовали lnX˜(tc)≫E˜=O(ϵ) в пределе ϵ→0. Далее определим L12 и L22. L12 можно определить из условия Wtot=0, т. е. трудоемкого состояния: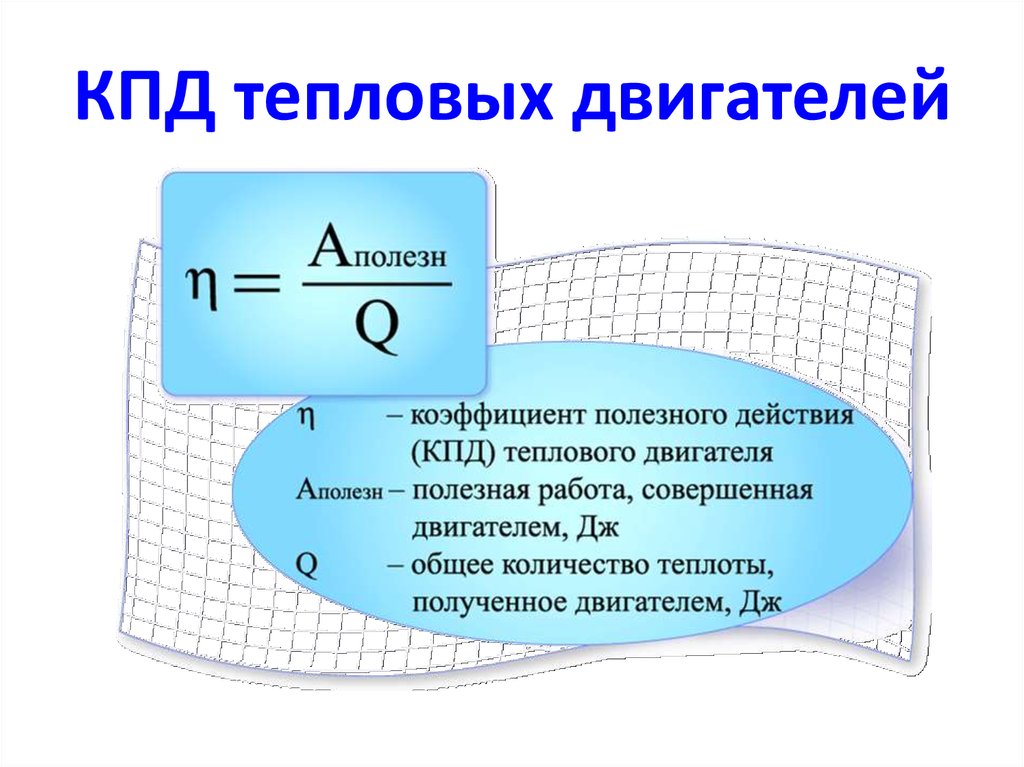 (40), т. е. lnX˜(tc)/2E˜=1/ηC и lnX˜=−αln(1−ηC)≃αηC+αηC2/2+O(ηC3) при условии, близком к равновесию ηC→0. Предел сильной связи detLij=0 соответствует α=3/2, что равно значению, полученному в разд. 5. Эффективность CNCA определяется на основе уравнений. (35) и (36) в пределе сильной связи, следуя аналогичной процедуре в [1]. [17]. Следует отметить, что параметром управления для нашего двигателя является не X1, а J1, в отличие от Ref. [17].
(40), т. е. lnX˜(tc)/2E˜=1/ηC и lnX˜=−αln(1−ηC)≃αηC+αηC2/2+O(ηC3) при условии, близком к равновесию ηC→0. Предел сильной связи detLij=0 соответствует α=3/2, что равно значению, полученному в разд. 5. Эффективность CNCA определяется на основе уравнений. (35) и (36) в пределе сильной связи, следуя аналогичной процедуре в [1]. [17]. Следует отметить, что параметром управления для нашего двигателя является не X1, а J1, в отличие от Ref. [17]. 6.2. Умеренно плотный случай
 См. также уравнение (20) для сравнения с разреженным случаем. Поскольку дополнительный тепловой поток dQJ существует, уравнения. (37) и (44) заменены соответственно на
См. также уравнение (20) для сравнения с разреженным случаем. Поскольку дополнительный тепловой поток dQJ существует, уравнения. (37) и (44) заменены соответственно на Следуя процедуре, аналогичной разд. 6.1, мы получаем матрицу Онзагера Ji*=∑jLij*Xj* с i,j=1,2 при
Следуя процедуре, аналогичной разд. 6.1, мы получаем матрицу Онзагера Ji*=∑jLij*Xj* с i,j=1,2 при

7. Обсуждение
 Когда мы прикрепляем термованну к газу, величина теплового потока за конечное время цикла Карно слишком мала и dQJ не существует, так как температура газа и баня практически идентичны из-за адиабатического процессы с механическим управлением поршнем. С другой стороны, величина теплового потока в нашем двигателе велика, потому что температура газа и температура ванны различны, когда мы присоединяем ванну к газу. Таким образом, влияние теплового потока dQJ существенно для КПД двигателя с пассивным поршнем.
Когда мы прикрепляем термованну к газу, величина теплового потока за конечное время цикла Карно слишком мала и dQJ не существует, так как температура газа и баня практически идентичны из-за адиабатического процессы с механическим управлением поршнем. С другой стороны, величина теплового потока в нашем двигателе велика, потому что температура газа и температура ванны различны, когда мы присоединяем ванну к газу. Таким образом, влияние теплового потока dQJ существенно для КПД двигателя с пассивным поршнем. Однако наша модель будет экспериментально реализована на двух типах установок: коллоидных суспензиях с полупроницаемой мембраной и высоковозбужденном гранулированном газе с подвижным поршнем. Хотя гидродинамическое взаимодействие между коллоидами важно, осмотическое давление между двумя разбавленными растворами, разделенными полупроницаемой мембраной, описывается формулой Вант-Гоффа, которая имеет форму, идентичную уравнению состояния идеальных газов. Точно так же можно подавить неоднородность и негауссовость гранулированных газов, по крайней мере, для конкретной установки сильно взволнованного гранулированного газа [47]. Таким образом, нашу модель можно рассматривать как упрощенную и идеализированную для таких систем. Мы также отмечаем, что наш результат, как ожидается, будет в основном верным даже в термодинамическом пределе, хотя в этой статье обсуждаются только небольшие системы, содержащие всего 200 частиц.
Однако наша модель будет экспериментально реализована на двух типах установок: коллоидных суспензиях с полупроницаемой мембраной и высоковозбужденном гранулированном газе с подвижным поршнем. Хотя гидродинамическое взаимодействие между коллоидами важно, осмотическое давление между двумя разбавленными растворами, разделенными полупроницаемой мембраной, описывается формулой Вант-Гоффа, которая имеет форму, идентичную уравнению состояния идеальных газов. Точно так же можно подавить неоднородность и негауссовость гранулированных газов, по крайней мере, для конкретной установки сильно взволнованного гранулированного газа [47]. Таким образом, нашу модель можно рассматривать как упрощенную и идеализированную для таких систем. Мы также отмечаем, что наш результат, как ожидается, будет в основном верным даже в термодинамическом пределе, хотя в этой статье обсуждаются только небольшие системы, содержащие всего 200 частиц. 8. Заключительные замечания
 Мы рассмотрели протокол операции для твердого газа, разделенного массивным поршнем (рис. 1 и 2). Было предложено SMF, и его актуальность была продемонстрирована путем сравнения его результатов с результатами моделирования МД как для разбавленного газа (рис. 4), так и для газа средней плотности (рис. 5). Мы обнаружили наличие МП на рис. 6 и исследовали эффективность при МП для разбавленного газа на рис. 7. Эффективность при МП для разбавленных газов близка к эффективности CNCA для упругого и массивного поршня. Мы получили аналитические выражения для эффективности в МП на основе SMF в виде уравнений. (32) и (33). Чтобы понять линейный неравновесный режим, мы вывели матрицу Онзагера в явном виде [уравнения. (42), (46), (48) и (50)] и обнаружили, что условие сильной связи выполняется для разбавленного газа. В отличие от разбавленного газа, мы обнаружили, что эффективность на МП для умеренно плотных газов меньше, чем эффективность CNCA даже для упругого и массивного поршня в линейно-неравновесном режиме (рис.
Мы рассмотрели протокол операции для твердого газа, разделенного массивным поршнем (рис. 1 и 2). Было предложено SMF, и его актуальность была продемонстрирована путем сравнения его результатов с результатами моделирования МД как для разбавленного газа (рис. 4), так и для газа средней плотности (рис. 5). Мы обнаружили наличие МП на рис. 6 и исследовали эффективность при МП для разбавленного газа на рис. 7. Эффективность при МП для разбавленных газов близка к эффективности CNCA для упругого и массивного поршня. Мы получили аналитические выражения для эффективности в МП на основе SMF в виде уравнений. (32) и (33). Чтобы понять линейный неравновесный режим, мы вывели матрицу Онзагера в явном виде [уравнения. (42), (46), (48) и (50)] и обнаружили, что условие сильной связи выполняется для разбавленного газа. В отличие от разбавленного газа, мы обнаружили, что эффективность на МП для умеренно плотных газов меньше, чем эффективность CNCA даже для упругого и массивного поршня в линейно-неравновесном режиме (рис. 9).). Мы выяснили важность теплового потока при переключении Tbath, что вызывает неизбежную слабую связь для матрицы Онзагера.
9).). Мы выяснили важность теплового потока при переключении Tbath, что вызывает неизбежную слабую связь для матрицы Онзагера. Благодарности

Приложение A. Вывод уравнений. (11), (12) и (14)
 (A4) и (A5) в dQˆwall=(qˆwallin−qˆwallout)dt, мы получаем уравнения. (11), (12) и (14).
(A4) и (A5) в dQˆwall=(qˆwallin−qˆwallout)dt, мы получаем уравнения. (11), (12) и (14). Приложение B. Изменение профиля температуры во времени
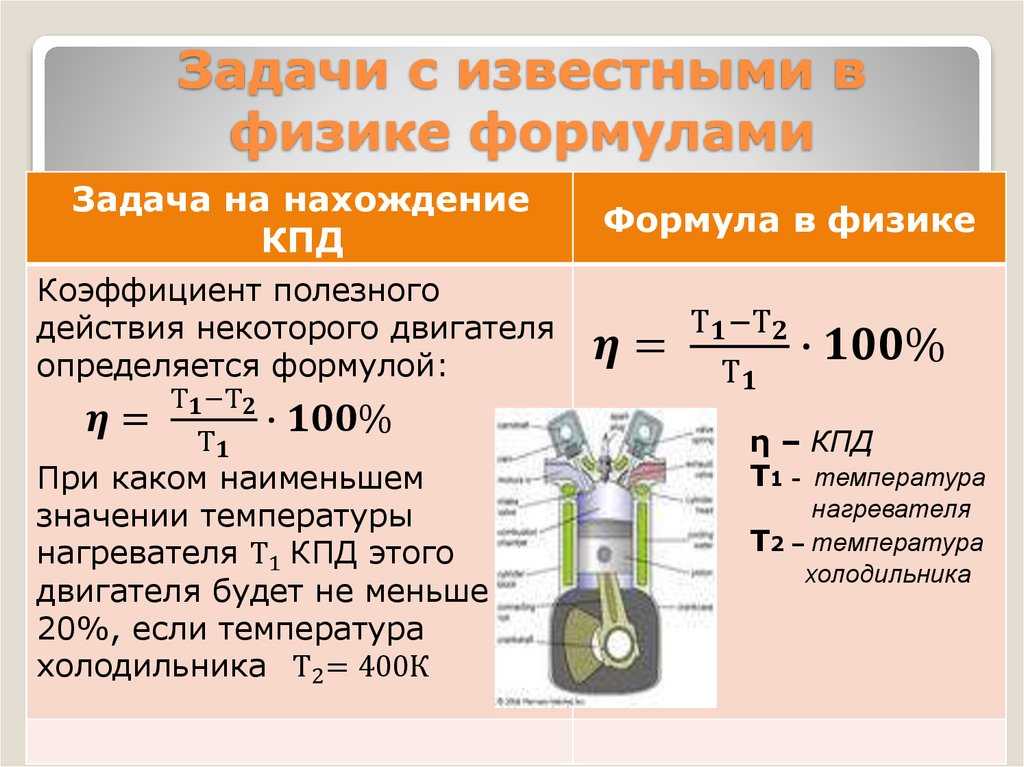 0×10-3MA/Tout сразу после изменения Tванн. Сплошная и пунктирная кривые представляют профиль температуры для плотного (din/A=0,1) и разбавленного (din/A=0,01) газа соответственно. Вертикальные сплошные и пунктирные линии показывают положение поршня, содержащего плотный и разреженный газ соответственно.
0×10-3MA/Tout сразу после изменения Tванн. Сплошная и пунктирная кривые представляют профиль температуры для плотного (din/A=0,1) и разбавленного (din/A=0,01) газа соответственно. Вертикальные сплошные и пунктирные линии показывают положение поршня, содержащего плотный и разреженный газ соответственно. Приложение С. Об определении работы

 сокращение V0≡Vˆ(0), Xτ≡Xˆ(τ) и Vτ≡Vˆ(τ). Из уравнения (С10) изменение внутренней энергии замкнутого газа ΔEin, по-видимому, разлагается на изменение работы и теплоты. Таким образом, мы принимаем определение работы в уравнении. (22) в тексте. Для двигателей с принудительным управлением мы обычно определяем работу, используя только Pout. Однако мы определяем работу, используя разность давлений, потому что наш двигатель не имеет принудительного управления.
сокращение V0≡Vˆ(0), Xτ≡Xˆ(τ) и Vτ≡Vˆ(τ). Из уравнения (С10) изменение внутренней энергии замкнутого газа ΔEin, по-видимому, разлагается на изменение работы и теплоты. Таким образом, мы принимаем определение работы в уравнении. (22) в тексте. Для двигателей с принудительным управлением мы обычно определяем работу, используя только Pout. Однако мы определяем работу, используя разность давлений, потому что наш двигатель не имеет принудительного управления. Приложение D. Масса и неупругость поршня
 Мы строим уравнение (32) в (а), в то время как наблюдаемые эффективности также меньше, чем уравнение. (32). Существование ϵ снижает эффективность ηCA даже при ведущем порядке O(ηC), поскольку α=0,79<3/2 для ϵ=0,1. Поправка более высокого порядка для ε была бы необходима для лучшего согласия.
Мы строим уравнение (32) в (а), в то время как наблюдаемые эффективности также меньше, чем уравнение. (32). Существование ϵ снижает эффективность ηCA даже при ведущем порядке O(ηC), поскольку α=0,79<3/2 для ϵ=0,1. Поправка более высокого порядка для ε была бы необходима для лучшего согласия. Приложение E. Влияние трения о боковые стенки
 Реализуем линейное трение на боковине как Fˆfri=−γVˆ. Тогда уравнение движения Eq. (5) оказывается
Реализуем линейное трение на боковине как Fˆfri=−γVˆ. Тогда уравнение движения Eq. (5) оказывается Таким образом, как и ожидалось, трение о боковину снижает эффективность.
Таким образом, как и ожидалось, трение о боковину снижает эффективность. Ссылки



 I.
I.
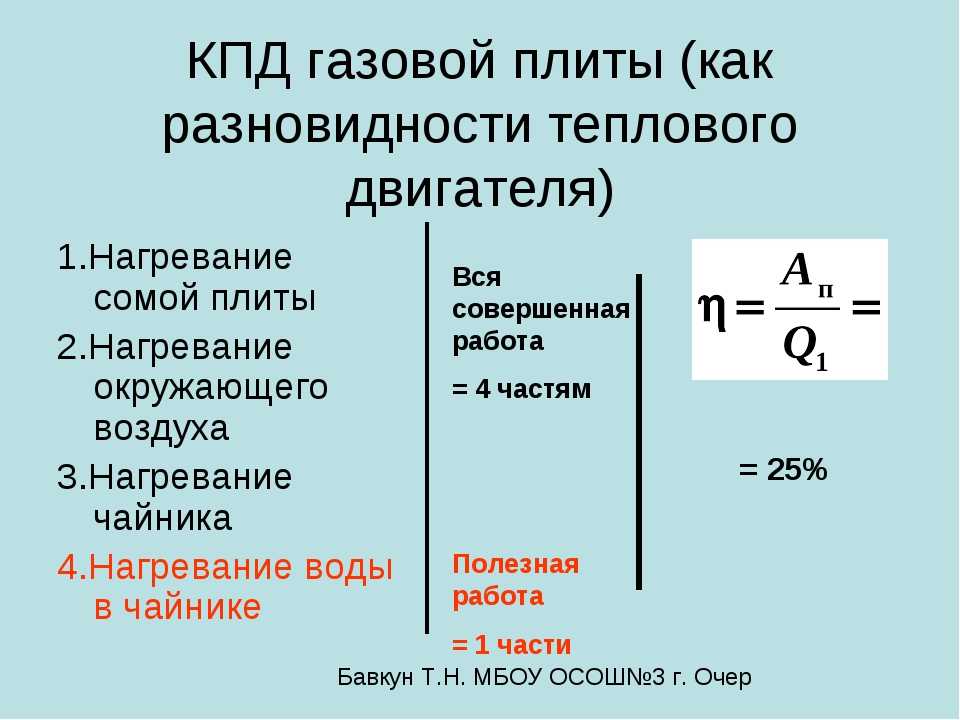

9, лат.
97
10004
(
2012
).
10.1209/0295-5075/97/10004
[22]
Hoppenau
J.
Niemann
M.
Engel
A.
,
Physel. E
87
,
062127
(
2013
).
10.1103/PhysRevE.87.062127
[23]
Seifert
U.
,
Физ. Преподобный Летт.
106
,
020601
(
2011
).
10.1103/physrevlett.106.020601
[24]
Van Den Broeck
C.
Kumar
N.
Linenberg
K.
,
Phys. Преподобный Летт.
108
210602
(
2012
).
10.1103/PhysRevLett.108.210602
[25]
Мозуркевич
M.
Berry
R. S.
,
J. Appl. физ.
53
,
34
(
1982
).
10.1063/1,329894
[26]
Ангуло-коричневый
F.
Rocha-Martínez
J. A.
Navarrete-González
T. D.
,
9
9
9
9
9
9
9
9. Д: заявл. физ.
29
,
80
(
1996
).
10.1088/0022-3727/29/1/014
[27]
Chen
L.
,
Евро. Дж. Физ.
24
359
(
2003
).
10.1088/0143-0807/24/4/354
[28]
Quan
H. T.
Wang
Y. D.
Liu
Y. X.
Sun
C. P.
Nori
F.
,
Физ. Преподобный Летт.
Преподобный Летт.
97
,
180402
(
2006
).
10.1103/physRevlett.97.180402
[29]
Quan
H. T.
Liu
Y. X.
Sun
C.
. E
76
,
031105
(
2007
).
[30]
Abah
O.
Roßnagel
J.
Jacob
G.
Deffner
S.
Schmidt-Kaler
F.
Singer
K.
Lutz
E
,
Физ. Преподобный Летт.
109
,
203006
(
2012
).
10.1103/PhysRevLett.109.203006
[31]
Schmiedl
T.
Seifert
U.
,
Phys. Преподобный Летт.
98
,
108301
(
2007
).
10.1103/PhysRevLett.98.108301
[32]
Schmiedl
T.
Seifert
U.
9, лат.
81
20003
(
2008
).
10.1209/0295-5075/81/20003
[33]
Tu
Z.C.
,
J. Phys. А: Математика. Теор.
41
312003
(
2008
).
10. 1088/1751-8113/41/31/312003
1088/1751-8113/41/31/312003
[34]
Blickle
V.
Bechinger
C.
6 Na
, 904 физ.
8
,
143
(
2012
).
10.1038/nphys2163
[35]
RANA
S.
PAL
P. S.
SAHA
A.
Jayannavar
A. M.
,
Phys. Ред. E
90
,
042146
(
2014
).
10.1103/PhysRevE.90.042146
[36]
Torquato
S.
,
Физ. Ред. E
51
,
3170
(
1995
).
10.1103/PhysRevE.51.3170
[37]
Gardiner
C.
,
Stochastic Methods
(
Springer-Verlag
,
Berlin
,
2009
), 4-е изд.
[38]
van Kampen
N. G.
,
Случайные процессы в физике и химии
(
North-Holland Personal Library
,
Амстердам
,
2007
), 3-е изд.
[39]
Sano
T. G.
Hayakawa
H.
,
Phys. E
E
89
,
032104
(
2014
).
10.1103/physreve.89.032104
[40]
Résibois
P.
De Leener
M.
,
Классическая кинетическая теория жидкости
,
.0006
(
Wiley
,
Нью-Йорк
,
1977
).
[41]
Garzó
V.
Dufty
J. W.
,
Phys. Ред. E
59
5895
(
1999
).
10.1103/PhysRevE.59.5895
[42]
Verley
G.
Esposito
M.
0
Willaert
0006
Van den Broeck
C.
,
Nature Comm.
5
,
4721
(
2014
).
10.1038/ncomms5721
[43]
Prigogine
I.
,
Etude Thermodynamique des Phénomènes Irreéversibles
(
Desoer
,
Liège
,
1947
).
[44]
de Groot
S. R.
Mazur
P.
,
Non-Equilibrium Thermodynamics
(
Dover
,
New York
,
1984
).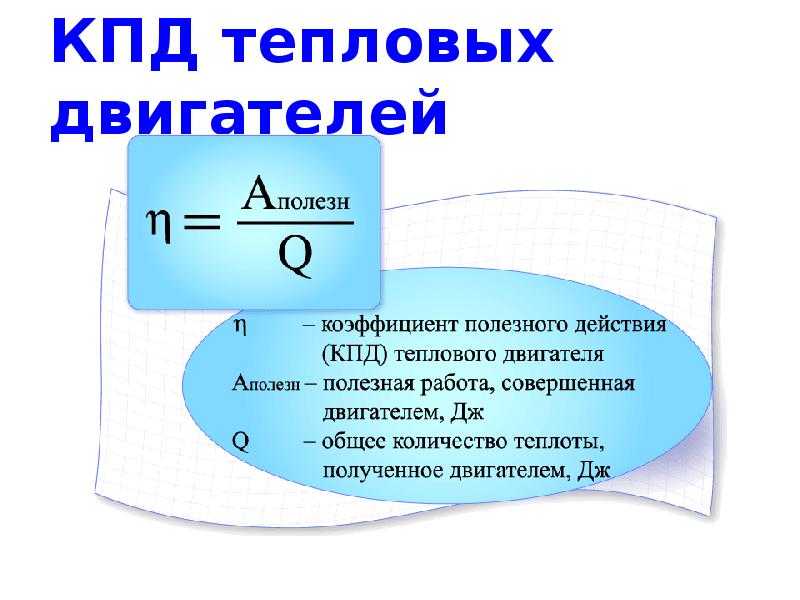
[45]
Bizzaro
J. P. S.
,
J. App. физ.
108
,
054907
(
2010
).
10.1063/1.3477189
[46]
Итами
М.
Саса
С.-и.
,
Физ. Ред. E
89
,
052106
(
2014
).
10.1103/PhysRevE.89.052106
[47]
Gnoli
A.
Petri
A.
Dalton
F.
Pontuale
G.
Gradenigo
G.
Sarracino
А.
Пуглиси
А.
,
Физ. Преподобный Летт.
Преподобный Летт.
110
,
120601
(
2013
).
10.1103/PhysRevLett.110.120601
[48]
Itami
M.
Sasa
S.-i.
,
J. Стат. физ.
158
,
37
(
2015
).
10.1007/s10955-014-1115-7
Примечания автора
† Текущий адрес: Факультет физики Университета Рицумейкан, Кусацу, Сига 525-8577, Япония. Электронная почта: [email protected]
© Автор(ы), 2016 г. Опубликовано Oxford University Press от имени Физического общества Японии.
Это статья в открытом доступе, распространяемая в соответствии с лицензией Creative Commons Attribution License (http://creativecommons. org/licenses/by/4.0/), которая разрешает неограниченное повторное использование, распространение и воспроизведение на любом носителе при условии, что оригинальная работа правильно цитируется.
org/licenses/by/4.0/), которая разрешает неограниченное повторное использование, распространение и воспроизведение на любом носителе при условии, что оригинальная работа правильно цитируется.
© Автор(ы), 2016 г. Опубликовано Oxford University Press от имени Физического общества Японии.
Тема
А47 Другие темы равновесной статистической механики А50 Стохастические процессы, стохастические модели и протекания А56 Нелинейные и неравновесные явления А58 Другие темы неравновесной статистической механики
Выпуск Раздел:
Общая и математическая физика
Скачать все слайды
Реклама
Цитаты
Альтметрика
Дополнительная информация о метриках
Оповещения по электронной почте
Оповещение об активности статьи
Предварительные уведомления о статьях
Оповещение о новой проблеме
Оповещение о текущей проблеме
Оповещение о теме
Получайте эксклюзивные предложения и обновления от Oxford Academic
Система астрофизических данных
Резюме объявлений
Ссылки на статьи по телефону
Последний
Самые читаемые
Самые цитируемые
Эффекты инстантона на электромагнитные переходы чармония
Мягкий дипольный резонанс в богатом нейтронами 8 He
Поиск аксионоподобных частиц электронными и позитронными пучками на ускорительном ускорителе KEK
Реакция подземной среды обсерватории KAGRA на возмущение атмосферного давления от извержения вулкана Тонга 15 января 2022 г.
Расчет голографического индекса для теорий Аргиреса-Дугласа и Минахана-Немещанского
Реклама
15.3 Введение во второй закон термодинамики: тепловые двигатели и их эффективность — College Physics 2e
Цели обучения
К концу этого раздела вы сможете:
- Назовите выражения второго закона термодинамики.
- Рассчитайте КПД и выбросы углекислого газа угольной электростанции, используя характеристики второго закона.
- Опишите и дайте определение циклу Отто.
Рисунок
15.14
Эти льдины тают во время арктического лета. Некоторые из них замерзают зимой, но второй закон термодинамики предсказывает, что молекулам воды, содержащимся в этих конкретных льдинах, крайне маловероятно, чтобы они преобразовали характерную аллигатороподобную форму, которую они сформировали, когда снимок был сделан летом 2009 года.. (кредит: Патрик Келли, Береговая охрана США, Геологическая служба США)
Второй закон термодинамики касается направления самопроизвольных процессов. Многие процессы протекают самопроизвольно только в одном направлении, т. е. необратимы при данном наборе условий. Хотя необратимость наблюдается в повседневной жизни — например, разбитое стекло не возвращается в исходное состояние — полная необратимость — это статистическое утверждение, которое нельзя увидеть в течение жизни Вселенной. Точнее, необратимый процесс — это процесс, зависящий от пути. Если процесс может идти только в одном направлении, то обратный путь принципиально иной и процесс не может быть обратимым. Например, как отмечалось в предыдущем разделе, теплота включает передачу энергии от более высокой температуры к более низкой. Холодный объект при соприкосновении с горячим никогда не становится холоднее, передавая тепло горячему объекту и делая его горячее. Кроме того, механическая энергия, например кинетическая энергия, может быть полностью преобразована в тепловую энергию трения, но обратное невозможно. Горячий неподвижный объект никогда самопроизвольно не остывает и не приходит в движение.
Многие процессы протекают самопроизвольно только в одном направлении, т. е. необратимы при данном наборе условий. Хотя необратимость наблюдается в повседневной жизни — например, разбитое стекло не возвращается в исходное состояние — полная необратимость — это статистическое утверждение, которое нельзя увидеть в течение жизни Вселенной. Точнее, необратимый процесс — это процесс, зависящий от пути. Если процесс может идти только в одном направлении, то обратный путь принципиально иной и процесс не может быть обратимым. Например, как отмечалось в предыдущем разделе, теплота включает передачу энергии от более высокой температуры к более низкой. Холодный объект при соприкосновении с горячим никогда не становится холоднее, передавая тепло горячему объекту и делая его горячее. Кроме того, механическая энергия, например кинетическая энергия, может быть полностью преобразована в тепловую энергию трения, но обратное невозможно. Горячий неподвижный объект никогда самопроизвольно не остывает и не приходит в движение. Еще одним примером является расширение струи газа, введенной в один из углов вакуумной камеры. Газ расширяется, заполняя камеру, но никогда не собирается в углу. Беспорядочное движение молекул газа могло бы привести их всех обратно в угол, но этого никогда не происходит. (См. рис. 15.15.)
Еще одним примером является расширение струи газа, введенной в один из углов вакуумной камеры. Газ расширяется, заполняя камеру, но никогда не собирается в углу. Беспорядочное движение молекул газа могло бы привести их всех обратно в угол, но этого никогда не происходит. (См. рис. 15.15.)
Рисунок
15.15
Примеры односторонних процессов в природе. а) Теплопередача происходит самопроизвольно от горячего к холодному, а не от холодного к горячему. (b) Тормоза этого автомобиля преобразуют его кинетическую энергию в передачу тепла окружающей среде. Обратный процесс невозможен. (c) Выброс газа, впущенного в эту вакуумную камеру, быстро расширяется, чтобы равномерно заполнить все части камеры. Беспорядочные движения молекул газа никогда не вернут их в угол.
Тот факт, что некоторые процессы никогда не происходят, говорит о том, что существует закон, запрещающий им происходить. Первый закон термодинамики допускает их возникновение — ни один из этих процессов не нарушает закон сохранения энергии. Закон, запрещающий эти процессы, называется вторым законом термодинамики. Мы увидим, что второй закон можно сформулировать разными способами, которые могут показаться разными, но на самом деле они эквивалентны. Как и все законы природы, второй закон термодинамики дает представление о природе, и несколько его утверждений подразумевают, что он широко применим, коренным образом влияя на многие, казалось бы, несопоставимые процессы.
Закон, запрещающий эти процессы, называется вторым законом термодинамики. Мы увидим, что второй закон можно сформулировать разными способами, которые могут показаться разными, но на самом деле они эквивалентны. Как и все законы природы, второй закон термодинамики дает представление о природе, и несколько его утверждений подразумевают, что он широко применим, коренным образом влияя на многие, казалось бы, несопоставимые процессы.
Уже знакомое нам направление теплопередачи от горячего к холодному лежит в основе нашей первой версии второго закона термодинамики.
Второй закон термодинамики (первое выражение)
Теплопередача происходит самопроизвольно от тел с более высокой температурой к телам с более низкой температурой, но никогда самопроизвольно в обратном направлении.
Другой способ выразить это: ни один процесс не может иметь своим единственным результатом передачу тепла от более холодного объекта к более горячему.
Тепловые двигатели
Теперь давайте рассмотрим устройство, которое использует теплопередачу для выполнения работы. Как отмечалось в предыдущем разделе, такое устройство называется тепловым двигателем, и оно схематически показано на рис. 15.16(b). Бензиновые и дизельные двигатели, реактивные двигатели и паровые турбины — все это тепловые двигатели, которые работают, используя часть теплопередачи из какого-либо источника. Теплоотдача от горячего тела (или горячего резервуара) обозначается как QhQh, теплопередача в холодный предмет (или холодный резервуар) – QcQc, а работа, совершаемая двигателем, – WW. Температуры горячего и холодного резервуаров равны ThTh и TcTc соответственно.
Как отмечалось в предыдущем разделе, такое устройство называется тепловым двигателем, и оно схематически показано на рис. 15.16(b). Бензиновые и дизельные двигатели, реактивные двигатели и паровые турбины — все это тепловые двигатели, которые работают, используя часть теплопередачи из какого-либо источника. Теплоотдача от горячего тела (или горячего резервуара) обозначается как QhQh, теплопередача в холодный предмет (или холодный резервуар) – QcQc, а работа, совершаемая двигателем, – WW. Температуры горячего и холодного резервуаров равны ThTh и TcTc соответственно.
Рисунок
15.16
а) Теплопередача происходит самопроизвольно от горячего тела к холодному в соответствии со вторым законом термодинамики. б) Тепловая машина, представленная здесь кружком, использует часть теплопередачи для совершения работы. Горячие и холодные объекты называются горячими и холодными резервуарами. QhQh — теплоотдача из горячего резервуара, WW — работа, QcQc — теплоотдача в холодный резервуар.
Поскольку горячий резервуар нагревается снаружи, что требует больших затрат энергии, важно, чтобы работа выполнялась максимально эффективно. На самом деле хотелось бы, чтобы WW было равно QhQh, и чтобы не было передачи тепла в окружающую среду (Qc=0Qc=0). К сожалению, это невозможно. Второй закон термодинамики также утверждает относительно использования теплопередачи для совершения работы (второе выражение второго закона):
Второй закон термодинамики (второе выражение)
Ни в одной системе теплопередачи от резервуара невозможно полное преобразование в работу в циклическом процессе, при котором система возвращается в исходное состояние.
Циклический процесс возвращает систему, например газ в баллоне, в исходное состояние в конце каждого цикла. В большинстве тепловых двигателей, таких как поршневые двигатели и вращающиеся турбины, используются циклические процессы. Второй закон, только что изложенный в его второй форме, ясно утверждает, что такие двигатели не могут иметь совершенного преобразования теплопередачи в совершенную работу. Прежде чем перейти к основным причинам ограничений на преобразование теплопередачи в работу, нам необходимо изучить взаимосвязь между WW, QhQh и QcQc и определить эффективность циклической тепловой машины. Как уже отмечалось, циклический процесс возвращает систему в исходное состояние в конце каждого цикла. Внутренняя энергия такой системы UU одинакова в начале и в конце каждого цикла, то есть ΔU=0ΔU=0. Первый закон термодинамики гласит, что
Прежде чем перейти к основным причинам ограничений на преобразование теплопередачи в работу, нам необходимо изучить взаимосвязь между WW, QhQh и QcQc и определить эффективность циклической тепловой машины. Как уже отмечалось, циклический процесс возвращает систему в исходное состояние в конце каждого цикла. Внутренняя энергия такой системы UU одинакова в начале и в конце каждого цикла, то есть ΔU=0ΔU=0. Первый закон термодинамики гласит, что
ΔU=Q-W, ΔU=Q-W,
15,22
, где QQ — чистая теплопередача во время цикла (Q=Qh−QcQ=Qh−Qc), а WW — чистая работа, выполненная системой. Поскольку ΔU=0ΔU=0 для полного цикла, имеем
0=Q−W,0=Q−W,
15,23
так что
Вт=Q.W=Q.
15,24
Таким образом, чистая работа, совершаемая системой, равна чистой передаче тепла в систему, или
W=Qh-Qc(циклический процесс),W=Qh-Qc(циклический процесс),
15,25
так, как схематично показано на рис. 15.16(b). Проблема в том, что во всех процессах происходит некоторая теплопередача QcQc в окружающую среду, и обычно очень значительная.
15.16(b). Проблема в том, что во всех процессах происходит некоторая теплопередача QcQc в окружающую среду, и обычно очень значительная.
При преобразовании энергии в работу мы всегда сталкиваемся с проблемой того, что получаем меньше, чем вкладываем. Мы определяем КПД преобразования EffEff как отношение выхода полезной работы к подводимой энергии (или, другими словами, словами, отношение того, что мы получаем, к тому, что мы тратим). В этом духе мы определяем КПД тепловой машины как его чистую выходную мощность WW, деленную на теплопередачу двигателю QhQh; то есть
Eff=WQh.Eff=WQh.
15,26
Поскольку W=Qh-QcW=Qh-Qc в циклическом процессе, мы также можем выразить это как
Eff=Qh-QcQh=1-QcQh(циклический процесс),Eff=Qh-QcQh=1-QcQh(циклический процесс),
15,27
поясняя, что эффективность 1 или 100% возможна только если нет передачи тепла в окружающую среду (Qc=0Qc=0). Обратите внимание, что все QQ положительны. Направление теплопередачи указывается знаком плюс или минус. Например, QcQc находится вне системы, поэтому ему предшествует знак минус.
Обратите внимание, что все QQ положительны. Направление теплопередачи указывается знаком плюс или минус. Например, QcQc находится вне системы, поэтому ему предшествует знак минус.
Пример
15,3
Ежедневная работа угольной электростанции, ее эффективность и выбросы углекислого газа
Угольная электростанция представляет собой огромную тепловую машину. Он использует теплопередачу от сжигания угля для выполнения работы по вращению турбин, которые используются для выработки электроэнергии. За один день крупная угольная электростанция имеет 2,50×1014J2,50×1014Дж теплоотдачи от угля и 1,48×1014J1,48×1014Дж теплоотдачи в окружающую среду. а) Какую работу совершает электростанция? б) Каков КПД электростанции? (c) В процессе горения происходит следующая химическая реакция: C+O2→CO2C+O2→CO2 . Это означает, что каждые 12 кг угля выбрасывают в атмосферу 12 кг + 16 кг + 16 кг = 44 кг углекислого газа. Предполагая, что 1 кг угля может обеспечить 2,5×106 Дж2,5×106 Дж теплопередачи при сгорании, сколько CO2CO2 выбрасывается в сутки этой электростанцией?
Стратегия для (a)
Мы можем использовать W=Qh-QcW=Qh-Qc, чтобы найти выход работы WW, предполагая, что на электростанции используется циклический процесс. В этом процессе вода кипятится под давлением с образованием высокотемпературного пара, который используется для работы паровых турбин-генераторов, а затем конденсируется обратно в воду, чтобы снова запустить цикл.
В этом процессе вода кипятится под давлением с образованием высокотемпературного пара, который используется для работы паровых турбин-генераторов, а затем конденсируется обратно в воду, чтобы снова запустить цикл.
Решение для (a)
Результат работы определяется как:
W=Qh-Qc.W=Qh-Qc.
15,28
Подставляя данные значения:
W=2,50×1014Дж–1,48×1014Дж=1,02×1014Дж.W=2,50×1014Дж–1,48×1014Дж=1,02×1014Дж.
15,29
Стратегия для (b)
Эффективность можно рассчитать с помощью Eff=WQhEff=WQh, поскольку QhQh задано, а работа WW была найдена в первой части этого примера.
Решение для (b)
Эффективность определяется по формуле: Eff=WQhEff=WQh. Только что было найдено, что работа WW равна 1,02 × 1014J1,02 × 1014J, и задано QhQh, поэтому эффективность равна
Eff=1,02×1014J2,50×1014J=0,408, или 40,8%Eff=1,02×1014J2,50×1014J=0,408, или 40,8%
15,30
Суточный расход угля 9 рассчитано с использованием информации о том, что каждый день происходит 2,50×1014 Дж2,50×1014 Дж теплопередачи от угля.
 В процессе горения мы имеем C+O2→CO2C+O2→CO2 . Таким образом, каждые 12 кг угля выбрасывают в атмосферу 12 кг + 16 кг + 16 кг = 44 кг CO2CO2 .
В процессе горения мы имеем C+O2→CO2C+O2→CO2 . Таким образом, каждые 12 кг угля выбрасывают в атмосферу 12 кг + 16 кг + 16 кг = 44 кг CO2CO2 .
Раствор для (с)
Ежедневное потребление угля составляет
2,50×1014J2,50×106Дж/кг=1,0×108кг.2,50×1014J2,50×106Дж/кг=1,0×108кг.
15,31
Если предположить, что уголь чистый и весь уголь идет на производство двуокиси углерода, то двуокиси углерода, производимой в день, составляет
1,0×108 кг угля×44 кг CO212 кг угля=3,7×108 кг CO2.1,0×108 кг уголь×44 кг CO212 кг уголь=3,7×108 кг CO2.
15.32
Ежедневно производится 370 000 метрических тонн CO2CO2 .
Обсуждение
Если вся выходная мощность преобразуется в электроэнергию в течение одного дня, средняя выходная мощность составит 1180 МВт (это остается вам решить в конце главы). Это значение примерно соответствует размеру крупной обычной электростанции. Найденный КПД приемлемо близок к значению 42%, данному для угольных электростанций. Это означает, что целых 59,2% энергии приходится на передачу тепла в окружающую среду, что обычно приводит к потеплению озер, рек или океана вблизи электростанции, а также к потеплению планеты в целом. Хотя законы термодинамики ограничивают эффективность таких установок, включая установки, работающие на ядерном топливе, нефти и природном газе, передача тепла в окружающую среду может использоваться и иногда используется для обогрева домов или для промышленных процессов. В целом низкая стоимость энергии не делает более экономичным более эффективное использование отработанного тепла от большинства тепловых двигателей. Электростанции, работающие на угле, производят наибольшее количество CO2CO2 на единицу выработки энергии (по сравнению с природным газом или нефтью), что делает уголь наименее эффективным ископаемым топливом.
Найденный КПД приемлемо близок к значению 42%, данному для угольных электростанций. Это означает, что целых 59,2% энергии приходится на передачу тепла в окружающую среду, что обычно приводит к потеплению озер, рек или океана вблизи электростанции, а также к потеплению планеты в целом. Хотя законы термодинамики ограничивают эффективность таких установок, включая установки, работающие на ядерном топливе, нефти и природном газе, передача тепла в окружающую среду может использоваться и иногда используется для обогрева домов или для промышленных процессов. В целом низкая стоимость энергии не делает более экономичным более эффективное использование отработанного тепла от большинства тепловых двигателей. Электростанции, работающие на угле, производят наибольшее количество CO2CO2 на единицу выработки энергии (по сравнению с природным газом или нефтью), что делает уголь наименее эффективным ископаемым топливом.
С информацией, приведенной в примере 15.3, мы можем найти такие характеристики, как КПД тепловой машины, не зная, как работает тепловая машина, но дальнейшее изучение механизма двигателя даст нам более глубокое понимание.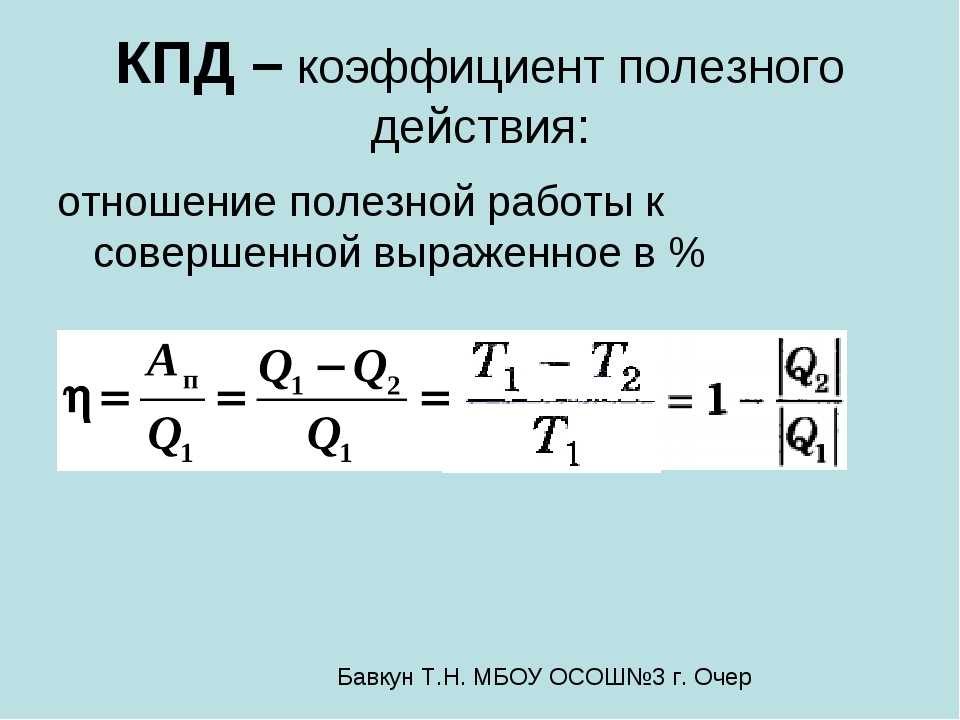 На рис. 15.17 показана работа обычного четырехтактного бензинового двигателя. Четыре показанных шага завершают цикл этой тепловой машины, возвращая смесь бензина и воздуха в исходное состояние.
На рис. 15.17 показана работа обычного четырехтактного бензинового двигателя. Четыре показанных шага завершают цикл этой тепловой машины, возвращая смесь бензина и воздуха в исходное состояние.
Цикл Отто, показанный на рис. 15.18(а), используется в четырехтактных двигателях внутреннего сгорания, хотя на самом деле траектории истинного цикла Отто не соответствуют точно тактам двигателя.
Адиабатический процесс AB соответствует почти адиабатическому такту сжатия бензинового двигателя. В обоих случаях над системой (газовой смесью в цилиндре) совершается работа, повышающая ее температуру и давление. На пути BC цикла Отто теплопередача QhQh в газ происходит при постоянном объеме, вызывая дальнейшее повышение давления и температуры. Этот процесс соответствует сжиганию топлива в двигателе внутреннего сгорания и происходит настолько быстро, что объем почти не меняется. Путь CD в цикле Отто — это адиабатическое расширение, которое действует на внешний мир точно так же, как рабочий ход двигателя внутреннего сгорания действует при его почти адиабатическом расширении. Работа, совершаемая системой на пути CD, больше, чем работа, совершаемая системой на пути AB, потому что давление больше, а значит, есть чистый выход работы. По пути DA в цикле Отто теплоотдача QcQc от газа при постоянном объеме снижает его температуру и давление, возвращая в исходное состояние. В двигателе внутреннего сгорания этот процесс соответствует выпуску горячих газов и впуску воздушно-бензиновой смеси при значительно более низкой температуре. В обоих случаях по этому конечному пути происходит передача тепла в окружающую среду.
Работа, совершаемая системой на пути CD, больше, чем работа, совершаемая системой на пути AB, потому что давление больше, а значит, есть чистый выход работы. По пути DA в цикле Отто теплоотдача QcQc от газа при постоянном объеме снижает его температуру и давление, возвращая в исходное состояние. В двигателе внутреннего сгорания этот процесс соответствует выпуску горячих газов и впуску воздушно-бензиновой смеси при значительно более низкой температуре. В обоих случаях по этому конечному пути происходит передача тепла в окружающую среду.
Чистая работа, выполненная циклическим процессом, представляет собой площадь внутри замкнутого пути на диаграмме PVPV, такой как внутренний путь ABCDA на рис. 15.18. Обратите внимание, что в каждом вообразимом циклическом процессе абсолютно необходима передача тепла от системы, чтобы получить чистую выходную мощность. В цикле Отто передача тепла происходит по пути DA. Если теплопередача не происходит, то обратный путь тот же, а чистая работа равна нулю. Чем ниже температура на пути АВ, тем меньшую работу необходимо совершить для сжатия газа. Площадь внутри замкнутого пути тогда больше, поэтому двигатель выполняет больше работы и, следовательно, более эффективен. Точно так же, чем выше температура на пути CD, тем больше выходная мощность. (См. рис. 15.19..) Таким образом, эффективность связана с температурами горячего и холодного резервуаров. В следующем разделе мы увидим, каков абсолютный предел эффективности тепловой машины и как он связан с температурой.
Чем ниже температура на пути АВ, тем меньшую работу необходимо совершить для сжатия газа. Площадь внутри замкнутого пути тогда больше, поэтому двигатель выполняет больше работы и, следовательно, более эффективен. Точно так же, чем выше температура на пути CD, тем больше выходная мощность. (См. рис. 15.19..) Таким образом, эффективность связана с температурами горячего и холодного резервуаров. В следующем разделе мы увидим, каков абсолютный предел эффективности тепловой машины и как он связан с температурой.
Рисунок
15.17
В четырехтактном бензиновом двигателе внутреннего сгорания передача тепла в работу происходит в циклическом процессе, показанном здесь. Поршень соединен с вращающимся коленчатым валом, который выполняет работу над газом в цилиндре. а) Воздух смешивается с топливом во время такта впуска. (b) Во время такта сжатия топливовоздушная смесь быстро сжимается в почти адиабатическом процессе, когда поршень поднимается при закрытых клапанах. Работа совершается на газе. (c) Рабочий такт состоит из двух отдельных частей. Во-первых, топливовоздушная смесь воспламеняется, почти мгновенно преобразовывая химическую потенциальную энергию в тепловую, что приводит к значительному увеличению давления. Затем поршень опускается, и газ работает, оказывая силу на расстоянии в почти адиабатическом процессе. (d) Такт выпуска выпускает горячий газ, чтобы подготовить двигатель к следующему циклу, начиная снова с такта впуска.
(c) Рабочий такт состоит из двух отдельных частей. Во-первых, топливовоздушная смесь воспламеняется, почти мгновенно преобразовывая химическую потенциальную энергию в тепловую, что приводит к значительному увеличению давления. Затем поршень опускается, и газ работает, оказывая силу на расстоянии в почти адиабатическом процессе. (d) Такт выпуска выпускает горячий газ, чтобы подготовить двигатель к следующему циклу, начиная снова с такта впуска.
Рисунок
15.18
Диаграмма PVPV для упрощенного цикла Отто, аналогичного используемому в двигателе внутреннего сгорания. Точка А соответствует началу такта сжатия двигателя внутреннего сгорания. Пути AB и CD являются адиабатическими и соответствуют такту сжатия и рабочему такту двигателя внутреннего сгорания соответственно. Траектории BC и DA являются изохорными и приводят к тем же результатам, что и части зажигания и выхлопа-впуска, соответственно, цикла двигателя внутреннего сгорания. Работа совершается газом по пути AB, но больше работы совершается газом по пути CD, так что получается чистая работа.
Рисунок
15.19
Этот цикл Отто производит больший объем работы, чем цикл на рис. 15.18, потому что начальная температура пути CD выше, а начальная температура пути AB ниже. Площадь внутри петли больше, что соответствует большему выходу чистой работы.
Инженеры находят новые способы повышения эффективности газовых двигателей: инженерное объяснение
Эрик С. Эвартс
Посмотреть галерею
Эрик С. Эвартс
По мере того, как электромобили совершенствуются и расширяются, есть вещи, в которых бензиновые двигатели работают лучше — многие эксперты сходятся во мнении, что бензиновые двигатели будут существовать еще несколько десятилетий.
Разработка электромобилей и переработка газовых двигателей не исключают друг друга. Электрификация транспортных средств будет продолжать быстро расширяться, а двигатели внутреннего сгорания могут продолжаться и в будущем, хотя их роль несколько уменьшится.
Если это так, то хорошо, что инженеры находят способы повысить эффективность внутреннего сгорания.
В течение многих лет газовые двигатели застряли на 30-процентном тепловом КПД (показатель того, сколько работы они могут выполнить на галлоне топлива), что примерно на треть меньше, чем у электродвигателя (не считая потерь от электростанций и линий электропередач). )
Некоторые из лучших современных автомобильных двигателей достигли 40-процентного теплового КПД.
Пришло время совершить следующий прыжок, о чем рассказывается в этом видеоролике от Engineering Explained.
ПРОВЕРИТЬ : Вот как работает двигатель Mazda HCCI
Следующим крупным скачком станет то, что инженеры называют HCCI: воспламенение от сжатия однородного заряда. Двигатели HCCI работают по тому же принципу, что и дизели, используя тепло от сжатия воздуха в цилиндре для воспламенения топлива. Хитрость заключалась в том, чтобы контролировать температуру в цилиндре и, следовательно, синхронизацию зажигания, поскольку двигатели с чистым HCCI не имеют топливных форсунок в камерах сгорания, как это делают дизели. Например, как запустить двигатель без свечи зажигания?
Хитрость заключалась в том, чтобы контролировать температуру в цилиндре и, следовательно, синхронизацию зажигания, поскольку двигатели с чистым HCCI не имеют топливных форсунок в камерах сгорания, как это делают дизели. Например, как запустить двигатель без свечи зажигания?
Двигатели
HCCI перспективны, потому что, как и дизели, они работают на более обедненной топливно-воздушной смеси, потребляют меньше газа и используют очень высокие степени сжатия, что также повышает эффективность.
НЕ ПРОПУСТИТЕ: первая поездка прототипа Mazda 3 2020 года: могут ли безискровые двигатели разжечь наши страсти?
Mazda объявила, что представит версию HCCI, которая называется Skyactiv-X и будет запущена в производство в 2019 году. худой ожог.
Несколько журналистов, в том числе наши коллеги из Motor Authority , управляли прототипами двигателя и были впечатлены.
Mazda заявляет о 30-процентном повышении эффективности по сравнению с текущей производственной линией бензиновых двигателей Skyactiv-G.
Mazda 2,0-литровый двигатель SkyActiv-X с искровым воспламенением от сжатия (SPCCI)
Теперь исследователи из Университета Висконсина пытаются сделать Mazda еще лучше: они разработали двухтопливный двигатель HCCI, который работает в основном на бензине с воспламенением от сжатия и частично — когда двигатель холодный или при малых нагрузках — на дизельном топливе. топливо.
Исследователи утверждают, что их двигатель с воспламенением от сжатия (RCCI) достиг 60-процентного теплового КПД на испытательном стенде, что представляет собой примерно 50-процентное улучшение по сравнению с лучшими современными двигателями.
Поскольку дизельное топливо воспламеняется намного легче, чем бензин, двигатель RCCI использует дизельное топливо, когда двигатель холодный или при низкой нагрузке. Благодаря очень высокой степени сжатия и низким температурам он позволяет избежать большинства проблем дизельных двигателей, связанных с выбросами оксидов азота и твердых частиц. Двигатель соответствует требованиям Агентства по охране окружающей среды США 2015 года по выбросам для дизелей без необходимости дополнительной обработки выхлопных газов, которая требуется для современных дизелей.
Двигатель соответствует требованиям Агентства по охране окружающей среды США 2015 года по выбросам для дизелей без необходимости дополнительной обработки выхлопных газов, которая требуется для современных дизелей.
При высоких нагрузках и прогретом двигателе в основном используется бензин, который даже в этих условиях работает чисто.
НЕ ПРОПУСТИТЕ: Mazda получила одобрение Калифорнии на дизель CX-5
Как и Skyactiv-X от Mazda, двигатель RCCI использует свечу зажигания для управления опережением зажигания. Он использует дизельное топливо, чтобы по возможности использовать более бедную смесь, смешивает бензин и дизельное топливо в камере сгорания и постоянно регулирует смесь для достижения максимальной эффективности.
Что плохого? В основном необходимость в двух отдельных топливных баках, за которыми водителям придется следить и заполнять.
Эти типы эффективных двигателей могут быть ключом к повышению эффективности грузовиков, которым приходится выполнять тяжелую работу и не тратить время на дозаправку электромобилей (а у большинства автомобилей они есть). Технологии можно даже комбинировать с гибридными системами. чтобы еще больше повысить эффективность.
Технологии можно даже комбинировать с гибридными системами. чтобы еще больше повысить эффективность.
Метки:
Автомобильная техника
Инженерное объяснение
Зеленый
Как это работает
Видео
ютуб
Добавить:
- Отправьте нам чаевые
- Связаться с редактором
Обзор: внедорожники Audi Q4 E-Tron 2023 года и Sportback больше ориентированы на практичность, чем на производительность. и материалы и супер-тихий, комфортный салон.
Союз государств Среднего Запада по производству водорода, потенциально для производства полуфабрикатов на топливных элементах
Коалиция также будет продвигать Средний Запад как многообещающую область для производства водорода с использованием автомобильных, железнодорожных, авиационных и морских перевозок в Великих озерах в качестве потенциальных применений.
Стивен Эдельштейн
Цены на Hyundai Ioniq 5, Tata EV за 10 000 долларов, производство Lordstown Endurance: сегодняшние автомобильные новости Лордстаун (медленно) производит серийные электрические грузовики Endurance. А где можно купить новый электромобиль примерно за 10 000 долларов? Это и многое другое здесь, в Green Car Reports. Индийский автопроизводитель Tata выпустил электрический автомобиль стоимостью 10 000 долларов…
Бенгт Халворсон
Первые электрические грузовики Endurance в Лордстауне еще не поступили в продажу
Лордстаун выпустил два первых серийных грузовика Endurance, хотя отсутствие сертификатов пока не позволяет осуществить поставки.
Бенгт Халворсон
Цена Hyundai Ioniq 5 2023 года выросла на 1500 долларов — до того, как дилеры наценят 10 000 долларов
Ioniq 5 больше не имеет права на налоговую льготу в размере 7 500 долларов США, но покупатели продолжают платить 10 000 долларов за наклейку — и эта наклейка вырастет примерно на 1 500 долларов в 2023 году.

Стивен Эдельштейн
Tata выпускает электромобиль стоимостью 10 000 долларов для Индии
Электрический хэтчбек Tiago.ev от индийского автопроизводителя считается одним из самых доступных новых электромобилей в мире; несколько моделей в Китае стоят еще ниже.
Стивен Эдельштейн
Цены на Nissan Ariya, Niro Hybrid на 53 мили на галлон, производительность Polestar 3: сегодняшние автомобильные новости
Бенгт Халворсон
Гибрид Kia Niro с расходом топлива 53 мили на галлон стоит намного меньше 30 000 долларов. Nissan Ariya 2023 года стоит около 45 000 долларов, но не имеет права на налоговый кредит на электромобиль.
 И Polestar готовится к презентации своей следующей модели 12 октября. Это и многое другое здесь, в Green Car Reports. Polestar раскрыла еще несколько подробностей о своем грядущем электрическом внедорожнике Polestar 3 американского производства, включая подтверждение пакета Performance Pack мощностью 510 л.с., управления вектором крутящего момента на основе сцепления, пневматической подвески и адаптивного демпфирования. Ожидается, что размер 3 будет близок к таким моделям, как Tesla Model X и BMW iX, но будет отличаться от…
И Polestar готовится к презентации своей следующей модели 12 октября. Это и многое другое здесь, в Green Car Reports. Polestar раскрыла еще несколько подробностей о своем грядущем электрическом внедорожнике Polestar 3 американского производства, включая подтверждение пакета Performance Pack мощностью 510 л.с., управления вектором крутящего момента на основе сцепления, пневматической подвески и адаптивного демпфирования. Ожидается, что размер 3 будет близок к таким моделям, как Tesla Model X и BMW iX, но будет отличаться от…Kia Niro Hybrid 2023 года стоит 27 785 долларов США, расход топлива составляет до 53 миль на галлон в смешанном цикле чем у предыдущей модели.
Стивен Эдельштейн
Nissan Ariya 2023 года начинается с 44 485 долларов США, цена на ранее анонсированные версии
9 повышенаПо данным Nissan, версии 0003 Base Engage с меньшим аккумуляторным блоком будут рассчитаны на 216 миль пробега, а версии с большим аккумулятором — до 304 миль по рейтингу EPA.

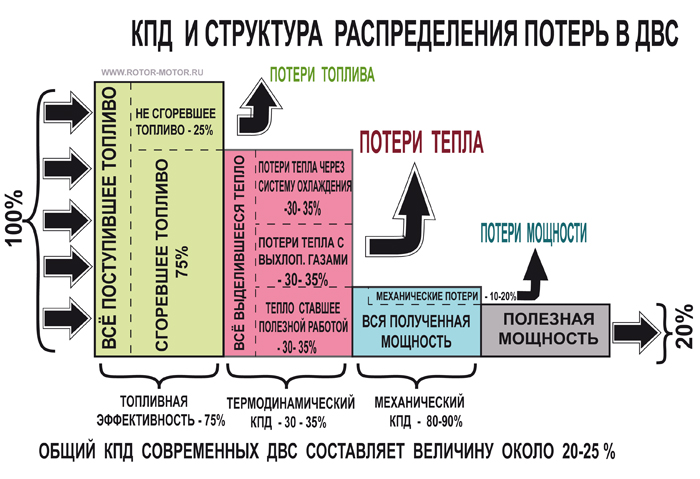
 Определите КПД машины.
Определите КПД машины. Определите КПД машины.
Определите КПД машины. Дзен
Дзен
 2/12000)*100%=83%
2/12000)*100%=83% 2)
2) Поэтому данное в условии задачи количество теплоты является количеством теплоты, полученным от нагревателя в течение цикла, — количеством теплоты, отданном холодильнику. Поэтому работа газа равна (ответ 1).
Поэтому данное в условии задачи количество теплоты является количеством теплоты, полученным от нагревателя в течение цикла, — количеством теплоты, отданном холодильнику. Поэтому работа газа равна (ответ 1).
 Если система
Если система
 Если реальный
Если реальный
 31 Рассчитайте изменение энтропии 250 г нагретой воды.
31 Рассчитайте изменение энтропии 250 г нагретой воды.
 Таблицу 20.2)
Таблицу 20.2) ; все права защищены
; все права защищены Сано, Хисао Хаякава, КПД при максимальной выходной мощности двигателя с пассивным поршнем, Прогресс теоретической и экспериментальной физики , том 2016 г., выпуск 8, август 2016 г., 083A03, https://doi.org/10.1093/ptep/ptw103
Сано, Хисао Хаякава, КПД при максимальной выходной мощности двигателя с пассивным поршнем, Прогресс теоретической и экспериментальной физики , том 2016 г., выпуск 8, август 2016 г., 083A03, https://doi.org/10.1093/ptep/ptw103
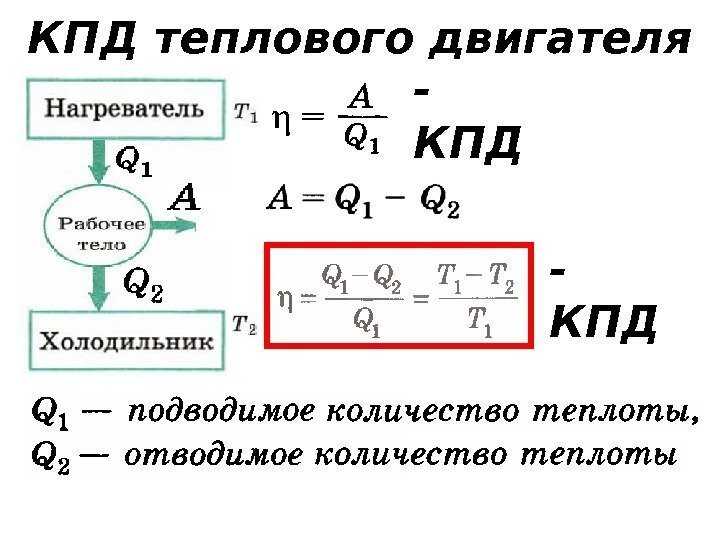 И Polestar готовится к презентации своей следующей модели 12 октября. Это и многое другое здесь, в Green Car Reports. Polestar раскрыла еще несколько подробностей о своем грядущем электрическом внедорожнике Polestar 3 американского производства, включая подтверждение пакета Performance Pack мощностью 510 л.с., управления вектором крутящего момента на основе сцепления, пневматической подвески и адаптивного демпфирования. Ожидается, что размер 3 будет близок к таким моделям, как Tesla Model X и BMW iX, но будет отличаться от…
И Polestar готовится к презентации своей следующей модели 12 октября. Это и многое другое здесь, в Green Car Reports. Polestar раскрыла еще несколько подробностей о своем грядущем электрическом внедорожнике Polestar 3 американского производства, включая подтверждение пакета Performance Pack мощностью 510 л.с., управления вектором крутящего момента на основе сцепления, пневматической подвески и адаптивного демпфирования. Ожидается, что размер 3 будет близок к таким моделям, как Tesla Model X и BMW iX, но будет отличаться от…