Физика. Механика

Представим снова элементарную работу в виде

Удельная величина, равная отношению работы совершенной за время dt к этому времени, называется мощностью:

Другими словами, мощность, развиваемая некоторой силой, равна скорости, с которой эта сила производит работу. Можно сказать и так: средняя за единицу времени мощность численно равна работе совершенной за единицу времени. Если мощность за выбранную единицу времени практически не меняется, то слово «средняя» можно опустить: мощность численно равна работе за единицу времени.

Как видно из определения, мощность равна скалярному произведению силы на скорость перемещения её точки приложения, поэтому работа силы за время от t1 до t2 может быть вычислена следующим образом:

Средняя мощность за этот же промежуток времени равна

За единицу мощности принимается такая мощность, при которой в единицу времени совершается единица работы.

В системе СИ единицей измерения мощности является ватт (Вт):

Внесистемная единица мощности — лошадиная сила (л.с.) — равна 736 Вт. В быту часто используют единицу энергии — 1 кВт•ч = 103 Вт•3600 с=3.6 МДж.

Пример. Вертолет массой m = 3 m висит в воздухе. Определить мощность, развиваемую мотором вертолета, если диаметр ротора равен d = 8 м. При расчете принять, что ротор отбрасывает вниз цилиндрическую струю воздуха диаметром, равным диаметру ротора. Плотность воздуха 1.29 кг/м3.

При решении этой задачи надо применить все известные нам законы динамики. Поскольку это — не одно- и не двухходовая задача, попробуем сначала найти вид окончательного выражения, пользуясь анализом размерности (см. тему 1.3). Искомая мощность зависит от: 1) веса вертолета mg; 2) диаметра винта d, 3) плотности воздуха , то есть искомая формула должна иметь вид

Размерность мощности будет [N] = [ML2T–3]. Составляем равенство размерностей в обеих частях искомой формулы:

Решая систему уравнений

находим

то есть искомая мощность двигателя вертолета будет

где C — некий числовой коэффициент.

Решим теперь эту же задачу точно. Пусть — скорость струи воздуха, отбрасываемой винтом. За время частицы воздуха проходят расстояние . Иными словами, за время винт вертолета придает скорость всем частицам воздуха, находящимся в цилиндре с площадью основания и высотой . Масса воздуха в этом объеме равна

а его кинетическая энергия дается выражением

Поскольку мотор передает воздуху кинетическую энергию , то такова и совершаемая им работа. Поэтому развиваемая мотором мощность (без учета потерь мощности во всех трансмиссиях на пути от двигателя до винта) равна

В этом выражении нам надо еще найти скорость струи воздуха, отбрасываемой винтом. Импульс , передаваемый частицам воздуха за время , равен

Из второго закона Ньютона следует, что средняя сила, действующая на отбрасываемый вниз воздух равна . По третьему закону Ньютона такая же сила действует на вертолет со стороны воздуха. Эта сила компенсирует вес вертолета:

Отсюда получаем уравнение

позволяющее найти скорость струи воздуха:

Подставляя найденную скорость в выражение для мощности двигателя вертолета, получаем окончательный результат:

Мы видим, что выражение для мощности действительно оказалось таким, каким ожидалось на основе анализа размерностей. Подставляя числовые данные, находим

Рис.4.5. Мощность в природе и технике

Урок физики «Мощность»

Цели урока:

  • Познакомиться с мощностью как новой физической величиной;

  • Развивать умения выводить формулы, пользуясь необходимыми знаниями прошлых уроков; развивать логическое мышление, умение анализировать, делать выводы;

  • Применять знания по физике в окружающем мире.

Ход урока

«И вечный бой! Покой нам только снится
Сквозь кровь и пыль…
Летит, летит степная кобылица
И мнет ковыль…
И нет конца! Мелькают вёрсты, кручи…
Останови! …Покоя нет! Степная кобылица несется вскачь!»

А. Блок «На поле Куликовом» (июнь 1908 г). ( Слайд 1).

Урок сегодня я хочу начать с вопросов к вам. (Слайд 2).

1. Как вы думаете, имеет ли какое-то отношение лошадь к физике?

2. С какой физической величиной связана лошадь?

Мощность – правильно, это и есть тема нашего урока. Запишем ее в тетрадь.

Действительно, мощность двигателей автомобилей, транспортных средств до сих пор измеряют в лошадиных силах. Сегодня на уроке мы с вами узнаем всё о мощности с точки зрения физики. Давайте подумаем вместе и определим, что мы должны знать о мощности, как о физической величине.

Существует план изучения физических величин: ( Слайд 3).

  1. Определение;

  2. Вектор или скаляр;

  3. Буквенное обозначение;

  4. Формула;

  5. Прибор для измерения;

  6. Единица величины.

Этот план и будут целью нашего урока.

Начнем с примера из жизни. Вам необходимо набрать бочку воды для полива растений. Вода находится в колодце. У вас есть выбор: набрать при помощи ведра или при помощи насоса. Напомню, что в обоих случаях механическая работа, совершенная при этом будет одинаковой. Конечно же, большинство из вас выберут, насос.

Вопрос: В чем разница при выполнении одной и той же работы?

Ответ: Насос выполнит эту работу быстрее, т.е. затратит меньшее время.

1) Физическая величина, характеризующая быстроту выполнения работы, называют мощностью. ( Слайд 4).

2) Скаляр, т.к. не имеет направления.

3) N.

4)

5) [N] = [ 1 Дж/с] = [1Вт ]

Название этой единицы мощности дано в честь английского изобретателя паровой машины (1784г) Джеймса Уатта. ( Слайд 5).

6) 1 Вт = мощности, при которой за время 1 с совершается работа в 1 Дж. ( Слайд 6).

Самолеты, автомобили, корабли и другие транспортные средства движутся часто с постоянной скоростью. Например, на трассах автомобиль достаточно долго может двигаться со скоростью 100 км/ч. ( Слайд 7).

Вопрос: от чего зависит скорость движения таких тел?

Оказывается, она напрямую зависит от мощности двигателя автомобиля.

Зная, формулу мощности мы выведем еще одну, но для этого давайте вспомним основную формулу для механической работы.

Учащийся выходит к доске для вывода формулы. ( Слайд 8).

Пусть сила совпадает по направлению со скоростью тела. Запишем формулу работы этой силы.

1.

2.При постоянной скорости движения , тело проходит путь определяемой формулой

Подставляем в исходную формулу мощности: , получаем — мощность.

У нас получилась еще одна формула для расчета мощности, которую мы будем использовать при решении задач.

Эта формула показывает ( Слайд 9), что при постоянной мощности двигателя, изменением скорости можно менять силу тяги автомобиля и наоборот, при изменении скорости автомобиля можно менять силу тяги двигателя.

При N = const

v > , F <.

v < , F >.

Вопрос. Когда нужна большая сила тяги?

Ответ:

а)При подъеме в гору. Правильно, тогда водитель снижает скорость.

б) При вспашке земли тракторист движется с малой скоростью, чтобы была большая сила тяги. Для этого водитель, тракторист, машинист, токарь, фрезеровщик часто используют коробку передач, которая позволяет менять скорость. ( Слайд 10).

Мощность всегда указывают в паспорте технического устройства. И в современных технических паспортах автомобилей есть графа:

Мощность двигателя: кВт / л.с.

Следовательно, между этими единицами мощности существует связь.

Вопрос: А откуда взялась эта единица мощности? ( Слайд 11).

Дж. Уатту принадлежит идея измерять механическую мощность в «лошадиных силах». Предложенная им единица мощности была весьма популярна, но в 1948　г. Генеральной конференцией мер и весов была введена новая единица мощности в международной системе единиц – ватт. ( Слайд 12).

1 л.с. = 735,5 Вт.

1 Вт = ,00013596 л.с.

Эта единица мощности была изъята из обращения с 1 января 1980 г.

Примеры мощностей современных автомобилей. ( Слайд 13,14).

Различные двигатели имеют разные мощности.

Учебник, страница 134, таблица 5. [1]

Вопрос: А какова мощность человека?

Текс учебника, § 54. Мощность человека при нормальных условиях работы в среднем составляет 70-80 Вт. Совершая прыжки, взбегая по лестнице, человек может развивать мощность до 730 Вт, а в отдельных случаях и большую.[1]

Вопрос: А чем «живые двигатели» отличаются от механических? ( Слайд 15).

Ответ: Тем, что «живые двигатели» могут изменять свою мощность в несколько раз.

Закрепление материала.

1.Расскажите все, что вы знаете о мощности. Ответ по плану изучения физической величины.

2. Упр. 29, задача №6. ( Слайд 16).

Дано: СИ Решение:
m = 125кг N = A / t
h = 70 см0,7 мA = F s s = h
t = 0,3 с F = P = mg
  N = mgh / t
N — ? N = 125 кг · 9,8 Н/ кг · 0,7 м / 0,3 с= 2858,3 Вт ≈ 2,9 кВт

Ответ : N ≈ 2,9 кВт.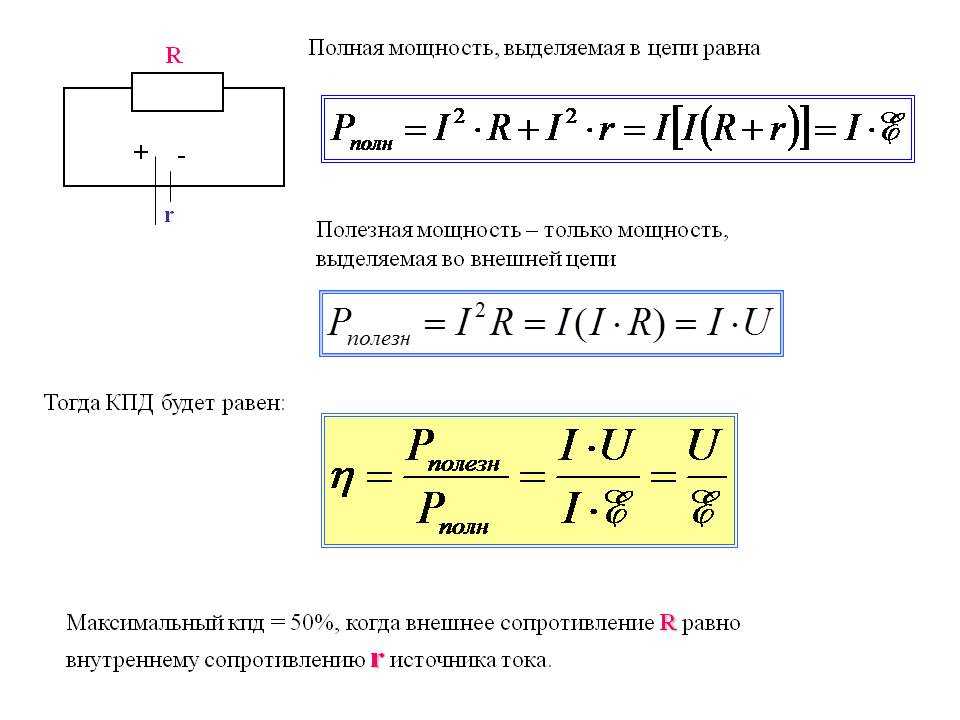

Домашнее задание: ( Слайд 17).

  1. § 54.

  2. Записать формулы мощности в таблицу формул.

  3. Упр. 29 (2,5) – 1 уровень.

  4. Упр. 29 (1,3) – 2 уровень.

  5. Упр. 29 (1,4) – 3 уровень.

  6. Задание 18 – на дополнительную оценку ( на листочках).

Литература:

  1. А.В. Перышкин «Учебник физики для 7 класса», Дрофа, Москва, 2006.

  2. А. Блок «На поле Куликовом».

  3. 1C: Школа Физика 7 класс

лошадиных сил двигателя — Physics LibreTexts

  1. Последнее обновление
  2. Сохранить как PDF
  • Идентификатор страницы
    3372

    • Введение

    В этом небольшом документе обсуждается измерение мощность двигателя, в частности лошадиных сил двигателя автомобиля или мотоцикла. Уровень обсуждения предназначен для начального курса физики университетского уровня.

    Поскольку количество лошадиных сил основано на британской системе единиц и до сих пор часто указывается производителями транспортных средств, мы будем игнорировать единицы СИ.

    Номера формул, указанные с SJ , являются номерами из R.A. Серуэй и Дж.В. Jewett, Основы физики: текст, основанный на исчислении , 3-е изд.; номера уравнений в скобках не из этого текста.

    Для эффективного просмотра этого документа на вашем компьютере должен быть установлен проигрыватель Flash Player версии не ниже 5. Проигрыватель Flash можно бесплатно загрузить с веб-сайта http://www.macromedia.com/.

    Работа и мощность

    Когда сила F действует в направлении движения на объект, после того как объект переместится на расстояние \(\Delta\) r , работа W , выполненная над объектом, равна:

    \[W=F\Delta r \tag{SJ:6. 2}\]

    Если над объектом совершена работа за время \(\Delta\) t , то мощность P равна скорость, с которой совершается работа:

    \[P=\frac{W}{\Delta t} \tag{SJ:6.25}\]

    после Джеймса Уатта, который изобрел современную паровую машину. Размеры указаны в Н-м/с. Британские единицы мощности — ft-lb/sec.

    Примерно в 1775 году Уатт ввел еще одну единицу измерения мощности: 9.0026 лошадиных сил (л.с.) . В то время для подъема угля из шахты использовались лошади, как показано справа.

    Ватт узнал, что «сильная лошадь может поднять 150 фунтов на высоту 220 футов за 1 минуту». Он определил это как одну лошадиную силу.

    1 л.с. составляет 150 фунтов x 220 футов / 60 секунд = 550 фут-фунтов/сек.

    Измерение мощности двигателя в лошадиных силах

    Прямое измерение

    В принципе, мы могли бы измерить мощность двигателя в лошадиных силах так же, как ее определил Уатт: посмотреть, какой вес двигатель может поднять на заданное расстояние за заданное время. .

    Анимация справа показывает двигатель мотоцикла. Шкив установлен на коленчатом валу и вращается вместе с двигателем. Груз подвешен к шкиву на веревке, и двигатель поднимает груз с постоянной скоростью. Вес имеет величину F , а радиус шкива r .

    На практике этот метод очень сложен, так как реальный двигатель вращается со скоростью тысячи оборотов в минуту.

    Косвенное измерение

    Способ, которым обычно выполняется измерение мощности двигателя, аналогичен показанному на рисунке справа. Шкив, прикрепленный к коленчатому валу двигателя, контактирует с другим шкивом через материал с высоким коэффициентом трения между ними. На втором шкиве подвешен груз, и его масса регулируется так, чтобы он оставался неподвижным.

    Эксперимент Механический эквивалент тепла в лаборатории использует очень похожую технику. Руководство по проведению эксперимента (pdf, 297к) здесь.

    Двигатель, показанный на этих анимациях, взят от мотоцикла Suzuki SV650. Изображение используется с разрешения. Исходный сайт: www.koups.com/sales/suzuki/sp…sv650_info.htm

    В приведенном выше Прямом измерении после одного оборота двигателя работа, выполненная им, равна длине окружности шкива. умноженное на силу:

    \[W_{1~rev}=2 \pi rF\tag{1}\]

    Когда приложенная сила F действует под углом \( \varphi \) по отношению к положению вектор r определение точки приложения силы, крутящий момент:

    \[\tau =rF \sin(\phi) \tag{SJ:10.18}\]

    Для прямого измерения , угол \( \varphi \) составляет 90 градусов, поэтому крутящий момент, создаваемый двигателем, равен r x F . Таким образом, мы перепишем уравнение (1) с точки зрения крутящего момента, создаваемого двигателем:

    \[W_{1~об}=2 \pi \tau \tag{2}\]

    , общий крутящий момент на втором шкиве равен нулю, так как он неподвижен. Таким образом, крутящий момент, действующий на него со стороны двигателя через первый шкив, равен и противоположен крутящему моменту, действующему на груз. Таким образом, крутящий момент, создаваемый двигателем, такой же, как и у 9-цилиндрового двигателя.0034 Прямое измерение : r x F . Точно так же уравнения (1) и (2) выше дают работу, совершаемую двигателем после одного оборота; энергия в этом случае переходит в теплоту, выделяемую трением.

    После того, как двигатель совершил \( \Delta \) n оборотов, работа будет равна:

    \[W_{\Delta n~об}=2 \pi \tau \Delta n \tag{3}\ ]

    Таким образом, скорость выполняемой работы, мощность, равна:

    \[P=2\pi \tau \left(\frac{\Delta n}{\Delta t}\right) \tag{4} \]

    Обычно скорость двигателя измеряется в оборотах в минуту ( об/мин ), что связано с оборотами в секунду соотношением:

    \[\frac{\Delta n}{\Delta t} =\frac{ rpm}{60} \tag{5}\]

    Таким образом, мощность равна:

    \[P=\frac{2~\pi~\tau ~rpm}{60}\tag{6}\]

    В британской системе единиц измерения мощности в уравнении (6) равны фут-фунт / сек . Так как 1 лошадиная сила равна 550 ft-lb/sec, то мощность двигателя равна:

    \[hp=\frac{2~\pi~\tau ~rpm}{60(550)} \tag{7a}\]

    \[hp=\frac{\tau ~rpm}{5252} \ tag{7b}\]

    Выводы

    Мы видели, что лошадиных сил двигателя получается из измерения его крутящего момента . Недолгое размышление может убедить вас в том, что крутящий момент действительно является основной величиной, представляющей интерес при измерении мощности двигателя, поскольку именно крутящий момент, воздействующий на колеса, заставляет автомобиль ускоряться.

    Вы также можете увидеть из уравнения. (7b), что при 5252 об/мин мощность всегда численно равна крутящему моменту. Когда частота вращения меньше 5252 об/мин, мощность меньше крутящего момента, а когда частота вращения больше 5252 об/мин, мощность больше крутящего момента.

    Прибор, измеряющий мощность двигателя, называется динамометром . Ниже приведен результат динамометрического измерения изготовленного на заказ V-образного двигателя мотоцикла объемом 1200 куб. см. Более светлая синяя кривая — это крутящий момент, а темно-синяя — мощность.

    Приведенный выше график был сделан для двигателя, модифицированного Моше К. Леви, и используется с разрешения. Оригинальный сайт: http://www.mklsportster.com/xlnallinstage2.htm.

    Наконец, для повседневного использования в автомобиле хороший двигатель обеспечивает высокий крутящий момент и обеспечивает этот крутящий момент в широком диапазоне оборотов. Полученное значение лошадиных сил далеко не так хорошо измеряет двигатель.

    Вопрос

    В системе единиц СИ мощность двигателя обычно выражается в киловаттах, а крутящий момент в Н-м. Что эквивалентно уравнению (7b) для динамометра, который измеряет крутящий момент в единицах СИ и для которого мы хотим выразить мощность в кВт?

    Лошадиная сила двигателя распространяется по недекларированной лицензии, автором, ремиксом и/или куратором является LibreTexts.

    1. Наверх
      • Была ли эта статья полезной?
      1. Тип изделия
        Раздел или Страница
        Показать оглавление
        нет
      2. Теги
        1. source@https://ocw.mit.edu/courses/electrical-engineering-and-computer-science/6-013-electromagnetics-and-applications-spring-2009

      Как рассчитать механическую мощность

      Обновлено 22 декабря 2020 г.

      Автор Kenrick Vezina

      Вы можете найти​ механическая мощность используется повсеместно в современном мире. Ты сегодня ездил на машине? Он использовал энергию топлива или батареи для перемещения взаимосвязанных механических компонентов — осей, шестерен, ремней и т. д. — пока, наконец, эта энергия не использовалась для вращения колес и движения автомобиля вперед.

      ​ Мощность ​ в физике является мерой ​ скорости ​ , с которой ​ работа ​ выполняется с течением времени. Слово «механический» является просто описательным; он говорит вам, что мощность связана с машиной и движением различных компонентов, таких как трансмиссия автомобиля или шестеренки часов.

      Формула механической энергии использует те же фундаментальные законы физики, что и другие формы энергии.

      TL;DR (слишком длинный; не читал)

      ​ Мощность ​ P ​ ​определяется как работа ​ Вт ​ ​ более 2 ​ 9 0 время ​ 39026 по следующей формуле. Примечание по единицам измерения: мощность должна быть в ваттах (Вт), работа в джоулях (Дж) и время в секундах (с) — всегда перепроверяйте, прежде чем вставлять свои значения.

      Механическая энергия подчиняется тем же законам, что и другие виды энергии, такие как химическая или тепловая. .

      Энергия, сила, работа и мощность

      Чтобы понять выражение для механической силы, полезно представить четыре взаимосвязанных термина: ​ энергия ​, ​ сила ​, ​ работа ​ и ​ мощность ​.

      • ​ энергия ​ E ​ ​ содержащаяся в объекте, является мерой того, какую работу он может выполнить; другими словами, сколько движения он может создать. Измеряется в джоулях (Дж).
      • A ​ сила ​ F ​ ​ является, по сути, толчком или тягой. Силы передают энергию между объектами. Как и скорость, сила имеет как величину , так и направление . Измеряется в ньютонах (Н).
      • Если сила перемещает объект ​ в том же направлении ​, в котором она действует, она выполняет​ работу ​. По определению, одна единица энергии необходима для выполнения одной единицы работы. Поскольку энергия и работа определяются друг через друга, они оба измеряются в джоулях (Дж).
      • ​ Мощность ​ является мерой​ скорости ​ , при которой выполняется​ работы ​ или ​ энергии используется ​с течением времени. Стандартной единицей мощности является ватт (Вт).

      Уравнение для механической мощности

      Из-за взаимосвязи между энергией и работой существует два распространенных способа математического выражения мощности. Во-первых, с точки зрения работы W и времени t ​:

      P=\frac{W}{t}

      Мощность в линейном движении 9027 25 9027 Если вы имеете дело с линейным движением, вы можете предположить, что любая приложенная сила либо перемещает объект вперед, либо назад по прямой траектории в соответствии с действием силы — подумайте о поездах на рельсах.

      Поскольку компонент направленности в основном заботится о себе сам, вы также можете выразить мощность с помощью простой формулы, используя сила ​, ​ расстояние ​ и ​ скорость ​.

      В этих ситуациях ​ работа ​ ​ W ​ может быть определена как ​ сила ​ ​ ​ F ​ × ​ расстояние ​ ​ ​ d ​. Подставьте это к основному уравнению выше, и вы получите:

      P=\frac{Fd}{t}

      Заметили что-нибудь знакомое? При линейном движении ​ расстояние ​ деленное на ​ время ​ является определением ​ скорости ​ (​ v ​), поэтому мы также можем выразить мощность как:

      P=F\frac{d}{t}=Fv

      Пример расчета: перенос белья

      Хорошо, это было много абстрактной математики, но давайте сейчас попробуем решить примерную задачу:

      ​ Ваши родители просят вас отнести наверх 10-килограммовую партию чистого белья. Если обычно вам требуется 30 секунд, чтобы подняться по лестнице, а высота лестницы составляет 3 метра, оцените, сколько энергии вам потребуется затратить, чтобы поднять одежду с нижней части лестницы наверх.

      Исходя из подсказки, мы знаем, что время t будет составлять 30 секунд, но у нас нет значения для работы W . Однако мы можем упростить сценарий ради оценки. Вместо того, чтобы беспокоиться о перемещении белья вверх и вперед на каждом отдельном шаге, давайте предположим, что вы просто поднимаете его по прямой линии от исходной высоты. Теперь мы можем использовать выражение механической силы P = F × d / t , но нам все еще нужно вычислить задействованную силу.

      Чтобы нести белье, вы должны противодействовать силе тяжести, действующей на него. Поскольку сила тяжести ​ F = мг ​ в направлении вниз, вы должны приложить ту же силу в направлении вверх. Обратите внимание, что ​ г ​ — это ускорение свободного падения, которое на Земле равно 9,8 м/с 2 .

      Posted inДвигатель