Мощность | Физика

Как вы уже знаете, система тел, обладающая механической энергией, может совершить работу над внешними телами. В этом случае говорят, что тела этой системы являются источниками силы.

Одна и та же работа разными источниками силы может быть совершена за разное время. Например, человек может поднять сотню кирпичей на верхний этаж строящегося дома за несколько часов. Эти же кирпичи на тот же этаж подъемным краном можно поднять за несколько минут. То есть подъемный кран может выполнить работу по подъему кирпичей во много раз быстрее человека. Быстроту совершения работы характеризуют мощностью.
Мощность – физическая величина, характеризующая быстроту совершения работы.

Чтобы определить мощность источника силы, надо работу A силы этого источника разделить на время Δt, за которое была совершена работа:

N = A / Δt

Если за любые равные промежутки времени источник силы совершает одинаковую работу A, то указанное отношение называют мгновенной мощностью (или просто мощностью) этого источника.

В других случаях указанное отношение называют средней мощностью за заданный промежуток времени.

В СИ единицу мощности называют ваттом (Вт):

1 Вт = 1 Дж / 1 с

Единица мощности названа в честь английского физика Джеймса Уатта 1873 г. Сам Уатт использовал в качестве единицы мощности лошадиную илу. Это работа, совершаемая за 1 секунду лошадью, которая работает целый день.

1 л. с. = 735 Вт.

Для примера отметим, что средняя мощность, развиваемая сердцем человека, примерно равна 2 Вт. При интенсивной работе в течение нескольких минут человек может развивать мощность около 1 кВт, а при отдельных движениях (прыжок с места, рывок при поднятии тяжести) мощность может достигать 4-5 кВт. Двигатели различных технических устройств, используемых в быту, имеют мощности от долей милливатта (электронно-механические часы) до сотен ватт (двигатели стиральной машины, электрического точила). Мощность же двигателей ракеты космического корабля «Энергия» достигает величины 1,2 · 10¹¹ Вт.

Мощность источника силы F можно вычислить, зная силу и скорость v точечного тела, на которое она действует. Как вы помните, скорость точки – это отношение перемещения точки к промежутку времени, в течение которого движение точки было практически равномерным и прямолинейным. Следовательно, за такой промежуток времени Δt перемещение точки Δx = v · Δt. В течение этого промежутка времени ускорение точки можно считать равным нулю. Следовательно, сумма действующих на точку сил согласно второму закону Ньютона должна быть равна нулю, а каждую из действующих сил можно считать постоянной. Поэтому работа силы, направление которой совпадает с направлением скорости точки, будет равна A = F · v · Δt. Следовательно, мощность источника силы, которая совпадает по направлению со скоростью, равна

N = F · v

Таким образом, если направления скорости и силы совпадают, то мощность источника силы положительна (значения F и v имеют одинаковые знаки).

Напротив, если скорость тела и действующая на него сила направлены в противоположные стороны, то мощность источника силы отрицательна (значения F и v имеют разные знаки).

Из полученной формулы следует, что, когда мощность двигателя постоянна, сила, которая приложена к движущемуся телу, благодаря работе двигателя увеличивается при уменьшении скорости. Именно поэтому водитель автомобиля, преодолевая участок, на котором сила сопротивления движению автомобиля велика, включает пониженную передачу. Уменьшая скорость автомобиля, он увеличивает силу, вращающую колеса.

Рассмотрим теперь, как можно вычислить мощность источника силы, на примере решения следующих задач.

Задача 1

Спортсмен поднялся по вертикальному канату за время Δt = 16 с на высоту h = 10 м. Какую среднюю мощность развивал этот спортсмен? Масса спортсмена M = 80 кг. Модуль ускорения свободного падения считайте равным g = 10 м/с².

Решение. При подъеме по канату спортсмен совершил работу против силы тяжести, равную A = M · g · h = 80 кг · 10 м/с² · 10 м = 8000 Дж. Следовательно, средняя мощность которую развивал спортсмен, равна
N = A / Δt = 8000 Дж / 16 с = 500 Вт.

Ответ: средняя мощность равна 500 Вт.

Задача 2

Определите массу груза, который может поднимать кран с постоянной скоростью v = 90 м/мин. Мощность двигателя крана N = 15 кВт. Модуль ускорения свободного падения считайте равным g = 10 м/с².

Решение. Из формулы N = F · v найдем модуль силы, с которой кран действует на равномерно поднимаемый груз: F = N/v. При равномерном подъеме эта сила должна уравновешивать действующую на груз силу тяжести F = m · g. Следовательно,

Итоги
Мощность – физическая величина, характеризующая быстроту совершения работы.

Чтобы определить мощность источника силы, надо работу A силы этого источника разделить на время Δt, за которое была совершена работа:

N = A / Δt

Вопросы

1. Что такое мощность?
2. Как называют единицу мощности в СИ?
3. Может ли мощность источника силы быть отрицательной? Приведите примеры источника силы с отрицательной мощностью.

Упражнения

1. Какую работу совершили за год генераторы электростанции, если их средняя мощность за год была равна N = 2,5 МВт? Ответ выразите в джоулях.
2. Определите среднюю мощность человека при быстрой ходьбе, если за Δt = 0,5 ч он делает 2500 шагов. Известно, что, делая один шаг, человек совершает работу A = 36 Дж.
3. Оцените вашу мощность при ходьбе. Для этого подсчитайте, сколько шагов вы делаете в минуту, в час при равномерном движении. Как изменится мощность, если вы будете идти тот же час с вдвое меньшей скоростью, с вдвое большей скоростью?
4. Проанализируйте решение задачи 1 из параграфа. Уменьшится ли время подъема на ту же высоту другого спортсмена, если он будет развивать ту же мощность, а его масса равна 60 кг? Найдите время подъема более легкого спортсмена.
5. Самолет летит прямолинейно горизонтально с постоянной скоростью 1000 км/ч. Вычислите силу сопротивления движению самолета, если его двигатели развивают мощность 1,8 МВт.
6. Автомобиль массой m = 2т движется прямолинейно по горизонтальной дороге со скоростью v = 72 км/ч, преодолевая силу сопротивления, равную 0,05 его веса. Какую мощность развивает двигатель автомобиля?

Физика. Механика

Представим снова элементарную работу в виде

Удельная величина, равная отношению работы совершенной за время dt к этому времени, называется мощностью:

Другими словами, мощность, развиваемая некоторой силой, равна скорости, с которой эта сила производит работу. Можно сказать и так: средняя за единицу времени мощность численно равна работе совершенной за единицу времени. Если мощность за выбранную единицу времени практически не меняется, то слово «средняя» можно опустить: мощность численно равна работе за единицу времени.

Как видно из определения, мощность равна скалярному произведению силы на скорость перемещения её точки приложения, поэтому работа силы за время от t₁ до t₂ может быть вычислена следующим образом:

Средняя мощность за этот же промежуток времени равна

За единицу мощности принимается такая мощность, при которой в единицу времени совершается единица работы.

В системе СИ единицей измерения мощности является ватт (Вт):

Внесистемная единица мощности — лошадиная сила (л.с.) — равна 736 Вт. В быту часто используют единицу энергии — 1 кВт•ч = 103 Вт•3600 с=3.6 МДж.

Пример. Вертолет массой m = 3 m висит в воздухе. Определить мощность, развиваемую мотором вертолета, если диаметр ротора равен d = 8 м. При расчете принять, что ротор отбрасывает вниз цилиндрическую струю воздуха диаметром, равным диаметру ротора. Плотность воздуха 1.29 кг/м3.

При решении этой задачи надо применить все известные нам законы динамики. Поскольку это — не одно- и не двухходовая задача, попробуем сначала найти вид окончательного выражения, пользуясь анализом размерности (см. тему 1.3). Искомая мощность зависит от: 1) веса вертолета mg; 2) диаметра винта d, 3) плотности воздуха , то есть искомая формула должна иметь вид

Размерность мощности будет [N] = [ML2T–3]. Составляем равенство размерностей в обеих частях искомой формулы:

Решая систему уравнений

находим

то есть искомая мощность двигателя вертолета будет

где C — некий числовой коэффициент.

Решим теперь эту же задачу точно. Пусть — скорость струи воздуха, отбрасываемой винтом. За время частицы воздуха проходят расстояние . Иными словами, за время винт вертолета придает скорость всем частицам воздуха, находящимся в цилиндре с площадью основания и высотой . Масса воздуха в этом объеме равна

а его кинетическая энергия дается выражением

Поскольку мотор передает воздуху кинетическую энергию , то такова и совершаемая им работа. Поэтому развиваемая мотором мощность (без учета потерь мощности во всех трансмиссиях на пути от двигателя до винта) равна

В этом выражении нам надо еще найти скорость струи воздуха, отбрасываемой винтом. Импульс , передаваемый частицам воздуха за время , равен

Из второго закона Ньютона следует, что средняя сила, действующая на отбрасываемый вниз воздух равна . По третьему закону Ньютона такая же сила действует на вертолет со стороны воздуха. Эта сила компенсирует вес вертолета:

Отсюда получаем уравнение

позволяющее найти скорость струи воздуха:

Подставляя найденную скорость в выражение для мощности двигателя вертолета, получаем окончательный результат:

Мы видим, что выражение для мощности действительно оказалось таким, каким ожидалось на основе анализа размерностей. Подставляя числовые данные, находим

Рис.4.5. Мощность в природе и технике

Как рассчитать мощность — Power Test, LLC

Уравнение для расчета лошадиных сил простое: лошадиных сил = крутящий момент x об/мин / 5,252 . Вы можете использовать наш калькулятор лошадиных сил ниже, чтобы проверить это самостоятельно. Когда дело доходит до понимания того, как динамометр измеряет крутящий момент и рассчитывает мощность, полезно знать еще несколько основных определений и формул.

Сила и работа

Если мы держим груз в 10 фунтов, мы применяем силу в 10 фунтов. Если мы переместим (сместим) вес на расстояние 3 фута, мы проделаем работу. Мы сделали 30 фунтов-футов работы.

Работа = Сила x Перемещение

Мощность

Мощность — это то, сколько работы можно выполнить за определенный период времени.

Мощность = Работа/Время или Сила x Смещение/Время

Лошадиная сила

Определение 1 лошадиной силы – это перемещение 1 фунта 33 000 футов за одну минуту или 33 000 фунтов-футов в минуту.

1 л.с. = 1 фунт x 33 000 футов / 1 минута

Попробуйте сами

Калькулятор мощности в л.с.

Крутящий момент: фунт-фут.

Скорость: об/мин

Лошадиная сила:
{{calculation.findHorsePower | число : 0}} л.с.

Лошадиная сила = Крутящий момент x RPM / 5 252

{{calculation.findHorsePower | число: 0}} ^л.с. = {{расчет.момент}} ^{фунт-фут.} x {{расчет.об/мин}} ^об/мин / 5 252

Применение к вращательному движению

Мы имеем дело с двигателями, в которых сила и мощность передаются во вращательном движении. Это немного меняет дело.

Крутящий момент – это сила, приложенная или полученная посредством рычага или рычага крутящего момента, который будет вращаться вокруг точки опоры или оси вращения. Для наших целей плечо — это радиус. Если сила в 10 фунтов приложена к радиусу 3 фута, мы применяем крутящий момент в 30 фунтов на фут. Мы будем использовать тормоз и моментный рычаг при измерении крутящего момента двигателя. Обратите внимание, что хотя физически крутящий момент является силой, математически он уже имеет те же единицы измерения, что и работа. (фунт-фут)

Мы знаем, что Работа достигается, когда есть Сила и Смещение. Сила — это работа, зависящая от скорости. Поскольку мы имеем дело с вращательным движением, оно называется угловой скоростью и выражается в радианах в секунду или оборотах в минуту. Радиан — это угол, радиус которого равен длине дуги, образованной этим углом. Это то же самое, независимо от размера круга. Следовательно, на каждый оборот приходится 2π радиан.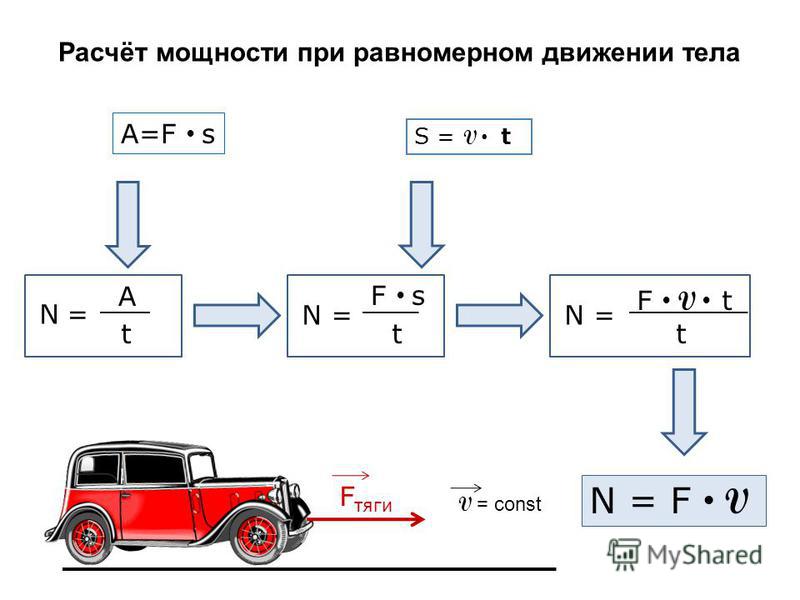 Как и у оборота, у радиана нет единицы измерения, что хорошо работает, потому что крутящий момент уже имеет единицу смещения (футы).

Теперь формула силы выглядит так.

Мощность = Крутящий момент x 2π x оборотов в минуту

Мы хотели бы избавиться от 2π и нам нужно учитывать, что 1 л.с. = 33 000 фунтов-футов. / мин.

Вот что у нас получилось для уравнения.

33 000 lb-ft/мин = lb-ft. x 2π x оборотов/мин

Разделите каждую сторону на 2π (6,28315), и вы получите 5252 фунт-фут/мин = фунт-фут. х оборотов/мин.

Затем разделите каждую сторону на 5252, и вы получите следующее уравнение:

1 Мощность = крутящий момент x об/мин. / 5252

Из-за этой математики крутящий момент в фунто-футах и ​​мощность всегда будут одинаковыми при 5252 об/мин.

Калькулятор работы и мощности

Создано Bogna Szyk

Отзыв Стивена Вудинга

Последнее обновление: 20 июня 2022 г.

Содержание:

• Определение работы
• Определение мощности с использованием
• Калькулятор работы и мощности
• Часто задаваемые вопросы

Этот калькулятор работы и мощности поможет вам определить механическую мощность конкретного устройства. Вы также можете использовать его, чтобы узнать, какую работу будет выполнять машина данной мощности за определенный промежуток времени.

Если вы хотите рассчитать электрическую мощность, попробуйте наш калькулятор закона Ома.

Определение работы

В физике работа, совершаемая объектом, понимается как количество энергии, которое необходимо приложить для перемещения на определенное расстояние. Например, это может быть энергия, необходимая для подъема по лестнице тяжелых сумок, или кинетическая энергия, приводящая к движению тела.

Как правило, он рассчитывается как силы, умноженной на перемещение объекта. Точнее говоря, это скалярное произведение этих двух величин. Измеряется в джоулях (Дж), выражается как кг·м²/с² в единицах СИ или киловатт-часах (кВтч).

Говоря о джоулях, вы можете найти наш конвертер нм в джоули интересным чтением.

Определение мощности

Мощность – это скорость изменения работы или количество работы, выполненной за определенный промежуток времени. Чем выше мощность устройства, тем больше работы оно может выполнить за заданный период времени. Измеряется в ваттах (Вт), что эквивалентно кг·м²/с³ в единицах СИ.

Как рассчитать мощность с помощью калькулятора работы и мощности

1. Определить значение работы. Вы можете либо напрямую ввести это значение в наш калькулятор, либо использовать расширенный режим , чтобы найти его на основе силы и перемещения. В этом примере мы примем Вт = 9000 Дж .
2. Определить время , за которое будет выполнена работа. Здесь мы можем взять t = 60 с .
3. Мощность равна работе, деленной на время . В этом примере P = 9000 Дж/60 с = 150 Вт .
4. Вы также можете использовать наш калькулятор мощности для поиска работы – просто введите значения мощности и времени .

Чтобы узнать о некоторых реальных применениях энергии, воспользуйтесь калькулятором циклической мощности!

Часто задаваемые вопросы

Как вы считаете время от питания и работы?

Поскольку мощность равна работы в единицу времени , продолжительность работы можно рассчитать на , разделив работа, совершенная силой.

Какие единицы используются для расчета работы и мощности?

Единицей работы является джоулей (Дж) , что составляет кг·м²/с² в единицах СИ. Другой стандартной единицей работы является кВтч .

Единицей мощности является ватт (Вт) , что равно числу джоулей работы, выполняемой в секунду .