Вращающий момент | это… Что такое Вращающий момент?

Момент силы (синонимы: крутящий момент; вращательный момент; вращающий момент) — физическая величина, характеризующая вращательное действие силы на твёрдое тело.

Момент силы приложенный к гаечному ключу

Отношение между векторами силы, момента силы и импульса во вращающейся системе

Момент силы

В физике момент силы можно понимать как «вращающая сила». В системе СИ единицами измерения для момента силы является ньютон-метр, хотя сантиньютон-метр (cN•m), футо-фунт (ft•lbf), дюйм-фунт (lbf•in) и дюйм-унция (ozf•in) также часто используются для выражения момента силы. Символ момента силы τ (тау). Момент силы иногда называют моментом пары сил, это понятие возникло в трудах Архимеда над рычагами. Вращающиеся аналоги силы, массы и ускорения есть момент силы, момент инерции и угловое ускорение соответственно. Сила, приложенная к рычагу, умноженная на расстояние до оси рычага, есть момент силы. Например, сила в 3 ньютона, приложенная к рычагу, расстояние до оси которого 2 метра, это то же самое, что 1 ньютон, приложенный к рычагу, расстояние до оси которого 6 метров. Более точно, момент силы частицы определяется как векторное произведение:

где  — сила, действующая на частицу, а  — радиус-вектор частицы!

Предыстория

Строго говоря, вектор, обозначающий момент сил, введен искуственно, так как является удобным при вычислении работы по криволинейному участку относительно неподвижной оси и удобен при вычислении общего момента сил всей системы, так как может суммироваться. Для того, чтобы понять откуда появилось обозначение момента сил и как до него додумались, стоит рассмотреть действие силы на рычаг, относительно неподвижной оси.

Работа, совершаемая при действии силы на рычаг , совершающего вращательное движение вокруг неподвижной оси, может быть рассчитана исходя из следующих соображений.

Пусть под действием этой силы конец рычага смещается на бесконечно малый отрезок , которому соответствует бесконечно малый угол . Обозначим через вектор, который направлен вдоль бесконечно малого отрезка и равен ему по модулю. Угол между вектором силы и вектором равен , а угол и вектором силы .

Следовательно, бесконечно малая работа , совершаемая силой на бесконечно малом участке равна скалярному произведению вектора и вектора силы, то есть .

Теперь попытаемся выразить модуль вектора через радиус вектор , а проекцию вектора силы на вектор , через угол .

В первом случае, используя теорему Пифагора, можно записать следующее равенство , где в случае малого угла справедливо и следовательно

Для проекции вектора силы на вектор , видно, что угол , так как для бесконечно малого перемещения рычага , можно считать, что траектория перемещения перпендикулярна рычагу , а так как , получаем, что .

Теперь запишем бесконечно малую работу через новые равенства или .

Теперь видно, что произведение есть ни что иное как модуль векторного произведения векторов и , то есть , которое и было принято обозначить за момент силы или модуля вектора момента силы .

И теперь полная работа записывается очень просто или .

Единицы

Момент силы имеет размерность сила на расстояние, и в системе СИ единицей момента силы является «ньютон-метр». Джоуль, единица СИ для энергии и работы, тоже определяется как 1Н*м, но эта единица не используется для момента силы. Когда энергия представляется как результат «сила на расстояние», энергия скалярная, тогда как момент силы — это «сила, векторно умноженная на расстояние» и таким образом она (псевдо) векторная величина. Конечно, совпадение размерности этих величин не простое совпадение; момент силы 1Н*м, приложенный через целый оборот, требует энергии как раз 2*π джоулей. Математически

,

где Е — энергия, τ — вращающий момент, θ — угол в радианах.

Специальные случаи

Формула момента рычага

Момент рычага

Очень интересен особый случай, представляемый как определение момента силы в поле:

τ = МОМЕНТ РЫЧАГА * СИЛУ

Проблема такого представления в том, что оно не дает направления момента силы, а только его величину, поэтому трудно рассматривать в.м. в 3-хмерном случае. Если сила перпендикулярна вектору r, момент рычага будет равен расстоянию до центра и момент силы будет максимален

= РАССТОЯНИЕ ДО ЦЕНТРА * СИЛУ

Сила под углом

Если сила F направлена под углом θ к рычагу r, то τ = r*F*sinθ, где θ это угол между рычагом и приложенной силой

Статическое равновесие

Для того чтобы объект находился в равновесии, должна равняться нулю не только сумма всех сил, но и сумма всех моментов силы вокруг любой точки. Для 2-хмерного случая с горизонтальными и вертикальными силами: сумма сил в двух измерениях ΣH=0, ΣV=0 и момент силы в третьем измерении Στ=0.

Момент силы как функция от времени

Момент силы — производная по времени от момент импульса,

,

где L — момент импульса. Момент импульса твердого тела может быть описан через произведение момента инерции и угловой скорости.

,

То есть если I постоянная, то

,

где α — угловое ускорение, измеряемое в радианах в секунду за секунду.

Отношение между моментом силы и мощностью

Если сила совершает действие на каком-либо расстоянии, то она совершает механическую работу. Также если момент силы совершает действие через угловое расстояние, он совершает работу.

= МОМЕНТ СИЛЫ * УГЛОВАЯ СКОРОСТЬ

В системе СИ мощность измеряется в Ваттах, момент силы в ньютон-метрах, а УГЛОВАЯ СКОРОСТЬ в радианах в секунду.

Отношение между моментом силы и работой

= МОМЕНТ СИЛЫ * УГОЛ

В системе СИ работа измеряется в Джоулях, момент силы в Ньютон * метр, а УГОЛ в в радианах.

Обычно известна угловая скорость в радианах в секунду и время действия МОМЕНТА .

Тогда совершенная МОМЕНТОМ силы РАБОТА рассчитывается как:

= МОМЕНТ СИЛЫ * *

Момент силы относительно точки

Если имеется материальная точка , к которой приложена сила , то момент силы относительно точки равен векторному произведению радиус-вектора , соединяющий точки O и O_F, на вектор силы :

.

Момент силы относительно оси

Моментом силы относительно оси называется момент проекции силы на плоскость, перпендикулярную оси относительно точки пересечения оси с этой плоскостью.

Единицы измерения

Момент силы измеряется в ньютон-метрах. 1 Н•м — момент силы, который производит сила 1 Н на рычаг длиной 1 м.

Измерение момента

На сегодняшний день измерение момента силы осуществляется с помощью тензометрических, оптических и индуктивных датчиков нагрузки. В России при решении задач измерения момента в основном используется оборудование зарубежных производителей (HBM (Германия), Kyowa (Япония), Dacell (Корея) и ряда других).

См. также

• Момент инерции
• Момент импульса
• Теорема Вариньона

Вращающий момент | это… Что такое Вращающий момент?

Момент силы (синонимы: крутящий момент; вращательный момент; вращающий момент) — физическая величина, характеризующая вращательное действие силы на твёрдое тело.

Момент силы приложенный к гаечному ключу

Отношение между векторами силы, момента силы и импульса во вращающейся системе

Момент силы

В физике момент силы можно понимать как «вращающая сила». В системе СИ единицами измерения для момента силы является ньютон-метр, хотя сантиньютон-метр (cN•m), футо-фунт (ft•lbf), дюйм-фунт (lbf•in) и дюйм-унция (ozf•in) также часто используются для выражения момента силы. Символ момента силы τ (тау). Момент силы иногда называют моментом пары сил, это понятие возникло в трудах Архимеда над рычагами. Вращающиеся аналоги силы, массы и ускорения есть момент силы, момент инерции и угловое ускорение соответственно. Сила, приложенная к рычагу, умноженная на расстояние до оси рычага, есть момент силы. Например, сила в 3 ньютона, приложенная к рычагу, расстояние до оси которого 2 метра, это то же самое, что 1 ньютон, приложенный к рычагу, расстояние до оси которого 6 метров. Более точно, момент силы частицы определяется как векторное произведение:

где  — сила, действующая на частицу, а  — радиус-вектор частицы!

Предыстория

Строго говоря, вектор, обозначающий момент сил, введен искуственно, так как является удобным при вычислении работы по криволинейному участку относительно неподвижной оси и удобен при вычислении общего момента сил всей системы, так как может суммироваться. Для того, чтобы понять откуда появилось обозначение момента сил и как до него додумались, стоит рассмотреть действие силы на рычаг, относительно неподвижной оси.

Работа, совершаемая при действии силы на рычаг , совершающего вращательное движение вокруг неподвижной оси, может быть рассчитана исходя из следующих соображений.

Пусть под действием этой силы конец рычага смещается на бесконечно малый отрезок , которому соответствует бесконечно малый угол . Обозначим через вектор, который направлен вдоль бесконечно малого отрезка и равен ему по модулю. Угол между вектором силы и вектором равен , а угол и вектором силы .

Следовательно, бесконечно малая работа , совершаемая силой на бесконечно малом участке равна скалярному произведению вектора и вектора силы, то есть .

Теперь попытаемся выразить модуль вектора через радиус вектор , а проекцию вектора силы на вектор , через угол .

В первом случае, используя теорему Пифагора, можно записать следующее равенство , где в случае малого угла справедливо и следовательно

Для проекции вектора силы на вектор , видно, что угол , так как для бесконечно малого перемещения рычага , можно считать, что траектория перемещения перпендикулярна рычагу , а так как , получаем, что .

Теперь запишем бесконечно малую работу через новые равенства или .

Теперь видно, что произведение есть ни что иное как модуль векторного произведения векторов и , то есть , которое и было принято обозначить за момент силы или модуля вектора момента силы .

И теперь полная работа записывается очень просто или .

Единицы

Момент силы имеет размерность сила на расстояние, и в системе СИ единицей момента силы является «ньютон-метр». Джоуль, единица СИ для энергии и работы, тоже определяется как 1Н*м, но эта единица не используется для момента силы. Когда энергия представляется как результат «сила на расстояние», энергия скалярная, тогда как момент силы — это «сила, векторно умноженная на расстояние» и таким образом она (псевдо) векторная величина. Конечно, совпадение размерности этих величин не простое совпадение; момент силы 1Н*м, приложенный через целый оборот, требует энергии как раз 2*π джоулей. Математически

,

где Е — энергия, τ — вращающий момент, θ — угол в радианах.

Специальные случаи

Формула момента рычага

Момент рычага

Очень интересен особый случай, представляемый как определение момента силы в поле:

τ = МОМЕНТ РЫЧАГА * СИЛУ

Проблема такого представления в том, что оно не дает направления момента силы, а только его величину, поэтому трудно рассматривать в.м. в 3-хмерном случае. Если сила перпендикулярна вектору r, момент рычага будет равен расстоянию до центра и момент силы будет максимален

= РАССТОЯНИЕ ДО ЦЕНТРА * СИЛУ

Сила под углом

Если сила F направлена под углом θ к рычагу r, то τ = r*F*sinθ, где θ это угол между рычагом и приложенной силой

Статическое равновесие

Для того чтобы объект находился в равновесии, должна равняться нулю не только сумма всех сил, но и сумма всех моментов силы вокруг любой точки. Для 2-хмерного случая с горизонтальными и вертикальными силами: сумма сил в двух измерениях ΣH=0, ΣV=0 и момент силы в третьем измерении Στ=0.

Момент силы как функция от времени

Момент силы — производная по времени от момент импульса,

,

где L — момент импульса. Момент импульса твердого тела может быть описан через произведение момента инерции и угловой скорости.

,

То есть если I постоянная, то

,

где α — угловое ускорение, измеряемое в радианах в секунду за секунду.

Отношение между моментом силы и мощностью

Если сила совершает действие на каком-либо расстоянии, то она совершает механическую работу. Также если момент силы совершает действие через угловое расстояние, он совершает работу.

= МОМЕНТ СИЛЫ * УГЛОВАЯ СКОРОСТЬ

В системе СИ мощность измеряется в Ваттах, момент силы в ньютон-метрах, а УГЛОВАЯ СКОРОСТЬ в радианах в секунду.

Отношение между моментом силы и работой

= МОМЕНТ СИЛЫ * УГОЛ

В системе СИ работа измеряется в Джоулях, момент силы в Ньютон * метр, а УГОЛ в в радианах.

Обычно известна угловая скорость в радианах в секунду и время действия МОМЕНТА .

Тогда совершенная МОМЕНТОМ силы РАБОТА рассчитывается как:

= МОМЕНТ СИЛЫ * *

Момент силы относительно точки

Если имеется материальная точка , к которой приложена сила , то момент силы относительно точки равен векторному произведению радиус-вектора , соединяющий точки O и O_F, на вектор силы :

.

Момент силы относительно оси

Моментом силы относительно оси называется момент проекции силы на плоскость, перпендикулярную оси относительно точки пересечения оси с этой плоскостью.

Единицы измерения

Момент силы измеряется в ньютон-метрах. 1 Н•м — момент силы, который производит сила 1 Н на рычаг длиной 1 м.

Измерение момента

На сегодняшний день измерение момента силы осуществляется с помощью тензометрических, оптических и индуктивных датчиков нагрузки. В России при решении задач измерения момента в основном используется оборудование зарубежных производителей (HBM (Германия), Kyowa (Япония), Dacell (Корея) и ряда других).

См. также

• Момент инерции
• Момент импульса
• Теорема Вариньона

Калькулятор крутящего момента

Создано Bogna Szyk

Отзыв Стивена Вудинга

Последнее обновление: 05 июня 2023 г.

Содержание:

• Уравнение крутящего момента
• Как рассчитать крутящий момент
• Часто задаваемые вопросы

Этот калькулятор крутящего момента поможет вам найти крутящий момент, возникающий при вращении тела. Что именно представляет собой этот крутящий момент? Представьте себе объект, который может вращаться вокруг некоторой точки, называемой точкой вращения. Если приложить силу на некотором расстоянии от точки опоры, то хоть сила и будет действовать по прямой линии, объект начнет вращаться. Продолжайте читать, если вы хотите узнать, как рассчитать крутящий момент, и получить подробное объяснение формулы крутящего момента.

Если вам нужен крутящий момент в контексте автомобильной промышленности, то калькулятор крутящего момента в л. с. может быть для вас!

Уравнение крутящего момента

Крутящий момент (склонность объекта к вращению) зависит от трех различных факторов:

τ = rFsin(θ)

где:

• r — плечо рычага — расстояние между точка поворота и точка приложения силы;
• F — сила, действующая на объект;
• θ — угол между вектором силы и плечом рычага. Обычно он равен 90°; и
• τ — крутящий момент. Единицами крутящего момента являются ньютон-метры (обозначение: Н·м).

Представьте, что вы пытаетесь открыть дверь. Точка поворота — это просто место, где расположены петли. Чем ближе вы к петлям, тем большее усилие вы должны приложить. Однако, если вы используете ручку, плечо рычага увеличится, и дверь откроется с меньшим усилием.

💡 Не путайте это понятие с центробежной силой — центробежная сила направлена ​​к точке поворота, параллельно плечу рычага. Такая сила не вызывает крутящего момента (это можно проверить, подставив угол 0° в формулу крутящего момента).

Как рассчитать крутящий момент

1. Начните с определения силы, действующей на объект. Предположим, что F = 120 N .
2. Выберите длину плеча рычага. В нашем примере r = 0,5 м .
3. Выберите угол между вектором силы и плечом рычага. Если он не равен 90° по умолчанию, откройте расширенный режим калькулятора, чтобы изменить его. Предположим, что θ = 90° . Используйте расширенный режим, чтобы изменить значение θ.
4. Введите эти значения в наш калькулятор крутящего момента. В нем используется уравнение крутящего момента: τ = rFsin(θ) = 0,5 * 120 * sin(90°) = 60 Н·м .
5. Калькулятор крутящего момента также может работать в обратном направлении, определяя силу или плечо рычага, если задан крутящий момент.

Если вы хотите узнать больше о концепции силы и втором законе Ньютона, попробуйте калькулятор ускорения и калькулятор второго закона Ньютона.

Часто задаваемые вопросы

Как рассчитать крутящий момент?

Для расчета крутящего момента следуйте данным инструкциям:

1. Узнать величину приложенной силы, F .

2. Измерьте расстояние , r , между точкой вращения и точкой приложения силы.

3. Определите угол θ между направлением приложенной силы и вектором между точкой приложения силы и точкой поворота.

4. Умножьте r на F и sin θ и вы получите крутящий момент.

Что такое единица крутящего момента в системе СИ?

Единицей крутящего момента в системе СИ является ньютон-метр или Н⋅м . Чтобы выразить крутящий момент в имперские единицы мы используем фунт-сила-фут или lbf·ft .

Какова формула измерения крутящего момента?

Величина крутящего момента равна произведению величины силы на плечо рычага. Формула измерения силы — [M¹L¹T⁻²], а для плеча рычага — [L]. Следовательно, размерная формула для крутящего момента равна [M¹L²T⁻²] .

Как преобразовать крутящий момент в lbf·ft из Н⋅м?

Как мы знаем, 1 фунт-сила (фунт-сила) = 4,448 ньютона (Н) и 1 фут (фут) = 0,3048 метра (м). Следовательно, К преобразовать крутящий момент из Н⋅м в lbf·ft, разделить на 1,355818 или умножить на 0,737562.

Богна Шик

Расстояние (r)

Сила (F)

Крутящий момент (τ)

9 0002 Ознакомьтесь с 22 похожими калькуляторами вращательного и периодического движения 🌎

Угловое ускорениеУгловое смещениеУгловая частота… Еще 19

10.7: Torque — Physics LibreTexts

1. Последнее обновление

2. Сохранить как PDF

• OpenStax
• OpenStax

Цели обучения

• Описать, как величина крутящего момента зависит от величины плеча рычага и угла, который вектор силы образует с плечом рычага
• Определите знак (положительный или отрицательный) крутящего момента с помощью правила правой руки
• Рассчитайте отдельные крутящие моменты относительно общей оси и просуммируйте их, чтобы найти чистый крутящий момент

Важной величиной для описания динамики вращающегося твердого тела является крутящий момент. Мы видим применение крутящего момента во многих отношениях в нашем мире. У всех нас есть интуитивное представление о крутящем моменте, например, когда мы используем большой гаечный ключ, чтобы открутить упрямый болт. Крутящий момент действует невидимым образом, например, когда мы нажимаем на педаль акселератора в автомобиле, заставляя двигатель передавать дополнительный крутящий момент на трансмиссию. Или каждый раз, когда мы перемещаем наше тело из положения стоя, мы прикладываем крутящий момент к нашим конечностям. В этом разделе мы определяем крутящий момент и аргументируем уравнение для расчета крутящего момента для твердого тела с вращением с фиксированной осью.

Определение крутящего момента

До сих пор мы определили множество переменных, которые являются вращательными эквивалентами своих поступательных аналогов. Рассмотрим, каким должен быть аналог силы. Поскольку силы изменяют поступательное движение объектов, вращательный аналог должен быть связан с изменением вращательного движения объекта вокруг оси. Мы называем этот вращательный аналог крутящим моментом .

В повседневной жизни мы постоянно вращаем объекты вокруг оси, поэтому интуитивно мы уже многое знаем о крутящем моменте. Рассмотрим, например, как мы поворачиваем дверь, чтобы открыть ее. Во-первых, мы знаем, что дверь открывается медленно, если мы прислоняем ее слишком близко к петлям; более эффективно повернуть дверь, если мы нажмем далеко от петель. Во-вторых, мы знаем, что толкать надо перпендикулярно плоскости двери; если мы нажмем параллельно плоскости двери, мы не сможем ее повернуть. В-третьих, чем больше сила, тем эффективнее она открывает дверь; чем сильнее вы нажимаете, тем быстрее открывается дверь. Первый пункт подразумевает, что чем дальше приложена сила от оси вращения, тем больше угловое ускорение; второй подразумевает, что эффективность зависит от угла приложения силы; третий подразумевает, что величина силы также должна быть частью уравнения. Обратите внимание, что при вращении в плоскости крутящий момент имеет два возможных направления. Крутящий момент либо по часовой стрелке, либо против часовой стрелки относительно выбранной точки поворота. На рисунке \(\PageIndex{1}\) показано вращение против часовой стрелки.

Рисунок \(\PageIndex{1}\): Крутящий момент — это эффективность силы при повороте или скручивании, показанная здесь для вращения двери на петлях (если смотреть сверху). Крутящий момент имеет как величину, так и направление. (a) Крутящий момент против часовой стрелки создается силой \(\vec{F}\), действующей на расстоянии r от шарниров (точки поворота). (b) Меньший крутящий момент против часовой стрелки создается, когда меньшая сила \(\vec{F}′\) действует на том же расстоянии r от шарниров. (c) Та же сила, что и в (a), создает меньший крутящий момент против часовой стрелки, когда она приложена на меньшем расстоянии от шарниров. (d) Меньший крутящий момент против часовой стрелки создается силой той же величины, что и (а), действующей на том же расстоянии, что и (а), но под углом \(\theta\), который меньше 90°.

Теперь рассмотрим, как определить крутящие моменты в общем трехмерном случае.

Крутящий момент

Когда сила \(\vec{F}\) приложена к точке P, положение которой равно \(\vec{r}\) относительно точки O (рисунок \(\PageIndex{2}\)) , крутящий момент \(\vec{\tau}\) вокруг O равен

\[\vec{\tau} = \vec{r} \times \vec{F} \ldotp \label{10.22}\]

Рисунок \(\PageIndex{2}\): направление определяется по правилу правой руки.

Из определения векторного произведения крутящий момент \(\vec{\tau}\) перпендикулярен плоскости, содержащей \(\vec{r}\) и \(\vec{F}\), и имеет величина

\[|\vec{\tau}| = |\vec{r} \times \vec{F}| = rF \sin \theta,\]

, где \(\theta\) — угол между векторами \(\vec{r}\) и \(\vec{F}\). Единицей крутящего момента в СИ является ньютон, умноженный на метр, обычно записывается как Н • м. Величина r _\(\perp\) = rsin \(\theta\) представляет собой перпендикулярное расстояние от O до линии, определяемой вектором \(\vec{F}\), и называется рычаг .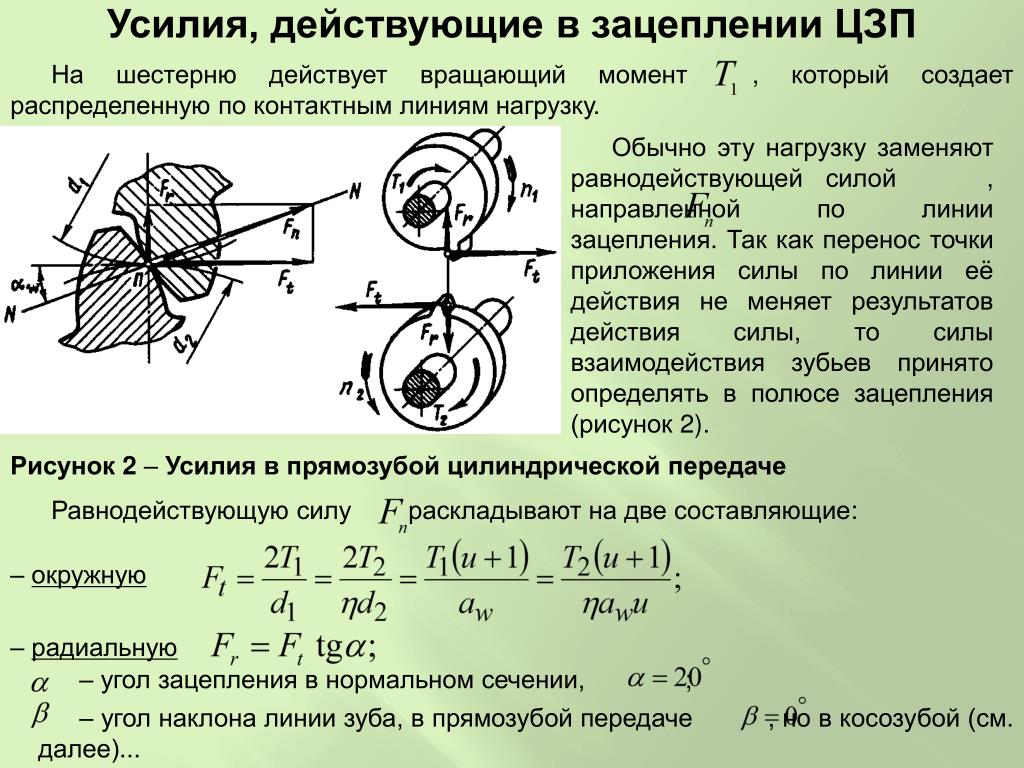 Обратите внимание, что чем больше плечо рычага, тем больше величина крутящего момента. В терминах плеча рычага величина крутящего момента составляет

\[|\vec{\tau}| = r_{\perp} F \ldotp \label{10.23}\]

Перекрестное произведение \(\vec{r} \times \vec{F}\) также сообщает нам знак крутящего момента. На рисунке \(\PageIndex{2}\) векторное произведение \(\vec{r} \times \vec{F}\) расположено вдоль положительной оси z, что по соглашению представляет собой положительный крутящий момент. Если \(\vec{r} \times \vec{F}\) вдоль отрицательной оси z, это создает отрицательный крутящий момент.

Если мы рассмотрим диск, который может свободно вращаться вокруг оси, проходящей через центр, как показано на рисунке \(\PageIndex{3}\), мы увидим, как угол между радиусом \(\vec{r}\ ), а сила \(\vec{F}\) влияет на величину крутящего момента. Если угол равен нулю, крутящий момент равен нулю; если угол равен 90°, крутящий момент максимальный. Крутящий момент на рисунке \(\PageIndex{3}\) положительный, потому что направление крутящего момента по правилу правой руки выходит за пределы страницы вдоль положительной оси z. Диск вращается против часовой стрелки за счет крутящего момента в том же направлении, что и положительное угловое ускорение.

Рисунок \(\PageIndex{3}\): Диск может свободно вращаться вокруг своей оси, проходящей через центр. Величина крутящего момента на диске равна rFsin \(\theta\). Когда \(\theta\) = 0°, крутящий момент равен нулю и диск не вращается. Когда \(\theta\) = 90°, крутящий момент максимален и диск вращается с максимальным угловым ускорением.

Любое количество крутящих моментов может быть рассчитано относительно данной оси. Отдельные крутящие моменты складываются, чтобы создать чистый крутящий момент вокруг оси. Когда соответствующий знак (положительный или отрицательный) присваивается величинам отдельных крутящих моментов относительно заданной оси, чистый крутящий момент вокруг оси представляет собой сумму отдельных крутящих моментов:

\[\vec{\tau}_{net} = \sum_{i} |\vec{\tau}_{i}| \ldotp \label{10.24}\]

Расчет чистого крутящего момента для твердых тел на неподвижной оси

В следующих примерах мы вычисляем крутящий момент как абстрактно, так и применительно к твердому телу. Сначала мы вводим стратегию решения проблем.

Стратегия решения проблем: определение чистого крутящего момента

1. Выберите систему координат с точкой вращения или осью вращения в качестве начала выбранной системы координат.
2. Определите угол между плечом рычага \(\vec{r}\) и вектором силы.
3. Возьмите векторное произведение \(\vec{r}\) и \(\vec{F}\), чтобы определить, является ли крутящий момент положительным или отрицательным относительно точки вращения или оси.
4. Оценить величину крутящего момента с помощью r _\(\perp\) F.
5. Присвойте величине соответствующий знак, положительный или отрицательный.
6. Суммируйте крутящие моменты, чтобы найти чистый крутящий момент.

Пример 10.14: Расчет крутящего момента

Четыре силы показаны на рисунке \(\PageIndex{4}\) в определенных местах и ​​ориентациях по отношению к данной системе координат xy. Найдите крутящий момент, вызванный каждой силой относительно начала координат, а затем используйте полученные результаты, чтобы найти чистый крутящий момент вокруг начала координат.

Рисунок \(\PageIndex{4}\): Четыре силы, создающие крутящие моменты.

Стратегия

Эта задача требует расчета крутящего момента. Все известные величины — силы с направлениями и плечами рычага — приведены на рисунке. Цель состоит в том, чтобы найти каждый отдельный крутящий момент и чистый крутящий момент путем суммирования отдельных крутящих моментов. Будьте осторожны, чтобы присвоить правильный знак каждому крутящему моменту, используя векторное произведение \(\vec{r}\) и вектора силы \(\vec{F}\).

Решение

Использование |\(\vec{\tau}\)| = r _\(\perp\) F = rFsin \(\theta\) для нахождения величины и \(\vec{r} = \vec{r} \times \vec{F}\) для определения знака крутящего момента.

Крутящий момент от силы 40 Н в первом квадранте определяется формулой (4)(40)sin 90° = 160 Н • м.

Перекрестное произведение \(\vec{r}\) и \(\vec{F}\) вне страницы, положительное.

Крутящий момент от силы 20 Н в третьем квадранте определяется выражением −(3)(20)sin 90° = − 60 Н • м.

Перекрестное произведение \(\vec{r}\) и \(\vec{F}\) находится на странице, поэтому оно отрицательно.

Крутящий момент от силы 30 Н в третьем квадранте определяется выражением (5)(30)sin 53° = 120 Н • м.

Перекрестное произведение \(\vec{r}\) и \(\vec{F}\) вне страницы, положительное.

Крутящий момент от силы 20 Н во втором квадранте определяется выражением (1)(20)sin 30° = 10 Н • м.

Перекрестное произведение \(\vec{r}\) и \(\vec{F}\) находится за пределами страницы.

Таким образом, чистый крутящий момент равен \(\tau_{net} = \sum_{i} |\tau_{i}|\) = 160 − 60 + 120 + 10 = 230 Н • м.

Значение

Обратите внимание, что каждая сила, действующая против часовой стрелки, имеет положительный крутящий момент, тогда как каждая сила, действующая по часовой стрелке, имеет отрицательный крутящий момент. Крутящий момент больше, когда расстояние, сила или перпендикулярные компоненты больше.

Пример 10.15: Расчет крутящего момента на твердом теле

На рисунке \(\PageIndex{5}\) показано несколько сил, действующих в разных местах и ​​под разными углами на маховик. Имеем \(|\vec{F}_{1}|\) = 20 Н, \(|\vec{F}_{2}|\) = 30 Н, \(|\vec{F}_{ 3}|\) = 30 Н, r = 0,5 м. Найдите чистый крутящий момент на маховике относительно оси, проходящей через центр.

Рисунок \(\PageIndex{5}\): Три силы, действующие на маховик.

Стратегия

Мы рассчитываем каждый крутящий момент отдельно, используя векторное произведение, и определяем знак крутящего момента. Затем мы суммируем крутящие моменты, чтобы найти чистый крутящий момент. Решение Начнем с \(\vec{F}_{1}\). Если мы посмотрим на рисунок \(\PageIndex{5}\), то увидим, что \(\vec{F}_{1}\) составляет угол 90° + 60° с радиус-вектором \(\vec{r }\). Взяв векторное произведение, мы видим, что оно находится вне страницы и, следовательно, является положительным. Мы также видим это из расчета его величины: 9{о} = (-0,5\; m)(30\; N) = -15,0\; Н\; \cdotp m \ldotp\]

Когда мы оцениваем крутящий момент из-за \(\vec{F}_{3}\), мы видим, что угол, который он образует с \(\vec{r}\), равен нулю, поэтому \(\vec{r} \times \vec{F}_{3}\) = 0. Следовательно, \(\vec{F}_{3}\) не создает крутящего момента на маховике.

Оцениваем сумму моментов:

\[\tau_{net} = \sum_{i} |\tau_{i}| = 5 — 15 = -10\; Н\; \cdotp m \ldotp\]

Значение

Ось вращения находится в центре масс маховика. Поскольку маховик находится на неподвижной оси, он не может свободно перемещаться. Если бы он находился на поверхности без трения и не был зафиксирован на месте, \(\vec{F}_{3}\) вызвал бы перемещение маховика, а также \(\vec{F}_{1}\). Его движение было бы комбинацией поступательного движения и вращения.

Упражнение 10.6

Большое океанское судно садится на мель у береговой линии, как и Costa Concordia , и лежит под углом, как показано ниже. Спасательные бригады должны приложить крутящий момент, чтобы выровнять судно, чтобы поднять его на воду для транспортировки. Чтобы выровнять судно, необходимо приложить силу 5,0 x 10 ⁵ Н, действующую в точке А. Каков крутящий момент относительно точки контакта корабля с землей (рис.