Раздел 2.4 Тепловые машины

2.4.1
Определить, на сколько процентов
изменится КПД цикла Карно при понижении
температуры холодильника от 404 К до 394
К. Темпеpатуpа нагревателя 804 К. Изобразить
цикл Карно в координатах p—V
и S—T.
(Увеличится
на 1,2%)

2.4.2
Газ совершает цикл Карно. Температура
теплоотдатчика в три раза выше, чем
температура теплоприемника. Теплоотдатчик
передал газу 41,9 кДж теплоты. Какую работу
совершил газ? Изобразить цикл Карно в
координатах p—V
и S—T.
(А =
27,9
кДж)

2.4.3
Тепловая машина работает по циклу Карно.
Темпеpатуpа нагревателя в три раза выше
темпеpатуpы холодильника. Количество
теплоты, переданное нагревателем газу,
30 кДж. Какую работу совершил газ?
Изобразить цикл Карно в координатах
p—V
и S—T.
(А
=
20
кДж)

2. 4.4
Идеальная тепловая машина работает по
циклу Карно. Температура холодильника
Т₂
в два раза ниже температуры нагревателя
Т₁.
Во сколько раз увеличится КПД машины,
если температуру нагревателя увеличить
вдвое? Изобразить цикл Карно в координатах
p—V
и S—T.
(В
1,5 раза)

2.4.5
Идеальная тепловая машина работает по
циклу Карно. Температура нагревателя
Т₁
в 3 раза выше температуры холодильника
Т₂.
Во сколько раз увеличилась температура
нагревателя Т₁
при неизменной температуре Т₂,
если КПД цикла вырос на 15%? Изобразить
цикл Карно в координатах p—V
и S—T.
(В
1,8 раза)

2.4.6
Газ совершает цикл Карно. Температура
теплоотдатчика в два раза выше температуры
теплоприемника. Теплоотдатчик передал
газу Q₁
= 42 кДж теплоты. Какую работу совершил
газ? Изобразить цикл Карно в координатах
p—V
и S—T.
(А = 21
кДж)

2.4.7
Идеальный газ совершает цикл Карно.
Темпеpатуpа Т₁
теплоотдатчика в четыре раза (n
= 4) больше темпеpатуpы теплоприемника.
Какую долю w
количества теплоты, полученного за один
цикл от теплоотдатчика, газ отдаст
теплоприемнику? Изобразить цикл Карно
в координатах p—V
и S—T.
(w
= 0,25)

2.4.8
Определить работу А₂
изотермического сжатия газа, совершающего
цикла Карно, КПД которого η
= 0,4, если работа изотермического
расширения равна А₁
= 8 Дж. Изобразить цикл Карно в координатах
p—V
и S—T.
(А₂
=
4,8
Дж)

2.4.9
Газ, совершая цикл Карно, отдал
теплоприемнику теплоту Q₂ = 14 кДж.
Определить темпеpатуpу Т₁
теплоотдатчика, если при темпеpатуpе
теплоприемника Т₂
= 280 К работа цикла А
= 6 кДж. Изобразить цикл Карно в координатах
p—V
и
S—T.
(Т₁
=
400
К)

2.4.10
Газ, являясь рабочим веществом в цикле
Карно, получил от теплоотдатчика теплоту
Q₁
= 4,38 кДж и совершил работу А
= 2,4 кДж. Определить темпеpатуpу
теплоотдатчика, если темпеpатуpа
теплоприемника Т₂
= 273 К. Изобразить цикл Карно в координатах
p—V
и S—T.
(Т₁
=
604
К)

2.4.11
Газ, совершающий цикл Карно, отдал
теплоприемнику 67 % теплоты, полученной
от теплоотдатчика. Определить темпеpатуpу
Т₂
теплоприемника, если темпеpатуpа
теплоотдатчика Т₁
= 430 К. Изобразить цикл Карно в координатах
p—V
и S—T.
(Т₂
= 288
К)

2.4.12
Во сколько раз увеличится коэффициент
полезного действия цикла Карно при
повышении температуры теплоотдатчика
от Т₁
= 380 К до Т₁
= 560 К? Температура теплоприемника Т₂
= 280 К. Изобразить цикл Карно в координатах
p—V
и S—T.
(В
1,92 раза)

2.4.13
В цилиндре двигателя внутреннего
сгорания при работе образуется газы,
температура которых 727˚С. Температура
отработанного газа 100˚С. Двигатель
расходует в час 36 кг топлива, теплота
сгорания которого 4.2·10⁷
Дж/кг.
Какую максимальную полезную мощность
может развить этот двигатель? (Р = 263 кВт)

2.4.14
Во сколько раз максимально возможный
КПД двигателя внутреннего сгорания
больше, чем максимально возможный КПД
паровой машины, работающей на перегретом
паре с температурой 300˚С, если температура
газов в цилиндре двигателя достигает
1000˚С? Отработанные газы и пар имеют
одинаковую температуру 100˚С. (В
2 раза)

2.4.15
Определить работу изотермического
расширения газа, совершающего цикл
Карно с КПД 50%, если работа изотермического
сжатия 10 Дж. Изобразить цикл Карно в
координатах p—V
и
S—T.
(А₂
=
20Дж)

2.4.16
Идеальная тепловая машина работает по
циклу Карно. При этом 80% тепла, полученного
от нагревателя, передается холодильнику.
Количество тепла, получаемое от
нагревателя, равно 3,5 кДж. Найти КПД
цикла и работу, совершенную при полном
цикле. Изобразить цикл Карно в координатах
p—V
и S—T.
(
= 20%, А =
0,7
кДж)

2.4.17
Идеальная тепловая машина работает по
циклу Карно. Температура теплоотдатчика
Т₁
= 500 К, температура теплоприемника Т₂
= 250 К. Определить термический КПД цикла,
а также работу А₁
рабочего вещества при изотермическом
расширении, если при изотермическом
сжатии совершена работа А₂
= 70 Дж. Изобразить цикл Карно в координатах
p—V
и S—T.
(
= 50%; А₁
= 140 Дж)

2.4.18
Газ, совершающий цикл Карно, получает
теплоту Q₁
= 84 кДж. Определить работу А
газа, если темпеpатуpа Т₁
теплоотдатчика в три раза выше темпеpатуpы
Т₂
теплоприемника. Изобразить цикл Карно
в координатах p—V
и S—T.
(А
=
56,3
кДж)

2.4.19
В цикле Карно газ получил от теплоотдатчика
теплоту Q₁
= 500 Дж и совершил работу А
= 100 Дж. Темпеpатуpа теплоотдатчика Т₁
= 400 К. Определить темпеpатуpу Т₂
теплоприемника. Изобразить цикл Карно
в координатах p—V
и S—T.
(Т₂
=
320
К)

2.4.20
Идеальная тепловая машина работает по
циклу Карно.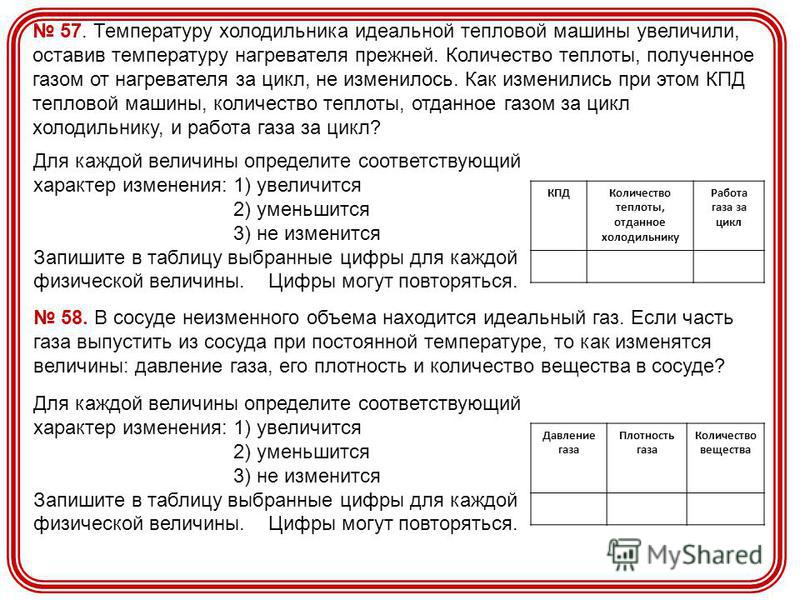 Темпеpатуpа нагревателя
17˚С, темпеpатуpа холодильника -10˚С. Найти
КПД цикла и количество теплоты, полученное
от нагревателя за один цикл, если
совершаемая за один цикл работа равна
37 кДж. Изобразить цикл Карно в координатах
p—V
и S—T.
( = 9,3 %;
Q =
398
кДж)

2.4.21
Тепловая машина работает по циклу Карно.
При этом 60 % количества теплоты, получаемого
от нагревателя, передается холодильнику.
За один цикл рабочее тело получает от
нагревателя Q₁
= 6,28 кДж теплоты. Найти КПД цикла и работу
A,
совершаемую за один цикл. Изобразить
цикл Карно в координатах p—V
и S—T.
( = 40%,
A
= 2,51 кДж)

2.4.22
Газ, совершающий цикл Карно, совершил
работу, затратив при этом 30% тепла,
полученного от нагревателя. Найти
температуру T₂
холодильника, если температура нагревателя
T₁
= 400 К. Изобразить цикл Карно в координатах
p—V
и S—T.
(T₂
= 280
К)

2.4.23
Совершая цикл Карно, газ получил от
нагревателя теплоту Q₁ = 1 кДж.
Сколько теплоты было отдано охладителю,
если КПД идеальной тепловой машины 25%?
Во сколько раз температура нагревателя
выше температуры охладителя? Изобразите
цикл Карно в координатах p—V
и S—T.
(Q₂
= 750
Дж, в 1,33 раза)

2.4.24
Газ совершает цикл Карно. Термодинамическая
температура нагревателя в два раза выше
температуры охладителя. Определить КПД
цикла. Какую долю количества тепла,
полученного от нагревателя, газ отдают
охладителю? Изобразите цикл Карно в
координатах p—V
и S—T.
(
= 50%, w
= 0,5)

2.4.25
Температура нагревателя тепловой машины
500 К. Температура холодильника 400 К.
Определить КПД тепловой машины, работающей
по циклу Карно, и полезную мощность
машины, если нагреватель ежесекундно
передает газу 1675 Дж теплоты. Изобразить
цикл Карно в координатах p—V
и S—T.
( = 20%;Р_полез
= 335 Вт)

get_2 физика — Стр 17

пература воздуха была понижена до первоначальной. Определить давление газа в конце процесса.

13.40.Кислород массой 200 г занимает объем 100 л и находится под давлением 200 кПа. При нагревании газ расширился при постоянном давлении до объема 300 л, а затем его давление возросло до 500 кПа при неизменном объеме. Найти изменение внутренней энергии газа, совершенную газом работу и теплоту, переданную газу. Построить график процесса.

13.41.Объем водорода при изотермическом расширении при температуре 300 К увеличился в 3,0 раза. Определить работу, совершенную газом, и теплоту, полученную при этом. Масса водорода равна 200 г.

13.42.Азот массой 0,10 кг был изобарно нагрет от температуры 200 К до температуры 400 К. Определить работу, совершенную газом, полученную им теплоту и изменение внутренней энергии азота.

13.43.Во сколько раз увеличится объем водорода, содержащий количество вещества 0,40 моль, при изотермическом расшире-

нии, если при этом газ получит количество теплоты 800 Дж? Температура водорода 300 К.

13.44.Какая работа совершается при изотермическом расширении водорода массой 5,0 г, взятого при температуре 290 К, если объем газа увеличить в три раза?

13.45.Какая доля количества теплоты, подводимого к идеальному двухатомному газу при изобарном процессе, расходуется на увеличение внутренней энергии газа и какая доля – на работу расширения? Рассмотреть три случая, если газ: 1) одноатомный: 2) двухатомный; 3) трехатомный.

13.46.Определить работу, которую совершит азот, если ему при постоянном давлении сообщить количество теплоты 21 кДж. Найти также изменение внутренней энергии газа.

14.ТЕПЛОВЫЕ МАШИНЫ

14.1.Определить работу идеальной тепловой машины за один цикл, если она в течение цикла получает от нагревателя ко-

161

личество теплоты 2095 Дж. Температура нагревателя 500 К, холодильника 300 К.

14.2.Температура нагревателя тепловой машины, работающей по циклу Карно, 480 К, температура холодильника 390 К. Какова должна быть температура нагревателя при неизменной температуре холодильника, чтобы КПД машины увеличился в 2,0 раза?

14.3.За счет 1,0 кДж теплоты, получаемого от нагревателя, машина, работающая по циклу Карно, совершает работу 0,50 кДж. Температура нагревателя 500 К. Определить температуру холодильника.

14.4.При прямом цикле Карно тепловая машина совершает работу 200 Дж. Температура нагревателя 375 К, холодильника 300 К. Определить количество теплоты, получаемое машиной от нагревателя.

14.5.Определить, на сколько процентов изменится КПД прямого цикла Карно, если температура нагревателя 894 К, а температура холодильника уменьшилась от 494 до 394 К.

14.6.Совершая прямой цикл Карно, газ отдал холодильнику 0,25 теплоты, полученной от нагревателя. Определить температуру холодильника, если температура нагревателя 500 К.

14.7.Какая часть теплоты, полученной от нагревателя, отдается холодильнику при прямом цикле Карно, если температура нагревателя 500 К, температура холодильника 125 К?

14.8.Найти КПД цикла, состоящего из двух изобар и двух адиабат, если температуры характерных точек равны 370 К, 600 К, 500 К, 350 К. Решение пояснить диаграммой p − V .

14.9.Сравните КПД двух циклов Карно. В первом цикле к рабочему телу теплота подводится при температуре 500 К и отводится при температуре 300 К, а во втором теплота подводится при температуре 400 К и отводится при температуре

200 К.

14.10.Цикл Карно осуществляется в интервале температур 600 К и 200 К. Давления в конце изотермического расширения и в

начале адиабатического сжатия одинаковы и равны 2,0 ×105 Па. Рабочим телом является воздух. Определить па-

162

раметры точек цикла и полезную работу, совершаемую 1,0 кг воздуха за цикл.

14.11.Коэффициент полезного действия цикла Карно равен 0,30. При изотермическом расширении газ получил от нагревателя 300 Дж энергии. Определить работу, совершаемую при изотермическом сжатии.

14.12.Температура нагревателя в 3,0 раза выше температуры холодильника. Какую часть энергии, полученной в цикле Карно от нагревателя, газ отдает холодильнику?

14.13.При совершении цикла Карно газ получил от нагревателя

14.14.Идеальный газ совершает цикл Карно при температурах холодильника 290 К и нагревателя 400 К. Во сколько раз увеличится коэффициент полезного действия цикла, если температура нагревателя возрастет до 600 К?

14.15.Идеальный газ совершает цикл Карно. Температура нагревателя в четыре раза больше температуры холодильника. Какую долю количества теплоты, полученного за один цикл от нагревателя, газ отдаст холодильнику?

14.16.Определить работу изотермического сжатия газа, совершающего цикл Карно, КПД которого равен 0,40, если работа изотермического расширения равна 8,0 Дж.

14.17.Газ, совершающий цикл Карно, отдал холодильнику теплоту 14 кДж. Определить температуру нагревателя, если при температуре холодильника 280 К работа цикла 6,0 кДж.

14.18.Газ, являясь рабочим веществом в цикле Карно, получил от нагревателя теплоту 4,38 кДж и совершил работу 2,4 кДж. Определить температуру нагревателя, если температура холодильника 273 К.

14.19.Газ, совершающий цикл Карно, отдал холодильнику 67 % теплоты, полученной от нагревателя. Определить температуру холодильника, если температура нагревателя 430 Κ.

14.20.Во сколько раз увеличится коэффициент полезного действия цикла Карно при повышении температуры нагревателя от 380 К до 560 К? Температура холодильника 280 К.

163

14.21.Идеальная тепловая машина работает по циклу Карно. Температура нагревателя 500 К, температура холодильника 250 К. Определить термический КПД цикла, а также работу рабочего вещества при изотермическом расширении, если при изотермическом сжатии совершена работа 70 Дж.

14.22.Газ, совершающий цикл Карно, получает теплоту 84 кДж. Определить работу газа, если температура нагревателя в три раза выше температуры холодильника.

14.23.В цикле Карно газ получил от нагревателя теплоту 500 Дж и

совершил работу 100 Дж. Температура нагревателя

400 К. Определить температуру холодильника.

15.ЭНТРОПИЯ

15.1.Определить изменение энтропии 4,0 кг свинца при охлаждении его от 327 до 0 °С.

15.2.Найти изменение энтропии при нагревании массы 10 г льда от –25 °С до 0 °С.

15.3.Найти изменение энтропии при нагревании 1,0 кг воды от 0 до 100 °С и последующем превращении ее в пар при той же температуре.

15.4.Лед массой 100 г, находящийся при температуре –30 °С, превращается в пар. Определить изменение энтропии при данном процессе.

15.5.Железо массой 1,0 кг при температуре 100 °С находится в тепловом контакте с таким же куском железа при 0 °С. Чему будет равно изменение энтропии при достижении равновесной температуры 50 °С? Считать, что молярная теплоемкость железа равна 25,14 Дж/(моль×К).

15.6.Определить изменение энтропии, происходящее при смешивании 5,0 кг воды, находящейся при температуре 280 К, и 8,0 кг воды, находящейся при температуре 350 К.

15.7.Как изменится энтропия при изотермическом расширении 0,10 кг кислорода, если при этом объем его изменится от

2,5 до 10 л?

164

15.8.Определить изменение энтропии при изобарном нагревании 0,10 кг азота от 17 до 100 °С.

15.9.Объем гелия, масса которого 2,0 кг, увеличился в 5,0 раз: а) изотермически; б) адиабатно. Каково изменение энтропии в этих случаях?

15.10.Определить изменение энтропии 1,0 моля идеального газа при изохорном, изобарном и изотермическом процессах. Задачу решить в общем виде.

15.11.Водород массой 10 г изобарно расширяется, при этом объем его увеличивается в 2,0 раза. Определить изменение энтропии водорода при этом процессе.

15.12.В политропном процессе энтропия одного килограмма азота увеличилась на 140 Дж/К; при этом температура газа изменилась от 20 °C до 120 °С. Определить показатель политропы.

15.13.В процессе политропного расширения воздуха к нему было подведено 90 кДж тепла, и все же его температура снизилась от 25 °С до –37 °С. Масса воздуха 4,0 кг, начальное давление воздуха 4,0×105 Па. Определить изменение энтропии в этом процессе.

15.14.Найдите изменение энтропии 1,0 кг воздуха, если его давление увеличилось от 2,0 ×105 Па до 1,0 ×106 Па, а температура понизилась от 327 °С до 127 °С.

15.15.Найти изменение энтропии при переходе массы 8,0 г кислорода от объема 10 л при температуре 80 °С к объему 40 л при температуре 300 °С.

15.16.Найти изменение энтропии при переходе массы 6,0 г водорода от объема 20 л под давлением 150 кПа к объему 60 л под давлением 100 кПа.

15.17.Найти изменение энтропии при изобарном сжатии массы 8,0 г гелия от объема 25 л до объема 10 л.

15.18.Найти изменение энтропии при изотермическом расширении массы 5,0 г водорода от давления 100 кПа до давления

50 кПа.

15.19.Масса 10 г кислорода нагревается от температуры 50 °С до температуры 150 °С. Найти изменение энтропии, если нагревание происходит: а) изохорно; б) изобарно.

165

15.20. При нагревании количества 1,0 кмоль двухатомного газа его термодинамическая температура увеличивается от T1 до

T2 =1,5T1 . Найти изменение энтропии, если нагревание происходит: а) изохорно; б) изобарно.

15.21.В результате нагревания массы 22 г азота его термодинамическая температура увеличилась от T1 до T2 =1,2T1 , а энтропия – на 4,19 Дж/К. При каких условиях производилось нагревание азота (при постоянном объеме или при постоянном давлении)?

16.РЕАЛЬНЫЕ ГАЗЫ

16.1.Зная поправки для воды в уравнении Ван-дер-Ваальса, определить критический объем для 1,0 кг воды.

16.2.Зная поправки для воды в уравнении Ван-дер-Ваальса, определить значения критического давления и критической температуры для 1,0 кг воды.

16.3.Вычислить постоянные в уравнении Ван-дер-Ваальса для азота, если его критическая температура 126 К, а критическое давление 3383 кПа.

16.4.Найти критические параметры неона, если считать известными его постоянные в уравнении Ван-дер-Ваальса.

16.5.Азот массой 14 кг занимает объем 0,50 м3 при температуре 0 °С. Пользуясь уравнением Ван-дер-Ваальса, найти, на сколько нужно изменить температуру газа, чтобы его давление увеличилось вдвое.

16.6.В сосуде, объем которого 10 л, находится 360 г водяного пара при температуре 470 К. Вычислить давление пара, используя уравнение Ван-дер-Ваальса.

16.7.Определить эффективный диаметр молекулы газа, для которого критическая температура равна 282,7 К, поправка в уравнении Ван-дер-Ваальса a = 45,3×10-2 Н×м4/моль2.

16.8.Найти эффективный диаметр молекулы кислорода, считая известными для кислорода критические значения температуры и давления.

166

16.9.Найти эффективный диаметр молекулы азота двумя способами: а) по данному значению средней длины свободного пробега молекул при нормальных условиях 95 нм; б) по известному значению постоянной b в уравнении Ван-дер- Ваальса.

16.10.По уравнению Ван-дер-Ваальса определить давление, под которым находится 1,0 кмоль азота в сосуде объемом 2,5 м3, если его температура 310 К.

16.11.Найти постоянные в уравнении Ван-дер-Ваальса для углекислого газа, считая известными его критическую температуру и критическое давление.

16.12.Давление кислорода, имеющего плотность 100 кг/м3, составляет 7,0 ×106 Па. Определить внутреннее давление (давление, обусловленное взаимодействием молекул) и температуру газа, пользуясь уравнениями Ван-дер-Ваальса и МенделееваКлапейрона.

16.13.В сосуде объемом 8,0 л находится 0,30 кг кислорода при температуре 37 °С. Какую часть давления газа составляет давление, обусловленное силами притяжения молекул? Какую часть объема сосуда составляет собственный объем молекул?

16.14.При каком давлении должен находиться кислород в количе-

стве 0,10 кмоль, чтобы при температуре 320 К он занимал объем 0,10 м3? Задачу решить, рассматривая кислород: а) как идеальный газ; б) как реальный газ. Поправки в уравнении Ван-дер-Ваальса для кислорода считать известными.

16.15.В сосуде содержится 1,0 моль газа. Его давление в 20 раз больше критического давления, а объем равен половине критического объема. Определить отношение температуры этого газа к критической температуре.

16.16.Масса 10 г гелия занимает объем 100 см3 при давлении 100 МПа. Найти температуру газа, считая его: а) идеальным; б) реальным.

16.17.Считая известными критическое давление и критическую температуру для аргона, определить: а) постоянные в урав-

167

нении Ван-дер-Ваальса; б) критический объем 1,0 моль аргона.

16.18.При температуре 310 К 1,0 кмоль азота занимает объем 2,5 м3. Используя критические параметры азота, определить давление и эффективный диаметр молекул азота.

16.19.Во сколько раз давление газа больше его критического давления, если известно, что его объем и температура вдвое больше критических значений этих величин?

16.20.Найти среднюю длину свободного пробега молекул углекислого газа при нормальных условиях. Эффективный диаметр молекулы вычислить, считая известными для углекислого газа критические значения температуры и давления.

17.ПОВЕРХНОСТНЫЕ ЯВЛЕНИЯ

17.1.Из вертикальной трубки, внутренний радиус которой 1,0 мм, вытекают капли воды. Найдите радиус капли в момент отрыва. Каплю считать сферической. Диаметр шейки капли во время отрыва считать равным внутреннему диаметру трубки.

17.2.На сколько нагреется капля ртути, полученная от слияния двух капель радиусом 1,0 мм каждая?

17.3.Какую работу против сил поверхностного натяжения надо совершить, чтобы разбить сферическую каплю ртути радиусом 3,0 мм на две одинаковые капли?

17.4.Определить давление воздуха (в мм рт. ст.) в воздушном пузырьке диаметром 0,010 мм, находящемся на глубине 20 см под поверхностью воды. Внешнее давление 765 мм рт. ст.

17.5.Найдите, на какой глубине под водой находится пузырек воздуха, если известно, что плотность воздуха в нем равна 2,0 кг/м3. Диаметр пузырька 0,015 мм, температура 20 °С и атмосферное давление 760 мм pт. ст.

17.6.Во сколько раз плотность воздуха в пузырьке, находящемся на глубине 5,0 м под водой, больше плотности воздуха при атмосферном давлении 760 мм рт. ст.? Радиус пузырька

5,0 ×10−4 мм.

17.7. В сосуд с ртутью опущен открытый капилляр, внутренний

168

диаметр которого 3,0 мм. Разность уровней ртути в сосуде и капилляре 3,7 мм. Чему равен радиус кривизны ртутного мениска в капилляре?

17.8.В сосуд с водой опущен открытый капилляр с внутренним диаметром 1,0 мм. Разность уровней воды в сосуде и капилляре 3,7 мм. Чему равен радиус кривизны мениска в капилляре? Чему была бы равна разность уровней в сосуде и в капилляре, если бы смачивание было полным?

17.9.Найдите разность уровней ртути в двух сообщающихся капиллярах с диаметрами 1,0 мм и 2,0 мм. Несмачивание считать полным.

17.10.Капилляр внутренним радиусом 2,0 мм опущен в жидкость. Найдите коэффициент поверхностного натяжения жидкости, если известно, что масса жидкости, поднявшейся в капилляре, равна 9,0 ×10−5 кг.

17.11.На нижнем конце трубки диаметром 0,20 см повисла шарообразная капля воды. Найти диаметр этой капли.

17.12.В сосуд с ртутью частично погружены две вертикально расположенные и параллельные друг другу стеклянные пластинки. Расстояние между пластинками 1,0 мм. Определить разность уровней ртути в сосуде и между пластинками, краевой угол принять равным 138°.

17.13.Найти массу воды, вошедшей в стеклянную трубку с диаметром канала 0,80 мм, опущенную в воду на малую глубину. Считать смачивание полным.

17.14.Какую работу надо совершить при выдувании мыльного пузыря, чтобы увеличить его объем от 8,0 см3 до 16 см3? Считать процесс изотермическим.

17.15.Какая энергия выделится при слиянии двух капель ртути диаметром 0,80 мм и 1,2 мм в одну каплю?

17.16.Определить давление внутри воздушного пузырька диаметром 4,0 мм, находящегося в воде у самой ее поверхности. Считать атмосферное давление нормальным.

17.17.Пространство между двумя стеклянными параллельными пластинками с площадью поверхности 100 см2 каждая, расположенными на расстоянии 20 мкм друг от друга, заполнено водой. Определить силу, прижимающую пластинки друг

169

к другу. Считать мениск вогнутым с диаметром, равным расстоянию между пластинками.

17.18.Глицерин поднялся в капиллярной трубке диаметром канала 1,0 мм на высоту 20 мм. Определить коэффициент поверхностного натяжения глицерина. Считать смачивание полным.

17.19.В воду опущена на очень малую глубину стеклянная трубка с диаметром канала 1,0 мм. Определить массу воды, вошедшей в трубку.

17.20.На сколько давление воздуха внутри мыльного пузыря больше нормального атмосферного давления, если диаметр пузыря 5,0 мм?

17.21.Воздушный пузырек диаметром 2,2 мкм находится в воде у самой ее поверхности. Определить плотность воздуха в пузырьке, если воздух над поверхностью воды находится при нормальных условиях.

170

Второй закон термодинамики в новой редакции – Колледж физики, главы 1-17

15 Термодинамика

Резюме

• Определение цикла Карно.
• Рассчитайте максимальный теоретический КПД ядерного реактора.
• Объясните, как диссипативные процессы влияют на идеальную машину Карно.

Рисунок 1. Эта новая игрушка, известная как пьющая птица, является примером двигателя Карно. Он содержит хлористый метилен (смешанный с красителем) в брюшной полости, который кипит при очень низкой температуре — около 100ºF . Для работы нужно намочить голову птицы. Когда вода испаряется, жидкость поднимается в голову, заставляя птицу утяжеляться и нырять вперед обратно в воду. Это охлаждает хлористый метилен в голове, и он возвращается в брюшную полость, в результате чего низ птицы становится тяжелым и опрокидывается. Если не считать очень небольшого вклада энергии — первоначального смачивания головы — птица становится своего рода вечным двигателем. (кредит: Arabesk.nl, Wikimedia Commons)

Из второго закона термодинамики мы знаем, что тепловая машина не может быть на 100 % эффективнее, так как всегда должна существовать некоторая теплопередача[латекс]\boldsymbol{Q _{\textbf{c} }}[/latex]в окружающую среду, которую часто называют отходящим теплом. Насколько эффективной может быть тепловая машина? На этот вопрос на теоретическом уровне ответил в 1824 г. молодой французский инженер Сади Карно (179 г.6–1832), в своем исследовании появившейся тогда технологии теплового двигателя, имеющей решающее значение для промышленной революции. Он разработал теоретический цикл, который теперь называется циклом Карно , который является наиболее эффективным из возможных циклических процессов. Второй закон термодинамики можно переформулировать в терминах цикла Карно, и, таким образом, Карно на самом деле открыл этот фундаментальный закон. Любая тепловая машина, использующая цикл Карно, называется двигателем Карно .

Важнейшее значение цикла Карно — и, по сути, его определение — заключается в том, что используются только обратимые процессы. Необратимые процессы связаны с диссипативными факторами, такими как трение и турбулентность. Это увеличивает передачу тепла[латекс]\boldsymbol{Q_{\textbf{c}}}[/латекс]в окружающую среду и снижает эффективность двигателя. Очевидно, что обратимые процессы предпочтительнее.

ДВИГАТЕЛЬ КАРНО

Сформулированный в терминах обратимых процессов, второй закон термодинамики имеет третью форму:

Двигатель Карно, работающий между двумя заданными температурами, имеет максимально возможный КПД любой тепловой машины, работающей между этими двумя температурами. Кроме того, все двигатели, использующие только обратимые процессы, имеют одинаковый максимальный КПД при работе в пределах одних и тех же заданных температур.

На рис. 2 показана диаграмма[latex]\boldsymbol{PV}[/latex]для цикла Карно. Цикл включает два изотермических и два адиабатических процесса. Напомним, что и изотермические, и адиабатические процессы в принципе обратимы.

Карно также определил КПД идеальной тепловой машины, то есть машины Карно. Всегда верно, что КПД циклической тепловой машины определяется выражением:

.

[латекс]\boldsymbol{Эфф\:=}[/латекс][латекс]\boldsymbol{\frac{Q _{\textbf{h}} -Q _{\textbf{c}}}{Q _{\textbf{h }}}}[/латекс][латекс]\boldsymbol{=1-}[/латекс][латекс]\boldsymbol{\frac{Q_{\textbf{c}}}{Q_{\textbf{h}}} }. [/латекс]

Карно обнаружил, что для идеальной тепловой машины отношение [латекс]\жирный символ{Q_{\textbf{c}}/Q_{\textbf{h}}}[/латекс] равно отношению абсолютных температур тепловые резервуары. То есть [латекс]\boldsymbol{Q_{\textbf{c}}/Q_{\textbf{h}}=T_{\textbf{c}}/T_{\textbf{h}}}[/latex]для двигатель Карно, так что максимум или Эффективность Карно [латекс]\boldsymbol{Eff _{\textbf{C}}}[/латекс] определяется как

[латекс]\boldsymbol{Eff _{\textbf{C}}=1-}[/latex][латекс]\boldsymbol{\frac{T_{\textbf{c}}}{T_{\textbf{h}} }},[/латекс]

, где[latex]\boldsymbol{T_{\textbf{h}}}[/latex]и[latex]\boldsymbol{T_{\textbf{c}}}[/latex]в градусах Кельвина (или любая другая абсолютная температура шкала). Ни одна настоящая тепловая машина не может работать так же хорошо, как КПД Карно — фактический КПД около 0,7 от этого максимума обычно является лучшим, чего можно достичь. Но идеальный двигатель Карно, как и пьющая птица выше, хотя и является увлекательной новинкой, но имеет нулевую мощность. Это делает его нереальным для любых приложений.

Интересный результат Карно подразумевает, что 100%-ная эффективность была бы возможна только в том случае, если[latex]\boldsymbol{T_{\textbf{c}}=0\textbf{K}}[/latex]—то есть, только если бы холодный резервуар был при абсолютном нуле, практическая и теоретическая невозможность. Но физический смысл таков: единственный способ заставить всю теплопередачу пойти на работу — это убрать всю тепловую энергию, а для этого требуется холодный резервуар при абсолютном нуле.

Также очевидно, что наибольшая эффективность достигается, когда отношение[латекс]\жирныйсимвол{Т_{\textbf{с}}/Т_{\textbf{h}}}[/латекс] является как можно меньшим. Как обсуждалось для цикла Отто в предыдущем разделе, это означает, что эффективность максимальна при максимально возможной температуре горячего резервуара и минимально возможной температуре холодного резервуара. (Эта установка увеличивает площадь внутри замкнутого контура на диаграмме [латекс]\boldsymbol{PV}[/латекс]; кроме того, кажется разумным, что чем больше разница температур, тем легче направить теплопередачу на работу. ) Фактические температуры резервуара тепловой машины обычно связаны с типом источника тепла и температурой окружающей среды, в которую происходит передача тепла. Рассмотрим следующий пример.

Рис. 2. PV Диаграмма цикла Карно с использованием только обратимых изотермических и адиабатических процессов. Теплопередача Q _h происходит в рабочее тело на изотермическом пути AB, который протекает при постоянной температуре Th. Теплообмен Q _c происходит вне рабочего тела по изотермическому пути CD, который происходит при постоянной температуре T _с . Чистый результат работы W равен площади внутри пути ABCDA. Также показана схема двигателя Карно, работающего между горячим и холодным резервуарами при температурах T _h и T _c . Любая тепловая машина, использующая обратимые процессы и работающая между этими двумя температурами, будет иметь такой же максимальный КПД, как и машина Карно.

Пример 1: Максимальная теоретическая эффективность ядерного реактора 9{\circ}\textbf{C}}[/latex], а затем снова нагревают, чтобы начать цикл заново. Рассчитайте максимальный теоретический КПД тепловой машины, работающей между этими двумя температурами.

Рисунок 3. Схематическая диаграмма ядерного реактора с водой под давлением и паровых турбин, преобразующих работу в электрическую энергию. Теплообмен используется для производства пара, отчасти для того, чтобы избежать загрязнения генераторов радиоактивностью. Две турбины используются, потому что это дешевле, чем работа одного генератора, который производит такое же количество электроэнергии. Пар конденсируется в жидкость перед возвратом в теплообменник, чтобы поддерживать низкое давление пара на выходе и способствовать прохождению пара через турбины (эквивалентно использованию холодного резервуара с более низкой температурой). Значительная энергия, связанная с конденсацией, должна рассеиваться в окружающей среде; в этом примере используется градирня, поэтому прямая передача тепла в водную среду отсутствует. (Обратите внимание, что вода, поступающая в градирню, не контактирует с паром, проходящим через турбины.) 9{\circ}\textbf{C}},[/latex] соответственно. Тогда в кельвинах [латекс]\boldsymbol{T_{\textbf{h}}=573\textbf{K}}[/latex]и [латекс]\boldsymbol{T_{\textbf{c}}=300\textbf { K}},[/latex], так что максимальная эффективность равна

[латекс]\boldsymbol{Eff _{\textbf{C}}=1-}[/latex][латекс]\boldsymbol{\frac{T_{ \textbf{c}}}{T_{\textbf{h}}}}.[/latex]

Таким образом,

[латекс]\begin{array}{lcl} \boldsymbol{Eff_{\textbf{C} }} & \boldsymbol{=} & \boldsymbol{1-\frac{300\textbf{ K}}{573\textbf{ K}}} \\ {} & \boldsymbol{=} & \boldsymbol{0.476\textbf {, или }47,6\%.} \end{массив}[/latex]

Обсуждение

Фактический КПД типичной атомной электростанции составляет около 35%, что немногим лучше, чем в 0,7 раза больше максимально возможного значения, что является данью превосходной инженерной мысли. Электростанции, работающие на угле, нефти и природном газе, имеют больший фактический КПД (около 42%), потому что их котлы могут достигать более высоких температур и давлений. Температура холодного резервуара на любой из этих электростанций ограничена местными условиями. На рис. 4 показан (а) внешний вид атомной электростанции и (б) внешний вид угольной электростанции. Оба имеют градирни, в которые вода из конденсатора поступает в градирню в верхней части и распыляется вниз, охлаждаясь за счет испарения.

Рисунок 4. (а) Атомная электростанция (фото: BlatantWorld.com) и (б) угольная электростанция. Оба имеют градирни, в которых вода испаряется в окружающую среду, представляя Q _c . Ядерный реактор, поставляющий Q _h , расположен внутри куполообразной защитной оболочки. (Фото: Роберт и Михаэла Викол, publicphoto.org)

Поскольку все реальные процессы необратимы, фактическая эффективность тепловой машины никогда не может быть такой же высокой, как у машины Карно, как показано на рис.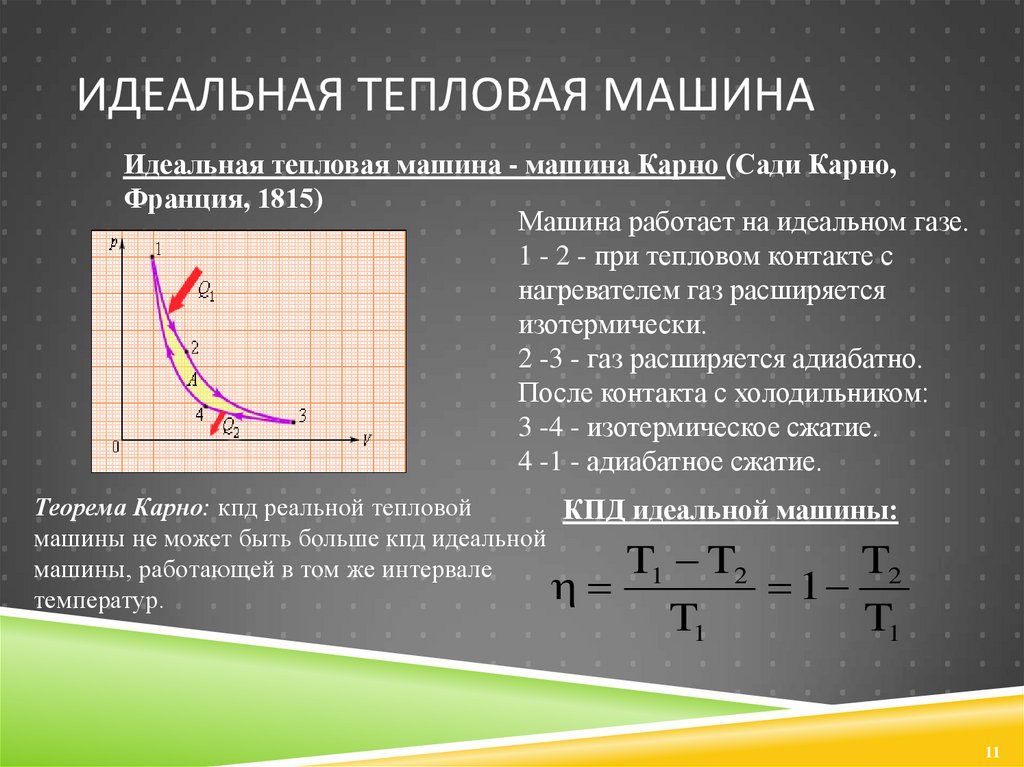 5(а). Даже при наличии наилучшей тепловой машины в периферийном оборудовании, таком как электрические трансформаторы или автомобильные трансмиссии, всегда присутствуют диссипативные процессы. Это еще больше снижает общую эффективность за счет преобразования части выходной мощности двигателя обратно в теплопередачу, как показано на рис. 5(b).

Рис. 5. Реальные тепловые двигатели менее эффективны, чем двигатели Карно. (а) В реальных двигателях используются необратимые процессы, уменьшающие передачу тепла на работу. Сплошные линии представляют реальный процесс; пунктирные линии — это то, что двигатель Карно сделал бы между теми же двумя резервуарами. б) Трение и другие диссипативные процессы в выходных механизмах тепловой машины преобразуют часть ее работы в теплопередачу окружающей среде.

• Цикл Карно — это теоретический цикл, который является наиболее эффективным из возможных циклических процессов. Любой двигатель, использующий цикл Карно, в котором используются только обратимые процессы (адиабатический и изотермический), известен как двигатель Карно.
• Любой двигатель, использующий цикл Карно, обладает максимальным теоретическим КПД.
• Хотя двигатели Карно являются идеальными двигателями, в действительности ни один двигатель не достигает теоретического максимального КПД Карно, поскольку определенную роль играют диссипативные процессы, такие как трение. Циклы Карно без потери тепла могут быть возможны при абсолютном нуле, но это никогда не наблюдалось в природе.

Цикл Карно

циклический процесс, в котором используются только обратимые процессы, адиабатические и изотермические процессы

Двигатель Карно

тепловой двигатель, использующий цикл Карно

Эффективность Карно

максимальный теоретический КПД тепловой машины

Лекция 42

Лекция 42

Резюме

• Первый закон термодинамики
• Термодинамические процессы
• Тепловые двигатели

• Викторина по чтению
• тепловые двигатели Карно
  • диаграмма и апплет
  • максимальная теоретическая эффективность
    
    Пример №1
    Пример №2
    Пример №3
  • второй закон термодинамики
  • сохранение энтропии

• Холодильники
  • диаграмма и апплет
  • коэффициент полезного действия
  • Цикл Карно
    
    Пример #4
    Пример №5
    Пример №6
    Пример №7
    Пример №8
    Пример №9

Walker4e
Тест по чтению Предположим, у вас есть идеальная тепловая машина, которая может работать в одном из двух режимов.
В режиме 1 T _h = 400 K и T _c = 200 K.
В режиме 2 T _h = 600 K и T _c = 400 K.
КПД режима 2 равен _______ КПД режима 1.

А. больше
Б. менее
C. то же, что и
Ответ

gc6 15.q10mod
Как вы должны установить рабочие температуры, чтобы максимизировать эффективность тепловой машины?
A. Сделайте T _L максимально теплым.
B. Сделайте Δ T как можно больше.
C. Сделайте Δ T как можно меньше.
D. Сделайте T _H как можно более крутым.
Ответ

кВт4
Тепловая машина потребляет 1000 Дж энергии при 1000 К и выбрасывает 700 Дж при 400 К. Каков фактический КПД этой тепловой машины?
А. 30%
Б. 40%
С. 60%
Д. 70%
Ответ

кВт4
Каков теоретический максимальный КПД этой тепловой машины?
А. 30%
Б. 40%
С. 60%
Д. 70%
Ответ

км
Как вы должны установить рабочие температуры, чтобы максимизировать производительность холодильника?
A. Сделайте T _L максимально теплым.
B. Сделайте Δ T как можно больше.
C. Сделайте Δ T как можно меньше.
D. Сделайте T _H как можно более крутым.
Ответ

кВт4
Может ли КПД холодильника быть больше единицы?
А. Да
B. №

Ответ

sj6 22,28
Идеальный холодильник работает при температуре от 0°C до 25°C. Он удаляет 8000 кДж/ч из холодной области. Какая минимальная мощность требуется?
А. 204 Вт
Б. 320 Вт
С. 400 Вт
Д. 733 З
Ответ

sj6 22,28
Идеальный холодильник работает при температуре от 0°C до 25°C. Он удаляет 8000 кДж/ч из холодной области. С какой скоростью он истощается
энергия?
А. 0,320 кВт
Б. 2,22 кВт
С.